频域滤波(基础)
频域滤波的基本原理

频域滤波的基本原理频域滤波的基本原理频域滤波是一种信号处理技术,它根据信号的频率特征对信号进行处理,从而达到去噪、滤波等目的。
频域滤波的基本原理就是将时域中的信号转化为频域中的信号,利用频域中的特征进行处理,最后再将处理后的信号转回时域。
一、时域和频域时域和频域是信号处理中常用的两个概念。
时域是指信号随时间变化的情况,它通常用时域波形来表示。
例如,我们平常看到的声音、图像等都是时域信号。
频域是指信号在频率上的特征,与时域不同,它通常用其频谱图表示。
频谱图是一种表示信号频率分布情况的图形,它能够显示信号中存在的各种频率成分。
例如,下图分别是一个声音信号的时域波形和频谱图:二、傅里叶变换频域处理的基础是傅里叶变换。
傅里叶变换是一种将时域信号转换为频域信号的方法,它可以将任意周期的连续信号分解成一系列正弦和余弦函数的和。
傅里叶变换的基本形式为:F_freq(x) = ∫_{-∞}^∞f_time(t)e^{-2πif t}dt其中,f_{time}是时域信号,F_{freq}是频域信号,i表示虚数单位。
需要注意的是,傅里叶变换通常是定义在连续信号上的,在实际应用中,离散信号也常常需要进行傅里叶变换,这时候可以使用离散傅里叶变换(DFT)。
三、频域滤波的基本原理频域滤波是指利用傅里叶变换将信号从时域转换到频域,然后在频域中对信号进行滤波,最后再将信号从频域转回时域的一种信号处理方法。
在频域中,我们可以通过观察信号的频谱图来判断信号中是否存在噪声或需要滤除的部分。
例如,下图中的频谱图显示了一个信号中存在高频噪声:为了去除这种噪声,我们可以在频域中将高频的部分过滤掉,实现去噪的效果。
具体而言,频域滤波通常包括以下几个步骤:1. 将时域信号x(t)进行傅里叶变换,得到频域信号X(f);2. 在频域中对X(f)进行滤波处理,得到滤波后的频域信号Y(f),过滤方式包括低通、高通、带通滤波等;3. 将Y(f)进行傅里叶反变换,得到处理后的时域信号。
频率域特征

频率域特征频率域特征是指对信号或图像在频率域进行表示和分析的特征。
在频率域中,信号或图像可以看作是由一系列不同频率的正弦波组成的。
通过对频率域特征的提取和分析,可以从信号或图像中获取有关频率分布、频谱特征等信息,为信号处理、图像处理等领域的相关任务提供基础。
频率域特征在很多领域都有广泛的应用。
在音频处理中,频率域特征可以用于音乐识别、语音识别等任务。
在图像处理中,频率域特征可以用于图像去噪、图像压缩、图像识别等任务。
在通信领域,频率域特征可以用于信号调制、信道估计等任务。
下面将介绍一些常见的频率域特征及其应用。
1.傅里叶变换(Fourier Transform)是频率域分析的基础。
傅里叶变换将一个时域信号转换为频域信号,将信号表示为一系列正弦波的叠加。
傅里叶变换的应用包括音频信号的频谱分析、频带滤波等。
2.快速傅里叶变换(Fast Fourier Transform,FFT)是一种高效计算傅里叶变换的方法。
FFT算法大大提高了傅里叶变换的计算速度,使得频域分析可以在实时系统中应用。
FFT在音频处理、图像处理、通信系统中都有广泛的应用。
3.频谱分析是一种常见的频率域特征提取方法。
频谱分析通过计算信号的功率谱密度或能量谱密度来描述信号的频率分布情况。
频谱分析的结果常常反映了信号的主要频率成分和能量分布。
4.频域滤波是一种基于频率域特征的滤波方法。
频域滤波通过将信号转换到频率域进行滤波操作,然后再将滤波后的频率域信号转换回时域。
频域滤波可以实现对特定频率成分的增强或抑制,常用于音频去噪、图像增强等任务。
5.小波变换(Wavelet Transform)是一种在时频域上具有局部性的分析方法。
小波变换可以将信号表示为一组小波基函数的线性组合,从而提供了更灵活的频率域分析方式。
小波变换在信号处理、图像处理等领域有广泛的应用。
6.频率矩形(Spectral Moments)是频率域特征的一种度量方式。
频率矩形可用于对频谱分布进行描述,包括中心频率、带宽、能量等方面。
matlab 频域高斯低通滤波

matlab 频域高斯低通滤波一、前言在数字图像处理中,滤波是一种常用的技术。
频域滤波是其中一种基于傅里叶变换的滤波方法,可以有效地去除图像中的噪声。
高斯低通滤波是其中一种常用的频域滤波方法,可以平滑图像并去除高频噪声。
本文将详细介绍 MATLAB 中如何实现频域高斯低通滤波。
二、MATLAB 中的频域滤波MATLAB 中提供了许多函数来实现频域滤波,例如 fft2, ifft2, fftshift, ifftshift 等。
其中 fft2 和 ifft2 分别表示二维快速傅里叶变换和逆变换,fftshift 和 ifftshift 分别表示将零频分量移到中心位置和将中心位置移到零频分量处。
三、高斯低通滤波原理在进行高斯低通滤波之前,需要先了解高斯函数和低通滤波器的概念。
1. 高斯函数高斯函数是一个连续函数,其形式为:$$g(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} $$其中 $\sigma$ 是标准差。
在图像处理中,高斯函数可以用来平滑图像并去除噪声。
2. 低通滤波器低通滤波器是一种可以通过去除高频信号来平滑图像的滤波器。
在频域中,低通滤波器可以通过将高频信号设置为零来实现。
3. 高斯低通滤波原理高斯低通滤波是一种将高斯函数与低通滤波器相结合的方法。
具体来说,可以通过以下步骤来实现:1)对输入图像进行二维傅里叶变换,得到频域图像。
2)在频域图像中心位置创建一个和输入图像大小相同的矩形掩膜,掩膜内部数值为 1,外部数值为 0。
3)将掩膜与一个高斯函数卷积,得到一个新的掩膜。
4)将新的掩膜应用于频域图像,得到经过高斯低通滤波后的频域图像。
5)对经过滤波后的频域图像进行逆傅里叶变换,得到经过高斯低通滤波后的空域图像。
四、MATLAB 中实现高斯低通滤波在 MATLAB 中实现高斯低通滤波可以通过以下步骤来完成:1)读入图像并显示。
滤波器的基础知识2

一.滤波器的基础知识1.滤波器的功能滤波器的功能就是允许某一部分频率的信号顺利的通过,而另外一部分频率的信号则受到较大的抑制,它实质上是一个选频电路。
滤波器中,把信号能够通过的频率范围,称为通频带或通带;反之,信号受到很大衰减或完全被抑制的频率范围称为阻带;通带和阻带之间的分界频率称为截止频率;理想滤波器在通带内的电压增益为常数,在阻带内的电压增益为零;实际滤波器的通带和阻带之间存在一定频率范围的过渡带。
2.滤波器的分类( 1)按所处理的信号分为模拟滤波器和数字滤波器两种。
( 2)按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。
低通滤波器:它允许信号中的低频或直流分量通过,抑制高频分量或干扰和噪声。
高通滤波器:它允许信号中的高频分量通过,抑制低频或直流分量。
带通滤波器:它允许一定频段的信号通过,抑制低于或高于该频段的信号、干扰和噪声。
带阻滤波器:它抑制一定频段内的信号,允许该频段以外的信号通过。
( 3)按所采用的元器件分为无源和有源滤波器两种。
①.无源滤波器:仅由无源元件(R、L 和C)组成的滤波器,它是利用电容和电感元件的电抗随频率的变化而变化的原理构成的。
这类滤波器的优点是:电路比较简单,不需要直流电源供电,可靠性高;缺点是:通带内的信号有能量损耗,负载效应比较明显,使用电感元件时容易引起电磁感应,当电感L较大时滤波器的体积和重量都比较大,在低频域不适用。
②.有源滤波器:由无源元件(一般用R和C)和有源器件(如集成运算放大器)组成。
这类滤波器的优点是:通带内的信号不仅没有能量损耗,而且还可以放大,负载效应不明显,多级相联时相互影响很小,利用级联的简单方法很容易构成高阶滤波器,并且滤波器的体积小、重量轻、不需要磁屏蔽(由于不使用电感元件);缺点是:通带范围受有源器件(如集成运算放大器)的带宽限制,需要直流电源供电,可靠性不如无源滤波器高,在高压、高频、大功率的场合不适用。
3. 滤波器的主要参数(1)通带增益A0:滤波器通带内的电压放大倍数。
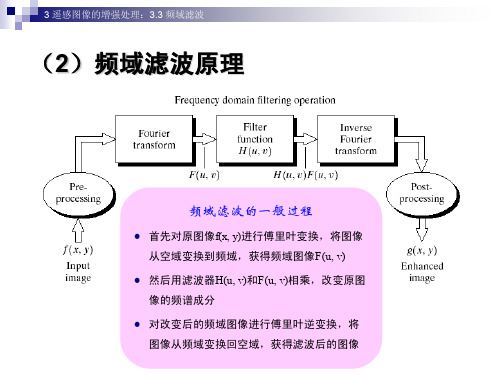
频域滤波原理
cut-off=14, power=99.85%
cut-off=12, power=99.84%
cut-off=10, power=99.82%
用不同的功率百分比恢复的水田图像 Paddy (泗洪)
3 遥感图像的增强处理:3.3 频域滤波
power=100% cut-off=40, power=99.98% cut-off=38, power=99.98% cut-off=36, power=99.98% cut-off=34, power=99.98%
cut-off=49, power=99.18%
cut-off=45, power=99.04%
cut-off=41, power=98.88%
cut-off=37, power=98.67%
cut-off=33, power=98.41%
cut-off=29, power=98.06%
cut-off=25, power=97.6
Smoothing with a Gaussian
3 遥感图像的增强处理:3.3 频域滤波
The Gaussian pyramid
3 遥感图像的增强处理:3.3 频域滤波
Character recognition
using a GLPF with D0 80
• Although humans fill these gaps visually without difficulty, • A machine recognition system has real difficulties reading broken characters.
3 遥感图像的增强处理:3.3 频域滤波
the average value of the resulting image will be zero make prominent edges stand out pixels which have negative values will be produced
数字信号处理中的频域滤波方法

数字信号处理中的频域滤波方法数字信号处理(Digital Signal Processing,DSP)是一门研究如何对数字信号进行变换、操作和分析的学科。
其中,频域滤波方法是一种常用的信号处理技术,用于去除信号中的噪声或改善信号质量。
本文将介绍数字信号处理中的频域滤波方法,包括傅里叶变换、傅里叶变换的性质以及滤波器设计。
一、傅里叶变换傅里叶变换是一种将信号从时域(时序)转换到频域(频率)的方法,它将信号表示为正弦和余弦函数的线性组合。
傅里叶变换可以将信号分解为不同频率成分的和,通过分析这些频率成分可以实现频域滤波。
在数字信号处理中,傅里叶变换通常使用离散傅里叶变换(Discrete Fourier Transform,DFT)来实现。
DFT将连续时域信号离散化为一系列离散频率,从而可以在计算机上进行处理。
二、傅里叶变换的性质1. 线性性质:傅里叶变换具有线性性质,即信号的线性组合的傅里叶变换等于信号各自的傅里叶变换的线性组合。
2. 积移性质:信号在时域上的平移会导致其在频域上的相位变化,即频谱随时间的平移而变化。
3. 对称性质:实信号的傅里叶变换具有共轭对称性,即其频谱是一个关于零频率对称的函数。
三、频域滤波器设计频域滤波器是根据信号在频域的特性来选择和调整信号成分的方法。
常见的频域滤波器有低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
1. 低通滤波器:低通滤波器用于去除高频成分,只保留低频成分。
在频域上,低通滤波器会在截止频率以下的频率范围内透传,而在截止频率以上的频率范围内抑制信号。
2. 高通滤波器:高通滤波器用于去除低频成分,只保留高频成分。
高通滤波器在截止频率以下的频率范围内抑制信号,而在截止频率以上的频率范围内透传。
3. 带通滤波器:带通滤波器用于滤除不在指定频率范围内的信号。
它可以让指定范围的频率通过,而将其他频率抑制。
4. 带阻滤波器:带阻滤波器用于滤除指定频率范围内的信号。
它可以让指定范围外的频率通过,而将指定范围内的频率抑制。
matlab频域低通滤波

matlab频域低通滤波Matlab频域低通滤波的过程包括以下几个步骤:准备工作、载入信号、转换信号、频域滤波、逆傅里叶变换、结果分析和可视化。
1. 准备工作:在进行频域低通滤波之前,需要先了解滤波的基本概念和频域变换的原理。
频域滤波是一种在频域中操作信号的方法,它能够消除或削弱不需要的频率成分,实现对信号的有选择性地处理。
常见的频域变换方法包括傅里叶变换和离散傅里叶变换。
2. 载入信号:使用Matlab自带的`audioread`函数或者其他适用的载入函数,将待处理的音频文件读入到工作环境中。
例如,我们可以读取一个.wav格式的音频文件并将其存储为一个向量。
matlab[x, Fs] = audioread('audio.wav');3. 转换信号:由于频域滤波需要将信号转换为频域表示,因此需要对信号进行频域变换。
在Matlab中,可以使用`fft`函数对信号进行快速傅里叶变换(FFT)。
matlabX = fft(x);4. 频域滤波:根据滤波的需求,选择合适的滤波器类型进行滤波。
常用的低通滤波器有理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器。
这里以理想低通滤波器为例。
理想低通滤波器的特点是在截止频率之前保留信号的全部频谱成分,并在截止频率之后完全削弱信号的高频成分。
使用以下代码可以生成一个理想低通滤波器的频域响应:matlabN = length(X);cutoff_freq = 1000; 设定截止频率H = zeros(N, 1);H(1:cutoff_freq) = 1;H(N-cutoff_freq+2:N) = 1;5. 滤波:将信号的频谱与滤波器的频谱相乘,可以实现滤波效果。
matlabY = X .* H;6. 逆傅里叶变换:将频域滤波后的信号进行逆变换,转换回时域表示。
在Matlab中,可以使用`ifft`函数对信号进行逆傅里叶变换。
matlaby = ifft(Y);7. 结果分析和可视化:经过频域低通滤波后得到的信号,可以通过时域分析和频谱分析来验证和评估滤波效果。
时域滤波器和频域滤波器的变换

时域滤波器和频域滤波器的变换卷积定理函数空间域的卷积的傅⾥叶变换是函数傅⾥叶变换的乘积。
对应地,频率域的卷积与空间域的乘积存在对应关系。
由卷积定理可知所有频域的滤波理论上都可以转化为空域的卷积操作。
给定频率域滤波器,可对其进⾏傅⾥叶逆变换得到对应的空域滤波器;滤波在频域更为直观,但空域适合使⽤更⼩的滤波模板以提⾼滤波速度。
因为相同尺⼨下,频域滤波器效率⾼于空域滤波器,故空域滤波需要⼀个更⼩尺⼨的模板近似得到需要的滤波结果。
空域卷积将模板在图像中逐像素移动,将卷积核的每个元素分别和图像矩阵对应位置元素相乘并将结果累加,累加和作为模板中⼼对应像素点的卷积结果。
通俗的讲,卷积就是对整幅图像进⾏加权平均的过程,每⼀个像素点的值,都由其本⾝和邻域内的其他像素值经过加权平均后得到。
在像素的处理上,是先将结果暂存在于⼀个副本,最后统⼀拷贝,故不会出现处理顺序不同⽽结果不同的情况。
⼆维连续卷积的数学定义:离散形式:频域滤波频率域是由傅⾥叶变换和频率变量 (u,v)定义的空间,频域滤波处理过程:先对图像进⾏傅⾥叶变换,转换⾄频率域,在频域使⽤滤波函数进⾏滤波,最后将结果反变换⾄空间域。
即:⾼斯函数公式:形状:空域⾼斯平滑滤波⾼斯模板的⽣成因为图像是离散存储的,故我们需要⼀个⾼斯函数的离散近似。
具体地,对⾼斯函数进⾏离散化,以离散点上的⾼斯函数值作为权值,组成⼀定尺⼨的模板,⽤此模板对图像进⾏卷积。
由于⾼斯分布在任意点处都⾮零,故理论上需要⼀个⽆穷⼤的模板,但根据" 准则",即数据分布在的概率是0.9974,距离函数中⼼超过数据所占权重可以忽略,因此只需要计算的矩阵就可以保证对⾼斯函数的近似了。
假设⼆维模板⼤⼩,则模板上元素处的值为:前⾯的系数在实际应⽤中常被忽略,因为是离散取样,不能使取样和为1,最后还要做归⼀化操作。
程序:function filt=mygaussian(varargin)%参数初始化,使⽤varargin处理可变参数情况siz=varargin{1};%模板尺⼨if(numel(siz)==1)siz=[siz,siz];endstd=varargin{2};%⽅差centa = (siz(1)+1)/2;%此处不要取整centb = (siz(1)+1)/2;filt = zeros(siz(1),siz(2));summ=0;for i=1:siz(1)for j=1:siz(2)radius = ((i-centa)^2+(j-centb)^2);filt(i,j) = exp(-(radius/(2*std^2)));summ=summ+filt(i,j);endendfilt=filt/summ;%归⼀化测试:执⾏mygaussian(4,1)得:0.0181 0.0492 0.0492 0.01810.0492 0.1336 0.1336 0.04920.0492 0.1336 0.1336 0.04920.0181 0.0492 0.0492 0.0181执⾏fspecial('gaussian',4,1)得:0.0181 0.0492 0.0492 0.01810.0492 0.1336 0.1336 0.04920.0492 0.1336 0.1336 0.04920.0181 0.0492 0.0492 0.0181可以看出与Matlab结果相同。
