【强烈推荐】小学六年级数学上册长方体正方体典型练习题
小学数学苏教版六年级上册长方体和正方体表面积和体积练习题

小学数学苏教版六年级上册长方体和正方体表面积和体积练习题小学数学苏教版六年级上册长方体和正方体表面积和体积练题1、有一根长52厘米的铁丝,恰好可以焊接成一个长6厘米,宽4厘米,高多少厘米的长方体?2.一个房间的长6米,宽3.5米,高3米,门窗面积是8平方米。
现在要把这个房间的四壁和顶面粉刷水泥,粉刷水泥的面积是多少平方米?如果每平方米需要水泥4千克,一共要水泥多少千克?3、用96厘米长的铁丝焊接成一个正方体的框架,然后用纸给它的表面包裹起来,至少需要多少平方厘米的纸?4.一盒饼干长20厘米,宽15厘米,高30厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?5、用两个棱长为5厘米的正方体拼成一个长方体,这个长方体的表面积是多少平方厘米?6、一个长方体和一个正方体的棱长之和相等,已知长方体的长为5厘米,宽为3厘米,高为4厘米,求正方体的棱长。
7、用两个同样的长、宽、高划分为4厘米、3厘米和2厘米的小长方体,拼成一个外表积最大的长方体,这个大长方体的外表积是多少平方厘米?8.做一个长方体的浴缸(无盖),长8分米,宽4分米,高6分米,至少需要多少平方分米的玻璃?如果每平方分米玻璃4元钱,至少需要多少钱买玻璃?9.一个抽屉,长50厘米,宽30厘米,高10厘米,做2个这样的抽屉,至少需要木板多少平方厘米?1、用一根铁丝恰好焊成一个棱长8厘米的正方体框架,假如用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?2、一种长方体硬纸盒,长10厘米,宽6厘米,高5厘米,有2平方米的硬纸板210张,可以做这样的硬纸盒多少个?(不计接口)3、一个面的面积是36平方米的正方体,它所有的棱长的和是多少厘米?4、一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是多少平方厘米?5、一个长方体的告白箱长是1.2米,宽是5分米,高是2米,做这样一个长方体告白箱需要多少平方米的塑料薄膜?6、一个正方体棱长是1.3米,它的表面积是多少?7、一个长方体铁皮油箱,长8分米,宽6分米,高4.5分米.做10个这样的油箱至少需要多少铁皮?8、一个正方体的棱长总和是24厘米,它的外表积是多少平方厘米?9、用36厘米的铁丝折一个正方体框架,这个正方体棱长是多少?假如用纸糊满框架的外表,最少需要纸多少平方厘米?10、长方体不同的三个面的面积分别为10平方分米,6平方分米,15平方分米,这个长方体的表面积是多少?11、做20个棱长为30厘米的小正方体纸箱,至少需要多少平方米硬纸?12、把一个长方体锯成18块,要锯几次呢?13.用72分米长的铁丝做一个正方体的框架,然后在外面贴上一层纸,至少需要多少平方分米的纸?14、一个正方体的外表积是384平方厘米,它的棱长是多少?15、一个长方体侧面积是360平方厘米,高是9厘米,长是宽的1.5倍,求它的外表积。
苏教版小学数学六年级上册第一单元《长方体和正方体》试题共10套

计算。(
)
6、在一个长方体中,从一个顶点出发的三条棱长的和是
7.5 分米,这个长方体的棱长总和是 30 分米。( )
7.长方体是特殊的
正方体。 ( )
8.把两个一样的正方体拼成一个长方体后,体积和表面
积都不变。( ) 9.正方体的棱长扩大 3 倍,体积就扩大 9 倍。( ) 10.棱
长是 5 厘米的正方体的表面积比体积大。 ( )
6、有一个长方体,若用三种不同的方法切成两个完全一样的长方体,它们的表
面积分别增加 30 平方厘米、 20 平方厘米、 12 平方厘米。这个长方体的表面积
是( )平方厘米。
A 、62
B
、 124
C
、248
六年级上册长方体和正方体题库 二
1、希望小学准备挖一个长方体沙坑,设计这个沙坑的长是 4 米,宽是 3 米,深 是 0.5 米。 (1) 这个沙坑的占地面积是多少平方米 ? (2) 如果把沙坑填满黄沙,希望小学要准备多少立方米的黄沙 ? 2、一个无盖的铁箱,长 5 分米,宽 4 分米,高 3 分米,做 20 个这样的铁箱至 少需要铁皮多少平方分米 ? 3、一个长方体油箱,底面是边长为 4dm 的正方形,铁箱高 5dm。做一个这样的 铁箱用铁皮多少平方分米? 如果每升汽油重 0.8 千克,这个油箱能盛油多少千 克/ 4、一个养鱼池长 60m,宽 30m,深 2m,现改建成游泳池,在四壁和底面涂上 一层水泥,涂水泥的面积是多少平方米?如果每平方米用水泥 6 千克,共需用 水泥多少千克? ★★★ 5、在一个练功房里铺设了 1600 块长 50cm,宽 10cm,厚 3cm 的木质地 板。这个练功房的面积有多大?铺设地板至少要用木材多少立方米?
大。 ( ) 17、.求水箱的容积就是求它的体积。 ( )
(整理)苏教版小学数学六年级上册第一单元《长方体和正方体》试题共八套

长方体与正方体的体积一、谨慎填空。
1.长方体的体积=( )×( )×( ),正方体的体积=( )×( )×( ),长方体(或正方体)体积=( )×( )2.如图是一个边长为10厘米的正方体,从它的顶角切下一个棱长为2厘米的小正方体后,余下部分表面积是( )平方厘米,体积是( )立方厘米。
3. 一个长方形的长、宽、高分别是5厘米、3厘米、4厘米,这个长方体切成一个最大的正方体,正方体的体积是( )。
4. 建房时需挖一个长48米、宽8米、深1.5米的地基,挖出的土填在底面积1000平方米的废沟里,填土的厚度是( )米。
5.一个底面是正方形的长方体木块,如果它的高增加4厘米,则表面积增加96平方厘米;如果高减少5厘米,则长方体木块的体积减少( )立方厘米。
6.一个长4分米,宽2分米,高5分米的长方体木块,可以切成( )个1立方厘米的小正方体。
把这些小正方体排成一行,长( )米。
7.一个底面是正方形的长方体,侧面展开是边长12厘米的正方形,它的体积是( )。
8.我们常用单位面积降雨的高度来描述降雨量的大小,据统计:去年七月份某市降雨量为4厘米。
那么该市平均每公顷地面降雨( )立方米。
9.把一个长方体木块,截成两段完全一样的正方体,这两个正方体的棱长之和比原长方体增加40厘米,每个正方体的体积是( )立方厘米。
10.把一个正方体的棱长增加2倍,那么这个正方体的棱长总和扩大( )倍,表面积扩大( )倍,体积增加( )倍。
11.把两个相同的正方体拼成一个长方体,这个长方体的棱长总和是48厘米,这个长方体的体积是( )立方厘米。
12.用一块棱长是6米的正方体钢坯,可镕锻成横截面是边长0.2米正方形的长方体钢材( )米长。
13.一个底面是正方形的长方体,侧面展开是边长12厘米的正方形,它的体积是( )。
14.右图是一个正方体的表面展开图。
使得对面两数之和为7,A 、B 、C 处所填的数分别是( )、( )、( )。
六年级长方体和正方体练习题

六年级长方体和正方体练习题一.填空题。
1、表面积是54平方分米的正方体,它的体积是立方分米。
2、把一个长、宽、高分别是2分米、12厘米、10厘米的长方体铁块熔铸成一个正方体铁块。
这个正方体铁块的体积是立方厘米。
3.一个正方体的棱长总和是72厘米,它的一个面是边长厘米的正方形,它的体积是。
4.至少要个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是5厘米,那么大正方体的表面积是平方厘米。
5、一根96厘米的铁丝正好做成了一个长8厘米,宽6厘米的长方体,它的高是厘米。
6、把一根长6米的长方体,切成3段一样的小长方体,表面积增加了3.6平方米。
这个长方体的体积是。
7.把三个棱长都是4厘米的正方体拼成一个长方体,表面积减少了平方厘米,它的体积是立方厘米。
8、做一个长方体的烟囱需要多少平方米铁皮,是求长方体的9、正方体的棱长扩大3倍,体积扩大倍。
10、把一个长8厘米、宽6厘米、高4厘米的的木块锯一个最大的正方体,剩下部分的体积是立方厘米。
二.看图求它们的表面积与体积。
三.实践与应用。
1、正方体的棱长总和是120厘米,它的表面积是多少平方厘米?2、一个底面是正方形的长方体,所在棱长的和是100厘米,它的高是7厘米,这个长方体的体积是多少立方厘米?3、一个长方体水箱,底面是一个边长2分米的正方形,高是30厘米,水面高度是15厘米,放入一个石头后,水面的高度是18厘米,石头的体积是多少?4、一个长方体的药水箱里装了60升的药水,已知药水箱里面长5分米,宽3分米,它的深是多少分米?5、一块长方形的铁皮,长40厘米,宽30厘米。
从四个角都剪掉边长为5厘米的小正方形后,焊成一个无盖的长方体盒子,这个盒子最多能容纳多少毫升的液体?小学六年级总复习长方体和正方体练习题一、填空题。
1.一个长方体的长是25厘米,宽是20厘米,高是18厘米,最大的面的长是厘米,宽是厘米,一个这样的面的面积是平方厘米;最小的面长是厘米,宽是厘米,一个这样的面的面积是平方厘米。
数学苏教版六年级上册长方体和正方体表面积和体积专项练习题(分类练习、综合练习100道)

数学苏教版六年级上册长方体和正方体表面积和体积专项练习1、一个无盖的长方体金鱼缸,长8分米,宽6分米,高7分米。
制作这个鱼缸共需玻璃多少平方分米?这个鱼缸能装水多少升?(玻璃厚度忽略不计)2、一个长方体铁块,长10分米,宽5分米,高4分米,每立方分米铁块重7.8千克,这个铁块重多少千克?3、一节长方体形状的铁皮通风管长2米,横截面是边长为10厘米的正方体,做这节通风管至少需要多少平方厘米铁皮?4、有一个底面积是300平方厘米、高10厘米的长方体,里面盛有5厘米深的水。
现在把一块石头浸没到水里,水面上升2厘米。
这块石头的体积是多少立方厘米?5、一个面的面积是36平方米的正方体,它所有的棱长的和是多少厘米?6、用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?7、天天游泳池,长25米,宽10米,深1.6米,在游泳池的四周和池底砌瓷砖,如果瓷砖的边长是1分米的正方形,那么至少需要这种瓷砖多少块?8、一种长方体硬纸盒,长10厘米,宽6厘米,高5厘米,有2平方米的硬纸板210张,可以做这样的硬纸盒多少个?(不计接口)9、一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是多少平方厘米?9、把棱长12厘米的正方体切割成棱长是3厘米的小正方体,可以切割成多少块?数学苏教版六年级上册长方体和正方体表面积和体积专项练习1.一个正方体木块,表面积是30平方分米,如果把它据成大小一样的8个小正方体木块,每个小木块的表面积是多少?2.2.把长5厘米、宽4厘米、高3厘米的两块相同的长方体拼成一个新长方体,有几种拼法,表面积分别是多少?3把两块棱长5厘米的正方体的拼成一个长方体,这个长方体的表面积是多少平方厘米?(你能用几种方法解答)4一个正方体的底面周长是16厘米,它的表面积是多少平方厘米,体积是多少立方厘米。
5.把一个长16厘米,宽6厘米,高8厘米的大长方体切成两个小长方体,这两个小长方体的表面积的和最大是多少平方厘米,最小是多少?6.一个正方体的表面积是24平方分米,把它分成两个完全相同的长方体,每个长方体的表面积是多少平方分米?7.把一个长6厘米,宽5厘米,高4厘米的长方体木块锯成两个小长方体,表面积最少增加多少平方厘米?最多增加多少平方厘米?8.把1立方米的正方体木料,全锯成1立方厘米的小木块(损耗不在计算之内),把这些小木块一个紧挨一个地排成一行,这一行总共有多少米?9.至少要几个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是5厘米,那么大正方体的表面积是多少平方厘米,体积是多少立方厘米。
六年级上册《长方体与正方体》专项练习试题(10套)

苏教版小学数学六年级上册《长方体与正方体》专项练习试题(10套)(1)(长方体和正方体的认识)一、填空:(38%)1、长方体和正方体都有( ) 个面,( ) 条棱,( ) 个顶点。
2、长方体的每个面都是( )形或有一组对面是( )。
它有( )条棱,平行的( )条棱都相等。
3、相交于长方体一个顶点的三条棱的长度分别叫做它的()、()和()。
4、长方体有()个面,从不同的角度观察一个长方体,最多能看到()个面。
5、一个长方体的长是5分米,宽是4分米,高是3分米,6个面中最小的一个面的面积是(),最大的一个面的面积是()。
6、一个长方体,长4米,宽3米,高2米,它的占地面积最大是()平方米。
7、一个长方体模型,从前面看是从上面看是长方体右面的面积是()平方厘米。
8、长方体的右侧面面积是12平方厘米,前面面积是8平方厘米,上面面积是6平方厘米,这个长方体的长、宽、高分别是()、()、()。
二、选择(8%):1、一个长方体水池,长20米,宽10米,深2米,这个水池占地()平方米。
A、200B、400C、5202、下面的图形中,能按虚线折成正方体的是()。
3、从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如下图) ,它的表面积( ) 。
A.和原来同样大 B.比原来小 C.比原来大 D.无法判断4、用一根52厘米长的铅丝,正好可以焊成长6厘米,宽4厘米,高()厘米的长方体教具。
A、2B、3C、4D、5三、计算下面每个形体的棱长和(6%)。
四、下面各题,列式计算,不写答。
(40%)1、一个长方体,长5分米,宽3分米,高4分米,求它的所有棱长的和。
2、用钢筋做一个长和宽都是3.5分米,高是10厘米的长方体,需多少分米的钢筋?3、棱长是4分米的正方体,棱长总和是多少分米?4、一个长方体的棱长和是36厘米,从一个顶点出发的三条棱的长度总和是多少厘米?5、同一根长96厘米的铁丝折成一个最大的正方体框架,求正方体框架的棱长。
第一单元 长方体和正方体 单元测试(含答案) 2024-2025学年六年级上册数学苏教版

第一单元长方体和正方体单元测试一、单选题1.棱长6厘米的正方体表面积和体积相比较,( )A.体积大B.表面积大C.相等D.无法判断2.一个长方体的长、宽、高分别是10米、8米、6米,如果高增加3米,则体积增加( )立方米。
A.3B.90C.180D.2403.一根长方体木料,它的横截面积是9cm2,把它截成2 段,表面积增加了( )cm2。
A.9B.27C.18D.04.一个长方体,如果高增加3厘米,就成为一个正方体。
这时表面积比原来增加了96平方厘米。
原来的长方体的体积是( )立方厘米。
A.320B.348C.372D.4205.如图折成一个正方体后,相交于同一顶点的三个面上的数的乘积最大的是( )A.120B.60C.40D.90二、判断题6.如果两个长方体的表面积相等,它们的长、宽、高也一定分别相等。
( )7.棱长2分米的正方体,它的棱长总和与它的表面积相等。
( )8.一根3米长的方钢,把它横截成3段时,表面积增加12平方分米,原来方钢的体积是90立方分米。
( )9.一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的27倍. ( )10.棱长为6cm的正方体.它的表面积和体积相等。
( )三、填空题11.一个正方体的棱长和是36cm,它的体积是 。
12.把2个棱长是2cm的小正方体拼成一个长方体,这个长方体的体积是 ,表面积是 。
13.(正方体体积)有小、中、大三个正方体水池,从里面测,它们的边长分别是2米,3米,6米。
把两堆沙分别倒入小、中号水池,两个水池水面分别上升了4厘米,6厘米,如果把两堆沙都倒人大号水池,大号水池水面上升 。
14.一个长方体长0.7米,宽0.5米,高0.3米,占地面积最小是 。
15.把一个长方体木块截成两个完全一样的正方体,这两个正方体的棱长之和比原长方体棱长之和增加40厘米,每个正方体的体积是 立方厘米。
16.将“致敬逆行英雄”六个字分别写在一个正方体的六个面上,这个正方体的展开图如图所示,那么在这个正方体中,和“致”相对的字是 。
六年级长方体正方体练习(含解析)
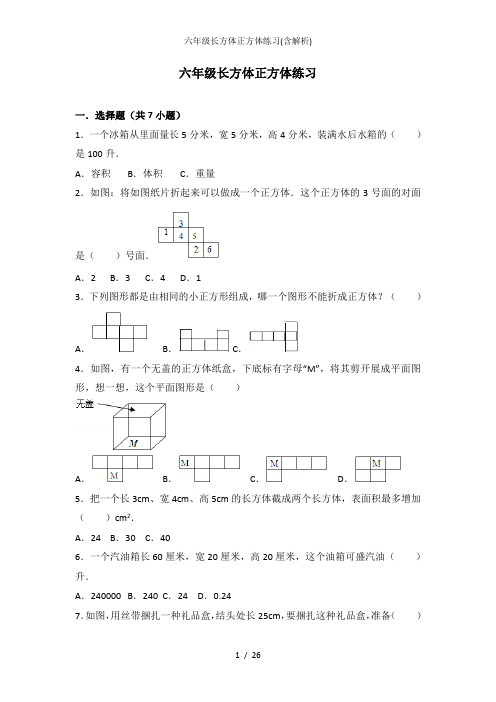
六年级长方体正方体练习一.选择题(共7小题)1.一个冰箱从里面量长5分米,宽5分米,高4分米,装满水后水箱的()是100升.A.容积B.体积C.重量2.如图:将如图纸片折起来可以做成一个正方体.这个正方体的3号面的对面是()号面.A.2 B.3 C.4 D.13.下列图形都是由相同的小正方形组成,哪一个图形不能折成正方体?()A.B.C.4.如图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是()A.B.C.D.5.把一个长3cm、宽4cm、高5cm的长方体截成两个长方体,表面积最多增加()cm2.A.24 B.30 C.406.一个汽油箱长60厘米,宽20厘米,高20厘米,这个油箱可盛汽油()升.A.240000 B.240 C.24 D.0.247.如图,用丝带捆扎一种礼品盒,结头处长25cm,要捆扎这种礼品盒,准备()分米的丝带比较合理.A.10 B.15 C.20 D.22.5二.填空题(共10小题)8.棱长总和是72cm的正方体,表面积是,体积是.9.如果正方体的棱长扩大到原来的3倍,那么它的表面积就扩大到原来的倍.10.用铁丝焊接一个棱长是5 厘米的正方体框架,至少需要铁丝厘米.如果用白纸贴满正方体的各个面,至少要用白纸平方厘米;这个正方体的体积是立方厘米.11.长方形的右侧面积是12平方厘米,前面面积是8平方厘米,上面面积是6平方厘米,这个长方体的表面积是平方厘米.12.一个长方体,如果宽增加2厘米,就变成一个正方体,这时表面积比原来增加32平方厘米.原来长方体的表面积是平方厘米,体积是立方厘米.13.一个正方体木块,把它割成2个长方体后.表面积增加了18m2,这个木块原来的表面积是,体积是.14.一个棱长4dm的正方体钢坯的体积是dm3,如果把它锻造成一个底面积是20dm2的长方体,这个长方体的高是dm.15.一根长2米的长方体钢材,沿横截面截成两段后,表面积增加了0.8平方米,这段长方体钢材的体积是立方分米.16.用一根24分米长的铁丝围成一个最大的正方体形状的框架,这个正方体的体积是立方米.17.一根60厘米长的铁丝,如果做一个长8厘米、宽5厘米的长方体模型,这个长方体的高是厘米,这个长方体的表面积是平方厘米,体积是立方厘米.三.判断题(共5小题)18.正方体的棱长扩大到原来的2倍,它的表面积也就扩大到原来的2倍..(判断对错)19.棱长为6cm的正方体的体积与表面积相等..(判断对错)20.底面周长是8分米的正方体,它的表面积是24平方分米..(判断对错)21.如果长方体的长、宽、高都扩大3倍,则它的体积扩大3倍.(判断对错)22.把一个长方体锻造成一个正方体铁块,形状变了,但体积不变.(判断对错)四.解答题(共10小题)23.如图,如果把这个长方体完全沉没于盛满水的水槽中,会有多少水溢出来?如果要包装这个盒子,至少需要多少平方厘米的包装纸?(单位:厘米)24.求出如图中长方体的体积和表面积.(单位:米)25.看图计算,如图是长方体纸箱的展开图,请你根据有关数据,求出纸箱的体积.(单位:分米)26.一间平顶教室,长是8.5米,宽6米,高4.2米.教室的门窗和黑板的面积一共有35.8平方米.要粉刷教室的顶面和四面墙壁,粉刷的面积有多少平方米?27.一个长方形的游泳池,从里面量长50米,宽20米,高2米,平均水深1.5米.粉刷它的四壁和地面,粉刷面积是多少平方米?28.一块长32厘米、宽25厘米的铁皮,从四个角各切掉一个边长为3厘米的正方形,然后做成盒子.这个盒子用了多少铁皮?它的容积有多少立方厘米?(如图)29.有一个长方体,从上面截下一个高是2厘米的长方体后正好得到一个正方体,如图,正方体的表面积比原长体的表面积减少了48平方厘米,求原来长方体的体积.30.一个长方体水箱,从里面量长是40cm,宽是35cm,水箱中浸没一个钢球(水末溢出),水深15cm,取出钢球后,水深12cm.如果每立方分米钢重7.8千克,这个钢球重多少千克?31.把棱长为4dm的正方形钢坯熔铸成横截面是边长8cm的正方形的长方体钢条,这个钢条的长是多少分米?32.李老师用一根长56cm的铁丝,做成一个长6cm,宽5cm的长方体框架教具,这个教具的高是多少厘米?六年级长方体正方体练习(2)参考答案与试题解析一.选择题(共7小题)1.(2016春•卧龙区校级期中)一个冰箱从里面量长5分米,宽5分米,高4分米,装满水后水箱的()是100升.A.容积B.体积C.重量【考点】AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】根据容积的意义,某容器所能容纳别的物体的体积叫做这个容器的容积.据此解答即可.【解答】解:根据容积的意义可知:一个木箱装满水后水箱的容积是100升故选:A.【点评】此题考查的目的是理解掌握容积的意义及应用.2.(2016秋•如皋市月考)如图:将如图纸片折起来可以做成一个正方体.这个正方体的3号面的对面是()号面.A.2 B.3 C.4 D.1【考点】8M:正方体的展开图.【专题】462:立体图形的认识与计算.【分析】根据正方体展开图的11种特征,属于“1﹣3﹣2”型,折叠成正方体后,1号面与5号面相对,2号面与3号面相对,4号面与6号面相对.【解答】解:如图,折叠成正方体后,1号面与5号面相对,2号面与3号面相对,4号面与6号面相对.故选:A.【点评】此题是考查正方体展开图的特征,正方体展开图有11种情况,折叠成正方体后哪些面相对是有规律的,最好是掌握规律,能快速解答此类题.3.(2016春•乐亭县校级月考)下列图形都是由相同的小正方形组成,哪一个图形不能折成正方体?()A.B.C.【考点】8M:正方体的展开图.【专题】462:立体图形的认识与计算.【分析】根据正方体展开图的11种特征,选项B不属于正方体展开图,不能折成正方体;选项A和选项C都属于正方体展开图的“1﹣4﹣1”型,都能折成正方体.【解答】解:根据正方体展开图的特征,选项B不能折成正方体;选项B和选项C都能折成正方体.故选:B.【点评】本题主要是考查正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.4.(2015•绵阳)如图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是()A.B.C.D.【考点】8M:正方体的展开图.【专题】462:立体图形的认识与计算.【分析】我们可以对四个选项用排除法,根据正方体展开图的特征,选项D不能折成无盖的正方体纸盒;选项A、B、C都能折成无盖的正方体纸盒,选项B、C中字母“M”都在侧面,只有选项A折成无盖的正方体纸盒,下底标有字母“M”.【解答】解:如图,根据正方体展开图的特征,将其剪开展成平面图形是:故选:A.【点评】此题是考查正方体展开图的特征,四个选项中除D外,其余几个都能折成无盖的正方体盒,关键是看哪个字母“M”在底上.5.(2015•德江县模拟)把一个长3cm、宽4cm、高5cm的长方体截成两个长方体,表面积最多增加()cm2.A.24 B.30 C.40【考点】AB:长方体和正方体的表面积.【专题】12 :应用题;33 :假设法;462:立体图形的认识与计算.【分析】抓住长方体的切割特点可得,要使增加的表面积最多,则平行于最大面5×4面切割,则表面积就是增加2个5×4面,据此即可解答.【解答】解:5×4×2=20×2=40(平方厘米)答:表面积最多能增加40平方厘米.故选:C.【点评】根据长方体切割小长方体的方法,明确表面积增加的2个面是解决本题的关键.6.(2015•徐州模拟)一个汽油箱长60厘米,宽20厘米,高20厘米,这个油箱可盛汽油()升.A.240000 B.240 C.24 D.0.24【考点】AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】根据长方体的容积(体积)公式:v=abh,把数据代入公式解答.【解答】解:60×20×20=24000(立方厘米),24000立方厘米=24(升),答:这个油桶可以盛汽油24升.故选:C.【点评】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算.7.(2015秋•射阳县校级期末)如图,用丝带捆扎一种礼品盒,结头处长25cm,要捆扎这种礼品盒,准备()分米的丝带比较合理.A.10 B.15 C.20 D.22.5【考点】8G:长方体的特征.【专题】12 :应用题;3B :代数方法;462:立体图形的认识与计算.【分析】由图形可知:丝带的长度等于长方体的两条长+两条宽+4条高,然后再加上打结用的25厘米就是所需要的长度,列式解答即可.【解答】解:30×2+20×2+25×4+25=60+40+100+25=225(厘米)=22.5(分米答:准备22.5分米的丝带比较合理.故选:D.【点评】此题考查的目的是理解掌握长方体的特征,相对棱的长度相等,关键是弄清如何捆扎的,进而确定是求哪几条棱的长度和.二.填空题(共10小题)8.(2016春•玉林期末)棱长总和是72cm的正方体,表面积是216平方厘米,体积是216立方厘米.【考点】AB:长方体和正方体的表面积;AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】正方体的12条棱的长度都相等,用棱长总和除以12求出棱长,再根据正方体的表面积公式:s=6a2,体积公式:v=a3,把数据分别代入公式解答.【解答】解:72÷12=6(厘米),6×6×6=216(平方厘米),6×6×6=216(立方厘米),答:这个正方体的表面积是216平方厘米,体积是216立方厘米.故答案为:216平方厘米,216立方厘米.【点评】此题主要考查正方体的表面积公式、体积公式的灵活运用.9.(2016春•克州校级期中)如果正方体的棱长扩大到原来的3倍,那么它的表面积就扩大到原来的9倍.【考点】AB:长方体和正方体的表面积.【专题】462:立体图形的认识与计算.【分析】根据正方体的表面积公式s=6a2,再根据积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,由此解答.【解答】解:根据正方体的表面积公式s=6a2,一个正方体的棱长扩大到原来的3倍,表面积扩大到原来的3×3=9倍.答:它的表面积扩大到原来的9倍.故答案为:9.【点评】此题主要根据正方体表面积计算方法和积的变化规律解决问题.10.(2016秋•玄武区期末)用铁丝焊接一个棱长是5 厘米的正方体框架,至少需要铁丝60厘米.如果用白纸贴满正方体的各个面,至少要用白纸150平方厘米;这个正方体的体积是125立方厘米.【考点】AB:长方体和正方体的表面积;8G:长方体的特征;AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】根据正方体的棱长总和=棱长×12,正方体的表面积公式:S=6a2,体积公式:v=a3,把数据分别代入公式解答.【解答】解:5×12=60(厘米);5×5×6=25×6=150(平方厘米);5×5×5=125(立方厘米);答:至少需要铁丝60厘米,至少要用白纸150平方厘米,它的体积是125立方厘米.故答案为:60、150、125.【点评】此题主要考查正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式.11.(2016春•扬州校级期末)长方形的右侧面积是12平方厘米,前面面积是8平方厘米,上面面积是6平方厘米,这个长方体的表面积是52平方厘米.【考点】AB:长方体和正方体的表面积.【专题】462:立体图形的认识与计算.【分析】根据长方体的特征.相对面的面积相等,已知长方体相邻三个面的面积,求这个长方体的表面积,也就是用相邻三个面的面积和乘2即可,据此解答.【解答】解:(6+8+12)×2=26×2=52(平方厘米)答:这个长方体的表面积是52平方厘米.故答案为:52.【点评】此题考查的目的是理解掌握长方体的特征,以及长方体的表面积公式的灵活运用.12.(2016秋•无锡期末)一个长方体,如果宽增加2厘米,就变成一个正方体,这时表面积比原来增加32平方厘米.原来长方体的表面积是64平方厘米,体积是32立方厘米.【考点】AB:长方体和正方体的表面积;AC:长方体和正方体的体积.【专题】12 :应用题;17 :综合填空题;462:立体图形的认识与计算.【分析】根据题意可知,一个长方体如果宽增加2厘米,就变成了一个正方体;说明长和高相等且比宽大2厘米,因此增加的32平方厘米是4个同样的长方形的面积和;由此可以求长方体的长=(32÷4)÷2=4厘米,由于长比宽多2厘米,那么宽=4﹣2=2厘米,由此再利用长方体的体积公式和表面积计算公式计算即可解答.【解答】解:32÷4÷2=4(厘米)4﹣2=2(厘米)(1)4×4×2+4×2×4=32+32=64(平方厘米)答:原来长方体的表面积是64平方厘米.(2)4×4×2=16×2=32(立方厘米)答:原来长方体的体积是32立方厘米.故答案为:64,32.【点评】本题主要考查长方体正方体表面积的实际应用,解答本题的关键是根据宽增加2cm,就变成一个正方体,可知增加的部分是长为2厘米的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体的表面积和体积的计算方法即可求解.13.(2016春•未央区期末)一个正方体木块,把它割成2个长方体后.表面积增加了18m2,这个木块原来的表面积是54平方米,体积是27立方米.【考点】AB:长方体和正方体的表面积;AC:长方体和正方体的体积.【专题】17 :综合填空题;462:立体图形的认识与计算.【分析】把一个正方体切成两个完全相同的长方体后,则表面积增加了两个边长和原来正方体棱长相同的两个横截面的面积,表面积增加了18平方米,则每个横截面的面积为18÷2=9平方米,即可求出正方体的边长为3米,再利用正方体的表面积公式S=6a2,体积公式V=a3,即可解答.【解答】解:18÷2=9(平方米)因为3×3=9,所以原来正方体的棱长是3米,表面积:3×3×6=9×6=54(平方米)体积:3×3×3=9×3=27(立方米)答:这个木块原来的表面积是54平方米,体积是27立方米.故答案为:54平方米、27立方米.【点评】此题主要考查正方体表面积公式和体积的计算,关键是求出正方体的棱长,再把数据代入表面积和体积公式解答即可.14.(2016春•仁怀市校级期末)一个棱长4dm的正方体钢坯的体积是64dm3,如果把它锻造成一个底面积是20dm2的长方体,这个长方体的高是 3.2dm.【考点】AC:长方体和正方体的体积.【分析】(1)根据正方体的体积=棱长×棱长×棱长即可解答;(2)锻造前后的体积不变,根据长方体的体积公式,用上面求出的正方体的体积,除以这个长方体的底面积,即可得出长方体的高.【解答】解:(1)正方体钢坯的体积是:4×4×4=64(立方分米);(2)64÷20=3.2(分米),答:一个棱长4dm的正方体钢坯的体积是64dm3,如果把它锻造成一个底面积是20dm2的长方体,这个长方体的高是3.2分米.故答案为:64;3.2.【点评】此题考查了正方体和长方体的体积公式的灵活应用,抓住锻造前后的体积不变,是解决此类问题的关键.15.(2016春•日照期末)一根长2米的长方体钢材,沿横截面截成两段后,表面积增加了0.8平方米,这段长方体钢材的体积是800立方分米.【考点】AC:长方体和正方体的体积.【分析】根据长方体的面的特征,它的6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;由题意可知,一根长2米的长方体钢材,沿横截面截成两段后,表面积增加了0.8平方米,增加了两个截面的面积,0.8÷2=0.4平方米,长方体的体积=底面积×高;由此解答.【解答】解:1立方米=1000立方分米;0.8÷2×2=0.4×2=0.8(立方米);0.8立方米=800立方分米;答:这段长方体钢材的体积是800立方分米.故答案为:800.【点评】此题主要考查长方体的体积计算,关键是理解沿横截面截成两段后,表面积增加了0.8平方米,增加的是两个截面的面积即底面积,然后根据体积公式解答.16.(2016春•抚州校级期末)用一根24分米长的铁丝围成一个最大的正方体形状的框架,这个正方体的体积是8立方米.【考点】AC:长方体和正方体的体积;8G:长方体的特征.【专题】462:立体图形的认识与计算.【分析】用一根24分米长的铁丝围成一个最大的正方体形状的框架,也就是这个正方体的棱长总和是24分米,首先用棱长总和除以12求出棱长,再根据正方体的体积公式:v=a3,把数据代入公式解答即可.【解答】解:24÷12=2(分米),2×2×2=8(立方分米),答:这个正方体的体积是8立方分米.故答案为:8.【点评】此题主要考查正方体的棱长总和公式、体积公式的灵活运用,关键是熟记公式.17.(2016秋•泰兴市校级期中)一根60厘米长的铁丝,如果做一个长8厘米、宽5厘米的长方体模型,这个长方体的高是2厘米,这个长方体的表面积是124平方厘米,体积是80立方厘米.【考点】8G:长方体的特征;AB:长方体和正方体的表面积;AC:长方体和正方体的体积.【专题】17 :综合填空题;462:立体图形的认识与计算.【分析】用长60厘米的铁丝围一个长方体框架,也就是这个长方体的棱长总和是60厘米,用棱长总和除以4求出长、宽、高的和,已知长方体的长是8厘米,宽是5厘米,用长、宽、高的和减去长、宽,即可求出高,再根据长方体的表面积公式:s=(ab+ah+bh)×2,体积公式:v=abh,把数据分别代入公式解答.【解答】解:60÷4﹣8﹣5=15﹣8﹣5=2(厘米)表面积:(8×5+5×2+8×2)×2=(40+10+16)×2=62×2=124(平方厘米)体积:8×5×2=40×2=80(立方厘米)答:这个长方体的高是2厘米,这个长方体的表面积是124平方厘米,体积是80立方厘米.故答案为:2、124、80.【点评】此题主要考查长方体的棱长占公式、表面积公式、体积公式的灵活运用,关键是求出长方体的高.三.判断题(共5小题)18.(2017春•渭源县校级期末)正方体的棱长扩大到原来的2倍,它的表面积也就扩大到原来的2倍.×.(判断对错)【考点】AB:长方体和正方体的表面积.【专题】18 :综合判断题;39 :找“定”法;462:立体图形的认识与计算.【分析】依据正方体的表面积公式S=a×a×6进行解答即可.【解答】解:原来的表面积:S=a×a×6=6a2,现在的表面积:S=2a×2a×6=24a2,表面积扩大:24a2÷6a2=4倍.所以题干的说法是错误的.故答案为:×.【点评】此题主要考查正方体的表面积公式的灵活应用.19.(2016•玉溪模拟)棱长为6cm的正方体的体积与表面积相等.×.(判断对错)【考点】AC:长方体和正方体的体积;AB:长方体和正方体的表面积.【专题】18 :综合判断题;462:立体图形的认识与计算.【分析】根据正方体的表面积公式:s=6a2,正方体的体积公式:v=a3,因为表面积和体积不是同类量,无法进行比较.由此解答.【解答】解:表面积:6×6×6=216(平方厘米)体积:6×6×6=216(立方厘米)因为表面积和体积不是同类量,无法进行比较.故答案为:×.【点评】此题解答关键是明确:只有同类量才能进行比较大小,不是同类量无法进行比较.20.(2016春•正定县校级期末)底面周长是8分米的正方体,它的表面积是24平方分米.√.(判断对错)【考点】AB:长方体和正方体的表面积.【专题】462:立体图形的认识与计算.【分析】根据正方体的特征,正方体的6个面是完全相同的正方形,已知它的底面周长是8分米,首先用底面周长除以4求出底面边长,再根据正方体的表面积公式:s=6a2,把数据代入公式求出它的表面积,然后与24平方分米进行比较即可.【解答】解:8÷4=2(分米),2×2×6=4×6=24(平方分米),答:它的表面积是24平方分米.故答案为:√.【点评】此题主要考查正方形的周长公式、正方体的表面积公式的灵活运用,关键是熟记公式.21.(2016春•仁怀市校级期末)如果长方体的长、宽、高都扩大3倍,则它的体积扩大3倍.×(判断对错)【考点】AC:长方体和正方体的体积.【专题】18 :综合判断题;462:立体图形的认识与计算.【分析】根据长方体的体积计算方法和积的变化规律,长方体的体积=长×宽×高,积扩大的倍数等于因数扩大倍数的乘积.由此解答.【解答】解:长方体的体积=长×宽×高,长、宽、高都扩大3倍,它的体积就扩大:3×3×3=27倍;所以“如果长方体的长、宽、高都扩大3倍,则它的体积扩大3倍”的说法是错误的.故答案为:×.【点评】此题主要根据长方体的体积计算方法和积的变化规律解决问题.22.(2016春•黎平县校级期末)把一个长方体锻造成一个正方体铁块,形状变了,但体积不变.√(判断对错)【考点】AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】根据体积的意义,物体所占空间的大小叫做物体的体积.将一个长方体铁块锻造成正方体,只是形状变了,但体积不变.据此解答.【解答】解:把一块长方体的铁块锻造成正方体的铁块,形状改变了,但体积不变,所以本题说法正确;故答案为:√.【点评】此题主要考查了学生对正方体表面积及体积公式的掌握应用情况.四.解答题(共10小题)23.(2017春•渭源县校级期末)如图,如果把这个长方体完全沉没于盛满水的水槽中,会有多少水溢出来?如果要包装这个盒子,至少需要多少平方厘米的包装纸?(单位:厘米)【考点】AC:长方体和正方体的体积;AB:长方体和正方体的表面积.【专题】462:立体图形的认识与计算.【分析】(1)溢出的水的体积就等于长方体的体积,利用长方体的体积公式即可得解;(2)求包装纸的面积实际上是求长方体的面积,利用长方体的表面积公式即可求解.【解答】解:(1)13×2×8=208(立方厘米);答:会有208立方厘米水溢出来.(2)(13×2+13×8+2×8)×2,=(26+104+16)×2,=146×2,=292(平方厘米);答:至少需要292平方厘米的包装纸.【点评】此题主要考查长方体的表面积和体积的计算方法的灵活应用.24.(2016•安溪县模拟)求出如图中长方体的体积和表面积.(单位:米)【考点】AB:长方体和正方体的表面积;AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,已知长是5厘米,宽是3厘米,高是4厘米.把数据分别代入公式解答.【解答】解:(3×4+3×5+4×5)×2=(12+15+20)×2=47×2=94(平方米)3×4×5=60(立方米)答:这个长方体的表面积是94平方米,体积是60立方米.【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式.25.(2016秋•玄武区期末)看图计算,如图是长方体纸箱的展开图,请你根据有关数据,求出纸箱的体积.(单位:分米)【考点】8L:长方体的展开图;AC:长方体和正方体的体积.【专题】462:立体图形的认识与计算.【分析】我们通过观察得到这个长方体的长是6分米,宽是9﹣6=3分米,高是11﹣3=8厘米,由此运用长方体的体积公式进行解答即可.【解答】解:长方体的体积:6×(9﹣6)×(11﹣3),=6×3×8,=144(立方厘米);答;这个纸盒的表面积是136平方厘米,体积是80立方厘米.【点评】本题考查了学生对长方体的体积公式的运用掌握情况.重点考查了空间想象能力.26.(2016秋•毕节市期中)一间平顶教室,长是8.5米,宽6米,高4.2米.教室的门窗和黑板的面积一共有35.8平方米.要粉刷教室的顶面和四面墙壁,粉刷的面积有多少平方米?【考点】AB:长方体和正方体的表面积.【分析】由题意知,粉刷的面积=教室的顶面面积+四面墙壁的面积﹣门窗和黑板的面积,据此列式解答即可.【解答】解:2×(8.5×4.2+6×4.2)+8.5×6﹣35.8=2×60.9+51﹣35.8=121.8+51﹣35.8=137(平方米).答:粉刷的面积有137平方米.【点评】本题主要考查长方体的表面积的知识点,长方体的表面积=2(长×宽+长×高+宽×高).本题需要注意减去地面的面积和教室的门窗和黑板的面积.27.(2016春•扬州校级期末)一个长方形的游泳池,从里面量长50米,宽20米,高2米,平均水深1.5米.粉刷它的四壁和地面,粉刷面积是多少平方米?【考点】AB:长方体和正方体的表面积.【专题】12 :应用题;462:立体图形的认识与计算.【分析】要在四壁和池底粉刷,只求它的5个面的总面积,根据长方体的表面积公式:S=2ab+2ah+2bh进行解答.【解答】解:(50×20+50×2+20×2)×2﹣50×20=(1000+100+40)×2﹣1000=1140×2﹣1000=2280﹣1000=1280(平方米)答:粉刷面积是1280平方米.【点评】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行解答问题.。
六年级上册《长方体与正方体》专项练习试题(10套)

(1)(长方体和正方体的认识)一、填空:(38%)1、长方体和正方体都有( ) 个面,( ) 条棱,( ) 个顶点。
2、长方体的每个面都是()形或有一组对面是()。
它有()条棱,平行的()条棱都相等。
3、相交于长方体一个顶点的三条棱的长度分别叫做它的()、()和()。
4、长方体有()个面,从不同的角度观察一个长方体,最多能看到()个面。
5、一个长方体的长是5分米,宽是4分米,高是3分米,6个面中最小的一个面的面积是(),最大的一个面的面积是()。
6、一个长方体,长4米,宽3米,高2米,它的占地面积最大是()平方米。
7、一个长方体模型,从前面看是从上面看是长方体右面的面积是()平方厘米。
8、长方体的右侧面面积是12平方厘米,前面面积是8平方厘米,上面面积是6平方厘米,这个长方体的长、宽、高分别是()、()、()。
二、选择(8%):1、一个长方体水池,长20米,宽10米,深2米,这个水池占地()平方米。
A、200B、400C、5202、下面的图形中,能按虚线折成正方体的是()。
3、从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如下图) ,它的表面积( ) 。
A.和原来同样大B.比原来小C.比原来大D.无法判断4、用一根52厘米长的铅丝,正好可以焊成长6厘米,宽4厘米,高()厘米的长方体教具。
A、2B、3C、4D、5三、计算下面每个形体的棱长和(6%)。
四、下面各题,列式计算,不写答。
(40%)1、一个长方体,长5分米,宽3分米,高4分米,求它的所有棱长的和。
2、用钢筋做一个长和宽都是分米,高是10厘米的长方体,需多少分米的钢筋3、棱长是4分米的正方体,棱长总和是多少分米4、一个长方体的棱长和是36厘米,从一个顶点出发的三条棱的长度总和是多少厘米5、同一根长96厘米的铁丝折成一个最大的正方体框架,求正方体框架的棱长。
6、一个长方体的长是15厘米,宽是12厘米,棱长总和是148厘米,求它的高。
7、两根同样长的铁丝焊一个长方体和正方体,长方体长7厘米,宽5厘米,高3厘米,求正方体的棱长。
六年级数学上册长方体和正方体练习题

长方体和正方体练习题1、 一个长方体是由3个2、 棱长为4厘米的正方体拼成的。
这个长方体的长、宽、高各是多少厘米?2、一个长方体的长、宽、高分别是15厘米、13厘米、17厘米,这个长方体最大面的面积比最小面的面积多多少平方厘米?3、林月12周岁生日,表姐送给她一组奥运福娃作生日礼物,生日礼物用长方体礼品盒包装,并用彩带扎好,你能算出彩带的长吗?(接头处长25厘米)4、李师傅要用两根同样长的铁丝分别围成一个长方体框架和一个整体框架,已知长方体框架的长是10厘米,宽是6厘米,高是5厘米。
正方体框架的棱长是多少?5、下图中的立方体表面都已涂上油漆,并被分成许多小的立方体,请你数一数:(1)它有( )个小的立方体。
(2)它有( )个小立方体是四面涂漆的。
(3)它有( )个小立方体是三面涂漆的。
(4)它有( )个小立方体是两面涂漆的。
(5)它有( )个小立方体是一面涂漆的。
(6)它有( )个小立方体是没有涂漆的。
6、学校礼堂的门口有8级台阶,每级台阶长6米,宽0.4米,高0.2米。
艺术节学校准备给礼堂门口的台阶铺上红地毯,至少需要买多少平方米的红地毯?7、礼堂内有四根长方体形状的柱子,底面积是正方形,边长为6分米,高为5米。
要油漆这四根柱子,油漆部分的面积是多少平方米?8、一种长方体形状的铁皮烟筒,每节长1.5米,截面是边长为4分米的正方形,做10节这样的烟筒需要多少平方米铁皮?9、枫叶学校建一个长方体游泳池,长50米,宽25米,深2米。
请你算一算:(1)游泳池的占地面积是多少平方米?(2)在游泳池底面和内壁抹一层水泥,抹水泥的面积是多少平方米? 10、把一个棱长为4分米的正方体的一个角挖掉一个棱长为1分米的小正方体(如图),这个形体的表面积是多少? 11、如图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个棱长为1厘米的正方体,做一种玩具。
它的表面积是多少平方厘米?12、从一个长10厘米、宽8厘米、高5厘米的长方体中裁出一个体积最大的正方体,这个正方体的体积是多少?13、一个正方体的棱长之和是8.4分米。
六年级上册数学试题长方体和正方体的表面积和体积专项练习

长方体和正方体的表面积和体积专项练习一、高减少或增加引起表面积的变化:例题:一个长方体高减少3厘米后,表面积减少了72平方厘米,剩下的刚好是一个正方体,原来长方体的表面积是多少平方厘米?试一试:一个长方体,如果高增加2厘米,就成为一个正方体,这时表面积比原来增加了64平方厘米,原来的长方体的表面积是多少平方厘米?二、拼接引起表面积的变化:例题:1.用两个长、宽、高分别是6分米、4分米、2分米的长方体拼成一个较大的长方体,这个长方体怎样拼表面积最大?怎样拼表面积最小?2.用6个棱长是1厘米的小正方体拼成一个较大的长方体,拼成的长方体的表面积比原来减少了多少平方厘米?试一试:10包长、宽、高分别为8厘米、5厘米、2厘米的中华牌香烟,若用包装纸将他们打包成一个长方体,不计接头处,至少需要多少平方厘米的包装纸?三、切割引起表面积的变化:例题:将一个长10厘米、宽6厘米、高5厘米的长方体切成两个完全相同的小长方体,这两个小长方体的表面积总和比原来增加了多少平方厘米?试一试:(1)有一个长方体,若用三种不同的方法切成两个完全一样的长方体,它们的表面积分别增加30平方厘米、20平方厘米、12平方厘米。
这个长方体的表面积是多少平方厘米?(2)如右图,一个正方体木块的表面积是36平方分米,把它沿虚线截成体积相等的8个小正方体木块,这时,表面积增加了多少平方厘米?四、挖去部分引起表面积的变化:例题:在一个长6厘米、宽4厘米、高3厘米的长方体上挖去一个棱长1厘米的小正方体,剩余部分的表面积可能是多少平方厘米?试一试:用橡皮泥做一个棱长为4厘米的正方体。
(1)如右图,在顶面中心位置从上到下打一个边长为1厘米的正方形通孔,打孔后的橡皮泥块的表面积为多少平方厘米?(2)在第(1)题打孔后,再在正面中心位置处,从前到后打一个边长1厘米的正方形通孔(如右图所示),那么打孔后的橡皮泥内外的表面积总和是多少平方厘米?(3)在棱长为3厘米的正方体木块的每个面的中心上打一个直穿木块的洞,洞口呈边长为1厘米的正方形(如图)。
2022-2023学年六年级数学上册典型例题之第一单元长方体和正方体体积的生活实际问题专项练习

20222023学年六年级数学上册典型例题系列之第一单元:长方体和正方体体积的生活实际问题专项练习(解析版)1.一根长方体方钢,长是6米,横截面是一个边长为5厘米的正方形,如果每立方厘米方钢重0.0069千克,这根方钢重多少千克?【答案】103.5千克【分析】方钢看作是底面积为5×5=25平方厘米,高是6米的长方体,先计算其体积,再用乘法计算出其重量。
【详解】6米=600厘米5×5×600=25×600=15000(立方厘米)15000×0.0069=103.5(千克)答:这根方钢重103.5千克。
【点睛】本题考查长方体体积公式,长方体体积=长×宽×高=底面积×高,计算时先统一单位。
2.一个长方体油桶从里面量,长、宽、高分别是8分米,4分米,5分米。
如果每升油重0.8千克,这个油桶可以装油多少千克?【答案】128千克【分析】要求油桶可以装油多少千克,首先要先求出长方体油桶的体积,根据长方体的体积公式V=abh,代入数据计算即可;再用所求体积乘每升油的质量,即可求出油桶可装油的质量。
【详解】8×4×5=32×5=160(立方分米)160立方分米=160升160×0.8=128(千克)答:这个油桶可以装油128千克。
【点睛】本题主要考查对长方体体积公式的掌握与实际应用。
3.只列综合算式不计算。
育英小学要砌一道长120米,厚0.24米,高2米的围墙,如果每立方米用砖525块,这道围墙要用砖多少块?【答案】1200.242525⨯⨯⨯【分析】根据长方体体积=长×宽×高,求出围墙体积,围墙体积×每立方米用砖块数=这道围墙用砖块数,据此分析。
【详解】1200.242525⨯⨯⨯⨯=57.6525=30240(块)答:这道围墙要用砖30240块。
【点睛】关键是掌握并灵活运用长方体体积公式。
(完整版)“长方体和正方体”练习题及答案

六年级第一学期“长方体和正方体”练习题姓名成绩一、填空题。
(每空1分,共24分)1、在括号里填上合适的单位名称。
⑴一小瓶红墨水是60()⑵一台电冰箱的体积约是240()⑶一种油箱的容积是0.6()⑷一只火柴盒的体积约是9.6()⑸一种水箱可容水约24()2、一个长方体长5厘米,宽5厘米,高4厘米,这个长方体有2个面是()形,还有()个面的面积相等,长方体的表面积是()。
3、一个长方体的体积是162立方厘米,它的底面积是32.4平方厘米,底面长8.1厘米,这个长方体的高是( )厘米,宽是( )厘米。
4、一个长方体的体积是240立方厘米,长是8厘米,宽是6厘米,高是()厘米。
5、 6.4立方米=( )立方分米 4500毫升=( )升80立方厘米=()立方分米 3.8升 = ( )毫升7.05立方分米=( )升 50平方厘米=()平方分米6、右图是由棱长1厘米的小正方体拼成的,它的体积是()立方厘米,至少再加上()个小正方体,就能成为一个较大的正方体。
7、一个长方体,长、宽、高分别为a米、b米、c米,如果高增加4米,新的长方体比原来长方体增加了()立方米。
8、一个长方体的表面积是90平方分米,把它平均分开正好成两个相等的正方体,每个正方体的表面积是()平方分米。
9、用3个棱长4厘米的正方体粘合成一个长方体,长方体的表面积比3个正方体的表面积少()平方厘米。
10、一个长方体相邻三个面的面积分别为10平方厘米、15平方厘米和6平方厘米,这个长方体的体积为()。
11、一个长方体的宽和高都是5厘米,把它从长的中点截成两个相同的长方体后,得到其中一个长方体的表面积比原来大长方体的表面积减少120平方厘米。
原来长方体的体积是()立方厘米。
二、判断题。
(每题2分,共12分)1、正方体棱长扩大到原来的2倍,体积扩大到原来的8倍。
……………()2、a3=3a。
……………………………………………………………………()3、一个长方体茶叶罐,体积和容积相等。
小学六年级数学上册长方体正方体典型练习题

六上数学-长方体、正方体单位换算:1立方米=1000立方分米=1000000立方厘米1升=1立方分米 1毫升=1立方厘米1升=1000毫升一.单位换算1立方米=〔〕立方分米 1立方分米=〔〕立方厘米1升=〔〕毫升 1立方厘米=〔〕毫升1.8立方米=〔〕立方分米 0.14立方分米=〔〕立方厘米5400立方分米=〔〕立方米 14200立方厘米=〔〕立方分米1.8立方分米=〔〕升 25毫升=〔〕立方厘米0.72升=〔〕毫升 1508毫升=〔〕升8.5立方分米=〔〕升=〔〕毫升0.42立方米=〔〕立方分米=〔〕升400立方厘米=〔〕毫升=〔〕升1.56升=〔〕立方分米=〔〕立方厘米此类考题需要细心:小单位大数字、大单位小数字;二.比较大小36立方分米○ 3.6立方米 2040毫升○ 2.04升7.08立方分米○ 7080升 1.5升○ 1500立方厘米680平方米○ 6.8平方分米 0.024立方米○ 120升此类考题需要细心:首先化成相同单位的数量,并把换算的数字记录在原数字上,然后再比较。
三.在括号里填上适宜的单位名称一桶纯洁水的净含量大约是16.8〔〕一盒白色粉笔的体积大约是1〔〕一个橱柜的容积大约是2〔〕此类考题需要联系实际问题考虑用什么单位更适宜:容量较小的用"毫升〞〔如小瓶装饮料、香水等〕作单位,体积小用"立方厘米〞作单位;容量略大的用"升〞〔饮水用、食用油等〕作单位,体积略大的用"立方分米〞作单位;容量和体积较大的用"立方米〞作单位。
四.判断题1.正方体的棱长扩大为原来的2倍,它的体积扩大原来的8倍。
2.长方体的体积就是它的容积。
3.棱长为1分米的正方体体积是1升。
4.把棱长为1分米的正方体放在地上,这个正方体的占地面积是1立方分米。
5.外表积相等的两个长方体,它们的体积不一定相等。
6.一个棱长6分米的正方体,它的体积和外表积相等7.把一个正方体的棱长扩大2位,那么它的外表积扩大4倍,体积扩大8倍。
【精品】苏教版小学数学六年级上册第一单元《长方体正方体》同步练习试题共3套

长方体正方体同步练习1、一个长方体的底面积是80平方厘米,高是7厘米,体积是()立方厘米。
2、一个长方体有一组相对的面是正方形,那么另外4个面()。
A、一定相等B、不一定相等C、一定不相等3、把棱长1米的正方体截成棱长1分米的小正方体,再把这些小正方体排成一排拼成一个长方体,长方体的长是多少米?4、将一个长方体截下一个体积800立方厘米的长方体后,剩下的正好是一个棱长10厘米的正方体,原长方体的表面积是多少平方厘米?5、一种液体饮料采用长方体塑封纸盒密封包装,从外面量盒子长6厘米、宽4厘米、10厘米,盒子上注明“净含量:240毫升”。
你觉得这个数据真实吗?为什么?6、一个无盖的正方体盒,下底标有字母M,沿其棱将它剪开展成平面图形,这个图形可能是()。
7、大正方体的棱长是小正方体的2倍,而体积比小正方体大420立方厘米,那么小正方体的体积是()立方厘米。
8、一个正方体表面积是96平方厘米,把它分成8个同样的小正方体后,每个小正方体的表面积是多少平方厘米?9、大厅里有8根长方体立柱,其底面是边长2分米的正方形,高6米.现在要油漆这些立柱,那么油漆面积共多少平方米?10、在一个长20厘米、宽15厘米、高10厘米的长方体容器中,装的水深8厘米,在里面放入一个棱长10厘米的铁块,这时水溢出多少立方厘米?附加题:1、一个正方体所有棱长的和是36厘米,它的表面积是()平方厘米,体积()立方厘米.2、把1立方米的木料全部锯成1立方厘米的小方块,再把这些小木块一面挨着一面地向前摆成一长串,那么这一长串小木块总共有多少厘米长?3、把一个长方体的高锯掉4厘米后变成一个正方体,表面积减少80平方厘米。
这个长方体原来的体积是多少立方厘米?4、从一个长方体上截下一个体积是32立方厘米的小长方体后剩下的部分正好是棱长4厘米的正方体,原来这个长方体的表面积是多少平方厘米?5、用一张长50厘米、宽40厘米的长方形铁皮,做一只深10厘米的无盖长方体盒(焊接处铁皮厚度不计)。
小学六年级数学长方体和正方体练习题精选

小学六年级数学长方体和正方体练习题精选1.一个长方体玻璃容器,向容器里倒入6L升水,这时水面高度是15厘米,再把一个苹果放入水中,量得这时水面的高度是16.5厘米,请你计算苹果的体积。
2.一个长方体玻璃容器,从里面量长、宽均为2dm,向容器中倒入5L的水,再把一个土豆放入水中。
这时量得容器内的水深是13cm。
这个土豆的体积是多少?3.一个长方体,如果长減少2厘米,宽和高不变,它的体积减少48立方厘米如果宽增加3厘米,长和高不变,它的体积增加99立方厘米,如果高增加4厘米,长和宽不变,它的体积增加352立方厘米,原来长方体的表面积是多少平方厘米?4.一个长方体,如果高截掉2厘米,表面积就减少了32平方厘米,剩下的正好是一个正方体,原来长方体的体积和表面积分别是多少?5.一个长方体,如果长增加2厘米,则体积增加40立方厘米,如果宽增加3厘米,则体积增加90立方厘米,如果高增加4厘米,则体积增加96立方厘米,原长方体的表面积是多少平方厘米?6.工地上有一个长方体沙堆,底面积18平方米,高8米。
用这些沙子铺在6米长、4米宽的长方体池子里,能铺多厚?7.现有一张长40厘米、宽20厘米的长方形铁皮,请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计,容积越大越好),你做出的铁皮盒容积是多少立方厘米?8.长方形铁皮长24厘米,四角剪去连长3厘米的正方形后,再焊接成长方形盒子,盒子容积是486立方厘米,求原长方形铁皮宽。
9.有一块长方形的铁皮,长60厘米,宽40厘米。
在这块铁皮的四角剪去边长5厘米的小正方形,然后制成一个无盖的长方体盒子,求这个长方体盒子的体积。
10.把一个长方体截去一个高为8厘米的长方形后,剩下的部分是一个正方体。
正方体的表面积比原来长方体的表面积减少320平方厘米。
求原来长方体的体积。
11.有一个长方体,它的前面和上面的面积之和是209平方厘米,如果它的长、宽、高都是质数,那么这个长方体的体积是多少立方厘米?12.如果一个小正方体的表面积是6平方厘米,由27个这样的小正方体组成一个大正方体,大正方体的表面积是多少平方厘米?13.两个完全相同的长方体,长6厘米,宽4厘米,高2厘米,拼成一个表面积最大的长方体,拼成后的长方体表面积比原来两个长方体的表面积减少多少平方厘米?14.一个长方体的纸盒,底面是周长为12厘米的正方形,高是2.5厘米,这个长方体纸盒的表面积和体积各是多少?15.一个正方体棱长总和是96厘米,它的表面积和体积分别是多少?16.把一个表面积是54平方分米的正方体木料锯成两个长方体,这两个长方体的表面积是多少平方分米?17.建造一个长方体游泳池,长30米,宽10米,深1.6厘米,池的四壁和底面用瓷砖铺砌,如果每平方米用瓷砖25块,共需要多少块?18.将棱长是6厘米的正方体铁块,锻造成长3厘米,宽2厘米的长方体,锻造成的这个长方体的高是多少厘米?19.在一个长3分米,宽24厘米,高22厘米的玻璃缸中,水深19厘米,小明将一块棱长12厘米的正方形铁块投入水中,投入后缸中的水会溢出吗?分析与答案20.分析与答案。
第1单元 长方体和正方体 应用题专项训练 数学六年级上册苏教版(含答案)

第1单元长方体和正方体应用题专项训练数学六年级上册苏教版1.(2024春•临颍县期中)五月初,杭州各地茶农忙于采摘售卖茶叶。
小聪正在打包一个茶叶礼盒(如图),打结处用了13cm长的绸带。
打包这个茶叶礼盒至少需要用多少厘米长的绸带?2.(2024春•泌阳县期中)一个长方体游泳池长50米,宽25米,深2米,如果在它的四周和底面贴瓷砖,贴瓷砖部分的面积是多少?3.(2024春•镇原县期中)鸟类是人类的朋友,爱护鸟类,人人有责。
希望小学用木板在树林中设置了若干个简易的人工鸟巢(如图),鸟巢的形状是长方体,长3dm、宽3dm、高2dm。
做一个这样的人工鸟巢,至少需要多少平方分米的木板?(人工鸟巢没有右侧面)4.(2024春•路北区期中)一个正方体礼品盒的棱长总和为12dm。
如果包装这个礼品盒的用纸是其表面积的1.2倍,至少要用多少平方分米的包装纸?5.(2024春•内乡县期中)如图所示,一个正方体的礼盒,包装盒上的彩带总长是209cm,其中打结处的蝴蝶结用了17cm。
做这个正方体礼盒至少需要多少平方厘米的硬纸板?6.(2024春•内乡县期中)把一块体积是16dm3的石头放进一个正方体的水箱里,水面上升了10cm,此时水箱的水面达到最高值。
求水箱的容积?7.(2024春•玉田县期中)用金属条制作一个长方体柜台的框架,柜台长3米,宽0.8米,高1.2米,做这个柜台需要多少米长的金属条?8.(2024春•林州市期中)一根长2m的长方体木料,沿着横截面平行的方向锯成三段,这三段木料总的表面积比原来多6dm2。
原来这根长方体木料的体积是多少立方分米?9.(2024春•博罗县期中)要做一个无盖的正方体鱼缸,棱长为60厘米,需要多少平方厘米的玻璃?10.(2024春•新野县期中)一个长方体的底面是一个周长为40cm的长方形。
高为10cm,如果长和宽的厘米数都是质数,那么这个长方体的体积最大是多少?11.(2024春•洞头区期中)一根铁丝可以搭一个长6dm,宽5dm,高4dm的长方体,如果用这根铁丝搭成一个正方体,那么正方体的体积是多少?12.(2024春•洞头区期中)笑笑将一块棱长6dm的正方体橡皮泥,捏成一个横截面的边长为3dm 的正方形,这个长方体的长是多少分米?13.(2024春•微山县期中)在一个长50cm,宽40cm,高10cm的长方体容器中,盛有5cm深的水,把一块石头浸没到水中后,水面升到了8cm,这块石头的体积是多少?14.(2024•嘉定区模拟)南京奥体中心的体育场里部分场馆翻修,铺设了20块长30米、宽3.5米、厚0.3分米的木质地板,所铺地板的体积一共是多少立方米?15.(2024春•上杭县期中)某村委会服务大厅长8m,宽5m,高3m,门窗面积7.5m2。
小学数学六年级上册长方体和正方体练习题

新版苏教版小学数学六年级上册长方体和正方体练习题(2018最新编写)一、认真读题,谨慎填写.1长方体有()个面,每一个面一般都是()形,也可能有两个相对的面是()形,相对的面的面积相等.2、长方体两个面相交的线叫做().长方体有()条棱.相交于同一顶点的三条棱分别叫做长方体的()、()、().3、正方体有()个面,每个面都是()形,每个面的面积都().从不同的位置观察最多能看到()面.4、长方体和正方体都有()个面,()条棱,()个顶点.5、长方体或正方体(),叫做它的表面积.6、一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,修理时配上的玻璃的面积是()平方分米.7、()叫做物体的体积.8、常用的体积单位有()、()、(),计量液体的体积常用()、().9、在括号里填上适当的数.90020立方厘米=()升 4.07立方米=()立方分米3.02立方米=()立方分米.3.5dm3=()L26cm2=()dm2360dm3=()m3 2.3L=()ml10.用36cm长的铁丝,弯制成一个正方体的框架,在框架的表面蒙上一层彩纸制成一个无盖的纸盒,至少需要彩纸()cm2,这个纸盒的容积是()cm3.11.一根长方体的木料长2m,横截面积是0.04m2,它的体积是()m3.(原创题)12.做一个长6dm,宽4dm,高5dm的无盖的长方体玻璃鱼缸,至少需要玻璃()dm2.13.用棱长为6cm的正方体木块堆成一个较大的正方体,至少需要()块,拼成的正方体的表面积是()cm2,体积是()cm3.14.一个正方体石头的占地面积是9m2,它的表面积是()m2,体积是()m3.15.将一个长为12cm,宽为6cm,高为4cm的长方体木块锯成两个完全一样的长方体木块,表面积最多增加()cm2,最少增加()cm2.二、巧思妙断,判断对错.(对的打“√”,错的打“×”.)1、把两个一样的正方体拼成一个长方体后,体积和表面积都不变.()2、棱长1分米的正方体,体积是1立方分米.()3、相交于同一顶点的三条棱分别叫做这个长方体的长、宽、高.()4、把一块正方体橡皮泥捏成一个长方体后,虽然它的形状变了,但是它所占有的空间大小不变.()5、正方体和长方体的体积都可以用底面积乘高来进行计算.()1.所有的长方体和正方体都有6个面,8个顶点,12条棱.()6.一个容器的容积一定小于它的体积.()7.正方体是特殊的长方体.()8.把一个正方体的橡皮泥揉捏成一个长方体,它的体积和表面积都不变.()(创新题)9.棱长是6厘米的正方体的体积和表面积相等.()三、反复比较,精心选择.1、我们在画长方体时一般只画出三个面,这是因为长方体().A.只有三个面B.只能看到三个面C.最多只能看到三个面2、用一根长()铁丝正好可以做一个长6厘米、宽5厘米、高3厘米的长方体框架.A.28厘米B.126平方厘米C.56厘米D.90立方厘米3、做一个长方体抽屉,需要()块长方形木板.A.4B.5C.64、一个长方体水池,长20米,宽10米,深2米,这个水池占地()平方米.A.200B.400C.5205、下面的图形中,能按虚线折成正方体的是().6、从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如右图),它的表面积().A.和原来同样大B.比原来小C.比原来大D.无法判断7、文具盒的体积和容积相比().A.体积大B.容积大C.相等8、一台电脑显示器的占地面积是9(),占据的空间是27()A.平方厘米B.立方分米C.平方分米D.立方厘米1.一个正方体的棱长总和是24厘米,它的表面积是().(原创题)A.3456平方厘米B.24平方厘米C.8立方厘米9.27个小正方体拼成一个较大的正方体,在这个大正方体表面涂色,那么三个面涂色的小正方体有().(创新题)A.4个B.6个C.8个D.不能确定10.用一根长()铁丝正好可以做一个长5厘米、宽4厘米、高3厘米的长方体框架.(原创题)A.12厘米B.94平方厘米C.48厘米D.60立方厘米11.正方体的棱长扩大2倍,它的表面积扩大(),体积扩大().A.2倍B.4倍C.8倍D.16倍12.把一个长方体分成几个小长方体后,体积(),表面积().A.不变B.比原来大了C.比原来小了四、注意审题,细心计算.1、求下图的棱长总和.2、求下图的表面积.3、求下图的体积.五、动手实践,操作应用.1、动手操作:根据下面给出的长、宽、高,画出长方体图.2、右图是长方体展开图,测量需要的数据,并求长方体体积.六、解决问题.1、一块木料,长6分米,宽和高都是4分米,它的体积是多少?2、一个长方体的长、宽、高分别是9分米,7.5分米、3分米,棱长总和是多少厘米?5cm40cm6cm3、一个正方体油箱棱长14分米,如果制造20个这样的油箱,至少要铁皮多少平方分米?4、生产50个如下图的包装袋共需多少平方分米的包装纸?5、一个长方体水池,长10米,宽8米,高4米,这个水池能蓄水有多少吨?(1立方米水重1吨)6.一个月饼盒长20厘米,宽18厘米,高15厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?X k B1.c o m7.湖滨新城新建一所学校,学校要砌一道长100米,宽24厘米、高2.5米的围墙,每立方米需要砖525块,一共需要多少块砖?8.为了方便学生体育锻炼,我校要在操场上挖一个长5米,宽3米,深0.4米的沙坑.(1)这个沙坑的占地面积是多少平方米?(2)这个沙坑的容积是多少立方米?(3)要往这个沙坑里倒入4.5立方米的沙子,沙子可以铺多厚?(用方程解)9.将40升的水倒入一个长5分米,宽4分米,高7分米的长方体水池中,水深多少分米?10.一个教室的长10米,宽6米,高3米,门窗面积是8平方米.现在要把这个房间的四壁和顶面粉刷涂料,如果每平方米需要涂料2千克,一共要涂料多少千克?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六上数学-长方体、正方体
单位换算:1立方米=1000立方分米=1000000立方厘米
1升=1立方分米 1毫升=1立方厘米
1升=1000毫升
一.单位换算
1立方米=()立方分米 1立方分米=()立方厘米
1升=()毫升 1立方厘米=()毫升
1.8立方米=()立方分米 0.14立方分米=()立方厘米
5400立方分米=()立方米 14200立方厘米=()立方分米
1.8立方分米=()升 25毫升=()立方厘米
0.72升=()毫升 1508毫升=()升
8.5立方分米=()升=()毫升
0.42立方米=()立方分米=()升
400立方厘米=()毫升=()升
1.56升=()立方分米=()立方厘米
此类考题需要细心:小单位大数字、大单位小数字;
二.比较大小
36立方分米○ 3.6立方米 2040毫升○ 2.04升
7.08立方分米○ 7080升 1.5升○ 1500立方厘米
680平方米○ 6.8平方分米 0.024立方米○ 120升此类考题需要细心:首先化成相同单位的数量;并把换算的数字记录在原数字上;然后再比较。
三.在括号里填上合适的单位名称
一桶纯净水的净含量大约是16.8()一盒白色粉笔的体积大约是1()
一个橱柜的容积大约是2()
此类考题需要联系实际问题考虑用什么单位更合适:容量较小的用“毫升”(如小瓶装饮料、香水等)作单位;体积小用“立方厘米”作单位;容量略大的用“升”(饮水用、食用油等)作单位;体积略大的用“立方分米”作单位;容量和体积较大的用“立方米”作单位。
四.判断题
1.正方体的棱长扩大为原来的2倍;它的体积扩大原来的8倍。
2.长方体的体积就是它的容积。
3.棱长为1分米的正方体体积是1升。
4.把棱长为1分米的正方体放在地上;这个正方体的占地面积是1立方分米。
5.表面积相等的两个长方体;它们的体积不一定相等。
6.一个棱长6分米的正方体;它的体积和表面积相等
7.把一个正方体的棱长扩大2位;则它的表面积扩大4倍;体积扩大8倍。
8.容积和体积的计算方法相同;所以物体的体积等于它的容积。
9.表面积相等的两个长方体;它们的体积也一定相等。
10.用9个完全一样的小正方体能拼成一个大正方体。
11.一个长、宽、高分别是10厘米、8厘米、7厘米的长方体;可以从一个边长是8厘米的正方形洞中穿过去。
12.把两个同样的正方体拼成一个长方体后;表面积和体积都不变。
13.把体积为1立方厘米的纸盒放在桌面上;纸盒所占桌面的面积是1立方厘米。
14.长方体相对的面完全相同;相邻的两个面也有可能完全相同。
15.将一个正方体橡皮泥捏成一个长方体后;它的形状发生了变化;但它的体积没有变。
16.正方体是长、宽、高都相等的特殊的长方体。
17.如果两个长方体的体积相等;那么它们的长、宽、高一定相等。
对待改错题;必须做到把错误的内容改到正确;切不可猜、或以大概、可能这种模棱两可的想法作判断。
四.解决问题
解决问题部分的习题必须认真读题:
(一)单位名称要统一;必须按答句要求的单位名称换算;
(二)圈出关键词-有盖还是无盖;通风管、落水管、烟囱只算四个面的面积;游泳池贴瓷砖、教室刷墙面确定好哪个面不用计算……;
(三)每一步求的是什么答案;可用文字做好提示;以免自己解题混乱;答非所问;
1.金水湾度假村要建一个长方体游泳池;长50米;宽36米;深2米;请算一算。
(1)这个游泳池占地多少平方米?
(2)在游泳池的底面和内壁抹一层水泥;抹水泥的面积是多少平方米?
(3)在游泳池的内壁1.6米高处用红漆画一条水位线;水位线全长多少米?
(4)按水位线进水;游泳池共可注水多少立方米?
2.一间长方体的房间;长为5.2米;宽为3米;高为2.6米;它的四面墙的下部涂了1.1米高的浅绿色油漆(开门处1平方米不刷);涂油漆的面积有多少平方米?四面墙的上部和房顶刷上白色涂料(其中门窗占10平方米不刷);粉刷白色涂料的面积有多少平方米?
3.一个长方体的高减少了2厘米后;它就变成了一个正方体;表面积比原来减少了32平方厘
米;长方体的体积是多少?
4.把一个棱长4分米的正方体的一个角挖掉一个棱长1分米的小正方体;这个形体的表面积是多少?体积是多少?
5.一个边长4厘米的正方体;分别在前、后、左、右、上、下各面的中心位置挖去一个棱长为1厘米的正方体。
所得形体的表面积是多少平方厘米?体积是多少?
6.在一个长方体的一端截下一个体积为1800立方厘米的长方体后;正好剩下一个棱长为30厘米的正方体。
原来长方体的体积是多少立方厘米?表面积是多少平方厘米?
7.一根长方体木料;长2.5米;横截面是边长为1.2分米的正方形。
这根木料的体积是多少立方米?
8.一个正方体的高增加2厘米;得到的新长方体的表面积比原正方体的表面积增加了56平方厘米;求原正方体的体积。
9.一个封闭的长方体容器;里面装着水;它的长、宽、高分别是20厘米、20厘米、30厘米;这个长方形容器里的水高15厘米。
这时红红不小心把容器碰倒了;现在的长方体容器里水的高度是多少厘米?
10.一个长方体的表面积是40平方厘米;正好可以把它平均分成两个相同的正方体;每个正
方体的表面积是多少平方厘米?
11.用27块棱长为1厘米的小正方体拼成一个大正方体;大正方体的表面积比原来所有小正体的表面积之和少多少平方厘米?
12.一个长方体的底面积是12平方分米;如果它的高增加5分米;那么它的体积增加多少?
13.把一根长2.4米的长方体木料锯成5段;表面积比原来增加96平方厘米。
求这根木料原来的体积是多少?
14.某综合大楼前有6级台阶;每级台阶长8米、宽0.3米、高0.2米。
(1)6级台阶一共占地多少平方米?
(2)给这些台阶铺上地砖(忽略台阶两侧);至少需要铺多少平方米的地砖?
15.一个长方体玻璃鱼缸(无盖);长50厘米、宽40厘米、高30厘米。
(1)做这个鱼缸至少需要多少平方厘米?
(2)在鱼缸里注入4升水;水深大约是多少厘米?
(3)再往水里放入鹅卵石、水草和鱼;水面上升了2.5厘米;这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
16.在一个练功房里铺设了1600块长50厘米、宽10厘米、厚3厘米的木质地板。
这个练功房的面积是多少平方米?铺设地板至少要用木材多少立方米?
17.把10升水倒入一个长2.5分米、宽2分米、高6分米的长方体水缸中;再将一个正方体铁块全部浸入水中;水面离水缸口还有2.4分米;求出正方体铁块的棱长。
18.在一个长48厘米、宽25厘米、高20厘米的长方体水箱中注入15厘米深的水;把一个棱长为12厘米的正方体铁块沉入水中;则水箱内的水面将上升到几厘米?
19.把一个长124厘米、宽10厘米、高10厘米的长方体锯成最大的正方体;最多可以锯多少个这样的正方体?
20.在一个长8分米、宽7分米、高5分米的长方体木盒内;最多可以放多少棱长为2分米的小正方体木块?
21.下图中的①和②是两块形状不同的铁皮;将每块铁皮弯折后焊接成一个无盖的长方体铁桶(②号焊接成的是一个底面为正方形的无盖长方体);几号铁桶装水更多一些?请用计算说明
100厘米
60厘米
②
80 厘米
120厘米
22.用丝带捆扎一种长、宽、高分别是30厘米、20厘米、25厘米的礼品盒;接头处长25厘米;捆扎这种礼品盒至少需要准备多少分米的丝带?
23.一个密封的长方体容器;长4分米;宽1分米;高2分米;里面的水深16厘米;如果以这个容器的左侧面为底放在桌上?
(1)这是水深多少?
(2)此时;水与容器接触的面积是多少平方厘米?
24.一个长方体水缸;长20厘米;宽15厘米;水深6厘米;将一块石头投入水中(石头完全浸入水)水面上升2厘米;这块石头的体积是多少?
其他
1.把一个正方体的六个面均涂上红色;然后再切成完全相同的27块小正方体。
这些小正方体中;一个面涂上红色的有多少块?两个面涂上红色的有多少块?三个面涂上红色的有多少块?
2.某校开运动会前要给长8米、宽2.5米的沙坑填上15-20厘米厚的沙;找了一个车厢为长 2.2米、宽1.2米、深50厘米的三轮车来拉沙;拉几车比较合适?
3.一块长32厘米的长方形铁皮;四角各剪去边长为4厘米的正方形铁皮;然后做成一个无盖铁盒;这个铁盒的容积是1920立方厘米;那么这块铁皮的面积是多少平方厘米?。
