国密SM2密码算法的C语言实现
基于Java语言的国密SM2SM3SM4算法库,包含加密解密、签名验签、摘要计算的实现代码。。。

基于Java语⾔的国密SM2SM3SM4算法库,包含加密解密、签名验签、摘要计算的实现代码。
SM2_SM3_SM4Encrypt项⽬介绍最近有⼀个项⽬需要⽤到国密算法 , 具体是需要对接硬件加密机调⽤加密机的JAVA接⼝实现国密的⼀整套流程 , 但是由于公司测试环境和阿⾥云硬件加密机不通 , 所以只能⾃⼰模拟加密机的接⼝实现⼀套国密的软加密实现。
将有关国密的代码提取并分享出来 , 并且提供了详细的测试代码以供参考。
项⽬中包括SM2算法的加密/解密/签名/验签 , SM3算法的摘要计算 , SM4算法的对称加密/解密 , 以及相应算法的公私钥对的⽣成⽅法。
项⽬测试脚本使⽤在项⽬中的test包下SecurityTestAll.java类中的main⽅法下有SM2/SM3/SM4的按照加解密流程实现的⼀整套测试脚本 , 直接直接执⾏可以输出如下测试结果:--产⽣SM2秘钥--:公钥:04ec7e40b8dfa4b14383f703ec5403b71db0ab505b9fc41f0df45a9910a307dfbd5b3c5afdd4b90d79fa0ab70d53fd88422df77e09b254a53e72b4857f74ab1da4私钥:58967e2beb6fffd3c96545eebd3000b39c10087d48faa0d41f9c7bf3720e0ea4--测试加密开始--原⽂UTF-8转hex:49204c6f766520596f75加密:密⽂:1b40e51d8462d97ac1cc9929039313152b8067eecfcff7ba0348a721d3f4d257e83f924364b84147879906d62a72472403a3c3d36d4cf243055ff77a4c794909673cc0e39954fbc8b01c50a4b708216d4d19c400719734b98bc0a6d7da92a078b6ef8dd971解密:I Love You--测试加密结束----测试SM2签名--原⽂hex:49204c6f766520596f75签名测试开始:软加密签名结果:3046022100d2665f92221efd00aa96d2729475aa05690bd10766641fd169c6e13c1a441b87022100c8ff9f00c7bb0a8308e183629cebef53e4fd65542c7ee6068275a606e3010088加密机签名结果:d2665f92221efd00aa96d2729475aa05690bd10766641fd169c6e13c1a441b87c8ff9f00c7bb0a8308e183629cebef53e4fd65542c7ee6068275a606e3010088验签1,软件加密⽅式:软件加密⽅式验签结果:true验签2,硬件加密⽅式:签名R:d2665f92221efd00aa96d2729475aa05690bd10766641fd169c6e13c1a441b87签名S:c8ff9f00c7bb0a8308e183629cebef53e4fd65542c7ee6068275a606e3010088硬件加密⽅式验签结果:true--签名测试结束----SM3摘要测试--hash:700B1D31B7BF81A3CE2B5AC97057AE783C9C51F56FA4EA14E13CF3EC6E58159A--SM3摘要结束----⽣成SM4秘钥--sm4Key:c8e8e733ac8c4043a1d6464ae82d70e6--⽣成SM4结束----SM4的CBC加密--密⽂:046be2948f89c9f78e9248fc562a9d0cCBC解密解密结果:I Love You--ECB加密--ECB密⽂:851b68592ac1a029976204ef66f62a5dECB解密ECB解密结果:I Love You下⾯将会说明使⽤此加解密包会遇到的问题以及解决⽅案 , 没有发现的问题后续还会做补充。
面向SOC的SM2加解密算法的实现

面向SOC的SM2加解密算法的实现随着信息技术的高速发展,网络安全成为了一个日益重要的话题,加密算法也成为了保证网络安全的重要手段之一。
在众多的加密算法中,SM2被广泛应用于数字证书、电子邮件、电子签名等领域。
SM2加解密算法是一种基于椭圆曲线密码学的公开密钥算法,它采用了国密标准体系,适用于中国特有的政府、金融、电信、物联网等领域。
实现面向SOC的SM2加解密算法,则需要对SM2算法进行一定程度的优化,并将其应用于SOC芯片等具有特定用途的计算平台上。
为了展示SM2加解密算法的优秀性能和广泛应用,以下列举了三个面向SOC的SM2加解密算法的实现案例。
1. 基于ARM处理器的SM2算法实现该案例使用ARM Cortex-M系列处理器实现了SM2算法的加解密和签名验签功能。
通过对SM2算法中的模幂、模乘等运算进行优化,使其在ARM芯片上运行效率更高。
同时,该实现还采用了硬件加速模块,进一步提升了SM2算法的加解密速度,使其适用于低功耗、高效率的物联网设备。
2. 基于Xilinx FPGA的SM2算法实现该案例使用Xilinx FPGA芯片实现了SM2算法的加解密和签名验签功能。
利用FPGA芯片的可编程性,将SM2算法中的运算模块进行并行化,进一步提高了算法的性能。
同时,该实现还采用了FPGA芯片的硬核模块,将SM2算法中的乘法运算转化为硬件实现,使其运行效率更高。
3. 基于高通骁龙处理器的SM2算法实现该案例使用高通骁龙处理器实现了SM2算法的加解密和签名验签功能。
通过对SM2算法中的运算模块进行SIMD优化,使其能够更好地利用处理器中的多核心,提高算法的运行速度。
同时,该实现还采用了高通骁龙处理器上的硬件安全保护模块,加强了SM2算法在处理器上的安全性。
总之,面向SOC的SM2加解密算法的实现具有高效、安全、广泛应用等特点,可应用于物联网、金融、政府等多个领域,有效保障了信息的安全性。
同时,随着物联网和5G技术的发展,对SM2算法的要求也越来越高,需要在保证安全性的同时,考虑到处理器的低功耗、高效率等需求。
bouncycastle(BC)实现SM2国密加解密、签名、验签

bouncycastle(BC)实现SM2国密加解密、签名、验签SM2国密加解密⼀个类就够了<dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15on</artifactId><version>1.65</version></dependency>版本库经测试适⽤(1.61-1.68) 如有问题请留⾔纠正本⽂参考博主「RisenMyth」:https:///RisenMyth/article/details/107212156若要使⽤⽼版本的写法可以参考 https:///fenglongmiao/article/details/79501757import org.bouncycastle.asn1.gm.GMNamedCurves;import org.bouncycastle.asn1.gm.GMObjectIdentifiers;import org.bouncycastle.asn1.x9.X9ECParameters;import org.bouncycastle.jcajce.provider.asymmetric.ec.BCECPrivateKey;import org.bouncycastle.jcajce.provider.asymmetric.ec.BCECPublicKey;import org.bouncycastle.jcajce.provider.asymmetric.x509.CertificateFactory;import org.bouncycastle.jce.provider.BouncyCastleProvider;import org.bouncycastle.jce.spec.ECParameterSpec;import org.bouncycastle.jce.spec.ECPrivateKeySpec;import org.bouncycastle.jce.spec.ECPublicKeySpec;import org.bouncycastle.math.ec.ECPoint;import org.bouncycastle.util.encoders.Hex;import ponent;import javax.crypto.BadPaddingException;import javax.crypto.Cipher;import javax.crypto.IllegalBlockSizeException;import javax.crypto.NoSuchPaddingException;import java.io.ByteArrayInputStream;import java.math.BigInteger;import java.security.*;import java.security.cert.CertificateException;import java.security.cert.X509Certificate;import java.security.spec.ECGenParameterSpec;import java.security.spec.InvalidKeySpecException;import java.util.Base64;/*** bcprov-jdk15on 版本适⽤(1.61-1.68)* @author dashou* @date 2021-4-13*/@Componentpublic class SM2Util {private BouncyCastleProvider provider;// 获取SM2相关参数private X9ECParameters parameters;// 椭圆曲线参数规格private ECParameterSpec ecParameterSpec;// 获取椭圆曲线KEY⽣成器private KeyFactory keyFactory;private SM2Util(){try {provider = new BouncyCastleProvider();parameters = GMNamedCurves.getByName("sm2p256v1");ecParameterSpec = new ECParameterSpec(parameters.getCurve(),parameters.getG(), parameters.getN(), parameters.getH());keyFactory = KeyFactory.getInstance("EC", provider);} catch (Exception e) {e.printStackTrace();}}/*** SM2算法⽣成密钥对** @return密钥对信息*/public KeyPair generateSm2KeyPair() throws InvalidAlgorithmParameterException, NoSuchAlgorithmException {final ECGenParameterSpec sm2Spec = new ECGenParameterSpec("sm2p256v1");// 获取⼀个椭圆曲线类型的密钥对⽣成器final KeyPairGenerator kpg = KeyPairGenerator.getInstance("EC", provider);SecureRandom random = new SecureRandom();// 使⽤SM2的算法区域初始化密钥⽣成器kpg.initialize(sm2Spec, random);// 获取密钥对KeyPair keyPair = kpg.generateKeyPair();return keyPair;}/*** 加密** @param input 待加密⽂本* @param pubKey 公钥* @return*/public String encode(String input, String pubKey)throws NoSuchPaddingException, NoSuchAlgorithmException,BadPaddingException, IllegalBlockSizeException,InvalidKeySpecException, InvalidKeyException {// 获取SM2相关参数X9ECParameters parameters = GMNamedCurves.getByName("sm2p256v1");// 椭圆曲线参数规格ECParameterSpec ecParameterSpec = new ECParameterSpec(parameters.getCurve(), parameters.getG(), parameters.getN(), parameters.getH());// 将公钥HEX字符串转换为椭圆曲线对应的点ECPoint ecPoint = parameters.getCurve().decodePoint(Hex.decode(pubKey));// 获取椭圆曲线KEY⽣成器KeyFactory keyFactory = KeyFactory.getInstance("EC", provider);BCECPublicKey key = (BCECPublicKey) keyFactory.generatePublic(new ECPublicKeySpec(ecPoint, ecParameterSpec));// 获取SM2加密器Cipher cipher = Cipher.getInstance("SM2", provider);// 初始化为加密模式cipher.init(Cipher.ENCRYPT_MODE, key);// 加密并编码为base64格式return Base64.getEncoder().encodeToString(cipher.doFinal(input.getBytes()));}/*** 解密** @param input 待解密⽂本* @param prvKey 私钥* @return*/public byte[] decoder(String input, String prvKey) throws NoSuchPaddingException, NoSuchAlgorithmException,InvalidKeySpecException, InvalidKeyException, BadPaddingException, IllegalBlockSizeException {// 获取SM2加密器Cipher cipher = Cipher.getInstance("SM2", provider);// 将私钥HEX字符串转换为X值BigInteger bigInteger = new BigInteger(prvKey, 16);BCECPrivateKey privateKey = (BCECPrivateKey) keyFactory.generatePrivate(new ECPrivateKeySpec(bigInteger,ecParameterSpec));// 初始化为解密模式cipher.init(Cipher.DECRYPT_MODE, privateKey);// 解密return cipher.doFinal(Base64.getDecoder().decode(input));}/*** 签名** @param plainText 待签名⽂本* @param prvKey 私钥* @return* @throws NoSuchAlgorithmException* @throws InvalidKeySpecException* @throws InvalidKeyException* @throws SignatureException*/public String sign(String plainText, String prvKey) throws NoSuchAlgorithmException, InvalidKeySpecException,InvalidKeyException, SignatureException {// 创建签名对象Signature signature = Signature.getInstance(GMObjectIdentifiers.sm2sign_with_sm3.toString(), provider);// 将私钥HEX字符串转换为X值BigInteger bigInteger = new BigInteger(prvKey, 16);BCECPrivateKey privateKey = (BCECPrivateKey) keyFactory.generatePrivate(new ECPrivateKeySpec(bigInteger,ecParameterSpec));// 初始化为签名状态signature.initSign(privateKey);// 传⼊签名字节signature.update(plainText.getBytes());// 签名return Base64.getEncoder().encodeToString(signature.sign());}public boolean verify(String plainText, String signatureValue, String pubKey) throws NoSuchAlgorithmException, InvalidKeySpecException, InvalidKeyException, SignatureException {// 创建签名对象Signature signature = Signature.getInstance(GMObjectIdentifiers.sm2sign_with_sm3.toString(), provider);// 将公钥HEX字符串转换为椭圆曲线对应的点ECPoint ecPoint = parameters.getCurve().decodePoint(Hex.decode(pubKey));BCECPublicKey key = (BCECPublicKey) keyFactory.generatePublic(new ECPublicKeySpec(ecPoint, ecParameterSpec));// 初始化为验签状态signature.initVerify(key);signature.update(plainText.getBytes());return signature.verify(Base64.getDecoder().decode(signatureValue));}/*** 证书验签** @param certStr 证书串* @param plaintext 签名原⽂* @param signValueStr 签名产⽣签名值此处的签名值实际上就是 R和S的sequence* @return* @throws NoSuchAlgorithmException* @throws InvalidKeyException* @throws SignatureException*/public boolean certVerify(String certStr, String plaintext, String signValueStr)throws NoSuchAlgorithmException, InvalidKeyException, SignatureException, CertificateException {byte[] signValue = Base64.getDecoder().decode(signValueStr);/** 解析证书*/CertificateFactory factory = new CertificateFactory();X509Certificate certificate = (X509Certificate) factory.engineGenerateCertificate(new ByteArrayInputStream(Base64.getDecoder().decode(certStr)));// 验证签名Signature signature = Signature.getInstance(certificate.getSigAlgName(), provider);signature.initVerify(certificate);signature.update(plaintext.getBytes());return signature.verify(signValue);}public static void main(String[] args) throws InvalidAlgorithmParameterException, NoSuchAlgorithmException {String str = "看看能不能⼀次通过";SM2Util sm2 = new SM2Util();KeyPair keyPair = sm2.generateSm2KeyPair();BCECPrivateKey privateKey = (BCECPrivateKey) keyPair.getPrivate();BCECPublicKey publicKey = (BCECPublicKey) keyPair.getPublic();// 拿到密钥String pubKey = new String(Hex.encode(publicKey.getQ().getEncoded(true)));String prvKey = privateKey.getD().toString(16);System.out.println("Private Key: " + prvKey);System.out.println("Public Key: " + pubKey);// 加解密测试try {System.out.println("加密前:" + str);String encode = sm2.encode(str, pubKey);System.out.println("加密后:" + encode);String decoder = new String(sm2.decoder(encode, prvKey));System.out.println("解密后:" + decoder);} catch (Exception e) {System.out.println("加解密测试错误");}// 签名和验签测试try {System.out.println("签名源数据:" + str);String signStr = sm2.sign(str, prvKey);System.out.println("签名后数据:" + signStr);boolean verify = sm2.verify(str, signStr, pubKey);System.out.println("签名验证结果:" + verify);} catch (Exception e) {System.out.println("签名和验签测试错误");}}}。
国密SM2加密算法的RCCA安全设计

国密SM2加密算法的RCCA安全设计国密SM2加密算法的RCCA安全设计摘要:随着互联网的快速发展,信息安全成为了重要的关注领域。
作为一种新兴的密码算法,国密SM2被广泛应用于加密通信领域。
然而,随着计算机技术的不断发展,攻击者的攻击手段也越来越复杂。
为了提高SM2算法的安全性,本文提出了一种RCCA安全设计策略,旨在进一步保护SM2算法免受不同类型的攻击。
1. 引言SM2算法是我国自主设计的一种椭圆曲线公钥密码算法,具有高效、安全等特点,在我国加密通信中被广泛应用。
然而,随着计算机技术和密码分析的发展,SM2算法的安全性也面临着新的威胁。
2. SM2算法简介SM2算法基于椭圆曲线离散对数问题,主要包括密钥生成、加密和解密三个过程。
其中,密钥生成过程中使用了随机数生成算法;加密过程使用了随机数生成算法和点压缩算法;解密过程使用了椭圆曲线点恢复算法。
3. RCCA安全设计策略为了进一步提高SM2算法的安全性,本文提出了RCCA (Random Oracle ConvIncability against Chosen-Ciphertext Attacks)安全设计策略。
该策略主要包括以下几个方面的设计:3.1 随机数的生成与保密在SM2算法的密钥生成、加密和解密过程中,随机数的生成非常重要。
为了保证随机数的安全性,可以采用硬件随机数生成器和伪随机数生成器相结合的方式。
同时,需要确保生成的随机数在传输和存储过程中的保密性,可以采用加密传输和存储等措施。
3.2 密钥的保护与管理密钥是SM2算法安全性的关键因素,因此密钥的保护与管理非常重要。
可以采用密钥集中存储和密钥分散存储相结合的方式,将密钥分散存储在多个地方,以提高密钥的安全性。
同时,还可以使用密码学方法对密钥进行加密和保护。
3.3 对抗选择密文攻击选择密文攻击是一种常见的密码攻击方法,为了对抗这种攻击方式,可以采用密文检验和验证机制。
密文检验可以通过对密文的合法性和完整性进行验证,以识别篡改的密文。
sm2 C语言实现加密算法详解教程

SM2算法1、公钥密码算法介绍消息鉴别:是一个证实收到的消息来自可信的源点并且未被篡改的过程。
它的目的是信源识别,保证信息完整性。
数字签名:是一种确保数据完整性和非否认的手段,通过给消息附加一段数据来实现。
公钥密码学与其他密码学完全不同, 使用这种方法的加密系统,不仅公开加密算法本身,也公开了加密用的密钥。
公钥密码系统与只使用一个密钥的对称传统密码不同,算法是基于数学函数而不是基于替换和置换。
公钥密码学是非对称的,它使用两个独立的密钥,即密钥分为公钥和私钥,因此称双密钥体制。
双钥体制的公钥可以公开,因此称为公钥算法。
公钥算法的出现,给密码的发展开辟了新的方向。
公钥算法虽然已经历了20多年的发展,但仍具有强劲的发展势头,在鉴别系统和密钥交换等安全技术领域起着关键的作用公钥算法的加密与解密由不同的密钥完成,并且从加密密钥得到解密密钥在计算上是不可行的。
通常,公钥算法的两个密钥中任何一个都可以作为加密而另一个用作解密,但不是所有的公钥算法都是如此。
2. SM2椭圆曲线公钥密码算法SM2算法就是ECC椭圆曲线密码机制,但在签名、密钥交换方面不同于ECDSA、ECDH等国际标准,而是采取了更为安全的机制。
另外,SM2推荐了一条256位的曲线作为标准曲线。
SM2标准包括总则,数字签名算法,密钥交换协议,公钥加密算法四个部分,并在每个部分的附录详细说明了实现的相关细节及示例。
SM2算法主要考虑素域Fp和F2m上的椭圆曲线,分别介绍了这两类域的表示,运算,以及域上的椭圆曲线的点的表示,运算和多倍点计算算法。
然后介绍了编程语言中的数据转换,包括整数和字节串,字节串和比特串,域元素和比特串,域元素和整数,点和字节串之间的数据转换规则。
详细说明了有限域上椭圆曲线的参数生成以及验证,椭圆曲线的参数包括有限域的选取,椭圆曲线方程参数,椭圆曲线群基点的选取等,并给出了选取的标准以便于验证。
最后给椭圆曲线上密钥对的生成以及公钥的验证,用户的密钥对为(s,sP),其中s为用户的私钥,sP为用户的公钥,由于离散对数问题从sP难以得到s,并针对素域和二元扩域给出了密钥对生成细节和验证方式。
国密算法SM2证书制作

国密算法SM2证书制作原⽂:前段时间将系统的RSA算法全部升级为SM2国密算法,密码机和UKey硬件设备⼤都同时⽀持RSA和SM2算法,只是应⽤系统的加解密签名验证需要修改,这个更改底层调⽤的加密动态库来,原来RSA⽤的对称加密算法DES(AES)和摘要MD5(SHA1)也相应改变,分别对应SM1、SM3算法,SM1算法基于硬件实现,SM2、SM3算法已公开。
SM2签名验证算法SM2签名同样也是需要先摘要原⽂数据,即先使⽤SM3密码杂凑算法计算出32byte摘要。
SM3需要摘要签名⽅ID(默认1234567812345678)、曲线参数a,b,Gx,Gy、共钥坐标(x,y)计算出Z值,然后再杂凑原⽂得出摘要数据。
这个地⽅要注意曲线参数和坐标点都是32byte,在转换为BigInteger⼤数计算转成字节流时要去掉空补位,否则可能会出现摘要计算不正确的问题。
SM2签名实现如下:[java]1. public static BigInteger[] Sm2Sign(byte[] md, AsymmetricCipherKeyPair keypair)2. {3. SM3Digest sm3 = new SM3Digest();4.5. ECPublicKeyParameters ecpub = (ECPublicKeyParameters)keypair.Public;6.7. byte[] z = SM2CryptoServiceProvider.Sm2GetZ(Encoding.Default.GetBytes(erId), ecpub.Q);8. sm3.BlockUpdate(z, 0, z.Length);9.10. byte[] p = md;11. sm3.BlockUpdate(p, 0, p.Length);12.13. byte[] hashData = new byte[32];14. sm3.DoFinal(hashData, 0);15.16. // e17. BigInteger e = new BigInteger(1, hashData);18. // k19. BigInteger k = null;20. ECPoint kp = null;21. BigInteger r = null;22. BigInteger s = null;23. BigInteger userD = null;24.25. do26. {27. do28. {29.30. ECPrivateKeyParameters ecpriv = (ECPrivateKeyParameters)keypair.Private;31. k = ecpriv.D;32. kp = ecpub.Q;33.34. userD = ecpriv.D;35.36. // r37. r = e.Add(kp.X.ToBigInteger());38. r = r.Mod(ecc_n);39. }40. while (r.Equals(BigInteger.Zero) || r.Add(k).Equals(ecc_n));41.42. // (1 + dA)~-143. BigInteger da_1 = userD.Add(BigInteger.One);44. da_1 = da_1.ModInverse(ecc_n);45. // s46. s = r.Multiply(userD);47. s = k.Subtract(s).Mod(ecc_n);48. s = da_1.Multiply(s).Mod(ecc_n);49. }50. while (s.Equals(BigInteger.Zero));51.52. byte[] btRS = new byte[64];53. byte[] btR = r.ToByteArray();54. byte[] btS = s.ToByteArray();55. Array.Copy(btR, btR.Length - 32, btRS, 0, 32);56. Array.Copy(btS, btS.Length - 32, btRS, 32, 32);57.58. return new BigInteger[] { r, s };59. }SM2算法是基于ECC算法的,签名同样返回2个⼤数,共64byte。
[转]国密SM2非对称算法与实现
![[转]国密SM2非对称算法与实现](https://img.taocdn.com/s3/m/cb58f179a88271fe910ef12d2af90242a895ab35.png)
[转]国密SM2⾮对称算法与实现国密SM2算法标准包括4个部分,第1部分为总则,主要介绍了ECC基本的算法描述,包括素数域和⼆元扩域两种算法描述,第2部分为数字签名算法,这个算法不同于ECDSA算法,其计算量⼤,也⽐ECDSA复杂些,也许这样会更安全吧,第3部分为密钥交换协议,与ECDH功能相同,但复杂性⾼,计算量加⼤,第4部分为公钥加密算法,使⽤ECC公钥进⾏加密和ECC私钥进⾏加密算法,其实现上是在ECDH上分散出流密钥,之后与明⽂或者是密⽂进⾏异或运算,并没有采⽤第3部分的密钥交换协议产⽣的密钥。
对于SM2算法的总体感觉,应该是国家发明,其计算上⽐国际上公布的ECC算法复杂,相对来说算法速度可能慢,但可能是更安全⼀点。
SM2标准还公布了⼀条建议的256位的ECC曲线,但没有在国际上被公认。
SM2算法是好,但要使⽤,⼜有很多障碍,就是统⼀的国际标识与互认,如算法没有OID标识,曲线也没有公认OID标识,这在通⽤上就⼤打折扣了,这⼀点需要考虑的。
⽹上可以查到⼀些SM2算法的实现代码,有C#的、有Java的,还有C的,但想找到⼀个完整的C语⾔代码还是很难,⼈家做了不公开,算法标准都公开的,代码不开源啊,但⽐较有意义的是这些代码都是使⽤Openssl或bouncycastle这些开源的算法库实现的。
但⾄少给你个信息,使⽤开源密码算法可以实现SM2算法。
要实现SM2算法,⾸先要实现ECC曲线基本描述,这个要独⽴去写还是需要很多计算算法能⼒的,不是搞数学的,还是有许多难度的。
Openssl的ECC算法是SUN公司奉献的,⼤家就是⼤家,写的就是好。
Bouncycastle也是⼀个⽐较好的算法,有Java版和C#版,⽹上可以得到C#的SM2算法,但是使⽤C语⾔的代码能够下载的SM2都有⼀点骗⼈感情啊,只给了代码测试运⾏包,没有公开源码。
笔者按着这些信息,细细分析了Openssl的ECC、ECDSA、ECDH算法,可以作为基础⽤来实现SM2是豪⽆问题的,待代码进⼀步完善后可以与⼤家分享。
SM2加解密代码示例

SM2加解密代码⽰例pom.xml<!--国密--><dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15on</artifactId><version>1.56</version></dependency>1、Cipherimport org.bouncycastle.crypto.AsymmetricCipherKeyPair;import org.bouncycastle.crypto.digests.SM3Digest;import org.bouncycastle.crypto.params.ECPrivateKeyParameters;import org.bouncycastle.crypto.params.ECPublicKeyParameters;import org.bouncycastle.math.ec.ECPoint;import java.math.BigInteger;public class Cipher {private int ct;private ECPoint p2;private SM3Digest sm3keybase;private SM3Digest sm3c3;private byte key[];private byte keyOff;public Cipher(){this.ct = 1;this.key = new byte[32];this.keyOff = 0;}private void Reset(){this.sm3keybase = new SM3Digest();this.sm3c3 = new SM3Digest();byte p[] = Util.byteConvert32Bytes(p2.getX().toBigInteger());this.sm3keybase.update(p, 0, p.length);this.sm3c3.update(p, 0, p.length);p = Util.byteConvert32Bytes(p2.getY().toBigInteger());this.sm3keybase.update(p, 0, p.length);this.ct = 1;NextKey();}private void NextKey(){SM3Digest sm3keycur = new SM3Digest(this.sm3keybase);sm3keycur.update((byte) (ct >> 24 & 0xff));sm3keycur.update((byte) (ct >> 16 & 0xff));sm3keycur.update((byte) (ct >> 8 & 0xff));sm3keycur.update((byte) (ct & 0xff));sm3keycur.doFinal(key, 0);this.keyOff = 0;this.ct++;}public ECPoint Init_enc(SM2 sm2, ECPoint userKey){AsymmetricCipherKeyPair key = sm2.ecc_key_pair_generator.generateKeyPair();ECPrivateKeyParameters ecpriv = (ECPrivateKeyParameters) key.getPrivate();ECPublicKeyParameters ecpub = (ECPublicKeyParameters) key.getPublic();BigInteger k = ecpriv.getD();ECPoint c1 = ecpub.getQ();this.p2 = userKey.multiply(k);Reset();return c1;}public void Encrypt(byte data[]){this.sm3c3.update(data, 0, data.length);for (int i = 0; i < data.length; i++)if (keyOff == key.length){NextKey();}data[i] ^= key[keyOff++];}}public void Init_dec(BigInteger userD, ECPoint c1){this.p2 = c1.multiply(userD);Reset();}public void Decrypt(byte data[]){for (int i = 0; i < data.length; i++){if (keyOff == key.length){NextKey();}data[i] ^= key[keyOff++];}this.sm3c3.update(data, 0, data.length);}public void Dofinal(byte c3[]){byte p[] = Util.byteConvert32Bytes(p2.getY().toBigInteger());this.sm3c3.update(p, 0, p.length);this.sm3c3.doFinal(c3, 0);Reset();}}2、SM2import org.bouncycastle.crypto.generators.ECKeyPairGenerator;import org.bouncycastle.crypto.params.ECDomainParameters;import org.bouncycastle.crypto.params.ECKeyGenerationParameters;import org.bouncycastle.math.ec.ECCurve;import org.bouncycastle.math.ec.ECFieldElement;import org.bouncycastle.math.ec.ECFieldElement.Fp;import org.bouncycastle.math.ec.ECPoint;import java.math.BigInteger;import java.security.SecureRandom;public class SM2 {//国密参数public static String[] ecc_param = {"FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF", "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC", "28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93", "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123", "32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7","BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0"};public static SM2 Instance() {return new SM2();}/** 素数p */public final BigInteger ecc_p;/** 系数a */public final BigInteger ecc_a;/** 系数b */public final BigInteger ecc_b;/** 基点G, G=(xg,yg),其介记为n */public final BigInteger ecc_n;/** 坐标x */public final BigInteger ecc_gx;/** 坐标y */public final BigInteger ecc_gy;public final ECCurve ecc_curve;public final ECPoint ecc_point_g;public final ECDomainParameters ecc_bc_spec;public final ECKeyPairGenerator ecc_key_pair_generator;public final ECFieldElement ecc_gx_fieldelement;public final ECFieldElement ecc_gy_fieldelement;this.ecc_a = new BigInteger(ecc_param[1], 16);this.ecc_b = new BigInteger(ecc_param[2], 16);this.ecc_n = new BigInteger(ecc_param[3], 16);this.ecc_gx = new BigInteger(ecc_param[4], 16);this.ecc_gy = new BigInteger(ecc_param[5], 16);this.ecc_gx_fieldelement = new Fp(this.ecc_p, this.ecc_gx);this.ecc_gy_fieldelement = new Fp(this.ecc_p, this.ecc_gy);this.ecc_curve = new ECCurve.Fp(this.ecc_p, this.ecc_a, this.ecc_b);this.ecc_point_g = new ECPoint.Fp(this.ecc_curve, this.ecc_gx_fieldelement, this.ecc_gy_fieldelement);this.ecc_bc_spec = new ECDomainParameters(this.ecc_curve, this.ecc_point_g, this.ecc_n);ECKeyGenerationParameters ecc_ecgenparam;ecc_ecgenparam = new ECKeyGenerationParameters(this.ecc_bc_spec, new SecureRandom());this.ecc_key_pair_generator = new ECKeyPairGenerator();this.ecc_key_pair_generator.init(ecc_ecgenparam);}}3、SM2EncDecUtilsimport org.bouncycastle.crypto.AsymmetricCipherKeyPair;import org.bouncycastle.crypto.params.ECPrivateKeyParameters;import org.bouncycastle.crypto.params.ECPublicKeyParameters;import org.bouncycastle.math.ec.ECPoint;import java.io.IOException;import java.math.BigInteger;import java.util.HashMap;import java.util.Map;public class SM2EncDecUtils {public static final String public_key = "public_key";public static final String private_key = "private_key";public static void main(String[] args) throws Exception {singleThreadTest();//mutiThreadTest();}// ⽣成随机秘钥对public static Map<String, String> generateKeyPair() {SM2 sm2 = SM2.Instance();AsymmetricCipherKeyPair key = null;while (true) {key = sm2.ecc_key_pair_generator.generateKeyPair();if (((ECPrivateKeyParameters) key.getPrivate()).getD().toByteArray().length == 32) {break;}}ECPrivateKeyParameters ecpriv = (ECPrivateKeyParameters) key.getPrivate();ECPublicKeyParameters ecpub = (ECPublicKeyParameters) key.getPublic();BigInteger privateKey = ecpriv.getD();ECPoint publicKey = ecpub.getQ();String pubk = Util.byteToHex(publicKey.getEncoded());String prik = Util.byteToHex(privateKey.toByteArray());System.out.println("公钥: " + pubk);System.out.println("公钥长度: " + pubk.length());System.out.println("私钥: " + prik);System.out.println("私钥长度: " + prik.length());Map<String, String> result = new HashMap<>();result.put(public_key, pubk);result.put(private_key, prik);return result;}// 数据加密public static String encrypt(byte[] publicKey, byte[] data) throws IOException {if (publicKey == null || publicKey.length == 0) {return null;}if (data == null || data.length == 0) {return null;}System.arraycopy(data, 0, source, 0, data.length);Cipher cipher = new Cipher();SM2 sm2 = SM2.Instance();ECPoint userKey = sm2.ecc_curve.decodePoint(publicKey);ECPoint c1 = cipher.Init_enc(sm2, userKey);cipher.Encrypt(source);byte[] c3 = new byte[32];cipher.Dofinal(c3);return new StringBuffer(Util.byteToHex(c1.getEncoded())).append(Util.byteToHex(c3)).append(Util.byteToHex(source)).toString();}// 数据解密public static byte[] decrypt(byte[] privateKey, byte[] encryptedData) throws IOException {if (privateKey == null || privateKey.length == 0) {return null;}if (encryptedData == null || encryptedData.length == 0) {return null;}// 加密字节数组转换为⼗六进制的字符串长度变为encryptedData.length * 2String data = Util.byteToHex(encryptedData);byte[] c1Bytes = Util.hexToByte(data.substring(0, 130));int c2Len = encryptedData.length - 97;byte[] c3 = Util.hexToByte(data.substring(130, 130 + 64));byte[] c2 = Util.hexToByte(data.substring(194, 194 + 2 * c2Len));SM2 sm2 = SM2.Instance();BigInteger userD = new BigInteger(1, privateKey);// 通过C1实体字节来⽣成ECPointECPoint c1 = sm2.ecc_curve.decodePoint(c1Bytes);Cipher cipher = new Cipher();cipher.Init_dec(userD, c1);cipher.Decrypt(c2);cipher.Dofinal(c3);// 返回解密结果return c2;}/*** 单线程* @throws Exception*/private static void singleThreadTest() throws Exception {String plainText = "张三123zhangsan";//获取⽂本内容的字节数byte[] sourceData = plainText.getBytes();// ⽣成随机秘钥对Map<String, String> keymap = generateKeyPair();//获取当前系统时间long start = System.currentTimeMillis();int counts = 100000;for (int j = 0; j < counts; j++) {//数据加密+⼗六进制串转化为byte数组//本本转字节--⽣成随机密钥对--得到公钥---⼗六进制串转化为byte数组--数据加密String cipherText = SM2EncDecUtils.encrypt(Util.hexToByte(keymap.get(public_key)), sourceData);System.out.println("加密前长度: " + plainText.length() + " ;加密后长度: " + cipherText.length());System.out.println("加密前原⽂本内容:" + plainText );System.out.println("加密后⽂本内容:" + cipherText);String plainTextEncripted = new String(SM2EncDecUtils.decrypt(Util.hexToByte(keymap.get(private_key)), Util.hexToByte(cipherText))); System.out.println("解密后⽂本内容: " + plainTextEncripted);if (plainText.equals(plainTextEncripted)) {System.out.println("------解密后同原⽂是否⼀致: " + plainText.equals(plainTextEncripted) + "----------------------");}}long end = System.currentTimeMillis();System.out.println("平均耗时:" + (end - start) / counts + "ms。
谈谈PBOC3.0中使用的国密SM2算法.
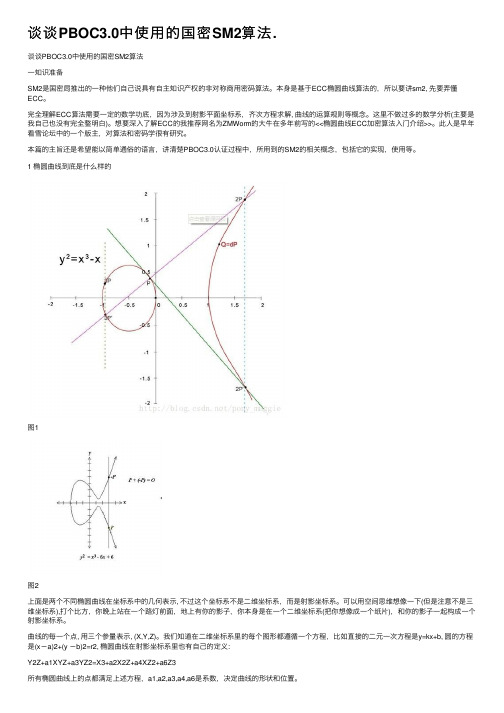
谈谈PBOC3.0中使⽤的国密SM2算法.谈谈PBOC3.0中使⽤的国密SM2算法⼀知识准备SM2是国密局推出的⼀种他们⾃⼰说具有⾃主知识产权的⾮对称商⽤密码算法。
本⾝是基于ECC椭圆曲线算法的,所以要讲sm2, 先要弄懂ECC。
完全理解ECC算法需要⼀定的数学功底,因为涉及到射影平⾯坐标系,齐次⽅程求解, 曲线的运算规则等概念。
这⾥不做过多的数学分析(主要是我⾃⼰也没有完全整明⽩)。
想要深⼊了解ECC的我推荐⽹名为ZMWorm的⼤⽜在多年前写的<<椭圆曲线ECC加密算法⼊门介绍>>。
此⼈是早年看雪论坛中的⼀个版主,对算法和密码学很有研究。
本篇的主旨还是希望能以简单通俗的语⾔,讲清楚PBOC3.0认证过程中,所⽤到的SM2的相关概念,包括它的实现,使⽤等。
1 椭圆曲线到底是什么样的图1图2上⾯是两个不同椭圆曲线在坐标系中的⼏何表⽰, 不过这个坐标系不是⼆维坐标系,⽽是射影坐标系。
可以⽤空间思维想像⼀下(但是注意不是三维坐标系),打个⽐⽅,你晚上站在⼀个路灯前⾯,地上有你的影⼦,你本⾝是在⼀个⼆维坐标系(把你想像成⼀个纸⽚),和你的影⼦⼀起构成⼀个射影坐标系。
曲线的每⼀个点, ⽤三个参量表⽰, (X,Y,Z)。
我们知道在⼆维坐标系⾥的每个图形都遵循⼀个⽅程,⽐如直接的⼆元⼀次⽅程是y=kx+b, 圆的⽅程是(x-a)2+(y -b)2=r2, 椭圆曲线在射影坐标系⾥也有⾃⼰的定义:Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3所有椭圆曲线上的点都满⾜上述⽅程,a1,a2,a3,a4,a6是系数,决定曲线的形状和位置。
⼆维坐标和射影坐标有⼀个对应关系,即x=X/Z, y=Y/Z, 这样就可以把上⾯的⽅程转成普通的⼆维坐标系⽅程:y2+a1xy+a3y= x3+a2x2+a4x+a62 离散的椭圆曲线上⾯的坐标系都是基于实数的,椭圆曲线看起来都是平滑的,如果我们限制曲线的点都必须是整数,曲线就变成离散的了,如图3所⽰:图3再进⼀步限制,要求整数必须⼤于0, ⼩于某个⼤整数P, 这样就形成了⼀个有限域F p.然后我们在这个有限域⾥定义⼀些点与点之间的加减乘除运算规则,⽐如A点加B点得到C点(记做A+B≡C (mod p)),或者A点乘以n得到K点(记做A×n≡K (mod p))。
C#SM2算法加密,解密,签名,验签

C#SM2算法加密,解密,签名,验签最近时间在整SM2算法,在⽹上看到不少代码,基本都是使⽤BouncyCastle库,现在这个版本算⽐较好的拿来分享给⼤家。
⾸先引⼊包 Portable.BouncyCastlepublic class SM2CryptoUtil{public SM2CryptoUtil(byte[] pubkey, byte[] privkey, Mode mode){this.pubkey = pubkey;this.privkey = privkey;this.mode = mode;}public SM2CryptoUtil(string pubkey, string privkey, Mode mode = Mode.C1C2C3, bool isPkcs8 = false){if (!isPkcs8){if (pubkey != null) this.pubkey = Decode(pubkey);if (privkey != null) this.privkey = Decode(privkey);}else{if (pubkey != null) this.pubkey = ((ECPublicKeyParameters)PublicKeyFactory.CreateKey(Convert.FromBase64String(pubkey))).Q.GetEncoded();if (privkey != null) this.privkey = ((ECPrivateKeyParameters)PrivateKeyFactory.CreateKey(Convert.FromBase64String(privkey))).D.ToByteArray();}this.mode = mode;}byte[] pubkey;byte[] privkey;Mode mode;ICipherParameters _privateKeyParameters;ICipherParameters PrivateKeyParameters{get{var r = _privateKeyParameters;if (r == null) r = _privateKeyParameters = new ECPrivateKeyParameters(new BigInteger(1, privkey), new ECDomainParameters(GMNamedCurves.GetByName("SM2P256V1")));return r;}}ICipherParameters _publicKeyParameters;ICipherParameters PublicKeyParameters{get{var r = _publicKeyParameters;if (r == null){var x9ec = GMNamedCurves.GetByName("SM2P256V1");r = _publicKeyParameters = new ECPublicKeyParameters(x9ec.Curve.DecodePoint(pubkey), new ECDomainParameters(x9ec));}return r;}}public static void GenerateKeyHex(out string pubkey, out string privkey){GenerateKey(out var a, out var b);pubkey = Hex.ToHexString(a);privkey = Hex.ToHexString(b);}public static void GenerateKey(out byte[] pubkey, out byte[] privkey){var g = new ECKeyPairGenerator();g.Init(new ECKeyGenerationParameters(new ECDomainParameters(GMNamedCurves.GetByName("SM2P256V1")), new SecureRandom()));var k = g.GenerateKeyPair();pubkey = ((ECPublicKeyParameters)k.Public).Q.GetEncoded(false);privkey = ((ECPrivateKeyParameters)k.Private).D.ToByteArray();}public byte[] Decrypt(byte[] data){if (mode == Mode.C1C3C2) data = C132ToC123(data);var sm2 = new SM2Engine(new SM3Digest());sm2.Init(false, this.PrivateKeyParameters);return sm2.ProcessBlock(data, 0, data.Length);}public byte[] Encrypt(byte[] data){var sm2 = new SM2Engine(new SM3Digest());sm2.Init(true, new ParametersWithRandom(PublicKeyParameters));data = sm2.ProcessBlock(data, 0, data.Length);if (mode == Mode.C1C3C2) data = C123ToC132(data);return data;}public byte[] Sign(byte[] msg, byte[] id = null){var sm2 = new SM2Signer(new SM3Digest());ICipherParameters cp;if (id != null) cp = new ParametersWithID(new ParametersWithRandom(PrivateKeyParameters), id);else cp = new ParametersWithRandom(PrivateKeyParameters);sm2.Init(true, cp);sm2.BlockUpdate(msg, 0, msg.Length);return sm2.GenerateSignature();}public bool VerifySign(byte[] msg, byte[] signature, byte[] id = null){var sm2 = new SM2Signer(new SM3Digest());ICipherParameters cp;if (id != null) cp = new ParametersWithID(PublicKeyParameters, id);else cp = PublicKeyParameters;sm2.Init(false, cp);sm2.BlockUpdate(msg, 0, msg.Length);return sm2.VerifySignature(signature);}static byte[] C123ToC132(byte[] c1c2c3){var gn = GMNamedCurves.GetByName("SM2P256V1");int c1Len = (gn.Curve.FieldSize + 7) / 8 * 2 + 1;int c3Len = 32;byte[] result = new byte[c1c2c3.Length];Array.Copy(c1c2c3, 0, result, 0, c1Len); //c1Array.Copy(c1c2c3, c1c2c3.Length - c3Len, result, c1Len, c3Len); //c3Array.Copy(c1c2c3, c1Len, result, c1Len + c3Len, c1c2c3.Length - c1Len - c3Len); //c2return result;}static byte[] C132ToC123(byte[] c1c3c2){var gn = GMNamedCurves.GetByName("SM2P256V1");int c1Len = (gn.Curve.FieldSize + 7) / 8 * 2 + 1;int c3Len = 32;byte[] result = new byte[c1c3c2.Length];Array.Copy(c1c3c2, 0, result, 0, c1Len); //c1: 0->65Array.Copy(c1c3c2, c1Len + c3Len, result, c1Len, c1c3c2.Length - c1Len - c3Len); //c2Array.Copy(c1c3c2, c1Len, result, c1c3c2.Length - c3Len, c3Len); //c3return result;}static byte[] Decode(string key){return Regex.IsMatch(key, "^[0-9a-f]+$", RegexOptions.IgnoreCase) ? Hex.Decode(key) : Convert.FromBase64String(key);}public enum Mode{C1C2C3, C1C3C2}}踩坑记录:1. ⽹上有不少教程也是使⽤ Portable.BouncyCastle库类,但SM2算法写了很多代码(我也没看懂,估计是⾃⼰计算椭圆曲线),但加密起来通过在线⼯具有时可以解密有时⼜不⾏。
国密算法java语言的实现

国密算法java语言的实现国密算法是我国自主研发的密码算法标准,被广泛应用于信息安全领域。
在本文中,将介绍国密算法在Java语言中的实现。
一、国密算法简介国密算法是指中国密码技术及标准化研究中心(简称“国密中心”)发布的一系列密码算法,包括SM1、SM2、SM3和SM4。
其中,SM1是对称加密算法,SM2是非对称加密算法,SM3是哈希算法,SM4是对称加密算法。
二、国密算法的Java实现1. SM1算法的Java实现SM1算法是一种对称加密算法,它使用了Feistel结构和S盒代换。
在Java中,可以通过使用Bouncy Castle库来实现SM1算法。
以下是使用Bouncy Castle库实现SM1算法的代码示例:```javaimport org.bouncycastle.crypto.CipherParameters;import org.bouncycastle.crypto.engines.SM1Engine;import org.bouncycastle.crypto.params.KeyParameter;public class SM1Example {public static void main(String[] args) {byte[] key = new byte[]{/* 密钥 */};byte[] plaintext = new byte[]{/* 明文 */};SM1Engine engine = new SM1Engine();CipherParameters params = new KeyParameter(key);engine.init(true, params);byte[] ciphertext = new byte[plaintext.length];engine.processBlock(plaintext, 0, ciphertext, 0);System.out.println("密文:" + new String(ciphertext));}}```2. SM2算法的Java实现SM2算法是一种非对称加密算法,它基于椭圆曲线密码体制。
SM2算法

有限域上的椭圆曲线 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
4 数据类型及其转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 数据类型 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 数据类型转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 4.2.1 4.2.2 4.2.3 4.2.4 4.2.5 4.2.6 4.2.7 4.2.8 4.2.9 5.1 5.2 整数到字节串的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 字节串到整数的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 比特串到字节串的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 字节串到比特串的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 域元素到字节串的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 字节串到域元素的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 域元素到整数的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 点到字节串的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 字节串到点的转换 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
python实现sm2和sm4国密(国家商用密码)算法的示例

python实现sm2和sm4国密(国家商⽤密码)算法的⽰例GMSSL模块介绍GmSSL是⼀个开源的加密包的python实现,⽀持SM2/SM3/SM4等国密(国家商⽤密码)算法、项⽬采⽤对商业应⽤友好的类BSD开源许可证,开源且可以⽤于闭源的商业应⽤。
安装模块pip install gmsslSM2算法RSA算法的危机在于其存在亚指数算法,对ECC算法⽽⾔⼀般没有亚指数攻击算法 SM2椭圆曲线公钥密码算法:我国⾃主知识产权的商⽤密码算法,是ECC(Elliptic Curve Cryptosystem)算法的⼀种,基于椭圆曲线离散对数问题,计算复杂度是指数级,求解难度较⼤,同等安全程度要求下,椭圆曲线密码较其他公钥算法所需密钥长度⼩很多。
gmssl是包含国密SM2算法的Python实现,提供了 encrypt、decrypt等函数⽤于加密解密,⽤法如下:1. 初始化CryptSM2import base64import binasciifrom gmssl import sm2, func#16进制的公钥和私钥private_key = '00B9AB0B828FF68872F21A837FC303668428DEA11DCD1B24429D0C99E24EED83D5'public_key = 'B9C9A6E04E9C91F7BA880429273747D7EF5DDEB0BB2FF6317EB00BEF331A83081A6994B8993F3F5D6EADDDB81872266C87C018FB4162F5AF347B483E24620207' sm2_crypt = sm2.CryptSM2(public_key=public_key, private_key=private_key)2. encrypt和decrypt#数据和加密后数据为bytes类型data = b"111"enc_data = sm2_crypt.encrypt(data)dec_data =sm2_crypt.decrypt(enc_data)assert dec_data == data3. sign和verifydata = b"111" # bytes类型random_hex_str = func.random_hex(sm2_crypt.para_len)sign = sm2_crypt.sign(data, random_hex_str) # 16进制assert sm2_crypt.verify(sign, data) # 16进制SM4算法国密SM4(⽆线局域⽹SMS4)算法,⼀个分组算法,分组长度为128bit,密钥长度为128bit,算法具体内容参照SM4算法。
基于Gmssl的SM2加解密算法Demo

基于Gmssl的SM2加解密算法Demo存储⼩咖 2018-12-28 18:38:11 4739 收藏 5展开GmSSL介绍Gmssl介绍:/当然本⽂也是参考 /其中SM2为⾮对称算法SM2密钥⽣成pair<string, string> GenKey(void){EC_KEY *keypair = NULL;EC_GROUP *group1 = NULL;keypair = EC_KEY_new();if(!keypair) {cout << "Failed to Gen Key" << endl;exit(1);}group1 = EC_GROUP_new_by_curve_name(NID_sm2p256v1);if(group1 == NULL){cout << "Failed to Gen Key" << endl;exit(1);}int ret1 = EC_KEY_set_group(keypair, group1);if(ret1 != 1){cout << "Failed to Gen Key" << endl;exit(1);}int ret2 = EC_KEY_generate_key(keypair);if(ret2 != 1){cout << "Failed to Gen Key" << endl;exit(1);}size_t pri_len;size_t pub_len;char *pri_key = NULL;char *pub_key = NULL;BIO *pri = BIO_new(BIO_s_mem());BIO *pub = BIO_new(BIO_s_mem());PEM_write_bio_ECPrivateKey(pri, keypair, NULL, NULL, 0, NULL, NULL);PEM_write_bio_EC_PUBKEY(pub, keypair);pri_len = BIO_pending(pri);pub_len = BIO_pending(pub);pri_key = new char[pri_len + 1];pub_key = new char[pub_len + 1];BIO_read(pri, pri_key, pri_len);BIO_read(pub, pub_key, pub_len);pri_key[pri_len] = '\0';pub_key[pub_len] = '\0';string public_key = pub_key;string private_key = pri_key;EC_KEY_free(keypair);BIO_free_all(pub);BIO_free_all(pri);delete [] pri_key;delete [] pub_key;return std::pair<string, string>(public_key, private_key); }1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465已字符串形式的返回,主要考虑我们在实际运⽤中,可能需要传递密钥信息,所以⽣成的SM2公钥和私钥以字符串形式返回。
C#国密加密SM2-SM4(.net)

C#国密加密SM2-SM4(.net)新建⼀个控制台来做demonuget引⽤程序集:KYSharp.SM安装 2.0 版本,⾥⾯才有sm3和sm4的加密⼀、SM2的⽤法static void SM2Console(){//公钥string publickey = "";//私钥string privatekey = "";//⽣成公钥和私钥SM2Utils.GenerateKeyPair(out publickey, out privatekey);System.Console.Out.WriteLine("加密明⽂: " + "000000");System.Console.Out.WriteLine("publickey:" + publickey);//开始加密string cipherText = SM2Utils.Encrypt(publickey, "000000");System.Console.Out.WriteLine("密⽂: " + cipherText);System.Console.Out.WriteLine("privatekey:" + privatekey);//解密string plainText = SM2Utils.Decrypt(privatekey, cipherText);System.Console.Out.WriteLine("明⽂: " + plainText);Console.ReadLine();}static void Main(string[] args){SM2Console();Console.ReadLine();}效果如下:该种加密⽅式得到的密⽂是长度不固定的密⽂串,可能⼏百位。
国密算法python

国密算法python
国密算法是中国国家密码管理局发布的一系列密码算法标准,其中包括SM1、SM2、SM3、SM4等算法。
这些算法用于保护国家机密、个人隐私等信息。
Python中可以使用gmssl库来实现国密算法。
以下是一个使用Python和gmssl库实现SM3摘要算法的示例代码:
```python
from gmssl.sm3 import sm3_hash
# 输入数据
data = b"hello world"
# 计算SM3摘要值
hash_value = sm3_hash(data)
# 输出摘要值
print(hash_value)
```
在上面的代码中,我们首先导入了gmssl库中的sm3_hash函数,然后定义了一个输入数据,并使用sm3_hash函数计算了该数据的SM3摘要值。
最后,我们将摘要值打印出来。
除了SM3摘要算法外,gmssl库还提供了SM2、SM4等其他国密算法的实现。
您可以根据需要选择适合的算法。
基于国密SM4和SM2的混合密码算法研究与实现

基于国密SM4和SM2的混合密码算法研究与实现现代密码技术在保障信息安全方面起着至关重要的作用。
然而,SM4算法虽然运算速度快,但存在密钥管理复杂并且安全性低的缺点;而SM2算法虽然安全性高、密钥管理简单,但存在对大块数据加解密速度慢和效率较低的缺点。
为了克服这些问题,本文提出了一种基于SM4和SM2算法的混合加密算法。
具体来说,大量的主体明文数据采用加密速度极快的SM4算法,然后利用SM2算法加密SM4算法的密钥,并将其与密文一起传输,从而避免了SM4复杂的密钥管理,提高了数据安全性。
经过理论分析和在同方THD86芯片上的实验验证,该算法方便可行,加密、解密速度快且安全性高,在电子商务和电子政务中的应用具有良好的效果。
随着计算机网络和通信技术的高速发展,电子商务和电子政务的需求和应用日益增加。
大量的敏感信息常常通过公共通信设施或计算机网络进行交换,密码技术是确保信息安全的主导力量,密码算法的研究与应用是信息安全技术的核心研究领域。
目前,密码算法主要分为两类:一类为对称密钥算法,另一类为非对称密钥算法。
对称密钥算法又叫传统密码算法,就是加密密钥能够从解密密钥中推算出来,反过来也成立。
在大多数对称算法中,加密和解密密钥是相同的。
对称密钥算法的优点是:算法实现的效率高、速度快和便于实现,尤其是对大块数据的加密。
然而,密钥管理复杂和安全性难以实现。
首先,在对称密钥密码系统中,每两个相互通信的人就需要一对密钥,这就导致了当用户增加时密钥量的成倍增长。
其次,加解密的安全性完全依赖于对密钥的保护,由于通信双方使用的是相同密钥,为了保证安全必须使用另外的安全信道来分发密钥,但这种做法往往难以实现。
非对称密钥算法突破性地解决了对称密钥算法无法解决的密钥分发和管理问题。
在非对称密钥算法中,加密和解密使用不同的密钥,加密密钥公开,谁都可以使用,解密密钥只有解密方自己知道,非法者根据公开的加密密钥无法推算出解密密钥。
基于SM2-SM3的IEC61850通信报文加密算法

技术&应用基于 S M2-S M3 的IEC61850通信报文加密算法IEC 61850 Com m unication Message Encryption Algorithm Based on SM2-SM3★谢敏敏,王勇,周林上海电力大学摘耍:本文针对IE C61850协议报文存在的安全问题,利用仿真软件模拟了IE C 61850通信过程,对其网络环境进行了重放攻击,验证了该协议的安全缺陷,为了增强报文的安全性,利用WINPCAP开发工具捕获IE C 61850数据报文,提出了一种基于SM2-SM3国密体系算法,对其报文进行了数字签名并验证,实验结果表明报文安全性得到了改善。
关键间:IEC61850;重放攻击;SM2-SM3;报文安全Abstract:Aiming at the security problem of IEC 61850 protocol message, the com m unication process of IEC 61850 is sim ulated by using simulation software, and the replay attack on its network environment is carried out to verify the security defects of the protocol. In order to enhance the security of the message, WINPCAP development tool is used to capture the IEC 61850 data packets, this paper proposes an algorithm based on SM2-SM3 national security system, carries on the digital signature to its message and verifies. The experimental results show that message security has improved.Key words:IEC 61850; Replay attack; SM2-SM3; Message security1研究背景IEC 61850是电力系统的一项国际标准,该标准 能够解决不同厂商设备之间的通信问题,却没有为变电站网络系统提供相关的安全规范。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
国密SM2密码算法的C语言实现
作者:邢维哲
来源:《中国新通信》2017年第18期
【摘要】 N.Koblitz和ler在1985年各自独立地提出将椭圆曲线应用于公钥密码系统。
SM2椭圆曲线密码算法是国家密码管理局批准的一组算法,在电力自动化通讯中得到了广泛应用。
本文介绍了SM2椭圆曲线公钥密码算法和加密解密算法中一部分过程的C语言实现。
【关键词】椭圆曲线 SM2 密码算法公钥加密解密
Implementation of Public Key Cryptographic Algorithm SM2 based on C language XINGWEIZHE (1. XINGWEIZHE COLLEGE OF ENGINEERING, PEKING UNIVERSITY,BEIJING,100871)
Abstract: Applying elliptic curves on public key cryptosystem was put forward independently by Koblitz and ler in 1985. Public Key Cryptographic Algorithm SM2 is Public Key Cryptographic Algorithm SM2, as the Chinese national cryptographic standard, is widely used in communications of automation system. This paper introduces elliptic curve cryptosystem and gives an implementation based on C language.
Key word: elliptic curve cryptosystem; Public Key Cryptographic Algorithm SM2; elliptic curve。
