初中奥数分式方程应用题

合集下载

关于分式方程奥数题

4 1
x

0
为整式方程时，方程两边必须同乘（
）
（A） (5x2 5)(x2 1)(1 x)
（B） 5(x2 1)(1 x)
（C） 5(x2 1)(x 1)
（D）5(x 1)(x 1)
10．下列说法中错误的是（）
（A）分式方程的解等于 0，就说明这个分式方程无解
（B）解分式方程的基本思路是把分式方程转化为整式方程
分式方程练习题
一；填空题
1．当 x ______时， 1 x 的值等于 1 ．
5 x
2
2．当 x ______时， 4 2x 的值与 x 5 的值相等．
4x
x4
3．若 1 与 1 互为相反数，则可得方程___________,解得 x _________. x 1 x 1
x
23 5
32
32
8．解分式方程 1 2x 1 3 ，去分母后所得的方程是（） 3x x
（A）1 3(2x 1) 3
（B）1 3(2x 1) 3x
（C）1 3(2x 1) 9x
（D）1 6x 3 9x
9.．化分式方程
1 5x2
5

3 x2 1
(C)解这个整式方程，得 x 1 (D) 原方程的解为 x 1
12．下列结论中，不正确的是（）
1
PS:双击获取文档，ctrl+A,ctrl+C，然后粘贴到word即可。未能直接提供word版本，抱歉。
（C）检验是解分式方程必不可少的步骤
（D）能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解．
11.解分式方程
2 x 1

(完整版)分式方程应用题及答案

分式方程应用题及答案1甲、乙两个清洁队共同参与了城中垃圾场的清运工作．甲队单独工作2天完成总量的三分之一，这时增加了乙队，两队又共同工作了1天，总量全部完成．那么乙队单独完成总量需要（）Ａ．6天Ｂ．4天Ｃ．3天Ｄ．2天2甲安装队为小区安装66台空调，乙安装队为B 小区安装60台空调，两队同时开工且恰好同时完工，甲队比乙队每天多安装2台．设乙队每天安装x 台，根据题意，下面所列方程中正确的是（）A ．66602x x =-B ．66602x x =-C ．66602x x =+D ．66602x x=+ 3有两块面积相同的试验田，分别收获蔬菜900kg 和1500kg ，已知第一块试验田每亩收获蔬菜比第二块少300kg ，求第一块试验田每亩收获蔬菜多少千克．设一块试验田每亩收获蔬菜x kg ，根据题意，可得方程（）A ．9001500300x x =+ B ．9001500300x x =- C ．9001500300x x =+ D ．9001500300x x=- 4轮船先顺水航行46千米再逆水航行34千米所用的时间，恰好与它在静水中航行80千米所用的时间相等，水的流速是每小时3千米，则轮船在静水中的速度是_________5南水北调东线工程已经开工，某施工单位准备对运河一段长2240m 的河堤进行加固，由于采用新的加固模式，现在计划每天加固的长度比原计划增加了20m ，因而完成河堤加固工程所需天数将比原计划缩短2天，若设现在计划每天加固河堤x m ，则得方程为 ________ ．6某市在旧城改造过程中，需要整修一段全长2400m 的道路．为了减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务．求原计划每小时修路的长度．若设原计划每小时修x m ，则根据题意可得方程 ________7、甲、乙两人准备整理一批新到的实验器材，甲单独整理需要40分完工；若甲、乙共同整理20分钟后，乙需要再单独整理20分才能完工。

初二年级奥数分式方程试题及答案

初二年级奥数分式方程试题及答案1．下列是分式方程的是(D)A.xx＋1＋x＋43B.x4＋x－52＝0C.34(x－2)＝43xD.1x＋2＋1＝02．为加快“最美毕节”环境建设，某园林公司增加了人力实行大型树木移植，现在平均每天比原计划多植树30棵，现在植树400棵所需时间与原计划植树300棵所需时间相同，设现在平均每天植树x棵，则列出的分式方程为(A)A.400x＝300x－30B.400x－30＝300xC.400x＋30＝300xD.400x＝300x＋303．已知x＝1是分式方程1x＋1＝3kx的根，则实数k＝16.4．把分式方程2x＋4＝1x转化为一元一次方程时，方程两边需同乘以(D)A．x B．2xC．x＋4 D．x(x＋4)5．解分式方程2x＋1＋3x－1＝6x2－1分以下几步，其中错误的一步是(D)A．方程两边分式的最简公分母是(x－1)(x＋1)B．方程两边都乘以(x－1)(x＋1)，得整式方程2(x－1)＋3(x＋1)＝6C．解这个整式方程，得x＝1D．原方程的解为x＝16．解分式方程1x－1＋1＝0，准确的结果是(A)A．x＝0 B．x＝1C．x＝2 D．无解7．已知x＝3是关于x的方程10x＋k－3x＝1的一个解，则k＝2．8．解下列方程：(1)2xx－2＝1－12－x；解：方程两边同乘以(x－2)，得2x＝x－2＋1.解得x＝－1.经检验，x＝－1是原方程的解．(2)6x－2＝xx＋3－1；解：方程两边同乘以(x－2)(x＋3)，得6(x＋3)＝x(x－2)－(x－2)(x＋3)．解得x＝－43.经检验，x＝－43是原方程的解．(3)xx2－4＋2x＋2＝1x－2；解：方程两边都乘以(x＋2)(x－2)，得x＋2(x－2)＝x＋2.解得x＝3.经检验，x＝3是原方程的解．(4)23＋x3x－1＝19x－3.解：方程两边同乘以9x－3，得2(3x－1)＋3x＝1.解得x＝13.检验：当x＝13时，9x－3＝0.所以x＝13不是原方程的解．∴原分式方程无解．9．某机加工车间共有26名工人，现要加工2 100个A零件，1 200个B零件，已知每人每天加工A零件30个或B零件20个，问怎样分工才能确保同时完成两种零件的加工任务(每人只能加工一种零件)？设安排x人加工A零件，由题意列方程得(A)A.2 10030x＝1 20020（26－x）B.2 100x＝1 20026－xC.2 10020x＝1 20030（26－x）D.2 100x×30＝1 20026－x×2010．在求3x的倒数的值时，嘉淇同学将3x看成了8x，她求得的值比准确答案小5.依上述情形，所列关系式成立的是(B)A.13x＝18x－5B.13x＝18x＋5C.13x＝8x－5D.13x＝8x＋511．用换元法解方程x2－12x－4xx2－12＝3时，设x2－12x＝y，则原方程可化为(B)A．y－1y－3＝0 B．y－4y－3＝0C．y－1y＋3＝0 D．y－4y＋3＝012．当x＝56时，xx－5－2与x＋1x互为相反数．13．若关于x的方程x－1x－5＝m10－2x无解，则m＝－8．14．解下列方程：(1)3x2－9＋xx－3＝1；。

初中奥数讲义分式方程(组)附答案

初中奥数讲义分式方程（组）附答案初中奥数讲义-分式方程（组）附答案分数阶方程本讲我们将介绍分式方程(组)的解法及其应用．【知识拓展】分母中含有未知量的方程称为分数阶方程。

解分数阶方程的基本思想是将它们转化为积分方程。

通常有两种方法：一种是去除分母；第二种是替代。

解分数阶方程时必须检验根解分式方程组时整体代换的思想体现得很充分．常见的思路有：取倒数法方程迭加法，换元法等．解决分数阶方程应用问题的关键是找到等价关系并列出方程。

如果方程包含以字母表示的已知数，则需要根据问题的变换条件实现变换。

在不求解的情况下设置未知数是常见的技能之一例题求解一、分数阶方程（组）解的例子1。

拆分项目并重新组织以解分数方程[示例1]以解方程x?5x?2x?3x?4．x?7x?4x?5x?6解析直接去分母太繁琐，左右两边分别通分仍有很复杂的分子．考虑将每一项分拆：如11x?52，这样可降低计算难度．经检验x?为原方程的解．?1?2x?7x?7注本题中用到两个技巧：一是将分式拆成整式加另一个分式；二是交换了项，避免通分后分子出现x．这样大大降低了运算量．本讲趣题引路中的问题也属于这种思路．2.用元素交换法求解分数阶方程[例2]1x?11x?82?1x?2x?82?1x?13x?82?0．如果在解析时考虑去除分母，则计算量过大；分裂是不够的，但每个分母都是一个二次三项式。

试试替代法。

解为x+2x-8=y，原始方程可转化为2111 0岁？9xyy？15x解关于y的分数方程，得到y=9x或y=-5x。

因此，当y=9x，x+2x-8=9x时，解得到X1=8，X2=-1。

当y=-5x，x+2x-8=-5x时，解得到X3=-8，X4=1。

经检验，上述四种解均为原方程的解注当分式方程的结构较复杂且有相同或相近部分时，可通过换元将之简化．3．形如x?形如x?11?a?结构的分式方程的解法xa22111? A.分数阶方程的解是：X1？a、 x2？。

奥数数的方程练习题

奥数数的方程练习题一、一元一次方程1. 解方程：3x 7 = 112. 解方程：5 2x = 3x + 13. 解方程：4(x 2) = 3(x + 5)4. 解方程：7 (2x + 3) = 4 x5. 解方程：2(3x 1) 5(x + 2) = 8二、一元二次方程1. 解方程：x^2 5x + 6 = 02. 解方程：2x^2 4x 6 = 03. 解方程：x^2 3x = 04. 解方程：4x^2 + 8x + 4 = 05. 解方程：x^2 4 = 0三、二元一次方程组1. 解方程组：\[\begin{cases}2x + 3y = 8 \\x y = 1\end{cases}\]2. 解方程组：\[3x 2y = 7 \\ 5x + y = 9\end{cases}\]3. 解方程组：\[\begin{cases} 4x + 5y = 14 \\ 2x 3y = 5\end{cases}\]4. 解方程组：\[\begin{cases} x + 2y = 6 \\ 3x y = 4\end{cases}\]5. 解方程组：\[\begin{cases} 2x + 3y = 11 \\ 5x 2y = 13\]四、不等式与不等式组1. 解不等式：3x 5 > 22. 解不等式：2(x 3) < 4 x3. 解不等式：5 2x ≥ 3x + 14. 解不等式组：\[\begin{cases}2x 3 > 1 \\x + 4 < 7\end{cases}\]5. 解不等式组：\[\begin{cases}3x + 2y ≥ 6 \\x y < 2\end{cases}\]五、应用题1. 某数的2倍与3的差是7，求这个数。

2. 甲、乙两人年龄之和为35岁，甲的年龄是乙的2倍，求甲、乙的年龄。

3. 一辆汽车从甲地出发，以60km/h的速度行驶，另一辆汽车从乙地出发，以80km/h的速度行驶，两车相向而行，2小时后相遇，求甲、乙两地之间的距离。

初二奥数辅导分式方程的解法

奥数辅导分式方程
分母中含有未知数的方程叫分式方程.解分式方程的基本思想是转化为整式方程求解，转化的基本方法是去分母、换元，但也要灵活运用，注意方程的特点进行有效的变形•变形时可能会扩大(或缩小)未知数的取值范围，故必须验根.
例1解方程
解令y=X+2x-8，那么原方程为
111,
+_*=a
y+9y y y亠15k
分析与解形式与上例相似.本题中分子与分母只是一次项的符号相反，故
可考虑用合分比定理化简•原方程变形为
(3x2+4x~1)+(3x2-4x -1)(x2++1) +(x2-4x+1)
去分母得
y(y-15x)+(y+9x)(y-15x)+y(y+9x)=0，
y2-4xy-45x2=0,
(y+或y=-5x .
由y=9x得x2+2x-8=9x，即x2-7x-8=0，所以Xi=-1 ,X2=8;由y=-5x，得x2+2x-8=-5x，即x2+7x-8=0，所以X3=-8，X4=1.
经检验，它们都是原方程的根.
例2解方程
x2+72x~72
——+_-18 =0・'
X2+4x
解设厂则原方費化为
整理得
\3茎一2
黑十！x+2x2+3x+2
去分母、整理得
x+ 9=0,x=-9 .
经检验知，x=-9是原方程的根.
例4解方程x+ 1 X +6x+ 2x+5
+=+
黑 +2x+ 7x+3x+ 6

七年级奥数20分式及分式的应用

七年级奥数20分式及分式的应用1、如果234x y z ==，则222(4)x y y z -+= ；2、如果2xy x y =+，则3533x xy y x xy y -+-+-= 。

3、若a b c a b c a b c c b a +--+-++==，则()()()a b b c c a abc+++= 。

4、若1,2,3xy yz zx x y y z z x ===+++，则x = ，y = ，z = 。

5、若01282=+-x x ，则分式4322621823815x x x x x x --++-+= 。

6、化简分式：222211113256712920x x x x x x x x +++++++++++= 。

7、已知0a b c ++=，则：)111(32333222c b a cb ac b a +++++++= 。

8、化简：222222a b c b a c c a b a ab ac bc b ab bc ac c ac bc ab------++--+--+--+= 。

9、已知2b ac =，求222333333111()a b c a b c a b c ⋅++++的值。

10、解方程组25121312x y y x yy ⎧+=⎪--⎪⎨⎪+=⎪--⎩11、已知1abc =，2a b c ++=，2223ab c ++=，求111111ab c bc a ca b +++-+-+-的值。

12、解分式方程：596841922119968x x x x x x x x ----+=+----13、已知4360x y z --=，24140x y z +-=且0xyz ≠，求22222223657x y z x y z ++++14、A 、B 两地相距80km,一辆公共汽车从A 地出发开往B 地，2小时后，又从A 地同向开出一辆小汽车，小汽车的速度是公共汽车的3倍，结果小汽车比公共汽车早40分钟到达B 地。

分式方程应用题总汇和答案

分式方程应用题总汇及答案1、A、B两地的距离是80公里.一辆公共汽车从A地驶出3小时后.一辆小汽车也从A地出发.它的速度是公共汽车的3倍.已知小汽车比公共汽车迟20分钟到达B 地.求两车的速度。

【提示】设共交车速度为x.小汽车速度为3x.列方程得：80/(3x) +3=80/x +20/602、为加快西部大开发.某自治区决定新修一条公路.甲、乙两工程队承包此项工程。

如果甲工程队单独施工.则刚好如期完成；如果乙工程队单独施工就要超过6个月才能完成.现在甲、乙两队先共同施工4个月.剩下的由乙队单独施工.则刚好如期完成。

问原来规定修好这条公路需多长时间？【提示】设时间为x个月.列方程得：[1/x+1/(x+6)]*4+(x-4)/(x+6)=13、某工人原计划在规定时间恰好加工1500个零件.改进了工具和操作方法后.工作效率提高为原来的2倍.因此加工1500个零件时.比原计划提前了五小时.问原计划每小时加工多少个零件？【提示】设原计划每小时加工x个零件.列方程得：1500/2x +5=1500/x4、甲、乙两组学生去距学校4.5千米的敬老院打扫卫生.甲组学生步行出发半小时后.乙组学生骑自行车开始出发.结果两组学生同时到达敬老院.如果步行的速度是骑自行车的速度的1/3.求步行和骑自行车的速度各是多少？【提示】设步行的速度是每小时x千米.则4.5/3x +0.5=4.5/x5、某质检部门抽取甲、乙两个相同数量的产品进行质量检测.结果甲厂有48件合格产品.乙厂有45件合格产品.甲厂合格率比乙厂高5%.求抽取检验的产品数量及甲厂的合格率。

【提示】设抽取检验的产品数量为x.则(48/x -45/x)*100％=5％6、某车间加工1200个零件后.采用了新工艺.工效提高50%.这样加工同样多的零件就少用10小时.采用新工艺前后每小时分别加工多少个零件？7、A 、B 两地相距48千米.一艘轮船从A 地顺流航行至B 地.又立即从B 地逆流返回A 地.共用去9小时.已知水流速度为4千米/时.若设该轮船在静水中的速度为x 千米/时.则可列方程求解。

初一奥数之分式方程

初一奥数之分式方程专题08 分式方程阅读与思考分母含有未知数的方程叫分式方程．解分式方程的主要思路是去分母，把分式方程化为整式方程，常用的方法有直接去分母、换元法等．在解分式方程中，有可能产生增根．尽管增根必须舍去，但有时却要利用增根，挖掘隐含条件．例题与求解【例1】若关于x 的方程22x ax +-＝－1的解为正数，则a 的取值范围是______．（黄冈市竞赛试题）解题思路：化分式方程为整式方程，注意增根的隐含制约．【例2】已知()22221111x x A B Cx x x x x +-=++--，其中A ，B ，C 为常数．求A ＋B ＋C 的值．（“五羊杯”竞赛试题）解题思路：将右边通分，比较分子，建立A ，B ，C 的等式．【例3】解下列方程：（1）596841922119968x x x x x x x x ----+=+----；（“五羊杯”竞赛试题）（2）222234112283912x x x x x x x x ++-+=+-+；（河南省竞赛试题）（3）2x ＋21x x ⎛⎫ ⎪+⎝⎭＝3．（加拿大数学奥林匹克竞赛试题）解题思路：由于各个方程形式都较复杂，因此不宜于直接去分母．需运用解分式问题、分式方程相关技巧、方法解．【例4】（1）方程18272938x x x x x x x x +++++=+++++的解是___________．（江苏省竞赛试题）（2）方程222111132567124x x x x x x x ++=+++++++的解是________．（“希望杯”邀请赛试题）解题思路：仔细观察分子、分母间的特点，发现联系，寻找解题的突破口．【例5】若关于x 的方程2211k x kx x x x x+-=--只有一个解，试求k 的值与方程的解．（江苏省竞赛试题）解题思路：化分式方程为整式方程，解题的关键是对原方程“只有一个解”的准确理解，利用增根解题．【例6】求方程11156x y z ++=的正整数解．（“希望杯”竞赛试题）解题思路：易知,,x y z 都大于1，不妨设1＜x ≤y ≤z ，则111x y z≥≥，将复杂的三元不定方程转化为一元不等式，通过解不等式对某个未知数的取值作出估计．逐步缩小其取值范围，求出结果．能力训练A 级1．若关于x 的方程1101ax x +-=-有增根，则a 的值为________．（重庆市中考试题） 2．用换元法解分式方程21221x x x x --=-时，如果设21x x-＝y ，并将原方程化为关于y 的整式方程，那么这个整式方程是___________．（上海市中考试题） 3．方程2211340x x x x ⎛⎫+-++= ⎪⎝⎭的解为__________．（天津市中考试题） 4．两个关于x 的方程220x x --=与132x x a=-+有一个解相同，则a ＝_______．（呼和浩特市中考试题）5．已知方程11x a x a+=+的两根分别为a ，1a ，则方程1111x a x a +=+--的根是（）．A ．a ，11a - B ．11a -，1a - C ．1a ，1a - D ．a ，1a a - （辽宁省中考试题）6．关于x 的方程211x mx +=-的解是正数，则m 的取值范围是（） A ．m ＞－1 B ．m ＞－1且m ≠0 C ．m ＜－1 D ．m ＜－l 且m ≠－2（孝感市中考试题）7．关于x 的方程22x c x c +=+的两个解是x 1＝c ，x 2＝2c ，则关于x 的方程2211x a x a +=+--的两个解是（）． A ．a ，2a B ．a －1，21a - C ．a ，21a - D ．a ，11a a +- 8．解下列方程：（1）()2221160x x x x+++-=；（苏州市中考试题）（2）2216104933x x x x ⎛⎫+=-- ⎪⎝⎭．（盐城市中考试题）9．已知13x x +=．求x 10＋x 5＋51011x x+的值．10．若关于x 的方程2211k x kx x x x x+-=--只有一个解（相等的两根算作一个），求k 的值．（黄冈市竞赛试题）11．已知关于x 的方程x 2＋2x ＋221022m x x m-=+-，其中m 为实数.当m 为何值时，方程恰有三个互不相等的实数根?求出这三个实数根.（聊城市中考试题）12．若关于x 的方程()()122112x x ax x x x x ++-=+--+无解，求a 的值．（“希望杯”邀请赛试题）B 级1．方程222211114325671221x x x x x x x x +++=+++++++的解是__________．（“祖冲之杯”邀请赛试题）2．方程222111011828138x x x x x x ++=+-+---的解为__________． 3．分式方程()()1112x m x x x -=--+有增根，则m 的值为_________． 4．若关于x 的分式方程22x ax +-＝－1的解是正数，则a 的取值范围是______．（黑龙江省竞赛试题）5．（1）若关于x 的方程2133m x x =---无解，则m ＝__________．（沈阳市中考试题）（2）解分式方程225111m x x x +=+--会产生增根，则m ＝______．（“希望杯”邀请赛试题） 6．方程33116x x x x ⎛⎫+=+ ⎪⎝⎭的解的个数为（）． A ．4个 B ．6个 C ．2个 D ．3个 7．关于x 的方程11ax =+的解是负数，则a 的取值范围是（）． A ．a ＜l B ．a ＜1且a ≠0 C ．a ≤1 D ．a ≤1且a ≠0（山西省竞赛试题）8．某工程，甲队独做所需天数是乙、丙两队合做所需天数的a 倍，乙队独做所需天数是甲、丙两队合做所需天数的b 倍，丙队独做所需天数是甲、乙两队合做所需天数的c 倍，则111111a b c +++++的值是（）．A ．1B ．2C ．3D ．4（江苏省竞赛试题）9．已知关于x 的方程（a 2－1）()2271011x x a x x ⎛⎫⎛⎫-++= ⎪ ⎪--⎝⎭⎝⎭有实数根．（1）求a 的取值范围；（2）若原方程的两个实数根为x 1，x 2，且121231111x x x x +=--，求a 的值. （TI 杯全国初中数学竞赛试颞）10．求方程22x －xy 3x -＋y ＋2006＝0的正整数解.（江苏省竞赛试题）11．某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降. 今年三月份的电脑售价比去年同期每台降价1 元．如果卖出相同数量的电脑，去年销售额为10万元．今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元?（2）为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案?（3）如果乙种电脑每台售价为3 800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a 元．要使（2）中所有方案获利相同，a 值应是多少？此时，哪种方案对公司更有利？（齐齐哈尔市中考试题）专题08 分式方程例1 a ＜2且a ≠－4例2 原式右边＝22(1)+B(1)(1Ax x x Cx x x --+-）＝2222()()211(1)(1)A C xB A x B x x x x x x ++--+-=--得2111A C B A B +=⎧⎪-=⎨⎪-=-⎩∴1011,8.A B C =⎧⎪=⎨⎪=-⎩，∴A ＋B ＋C ＝13．例3 （1）x ＝12314提示：1155(5)(1)(4)(2)191968x x x x -++=++-----．（2）1,2x =，x 3＝－1，x 4＝－4 提示：令223.4x xy x x +=+-（3）1,2x =提示222222()().111x x x x x x x +=++++例4 （1）原方程化为11111+111+2+9+3+8x x x x --=-+-，即1111+3+2+9+8x x x x -=-，进一步可化为(x ＋2) (x ＋3)＝(x ＋8) (x ＋9)，解得x ＝－112．（2）原方程化为1111111+1+2+2+3+3+4+4x x x x x x x -+-+-=，即12+14x x =+，解得x ＝2．例5 原方程化为kx 2－3kx ＋2x －1＝0①，当k ＝0时，原方程有唯一解x ＝12；当k ≠0，Δ＝5k 2＋4(k －1)2＞0．由题意知，方程①必有一根是原方程的曾根，即x ＝0或x ＝1，显然0不是①的根，故x ＝1是方程①的根，代入的k ＝12．∴当k ＝0或12时，原方程只有一个解．例6 11113x x y z x <++≤，即1536x x <≤，因此得x ＝2或3．当x ＝2时，111x x y <+＝511112623y y y -=≤+=，即1123y y<≤，由此可得y ＝4或5或6；同理，当x ＝3时，y ＝3或4，由此可得当1≤x ≤y ≤z 时，(x ，y ，z )共有(2，4，12)，(2，6，6)，(3，3，6)，(3，4，4)4组；由于x ，y ，z 在方程中地位平等，可得原方程组的解共15组：(2，4，12)，(2，12，4)， (4，2，12)，(4，12，2)，(12，2，4)，(12，4，2)，(2，6，6)，(6，2，6)，(6，6，2)，(3，3，6)，(3，6，3)，(6，3，3)，(3，4，4) ，(4，4，3) ，(4，3，4)．A 级1．－1 2．y 2－2y －1＝0 3．1 4．－8 5．D 6．D 7．D8．(1)12123x x ==-， (2)1226x x ==-，,3,43x =-9．15250 提示：由x ＋13x =得2217.x x +=则2211()()21x x x x ++=，得33118x x+=．于是221()x x +331()126x x +=，得551123x x +=．进一步得1010115127x x +=．故原式＝15250．10．k ＝0或k ＝12提示：原方程化为kx 2－3kx ＋2x －1＝0，分类讨论． 11．设x ＋2x ＝y ，则原方程可化为y 2－2my ＋m 2－1＝0，解得y 1＝m ＋1，y 2＝m －1．∵x 2＋2x －m －1＝0①，x 2＋2x －m ＋1＝0②，从而Δ1＝4m ＋8，Δ2＝4m 中应有一个等于零，一个大于零．经讨论，当Δ2＝0即m ＝0时，Δ1＞0，原方程有三个实数根．将m ＝0代入原方程，解得123111.x x x ⎧=⎪⎪=⎨⎪=⎪⎩12 原方程“无解”内涵丰富:可能是化得的整式方程无解,亦可能是求得的整式方程的解为増根,故需全面讨论.原方程化为(a+2)x =－3 ① , ∵原方程无解,∴a+2=0或x －1=0,x+2=0,得B 级1. 3或－ 72. x ₁=8 , x ₂=－1 , x ₃=－8 , x ₄=1 提示: 令x ²－8=y3. 3 提示:由有増根可得m=0或 m=3,但当 m=0,化为整式方程时无解4. a<2 且 a ≠－45. ⑴ －2 ⑵ －4 或－106. A7.8. 设甲单独做需要x 天完成,乙单独做需要y 天完成,丙单独做需要z 天完成则.解 . 当a ≠±1时,则Δ≥0,原方程有实数解.由Δ=[-﹙2a+7﹚]²-4﹙a ²-1﹚≥0,解得.21-5,2,21-a 5,－=a 分别别代入①2－= x 1,=x 把 2,－=a 或综上知--==a 0≠1a ∴ 0,≠11 0≠1x 1a 01-a x ∴,111x a: a a x a B 且即且由提示<+-+<⇒<=+=⇒=+1xy +=++a yz yzxz 得⑥⑤④, ⑥11yz xz xy xy ⑤,11yz xz xy xz ④.11yz xz xy yz ∴+++=+++=+++=++c b a 同理可得111111a 1=+++++c b 得,01.01)72(1)t -(a 1,≠,1⑴....9222=-=++-=-a t a t t x x当原方程可化为则设.,?=a , 41-=x 81-=x ∴, 51=1-x 91=1-x 0=1+5-0=1+9-, ?=原方程有实数解时当故或或即或则方程为时即x x t t a 且当综上可知由于解得时但当又,2853－≥,,2853－>22±1,22±1=a ,1=t 1,≠t ,2853－≥a a .,22±1≠原方程有实数解时a253,,10.28a a <-=∴=故应当舍去22232006()2321006,1,10.? 1x x y x x x y x x -+=-+≠--∴=把原方程变形为200521,2005120055401,11,5,401,2005,1(x,y)=(2,2008),(6,412),(402,808),(2006,4012)x x x =-+=⨯=⨯-=-分别取从而 1000008000011 (1),,10004000,4000,4000.(2),48003500+3000(15)50000,6x 10.x ,,,,,.x x xx x x x x =+==≤-≤≤≤设今年三月份甲种电脑每台售价元由题意得解得经检验是原方程的根所以甲种电脑每台售价元设购进甲种电脑台由题意得解得因为的正整数解为678910所以共有5种进货方案(3)设总获利为W 元,则W=(4-35)x+(3800-3-a)(15-x)=(a-300)x+12-15a当a=300时,(2)中所有方案获利相同,此时购买甲种电脑6台,乙钟电脑9台时对公司更有利。

初二分式方程应用题及答案

初二分式方程应用题及答案
题目：某工厂生产一批零件，甲车间单独完成需要15天，乙车间单
独完成需要20天。

现在甲乙两个车间合作，共同完成这批零件的生产，问需要多少天？
解答：
设甲车间每天完成这批零件的$ \frac{1}{15} $，乙车间每天完成
这批零件的$ \frac{1}{20} $。

设甲乙两个车间合作完成这批零件
需要$ x $天。

根据题意，甲乙两个车间合作$ x $天完成的零件数等于这批零件的
总数，即：
\[ \frac{1}{15}x + \frac{1}{20}x = 1 \]
为了解这个方程，我们首先找到两个分数的最小公倍数，即60，然后
将方程两边同时乘以60，得到：
\[ 4x + 3x = 60 \]
合并同类项，得到：
\[ 7x = 60 \]
解得：
\[ x = \frac{60}{7} \]
所以，甲乙两个车间合作需要$ \frac{60}{7} $天完成这批零件的生产。

答案：甲乙两个车间合作需要$ \frac{60}{7} $天完成这批零件的生产。

八年级数学竞赛例题专题讲解8：分式方程附答案

八年级数学竞赛例题专题讲解8：分式方程附答案分式方程是含有未知数的方程，其中分母含有未知数。

解分式方程的主要思路是去分母，把分式方程化为整式方程，可以通过直接去分母或换元法等方法实现。

有时，在解分式方程时可能会出现增根的情况。

虽然增根必须舍去，但有时也可以利用增根，挖掘隐含条件。

例如，对于一个关于x的方程2x+a/(x-2)=-1，如果其解为正数，则a的取值范围需要注意增根的隐含制约。

另一个例子是已知2/(x(x-1))+A/(x-1)+B/x=C，其中A，B，C为常数，需要求出A+B+C的值。

可以将右边通分，然后比较分子，建立A，B，C的等式。

对于一些复杂的分式方程，不宜直接去分母。

需要运用解分式问题、分式方程相关技巧和方法来解决。

例如，对于方程5x-9/(x-19)+6x-8/(x-9)+4/(x-6)+2/(x-8)=0，或者方程x^2+3x/(x^2+x-4)+11/2=0，或者方程x/(x+1)+1/(x+1)^2=3，需要仔细观察分子、分母间的特点，寻找解题的突破口。

有时，解分式方程需要对原方程“只有一个解”的准确理解，利用增根解题。

例如，对于方程2kx/(kx+1)-2/(x-1)=0，如果该方程只有一个解，则需要化分式方程为整式方程，并利用增根解题。

对于一些复杂的不定方程，可以通过转化为一元不等式，逐步缩小未知数的取值范围，求出结果。

例如，对于方程1115/(xyz)=1，且x≤y≤z，≥111，然后通过解不等式对某个未知数的取值作出估计，逐步缩小其取值范围，求出结果。

最后，需要注意格式错误和明显有问题的段落，进行删除和小幅度改写，以提高文章的可读性。

1.当$x=\frac{1}{y}$时，原方程变为$\frac{y^2-1}{y}=2$，即$y^2-2y-1=0$。

因此，这个整式方程是$y^2-2y-1=0$。

2.将方程$x^2-3x+4=0$移项得$x^2=3x-4$，代入原方程得$\frac{2x(3x-4)}{x-1}=2x^2-2x-4=0$。

初二年级奥数分式方程试题及答案

【导语】奥林匹克数学竞赛或数学奥林匹克竞赛，简称奥数。

奥数体现了数学与奥林匹克体育运动精神的共通性：更快、更⾼、更强。

国际数学奥林匹克作为⼀项国际性赛事，由国际数学教育专家命题，出题范围超出了所有国家的义务教育⽔平，难度⼤⼤超过⼤学⼊学考试。

下⾯是为⼤家带来的初⼆年级奥数分式⽅程试题及答案，欢迎⼤家阅读。

1．下列是分式⽅程的是(D)A.xx＋1＋x＋43B.x4＋x－52＝0C.34(x－2)＝43xD.1x＋2＋1＝0 2．为加快“最美毕节”环境建设，某园林公司增加了⼈⼒进⾏⼤型树⽊移植，现在平均每天⽐原计划多植树30棵，现在植树400棵所需时间与原计划植树300棵所需时间相同，设现在平均每天植树x棵，则列出的分式⽅程为(A)A.400x＝300x－30B.400x－30＝300xC.400x＋30＝300xD.400x＝300x＋30 3．已知x＝1是分式⽅程1x＋1＝3kx的根，则实数k＝16. 4．把分式⽅程2x＋4＝1x转化为⼀元⼀次⽅程时，⽅程两边需同乘以(D) A．x B．2x C．x＋4 D．x(x＋4) 5．解分式⽅程2x＋1＋3x－1＝6x2－1分以下⼏步，其中错误的⼀步是(D) A．⽅程两边分式的最简公分母是(x－1)(x＋1) B．⽅程两边都乘以(x－1)(x＋1)，得整式⽅程2(x－1)＋3(x＋1)＝6 C．解这个整式⽅程，得x＝1 D．原⽅程的解为x＝1 6．解分式⽅程1x－1＋1＝0，正确的结果是(A) A．x＝0 B．x＝1 C．x＝2 D．⽆解 7．已知x＝3是关于x的⽅程10x＋k－3x＝1的⼀个解，则k＝2． 8．解下列⽅程： (1)2xx－2＝1－12－x；解：⽅程两边同乘以(x－2)，得 2x＝x－2＋1.解得x＝－1. 经检验，x＝－1是原⽅程的解． (2)6x－2＝xx＋3－1；解：⽅程两边同乘以(x－2)(x＋3)，得 6(x＋3)＝x(x－2)－(x－2)(x＋3)．解得x＝－43. 经检验，x＝－43是原⽅程的解． (3)xx2－4＋2x＋2＝1x－2；解：⽅程两边都乘以(x＋2)(x－2)，得 x＋2(x－2)＝x＋2.解得x＝3. 经检验，x＝3是原⽅程的解． (4)23＋x3x－1＝19x－3. 解：⽅程两边同乘以9x－3，得 2(3x－1)＋3x＝1.解得x＝13. 检验：当x＝13时，9x－3＝0. 因此x＝13不是原⽅程的解． ∴原分式⽅程⽆解． 9．某机加⼯车间共有26名⼯⼈，现要加⼯2 100个A零件，1 200个B零件，已知每⼈每天加⼯A零件30个或B零件20个，问怎样分⼯才能确保同时完成两种零件的加⼯任务(每⼈只能加⼯⼀种零件)？设安排x⼈加⼯A零件，由题意列⽅程得(A) A.2 10030x＝1 20020（26－x） B.2 100x＝1 20026－x C.2 10020x＝1 20030（26－x） D.2 100x×30＝1 20026－x×20 10．在求3x的倒数的值时，嘉淇同学将3x看成了8x，她求得的值⽐正确答案⼩5.依上述情形，所列关系式成⽴的是(B)A.13x＝18x－5B.13x＝18x＋5C.13x＝8x－5D.13x＝8x＋5 11．⽤换元法解⽅程x2－12x－4xx2－12＝3时，设x2－12x＝y，则原⽅程可化为(B) A．y－1y－3＝0 B．y－4y－3＝0 C．y－1y＋3＝0 D．y－4y＋3＝0 12．当x＝56时，xx－5－2与x＋1x互为相反数． 13．若关于x的⽅程x－1x－5＝m10－2x⽆解，则m＝－8． 14．解下列⽅程： (1)3x2－9＋xx－3＝1；解：去分母，得3＋x(x＋3)＝x2－9， 3＋x2＋3x＝x2－9.解得x＝－4. 经检验，x＝－4是原⽅程的解． (2)x＋1x－1＋4x2－1＝1；解：⽅程两边同乘以(x＋1)(x－1)，得 (x＋1)2＋4＝(x＋1)(x－1)，解得x＝－3. 检验：当x＝－3时，(x＋1)(x－1)≠0， ∴x＝－3是原⽅程的解． ∴原⽅程的解是x＝－3. (3)8x2－4＋1＝xx－2. 解：原⽅程可化为8（x＋2）（x－2）＋1＝xx－2. 去分母，得8＋(x＋2)(x－2)＝x(x＋2)．解得x＝2. 检验：当x＝2时，(x＋2)(x－2)＝0， ∴x＝2是原⽅程的增根，即原⽅程⽆解． 15．如图，点A，B在数轴上，它们所对应的数分别是－3和1－x2－x，且点A，B到原点的距离相等，求x的值．解：由题意，得1－x2－x＝3.解得x＝52. 经检验，x＝52是原⽅程的解． ∴x＝52. 16．解关于x的⽅程：mx－1x－1＝0(m≠0且m≠1)．解：⽅程两边同乘以x(x－1)，得 m(x－1)－x＝0.(m－1)x＝m. ∵m≠1，∴x＝mm－1. 检验：当x＝mm－1时，x(x－1)≠0. ∴原分式⽅程的解为x＝mm－1.。

2019初中奥数分式方程应用题两篇

2019初中奥数分式方程应用题两篇【篇一】1.汶川大地震后，各地人民纷纷捐款捐物支援灾区。

然后某企业向灾区捐助价值940000元的A,B两种帐篷共600顶，已知A帐篷每顶1700元，B帐篷每顶1300元，问A,B两种帐篷各捐多少顶？2.有一瓶纯蜂蜜，第一次倒出四分之一后，用水加满；第二次倒出三分之一后，用水加满；第三次倒出四分之三后，用水加满。

这时瓶中的水占几分之几？3.甲和乙都存粮10吨。

如果把甲的五分之一给乙。

然后现在两人的储存量一样多，原来两人各存粮多少吨？4.甲乙丙三人合修一围墙，甲乙合修5天完成1/3，乙丙合修2天完成余下的1/4，然后甲丙两人合修了5天才完工。

整修工程的劳动报酬是600元。

甲应分的多少元？5.丽丽和家家去书店买书,他们同时喜欢上了一本书,最后丽丽用自己的钱的5分之3,家家用自己的钱的3分之2各买了一本,丽丽剩下的钱比家家剩下的钱多5块.两人原来各有多少钱?书多少钱?6.一辆汽车每行8千米要耗油4/5千克,平均每千克汽油可行多少千米.行1千米路程要耗油多少千克?【篇二】1.小巧的爸爸出差到外地去了56天，途中遇到阴雨天气共计两个星期，其余全是晴天。

晴天有几个星期？2.学校举行朗诵比赛。

三年级有32人参加，四年级参加的人数是三年级的2倍，五年级参加的人数比三、四年级参加的总人数的2倍少26人。

五年级有多少人参加朗诵比赛？3.一块长方形的操场，原来长50米，宽30米。

扩建后，长和宽都增加了原来的一倍。

现在操场的面积是多少平方米？增加了多少平方米？4.科学考察船在某处测量海深，由海面向海底发射超声波，8秒钟后收到信号。

超声波在海水里的传播速度是每秒钟1250米，此处海水深多少米？5.一部电话机售价320元，一台彩电的售价是电话机的8倍，一台电脑的售价比一台彩电售价的2倍还多460元。

一台电脑的售价多少元？6.小亚抄写词语，第一天和第二天抄写的词语个数同样多，第三天抄写了26个，比第二天少抄写7个。

初中奥数分式方程应用题练习题

初中奥数分式方程应用题练习题【篇1】1.一个等腰三角形的一个底角度数是顶角的二分之一，这个三角形的顶角是多少度？2.一个圆的周长和直径相加的合适20.7米，这个圆的面积是多少平方米？3.加工一批零件,甲单独做12天完成,乙单独做15天完成.两队同时开工,几天能完成这批零件的五分之三?4.寒假开始，红领巾志愿者参加社区劳动。

有50%的同学扫楼道，有五分之二的同学运垃圾，在这些同学之中有7人两项都做，占志愿者总数的14%。

然后是志愿者共几人？除了扫楼道的和运垃圾的学生外，其他人擦窗户，擦窗户的几人？5.用1200米布做一批服装,其中做裤子的用布量是坐上衣的五分之一,做上衣和裤子各用布多少米?6.仓库里有30吨粮食,第一次运走总数的五分之一,第二次运走二分之九吨.两次共用去多少吨?【篇2】1.商店有红气球和黄气球，共有48只，其中黄气球的只数是红气球的3/5。

红气球和黄气球各多少只?2.某玩具厂去年生产玩具2.1万件，今年比去年多生产0.7万件，今年生产的件数是去年的百分之几?(百分号前面保留一位小数)3、白沙县计划造林20公顷，实际造林比计划多5公顷，实际造林比计划多百分之几？4、乐华收录机现在每台售价120元，比原来降低40元。

降低了百分之几？5、一项工程，甲队独做4小时完成，乙队独做6小时完成。

两队合做，需要几小时完成？6、陈家村要挖一条长150米的水渠，第一天挖了全长的1/10，第二天挖了全长的9/10米。

两天共挖了多少米？7、水果批发部要运进一批水果，第一次运进25%，第二次运进1.5吨，两次共运进这批水果的62%，这批水果有多少吨？【篇3】1.一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或者不盈不亏?2.某种商品的进价为400元,标价为600元,打折出售的利润率为5%,那么,此商品是按几折销售的?3.某商场将某种DVD产品按进价提升35%,然后打出“九折酬宾,外送50元打的费”的广告,结果每台DVD仍获利208元,则每台DVD的进价是多少元?4.某商店因换季销售打折商品,若按定价的6折出售,将赔20元,若按定价的8折出售,将赚15元,则该商品应定价多少元?成本为多少元?5.某玩具店两款进价不同的智力拼图都卖了80元,其中一个盈利60%,另一个亏本20%,在这次买卖中,这家玩具店是赔了还是赚了?赔了或赚了多少元?6.某商品的进价为800元,出售时标价为1200元,后来因为该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多打几折?7.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样两件共获利157元,则甲、乙两件服装的成本各是多少元?。

八年级奥数精讲与测试分式方程及其应用(无答案)

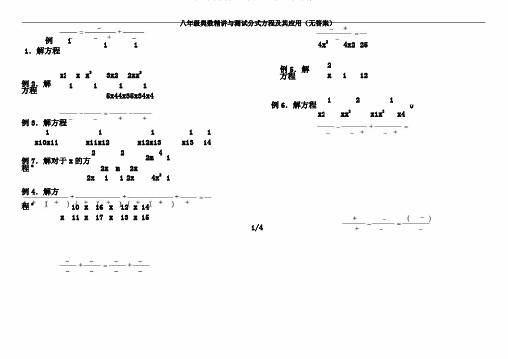
八年级奥数精讲与测试分式方程及其应用（无答案）例1．解方程111例5．解方程4x24x2252x22xx2 x x3x22x112例2．解方程11115x44x35x34x4121例6．解方程2xx2x1x2x x4例3．解方程11111 x10x11x11x12x12x13x1314222m 41例7．解对于x的方程m2x m2x4x212x112x例4．解方程x10x16x12x14x11x17x13x151/4八年级奥数精讲与测试卷一、填空题01.用换元法解方程6x1x2121x4时，一般令_______=y，比较适合。

x102.已知方程x 1a11，则方程x11的x的两个根是a、aa1a a x1根是_______。

03.使分式2x25x 12的值是零时x的值是_______。

x2x1204.若方程12k有增根，则k=_______。

4x2x211705.方程组x y12的解是_______。

1xy1244413b0，则a06.若1a2_______。

a2b772x6有_______个整数解。

07.方程62x2x3x2x3m 08.若x=1是方程1x2的增根，m=_______。

x x1x2x k只有一个根，则k≠_______。

09.若方程0x24分式方程及其应用（无答案）10.解方程4x2-2x+22=1宜用_______法来解，而且设_______=y2x x2较为适合。

二、解答题11.若解分式方程2x m1x1产生增根，求m的值。

x1x2x x12.解分式方程x24x72x72180.x1x24x卷一、填空题2/4八年级奥数精讲与测试x 28x 16 2 22x的解是_______。

01．方程 4x 4 1x2 x 2x202.已知x1+(xy-2)2=0,则 1 1 1xyx1 y1 x2y2 ? 1 _______。

x 1998 y 199803.使2n 3＋n ＋4能被n-3整除的正整数n 的最大值是_______。

特难的解方程奥数练习题

特难的解方程奥数练习题解方程是数学中非常重要的一部分，其中有些题目特别难，需要借助一些特殊的技巧和方法才能解决。

本文将给你介绍几个特难的解方程奥数练习题，并详细阐述解题思路和步骤。

题目一：一元二次方程已知一元二次方程$x^2 - 3x + 2 = 0$，求其解。

解题思路：1. 将方程化为标准形式：$x^2 - 3x + 2 = 0$；2. 利用求根公式：$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$，其中$a=1$，$b=-3$，$c=2$；3. 将数值代入公式，进行计算；4. 得到解：$x_1=1$，$x_2=2$。

题目二：绝对值方程已知绝对值方程$|2x-3| = 5$，求其解。

解题思路：1. 将方程分为两种情况讨论：- 当$2x-3 \geq 0$时，$|2x-3| = 2x-3$，则原方程可化为$2x-3=5$；- 当$2x-3 < 0$时，$|2x-3| = -(2x-3)$，则原方程可化为$-(2x-3)=5$；2. 分别求解上述两个一元方程：- 当$2x-3=5$时，计算得$x=4$；- 当$-(2x-3)=5$时，计算得$x=-1$；3. 综合两种情况的解：$x=4$，$x=-1$。

题目三：分式方程已知分式方程$\frac{x-4}{x+1} + \frac{x+2}{3} = \frac{9}{x+1}$，求其解。

解题思路：1. 将分式方程的分母通分：$(x+1)(3) = 3(x+1)$；2. 化简并合并同类项，得到方程$3(x-4) + (x+2) = 9$；3. 解方程：$4x - 10 = 9$；4. 计算得解$x = \frac{19}{4}$。

题目四：无理方程已知无理方程$\sqrt{x+3} - \sqrt{x+1} + 1 = 0$，求其解。

解题思路：1. 将方程两边移项，得到$\sqrt{x+3} - \sqrt{x+1} = -1$；2. 平方两边，得到$x+3 - 2\sqrt{(x+3)(x+1)} + x+1 = 1$；3. 合并同类项，化简，得到$2x - 2\sqrt{x^2+4x+3} = -1$；4. 平方两边，得到$4x^2 -4x+1 = 4x^2 +16x + 12$；5. 合并同类项，化简，得到$x= \frac{-9}{20}$；6. 检验解，代入原方程，左右两边均为$0$，验证通过。

初中奥数分式方程应用题

关于分式方程奥数题

(完整版)分式方程应用题及答案

初二年级奥数分式方程试题及答案

初中奥数讲义 分式方程(组)附答案

奥数数的方程练习题

初二奥数辅导分式方程的解法

七年级奥数20分式及分式的应用

分式方程应用题总汇和答案

初一奥数之分式方程

初二分式方程应用题及答案

八年级数学竞赛例题专题讲解8：分式方程附答案

初二年级奥数分式方程试题及答案

2019初中奥数分式方程应用题两篇

初中奥数分式方程应用题练习题

八年级奥数精讲与测试分式方程及其应用(无答案)

特难的解方程奥数练习题

初中奥数讲义分式方程(组)附答案