核辐射测量原理课后习题解析
核辐射测量数据处理习题及答案

核数据处理理论知识核辐射测量数据特征:随机性(被测对象测量过程)局限性混合型空间性数据分类:测量型计数型级序型状态型名义型精度:精密度正确度准确度统计误差:核辐射测量中,待测物理量本身就是一个随机变量。
准确值为无限次测量的平均值,实际测量为有限次,把样本的平均值作为真平均值,因此存在误差。
变量分类:(原始组合变换)变量误差来源:(设备方法人员环境被测对象)误差误差分类:系统误差随机误差统计误差粗大误差放射性测量统计误差的规律答:各次测量值围绕平均值涨落二项分布泊松分布高斯分布精度的计算,提高测量精度的方法?答:采用灵敏度高的探测器增加放射源强度增加测量次数延长测量时间减少测量时本底计数放射性测量中的统计误差与一般测量的误差的异同点?答:不同点:测量对象是随机的,核衰变本身具有统计性,放射性测量数据间相差可能很大。
测量过程中存在各种随机因素影响。
相同点:测量都存在误差。
样本的集中性统计量?答:算术平均值几何平均值中位数众数(最大频数)样本的离散性统计量?答:极差方差变异系数或然系数算术平均误差单变量的线性变换方法?答:1.标准化变换 2.极差变换 3.均匀化变换 4.均方差变换单变量的正态化变换方法?答:标准化变化角度变换平方根变换对数变换数据网格化变换的目的?答:1.把不规则的网点变为规则网点 2.网格加密数据网格变换的方法?答:1.插值法(拉格朗日插值三次样条插值距离导数法方位法)2.曲面拟合法(趋势面拟合法趋势面和残差叠加法加权最小二乘拟合法)边界扩充的方法有哪些?答:拉格朗日外推法余弦尖灭法偶开拓法直接扩充法补零法核数据检验目的:1.帮助检查测量系统的工作和测量条件是否正常和稳定,判断测量除统计误差外是否存在其它的随机误差或系统误差2.确定测量数据之间的差异是统计涨落引起的,还是测量对象或条件确实发生了变化引起的变量选择的数学方法:几何作图法(点聚图数轴)相关法(简单相关系数逐步回归分析秩相关系数)秩和检验法谱数据处理—问答题谱的两大特点?答:1.放射性核素与辐射的能量间存在一一对应关系2.放射性核素含量和辐射强度成正比谱光滑的意义是什么?方法有哪些?答:意义1.由于核衰变及测量的统计性,当计数较小时,计数的统计涨落比较大,计数最多的一道不一定是高斯分布的期望,真正峰被湮没在统计涨落中2.为了在统计涨落的影响下,能可靠的识别峰的存在,并准确确定峰的位置和能量,从而完成定性分析,就需要谱光滑3.由于散射的影响,峰边界受统计涨落较大,需要谱光滑方法算术滑动平均法重心法多项式最小二乘法其他(傅里叶变换法)寻峰的方法有哪些?答:简单比较法导数法对称零面积变换法二阶插值多项式计算峰位法重心法拟合二次多项式计算峰位法峰面积计算的意义和方法?答:1)峰面积的计算是定量分析的基础。
核电站辐射测量技术课后题(优秀范文5篇)

核电站辐射测量技术课后题(优秀范文5篇)第一篇:核电站辐射测量技术课后题2.1核辐射测量的分类:一是测量核辐射的粒子数如放射源活度、射线强度及通量密度等;二是测量核辐射粒子的能量。
2.2测量装置包括:辐射源、探测器、电子学记录系统及计算机系统。
2.3低水平放射性测量:辐射防护、环境检测、核电站的辐射测量等通常都是极其微弱的放射性测量被称作低水平放射性测量。
2.4低水平放射性测量通常分3步进行:1.在所关心的地点采集具有代表性的样品;2.用物理或者化学方法处理样品3.测量样品并对测量结果作统计学方面的分析判断。
2.5用于低水平放射性测量的测量装置应该具有这样的特点:能用最少的测量时间得到满足测量精度要求的测量数据,可以探测到的最少样品的放射性活度要大。
(这就需要定义优质因子)2.6本底的主要来源:宇宙射线、周围环境的放射性核素、屏蔽材料及探测器件中的放射性核素2.7降低本底的措施:降低本底,要根据本底的来源,采用不同的措施。
1.铅屏蔽材料中有微量放射性核素,选择放置较长时间的老铅或特殊精练过的铅,可使本底降低2.为减少氡钍射气造成的本底,可以采用有效的通风3.为了降低探测元器件的放射性核素带来的本底,可以采用以石英玻璃代替玻璃壳的光电倍增管,可以先对NAI(T1)晶体经过去钾提纯4.降低宇宙射线中的硬成分的影响可采用反符合屏蔽5.对于接地不良造成的对电子学线路的干扰,可以尽可能缩短放大器与探测器之间的距离,所有电子学仪器都一点接地。
4.1、燃料元件破损监测的方法?①一回路冷却剂γ放射性的连续监测②一回路冷却剂放射性的采样测量③辐照后燃料元件包壳破损的啜漏检测2、燃料元件包壳破损的啜漏检测系统的组成和工作原理?在线:固定在装卸料机上的压缩空气注入单元和抽真空单元;控制和测量单元;记录单元。
离线:水循环采样回路、气体回路、隔热回路;啜漏套筒、过滤器原理:在停堆期间,根据一回路冷却剂放射性跟踪监测提供的信息,将全部或部分燃料燃耗未达到额定值的燃料组件从反应堆卸到燃料水池,先采取在线检测系统对元件包壳破损泄漏监测,进而把泄漏的有破损燃料组件和不带泄漏的完好燃料组件区分开,然后采用离线检测系统定量的测定破损情况。
核辐射探测习题解答

第二章 气体探测器1、设由平行金属板构成的电极系统,极间距离2cm ,内充氩气1.5个大气压,二极板上加了1000伏的电位差。
问正离子由正极表面漂移到负极表面所需的时间为多少? 解:由w p dp εμμμ+++=()=(公式2.6a )和d t w +=得 ddp t u μ+==22 1.51.371000⨯⨯⨯=4.38(ms )2、气体探测器两端收集到的离子对数和两端外加电压存在一定的关系,具体分为哪几个区? 答:复合区、饱和区、正比区、有限正比区、G-M 计数区、连续放电区。
3、设在平行板电离室中α离子的径迹如图所示,径迹长度为L 。
假设沿径迹各处的单位路程上产生的离子对数N 相等,且电子的漂移速度W -,求电子的电流脉冲。
(假设α粒子的径迹是在瞬间完成的)解:(1)当o t t 0<<时,o D L cos t w --=θ eNL I t w D -()= (2)当0max t t t ≤≤时,exN I t w d-()= 由三角形相似,可推知,D tw x cos --=θ因此,New I t D tw Dcos ---()=()θ(3)当max t>t 时,max d t w-= ,I t ()=0 4、离子脉冲电离室与电子脉冲电离室的主要差别是什么?答:(1)工作条件:前者 RC<<T +后者 T -<RC<<T +(2) 脉冲贡献:前者是正离子的贡献,后者是电子飘移贡献;(3)优点:前者可用于测量入射粒子的能量。
后者可获得较高计数率。
(4)缺点:前者脉冲较宽,限制了计数速度。
后者不能精确测量粒子的能量。
5、有一累积电离室,每秒有104,粒子射入其灵敏体积并将全部能量损耗于其中,已知E α=3.5MeV ,电离室内充的纯氩气,试求累积电离室输出的平均电流。
解: 064195.31010 1.61026.4E n e Q ne I t t tαϖ-===⨯=⨯⨯⨯ =3.211010-⨯(A )6、有一充氩的电离室(F=0.2),试计算用它来测定5MeV 的粒子能量时,所能达到的最佳分辨率。
原子核物理及核辐射探测学第6章习题答案new(免费)

Ee
2.04 1.326 MeV 0.511 1 2.04(1 cos57.65)
6-11 解:
I (t ) I 0 e t ln 4 0.277 cm 1 5 cm
-1
6-12 某一能量的 射线在铅中的线性吸收系数为 0.6cm ,试问它的质量吸收系数及原子的 吸收截面是多少?按防护要求,要用多厚的铅容器才能使源射到容器外的 射线强度减弱 1000 倍? 解: (1) 线性吸收系数的定义为: N ,这里 是γ射线与物质相互作用的截面,N 为铅原子数的密度,关于 N,我们可由它的原子量和密度共同得到:
h 代入光子的能量 2.04MeV, 电子质量 0.511MeV tg , m0c 2 2
需要做个转换: 1 ctg
和 20 度角,得到 ctg 20 1 度方向的能量为:
2.04 tg 57.65 ,于是康普顿反冲电子在 20 0.511 2
6-8 试证明入射光子不能与自由电子发生光电效应。 (这是假设初始电子静止的情况计算得 到的,这个结论是可以推广的,因为总可以找到这样的一个参考系) 证明: 对于某个任意能量 E h 的γ光子,其动量为: P
h 。 c
发生光电效应后,光子消失,则自由电子继承γ光子的动能与动量,于是:
质量厚度为: 2.13 10
3
cm 4.1 g/cm3 8.7 103 g/cm 2
6-3 如果已知质子在某一物质中的射程和能量关系曲线,能否从这一曲线求得 d (氘核)与
t (氚核)在同一物质中的射程值?如能够,请说明如何计算。
解:可以。 某种带电粒子在介质中的射程具有这样的特性: M 其中 M 和 z 是入射带电粒子的质量与电荷,F(v)由 R(v ) 2 F (v ) 入射粒子的速度和 z 介质特性决定。 为求得某种能量下 d 和 t 在该介质中 的射程,首先需要 计算出 d 和 t 速度 v 的大小, 然后在质子的射程-能量关系曲线中找出与该速度 v 对应的射 程 Rp 。 由于同样速度下 d 和 t 的动能分别是质子的 2 和 3 倍, 则对具有某个能量 E 的 d 或 t, 只需在质子的射程-能量关系曲线中找到与质子能量 E/2 或 E/3 对应的射程 Rp, 再分别乘以 2 d 和 t 的 M/z 因子即可得到能量为 E 的 d 和 t 在该介质中的射程。即:d 和 t 的射程分别 Rp 的 2 和 3 倍。 6-4 请估算 4MeV 粒子在硅中的阻止时间。已经 4MeV 粒子在硅中射程为 17.8m。 解: 阻止时间:指的是将带电粒子阻止在吸收体内所需的时间。
核辐射探测1234章习题答案

1000 2 cm 2 atn V E 2 u 1.37 4.57 10 cm s P 1. 5 s V cm atm
漂移时间 t d u 2 4.57 10 2 4.37 ms 3.计算出如图所示电离室中在(a)、(b)、(c)三处产生的一对离子因漂移而产生的 I (t ) 、
ph 1.33 10 32 82 5 4.93 10 23 cm 2
E e 661.661 88.001 573.660 KeV
1
对 Fe , Z 26 , K 7.111KeV
ph 1.33 10 32 265 1.58 10 25 cm 2
2
对(a): I (t )
eu 0 ; Q t 0 ; Q 0 。 d eu 1.6 10 19 10 3 I (t ) 0.8 10 16 A d 2 I (t ) 0
( 0 t 2ms ); ( t 2ms )。 ( t 2 ms ); ( t 2ms )。
2.36
F 0.68 N0
式中 N 0 为入射粒子在灵敏体积内产生的离子对数
E 200 10 3 7.60 10 3 W 26.3 取法诺因子 F 0.3 F 0.68 0.3 0.68 2.36 2.36 2.68 10 2 2.68% N0 7.60 10 3 N 0
A
z2 p
R0 3.2 10 4 2 3.88 24.8m
z2 p mp Ep
2. 已知 1MeV 质子在某介质中的电离损失率为 A ,求相同能量的 粒子的电离损失率。 答: 所以 3. 试计算 答: 4. 计算 答:
核辐射测量数据处理习题及答案汇编

核数据处理理论知识核辐射测量数据特征:随机性(被测对象测量过程)局限性混合型空间性数据分类:测量型计数型级序型状态型名义型精度:精密度正确度准确度统计误差:核辐射测量中,待测物理量本身就是一个随机变量。
准确值为无限次测量的平均值,实际测量为有限次,把样本的平均值作为真平均值,因此存在误差。
变量分类:(原始组合变换)变量误差来源:(设备方法人员环境被测对象)误差误差分类:系统误差随机误差统计误差粗大误差放射性测量统计误差的规律答:各次测量值围绕平均值涨落二项分布泊松分布高斯分布精度的计算,提高测量精度的方法?答:采用灵敏度高的探测器增加放射源强度增加测量次数延长测量时间减少测量时本底计数放射性测量中的统计误差与一般测量的误差的异同点?答:不同点:测量对象是随机的,核衰变本身具有统计性,放射性测量数据间相差可能很大。
测量过程中存在各种随机因素影响。
相同点:测量都存在误差。
样本的集中性统计量?答:算术平均值几何平均值中位数众数(最大频数)样本的离散性统计量?答:极差方差变异系数或然系数算术平均误差单变量的线性变换方法?答:1.标准化变换 2.极差变换 3.均匀化变换 4.均方差变换单变量的正态化变换方法?答:标准化变化角度变换平方根变换对数变换数据网格化变换的目的?答:1.把不规则的网点变为规则网点 2.网格加密数据网格变换的方法?答:1.插值法(拉格朗日插值三次样条插值距离导数法方位法)2.曲面拟合法(趋势面拟合法趋势面和残差叠加法加权最小二乘拟合法)边界扩充的方法有哪些?答:拉格朗日外推法余弦尖灭法偶开拓法直接扩充法补零法核数据检验目的:1.帮助检查测量系统的工作和测量条件是否正常和稳定,判断测量除统计误差外是否存在其它的随机误差或系统误差2.确定测量数据之间的差异是统计涨落引起的,还是测量对象或条件确实发生了变化引起的变量选择的数学方法:几何作图法(点聚图数轴)相关法(简单相关系数逐步回归分析秩相关系数)秩和检验法谱数据处理—问答题谱的两大特点?答:1.放射性核素与辐射的能量间存在一一对应关系2.放射性核素含量和辐射强度成正比谱光滑的意义是什么?方法有哪些?答:意义1.由于核衰变及测量的统计性,当计数较小时,计数的统计涨落比较大,计数最多的一道不一定是高斯分布的期望,真正峰被湮没在统计涨落中2.为了在统计涨落的影响下,能可靠的识别峰的存在,并准确确定峰的位置和能量,从而完成定性分析,就需要谱光滑3.由于散射的影响,峰边界受统计涨落较大,需要谱光滑方法算术滑动平均法重心法多项式最小二乘法其他(傅里叶变换法)寻峰的方法有哪些?答:简单比较法导数法对称零面积变换法二阶插值多项式计算峰位法重心法拟合二次多项式计算峰位法峰面积计算的意义和方法?答:1)峰面积的计算是定量分析的基础。
核辐射探测习题解答6

第一章习题答案1. 计算Po 210放射源发射的α粒子()MeV E 304.5=α 在水中的射程。
答:先求α粒子在空气中的射程cm E R 88.3304.5318.0318.05.15.10=⨯==α由1001A A R R ρρ= 对多种元素组成的化合物或混合物,因为与入射粒子的能量相比,原子间的化学键能可以忽略,所以其等效原子量∑=ii i A n A式中i n 为各元素的原子百分数。
对空气而言,81.30=A ,在标准状态下,33010226.1--⋅⨯=cm g ρ,所以04102.3R AR ρ-⨯=对水而言 21631132=+==∑ii i A n A 在水中的射程m R AR μρ8.2488.32102.3102.3404=⨯⨯⨯=⨯=--2. 已知MeV 1质子在某介质中的电离损失率为A ,求相同能量的α粒子的电离损失率。
答:1611144222222,,=⨯⨯=⋅⋅==pp p ppp ion ion E m z E m z v z v z S S αααααα所以 A S ion 16.=α3. 试计算Cs 137KeV E 662=γγ射线发生康普顿效应时,反冲电子的最大能量。
答: MeV h c m h E e 478.0662.02511.01662.02120max ,=⨯+=+=νν4. 计算Cs 137的γ射线对Al Fe Pb ,,的原子光电吸收截面及光电子能量。
从中可得到什么规律性的启迪?已知k ε分别为KeV KeV KeV 559.1,111.7,001.88。
答:Cs 137的γ射线能量为MeV h 662.0=ν,525410625.61371324545Z K ph ⨯⨯⨯⎪⎭⎫ ⎝⎛⨯⨯==-σσ25321033.1cm Z ⨯⨯=-对Pb ,82=Z ,KeV K 001.88=ε()2235321093.4821033.1cm ph --⨯=⨯⨯=σKeV E e 660.573001.88661.661=-=对Fe ,26=Z ,KeV K 111.7=ε()2255321058.1261033.1cm ph --⨯=⨯⨯=σKeV E e 550.654111.7661.661=-= 对Al ,13=Z ,KeV K 559.1=ε()22753210938.4131033.1cm ph --⨯=⨯⨯=σKeV E e 102.660559.1661.661=-=5.试证明γ光子只有在原子核或电子附近,即存在第三者的情况下才能发生电子对效应,而在真空中是不可能的。
核辐射测量原理课后习题解析

第一章 辐射源1、实验室常用辐射源有哪几类?按产生机制每一类又可细分为哪几种?2、选择放射性同位素辐射源时,需要考虑的几个因素是什么? 答题要点:射线能量、放射性活度、半衰期。
3、252Cf 可作哪些辐射源?答题要点:重带电粒子源(α衰变和自发裂变均可)、中子源。
4、137Cs 和60Co 是什么辐射源?能量分别为多少? 答题要点:γ辐射源;137Cs :0.662MeV 或0.661MeV ; 60Co :1.17MeV 和1.33MeV ;第二章 射线与物质的相互作用1、某一能量的γ射线在铅中的线性吸收系数是0.6cm -1,它的质量吸收系数和原 子的吸收截面是多少?按防护要求,源放在容器中,要用多少厚度的铅容器才能 使容器外的γ强度减为源强的1/1000? 解:已知μ=0.6cm -1,ρ=11.34g/cm 3,则由μm =μ/ρ得质量吸收系数μm =0.6/11.34cm 2/g=0.0529 cm 2/g 由 得原子的吸收截面: A m N Aγμμσρ==232322070.0529 6.02101.8191018.19m A A N cm bγσμ-⎛⎫==⨯ ⎪⨯⎝⎭≈⨯=由 得:()000111000ln ln 33ln 10 2.311.50.60.6I I t I I cm μμ⎛⎫⎛⎫ ⎪== ⎪ ⎪⎝⎭ ⎪⎝⎭==⨯=或由 得01()1000I t I =时铅容器的质量厚度t m 为: ()()()000332111000ln ln11ln 10ln 100.052933 2.3ln 100.05290.0529130.435/m m m m I I t I I g cm μμμ--⎛⎫⎛⎫ ⎪=-=- ⎪ ⎪⎝⎭ ⎪⎝⎭=-=-⨯==≈10、如果已知质子在某一物质中的射程和能量关系曲线,能否从这一曲线求得d (氘核)与t (氚核)在物质中的射程值?如果能够求得,请说明如何计算? 答题要点:方式一:若已知能量损失率,从原理上可以求出射程: 整理后可得:在非相对论情况下:()m m t I t I e μ-=0()t I t I e μ-=0001(/)RE E dE R dx dxdE dE dE dx ===-⎰⎰⎰0202404πE m v R dEz e NB=⎰22E v M =0024'02πE m E R dE z e NM B=⎰212E Mv =则在能量相同的情况下:从而得:方式二:若已知能量损失率,从原理上可以求出射程: 整理后可得:在非相对论情况下:从而得: 在速度v 相同的情况下,上式积分项相同,则12、当10MeV 氘核与10MeV 电子穿过铅时,请估算他们的辐射损失之比是多少?当20MeV 电子穿过铅时,辐射损失与电离损失之比是多少? 答题要点:已知辐射能量损失率理论表达式为:对于氘核而言,m d =1875.6139MeV ;对于电子而言,m e =0.511MeV ,而它们的电荷数均为1,则10MeV 的氘核与10MeV 的电子穿过铅时,它们的辐射损失率之比为:22222228222220.5117.42101857.6139d e d e de e d Z Z Z m Z NE Z NE m m Z m -==≈⨯222NZm E z dx dE S radrad∝⎪⎭⎫ ⎝⎛-=00001(/)R E E dE R dx dx dEdEdE dx ===-⎰⎰⎰0202404πE m v R dEz e NB =⎰212E Mv =dE Mvdv =21222211R M z R M z =0302404πv m Mv R dv z e N B=⎰222222aa ab ab b b ab a ba bb aM R M z z M R M z z M z R R M z ==⋅=⋅⋅22212211M z R R M z =E e =20MeV 时,在相对论区,辐射损失和电离损失之比有如下表达式:()()700re ZE dE dx dE dx -=-则 20MeV 的电子穿过铅时,辐射损失和电离损失之比为:20822.34700⨯≈第三章 核辐射测量的统计误差和数据处理3 本底计数率是10±1s -1,样品计数率是50±2s -1, 求净计数率及误差。
哈工程辐射探测习题答案

E Z ,这里 E 为电子的动能,Z 为介质的原子序数,分别代入 20MeV 700
和 82,于是:
4MeV 的α粒子还不是相对论粒子,因此:
dE / dx rad dE / dx ion
20 82 =2.34 700
E
1 Mv 2 , v 2
2E 2E 2E c , v kv kc ,这里 k 一般取 0.6 而非匀减 M Mc 2 Mc 2
6. 若在时间 t 内,放射源放出粒子的平均数为 n 100 ,试求: 1. 2. 在相同时间内放出 n=108 个粒子的概率; 出现绝对偏差 n n 6 的概率
第八章习题答案
1. 为什么射线在气体中产生一对离子对平均消耗的能量要比气体粒子的电离能大? 答:射线与气体原子或分子的作用过程中,除使气体原子或分子电离外,还可使其激发 而损失能量,这部分能量包括在产生一对离子对平均消耗的能量中。
4. 试证明入射光子不能与自由电子发生光电效应。 证明: 对于某个任意能量 E h 的γ光子,其动量为: P
速时的 0.5,则:
T
R R R Mc 2 Ma 7 , T 1.2 10 R ,R 的单位是 m,M 的单位是原子质 v kv kc 2E E
h 。 c
i 1 4
N
i 1 4
b ,i
222.85 21.2 201.65/ min
b ,i
t
i 1
S ,i
t
i 1
2. 进行放射性测量时, 若要求计数率的相对误差不大于 1%,2%,5%时, 要求总的计数 N 应分 别不小于多少? 解: 由 N ( ) 2 ,则总计数分别对应 10000,2500,400。
核辐射探测学习题参考答案(修改)

第一章射线与物质的相互作用1.不同射线在同一物质中的射程问题如果已知质子在某一物质中的射程和能量关系曲线,能否从这一曲线求得d (氘核)与t (氚核)在同一物质中的射程值?如能够,请说明如何计算?解:P12”利用Bethe 公式,也可以推算不同带点例子在某一种吸收材料的射程。
”根据公式:)()(22v R M M v R b ab b a a Z Z =,可求出。
步骤:1先求其初速度。
2查出速度相同的粒子在同一材料的射程。
3带入公式。
2:阻止时间计算:请估算4MeV α粒子在硅中的阻止时间。
已知4MeV α粒子的射程为17.8μm 。
解:解:由题意得 4MeV α粒子在硅中的射程为17.8um 由T ≌1.2×107-REMa,Ma=4得 T ≌1.2×107-×17.8×106-×44()s =2.136×1012-()s3:能量损失率计算课本3题,第一小问错误,应该改为“电离损失率之比”。
更具公式1.12-重带点粒子电离能量损失率精确表达式。
及公式1.12-电子由于电离和激发引起的电离能量损失率公式。
代参数入求解。
第二小问:快电子的电离能量损失率与辐射能量损失率计算:()20822.34700700()rad iondE E Z dx dEdx*⨯≅=≈4光电子能量:光电子能量:(带入B K ) 康普顿反冲电子能量:200.511m c Mev =ie hv E ε-=220200(1cos ) 2.04(1cos 20) 4.16160.060.3947(1cos )0.511 2.04(1cos 20)0.511 2.040.06Er Ee Mev m c Er θθ--⨯====+-+-+⨯5:Y 射线束的吸收解:由题意可得线性吸收系数10.6cm μ-=,311.2/pb g cm ρ=12220.6 5.3610/11.2/m pb cm cm g g cmμμρ--∴===⨯质量吸收系数 由r N μσ=*可得吸收截面:12322230.61.84103.2810/r cm cm N cm μσ--===⨯⨯ 其中N 为吸收物质单位体积中的原子数2233.2810/N cm =⨯ 0()t I t I e μ-=要求射到容器外时强度减弱99.9% 0()0.1%0.001t I t e I μ-∴=∴=即t=5In10 =11.513cm6:已知)1()(tι--=e A t f t 是自变量。
核辐射探测习题解答7

μ x
θ
μ = 0.6
1 ?6.907755 x= = 1000 = = 11.51(cm) ?μ ?0.6 ?0.6 ln ln
6.当电子在铝中的辐射损失是全部能量损失的 1/4 时,试估计电子的动能。27MeV 的电子 在铝中的总能量损失率是多少? 解:
3
3
dE dE dE ) = (? ) rad + (? )ion dX dX dX dE (? )rad 1 已知 dX = 得到 dE 4 (? ) dX dE 1 (? ) rad 1 dX =4= dE 3 3 (? )ion dX 4 (?
11. 一个 2MeV 的γ光子射在探测器上,遭受两次相继的康普顿散射逃离。若两次散射的散 射角度分别是 解: 由 Er =
'
I I0
30 和60 ,沉积在探测器中的反冲电子的总能量是多少?
Er Er 1+ (1 ? 轨道电子屏蔽时
(?
4 z 2 NEe 2 2 Ee 1 dE ) rad = re (ln ? ) dX 137 me c 2 3
2.7 × 6.022 × 1023 × 27 2 × 27 1 27 = × (2.82 × 10?13 )2 [ln ? ] 137 0.511 3 = 6.38 ×10 2 × 1023 × 10?26 × (4.66 ? 0.33) = 2.76 MeV / cm dE (? )rad ( Ee + me c 2 ) × z 357.643 dX 根据 = = = 0.437 dE 1600 × me c 2 817.6 (? )ion dX 4 × 132 ×
核辐射测量原理-作业答题要点.doc配套清华大学,复旦大学,北京大学合编的原子核物理实验方法

第一章 辐射源1、谈谈你所感兴趣的一种辐射源。
答题要点(略)。
第二章 射线与物质的相互作用8、10MeV 的氘核与10MeV 的电子穿过铅时,它们的辐射损失率之比是多少?20MeV 的电子穿过铅时,辐射损失和电离损失之比是多少?解:已知辐射能量损失率理论表达式为:对于氘核而言,m d =1875.6139MeV ;对于电子而言,m e =0.511MeV ,则10MeV 的氘核与10MeV 的电子穿过铅时,它们的辐射损失率之比为:222222822227.4210d e d e d e e dZ Z Z m Z NE Z NE m m Z m -=≈⨯Ee=20MeV 时,在相对论区,辐射损失和电离损失之比有如下表达式:()()800r e ZE dE dx dE dx -=-则 20MeV 的电子穿过铅时,辐射损失和电离损失之比为:2082 2.05800⨯≈ 11、某一能量的γ射线在铅中的线性吸收系数是0.6cm -1,它的质量吸收系数和原子的吸收截面是多少?这γ射线的能量是多少?按防护要求,源放在容器中,要用多少厚度的铅容器才能使容器外的γ强度减为源强的1/1000? 解:已知μ=0.6cm -1,ρ=11.34g/cm 3,则由μm=μ/ρ得质量吸收系数μm=0.6/11.34cm 2/g=0.0529 cm 2/g由 得原子的吸收截面: 232322070.0529 6.02101.8191018.19m A A N cm bγσμ-⎛⎫==⨯ ⎪⨯⎝⎭≈⨯= 查γ射线与物质相互作用截面和元素的质量衰减系数表可知,在μm=0.0517cm 2/g 时相对应的γ射线的能量为1.5 MeV ,μm=0.0703 cm 2/g 时,222NZ m E z dx dE S radrad ∝⎪⎭⎫ ⎝⎛-=A m N Aγμμσρ==相对应的γ射线的能量为1.0 MeV ,如果以y 轴表示能量,x 轴表示质量吸收系数,则相对应的两个点(x1,y1)、(x2,y2)分别为(0.0517,1.5)、(0.0703,1.0):利用插值与多项式逼近中的拉格朗日逼近:21121221x x x x y y y x x x x --=+--可得μm =0.0529 cm 2/g 时所对应的能量:0.05290.07030.05290.05171.5 1.00.05170.07030.07030.0517174121.5 1.01861861.50.935 1.00.0651.4030.065 1.468y MeV--=⨯+⨯--=⨯+⨯=⨯+⨯=+=(这里用的是两点式逼近,同学们有兴趣的话可以查表多找几个点用多项式逼近计算)由 得01()1000I t I =时铅容器的质量厚度t m 为: ()()()000332111000ln ln 11ln 10ln 100.052933 2.3ln 100.05290.0529130.435/m m m m I I t I I g cm μμμ--⎛⎫⎛⎫ ⎪=-=- ⎪ ⎪⎝⎭ ⎪⎝⎭=-=-⨯==≈ 或由 得: ()000111000ln ln 33ln 10 2.311.50.60.6I I t I I cm μμ⎛⎫⎛⎫ ⎪== ⎪ ⎪⎝⎭ ⎪⎝⎭==⨯=第三章 放射性测量中的统计涨落3、本底计数率是500±20min -1,样品计数率是750±25min -1,求净计数率及误差。
核辐射探测习题解答2

第七章作业答案1.设测量样品的平均计数率是5计数/s,使用泊松分布公式确定在任1s 内得到计数小于或等于2个的概率。
解:51525(,)!5(0;5)0.00670!5(0;5)0.03371!5(0;5)0.08422!NNr r r r N P N N e N P e P e P e ----=⋅=⋅==⋅==⋅= 在1秒内小于或等于2的概率为:(0;5)(1;5)(2;5)0.00670.03370.08420.1246r r r P P P ++=++=2.若某时间内的真计数值是100,求得到计数为104的概率。
解:高斯概率密度函数为:222220.012102()2(100104)4(;,)100,10104(104;100;10)0.0145N N P N N e N N P e e σσσ⋅-----======== 5.本底计数率n b =15计数/min,测量样品计数率n 0=60计数/min,试求对给定的测量时间t b +t s 来说净计数率精确度最高时的最优比值t b /t s ;若净计数率的误差为5%,t b 和t s 的最小值是多少?解:2:2:1s b s b t t t t ====若要使净计数率的误差为5%1122222211222222()60(6015)17.778().(6015).(5%)()15(6015)8.889().(6015).(5%)s s s s b s s b n b s b b s b n n n n t n n n n n t n n δδ+⋅+⋅===--+⋅+⋅===-- 6.为了探测α粒子,有两种探测器可以选择,一种的本底为7计数/min,效率为0.02;另一种的本底为3计数/min,效率为0.016,对于低水平测量工作,应选用哪一种探测器更好些?解:Q 为探测器的优质因子,其值越大,探测器性能越好。
2251252120.02 5.71070.0168.53103bQ n Q Q Q Q --===⨯==⨯<∑∴选用效率为0.016的探测器更好.。
核辐射物理与探测学课后习题

核辐射物理与探测学课后习题第一章原子核的基本性质1-1 当电子的速度为18105.2-?ms 时,它的动能和总能量各为多少?1-2 将α粒子的速度加速至光速的0.95时,α粒子的质量为多少? 1-5 已知()()92,23847.309,92,23950.574MeV MeV ?=?= ()()92,23540.921,92,23642.446MeV MeV ?=?=试计算239U ,236U 最后一个中子的结合能。
1-8 利用结合能半经验公式,计算U U 239236,最后一个中子的结合能,并与1-5式的结果进行比较。
第二章原子核的放射性2.1经多少半衰期以后,放射性核素的活度可以减少至原来的3%,1%,0.5%,0.01%?2.7 人体内含%18的C 和%2.0%的K 。
已知天然条件下C C 1214与的原子数之比为12102.1,C 14的573021=T 年;K 40的天然丰度为%0118.0,其半衰期a T 911026.1?=。
求体重为Kg 75的人体内的总放射性活度。
2-8 已知Sr 90按下式衰变:Zr Y Sr h a 9064,901.28,90??→→?--ββ(稳定) 试计算纯Sr 90放置多常时间,其放射性活度刚好与Y 90的相等。
2-11 31000cm 海水含有g 4.0K 和g 6108.1-?U 。
假定后者与其子体达平衡,试计算31000cm 海水的放射性活度。
第三章原子核的衰变3.1 实验测得Ra 226的α能谱精细结构由()%95785.41MeV T =α和()%5602.42MeV T =α两种α粒子组成,试计算如下内容并作出Ra 226衰变网图(简图)(1)子体Rn 222核的反冲能;(2)Ra 226的衰变能;(3)激发态Rn 222发射的γ光子的能量。
3.2 比较下列核衰变过程的衰变能和库仑位垒高度:Th He U 2304234+→;Rn C U 22212234+→;Po O U 21816234+→。
核辐射探测习题解答5.

第一章习题1. 计算Po 210放射源发射的α粒子()MeV E 304.5=α 在水中的射程。
2. 已知MeV 1质子在某介质中的电离损失率为A ,求相同能量的α粒子的电离损失率。
3. 试计算Cs 137KeV E 662=γγ射线发生康普顿效应时,反冲电子的最大能量。
4. 计算Cs 137的γ射线对Al Fe Pb ,,的原子光电吸收截面及光电子能量。
从中可得到什么规律性的启迪?已知k ε分别为KeV KeV KeV 559.1,111.7,001.88。
5.试证明γ光子只有在原子核或电子附近,即存在第三者的情况下才能发生电子对效应,而在真空中是不可能的。
第二章习题1. 为什么射线在气体中产生一对离子对平均消耗的能量要比气体粒子的电离能大?2. 设一由二平行金属板构成的电极系统,极间距离2cm ,内充氩气1.5大气压,二极板上加了1000伏的电位差。
问正离子+A 由正极表面漂移到负极表面所需时间为何?3.计算出如图所示电离室中在(a)、(b)、(c)三处产生的一对离子因漂移而产生的)(t I +、)(t I -、)(t Q +、)(t Q -以及+Q 、-Q 分别为何?(假定所加电压使电子漂移速度为105cm/s ,正离子漂移速度为103cm/s )。
4.画出下列各种输出电路的等效电路,并定性地画出输出电压脉冲形状,标明极性及直流电位。
题4之图5.有一累计电离室,每秒有104个α粒子射入其灵敏体积并将全部能量损耗于其中。
已知3.5=αE MeV ,电离室内充的纯氩气,试求出累计电离室输出的平均电流=0I ?6.在上题条件下,若选择输出电路之Ω10010=R ,pf C 200=,问该电离室输出电压信号的相对均方根涨落为何?7.为什么圆柱形电子脉冲电离室的中央极必须为正极?8.试说明屏栅电离室栅极上感应电荷的变化过程。
9.什么屏栅电离室的收集极必须是正极?10.离子脉冲电离室与电子脉冲电离室的主要差别是什么?11.累计电离室所能测的最大幅射强度受何因素限制?脉冲电离室呢?12.为什么正比计器的中央丝极必须是正极?13.圆柱形电子脉冲电离室的输出电荷主要是由电子所贡献,但在圆柱形正比计数器中输出电荷却主要是正离子的贡献,这是什么原因?14.有一充氩之正比计数器。
《核辐射探测学》研究生课程习题与思考题

《核辐射探测学》研究生课程习题与思考题第一套1. 当电子的速度为2.5×108m/s 时,它的动能和总能量各为多少MeV ?2. 已知32P ,14C ,238U 的半衰期分别为14.26d,5370a,4.468×109a ,试求它们的衰变常数(以s -1为单位)。
3.238Pu 的重要用途之一为制造核电池。
假定238Pu (1/2T 87.75, 5.4992a E MeV α==)的α衰变能的5%转变为电能,当电池的输出 功率为20W 时,此电池应装多少克238Pu ?4. 确定下列核反应中的未知粒子x :(a) 188(,)O d p x , (b) 8739(,)x p Y α , (c) 1231245253(,)Te x d I 。
5. 试计算234U 和241m A 的裂变阈能。
第二套1. 已知: △(92,238)= 47.307MeV ; △(92,239) = 50.572MeV ; △ ( 92, 235) = 40.916MeV ; △(92,236)= 42.442MeV ; 试计算239U,236U 最后一个中子的结合能。
2. 计算下面1.0Ci 的放射源的原子核数?(a )18F ; (b)14C ; (c)222Rn ; (d)235U 。
3. 设Bb (A,Z ),Bb (4He ),Bb (A-4,Z-2)分别为母核、α粒子、子核的结合能,试证明 4Bb(A-4,Z-2)+Bb(He)-Bb(A,Z)Q α=。
4. 能量为6MeV 的质子投射到静态的12C 核上,试求质心的运动速度,取质子的质量为1u 。
5. 设一个聚变堆的功率为100万kW ,以d+T 为燃料,试计算一年要消耗多少氘?这么大功率的电站,若改用煤作燃料,则每年要消耗多少煤(煤的燃料热约为3.3×710 J/kg )?第三套1. 当质子在球形核里均匀均匀分布时,原子核的库仑能为:203(1)54C e Z Z E Rπ-=ε Z 为核电荷数,R 为核半径,r 0 取1.5×10-15m 。
核辐射探测复习题第二章练习题答案
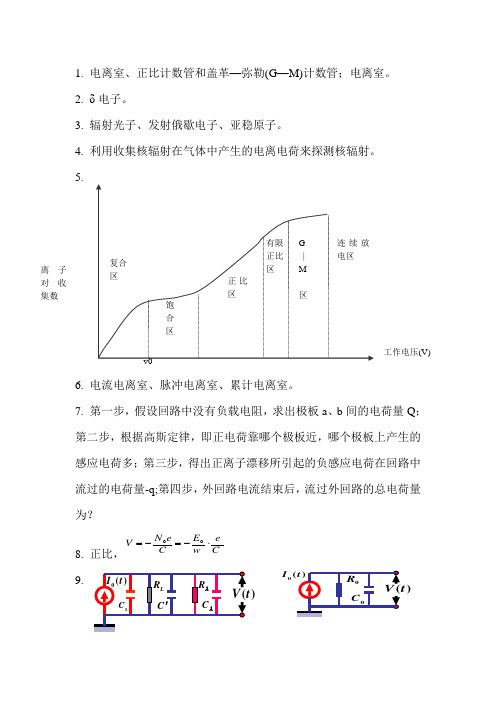
复合 区饱合 区正比区有限 正比 区G | M 区工作电压(V)离子对收集数v0连续放电区1. 电离室、正比计数管和盖革—弥勒(G —M)计数管;电离室。
2. δ电子。
3. 辐射光子、发射俄歇电子、亚稳原子。
4. 利用收集核辐射在气体中产生的电离电荷来探测核辐射。
5.6. 电流电离室、脉冲电离室、累计电离室。
7. 第一步,假设回路中没有负载电阻,求出极板a 、b 间的电荷量Q ;第二步,根据高斯定律,即正电荷靠哪个极板近,哪个极板上产生的感应电荷多;第三步,得出正离子漂移所引起的负感应电荷在回路中流过的电荷量-q;第四步,外回路电流结束后,流过外回路的总电荷量为? 8. 正比,Cew E C e N V ⋅-=-=009.λR λCLR C '1C)(0t I )(t V 0C)(0t IR )(t V10. 脉冲幅度谱峰值一半处所对应的全宽度称为半高宽,用FWHM表示,V V FW HM σ355.2=∆=;能量分辨率定义为探测器微分脉冲幅度分布谱中的特征峰半高宽与峰值所对应的脉冲幅度之比,用η表示,EEV V ∆=∆=ηη或 11. 入射带电粒子进入正比计数管灵敏体积后,使气体分子或原子电离,生成N0个离子对(初电离)。
初电离电子在电场作用下向中心阳极漂移过程中,不断和气体分子或原子碰撞而损失能量,又不断地从电场获得能量,离中心收集极越近,电场越强,在r=r0处,电场强度足够大,可以使初电离电子获得更大冲量而使气体分子或原子电离(次电离),次电离电子又会产生新的次电离。
于是电子不断地增殖,增殖的结果将产生大量的电子和正电子,这就是气体放大的过程。
12. 非自持放电、同轴圆柱型。
13. 坪特性。
14. 【优点】:制造简单,价格便宜,易于操作,输出脉冲幅度大,对电子学线路要求简单;【缺点】:死时间长,不能用于高计数率场合。
15. 10≈νM16. ①G-M 计数管的电荷增殖主要是由光电子引起的雪崩决定的,而正比计数管主要是由电离电子引起;②正比计数管每次雪崩在管内都是对应于入射辐射产生初始自由电子的那一侧,即气体放大只是在管内局部区域发生,而对于G-M 技术管,光子是各个方向发射的,所以雪崩放大是在整个管子范围内,不管初始电离发生在管内何处,雪崩放电都会逐渐包围整个阳极丝。
【精品】核辐射探测学习题参考答案(修改).doc

E e =hv-与第一章射线与物质的相互作用1.不同射线在同一物质中的射程问题如果已知质子在某一物质中的射程和能量关系曲线,能否从这一曲线求得d (兔核)与t (M 核)在同一物质中的射程值?如能够,请说明如何计算?解:P12”利用Bethe 公式,也可以推算不同带点例子在某一种吸收材料的射M程。
"根据公式:R«(v ) =」^Rb (v ),可求出。
MZ步骤:1先求其初速度。
2查出速度相同的粒子在同一材料的射程。
3带入公式。
2:阻止时间计算:请估算4MeVa 粒子在硅中的阻止时间。
伽 4MeV a 粒子的射程为17.8 u m 。
解:解:由题意得4MeVa 粒子在硅中的射程为17. 8um由 TM1.2X10—7R J 平,Ma=4 得T 竺1. 2X 10一7 X17. 8X 10一6 X =2. 136 X 10-口($)3:能量损失率计算课本3题,第一小问错误,应该改为“电离损失率之比”。
更具公式1.12-重 带点粒子电离能量损失率精确表达式。
及公式1.12-电子由于电离和激发引起的 电离能量损失率公式。
代参数入求解。
第二小问:快电子的电离能量损失率与辐射能量损失率计算:= 20x82 @ ? 34(dE/) — 700700' / dxJlon4光电子能量:光电子能量:(带入B K ) 康普顿反冲电子能量:m o c 2 = 0.511Mev2.042(1 —cos 20。
) = 1.84x10-23(^2厂 Er 2(l-cos0) 2.042(1 —cos 20°) 4.1616x0.06 八。
〜、,Be = ------------------------- — -------------------------------- —------------------------- — n m 0c 2+Er(l-cos^) 0.511 + 2.04(1-cos 20°) 0.511 + 2.04x0.06 '5:Y 射线束的吸收解:由题意可得线性吸收系数n = Q.6cm~', p pb = 11.2g /cm质量吸收系叽=土= °成〃广,=5.36x 10~2cm 2 /gPpb lL2g/cm 由〃 =b,. * N 可得吸收截面:以 _0.6cm -1万—3.28x1()22 /c 〃3其中N 为吸收物质单位体积中的原子数N = 3.28X 1()22 /凯3I(t) = y 要求射到容器外时强度减弱99.9%坐=0.1% .•"*= 0.00唧t=5Inl0 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 辐射源
1、实验室常用辐射源有哪几类?按产生机制每一类又可细分为哪几种?
2、选择放射性同位素辐射源时,需要考虑的几个因素是什么? 答题要点:射线能量、放射性活度、半衰期。
3、252Cf 可作哪些辐射源?
答题要点:重带电粒子源(α衰变和自发裂变均可)、中子源。
4、137Cs 和60Co 是什么辐射源?能量分别为多少? 答题要点:γ辐射源;
137
Cs :0.662MeV 或0.661MeV ; 60
Co :1.17MeV 和1.33MeV ;
第二章 射线与物质的相互作用
1、某一能量的γ射线在铅中的线性吸收系数是0.6cm -1,它的质量吸收系数和原 子的吸收截面是多少?按防护要求,源放在容器中,要用多少厚度的铅容器才能 使容器外的γ强度减为源强的1/1000? 解:
已知μ=0.6cm -1,ρ=11.34g/cm 3,
则由μm =μ/ρ得质量吸收系数μm =0.6/11.34cm 2/g=0.0529 cm 2/g 由 得原子的吸收截面: A m N A
γ
μ
μσρ==
23
232
207
0.0529 6.02101.8191018.19m A A N cm b
γσμ-⎛⎫==⨯ ⎪⨯⎝⎭
≈⨯=
由 得:
()00011
1000ln ln 33ln 10 2.311.50.60.6
I I t I I cm μμ⎛⎫⎛⎫ ⎪
== ⎪ ⎪⎝⎭ ⎪
⎝⎭==⨯=
或由 得01
()1000
I t I =
时铅容器的质量厚度t m 为: ()()()0003
32111000ln ln
11ln 10ln 100.052933 2.3
ln 100.05290.0529130.435/m m m m I I t I I g cm μμμ--⎛⎫
⎛⎫ ⎪=-=- ⎪ ⎪⎝⎭ ⎪
⎝⎭
=-=-⨯=
=≈
10、如果已知质子在某一物质中的射程和能量关系曲线,能否从这一曲线求得d (氘核)与t (氚核)在物质中的射程值?如果能够求得,请说明如何计算? 答题要点:
方式一:
若已知能量损失率,从原理上可以求出射程: 整理后可得:
在非相对论情况下:
()m m t I t I e μ-=0()t I t I e μ-=00
01(/)
R
E E dE R dx dx
dE dE dE dx ===-⎰⎰⎰02
02404πE m v R dE
z e NB
=⎰22E v M =00
24'02πE m E R dE z e NM B
=⎰212
E Mv =
则在能量相同的情况下:
从而得:
方式二:
若已知能量损失率,从原理上可以求出射程: 整理后可得:
在非相对论情况下:
从而得: 在速度v 相同的情况下,上式积分项相同,
则
12、当10MeV 氘核与10MeV 电子穿过铅时,请估算他们的辐射损失之比是多少?当20MeV 电子穿过铅时,辐射损失与电离损失之比是多少? 答题要点:已知辐射能量损失率理论表达式为:
对于氘核而言,m d =1875.6139MeV ;对于电子而言,m e =0.511MeV ,而它们的电荷数均为1,则10MeV 的氘核与10MeV 的电子穿过铅时,它们的辐射损失率之比为:
2
222
22
28
22222
0.5117.42101857.6139d e d e d
e e d Z Z Z m Z NE Z NE m m Z m -==≈⨯
2
22NZ
m E z dx dE S rad
rad
∝⎪⎭⎫ ⎝⎛-=000
01
(/)R E E dE R dx dx dE
dE
dE dx ===-⎰
⎰⎰02
02404πE m v R dE
z e NB =⎰2
1
2
E Mv =
dE Mvdv =2
1
222211R M z R M z =
0302404πv m M
v R dv z e N B
=⎰22
2
22
2a
a a
b a
b b b a
b a b
a b
b a
M R M z z M R M z z M z R R M z ==⋅=⋅⋅2
22
12
2
11M z R R M z =
E e =20MeV 时,在相对论区,辐射损失和电离损失之比有如下表达式:
()()700r
e ZE dE dx dE dx -=
-
则 20MeV 的电子穿过铅时,辐射损失和电离损失之比为:
2082
2.34700
⨯≈
第三章 核辐射测量的统计误差和数据处理
3 本底计数率是10±1s -1,样品计数率是50±2s -1, 求净计数率及误差。
答题要点:
由50±2s -1可知样品的n s =50s -1,σs =2s -1 由10±1s -1可知本底的n b =10s -1,σb =1s -1
则净计数率:11
0(5010)40n s s --=-=
误差:0 2.236σ====
数据结果表示:1
00
(40 2.236)n s σ-±=± 4、样品测量时间为480s ,得平均计数率为25s -1,本底测量时间为240s ,得平均计数率18s -1,求样品的净计数率及误差。
答题要点:
由已知条件1
1
s 480,25;240,18s b b t s n s t s n s --====
得1
10(2518)7s b n n n s s --=-=-=
又
s N
s
s t σσ=====
b B
b
b
t σσ=
=
=
==
由0σ=
得:
0.36σ====≈≈
数据结果表示:
1
00
(70.36)
n s
σ-
±=±
6 某放射性测量中,测得样品计数率约20s-1,本底计数率约为4s-1。
若要求测量误差≤1%,求测量样品和本底的时间各取多少?
答题要点:
由题意可知n s=20s-1, n d=4s-1, υn ≤1℅
由公式:
min2
2
1
1
b n
T
n v
=
⎫
⎪
⎭
可得测量误差υn ≤1℅时实验需要的最小测量时间T min
(
)()(
)()
()
min22
2
2
4
2
11
40.011
40.011
110
27.3min
6.112
40.01 1.528
T s s
s s
≥=
⨯⨯
⨯⨯
==≈
⨯⨯
由
,
s b
t t
==得:
2.236
27.3min27.3min18.9min
3.236
1
27.3min27.3min8.4min
3.236
s
b
t
t
==⨯=
==⨯=。
