[实用参考]勾股定理拓展提高题

合集下载

(2021年整理)勾股定理拓展提高题

(完整版)勾股定理拓展提高题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)勾股定理拓展提高题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)勾股定理拓展提高题的全部内容。

（完整版）勾股定理拓展提高题编辑整理：张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是我们任然希望 (完整版）勾股定理拓展提高题这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为 <(完整版)勾股定理拓展提高题> 这篇文档的全部内容。

B A6cm3cm1cmCBA勾股定理拓展提高题1、如图,长方体的底面边长分别为1cm 和3cm,高为6cm ．①如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ，那么所用细线最短需要__________cm ；②如果从点A 开始经过4个侧面缠绕3圈到达点B ，那么所用细线最短需要__________cm ．2、如图1，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数_________图1 图2 图33、如图2，直线l 上有三个正方形a b c ，，，若a c ，的面积分别为5和11，则b 的面积4、如图3，数轴上的点A 所表示的数为x,则x 2-10的立方根为5、如图4,一只蚂蚁沿棱长为a 的正方体表面从顶点A 爬到顶点B,则它走过的最短路程为图4 图56、2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图5所示）．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边为a ，较长直角边为b,那么()2b a +的值为（）（A ）13 (B)19 （C)25 （D ）169• •ABADEBC7、已知△ABC 的三边长满足18,10==+ab b a ，8=c ，则为三角形8、如图，铁路上A ，B 两点相距25km ，C ，D 为两村庄,DA⊥AB 于A ，CB⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个土特产品收购站E ，使得C ，D 两村到E 站的距离相等，则E 站应建在离A 站多少km 处？9、已知：正方形ABCD 的边长为1，正方形ABCD 的边长为1，正方形EFGH 内接于ABCD ，AE=a,AF=b ，且32=EFGH S 正方形。

[实用参考]勾股定理及其逆定理复习典型例题

勾股定理及其逆定理复习典型例题1. 勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

（即：a 2+b 2=c 2）2.勾股定理的逆定理：如果三角形的三边长：a 、b 、c 有关系a 2+b 2=c 2，那么这个三角形是直角三角形。

3. 勾股定理与勾股定理逆定理的区别与联系4. 区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理5. 联系：勾股定理与其逆定理的题设和结论正好相反，都与直角三角形有关。

6. 如果用勾股定理的逆定理判定一个三角形是否是直角三角形7. （1）首先确定最大边（如：C ，但不要认为最大边一定是C ）8.（2）验证c 2与a 2+b 2是否具有相等关系，若c 2=a 2+b 2，则△ABC 是以∠C 为直角的三角形。

（若c 2>a 2+b 2则△ABC 是以∠C 为钝角的三角形，若c 2<a 2+b 2则△ABC 是以∠C 为锐角三角形）二、例题分析例1、若直角三角形两直角边的比是3：4，斜边长是20，求此直角三角形的面积。

解：设此直角三角形两直角边分别是3R ，4R ，根据题意得：（3R ）2+（4R ）2=202 化简得R 2=16；∴直角三角形的面积=21×3R ×4R =6R 2=96 注：直角三角形边的有关计算中，常常要设未知数，然后用勾股定理列方程（组）求解。

例2、等边三角形的边长为2，求它的面积。

解：如图，等边△ABC ，作AD ⊥BC 于D则：BD=21BC （等腰三角形底边上的高与底边上的中线互相重合）∵AB=AC=BC=2（等边三角形各边都相等） ∴BD=1在直角三角形ABD 中AB 2=AD 2+BD 2，即：AD 2=AB 2－BD 2=4－1=3 ∴AD=3S △ABC =21BC·AD=3ABCD注：等边三角形面积公式：若等边三角形边长为a ，则其面积为43a 例3、直角三角形周长为12cm ，斜边长为5cm ，求直角三角形的面积。

股市勾股定理

股市勾股定理
（原创实用版）
目录
1.股市勾股定理的概念和原理
2.股市勾股定理的应用
3.股市勾股定理的优缺点
正文
1.股市勾股定理的概念和原理
股市勾股定理，是一种在股票市场中，通过计算三角形斜边长度来预测股票价格的方法。

它的原理来源于数学中的勾股定理，即在直角三角形中，斜边的平方等于两直角边的平方和。

在股市勾股定理中，直角边代表股票价格的变动幅度，而斜边则代表股票价格的平均变动幅度。

通过计算斜边的长度，投资者可以预测股票价格的未来走势。

2.股市勾股定理的应用
股市勾股定理的应用主要体现在以下几个方面：
（1）预测股票价格的走势：通过计算斜边的长度，投资者可以预测股票价格的未来走势，从而为投资决策提供参考。

（2）分析股票价格的波动幅度：通过计算直角边的长度，投资者可以了解股票价格的波动幅度，从而评估投资的风险。

（3）分析股票价格的合理性：当股票价格偏离预测价格较多时，投资者可以通过股市勾股定理来判断股票价格是否合理，从而决定是否进行投资。

3.股市勾股定理的优缺点
股市勾股定理的优点在于，它能够为投资者提供一种预测股票价格走
势的方法，有助于投资者做出更为明智的投资决策。

然而，股市勾股定理也存在一些缺点：
（1）预测结果存在一定误差：股市勾股定理的预测结果并非绝对准确，因为股票价格的波动受到多种因素的影响，包括宏观经济、政策、公司基本面等。

（2）适用范围有限：股市勾股定理适用于具有一定规律的股票价格波动，对于波动幅度过大或者规律性较差的股票价格，预测效果可能会大打折扣。

[实用参考]常见的勾股数及公式.doc

常见的勾股数及公式武安市黄冈实验学校翟升华搜集整理我们知道，如果∠C=90°，a 、b 、c 是直角三角形的三边，则由勾股定理，得a 2+b 2=c 2；反之，若三角形的三边a 、b 、c 满足a 2+b 2=c 2，则该三角形是直角三角形，c 为斜边．与此相类似，如果三个正整数a 、b 、c 满足a 2+b 2=c 2，则称a 、b 、c 为勾股数，记为（a ，b ，c ）．勾股数有无数多组，下面向同学们介绍几种：一、三数为连续整数的勾股数（3，4，5）是我们所熟悉的一组三数为连续整数的勾股数，除此之外是否还有第二组或更多组呢？设三数为连续整数的勾股数组为（G －１，G ，G ＋１），则由勾股数的定义，得（G+1）2+G 2=（G+1）2，解得G ＝４或G ＝０（舍去），故三数为连续整数的勾股数只有一组（３，４，５）；类似有3n,4n,5n(n 是正整数)都是勾股数。

二、后两数为连续整数的勾股数易知：（５，１２，１３），（９，４０，４１），（１１３，６３３８，６３８５），…，都是勾股数，如此许许多多的后两数为连续整数的勾股数，它的一般形式究竟是什么呢？a=2n+1,b=2n 2+2n,c=2n 2+2n+1（其特点是斜边与其中一股的差为1）.分别取n ＝１，２，３，…就得勾股数组（３，４，５），（５，１２，１３），（７，２４，２５），…三、前两数为连续整数的勾股数你知道（２０，２１，２９），（１１９，１２０，１６９），（４０５９，４０６０，５７４１）…，这些都是前两数为连续整数的勾股数组。

其公式为：（G ，G ＋１，1222++x x ）（G 为正整数）。

设前两数为连续整数的勾股数组为（G ，G ＋１，P ），P=1222++x x 则()2221y x x =++（＊）整理，得1222++x x ＝2y ，化为()121222-=-+y x ，即()y x 212++()y x 212-+＝－１，又()()2121-+＝－１，∴()1221++n ()1221+-n ＝－１（ｎ∈Ｎ），故取()y x 212++＝()1221++n ，()y x 212-+＝()1221+-n ，解之，得G ＝41〔()1221++n ＋()1221+-n －２〕，P ＝42〔()1221++n －()1221+-n 〕，故前两数为连续整数的勾股数组是（41〔()1221++n ＋()1221+-n －２〕，41〔()1221++n ＋()1221+-n －２〕＋１，42〔()1221++n －()1221+-n 〕）．四、后两数为连续奇数的勾股数如(8，15，17),(12，35，37)…其公式为：4(n+1),4(n+1)2-1,4(n+1)2+1(n 是正整数).五、其它的勾股数组公式：1.a=2m,b=m 2－1,c=m 2+1（m 大于1的整数）.2.a=21（m 2－n 2）,b=mn,c=21（m 2+n 2）（其中m>n 且是互质的奇数）. 3.a=2m,b=m 2－n 2,c=m 2+n 2（m>n,互质且一奇一偶的任意正整数）.下面我们把100以内的勾股数组列出来，供同学们参考：34 5；512 13；6810；72425；81517；9 1215；940 41；102426；116061；12 16 20；12 35 37；13 84 85；14 48 50；15 20 25；15 36 39；15112 113；16 30 34；16 63 65 17144 145；18 24 30；18 80 82；19 180 181；20 21 29；20 48 52；20 99 101；21 28 35 21 72 75；21 220 221；22 120 122；23 264 265；24 32 40；24 45 51；24 70 74；24 143 145 25 60 65；25 312 313；26 168 170；27 36 45；27120 123；27 364 365；28 45 53；28 96 100 28 195 197；29 420 421；30 40 50；30 72 78；30 224 226；31 480 481；32 60 68；32 126 130 32 255 257；33 44 55；33 56 65；33 180 183；33 544 545；34 288 290；35 84 91；35 120 125 35 612 613；36 48 60；36 77 85；36 105 111；36 160 164；36 323 325；37 684 685；38 360 362 39 52 65；39 80 89；39 252 255；39 760 761；40 42 58；40 75 85；40 96 104；40 198 202 40 399 401；41 840 841；42 56 70；42 144 150；42 440 442；43 924 925；44 117 125；44 240 244 44 483 485；45 60 75；45 108 117；45 200 205；45 336 339；46 528 530；48 55 73；48 64 80 48 90 102；48 140 148；48 189 195；48 286 290；48 575 577；49 168 175；50 120 130；50 624 62651 68 85；51 140 149；51 432 435；52 165 173；52 336 340；52 675 677；54 72 90；54 240 246 54 728 730；55 132 143；55 300 305；56 90 106；56 105 119；56 192 200；56 390 394；56 783 785 57 76 95；57176 185；57 540 543；58 840 842；60 63 87；60 80 100；60 91 109；60 144 156 60 175 185；60 221 229；60 297 303；60 448 452；60 899 901；62 960 962；63 84 105；63 216 225 63 280 287；63 660 663；64 120 136；64 252 260；64 510 514；65 72 97；65 156 169；65 420 425 66 88 110；66 112 130；66 360 366；68 285 293；68 576 580；69 92 115；69 260 269；69 792 795 70 168 182；70 240 250；72 96 120；72 135 153；72 154 170；72 210 222；72 320 328；72 429 435 72 646 650；75 100 125；75 180 195；75 308 317；75 560 565；75 936 939；76 357 365；76 720 724 77 264 275；77 420 427；78 104 130；78 160 178；78 504 510；80 84 116；80 150 170；80 192 208 80 315 325；80 396 404；80 798 802；81 108 135；81 360 369；84 112 140；84 135 159；84 187 205 84 245 259；84 288 300；84 437 445；84 585 591；84 880 884；85 132 157；85 204 221；85 720 725 87 116 145；87 416 425；88 105 137；88 165 187；88 234 250；88 480 488；88 966 970；90 120 150 90 216 234；90 400 410；90 672 678；91 312 325；91 588 595；92 525 533；93 124 155；93 476 48595 168 193；95 228 247；95 900 905；96 110 146；96 128 160；96 180 204；96 247 265；96 280 29696 378 390；96 572 580；96 765 771；98 336 350；99 132 165；99 168 195；99 440 451；99 540 549 100 105 145；100240260；100 495 505；100621629.以下是大于100的勾股数：第223组：102 136 170第224组：102 280 298第225组：102 864 870第226组：104 153 185第227组：104 195 221第228组：104 330 346第229组：104 672 680第230组：105 140 175第231组：105 208 233第232组：105 252 273第233组：105 360 375第234组：105 608 617第235组：105 784 791第236组：108 144 180第237组：108 231 255第238组：108 315 333第239组：108 480 492第240组：108 725 733第241组：108 969 975第242组：110 264 286第243组：110 600 610第244组：111 148 185第245组：111 680 689第246组：112 180 212第247组：112 210 238第248组：112 384 400第249组：112 441 455第250组：112 780 788第251组：114 152 190第252组：114 352 370第253组：115 252 277第254组：115 276 299第255组：116 837 845第256组：117 156 195第259组：117 756 765 第260组：119 120 169 第261组：119 408 425 第262组：120 126 174 第263组：120 160 200 第264组：120 182 218 第265组：120 209 241 第266组：120 225 255 第267组：120 288 312 第268组：120 350 370 第269组：120 391 409 第270组：120 442 458 第271组：120 594 606 第272组：120 715 725 第273组：120 896 904 第274组：121 660 671 第275组：123 164 205 第276组：123 836 845 第277组：124 957 965 第278组：125 300 325 第279组：126 168 210 第280组：126 432 450 第281组：126 560 574 第282组：128 240 272 第283组：128 504 520 第284组：129 172 215 第285组：129 920 929 第286组：130 144 194 第287组：130 312 338 第288组：130 840 850 第289组：132 176 220 第290组：132 224 260 第291组：132 351 375 第292组：132 385 407 第293组：132 475 493 第294组：132 720 732 第295组：133 156 205 第296组：133 456 475 第297组：135 180 225 第298组：135 324 351 第299组：135 352 377 第300组：135 600 615 第301组：136 255 289 第302组：136 273 305 第303组：136 570 586 第304组：138 184 230 第305组：138 520 538 第306组：140 147 203 第307组：140 171 221第310组：140 480 500 第311组：140 693 707 第312组：140 975 985 第313组：141 188 235 第314组：143 780 793 第315组：143 924 935 第316组：144 165 219 第317组：144 192 240 第318组：144 270 306 第319组：144 308 340 第320组：144 420 444 第321组：144 567 585 第322组：144 640 656 第323组：144 858 870 第324组：145 348 377 第325组：145 408 433 第326组：147 196 245 第327组：147 504 525 第328组：150 200 250 第329组：150 360 390 第330组：150 616 634 第331组：152 285 323 第332组：152 345 377 第333组：152 714 730 第334组：153 204 255 第335组：153 420 447 第336组：153 680 697 第337组：154 528 550 第338组：154 840 854 第339组：155 372 403 第340组：155 468 493 第341组：156 208 260 第342组：156 320 356 第343组：156 455 481 第344组：156 495 519 第345组：156 667 685 第346组：159 212 265 第347组：160 168 232 第348组：160 231 281 第349组：160 300 340 第350组：160 384 416 第351组：160 630 650 第352组：160 792 808 第353组：161 240 289 第354组：161 552 575 第355组：162 216 270 第356组：162 720 738 第357组：165 220 275 第358组：165 280 325第361组：165 900 915 第362组：168 224 280 第363组：168 270 318 第364组：168 315 357 第365组：168 374 410 第366组：168 425 457 第367组：168 490 518 第368组：168 576 600 第369组：168 775 793 第370组：168 874 890 第371组：170 264 314 第372组：170 408 442 第373组：171 228 285 第374组：171 528 555 第375组：171 760 779 第376组：174 232 290 第377组：174 832 850 第378组：175 288 337 第379组：175 420 455 第380组：175 600 625 第381组：176 210 274 第382组：176 330 374 第383组：176 468 500 第384组：176 693 715 第385组：176 960 976 第386组：177 236 295 第387组：180 189 261 第388组：180 240 300 第389组：180 273 327 第390组：180 299 349 第391组：180 385 425 第392组：180 432 468 第393组：180 525 555 第394组：180 663 687 第395组：180 800 820 第396组：180 891 909 第397组：182 624 650 第398组：183 244 305 第399组：184 345 391 第400组：184 513 545 第401组：185 444 481 第402组：185 672 697 第403组：186 248 310 第404组：186 952 970 第405组：189 252 315 第406组：189 340 389 第407组：189 648 675 第408组：189 840 861 第409组：190 336 386第411组：192 220 292 第412组：192 256 320 第413组：192 360 408 第414组：192 494 530 第415组：192 560 592 第416组：192 756 780 第417组：195 216 291 第418组：195 260 325 第419组：195 400 445 第420组：195 468 507 第421组：195 748 773 第422组：196 315 371 第423组：196 672 700 第424组：198 264 330 第425组：198 336 390 第426组：198 880 902 第427组：200 210 290 第428组：200 375 425 第429组：200 480 520 第430组：200 609 641 第431组：201 268 335 第432组：203 396 445 第433组：203 696 725 第434组：204 253 325 第435组：204 272 340 第436组：204 560 596 第437组：204 595 629 第438组：204 855 879 第439组：205 492 533 第440组：205 828 853 第441组：207 224 305 第442组：207 276 345 第443组：207 780 807 第444组：207 920 943 第445组：208 306 370 第446组：208 390 442 第447组：208 660 692 第448组：208 819 845 第449组：210 280 350 第450组：210 416 466 第451组：210 504 546 第452组：210 720 750 第453组：213 284 355 第454组：215 516 559 第455组：215 912 937 第456组：216 288 360 第457组：216 405 459 第458组：216 462 510 第459组：216 630 666 第460组：216 713 745第462组：217 456 505 第463组：217 744 775 第464组：219 292 365 第465组：220 231 319 第466组：220 459 509 第467组：220 528 572 第468组：220 585 625 第469组：222 296 370 第470组：224 360 424 第471组：224 420 476 第472组：224 768 800 第473组：224 882 910 第474组：225 272 353 第475组：225 300 375 第476组：225 540 585 第477组：225 924 951 第478组：228 304 380 第479组：228 325 397 第480组：228 665 703 第481组：228 704 740 第482组：230 504 554 第483组：230 552 598 第484组：231 308 385 第485组：231 392 455 第486组：231 520 569 第487组：231 792 825 第488组：232 435 493 第489组：232 825 857 第490组：234 312 390 第491组：234 480 534 第492组：235 564 611 第493组：237 316 395 第494组：238 240 338 第495组：238 816 850 第496组：240 252 348 第497组：240 275 365 第498组：240 320 400 第499组：240 364 436 第500组：240 418 482 第501组：240 450 510 第502组：240 551 601 第503组：240 576 624 第504组：240 700 740 第505组：240 782 818 第506组：240 884 916 第507组：240 945 975 第508组：243 324 405 第509组：245 588 637 第510组：245 840 875 第511组：246 328 410第514组：249 332 415 第515组：250 600 650 第516组：252 275 373 第517组：252 336 420 第518组：252 405 477 第519组：252 539 595 第520组：252 561 615 第521组：252 735 777 第522组：252 864 900 第523组：255 340 425 第524组：255 396 471 第525组：255 612 663 第526组：255 700 745 第527组：256 480 544 第528组：258 344 430 第529组：259 660 709 第530组：259 888 925 第531组：260 273 377 第532组：260 288 388 第533组：260 624 676 第534组：260 651 701 第535组：260 825 865 第536组：261 348 435 第537组：261 380 461 第538组：264 315 411 第539组：264 352 440 第540组：264 448 520 第541组：264 495 561 第542组：264 702 750 第543组：264 770 814 第544组：264 950 986 第545组：265 636 689 第546组：266 312 410 第547组：266 912 950 第548组：267 356 445 第549组：270 360 450 第550组：270 648 702 第551组：270 704 754 第552组：272 510 578 第553组：272 546 610 第554组：273 364 455 第555组：273 560 623 第556组：273 736 785 第557组：273 936 975 第558组：275 660 715 第559组：276 368 460 第560组：276 493 565 第561组：276 805 851 第562组：279 372 465第565组：280 342 442 第566组：280 351 449 第567组：280 450 530 第568组：280 525 595 第569组：280 672 728 第570组：280 759 809 第571组：280 960 1000 第572组：282 376 470 第573组：285 380 475 第574组：285 504 579 第575组：285 684 741 第576组：285 880 925 第577组：287 816 865 第578组：288 330 438 第579组：288 384 480 第580组：288 540 612 第581组：288 616 680 第582组：288 741 795 第583组：288 840 888 第584组：290 696 754 第585组：290 816 866 第586组：291 388 485 第587组：294 392 490 第588组：295 708 767 第589组：296 555 629 第590组：297 304 425 第591组：297 396 495 第592组：297 504 585 第593组：300 315 435 第594组：300 400 500 第595组：300 455 545 第596组：300 589 661 第597组：300 720 780 第598组：300 875 925 第599组：301 900 949 第600组：303 404 505 第601组：304 570 646 第602组：304 690 754 第603组：305 732 793 第604组：306 408 510 第605组：306 840 894 第606组：308 435 533 第607组：308 495 583 第608组：308 819 875 第609组：309 412 515 第610组：310 744 806 第611组：310 936 986 第612组：312 416 520 第613组：312 459 555第614组：312 585 663 第615组：312 640 712 第616组：312 910 962 第617组：315 420 525 第618组：315 572 653 第619组：315 624 699 第620组：315 756 819 第621组：318 424 530 第622组：319 360 481 第623组：320 336 464 第624组：320 462 562 第625组：320 600 680 第626组：320 768 832 第627组：321 428 535 第628组：322 480 578 第629组：324 432 540 第630组：324 693 765 第631组：324 945 999 第632组：325 360 485 第633组：325 780 845 第634组：327 436 545 第635组：328 615 697 第636组：330 440 550 第637组：330 560 650 第638组：330 792 858 第639组：333 444 555 第640组：333 644 725 第641组：335 804 871 第642组：336 377 505 第643组：336 385 511 第644组：336 448 560 第645组：336 527 625 第646组：336 540 636 第647组：336 630 714 第648组：336 748 820 第649组：336 850 914 第650组：339 452 565 第651组：340 357 493 第652组：340 528 628 第653组：340 816 884 第654组：341 420 541 第655组：342 456 570 第656组：344 645 731 第657组：345 460 575 第658组：345 756 831 第659组：345 828 897 第660组：348 464 580 第661组：348 805 877 第662组：350 576 674 第663组：350 840 910 第664组：351 468 585。

勾股定理的优秀教案5篇

勾股定理的优秀教案5篇（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如总结报告、心得体会、讲话致辞、条据文书、合同协议、策划方案、规章制度、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as summary reports, insights, speeches, written documents, contract agreements, planning plans, rules and regulations, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!勾股定理的优秀教案5篇教案的制定可以帮助教师思考教学策略和方法是否合理，激发学生的学习兴趣和积极参与，写好教案帮助教师评估学生的学习情况和教学效果，及时调整教学计划和教学内容，以下是本店铺精心为您推荐的勾股定理的优秀教案5篇，供大家参考。

八年级数学下册《勾股定理》教案、教学设计

（3）组织学生进行小组讨论，分享探究成果，互相启发，加深对勾股定理的理解。
3.精讲精练，突破难点
（1）教师针对勾股定理的证明方法进行详细讲解，引导学生理解并掌握。
（2）设计具有层次性的课堂练习，让学生在实际操作中巩固勾股定理的应用。
（3）针对学生在练习中遇到的问题，教师进行个别辅导，帮助他们突破难点。
2.各小组选取一位代表进行汇报，分享他们的讨论成果和心得体会。
3.组织学生互相提问、解答，共同探讨勾股定理的证明方法和应用技巧。
4.引导学生思考勾股定理在生活中的具体应用，鼓励他们举例说明。
5.对各小组的表现进行评价，鼓励积极参与、合作交流的学生。
（四）课堂练习，500字
在课堂练习环节，我会设计以下练习题：
五、作业布置
为了巩固学生对勾股定理的理解和应用，以及提高他们的数学思维能力，我设计了以下作业：
1.基础巩固题：完成课本第56页的练习题1、2、3，要求学生通过计算给定直角三角形的斜边长度，加强对勾股定理的直接应用。
2.实践应用题：选择一道生活中的实际问题，如测量学校旗杆的高度、计算三角形广告牌的面积等，运用勾股定理解决问题，并撰写解题报告。此题旨在培养学生将数学知识应用于实际情境的能力。
1.直角三角形的两条直角边和斜边之间有什么关系？
2.在直角三角形中，是否有一个规律可以计算斜边的长度？
3.你听说过勾股定理吗？它是什么意思？
（二）讲授新知，500字
在讲授新知环节，我会按照以下步骤进行：
1.回顾直角三角形的基本概念和性质，如直角、斜边、直角边等。
2.引导学生观察直角三角形中斜边与直角边之间的关系，发现斜边的平方等于两条直角边平方和的规律。
（2）引导学生进行自我反思，总结学习经验，提高自主学习能力。

勾股定理

A C
B c
b c
a
a b
A
A B
b
B C
A
C a
友情提示：
直角三角形的三边之间存在勾股定理这个数量关系！
运用勾股定理时先找出要找出斜边。
题组一
应用勾股定理
1、在△ABC中，∠A=900， ∠A、 ∠B、 ∠C的对边分别为a、b、c，则下列结论不正确的是（） A
A、a2+b2=c2 B、b2+c2=a2 C、a2-b2=c2 D、a2-c2=b2
1、一个直角三角形的两边长分别为3与4，则第三边长为 5或 7 。 2、直角三角形的两条直角边分别为3、4，则斜边 12 上的高为。 5
3、将一根长24cm的筷子，置于底面直径为5cm、高为12cm 的圆柱形水杯中，设筷子露在外面的长度为hcm,则h的取值范围是 11≤h≤12 。
勾股定理
应用勾股定理
3、在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
题组三
应用勾股定理
B
a
c
C
b
A
临朐新华中学
问题一
受台风影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
4米 3米
临朐新华中学
学习目标：
1、探索直角三角形中两条直角边与斜边的数量关系. 2、掌握勾股定理，会用勾股定理解决一些与直角三角形有关的实际问题. 3、感受数形结合、方程等数学思想.

股市勾股定理

股市勾股定理
（实用版）
目录
1.股市勾股定理的概念
2.股市勾股定理的公式
3.股市勾股定理的应用
4.股市勾股定理的局限性
正文
一、股市勾股定理的概念
股市勾股定理，是一种用于预测股票价格走势的数学模型，该模型基于直角三角形的勾股定理，通过计算三角形的斜边长度来预测股票价格的变化。

在股市中，该定理主要应用于短期趋势的预测，帮助投资者更好地把握市场机会。

二、股市勾股定理的公式
股市勾股定理的公式为：c = a + b，其中 c 表示斜边（即未来股票价格），a 和 b 分别表示直角边（即过去两个交易日的股票价格）。

通过这个公式，可以计算出未来股票价格的大致范围。

三、股市勾股定理的应用
1.确定买入点：当预测的未来股票价格高于当前价格时，投资者可以考虑在当前价格买入股票，等待未来价格上涨获利。

2.确定卖出点：当预测的未来股票价格低于当前价格时，投资者可以考虑在当前价格卖出股票，避免未来价格下跌造成损失。

3.风险控制：通过股市勾股定理，投资者可以对未来股票价格的波动范围进行预测，从而在投资过程中做好风险控制，降低投资风险。

四、股市勾股定理的局限性
1.股市勾股定理只能预测短期趋势，对于中长期趋势的预测能力较弱。

2.股市勾股定理的预测结果受到市场诸多因素的影响，如政策、经济环境、公司基本面等，因此预测结果仅供参考，投资者需结合其他分析方法进行投资决策。

3.股市勾股定理不适用于所有股票，对于一些走势异常的股票，该定理的预测能力可能会失效。

人教版八年级勾股定理教学设计第一课时

-设计意图：通过基础练习，使学生熟练掌握勾股定理的基本运用，增强对定理的记忆和理解。
2.实践应用题：选择生活中一个直角三角形的实例，运用勾股定理计算其边长，并简述解题过程。
-设计意图：培养学生将数学知识应用于实际生活的能力，体会数学的实用价值。
3.思考提高题：结合勾股定理，探讨直角三角形其他相关性质，如相似三角形的判定、特殊角的三角函数值等。
3.布置课后作业：根据学生的学习情况，布置适量的课后作业，帮助学生巩固所学知识，提高解题能力。
五、作业布置
为了巩固学生对勾股定理的理解和应用，确保学生对课堂所学知识的内化，特布置以下作业：
1.基础知识巩固题：完成教材第十五章第二节后的练习题，包括勾股定理的概念理解、定理的直接应用以及简单问题的解决。
针对以上学情，教师在教学过程中应关注学生的个体差异，因材施教，充分调动学生的学习兴趣，引导学生主动探究，提高学生的几何素养。
三、教学重难点和教学设想
（一）教学重难点
1.理解并掌握勾股定理的表述及其证明方法。
2.能够运用勾股定理解决实际问题，如计算直角三角形的边长、判断直角三角形等。
3.理解勾股定理在实际生活中的应用，提高学生的几何素养。
4.学会使用勾股定理进行简单的几何作图，如构造直角三角形、等腰直角三角形等。
5.能够运用勾股定理推导出其他相关定理，如相似三角形的性质、正弦、余弦函数的定义等。
（二）过程与方法
在教学过程中，教师应采用以下方法引导学生学习勾股定理：
1.创设情境，导入新课：通过介绍勾股定理的历史背景，激发学生的学习兴趣。
3.解释勾股定理的应用：通过讲解典型例题，让学生了解勾股定理在实际问题中的应用，如计算直角三角形的边长、判断直角三角形等。
（三）学生小组讨论，500字

勾股定理的题类分类和提高拓展题

勾股定理的复习考点一：利用勾股定理求面积1．求：（1）阴影部分是正方形；（2）阴影部分是长方形；（3）阴影部分是半圆．2. 如图1-1，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，则这个半圆的面积是____________.图1-1 图1-2 图1-3 3.如图，如果半圆的直径恰为直角三角形的一条直角边，那么这个半圆的面积为（） A.π4 B.π6 C.π12 D.π244. 如图，以Rt △ABC 的三边为直径分别向外作三个半圆，试探索三个半圆的面积之间的关系．考点二：在直角三角形中，已知两边求第三边1．在直角三角形中,若两直角边的长分别为1cm ，2cm ，则斜边长为．2．（易错题、注意分类的思想）已知直角三角形的两边长为3、2，则另一条边长的平方是3、已知直角三角形两直角边长分别为5和12，求斜边上的高．4.已知△ABC中，AB＝17，AC＝10，BC边上的高，AD＝8，则边BC的长为考点三：应用勾股定理在等腰三角形中求底边上的高1.如图1所示，等腰中，，是底边上的高，若，求①AD的长；②ΔABC的面积．2.如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.考点四:应用勾股定理解决楼梯上铺地毯问题1. 如图4-1，相邻的两边互相垂直，则从点B到点A的最短距离为（）A.13B.12C.8D.52.如图4-1，在一个高为3米，长为5米的楼梯表面铺地毯，则地毯长度为米。

考点五、利用列方程求线段的长（折叠问题）1.折叠矩形ABCD 的一边AD,点D 落在BC 边上的点F 处,已知，AB=8cm ，BC=10cm,求 CF 和EC .2.如图，有一个直角三角形纸片，两直角边AC=6cm ，BC=8cm ，现将直角边AC 沿直线AD折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD 的长吗？3．在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A 处。

勾股定理习题(附答案)

C勾股定理评估试卷（1）一、选择题（每小题3分，共30分）1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长（A ）4 cm（B ）8 cm （C ）10 cm（D ）12 cm3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（）（A ）25（B ）14（C ）7（D ）7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）645. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）715242520715202425157252024257202415(A)(B)(C)(D)6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )（A ）钝角三角形（B ）锐角三角形（C ）直角三角形（D ）等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) （A ） 25 （B ） 12.5 （C ） 9 （D ） 8.5 8. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( ) （A ）等边三角形（B ）钝角三角形（C ）直角三角形（D ）锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（）. （A ）50a 元（B ）600a 元（C ）1200a 元（D ）1500a 元 10.如图，A B ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.（A ）12 （B ）7 （C ）5 （D ）135米3米（第10题）（第11题）（第14题）二、填空题（每小题3分，24分）11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12. 在直角三角形ABC 中，斜边AB =2，则222AB AC BC ++=______. 13. 直角三角形的三边长为连续偶数，则其周长为 .14. 如图，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，则这个半圆的面积是____________.（第15题）（第16题）（第17题） 15. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米. 16. 如图，△ABC 中，∠C =90°，AB 垂直平分线交BC 于D若BC =8，AD =5，则AC 等于______________. 17. 如图，四边形ABCD 是正方形，AE 垂直于BE ，且AE =3，BE =4，阴影部分的面积是______.18. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2.C三、解答题（每小题8分，共40分）19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：“小溪边长着两棵棕榈树，恰好隔岸相望.一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻飞去抓鱼，并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？20. 如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.21. 如图，A 、B 两个小集镇在河流CD 的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A 、B 两镇供水，铺设水管的费用为每千米3万，请你在河流CD 上选择水厂的位置M ，使铺设水管的费用最节省，并求出总费用是多少？22. 如图所示的一块地，∠ADC=90°，AD=12m ，CD=9m ，AB=39m ，BC=36m ，求这块地的面积。

勾股定理经典提高题

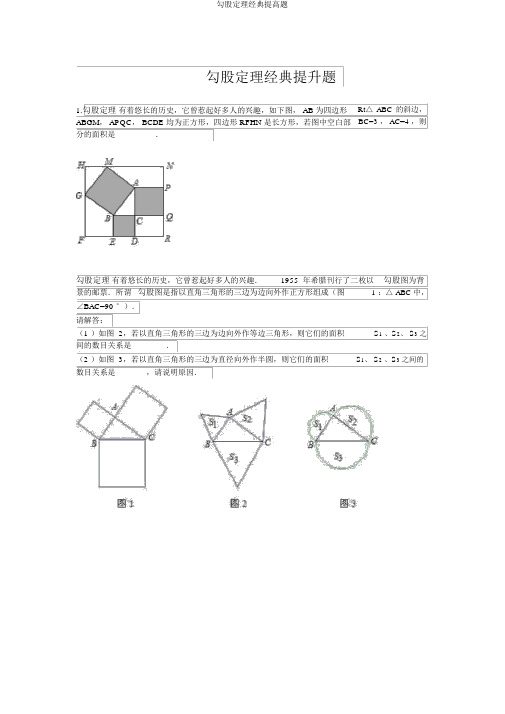
勾股定理经典提升题1.勾股定理有着悠长的历史，它曾惹起好多人的兴趣，如下图， AB 为四边形ABGM， APQC， BCDE 均为正方形，四边形 RFHN 是长方形，若图中空白部分的面积是 ________ ．Rt△ABC 的斜边，BC=3 ， AC=4 ，则勾股定理有着悠长的历史，它曾惹起好多人的兴趣．1955 年希腊刊行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形组成（图 1 ：△ ABC 中，∠BAC=90 °）．请解答：（1 ）如图 2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、 S3之间的数目关系是______ ．（2 ）如图 3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、 S2、S3之间的数目关系是 ______ ，请说明原因．3 学过《勾股定理》后，八年级某班数学兴趣小组到达操场上丈量旗杆AB 的高度．小华测得从旗杆顶端垂直挂下来的升旗用的绳索比旗杆长1m（如图 1 ），小明拉着绳索的下端今后退，当他将绳索拉直时，小凡测得此时小明拉绳索的手到地面的距离CD 为 1m ，到旗杆的距离CE 为 8m ，（如图 2 ）．于是，他们很快算出了旗杆的高度，请你也来试一试．4.研究学习：研究勾股定理时，我们发现“用不一样的方式表示同一图形的面积”能够解决线段和（或差）的相关问题，这类方法称为面积法．请你运用面积法求解以下问题：在等腰三角形 ABC 中， AB=AC ，BD 为腰 AC 上的高（如图1）．（1）若等腰△ ABC 的面积为 24 cm 2，腰的长为 8 cm ，则腰 AC 上的高 BD 的长为 ______cm ；（2）若 BD=h ，M 是直线 BC 上的随意一点， M 到 AB、 AC 的距离分别为 h 1、h 2．①若 M 在线段 BC 上，请你联合图 2 证明： h 1+h 2=h ；②当点 M 在 BC 延伸线上时， h1、h 2、h 之间的关系为 ______ ．（直接写出结论，不用证明）5. 一个直立的火柴盒在桌面上倒下，启示人们发现了勾股定理的一种新的考证方法．如图，火柴盒的一个侧面ABCD 倒下到 AB′ C′D′的地点，连结 CC′，设 AB=a ，BC=b ，AC=c ，请利用四边形BCC′D′的面积考证勾股定理：a2+b2=c2．6.在直线 l 上挨次摆放着七个正方形（如下图）．已知斜搁置的三个正方形的面积分别是 1、2、3，正搁置的四个正方形的面积挨次是 S1、S2、S3、S4，则S1+S2+S3+S4等于A.4B.5C.6D.147.如图，已知AB： BC： CD： DA=2 ： 2： 3： 1，且∠ ABC=90 °，求∠ DAB 的度数8 如下图，有高为 3 米，斜坡长为 5 米的楼梯表面铺地毯，那么地毯起码需要多少米？9 如下图，折叠长方形（四个角都是直角）的一边 AD使点 D落在 BC 边的点 F 处，已知 AB=DC=8cm， AD=BC=10cm，求 EC 的长．10.如图，长方体的长 BE=20cm，宽 AB=10cm，高 AD=15cm，点 M 在 CH 上，且 CM=5cm，一只蚂蚁假如要沿着长方体的表面从点 A 爬到点 M，需要爬行的最短距离是多少？11.柱子是圆柱体 ,它的周长是 1.6 米 ,高 4.8 米 ,如图是柱子的一个侧面 ,左上是彩带的起点 ,左下彩带的终点 , 彩带绕圆柱四圈 , 这根柱子最少需要多少米的彩带 ?...12. 如图有一个三级台阶，每级台阶长、宽、高分别为 2 米、0.3 米 0.2 米，A 处有一只蚂蚁，它想吃到B 处食品，你能帮蚂蚁设计一条最短的线路吗？并求出最短的线路长。

数学家毕达哥拉斯+勾股定理

7

课堂小结
2、直角三角形ABC中，AB边为13， BC边为12，那AC边为：
A、15 B、12 C、10 D、 5
回答错误哦，你再继续想想！方法小结：运用勾股定理
a2+b2=c2
我要继续继续奋斗

为
()
C
A.3 米 B.4 米 C.5米 D.6米
３

４
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结

数学语言符号语言
结论变形
勾股定理：直角三角形两直角边的平方和等于斜边的平方．

1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结

1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结

继续下一题结束学习

如图,折叠长方形（四个角都是直角，
对边相等）的一边，使点D落在BC边
上的点F处，若AB=8，AD=10.
（1）你能说出图中哪些线段的长?
A
10
D
（2）求EC的长.
8 10
8-x E 8-x x
B 6 F4 C
盛开的水莲
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结

探索勾股定理视频
勾股定理动画演示
ห้องสมุดไป่ตู้

1 定理简介
21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结

八年级初二数学提高题专题复习勾股定理练习题及答案

∵∠DAE=90°，∠ADE=45°，
∴∠ADE=∠AED=45°， ∴AE=AD=1，
∴在 Rt△ADE 中，DE= 12 12 2 ，
∵∠DAE=∠BAC=90°， ∴∠DAE+∠EAC=∠BAC+∠EAC，即∠CAD=∠BAE，又∵AB=AC, ∴△BAE≌△CAD(SAS)， ∴CD=BE=3，∠AEB=∠ADC=45°， ∴∠BED=90°，
B，C 都在格点上，同时构造长方形 CDEF，使它的顶点都在格点上，且它的边 EF 经过点
A，ED 经过点 B．同学们借助此图求出了△ABC 的面积．
（1）在图（1）中，△ABC 的三边长分别是 AB＝
，BC＝
，AC＝
．△ABC
的面积是
．
（2）已知△PMN 中，PM＝ 17 ，MN＝2 5 ，NP＝ 13 ．请你根据启航小组的思路，在
17．如图，Rt△ABC 中，∠BCA＝90°，AB＝ 5 ，AC＝2，D 为斜边 AB 上一动点（不与点 A，B 重合），DE⊥AC，DF⊥BC，垂足分别为 E、F，连接 EF，则 EF 的最小值是_____．
18．如图，直线 y 4 x 2 与 x 轴、 y 轴分别交于点 B 和点 A ，点 C 是线段 OA 上的一 3
9．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而
成，其中 AE=10，BE=24，则 EF 的长是（）
A．14
B．13
C．14 3
10．以下列各组数为边长，能组成直角三角形的是（）
D．14 2
A．1，2，3
B．2，3，4
C．3，4，6
D．1， 3 ，2
二、填空题
得出 BD，利用勾股定理即可求出 AD，再利用三角形面积公式即可解决问题．

探索勾股定理练习题精选

基础训练1．为迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小刚搬来一架高为米的木梯，准备把拉花挂到米的墙上，则梯脚与墙角的距离应为米．2．如图1-1-1 ，小张为测量校园内池塘A，B 两点的距离，他在池塘边选定一点C，使∠ ABC ＝90°，并测得AC 长26m，BC 长24m，则A， B 两点间的距离为m ．3．如图1-1-2 ，阴影部分是一个半圆，则阴影部分的面积为不取近似值）4．底边长为16cm ，底边上的高为6cm 的等腰三角形的腰长为5．一艘轮船以16km/h 的速度离开港口向东北方向航行，另一艘轮船同时离开港口以东南方向航行，它们离开港口半小时后相距km ．提高训练6．一个长为10m 为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为8m ，梯子的顶端下滑2m 后，底端滑动m ．7．如图1-1-3 所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，Dcm2．D）60cm2分别以直角三角形的三边为边长向外作正方形，然后分别以三个探索勾股定理1）正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为S1，S2，S3，则S1，S2，S3 之间的关系是（）．12km/h 的速度向的面积的和8．已知Rt△ ABC 中，∠ C＝a b 14cm， c 10 cm ，则的面积为（）．Rt△ABCA ）24cm 2B ）36cm 248cm2 9．如图1-1-4 ，A）S1 S2 S3 （B）S1 S2 S3 （C）S1 S2 S3 （D）无法确定图 1-1-1210．暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的路线探宝又往北走 2km ，遇到障碍后又往西走 3km ，再折向北走知识拓展11．如图 1-1-6 ，已知直角△ ABC 的两直角边分别为影部分的面积．12．如图 1-1-7 ，有一块直角三角形纸片，两直角边AD 折叠，使它恰好落在斜边 AB 上，且与 AE 重合，求基础训练登陆点到埋宝藏点的直线距离为 km ．1．斜边为 17cm ，一条直角边长为（A ） 60（B ） 30 （C ） 902. 等腰三角形的腰长为 10, 底长为（A ）13 （ B ）8 3. 已知一个 Rt △的两边长分别为（ A ） 25 （ B ） 14 15cm 的直角三角形的面积是（（D ） 12012, 则其底边上的高为（）（C ） 253和 4，则第三边长的平方是（（ C ） 7 （ D） 7或 4. 在直角三角形 ABC 中，斜边 AB =2，则 AB2AC 2 BC 2直角三角形的三边长为连续偶数，如图 1-1-8 为某楼梯 , 测得楼梯的长为至少需要 _______米 . 5.6. 则其周长为（D ））25 64提高训练毯的长度 3米 7. 如图 1-1-9 ，校园内有两棵树，相距顶端飞到另一棵树的顶端，小鸟至少要飞8. 如图 1-1-10 ，小李准备建一个蔬菜大棚，棚宽 4 米，计墙的厚度，请计算阳光透过的最大面积 . 12 米，一棵树高 13 米，另一棵树高 8 米，一只小鸟从一棵树的 __________ 米. 高 3 米，长 20 米，棚的斜面用塑料布遮盖，不图 1-1-109．伽菲尔德图（1-1G -9a rfield ， 1881 年任美国第 20 届总统）利用两个全等的三角形拼成如图图形， Rt △ABC≌Rt △CDE ， B D 90 ，且 B ， C ，D 三点共线，证明了勾股定理（ 1876 年 4 月 1 日，发表在《新英格兰教育日志》上），现请你尝试该证明过程．知识拓展 10．如图，已知长方形 ABCD 中 AB=8 cm,BC=10 cm,在边 CD 上取一点将△ ADE 折叠使点 D 恰好落在 BC 边上的点 F ，求 CE 的长 .E ，他们登陆后先往东走 8km ，6km 处往东一拐，仅走 1km 就找到了宝藏，则探索勾股定理AC6，8CD图 1-2-1探索勾股定理（ 3）2 2 2 2（ A ）60cm 2 （B ）64 cm 2 （C ）24 cm 2 （D ）48 cm 22．如图 1-1-3 ，把矩形纸条 ABCD 沿 EF ，GH 同时折叠， B ，C 两点恰好落在 AD 边的 P 点处，若∠FPH 90 ， PF 8， PH 6，则矩形 ABCD 的边 BC 长为（）提高训练5．一个直角三角形的三边长的平方和为 200 ，则斜边长为6．我国古代数学家赵爽的 “勾股圆方图” 是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形（如图 1-1-16 所示）．如果大正方形的面积是 13，小正方形的面积是 1，直角三角形的两直角边长分别为 a ，b ，那么（a b ）2 的值是7．如图，直线 l 上有三个正方形Ａ． 4 Ｂ． 6 a ，b ，c ，若 a ，c 的面积分别为5 和 11 ，则 b 的面积为（Ｃ． 16 Ｄ． 55图 1-1-16 8．如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位：mm ），计算两圆孔中心 A 和 B 的距离为 _____ mm ． 9．如图 1-1-19，已知 Rt △ ABC 中， C 90 ， AC BC 3cm ．现将 △ ABC 进行折叠，使顶点 A ，B 重合， DE cm ． 4cm ，则折痕图 1-1E -1910．图 1-1-20 是我国古代着名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若 AC 6 ， BC 将四个直角三角形中边长为 6 的直角边分别向外延长一倍，图-2所示的“数学风车” ，则这个风车的外围周长是 5，得到图 1-1-20BA图 1-1-20基础训练1．长方形的一条对角线的长为 10cm ，一边长为 6cm ，它的面积是（Ａ． 20 Ｂ． 22Ｃ． 24Ｄ． 30图 1-1-14图 1-1-133．如图 1-1-14, 一圆柱高 8cm, 底面半径 2cm, 一只蚂蚁从点 A 爬到点 B 爬行的最短路程（取 3）是（）. A )20cm B ） 10cm （ C ） 14cm （ D ）无法确定4．如图 1-1-15 是一个圆柱形饮料罐，底面半径是 5，高是 12，上底面小圆孔，则一条到达底部的直吸管在罐内部．分． a 的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是)A ．12≤ a ≤13B ．12≤a ≤15C ． 5≤ a ≤12D ． 5≤ a ≤13处吃食 , 要中心有一个11. 如图 1-1-21 ，铁路上 A ，B 两点相距 25km ，C ，D 为两村庄， DA ⊥AB 于 A ，CB ⊥ AB 于 B ，已知 DA=15km ， CB=10km ，现在要在铁路 AB 上建一个土特产品收购站 E ，使得 C ，D 两村到 E 站的距离相等，则 E 站应建在离 A 站多少 km 处？ 12. 已知，如图 1-1-22 ，四边形 ABCD 中， AB=3cm ， AD=4cm ，BC=13cm ， ABCD 的面积。

人教版八年级下册17.1《勾股定理》第一课时教学设计

1.使学生认识到数学在生活中的广泛应用，增强学生学习数学的信心和兴趣。
2.培养学生严谨、细致的学习态度，养成科学的学习方法。
3.引导学生体会数学的简洁美、逻辑美，提高学生的审美情趣。
4.培养学生团队合作意识，学会倾听、尊重他人的意见，形成良好的沟通能力。
二、学情分析
八年级下册的学生已经具备了一定的数学基础，掌握了直角三角形的基本概念和性质，能够进行简单的几何图形的推理和计算。在此基础上，他们对勾股定理这一章节的学习将更加深入地理解直角三角形的内在联系。然而，学生在解决实际问题时，可能仍存在以下困难：对勾股定理的理解不够深入，不能灵活运用；在计算过程中容易出现粗心大意的情况；对于定理的证明过程，可能感到困惑。因此，在教学过程中，教师应关注学生的个体差异，提供充足的实践机会，引导学生通过自主探究、合作交流等方式，逐步提高解决问题的能力，增强数学思维能力。同时，注重激发学生的学习兴趣，培养他们面对困难的勇气和毅力，使学生在轻松愉快的氛围中学习数学。
3.拓展提高题：针对学有余力的学生，设计一道涉及勾股定理与其他数学知识相结合的题目，鼓励学生进行思考和探究。
4.小组合作作业：布置一道小组合作完成的作业，要求学生相互讨论、分工合作，共同解决一个较为复杂的勾股定理问题。培养学生团队合作意识，提高交流沟通能力。
5.思考题：提出一个关于勾股定理的思考题，引导学生深入思考定理的本质和内涵，激发学生的求知欲。
2.创设情境：展示一个实际情境，如一块直角三角形的土地，要求学生计算斜边的长度。让学生意识到勾股定理在实际生活中的应用，为新课的学习奠定基础。
（二）讲授新知
1.勾股定理的概念：通过导入环节的实际问题，引导学生观察直角三角形的边长关系，发现勾股定理。用数学符号表示勾股定理，并解释定理的含义。