完整三角函数公式表

合集下载

三角函数公式表（初中物理公式）

三角函数公‎式表物理量计算公式备注速度υ= S / t1m / s = 3.6 Km / h声速υ= 340m / s光速C = 3×108 m /s密度ρ= m / V 1 g / c m3 = 103 Kg / m3合力 F = F1 - F2F = F1 + F2 F1、F2在同一直线线上且方向相反F1、F2在同一直线线上且方向相同压强p = F / Sp =ρg h p = F / S适用于固、液、气p =ρg h适用于竖直固体柱p =ρg h可直接计算液体压强1标准大气压= 76 cmHg柱= 1.01×105 Pa = 10.3 m水柱浮力①F浮= G – F②漂浮、悬浮：F浮= G③F浮= G排=ρ液g V排④据浮沉条件判浮力大小（1）判断物体是否受浮力（2）根据物体浮沉条件判断物体处于什么状态（3）找出合适的公式计算浮力物体浮沉条件（前提：物体浸没在液体中且只受浮力和重力）：①F浮＞G（ρ液＞ρ物）上浮至漂浮②F浮=G（ρ液=ρ物）悬浮③F浮＜G（ρ液＜ρ物）下沉杠杆平衡条件F1 L1 = F2 L 2 杠杆平衡条件也叫杠杆原理滑轮组 F = G / nF =（G动+ G物）/ nSF = n SG 理想滑轮组忽略轮轴间的摩擦n：作用在动滑轮上绳子股数功W = F S = P t 1J = 1N•m = 1W•s功率P = W / t = Fυ1KW = 103 W，1MW = 103KW有用功W有用= G h（竖直提升）= F S（水平移动）= W总– W额=ηW总额外功W额= W总– W有= G动h（忽略轮轴间摩擦）= f L（斜面）总功W总= W有用+ W额= F S = W有用/ η机械效率η= W有用/ W总η=G /（n F）= G物/（G物+ G动）定义式适用于动滑轮、滑轮组中考物理所有的公式特点或原理串联电路并联电路时间：t t=t1=t2 t=t1=t2电流：I I = I 1= I 2 I = I 1+ I 2电压：U U = U 1+ U 2 U = U 1= U 2电荷量：Q电Q电= Q电1= Q电2 Q电= Q电1+ Q电2电阻：R R = R 1= R 2 1/R=1/R1+1/R2 [R=R1R2/(R1+R2)]电功：W W = W 1+ W 2 W = W 1+ W 2电功率：P P = P 1+ P 2 P = P 1+ P 2电热：Q热Q热= Q热1+ Q热 2 Q热= Q热1+ Q热 2物理量（单位）公式备注公式的变形速度V（m/S）v= S：路程/t：时间重力G（N）G=mg m：质量g：9.8N/kg或者10N/kg密度ρ（kg/m3）ρ=m：质量V：体积合力F合（N）方向相同：F合=F1+F2方向相反：F合=F1—F2 方向相反时，F1>F2浮力F浮(N) F浮=G物—G视G视：物体在液体的重力浮力F浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F浮(N) F浮=G排=m排g=ρ液gV排G排：排开液体的重力m排：排开液体的质量ρ液：液体的密度V排：排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1：动力 L1：动力臂F2：阻力 L2：阻力臂定滑轮F=G物S=h F：绳子自由端受到的拉力G物：物体的重力S：绳子自由端移动的距离h：物体升高的距离动滑轮F= （G物+G轮）S=2 h G物：物体的重力G轮：动滑轮的重力滑轮组F= （G物+G轮）S=n h n：通过动滑轮绳子的段数机械功W（J）W=Fs F：力s：在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs 适用滑轮组竖直放置时机械效率η= ×100%功率P（w）P=W：功t：时间压强p（Pa）P=F：压力S：受力面积液体压强p（Pa）P=ρgh ρ：液体的密度h：深度（从液面到所求点的竖直距离）热量Q（J）Q=cm△t c：物质的比热容 m：质量△t：温度的变化值燃料燃烧放出的热量Q（J）Q=mq m：质量q：热值常用的物理公式与重要知识点一．物理公式单位）公式备注公式的变形串联电路电流I（A）I=I1=I2=…… 电流处处相等串联电路电压U（V）U=U1+U2+…… 串联电路起分压作用串联电路电阻R（Ω）R=R1+R2+……并联电路电流I（A）I=I1+I2+…… 干路电流等于各支路电流之和（分流）并联电路电压U（V）U=U1=U2=……并联电路电阻R（Ω）= + +……欧姆定律I=电路中的电流与电压成正比，与电阻成反比电流定义式I=Q：电荷量（库仑）t：时间（S）电功W（J）W=UIt=Pt U：电压 I：电流t：时间 P：电功率电功率P=UI=I2R=U2/R U:电压 I：电流R：电阻电磁波波速与波长、频率的关系C=λν C：波速（电磁波的波速是不变的，等于3×108m/s）λ：波长ν：频率二．知识点1．需要记住的几个数值：a．声音在空气中的传播速度：340m/s b光在真空或空气中的传播速度：3×108m/sc．水的密度：1.0×103kg/m3 d．水的比热容：4.2×103J/（kg•℃）e．一节干电池的电压：1.5V f．家庭电路的电压：220Vg．安全电压：不高于36V2．密度、比热容、热值它们是物质的特性，同一种物质这三个物理量的值一般不改变。

(完整版)三角函数三角函数公式表

(完整版)三角函数公式表1. 正弦函数 (sin):定义：正弦函数是直角三角形中对边与斜边的比值。

公式：sin(θ) = 对边 / 斜边范围：1 ≤ sin(θ) ≤ 1特殊值：sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义：余弦函数是直角三角形中邻边与斜边的比值。

公式：cos(θ) = 邻边 / 斜边范围：1 ≤ cos(θ) ≤ 1特殊值：cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义：正切函数是直角三角形中对边与邻边的比值。

公式：tan(θ) = 对边 / 邻边范围：tan(θ) 可以取任意实数值特殊值：tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在（无穷大）4. 余切函数 (cot):定义：余切函数是直角三角形中邻边与对边的比值。

公式：cot(θ) = 邻边 / 对边范围：cot(θ) 可以取任意实数值特殊值：cot(0°) 不存在（无穷大）, cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义：正割函数是直角三角形中斜边与邻边的比值。

公式：sec(θ)= 1 / cos(θ)范围：sec(θ) 可以取任意实数值特殊值：sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在（无穷大）6. 余割函数 (csc):定义：余割函数是直角三角形中斜边与对边的比值。

三角函数公式表

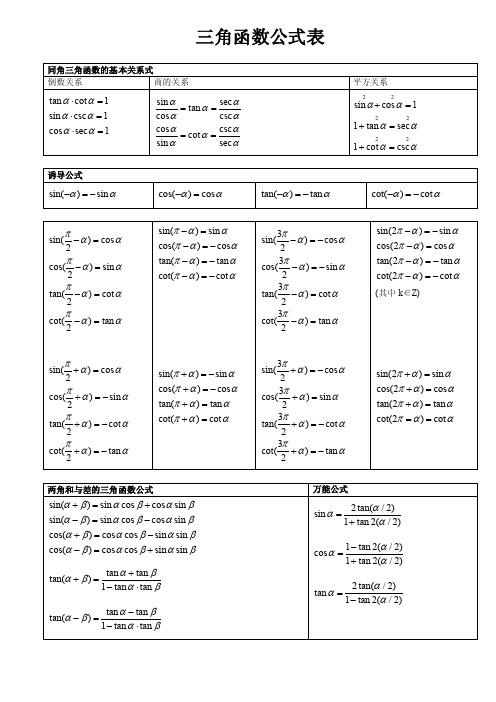
三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系：平方关系： tan α ²cot α＝1 sin α ²csc α＝1 cos α ²sec α＝1sin α/cos α＝tan α＝sec α/csc αcos α/sin α＝cot α＝csc α/sec α sin2α＋cos2α＝1 1＋tan2α＝sec2α 1＋cot2α＝csc2α（六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”）诱导公式（口诀:奇变偶不变，符号看象限。

） sin （－α）＝－sin αcos （－α）＝cos α tan （－α）＝－tan α cot （－α）＝－cot αsin （π/2－α）＝cos αcos （π/2－α）＝sin αtan （π/2－α）＝cot αcot （π/2－α）＝tan αsin （π＋α）＝－sin αcos （π＋α）＝－cos αtan （π＋α）＝tan α cot （π＋α）＝cot αsin （2π－α）＝－sin αcos （2π－α）＝cos α tan （2π－α）＝－tan α cot （2π－α）＝－cot α两角和与差的三角函数公式万能公式sin （α＋β）＝sin αcos β＋cos αsin β sin （α－β）＝sin αcos β－cos αsin βtan （α＋β）＝（tanα＋tanβ）/（1－tanα ·tanβ） tan （α－β）＝（tanα－tanβ）/（1＋tanα ·tanβ）半角的正弦、余弦和正切公式三角函数的降幂公式 sinα＝（2tan(α/2) ）/（1＋tan2(α/2)） cosα＝(1－tan2(α/2))/(1＋tan2(α/2)) tanα＝(2tan(α/2))/(1－tan2(α/2))二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式 sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α tan2α＝2tanα/(1－tan2α) sin3α＝3sinα－4sin3α cos3α＝4cos3α－3cosαtan3α＝(3tanα－tan3α)/( 1－3tan2α)三角函数的和差化积公式三角函数的积化和差公式sin （π/2＋α）＝cosα cos （π/2＋α）＝－sinα tan （π/2＋α）＝－cotα cot （π/2＋α）＝－tanα sin （π－α）＝sinα cos （π－α）＝－cosα tan （π－α）＝－tanα cot （π－α）＝－cotα sin （3π/2－α）＝－cosα cos （3π/2－α）＝－sinα tan （3π/2－α）＝cotα cot （3π/2－α）＝tanαsin （3π/2＋α）＝－cosα cos （3π/2＋α）＝sinα tan （3π/2＋α）＝－cotα cot （3π/2＋α）＝－tanα sin （2kπ＋α）＝sinα cos （2kπ＋α）＝cosα tan （2kπ＋α）＝tanα cot （2kπ＋α）＝cotα (其中k ∈Z) cos （α＋β）＝cos αcos β－sin αsin β cos （α－β）＝cos αcos β＋sin αsin βsin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)−sin(b)=2cos((a+b)/2)sin((a -b)/2) cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)化asin α ±b cos α为一个角的一个三角函数的形式（辅助角的三角函数的公式集合、函数集合简单逻辑任一x∈A x∈B，记作A B A B ，B A A ＝BA B ＝{x|x∈A，且x∈B} A B ＝{x|x∈A，或x∈B}card （A B ）＝card （A ）+card （B ）－card （A B ）（1）命题原命题若p 则q 逆命题若q 则p 否命题若 p 则 q 逆否命题若 q ，则 p （2）四种命题的关系（3）A B ，A 是B 成立的充分条件 B A ，A 是B 成立的必要条件 A B ，A 是B 成立的充要条件函数的性质指数和对数（1）定义域、值域、对应法则（2）单调性对于任意x1，x2∈D若x1＜x2 f （x1）＜f （x2），称f （x ）在D 上是增函数若x1＜x2 f （x1）＞f （x2），称f （x ）在D 上是减函数（3）奇偶性对于函数f （x ）的定义域内的任一x ，若f （－x ）＝f （x ），称f （x ）是偶函数若f （－x ）＝－f （x ），称f （x ）是奇函数（4）周期性对于函数f （x ）的定义域内的任一x ，若存在常数T ，使得f （x+T ）＝f(x)，则称f （x ）是周期函数（1）分数指数幂正分数指数幂的意义是负分数指数幂的意义是（2）对数的性质和运算法则 loga （MN ）＝logaM+logaN logaMn ＝nlogaM （n∈R）指数函数对数函数（1）y ＝ax （a ＞0，a≠1）叫指数函数（2）x∈R，y ＞0 图象经过（0，1）a ＞1时，x ＞0，y ＞1；x ＜0，0＜y ＜1 0＜a ＜1时，x ＞0，0＜y ＜1；x ＜0，y ＞1 a ＞ 1时，y ＝ax 是增函数0＜a ＜1时，y ＝ax 是减函数（1）y ＝logax （a ＞0，a≠1）叫对数函数（2）x ＞0，y∈R 图象经过（1，0）a ＞1时，x ＞1，y ＞0；0＜x ＜1，y ＜0 0＜a ＜1时，x ＞1，y ＜0；0＜x ＜1，y ＞0 a ＞1时，y ＝logax 是增函数 0＜a ＜1时，y ＝logax 是减函数sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]指数方程和对数方程基本型logaf(x)＝b f （x ）＝ab （a ＞0，a≠1）同底型logaf （x ）＝logag （x ） f （x ）＝g （x ）＞0（a ＞0，a≠1）换元型 f （ax ）＝0或f (logax)＝0数列数列的基本概念等差数列（1）数列的通项公式an ＝f （n ）（2）数列的递推公式（3）数列的通项公式与前n 项和的关系 an+1－an ＝dan ＝a1+（n －1）da ，A ，b 成等差 2A ＝a+b m+n ＝k+l am+an ＝ak+al等比数列常用求和公式 an ＝a1qn ＿1a ，G ，b 成等比 G2＝ab m+n ＝k+l aman ＝akal不等式不等式的基本性质重要不等式 a ＞b b ＜aa ＞b ，b ＞c a ＞c a ＞b a+c ＞b+c a+b ＞c a ＞c －b a ＞b ，c ＞d a+c ＞b+d|a|－|b|≤|a±b|≤|a|+|b| 证明不等式的基本方法比较法（1）要证明不等式a ＞b （或a ＜b ），只需证明 a －b ＞0（或a －b ＜0＝即可（2）若b ＞0，要证a ＞b ，只需证明，要证a ＜b ，只需证明综合法综合法就是从已知或已证明过的不等式出发，根据不等式的性质推导出欲证的不等式（由因导果）的方法。

完整三角函数公式表

完整三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系: 平方关系:22tanα ?cotα,1 sinα，cosα,1 sinα/cosα,tanα,secα/cscα 22sinα ?cscα,1 1，tanα,secα cosα/sinα,cotα,cscα/secα22cosα ?secα,1 1，cotα,cscα(六边形记忆法:图形结构“上弦中切下割，左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”)诱导公式(口诀:奇变偶不变，符号看象限。

)sin(,α),,sinα cos(,α),cosα tan(,α),,tanα cot(,α),,cotα sin(2π,α),,sinα sin(π/2,α),cosα sin(3π/2,α),,cosαsin(π,α),sinαcos(2π,α),cosα cos(π/2,α),sinα cos(3π/2,α),,sinαcos(π,α),,cosαtan(2π,α),,tanα tan(π/2,α),cotα tan(3π/2,α),cotαtan(π,α),,tanαcot(2π,α),,cotα cot(π/2,α),tanα cot(3π/2,α),tanαcot(π,α),,cotαsin(2kπ，α),sinα sin(π，α),,sinα sin(π/2，α),cosαsin(3π/2，α),,cosαcos(2kπ，α),cosα cos(π，α),,cosα cos(π/2，α),,sinαcos(3π/2，α),sinαtan(2kπ，α),tanα tan(π，α),tanα tan(π/2，α),,cotαtan(3π/2，α),,cotαcot(2kπ，α),cotα cot(π，α),cotα cot(π/2，α),,tanαcot(3π/2，α),,tanα(其中k?Z)两角和与差的三角函数公式万能公式sin(α，β),sinαcosβ，cosαsinβ 2tan(α/2)sin(α,β),sinαcosβ,cosαsinβ sinα,——————cos(α，β),cosαcosβ,sinαsinβ 2 1，tan(α/2) cos(α,β),cosαcosβ，sinαsinβ2 1,tan(α/2) tanα，tanβ cosα,——————tan(α，β),—————— 2 1，tan(α/2) 1,tanα ?tanβ2tan(α/2) tanα,tanβ tanα,——————tan(α,β),—————— 2 1,tan(α/2) 1，tanα ?tanβ半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式3sin2α,2sinαcosα α sin3α,3sinα,4sin22223cos2α,cosα,sinα,2cosα,1,1,2sinα cos3α,4cosα,3cosα3 3tanα,tanα 2tanαtan3α,——————tan2α,—————22 1,3tanα 1,tanα三角函数的和差化积公式三角函数的积化和差公式α，β α,β 1sinα，sinβ,2sin———?cos———sinα ?cosβ,-[sin(α，β)，sin(α,β)]2 2 2α，β α,β 1sinα,sinβ,2cos———?sin———cosα ?sinβ,-[sin(α，β),sin(α,β)]2 2 2α，β α,β 1cosα，cosβ,2cos———?cos———cosα ?cosβ,-[cos(α，β)，cos(α,β)]2 2 2α，β α,β 1cosα,cosβ,,2sin———?sin———sinα ?sinβ,— -[cos(α，β),cos(α,β)]2 2 2化asinα ?bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)RAID0、RAID1、RAID0+1(又叫RAID10)、RAID5做服务器，选 REDHAT 或者 SUSE做开发，选 FEDORA做客户端，选 UBUNTU。

三角函数公式表及其图表

三角函数公式表及其图表三角函数常用公式：（^表示乘方，例如^2表示平方）正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ =1-cosθ余矢函数vercosθ =1-sinθ同角三角函数间的基本关系式：·平方关系：sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式：Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式：sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]两角和公式sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-cos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinbtan(a+b)=(tana+tanb)/(1-tanatanb)tan(a-b)=(tana-tanb)/(1+tanatanb)cot(a+b)=(cotacotb-cot(a-b)=(cotacotb+1)/(cotb-cota)倍角公式tan2a=2tana/[1-(tana)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2sin2a=2sina*cosa半角公式sin(a/2)=√((1-cosa)/2) sin(a/2)=-√((1-cosa)/2)cos(a/2)=√((1+cosa)/2) cos(a/2)=-√((1+cosa)/2)tan(a/2)=√((1-cosa)/((1+cosa)) tan(a/2)=-√((1-cosa)/((1+cosa)) cot(a/2)=√((1+cosa)/((1-cosa)) cot(a/2)=-√((1+cosa)/((1-tan(a/2)=(1-cosa)/sina=sina/(1+cosa)和差化积2sinacosb=sin(a+b)+sin(a-b)2cosasinb=sin(a+b)-sin(a-b) )2cosacosb=cos(a+b)-sin(a-b)-2sinasinb=cos(a+b)-cos(a-b)sina+sinb=2sin((a+b)/2)cos((a-b)/2cosa+cosb=2cos((a+b)/2)sin((a-b)/2)tana+tanb=sin(a+b)/cosacosb积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tga=tana=sina/cosa万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b] 1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)。

完整版三角函数常用公式表

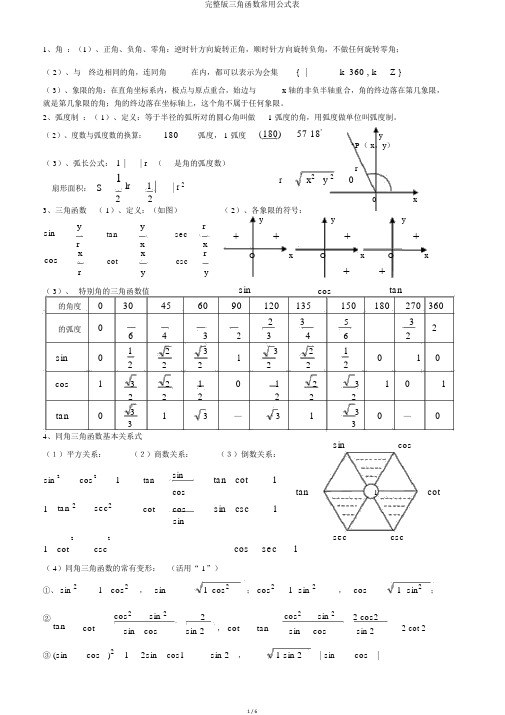
1、角：（1）、正角、负角、零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角；（ 2）、与终边相同的角，连同角在内，都可以表示为会集{ |k 360 , k Z }（ 3）、象限的角：在直角坐标系内，极点与原点重合，始边与x 轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限。

2、弧度制：（ 1）、定义：等于半径的弧所对的圆心角叫做 1 弧度的角，用弧度做单位叫弧度制。

（ 2）、度数与弧度数的换算：180弧度， 1 弧度( 180 )57 18'yP （ x ，y ）（ 3）、弧长公式： l || r （是角的弧度数）rx 2 y 2扇形面积： S1lr 1 | | r 2 r22x 3、三角函数（ 1）、定义：（如图）（ 2）、各象限的符号：siny y r tan x secr x cosx x r cotycscryyyy++_+_+OxOxOx___++_（ 3）、特别角的三角函数值sincostan的角度 0 30456090120 135 150180270 360的弧度2 353 26432 3462sin1 2 3 1 32 1 012 2 2222cos13 2 1 01 2 3 112 22222tan3 13—3 13 0—334、同角三角函数基本关系式sincos（１）平方关系：（２）商数关系：（３）倒数关系：sin 2cos21tansin tan cot1costancot11 tan 2sec 2cotcos sin csc1sin1 2csc 2cossec1seccsccot（ 4）同角三角函数的常有变形：（活用“ 1”）①、 sin 21 cos2 ， sin1 cos2 ； cos 21 sin2 ， cos1 sin2 ；②tancotcos 2sin 22 ， cottancos 2sin 2 2 cos2 2 cot 2sin cossin 2sin cos sin 2③ (sincos )2 1 2sin cos1sin 2 ，1 sin 2| sincos |5、引诱公式：（奇变偶不变，符号看象限）公式一： sin( k 360 ) sincos(k360 ) costan(k 360 ) tan公式二：公式三：公式四：公式五：sin(180 ) sinsin(180 ) sin sin( ) sinsin(360 ) sin cos(180 ) cos cos(180 )coscos( ) cos cos(360 ) costan(180)tantan(180) tantan()tantan(360)tansin( )cossin()cos3)cossin(3) cossin(2222补充：cos()sincos()sincos(3)sincos(3)sin2222tan()cottan()cottan(3) cottan(3)cot22226、两角和与差的正弦、余弦、正切两角和与差的三角函数公式全能公式sin( ) sin cos cos sinsin2 tan( / 2) sin( ) sin coscos sin1 tan 2( / 2)cos( ) cos cos sin sin1 tan 2( / 2)cos() coscossin sincos1 tan 2(/ 2)tan tantan()1 tantan2 tan( / 2)tan1 tan 2( / 2)tan tantan()1 tantan7 . 辅角公式a sin x bcosxa 22asin xb2 cosxb22 a 2ba ba 2b 2 (sin x coscos x sin ) a 2 b 2 sin(x)（其中称为辅助角，的终边过点 (a,b) ， tanb）（多用于研究性质）a8、二倍角公式：（ 1）、 S 2 ：sin 22 sin cos（ 2）、降次公式：（多用于研究性质）C 2 ： cos 2cos2sin2sin cos1sin 221 2 sin22cos21sin21 cos21cos212 22 T 2 ：tan 22 tancos 21 cos21 cos2 11 tan 222 2 （ 3）、二倍角公式的常用变形：①、1cos22 | sin | ， 1 cos22 | cos|；②、 11cos2| sin |，11cos2| cos |2 222③ sin 4cos 41 2sin 2cos 21 sin2 2；cos 4sin 4cos2 ；2④半角： sin1 cos， cos1 cos ， tan 1 cos1 cos sin22 1 cossin1 cos222三角函数的和差化积公式三角函数的积化和差公式sinsin 2sincossincos 1 sin() sin()222sinsin2cossincos sin1 sin( ) sin()222coscos 2coscoscoscos 1 cos( ) cos()2 22coscos2sinsinsinsin1cos( ) cos()2229、三角函数的图象性质（ 1）、函数的周期性：①、定义：关于函数f （ x ），若存在一个非零常数 T ，当 x 取定义域内的每一个值时，都有： f （ x+T ） = f （x ），那么函数 f （ x ）叫周期函数，非零常数 T 叫这个函数的周期；②、若是函数 f （ x ）的所有周期中存在一个最小的正数，这个最小的正数叫f （ x ）的最小正周期。

三角函数公式大全图解

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a -cosa+cosb = 2cos2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式sin(-a) = -sinacos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +-tana=2)2(tan 12tan2a a- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinαcos （2kπ＋α）= cosαtan （2kπ＋α）= tanαcot （2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）= -sinαcos （π＋α）= -cosαtan （π＋α）= tanαcot （π＋α）= cotα公式三：任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinαcos （-α）= cosαtan （-α）= -tanαcot （-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin （π-α）= sinαcos （π-α）= -cosαtan （π-α）= -tanαcot （π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin （2π-α）= -sinαcos （2π-α）= cosαtan （2π-α）= -tanαcot （2π-α）= -cotα公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosαcos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明（全部）2009-07-08 16:13公式表达式乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式 |a+b|≤|a|+|b| |a -b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系 X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式 b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注：角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦：cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减，可以得到2组积化和差:相加：cosAcosB=[cos(A+B)+cos(A-B)]/2相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减，可以得到2组积化和差:相加：sinAcosB=[sin(A+B)+sin(A-B)]/2相减：sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1) tan(α+β)=(1+m)/(1-m)tanβ。

三角函数常用公式大全

三角函数公式看似很多、很复杂，但只要掌握了三角函数的本质及内部规律，就会发现三角函数各个公式之间有强大的联系。

而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。

三角函数半角公式sin(A/2)=±√((1-cosA)/2)cos(A/2)=±√((1+cosA)/2)tan(A/2)=±√((1-cosA)/((1+cosA))三角函数倍角公式Sin2A=2SinA*CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)三角函数两角和与差公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cossinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)平方关系公式sin²α+cos²α=1cos²a=(1+cos2a)/2tan²α+1=sec²αsin²a=(1-cos2a)/2cot²α+1=csc²α倒数关系公式tanα·cotα=1sinα·cscα=1cosα·secα=1商数关系公式tana=sina/cosacota=cosa/sinatan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数积化和差sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数和差化积sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 三角函数诱导公式诱导公式一：终边相同的角的同一三角函数的值相等设α为任意锐角，弧度制下的角的表示：sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)诱导公式二：π+α的三角函数值与α的三角函数值之间的关系设α为任意角，弧度制下的角的表示：sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα诱导公式三：任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα诱导公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα诱导公式六：π/2±α及3π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα三角函数的万能公式sin(A)=[2tan(A/2)]/[1+tan2(A/2)]cos(A)=[1-tan2(A/2)]/[1+tan2(A/2)]tan(A)=[2tan(A/2)]/[1-tan2(A/2)]。

三角函数公式大全

三角函数十组诱导公式公式一公式二sin(2kπ+x)=sin x cos(2kπ+x)=cos x tan(2kπ+x)=tan x cot(2kπ+x)=cot x sec(2kπ+x)=sec x csc(2kπ+x)=csc x sin(π+x)=-sin x cos(π+x)=-cos x tan(π+x)=tan x cot(π+x)=cot x sec(π+x)=-sec x csc(π+x)=-csc x公式三公式四sin(-x)=-sin x cos(-x)=cos x tan(-x)=-tan x cot(-x)=-cot x sec(-x)=sec x csc(-x)=-csc x sin(π-x)=sin x cos(π-x)=-cos x tan(π-x)=-tan x cot(π-x)=-cot x sec(π-x)=-sec x csc(π-x)=csc x公式五公式六sin(x-π)=-sin x cos(x-π)=-cos x tan(x-π)=tan x cot(x-π)=cot x sec(x-π)=-sec x csc(x-π)=-csc x sin(2π-x)=-sin x cos(2π-x)=cos x tan(2π-x)=-tan x cot(2π-x)=-cot x sec(2π-x)=sec x csc(2π-x)=-csc x公式七公式八sin(π/2+x)=cosx cos(π/2+x)=−sinx tan(π/2+x)=-cotx cot(π/2+x)=-tanx sec(π/2+x)=-cscx csc(π/2+x)=secx sin(π/2-x)=cosx cos(π/2-x)=sinx tan(π/2-x)=cotx cot(π/2-x)=tanx sec(π/2-x)=cscx csc(π/2-x)=secx公式九公式十sin(3π/2+x)=-cosx cos(3π/2+x)=sinx tan(3π/2+x)=-cotx cot(3π/2+x)=-tanx sec(3π/2+x)=cscx csc(3π/2+x)=-secx sin(3π/2-x)=-cosx cos(3π/2-x)=-sinx tan(3π/2-x)=cotx cot(3π/2-x)=tanx sec(3π/2-x)=-cscx csc(3π/2-x)=-secx两角和差设A（cosα,sinα)，B (cosβ,sinβ)，O(0,0)∴=(cosα,sinα)，=(cosβ,sinβ)∴·=|| || cos (α-β) =coα cosβ + sinα sinβ∴cos(α-β)=cosαcosβ+sinαsinβ取β=-β，可得cos(α+β)=cosαcosβ-sinαsinβ和差化积积化和差二倍角公式三倍角公式sin(3α)=3sinα-4sin3α=4sinα·sin(60°+α)sin(60°-α)cos(3α)=4cos3α-3cosα=4cosα·cos(60°+α)cos(60°-α)tan(3α)=(3tanα-tan3α)/(1-3tan²α)=ta nα·tan(π/3+α)tan(π/3-α)cot(3α)=(cot3α-3cotα)/(3cot²α-1)倍角公式根据欧拉公式(cosθ+isinθ)n=cosnθ+isinnθ将左边用二项式定理展开分别整理实部和虚部可以得到下面两组公式sin(nα)=ncos n-1α·sinα-Cn 3cos n-3α·sin3α+Cn5cos n-5α·sin5α-…cos(nα)=cos nα-Cn 2cos n-2α·sin2α+Cn4cos n-4α·sin4α-…半角公式sin(α/2)=±√[(1-cosα)/2]cos(α/2)=±√[(1+cosα)/2]tan(α/2)=±√[(1-cosα)/(1+cosα)]=sinα/(1+cosα)=(1-cosα)/sinα=cscα-cotαcot(α/2)=±√[(1+cosα)/(1-cosα)]=(1+cosα)/sinα=sinα/(1-cosα)=cscα+cotαsec(α/2)=±√[(2secα/(secα+1)]csc(α/2)=±√[(2secα/(secα-1)]辅助角公式万能公式sinα=[2tan(α/2)]/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=[2tan(α/2)]/[1-tan²(α/2)]三角函数降幂公式sin²α=[1-cos(2α)]/2cos²α=[1+cos(2α)]/2tan²α=[1-cos(2α)]/[1+cos(2α)]三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·ta nα)泰勒展开式sin x = x-x3/3!+x5/5!-……+(-1)(k-1)(x(2k-1))/(2k-1)!+…… (-∞<x<∞)cos x = 1-x2/2!+x4/4!-……+(-1)k(x(2k))/(2k)!+…… (-∞<x<∞)arcsinx=x+x3/(2·3)+(1·3)x5/(2·4·5)+1·3·5(x7)/(2·4·6·7)……(2k+1)/(2k!!(2k+1))+……(|x|<1) (!!表示双阶乘) +(2k+1)!!·xarccosx=π/2-(x+x3/(2·3)+(1·3)x5/(2·4·5)+1·3·5(x7)/(2·4·6·7)……)(|x|<1)arctan x = x - x3/3 + x5/5 -……(x≤1)sinh x = x+x3/3!+x5/5!+……+(x(2k-1))/(2k-1)!+…… (-∞<x<∞)cosh x = 1+x2/2!+x4/4!+……+(x(2k))/(2k)!+……(-∞<x<∞)arcsinh x =x - x3/(2·3) + (1·3)x5/(2·4·5) -1·3·5(x7)/(2·4·6·7)……(|x|<1)arctanh x = x + x3/3 + x5/5 + ……(|x|<1)导数y=sinx→y'=cosxy=cosx→y'=-sinxy=tanx→y'=1/cos²x =sec²xy=cotx→y'= -1/sin²x= - csc²xy=secx→y'=secxtanxy=cscx→y'=-cscxcotxy=arcsinx→y'=1/√(1-x²)y=arccosx→y'= -1/√(1-x²)y=arctanx→y'=1/(1+x²)y=arccotx→y'= -1/(1+x²)三角函数指数形式sinz=[e iz-e-iz]/(2i)cosz=[e iz+e-iz]/2tanx=[e iz-e-iz]/[ie iz+ie-iz]复数三角函数sin(a+bi)=sinacosbi+sinbicosa =sinachb+ishbcosacos(a-bi)=cosacosbi+sinbisina =cosachb+ishbsinatan(a+bi)=sin(a+bi)/cos(a+bi) cot(a+bi)=cos(a+bi)/sin(a+bi) sec(a+bi)=1/cos(a+bi)csc(a+bi)=1/sin(a+bi)正弦定理S=½absinC=½bcsinA=½acsinB余弦定理a² = b² + c²- 2bc·cosAb² = a² + c² - 2ac·cosBc² = a² + b² - 2ab·cosCcosC=（a² +b² -c²）/ 2abcosB=（a² +c² -b²）/ 2accosA=（c² +b² -a²）/ 2bc延伸定理：第一余弦定理a=b·cos C+c·cos B， b=c·cos A+a·cos C， c=a·cos B+b·cos A 正切定理(a+b)/(a-b) = tan[(A+B)/2]/tan[(A-B)/2]三角恒等式tanA+tanB+tanC=tanAtanBtanC （A+B+C=π）当α+β+γ=nπ(n∈Z)时，总有tanα+tanβ+tanγ=tanαtanβtanγ 三角函数记忆口诀三角函数是函数，象限符号坐标注。

三角函数公式表

y cot x
y A sinx
（A、＞0） R
定义域值域周期性奇偶性
R
[1,1]
R
[1,1]
x | x R且x k , k Z
R

R

A, A
2
2
2
奇函数
偶函数
奇函数
奇函数
当 0, 非奇非偶当 0, 奇函数
（一）基本关系
公式组一 sinx·cscx=1 cosx·secx=1 tanx·cotx=1
sin x tanx= cos x
sin2x+cos2x=1 1+tan2 x =sec2x 1+cot2x=csc2x
x=
cos x sin x
公式组二 sin(2k x) sin x cos(2k x) cos x tan(2k x) tan x cot(2k x) cot x 公式组六

2
2
sin cos
公式组四 1

2
cos
1 tan 2 1 tan
2

2 2
tan
2 tan

2
1 tan2
sin 15 cos75

2
2 1 cos sin sin sin 2 1 cos cos cos cos 2 1 sin sin cos cos 2 sin sin 2 sin cos 2 2 sin sin 2 cos sin 2 2 cos cos 2 cos cos 2 2 cos cos 2 sin sin 2 2

(完整版)三角函数常用公式表

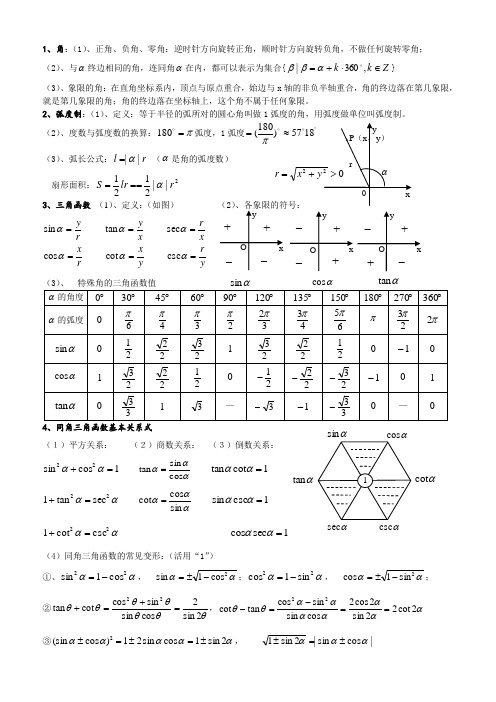
1、角：（1）、正角、负角、零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角；（2）、与α终边相同的角，连同角α在内，都可以表示为集合{Z k k ∈⋅+=,360|αββ}（3）、象限的角：在直角坐标系内，顶点与原点重合，始边与x 轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限。

2、弧度制：（1）、定义：等于半径的弧所对的圆心角叫做1弧度的角，用弧度做单位叫弧度制。

（2）、度数与弧度数的换算：π=180弧度，1弧度)180( =π（3）、弧长公式：r l ||α= （α是角的弧度数）扇形面积：2||2121r lr S α===3、三角函数（1）、定义：（如图）（2）yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin 4、同角三角函数基本关系式（１）平方关系：（２）商数关系：（３）倒数关系：1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα（4）同角三角函数的常见变形：（活用“1”） ①、αα22cos 1sin-=， αα2cos 1sin -±=；αα22sin 1cos -=， αα2sin 1cos -±=；②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+，αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±， |cos sin |2sin 1ααα±=±xy+ +_ _O xy++__ Oαtanxy+ +__O=r αsec αsinαtan αcotcsc5、诱导公式：（奇变偶不变，符号看象限）公式一： ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k公式二：公式三：公式四：公式五：ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充：ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切 7 .辅角公式 ⎪⎪⎭⎫ ⎝⎛++++=+x b a b x b a a b a xb x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a（其中ϕ称为辅助角，ϕ的终边过点),(b a ，ab =ϕtan ）（多用于研究性质） 8、二倍角公式：（1）、α2S ： αααcos sin 22sin = （2）、降次公式：（多用于研究性质） α2C ： ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin 2122-=-=αα 212cos 2122cos 1sin 2+-=-=αααα2T ： ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα （3）、二倍角公式的常用变形：①、|sin |22cos 1αα=-， |cos |22cos 1αα=+；②、|sin |2cos 2121αα=-， |cos |2cos 2121αα=+③22sin 1cos sin 21cos sin 22244ααααα-=-=+； ααα2cos sin cos 44=-；④半角：2cos 12sin αα-±=，2cos 12cos αα+±=，αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-=9、三角函数的图象性质（1）、函数的周期性：①、定义：对于函数f （x ），若存在一个非零常数T ，当x 取定义域内的每一个值时，都有：f （x +T ）= f （x ），那么函数f （x ）叫周期函数，非零常数T 叫这个函数的周期；②、如果函数f （x ）的所有周期中存在一个最小的正数，这个最小的正数叫f （x ）的最小正周期。

三角函数公式大全

三角函数公式大全诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b) sin(a-b)=sin(a)cos(b)-cos(a)sin(b) cos(a-b)=cos(a)cos(b)+sin(a)sin(b) tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b)) 和差化积公式a-b)/2)sin(a)+sin(b)=2sin((a+b)/2)cos((sin(a)?sin(b)=2cos((a+b)/2)sin((a-b)/2) cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2) cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2) 积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)] 二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半角公式sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2)) tan(a)= (2tan(a/2))/(1-tan^2(a/2)) 其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b]1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 其他非重点csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式 |a+b|?|a|+|b| |a-b|?|a|+|b| |a|?b<=>-b?a?b|a-b|?|a|-|b| -|a|?a?|a|一元二次方程的解 -b+?(b2-4ac)/2a -b-b+?(b2-4ac)/2a根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) -1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) ctg(A+B)=(ctgActgB 倍角公式 tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式 sin(A/2)=?((1-cosA)/2) sin(A/2)=-?((1-cosA)/2)cos(A/2)=?((1+cosA)/2) cos(A/2)=-?((1+cosA)/2)tan(A/2)=?((1-cosA)/((1+cosA)) tan(A/2)=-?((1-cosA)/((1+cosA))ctg(A/2)=?((1+cosA)/((1-cosA)) ctg(A/2)=-?((1+cosA)/((1-cosA))和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB 某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注: 其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角圆的标准方程 (x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r 锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h 斜棱柱体积 V=S'L 注:其中,S'是直截面面积， L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h。

三角函数常用公式表

2、弧度制：（1）、定义：等于半径的弧所对的圆心角叫做1弧度的角，用弧度做单位叫弧度制。

（2）、度数与弧度数的换算：π=180弧度，1弧度)180( =π（3）、弧长公式：r l ||α= （α是角的弧度数）扇形面积：2||2121r lr S α===3、三角函数（1）、定义：（如图）（2）yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin 4、同角三角函数基本关系式（１）平方关系：（２）商数关系：（３）倒数关系：1cos sin 22=+αα αααc o ss i nt a n = 1c o t t a n =αα αα22sec tan 1=+ αααs i nc o sc o t =1c s c s i n =αα αα22csc cot 1=+ 1sec cos =αα（4）同角三角函数的常见变形：（活用“1”） ①、αα22cos 1sin-=， αα2cos 1sin -±=；αα22sin 1cos -=， αα2sin 1cos -±=；②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+，αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±， |cos sin |2sin 1ααα±=±xy+ +_ _O xy++__ Oαtanxy+ +__O=r αsec αsinαtan αcotcsc5、诱导公式：（奇变偶不变，符号看象限）公式一： ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k公式二：公式三：公式四：公式五：ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充：ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切 7 .辅角公式 ⎪⎪⎭⎫ ⎝⎛++++=+x b a b x b a a b a xb x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a（其中ϕ称为辅助角，ϕ的终边过点),(b a ，ab =ϕtan ）（多用于研究性质） 8、二倍角公式：（1）、α2S ： αααcos sin 22sin = （2）、降次公式：（多用于研究性质） α2C ： ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin 2122-=-=αα 212cos 2122cos 1sin 2+-=-=αααα2T ： ααα2t a n1t a n 22t a n -= 212cos 2122cos 1cos 2+=+=ααα （3）、二倍角公式的常用变形：①、|sin |22cos 1αα=-， |cos |22cos 1αα=+；②、|sin |2cos 2121αα=-， |cos |2cos 2121αα=+③22sin 1cos sin 21cos sin 22244ααααα-=-=+； ααα2cos sin cos 44=-；④半角：2cos 12sin αα-±=，2cos 12cos αα+±=，αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-=9、三角函数的图象性质（1）、函数的周期性：①、定义：对于函数f （x ），若存在一个非零常数T ，当x 取定义域内的每一个值时，都有：f （x +T ）= f （x ），那么函数f （x ）叫周期函数，非零常数T 叫这个函数的周期；②、如果函数f （x ）的所有周期中存在一个最小的正数，这个最小的正数叫f （x ）的最小正周期。

完整三角函数公式表

完整三角函数公式表 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系：平方关系：tanα ·cotα＝1 sinα ·cscα＝1 cosα ·secα＝1sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secαsin2α＋cos2α＝11＋tan2α＝sec2α1＋cot2α＝csc2α（六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”）?诱导公式（口诀:奇变偶不变，符号看象限。

）sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα??sin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotαsin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotαsin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotαcot（π/2＋α）＝－tanαcotαcot（3π/2＋α）＝－tanαcotα(其中k∈Z)?两角和与差的三角函数公式万能公式sin（α＋β）＝sinαcosβ＋cosαsinβsin（α－β）＝sinαcosβ－cosαsinβcos（α＋β）＝cosαcosβ－sinαsinβcos（α－β）＝cosαcosβ＋sinαsinβ??????????????tanα＋tanβtan（α＋β）＝——————?????????????1－tanα ·tanβ??????????????tanα－tanβtan（α－β）＝——————?????????????1＋tanα ·tanβ??????? 2tan(α/2)sinα＝——————?????? 1＋tan2(α/2)???????1－tan2(α/2)cosα＝——————?????? 1＋tan2(α/2)???????2tan(α/2)tanα＝——————??????1－tan2(α/2)?半角的正弦、余弦和正切公式三角函数的降幂公式??二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－sin3α＝3sinα－4sin3α2sin2α??????? ?2tanαtan2α＝—————?????? ?1－tan2αcos3α＝4cos3α－3cosα???????3tanα－tan3αtan3α＝——————?????? ?1－3tan2α??三角函数的和差化积公式三角函数的积化和差公式?????????????????α＋β???????α－βsinα＋sinβ＝2sin———·cos———??????????????????2??????????2 ?????????????????α＋β???????α－βsinα－sinβ＝2cos———·sin———??????????????????2??????????2 ?????????????????α＋β???????α－βcosα＋cosβ＝2cos———·cos———??????????????????2??????????2 ???????????????????α＋β???????α－βcosα－cosβ＝－2sin———·sin———????????????????????2??????????2???????????1sinα ·cosβ＝-[sin（α＋β）＋sin（α－β）]???????????2???????????1cosα ·sinβ＝-[sin（α＋β）－sin（α－β）]???????????2???????????1cosα ·cosβ＝-[cos（α＋β）＋cos（α－β）]???????????2??????????????1sinα ·sinβ＝— -[cos（α＋β）－cos（α－β）]??????????????2?化asinα±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）arc sin x + arc sin y = arc sin x – arc sin y =?arc cos x + arc cos y = arc cos x – arc cos y =??arc tan x + arc tan y = arc tan x – arc tan y =?2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =?三角形中三角函数基本定理Tag： ? 点击：1522 【正弦定理】式中R为ABC的外接圆半径(图.【余弦定理】【勾股定理】在直角三角形(C为直角)中，勾方加股方等于弦方(图，即勾股定理也称商高定理，外国书刊中称毕达哥拉斯定理.【正切定理】或【半角与边长的关系公式】式中，r为ABC的内切圆半径，且式中S为ABC的面积.。

高中三角函数公式总表

三角公式总表⒈L弧长=R= S扇=LR=R2=⒉正弦定理：=== 2R（R为三角形外接圆半径）⒊余弦定理：a=b+c-2bc b=a+c-2ac c=a+b-2ab⒋S⊿=a=ab=bc=ac==2R====pr=(其中, r为三角形xx半径)⒌同角关系：⑴商的关系：①=== ②③④⑤⑥⑵倒数关系：⑶平方关系：⑷ （其中辅助角与点（a,b）在同一象限，且）⒍函数y=k的图象及性质：（）振幅A，周期T=, 频率f=, 相位，初相⒎五点作图法：令依次为求出x与y，依点作图⒏诱导公试三角函数值，前面加上一个把看作锐角时，原三角函数值的符号；即：函数名不变，符号看象限三角函数值等于的异名三角函数值，前面加上一个把看作锐角时，原三角函数值的符号;即：函数名改变，符号看象限⒐和差角公式① ②③④⑤ 其中当A+B+C=π时,有:i). ii).⒑二倍角公式：(含万能公式)①②③ ④ ⑤⒒三倍角公式：①②③⒓半角公式：（符号的选择由所在的象限确定）①② ③④⑤ ⑥⑦⑧⒔积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin ⒕和差化积公式： ① ② ③ ④⒖反三角函数： ⒗最简单的三角方程。

三角函数公式大全(很详细)

三角函数公式大全(很详细)在三角函数的定义方面，可以通过在直角三角形和直角坐标系中定义六个三角函数来理解。

其中包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

转化关系方面，倒数关系和平方关系都是常见的转化方式。

此外，还有和角公式、倍角公式、半角公式和万能公式等。

在积化和差、和差化积方面，可以利用正弦和余弦的和角、差角公式来得到“积化和差公式”。

同样地，余弦的和角、差角公式也可以用来得到相应的公式。

需要注意的是，在文章中有明显的格式错误和段落缺失，需要进行删除和修改。

Cosine of the sum and difference of two angles can be expressed as follows using the product-to-sum identities:cos(α + β) = cosα cosβ - sinα sinβcos(α - β) = cosα cosβ + sinα sinβSimilarly。

sine of the sum and difference of two angles can be expressed as follows:sin(α + β) = sinα cosβ + cosα sinβsin(α - β) = sinα cosβ - cosα sinβThese are known as the sum-to-product identities.Another set of identities that relate the sum and difference of two angles to their sines and cosines are the difference-to-product identities:sinα - sinβ = 2 cos((α + β)/2) sin((α - β)/2)sinα + sinβ = 2 sin((α + β)/2) cos((α - β)/2)cosα - cosβ = -2 sin((α + β)/2) sin((α - β)/2)cosα + cosβ = 2 cos((α + β)/2) cos((α - β)/2)These can be derived using the sum-to-product identities and some algebraic n.There are also several trigonometric identities that involve negative angles or angles that differ by π/2.For example:sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = -sin(a)sin(π - a) = sin(a)cos(π - a) = -cos(a)sin(π + a) = -sin(a)cos(π + a) = -cos(a)Finally。

完整版)完整三角函数公式表

完整版)完整三角函数公式表三角函数公式表同角三角函数的基本关系式三角函数是数学中的重要概念，它们在数学和物理学中都有广泛的应用。

同角三角函数的基本关系式包括倒数关系、商的关系和平方关系。

其中，倒数关系式如下：tan\alpha\cdot\cot\alpha=1$$sin\alpha\cdot\csc\alpha=1$$cos\alpha\cdot\sec\alpha=1$$商的关系式如下：frac{\sin\alpha}{\cos\alpha}=\tan\alpha=\frac{\sec\alpha}{\csc\alpha}$$frac{\cos\alpha}{\sin\alpha}=\cot\alpha=\frac{\csc\alpha}{\sec\alpha}$$平方关系式如下：sin^2\alpha+\cos^2\alpha=1$$2^2+ \tan^2\alpha=\sec^2\alpha$$1+\cot^2\alpha=\csc^2\alpha$$这些关系式可以用六边形记忆法和记忆方法来记忆。

其中，六边形记忆法是指图形结构“上弦中切下割，左正右余中间1”，而记忆方法是指对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

诱导公式诱导公式是指通过已知的三角函数值来推导其他角度的三角函数值的公式。

它们可以用口诀“奇变偶不变，符号看象限”来记忆。

具体来说，诱导公式包括三角函数的奇偶性和象限问题。

奇偶性公式如下：sin(-\alpha)=-\sin\alpha$$cos(-\alpha)=\cos\alpha$$tan(-\alpha)=-\tan\alpha$$cot(-\alpha)=-\cot\alpha$$象限问题公式如下：sin\left(\frac{3\pi}{2}-\alpha\right)=-\cos\alpha$$ cos\left(\frac{3\pi}{2}-\alpha\right)=-\sin\alpha$$ sin(2\pi-\alpha)=-\sin\alpha$$cos(2\pi-\alpha)=\cos\alpha$$tan\left(\frac{3\pi}{2}-\alpha\right)=\cot\alpha$$ tan(2\pi-\alpha)=-\tan\alpha$$cot\left(\frac{3\pi}{2}-\alpha\right)=\tan\alpha$$ cot(2\pi-\alpha)=-\cot\alpha$$另外，还有两个特殊的角度：sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha$$cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha$$ tan\left(\frac{\pi}{2}-\alpha\right)=\cot\alpha$$ cot\left(\frac{\pi}{2}-\alpha\right)=\tan\alpha$$ sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha$$ cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha$$ tan\left(\frac{\pi}{2}+\alpha\right)=-\cot\alpha$$ cot\left(\frac{\pi}{2}+\alpha\right)=-\tan\alpha$$ sin(\pi-\alpha)=\sin\alpha$$cos(\pi-\alpha)=-\cos\alpha$$tan(\pi-\alpha)=-\tan\alpha$$cot(\pi-\alpha)=-\cot\alpha$$sin(\pi+\alpha)=-\sin\alpha$$cos(\pi+\alpha)=-\cos\alpha$$tan(\pi+\alpha)=\tan\alpha$$cot(\pi+\alpha)=\cot\alpha$$两角和与差的三角函数公式最后，还有两角和与差的三角函数公式。