电磁场与电磁波期末试卷B卷答案
电磁场与电磁波期末考试复习试题4套(部分含答案)

电磁场与电磁波期末考试复习资料11.圆柱坐标系中单位矢量 , 。
2.对于矢量A ,若 ,则=+•y x a y x a x )(2 ,=⨯x z a y a x 2 。
3.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ,矢量B A ⋅= 。
4.已知直角坐标系中点P 1(5,-2,1),P 2(3,1,2),则P1的位置矢量为 ,P1到P2的距离矢量为 。
5.已知球坐标系中单位矢量 。
6.在两半无限大导电平面组成的直角劈形中间放置一点电荷,此时点电荷的镜像电荷个数为 。
7.点电荷q 在自由空间任一点r 处电场强度为 。
8.静电场中导体内的电场为 ,电场强度与电位函数的关系为 。
9.高斯散度定理的积分式为 ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
10.已知任意一个矢量场A ,则其旋度的散度为 。
11.真空中静电场的基本方程的微分形式为 、 、 。
12.分析恒定磁场时,在无界真空中,两个基本场变量为 ,它们之间的关系为 。
13.斯托克斯定理为 ,它表明矢量场A 的旋度沿曲面S 的方向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。
14.任意一个标量场u ,则其梯度的旋度为 。
15.对于某一矢量 ,它的散度定义式为 ,用哈密顿算子表示为 。
16.介质中静电场的基本方程的积分式为 , , 。
17.介质中恒定磁场的基本方程的微分形式为 、 、 。
18.介质中恒定磁场的基本方程的积分式为 , , 。
19.静电场中两种介质分界面的边界条件是 , 。
20.在无限大的导体平面上方d 处放一点电荷q ,则其镜像电荷电量为 ,位置位于 ;如果一个点电荷置于两平行导体中间,则此点电荷有 镜像电荷。
21.矢量场223z a yz a y x a A z y x ++=在点P(1,1,0)的散度为 。
22.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ,位置位于 ;当点电荷q 向无限远处运动时,其镜像电荷向 运动。
电磁场与电磁波期末试卷B卷答案

.;.淮 海 工 学 院10 - 11 学年 第 2 学期 电磁场与电磁波期末试卷(B 闭卷)答案及评分标准一、判断题(本大题共10小题,每题1分,共10分)1.导体或介质所受到的静电力可以由能量的空间变化率计算得出。
(√ )2.在恒定电流场中,电流密度通过任一闭合面的通量一定为零。
(√ )3.均匀导体中没有净电荷,在导体面上,也没有电荷分布。
(× )4. 标量场梯度的方向沿其等值面的切线方向。
(× )5.在理想导电体的表面上电场强度的切向分量等于零。
(√ )6.在无限大理想介质中传播的平面电磁波不衰减。
(√ )7.复能流密度矢量的实部代表能量的流动,虚部代表能量交换。
(√ ) 8.平面波的频率是由波源决定的。
(√ )9.用单站雷达可以发现隐形飞机。
(× )10.地面雷达存在低空盲区。
(√ )二、单项选择题(本大题共10小题,每题3分,共30分)1.一个点电荷q 位于一无限宽和厚的导电板上方(0,0,d )点,如图1所示,则求解上半空间p(x,y,z)点的电场时,导体板上的感应电荷可用位于[ B ]的像电荷q -代替。
A 、(0,0,-z );B 、(0,0,-d );C 、(x ,y ,-z );D 、(x ,y ,-d )。
2. 设在无源的自由空间中,电场强度复矢量的表达式为 j 0(34e )e kz x y E e E -=-则以下说法正确的是[ A ] 。
A 、此电磁波沿z 轴正向传播; B 、该电磁波为椭圆极化波; C 、该电磁波沿z 轴方向衰减;D 、该电磁波为右旋椭圆极化波。
3.当平面波在介质中传播时,其传播特性与比值σωε有关。
此比值实际上反映了[ A ] 。
A 、介质中传导电流与位移电流的幅度之比; B 、复介电常数的实部与虚部之比; C 、电场能量密度与磁场能量密度之比; D 、介质中位移电流与传导电流的幅度之比。
4.已知一电磁波电场强度复矢量表达式为 由此可知它的极化特性为[ C ] 。
《电磁场与电磁波》期末复习题及答案

《电磁场与电磁波》期末复习题及答案一,单项选择题1.电磁波的极化特性由__B ___决定。
A.磁场强度B.电场强度C.电场强度和磁场强度D. 矢量磁位2.下述关于介质中静电场的基本方程不正确的是__D ___A. ρ??=DB. 0??=EC. 0C d ?=? E lD.0S q d ε?=? E S 3. 一半径为a 的圆环(环面法向矢量z = n e )通过电流I ,则圆环中心处的磁感应强度B 为__D ___A. 02r Ia μe B.02I a φμe C. 02z Ia μe D. 02z I a μπe4. 下列关于电力线的描述正确的是__D ___A.是表示电子在电场中运动的轨迹B. 只能表示E 的方向,不能表示E 的大小C. 曲线上各点E 的量值是恒定的D. 既能表示E 的方向,又能表示E 的大小5. 0??=B 说明__A ___A. 磁场是无旋场B. 磁场是无散场C. 空间不存在电流D. 以上都不是6. 下列关于交变电磁场描述正确的是__C ___A. 电场和磁场振幅相同,方向不同B. 电场和磁场振幅不同,方向相同C. 电场和磁场处处正交D. 电场和磁场振幅相同,方向也相同7.关于时变电磁场的叙述中,不正确的是:(D )A. 电场是有旋场B. 电场和磁场相互激发C.电荷可以激发电场D. 磁场是有源场8. 以下关于在导电媒质中传播的电磁波的叙述中,正确的是__B ___A. 不再是平面波B. 电场和磁场不同相C.振幅不变D. 以TE波形式传播9. 两个载流线圈之间存在互感,对互感没有影响的是_C ____A. 线圈的尺寸B. 两个线圈的相对位置C. 线圈上的电流D. 空间介质10. 用镜像法求解静电场边值问题时,判断镜像电荷的选取是否正确的根据__C ___A. 镜像电荷是否对称B.电位?所满足的方程是否改变C. 边界条件是否保持不变D. 同时选择B和C11. 区域V全部全部用非导电媒质填充,当此区域中的电磁场能量减少时,一定是_A ___A. 能量流出了区域B.能量在区域中被损耗C.电磁场做了功D. 同时选择A和C12. 磁感应强度为(32)x y z B axe y z e ze =+-+ , 试确定常数a 的值。
《电磁场与电磁波》试题含答案

E
;
E x 分量
� ˆ x + ye ˆ y + xe ˆz A = − x 2e
,试求
�
(2)若在 xy 平面上有一边长为 2 的正方形,且正方形的中心在坐标原点,试求该矢量 A 穿 过此正方形的通量。 17.已知某二维标量场 u ( x, y ) = x + y ,求 (1)标量函数的梯度; (2)求出通过点 (1,0) 处梯度的大小。
三、计算题
15.矢量函数
(每小题 10 分,共 30 分) � ˆ x + yze ˆz A = − yx 2 e
,试求
� ∇ ⋅ A (1) � (2) ∇ × A � � ˆx − e ˆy ˆ x − 2e ˆz B = e A = 2 e 16.矢量 , ,求
(1 ) A − B (2)求出两矢量的夹角 17.方程 u ( x, y, z ) = x + y + z 给出一球族,求 (1)求该标量场的梯度; (2)求出通过点 (1,2,0) 处的单位法向矢量。
。
等于零,则此两个矢量必然相互垂直。 关系。 函
9.对平面电磁波而言,其电场、磁场和波的传播方向三者符合 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 数的旋度来表示。
二、简述题
(每小题 5 分,共 20 分) � � ∂B ∇×E = − ∂t ,试说明其物理意义,并写出方程的积分形式。 11.已知麦克斯韦第二方程为
(1) 求出入射波磁场表达式; (2) 画出区域 1 中反射波电、磁场的方向。
�
区域 1 图3
区域 2《电磁场与电磁波》试题2一、填空题(每小题 1 分,共 10 分)
1.在均匀各向同性线性媒质中,设媒质的介电常数为 ε ,则电位移矢量 D 和电场 E 满足的 方程为: 。
电磁场与电磁波考试题答案参考资料

第一章 静电场一、选择题(每题三分)1) 将一个试验电荷Q (正电荷)放在带有正电荷的大导体附近P 点处,测得它所受力为F ,若考虑到电量Q 不是足够小,则:()A 、F/Q 比P 点处原先的场强数值大 C 、F/Q 等于原先P 点处场强的数值B 、F/Q 比P 点处原先的场强数值小 D 、F/Q 与P 点处场强数值关系无法确定 答案(B )·P+Q2) 图中所示为一沿X 轴放置的无限长分段均匀带电直线,电荷线密度分别为+λ(X<0)和一个-λ(X>0),则OXY 坐标平面上点(0,a )处的场强E为( )A 、0B 、a 2i 0πελC 、a 4i 0πελD 、a 4)j i (0πε+λ3) 图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系,请指出该曲线可描述下面那方面内容(E 为电场强度的大小,U为静电势)()A 、半径为R 的无限长均匀带电圆柱体电场的E-r 关系 C 、半径为R 的均匀带正电球体电场的U-r 关系B 、半径为R 的无限长均匀带电圆柱面电场的E-r 关系 D 、半径为R 的均匀带正电球面电场的U-r 关系答案(B )4) 有两个点电荷电量都是+q ,相距2a,今以左边的点电荷为球心,以a 为半径作一球形高斯面,在球面上取两块相等的小面积1S 和 2S 的电场强度通量分别为1ϕ和 2ϕ,通过整个球面的电场强度通量为3ϕ,则()为零D 、以上说法都不对 答案(C ) 6) 两个同心带电球面,半径分别为)(,b a b a R R R R <,所带电量分别为b a Q Q ,。
设某点与球心相距r,当b a R r R <<时,该点的电场强度的大小为() A 、2ba 0rQ Q 41+∙πε B 、2ba 0rQ Q 41-∙πε C 、)R Q r Q (412bb 2a 0+∙πε D 、2a 0r Q 41∙πε 答案(D )7) 如图所示,一个带电量为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量为() A 、6q ε B 、12qε C 、24q ε D 、048qε 答案(C )8) 半径为R 的均匀带电球面,若其电荷密度为σ,则在距离球面R 处的电场强度为()A 、0εσ B 、02εσC 、04εσD 、8εσ答案(C )9) 高斯定理⎰⎰ερ=∙vs dV S d E ()A 、适用于任何静电场 C 、只适用于具有球对称性,轴对称性和平面对称性的静电场B 、只适用于真空中的静电场 D 、只适用于虽然不具有(C)中所述的对称性,但可以找到合适的高斯面的静电场 答案(B ) 10) 关于高斯定理的理解正确的是()A 、 如果高斯面上处处E为零,则该面内必无电荷 C 、如果高斯面内有许多电荷,则通过高斯面的电通量必不为零B 、 如果高斯面内无电荷,则高斯面上处处E为零 D 、如果高斯面的电通量为零,则高斯面内电荷代数和必为零 答案(D ) 11) 如图两同心的均匀带电球面,内球面半径为1R ,电量1Q ,外球面半径为2R ,电量2Q ,则在内球面内距离球心为r 处的P 点场强大小E 为() A 、2021r 4Q Q πε+ B 、+πε2101R 4Q 2202R 4Q πε C 、201r 4Q πε D 、0 答案(D )12)若均匀电场的场强为E,其方向平行于半径为R 的半球面的轴,则通过此半球面的电通量Φ为()13) 下列说法正确的是()A 、 闭合曲面上各点场强为零时,面内必没有电荷 C 、闭合曲面的电通量为零时,面上各点场强必为零B 、 闭合曲面内总电量为零时,面上各点场强必为零 D 、通过闭合曲面的电通量仅决定于面内电荷 答案(D )14) 在空间有一非均匀电场,其电力线分布如图,在电场中作一半径为R 的闭合球面S ,已知通过球面上某一面元S ∆的电场线通量为e ∆Φ,则通过该球面其余部分的电场强度通量为()A 、e ∆Φ-B 、e S r ∆Φ⋅∆24π C 、e SSr ∆Φ⋅∆∆-24π D 、0 答案(15) 在电荷为q +的电场中,若取图中点P 处为电势零点,则M 点的电势为()16)下列说法正确的是()A 、 带正电的物体的电势一定是正的 C 、带负电的物体的电势一定是负的B 、 电势等于零的物体一定不带电 D 、物体电势的正负总相对电势参考点而言的 答案(D )17) 在点电荷q 的电场中,选取以q 为中心,R 为半径的球面上一点P 处作电势零点,则与点电荷q 距离为r 的P ‘点电势为()A 、r 4q 0πε B 、)R 1r 1(4q 0-πε C 、)R r (4q 0-πε D 、)R1r 1(4q 0-πε-答案(B )18) 半径为R的均匀带电球面,总电量为Q ,设无穷远处的电势为零,则球内距球心为r 的P 强度和 电势为() A 、E=0, U=r 4Q 0πε B 、 E=0, U=R 4Q 0πε C 、E=2r 4Q0πε. U=r 4Q 0πε D 、E=2r 4Q0πε答案(B )19) 有N 个电量为q 布,比较在这两种情况下在通过圆心O 并垂直与圆心的Z 轴上任意点P 的 场强与电势,则有() A 、场强相等,电势相等B 、场强不相等,电势不相等C 、场强分量z E 相等,电势相等D 、场强分量z E 答案(C )20)在边长为a 正方体中心处放置一电量为Q A 、a 4Q 0πε B 、R 2Q 0πε C 、R Q 0πε D 、R22Q0πε答案(B )21)如图两个同心的均匀带电球面,内球面半径为1R ,电量1Q ,外球面半径为2R ,电量2Q ,则在内球面内距离球心为r 处的P 点的电势U 为()A 、r4Q Q 021πε+ B 、101R 4Q πε+202R 4Q πε C 、0 D 、101R 4Q πε 答案(B )22) 真空中一半径为R 的球面均匀带电为Q ,,在球心处有一带电量为q 的点电荷,如图设无穷远处为电势零点,则在球内离球心O 距离为r 的P 点处的电势为()A 、E R 2π B 、E R 22π C 、E R 221π D 、E R 22πE 、22ERπ 答案(A )A 、a 4q 0πε B 、a8q 0πε C 、a 4q 0πε-D 、a8q0πε- 答案(D )A 、r4Q 0πε B 、)R Q r q (410+πε C 、r 4q Q 0πε+ D 、)RqQ r q (410-+πε 答案(B )23)当带电球面上总的带电量不变,而电荷的分布作任意改变时,这些电荷在球心出产生的电场强度E和电势U 将()A 、E 不变,U 不变 B 、E 不变,U 改变 C 、E 改变 ,U 不变 D 、E改变,U 也改变 答案(C )24) 真空中有一电量为Q 的点电荷,在与它相距为r 的A 点处有一检验电荷q,现使检验电荷q 从A 点沿半圆弧轨道运动到B 点,如图则电场场力做功为()A 、q2r r 4Q 220⋅π⋅πε B 、rq 2r 4Q 20⋅πε C 、rq r 4Q 20π⋅πε D 、0 答案(D ) 25) 两块面积为S 的金属板A 和B 彼此平行放置,板间距离为d (d 远远小于板的线度),设A 板带电量1q , B 板带电量2q ,则A,B 板间的电势差为() A 、S2q q 021ε+ B 、d S 4q q 021⋅ε+ C 、d S 2q q 021⋅ε- D 、d S4q q 021⋅ε- 答案(C )26)图中实线为某电场中电力线,虚线表示等势(位)面,由图可以看出() A 、c E >>b a E E c U >>b a U U C 、c E >>b a E E c U <<b a U UB 、c E <<b aE E c U <<ba U U D 、c E <<b a E Ec U >>b a U U 答案(A )27) 面积为S 的空气平行板电容器,极板上分别带电量为q ±,若不考虑边缘效应,则两极板间的相互作用力为()A 、S q 02ε- B 、S 2q 02ε- C 、202S 2q ε D 、202S q ε 答案(B )28)长直细线均匀带电。
《电磁场与电磁波》期末考试参考题

1、一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心o 点为z 处的电场强度E。
解:设圆环电荷线密度为λ,再在圆环上任取微元dl ,则dl dq λ=∴圆环上点电荷元dq 在p 处产生的电场强度为204RdqE d πε=根据对称性原理可,整个圆环在p 点产生的场强为沿轴线方向分量之和,即()232202044cos za dl z RzR dq E d E d z +===πελπεθ∴ ()⎰+=lz dl za z E 232204πελ又a dl lπ2=⎰ λπa q 2=∴ ()232204za zq E z +=πε2、在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。
解:导体在空间各点产生的电场为)(4)0(02a r r q E a r E r w >=<<=πε故静电能量为a q dr r r q dV E dV E D W V V πεππεεε844212121202222=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰∞ 3、一电荷面密度为σ的“无限大”平面,在距离平面a 的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生。
圆半径的大小。
解:电荷面密度为σ的“无限大”平面,在其周围任意点的场强为:2εσ=E 以图中O 点为圆心,取半径为r 的环形圆,其电量为:rdr dq πσ2=它在距离平面为a 的一点处产生的场强为:()2/32202ra ardrdE +=εσ则半径为R 的圆面积内的电荷在该点的场强为:()⎪⎪⎭⎫⎝⎛+-=+=⎰22002/322122R a a r ardra E Rεσεσ 0220412εσεσ=⎪⎪⎭⎫ ⎝⎛+-R a a∴ a R 3=4、已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器,其电位差为V 。
试证:将半径分别为a 和b ,介电常数为ε的介质管拉进电容器时,拉力为abV F ln )(20εεπ-=证明:内外导体间的电场为ab r V E r ln=插入介质管后的能量变化为a b zV dz dr r a b r B dV E W z b a v ln )(ln 2)(21)(21200222020εεππεεεε-=⎪⎭⎫ ⎝⎛-=-=⎰⎰⎰ 式中z 为介质管拉进电容器内的长度。
(完整word版)电磁场与电磁波波试卷3套含答案

《电磁场与电磁波》试卷1一. 填空题(每空2分,共40分)1.矢量场的环流量有两种特性:一是环流量为0,表明这个矢量场 无漩涡流动 .另一个是环流量不为0,表明矢量场的 流体沿着闭合回做漩涡流动 .2.带电导体内静电场值为 0 ,从电位的角度来说,导体是一个 等电位体 ,电荷分布在导体的 表面 。
3.分离变量法是一种重要的求解微分方程的方法,这种方法要求待求的偏微分方程的解可以表示为 3个 函数的乘积,而且每个函数仅是 一个 坐标的函数,这样可以把偏微分方程化为 常微分方程 来求解。
4.求解边值问题时的边界条件分为3类,第一类为 整个边界上的电位函数为已知 ,这种条件成为狄利克莱条件.第二类为已知 整个边界上的电位法向导数 ,成为诺伊曼条件。
第三类条件为 部分边界上的电位为已知,另一部分边界上电位法向导数已知 ,称为混合边界条件。
在每种边界条件下,方程的解是 唯一的 。
5.无界的介质空间中场的基本变量B 和H 是 连续可导的 ,当遇到不同介质的分界面时,B 和H 经过分解面时要发生 突变 ,用公式表示就是 12()0n B B ⋅-=,12()s n H H J ⨯-=.6.亥姆霍兹定理可以对Maxwell 方程做一个简单的解释:矢量场的 旋度 ,和 散度 都表示矢量场的源,Maxwell 方程表明了 电磁场 和它们的 源 之间的关系。
二.简述和计算题(60分)1.简述均匀导波系统上传播的电磁波的模式。
(10分)答:(1)在电磁波传播方向上没有电场和磁场分量,即电场和磁场完全在横平面内,这种模式的电磁波称为横电磁波,简称TEM 波.(2)在电磁波传播方向上有电场和但没有磁场分量,即磁场在横平面内,这种模式的电磁波称为横磁波,简称TM 波。
因为它只有纵向电场分量,又成为电波或E 波.(3)在电磁波传播方向上有磁场但没有电场分量,即电场在横平面内,这种模式的电磁波称为横电波,简称TE 波。
因为它只有纵向磁场分量,又成为磁波或M 波。
浙江大学 春夏学期《电磁场与电磁波》期末考试试卷及答案
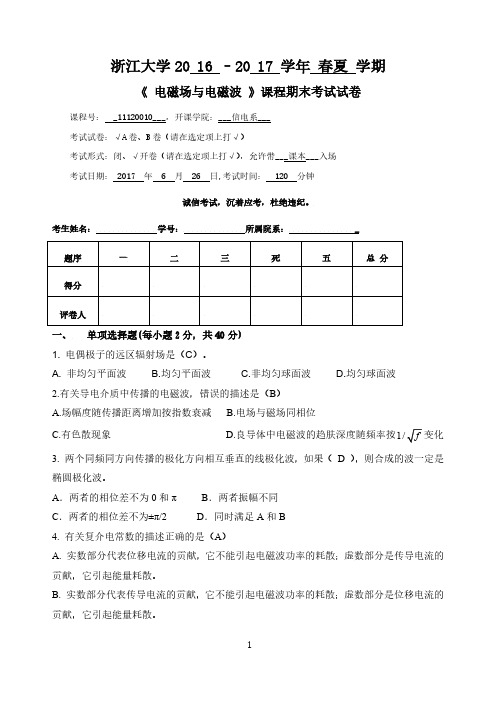
z015.02103 mW / m2
(3)透射波
E2 x0Em2e j2z x01.21510e j1.66z x012.15e j1.66zmV / m
5
H2
1 2
z0
x0 Em2e j2z
1 238.44
y
012.15e
j1.66
z
y0 51103 e j1.66zmA / m
A.都是连续的 B. 不连续的;连续的 C. 连续的;不连续的 D.都不连续
8. z=0 是空气( 0 )与介质( 2 30 )的分界面,若已知空气中的电场强度 E1 3x0 3z0 , 则介质中的电场强度应为(C)。
A. E2 3x0 9z0
B. E2 x0 3z0
D. 实数部分代表传导电流的贡献,它引起电磁波功率的耗散;虚数部分是位移电流的贡献,
它不能引起能量耗散。
5. 有关天线增益和天线方向性的描述,不正确的是(B)
A.天线增益考虑了天线材料中的欧姆损耗,而天线方向性则没有;
B.天线增益是馈入天线电磁信号的放大倍数,方向性是指波束的指向方向;
C.方向图主瓣越窄,副瓣越小,天线方向性就越大,天线增益也越高
浙江大学 20 16 –20 17 学年 春夏 学期
《 电磁场与电磁波 》课程期末考试试卷
《电磁场与电磁波》期末复习题及答案

《电磁场与电磁波》期末复习题及答案一,单项选择题1.电磁波的极化特性由__B ___决定。
A.磁场强度B.电场强度C.电场强度和磁场强度D. 矢量磁位2.下述关于介质中静电场的基本方程不正确的是__D ___A. ρ??=DB. 0??=EC. 0C d ?=? E lD.0S q d ε?=? E S 3. 一半径为a 的圆环(环面法向矢量z = n e )通过电流I ,则圆环中心处的磁感应强度B 为__D ___A. 02r Ia μe B.02I a φμe C. 02z Ia μe D. 02z I a μπe4. 下列关于电力线的描述正确的是__D ___A.是表示电子在电场中运动的轨迹B. 只能表示E 的方向,不能表示E 的大小C. 曲线上各点E 的量值是恒定的D. 既能表示E 的方向,又能表示E 的大小5. 0??=B 说明__A ___A. 磁场是无旋场B. 磁场是无散场C. 空间不存在电流D. 以上都不是6. 下列关于交变电磁场描述正确的是__C ___A. 电场和磁场振幅相同,方向不同B. 电场和磁场振幅不同,方向相同C. 电场和磁场处处正交D. 电场和磁场振幅相同,方向也相同7.关于时变电磁场的叙述中,不正确的是:(D )A. 电场是有旋场B. 电场和磁场相互激发C.电荷可以激发电场D. 磁场是有源场8. 以下关于在导电媒质中传播的电磁波的叙述中,正确的是__B ___A. 不再是平面波B. 电场和磁场不同相C.振幅不变D. 以TE波形式传播9. 两个载流线圈之间存在互感,对互感没有影响的是_C ____A. 线圈的尺寸B. 两个线圈的相对位置C. 线圈上的电流D. 空间介质10. 用镜像法求解静电场边值问题时,判断镜像电荷的选取是否正确的根据__C ___A. 镜像电荷是否对称B.电位?所满足的方程是否改变C. 边界条件是否保持不变D. 同时选择B和C11. 区域V全部全部用非导电媒质填充,当此区域中的电磁场能量减少时,一定是_A ___A. 能量流出了区域B.能量在区域中被损耗C.电磁场做了功D. 同时选择A和C12. 磁感应强度为(32)x y z B axe y z e ze =+-+ , 试确定常数a 的值。
电磁波与电磁场期末复习题(试题+答案)

电磁波与电磁场期末复习题(试题+答案)电磁波与电磁场期末试题一、填空题(20分)1.旋度矢量的散度恒等与零,梯度矢量的旋度恒等与零。
2.在理想导体与介质分界面上,法线矢量n r由理想导体2指向介质1,则磁场满足的边界条件:01=?B n ρρ,s J H n =?1ρρ。
3.在静电场中,导体表面的电荷密度σ与导体外的电位函数?满足的关系式n ??=?εσ-。
4.极化介质体积内的束缚电荷密度σ与极化强度P 之间的关系式为P ?-?=σ。
5.在解析法求解静态场的边值问题中,分离变量法是求解拉普拉斯方程的最基本方法;在某些特定情况下,还可用镜像法求拉普拉斯方程的特解。
6.若密绕的线圈匝数为N ,则产生的磁通为单匝时的N 倍,其自感为单匝的2N 倍。
7.麦克斯韦关于位移电流的假说反映出变化的电场要产生磁场。
8.表征时变场中电磁能量的守恒关系是坡印廷定理。
9.如果将导波装置的两端短路,使电磁波在两端来回反射以产生振荡的装置称为谐振腔。
10.写出下列两种情况下,介电常数为ε的均匀无界媒质中电场强度的量值随距离r 的变化规律:带电金属球(带电荷量为Q )E = 24r Qπε;无限长线电荷(电荷线密度为λ)E =r2。
11.电介质的极性分子在无外电场作用下,所有正、负电荷的作用中心不相重合,而形成电偶极子,但由于电偶极矩方向不规则,电偶极矩的矢量和为零。
在外电场作用下,极性分子的电矩发生转向,使电偶极矩的矢量和不再为零,而产生极化。
12.根据场的唯一性定理在静态场的边值问题中,只要满足给定的边界条件,则泊松方程或拉普拉斯方程的解是唯一的。
二、判断题(每空2分,共10分)1.应用分离变量法求解电、磁场问题时,要求整个场域内媒质必须是均匀、线性的。
(×)2.一个点电荷Q 放在球形高斯面中心处。
如果此电荷被移开原来的球心,但仍在球内,则通过这个球面的电通量将会改变。
(×)3.在线性磁介质中,由IL ψ=的关系可知,电感系数不仅与导线的几何尺寸、材料特性有关,还与通过线圈的电流有关。
电磁场与电磁波B答案

江西科技师范学院理工学院-2010-2011学年第二学期期末考试B 卷―标准答案及评分标准课程编号: 课程名称:电磁场与电磁波 课程归属院(系、部):通电学院 适用专业(班级):08电信 出卷人:杨伟松 教研室主任:邹珊珊 系主任:王建敏 ――――――――――――――――――――――――――――――――――一、单项选择题(每题2分,共10分)1.C2.D3.B4.C5.C二、填空题(每空2分,共12分)1. 电场的变化率, t D ∂∂2.z e a 02μ 3. J A 02μ-=∇ 4. 001εμ=c 5. 振幅随传播距离迅速衰减三、(15分)简述0=⋅∇B 和J B 0μ=⨯∇所表征的静磁场特性。
答:静磁场是有旋场(5分)和无源场(5分)。
所以静磁场存在矢势(5分)。
四、(16分)一个半径为a 的导体球带电荷量为q ,当球体以均匀角速度ω绕一个直径旋转时,试求球心处的磁感应强度B 。
解:导体球面上的电荷面密度为24a qπρ=(2分) 球面上位置矢量a e r r =点处的电流面密度θπωωρρωφsin 4aqe a e e r J r z =⨯=⨯= (2分)将球面划分为无数个宽度为θad dl =的细圆环,则任一细圆环的电流为θθπωd qJdl dI sin 4== (2分) 细圆环的半径θsin a b =,细圆环平面到球心的距离θcos a d = (2分)该细圆环电流在球心处产生的磁场为 θπθωμμd aq e d b dI b e dB z z 8sin )(230232220=+= (4分)所以整个球面电流在球心处产生的磁场为(4分)aq e d a q e dB B z z πωμθπθωμπ68sin 0300===⎰⎰五、(14分)证明矢量恒等式:ϕψψϕϕψ∇+∇=∇)(证:→→→∂∂+∂∂+∂∂=∇k zj y i x )()()()(ϕψϕψϕψϕψ (7分) ϕψψϕ∇+∇= (7分)六、(18分)两平行的金属板,板间距离为d , 竖直地插入介电常数为ε的液态介质中,两板间加电压0U ,试证明液面升高200))((21d Ug h εερ-=。
电磁场与电磁波期末B卷+答案+评分标准

武夷学院期末考试试卷 ( 2011 级 通信 专业2012~2013 学年 第 一 学期) 课程名称 电磁场与电磁波 B 卷 考试形式 闭卷 考核类型 考试 本试卷共 四 大题,卷面满分100分,答题时间120分钟。
一、选择题:(本大题共6题,每题3分,共18分) (注:请将选项填在下面表格里。
) 1、边界条件0)(21=-⋅B B n 仅在下列边界上成立( ) A 在两种非导电媒质的分界面上 B 在任何两种介质的分界面上 C 在理想介质与理想导电媒质的分界面上 D 在真空中的导体表面上 2、介质和边界的形状完全相同的两个均匀区域内,若静电场分布相同,则有( )A 区域内自由电荷分布相同B 区域内和区域外自由电荷分布均相同C 区域内自由电荷分布相同并且边界条件相同D 区域内自由电荷分布相同并且束缚电荷分布相同 3、恒定电场中的导电媒质必满足边界条件( ) A n n D D 21 = B n n J J 21 = C t tE E 21 = D 同时选择B 和C 4、电场中试验电荷受到的作用力与试验电荷电量为( )关系 A 正比 B 反比 C 平方 D 平方根5、单位时间通过某面积S 的电荷量,定义为穿过该面积的( )A 通量B 电流C 电阻D 环流6、用磁场矢量B 、H 表示的磁场能量密度计算公式为( )。
A H B ∙21 B H B ⨯21 C dV B v ⎰⨯ H 21 D →→∙H B二、填空题:(本大题共11个空,每空2分,共22分)1、只有大小没有方向的量称 标量 ,既有大小又有方向的量称 矢量 。
2、泊松方程 ,拉普拉斯方程 。
3、设23242),,(z y y x z y x -=ϕ,求点M (1,-2,1)的ϕ∇= _。
4、电场强度的方向是 运动的方向。
磁场强度的单位是 。
5、两个矢量的点积是是 量,两个矢量的叉积是 量。
6、电位参考点就是指定电位值恒为 的点,电位参考点选定后,电场中各点的电位值是 。
《电磁场与电磁波》试题含答案

�
(1)标量函数的梯度; (2)求出通过点 (1,0 ) 处梯度的大小。
四、应用体 (每小题 10 分,共 30 分) � ˆ x 3E 0 e − jkz E =e 18.在无源的自由空间中,电场强度复矢量的表达式为
(3) 试写出其时间表达式; (4) 判断其属于什么极化。 19. 两点电荷 q1 = −4C , 位于 x 轴上 x = 4 处, q 2 = 4C 位于轴上 y = 4 处, 求空间点 (0,0,4 ) 处的 (1) 电位; (2) 求出该点处的电场强度矢量。 20.如图 1 所示的二维区域,上部保持电位为
,使电磁场以波的形式
。 。
可以构成电容器。
9.电介质中的束缚电荷在外加电场作用下,完全脱离分子的内部束缚力时,我们把这种现 象称为 。 函数表示成几个单变量函数乘积的方法。
10.所谓分离变量法,就是将一个
二、简述题(每ຫໍສະໝຸດ 题 5 分,共 20 分) � � � ∂D ∇×H = J + ∂t ,试说明其物理意义,并写出方程的积分形 11.已知麦克斯韦第一方程为
5.在无源区域中,变化的电场产生磁场,变化的磁场产生电场,使电磁场以 播出去,即电磁波。 6.随时间变化的电磁场称为 场。 。
的形式传
7.从场角度来讲,电流是电流密度矢量场的
8.一个微小电流环,设其半径为 a 、电流为 I ,则磁偶极矩矢量的大小为 9.电介质中的束缚电荷在外加
。
作用下,完全脱离分子的内部束缚力时,我们把这种
(1) A + B (2) A ⋅ B 17.在无源的自由空间中,电场强度复矢量的表达式为
�
�
� �
� ˆ x 3E 0 − e ˆ y 4 E 0 )e − jkz E = (e
电磁场与电磁波试题含答案

函数乘积的方法。
二、简述题 (每小题 5 分,共 20 分)
11.简述高斯通量定理,并写出其积分形式和微分形式的表达式。
12.试简述电磁场在空间是如何传播的?
13.试简述何谓边界条件。
E
q 4 0r 2
eˆr
(1)求出电力线方程;(2)画出电力线。
19.设点电荷位于金属直角劈上方,如图 1 所示,求
(1) 画出镜像电荷所在的位置
(2) 直角劈内任意一点 (x, y, z) 处的电位表达式
图1
20.设时变电磁场的电场强度和磁场强度分别为:
E E0 cos(t e )
14.什么是色散?色散将对信号产生什么影响?
三、计算题 (每小题 10 分,共 30 分)
15.标量场 x, y, z x2 y3 ez ,在点 P1,1,0处
7
(1)求出其梯度的大小
(2)求梯度的方向
16.矢量
A
eˆx
2eˆy
,B
eˆx
3eˆz
,求
(1) A B
。
9.电介质中的束缚电荷在外加
作用下,完全脱离分子的内部束缚力时,我们把这种
现象称为击穿。
10.法拉第电磁感应定律的微分形式为
。
二、简述题 (每小题 5 分,共 20 分)
11.简述恒定磁场的性质,并写出其两个基本方程。
12.试写出在理想导体表面电位所满足的边界条件。
13.试简述静电平衡状态下带电导体的性质。
(1) A B
(2) A B
17.在无源的自由空间中,电场强度复矢量的表达式为
E eˆ x 3E0 eˆ y 4E0 e jkz
北工大电磁场与电磁波期末试题B答案

北京工业大学 2014——2015学年第一学期《电磁场与电磁波》期末考试试卷 B 卷考试说明:考试时间:95分钟考试形式(开卷/闭卷/其它):闭卷适用专业:电子信息工程、通信工程承诺:本人已学习了《北京工业大学考场规则》和《北京工业大学学生违纪处分条例》,承诺在考试过程中自觉遵守有关规定,服从监考教师管理,诚信考试,做到不违纪、不作弊、不替考。
若有违反,愿接受相应的处分。
承诺人:学号:班号:。
注:本试卷共三大题,共十页,满分100分,考试时必须使用卷后附加的统一答题纸和草稿纸。
请将答案统一写在试题下方或指定位置,如因答案写在其他位置而造成的成绩缺失由考生自己负责。
卷面成绩汇总表(阅卷教师填写)一、单选题(每题3分,共15分)1.下列关于梯度、散度和旋度描述中,错误的是:(B)A.梯度的旋度恒等于0;B.梯度的散度恒等于0;C.旋度的散度恒等于0;D.常矢量的散度恒等于0。
2.下列电磁场边界条件中,适用于理想导体的是:(C)A.()()()()12121212SSρ⨯-=⎧⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩n H H Jn E En B Bn D DB.()()()()12121212⨯-=⎧⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩n H Hn E En B Bn D DC.1111SSρ⨯=⎧⎪⨯=⎪⎨⋅=⎪⎪⋅=⎩n H Jn En Bn D3. 下列均匀平面波中,是右旋圆极化的为:(B)A.B.C.D.4. 当电磁波以布儒斯特角入射到两种非磁性煤质分界面上时,哪个是正确的: ( A )A . 平行极化分量全部透射;B . 垂直极化分量全部透射;C . 平行极化分量全部反射;D . 垂直极化分量全部反射。
5. 下列关于均匀波导的假设,哪个是错误的:( D )A . 波导的横截面沿z 方向是均匀的,即波导内的电场和磁场分布只与坐标x 、y 有关,与坐标z 无关;B . 构成波导壁的导体是理想导体;C . 波导内填充的媒质为理想媒质,且各向同性;D . 所讨论的区域内只有自由电荷;E . 波导内的电磁场是时谐场。
《电磁场与电磁波》(B卷)考试试卷答案及评分标准

《电磁场与电磁波》(B 卷)考试试卷答案及评分标准一.填空(20分,每空2分) 1. 12916x y z --+e e e 2.54,1516± 3. =53x y z --R e e e,0=53)x y z R =--R R e e e 4. -2,336x y z ---e e e5. 21()s ρ-=n D D ,21()⨯-0n E E =,21()s ⨯-n H H =J6. ()()()t t t =⨯S E H二、判断题:(每题2分,共16分)1. B2. A3. D4. C5. A6. C7. A8. B 三、证明题(共2题,每题8分,总计16分) 1.证明:(1)=()+()+()=xy zx y z z y x z y xx y z y z z x x y xyz∂∂∂∂∂∂∂∂∂∇⨯---∂∂∂∂∂∂∂∂∂0e e e R =e e e (4分)(2)设常矢A 为=x x y y z z A A A ++A e e e 则=()()=x x y y z z x y z x y z A A A x y z A x A y A z++++++A R e e e e e e (2分)所以()=()()()=xx y x z z x x y y z zA x A y A z x y z A A A ∂∂∂∇++∂∂∂++A R e e e e e e (2分) 2. 根据已知可以得到(1)证明:三个顶点的位置矢量分别为12y z -r =e e ,243x y z -r =e +e e ,3625x y z +r =e +e e (2分)则12214x z-=-R =r r e e ,233228x y z-=++R =r r e e e ,311367x y z -=---R =r r e e e (2分)由此可见,1223(4)(28)=0x z x y z -++R R =e e e e e (2分)所以,123PP P ∆是直角三角形。
电磁场期末考试参考答案B电信06

莆田学院期末考试参考答案及评分标准2008 — 2009 学年第 一 学期 (B )卷课程名称: 电磁场 适用年级/专业: 06/电信 试卷类别 开卷( )闭卷(√) 学历层次 本科 考试用时 120 分钟 一、填空题(每空3分,共30分) 1. ①z y x 43++- 2. ① 1 ② 03. ① 4.①y 2 5.① 26.① ;② 变化的磁场能够激发电场 (或类似描述)7.①l ρ- ② 位于线电荷与圆柱轴线的连线上,且距轴心距离为d a 2二、简答题(每小题6分,共18分) 1.答:介质恒定磁场的基本方程2.答:介质的极化过程未加电场时,由于分子热运动,不同电偶极子的偶极距的方向不规则,宏观上说,所有分子的等效电偶极距的矢量和为零,对外不成电性;-----2分外加电场作用下,各分子电距发生转向,均沿外加电场方向,对外呈电性;---2分 极化的结果是在电介质的内部和表面形成极化电荷。
---2分 3.答:一般的波动方程为14222=++z y x 或---------2分 ---------2分 ---------2分tE ∂∂=⨯∇J H B μ==⨯∇=⋅∇(有旋)(无源)0⎰⎰⎰=⋅=⋅=⋅SCS Id l d d 02∂E三、计算题1.(8分)解:由题得,方向余弦为{}⎭⎬⎫⎩⎨⎧=21,22,21cos ,cos ,cos γβα再由方向导数的计算公式 得2.(10分)解:球体上电荷分布是球对称的, 仅有径向分量Er ,且具有球对称性质,作一个与带电体同心、半径为r 的球面,应用高斯定理的积分式 得 当r >a 时, 即当r <a 时, 即当r >a 时, 当r <a 时,3.(8分)解:媒质内的漏电电流沿径向从内导体流向外导体, 设沿轴向方向单位长度(L =1)---------3分--------2分 ----2分 0222=∂∂-∇tHμεγβαcos cos cos 0zuy u x u luP ∂∂+∂∂+∂∂=∂∂221)1122(22)21112(21)211(cos )2(cos )2(cos )(22)2,1,1(=⨯-⨯+⨯-⨯⨯+⨯-=-+-+-=∂∂γβαxy z xz xy yz y lu---------2分---------3分 ---------3分⎰=⋅SQd 0ε3002344a r E r περπ=故 )(32030αερ>=r ra E r 3002344r r E rπερπ=)(300αερ<=r rE r )(32030αερ>=r r a a r )(300αερ<=r r a E r -------2分ra dr r a dr E rr r 030203033ερερϕ===⎰⎰∞∞⎪⎪⎭⎫⎝⎛-=+=⎰⎰∞332200r a dr E dr E arar r ερϕ-------2分-------2分从内导体流向外导体的漏电电流为I ,则媒质内任一点的电流密度和电场为内、外导体间的电压为 单位长度的漏电电导为4.(8分)解:取圆柱坐标系的z 轴和磁介质柱的中轴线重合, 磁介质的下底面位于z =0处,上底面位于z =L 处。
电磁场与波期末考试试题3套含答案(大学期末复习资料)

莆田学院期末考试试卷 (A )卷2011 — 2012 学年第 一 学期课程名称: 电磁场与波 适用年级/专业: 09/电信 试卷类别 开卷( ) 闭卷(√) 学历层次 本科 考试用时 120分钟《.考生注意:答案要全部抄到答题纸上,做在试卷上不给分.........................》.一、填空题(每空2分,共30分)1.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ① ,矢量B A ⋅= ② 。
2.高斯散度定理的积分式为 ① ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
3.已知任意一个矢量场A ,则其旋度的散度为 ① 。
4.介质中恒定磁场的基本方程的积分式为 ① , ② , ③ 。
5.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ① ,位置位于 ② ;当点电荷q 向无限远处运动时,其镜像电荷向 ③ 运动。
6.标量场2),,(x xyz z y x +=ψ通过点P(1,1,2)的梯度为① 。
7.引入位移电流的概念后,麦克斯韦对安培环路定律做了修正,其修正后的微分式是 ① ,其物理含义是: ② 。
8.自由空间传播的电磁波,其磁场强度)sin(z t H a H m y βω-=,则此电磁波的传播方向是 ① ,磁场强度复数形式为 ② 。
二、单项选择题(每小题2分,共20分)1.自由空间中的平行双线传输线,导线半径为a ,线间距为D ,则传输线单位长度的电容为 。
A .)ln(1aaD C -=πε B. )ln(201aa D C -=πε C. )ln(2101a a D C -=πε2.如果某一点的电场强度为零,则该点的电位为 。
A.一定为零 B.不一定为零 C.为无穷大3.真空中一个电流元在某点产生的磁感应强度dB 随该点到电流元距离变化的规律为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
淮海工学院
10 - 11 学年第 2 学期电磁场与电磁波期末试卷(B闭卷)
答案及评分标准
题号一二三四五1 五2 五3 五4 总分核分人分值10 30 10 10 10 10 10 10 100
得分
一、判断题(本大题共10小题,每题1分,共10分)
1.导体或介质所受到的静电力可以由能量的空间变化率计算得出。
(√)2.在恒定电流场中,电流密度通过任一闭合面的通量一定为零。
(√)3.均匀导体中没有净电荷,在导体面上,也没有电荷分布。
(×)4. 标量场梯度的方向沿其等值面的切线方向。
(×)5.在理想导电体的表面上电场强度的切向分量等于零。
(√)6.在无限大理想介质中传播的平面电磁波不衰减。
(√)7.复能流密度矢量的实部代表能量的流动,虚部代表能量交换。
(√)8.平面波的频率是由波源决定的。
(√)9.用单站雷达可以发现隐形飞机。
(×)10.地面雷达存在低空盲区。
(√)二、单项选择题(本大题共10小题,每题3分,共30分)
1.一个点电荷q位于一无限宽和厚的导电板上方(0,0,d)点,如图1所示,
则求解上半空间p(x,y,z)点的电场时,导体板上的感应电荷可用位于[ B ]的像电荷q
-代替。
A、(0,0,-z);
B、(0,0,-d);
C、(x,y,-z);
D、(x,y,-d)。
2.设在无源的自由空间中,电场强度复矢量的表达式为
j
(34e)e kz
x y
E e E-
=-
则以下说法正确的是[ A ] 。
A、此电磁波沿z轴正向传播;
B、该电磁波为椭圆极化波;
C、该电磁波沿z轴方向衰减;
D、该电磁波为右旋椭圆极化波。
3.当平面波在介质中传播时,其传播特性与比值
σ
ωε
有关。
此比值实际上反映了[ A ] 。
A、介质中传导电流与位移电流的幅度之比;
B、复介电常数的实部与虚部之比;
C、电场能量密度与磁场能量密度之比;
D、介质中位移电流与传导电流的幅度之比。
4.已知一电磁波电场强度复矢量表达式为
由此可知它的极化特性为[ C ] 。
A、线极化;
B、左旋椭圆极化;
C、右旋圆极化;
D、右旋椭圆极化。
5.光导纤维即是由两种介电常数不同的介质层构成的。
其内部芯线的介电常数大于外层介质的介电常数。
当光束以大于临界角的入射角度自芯线内部向边界投射时,即发生[ C ],光波局限在芯线内部传播,这就是光导纤维的导波原理。
A、散射;
B、无反射;
C、全反射;
D、折射。
6.以下四个矢量函数中,只有[ A ]中的矢量函数,才可能是磁感应强度。
A、
x y
B e y e x
=+;B、
x y
B e x e y
=+;
C、22
x y
B e x e y
=+;D、2
x y
B e x e x
=+。
7.两个载流线圈之间存在互感,对互感没有影响的是[ D ]。
A、线圈的尺寸;
B、线圈的形状;
C、两线圈的相对位置;
D、线圈上的电流。
8.如两个频率相等、传播方向相同、振幅相等,且极化方向相互正交的线极化波合成新的线极化波,则这两个线极化波的相位差为[ A ]。
图1
j
(je)e kz
x y
E E e-
=-
1
2
A 、零;
B 、90度;
C 、270度;
D 、任意值。
9.一平面电磁波向一无限大界面入射,则与入射波电场强度相伴生(即入射波电场激发的)的磁场强度是[ B ]。
A 、反射波磁场强度;
B 、入射波磁场强度;
C 、入射波与反射波的合成波磁场强度;
D 、透射波的磁场强度。
10.以下关于时变电磁场的叙述中,不正确的是[ B ]。
A 、电场是有旋场; B 、磁场是有源场;
C 、电场和磁场相互激发;
D 、电磁波的相位速度,可以大于真空中的光速。
三、填空题(本大题共5小题,每题2分,共10分)
1.已知,,)x y z ϕϕ
=(,x y z e e e x y z
∂∂∂
∇=++∂∂∂则ϕ∇⨯∇=_0_________。
2.当点电荷q 位于无限大的导体平面附近时,导体表面上的总感应电荷等于
______-q____。
3.矢量x y z A xe ye ze =++的散度A ∇⋅=_3_________。
4.静电场中,在给定的边界条件下,拉普拉斯方程或泊松方程的解是唯一的,这一定理称为 唯一性定理 。
5.已知无限长直导体圆柱,电导率为σ,电流密度J 沿轴线且均匀分布,则导体内电场强度矢量为___J σ______。
四、证明题(本大题10分)
1.利用高斯散度定理证明高斯定理
的微分形式为
E ρε∇⋅=
证明:高斯散度定理为 (2分)
利用散度定理高斯定理可写为: (3分) 因为V 为任意体积,所以,以上积分等式相等,(2分) 必然有被积函数相等,即
E ρ
ε∇⋅=
(2分) 命题得证。
(1分)
五、计算题(本大题共4小题,每题10分,共40分)
1.某矢量函数为2x y E x e ye =-+
(1)判断此矢量函数是否可能是某区域的静电场场强? (2)如是,求其电荷密度。
解:(1)静电场强满足0E ∇⨯= (1分) 对此函数有
2
ˆˆˆ0
01x y z e
e e E x y z x y
∂∂∂∇⨯=
∂∂∂-=(2分)
(分)
所以,它可能是静电场场强。
(1分)
(2)静电场满足0
E ρ
ε∇⋅=
(1分) z
E y E x E E z y x ∂∂+∂∂+∂∂=⋅∇ (2分)
s
v
1
d dV
E S ρε⋅=
⎰
⎰
v v
01dV dV
E ρε∇⋅=⎰⎰
v
dV s
A A dS ∇⋅=⋅⎰⎰
3
21x ρ
ε=-+=
(1分) 即:0(21)x ρε=-+ (1分)
2.已知无限长圆柱导体半径为a ,通过的电流为I ,且电流均匀分布,试求:(1)柱内的磁感应强度矢量;(2)柱外的磁感应强度矢量。
解:由安培环路定律
l
H dl
I ⋅=⎰(2分)
得
2222
I J r Jr
H r r πππ===
内
内 (2分)
002Jr
B H μμ==内内 (1分)
02
Jr
B e ϕμ=内 (1分)
同理22I I H r
r
ππ=
=
内外
(2分)
002I B H r
μμπ==外外(1分)
2I B e r
ϕμπ=外(1分)
3.设沿z +方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,该电磁波电场只有x 分量,其电场强度复矢量为 00()jk z
x E Z e E e -=
(1) 求出反射波电场强度复矢量表达式;
(2) 画出区域1中反射波电、磁场以及传播的方向。
解:(1)设反射波电场
ˆjkz r x r E e
E e = (2分) 区域1中的总电场为
0ˆ()jkz jkz
r x r E E e E e E e -+=+ (2分)
根据0=z 导体表面电场的切向分量等于零的边界条件得
0E E r -= (2分)
因此,反射波电场的表达式为
0ˆjkz r x E e
E e =- (1分) (2)电场方向沿x 负向;磁场沿y 轴正向,传播方向沿z 轴负向。
(各1分)
区域1 区域2
图2。
