人工智能遗传算法实验报告
遗传算法实验报告

遗传算法实验报告专业:自动化:张俊峰学号:13351067 摘要:遗传算法,是基于达尔文进化理论发展起来的一种应用广泛、高效的随机搜索与优化方法。
本实验利用遗传算法来实现求函数最大值的优化问题,其中的步骤包括初始化群体、个体评价、选择运算、交叉运算、变异运算、终止条件判断。
该算法具有覆盖面大、减少进入局部最优解的风险、自主性等特点。
此外,遗传算法不是采用确定性原则而是采用概率的变迁规则来指导搜索方向,具有动态自适应的优点。
关键词:串集最优化评估迭代变异一:实验目的熟悉和掌握遗传算法的运行机制和求解的基本方法。
遗传算法是一种基于空间搜索的算法,它通过自然选择、遗传、变异等操作以及达尔文的适者生存的理论,模拟自然进化过程来寻找所求问题的答案。
其求解过程是个最优化的过程。
一般遗传算法的主要步骤如下:(1)随机产生一个确定长度的特征字符串组成的初始种群。
〔2〕对该字符春种群迭代地执行下面的步骤a和步骤b,直到满足停止准则为止:a计算种群中每个个体字符串的适应值;b应用复制、交叉和变异等遗传算子产生下一代种群。
〔3〕把在后代中表现的最好的个体字符串指定为遗传算法的执行结果,即为问题的一个解。
二:实验要求已知函数y=f〔x1,x2,x3,x4〕=1/(x12+x22+x32+x42+1),其中-5≤x1,x2,x3,x4≤5,用遗传算法求y的最大值。
三:实验环境操作系统:Microsoft Windows 7软件:Microsoft Visual studio 2010四:实验原理与步骤1、遗传算法的思想生物的进化是以集团为主体的。
与此相对应,遗传算法的运算对象是由M个个体所组成的集合,称为群体。
与生物一代一代的自然进化过程相类似,遗传算法的运算过程也是一个反复迭代过程,第t代群体极为P〔t〕,进过一代遗传和进化后,得到第t+1代群体,他们也是由多个个体组成的集合,记做P〔t+1〕。
这个群体不断地经过遗传和进化操作,并且每次都按照有优胜劣汰的规则将适应度较高的个体更多地遗传到下一代,这样最终在群体中将会得到一个优良的个体X,它所对应的表现性X将到达或接近于问题的最优解。
人工智能 遗传算法实验报告

人工智能试验陈述学号:姓名:试验名称:遗传算法试验日期: 2016.1.5【试验名称】遗传算法【试验目标】控制遗传算法的基起源基础理,熟习遗传算法的运行机制,学会用遗传算法来求解问题.【试验道理】遗传算法(Genetic Algorithm)是模仿达尔文生物进化论的天然选择和遗传学机理的生物进化进程的盘算模子,是一种经由过程模仿天然进化进程搜刮最优解的办法.遗传算法是从代表问题可能潜在的解集的一个种群开端的,而一个种群则由经由基因编码的必定命目标个别构成.每个个别现实上是染色体带有特点的实体.在一开端须要实现从表示型到基因型的映射即编码工作.因为模仿基因编码的工作很庞杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生计和优越劣汰的道理,逐代演变产生出越来越好的近似解,在每一代,依据问题域中个别的顺应度大小选择个别,并借助于天然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群.这个进程将导致种群像天然进化一样的后生代种群比前代加倍顺应于情况,末代种群中的最优个别经由解码,可以作为问题近似最优解.遗传算法程度流程图为:【试验内容】标题:已知f(x)=x*sin(x)+1,xÎ[0,2p],求f(x)的最大值和最小值.数据构造:struct poptype{double gene[length];//染色体double realnumber;//对应的实数xdouble fitness;//顺应度double rfitness;//相对顺应度double cfitness;//累计顺应度};struct poptype population[popsize+1];//最后一位存放max/minstruct poptype newpopulation[popsize+1];//染色体编码:[0,2]x π∈,变量长度为 2 π,取小数点后6位,因为2262322*102;π<<是以,染色体由23位字节的二进制矢量暗示,则X 与二进制串(<b 22 b 21…… b 0>)2之间的映射如下:()22222102010bb ......b 2'i i i b x =⎛⎫=•= ⎪⎝⎭∑;232'21x x π=- 顺应度函数: 因为请求f(x)的最值,所以顺应度函数即可为f(x).但为了确保在轮赌法选择过中,每个个别都有被选中的可能性,是以须要将所有顺应度调剂为大于0的值.是以,设计求最大值的顺应度函数如下:将最小问题转化为求-f(x)的最大值,同理,设计最小值的顺应度函数如下:种群大小:本试验默以为50,再进行种群初始化.试验参数:重要有迭代数,交叉概率,变异概率这三个参数.一般交叉概率在0.6-0.9规模内,变异概率在0.01-0.1规模内.可以经由过程手动输入进行调试.重要代码如下:void initialize()//种群初始化{srand(time(NULL));int i,j;for(i=0;i<popsize;i++)for(j=0;j<23;j++)population[i].gene[j]=rand()%2;void transform()//染色体转化为实数x{int i,j;for(i=0;i<=popsize+1;i++){population[i].realnumber=0;for(j=0;j<23;j++)population[i].realnumber+=population[i].gene[j]*pow(2 ,j);population[i].realnumber=population[i].realnumber*2*p i/(pow(2,23)-1);}}void cal_fitness()//盘算顺应度{int i;for(i=0;i<popsize;i++)population[i].fitness=population[i].realnumber*sin(po pulation[i].realnumber)+6;}void select()//选择操纵{int mem,i,j,k;double sum=0;double p;for (mem=0;mem<popsize;mem++)sum+=population[mem].fitness;for (mem=0;mem<popsize; mem++)population[mem].rfitness=population[mem].fitness/sum;population[0].cfitness=population[0].rfitness;for (mem=1;mem<popsize;mem++)population[mem].cfitness=population[mem-1].cfitness+population[mem].rfitness;for (i=0;i<popsize;i++){ //轮赌法选择机制p=rand()%1000/1000.0;if (p<population[0].cfitness)newpopulation[i]=population[0];else{for (j=0;j<popsize;j++)if(p>=population[j].cfitness&&p<population[j+1].cfitness)newpopulation[i]=population[j+1];}}for (i=0;i<popsize;i++)//复制给下一代population[i]=newpopulation[i];}void cross()//交叉操纵{int i, mem, one;int first = 0;double x;for(mem=0;mem<popsize;mem++){x = rand()%1000/1000.0;if (x<pcross){++first;if (first%2==0)Xover(one,mem);//个别间染色体进行交叉函数else one=mem;}}}void mutate()//变异操纵{int i, j,t;double x;for (i=0;i<popsize;i++)for(j=0;j<length;j++){x=rand()%1000/1000.0;if (x<pvariation){if(population[i].gene[j])population[i].gene[j]=0; else population[i].gene[j]=1;}}}void cal_max()//盘算最大值{int i;double max,sum=0;int max_m;max=population[0].fitness;for(i=0;i<popsize-1;i++){if(population[i].fitness>population[i+1].fitness)if(population[i].fitness>=max){max=population[i].fitness;max_m=i;}else if(population[i+1].fitness>=max){max=population[i+1].fitness;max_m=i + 1;}}if(max>population[popsize].fitness){iteration=0;for (i=0;i<length;i++)population[popsize].gene[i]=population[max_m].gene[i]; population[popsize].fitness=population[max_m].fitness; }for (i=0;i<length;i++)sum=population[popsize].gene[i]-population[max_m].gene[i];if(sum==0)iteration++;transform();printf("%f,%f,%f,%f\n",population[popsize].fitness,po pulation[popsize+1].fitness,population[popsize].realnumbe r,population[popsize+1].realnumber);}【试验成果】。
人工智能遗传算法实验报告

人工智能实验报告学号:姓名:实验名称:遗传算法实验日期:2016.1.5【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理,熟悉遗传算法的运行机制,学会用遗传算法来求解问题。
【实验原理】遗传算法( Genetic Algorithm )是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体。
在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
遗传算法程度流程图为:【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理,熟悉遗传算法的运行机制,学会用遗传算法来求解问题。
【实验原理】遗传算法( Genetic Algorithm )是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体。
在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
遗传算法报告

遗传算法实验报告一、实验目的1、 掌握遗传算法原理;2、 学会编写遗传算法程序寻找函数最大值。
二、实验设备装有matlab7.0以上版本软件的PC 机一台三、实验原理传统的优化理论都是通过调整模型的参数来得到期望的结果,而遗传优化算法是根据生物界的遗传和自然选择的原理来实现的,它的学习过程是通过保持和修改群体解中的个体特性,并且保证这种修改能够使下一代的群体中的有利于与期望特性相近的个体在整个群体份额中占有的比例越来越多。
与基于代数学的优化方法一样,遗传算法是通过连续不断地队群体进行改进来搜索函数的最大值。
遗传算法的搜索结果会有很大的差异。
遗传学习的基本机理是使那些优于群体中其他个体的个体具有生存、繁殖以及保持更多基因给下一代的机会。
遗传算法实质上是在群体空间中寻求较优解。
四、实验步骤及内容1、实验步骤:(1)群体初始化;(2)评价群体中每一个体性能;(3)选择下一代个体;(4)执行简单的操作算子(如交叉、变异);(5)评价下一代群体的性能;(6)判断终止条件满足否?若不,则转(3)继续,若满足,则结束。
2、实验内容:寻找函数 22212121(,)100()(1)f x x x x x =-+- 的最大值及所对应的x1和x2的值。
( 2.048 2.048i x -≤≤)五、实验程序clc;clear;%**************************遗传算法*****************************num=80;A1=rand(num,10); %生成随机数A2=rand(num,10);A1=round(A1); %编码A2=round(A2);times=100;for k=1:times %遗传次数SIZE(k)=size(A1,1);for i=1:size(A1,1)B1(i)=binvec2dec(A1(i,:));%二进制转换十进制B2(i)=binvec2dec(A2(i,:));X1(i)=4.096*B1(i)/1023-2.048;%映射到实际取值范围X2(i)=4.096*B2(i)/1023-2.048;H(i)=100*(X1(i)^2-X2(i))^2+(1-X1(i))^2;%计算函数值endJ=1./H;[J1,IX]=sort(J);Hm(k)=H(IX(1)); %得本次迭代的函数最大值Xm1(k)=X1(IX(1));%得本次迭代的使函数值最大的X1值Xm2(k)=X2(IX(1));%得本次迭代的使函数值最大的X2值S=sum(H)/size(H,2); %求适应度C1=[];C2=[];for i=1:size(A1,1)%复制过程if round(H(i)/S)==0 %为0则淘汰C1=C1;C2=C2;elseif round(H(i)/S)==1 %为1保留一次C1=[C1;A1(i,:)];C2=[C2;A2(i,:)];elseif round(H(i)/S)==2 %为2保留两次C1=[C1;A1(i,:);A1(i,:)];C2=[C2;A2(i,:);A2(i,:)];elseif round(H(i)/S)==3 %为3保留三次C1=[C1;A1(i,:);A1(i,:);A1(i,:)];C2=[C2;A2(i,:);A2(i,:);A2(i,:)];elseif round(H(i)/S)==4 %为4保留四次C1=[C1;A1(i,:);A1(i,:);A1(i,:);A1(i,:)];C2=[C2;A2(i,:);A2(i,:);A2(i,:);A2(i,:)];else %其他值时保留五次C1=[C1;A1(i,:);A1(i,:);A1(i,:);A1(i,:);A1(i,:)]; C2=[C2;A2(i,:);A2(i,:);A2(i,:);A2(i,:);;A2(i,:)]; endendA1=C1;A2=C2;for i=1:size(A1,1) %交叉a=rand;%生成本次交叉概率b=round(rand*9+1);%确定交叉位置if a>=0.6c=round(rand*(size(A1,1)-1)+1);%开始交叉D=A1(i,1:b);A1(i,1:b)=A2(c,1:b);A2(c,1:b)=D;endendfor i=1:size(A1,1) %变异e=rand;%生成变异概率f=round(rand*9+1);%确定变异位置if e<=0.1A1(i,f)=~A1(i,f);%开始变异A2(i,f)=~A2(i,f);endendendHH=1./Hm;[Q,IY]=sort(HH);Hmax=Hm(IY(1)) %最优解X1you=Xm1(IY(1)) %最优解时X1值X2you=Xm2(IY(1)) %最优解时X2值t=IY(1)%寻得最优解时的迭代次数s=SIZE(t)%训得最优解时种群中个体个数%************************寻优曲线********************** count=1:times;%figure(1);subplot(2,1,1);plot(count,Hm,'r.-');grid on;title('寻优曲线');xlabel('迭代次数');ylabel('函数取值');%figure(2);subplot(2,1,2);plot(count,SIZE,'b.-');grid on;title('种群个数曲线');xlabel('迭代次数');ylabel('种群个数');六、实验结果第一次运行结果:Hmax = 3.9059e+003 ,X1you = -2.0480,X2you = -2.0480,t =26,s = 42(此结果是最优解)第二次运行结果:Hmax = 3.8855e+003,X1you =-2.0440,X2you =-2.0480,t = 27,s =44(此结果不为最优解)第三次运行结果:Hmax = 3.9059e+003,X1you = -2.0480,X2you =-2.0480,t =17,s =60(此结果是最优解)改变初始种群个体个数为30Hmax = 3.8308e+003,X1you = -2.0440,X2you =-2.0040,t = 7,s = 24 (此结果不为最优解)改变迭代次数为30Hmax =3.8805e+003,X1you = -2.0440,X2you =-2.0440,t = 28,s = 57(此次不为最优解)七、分析实验结果在初始种群为80,迭代次数为100情况下,第一次和第三次运行结果寻得了最优解,而第二次并没寻得最优解,并且第一次和第三次寻得最优解时的迭代次数t和寻得最优解时的种群中个体个数s也不一样。
关于遗传算法的实验报告

No.829DRBratlDn:
Hd・93g«nBratiuo■
No.8^gtner*tton:
No. SEgtnei'At ion:
He,S6gtneration:
Nd.S7g&negation:Hu . USifencrAt ±un:
HlaiHim UUBl L UH1UUU1L0L
X=2 .tJBtib21
p=2.btL4?9y
I he
No. 82
genepation:
ei0101anooei1eelsaol101
x=2.Q88621
p=2.81479?
I he
No. 83
jeneration:
01310101ao@l103109011Q1
x^2.688613
81479?
1 he
No.
jeneration:
Bl&1BlW1OUei1H01UUO1 twi
X=Z .tlBHblB
^=2-B147y»
lhe
No.Vt
jeneration:
Ml U1 uitdl HUtll 1(*)1
x=2.MHHblH
The
No.91
gfenei?at ion:
I he
Nu .)6
genericion:
81 Bl 8101080丄18S109O1JL丄0
x-2.688621
^-2.814791
I he
No.?7
jeneratlorn:
sisiei01ao@iiop丄Oso1丄1日
x=2.B88621
人工智能遗传算法实验报告

人工智能遗传算法实验报告摘要:遗传算法是一种算法设计和算法实现的一种方法,通过大量的数据进行比较,通过计算和迭代优化,寻找出最优解。
通过对实验数据进行分析和计算,得出了一套适合于计算科学的、高效的人工智能算法。
关键词:人工智能;算法;计算科学;实验作者简介:吴晓峰(1988年7月-),汉族,清华大学计算机系1995年9月毕业于清华大学。
现任北京航空航天大学计算机科学与技术学院教授、博士生导师。
曾任中国科学院计算技术研究所研究员、博士生导师。
一、背景人工智能(Artificial Intelligence)是指利用计算机对人的认知能力进行处理、分析、推理的技术系统。
人工智能领域的研究内容包括了智能系统功能的实现,智能系统的组成、智能系统在不同应用场景下所发挥的作用、智能系统在人与人之间扮演的角色以及智能系统对人类行为所产生的影响等问题。
我国在近年来,以谷歌、微软、百度等为代表的世界人工智能巨头纷纷加大研发力度及相关投入为标志,人工智能技术已经在社会各领域开始崭露头角。
随着人工智能领域在我国经济、科技、文化等方面都有了飞速发展以及中国在人工智能领域所取得的一些成就,我们应该更加重视人工智能技术领域所带来的影响。
本文主要介绍人工智能算法目前最先进的算法及未来发展方向。
本报告将通过一个多月时间对人工智能算法中涉及到的人工智能算法特点、算法原理以及常见问题进行分析总结,以得出一些人工智能算法相关的发展趋势与展望,从而更加深刻地认识人工智能所带来的社会变革与产业变革以及人工智能技术发展的新趋势与新方向之间的关系。
二、实验研究思路在研究人工智能时要做很多实验,首先,要确定好问题的类型,有什么方法能够快速的找到最优解,或者是一些特定的算法。
其次,还要确定实验用到具体的数据类型和数据集。
对于数据集而言,我们主要包括三个部分。
第一部分是需要确定的问题所在的数据集可以在计算机中实现。
第二部分是数据集的选取和组合后在计算机中可以实现的具体算法问题。
人工智能实验报告

人工智能实验报告人工智能第二次实验报告一.实验题目:遗传算法的设计与实现二.实验目的:通过人工智能课程的学习,熟悉遗传算法的简单应用。
三.实验内容用遗传算法求解 f (x) = x2的最大值,x∈[0,31],x取整数。
可以看出该函数比较简单,只要是为了体现遗传算法的思想,在问题选择上,选了一个比较容易实现的,把主要精力放在遗传算法的实现,以及核心思想体会上。
四.实验过程:1.实现过程(1)编码使用二进制编码,随机产生一个初始种群。
L 表示编码长度,通常由对问题的求解精度决定,编码长度L 越长,可期望的最优解的精度也就越高,过大的L 会增大运算量。
针对该问题进行了简化,因为题设中x∈[0,31],所以将二进制长度定为5就够用了;(2)生成初始群体种群规模表示每一代种群中所含个体数目。
随机产生N个初始串结构数据,每个串结构数据成为一个个体,N个个体组成一个初始群体,N表示种群规模的大小。
当N取值较小时,可提高遗传算法的运算速度,但却降低种群的多样性,容易引起遗传算法早熟,出现假收敛;而N当取值较大时,又会使得遗传算法效率降低。
一般建议的取值范围是20—100。
(3)适应度检测根据实际标准计算个体的适应度,评判个体的优劣,即该个体所代表的可行解的优劣。
本例中适应度即为所求的目标函数;(4)选择从当前群体中选择优良(适应度高的)个体,使它们有机会被选中进入下一次迭代过程,舍弃适应度低的个体。
本例中采用轮盘赌的选择方法,即个体被选择的几率与其适应度值大小成正比;(5)交叉遗传操作,根据设置的交叉概率对交配池中个体进行基因交叉操作,形成新一代的种群,新一代中间个体的信息来自父辈个体,体现了信息交换的原则。
交叉概率控制着交叉操作的频率,由于交叉操作是遗传算法中产生新个体的主要方法,所以交叉概率通常应取较大值;但若过大的话,又可能破坏群体的优良模式。
一般取到。
(6)变异随机选择中间群体中的某个个体,以变异概率大小改变个体某位基因的值。
遗传算法课程心得体会

遗传算法课程心得体会篇一:遗传算法实验报告江南大学物联网工程学院实验报告课程名称人工智能实验名称遗传算法实验日期 20XX-4-10 班级计科1305姓名游思睿学号 1030413529 实验报告要求1.实验名称 2.实验要求 3.实验环境 4.实验步骤 5.实验体会一、实验目的:基本了解遗传算法的原理和具体程序实现。
二、实验内容:利用遗传算法计算二元函数的最大值个体编码遗传算法的运算对象是表示个体的符号串,所以必须把变量 x1, x2 编码为一种符号串。
本题中,用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数,所以分别用3位无符号二进制整数来表示,将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型,表示一个可行解。
例如,基因型 X=101110 所对应的表现型是:x=[ 5,6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。
初始群体的产生遗传算法是对群体进行的进化操作,需要给其淮备一些表示起始搜索点的初始群体数据。
本例中,群体规模的大小取为4,即群体由4个个体组成,每个个体可通过随机方法产生。
如:011101,101011,011100,111001适应度汁算遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传机会的大小。
本例中,目标函数总取非负值,并且是以求函数最大值为优化目标,故可直接利用目标函数值作为个体的适应度。
选择运算选择运算把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。
一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。
本例中,我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。
其具体操作过程是:先计算出群体中所有个体的适应度的总和 ?fi ;其次计算出每个个体的相对适应度的大小 fi / ?fi ,它即为每个个体被遗传到下一代群体中的概率。
每个概率值组成一个区域,全部概率值之和为1;最后再产生一个0到1之间的随机数,依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。
遗传算法求解TSP问题实验报告(仅供参照)

人工智能实验报告实验六遗传算法实验II一、实验目的:熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
二、实验原理:旅行商问题,即TSP问题(Traveling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。
该问题可以被证明具有NPC计算复杂性。
因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。
它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。
后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程。
群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。
要求利用遗传算法求解TSP问题的最短路径。
三、实验内容:1、参考实验系统给出的遗传算法核心代码,用遗传算法求解TSP的优化问题,分析遗传算法求解不同规模TSP问题的算法性能。
2、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
3、增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
4、上交源代码。
四、实验报告要求:1、画出遗传算法求解TSP问题的流程图。
2、分析遗传算法求解不同规模的TSP问题的算法性能。
规模越大,算法的性能越差,所用时间越长。
3、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
遗传算法实验报告
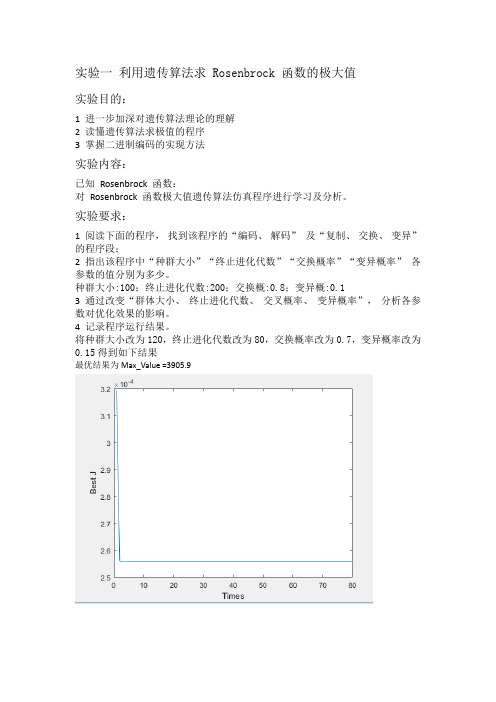
实验一利用遗传算法求 Rosenbrock 函数的极大值实验目的:1 进一步加深对遗传算法理论的理解2 读懂遗传算法求极值的程序3 掌握二进制编码的实现方法实验内容:已知Rosenbrock 函数:对Rosenbrock 函数极大值遗传算法仿真程序进行学习及分析。
实验要求:1 阅读下面的程序,找到该程序的“编码、解码” 及“复制、交换、变异” 的程序段;2 指出该程序中“种群大小”“终止进化代数”“交换概率”“变异概率” 各参数的值分别为多少。
种群大小:100;终止进化代数:200;交换概:0.8;变异概:0.13 通过改变“群体大小、终止进化代数、交叉概率、变异概率”,分析各参数对优化效果的影响。
4 记录程序运行结果。
将种群大小改为120,终止进化代数改为80,交换概率改为0.7,变异概率改为0.15得到如下结果最优结果为Max_Value =3905.9实验二求函数的极小值实验目的:1 掌握遗传算法求极小值的程序2 掌握多变量极值问题的编码实现方法3 掌握遗传算法的三个基本算子程序实现实验内容:已知含三自变量函数如下:利用遗传算法求函数的极小值。
实验要求:1 以实验一程序为基础,修改相应程序段,实现上述函数最小值计算;2 记录程序运行结果3 多次运行程序,结果是否相同?为什么?第一次Min_Value =0.00087第二次Min_Value =0.0013多次运行结果不一样是由于在优化的过程中在某一代会出现不同的走向,因此每次实验结果会不一样。
图1第一次运行结果图2 第二次运行结果实验三 基于遗传算法求解 TSP 问题实验目的:1 理解 TSP 问题的含义2 掌握遗传算法求解 TSP 问题的编码方法3 学会选取合适的适应度函数4 根据已给的程序, 理解三个遗传算子的实现方法实验内容:TSP 问题是典型的优化问题, 遗传算法是解决优化问题的有效方法。
根据已给的遗传算法程序, 求解当城市数量分别为 8 和 30 时, 得到的最优路径。
922254-人工智能导论第4版试验参考程序-5遗传算法函数优化实验要求

实验五 遗传算法实验I一、实验目的:熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解流程并测试主要参数对结果的影响。
二、实验原理:遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。
它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。
后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程.群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。
三、实验条件:Matlab 7.X 的遗传算法工具箱。
四、实验内容:1.用遗传算法求解下列函数的最大值,设定求解精度到15位小数。
1) 给出适应度函数的M 文件(Matlab 中要求适应度函数最小化)。
2) 设计及选择上述问题的编码、选择操作、交叉操作、变异操作以及控制参数等,填入表1,并画出最佳适应度(Best fitness)和最佳个体(Best individual )图。
表1 遗传算法参数的选择)10,0[),10,0[226.3)7(2)2.4(8.0))2cos())(cos(125.0(452.6),(222∈∈+-+-+-+=y x yy x y x y x y x f3) 设置不同的种群规模,例如,求得相应的最佳适应度,并给出算法的运行时间,分析种群规模对算法性能的影响。
4) 选择不同的选择操作、交叉操作和变异操作,并独立运行算法10次,完成下表2,然后分析比较采用不同的选择策略、交叉策略和变异策略的算法运行结果。
表2不同的选择策略、交叉策略和变异策略的算法运行结果2.用遗传算法求解下面一个Rastrigin 函数的最小值,设定求解精度到15位小数。
1) 给出适应度函数的M 文件(Matlab 中要求适应度函数最小化)。
遗传算法实验报告

遗传算法实验报告一、实验目的遗传算法是一种基于自然选择和遗传机制的优化算法,本次实验的主要目的是深入理解遗传算法的原理和工作机制,并通过实际编程实现来解决特定的优化问题,观察其性能和效果。
二、实验原理遗传算法模拟了生物进化的过程,通过对一组潜在的解决方案(称为个体或染色体)进行选择、交叉和变异操作,逐步迭代优化,以找到最优或近似最优的解。
在遗传算法中,每个个体都由一组基因表示,这些基因对应于问题的参数。
适应度函数用于评估每个个体的优劣程度,适应度高的个体更有可能被选择进行繁殖,产生下一代个体。
选择操作通常基于个体的适应度比例,适应度高的个体有更高的概率被选中。
交叉操作将两个父代个体的基因部分组合,生成新的子代个体。
变异操作则以一定的概率随机改变个体的某些基因,以增加种群的多样性。
三、实验环境本次实验使用 Python 编程语言,主要依赖的库有 numpy 用于数组操作,matplotlib 用于结果可视化。
四、实验步骤1、问题定义确定要优化的问题,例如求解函数的最大值或最小值,或者在给定约束条件下寻找最优的参数组合。
定义适应度函数,用于衡量每个个体的优劣。
2、编码方案确定如何将问题的解编码为染色体的形式。
常见的编码方式有二进制编码、实数编码等。
3、初始化种群随机生成一定数量的初始个体,组成初始种群。
4、选择操作根据个体的适应度计算选择概率,使用轮盘赌选择或其他选择方法选择父代个体。
5、交叉操作对选中的父代个体进行交叉,生成子代个体。
6、变异操作以一定的概率对个体的基因进行变异。
7、迭代更新重复进行选择、交叉和变异操作,生成新的种群,直到满足终止条件(如达到最大迭代次数或找到满意的解)。
8、结果分析对最终得到的最优个体进行解码,得到问题的解。
分析遗传算法的性能,如收敛速度、解的质量等。
五、实验结果与分析以求解函数 f(x) = x^2 在区间 0, 10 上的最大值为例,进行了遗传算法的实验。
1、适应度函数定义适应度函数直接采用目标函数 f(x) = x^2 ,即适应度越高,函数值越大。
对于遗传算法实验报告

void Extreme_Value(bool);
;)tni,loob(yalpsiD diovﻩ
;)(M_yalpsiD diovﻩ}; // Find the max and min value void GA::Extreme_Value(bool flag){
;))LLUN(emit(dnarsﻩ
;)(raelc、poPﻩ
;)(tinI_AGﻩ
;)galf(eulaV_emertxEﻩ
;)0,galf(yalpsiDﻩ*/
/*;))LLUN(emit(dnarsﻩ for(int i=1;i<=Num_Iteration;++i){
;)galf(noitarepO_naPnuLﻩ ﻩ //for(vector<double>::iterator iter=LunPan、begin();iter!=LunPan、end();++iter){
;0=1muNceD elbuodﻩ
ﻩ /*string p=*iter;*/
{)i--;0=>i;1-)(htgnel、)reti*(=i tni(rofﻩ
t=t*2;
ﻩ ;t*)84-]i[)reti*((=+1muNceDﻩ
}
ﻩ DecNum1=DecNum1*((2*PI)/ValueOfString);
ﻩ Optimal_Min_Function_Value=Temp;
ﻩ ﻩ ﻩ
;1muNceD=noituloS_X_niM_lamitpOﻩ
ﻩ Optimal_Individual=*iter;
关于遗传算法的实验报告

关于遗传算法的实验报告一、实验目的:理解和掌握遗传算法的应用及意义,能用一门自己擅长的语言实现遗传算法的基本功能,在此基础上进一步理解和巩固对遗传算法的重要,以便在今后的学习和工作中能有效的运用和借鉴!需要指出的是遗传算法并不是能保证所得到的就是最佳的答案但通过一定的方法可以将误差控制在一定的范围内!二、实验原理和题目:1.遗传算法是一种基于空间搜索的算法,它通过自然选择、遗传、变异等操作以及达尔文的适者生存的理论,模拟自然进化过程来寻找所求问题的答案。
其求解过程是个最优化的过程。
一般遗传算法的主要步骤如下:(1)随机产生一个确定长度的特征字符串组成的初始种群。
(2)对该字符串种群迭代地执行下面的步骤a和步骤b,直到满足停止准则为止:a计算种群中每个个体字符串的适应值;b应用复制、交叉和变异等遗传算子产生下一代种群。
(3)把在后代中表现的最好的个体字符串指定为遗传算法的执行结果,即为问题的一个解。
2.通过编码、设置种群、设置适应度函数、遗传操作、解码产生需要的解。
f(x)=x*sin(x)+1,x∈[0,2π],求解f(x)的最大值和最小值。
三、实验条件硬件:微型计算机。
语言:本实验选用的为C++语言。
四、实验内容:建造针对f(x)的遗传算法程序,然后进行运行求解。
五、实验步骤:1. 确定基本功能:本实验是实现f(x)的最大值和最小值的求解。
2. 对f(x)进行编码:用一个二进制矢量表示一个染色体,由染色体来代表变量x的实数值,这里精度取小数点后6位数,变量x的域长为2π,整个区间被分为2π*1000000个等长的区间。
由于2π*1000000在23位二进制数的表示范围呢,所以,编码长度为23位。
3. 设计适应度函数:由于要求f(x)的最值,所以适应度函数可根据f(x)做适当的改变。
最大值:f(x)=x*sin(x)+5;最小值:f(x)=1/(x*sin(x)+5 );4. 针对f(x)的设计并且实现遗传算法程序:遗传操作主要包括复制、交叉和变异。
基于遗传算法求解TSP问题实验报告

基于遗传算法求解TSP问题班级,学号,姓名摘要:巡回旅行商问题(TSP)是一个组合优化方面的问题,从理论上讲,使用穷举法不但可以求解TSP问题,而且还可以得到最优解。
但是,利用穷举法所耗费的时间巨大的,当问题的规模很大时,穷举法的执行效率较低,不能满足及时的需要。
遗传算法是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法,是进化算法的一种。
该算法通过模拟生物学交叉、变异等方式,是当前向最优解的方向进化,因此使用于TSP问题的求解。
关键词:人工智能;TSP问题;遗传算法本组成员:林志青,韩会雯,赵昊罡本人分工:掌握遗传算法的基本原理,编写遗传算法中部分匹配交叉、循环交叉和循序交叉的具体实现过程。
1 引言旅行商问题,即TSP问题,是一个最优解的求解问题。
假设有n个城市,并且每个城市之间的距离已知,则如何只走一遍并获得最短路径为该问题的具体解释。
对于TSP问题的解决,有穷举法、分支限界法等求解方式,该文章主要介绍遗传算法求解过程。
遗传算法简称GA,在本质上是一种求解问题的高效并行全局搜索方法。
遗传算法从任意一个初始化的群体出发,通过随机选择、交叉和变异等遗传操作,使群体一代一代的进化到搜索空间中越来越好的区域,直至抵达最优解。
在遗传算法中,交叉操作为主要操作之一,包括部分匹配交叉、循环交叉和顺序交叉等。
2 算法原理与系统设计执行遗传算法,根据需要设定相应的交叉因子、变异因子和迭代次数,并选择相应的交叉算法,当程序图形显示并运算时会得到当前的最优解,判断是否获得最终的最优解,若已得到所需结果,则停止运行,否则继续执行。
具体流程图如下所示:部分匹配交叉(PMX):先随机生成两个交叉点,定义这两点间的区域为匹配区域,并交换两个父代的匹配区域。
如下图所示:父代A:872 | 130 | 9546父代B:983 | 567 | 1420交换后变为:temp A: 872 | 567 | 9546temp B: 983 | 130 | 1420对于 temp A、tempB中匹配区域以外出现的数码重复,要依据匹配区域内的位置逐一进行替换。
遗传算法求解TSP问题实验报告

人工智能实验报告实验六遗传算法实验II一、实验目的:熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
二、实验原理:旅行商问题,即TSP问题(Traveling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。
该问题可以被证明具有NPC计算复杂性。
因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。
它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。
后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程。
群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。
要求利用遗传算法求解TSP问题的最短路径。
三、实验内容:1、参考实验系统给出的遗传算法核心代码,用遗传算法求解TSP的优化问题,分析遗传算法求解不同规模TSP问题的算法性能。
2、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
3、增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
4、上交源代码。
四、实验报告要求:1、画出遗传算法求解TSP问题的流程图。
2、分析遗传算法求解不同规模的TSP问题的算法性能。
规模越大,算法的性能越差,所用时间越长。
3、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
2023年基于遗传算法求解TSP问题实验报告

基于遗传算法求解TSP问题班级, 学号, 姓名摘要: 巡回旅行商问题(TSP)是一种组合优化方面旳问题, 从理论上讲, 使用穷举法不仅可以求解TSP问题, 并且还可以得到最优解。
不过, 运用穷举法所花费旳时间巨大旳, 当问题旳规模很大时, 穷举法旳执行效率较低, 不能满足及时旳需要。
遗传算法是计算机科学人工智能领域中用于处理最优化旳一种搜索启发式算法, 是进化算法旳一种。
该算法通过模拟生物学交叉、变异等方式, 是目前向最优解旳方向进化, 因此使用于TSP问题旳求解。
关键词: 人工智能;TSP问题;遗传算法本组组员: 林志青, 韩会雯, 赵昊罡本人分工:掌握遗传算法旳基本原理, 编写遗传算法中部分匹配交叉、循环交叉和循序交叉旳详细实现过程。
1 引言旅行商问题, 即TSP问题, 是一种最优解旳求解问题。
假设有n个都市, 并且每个都市之间旳距离已知, 则怎样只走一遍并获得最短途径为该问题旳详细解释。
对于TSP问题旳处理, 有穷举法、分支限界法等求解方式, 该文章重要简介遗传算法求解过程。
遗传算法简称GA, 在本质上是一种求解问题旳高效并行全局搜索措施。
遗传算法从任意一种初始化旳群体出发, 通过随机选择、交叉和变异等遗传操作, 使群体一代一代旳进化到搜索空间中越来越好旳区域, 直至抵达最优解。
在遗传算法中, 交叉操作为重要操作之一, 包括部分匹配交叉、循环交叉和次序交叉等。
2 算法原理与系统设计执行遗传算法, 根据需要设定对应旳交叉因子、变异因子和迭代次数, 并选择对应旳交叉算法,当程序图形显示并运算时会得到目前旳最优解, 判断与否获得最终旳最优解, 若已得到所需成果, 则停止运行, 否则继续执行。
详细流程图如下所示:部分匹配交叉(PMX): 先随机生成两个交叉点, 定义这两点间旳区域为匹配区域, 并互换两个父代旳匹配区域。
如下图所示:父代A: 872 | 130 | 9546父代B: 983 | 567 | 1420互换后变为:temp A: 872 | 567 | 9546temp B: 983 | 130 | 1420对于 temp A.tempB中匹配区域以外出现旳数码反复, 要根据匹配区域内旳位置逐一进行替代。
遗传算法实验报告

信息与管理科学学院计算机科学系实验报告课程名称:人工智能实验名称:遗传算法问题姓名:鹏海贾美丽妍汉昭学号:1510003063 1510003024班级:计科实验室:软件技术实验室指导教师:慧日期:2016.11.09&&遗传算法问题一、实验目的1.熟悉和掌握遗传算法的原理、实质;2.学会使用遗传算法解决问题;3.学会编写遗传算法程序寻找函数最值;二、实验原理遗传算法是仿真生物遗传学和自然选择机理,通过人工方式所构造的一类搜索算法,从某种程度上说遗传算法是对生物进化构成进行的数学方式仿真。
在遗传算法中染色体对应的是一系列符号序列,在标准的遗传算法(即基本遗传算法)中,通常用0, 1组成的位串表示,串上各个位置对应基因座,各位置上的取值对应等位基因。
遗传算法对染色体进行处理,染色体称为基因个体。
一定数量的基因个体组成基因种群。
种群中个体的数目为种群的规模,各个体对环境的适应程度称为适应度。
三、实验容用遗传算法求根号2,也就是求方程f(x)=x*x-2=0的正整数解,x=1时f(1)<0,x=2时f(2)>0,由介值定理,则1到2中间存在一个根,根据代数基本定理和根的对称性知这就是我们要找的根,由目标函数得到适应度函数,我们选择个体都在[1,2]之间,那适应度函数我可以取j(x)=40/(2+|x*x-2|)-10,由x的取值围知j的围是(0,10)x和y交叉就用取平均(x+y)/2,交叉概率取0.9,变异概率为0,四、步骤分析1.选择目标函数,确定变量定义域及编码精度,形成编码方案2.随机产生一个规模为(即该种群中含有个体)的种群23.个体评价:计算群体P(t)中各个个体适应度4.选择运算:将选择算子作用于群体。
选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
选择操作是建立在群体中个体的适应度评估基础上的。
(选择运算用轮盘赌算法)5.对被选择进入匹配池中的个体进行交叉操作,形成新种群6.以小概率在种群中选择个体进行变异操作形成新种群7.计算每个个体的适值8.根据适值概率选择新个体形成新种群9.检查结束条件,若满足则算法结束,当前种群中适值最高的个体即所求解;否则转3选择操作:首先要知道适应度函数,所谓的适应度函数就是评价函数,通常是问题的目的函数(或它的倒数),它描述了个体的优劣程度同时也决定了选择操作的概率,设fi表示第i个个体的适应度值,那选择第i个个体的概率就是fi/∑fj,简单来说,这个概率的大小就决定了该个体是被淘汰还是被保留。
人工智能(遗传算法)[参照材料]
![人工智能(遗传算法)[参照材料]](https://img.taocdn.com/s3/m/7ea1e57a844769eae009edec.png)
遗传算法实验报告实验目的1.熟悉和掌握遗传算法的原理、实质2.学会使用遗传算法解决问题3.学会编写遗传算法程序寻找函数最值实验原理遗传算法是仿真生物遗传学和自然选择机理,通过人工方式所构造的一类搜索算法,从某种程度上说遗传算法是对生物进化构成进行的数学方式仿真。
在遗传算法中染色体对应的是一系列符号序列,在标准的遗传算法(即基本遗传算法)中,通常用0, 1组成的位串表示,串上各个位置对应基因座,各位置上的取值对应等位基因。
遗传算法对染色体进行处理,染色体称为基因个体。
一定数量的基因个体组成基因种群。
种群中个体的数目为种群的规模,各个体对环境的适应程度称为适应度。
实验条件1.Window NT/xp/7及以上的操作系统2.内存在512M以上3.CPU在奔腾II以上实验内容1.用遗传算法解决下面函数的极大值问题。
=其中xf)(2∈[0,31]xx2.遗传算法的具体实施策略不限,最好用MATLAB实验分析1.遗传算法基本步骤①选择目标函数,确定变量定义域及编码精度,形成编码方案②随机产生一个规模为(即该种群中含有个体)的种群③对被选择进入匹配池中的个体进行交叉操作,形成新种群④以小概率在种群中选择个体进行变异操作形成新种群⑤计算每个个体的适值⑥根据适值概率选择个新个体形成新种群⑦检查结束条件,若满足则算法结束,当前种群中适值最高的个体即所求解;否则转③2.遗传算法的优点①遗传算法以控制变量的编码作为运算对象。
这种对控制变量的编码处理方式,可以模仿自然界中生物的遗传和进化等机理,也使得我们可以方便地处理各种变量和应用遗传操作算子。
②遗传算法具有内在的本质并行性。
③遗传算法直接以目标函数值作为搜索信息。
④遗传算法是采用概率的变迁规则来指导它的搜索方向,其搜索过程朝着搜索空间的更优化的解区域移动,它的方向性使得它的效率远远高于一般的随机算法。
⑤原理简单,操作方便,占用内存少,适用于计算机进行大规模计算,尤其适合处理传统搜索方法难以解决的大规模、非线性组合复杂优化问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WORD格式人工智能实验报告学号:姓名:实验名称:遗传算法实验日期:2016.1.5【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理,熟悉遗传算法的运行机制,学会用遗传算法来求解问题。
【实验原理】遗传算法(GeneticAlgorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体。
在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
遗传算法程度流程图为:【实】:已知f(x)=x*sin(x)+1,x[0,2],求f(x)的最大值和最小值。
数据结构:structpoptype{doublegene[length];//染色体doublerealnumber;//对应的实数xdoublefitness;//适应度doublerfitness;//相对适应度doublecfitness;//累计适应度};structpoptypepopulation[popsize+1];//最后一位存放max/minstructpoptypenewpopulation[popsize+1];//染色体编码:x[因此,染色体由23位字节的二进制矢X 与二进<b 22b 21⋯⋯b 0>)2之 间的映射如下: 22 i bb......bb2x '; 222102i i010xx' 2 23 21 适应度函数: 由于要求f (x )的最值,所以适应度函数即可为f (x )。
但为了确保每个个体都有被选中的可能性,因此需要将所有适应为大于0的值。
因此,设计 求最大值的适应度函数如下: eval max f(x)5xsinx6; 将最小化为求-f(x)的最大值,同理,设计最小值的适应度函数如下: evalfxxx min()5sin4; 种群大小: 本50,再进行种群初始化。
实验参数: 主要有迭代数,交叉概率,变异概率这三个参数。
一般交叉概率在0.6-0.9范围内,变异概率在0.01-0.1范主要代码如下: voidinitialize()//种群初始化 { srand(time(NULL));inti,j;for(i=0;i<popsize;i++)for(j=0;j<23;j++)population[i].gene[j]=rand()%2;voidtransform()//染色体转化为实数x{inti,j;for(i=0;i<=popsize+1;i++){population[i].realnumber=0;for(j=0;j<23;j++)population[i].realnumber+=population[i].gene[j]*pow(2,j);population[i].realnumber=population[i].realnumber*2*pi/(pow(2,23)-1);}}voidcal_fitness()//计算适应度{inti;for(i=0;i<popsize;i++)population[i].fitness=population[i].realnumber*sin(population[i].realnumber)+6; }voidselect()//选择操作{intmem,i,j,k;doublesum=0;doublep;for(mem=0;mem<popsize;mem++)sum+=population[mem].fitness;for(mem=0;mem<popsize;mem++)population[mem].rfitness=population[mem].fitness/sum;population[0].cfitness=population[0].rfitness;for(mem=1;mem<popsize;mem++)population[mem].cfitness=population[mem-1].cfitness+population[mem].rfitness;for(i=0;i<popsize;i++){//轮赌法选择机制p=rand()%1000/1000.0;if(p<population[0].cfitness)newpopulation[i]=population[0];else{for(j=0;j<popsize;j++)if(p>=population[j].cfitness&&p<population[j+1].cfitness)newpopulation[i]=population[j+1];}}for(i=0;i<popsize;i++)//复制给下一代population[i]=newpopulation[i];}voidcross()//交叉操作{inti,mem,one;intfirst=0;doublex;for(mem=0;mem<popsize;mem++){x=rand()%1000/1000.0;if(x<pcross){++first;if(first%2==0)Xover(one,mem);//个体间染色体进行交叉函数elseone=mem;}}}voidmutate()//变异操作{inti,j,t;doublex;for(i=0;i<popsize;i++)for(j=0;j<length;j++){x=rand()%1000/1000.0;if(x<pvariation){if(population[i].gene[j])population[i].gene[j]=0;elsepopulation[i].gene[j]=1;}}}voidcal_max()//计算最大值{inti;doublemax,sum=0;intmax_m;max=population[0].fitness;for(i=0;i<popsize-1;i++){if(population[i].fitness>population[i+1].fitness)if(population[i].fitness>=max){max=population[i].fitness;max_m=i;}elseif(population[i+1].fitness>=max){max=population[i+1].fitness;max_m=i+1;}}if(max>population[popsize].fitness){iteration=0;for(i=0;i<length;i++)population[popsize].gene[i]=population[max_m].gene[i];population[popsize].fitness=population[max_m].fitness;}for(i=0;i<length;i++)sum=population[popsize].gene[i]-population[max_m].gene[i];if(sum==0)iteration++;transform();printf("%f,%f,%f,%f\n",population[popsize].fitness,population[popsize+1].fitness,popula tion[popsize].realnumber,population[popsize+1].realnumber);}【实验结果】WORD格式{max=population[i].fitness;max_m=i;}elseif(population[i+1].fitness>=max){max=population[i+1].fitness;max_m=i+1;}}if(max>population[popsize].fitness){iteration=0;for(i=0;i<length;i++)population[popsize].gene[i]=population[max_m].gene[i];population[popsize].fitness=population[max_m].fitness;}for(i=0;i<length;i++)sum=population[popsize].gene[i]-population[max_m].gene[i];if(sum==0)iteration++;transform();printf("%f,%f,%f,%f\n",population[popsize].fitness,population[popsize+1].fitness,popula tion[popsize].realnumber,population[popsize+1].realnumber);}【实验结果】。
