浮力习题中的液面变化问题-2019年文档
浮力整体法分析液面变化及冰化水问题

浮力整体法分析液面变化及冰化水问题第一篇:浮力整体法分析液面变化及冰化水问题捞放货物问题1、一艘船漂浮在湖面上,将船上的货物扔进湖里,请问船体将沉一些),湖面将(上升、下降或不变)。
2、一艘船漂浮在湖面上,将船上的货物用钢丝吊在船下,请问船体将(上浮一些或下沉一些),湖面将(上升、下降或不变)。
冰化水问题3、容器里装满水,水面上漂浮着一块冰,问,并在融化后水面将或不变)。
冰包物问题1、容器里盛满水,一块冰包木块浮在水面上,溶化后液面怎么变化降或不变)。
2、容器里盛满水,一块冰包铁块浮在水面上,溶化后液面怎么变化降或不变)。
3、容器里盛满水,一块冰包气泡浮在水面上,溶化后液面怎么变化降或不变)。
1.有一个烧杯,烧杯中的冰块漂浮在水中,烧杯中的水面恰好与烧杯口相平。
待这些冰全部融化后,水是否会溢出,或水面是否会下降?解析:因为冰块处于漂浮状态,故有G冰=F浮,∴ρ冰V冰g=ρ水V排g化解得ρ冰V冰=ρ水V排∵冰融化成水后质量不变,故有m冰=m水融∴ρ冰V冰=ρ水V 水融综合两式:ρ冰V冰=ρ水V排,ρ冰V冰=ρ水V水融可得ρ水V排=ρ水V水融∴V排=V水融,∴水面既不会升高也不会降低答:。
还有以下的几种类型的浮冰问题:1.冰在果汁中浮着,叫你判断冰融化后液面的变化,其实这时冰融化后水面时会变化的。
2.冰中含有杂质小石块,冰此时可能悬浮也可能漂浮,然后让你计算一些数据,比如压强,密度(石块的),等等!我在举个例子:2.一杯浓橘汁加了冰块后,刚好不会溢出,如果冰块融化,则液面将怎么变化?解析:(我要偷懒了)和上面那个题一样的方法,可以得出如下结论ρ冰V冰=ρ汁V 排,ρ冰V冰=ρ水V水融综合可得:ρ汁V排=ρ水V水融因为ρ汁>ρ水所以V排<V水融所以会溢出。
答:.........浮冰问题种种冰、水是同种物质的不同状态,冰可由水凝固而成,水由冰熔化可得。
由于冰、水密度不等,带来了一些需要我们探究的问题。
1、冰山一角到底是冰山的多少?解析:设冰山体积为V,浮在水面上的冰山体积为V1,因为冰漂浮在水面上,F浮=G冰,即ρ水g(V-V1)= ρ冰 gV1化简得V1=V冰(ρ水-ρ冰)/ρ水=V冰/10,即浮于水面的冰山一角是冰山的十分之一。
总复习浮力液面高度变化专题(定稿)闫

V排
Δh
F浮
G
A
h1 h2
ΔP
ΔF压
甲
乙
情景一:V排变化导致液面高度变化
A
Δh液升 Δh物降
A
甲
乙
液面上升的高度Δh液升与Δh物降的关系? S物Δh物降=(S容-S物)Δh液升
情景一:V排变化导致液面高度变化
A
Δh液降 Δh物升
A
甲
乙
液面下降高度Δh液降与Δh物升的关系?
S物Δh物升=(S容-S物)Δh液降
若注入液体的过程中细线对物块的拉力F随液 体深度h的变化关系图像如图丙所示。 请问:能从图像中得到什么信息?
(1)
(2)
F浮=G物
h=30cm
h’=35cm F拉=8N
(4)
( 5)
H=60cm
(3)
绳恰好拉直
恰好浸没
例3.如图10甲所示,圆柱形平底容器置于水平桌面上, 其底面积为500cm2。在容器内放入一个底面积为 200cm2、高为20cm的圆柱形物块,物块底部的中心通 过一段细线与容器底部相连。向容器内缓慢注入某种 液体直至将其注满,如图10乙所示。已知在注入液体 的过程中细线对物块的拉力F随液体深度h的变化关系 图像如图10丙所示。若将细线剪断,当物块静止时, 液体对容器底部的压强为 Pa。(g=10N/kg)
S容=500cm2
S物= 200cm2、h物= 20cm
h=30cm h’=35cm h容=60cm Δh
(1)
(2)
刚好F浮=G物 F浮=G物
(3)
(4)
(5) 绳恰好直 F拉=0N F浮=G物
(6) 恰好浸没 F浮不变 F拉=8N
浮力液面变化(经典推荐)
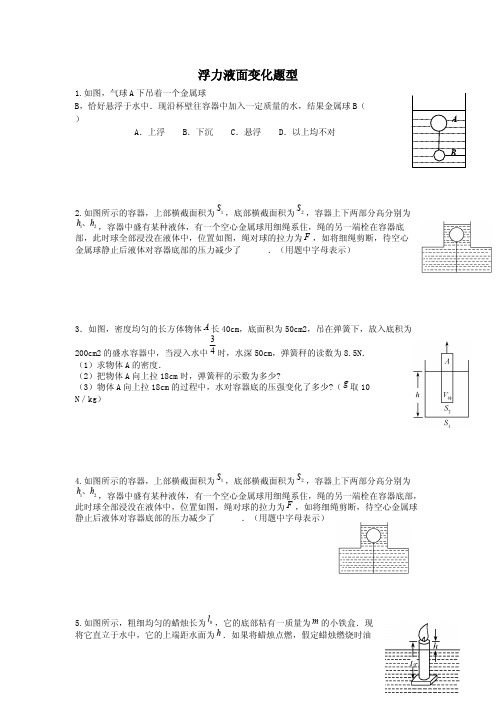
1.如图,气球 A 下吊着一个金属球 B,恰好悬浮于水中.现沿杯壁往容器中加入一定质量的水,结果金属球 B( ) A.上浮 B.下沉 C.悬浮 D.以上均不对
A
B
2.如图所示的容器,上部横截面积为 S1 ,底部横截面积为 S2 ,容器上下两部分高分别为 h1、h2 ,容器中盛有某种液体,有一个空心金属球用细绳系住,绳的另一端栓在容器底 部,此时球全部浸没在液体中,位置如图,绳对球的拉力为 F ,如将细绳剪断,待空心 金属球静止后液体对容器底部的压力减少了 .(用题中字母表示)
x
∴ 因每分钟烧去的蜡烛长为 l , 1h 1h x t l () 1 l (分).答案: () 1 l (分) ∴
1h 1
6.
<解析> 按题意,刻度线 a 和 b 所表示的密度分别为
a 1 103 kg/m3 ……………………①
b 2 103 kg/m3 ………………………②
3.如图,密度均匀的长方体物体 A 长 40cm,底面积为 50cm2,吊在弹簧下,放入底积为 3 200cm2 的盛水容器中,当浸入水中 4 时,水深 50cm,弹簧秤的读数为 8.5N. (1)求物体 A 的密度. (2)把物体 A 向上拉 18cm 时,弹簧秤的示数为多少? (3)物体 A 向上拉 18cm 的过程中,水对容器底的压强变化了多少?( g 取 10 N/kg)
4.如图所示的容器,上部横截面积为 S1 ,底部横截面积为 S2 ,容器上下两部分高分别为 h1、h2 ,容器中盛有某种液体,有一个空心金属球用细绳系住,绳的另一端栓在容器底部, 此时球全部浸没在液体中,位置如图,绳对球的拉力为 F ,如将细绳剪断,待空心金属球 静止后液体对容器底部的压力减少了 .(用题中字母表示)
2019年中考物理试题专题训练——浮力实验专题(word版含答案)

(2)分析图丙、丁可知,浮力大小跟物体浸没在水中的深度(选填“有关”或“无关”)。
(3)分析两图可知,浸在液体中的物体所受浮力大小跟液体密度有关。戊图中盐水的密度是kg/m3.如果在实验中不小心使戊图中的金属块接触了容器底且与容器底有力的作用,此时测量出的盐水密度值将如何变化,并分析原因。
(2)将合金块分别浸没在水和某液体中(如图1乙、丙所示),比较图1甲、乙、丙可知:。
(3)合金块的密度为ρ合金=g/cm3。
(4)若用此合金块制成一空心合金球,当合金球恰好能悬浮于图1丙所示液体中时,空心部分的体积是cm3。
12.(2019赤峰,20)如图所示,是探究同一物体所受浮力大小于哪些因素有关的实验过程。
(1)两次实验证明物体所受浮力随物体排开液体积的变化而变化(选填实验序号)
(2)进行乙、丙两次实验是为了探究物体所受浮力大小与关系。
(3)由丙、丁两次实验可知:完全浸没在同种液体中的物体,所受浮力大小与无关
13.(2019重庆A卷,18)小薇同学制作了如图1所示的探头进行了液体压强和浮力的综合探究。
3.(2019上海,26)某小组同学在“探究物体在液体中所受向上的力与哪些因素有关”实验中,用弹簧测力计拉着一个圆柱体,测力计示数为F0.现将圆柱体悬空放置在一个烧杯中,倒入液体A,圆柱体的下表面到液面的深度为 h,记录下此时弹簧测力计的示数为F,以及F0和F 的差为△F.接着,将液体A 钟换为液体B,重复上述实验,记录数据如下表二所示.
(1)金属块完全浸没在水中受到的浮力为N。
(2)金属块的密度是kg/m3。
(3)你还能求出有关金属块的哪些物理量:(写出三个物理量即可,不需要计算结果)
2.(2019 青岛,21)测量盐水的密度,方案如下:
浮力专题:浮力习题中的液面变化问题(有答案)

浮力专题:浮力习题中的液面变化问题【例1】(纯冰熔于液体)容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?【答案】(1)不变;(2)上升【解析】液面是否变化,关键是看V排是否等于V化水。
(1)①当冰漂浮时,依漂浮条件知,F浮=G冰即ρ水ɡV排= G冰= m冰g ∴V排=m冰/ρ水②冰化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水③所以V排=V化水即冰块完全熔化后水面高度不变。
(2)同理:纯冰浮在盐水液面上,当冰熔化后液面将上升。
练习1:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化?【答案】上升【解析】冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,∴熔化前F浮<G冰,即ρ水g V排<G冰,故得V排<m冰/ρ水。
熔化为水的体积V化水=m水/ρ水= m冰/ρ水,∴V排<V化水,即熔化后水面要上升。
【例2】(冰中有杂质)在盛水的烧杯中漂浮着一块冰,冰中夹着一小木块,问:(1)当冰完全熔化为水时,水面将如何变化?(2)若冰中夹杂着一小石块,冰熔化后液面如何变化?【答案】(1)不变;(2)下降【解析】方法一:比较体积变化法①冰块漂浮时:F浮=G冰+G木即ρ水gV排= G冰+G木,V前排= (m冰+m木)/ ρ水=m冰/ρ水+m木/ρ水②当冰块化成水时:m化水= m冰∴V化水=m冰/ρ水又因为木块仍漂浮,F木浮= G木即ρ水gV木排= m木g ∴V木排=m木/ρ水V后排=V化水+V木排= m冰/ρ水+ m木/ρ水 (2)由(1)(2)得:V前排= V后排故当冰完全熔化成水时,水面不变。
方法二:比较浮力变化法熔化前冰块和木块都漂浮∴F前浮= G冰+ G木熔化后熔化成的水悬浮,木块仍漂浮∴F后浮= G化水+ G木又G化水= G冰所以F前浮=F后浮,即熔化前后所受浮力不变,所以液面将不变。
3 浮力——液面升降问题(原卷版)

B.A的一半浸入水中前后,台秤的示数变化了
C.若剪断细线,A物体下表面受到的压强先变大后不变
D.若剪断细线,待液面静止后,水对容器底的压强为
11、小科在水盆中洗碗,发现一个大碗正漂浮在水盆中,如图所示。他将水盆中的一些水放入大碗中,但大碗仍然漂浮。与原先相比,水盆中的水面将会(填“上升”、“不变”或“下降”),一不小心倾斜沉入水底,水盆底受水的压强将会(填“变大”、“不变”或“变小”)。
一、液面升降的三种情形
1、物体浸没
2、物体部分浸入
方法一:
方法二:
V1=2V2
V3+V1=V3+2V2
3、剪断绳子
液面升降:
二、液体和固压变化量:Δp水、ΔF水、ΔF桌、Δp桌
柱形容器中装有0.2m深的水,容器底面积为0.02m2,将重为10N,体积为1×10-3m3的正方体A放入上述液体中,A完全浸没且完全没有水溢出,求:
(1)水对容器底部压强变化量Δp水;
(2)水对容器底部压力变化量ΔF水;
(3)容器对桌面压力变化量ΔF桌;
(4)容器对桌ρ水gΔh=1.0×103kg/m3×10N/kg×0.05m=500Pa
(2)ΔF=ΔpS=500Pa×0.02m2=10N
(3)F压1=F支1=G液+G容F压2=F支2=G液+G容+G物ΔF桌= F压2-F压1=G物=10N
A.下降B.上升C.不变D.无法判断
7、如图所示,柱形容器的底面积为500cm2,重为5N的木块A在水中处于静止状态,此时绳子的拉力为3N。若绳子突然断了,待木块再次静止时,容器中水面将下降的高度是( )
A.4.0×103mB.6.0×10-3mC.1.0×10-2mD.1.6×10-2m
初中物理:浮力-液面升降问题

G总
F浮总
乙图中
(2)冰熔化问题
思路:
冰漂浮
液面不变h1=h
点题:实际就是比较V排和V化水
S
h
水
S
h1
水
液面上升h1〉h
S S 淡盐水
S
盐水
盐水
1
2
3
(3)冰中物,冰熔化问题
S
h
水
S
h1
水
S
h
水
等效
熔化
液面不变h1=h
S 水 S 水 熔化 液面下降
h
h
h1
水
S
等效
4、浮力与压力、压强相结合问题
—总体积变化?
—物体排开液体的总体积变化?
—浮力变化?
思路:液面升降?
3、液面升降问题
S
h
S
h1
思路:整体法
船和物均漂浮
G总不变
F总浮不变
V排总不变
液面不变h1=h
(1)船中物问题
1
第一部分
2
第二部分
思路:
S
h
S
h2
甲图中 船和物漂浮
F总浮变小
V排总变小
液面下降
甲图
乙图
G球
N
F球浮
G船
h
S
h1
S
甲
h1
S
乙
h1
S
丙
h1
S
丁
液体对容器底的压力变化
从无到有
4、浮力与压力、压强相结合问题
S
h1
S
h2
液体对容器的压力变化
有中有变
01
边审题边画图,明确物理状态、过程和条件
浮力专题:液面升降问题

(3)
.
橡皮泥密度的表达式:
.
2.小红的妈妈有一只翠玉手镯,她想知道手镯的密度。现在只有如
下器材:一个水槽和足量的水、细线、刻度尺、一个正方体木块。请你
按照下面的实验设计思路,把实验步骤补充完整,并利用测量中的表
示符号和水的密度ρ水,写出测量翠玉手镯密度的数学表达式。实验 步骤:
①水槽中装入适量水,将木块放入水槽中,用刻度尺测出木块下表面到水面的距离 h1;
5
【浮力与密度实验练习】
1.用图所示的方法可以粗测出橡皮泥的密度.请你将李明同学测橡皮泥密度的实验步
骤补充完整,并用测得的物理量表示出橡皮泥密度的表达式.实验步骤:
(1)将适量的水倒入烧杯中,用刻度尺测出烧杯中水的深度 h1. (2)将橡皮泥捏成球状后放入烧杯中(如图甲所示),用刻度尺
测出此时烧杯中水的深度 h2.
9.下图是常见的厕所自动冲水装置原理图,水箱内有质量 m1=0.4kg,体积 V1=3×10-3m3 的浮筒 P,另有一厚度不计,质量 m2=0.2kg,面积 S2=8×10-3m2 的盖板 Q 盖在水箱底部 的排水管上,用细线将 P、Q 连接,当供水管上流进水箱的水使浮筒刚好浸没时,盖板 Q 恰好被拉开,水通过排水管流出冲洗厕所,当盖板 Q 恰好被拉开 的瞬间,求:(1)浮筒受到的浮力大小。 (2)细线对浮筒 P 的拉力大小。(3)水箱中水的深度。
量△V 水=
。
,加入水
*若木块被按压又下降 h(水未溢出),则水面升高高度△h2=
。
2、将木块(密度为ρ,底面积 S0,高为 h0)立放于容器中(容器底面积 S0),
向 容 器 中 加 水( ,密 度 为 ρ 水 ),水 面 高 度 为 h ,木 块 未 浮 起 ,则 V 排
冰融化液面变化问题(浮力专题)

冰融化液面变化问题
例题1:将冰块放在浓盐水中,液面位置如图所示,若冰完全熔化,杯中液面高度将()
A.上升B.下降C.不变D.无法确定
变式1:将冰块放在水中,液面位置如图所示,若冰
完全熔化,杯中液面高度将()
A.上升B.下降C.不变D.无法确定
解析:此类“冰融化问题”是一个重难点。
变式2:将冰块放在酒精中,液面位置如图所示,若冰
完全熔化,杯中液面高度将()
A.上升B.下降C.不变D.无法确定
变式3:烧杯中的一大块冰内含有一定量的砂子,冰块漂浮在水面,杯中水面恰好与杯口相平,且冰块上部高出杯口.在冰块熔化的过程中()
A.将有水从烧杯中溢出B.水面始终与杯口相平C.烧杯中水面会下降D.水面先有下降,后有水溢出
解析方法:
由于图中冰是漂浮的,
根据浮力公式g m g 冰冰排液浮===G V F ρ
冰融化成水的质量冰水冰m m =→
则:g m g 水冰排液→=V ρ ① 根据密度公式:g g m 水冰水水冰则:→→=⇒=⇒=V V m V m
ρρρ
② 公式①②连列可得:
g V g 水冰水排液→=ρρV 两边同除以g 可得
水冰水排液→=V ρρV 由此公式可以解决任何冰水融化问题
例题1:水液水浓盐水即ρρρρ〉〉
根据公式水冰水排液→=V ρρV
可得:水冰排→〈V V
冰融化得到的水的体积大于冰排开水的体积,则液面将上升 变式1、2、3都可以用此公式计算
欢迎下载,谢谢观看!资料仅供参考学习。
浮力典型液面变化

有关液面升降的浮力和液体压强计算1. 如图所示,容器重4.2N,放在水平桌面上,容器上部是边长为5cm的立方体,下部是边长为10cm的立方体.若向容器内注入1.1kg水,g取10N/kg,求:(1)这个装着水的容器对桌面的压强多大?(2)容器底部所受水的压强多大?(3)现用细线吊着一个体积为50cm3,质量为100g的物体浸没在水中,求此时容器对桌面的压强?2. 如图,弹簧测力计下挂一长方体金属块,弹簧测力计的示数为78N,在物体下方放一装有水的圆柱形容器(器壁厚不计),水深为10cm,金属块的下表面与水面相平,若此时将金属块下移5cm(水未溢出),金属块刚好浸没,此时弹簧测力计的示数为68N,若S容=5S物,g取10N/kg求:(1)金属块重力(2)金属块受到的浮力(3)金属块下移5cm(水未溢出)时水面变化高度(4)圆柱形容器内所装水的质量3. 如图所示,底面积为400cm2的圆柱形容器内盛有20厘米深的水,弹簧测力计(0刻度线与1N刻度线之间的间隔0.6cm)下端用细线挂着一个边长为10cm的正方体物块,物块的上表面与水面刚好相平,此时弹簧测力计的示数是15N。
从容器内向外缓慢抽水,直至物块有一半浸在水中,求:(取g=10N/kg)(1)未抽水时物块下表面所受的水的压强;(2)此物块的密度;(3)共抽了多少kg水;(4)抽水后容器底所受的压力。
4. 如图16所示:一个底面积为10m2的圆柱状容器,装有适量的水,现在将一个体积为20m3、质量1.6ⅹ104kg的物体A放入其中,最终物体A漂浮于水面上。
求:(1)物体A所受到的浮力是多少?(2)如图所示,若将画斜线部分载取下来并取出(其体积为浸入水中体积的一半),则取出的那部分物体的质量是多少?(3)待剩余部分再次静止后,容器底部受到压强减小了多少?5. 如图19所示,将装入一定量水的圆柱形容器放在天平上,并将高为8cm、横截面积为10cm2的柱形物块挂在弹簧测力计下端,缓慢放入底面积为50cm2的圆柱形容器内的水中。
备考2019年中考物理一轮复习:专题06浮力液面变化(注水抽水过程分析)(含答案及解析)

备考2019年中考物理一轮复习:专题06 浮力液面变化(注水抽水过程分析)一、综合题(共2题;共30分)1. ( 15分) 如图甲,水平地面上有一底面积为400cm2,重为2N的圆柱形容器(容器重和容器壁厚度不计),容器内盛有20cm深的水,一个量程选择合适的弹簧测力计下端用细线挂着一个边长为10cm的不吸水的正方体物块缓慢放入水中,物块的上表面与水面刚好相平,此时测力计示数为10N,如图乙.已知在一定范围内,弹簧受到的拉力每减少1N,弹簧的长度就缩短0.6cm.(g=10N/kg)求:(1)图甲中水对容器底部的压强是多少?(2)物体的密度是多少?(3)图乙中从容器内向外缓慢抽水,直至物块有一半浸在水中,此时容器对桌面的压强?2. ( 15分) 如图甲所示,一个柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2,高为12cm 均匀实心长方体木块A,A的底部与容器底用一根细绳连在一起,现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,此时容器中的水的深度为9cm.已知细绳长度为L=8cm,ρ水=1.0×103kg/m3.求:(1)当木块A对容器底部的压力刚好为0,A受到的浮力;(2)木块A的密度;(3)若继续缓慢向容器中加水,当容器中的水的总质量为4.5kg时,停止加水,如图丙所示,此时将与A 相连的细绳剪断,求细绳剪断前、剪断后木块静止时,水对容器底部压强的变化量.(整个过程中无水溢出)答案解析部分一、综合题1.【答案】(1)解:图甲中水对容器底部的压强:p甲=ρ水gh甲=1.0×103kg/m3×10N/kg×0.2m=2000Pa;答:图甲所示中水对容器底部的压强是2000Pa;(2)解:物块的上表面与水面刚好相平时排开水的体积:V排=V=L3=(10cm)3=1000cm3=0.001m3,物块受到水的浮力:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.001m3=10N,由F浮=G﹣F′可得,物体的重力:G=F浮+F′=10N+10N=20N,物体的密度为:ρ= = = =2×103kg/m3;答:物体的密度为2×103kg/m3;(3)解:图乙容器内水的深度:h乙= = =22.5cm,物块有一半浸在水中时,由F浮=ρgV排可知,F浮′= F浮= ×10N=5N,由F浮=G﹣F′可知,此时弹簧测力计的示数:F″=G﹣F浮′=20N﹣5N=15N,即弹簧的拉力增加了5N,因在一定范围内,弹簧受到的拉力每减少1N,弹簧的长度就缩短0.6cm,所以,弹簧伸长了0.6cm/N×5N=3cm,即物体下降了3cm,而新的液面在物体高的中点位置,液面下降了3cm+5cm=8cm,剩余部分水的深度为22.5cm﹣8cm=14.5cm,剩余部分水的体积:V水剩=S容h剩﹣V=400cm2×14.5cm﹣×1000cm3=5300cm3,则剩余的水的质量:m水剩=ρ水V水剩=1.0g/cm3×5300cm2=5300g=5.3kg,剩余的水的重力:G水剩=m水剩g=5.3kg×10N/kg=53N,因物块受到水的浮力和物块对水的压力是一对相互作用力,二力大小相等,所以,容器对桌面的压力:F压=G容+G剩水+F浮=2N+53N+5N=60N,容器对桌面的压强:p= = =1500Pa.答:容器对桌面的压强为1500Pa.【考点】密度公式及其应用,压强的大小及其计算,液体的压强的计算【解析】【分析】(1)已知甲中水的深度,根据p=ρgh求出水对容器底部的压强;(2)物块的上表面与水面刚好相平时排开水的体积和其体积相等,根据阿基米德原理求出物块受到水的浮力,根据F浮=G﹣F′求出物体的重力,根据ρ= = 求出物体的密度;(3)水的体积加上物体排开水的体积然后除以容器的底面积即为图乙容器内水的深度,根据阿基米德原理求出物块有一半浸在水中时受到的浮力,根据F浮=G﹣F′可知此时弹簧测力计的示数,进一步得出弹簧的拉力增加了量,根据题意求出弹簧的伸长量即物体下降的高度,进一步求出剩余部分水的深度以及剩余部分水的体积,根据m=ρV求出剩余的水的质量,根据G=mg求出剩余的水的重力,物块受到水的浮力和物块对水的压力是一对相互作用力,二力大小相等,则容器对桌面的压力等于容器和水的重力加上物体受到的浮力,根据p= 求出容器对桌面的压强.2.【答案】(1)解:已知木块A的底面积S木=100cm2,由乙图可知:当木块A对容器底部的压力刚好为0,水的深度为h水=9cm;则木块A排开水的体积:V排=S木h水=100cm2×9cm=900m3=9×10﹣4m3,木块受到的浮力:F浮=ρ水V排g=1×103kg/m3×9×10﹣4m3×10N/kg=9N(2)解:木块A的体积:V木=S木h木=100cm2×12cm=1200cm3=1.2×10﹣3m3,由于木块A对容器底部的压力刚好为0,木块A处于漂浮,则G=F浮=9N,由G=mg=ρVg可得木块的密度:ρ木= = =0.75×103kg/m3(3)解:木块A对容器底部的压力刚好为0时,由ρ= 可得所加水的体积为:V水1= ==1.8×10﹣3m3=1800cm3;由乙图可知:V水1=(S容﹣S木)h水,(其中h水=9cm)则容器的底面积为:S容= +S木= +100cm2=300cm2;再次加水后容器中水的总体积为:V水2= = =4.5×10﹣3m3=4500cm3;如上图丙中可知,木块下表面以下水的体积(图中红线以下)为:V1=S容L=300cm2×8cm=2400cm3,则红线以上水的体积为:V2=V水2﹣V1=4500cm3﹣2400cm3=2100cm3,设此时木块浸入水的深度为h′,则V2=(S容﹣S木)h′,所以,木块浸入水的深度:h′= = =10.5cm,此时木块排开水的体积为V排′=S木h′=100cm2×10.5cm=1050cm3;若将细线剪断,木块将上浮,当木块静止时漂浮如上图丁,由于图丁与图甲中的木块都是漂浮,则木块受到的浮力相等,排开水的体积相等,所以,细线剪断后木块漂浮时,其排开水的体积为V排″=V排=900cm3,细绳剪断前、剪断后,排开水的体积变化量:△V排=V排′﹣V排″=1050cm3﹣900cm3=150cm3,则水的深度变化量:△h═= =0.5cm=5×10﹣3m,所以,水对容器底部压强的变化量:△p=ρ水g△h=1×103kg/m3×10N/kg×5×10﹣3m=50Pa.【解析】【分析】(1)根据木块A底面积和水的深度,可求木块A排开水的体积,再利用阿基米德原理求物块受到的浮力;(2)由于木块A对容器底部的压力刚好为0,则重力与浮力相等;利用G=mg求木块的质量,再利用密度公式求木块的密度;(3)根据水的体积求出木块A浸入水的体积,进一步求细绳剪断前、剪断后排开水的体积变化,知道容器底面积,可求水深的变化量,再利用液体压强公式求容器底所受压强改变量.。
]与浮力有关的液面变化类问题.pdf
![]与浮力有关的液面变化类问题.pdf](https://img.taocdn.com/s3/m/b2c06938caaedd3383c4d3a4.png)
]与浮力有关的液面变化类问题液面变化类(与浮力有关)问题【模块一】考点解析知识复习:1.阿基米德原理:浸在液体中的物体受到向上的浮力,浮力的大小等于它排开的液体受到的重力。
F浮=G排液=ρ液gV排浸没时V排=V物部分浸入时V排=V-V出2.物体的浮沉条件(1)浸没在液体中的物体(V排=V物)F浮<G物,下沉(ρ液<ρ物)F浮>G物,上浮(ρ液>ρ物)F浮=G物,悬浮(ρ液=ρ物)(2)漂浮在液面上的物体:F浮=G物(V排<V物)液面升降问题类型一:容器中的固态物质投入水中后判断液面升降实质是比较前后V排的变化。
实验:情景如图所示,小船和石块一起漂浮在水中,将石块(或金属块)从船中取出放入水中后,你观察到的现象是水面。
怎样用理论知识解释你看到的现象?理论推导:变化:如果将沉在水底的石块放入船中使船漂浮,液面如何变化?原因是:。
进一步探讨:从船中取出怎样的固态物质放入水中,水面不变?答:。
原因是:。
类型一的结论是:此类问题判断前后液面变化,实质是比较V排的变化,因为液体密度不变,浮力跟V排有关,所以转化为判断浮力的变化。
若浮力变大,则V排变大,液面;若浮力变小,则V排变小,液面;若浮力不变,则V排不变,液面。
从容器中往水中投放固态物质,也可以比较ρ物和ρ液的关系,若ρ物>ρ液,则液面;若ρ物≤ρ液,则液面。
反馈练习:如图所示,一个小船中放有ABC三个小球,小船和球一起漂浮在水面上,其中A球密度小于水,B球密度等于水,C球密度大于水,小船可以自由的漂浮在水面上。
①只将A球放入水中,则A球(填浮沉状况),液面(填“上升”或“下降”或“不变”)②只将B球放入水中,则B球(填浮沉状况),液面(填“上升”或“下降”或“不变”)③只将C球放入水中,则C球(填浮沉状况),液面(填“上升”或“下降”或“不变”)④若将ABC三球同时从船中取出放入水中,则液面(填“上升”或“下降”或“不变”)。
液面升降问题类型二:纯冰浸于液体,熔化后判断液面升降分析:冰块熔化后化成水,体积变小且水具有流动性。
专题二:液面变化问题【含答案及解析】

专题二:液面变化问题【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 在远洋轮船的船舷上,都漆着五条“吃水线”,又称“载重线”。
如图所示,其中标有W的是北大西洋载重线,标有S的是印度洋载重线。
当船从北大西洋驶向印度洋时,轮船受到的浮力以及北大西洋与印度洋的海水密度ρ1和ρ2的关系,正确的是()A.浮力增大,ρ1=ρ2B.浮力减小,ρ1=ρ2C.浮力不变,ρ1>ρ2D.浮力不变,ρ1<ρ22. 如图,小瓷碗漂浮在水面上,倾斜后能沉入水底,关于这一情景分析正确的是()A.小瓷碗能沉入水底是因为它的重力变大了B.小瓷碗漂浮时受到的浮力大于它的重力C.小瓷碗浸没时受到的浮力比漂浮时受到的浮力大D.小瓷碗浸没后容器底受到水的压强变小了二、填空题3. 小明在水盆中洗碗,发现一个大碗正漂浮在水盆中,如图所示。
他将水盆中的一些水放入大碗中,但大碗仍然漂浮。
与原先相比,大碗所受到的浮力将(选填“变大”、“不变”或“变小”),水盆中的水面将会(选填“上升”、“不变,,或“下降,,)。
4. 如图,放有铁块的杯子漂浮在水面上,如果把铁块用细线悬挂在杯底,杯子和铁块受到的浮力将,水对容器底部的压强将。
(填增大、减小或不变)如果把细线断了,水面将。
三、选择题5. 容器内盛有水,在一试管里面放一小球后,浮在水面上。
如图所示,现将小球取下沉入水中,试管仍浮在水面上,则()A.液面下降B.液面上升C.容器底部受到的液体的压强不变D.试管下表面受到的液体压强变小6. 如图所示,容器内有水,有一塑料试管下面挂一小铁块,浮在水面上.现将小铁块取下放入试管中,试管仍浮在水面,则()A.液面上升B.液面下降C.容器底部受到液体的压强不变D.试管外壁上A点受到液体的压强不变7. 如图所示,四个相同的容器内水面一样高,a的容器内只有水,b容器内有木块漂浮在水面上,c容器内漂浮着一块冰块,d容器中悬浮着一个空心球,下列说法正确的一组是()①四个容器对水平面的压力相等②四个容器中,液体对容器底的压强相同③在b容器中倒入酒精后,木块在液面下体积不变④c容器中冰块熔化后水面高度下降⑤空心球的材料密度可能等于水的密度A.①②⑤ B.①③⑤ C.②⑤ D.①②8. 容器中装有一定质量的水,先后按甲、乙两种方式使物体A和小玻璃杯漂浮在水面上(图中细线重力及体积均不计).设甲、乙两图中物体A和小玻璃杯共同受到的浮力分别为F甲和F乙,水对容器底的压强分别为p甲和p乙,则()A.F甲<F乙 p甲=p乙.B.F甲>F乙 p甲>p乙C.F甲=F乙 p甲<p乙.D.F甲=F乙 p甲=p乙9. (多选)如图(a),在一个较大的容器中盛有水,水中放有一个木块,木块上面放有物体A,此时木块漂浮;如果将A从木块上拿下,并放入水中,当木块和A都静止时(水未溢出),下面说法正确的是()A.当A的密度小于水的密度时,容器中水面上升B.当A的密度大于水的密度时,容器中水面下降C.当A的密度等于水的密度时,容器中水面下降D.当A的密度大于水的密度时,将A拿下后悬挂在木块下面,如图(b),容器中水面不变10. 如图所示,一块0℃的冰放在盛有0℃水的容器中,已知冰块与容器底部相接触并相互间有压力,当冰块完全熔化为0℃的水后,则容器中水面的位置将()A.上升B.下降C.保持不变D. 水面的升或降决定于冰和容器内水的体积11. 如图所示,在水平桌面上放置一个装有适量水的锥形瓶,瓶内漂浮着一块冰,冰融化过程中()A.瓶内水面上升B.水对瓶底的压强减少C.桌面受到的压力增大D.桌面受到的压强不变四、填空题12. 容器内水中放有长方体木块A,木块上方压有密度为4g/cm3的金属块B,此时,木块露出水面的高度为2cm,如图甲所示;用细绳将该金属块系在木块的下方,木块露出水面的高度为3cm,如图乙所示;将细绳剪断后,如图丙所示,则木块露出水面的高度为cm。
备考2019年中考物理一轮复习:专题06浮力液面变化(物体上升下降引起液面变化)(含答案及解析)

备考2019年中考物理一轮复习:专题06 浮力液面变化(物体上升下降引起液面变化)一、填空题(共2题;共4分)1. ( 2分) 如图甲所示,圆柱形容器中盛有适量的水,其内底面积为100cm2.弹簧测力计的下端挂着一个正方体花岗岩,将花岗岩从容器底部开始缓慢向上提起的过程中,弹簧测力计的示数F与花岗岩下底距容器底部的距离h的关系如图乙所示.则花岗岩未露出水面前所受水的浮力为________ N,从开始提起到花岗岩完全离开水面,水对容器底部减小的压强为________ Pa.(g取10N/kg)2. ( 2分) 如图所示,底面积为S1的圆柱体放在水平桌面上,当把一质量为m的物体A放在它上面时.圆柱体对桌面压强的变化量为________;另有一个底面积为S2、内装某液体的薄壁圆柱形容器,也放在同一水平桌面上,当把物体A浸没在液体中时(液体未溢出),液体对容器底压强的变化量与圆柱体对桌面压强的变化量相等.若物体A的密度为ρ,则该液体的密度为________.(用物理量符号表示)二、单选题(共2题;共4分)3. ( 2分) 已知小球甲能漂浮在水面上,小球乙能悬浮在水中,小球丙将在水中下沉,现把三只小球放在同一个小盒中,小盒在盛水的容器中漂浮,则下列说法中正确的是()A. 只把小球甲从小盒中拿出放入水中,容器中水面下降B. 只把小球乙从小盒中拿出放入水中,容器中水面不变C. 只把小球丙从小盒中拿出放入水中,容器中水面上升D. 若将三只小球同时从小盒中拿出放入水中,容器中水面上升4. ( 2分) 如图所示,水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器.其中甲容器内只有水,乙容器内有木块漂浮在水面上,丙容器内有一个装有铝块的平底塑料盒漂浮在水面上,塑料盒底始终与容器底平行,且塑料盒的底面积等于圆柱形容器底面积的一半,丁容器中用细线悬吊着一个实心的铝球浸没在水中.已知四个容器中的水面一样高,ρ木=0.6×103kg/m3;ρ酒精=0.8×103 kg/m3;ρ铝=2.7×103 kg/m3,对于这一情景,有如下一些说法,其中说法正确的是()A. 向乙容器中倒入酒精后,木块底部受到的压强将增大B. 各容器对水平桌面的压强不同C. 将悬吊铝球的细线剪断后,丁容器对水平桌面压力的增大值等于铝球所受重力的大小D. 将塑料盒内的铝块取出放入到丙容器中,待塑料块和铝块稳定后,则丙容器中的液面会下降三、解答题(共1题;共5分)5. ( 5分) 水平桌面上放置底面积为80cm2,质量为400g圆筒,筒内装有16cm深的某液体,弹簧测力计悬挂底面积为40cm2、高为8cm的圆柱体,从液面逐渐浸入直到浸没,弹簧测力计示数F与圆柱体浸入液体深度h的关系如图所示.(圆筒的厚度忽略不计,筒内液体没有溢出)求:(1)圆柱体浸没在液体中所受浮力是多少?(2)筒内液体的密度是多少?(3)圆柱体浸没时,圆筒对桌面的压强是多少?答案解析部分一、填空题1.【答案】2;200【考点】液体的压强的计算,浮力大小的计算【解析】【解答】解:(1)由图乙可知,花岗岩的重力G=5.6N,花岗岩在未露出水面前弹簧测力计的示数F=3.6N,则未露出水面前花岗岩所受水的浮力:F浮=G﹣F=5.6N﹣3.6N=2N;(2)由F浮=ρ水gV排可得花岗岩的体积:V=V排= = =2×10﹣4m3;花岗岩离开水面后,水面下降的高度:△h= = =0.02m,水对容器底部减小的压强:△p=ρ水g△h=1×103kg/m3×10N/kg×0.02m=200Pa.故答案为:2;200.【分析】(1)由图乙可知,花岗岩在露出水面时,弹簧测力计的示数,可得花岗岩的重力;又可得花岗岩在未露出水面前弹簧测力计的拉力,利用称重法可得花岗岩所受水的浮力大小;(2)由阿基米德原理F浮=ρ水gV排可得花岗岩的体积;花岗岩离开水面后,水面下降的高度等于排开水的体积除以容器底面积,再利用液体压强公式求水对容器底部减小的压强.2.【答案】;ρ【考点】压强的大小及其计算【解析】【解答】解:①圆柱体对桌面压力变化量△F=G A=mg,压强的变化量:△p1= = ;②物体A浸没在液体中,根据ρ= 可得,物体A的排开液体的体积为:V排=V A= ,当把物体A浸没在液体中时(液体未溢出),液面升高的高度h= = ,由题知,液体对容器底压强的变化量△p2=△p1= ;所以有:△p2=ρ液gh=ρ液g = ,解得,ρ液= ρ.故答案为:;ρ.【分析】①求出圆柱体对桌面压力变化量,利用p= 计算圆柱体对桌面压强的变化量;②物体A浸没在液体中,排开液体的体积等于其自身体积,利用密度公式写出其表达式,再利用求出液面升高的高度,再根据液体对容器底压强的变化量与圆柱体对桌面压强的变化量相等,结合液体压强公式列出等式求解即可.二、单选题3.【答案】B【考点】物体的浮沉条件及其应用【解析】【解答】解:当三个小球放在盒中漂浮于水面时,则F浮总=G甲+G乙+G丙;A、当把小球甲从小盒中拿出放入水中后,小球甲在水中漂浮,说明F浮甲=G甲,小球甲出放入水中后F还是G甲,因为两个物体都是漂浮,浮力不变,所以水面高度不变,故A错误;浮甲B、当把小球乙从小盒中拿出放入水中后,小球乙在水中悬浮,说明F浮乙=G乙,小球乙出放入水中后F还是G乙,因为两个物体一个漂浮,一个悬浮,浮力不变,所以水面高度不变,故B正确;浮乙C、把小球丙从小盒中拿出放入水中,因小球丙在水中会沉至水底,则F浮丙<m丙g,也就是总的浮力比之前小了,所以V排变小,水面下降,故C错误;D、通过前面的分析已然明确,甲乙两个拿出放入水中时水面不变,而将丙拿出放入水中时,容器中的水面高度会下降,所以若将三只小球从小盒中拿出放入水中,水面高度会下降,故D错误.故选B.【分析】由物体的浮沉条件可知三个球在盒子中时,盒子所受到的浮力,由浮力公式可得排开水的体积;则分别将三个小球放入水中时可由浮力公式求得排开水的体积,则可知水面高度的变化.4.【答案】D【考点】压强大小比较【解析】【解答】解:A、乙容器中再倒入酒精后,使水的密度减小,但木块还是漂浮,受到的浮力相等,根据F浮=ρ水V排g可知,排开水的体积增大,使木块在液面下的体积增大,根据p= 可得,F浮=pS木块底,木块的底面积不变,所以木块底部受到的压强不变,故A错误;B、木块漂浮,受到的浮力等于木块重等于排开的水重,甲、乙容器水面等高,则乙容器的总重等于甲容器的总重,乙容器的总质量与甲容器的总质量相同,则甲乙对桌面的压力相等;同理可以得出,丙容器的总质量与甲容器的总质量相同,则甲丙对桌面的压力相等;丁容器中水重力的增加的量等于小球排开液体的重力,因液面与甲容器的相平,所以甲丁对桌面的压力相等;因四个容器底面积相同,由p= 可知它们的压强相同,故B错误;C、细线剪断前,桌面受到的压力等于容器与水的重力、小球排开液体的重力之和,将悬吊铝球的细线剪断后,桌面受到的压力等于容器与水的重力、铝球对容器底部的压力之和,而铝球对容器底部的压力等于铝球的重力减去受到的浮力,根据阿基米德原理可知铝球受到的浮力等于小球排开液体的重力,所以容器对水平桌面压力的增大值等于铝球所受重力减去受到的浮力,不等于铝球所受重力的大小,故C错误;D、由图丙图可知,塑料盒和铝块漂浮,浮力等于塑料盒的重力与铝块的重力之和,将塑料盒内的铝块取出放入到丙容器中,待塑料块和铝块稳定后,塑料盒漂浮,浮力等于其重力,铝块沉底,浮力小于其重力,故将塑料盒内的铝块取出放入到丙容器中后塑料盒与铝块受到的总浮力减小,根据F浮=ρ水V排g可知,排开水的体积减小,所以,待塑料块和铝块稳定后,则丙容器中的液面会下降.故选D.【分析】(1)乙容器中再倒入酒精后,使水的密度减小,但木块还是漂浮,受到的浮力相等,根据浮力产生的原因可知压力压强的变化;(2)乙丙两个容器的物体漂浮,受到的浮力都等于物体重,丁容器中用细线悬吊着一个实心的铝球,由阿基米德原理可知排开的水重等于物体重,由此可知每个容器对水平桌面的压力、压强.(3)细线剪断前,容器对桌面增大的压力等于容器中水的重力和铝球排开水的重力;将悬吊铝球的细线剪断后,铝球对容器底部的压力等于铝球的重力减去受到的浮力,进一步求出容器对桌面的压力.(4)比较图丙中塑料盒内的铝块取出放入到丙容器中前后所受总浮力的变化,根据阿基米德原理分析解答.三、解答题5.【答案】解:(1)由图象知,当h=0时,此时测力计的示数等于圆柱体的重力,所以G=10N;当h≥8cm时,测力计的示数不变,说明此时浮力不变,圆柱体完全浸没,此时F=2N;所以F浮=G﹣F=10N﹣2N=8N;(2)物体排开液体的体积V排=V物=40×8×10﹣6m3=3.2×10﹣4m3由F浮=ρ液gV排得,ρ液==2.5×103kg/m3(3)液体的质量m液=ρ液V液=2.5×103kg/m3×80×16×10﹣6m3=3.2kg将圆柱体、圆筒、液体看做一个整体,则其对地面的压力F′=(m液+m筒)g+G物﹣F拉=(3.2kg+400×10﹣3kg)×10N/kg+10N﹣2N=44Np==5.5×103Pa答:(1)圆柱体浸没在液体中所受浮力是8N;(2)筒内液体的密度是2.5×103kg/m3;(3)圆柱体浸没时,圆筒对桌面的压强是5.5×103Pa.【考点】密度的计算【解析】【分析】(1)根据图象分析出物体的重力和完全浸没时的拉力,根据公式F浮=G﹣F计算出浮力的大小;(2)根据F浮=ρ液gV排的变形公式ρ液=计算出液体的密度;(3)判断出此时圆筒对桌面的压力,等于圆筒和液体的总重加浮力,根据公式p=计算出压强;也可将圆柱体、圆筒、液体看做一个整体进行受力分析.。
浮力专题:液面升降问题

浮力专题:液面升降问题、判断液面升降方法:比较V排的变化物体浸在液体中,若浮力变大,V排变大,液面____________ ;若浮力变小,则V排变小, 液面__________ ;若浮力不变,则V排不变,液面_________________ 。
(填“上升”或“下降”或“不变”)1、如图所示,将两块相同的橡皮泥做成实心球形和碗形,分别放入相同的甲、乙两杯水中.静止时甲杯中橡皮泥所受的浮力(填“大于” “小于”或“等于”)乙杯中橡皮泥所受的浮力,杯中水面•2、(1)如图所示,小船和石块一起漂浮在水中,将石块(或金属块)从船中取出放入水中后,水面____________________ 。
(2)如图2所示,在一较大容器的水面上放一木块,木块上面放一个体积为1dm3、重7.84N的物体,此时木块漂浮.如果将物体从木块上拿下并放入水中,当木块和物体都静止时,容器中的水面将()A.上升E.下降C.不变D.无法判断3、将冰块分别放在水、盐水和煤油(或酒精)中,冰块完全熔化后,判断液面的变化。
1)冰块放在水中,漂浮,熔化后,液面 ___________________ 。
2 )冰块放在盐水中,漂浮,熔化后,液面___________________3)冰块放在煤油(或酒精)中,沉底,熔化后,液面4、冰块内包有一个木块漂浮在水面上,冰块熔化后,水面O5、冰块内包有一个石块(石块密度大于水的密度)漂浮在水面上,冰块熔化后,石块______________ (填浮沉状况),则水面_________________ 。
检测:1.(1)在图中,容器内装有一定量的水,水面上浮有木块甲,在甲上放有铁块乙,甲与乙之间用细绳相连,当木块翻转,铁块乙没入水中时,则()A.容器内液面高度一定不变 B .容器内液面高度一定降低C.容器内液面高度一定升高 D .容器内液面高度先升高后降低(2)现将绳子剪断,当木块和铁块都静止后,下列分析正确的是()A.铁块沉底,木块漂浮 B .水面下降,容器底受到水的压强变小C.桌面受到的压力变小 D .桌面受到的压强不变2 .重为5N的木块A,在水中处于静止状态,此时绳子的拉力为3N,若绳子突然断了,水面(填“上升”或“下降”或“不变”),最终木块所受浮力为____________ ,水对容器底的压力_______________ (填“增加”或“减小”)二、液面升降的定量计算1、容器底面积S,盛有适量水,柱形木块底面积S o,放入水中,水面上升△ h,则木块排开液体的体积V排= _______________ 。
备考2019年中考物理一轮复习:专题06浮力液面变化(绳断后引起的液面变化)(含答案及解析)

备考2019年中考物理一轮复习:专题06 浮力液面变化(绳断后引起的液面变化)一、单选题(共2题;共4分)1. ( 2分) (2016•重庆)水平地面上有底面积为300cm2、不计质量的薄壁盛水柱形容器A,内有质量为400g、边长为10cm、质量分布均匀的正方体物块B,通过一根长10cm的细线与容器底部相连,此时水面距容器底30cm(如图),计算可得出()A. 绳子受到的拉力为14NB. 容器对水平地面的压力是90NC. 剪断绳子,待物块静止后水对容器底的压强变化了200PaD. 剪断绳子,待物块静止后水平地面受到的压强变化了200Pa2. ( 2分) (2014•贵港)如图所示,密度为0.6×103kg/m3,体积为1×10﹣3m3的正方体木块,用一质量可忽略不计的细线,一端系于木块底部中心,另一端系于圆柱形容器底部的中心,细线对木块的最大拉力为3N,容器内有一定质量的水,木块处于漂浮状态,但细线仍松弛.若圆柱形容器底面积为6×10﹣2m2,现在向容器中注水(容器的容量足够大)直到细线对木块的拉力达到最大值,在细线断裂瞬间停止注水.待木块稳定后,容器的水面与细线断裂前的瞬间的水面相比高度变化()A. 升高了2cmB. 降低了1.5cmC. 升高了1cmD. 降低了0.5cm二、解答题(共1题;共5分)3. ( 5分) 如图所示,将一个体积为1.0×10﹣3m3、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部.当容器中倒入足够的水使木块被浸没时,求:(g取10N/kg)(1)木块浸没在水中受到的浮力.(2)剪断细线后,木块处于静止时露出水面的体积多大.(3)容器底压强减小了多少?答案解析部分一、单选题1.【答案】C【考点】压力及重力与压力的区别,液体压强计算公式的应用,阿基米德原理【解析】【解答】解:A、木块的重力:G=m B g=0.4kg×10N/kg=4N,木块浸没在水中,则V排=V木=(10cm)3=1000cm3=1×10﹣3m3,物体浸没时受到的浮力为:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1×10﹣3m3=10N,绳子的拉力为:F=F浮﹣G=10N﹣4N=6N,故A错误;B、容器内水的体积V=Sh=300cm2×30cm=9000cm3=9×10﹣3m3,由ρ= 可得,水的质量m水=ρV=1.0×103kg/m3×9×10﹣3m3=9kg,因不计质量的薄壁盛水柱形容器,则容器对水平地面的压力F=G总=(m水+m B)g=(0.4kg+9kg)×10N/kg=94N,故B错误;C、木块漂浮,F浮′=G=4N;由F浮=ρ液gV排得,木块漂浮时排开水的体积:V排′= = =4×10﹣4m3;所以液面下降的深度为:△h= = =0.02m;则△p=ρ水g△h=1.0×103kg/m3×10N/kg×0.02m=200Pa.故C正确;D、绳子断和断之前,容器对桌面的压力不变,受力面积不变,故剪断绳子,待物块静止后水平地面受到的压强没有变化,故D错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浮力习题中的液面变化问题
浮力是初中物理教学中的重点和难点。
在浮力习题教学中经常会涉及到求液面变化的问题。
这种问题的综合性较强,是对学生综合运用物理知识分析并解决相关问题的考查。
本文由生活中初春开化时河面将如何变化这一问题引入,对漂浮于水面的冰块融化后液面将如何变化这一问题做了讨论并以此展开联想,分别论述了浮力习题中经常涉及到的求解液面变化的几种情况。
每当初春河开化时,我们都会发现河面上漂浮着很多冰排,那么当这些冰排融化后,河面将如何变化呢?我们可以把漂浮在河面上的冰排看作是漂浮在量杯中的冰块,计算冰块融化后量杯内液面示数的变化,并对冰中混有石子、汽泡、油滴、蜡块这四种情况加以讨论。
例:纯冰漂在水面的情形
水槽中装有体积为V的水,水面上漂浮着重为G的一块冰。
求冰融化后,液面示数将如何变化?
分析:设冰块的重力为G,其质量为m,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
G=mg=P2gV2
整理可得P1gV1=P2gV2
当冰块熔化后,冰块融化成水的体积为V3
此时
故
也就是说,漂浮在水面上的冰排开水的体积恰好等于冰化成水的体积,所以冰融化后液面保持不变。
从这道题可以看出当纯冰漂浮在水面时冰融化后液面不变化。
但是漂浮的冰的内部混有其他物质时,液面将如何变化呢?下面我们对以下几种情况对该题进行讨论。
变试1:冰中混有石子的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有小石子的冰块,小石子的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2,小石子的质量为m0,小石子的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理
F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
整理可得
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,石子落入水中,此时石子排开水的体积为石子的体积V0。
因为P0>P1
故V12>V13
也就是说,当冰块中含有石块时,冰块融化后液面下降。
当然,这道题除了计算以外,还有一种简便的解法。
石块单独放入水中是要沉入水底的,但由于外面包裹了冰块而漂浮在水面上。
我们可以看做是石块借助冰增加了自身的体积,从而增大了浮力使自身漂浮在水面上。
当冰融化后这种凭借消失,浮力变小,石块下沉,排开水的体积变小,故液面下降。
变试2:冰中混有汽泡的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有汽泡的冰块,汽泡的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰
块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2,汽泡的质量为m0,汽泡的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
整理可得
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,气体释放,
V12>V13
故液面下降。
也就是说,当冰块中含有汽泡时,冰块融化之后气体释放,液面下降。
我们可以将冰块、水、汽泡看作一个整体。
由于纯冰化成水后液面不变,当冰块中含有汽泡时,冰块融化之后气体要从整体中释放出去,故液面下降。
变试3:冰中混有油滴的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有油滴的冰块,油滴的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为
G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后油平铺于水面总体积为V13,水的密度为P1,冰的密度为P2,油滴的质量为m0,油滴的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
因为m0=P0V0
所以
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,由于油的密度比水小,所以油会平铺于水面因为P0<P1
所以V12<V13 因为纯冰融化成水后液面不变。
本题相当于把原题中冰内的一部分变成油,如图2所示。
我们可以假定为将图甲中虚线部分的冰变为油。
在图甲中虚线部分为冰,当冰化成水后,虚线部分的冰体积变小而液面不变。
而图乙中虚线部分为等体积的油,油体积不变而平铺于液面。
既当冰化成水后,虚线部分的油体积不变故液面升高。
变试4:冰中混有蜡块的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有蜡
块的冰块,如图3所示。
蜡块的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的总体积为V2,冰块未融化时液面以下的总体积为V12,冰块融化成水的体积为V3,冰块融化后蜡块仍然漂浮,所受浮力为F2,冰块融化后蜡块在液面以下的体积为V30,液面以下的总体积为V13,水的密度为P1,冰的密度为P2,蜡块的质量为m0,蜡块的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
因为m0=P0V0
所以
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,由于蜡的密度比水小,所以蜡块会漂浮于水面
此时F2=G0
根据阿基米德原理F2=P1gV30
而G0=m0g=P0gV0
所以P1gV30=P0gV0
冰块融化后液面以下的总体积
所以V13=V12
故冰融化后液面不变。
由于蜡块无需借助冰块也能漂浮在水面上,所以冰的融化对蜡块没有影响,故冰融化后液面不变。
我们对上题及其几个变式比较后不难发现这样的结论:纯冰漂浮在水面上融化后液面不变,当冰中混有石子或汽泡时融化后液面下降,当冰中混有油滴时融化后液面上升,当冰中混有蜡块时融化后液面不变。
在解决浮力习题中的液面变化问题时,首先要对所研究对象的初始状态进行受力分析,列出平衡方程。
根据阿基米德原理将方程展开。
然后再分析当条件变化后的情形,并对两种情形加以比较,或进行相关的讨论得出结论。
同时要注意分析所得结论的物理意义以及与实际生活之间的联系。
除了理论计算分析以外,还可以用一些简便方法分析,即从定性的角度加以分析比较。
在分析了基本问题的基础上,再对该问题采用变换题设条件的方式进行变式,从而对该问题进行进一步拓展。
2.哈尔滨师范大学物理与电子工程学院)。
