八下数学专题突破:勾股定理(手拉手模型)(人教版)
初中数学几何模型之手拉手模型
即∠DAC=∠EAB,
在△ACD与△ABE中
,
∴△ACD≌△ABE(SAS);
(2)∵△ACD≌△ABE,
∴∠ADC=∠AEB,
∵△ADE是等腰直角三角形,
∴∠ADE=∠AED =45°,
∴∠AEB=∠ADE+∠CDE=45°+60°=105°.
【点睛】本题考查全等三角形的判定和性质,解题的关键是根据等腰直角三角形的性质和全等三角形的判定进行解答.
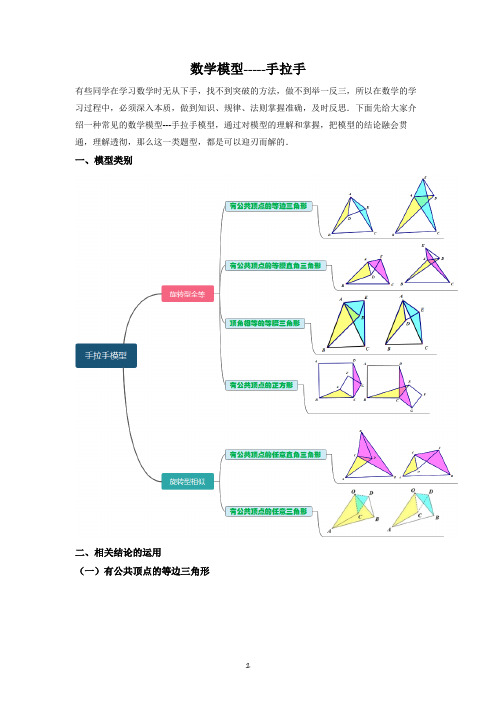
一、模型类别
二、相关结论的运用
(一)有公共顶点的等边三角形
典例精讲:
[问题提出]
(1)如图①, 均为等边三角形,点 分别在边 上.将 绕点 沿顺时针方向旋转,连结 .在图②中证明 .
[学以致用]
(2)在(1)的条件下,当点 在同一条直线上时, 的大小为度.
[拓展延伸]
(3)在(1)的条件下,连结 .若 直接写出 的面积 的取值范围.
(3)①
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE,
∵∠AOB=∠FOC,
∴∠BFC=∠BAC=90°,
∴S四边形BCDE=S△BCE+S△DCE ;
数学模型-----手拉手
有些同学在学习数学时无从下手,找不到突破的方法,做不到举一反三,所以在数学的学习过程中,必须深入本质,做到知识、规律、法则掌握准确,及时反思.下面先给大家介绍一种常见的数学模型---手拉手模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,那么这一类题型,都是可以迎刃而解的.
专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)(解析版)

专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。
3)双等腰三角形型条件:△ABC 和△DCE 均为等腰三角形,C 为公共点;连接BE ,AD 交于点F 。
结论:①△ACD ≌△BCE ;②BE =AD ;③∠ACM =∠BFM ;④CF 平分∠AFD 。
4)双正方形形型条件:△ABCFD 和△CEFG 都是正方形,C 为公共点;连接BG ,ED 交于点N 。
结论:①△△BCG ≌△DCE ;②BG =DE ;③∠BCM =∠DNM=90°;④CN 平分∠BNE 。
例1.(2022·黑龙江·中考真题)ABC V 和ADE V 都是等边三角形.(1)将ADE V 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE V 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE V 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC+=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,PA =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明CAP BAF ≌△△(SAS ),得CAP BAF Ð=Ð,AF AP =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明BAP CAF ≌△△(SAS ),得出CAF BAP Ð=Ð,AP AF =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∵△ABC 是等边三角形,∴AB =AC ,∵点P 与点A 重合,∴PB =AB ,PC =AC ,PA =0,∴PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC=+证明:在BP 上截取BF CP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AC =AB ,CP =BF , ∴CAP BAF ≌△△(SAS ),∴CAP BAF Ð=Ð,AF AP =,∴CAP CAF BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AB =AC ,BP =CF ,∴BAP CAF ≌△△(SAS ),∴CAF BAP Ð=Ð,AP AF =,∴BAF BAP BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.例2.(2023·湖南·长沙市八年级阶段练习)如图1,在Rt △ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE .(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长;(3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.例3.(2023·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B 重合时,如图2,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论.【详解】解:(1)CD 2+DB 2=2DF 2证明:∵DF =EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF = 连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =,CF AB ^,即90CFB Ð=° ∴45FCB FBC Ð=Ð=°,90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =,45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2 证明:连接CF 、BE∵CF =BF ,DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ,∠DCF =∠EBF =135°∵∠EBD =∠EBF -∠FBD =135°-45°=90° 在Rt △DBE 中,BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例4.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC V 和ADE V 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE V 均为等腰直角三角形,90ACB DCE Ð=Ð=°,点A ,D ,E 在同一条直线上,CM 为DCE V 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°;2AE AD DE BE CM=+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ≌△CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ≌△CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∵ABC V 和ADE V 是顶角相等的等腰三角形,∴AB AC =,AD AE =,BAC DAE Ð=Ð,∴BAC CAD DAE CAD Ð-Ð=Ð-Ð,∴BAD CAE Ð=Ð.在BAD V 和CAE V 中,AB AC BAD CAE AD AE =ìïÐ=Ðíï=î,∴()BAD CAE SAS ≌△△,∴BD CE =.(2)解:90AEB =°∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE V V ,∴AD BE =,ADC BEC ÐÐ=,∵CDE △是等腰直角三角形,∴45CDE CED Ð=Ð=°,∴180135ADC CDE Ð=°-Ð=°,∴135BEC ADC Ð=Ð=°,∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°.∵CD CE =,CM DE ^,∴DM ME =.∵90DCE Ð=°,∴DM ME CM ==,∴2DE CM =.∴2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ≌△BCE 是解本题的关键.3)15°模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④D AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。
人教版 八年级下册数学 第17章勾股定理 17.1.2勾股定理的实际运用(课件)(共18张PPT)

17.1.2 勾股定理
(勾股定理的实际运用)
知识回顾 :
勾股定理:
如果直角三角形的两条直角边长分别为a,
B b,斜边长为c,那么 a2 b2 c2 .
c a
b
C
A
知识回忆 :
在△ABC中,∠C=90°.
(1)若b=8,c=10,则a= 6
;
(2)若a=5,b=10,则c = ������ ������ ;
B
c a
30°
C
b
A
(5)∵ ∠A=30°, ∴ c =2a
设a =x,则c = 2x ∵������������ + ������������ = ������������ ∴������������ + ������������ = (������������)������ 解得: ������ = ������ ������ ∴ ������ = ������ ������,������ = ������ ������
A
在Rt△ABC中,由勾股定理得:
AC= ������������������ + ������������������= ������������������ + ������������=13cm
答:吸管至少要做 13+4.6=17.6cm.
C
Hale Waihona Puke B练习提高6. 如图,甲船以16海里/时的速度离开码头向东北方向航行,乙船同 时由码头向西北方向航行,已知两船离开码头1.5小时后相距30海里, 问乙船每小时航行多少海里?
30 24
练习提高
7.如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米. (1)这个梯子的顶端距地面有多高? (2)如果梯子的底端B外移了2米,那么梯子的顶端A沿墙下滑了多少米?
专题04 手拉手模型证全等(解析版)

专题04 手拉手模型证全等类型一等边手拉手1.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)线段AN与线段BM交于点O,求∠AOM的度数;(3)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.【答案】(1)AN=BM,见解析;(2)60°;(3)等边三角形,见解析【解析】【分析】(1)证△ACN≌△MCB(SAS),即可得出AN=BM;(2)由全等三角形的性质得∠ANC=∠MBC,则∠AOM=∠CAN+∠MBC=∠CAN+∠ANC =∠BCN=60°;(3)证△ACE≌△MCF(ASA),得CE=CF,即可得出结论.【详解】解:(1)AN=BM,理由如下:∵△ACM、△CBN都是等边三角形,∴AC=CM,CN=CB,∠ACM=∠BCN=60°,∴∠ACM +∠MCN =∠BCN +∠MCN ,∴∠ACN =∠BCM ,在△ACN 和△MCB 中,AC MC ACN MCB CN CB =⎧⎪∠=∠⎨⎪=⎩,∴△ACN ≌△MCB (SAS ),∴AN =BM ;(2)由(1)得:△ACN ≌△MCB ,∴∠ANC =∠MBC ,∴∠AOM =∠CAN +∠MBC =∠CAN +∠ANC =∠BCN =60°;(3)△CEF 是等边三角形,理由如下:∵△ACN ≌△MCB ,∴∠CAE =∠CMF ,∵∠MCF =180°﹣∠ACM ﹣∠BCN =60°,∴∠ACE =∠MCF ,在△ACE 和△MCF 中,CAE CMF AC MCACE MCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACE ≌△MCF (ASA ),∴CE =CF ,∵∠MCF =60°,∴△CEF 是等边三角形.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.2.如图,△ABD 和△BCE 都是等边三角形,∠ABC <105°,AE 与DC 交于点F . (1)求证:AE =DC ;(2)求∠BFE 的度数;(3)若AF =9.17cm ,BF =1.53cm ,CF =7.53cm ,求CD .【答案】(1)见解析;(2)60°;(3)18.23cm【解析】【分析】(1)由等边三角形的性质可知∠DBA=∠EBC=60°,BD=AB,BC=BE.从而可证∠DBC =∠ABE.即可利用“SAS”可证明△DBC≌△ABE,得出结论AE=DC.(2)过点B作BN⊥CD于N,BH⊥AE于H.由△DBC≌△ABE可知∠BEH=∠BCN,∠BDF =∠BAF.再结合等边三角形的性质可求出∠FDA+∠DAF=120°,进而求出∠DF A=180°-120°=60°,即求出∠DFE=180°-60°=120°.即可利用“AAS”证明△BEH≌△BCN,得出结论BH=BN,即得出BF平分∠DFE,即可求出∠BFE=60°.(3)延长BF至Q,使FQ=AF,连接AQ.根据所作辅助线可知∠AFQ=∠BFE=60°,即证明△AFQ是等边三角形,得出结论AF=AQ=BQ,∠F AQ=60°.又可证明∠DAF=∠BAQ.利用“SAS”可证明△DAF≌△BAQ,即得出DF=BQ=BF+FQ=BF+AF,最后即可求出CD=DF+CF=BF+AF+CF=1.53+9.17+7.53=18.23cm.【详解】(1)证明:∵△ABD和△BCE都是等边三角形,∴∠DBA=∠EBC=60°,BD=AB,BC=BE,∴∠DBA+∠ABC=∠EBC+∠ABC,即∠DBC=∠ABE,∵在△DBC和△ABE中,BD ABDBC ABE BC BE=⎧⎪∠=∠⎨⎪=⎩,∴△DBC≌△ABE(SAS),∴AE=DC;(2)解:如图,过点B作BN⊥CD于N,BH⊥AE于H.∵△DBC ≌△ABE ,∴∠BEH =∠BCN ,∠BDF =∠BAF ,∵△ABD 是等边三角形,∴∠BDA +∠BAD =120°,∴∠FDA +∠DAF =120°,∴∠DF A =180°-120°=60°,∴∠DFE =180°-60°=120°,在△BEH 和△BCN 中,90BEH BCN BHE BNC BE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△BEH ≌△BCN (AAS ),∴BH =BN ,∴BF 平分∠DFE ,∴∠BFE =12∠DFE =12×120°=60°;(3)解:如图,延长BF 至Q ,使FQ =AF ,连接AQ .则∠AFQ =∠BFE =60°,∴△AFQ 是等边三角形,∴AF =AQ =BQ ,∠F AQ =60°,∵△ABD 是等边三角形,∴AD =AB ,∠DAB =60°,∴∠DAB +∠BAF =∠BAF +∠F AQ ,即∠DAF =∠BAQ ,在△DAF 和△BAQ 中,AD AB DAF BAQ AF AQ =⎧⎪∠=∠⎨⎪=⎩,∴△DAF ≌△BAQ (SAS ),∴DF =BQ =BF +FQ =BF +AF ,∴CD =DF +CF =BF +AF +CF =1.53+9.17+7.53=18.23cm .【点睛】本题为三角形综合题.考查等边三角形的判定和性质,全等三角形的判定和性质,三角形内角和定理以及角平分线的判定和性质.正确的作出辅助线也是解答本题的关键. 3.如图,点C 为线段BD 上一点,,ABC CDE △△都是等边三角形,AD 与CE 交于点,F BE 与AC 相交于点G .(1)求证:≌ACD BCE ;(2)求证:ACF BCG ≌(3)若8,25CF CG BD +==,求ACD △的面积.【答案】(1)见解析;(2)见解析;(3)【解析】【分析】(1)根据SAS 即可证明△BCE ≌△ACD ;(2)由△ACD ≌△BCE 可得∠CBG =∠CAF ,从而利用ASA 可证明△ACF ≌△BCG ;(3)求出CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,求出GM ,FN ,根据S △ACD =S △ACF +S △CDF =S △BCG +S △CDF 可求出答案.【详解】解:(1)证明:∵△ABC ,△CDE 是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠ACE =∠DCE +∠ACE ,即∠BCE =∠DCA ,∴△ACD ≌△BCE (SAS ).(2)由(1)得△ACD ≌△BCE ,∴∠CBG =∠CAF ,又∵∠ACF =∠BCG =60°,BC =AC ,在△ACF 和△BCG 中,ACF BCG BC ACCAF CBG ∠=∠⎧⎪=⎨⎪∠=⎩, ∴△ACF ≌△BCG (ASA );(3)∵△ACF ≌△BCG ,∴S △ACF =S △BCG ,CG =CF ,而CF +CG =8,∴CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,又∵∠ACB =∠DCE =60°,∴GM=FN= ∴S △ACD =S △ACF +S △CDF=S △BCG +S △CDF =12BC •GM +12CD •FN=12⨯(BC +CD )=【点睛】本题考查了全等三角形的判定和性质以及等边三角形的判定和性质,利用全等三角形的性质得出CG =CF 是解答此题的关键.类型二 等直手拉手4.已知:两个等腰直角三角板△ACB 和△DCE (AC =BC ,DC =CE ,∠ACB =∠DCE =90°)如图所示摆放,连接AE 、BD 交于点O .AE 与DC 交于点M ,BD 与AC 交于点N .(1)如图1(两个等腰直角三角板大小不等),试判断AE 与BD 有何关系并说明理由; (2)如图2(两个等腰直角三角板大小相等,即AC =DC ),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.【答案】(1)AE =BD 且AE ⊥BD .理由见解析;(2)△ACB ≌△DCE ,△EMC ≌△BCN ,△AON ≌△DOM ,△AOB ≌△DOE【解析】【分析】(1)证明△ACE ≌△BCD ,可得AE =BD ,∠CEA =∠BDC ,由∠CME =∠DMO ,根据三角形内角和定理即可得∠DOM =∠ECM =90°,进而可证AE ⊥BD .(2)根据三角形全等的判定找出相等边和角,进而找出全等三角形.【详解】解:(1)结论;AE =BD 且AE ⊥BD .理由如下:∵∠ACB =∠DCE ,∴∠ACB +∠DCA =∠DCE +∠DCA ,即∠DCB =∠ACE ,∵AC =BC ,CD =CE ,在△ACE 与△BCD 中,AC BC ACE DCB CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD (SAS ),∴AE =BD ,∠CEA =∠BDC ,∵∠CME =∠DMO ,∴180()180()CEA CME DMO BDC ︒-∠+∠=︒-∠+∠,即∠DOM =∠ECM =90°,∴AE ⊥BD ,∴AE =BD 且AE ⊥BD ;(2)∵AC =DC ,∴AC =CD =EC =CB ,在△ACB 与△DCE 中,AC DC ACB DCE CB CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACB ≌△DCE (SAS );由(1)可知:∠AEC =∠BDC ,∠EAC =∠DBC ,∴∠DOM =90°,∵∠AEC =∠CAE =∠CBD ,∴△EMC ≌△BCN (ASA ),∴CM =CN ,∴DM =AN ,∴△AON ≌△DOM (AAS ),∵DE =AB ,AO =DO ,∴△AOB ≌△DOE (HL ).【点睛】本题考查了三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键. 5.已知Rt ABC △中,AB AC =,90BAC ∠=︒,点D 为直线BC 上的一动点(点D 不与点B 、C 重合),以AD 为边作Rt ADE △,AD AE =,连接CE .(1)发现问题:如图①,当点D 在边BC 上时,①请写出BD 和CE 之间的数量关系________,位置关系________;②线段CE 、CD 、BC 之间的关系是_________;(2)尝试探究:如图②,当点D 在边BC 的延长线上且其他条件不变时,(1)中CE 、CD 、BC 之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;(3)拓展延伸:如图③,当点D 在边CB 的延长线上且其他条件不变时,若6BC =,1CE =,则线段AD 的长为________.【答案】(1)①BD CE =,BD CE ⊥.②BC CE CD =+.(2)不成立,CE BC CD =+.(3)5【解析】【分析】(1)①根据全等三角形的判定定理证明△BAD ≌△CAE ,根据全等三角形的性质证明; ②根据全等三角形的对应边相等证明即可;(2)证明△BAD ≌△CAE ,根据全等三角形的性质解答即可;(3)根据△BAD ≌△CAE 得到BD =CE =1,再证明△DCE 是直角三角形,利用勾股定理求出DE ,即可求出AD 的长度;【详解】(1)①解:结论:BD =CE ,BD ⊥CE ,理由:∵∠ABC =∠ACB =45°,∠ADE =∠AED =45°,∴∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∠ACE =∠B =45°,∴∠BCE =90°,即BD ⊥CE ,故答案为:BD =CE ;BD ⊥CE ;②证明:∵BD =CE ,∴BC =BD +CD =CE +CD ;故答案为:BC CE CD =+.(2)解:(1)中BC 、CE 、CD 之间存在的数量关系不成立,新的数量关系是CE =BC +CD , 理由:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∴CE =BC +CD ;(3)解:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE =1,∠ABD =∠ACE =135°,∵∠ACB =45°,∴∠DCE =90°,在Rt △DCE 中,CD =BD +BC =7,CE =1,∴DE=∴52AD ==; 故答案为:5.【点睛】本题考查三角形综合题,等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.6.在△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点.(1)如图1,E 、F 分别是AB 、AC 上的点,且BE =AF 、求证:△DEF 是等腰直角三角形经过分析已知条件AB =AC ,D 为BC 的中点.容易联想等腰三角形三线合一的性质,因此,连结AD (如图2),以下是某同学由己知条件开始,逐步按层次推出结论的流程图.请帮助该同学补充完整流程图.补全流程图:①___≅____,②∠EDF =___(2)如果E 、F 分别为AB 、CA 延长线上的点,仍有BE =AF ,其他条件不变,试猜想△DEF是否仍为等腰直角三角形?请在备用图中补全图形、先作出判断,然后给予证明.【答案】(1)△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由见解析【解析】【分析】(1)连接AD ,根据∠BAC =90°,AB =AC ,D 为BC 的中点,可以得到∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===,从而可以证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,由∠ADE +∠BDE =∠BDA =90°,可得∠ADE +∠ADF =90°,即∠EDF =90°,即可证明;(2)连接AD ,同样证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,再由∠ADF +∠BDF =∠BDA =90°,即可得到∠BDE +∠BDF =90°,即∠EDF =90°,即可证明.【详解】解:(1)如图所示,连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠B =∠BAD =∠CAD ,在△BDE 和△ADF 中,BD AD B DAF BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴DE =DF ,∠BDE =∠ADF ,∵∠ADE +∠BDE =∠BDA =90°,∴∠ADE +∠ADF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形;故答案为:△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由如下:连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠ABC =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠F AD =180°-∠CAD =135°,∠EBD =180°-∠ABC =135°,∴∠F AD =∠EBD ,在△BDE 和△ADF 中,BD AD EBD FAD BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴∴DE =DF ,∠BDE =∠ADF ,∵∠ADF +∠BDF =∠BDA =90°,∴∠BDE +∠BDF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形.【点睛】本题主要考查了全等三角形的性质与判定,等腰直角三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.7.(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE 之间的数量关系__________;(2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)【答案】(1)90°,AD =BE ;(2)AD =BE ,AD ⊥BE ;(3)α【解析】【分析】(1)由已知条件可得AC BC =,CD CE =,进而根据∠ACB −∠DCB =∠DCE −∠DCB ,可得∠ACD =∠BCE ,证明△ACD ≌△BCE (SAS ),即可求得AD =BE ;∠BEC =∠CDA =135°;(2)延长AD 交BE 于点F ,同理可得△ACD ≌△BCE ,设∠F AB =α,则∠CAD =∠CBE =45°-α,根据∠ABE =45°+45°-α=90°-α,进而根据∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°,即可求解;(3)延长BE 交AD 于点G ,方法同(2)证明△ACD ≌△BCE ,进而根据三角形的内角和定理即可求得直线AD 和BE 的夹角.【详解】(1)∵ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,∴AC BC =,CD CE =,∠CDE =45°∴∠CDA =135°∵∠ACB −∠DCB =∠DCE −∠DCB ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠BEC =∠ADC =135°,AD =BE∴∠AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ⊥BE ,理由如下,同理可得△ACD ≌△BCE ,则AD =BE ,延长AD 交BE 于点F ,设∠F AB =α,则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE(3)如图,延长BE 交AD 于点G ,∵ACB △和DCE 均为等腰三角形,∴AC BC =,CD CE =,∵∠ACB =∠DCE =α,∵∠ACB +∠ACE =∠DCE +∠ACE ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD∵ACB DCE α∠=∠=∴∠CBA =∠CAB =()11180=9022αα︒-︒- ∴∠GAB +∠GBA =()()CAD CAB ABC CBE ∠+∠+∠-∠,ABC CAB =∠+∠180α=︒-,∴∠AGB =180°-(∠GAB +∠GBA )α= ,即直线AD 和BE 的夹角为α.故答案为:α.【点睛】本题考查了等腰三角形的性质,三角形内角和定理,全等三角形的性质与判定,掌握旋转模型证明三角形全等是解题的关键.8.已知:等腰Rt ABC 和等腰Rt ADE △中,AB AC =,AE AD =,90BAC EAD ∠=∠=︒.(1)如图1,延长DE 交BC 于点F ,若68BAE ∠=︒,则DFC ∠的度数为;(2)如图2,连接EC 、BD ,延长EA 交BD 于点M ,若90AEC ∠=︒,求证:点M 为BD 中点;(3)如图3,连接EC 、BD ,点G 是CE 的中点,连接AG ,交BD 于点H ,9AG =,5HG =,直接写出AEC △的面积.【答案】(1)68︒;(2)见解析;(3)36【解析】【分析】(1)由已知条件可得45D C ∠=∠=︒,对顶角AQD CQF ∠=∠,则DAC DFC ∠=∠,根据DAE CAB ∠=∠即可的DFC BAE ∠=∠;(2)过点B 作ME 的垂线交EM 的延长线于N ,证明AEC BNA △≌△,得AE BN =,进而可得AD NB =,再证明DAM BNM △≌△即可得证点M 为BD 中点;(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,先证明ABE ACD △≌△,进而证明AEG KCG △≌△,根据角度的计算以及三角形内角和定理求得BAD KCA ∠=∠,进而证明ABD CAK △≌△,再根据,90CAG ABD BAC ∠=∠∠=︒,证明AH BD ⊥,根据已知条件求得ABD S最后证明AEC ABD S S =即可.【详解】 (1)设DF 交AC 于Q ,如图1,ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △AQD CQF ∠=∠180,180DAQ D AQD QFC C CQF ∠=-∠-∠∠=-∠-∠DAQ QFC ∴∠=∠90BAC EAD ∠=∠=︒即BAE EAQ EAQ QAD ∠+∠=∠+∠BAE QAD ∴∠=∠DFC BAE ∴∠=∠68BAE ∠=︒68DFC ∴∠=︒故答案为68︒(2)如图2,过点B 作ME 的垂线交EM 的延长线于N ,90N ∴∠=︒90AEC =︒∠N AEC ∴∠=∠90BAC ∠=︒90EAC NAB ∴∠+∠=︒90NAC ACE ∠+∠=︒NAB ECA ∴∠=∠ ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AD AE ∴== 又AC AB =∴AEC BNA △≌△NB AE ∴=AE AD =AD NB ∴=90DAE ∠=︒DAM N ∴∠=∠又DMA BMN ∠=∠DAM BNM ∴△≌△DM BM ∴=即M 是BD 的中点(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,如图90BAC EAD ∠=∠=︒即BAE EAC EAC CAD ∠+∠=∠+∠BAE CAD ∴∠=∠ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AE AD ∴==在ABE △与ACD △中,AE AD BAE CAD AB AC =⎧⎪∠=∠⎨⎪=⎩∴ABE △≌ACD △(SAS )ABE ABD S S ∴=△△,BE CD = G 点是EC 的中点EG GC ∴=AGE KGC ∠=∠,AG GK =AGE KGC ∴△≌△(SAS )∴,AE CK AEG KCG =∠=∠,AE KC AD ∴==ACK ACB BCE KCG ∠=∠+∠+∠45AEC BCE =︒+∠+∠45ABC BAP =︒+∠+∠90BAE =︒+∠BAD =∠AKC ABD ∴△≌△(SAS )18BD AK ∴==,CAK ABD ∠=∠90BAG CAG ∠+∠=︒90ABD BAG ∴∠+∠=︒即90AHB ∠=︒9AG =,5HG =954AH AG HG ∴=-=-=111843622ABD S BD AH ∴=⋅=⨯⨯=△ 36AEC AEG AGC GCK AGC ACK ABD S S S S S S S =+=+===△△△△△△△∴AEC S 36=【点睛】本题考查了三角形全等的性质与判定,等腰直角三角形的性质,三角形内角和定理,三角形外角性质,构造辅助线是解题的关键.类型三 等腰手拉手9.已知:如图,在△ABC 中,AB =AC ,在△ADE 中,AD =AE ,且∠BAC =∠DAE ,连接BD ,CE 交于点F ,连接AF .(1)求证:△ABD ≌△ACE ;(2)求证:F A 平分∠BFE .【答案】(1)见解析(2)见解析【解析】【分析】(1)根据SAS 证明结论即可;(2)作AM ⊥BD 于M ,作AN ⊥CE 于N .由(1)可得BD =CE ,S △BAD =S △CAE ,然后根据角平分线的性质即可解决问题.(1)证明:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS );(2)证明:如图,作AM ⊥BD 于M ,作AN ⊥CE 于N .由△BAD ≌△CAE ,∴BD =CE ,S △BAD =S △CAE , ∵1122BD AM CE AN ⋅⋅=⋅⋅, ∴AM =AN ,∴点A 在∠BFE 平分线上,∴F A 平分∠BFE .【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.10.如图,在等腰△ABC 与等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE =α,连接BD 和CE 相交于点P ,交AC 于点M ,交AD 于点N .(1)求证:BD=CE.(2)求证:AP平分∠BPE.(3)若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.【答案】(1)见解析(2)见解析(3)PE=AP+PD,见解析【解析】【分析】(1)由“SAS”可证△BAD≌△CAE,可得BD=CE;(2)由全等三角形的性质可得S△BAD=S△CAE,由三角形面积公式可得AH=AF,由角平分线的性质可得AP平分∠BPE;(3)由全等三角形的性质可得∠BDA=∠CEA,由“SAS”可证△AOE≌△APD,可得AO=AP,可证△APO是等边三角形,可得AP=PO,可得PE=AP+PD,即可求解.(1)证明:∵∠BAC=∠DAE=α,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)证明:如图,过点A作AH⊥BD,AF⊥CE,∵△BAD≌△CAE,∴S△BAD=S△CAE,BD=CE,∴12BD×AH=12CE×AF,∴AH=AF,又∵AH⊥BD,AF⊥CE,∴AP平分∠BPE;(3)解:PE=AP+PD,理由如下:如图,在线段PE上截取OE=PD,连接AO,∵△BAD≌△CAE,∴∠BDA=∠CEA,又∵OE=PD,AE=AD,∴△AOE≌△APD(SAS),∴AP=AO,∵∠BDA=∠CEA,∠PND=∠ANE,∴∠NPD=∠DAE=α=60°,∴∠BPE=180°-∠NPD=180°-60°=120°,又∵AP平分∠BPE,∴∠APO=60°,又∵AP=AO,∴△APO是等边三角形,∴AP =PO ,∵PE =PO +OE ,∴PE =AP +PD .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的判定和性质以及角之间的关系,证明△BAD ≌△CAE 是解本题的关键.11.如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,连接BD ,CE ,BD 与CE 交于点O ,BD 与AC 交于点F .(1)求证:BD =CE .(2)若∠BAC =48°,求∠COD 的度数.(3)若G 为CE 上一点,GE =OD ,AG =OC ,且AG ∥BD ,求证:BD ⊥AC .【答案】(1)见解析;(2)132°;(3)见解析【解析】【分析】(1)根据∠BAC =∠DAE ,推出∠BAD =∠CAE ,从而结合“SAS ”证明△BAD ≌△CAE ,即可得出结论;(2)根据外角定理推出∠COD =∠OBC +∠BCA +∠ACE ,结合全等三角形的性质推出∠COD =∠ABC +∠BCA ,最后在△ABC 中利用内角和定理求解即可;(3)连接AO ,根据题意确定△ADO ≌△AEG ,得到∠OAD =∠GAE ,AO =AG ,再结合题干条件推出△AOC 为等腰三角形,以及∠BOA =∠BOC ,从而根据“三线合一”证明即可.【详解】(1)证:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即:∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE (SAS ),∴BD =CE ;(2)解:∵∠COD =∠OBC +∠BCO ,∠BCO =∠BCA +∠ACE ,∴∠COD =∠OBC +∠BCA +∠ACE ,∵△BAD ≌△CAE ,∴∠ABD =∠ACE ,∴∠COD =∠OBC +∠BCA +∠ABD =∠ABC +∠BCA ,∵∠BAC =48°,∴∠ABC +∠BCA =180°-48°=132°,∴∠COD =132°;(3)证:如图所示,连接AO ,∵△BAD ≌△CAE ,∴∠ADO =∠AEG ,在△ADO 和△AEG 中,E A ADO A G E E D G D A O =⎧⎪⎨⎪∠==⎩∠ ∴△ADO ≌△AEG (SAS ),∴∠OAD =∠GAE ,AO =AG ,∴∠AOG =∠AGO ,∴∠OAD +∠DAG =∠GAE +∠DAG ,即:∠OAG =∠DAE ,∵∠DAE =∠BAC ,∴∠BAC =∠OAG ,在△ABF 和△COF 中,∠BAC =180°-∠ABD -∠AFB ,∠BOC =180°-∠ACE -∠CFO , 由(2)知∠ABD =∠ACE ,∵∠AFB =∠CFO ,∴∠BAC =∠BOC ,∴∠BOC =∠OAG ,∵AG ∥BD ,∴∠BOA =∠OAG ,∴∠BOA =∠BOC ,∵AO =AG ,AG =CO ,∴AO =CO ,即:△AOC为等腰三角形,∵∠BOA=∠BOC,∴OF⊥AC,∴BD⊥AC.【点睛】本题考查全等三角形的判定与性质,等腰三角形的判定与性质等,掌握全等三角形的判定与性质,熟悉“手拉手”模型的证明是解题关键.类型四手拉手综合12.现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA 所在直线上.以MN为边作如图所示的等边△MNP.(1)如图1,当M在线段OA上时,证明:AM﹣AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.【答案】(1)见解析;(2)AM+AN=AP,理由见解析【解析】【分析】(1)在AB上取点C,使得AC=AM,则△ACM为等边三角形,结合“手拉手”模型证明△CMN≌△AMP,得到CN=AP,即可得证;(2)在射线AO上取点D,使得AN=AD,仿照(1)的过程证明△DNM≌△ANP,即可得到AP=DM,从而得出结论.【详解】证:(1)由题意可知,∠BAO =60°,如图所示,在AB 上取点C ,使得AC =AM ,则△ACM 为等边三角形,MC =MA ,∠CMA =60°,∵△NMP 为等边三角形,∴MN =MP ,∠NMP =60°,∴∠CMA =∠NMP ,∴∠CMA -∠NMA =∠NMP -∠NMA ,∴∠CMN =∠AMP ,在△CMN 和△AMP 中,M M CMN A P P A N M C M M =⎧⎪⎨⎪∠==⎩∠ ∴△CMN ≌△AMP (SAS ),∴CN =AP ,∴CN +AN =AP +AN =AC ,∵AC =AM ,∴AP +AN =AM ,∴AM -AN =AP ;(2)AM +AN =AP ,理由如下:如图所示,在射线AO 上取点D ,使得AN =AD ,∵∠BAO =60°,∴△AND 为等边三角形,ND =NA ,∠DNA =60°,∵△NMP 为等边三角形,∴NM =NP ,∠MNP =60°,∴∠DNA =∠MNP ,∴∠DNA +∠ANM =∠MNP +∠ANM ,∴∠DNM =∠ANP ,在△DNM 和△ANP 中,N N DNM A P P A M N D N N =⎧⎪⎨⎪∠==⎩∠ ∴△DNM ≌△ANP (SAS ),∴AP =DM ,∵AN =AD ,DA +AM =DM ,∴AN +AM =AP .【点睛】本题考查等边三角形的性质,全等三角形的判定与性质等,掌握双等边三角形中“手拉手”模型是解题关键.13.已知:△ABC 与△BDE 都是等腰三角形.BA =BC ,BD =BE (AB >BD )且有∠ABC =∠DBE .(1)如图1,如果A 、B 、D 在一直线上,且∠ABC =60°,求证:△BMN 是等边三角形; (2)在第(1)问的情况下,直线AE 和CD 的夹角是 °;(3)如图2,若A 、B 、D 不在一直线上,但∠ABC =60°的条件不变则直线AE 和CD 的夹角是 °;(4)如图3,若∠ACB =60°,直线AE 和CD 的夹角是 °.【答案】(1)证明见解析;(2)60;(3)60;(4)60;【解析】【分析】(1)根据题意,得∠ABC =∠DBE =60°,从而得ABE DBC ∠=∠;通过证明ABE CBD ≌,得BAE BCD ∠=∠;通过证明BAM BCN ≌,得BM BN =,根据等边三角形的性质分析,即可完成证明;(2)结合题意,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;结合(1)的结论,根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解;(3)同理,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;通过证明ABE CBD ≌,得BAE BCD ∠=∠;根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解; (4)根据题意,通过证明ABC 为等边三角形,推导得ABE CBD ∠=∠,通过证明ABE CBD ≌,得BAE BCD ∠=∠,结合三角形外角的性质计算,即可得到答案.【详解】(1)∵∠ABC =∠DBE =60°∴18060MBN ABC DBE ∠=︒-∠-∠=︒,ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠ ∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠ BAM 和BCN △中 60BAE BCD AB BC ABC MBN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴BAM BCN ≌∴BM BN =∴BMN △为等边三角形;(2)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒根据题意,AE 和CD 相交于点O∵BAE BCD ∠=∠∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(3)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒∵ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠,∠ABC =∠DBE =60°∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠如图,延长AE ,交CD 于点O∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(4)∵BA =BC ,∴ACB CAB ∠=∠∵∠ACB =60°∴60ACB CAB ∠=∠=︒∴ABC 为等边三角形∵BD =BE ,∠ABC =∠DBE∴60DBE ∠=︒∵ABE ABC CBE ∠=∠-∠,CBD DBE CBE ∠=∠-∠∴ABE CBD ∠=∠ABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠分别延长CD 、AE ,相较于点O ,如下图:∴AOF OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOF BAC BCA ∠=∠+∠=︒∴18060AOC AOF ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60.【点睛】本题考查了等腰三角形、等边三角形、全等三角形、补角、三角形外角的知识;解题的关键是熟练掌握等边三角形、全等三角形、三角形外角的性质,从而完成求解.14.在ABC 中,AB =AC ,点D 是直线BC 上一点(不与B ,C 重合),以AD 为一边在AD 的右侧作ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE .(1)(请直接写出你的结论)如图1,当点D 在线段BC 上:①如果∠BAC =90°,则∠BCE =°;②如果∠BAC =100°,则∠BCE =°;(2)设∠BAC =α,∠BCE =β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.【答案】(1)①90;②80;(2)①α+β=180°,理由见解析;②图见解析,α+β=180°或α=β【解析】【分析】、(1)①由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD≌△CAE,可得∠ABC=∠ACE=45°,可求∠BCE的度数;②由等腰三角形的性质求出∠ABD=∠ACB=40°,由“SAS”可证△ABD≌△ACE得出∠ABD =∠ACE=40°,则可得出结论;(2)①由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论;②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论.【详解】解:(1)①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;②∵∠BAC=100°,AB=AC,∴∠ABD=∠ACB=40°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=40°,∴∠BCE =∠ACE +∠ACB =40°+40°=80°,故答案为:80.(2)①α+β=180°,理由:∵∠BAC =∠DAE ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC .即∠BAD =∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B =∠ACE .∴∠B +∠ACB =∠ACE +∠ACB .∵∠ACE +∠ACB =β,∴∠B +∠ACB =β,∵α+∠B +∠ACB =180°,∴α+β=180°.②如图1:当点D 在射线BC 上时,α+β=180°,连接CE ,∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,在△ABC 中,∠BAC +∠B +∠ACB =180°,∴∠BAC +∠ACE +∠ACB =∠BAC +∠BCE =180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.【点睛】本题主要考查全等三角形的判定及性质,等腰三角形的性质和三角形内角和定理,掌握全等三角形的判定方法及性质是关键.15.小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;(2)拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由.【答案】(1)见解析;(2)60°,BE=AD;(3)∠AEB=90°,AE=BE+2CM,理由见解析【解析】【分析】(1)先判断出∠BAD=∠CAE,进而利用SAS判断出△BAD≌△CAE,即可得出结论;(2)同(1)的方法判断出△BAD≌△CAE,得出AD=BE,∠ADC=∠BEC,最后用角的差,即可得出结论;(3)同(2)的方法,即可得出结论.【详解】解:(1)∵△ABC和△ADE均是顶角为40°的等腰三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)∵△ABC和△ADE均是等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=∠CDE=∠CED=60°,∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵∠CDE=60°,∴∠BEC=∠ADC=180°﹣∠CDE=120°,∵∠CED=60°,∴∠AEB=∠BEC﹣∠CED=60°,故答案为:60°,BE=AD;(3)AE=BE+2CM,理由:同(1)(2)的方法得,△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵△CDE是等腰直角三角形,∴∠CDE=∠CED=45°,∴∠ADC=180°﹣∠CDE=45°,∴∠BEC=∠ADC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM=ME=CM.∴AE=AD+DE=BE+2CM.。
初中数学“手拉手”模型——共顶点的等腰三角形压轴题三种题型及答案

模型构建专题:“手拉手”模型【考点导航】目录【典型例题】【类型一共顶点的等边三角形】【类型二共顶点的等腰直角三角形】【类型三共顶点的一般等腰三角形】【典型例题】【类型一共顶点的等边三角形】1(2023·全国·八年级假期作业)如图所示,△ABC和△ADE都是等边三角形,且点B、A、E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.(1)求证:BD=CE;(2)求证:△ABM≌△ACN;(3)求证:△AMN是等边三角形.【变式训练】1(2023春·山西运城·八年级统考期中)如图,点C为线段AB上一点,△DAC、△ECB都是等边三角形,AE、DC交于点M,DB、EC交于点N,DB、AE交于点P,连接MN,下列说法正确的个数有个.①MN∥AB;②∠DPM=60°;③∠DAP=∠PEC;④△ACM≌△DCN;⑤若∠DBE=30°,则∠AEB=90°.2(2023秋·四川凉山·八年级统考期末)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.求证:(1)AD=BE;(2)△CPQ为等边三角形;3(2021春·广东佛山·八年级校考阶段练习)已知图1是边长分别为a和b a>b的两个等边三角形纸片ABC和三角形C DE叠放在一起(C与C 重合)的图形.(1)将△C DE绕点C按顺时针方向旋转30°,连接AD,BE.如图2:在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;(2)若将上图中的△C DE,绕点C按顺时针方向任意旋转一个角度α,连接AD、BE,如图3:在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论:(3)根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大,最大是多少?当α为多少度时,线段AD的长度最小,最小是多少?请直接写出答案.4(2023春·广东梅州·七年级校考期末)【初步感知】(1)如图1,已知ΔABC为等边三角形,点D为边BC上一动点(点D不与点B,点C重合).以AD为边向右侧作等边ΔADE,连接CE.求证:ΔABD≌ΔACE;【类比探究】(2)如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为:;②线段EC、AC、CD之间的数量关系为:;【拓展应用】(3)如图3,在等边ΔABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP为边向右侧作等边ΔDPE,连接CE、BE.请问:PE+BE是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.【类型二共顶点的等腰直角三角形】1(2023春·湖北黄冈·八年级统考期中)如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE= 90°.(1)【猜想】:如图1,点E在BC上,点D在AC上,线段BE与AD的数量关系是,位置关系是.(2)【探究】:把△DCE绕点C旋转到如图2的位置,连接AD,BE,(1)中的结论还成立吗?说明理由;(3)【拓展】:把△DCE绕点C在平面内自由旋转,若AC=5,CE=22,当A,E,D三点在同一直线上时,则AE的长是.【变式训练】1(2023·全国·九年级专题练习)如图,在等腰直角三角形ABC和DEC中,∠BCA=∠DCE=90°,点E在边AB上,ED与AC交于点F,连接AD.(1)求证:△BCE≌△ACD;(2)求证:AB⊥AD.2(2023春·八年级课时练习)(1)问题发现:如图1,△ABC与△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,则线段AE、BD的数量关系为,AE、BD所在直线的位置关系为;(2)深入探究:在(1)的条件下,若点A,E,D在同一直线上,CM为△DCE中DE边上的高,请判断∠ADB的度数及线段CM,AD,BD之间的数量关系,并说明理由.3(2023·山东枣庄·统考二模)感知:如图①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE =90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE,不需证明.(1)探究:如图②,将△ADE绕点A逆时针旋转α(0<α<90°),连接BD和CE,此时BD=CE是否依然成立?若成立,写出证明过程;若不成立,说明理由.(2)应用:如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上,连接CE.求:①∠ACE的度数;②若AB=AC=32,CD=3,则线段DE的长是多少?【类型三共顶点的一般等腰三角形】1(2023春·山东泰安·七年级校考开学考试)如图,△ABC与△CDE都是等腰三角形,AC=BC,CD= CE,∠ACB=∠DCE=42°,AD、BE相交于点M.(1)试说明:AD=BE;(2)求∠AMB的度数.【变式训练】1(2023秋·辽宁抚顺·八年级统考期末)如图,已知△ABC中,AB≠AC≠BC.分别以AB、AC为腰在AB左侧、AC右侧作等腰三角形ABD.等腰三角形ACE,连接CD、BE.(1)如图1,当∠BAD=∠CAE=60°时,①△ABD、△ACE的形状是;②求证:BE=DC.(2)若∠BAD=∠CAE≠60°,①如图2,当AB=AD,AC=AE时,BE=DC是否仍然成立?请写出你的结论并说明理由;②如图3,当AB=DB,AC=EC时,BE=DC是否仍然成立?请写出你的结论并说明理由.2(2023秋·全国·八年级专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,△ABC和△CDE为“同源三角形”,AC=BC,CD=CE,∠ACB 与∠DCE为“同源角”.(1)如图1,△ABC和△CDE为“同源三角形”,试判断AD与BE的数量关系,并说明理由.(2)如图2,若“同源三角形”△ABC和△CDE上的点B,C,D在同一条直线上,且∠ACE=90°,则∠EMD =°.(3)如图3,△ABC和△CDE为“同源三角形”,且“同源角”的度数为90°时,分别取AD,BE的中点Q,P,连接CP,CQ,PQ,试说明△PCQ是等腰直角三角形.3(2023春·辽宁丹东·七年级统考期末)(1)如图1,两个等腰三角形△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE.则△ADB≌,此时线段BD和线段CE的数量关系式;(2)如图2,两个等腰直角三角形△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和线段CE的关系,并说明理由;(3)如图3,分别以△ABC的两边AB,AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,两线交于点P.请直接写出线段BE和线段CD的数量关系及∠PBC+∠PCB的度数.模型构建专题:“手拉手”模型【考点导航】目录【典型例题】【类型一共顶点的等边三角形】【类型二共顶点的等腰直角三角形】【类型三共顶点的一般等腰三角形】【典型例题】【类型一共顶点的等边三角形】1(2023·全国·八年级假期作业)如图所示,△ABC和△ADE都是等边三角形,且点B、A、E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.(1)求证:BD=CE;(2)求证:△ABM≌△ACN;(3)求证:△AMN是等边三角形.【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】(1)由已知条件等边三角形,可知AB=AC,AD=AE,∠BAC=∠DAE,进一步求证∠BAD=∠CAE,从而△ABD≌△ACE(SAS),所以BD=CE.(2)由(1)知△ABD≌△ACE,得∠ABM=∠CAN,由点B、A、E共线,得∠CAN=60°=∠BAC,进一步求证△ABM≌△ACN(ASA).(3)由△ABM≌△ACN,得AM=AN,而∠CAN=60°,所以△AMN是等边三角形.【详解】(1)∵△ABC和△ADE都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE.在△ABD和△ACE中,AB=AC∠BAD=∠CAE AD=AE∴△ABD≌△ACE(SAS),∴BD=CE.(2)由(1)知△ABD≌△ACE,∴∠ABM=∠ACN.∵点B、A、E在同一直线上,且∠BAC=∠DAE=60°,∴∠CAN=60°=∠BAC.在△ABM和△ACN中,∠BAM=∠CAN AB=AC∠ABM=∠ACN∴△ABM≌△ACN(ASA).(3)由(2)知△ABM≌△ACN,∴AM=AN,∵∠CAN=60°,∴△AMN是等边三角形.【点睛】本题主要考查等边三角形的性质和判定、全等三角形判定和性质;将等边三角形的条件转化为相等线段和等角,选择合适的方法判定三角形全等是解题的关键.【变式训练】1(2023春·山西运城·八年级统考期中)如图,点C为线段AB上一点,△DAC、△ECB都是等边三角形,AE、DC交于点M,DB、EC交于点N,DB、AE交于点P,连接MN,下列说法正确的个数有个.①MN∥AB;②∠DPM=60°;③∠DAP=∠PEC;④△ACM≌△DCN;⑤若∠DBE=30°,则∠AEB=90°.【答案】①②③④⑤【分析】根据等边三角形的性质得到AC=CD,BC=CE,∠ACD=∠BCE=60°,得到∠ACE=∠BCE,∠DCE=60°,根据平行线的判定定理得到AD∥CE,根据平行线的性质得到∠DAP=∠PEC,故③正确;根据全等三角形的性质得到∠CAE=∠CDB,根据三角形的内角和得到∠DPM=∠ACM=60°,故②正确,推出△ACM≌△DCN,故④正确;根据全等三角形的性质得到CM=CN,得到△CMN是等边三角形,求得∠CMN=60°,根据平行线的判定定理得到MN∥AB,故①正确;根据三角形的内角和得到∠AEB= 90°.故⑤正确.【详解】解:∵△DAC 、△ECB 都是等边三角形,∴AC =CD ,BC =CE ,∠ACD =∠BCE =60°,∴∠ADC =∠DCE =60°,∴∠ACE =∠BCD ,∠DCE =60°,∴AD ∥CE ,∴∠DAP =∠PEC ,故③正确;在△ACE 与△BCD 中,AC =CD∠ACE =∠BCD CE =CB,∴△ACE ≌△BCD SAS ,∴∠CAE =∠CDB ,∵∠PMD =∠AMC ,∴∠DPM =∠ACM =60°,故②正确,在△ACM 与△DCN 中,∠CAM =∠CDNAC =CD ∠ACM =∠DCN =60°,∴△ACM ≌△DCN ,故④正确;∴CM =CN ,∴△CMN 是等边三角形,∴∠CMN =60°,∴∠CMN =∠ACD ,∴MN ∥AB ,故①正确;∵∠DBE =30°,∠BPE =∠APD =60°,∴∠AEB =90°.故⑤正确;故答案为:①②③④⑤.【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的判定,熟练掌握全等三角形的判定和性质是解题的关键.2(2023秋·四川凉山·八年级统考期末)如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边△ABC 和等边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ.求证:(1)AD =BE ;(2)△CPQ 为等边三角形;【答案】(1)见解析;(2)见解析.【分析】(1)由等边三角形的性质可知AC =BC ,CD =CE ,∠ACB =∠DCE =60°,从而可求出∠ACD =∠BCE ,即可利用“SAS ”证明△ADC ≌△BEC ,即得出AD =BE ;(2)由等边三角形的性质可知∠ACB =∠DCE =60°,AC =BC ,即可求证∠ACP =∠BCQ =60°.再根据△ADC ≌△BEC 可得出∠CAP =∠CBQ ,利用“ASA ”证明△APC ≌△BQC ,据此即可证明结论成立.【详解】(1)证明:∵△ABC 和△CDE 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∵∠ACD =∠ACB +∠BCD ,∠BCE =∠DCE +∠BCD ,∴∠ACD =∠BCE ,∴AC =BC∠ACD =∠BCE CD =CE,∴△ADC ≌△BEC (SAS ),∴AD =BE ;(2)证明:∵△ABC 和△CDE 是等边三角形,∴∠ACB =∠DCE =60°,AC =BC ,∴∠BCQ =180°-∠ACP -∠ECD =60°,∴∠ACP =∠BCQ =60°.∵△ADC ≌△BEC∴∠CAP =∠CBQ .∴∠CAP =∠CBQAC =BC∠ACP =∠BCQ∴△APC ≌△BQC ASA .∴CP =CQ ,又∵∠PCQ =60°,∴△CPQ 为等边三角形.【点睛】本题考查等边三角形的性质,全等三角形的判定和性质.熟练掌握全等三角形的判定条件是解题关键.3(2021春·广东佛山·八年级校考阶段练习)已知图1是边长分别为a 和b a >b 的两个等边三角形纸片ABC 和三角形C DE 叠放在一起(C 与C 重合)的图形.(1)将△C DE 绕点C 按顺时针方向旋转30°,连接AD ,BE .如图2:在图2中,线段BE 与AD 之间具有怎样的大小关系?证明你的结论;(2)若将上图中的△C DE ,绕点C 按顺时针方向任意旋转一个角度α,连接AD 、BE ,如图3:在图3中,线段BE 与AD 之间具有怎样的大小关系?证明你的结论:(3)根据上面的操作过程,请你猜想当α为多少度时,线段AD 的长度最大,最大是多少?当α为多少度时,线段AD 的长度最小,最小是多少?请直接写出答案.【答案】(1)BE =AD ,证明见解析(2)BE =AD ,证明见解析(3)当α为180度时,线段AD 的长度最大,最大值为a +b ;当α为0度或360度时,线段AD 的长度最小,最小值为a -b .【分析】(1)先由等边三角形判断出AC =BC ,CE =CD ,再由旋转判断出∠BCE =∠ACD ,进而判断出△BCE ≌△ACD ,即可得出结论;(2)同(1)的方法,即可得出结论;(3)当点D 在AC 的延长线上时,AD 最大,最大值为a +b ,当点D 在线段AC 上时,AD 最小,最小值为a -b ,即可得出结论.【详解】(1)解:BE =AD证明:∵点C 与C 1重合,△ABC 和△C 1DE ,∴△ABC 和△CDE 都是等边三角形,∴AC =BC ,CE =CD ,由旋转知,∠BCE =∠ACD =30°,在△BCE 和△ACD 中,BC =AC∠BCE =∠ACD CE =CD,∴△BCE ≌△ACD (SAS ),∴BE =AD ,(2)解:BE =AD ,证明:∵△ABC 和△CDE 都是等边三角形,∴AC =BC ,CE =CD ,由旋转知,∠BCE =∠ACD ,在△BCE 和△ACD 中,BC =AC∠BCE =∠ACD CE =CD,∴△BCE ≌△ACD (SAS ),∴BE =AD ;(3)解:当点D 在AC 的延长线上时,AD 最大,最大值为AC +CD =a +b ,如图,∴当α为180度时,线段AD 的长度最大,最大值为a +b ,当点D 在线段AC 上时,AD 最小,最小值为AC -CD =a -b ,如图,∴当α为0度或360度时,线段AD的长度最小,最小值为a-b.【点睛】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,判断出△BCE≌△ACD是解本题的关键.4(2023春·广东梅州·七年级校考期末)【初步感知】(1)如图1,已知ΔABC为等边三角形,点D为边BC上一动点(点D不与点B,点C重合).以AD为边向右侧作等边ΔADE,连接CE.求证:ΔABD≌ΔACE;【类比探究】(2)如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为:;②线段EC、AC、CD之间的数量关系为:;【拓展应用】(3)如图3,在等边ΔABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP 为边向右侧作等边ΔDPE,连接CE、BE.请问:PE+BE是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.【答案】(1)见解析(2)平行EC=AC+CD(3)有最小值,5【分析】(1)由ΔABC和ΔADE是等边三角形,推出AB=AC,AD=AE,∠BAC=∠DAE=60°,又因为∠BAC=∠DAE,则∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,从而利用“SAS”证明ΔABD≌ΔACE;(2)①由(1)得ΔABD≌ΔACE(SAS),得出∠B=∠ACE=60°,CE=BD,∠BAC=∠ACE,则AB∥CE;②因为CE=BD,AC=BC,所以CE=BD=BC+CD=AC+CD;(3)在BC上取一点M,使得DM=PC,连接EM,可证ΔEPC≌ΔEDM(SAS),EC=EM,求得∠CEM= 60°,得出ΔCEM是等边三角形,则∠ECD=60°,即点E在∠ACD角平分线上运动,在射线CD上截取CP =CP,当点E与点C重合时,BE+PE=BE+P E≥BP =5,进而解答此题.【详解】(1)证明:∵ΔABC和ΔADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE在ΔABD和ΔACE中,AB=AC∠BAD=∠CAE AD=AE,∴ΔABD≌ΔACE(SAS);(2)平行,EC=AC+CD,理由如下:由(1)得ΔABD≌ΔACE(SAS),∴∠B=∠ACE=60°,CE=BD,∴∠BAC=∠ACE,∴AB∥CE,∵CE=BD,AC=BC,∴CE=BD=BC+CD=AC+CD;(3)有最小值,理由如下:如图,在射线BC上取一点M,使得DM=PC,连接EM,∵ΔABC和ΔDPE是等边三角形,∴PE=ED,∠DEP=∠ACB=60°,∴∠ACD=180°-∠ACB=180°-60°=120°,∴∠ACD+∠DEP=120°+60°=180°,由三角形内角和为180°,可知:∠PCE+∠CEP+∠EPC=180°,∠ECD+∠CDE+∠CED=180°,∴∠PCE+∠CEP+∠EPC+∠ECD+∠CDE+∠CED=360°,又∵∠PCE+∠ECD+∠CEP+∠CED=∠ACD+∠DEP=180°,∴∠EPC+∠CDE=360°-180°=180°,∵∠EDM+∠CDE=180°,∴∠EPC=∠EDM,在ΔEPC和ΔEDM中,PE=ED∠EPC=∠EDM PC=DM,ΔEPC≌ΔEDM(SAS),∴EC=EM,∠PEC=∠DEM,∵∠PEC+∠CED=∠DEP=60°,∴∠CEM=∠DEM+∠CED=60°,∴ΔCEM是等边三角形,∴∠ECD=60°,∠ACE=180°-∠ECD-∠ACB=180°-60°-60°=60°,即点E在∠ACD的角平分线上运动,在射线CD上截取CP =CP,连接EP ,在ΔCEP和ΔCEP 中,PC=P C∠PCE=∠P CE=60°CE=CE,ΔCEP≌ΔCEP (SAS),∴PE=P E,由三角形三边关系可知,BE+P E≥BP ,即当点E与点C重合,BE+P E=BP 时,PE+BE有最小值BP ,∵BP =BE+CP =BC+CP=3+2=5,∴BE+PE=BE+P E≥BP =5,∴BE+PE最小值为5.【点睛】本题考查三角形综合,全等三角形的判定,正确添加辅助线、掌握相关图形的性质定理是解题的关键.【类型二共顶点的等腰直角三角形】90°.(1)【猜想】:如图1,点E在BC上,点D在AC上,线段BE与AD的数量关系是,位置关系是.(2)【探究】:把△DCE绕点C旋转到如图2的位置,连接AD,BE,(1)中的结论还成立吗?说明理由;(3)【拓展】:把△DCE绕点C在平面内自由旋转,若AC=5,CE=22,当A,E,D三点在同一直线上时,则AE的长是.【答案】(1)BE=AD,BE⊥AD(2)成立,理由见解析(3)21+2或21-2【分析】(1)利用等腰直角三角形的性质得出AC=BC,EC=DC,再作差,得出BE=AD,再用∠ACB= 90°,即可得出结论;(2)先由旋转的旋转得出∠BCE=∠ACD,进而判断出△BCE≌△ACD SAS,得出BE=AD,∠CAD=∠CBE,AC与BE交于M,AD与BE交于N,利用全等的性质和对顶角相等进而得出∠MAN+∠AMN=90°,即可得出结论;(3)分两种情况,①当点E在线段AD上时,如图3,过点C作CM⊥AD于M,求出CM=EM=12DE= 2,再用勾股定理求出AM,利用线段的加减即可得出结论;②当点D在线段AE上时,如图4,过点C作CN⊥AE于N,求出CM=EM=12DE=2,再由勾股定理求出根据勾股定理得,AN,利用线段的加减即可得出结论.【详解】(1)∵△ABC和△DCE都是等腰直角三角形,∴AC=BC,EC=DC,∴AC-DC=BC-EC,∴BE=AD,点E在BC上,点D在AC上,且∠ACB=90°,∴BE⊥AD,故:BE=AD,BE⊥AD;(2)成立;如图2,AC与BE交于M,AD与BE交于N,由题意可知:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACE=∠DCE+∠CE,∴∠BCE=∠ACD,在△BCE与△ACD中:BC=AC∠BCE=∠ACD CE=CD∴△BCE≌△ACD SAS,∴BE=AD,∠CAD=∠CBE,又∵∠ACB=90°,∠BMC=∠AMN,在△ANM中,∴∠MAN+∠AMN=∠CBE+∠BMC=90°,∴∠ANM=90°,∴BE⊥AD,所以结论成立;(3)①当点E在线段AD上时,如图3,过点C作CM⊥AD于M,∵△DCE是等腰直角三角形,且CE=22,∴DE=CE2+CD2=4,∵CM⊥AD,∴CM=EM=12DE=2,在Rt△ACM中,AC=5,∴AM=AC2-CM2=52-22=21,∴AE=AM-EM=21-2;②当点D在线段AE上时,如图4,过点C作CN⊥AE于N,∵△DCE是等腰直角三角形,且CE=22,∴DE=CE2+CD2=4,∵CN⊥AD,∴CN =NE =12DE =2,在Rt △ACN 中,AC =5,∴AN =AC 2-CN 2=52-22=21,∴AE =AN +NE =21+2,综上,AE 的长为21-2或21+2,故答案为:21-2或21+2.【点睛】此题是几何变换综合题,主要考查了等腰直角三角形的性质,旋转的旋转,全等三角形的判定和性质,勾股定理,作出辅助线构造出直角三角形是解本题的关键.【变式训练】1(2023·全国·九年级专题练习)如图,在等腰直角三角形ABC 和DEC 中,∠BCA =∠DCE =90°,点E 在边AB 上,ED 与AC 交于点F ,连接AD .(1)求证:△BCE ≌△ACD ;(2)求证:AB ⊥AD .【答案】(1)见解析(2)见解析【分析】(1)根据∠BCA =∠DCE =90°,可得∠BCE =∠ACD ,再由等腰直角三角形的性质可得BC =AC ,CE =CD ,可证明△BCE ≌△ACD ,即可求证;(2)根据△BCE ≌△ACD ,可得∠B =∠CAD ,从而得到∠CAD +∠CAE =90°,即可求证.【详解】(1)证明:∵∠BCA =∠DCE =90°,∴∠BCE +∠ECA =∠ECA +∠ACD =90°,∴∠BCE =∠ACD ,∵△ABC 和△DEC 是等腰直角三角形,∴BC =AC ,CE =CD ,在△BCE 和△ACD 中,BC =AC∠BCE =∠ACD CE =CD,∴△BCE ≌△ACD SAS ;(2)证明:∵△BCE ≌△ACD ,∴∠B =∠CAD ,∵∠ACB =90°,∴∠B +∠CAE =90°,∴∠CAD +∠CAE =90°,即∠DAE =90°,∴AB ⊥AD .【点睛】本题主要考查了全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定和性质,等腰直角三角形的性质是解题的关键.2(2023春·八年级课时练习)(1)问题发现:如图1,△ABC与△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,则线段AE、BD的数量关系为,AE、BD所在直线的位置关系为;(2)深入探究:在(1)的条件下,若点A,E,D在同一直线上,CM为△DCE中DE边上的高,请判断∠ADB 的度数及线段CM,AD,BD之间的数量关系,并说明理由.【答案】(1)AE=BD,AE⊥BD;(2)∠ADB=90°,AD=2CM+BD;理由见解析【分析】(1)延长AE交BD于点H,AH交BC于点O.只要证明△ACE≌△BCD SAS,即可解决问题;(2)由△ACE≌△BCD,结合等腰三角形的性质和直角三角形的性质,即可解决问题.【详解】解:(1)如图1中,延长AE交BD于点H,AH交BC于点O,∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,∴AC=BC,CD=CE,∴∠ACE+∠ECB=∠BCD+∠ECB=90°,∴∠ACE=∠BCD,∴△ACE≌△BCD(SAS),∴AE=BD,∠CAE=∠CBD,∵∠CAE+∠AOC=90°,∠AOC=∠BOH,∴∠BOH+∠CBD=90°,∴∠AHB=90°,∴AE⏊BD.故答案为:AE=BD,AE⏊BD.(2)∠ADB=90°,AD=2CM+BD;理由如下:如图2中,∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,∴∠CDE=∠CED=45°,∴∠AEC=180°-∠CED=135°,由(1)可知:△ACE≌△BCD,∴AE=BD,∠BDC=∠AEC=135°,∴∠ADB=∠BDC-∠CDE=135°-45°=90°;在等腰直角三角形DCE中,CM为斜边DE上的高,∴CM=DM=ME,∴DM=2CM,∴AD=DE+AE=2CM+BD.【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题.3(2023·山东枣庄·统考二模)感知:如图①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE,不需证明.(1)探究:如图②,将△ADE绕点A逆时针旋转α(0<α<90°),连接BD和CE,此时BD=CE是否依然成立?若成立,写出证明过程;若不成立,说明理由.(2)应用:如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上,连接CE.求:①∠ACE的度数;②若AB=AC=32,CD=3,则线段DE的长是多少?【答案】(1)BD=CE成立,证明见解析(2)①45° ②310【分析】(1)只需要利用SAS证明△ABD≌△ACE即可证明BD=CE;(2)①由等腰直角三角形的性质得到∠ABC=∠ACB=45°,再证明△ABD≌△ACE即可得到∠ABD=∠ACE=45°;②先由勾股定理得到BC=6,由全等三角形的性质得到∠ACE=∠ABD=45°,BD=CE,则∠BCE=90°,CE=9;则DE=CE2+CD2=310.【详解】(1)解:BD=CE成立,证明如下:∵△ABC和△ADE都是等腰直角三角形,∴AB=AC,AD=AE,由旋转的性质可得∠BAD=∠CAE,∴△ABD≌△ACE SAS,∴BD=CE;(2)解:①∵△ABC和△ADE都是等腰直角三角形,∴∠ABC=∠ACB=45°,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,∠BAD=CAE,AD=AE,∴△ABD≌△ACE SAS,∴∠ABD=∠ACE=45°;②∵AB=AC=32,∴BC=AB2+AC2=6,∵△ACE≌△ABD,∴∠ACE=∠ABD=45°,BD=CE,∴∠BCE=∠ACB+∠ACE=90°,CE=BD=BC+CD=6+3=9;∴DE=CE2+CD2=92+32=310.【点睛】本题主要考查了全等三角形的性质与判定,勾股定理,等腰直角三角形的性质,熟知全等三角形的性质与判定条件是解题的关键.【类型三共顶点的一般等腰三角形】1(2023春·山东泰安·七年级校考开学考试)如图,△ABC与△CDE都是等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE=42°,AD、BE相交于点M.(1)试说明:AD=BE;(2)求∠AMB的度数.【答案】(1)见解析(2)42°【分析】(1)由“SAS”可证△ACD≌△BCE,可得BE=AD;(2)根据全等三角形的性质可得∠CAD=∠CBE,再利用三角形内角和定理计算∠AMB.【详解】(1)解:证明:∵∠ACB=∠DCE,∴∠ACD=∠BCE,在△ACD和△BCE中,CA=CB∠ACD=∠BCE CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE;(2)∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠BAC+∠ABC=180°-42°=138°,∴∠BAM+∠ABM=∠BAC-∠CAD+∠ABC+∠CBE=∠BAC+∠ABC=138°,∴∠AMB=180°-138°=42°.【点睛】本题考查了全等三角形的判定和性质,三角形内角和,证明三角形全等是解题的关键.【变式训练】1(2023秋·辽宁抚顺·八年级统考期末)如图,已知△ABC中,AB≠AC≠BC.分别以AB、AC为腰在AB左侧、AC右侧作等腰三角形ABD.等腰三角形ACE,连接CD、BE.(1)如图1,当∠BAD=∠CAE=60°时,①△ABD、△ACE的形状是;②求证:BE=DC.(2)若∠BAD=∠CAE≠60°,①如图2,当AB=AD,AC=AE时,BE=DC是否仍然成立?请写出你的结论并说明理由;②如图3,当AB=DB,AC=EC时,BE=DC是否仍然成立?请写出你的结论并说明理由.【答案】(1)①等边三角形;②证明见解析(2)①成立,理由见解析;②不成立,理由见解析【分析】(1)①根据有一个内角是60度的等腰三角形是等边三角形即可求解;②根据等边三角形的性质可得AB=AD,AE=AC,∠DAB=∠CAE=60°,证明△BAE≌△DAC,根据全等三角形的性质即可证明;(2)①证明△BAE≌△DAC,根据全等三角形的性质即可得出结论;②根据已知可得△BAE与△DAC不全等,即可得出结论.【详解】(1)①∵△ABD是等腰三角形,△ACE是等腰三角形,∠BAD=∠CAE=60°∴△ABD、△ACE是等边三角形,故答案为:等边三角形.②证明:∵△ABD、△ACE是等边三角形,∴AB=AD,AE=AC,∠DAB=∠CAE=60°,∵∠DAC=∠DAB+∠BAC,∠BAE=∠CAE+∠BAC,∴∠DAC=∠BAE,在△BAE与△DAC中,∵AB=AD∠BAE=∠DAC AE=AC,∴△BAE≌△DAC SAS.∴BE=DC.(2)①当AB=AD,AE=AC时,成立.理由:如图,∵AB=AD,∠BAE=∠DAC,AE=AC,∴△BAE≌△DAC SAS,∴BE=DC;②当AB=DB,AC=EC时,不成立.理由:如图,∵∠BAD=∠CAE≠60°,∴AB=DB≠AD,AC=EC≠AE,∴△BAE与△DAC不全等,∴BE≠DC.【点睛】本题考查全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质等,熟练掌握全等三角形的判定与性质是解题的关键.2(2023秋·全国·八年级专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,△ABC 和△CDE 为“同源三角形”,AC =BC ,CD =CE ,∠ACB 与∠DCE 为“同源角”.(1)如图1,△ABC 和△CDE 为“同源三角形”,试判断AD 与BE 的数量关系,并说明理由.(2)如图2,若“同源三角形”△ABC 和△CDE 上的点B ,C ,D 在同一条直线上,且∠ACE =90°,则∠EMD =°.(3)如图3,△ABC 和△CDE 为“同源三角形”,且“同源角”的度数为90°时,分别取AD ,BE 的中点Q ,P ,连接CP ,CQ ,PQ ,试说明△PCQ 是等腰直角三角形.【答案】(1)AD =BE ,详见解析(2)45(3)详见解析【分析】(1)由“同源三角形”的定义可证∠ACD =∠BCE ,然后根据SAS 证明△ACD ≌△BCE 即可;(2)由“同源三角形”的定义和∠ACE =90°可求出∠DCE =ACB =45°,由(1)可知△ACD ≌△BCE ,得∠ADC =∠BEC ,然后根据“8”子三角形即可求出∠EMD 的度数;(3)由(1)可知△ACD ≌△BCE ,可得∠CAQ =∠CBP ,BE =AD .根据SAS 证明△ACQ ≌△BCP ,可得CQ =CP ,∠ACQ =∠BCP ,进而可证结论成立.【详解】(1)AD =BE .理由:因为△ABC 和△CDE 是“同源三角形”,所以∠ACB =∠DCE ,所以∠ACD =∠BCE .在△ACD 和△BCE 中,AC =BC ,∠ACD =∠BCE ,CD =CE ,所以△ACD ≌△BCE SAS .所以AD =BE .(2)∵△ABC 和△CDE 是“同源三角形”,∴∠ACB =∠DCE .∵∠ACE =90°,∴∠DCE =ACB =45°.由(1)可知△ACD ≌△BCE ,∴∠ADC =∠BEC .∵∠MOE =∠COD ,∴∠EMD =∠DCE =45°.故答案为:45;(3)由(1)可知△ACD ≌△BCE ,所以∠CAQ =∠CBP ,BE =AD .因为AD ,BE 的中点分别为Q ,P ,所以AQ =BP .在△ACQ 和△BCP 中,CA =CB ,∠CAQ =∠CBP ,AQ =BP ,所以△ACQ ≌△BCP SAS ,所以CQ =CP ,∠ACQ =∠BCP .又因为∠BCP +∠PCA =90°,所以∠ACQ +∠PCA =90°.所以∠PCQ =90°,所以△PCQ 是等腰直角三角形.【点睛】本题考查了新定义,全等三角形的判定与性质,等腰直角三角形的判定,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解答本题的关键.3(2023春·辽宁丹东·七年级统考期末)(1)如图1,两个等腰三角形△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,连接BD ,CE .则△ADB ≌,此时线段BD 和线段CE 的数量关系式;(2)如图2,两个等腰直角三角形△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE =90°,连接BD ,CE ,两线交于点P ,请判断线段BD 和线段CE 的关系,并说明理由;(3)如图3,分别以△ABC 的两边AB ,AC 为边向△ABC 外作等边△ABD 和等边△ACE ,连接BE ,CD ,两线交于点P .请直接写出线段BE 和线段CD 的数量关系及∠PBC +∠PCB 的度数.【答案】(1)△AEC ,BD =CE ;(2)BD =CE 且BD ⊥CE ;(3)CD =BE ,∠PBC +∠PCB =60°【分析】(1)先判断出∠DAB =∠EAC ,进而判断出△ADB ≌△AEC ,即可得出结论;(2)先判断出△DAB ≌△EAC ,得出BD =CE ,∠DBA =∠ECA ,进而判断出∠DBC +∠ECB ,即可得出结论;(3)先判断出△ACD ≌△AEB ,得出CD =BE ,∠ADC =∠ABE ,进而求出∠BPD =60°,最后用三角形外角的性质,即可得出结论.【详解】解:(1)∵∠DAE =∠BAC ,∴∠DAE +∠BAE =∠BAC +∠BAE .即∠DAB =∠EAC ,在△ADB 和△AEC 中,AD =AE∠DAB =∠EAC AB =AC,∴△ADB ≌△AEC SAS ,∴BD =CE ,故答案为:△AEC ,BD =CE ;(2)BD =CE 且BD ⊥CE ;理由如下:∵∠DAE =∠BAC =90°,∴∠DAE +∠BAE =∠BAC +∠BAE .即∠DAB =∠EAC .在△DAB 和△EAC 中,AD =AE∠DAB =∠EAC AB =AC,∴△ADB ≌△AEC SAS ,∴BD =CE ,∠DBA =∠ECA ,∵∠ECA +∠ECB +∠ABC =90°,∴∠DBA +∠ECB +∠ABC =90°,即∠DBC +∠ECB =90°,∴∠BPC =180°-(∠DBC +∠ECB )=90°,∴BD ⊥CE ,综上所述:BD =CE 且BD ⊥CE ;(3)如图3所示,BE =CD ,∠PBC +∠PCB =60°,理由如下:∵△ABD 和△ACE 是等边三角形,∴AD =AB ,AC =AE ,∠ADB =∠ABD =∠BAD =∠CAE =60°,∴∠BAD +∠BAC =∠CAE +∠BAC ,∴∠CAD =∠EAB ,在△ACD 和△AEB 中,AD =AB ∠CAD =∠EAB AC =AE,∴△ACD ≌△AEB (SAS ),∴CD =BE ,∠ADC =∠ABE ,∴∠BPD =180°-∠PBD -∠BDP=180°-∠ABE -∠ABD -∠BDP=180°-∠ABD -∠ABE +∠BDP=180°-∠ABD -∠ADC +∠BDP=180°-∠ABD -∠ADB=60°,∴∠PBC +∠PCB =∠BPD =60°.【点睛】此题是三角形综合题,主要考查了等腰三角形的性质,等腰直角三角形的性质,等边三角形的性质,三角形的内角和定理,三角形外角的性质,判断出△ADB ≌△AEC 是解本题的关键.。
初二数学手拉手模型

初二数学中的“手拉手”模型如图1:两个公共顶点并且顶角相等的等腰三角形所组成的图形具有很特别的性质,我们形象地称其为“手拉手”模型;在这个图形种蕴含这两个全等三角形,而且这两个全等三角形可以看成其中一个绕着顶点旋转顶角地度数后变成另外一个。
在图1中,只需要连结BD,CE则容易证明△ABD≌△ACE;同时△ACE可以看成△ABD绕着点A顺时针旋转∠BAC的度数得到。
熟悉手拉手模型对于解题是十分有帮助的。
下面以一些初二阶段的考题为例子一起来巩固强化一下这个模型。
例1(15石狮八年级期末26题)△ABC和△ADE都是等腰三角形,其中AB=AC,AD=AE,且∠BAC=∠DAE.(1)如图1,连结BE、CD,求证:CD=BE;(2)如图2,连结BD、CD,若∠BAC=∠DAE=60°,CD⊥AE,AD=3,CD=4,求BD的长;(3)如图3,若∠BAC=∠DAE=90°,以点A为旋转中心旋转△ABC,使得点C恰好落在斜边DE上,试探究、、之间的数量关系,并加以证明.本分析:本题就是一道典型的手拉手模型问题,这边的两个等顶角共定点的等腰三角形是△ABC和△AED,因此图形中一定存在着两个全等的可以看成旋转得到的三角形。
有了这个理念就不难想到第二题连结BE;第三题连结BE,得到全等三角形,第二题中两个全等三角形是△ABE与△ACD;第三问全等的三角形是△ABE与△ACD。
发现全等在本题中是关键;例如第二题、三题就是通过全等把已知条件集中到同一个直角三角形中;利用勾股定理求解。
例2:如图3,在三角形ABC中AB=AC,∠BAC=90°,P是BC上的一点,证明:BP²+CP²=2AP²分析:这个题目中并没有直接的“手拉手”模型;但是题目中有一个已知的等腰直角三角形ABC,要证明的式子中有一个线段AP是以A为端点的,因此我们可以考虑以AP为直角边,构造以点A为顶点的另一个等腰直角三角形APD,这样就出现“手拉手”模型了,而模型中存在的两个旋转三角形也随之显现,能把相关线段集中到同一个直角三角形中。
勾股定理(手拉手模型)(人教版)
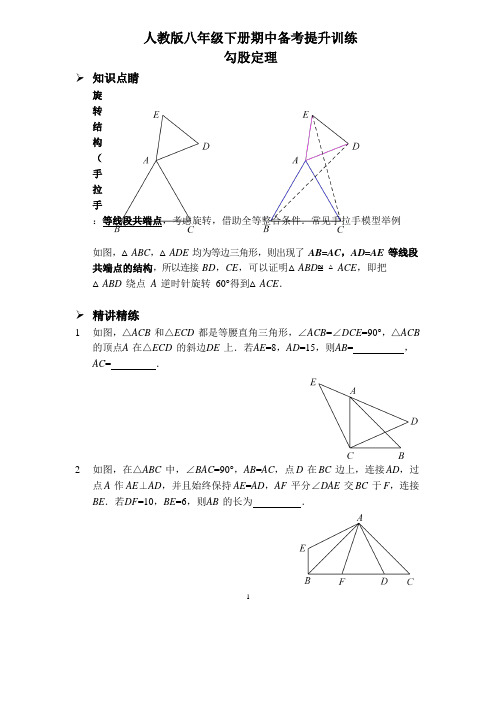
人教版八年级下册期中备考提升训练勾股定理➢知识点睛旋转结构(手拉手:等线段共端点,考虑旋转,借助全等整合条件.常见手拉手模型举例如图,△ABC,△ADE 均为等边三角形,则出现了AB=AC,AD=AE 等线段共端点的结构,所以连接BD,CE,可以证明△ABD≌△ACE,即把△ABD 绕点A 逆时针旋转60°得到△ACE.➢精讲精练1.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠DCE=90°,△ACB的顶点A在△ECD 的斜边D E 上.若A E=8,AD=15,则A B= ,AC= .2.如图,在△ABC 中,∠BAC=90°,AB=AC,点D 在BC 边上,连接AD,过点A 作AE⊥AD,并且始终保持AE=AD,AF 平分∠DAE 交BC 于F,连接BE.若D F=10,BE=6,则A B 的长为.117 3. 如图,已知 CA =CB ,CF =CE ,∠ACB =∠FCE =90°,且 A ,F ,E 三点共线,AE 与 CB 交于点 D .(1) 求证:AF 2+AE 2=AB 2;(2) 若 A C = ,BE =3,则 C E = .4. 如图,E 是正方形 ABCD 对角线 CA 的延长线上任意一点,以线段 AE 为边作一个正方形 AEFG ,线段 GB 与线段 ED ,AD 分别交于点 H ,M .(1) 求证:ED =GB ;(2) 判断 ED 与 GB 的位置关系,并说明理由;(3) 若 AB =2,AE = ,则 G B =.225.(1)如图1,O 是等边△ABC 内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO 绕点B 顺时针旋转后得到△BCD,连接OD.①旋转角是度;②线段O D 的长为;③求∠BDC 的度数.(2)如图2 所示,O 是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,∠AOB=135°,OA=1,OB=2,求OC 的长.小明同学借用了图1 的方法,将△BAO 绕点B 顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.36.如图,△ABC 是等腰直角三角形,∠BAC=90°,点D 为直线BC 上的动点(不与点B,C 重合),连接AD,将线段AD 绕点A 逆时针旋转90°,得到线段AE,连接DE.(1)如图1,当点D在线段B C 上时,请直接写出线段D B,DC,DE 之间的数量关系:.(2)如图2,当点D 在BC 延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由.(3)如图3,当点D 在CB 延长线上时,若∠DAB=30°,BD=2,请直接写出AB 的长.47.如图,在Rt△ABC 中,∠ACB=90°,AC=BC,CD⊥AB 于点D,点E 是直线AC 上一动点,连接DE,过点D 作FD⊥ED,交直线BC 于点F.(1)如图1,当点E 在线段AC 上时,①求证:△CDE≌△BDF;②直接写出B F2,CF2,DF2 之间的数量关系:.(2)如图2,当点E 在线段AC 的延长线上时,判断(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)58.某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD 中,AB=6,将三角板放在正方形ABCD 上,使三角板的直角顶点与D 点重合,三角板的一边交AB 于点P,另一边交BC 的延长线于点Q.(1)求证:DP=DQ;(2)如图2,小明在图1 的基础上作∠PDQ 的平分线DE 交BC 于点E,连接PE,他发现PE 和QE 存在一定的数量关系,请猜测他的结论并予以证明.(3)如图3,固定三角板直角顶点在D 点不动,转动三角板,使三角板的一边交AB 的延长线于点P,另一边交BC 的延长线于点Q,仍作∠PDQ 的平分线DE 交BC 延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP 的面积(直接写出答案即可).6 参考答案:。
手拉手模型(压轴题专项讲练)(人教版)(解析版)—2024-2025学年八年级数学上册(苏科版)

手拉手模型(压轴题专项讲练)【典例1】(1)问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,如图1,△ABC和△ADE是顶角相等的等腰三角形,即AB=AC,AD=AE,且∠BAC=∠DAE,分别连接BD,CE.求证:BD=CE;(2)类比探究:如图2,△ABC和△ADE都是等腰三角形,即AB=AC,AD=AE,且∠BAC=∠DAE=90°,B,C,D在同一条直线上.请判断线段BD与CE存在怎样的数量关系及位置关系,并说明理由.(3)问题解决:如图3,若△ACB和△DCE均为等腰直角三角形,且CA=CB,CD=CE,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE中DE边上的高,连接BE,若AE=7,BE=2,请直接写出四边形ABEC的面积.本题是三角形综合题,主要考查了全等三角形的判定和性质、等腰三角形、等腰直角三角形的性质、三线合一等性质,熟练掌握三角形的有关性质是解题的关键.(1)根据三角形全等的判定和性质即可解答.(2)根据(1)问中,“手拉手”全等的证明,可得△BAD≌△CAE(SAS),利用全等的性质可得BD=CE,∠ACE=∠ABC,又因为△ABC是等腰直角三角形,可得∠ABC=∠ACB=∠ACE=45°,从而可知∠BCE=90°,即BD⊥CE.(3)由△DCE是等腰直角三角形,CM为△DCE中DE边上的高,可证得CM=12DE=12(AE―AD),根据(1)问中,“手拉手”全等的证明,可得△ACD≌△BCE,从而得AD=BE,即可求出CM的长,最后求出四边形ABEC的面积.(1)证明:∵∠BAC=∠DAE∴∠BAC―∠CAD=∠DAE―∠CAD即∠BAD=∠CAE在△ABD和△ACE中AB=AC∠BAD=∠CAE,AD=AE∴△ABD≌△ACE(SAS)∴BD=CE.(2)BD与CE的数量关系是BD=CE,位置关系是BD⊥CE.理由如下:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),∴BD=CE,∠ACE=∠ABC,∵△ABC是等腰三角形且∠BAC,∴∠ABC=∠ACB=45°,∴∠ACE=∠ABC=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°,∴BD⊥CE.(3)解:由(1)的方法得,△ACD≌△BCE,∴AD=BE,∠CAD=∠CBE,∵△CDE是等腰直角三角形,∴∠CDE=∠CED=45°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM =ME =CM ,∴ CM =12DE =12(AE ―AD)=12(AE ―BE)=12×(7―2)=2.5.∵∠ACB =90°,∴∠CAD +∠EAB +∠CBA =90°,∴∠CBE +∠EAB +∠CBA =90°,∴∠AEB =90°,即四边形ABEC 的面积=S △ACE +S △AEB =12AE·CM +12AE·BE =12×7×2.5+12×7×2=634.1.(23-24七年级下·贵州毕节·期末)在△BCD 中,∠BCD <120°,分别以BC 、CD 和BD 为边在△BCD 外部作等边三角形ABC 、等边三角形CDE 和等边三角形BDF ,连结AD 、BE 和CF 交千点P ,则以下结论中①AD =BE =CF ;②∠BEC =∠ADC ;③∠DPE =∠EPC =∠CPA =60°;④PB +PC +PD =BE .正确的有( )A .1个B .2个C .3个D .4个【思路点拨】证明△ABD≌△CBF (SAS),△ACD≌△BCE (SAS),可得∠BAD =∠BCF ,∠CAD =∠CBE ,进一步可判断①②,证明∠APC =60°,求出∠BPC =120°,进一步可判断③,在PA 上截取PG =PB ,连接BG ,证明∠BGA =∠BPC =120°,再证△BAG≌△BCP (AAS),可得PC =GA ,进而可得PA =PB +PC ,进一步可判断④.【解题过程】解:∵△ABC ,△BDF是等边三角形,∴BA=BC,BD=BF,∠ABC=∠DBF=60°,∴∠ABD=∠CBF,∴△ABD≌△CBF(SAS),∴∠BAD=∠BCF,AD=CF,同理可得△ACD≌△BCE(SAS),∴∠CAD=∠CBE,AD=BE,∠BEC=∠ADC,∴AD=BE=CF,故①②符合题意;∵∠BAD+∠CAD=60°,∴∠BAD+∠CBE=60°,∵∠ABC=60°,∴∠BAD+∠ABC+∠CBE=∠BAD+∠ABE=120°,∴∠BPA=60°=∠DPE,同理可得∠APC=60°,∴∠BPC=120°,∠EPC=60°,∴∠DPE=∠EPC=∠CPA=60°,故③符合题意;如图,在PA上截取PG=PB,连接BG,∴△BPG是等边三角形,∴∠BGP=60°,∴∠BGA=120°,∴∠BGA=∠BPC,又∵∠BAG=∠BCP,AB=CB,∴△BAG≌△BCP(AAS),∴PC=GA,∴PA =PG +GA =PB +PC ,∵AD =BE ,∴PB +PC +PD =PA +PD =AD =BE ;故④符合题意;故选D2.(2023·吉林长春·模拟预测)两个大小不同的等腰直角三角板按图1所示摆放,将两个三角板抽象成如图2所示的△ABC 和△AED ,其中∠BAC =∠EAD =90°,点B 、C 、E 依次在同一条直线上,连结CD .若BC =4,CE =2,则△DCE 的面积是 .【思路点拨】本题考查了全等三角形的判定与性质、等腰直角三角形的性质等知识,根据SAS 证明△ACD≌△ABE ,由全等三角形的性质得出∠ACD =∠B ,CD =BE ,则可得出答案.【解题过程】解:∵∠BAC =∠EAD =90°,∴∠BAC +∠CAE =∠EAD +∠CAE ,即∠BAE =∠CAD ,在△ABD 和△ACD 中,AB =AC ∠BAE =∠CAD AD =AE,∴△ACD≌△ABE (SAS),∴∠ACD =∠B ,CD =BE ,∵∠B =45°,∴∠ACD =45°,∴∠BCD =∠ACB +∠ACD =90°,∵BC =4,CE =2,∴BE =6,∴CD =6,∴S △DCE =12CE ⋅DC =12×2×6=6,故答案为:6.3.(24-25八年级上·吉林长春·阶段练习)已知:如图,△ABC 和△DEC 都是等边三角形,D 是BC 延长线上一点,AD 与BE 相交于点P ,AC 与BE 相交于点M ,AD 与CE 相交于点 ,连接MN ,PC ,则下列四个结论:①∠BMC =∠BMA ;②∠APB =60°;③AN =BM ;④PC 平分∠BPD .其中,正确的是 (只填写序号)【思路点拨】当M 是AC 的中点或者BM 平分∠ABC 时,∠BMC =∠BMA ,故①错误;根据等边三角形的性质得CA =CB,CD =CE ,∠ACB =60°,∠DCE =60°,则∠ACE =60°,可得△ACD≌△BCE (SAS),故∠CAD =∠CBE ,再判断△ACN≌△BCM (ASA),所以AN =BM ;可以判断③正确,根据三角形内角和定理可得∠CAD +∠CDA =60°,而∠CAD =∠CBE ,则∠CBE +∠CDA =60°,然后再利用三角形内角和定理即可得到∠BPD =120°,故∠APB =②正确;作CH ⊥BE 于H ,CQ ⊥AD 于Q ,由△ACD≌△BCE 得到∠CAD =∠CBE ,即可证明△AQC≌△BHC (AAS),故CQ =CH ,根据角平分线的判定定理即可得到PC 平分∠BPD ,进而可以判断④正确.【解题过程】证明:∵△ABC 是等边三角形,∴当M 是AC 的中点或者BM 平分∠ABC 时,∴∠BMC =∠BMA ,但题中M 的位置不确定,∴∠BMC 和∠BMA 不一定相等,故①错误;∵△ABC 和△DEC 都是等边三角形,∴CA =CB,CD =CE ,∠ACB =60°,∠DCE =60°,∴∠ACE =60°,∴∠ACD =∠BCE =120°,在△ADC 和△BCE 中,CA =CB ∠ACD =∠BCE CD =CE∴△ACD≌△BCE (SAS),∴∠CAD =∠CBE ,在△ACN 和△BCM 中,∠ACN =∠BCM CA =CB ∠CAN =∠CBM,∴△ACN≌△BCM (ASA),∴AN =BM ,故③正确;∵∠CAD +∠CDA =60°,而∠CAD =∠CBE ,∴∠CBE +∠CDA =60°,∴∠BPD =120°,∴∠APB =60°,故②正确;作CH ⊥BE 于H ,CQ ⊥AD 于Q∵△ACD≌△BCE ,∴AC =BC ,∠CAD =∠CBE又∵∠BHC =∠AQC =90°∴△AQC≌△BHC (AAS)∴CQ =CH ,又∵∠CHP =∠CQP =90°,∴CP平分∠BPD,故④正确.综上所述:正确的是②③④.故答案为:②③④.4.(23-24九年级上·河南周口·期中)如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为______,线段AE与BD的数量关系为______.(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α≤360°)时,(1)中的结论是否还成立?若不成立,请说明理由:若成立,请就图2给予证明.(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.【思路点拨】本题考查了等边三角形性质的运用,全等三角形的判定及性质的运用,以及旋转的性质,解答时证明三角形全等是关键.(1)利用等边三角形的性质证明△ACE≌△BCD,结合三角形的外角就可以得出结论;(2)同(1)中方法证明△ACE≌△BCD,得出AE=BD,∠2=∠3,再根据三角形的内角和得出∠AFB=60°;(3)当B、C、D三点共线时得出BD的最大和最小值,即可得出结论.【解题过程】(1)解:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∵△ECD是等边三角形,∴CE=CD,∠DCE=60°,∴∠ACB=∠DCE=60°∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE =∠BCD ,在△ACE 和△BCD 中,AC =BC ∠ACE =∠BCD CE =CD∴△ACE≌△BCD ,∴AE =BD ,∠CAE =∠CBD ,∵∠AFB =∠CAE +∠BDC ,且∠ACB =60°∴∠AFB =∠CBD +∠BDC =∠ACB =60°(2)(1)中结论仍成立,∵△ABC 是等边三角形,∴AC =BC ,∠ACB =60°,∵△ECD 是等边三角形,∴CE =CD ,∠DCE =60°,∴∠ACB =∠DCE =60°∴∠ACB +∠1=∠DCE +∠1,即∠ACE =∠BCD ,在△ACE 和△BCD 中,AC =BC ∠ACE =∠BCD CE =CD∴△ACE≌△BCD ,∴AE =BD ,∠2=∠3,∵∠AFB +∠3=∠ACB +∠2,且∠ACB =60°,∴∠AFB =60°;(3)∵△ABC是等边三角形,∴AC=BC=4,当旋转α=60°时,B、C、D三点共线,此时BD=BC+CD=7,当旋转α=240°时,B、C、D三点共线,此时BD=BC―CD=1;∴1≤BD≤7.5.(23-24七年级下·四川成都·期中)数学模型可以用来解决一类问题,是数学应用基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:__________,∠BDC=;(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;(3)拓展应用:在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=90°,连接BE,CF,将△AEF 绕它们共同的顶点A旋转一定的角度后,若B,E,F三点刚好在同一直线上,求此时∠AFC的度数.【思路点拨】本题考查全等三角形的判定,等腰三角形以及等腰直角三角形的判定与性质,灵活运用相关知识成为解题的关键.(1)设AC交BD于点G,由∠BAC=∠EAF=30°可得∠BAE=∠CAF=30°+∠CAE,而AB=AC、AE=AF,即可根据“SAS”证明△ABE≌△ACF,所以BE=CF,∠ABE=∠ACF,则∠BDC=∠AGD―∠ACF=∠AGD―∠ABE=∠BAC=30°即可解答;(2)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF可得BE=CF,∠AEB=∠AFC,然后再根据等腰三角形的性质即可解答;(3)根据等腰直角三角形的性质,利用SAS证明△ABE≌△ACF可得∠AFC=AEB,AE=AF,再说明∠AEB=135°即可.【解题过程】(1)解:如图1,设AC 交BD 于点G ,∵∠BAC =∠EAF =30°,∴∠BAE =∠CAF =30°+∠CAE ,在△ABE 和△ACF 中,AB =AC ∠BAE =∠CAF AE =AF,∴△ABE≌△ACF (SAS),∴∠ABE =∠ACF ,BE =CF ,∴∠BDC =∠AGD ―∠ACF =∠ACD ―∠ABE =∠BAC =30°.故答案为:BE =CF ,30.(2)解:BE =CF ,∠BDC =60°,理由如下:∵∠BAC =∠EAF =120°,∴∠BAC ―∠EAC =∠EAF ―∠EAC ,即∠BAE =∠CAF ,在△ABE 和△ACF 中,AB =AC ∠BAE =∠CAF AE =AF,∴△ABE≌△ACF (SAS),∴BE =CF ,∠AEB =∠AFC ,∵∠EAF =120°,AE =AF ,∴∠AEF =∠AFE =30°,∴∠BDC =∠BEF ―∠EFD =∠AEB +30°―(∠AFC ―30°)=60°.(3)解:如图3所示:∵△ABC和△AEF都是等腰三角形,∴∠CAB=∠EAF=90°,AB=AC,AE=AF,∴∠CAB―∠CAE=∠FAE―∠CAE,即:∠BAE=∠CAF,∴△BAE≌△CAF(SAS),∴∠AFC=AEB,AE=AF,∵∠EAF=90°,∴∠AEF=45°,∴∠AEB=180°―∠AEF=135°,∴∠AFC=∠AEB=135°.6.(2024·河南·一模)如图,(1)问题发现:如图①,△ABC和△EDC都是等边三角形,点B、D、E在同一条直线上,连接AE.①∠AEC的度数为______;②线段AE、BD之间的数量关系为______;(2)拓展探究:如图②,△ABC和△EDC都是等腰直角三角形,∠ACB=∠DCE=90°,点B、D、E在同一条直线上,CM为△EDC中DE边上的高,连接AE,试求∠AEB的度数及判断线段CM、AE、BE之间的数量关系,并说明理由;(3)解决问题:如图③,△ABC和△EDC都是等腰三角形,∠ACB=∠DCE=36°,点B、D,E在同一条直线上,请直接写出∠EAB+∠ECB的度数.【思路点拨】本题考查了全等三角形的判定与性质,等边三角形的性质,等腰三角形的性质,灵活运用这些性质是解题的关键.(1)①根据等边三角形的性质可得∠BDC =120°,证明△ECA≌△DCB (SAS),根据全等三角形的性质即可求解;②根据全等三角形的性质即可解答;(2)证明△ECA≌△DCB (SAS),根据等腰直角三角形的性质可得∠CDB =135°,进而得到∠CEA =∠CDB =135°,∠AEB =∠CEA ―∠CEB ,即可得到∠AEB 的度数;由△DCE 是等腰直角三角形,CM 为△EDC 中DE 边上的高,可得BE =AE +2CM ,即可得到线段CM 、AE 、BM 之间的数量关系;(3)证明△ECA≌△DCB (SAS),得到∠CEA =∠CDB =108°,推出∠EAC +∠ECA =72°,最后根据∠EAB +∠ECB =∠EAC +∠CAB +∠ECA +∠ACB ,即可求解.【解题过程】(1)解:①∵ △ABC 和△EDC 都是等边三角形,∴ CE =CD ,CA =CB ,∠ECD =∠ACB =60°,∴ ∠BDC =180°―∠EDC =120°,∴ ∠ECD ―∠ACD =∠ACB ―∠ACD ,即∠ECA =∠DCB ,在△ECA 和△DCB 中,CE =CD ∠ECA =∠DCB CA =CB, ∴ △ECA≌△DCB (SAS),∴ ∠AEC =∠BDC =120°,故答案为:120°;②∵ △ECA≌△DCB ,∴ AE =BD ,故答案为:AE =BD ;(2)解:∵ △ABC 和△EDC 都是等腰直角三角形,∠ACB =∠DCE =90°,EC =DC,AC =BC,∠ECD =∠ACB =90°,∠CDE =∠CED =45°,∴∠ECD ―∠ACD =∠ACB ―∠ACD ,∴∠ECA =∠DCB ,在△AEC 与△BDC 中,EC =DC ∠ECA =∠DCB AC =BC,∴△AEC≌△BDC(SAS),∴∠AEC =∠BDC,AE =BD,∵∠CDE=45°,点B、D、E在同一条直线上,∴∠BDC=135°,∴∠AEC=∠BDC=135°,∴∠AEB=∠AEC―∠CEB=135°―45°=90°,∵△EDC都是等腰直角三角形,CM⊥DE,∴CM=EM=MD,∴ED=2CM,∴BE=BD+DE=AE+2CM,∠AEB的度数为90°,线段CM、AE、BE之间的数量关系为:BE=AE+2CM;(3)解:根据(1)(2)中结论可知:△AEC≌△BDC,得∠AEC=∠BDC,∵△ABC和△EDC都是等腰三角形,∠ACB=∠DCE=36°,=72°,∴∠CDE=∠ABC=180°―36°2∴∠AEC=∠BDC=180°―72°=108°,∴∠AEC+∠ABC=108°+72°=180°,∴∠EAB+∠ECB=360°―180°=180°.7.(23-24八年级上·重庆万州·阶段练习)(1)问题情境如图1,△ABC和△ADE都是等边三角形,连接BD,CE,求证:△ABD≌△ACE.(2)迁移应用如图2,△ABC和△ADE都是等边三角形,A,B,E三点在同一条直线上,M是AD的中点,N是AC的中点,P在BE上,△MNP是等边三角形,求证:P是BE的中点.(3)拓展创新如图3,P是线段BE的中点,BE=9,在BE的下方作等边△PFH(P,F,H三点按逆时针顺序排列,△PFH的大小和位置可以变化),连接EF,BH.当EF+BH的值最小时,直接写出等边△PFH 边长的最小值.【思路点拨】(1)证出∠BAD=∠CAE,根据SAS证明△ABD≌△ACE;(2)在AE 上取点K ,使得AK =AM ,连接KM ,证明△AMN≌△KMP(SAS),由全等三角形的性质得出AN =KP ,证出EP =BP ,则可得出结论;(3)作∠EPQ =60°, 使PQ =PE ,连接QE,QB ,证明△EPF≌△QPH(SAS),由全等三角形的性质得出EF =QH ,则EF +BH =QH +BH ,当点H 在线段QB 上时,EF +BH 的值最小,由直角三角形的性质可得出答案.【解题过程】(1)证明:∵△ABC 和△ADE 都是等边三角形,∴∠BAC =∠DAE =60°,AB =AC , AD =AE ,∴∠BAC ―∠ACD =∠DAE ―∠ACD ,∴∠BAD =∠CAE ,在△BAD 和△CAE 中AB =AC ∠BAD =∠CAE AD =AE,∴△BAD≌△CAE(SAS);(2)证明: 在AE 上取点K ,使得AK =AM ,连接KM ,∵△ABC 和△ADE 都是等边三角形.∴∠DAE =60°,AD =AE ,AC =AB ,∴△AMK 是等边三角形,∴AM =MK =AK ,∠AMK =60°,∵△MPN 是等边三角形,∴MN =MP ,∠PMN =60°,∴∠PMN =∠KMA ,∴∠PMN ―∠AMP =∠KMA ―∠AMP ,即∠AMN =∠KMP ,在△AMN 和△KMP中AM =KM∠AMN =∠KMP MN =MP,∴△AMN≌△KMP(SAS),∴AN =KP ,∴AM =AK =AP +AN ,∵M 为AD 的中点, 点N 为AC 的中点,∴AE =AD =2AM ,AB =AC =2AN ,设AP =x ,AN =y ,则AK =x +y ,AB =2y ,∴AE =2AK =2x +2y ,BP =AB +AP =x +2y ,∴EP =AE ―AP =x +2y ,∴ EP =BP ,∴点P 为BE 的中点;(3)作∠EPQ =60°,使PQ =PE ,连接EQ,QB ,∵△PFH 是等边三角形,∴ PF =PH ,∠FPH =60°,∴∠EPF =∠QPH ,∴△EPF≌△QPH (SAS),∴EF =QH ,∴EF +BH =QH +BH ,当点H 在线段QB 上时,EF +BH 的值最小,此时PH ⊥BQ ,PH 的值最小,∵PQ =PB =PE ,∴∠PBQ =∠PQB =30°,在Rt △PBH 中,PH =12PB =14BE =94,即当EF +BH 的值最小时,△PFH 边长的最小值为 94.8.(23-24七年级下·陕西咸阳·期末)【问题提出】(1)如图1,在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠BAC =∠EAF =30°,连接BE ,CF ,BE 交AC 于点O ,延长BE 交CF 于点D .①试说明:BE =CF ;②求∠BDC 的度数.【问题探究】(2)如图2,在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠BAC =∠EAF =120°,连接BE ,CF ,延长BE ,FC 交于点D ,请猜想BE 与CF 的数量关系及∠BDC 的度数,并说明理由.【思路点拨】(1)①利用SAS 证明△ABE≌△ACF ,即可得出结论;②由全等三角形的性质以及三角形外角的性质可得出结论;(2)利用SAS 证明△ABE≌△ACF ,由全等三角形的性质即可得出BE =CF ;然后,根据等腰三角形的性质,三角形的内角和定理以及三角形外角的性质即可求出∠BDC 的度数.【解题过程】解:(1)①∵∠BAC =∠EAF =30°,∴∠BAC +∠CAE =∠EAF +∠CAE ,即∠BAE =∠CAF ,在△ABE 和△ACF 中,AB =AC ∠BAE =∠CAF AE =AF,∴△ABE≌△ACF (SAS),∴BE =CF ;②如图,设AC 与BD 交于点O ,∵△ABE≌△ACF ,∴∠ABE =∠ACF ,∵∠AOE =∠ABE +∠BAC ,∠AOE =∠ACF +∠BDC ,∴∠BDC =∠BAC =30°;(2)BE =CF ,∠BDC =60°,理由如下:∵∠BAC =∠EAF =120°,∴∠BAC ―∠EAC =∠EAF ―∠EAC ,即∠BAE =∠CAF ,在△ABE 和△ACF 中,AB =AC ∠BAE =∠CAF AE =AF,∴△ABE≌△ACF (SAS),∴BE =CF ,∠AEB =∠AFC ,∵∠EAF =120°,AE =AF ,∴∠AEF =∠AFE =12(180°―∠EAF )=12×(180°―120°)=30°,∴∠BDC =∠BEF ―∠EFD=(∠AEB +∠AEF )―(∠AFC ―∠AFE )=∠AEB ―∠AFC +∠AEF +∠AFE=∠AEF +∠AFE=30°+30°=60°.9.(23-24七年级下·安徽宿州·期末)已知,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边在AD的右侧作等腰直角△ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①如图1,当点D在线段BC上时(与点B不重合),请直接写出线段CE与BD之间的数量关系:___________,位置关系:___________;(只写结论,不用证明)②如图2,当点D在线段BC的延长线上时,①中的结论是否仍然成立?若不成立,请说明理由;若成立,写出结论并加以论证;(2)如果AB≠AC,∠BAC<90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD (点C,E重合除外)?请写出条件,并借助图3简述CE⊥BD成立的理由.【思路点拨】本题主要考查了等腰直角三角形的旋转.熟练掌握等腰直角三角形的判断和性质,旋转性质,全等三角形(1)①根据等腰直角三角形性质得到∠B=∠ACB=45°,推出∠BAD=∠CAE,得到△ABD≌△ACE(SAS),得到CE=BD,∠ACE=∠B=45°,得到∠BCE=90°,CE⊥BD;②根据等腰直角三角形性质得到∠B=∠ACB=45°,推出∠BAD=∠CAE,推出△ABD≌△ACE(SAS),得到CE=BD,∠ACE=∠B=45°,得到∠BCE=90°,即得CE⊥BD;(2)当∠ACB=45°时,CE⊥BD.过点A作AF⊥AC交CB的延长线于点F,得到△AFC是等腰直角三角形,根据∠DAE=90°,AD=AE,推出∠FAD=∠CAE,得到△FAD≌△CAE(SAS),得到∠ACE=∠F=45°,得到∠BCE=90°,即得CE⊥BD.【解题过程】(1)①当AB=AC,∠BAC=90°时,∠B=∠ACB=45°,∵∠DAE=90°,AD=AE,∴∠BAD+∠CAD=∠CAD+∠CAE=90°,∴∠BAD=∠CAE,∴△ABD≌△ACE(SAS),∴CE=BD,∠ACE=∠B=45°,∴∠BCE=∠ACB+∠ACE=90°,∴CE⊥BD;故答案为:CE=BD,CE⊥BD;②CE=BD,CE⊥BD仍然成立,理由:∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵∠DAE=90°,AD=AE,∴∠BAD―∠CAD=∠CAE―∠CAD=90°,∴∠BAD=∠CAE,∴△ABD≌△ACE(SAS),∴CE=BD,∠ACE=∠B=45°,∴∠BCE=∠ACB+∠ACE=90°,∴CE⊥BD;(2)当∠ACB=45°时,CE⊥BD,理由:如答图,过点A作AF⊥AC交CB F,则∠FAC=90°,∵∠ACB=45°,∴∠F=90°―∠ACB=45°,∴AC=AF,∵∠DAE=90°,AD=AE,∴∠FAD+∠DAC=∠CAE+∠DAC=90°,∴∠FAD=∠CAE,∴△FAD≌△CAE(SAS),∴∠ACE=∠F=45°,∴∠BCE=∠ACB+∠ACE=90°,∴CE⊥BD.10.(23-24七年级下·河南郑州·期中)【综合实践】如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,可以形象地看作两双手,所以通常称为“手拉手模型”.(1)【初步把握】如图1,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,则有△ABD≌;线段BD和CE的数量关系是;(2)【深入研究】如图2,△ABC和△ADE是都是等腰三角形,即AB=AC,AD=AE,且∠BAC=∠DAE=90°,B,C,D BD与CE存在怎样的数量关系及位置关系,并说明理由;(3)【拓展延伸】如图3,直线l1⊥l2,垂足为点O,l2上有一点M在点O右侧且OM=4,点N是l1上一个动点,连接MN,在MN下方作等腰直角三角形NMP,MN=MP,∠NMP=90°,连接OP.请直接写出线段OP的最小值及此时ON的长度.【思路点拨】本题考查四边形综合应用,涉及全等三角形判定与性质,等腰直角三角形性质等,解题的关键是掌握全等三角形判定定理.(1)由∠BAC=∠DAE,可得∠BAD=∠CAE,根据SAS可得△ABD≌△ACE,则可得出结论;(2)由∠BAC=∠DAE=90°,得∠BAD=∠CAE,即可证△ABD≌△ACE(SAS),有BD=CE,∠ACE=∠ABC,而△ABC是等腰三角形且∠BAC=90°,知∠ABC=∠ACB=45°,故∠ACE=∠ABC=45°,即可得∠BCE=∠ACB+∠ACE=45°+45°=90°,BD⊥CE;(3)证明∠O′MO=45°,当OP有最小,即O′P′最小,即垂线段最短,当O′P′⊥y轴时,O′P′最小,则可得出答案.【解题过程】(1)∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,AB=AC∠BAD=∠CAE,AD=AE∴△ABD≌△ACE(SAS);故答案为:△ACE;BD=CE;(2)解:BD与CE的数量关系是BD=CE,位置关系是BD⊥CE ∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,AB=AC∠BAD=∠CAE,AD=AE∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC,∵△ABC是等腰三角形且∠BAC=,∴∠ABC=∠ACB=45°,∴∠ACE=∠ABC=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°,∴BD⊥CE;(3)∵△MNP是等腰直角三角形,∴∠MNP=∠NPM=45°,将△OPM绕M点顺时针旋转90°得△O′P′M(N与P′重合),连接OO′,∴△PMO≌△P′MO′,∴MO=MO′,OP=O′P′,∴∠O′MO=45°,当OP有最小,即O′P′最小,当O′P′⊥y轴时,由∠O′OP′=45°,∠O′P′O=90°,∴O′P′=OM=4,ON=OP′=4,∴ON=4,OP最小值为4.11.(23-24七年级下·浙江宁波·期末)【基础巩固】(1)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,求证:△AEC≌△ADB;【尝试应用】(2)如图2,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,B、D、E 三点在一条直线上,AC与BE交于点F,若点F为AC中点,①求∠BEC的大小;②CE=2,求△ACE的面积;【拓展提高】(3)如图3,△ABC与△ADE中,AB=AC,DA=DE,∠BAC=∠ADE=90°,BE与CA 交于点F,DC=DF,△BCF的面积为32,求AF的长.【思路点拨】(1)由SAS证△AEC≌△ADB即可;(2)①同(1)得△AEC≌△ADB (SAS),得∠AEC =∠ADB =135°,即可得出结论;②过点A 作AG ⊥DE 于点G ,证△AGF≌△CEF (ASA),得AG =CE =2,GF =EF ,再由等腰直角三角形的性质得DG =EG =AG =2,则GF =EF =1,然后由三角形面积关系即可得出结论;(3)连接CE ,同(2)得△CDE≌△FDA (SAS),则CE =AF ,∠DCE =∠DFA =135°,得∠ACE =90°,再证△ACE≌△BAF (SAS),得CE =AF ,S △ACE =S △BAF ,然后证CE∥AB ,得S △ABE =S △ABC =12AC 2,进而由S △ABC +S △ACE ―S △ABE ―S △CEF =S △BCF ,得AC ⋅AF ―AF ⋅CF =64,则AF 2=64,即可得出结论.【解题过程】(1)证明:∵∠BAC =∠DAE ,∴∠BAC ―∠BAE =∠DAE ―∠BAE ,即∠CAE =∠BAD ,在△AEC 和△ADB 中,AC =AB ∠CAE =∠BAD AE =AD,∴△AEC≌△ADB (SAS);(2)解:①∵AD =AE ,∠DAE =90°,∴∠ADE =∠AED =45°,∴∠ADB =180°―∠ADE =180°45°=135°,同(1)得:△AEC≌△ADB (SAS),∴∠AEC =∠ADB =135°,∴∠BEC =∠AEC ―∠AED =135°―45°=90°;②如图2,过点A 作AG ⊥DE 于点G ,则∠FGA =90°,由①可知,∠FEC =90°,∴∠FGA =∠FEC,∵点F 为AC 中点,∴AF =CF ,又∵∠AFG =∠CFE ,∴△AGF≌△CEF (AAS),∴AG =CE =2,GF =EF ,∵AD =AE ,∠DAE =90°,∴DG =EG =AG =2,∴GF =EF =12EG =1,∴S △ACE =2S △CEF =2×12CE ⋅EF =2×1=2;(3)解:如图3,连接CE ,同(2)得:△CDE≌△FDA (SAS),∴CE =AF ,∠DCE =∠DFA =135°∴∠ACE =∠DCE ―∠ACB =135°―45°=90°,在△ACE 和△BAF 中,AC =AB ∠ACE =∠BAF =90°CE =AF,∴△ACE≌△BAF (SAS),∴S △ACE =S △BAF ,∵∠ACE =∠BAC ,∴CE∥AB ,∴S △ABE =S △ABC =12AC ⋅AB =12AC 2,∵S △ABC +S △ACE ―S △ABE ―S △CEF =S △BCF ,∴ 1AC 2+1AC ⋅CE ―1AC 2―1CE ⋅CF =32,∴AC⋅AF―AF⋅CF=64,∴AF(AC―CF)=64,∴AF2=64,∴AF=8,负值舍去,即AF的长为8.12.(2023·甘肃张掖·模拟预测)在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化时,始终存在一对全等三角形.通过查询资料,他们得知这种模型称为“手拉手模型”.兴趣小组进行了如下操作:(1)观察猜想:如图①,已知△ABC,△ADE均为等边三角形,点D在边BC上,且不与点B、C重合,连接CE,易证△ABD≌△ACE,进而判断出AB与CE的位置关系是___________(2)类比探究:如图②,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,试说明点B,D,E在同一直线上;(3)解决问题:如图③,已知点E△ABC的外部,并且与点B位于线段AC的异侧,连接AE、BE、CE.若∠BEC=60°,AE=3,CE=2,请求出BE的长.【思路点拨】本题考查了等边三角形的判定与性质,全等三角形的判定与性质等知识,解题的关键是:(1)利用SAS证明△BAD≌△CAE,可求出∠BAC=∠ACE=60°,利用平行线的判定即可得出结论;(2)利用SAS证明△BAD≌△CAE,可得出∠ADB=∠AEC=120°,进而得出∠ADB+∠ADE=180°,即可得证;(3)在线段BE上取一点H,使得BH=CE,设AC交BE于点O,先利用外角的性质证明∠ABH=∠ACE,再利用SAS证明△ABH≌△ACE,得出∠BAH=∠CAE,AH=AE,则可证明△AEH是等边三角形,得出AE=EH,即可求解.【解题过程】(1)解:AB∥CE,理由如下:∵△ABC 、△ADE 都是等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =∠B =60°,∴∠BAC ―∠DAC =∠DAE ―∠DAC ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△BAD≌△CAE (SAS),∴∠B =∠ACE =60°,∴∠BAC =∠ACE =60°,∴AB∥CE ;故答案为:AB∥CE ;(2)证明:∵△ABC 、△ADE 都是等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =∠ADE =60°,∴∠BAC ―∠DAC =∠DAE ―∠DAC ,即∠BAD =∠CAE ,∵∠AED =60°,∠DEC =60°,∴∠AEC =120°,在△BAD 和△CAE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△BAD≌△CAE (SAS),∴∠ADB =∠AEC =120°,∴∠ADB +∠ADE =180°,∴点B ,D ,E 在同一直线上;(3)解:如图③,在线段BE 上取一点H ,使得BH =CE ,设AC 交BE 于点O ,∵△ABC是等边三角形,∴AB=BC,∠BAC=60°,∵∠BEC=60°,∴∠BAO=∠OEC=60°,∵∠AOB=∠EOC,∴∠ABH=∠ACE,在△ABH和△ACE中,AB=AC∠ABH=∠ACE,BH=CE∴△ABH≌△ACE(SAS),∴∠BAH=∠CAE,AH=AE,∴∠HAE=∠BAC=60°,∴△AEH是等边三角形,∴AE=EH,∴BE=BH+EH=EC+AE,即BE=AE+EC,∵AE=3,CE=2,∴BE=3+2=5.13.(23-24八年级上·河北沧州·期末)在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),把线路AD绕着点A逆时针旋转至AD=AE),使得∠DAE=∠BAC,连接DB、CE.(1)如图1,点D在线段BC上,如果∠BAC=90°,则∠BCE=__________度.Array(2)如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE=__________度.(3)如图3,设∠BAC =α,∠BCE =β,当点D 在线段BC 上移动时,α,β的数量关系是什么?请说明理由.(4)设∠BAC =α,∠BCE =β,当点D 在直线BC 上移动时,请直接写出α,β的数量关系,不用证明.【思路点拨】(1)由“SAS ”可证△BAD≌△CAE ,得∠ABC =∠ACE =45°,可求∠BCE 的度数;(2)由“SAS ”可证△BAD≌△CAE ,得∠ABC =∠ACE =60°,可求∠BCE 的度数;(3)由“SAS ”可证△BAD≌△CAE 得出∠ABD =∠ACE ,再用三角形的内角和即可得出结论;(4)由“SAS ”可证△BAD≌△CAE 得出∠ABD =∠ACE ,再用三角形的内角和即可得出结论.【解题过程】(1)解:∵∠BAC =90°,∴∠DAE =∠BAC =90°,∵AB =AC ,AD =AE ,∴∠B =∠ACB =45°,∠ADE =∠AED =45°,∵∠DAE =∠BAC ,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△BAD≌△CAE (SAS),∴∠ACE =∠B =45°,∴∠BCE =∠ACB +∠ACE =90°,故答案为:90;(2)∵∠BAC =60°,∴∠DAE =∠BAC =60°,∵AB =AC ,AD =AE,∴∠B=∠ACB=60°,∠ADE=∠AED=60°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),∴∠ACE=∠B=60°,∴∠BCE=∠ACB+∠ACE=120°,故答案为:120;(3)α+β=180°,理由如下:∵AB=AC,AD=AE,∠DAE=∠BAC,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),∴∠ACE=∠B,∴∠ACE+∠ACB=∠B+∠ACB,∵∠BCE=∠ACB+∠ACE=β,∴∠B+∠ACB=β,∵∠BAC=α,∠BAC+∠B+∠ACB=180°,∴α+β=180°;(4)如图4,当点D在BC的延长线上时,α+β=180°,证明方法同(3);如图5,当点D 在CB 的延长线上时,α=β,理由如下:∵∠DAE =∠BAC ,∴∠DAB +∠BAE =∠EAC +∠BAE ,∴∠DAB =∠EAC ,在△BAD 和△CAE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△BAD≌△CAE (SAS),∴∠ABD =∠ACE ,∵∠ABD =∠BAC +∠ACB ,∠ACE =∠BCE +∠ACB ,∴∠BAC =∠BCE ,∵∠BAC =α,∠BCE =β,∴α=β.综上,α+β=180°或α=β.14.(24-25九年级上·广东深圳·开学考试)【初步感知】(1)如图1,已知△ABC 为等边三角形,点D 为边BC 上一动点(点D 不与点B ,点C 重合).以AD 为边向右侧作等边△ADE ,连接CE .求证:△ABD≌△ACE;【类比探究】(2)如图2,若点D 在边BC 的延长线上,随着动点D 的运动位置不同,线段EC ,AC ,CD 之间的数量关系为__________,请证明你的结论.【拓展应用】(3)如图3,在等边△ABC 中,AB =5,点P 是边AC 上一定点且AP =2,若点D 为射线BC 上动点,以DP 为边向右侧作等边△DPE ,连接CE ,BE .请问:PE +BE 是否有最小值?若有,请求出其最小值;若没有,请说明理由.【思路点拨】本题考查三角形综合,全等三角形的判定,等边三角形的判定与性质,掌握相关知识是解题的关键.(1)由△ABC 和△ADE 是等边三角形,推出AB =AC ,AD =AE ,∠BAC =∠DAE =60°,又因为∠BAC =∠DAE ,则∠BAC ―∠DAC =∠DAE ―∠DAC ,即∠BAD =∠CAE ,利用SAS 证明△ABD≌△ACE 即可;(2)证明△ABD≌△ACE (SAS),得出CE =BD ,结合AC =BC ,则CE =BD =BC +CD =AC +CD ;(3)在射线BC 上截取PC =DM ,连接EM ,易证△EPC≌△EDM ,则EC =EM ,∠CEM =∠PED =60°,得出△CEM 是等边三角形,则∠ECM =60°,即点E 在∠ACD 角平分线上运动,在射线CD 上截取CP ′=CP ,连接EP ′,证明△CEP≌△CEP ′(SAS),得出PE =P ′E ,推出BE +PE =BE +P ′E ,由三角形三边关系可得,BE +P ′E ≥BP ′,即当点E 与点C 重合时,BE +P ′E =BP ′时,BE +PE 有最小值BP ′.【解题过程】(1)证明:∵ △ABC 和△ADE 是等边三角形,∴ AB =AC ,AD =AE ,∠BAC =∠DAE =60°.∵ ∠BAC =∠DAE ,∴ ∠BAC ―∠DAC =∠DAE ―∠DAC ,即∠BAD =∠CAE .在△ABD 和△ACE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△ABD≌△ACE(SAS).(2)解:EC=AC+CD,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°.∵∠BAC=∠DAE,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中,AB=AC∠BAD=∠CAE,AD=AE∴△ABD≌△ACE(SAS).∴CE=BD,∵AC=BC,∴CE=BD=BC+CD=AC+CD.(3)解:有最小值,在射线BC上截取PC=DM,连接EM,,∵△ABC和△DPE是等边三角形,∴PE=ED,∠DPE=∠ACB=60°,∴∠ACD=180°―∠ACB=120°,∴∠ACD+∠DEP=180°,∵∠PCE+∠CEP+∠EPC=180°,∠ECD+∠CDE+∠CED=180°,∴∠ECD+∠CDE+∠CED+∠PCE+∠CEP+∠EPC=360°,∵∠PCE+∠ECD+∠CEP+∠CED―∠ACD+∠DEP=180°,∴∠EPC+∠CDE=180°,∴∠EPC=∠EDM,在△EPC和△EDM 中,PE=ED∠EPC=∠EDM,PC=DM∴△EPC≌△EDM(SAS),∴EC=EM,∠PEC=∠DEM,∵∠PEC+∠CED=∠DEP=60°,∴∠CEM=∠DEM+∠CED=60°,∴△CEM是等边三角形,∴∠ECM=60°,∴∠ECD=60°,∠ACE=180°―∠ECD―∠ACB=60°,即点E在∠ACD角平分线上运动,在射线CD上截取CP′=CP,连接EP′,在△CEP和△CEP′中,PC=P′C,∠PCE=∠P′CECE=CE∴△CEP≌△CEP′(SAS),∴PE=P′E,∴BE+PE=BE+P′E,由三角形三边关系可得,BE+P′E BP′,即当点E与点C重合时,BE+P′E=BP′时,BE+PE有最小值BP′,∵AP=2,AC=BC=AB=5,∴PC=AC―AP=3,∴BE+PE=BE+P′E=BP′=BE+CP′=BC+CP=5+3=8∴BE+PE的最小值为8.15.(23-24七年级下·陕西西安·期末)问题发现:学习三角形全等的知识时,小明发现重合两个等腰直角三角形的顶点会产生一对新的全等三角形.如图1,Rt△ABC中,∠BAC=90°,AB=AC,点D在边BC上,连接AD,以AD为边作△ADE,使∠DAE=90°,AD=AE,请连接图中标有字母的点,补全图形,直接写出一对全等三角形和∠BCE的度数.问题探究:小明想,如果将上图中的等腰直角三角形换成等边三角形,那么这组全等三角形是否还存在?如图2,△ABC和△ADE是等边三角形,点B,D,E在同一直线.(1)证明:△ABD≌△ACE .(2)探索线段BE ,AE ,CE 三者间的数量关系,写出结论并说明理由.问题拓展:经过上面的探究,小明联想到几天前一道不会的题,请你帮小明再想一想,是否有新的发现.如图3,边长为a 的等边△ABC 中,D 是AC 中点,BD =b ,E 是线段BD 上一动点,连接AE ,在AE 右侧作等边△AEF ,连接FD ,求△AFD 周长的最小值(用含a ,b 的代数式表示),并直接写出取最小值时∠AFD 的度数.【思路点拨】问题发现:由∠BAC =90°,∠DAE =90°,得到∠BAD =∠CAE ,可证明△ABD≌△ACE ,推出∠ABD =∠ACE ,由Rt △ABC 中,∠BAC =90°,AB =AC ,可得∠ABC =∠ACB =45°,得到∠ACE =45°,即可求解;问题探究:(1)由△ABC 和△ADE 是等边三角形,得到∠BAC =∠DAE =60°,AB =BC =AC ,AD =AE =DE ,推出∠BAD =∠CAE ,即可证明;(2)由△ABD≌△ACE 可得BD =CE ,推出BE =DE +BD =AE +CE ;问题拓展:证明△ABE≌△ACF ,得到∠ACF =∠ABE ,由于∠ABE 是定值,所以∠ACF 为定值,P 在一条固定的线段上运动,延长CF 至点P ,使得BD =CP ,推出点F 在线段CP 上运动,以直线CP 为对称轴,作点A 的对称点A ′,得到AC =A ′C ,AF =A ′F ,根据三角形的三边关系可得AF +DF =A ′F +FD ≥A ′D ,令A ′D 与CP 交于点F ′,则有AF ′+F ′D =A ′D ,根据全等三角形的性质,等边三角形的判定与性质推出DA ′=BD ,得到C △AFD =AF +DF +AD ≤AF ′+DF ′+AD =DA ′+AD ,可求出△AFD 周长的最小值;延长AF ′交A ′C 于点D ′,由∠AF ′D =180°―∠ADF ′―∠F ′AD 可求出此时∠AFD 的度数.【解题过程】解:问题发现:∵ ∠BAC =90°,∠DAE =90°,∴ ∠BAC ―∠DAC =∠DAE ―∠DAC ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB =AC ∠BAD =∠CAE AD =AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵Rt△ABC中,∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∴∠ACE=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°;问题探究:(1)∵△ABC和△ADE是等边三角形,∴∠BAC=∠DAE=60°,AB=BC=AC,AD=AE=DE,∴∠BAC―∠DAC=∠DAE―∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△ABD≌△ACE(SAS);(2)BE=AE+CE,理由如下:∵△ABD≌△ACE,∴BD=CE,∵AE=DE,∴BE=DE+BD=AE+CE;问题拓展:连接CF,∵△ABC和△AEF是等边三角形,∴∠BAC=∠EAF=60°,AB=BC=AC,AE=AF=EF,∴∠BAC―∠EAD=∠EAF―∠EAD,即∠BAE=∠CAF,在△BAE和△CAF中,AB=AC∠BAE=∠CAF,AF=AE∴△ABE≌△ACF(SAS)∴∠ACF=∠ABE,由于∠ABE是定值,所以∠ACF为定值,P在一条固定的线段上运动,如图3,延长CF至点P,使得BD=CP,。
八年级手拉手模型典型例题及解析

八年级手拉手模型典型例题及解析1. 概述手拉手模型作为数学中一个重要的解题方法,是指通过将一道难题分解成多个简单的小问题,再逐一解决,最终得出整体的解题过程。
在八年级的数学学习中,手拉手模型的应用尤为重要,下面我们将以典型例题为例,介绍手拉手模型的具体应用。
2. 例题一题目:有一根长为14厘米的铁丝,要用它围成一个面积最大的矩形,求这个最大的矩形的面积。
解析:步骤一:分析问题,设矩形的长为x厘米,宽为(14-2x)厘米。
步骤二:列出等式,设矩形的面积为S,即S=x*(14-2x)。
步骤三:求导并求零点,对S求x的导数得S'=-2x+14,令S'=0,解得x=7。
步骤四:验证解的有效性,计算得到S=7*14-2*7*7=98。
步骤五:得出结论,当x=7时,面积最大,为98平方厘米。
3. 例题二题目:水桶的容积是15升,一管子每秒钟往水桶注入2升的水,另一管子每秒钟注入3升的水,现在两管子一起注水,问多长时间后,两管子总共注满水桶?解析:步骤一:设t为注水时间(秒),则第一管子注水量为2t,第二管子注水量为3t,总注水量为2t+3t=15。
步骤二:列出方程,得到5t=15,解得t=3。
步骤三:得出结论,三秒后,两管子总共注满水桶。
4. 例题三题目:甲、乙两人合作种植一片甘蔗地,甲单独干活需要6天,乙单独干活需要8天,两人合作干活,两天完成了一项任务,求两人的合作效率。
解析:步骤一:设甲乙合作的效率为x,甲的效率为y,则乙的效率为(1-x)。
步骤二:根据效率的定义,列出方程,得到2*(x+y)=1,2*(x+1-x)=1,解得x=1/12,y=1/6。
步骤三:得出结论,甲乙合作的效率为1/12,甲的效率为1/6,乙的效率为1/4。
5. 结论通过以上典型例题的解析,我们了解了手拉手模型在解题过程中的应用方法。
在实际的数学学习和解题中,我们可以根据不同问题的特点,灵活运用手拉手模型,将复杂的问题分解成简单的小问题,逐一解决,最终得出整体的解题过程。
模型11 手拉手模型(解析版)

模型介绍共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。
寻找共顶点旋转模型的步骤如下: (1)寻找公共的顶点(2)列出两组相等的边或者对应成比例的边(3)将两组相等的边分别分散到两个三角形中去,证明全等或相似即可。
两等边三角形两等腰直角三角形两任意等腰三角形*常见结论:连接BD 、AE 交于点F ,连接CF ,则有以下结论:(1)BCD ACE≅△△(2)AE BD=(3)AFB DFE∠=∠(4)FC BFE∠平分【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
【知识总结】【基本模型】一、等边三角形手拉手-出全等图1图2图3图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有:①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;图1图2图3图4手拉手模型的定义:两个顶角相等且有共顶点的等腰三角形形成的图形。
手拉手模型特点:“两等腰,共顶点”模型探究:例题精讲考点一:等边三角形中的手拉手模型【例1】.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.有下列结论:①AD=BE;②AP=BQ;③∠AOB=60°;④DC=DP;⑤△CPQ为正三角形.其中正确的结论有_____________.解:∵△ABC和△DCE是正三角形,∴AC=BC,DC=CE,∠BCA=∠DCE=60°,∴∠BCA+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,在△ACD和△BCE中∴△ACD≌△BCE(SAS),∴AD=BE,∴①正确;∵△ACD≌△BCE,∴∠CBE=∠CAD,∵∠ACB=∠DCE=60°,∴∠BCD=60°=∠ACB,在△ACP和△BCQ中∴△ACP≌△BCQ(ASA),∴AP=BQ,∴②正确;PC=QC,∴△CPQ为正三角形∴⑤正确∵△ACD≌△BCE,∴∠ADC=∠BEC,∠DCE=60°=∠CAD+∠ADC,∴∠CAD+∠BEC=60°,∴∠AOB=∠CAD+∠BEC=60°,∴③正确;∵△DCE 是正三角形,∴DE =DC ,∵∠AOB =60°,∠DCP =60°,∠DPC >∠AOB ,∴∠DPC >∠DCP ,∴DP <DC ,即DP <DE ,∴④错误;所以正确的有①②③⑤变式训练【变式1-1】.如图,ABD ∆,AEC ∆都是等边三角形,则BOC ∠的度数是()A .135︒B .125︒C .120︒D .110︒解:ABD ∆ ,AEC ∆都是等边三角形,AD AB ∴=,AE AC =,60DAB CAE ∠=∠=︒,60ADB DBA ∠==︒,DAB BAC CAE BAC ∴∠+∠=∠+∠,DAC BAE ∴∠=∠,()DAC BAE SAS ∴∆≅∆,ADC ABE ∴∠=∠,BOC BDO DBA ABE∴∠=∠+∠+∠BDO DBA ADC =∠+∠+∠ADB DBA=∠+∠6060=︒+︒120=︒,BOC ∴∠的度数是120︒故选:C .【变式1-2】.如图,△DAC 和△EBC 均是等边三角形,AE 、BD 分别与CD 、CE 交于点M 、N ,有如下结论:①△ACE ≌△DCB ;②CM =CN ;③AC =DN ;④∠DAE =∠DBC .其中正确的有()A .②④B .①②③C .①②④D .①②③④解:∵△DAC 和△EBC 均是等边三角形,∴AC =DC ,BC =CE ,∠ACE =∠BCD ,∴△ACE≌△DCB,①正确由①得∠AEC=∠CBD,∴△BCN≌△ECM,∴CM=CN,②正确假使AC=DN,即CD=CN,△CDN为等边三角形,∠CDB=60°,又∵∠ACD=∠CDB+∠DBC=60°,∴假设不成立,③错误;∵∠DBC+∠CDB=60°∠DAE+∠EAC=60°,而∠EAC=∠CDB,∴∠DAE=∠DBC,④正确,∴正确答案①②④故选:C.【变式1-3】.如图,△ABC和△ADE都是等边三角形,点D在BC上,DE与AC交于点F,若AB=5,BD=3,则=.解:连接CE,过点F作FM⊥BC于点M,FN⊥CE于点N,∵△ABC和△ADE为等边三角形,∴AB=AC,AD=AE,∠BAC DAE=60°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=CE=3,∠ABD=∠ACE=60°,∵AB=BC=5,∴DC=2,∵∠ACB=∠ACE=60°,FM⊥BC,FN⊥CE,∴FM=FN,=DC•FM,S△FCE=CE•FN,∵S△DFC∴,∴,故答案为:.考点二:等腰直角三角形中的手拉手模型【例2】.如图,ACB∆和ECD∆都是等腰直角三角形,90ACB ECD∠=∠=︒,D为AB边上一点,若5AD=,12BD=,则DE的长为__________解:ACB∆和ECD∆都是等腰直角三角形,CD CE∴=,AC BC=,90ECD ACB∠=∠=︒,ACE BCD∴∠=∠,在ACE∆和BCD∆中,CE CDACE BCD AC BC=⎧⎪∠=∠⎨⎪=⎩,()ACE BCD SAS∴∆≅∆,12BD AE∴==,45CAE CBD∠=∠=︒,90EAD∴∠=︒,222212513DE AE AD∴=+=+=.变式训练【变式2-1】.如图,3AB=,2AC=,连结BC,分别以AC、BC为直角边作等腰Rt ACD∆和等腰Rt BCE∆,连结AE、BD,当AE最长时,BC的长为()A.22B.3C.11D.17解:90ACD BCE∠=∠=︒,ACD ACB BCE ACB∴∠+∠=∠+∠,即ACE DCB∠=∠,在ACE ∆和DCB ∆中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,()ACE DCB SAS ∴∆≅∆,AE BD ∴=,AC CD == ,90ACD ∠=︒,2AD ∴=,3AB = ,∴当点A 在BD 上时,BD 最大,最大值为325+=,如图,过C 作CE AD ⊥于E ,由等腰三角形“三线合一”得1DE AE ==,314BE AB AE ∴=+=+=,再由直角三角形斜边中线等于斜边一半得1DE =,BC ∴=.故选:D .【变式2-2】.如图,在Rt ABC ∆中,AB AC =,点D 为BC 中点,点E 在AB 边上,连接DE ,过点D 作DE 的垂线,交AC 于点F .下列结论:①AED CFD ∆≅∆;②EF AD =;③BE CF AC +=;④212AEDF S AD =四边形,其中正确的结论是(填序号).解:AB AC = ,90BAC ∠=︒,点D 为BC 中点,12BD CD AD BC ∴===,45BAD CAD C ∠=∠=∠=︒,AD BC ⊥,BC =,DF DE ⊥ ,90EDF ADC ∴∠=∠=︒,ADE CDF ∴∠=∠,AD CD = ,BAD C ∠=∠,()AED CFD ASA ∴∆≅∆,故①正确;当E 、F 分别为AB 、AC 中点时,12EF BC AD ==,故②不一定正确;ADE CDF ∆≅∆ ,AE CF ∴=,BE AE AB += ,BE CF AC ∴+=,故③正确;ADE CDF ∆≅∆ ,ADE CDF S S ∆∆∴=,212ADF CDF ADC AEDF S S S S AD ∆∆∆∴=+==⨯四边形,故④正确;故答案为:①③④.【变式2-3】.如图,△ABC 和△CEF 均为等腰直角三角形,E 在△ABC 内,∠CAE +∠CBE =90°,连接BF .(1)求证:△CAE ∽△CBF .(2)若BE =1,AE =2,求CE 的长.(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴==,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;(2)解:∵△CAE∽△CBF,∴∠CAE=∠CBF,==,又∵==,AE=2∴=,∴BF=,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴EF2=BE2+BF2=12+()2=3,∴EF=,∵CE2=2EF2=6,∴CE=.考点三:任意等腰三角形中的手拉手模型【例3】.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD =36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论是_____.解:∵∠AOB=∠COD=36°,∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,在△AOC和△BOD中,∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,故②正确;∵∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OBD=∠OAC+∠AOB,∴∠AMB=∠AOB=36°,故①正确;法一:作OG⊥AM于G,OH⊥DM于H,如图所示,则∠OGA=∠OHB=90°,∵△AOC≌△BOD,∴OG=OH,∴MO平分∠AMD,故④正确;法二:∵△AOC≌△BOD,∴∠OAC=∠OBD,∴A、B、M、O四点共圆,∴∠AMO=∠ABO=72°,同理可得:D、C、M、O四点共圆,∴∠DMO=∠DCO=72°=∠AMO,∴MO平分∠AMD,故④正确;假设MO平分∠AOD,则∠DOM=∠AOM,在△AMO与△DMO中,,∴△AMO≌△DMO(ASA),∴AO=OD,∵OC =OD ,∴OA =OC ,而OA <OC ,故③错误;变式训练【变式3-1】.如图,等腰ABC ∆中,120ACB ∠=︒,4AC =,点D 为直线AB 上一动点,以线段CD 为腰在右侧作等腰CDE ∆,且120DCE ∠=︒,连接AE ,则AE 的最小值为()A .23B .4C .6D .8解:连接BE 并延长交AC 延长线于F ,120ACB ∠=︒ ,AC BC =,30CAB CBA ∴∠=∠=︒,120DCE ACB ∠=︒=∠ ,ACD BCE ∴∠=∠,AC BC = ,CD CE =,()ACD BCE SAS ∴∆≅∆,30CBE CAD ∴∠=∠=︒,CB 为定直线,30CBE ∠=︒为定值,∴当D 在直线AB 上运动时,E 也在定直线上运动,当AE BE ⊥时,AE 最小,30CAB ABC CBE ∠=︒=∠=∠ ,90AFB ∴∠=︒,∴当E 与F 重合时,AE 最小,在Rt CBF ∆中,90CFB ∠=︒,30CBF ∠=︒,122CF CB ∴==,6AF AC CF ∴=+=,AE ∴的最小值为6AF =,故选:C .【变式3-2】.如图,在△ABC 中,AB =AC =5,∠BAC =120°,以CA 为边在∠ACB 的另一侧作∠ACM =∠ACB ,点D 为边BC (不含端点)上的任意一点,在射线CM 上截取CE =BD ,连接AD ,DE ,AE .设AC 与DE 交于点F ,则线段CF 的最大值为.解:∵∠BAC=120°,AB=AC,∴∠B=∠ACB=30°.∵∠ACM=∠ACB,∴∠B=∠ACM=30°.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴AD=AE,∠BAD=∠CAE.∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120°.即∠DAE=120°.∵AD=AE,∴∠ADE=∠AED=30°;∵∠ADE=∠ACB=30°且∠DAF=∠CAD,∴△ADF∽△ACD.∴=.∴AD2=AF•AC.∴AD2=5AF.∴AF=.∴当AD最短时,AF最短、CF最长.∵当AD⊥BC时,AF最短、CF最长,此时AD=AB=.∴AF最短==.∴CF最长=AC﹣AF最短=5﹣=.故答案为:.【变式3-3】.【问题背景】(1)如图1,等腰ABC ∆中,AB AC =,120BAC ∠=︒,AQ BC ⊥于点Q ,则BC AB =;【知识应用】(2)如图2,ABC ∆和ADE ∆都是等腰三角形,120BAC DAE ∠=∠=︒,D 、E 、C 三点在同一条直线上,连接BD .求证:ADB AEC ∆≅∆.(3)请写出线段AD ,BD ,CD之间的等量关系,并说明理由.(1)解:AB AC = ,120BAC ∠=︒,AQ BC ⊥,30B C ∴∠=∠=︒,BQ QC =,12AQ AB ∴=,由勾股定理得:32BQ AB ===,BC ∴=,∴BC AB ==(2)证明:BAC DAE ∠=∠ ,BAC BAE DAE BAE ∴∠-∠=∠-∠,即DAB EAC ∠=∠,在ADB ∆和AEC ∆中,AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩,()ADB AEC SAS ∴∆≅∆;(3)解:CD BD =+,理由如下:由(1)可知:DE =,ADB AEC ∆≅∆ ,EC BD ∴=,CD DE EC BD ∴=+=+.实战演练1.风筝为中国人发明,相传墨翟以木头制成木鸟,研制三年有成,是人类最早的风筝起源.如图,小飞在设计的“风筝”图案中,已知AB AD =,B D ∠=∠,BAE DAC ∠=∠,那么AC 与AE 相等.小飞直接证明ABC ADE ∆≅∆,他的证明依据是()A .SSSB .SASC .ASAD .AAS证明:BAE DAC ∠=∠ ,BAE EAC DAC EAC ∴∠+∠=∠+∠,BAC DAE ∴∠=∠,AB AD = ,B D ∠=∠,()ABC ADE ASA ∴∆≅∆,AC AE ∴=,故选:C .2.如图,ABD ∆,AEC ∆都是等边三角形,则BOC ∠的度数是()A .135︒B .125︒C .120︒D .110︒解:ABD ∆ ,AEC ∆都是等边三角形,AD AB ∴=,AE AC =,60DAB CAE ∠=∠=︒,60ADB DBA ∠==︒,DAB BAC CAE BAC ∴∠+∠=∠+∠,DAC BAE ∴∠=∠,()DAC BAE SAS ∴∆≅∆,ADC ABE ∴∠=∠,BOC BDO DBA ABE∴∠=∠+∠+∠BDO DBA ADC =∠+∠+∠ADB DBA=∠+∠6060=︒+︒120=︒,BOC ∴∠的度数是120︒,故选:C .3.如图,点A 是x 轴上一个定点,点B 从原点O 出发沿y 轴的正方向移动,以线段OB 为边在y 轴右侧作等边三角形,以线段AB 为边在AB 上方作等边三角形,连接CD ,随点B 的移动,下列说法错误的是()A .BOA BDC∆≅∆B .150ODC ∠=︒C .直线CD 与x 轴所夹的锐角恒为60︒D .随点B 的移动,线段CD 的值逐渐增大解:A .OBD ∆ 和ABC ∆都是等边三角形,60ABC OBD ODB BOD ∴∠=∠=∠=∠=︒,BO BD =,BC AB =,ABC DBA OBD DBA ∴∠-∠=∠-∠,CBD ABO ∴∠=∠,()BOA BDC SAS ∴∆≅∆,故A 不符合题意;B .BOA BDC ∆≅∆ ,90BDC BOA ∴∠=∠=︒,6090150ODC BDO BDC ∴∠=∠+∠=︒+︒=︒,故B 不符合题意;C .延长CD 交x 轴于点E ,150ODC ∠=︒ ,18030ODE ODC ∴∠=︒-∠=︒,90BOA ∠=︒ ,60BOD ∠=︒,30DOA BOA BOD ∴∠=∠-∠=︒,60DEA DOA ODE ∴∠=∠+∠=︒,∴直线CD 与x 轴所夹的锐角恒为60︒,故C 不符合题意;D .BOA BDC ∆≅∆ ,CD OA ∴=,点A 是x 轴上一个定点,OA ∴的值是一个定值,∴随点B 的移动,线段CD 的值不变,故D 符合题意;故选:D .4.如图,3AB =,2AC =BC ,分别以AC 、BC 为直角边作等腰Rt ACD ∆和等腰Rt BCE ∆,连结AE 、BD ,当AE 最长时,BC 的长为()A .22B .3C .11D .17解:90ACD BCE ∠=∠=︒ ,ACD ACB BCE ACB ∴∠+∠=∠+∠,即ACE DCB ∠=∠,在ACE ∆和DCB ∆中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,()ACE DCB SAS ∴∆≅∆,AE BD ∴=,2AC CD == ,90ACD ∠=︒,222AD AC CD ∴=+=,3AB = ,∴当点A 在BD 上时,BD 最大,最大值为325+=,如图,过C 作CE AD ⊥于E ,由等腰三角形“三线合一”得1DE AE ==,314BE AB AE ∴=+=+=,再由直角三角形斜边中线等于斜边一半得1DE =,2217BC CE BE ∴=+=.故选:D .5.如图,线段OA 绕点O 旋转,线段OB 的位置保持不变,在AB 的上方作等边PAB ∆,若1OA =,3OB =,则在线段OA 旋转过程中,线段OP 的最大值是()A 10B .4C .5D .5解:如图,以AO 为边,在AO 的左侧作等边AOH ∆,连接BH ,AOH ∆ ,ABP ∆是等边三角形,1AO AH OH ∴===,AB AP =,60OAH BAP ∠=∠=︒,OAP HAB ∴∠=∠,在OAP ∆和HAB ∆中,AO AH OAP HAB AP AB =⎧⎪∠=∠⎨⎪=⎩,()OAP HAB SAS ∴∆≅∆,OP BH ∴=,在OPH ∆中,BH OH OB <+,∴当点H 在BO 的延长线上时,BH 的最大值4OH OB =+=,OP ∴的最大值为4,故选:B .6.如图,O 是等边△ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,则∠AOB =150°.解:连接OO ′,如图,∵线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,∴BO ′=BO =4,∠O ′BO =60°,∴△BOO ′为等边三角形,∴∠BOO ′=60°,∵△ABC 为等边三角形,∴BA =BC ,∠ABC =60°,∴∠O ′BO ﹣∠ABO =∠ABC ﹣∠ABO ,即∠O ′BA =∠OBC ,在△O ′BA 和△OBC中,∴△O ′BA ≌△OBC (SAS ),∴O ′A =OC =5,在△AOO ′中,∵OA ′=5,OO ′=4,OA =3,∴OA 2+OO ′2=O ′A 2,∴∠AOO ′=90°,∴∠AOB =60°+90°=150°,故答案为:150°.7.如图,△ABC与△ADE均是等腰直角三角形,点B,C,D在同一直线上,AB=AC=2,AD=AE=3,∠BAC=∠DAE=90°,则CD=﹣.解:∵AB=AC=2,AD=AE=3,∠BAC=∠DAE=90°,∴BC=AB=2,DE=AE=3,∠BAD=∠CAE,∠ABC=45°=∠ACB,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴EC=BD,∠ABD=∠ACE=45°,∴∠ECB=∠ECD=90°,∴DE2=EC2+CD2,∴18=(2+CD)2+CD2,解得:CD=﹣,CD=﹣﹣(不合题意舍去),故答案为:﹣.8.如图,△ABC和△ADE均为等腰直角三角形,连接CD、BE,点F、G分别为DE、BE 的中点,连接FG.在△ADE旋转的过程中,当D、E、C三点共线时,若AB=3,AD=2,则线段FG的长为.解:连接BD,∠BAD=90°﹣∠BAE,∠CAE=90°﹣∠BAE,∴∠BAD=∠CAE.又AD=AE,AB=AC,∴△ADB≌△AEC(SAS).∴BD=CE,∠ADB=∠AEC=135°,∴∠BDC=135°﹣45°=90°.∵△ABC和△ADE均为等腰直角三角形,AB=3,AD=2,∴DE=2,BC=3.设BD=x,则DC=2+x,在Rt△BDC中,利用勾股定理BD2+DC2=BC2,所以x2+(2+x)2=18,解得x1=﹣﹣(舍去),x2=﹣+.∵点F、G分别为DE、BE的中点,∴FG=BD=.故答案为.9.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.解:猜测AE=BD,AE⊥BD;理由如下:∵∠ACD=∠BCE=90°,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,又∵△ACD和△BCE都是等腰直角三角形,∴AC=CD,CE=CB,在△ACE与△DCB中,∴△ACE≌△DCB(SAS),∴AE=BD,∠CAE=∠CDB;∵∠AFC=∠DFH,∠FAC+∠AFC=90°,∴∠DHF=∠ACD=90°,∴AE⊥BD.故线段AE和BD的数量相等,位置是垂直关系.10.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.证明:(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠E=45°,由(1)知△BAC≌△DAE,∴∠BCA=∠E=45°,∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF到G,使得FG=FB,∵AF⊥BG,∴∠AFG=∠AFB=90°,在△AFB和△AFG中,,∴△AFB≌△AFG(SAS),∴AB=AG,∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,∵∠GCA=∠DCA=45°,在△CGA和△CDA中,,∴△CGA≌△CDA(AAS),∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.11.已知△ABC和△ADE都是等边三角形,点D在射线BF上,连接CE.(1)如图1,BD与CE是否相等?请说明理由;(2)如图1,求∠BCE的度数;(3)如图2,当D在BC延长线上时,连接BE,△ABE、△CDE与△ADE的面积有怎样的关系?并说明理由.解:(1)BD=CE,理由如下:∵△ABC和△ADE是都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∠ABC=∠ACB=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;(2)∵△ABD≌△ACE,∴∠ABD=∠ACE=60°,∴∠BCE=120°;+S△CDE=S△ADE,理由如下:(3)S△ABE∵△ABC和△ADE是都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∠ABC=∠ACB=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),=S△ACE,∠ABC=∠ACE=60°,∴S△ABD∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ABC=∠ECD,∴AB∥CE,=S△ABC,∴S△ABE+S△CDE=S△ADE+S△ACD,∵S△ACE+S△CDE=S△ADE+S△ACD,∴S△ABD+S△ACD+S△CDE=S△ADE+S△ACD,∴S△ABC+S△CDE=S△ADE.∴S△ABE12.如图,在△ABC中,分别以AB、AC为腰向外侧作等腰Rt△ADB与等腰Rt△AEC,∠DAB=∠EAC=90°,连接DC、EB相交于点O.(1)求证:BE⊥DC;(2)若BE=BC.①如图1,G、F分别是DB、EC中点,求的值.②如图2,连接OA,若OA=2,求△DOE的面积.(1)证明:∵∠DAB=∠EAC=90°,∴∠EAB=∠CAD,在△BAE和△DAC中,,∴△BAE≌△DAC(SAS),∴∠ABE=∠ADC,∵∠BAD=90°,∴∠DOB=90°,即BE⊥DC;(2)解:①取DE的中点H,连接GH、FH,∵点G是BD的中点,∴GH∥BE,GH=BE,同理,FH∥CD,FH=CD,∵BE=CD.BE⊥DC,∴GH=FH,GH⊥FH,∴△HGF为等腰直角三角形,∴GF=GH,∵GH=BE,∴GF=BE,∵BE=BC,∴=;②作AM⊥BE于M,AN⊥CD于N,在△BAE和△BAC中,,∴△BAE≌△BAC(SSS),∴∠BAE=∠BAC=135°,∴∠DAE=135°﹣90°=45°,即∠OAD+∠OAE=45°,∵△BAE≌△DAC,∴AM=AN,又AM⊥BE,AN⊥CD,∴OA平分∠BOC,∴∠BOA=∠COA=45°,∴∠DOA=∠EOA=135°,∴∠ODA+∠OAD=45°,∴∠OAE=∠ODA,∴△ODA∽△OAE,∴=,即OD•OE=OA2=4,∴△DOE的面积=×OD•OE=2.13.如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD 为一边在AD的右侧作等腰直角△ADF,∠ADE=∠AED=45°,∠DAE=90°,AD=AE,解答下列问题:(1)如果AB=AC,∠BAC=90°,∠ABC=∠ACB=45°.①当点D在线段BC上时(与点B不重合),如图(2),线段CE、BD之间的数量关系为CE=BD;位置关系为CE⊥BD;(不用证明)②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,请写出结论并说明理由.(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?请写出条件,并借助图(4)简述CE⊥BD成立的理由.解:(1)①CE与BD位置关系是CE⊥BD,数量关系是CE=BD.理由:如图(2),∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,∴∠BAD=∠CAE.又BA=CA,AD=AE,∴△ABD≌△ACE(SAS),∴∠ACE=∠B=45°且CE=BD.∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即CE⊥BD.故答案为:CE=BD;CE⊥BD.②当点D在BC的延长线上时,①的结论仍成立.如图(3),∵∠DAE=90°,∠BAC=90°,∴∠DAE=∠BAC,∴∠DAB=∠EAC,又AB=AC,AD=AE,∴△DAB≌△EAC(SAS),∴CE=BD,且∠ACE=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD;(2)如图(4)所示,当∠BCA=45°时,CE⊥BD.理由:过点A作AG⊥AC交BC于点G,∴AC=AG,∠AGC=45°,即△ACG是等腰直角三角形,∵∠GAD+∠DAC=90°=∠CAE+∠DAC,∴∠GAD=∠CAE,又∵DA=EA,∴△GAD≌△CAE(SAS),∴∠ACE=∠AGD=45°,∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.14.(注意:本题中的说理过程中的每一步必须注明理由,否则不得分)如图1,在△ABC 中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°;①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为CF⊥BD,线段CF、BD的数量关系为CF=BD;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立?并说明理由;(2)如图4,如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.解:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC(SAS),∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.故答案为:CF⊥BD,CF=BD;②当点D在BC的延长线上时①的结论仍成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC(SAS),∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD;(2)当∠ACB=45°时,CF⊥BD.理由如下:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF(SAS),∴∠ACF=∠AGC=45°,∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.15.背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了下列三个问题,请你帮助解答:(1)将正方形AEFG绕点A按逆时针方向旋转(如图1),还能得到BE=DG吗?若能,请给出证明;若不能,请说明理由;(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图2),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)把背景中的正方形分别改写成矩形AEFG和矩形ABCD,且,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.(1)证明:∵四边形AEFG为正方形,∴AE=AG,∠EAG=90°,又∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠EAB=∠GAD,∴△AEB≌△AGD(SAS),∴BE=DG;(2)当∠EAG=∠BAD时,BE=DG,理由如下:∵∠EAG=∠BAD,∴∠EAB=∠GAD,又∵四边形AEFG和四边形ABCD为菱形,∴AE=AG,AB=AD,∴△AEB≌△AGD(SAS),∴BE=DG;(3)解:方法一:过点E作EM⊥DA,交DA的延长线于点M,过点G作GN⊥AB交AB于点N,由题意知,AE=4,AB=8,∵=,∴AG=6,AD=12,∵∠EMA=∠ANG,∠MAE=∠GAN,∴△AME∽△ANG,设EM=2a,AM=2b,则GN=3a,AN=3b,则BN=8﹣3b,∴ED2=(2a)2+(12+2b)2=4a2+144+48b+4b2,GB2=(3a)2+(8﹣3b)2=9a2+64﹣48b+9b2,∴ED2+GB2=13(a2+b2)+208=13×4+208=260.方法二:如图2,设BE与DG交于Q,BE与AG交于点P,∵,AE=4,AB=8∴AG=6,AD=12.∵四边形AEFG和四边形ABCD为矩形,∴∠EAG=∠BAD,∴∠EAB=∠GAD,∵,∴△EAB∽△GAD,∴∠BEA=∠AGD,∴A,E,G,Q四点共圆,∴∠GQP=∠PAE=90°,∴GD⊥EB,连接EG,BD,∴ED2+GB2=EQ2+QD2+GQ2+QB2=EG2+BD2,∴EG2+BD2=42+62+82+122=260.。
初二数学培优专题 (1)——共点“手拉手”模型(又称旋转“一拖二”模型)(答案详解)

共点手拉手模型(又称旋转“一拖二”模型)——兼谈最值、轨迹问题特点——公共点是等腰三角形顶角的顶点如图,若连接BB’、CC’,易证明△ABB’≌△ACC’(SAS)。
这就是传说中的“旋转一拖二”,又称为“手拉手模型”。
典型问题:【例1】(成都高新区2017-2018八年级上期27题)【例2】(成都金牛区2017-2018八年上期27题)如图,在△ABC中,∠B=45°,AB=22,2=BC,等腰直角∆ADE中,∠DAE=90°,2+3且点D是边BC上一点。
(1)(3 分)求AC的长;(2)(4 分)如图1,当点E恰在AC上时,求点E到BC的距离;(3)(3 分)如图2, 当点D从点B向点C运动时,求点E到BC的距离的最大值。
图1【例3】(2017届初二上期七中联盟半期)已知:ABC △是等腰直角三角形,动点P 在斜边AB 所在的直线上,以PC 为直角边作等腰直角三角形PCQ ,其中90PCQ =∠,探究并解决下列问题:(1)如图①,若点P 在线段AB上,且AC =,12PA =,则: ①线段PB =________,PC =________;②猜想:222,,PQ PA PB 三者之间的数量关系为_______________________;(2)如图②,若点P 在AB 的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程; (3)若动点P 满足4PA PB =,求PQAC的值.(提示:请利用备用图进行探求)图① 图② 备用图QCBPAQCB ACBA【例4】如图,已知30MON ∠=︒ ,B 为OM 上一点,BA ON ⊥ 于A ,四边形ABCD 为正方形,P 为射线BM 上一动点,连结CP ,将CP 绕点C 顺时针方向旋转90︒ 得CE ,连结BE ,若 4AB = ,则BE 的最小值为【例5】(成都武侯区2016-2017八年上期27题)如图,已知直线x y =过点A ,y AB ⊥轴于点B ,x AC ⊥轴于点C ,点P 是y 轴上的一动点,连接AP 交直线BC 于点E .点N 在直线BC 上,连接AN 且︒=∠90PAN ,在射线AN 上截取AE AD =,连接DE .(1)求证:2222AE EC BE =+;(2)若点A 的坐标是(6,m ),点P 的坐标是(0,m 32),求线段AD 的长; (3)当31=EC BE 时,求BPDE的值.27题【例6】(成都青羊区2016-2017八上期27题)在Rt ACB ∆中,90ACB ∠=︒,AC=BC ,D 为AB 上一点,连结CD ,将CD 绕C 点逆时针旋转90︒至CE ,连结DE ,过C 作CF ⊥DE 交AB 于F ,连结BE.(1)求证:AD=BE ;(2)求证:222AD BF DF +=; (3)若15ACD ∠=︒,1CD =+,求BF.【例7】(1)问题发现:如图1,△ACB 和△DCE 均为等边三角形,当△DCE 旋转至点A ,D ,E 在同一直线上,连接BE ,易证△BCE ≌△ACD .则 ①∠BEC =;②线段AD 、BE 之间的数量关系是 . (2)拓展研究:如图2,△ACB 和△DCE 均为等腰三角形,且∠ACB =∠DCE =90°,点A 、D 、E 在同一直线上,若AE =15,DE =7,求AB 的长度.(3)探究发现:如图3,P 为等边△ABC 内一点,且∠APC =150°,且∠APD =30°,AP =5,CP =4,DP =8,求BD 的长.E答案典型问题:【例1】(2017-2018上期成都高新区27题)解:(1)∵∠BAC=∠DAE=︒90 ∴∠BAD=∠CAE∵AB=AC ,AD=AE ∴△ABD ≌△ACE (SAS )(2)取AB 的中点G ,连接DG(I )∵∠BAC=∠DAE=︒120且点D是边BC上一点。
八年级下册 第一章 模型构建专题:“手拉手”模型——共顶点的等腰三角形(3类热点题型讲练)(解析版)

第08讲模型构建专题:“手拉手”模型——共顶点的等腰三角形(3类热点题型讲练)目录【类型一共顶点的等边三角形】 (1)【类型二共顶点的等腰直角三角形】 (11)【类型三共顶点的一般等腰三角形】 (21)【类型一共顶点的等边三角形】例题:(2023上·内蒙古呼和浩特·八年级统考期末)如图,已知点C 是AB 上一点,ACM △、CBN △都是等边三角形,连接AN 交CM 于点E ,连接BM 交CN 于点F .(1)求证:NAC BMC(2)连接EF ,判断CEF △的形状,并说明理由.【答案】(1)证明见解析(2)CEF △是等边三角形,理由见解析【分析】本题考查全等三角形的判定及性质以及等边三角形的判定和性质,(1)由等边三角形可得其对应线段相等,对应角相等,证明 SAS ACN MCB ≌,即可得证;(2)由(1)可得EAC FMC ,继而得到ACE MCF ,证明 ASA ACE MCF ≌,得CE CF ,根据等边三角形的判定即可得出结论;掌握全等三角形的判定和性质及等边三角形的判定和性质是解题的关键.【详解】(1)证明:∵ACM △与CBN △为等边三角形,∴60ACM BCN ,AC MC ,NC BC ,∴ACM MCN BCN NCM ,即ACN MCB ,在ACN △和MCB △中,AC MC ACN MCB NC BC,∴ SAS ACN MCB ≌;∴NAC BMC ;(2)CEF △为等边三角形.理由:∵180ACB ,60ACM BCN ,∴180606060MCF ACE ,∵NAC BMC ,即EAC FMC ,在ACE △和MCF △中,EACFMC AC MC ACE MCF,∴ASA ACE MCF ≌∴CE CF,∵60MCF ,∴CEF △是等边三角形.【变式训练】1.(2023春·全国·七年级专题练习)如图1,等边三角形BCD 和等边三角形ACE ,连接AD ,BE ,其中AC BC .(1)求证:AD BE ;(2)如图2,当点A C 、、B 在一条直线上时,AD 交CE 于点F ,BE 交CD 于点G ,求证:BG DF ;(3)利用备用图补全图形,直线AD ,BE 交于点H ,连接CH ,若3DH ,5CH ,直接写出BH 的长.【答案】(1)见解析(2)见解析(3)8BH 【分析】(1)由“SAS ”可证ACD ECB △≌△,可得AD BE ;(2)由“ASA ”可证BCG D CF ≌,可得BG DF ;(3)如图3,过点C 作CP BE 于P ,CN AD 于N ,由面积法可求CP CN ,可证60BH C CH A ,由直角三角形的性质可求 2.5PH HN ,由“AAS ”可证BCP D CN ≌,可得 5.5D N BP ,即可求解.【详解】(1)证明:BCD ∵ 和ACE △是等边三角形,BC CD ,AC CE ,60BCD ACE ,BCE DCA ,在ACD 和ECB 中,AC CE ACD ECB CD BC,()ACD ECB ≌SAS ,AD BE ;(2)证明:AC D EC B ∵ ≌,EBC ADC ,∵点C 在线段AB 上,60BCD ACE ,60DCE BCD ,在BCG 和DCF 中,90EBC ADC BC CD BCG DCF,()BCG DCF ≌ASA ,BG DF ;(3)解:如图3,过点C 作CP BE 于P ,CN AD 于N ,EBC ADC∵,DBH EBC,60DHB DCB,120BHA2.(2023上·广西南宁·八年级校考期中)数学课上,张老师带领学生们对课本一道习题层层深入研究.教材再现:如图,ABD △,AEC △都是等边三角形.求证:BE DC .(1)请写出证明过程;继续研究:(2)如图,在图1的基础上若CD 与BE 交于点O ,AB 与CD 交于点M ,AC 与BE 交于点N ,连接AO ,求证:AO 平分DOE ;(3)在(2)的条件下再探索OA ,OC ,OE 之间的数量关系,并证明.【答案】(1)证明见解析;(2)证明见解析;(3)OE OA OC ,理由见解析.【分析】(1)根据等边三角形性质得出AB AD ,AE AC ,60BAD BDA DBA CAE ,求出BAE DAC ,根据SAS 证ABE ADC △≌△即可;(2)过点A 分别作AG BE ,AH DC ,垂足为点G ,H ,由得到ABE ADC △≌△,从而ABE ADC S S ,故有AM AN ,根据角平分线判定即可求证;(3)在OE 上截取一点Q ,使得OQ OA ,证明AOQ △是等边三角形,即可证明 SAS OAC QAE ≌,从而得证.由(1)知:ABE ADC △≌△,BE ∴ABE ADC S S ,∴11··22BE AM DC AN ,∴AM AN ,由(1)知:ABE ADC△≌△, ,∴ADC ABE∴ADC BDO ABE BDO 在BOD中,为边在直线AD 右侧作等边三角形ADE .(1)如图1,当点D 在BC 边上时,连接CE ,此时AB ,CD ,CE 之间的数量关系为______,ACE ______;(2)如图2,当点D 在BC 的延长线上时,连接CE ,(1)中AB ,CD ,CE 之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请写出新的结论及证明过程;(3)如图3,当点D 在射线BC 上运动时,取AC 的中点F ,连接EF ,当EF 的值最小时,请直接写出CFE 的度数.【答案】(1)CE CD AB ;60(2)不成立,CE CD AB ,证明见解析(3)30【分析】(1)根据等边三角形的性质,证明ABD ACE ≌△△,可得ACE B ,CE BD ,即可得到AB ,CD ,CE 之间的数量关系;(2)同(1)中原理证明ABD ACE ≌△△,可得AB ,CD ,CE 之间新的数量关系;(3)本题考查了等边三角形的性质,全等三角形的判定和性质,连接CE ,取AB 的中点G ,连接DG ,根据ABD ACE ≌△△,证明BDG CFE ≌,则可得EF DG ,当GD BC 时,取最小值,则EF 此时也去最小值,即可求得此时CFE 的值,见手拉手模型则考虑证全等,将EF 转换到ABD △中等量的中线看最小值,是解题的关键.【详解】(1)解:ABC ∵ 是等边三角形,ADE V 是等边三角形,,AB AC AD AE ,BAC DAE ,,60AB BC B ,BAC DAC DAE DAC ,即BAD CAE ,在BAD 与CAE V 中,AB AC BAD CAE AD AE, SAS BAD CAE △≌△,CE BD ,60ACE B ,CE DC BD DC BC AB ,即CE CD AB ,故答案为:CE CD AB ;60 ;(2)不成立,CE CD AB ,证明如下:证明:ABC ∵ 是等边三角形,ADE V 是等边三角形,,AB AC AD AE ,BAC DAE ,AB BC ,BAC DAC DAE DAC ,即BAD CAE ,在BAD 与CAE V 中,AB AC BAD CAE AD AE, SAS BAD CAE △≌△,CE BD ,CE CD BD CD BC AB ,即CE CD AB ;(3)解:如图,连接CE ,取AB 的中点G ,连接DG ,【类型二共顶点的等腰直角三角形】例题:(2023春·全国·八年级专题练习)ABC 和△ADE 都是等腰直角三角形,90BAC DAE .(1)如图1,点D 、E 在AB ,AC 上,则BD ,CE 满足怎样的数量关系和位置关系?(直接写出答案不证明)(2)如图2,点D 在ABC 内部,点E 在ABC 外部,连接BD ,CE ,则BD ,CE 满足怎样的数量关系和位置关系?请说明理由.【答案】(1)BD CE ,BD CE(2)BD CE ,BD CE ,理由见解析【分析】(1)根据等腰直角三角形结合线段的和差即可得到结论;(2)延长BD ,分别交AC 、CE 于F 、G ,证明ABD ACE ≌△△,根据全等三角形的性质、垂直的定义解答;【详解】(1)解:∵ABC 和△ADE 都是等腰直角三角形,90BAC DAE ,∴AB AC ,AD AE ,∴AB AD AC AE ,即BD CE ,∵点D ,E 在AB ,AC 上,AD AC ,∴BD CE ;(2)BD CE ,BD CE ,理由如下:延长BD ,分别交AC 、CE 于F 、G ,∵ABC 和△ADE 都是等腰直角三角形,90BAC DAE ,∴AB AC ,AD AE ,∵BAD BAC DAC ,CAE DAE DAC ,∴BAD CAE ,在ABC 和ADE V 中,AB AC BAD CAE AD AE,∴ABD ACE ≌△△,∴BD CE ,ABD ACE ,∵A F B G F C ,180AFB ABD BAC GFC ACE CGF ,∴90CGF BAF ,即BD CE ;【点睛】本题是三角形综合题,主要考查的是等腰直角三角形的性质、全等三角形的判定和性质,掌握相关的判定定理和性质定理是解题的关键.【变式训练】1.(2023春·八年级课时练习)(1)问题发现:如图1,ABC 与CDE 均为等腰直角三角形,90ACB DCE ,则线段AE 、BD 的数量关系为_______,AE 、BD 所在直线的位置关系为________;(2)深入探究:在(1)的条件下,若点A ,E ,D 在同一直线上,CM 为DCE △中DE 边上的高,请判断ADB 的度数及线段CM ,AD ,BD 之间的数量关系,并说明理由.【答案】(1)AE BD ,AE BD ;(2)90ADB ,2AD CM BD ;理由见解析【分析】(1)延长AE 交BD 于点H ,AH 交BC 于点O .只要证明 SAS ACE BCD ≌,即可解决问题;(2)由ACE BCD ≌,结合等腰三角形的性质和直角三角形的性质,即可解决问题.【详解】解:(1)如图1中,延长AE 交BD 于点H ,AH 交BC 于点O ,∵ACB △和DCE △均为等腰直角三角形,90ACB DCE ,∴AC BC ,CD CE ,∴90ACE ECB BCD ECB ,∴ACE BCD ,∴ SAS ACE BCD ≌,∴AE BD ,CAE CBD ,∵90CAE AOC ,AOC BOH ,∴90BOH CBD ,∴90AHB ,∴AE BD .故答案为:AE BD ,AE BD .(2)90ADB ,2AD CM BD ;理由如下:如图2中,∵ACB △和DCE △均为等腰直角三角形,90ACB DCE ,∴45CDE CED ,∴180135AEC CED ,由(1)可知:ACE BCD ≌,∴AE BD ,135BDC AEC ,∴1354590ADB BDC CDE ;在等腰直角三角形DCE 中,CM 为斜边DE 上的高,∴CM DM ME ,∴2DE CM ,∴2AD DE AE CM BD .【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题.2.(2023秋·山东日照·八年级校考阶段练习)已知△ABC 和△ADE 都是等腰直角三角形,点D 是直线BC 上的一动点(点D 不与B ,C 重合),连接CE .(1)在图1中,当点D 在边BC 上时,求证:BC =CE +CD ;(2)在图2中,当点D 在边BC 的延长线上时,结论BC =CE +CD 是否还成立?若不成立,请猜想BC ,CE ,CD 之间存在的数量关系,并说明理由;(3)在图3中,当点D 在边BC 的反向延长线上时,不需写证明过程,直接写出BC ,CE ,CD 之间存在的数量关系及直线CE 与直线BC 的位置关系.【答案】(1)见解析;(2)结论BC =CE +CD 不成立,猜想BC =CE -CD ,理由见解析;(3)BC CD CE ;CE BC ,理由见解析【分析】(1)证明△BAD ≌△CAE (SAS ),可得BD =CE ,即可证得BC =BD +CD =CE +CD 成立;(2)同样证明△BAD ≌△CAE (SAS ),可得BD =CE ,即可证得BC BD CD CE CD 成立,故BC =CE +CD 不成立;(3)补全图形,同样证明△BAD ≌△CAE (SAS ),利用全等三角形的性质即可作出结论:BC CD CE ;CE BC .【详解】(1)证明:∵△ABC 和△ADE 都是等腰直角三角形∴AB =AC ,AD =AE ,90BAC DAE∴90BAD DAC CAE DAC∴BAD CAE∴△BAD ≌△CAE (SAS )∴BD =CE∴BC =BD +CD =CE +CD(2)结论BC =CE +CD 不成立,猜想BC =CE -CD ,理由如下:∵90BAC DAEBAC CAD DAE CADBAD CAE又∵AB =AC ,AD =AEBAD CAE SAS BD CEBC BD CD CE CD(3)BC CD CE ;CE BC ;理由如下:补全图形如图3,∵△ABC 是等腰直角三角形,∴∠ACB =∠ABC =45°,∴∠ABD =135°,由(1)同理可得,在△ABD 和△ACE 中,AB AC BAD EAC AD AE,(1)如图1,若30CAD ,10DCB ,求DEB 的度数;(2)如图2,若A 、D 、E 三点共线,AE 与BC 交于点F ,且CF BF ,AD (3)如图3,BE 与AC 的延长线交于点G ,若CD AD ,延长CD 与AB 交于点△BNM≌△BNT (SAS ),利用全等三角形的性质,可得结论.【详解】(1)解:如图1中,90ACB DCE Q ,ACB BCD DCE BCD ,ACD BCE ,在ACD 和BCE 中,CA CB ACD BCE CD CE,ACD ≌ SAS BCE ,30CAD CBE ,10DCB ∵,901080ECB ,180803070CEB ,45CED ∵,704525DEB ;(2)如图2中,过点C 作CQ DE 于Q .∵,AD CD90ADC ,同理:ACD ≌BCE ,90ADC BEC ,90BCT ECB ∵,90ECB CBG ,BCT CBG ,在CBT 和BCG 中,90BCT CBG CB BC CBT BCG,CBT ≌ ASA BCG ,BT CG ,CT BG ,BM CG ∵,BM BT ,在BNM 和BNT 中,45BM BT NBM NBT BN BN,BNM ≌ SAS BNT ,MN NT ,CN MN CN NT CT BG .【点睛】本题属于三角形综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.【类型三共顶点的一般等腰三角形】例题:(2023秋·广东·八年级校联考期末)若ABC 和ADE V 均为等腰三角形,且AB AC AD AE ,当ABC 和ADE 互余时,称ABC 与ADE V 互为“底余等腰三角形”,ABC 的边BC 上的高AH 叫做ADE V 的“余高”.(1)如图1,ABC 与ADE V 互为“底余等腰三角形”,若连接BD ,CE ,判断ABD △与ACE △是否互为“底余等腰三角形”:______(填“是”或“否”);(2)如图1,ABC 与ADE V 互为“底余等腰三角形”,当0180BAC 时,若ADE V 的“余高”是AH .①请用直尺和圆规作出AH ;(要求:不写作法,保留作图痕迹)②求证:2DE AH .(3)如图2,当90BAC 时,ABC 与ADE V 互为“底余等腰三角形”,连接BD 、CE ,若6BD ,8CE ,请直接写出AB 的长.【答案】(1)是(2)见详解(3)5【分析】(1)根据题意可得90ABC ADE ,90ACB AED ,四边形内角和为360 ,求出【变式训练】1.(2023秋·辽宁抚顺·八年级统考期末)如图,已知ABC 中,AB AC BC .分别以AB 、AC 为腰在AB 左侧、AC 右侧作等腰三角形ABD .等腰三角形ACE ,连接CD 、BE .(1)如图1,当60BAD CAE 时,①ABD △、ACE △的形状是____________;②求证:BE DC .(2)若60BAD CAE ,①如图2,当AB AD AC AE ,时,BE DC 是否仍然成立?请写出你的结论并说明理由;②如图3,当AB DB AC EC ,时,BE DC 是否仍然成立?请写出你的结论并说明理由.【答案】(1)①等边三角形;②证明见解析(2)①成立,理由见解析;②不成立,理由见解析【分析】(1)①根据有一个内角是60度的等腰三角形是等边三角形即可求解;②根据等边三角形的性质可得AB AD ,AE AC ,60DAB CAE ,证明BAE DAC ≌ ,根据全等三角形的性质即可证明;(2)①证明BAE DAC ≌ ,根据全等三角形的性质即可得出结论;②根据已知可得BAE 与DAC △不全等,即可得出结论.【详解】(1)①∵ABD △是等腰三角形,ACE △是等腰三角形,60BAD CAE∴ABD △、ACE △是等边三角形,故答案为:等边三角形.②证明:∵ABD △、ACE △是等边三角形,∴AB AD ,AE AC ,60DAB CAE ,∵DAC DAB BAC ,BAE CAE BAC ,∴DAC BAE ,在△BAE 与△DAC 中,∵AB AD BAE DAC AE AC,∴ SAS BAE DAC ≌ .∴BE DC .(2)①当AB AD ,AE AC 时,成立.理由:如图,∵AB AD ,BAE DAC ,AE AC ,∴ SAS BAE DAC ≌ ,∴BE DC ;②当AB DB ,AC EC 时,不成立.理由:如图,∵60BAD CAE ,∴AB DB AD ,AC EC AE ,∴BAE 与DAC △不全等,∴BE DC .【点睛】本题考查全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质等,熟练掌握全等三角形的判定与性质是解题的关键.2.(2023秋·全国·八年级专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,ABC 和CDE 为“同源三角形”,AC BC ,CD CE ,ACB 与DCE 为“同源角”.(1)如图1,ABC 和CDE 为“同源三角形”,试判断AD 与BE 的数量关系,并说明理由.(2)如图2,若“同源三角形”ABC 和CDE 上的点B ,C ,D 在同一条直线上,且90ACE ,则 EMD ______°.(3)如图3,ABC 和CDE 为“同源三角形”,且“同源角”的度数为90°时,分别取AD ,BE 的中点Q ,P ,连接CP ,CQ ,PQ ,试说明PCQ △是等腰直角三角形.【答案】(1)AD BE ,详见解析(2)45(3)详见解析【分析】(1)由“同源三角形”的定义可证ACD BCE ,然后根据SAS 证明≌ACD BCE V V 即可;(2)由“同源三角形”的定义和90ACE 可求出45DCE ACB ,由(1)可知≌ACD BCE V V ,得ADC BEC ,然后根据“8”子三角形即可求出EMD 的度数;(3)由(1)可知≌ACD BCE V V ,可得CAQ CBP ,BE AD .根据SAS 证明ACQ BCP △≌△,可得CQ CP ,ACQ BCP ,进而可证结论成立.【详解】(1)AD BE .理由:因为ABC 和CDE 是“同源三角形”,所以ACB DCE ,所以ACD BCE .在ACD 和BCE 中,,,,AC BC ACD BCE CD CE所以 SAS ACD BCE △≌△.所以AD BE .(2)∵ABC 和CDE 是“同源三角形”,∴ACB DCE .∵90ACE ,∴45DCE ACB .由(1)可知≌ACD BCE V V ,∴ADC BEC .∵MOE COD ,∴45EMD DCE .故答案为:45;(3)由(1)可知≌ACD BCE V V ,所以CAQ CBP ,BE AD .因为AD ,BE 的中点分别为Q ,P ,所以AQ BP .在ACQ 和BCP 中,,,,CA CB CAQ CBP AQ BP所以 SAS ACQ BCP △≌△,所以CQ CP ,ACQ BCP .又因为90BCP PCA ,所以90ACQ PCA .所以90PCQ ,所以PCQ △是等腰直角三角形.【点睛】本题考查了新定义,全等三角形的判定与性质,等腰直角三角形的判定,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解答本题的关键.3.(2023上·浙江宁波·八年级统考期末)规定:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.(1)如图①,在ABC 与ADE V 中,AB AC ,当BAC BAD BAE 、、、满足条件____时,ABC 与ADE V 互为“兄弟三角形”;(2)如图②,在ABC 与ADE V 互为“兄弟三角形”,AB AC ,BE CD 、相交于点M ,连AM ,求证:MA 平分BMD(3)如图③,在四边形ABCD 中,180BAD BCD ,AD AB ,AC BC DC ,求BAD 的度数.【答案】(1)BAE BAC BAD ;(2)见解析(3)60BAD【分析】(1)顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.据此推导出BAC BAD BAE 、、的关系便可;(2)过点A 作AM BE 于点M ,作AN CD 于点N ,再证明ABE ACD ≌得AM AN ,再根据角平分线的判定定理得结论;(3)延长CD 至E ,使得DE BC ,连接AE ,证明ABC ADE △≌△,进而得ACE △是等边三角形,便可得60BAD CAE .【详解】(1)∵在ABC 与ADE V 中,AB AC ,∴当BAC DAE 时,ABC 与ADE V 互为“兄弟三角形”,∵BAE DAE BAD ,∴BAE BAC BAD ,故当BAE BAC BAD 时,ABC 与ADE V 互为“兄弟三角形”,故答案为BAE BAC BAD ;(2)过点A 作AH BE 于点H ,作AN CD 于点N ,∵在ABC 与ADE V 互为“兄弟三角形”,AB AC ,∴BAC DAE ,AD AE ,∴BAE CAD ,∴ SAS ABE ACD ≌,∴AH AN (全等三角形的对应高相等),∴MA 平分BMD ;(3)延长CD 至E ,使得DE BC ,如图③,∵180BAD BCD ,∴360180180 ABC ADC ,∵180ADC ADE ,∴ABC ADE ,∵AB AD ,∴ SAS ABC ADE ≌,∴AC AE BAC DAE ,,∴BAD CAE ,∵AC BC DC DE DC CE ,∴AC CE AE ,∴60CAE ,∴60BAD .【点睛】此题考查了新定义,等腰三角形的定义,等边三角形的判定与性质,角平分线的判定,全等三角形的判定和性质,构造等边三角形和全等三角形是解本题的关键.。
相似三角形重要模型-手拉手模型(解析版)-初中数学

相似三角形重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC =∠DAE =α,AD AB =AE AC=k ;结论:△ADE ∽△ABC ,△ABD ∽△ACE ;EC BD =k .2)手拉手相似模型(直角三角形)条件:如图,∠AOB =∠COD =90°,OC OA =OD OB =k (即△COD ∽△AOB );结论:△AOC ∽△BOD ;BD AC =k ,AC ⊥BD ,S ABCD =12AB ×CD .3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点;结论:△BME ∽△CMF ;BE CF =3.条件:△ABC 和ADE 是等腰直角三角形;结论:△ABD ∽△ACE .1(2023秋·福建泉州·九年级校考期末)问题背景:(1)如图①,已知△ABC ∽△ADE ,求证:△ABD ∽△ACE ;尝试应用:(2)如图②,在△ABC 和△ADE 中,∠BAC =∠DAE =90°,∠ABC =∠ADE =60°,AC 与DE相交于点F ,点D 在BC 边上,DF CF=233,求AD BD 的值;拓展创新:(3)如图③,D 是△ABC 内一点,∠BAD =∠CBD =30°,∠BDC =90°,AB =4,AC =23,求AD 的长.【答案】(1)见解析;(2)AD BD =2;(3)AD =5【分析】问题背景(1)由题意得出AB AD =AC AE ,∠BAC =∠DAE ,则∠BAD =∠CAE ,可证得结论;尝试应用(2)连接EC ,证明△ABC ∽△ADE ,由(1)知△ABD ∽△ACE ,由相似三角形的性质得出AE AD =EC BD =3,∠ACE =∠ABD =∠ADE ,可证明△ADF ∽△ECF ,得出DF CF =AD CE=233,则可求出答案.拓展创新(3)过点A 作AB 的垂线,过点D 作AD 的垂线,两垂线交于点M ,连接BM ,证明△BDC ∽△MDA ,由相似三角形的性质得出BD MD =DC DA ,证明△BDM ∽△CDA ,得出BM CA =DM AD=3,求出BM =6,由勾股定理求出AM ,最后由直角三角形的性质可求出AD 的长.【详解】问题背景(1)证明:∵△ABC ∽△ADE ,∴AB AD =AC AE ,∠BAC =∠DAE ,∴∠BAD =∠CAE ,AB AC =AD AE,∴△ABD ∽△ACE ;尝试应用(2)解:如图,连接EC ,∵∠BAC=∠DAE=90°,∠ABC=∠ADE=60°,∴△ABC∽△ADE,AE=3AD由(1)知△ABD∽△ACE,∴AEAD=ECBD=3,∠ACE=∠ABD=∠ADE=60°,∴AEEC=ADBD,∵∠AFD=∠AEFC∴△ADF∽△ECF∴DFCF =ADCE∵DF CF =233∴DFCF=ADCE=233∴AD=233CE∴AE=3AD=2CE∴ADBD=AEEC=2,拓展创新(3)解:如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,∵∠BAD=30°,∴∠DAM=60°,∴∠AMD=30°,∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴BDMD=DCDA,又∠BDC=∠ADM,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM=∠CDA,∴△BDM∽△CDA,∴BMCA=DMAD=3,∵AC=23,∴BM=23×3=6,∴AM=BM2-AB2=62-42=25,∴AD=12AM=5.【点睛】此题是相似形综合题,考查了直角三角形的性质,勾股定理,相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.2(2023秋·江苏无锡·九年级校考阶段练习)【模型呈现:材料阅读】如图,点B,C,E在同一直线上,点A,D在直线CE的同侧,△ABC和△CDE均为等边三角形,AE,BD 交于点F,对于上述问题,存在结论(不用证明):(1)△BCD≌△ACE(2)△ACE可以看作是由△BCD绕点C旋转而成;⋯【模型改编:问题解决】点A ,D 在直线CE 的同侧,AB =AC ,ED =EC ,∠BAC =∠DEC =50°,直线AE ,BD 交于F ,如图1:点B 在直线CE 上,①求证:△BCD ∽△ACE ; ②求∠AFB 的度数. 如图2:将△ABC 绕点C 顺时针旋转一定角度.③补全图形,则∠AFB 的度数为;④若将“∠BAC =∠DEC =50°”改为“∠BAC =∠DEC =m °”,则∠AFB 的度数为.(直接写结论)【模型拓广:问题延伸】如图3:在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =23,DG =6,连接AG ,BF ,求BF AG 的值.图1 图2 图3【答案】【模型改编:问题解决】①见解析;②65°;③图见解析,115°;④90°+m °2【模型拓广:问题延伸】233【分析】【模型改编:问题解决】①先证明△ABC ∽△EDC ,可得AC EC =BC DC,再证明∠ACE =∠BCD ,可得△BCD ∽△ACE ;②由△BCD ∽△ACE ,可得∠DBC =∠EAC ,再结合三角形的外角可得答案;③连接EA 并延长交BD 于F ,同理可得:△BCD ∽△ACE ,∠CEF =∠BDC ,再结合三角形的外角可得答案;④先求解∠CDE =∠DCE =12180°-m ° =90°-12m °,结合③的思路可得答案;【模型拓广:问题延伸】连接BD 、DF ,先证明△ADB ∽△GDF ,可得∠ADB =∠GDF ,AD DG =BD DF ,证明∠ADG =∠BDF ,可得△BDF ∽△ADG ,可得BF AG =BD AD,从而可得答案.【详解】【模型改编:问题解决】①∵AB =AC ,ED =EC ,∠BAC =∠DEC =50°,∴∠ABC =∠ACB =180°-50° ÷2=65°,∠EDC =∠ECD =180°-50° ÷2=65°,∴△ABC ∽△EDC ,∴AC EC =BC DC,∵∠ACE =180°-∠ACB =115°,∠BCD =180°-∠DCE =115°,∴∠ACE =∠BCD ,∴△BCD ∽△ACE ;②由①知,△BCD ∽△ACE ,∴∠DBC =∠EAC ,∴∠AFB =∠DBC +∠CEA =∠EAC +∠CEA =∠ACB =65°③补图如下:连接EA 并延长交BD 于F ,图2同理可得:△BCD ∽△ACE ∴∠CEF =∠BDC ,∴∠AFB =∠BDC +∠CDE +∠DEF =∠CEF +∠CDE +∠DEF =∠CED +∠CDE =50°+65°=115°,④∵∠BAC =∠DEC =m °,CE =DE ,∴∠CDE =∠DCE =12180°-m ° =90°-12m °,同理③可得∠AFB =∠CED +∠CDE =m °+90°-12m °=90°+m °2,故答案为:90°+m °2;【模型拓广:问题延伸】连接BD 、DF ,图3∵在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =FG =23,DG =6,∴AB AD =GF DG =33,又∵∠BAD =∠DGF =90°,∴△ADB ∽△GDF ,∴∠ADB =∠GDF ,AD DG=BD DF ,∵∠ADG =∠GDF +∠ADF ,∠BDF =∠ADB +∠ADF ,∴∠ADG =∠BDF ,∴△BDF ∽△ADG ,∴BF AG =BD AD,∵AD =23,AB =2,∴BD =AB 2+AD 2=4,∴BF AG =BD AD =423=233.【点睛】本题考查的是等腰三角形的性质,矩形的性质,勾股定理的应用,相似三角形的判定与性质,熟练的证明三角形相似是解本题的关键.3(2023春·湖北黄冈·九年级专题练习)【问题呈现】△CAB 和△CDE 都是直角三角形,∠ACB =∠DCE =90°,CB =mCA ,CE =mCD ,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当m =1时,直接写出AD ,BE 的位置关系:;(2)如图2,当m ≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当m =3,AB =47,DE =4时,将△CDE 绕点C 旋转,使A ,D ,E 三点恰好在同一直线上,求BE 的长.【答案】(1)BE ⊥AD (2)成立;理由见解析(3)BE =63或43【分析】(1)根据m =1,得出AC =BC ,DC =EC ,证明△DCA ≌△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(2)证明△DCA ∽△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(3)分两种情况,当点E 在线段AD 上时,当点D 在线段AE 上时,分别画出图形,根据勾股定理求出结果即可.【详解】(1)解:∵m =1,∴AC =BC ,DC =EC ,∵∠DCE =∠ACB =90°,∴∠DCA +∠ACE =∠ACE +∠ECB =90°,∴∠DCA =∠ECB ,∴△DCA ≌△ECB ,∴∠DAC =∠CBE ,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;故答案为:BE⊥AD.(2)解:成立;理由如下:∵∠DCE=∠ACB=90°,∴∠DCA+∠ACE=∠ACE+∠ECB=90°,∴∠DCA=∠ECB,∵DC CE =ACBC=1m,∴△DCA∽△ECB,∴∠DAC=∠CBE,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG =∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;(3)解:当点E在线段AD上时,连接BE,如图所示:设AE=x,则AD=AE+DE=x+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3x+4=3x+43,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE2+BE2=AB2,即x2+3x+432=472,解得:x=2或x=-8(舍去),∴此时BE=3x+43=63;当点D在线段AE上时,连接BE,如图所示:设AD=y,则AE=AD+DE=y+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3y,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE 2+BE 2=AB 2,即y +4 2+3y 2=47 2,解得:y =4或y =-6(舍去),∴此时BE =3y =43;综上分析可知,BE =63或43.【点睛】本题主要考查了全等三角形的判定和性质,相似三角形的判定和性质,三角形内角和定理的应用,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.4(2023秋·福建泉州·九年级校考阶段练习)如图,已知△ABC 中,AB =AC ,∠BAC =α.点D 是△ABC 所在平面内不与点A 、C 重合的任意一点,连接CD ,将线段CD 绕点D 顺时针旋转α得到线段DE ,连接AD 、BE .(1)如图1,当α=60°时,求证:BE =AD .(2)当α=120°时,请判断线段BE 与AD 之间的数量关系是,并仅就图2的情形说明理由.(3)当α=90°时,且BE ⊥AB 时,若AB =8,BE =2,点E 在BC 上方,求CD 的长.【答案】(1)见解析,(2)BE =3AD ,理由见解析(3)82【分析】(1)先证明△ABC 和△DCE 是等边三角形,再证明△ADC ≌△BEC ,可推出BE =AD ;(2)过A 作AH ⊥BC 与H ,先根据含30°的直角三角形的性质,等腰三角形的性质以及勾股定理可求出BC =3AC ,同理求出CE =3CD ,可得出BC EC =3AC 3DC=AC DC ,证明∠DCA =∠BCE ,然后证明△EBC ∽△DAC 即可求解;(3)过E 作EF ⊥BC 于F ,可判断△BEF 是等腰直角三角形,然后可求出EF ,BF ,CF 的长度,由(2)同理可证出△EBC ∽△DAC ,最后根据相似三角形的性质即可求解.【详解】(1)解:∵旋转,∴CD =ED ,当α=60°时,又AB =AC ,∴△ABC 和△DCE 是等边三角形,∴AC =BC ,DC =EC ,∠DCE =∠ACB =60°,∴∠ACD =∠BCE ,∴△ADC ≌△BEC ,∴AD =BE ;(2)解:BE =3AD 过A 作AH ⊥BC 与H ,∵AB =AC ,∠BAC =α=120°,∴∠ACB =30°,CH =12BC ,∴AC =2AH ,又由勾股定理得AH 2+CH 2=AC 2,∴CH =32AC ,∴BC =3AC ,同理CE =3CD ,∵DC =EC ,∠CDE =α=120°,∴∠DCE =30°=∠ACB ,∴∠DCA =∠BCE ,∵BC =3AC ,CE =3CD ,∴BC EC =3AC 3DC =AC DC ,∴△EBC ∽△DAC ,∴BE AD =BC AC =3,即BE =3AD (3)解:如图,过E 作EF ⊥BC 于F ,当α=90°时,∵AC =AB =8,∴∠ACB =45°,BC =AB 2+AC 2=2AC =82,∵BE ⊥AB ,∴∠EBF =45°=∠BEF ,∴BF =EF ,∵BE =EF 2+BF 2=2EF =2,∴EF =BF =2,∴CF =BF +BC =92,∴CE =EF 2+CF 2=241,由(2)同理可证△EBC ∽△DAC ,∴EC DC =BC AC=2,即241DC =2,∴DC =82.【点睛】本题属于三角形综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键在于正确寻找全等三角形或相似三角形.5(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠BAC =∠EAF =30°,连接BE ,CF,延长BE交CF于点D.则BE与CF的数量关系:,∠BDC=°;(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:;(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP=.【答案】(1)BE=CF,30(2)BE=CF,∠BDC=60°,证明见解析(3)BF=CF+2AM(4)7+74或7-74【分析】(1)根据已知得出∠BAE=∠CAF,即可证明△BAE≌△CAF,得出BE=CF,∠ABE=∠ACF,进而根据三角形的外角的性质即可求解;(2)同(1)的方法即可得证;(3)同(1)的方法证明△BAE≌△CAF SAS,根据等腰直角三角形的性质得出AM=12EF=EM=MF,即可得出结论;(4)根据题意画出图形,连接BD,以BD为直径,BD的中点为圆心作圆,以D点为圆心,1为半径作圆,两圆交于点P,P1,延长BP至M,使得PM=DP=1,证明△ADP∽△BDM,得出PA=22BM,勾股定理求得PB,进而求得BM,根据相似三角形的性质即可得出PA=221+7=2+142,勾股定理求得BQ,PQ,进而根据三角形的面积公式即可求解.【详解】(1)解:∵∠BAC=∠EAF=30°,∴∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF,∴BE=CF,∠ABE=∠ACF设AC,BD交于点O,∵∠AOD=∠ACF+∠BDC=∠ABE+∠BAO∴∠BDC=∠BAO=∠BAC=30°,故答案为:BE= CF,30.(2)结论:BE=CF,∠BDC=60°;证明:∵∠BAC=∠EAF=120°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF∴BE=CF,∠AEB=∠AFC∵∠EAF=120°,AE=AF,∴∠AEF=∠AFE=30°,∴∠BDC=∠BEF-∠EFD=∠AEB+30°-∠AFC-30°=60°,(3)BF=CF+2AM,理由如下,∵∠BAC=∠EAF=90°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵△ABC和△AEF均为等腰直角三角形∴AB=AC,AE=AF,∴△BAE≌△CAF SAS,∴BE= CF,在Rt △AEF 中,AM ⊥BF ,∴AM =12EF =EM =MF ,∴BF =BE +EF =CF +2AM ;(4)解:如图所示,连接BD ,以BD 为直径,BD 的中点为圆心作圆,以D 点为圆心,1为半径作圆,两圆交于点P ,P 1,延长BP 至M ,使得PM =DP =1,则△MDP 是等腰直角三角形,∠MDP =45°∵∠CDB =45°,∴∠MDB =∠MDP +∠PDC +∠CDB =90°+∠PDC =∠ADP ,∵AD DB =12,DP DM =12,∴△ADP ∽△BDM ∴PA BM =12=22,∴PA =22BM ,∵AB =2,在Rt △DPB 中,PB =DB 2-DP 2=22 2-12=7,∴BM =BP +PM =7+1∴PA =221+7 =2+142过点P 作PQ ⊥AB 于点Q ,设QB =x ,则AQ =2-x ,在Rt △APQ 中,PQ 2=AP 2-AQ 2,在Rt △PBQ 中,PQ 2=PB 2-BQ 2∴AP 2-AQ 2=PB 2-BQ 2∴2+142 2-2-x 2=7 2-x 2解得:x =7-74,则BQ =7-74,设PQ ,BD 交于点G ,则△BQG 是等腰直角三角形,∴QG =QB =7-74在Rt △DPB ,Rt △DP 1B 中,DP =DP 1DB =DB ∴Rt △DPB ≌Rt △DP 1B ∴∠PDB =∠P 1DB又PD =P 1D =1,DG =DG ∴△PGD ≌△P 1DG ∴∠PGD =∠P 1GD =45°∴∠PGP 1=90°,∴P 1G ∥AB ∴S △ABP 1=12AB ×QG =12×2×7-74=7-74,在Rt △PQB 中,PQ =PB 2-BQ 2=7 2-7-74 2=7+74∴S△ABP =12AB ×PQ =12×2×7+74=7+74,综上所述,S△ABP=7+74或7-74故答案为:7+74或7-74.【点睛】本题考查了全等三角形的性质与判定,相似三角形的性质与判定,正方形的性质,勾股定理,直径所对的圆周角是直角,熟练运用已知模型是解题的关键.6(2023·山东济南·九年级统考期中)问题背景:一次小组合作探究课上,小明将一个正方形ABCD和等腰Rt△CEF按如图1所示的位置摆放(点B、C、E在同一条直线上),其中∠ECF=90°.小组同学进行了如下探究,请你帮助解答:初步探究(1)如图2,将等腰Rt△CEF绕点C按顺时针方向旋转,连接BF,DE.请直接写出BF与DE的关系;(2)如图3,将(1)中的正方形ABCD和等腰Rt△CEF分别改成菱形ABCD和等腰△CEF,其中CE=CF,∠BCD=∠FCE,其他条件不变,求证:BF=DE;深入探究:(3)如图4,将(1)中的正方形ABCD和等腰Rt△CEF分别改成矩形ABCD和Rt△CEF,其中∠ECF=90°且CECF =CDBC=34,其它条件不变.①探索线段BF与DE的关系,说明理由;②连接DF,BE若CE=6,AB=12,直接写出DF2+BE2=.【答案】(1)BF=DE,BF⊥DE;(2)见解析;(3)①DEBF=34,DE⊥BF,见解析;②500【分析】(1)由正方形的性质,等腰直角三角形的性质,得到BC=CD,CE=CF,证明△BCF≌DCE,得到BF=DE,∠CBF=∠CDE,结合对顶角相等,即可得到BF⊥DE;(2)由菱形的性质,旋转的性质,先证明ΔBCF≌ΔDCE,即可得到结论成立;(3)①由矩形的性质,直角三角形的性质,先证明ΔBCF∽ΔDCE,得到BF与DE的数量关系,再由余角的性质证明位置关系即可;②连接BD,先求出矩形的边长,直角三角形的边长,与(1)同理先证明BF⊥DE,然后利用勾股定理,等量代换,即可得到DF2+BE2=500.【详解】解:(1)如图:∵正方形ABCD和等腰Rt△CEF中,∴BC=CD,CE=CF,∠BCD=∠ECF=90°,∴∠BCD+∠DCF=∠ECF+∠DCF,即∠BCF=∠DCE,∴△BCF≌DCE,∴BF=DE,∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DFG=90°∴BF⊥DE.(2)证明:如图:∵∠BCD=∠FCE,∴∠BCF=∠DCE,∵四边形ABCD为菱形∴BC=CD,又∵CE=CF∴△BCF≌△DCE(SAS),∴BF=DE;(3)①∵在矩形ABCD中,∠BCD=90°,∴∠BCD=∠FCE∴∠BCF=∠DCE,又∵CECF=CDBC=34∴△BCF∽△DCE,∴DEBF=CECF=34;∴∠CBF=∠CDE,设CD与BF交于点G∵∠BGC=∠DGF∴180°-∠CBF-∠BGC=180°-∠CDE-∠DGF,∴∠DQB=∠BCD=90°∴DE⊥BF.②如图:连接BD在矩形ABCD中,CD=AB=12,∵CE=6,6CF =12BC=34,∴CF=8,BC=16,∵△BCF∽△DCE,∴∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DQG=90°,∴BF⊥DE;在直角△BCD中,有BD2=BC2+CD2=162+122=400,在直角△BDQ中,BD2=BQ2+DQ2=400;在直角△CEF中,EF2=CE2+CF2=62+82=100,在直角△EFQ中,EF2=EQ2+FQ2=100;∴BQ2+DQ2+EQ2+FQ2=400+100=500;在直角△BEQ和直角△DFQ中,由勾股定理,则∵BQ2+EQ2=BE2,DQ2+FQ2=DF2,∴DF2+BE2=BQ2+DQ2+EQ2+FQ2=500;故答案为:500.【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,旋转的性质,勾股定理,以及等腰直角三角形的性质等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线,找到证明三角形相似和三角形全等的条件进行解题.7(2023春·广东·九年级专题练习)已知在△ABC中,O为BC边的中点,连接AO,将△AOC绕点O顺时针方向旋转(旋转角为钝角),得到△EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)如图2,当∠BAC =90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.【答案】(1)AE=CF;(2)成立,证明见解析;(3)511 3【分析】(1)结论AE=CF.证明ΔAOE≅ΔCOF(SAS),可得结论.(2)结论成立.证明方法类似(1).(3)首先证明∠AED=90°,再利用相似三角形的性质求出AE,利用勾股定理求出DE即可.【详解】解:(1)结论:AE=CF.理由:如图1中,∵AB=AC,∠BAC=90°,OC=OB,∴OA=OC=OB,AO⊥BC,∵∠AOC=∠EOF=90°,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(2)结论成立.理由:如图2中,∵∠BAC=90°,OC=OB,∴OA=OC=OB,∵∠AOC=∠EOF,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(3)如图3中,由旋转的性质可知OE =OA ,∵OA =OD ,∴OE =OA =OD =5,∴∠AED =90°,∵OA =OE ,OC =OF ,∠AOE =∠COF ,∴OA OC =OE OF ,∴ΔAOE ∽ΔCOF ,∴AE CF =OA OC,∵CF =OA =5,∴AE 5=53,∴AE =253,∴DE =AD 2-AE 2=102-253 2=5113.【点睛】本题属于几何变换综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.课后专项训练1(2023秋·北京顺义·九年级校考期中)如图,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .则BD CE的值为()A.12B.22C.2D.2【答案】B 【分析】由等腰直角三角形的性质可推出∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,从而可得出∠EAC =∠DAB ,AE AD =AC AB=2,证明△DAB ∽△EAC 即可得出结论.【详解】解:∵△ABC 和△ADE 都是等腰直角三角形,∴∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,∴∠EAC =∠DAB ,AE AD =AC AB =2,∴△DAB ∽△EAC ,∴BD CE =AD AE=22.故选B .【点睛】本题考查等腰直角三角形的性质,勾股定理,相似三角形的判定和性质.掌握三角形相似的判定条件是解题关键.2(2023春·浙江金华·九年级校考期中)如图,在Rt △ABC 中,∠ABC =90°,以AB ,AC 为边分别向外作正方形ABFG 和正方形ACDE ,CG 交AB 于点M ,BD 交AC 于点N .若GM CM =12,则CG BD=() A.12 B.34 C.255 D.13013【答案】D【分析】设AG =a =AB ,BC =2a ,由“AAS ”可证△ABC ≌△CHD ,可得AB =CH =a ,DH =BC =2a ,利用勾股定理分别求出CG ,BD 的长,即可求解.【详解】解:如图,过点D 作DP ⊥BC ,交AC 的延长线于点P,交BC 的延长线于点H ,∵AG ∥BF ,∴△AGM ∽△BCM ,∴AG BC =GM CM=12,∴设AG =a =AB ,BC =2a ,∴CG =GF 2+FC 2=a 2+(3a )2=10a ,∵DH ⊥BC ,AB ⊥BC ,∴∠DHC =∠ABC =∠ACD =90°,AB ∥DH ,∴∠DCH +∠ACB =90°=∠ACB +∠BAC ,∴∠DCH =∠BAC ,在△ABC 和△CHD 中,∠ABC =∠DHC ∠BAC =∠DCH AC =CD,∴△ABC ≌△CHD (AAS ),∴AB =CH =a ,DH =BC =2a ,∴BD =BH 2+DH 2=(3a )2+(2a )2=13a ,∴CG BD =10a 13a =13013.故选:D .【点睛】本题考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定和性质,添加恰当辅助线构造相似三角形是解题的关键.3(2023春·浙江丽水·九年级专题练习)如图,在△ABC 中,过点C 作CD ⊥AB ,垂足为点D ,过点D 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E ,F .连接EF 交线段CD 于点O ,若CO =22,CD =32,则EO ⋅FO 的值为( ).A.63B.4C.56D.6【答案】B【分析】由题意易得出∠DEC=∠DFC=90°,即说明点C,E,D,F四点共圆,得出∠DEO=∠FCO,从而易证△DOE∽△FOC,得出EOCO=DOFO.由题意可求出DO=CD-CO=2,即可求出EO⋅FO=CO⋅DO=4.【详解】解:∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°,∴点C,E,D,F四点共圆,∴∠DEF=∠FCD,即∠DEO=∠FCO.又∵∠DOE=∠FOC,∴△DOE∽△FOC,∴EOCO=DOFO,∴EO⋅FO=CO⋅DO.∵CO=22,CD=32,∴DO=CD-CO=2,∴EO⋅FO=CO⋅DO=22×2=4.故选B.【点睛】本题考查相似三角形的判定和性质,四点共圆的知识,圆周角定理.确定点C,E,D,F四点共圆,从而可得出证明△DOE∽△FOC的条件是解题关键.4(2022·广西梧州·统考一模)如图,在△ABC中,∠C=45°,将△ABC绕着点B逆时针方向旋转,使点C的对应点C′落在CA的延长线上,得到△A′BC′,连接AA′,交BC′于点O.下列结论:①∠AC′A′= 90°;②AA′=BC′;③∠A′BC′=∠A′AC′;④△A′OC′∽△BOA.其中正确结论的个数是()A.1B.2C.3D.4【答案】C【分析】利用旋转的性质和等腰三角形的性质推出∠AC A =90°,即可判断①的正确性;通过点A 、B、A、C 四点共圆可以判断出②③④的正确性.【详解】解:由题意可得:BC=BC ,∠C=∠A C B∵∠C=45°∴∠BC A=45°∵∠AC A =∠A C B+∠BC A∴∠AC A =90°,故①正确;∵∠BC A=∠C=45°∴∠C BC=90°∵∠ABC=∠A BC ∴∠A BA=90°∴∠A BA+∠AC A =180°,∠C AB+∠C A B=180°∴点A 、B、A、C 四点共圆∵∠AC A =90°,∠BAC ≠90°∴A A是直径,BC 不是直径∴A A≠BC ,故②错误;∵点A 、B、A、C 四点共圆∴∠A BC =∠A AC ,故③正确;∵点A 、B、A、C 四点共圆∴∠AA C =∠ABC ,∠A C B=∠A AB∴△A OC ∽△BOA,故④正确;∴正确结论的个数是3个故选C.【点睛】本题考查了图形的旋转、等腰三角形的性质、四点共圆、圆周角定理的推论以及相似的判定等知识点,灵活运用这些知识点是解题的关键.5(2023·广东深圳·校联考模拟预测)如图,已知▱ABCD ,AB =3,AD =8,将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,延长AB 交EF 于点H ,则FH 的长为.【答案】558【分析】先利用平行四边形的性质得到CD =AB =3,BC =AD =8,∠D =∠ABC ,再根据旋转的性质得到∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,接着证明△ADC ∽△AEH ,然后利用相似比求出EH ,从而得到FH 的长.【详解】解:∵四边形ABCD 为平行四边形,∴CD =AB =3,BC =AD =8,∠D =∠ABC ,∵将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,∴∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,∴∠E =∠D ,∵∠DAC =∠HAE ,∴△ADC ∽△AEH ,∴AD AE =DC EH ,∴83=3EH ,∴EH =98,∴FH =EF -EH =8-98=558,故答案为:558.【点睛】本题考查了平行四边形的性质,旋转、三角形相似的判定利用三角形相似比求线段的长,根据旋转的性质得到∠DAG =∠BAE ,然后根据两组对应角分别相等的两三角形相似得出AD AE=DC EH 是本题的关键.6(2022·安徽·模拟预测)如图,将边长为3的菱形ABCD 绕点A 逆时针旋转到菱形AB C D 的位置,使点B 落在BC 上,B C 与CD 交于点E .若BB =1,则CE 的长为.【答案】34/0.75【分析】延长D D 交BC 的延长线于点M ,过点C 作CN ∥DM 交B C 于点N ,根据菱形的性质和旋转的性质证明△ABB ≌△ADD ≌△DCM ≌B C M ,求得C D =B C =2,CM =C M =1,再根据CN ∥DM ,得CN MC =B C B M ,CN DC=CE DE ,代入即可求解.【详解】解:如图,延长D D 交BC 的延长线于点M ,过点C 作CN ∥DN 交B C 于点N ,∵四边形ABCD是菱形∴AB=BC=CD=AD=3,∠B=∠ADC=∠D ,AB∥CD∴∠DCM=∠B由旋转的性质得:AB =AB=3,AD =AD=3,∠BAB =∠DAD =∠MB C ,B C =D C =3,∠ADC=∠D ,∴△ABB ≌△ADD ∴DD =BB =1∴DC =D C -DD =2∵∠CDM+∠ADC=∠DAD +∠D ∴∠BAB =∠DAD =∠CDM∴△ABB ≌△DCM≌B C M,∴DM=AB =3,∠M=∠AB B∴C M=CM=3-2=1∵CN∥DM∴△B CN∽△B MC ∴CNMC =B CB M∵B C=BC-BB =2∴CN1=23∴CN=23∵CN∥DM∴△CNE∽△DC E∴CNDC =CEDE∴232=CE3-CE∴CE=34故答案为:34【点睛】本题考查菱形的性质,旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质,综合性较强,作辅助线构造全等三角形和相似三角形是解题的关键.7(2021·湖南益阳·统考中考真题)如图,Rt△ABC中,∠BAC=90°,tan∠ABC=32,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB C ,连接BB ,CC ,则△CAC 与△BAB 的面积之比等于.【答案】9:4【分析】先根据正切三角函数的定义可得ACAB=32,再根据旋转的性质可得AB=AB,AC=AC ,∠BAB=∠CAC =α,从而可得ACAC =ABAB=1,然后根据相似三角形的判定可得△CAC ∼△BAB ,最后根据相似三角形的性质即可得.【详解】解:∵在Rt△ABC中,∠BAC=90°,tan∠ABC=32,∴ACAB=32,由旋转的性质得:AB=AB ,AC=AC ,∠BAB =∠CAC =α,∴ACAC=ABAB=1,在△CAC 和△BAB 中,ACAC=ABAB∠CAC =∠BAB,∴△CAC ∼△BAB ,∴S△CACS△BAB=ACAB2=94,即△CAC 与△BAB 的面积之比等于9:4,故答案为:9:4.【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.8(2023秋·山东济南·九年级校考阶段练习)如图,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°.(1)求证:△ACD∽△BCE;(2)若AC=3,AE=8,求AD.【答案】(1)见详解(2)AD=103 3【分析】(1)根据30°的正切值得ACBC=DCEC,即可证明相似.(2)先证明∠BAE=90°,进而求出BE=10,再根据△ACD∽△BCE得出ADBE=ACBC=DCEC=33,即可求出AD=33BE=1033.【详解】(1)∵∠ACB=∠DCE=90°∴∠ACD=∠BCE∵∠ABC=∠CED=∠CAE=30°∴tan∠ABC=ACBC =33,tan∠CED=DCEC=33∴AC BC =DCEC∴△ACD∽△BCE(2)∵由(1),△ACD∽△BCE∴ADBE =ACBC=DCEC=33∵∠ABC=∠CED=∠CAE=30°∴∠BAC=60°∴∠BAE=90°∵AC=3,∠ABC=30°∴AB=2AC=6∵AE=8∴BE=10∴AD=33BE=1033【点睛】本题考查相似三角形的判定、特殊角三角函数值及勾股定理,根据特殊角得出对应线段成比例是解题关键.9(2023·安徽滁州·九年级校考阶段练习)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P、M.求证:(1)△BAE∽△CAD;(2)MP⋅MD=MA⋅ME.【答案】(1)证明见解析(2)证明见解析【分析】(1)由题意可得AC=2AB,AD=2AE,∠BAE=∠CAD=135°,即可证△BAE∽△CAD;(2)由△BAE∽△CAD可得∠BEA=∠CDA,即可证△PME∽△AMD,可得MP⋅MD=MA⋅ME.【详解】(1)证明:∵等腰Rt △ABC 和等腰Rt △ADE ,∴AB =BC ,AE =DE ,∠BAC =∠DAE =45°,∴AC =2AB ,AD =2AE ,∠BAE =∠CAD =135°,∴AC AB =AD AE=2,∴△BAE ∽△CAD ,(2)∵△BAE ∽△CAD ,∴∠BEA =∠CDA ,且∠PME =∠AMD ,∴△PME ∽△AMD ,∴ME MD =MP AM,∴MP ⋅MD =MA ⋅ME .【点睛】本题考查了相似三角形的判定和性质,等腰直角三角形性质,勾股定理的应用,熟练运用相似三角形的判定是本题的关键.10(2023秋·湖北孝感·九年级校联考阶段练习)问题背景:如图1,在△ABC 中,∠ACB =90°,AC =BC ,AD 是BC 边上的中线,E 是AD 上一点,将△CAE 绕点C 逆时针旋转90°得到△CBF ,AD 的延长线交BF 于点P .问题探究:(1)当点P 在线段BF 上时,证明EP +FP =2BP .①先将问题特殊化,如图2,当CE ⊥AD 时,证明:EP +FP =2BP ;②再探究一般情形,如图1,当CE 不垂直AD 时,证明:EP +FP =2BP ;拓展探究:(2)如图3,若AD 的延长线交BF 的延长线于点P 时,直接写出一个等式,表示EP ,FP ,BP 之间的数量关系.【答案】(1)①见解析,②见解析(2)EP -FP =2PB【分析】①结论:PE +PF =2PB .根据旋转的性质△ACE ≌△BCF ,再证明四边形CEPF 是正方形,可得结论.②结论不变,如图2中,过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .证明△CHF ≌△CGE ,可以推出FH =EG ,再利用正方形的性质解决问题即可.(2)结论:EP -FP =2PB ,证明方法类似②.【详解】(1)①证明:∵CE ⊥AD ,∴∠AEC =∠PEC =90°,在△ABC 中,∠ACB =90°,AC =AB ,∵将△CAE 绕点C 逆时针旋转90°得到△CBF ,∴△ACE ≌△BCF ,CF =CE ,∠ECF =90°,∠BFC =∠AEC =90°,∴∠BFC =∠ECF =∠PEC =90°,∴四边形CEPF 是矩形,∵CE =CF ,∴四边形CEPF 是正方形,∴CE =EP =FP =CF ,∠EPF =90°,∴∠BPD =90°=∠CED ,∵AD 是△ABC 中BC 边上的中线,∴BD =CD =12BC ,在△CED 和△BPD 中,∴∠CED =∠BPD∠CDE =∠BDP CD =BD,∴△CED ≌△BPD (AAS ),∴CE =BP ,∴BP =EP =CE =FP ,∴EP +FP =2BP②结论成立,证明:过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .则∠CGE =∠CGD =∠CHF =90°.由旋转性质可知,△CBF≌△CAE,∴CF=CE,∠CFB=∠CEA,∠ACE=∠BCF,∵∠CFH=180°-∠CFB,∠CEG=180°-∠CEA,∴∠CFH=∠CEG,∴△CHF≌△CGE,∴∠FCH=∠ECG,CH=CG,FH=EG.∴∠FCH+∠BCF+∠DCG=∠ECG+∠ACF+∠DCG=90°.∴∠HCG=90°.∴四边形CGPH是正方形.∴CG=GP=PH,∴EP+FP=GP+PH=2CG.∵CD=BD,∠CGD=∠BPD=90°,∠CDG=∠BDP,∴△CDG≌△BDP.∴CG=BP.∴EP+FP=2PB.(2)解:EP-FP=2PB.理由:如下图所示,过C作CN∥BP交AP于点N,CM∥DP交BP的延长线于点M,则四边形CNPM是平行四边形,△BPD∽△BMC,∴CN=PM,CM=PN,BPBM =BDBC=12,∴BM=2BP,∴PM=BP,∵∠APB=90°,∴∠NPM=90°,∴四边形CNPM是矩形,∴∠M=∠CNE=∠CNP=90°,在△CFM和△CEN中,∠H=∠CNE=90°∠CFH=∠CEN CF=CE,∴△CFM≌△CEN(AAS),∴CM=CN,FM=EN,∴四边形CNPM是正方形,∴PM=CN=PN,∴EP-FP=PN+EN-FP=PN+FM-FP=PN +PM=2PM,∴EP-FP=2BP.【点睛】本题属于几何变换综合题,考查相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质等知识,解题关键是正确寻找全等三角形解决问题,属于中考压轴题.11(2022·河南·九年级专题练习)规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.(1)问题联想:如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为,位置关系为;(2)类比探究:如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗?若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;(3)拓展延伸:如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.【答案】(1)BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由见解析;(3)BM =2DN ,BM ⊥DN .【分析】(1)根据SAS证明△ABM'≌△AND',进而得到BM =DN ,∠ABM'=∠ADN',再利用三角形内角和可推出∠BOD=90°,即BM ⊥DN ;(2)根据旋转和菱形的性质证明ΔABM ≌ΔADN ,再推出∠BOD=∠BAD=60°,故可求解;(3)根据旋转和矩形的性质证明ΔABM ∼ΔADN ,得到BM =2DN ,再推出∠BOD=∠BAD=90°即可求解.【详解】(1)如图设AB,DN 交于点H,,∵四边形ABCD,AMPN都是正方形,把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',∴AB=AD,AM'=AD', ∠BAM =∠DAN =150°∴△ABM'≌△AND',∴BM =DN ,∠ABM'=∠ADN',∵∠ADN'+∠DHA+∠DAH=180°,∠ABM'+∠BHO+∠BOD=180°,又∠DHA=∠BHO∴∠BOD=∠BAD=90°,即BM ⊥DN 故答案为:BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由:设AB,DN 交于点E,由旋转的性质可得∠BAM =∠DAN =150°.∵四边形ABCD,AM P N 都是菱形,∴AB=AD,AM =AN ,∴ΔABM ≌ΔADN ,∴BM =DN ,∠ABM =∠ADN .。
手拉手模型-含答案

手拉手模型一.填空题(共18小题)1.已知△ABC中,∠ABC=45°,AB=7,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为.2.如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为.3.四边形ABCD中,AC=BC,∠ACB=90°,∠ADB=30°,AD=,CD=14,则BD=.4.已知在四边形ABCD中,AB=AC,∠ABC=∠ADC=60°,连接BD,若CD=2,AB =2,则BD的长度为.5.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=,BC=,连接AC、BD,若AC⊥AB,则BD的长度为.6.如图,四边形ABCD中,∠ABC=∠ACD=∠ADC=45°,△DBC的面积为8,则BC 长为.7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC =.8.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC 的内部有一点P,P A=8,PB=4,PC=4,则线段AB的长为.9.如图,在△ABC中,∠ABC=60°,=,D为△ABC外一点,连接AD、CD.若∠ADC=30°,AC=AD,则的值为.10.如图,△ABC、△CDE是两个直角三角板,其中∠ECD=∠ACB=90°,∠CED=45°,∠CAB=30°,若AB=DE=2,将直角三角板CDE绕点C旋转一周,则|AD﹣BE|的最大值为.11.如图,点D为等边△ABC外一点,∠ADC=60°,连接BD,若AD=8,△BCD的面积为,则BD的长为.12.如图,△ABC中,∠ABC=45°,AB=2,BC=6,AD⊥AC,AD=AC,连接BD,则BD的长为.13.如图,在△ABC中,∠ABC=60°,AB=3,BC=12,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为.14.如图,△ABC为等腰直角三角形,∠ACB=90°,∠APC=165°,P A=3,PC=,则PB=.15.如图,在等腰直角三角形ABC中,已知∠ACB=90°,P是△ABC内一点,使P A=11,PB=7,PC=6,则∠BPC=.16.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3;⑤S△AOC+S△AOB═6+.其中正确的结论是.17.等边△ABC的边长为2,三角形外部有一点D,CD=2,连接AD、BD,若∠ADC =30°,则BD的长为.18.如图,在四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,∠BAD的平分线AE与DC边相交于点E,连接BE,AC,若AC=7,△BCE的周长为16,则线段BC 的长为.二.解答题(共22小题)19.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:已知△ABC如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)●类比探究:如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么数量关系?说明理由.●灵活运用:如图3,已知△ABC中,AB=,BC=3,∠ABC=45°,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.20.将图形中的三角形绕某一点作适当旋转,可帮助解决很多几何问题.(1)如图1,直角△ABC中,AB=AC,∠BAC=90°,D为BC边上的一点,将△ABD 绕点A逆时针旋转90°至△ACF,作AE平分∠DAF交BC于E,请证明:BD2+CE2=DE2;(2)如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是64cm2,则AC长是cm;(3)如图3,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC=30°,AD=2,BD=3,求CD的长.21.直线m∥n,点A、B分别在直线m,n上(点A在点B的右侧),点P在直线m上,AP=AB,连接BP,将线段BP绕点B顺时针旋转60°得到BC,连接AC交直线n于点E,连接PC,且△ABE为等边三角形.(1)如图①,当点P在A的右侧时,请直接写出∠ABP与∠EBC的数量关系是,AP与EC的数量关系是.(2)如图②,当点P在A的左侧时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.(3)如图②,当点P在A的左侧时,若△PBC的面积为,求线段AC的长.22.某校八年级数学兴趣小组在研究等腰直角三角形与图形变换时,作了如下研究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为腰作等腰直角三角形DAF,使∠DAF=90°,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①CF与BC的位置关系为;②CF,DC,BC之间的数量关系为(直接写出结论);(2)数学思考如图2,当点D在线段CB的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,将△DAF沿线段DF翻折,使点A与点E重合,连接CE,若已知4CD=BC,AC=2,请求出线段CE的长.23.在等腰△ADC和等腰△BEC中,∠ADC=∠BEC=90°,BC<CD,将△BEC绕点C 逆时针旋转,连接AB,点O为线段AB的中点,连接DO,EO.(1)如图1,当点B旋转到CD边上时,请直接写出线段DO与EO的位置关系和数量关系;(2)如图2,当点B旋转到AC边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由;(3)若BC=4,CD=2,在△BEC绕点C逆时针旋转的过程中,当∠ACB=60°时,请直接写出线段OD的长.24.如图1,在Rt△ABC中,AB=AC,D、E是斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF.(1)试说明:△AED≌△AFD;(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.25.已知正方形ABCD,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.(1)如图1,求证:①AE=CF;②AE⊥CF.(2)若BE=2,①如图2,点E在正方形内,连接EC,若∠AEB=135°,EC=5,求AE的长;②如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,求AE的长.26.(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=a,S=a2.(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;②求∠ADB的度数.③若AD=2,BD=4,求△ABC的面积.(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.①求∠EAF的度数;②若CD=5,BD=2,求BC的长.27.【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB、CD所在直线夹角(锐角)为;(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角.【运用拓广】运用所形成的结论解决问题:(3)如图③,四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD =,求AD的长.28.已知△AOB和△MON都是等腰直角三角形(OA<OM=ON),∠AOB=∠MON=90°.(1)如图1:连AM,BN,求证:△AOM≌△BON;(2)若将△MON绕点O顺时针旋转,①如图2,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;②当点A,M,N在同一条直线上时,若OB=4,ON=3,请直接写出线段BN的长.29.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由;(3)如图②,若∠ADC=90°,AD=5,AC=13,求BE2的值.30.(1)【操作发现】如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD =40°,连接AC,BD交于点M.①的值为;②∠AMB的度数为.(2)【类比探究】如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.计算的值及∠AMB的度数;(3)【实际应用】在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.31.△ABC中,BC=8,以AC为边向外作等边△ACD.(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;(2)如图②,若∠ABC=60°,AB=4,求BD的长.32.阅读下列材料:问题:如图1,在正方形ABCD内有一点P,P A=,PB=,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连接PP′.请你参考小明同学的思路,解决下列问题:(1)图2中∠BPC的度数为;(2)如图3,若在正六边形ABCDEF内有一点P,且P A=,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.33.(1)如图,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,问:BE与CD有什么数量关系?请说明理由;(2)如图2,已知△ABC,以AB、AC为边向外作正方向ABFD和正方形ACGE,连接BE,CD,则BE和CD之间的数量关系是;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,四边形ADBC中,∠ACB=45°,AC=40,BC=60,AB、CD是对角线,AB ⊥AD,AB=AD,求CD的长;(4)探究:①在图1中,当∠ACB=30°时,请直接写出DC、BC、AC之间的数量关系;②在图2中,当∠ACB=45°时,请直接写出DC、BC、AC之间的数量关系.34.(1)如图1,已知△ABC,以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,BD=2,∠ABC=∠ACB=∠ADB=45°,求CD的长;(3)如图3,四边形ABCD中,∠BAC=90°,∠ADB=∠ABC=α,tanα=,BD=5,AD=12,求CD的长.35.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:操作发现:(1)如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)类比探究:(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.灵活运用:(3)如图3,在四边形ABCD中,AC,BD是对角线,AB=BC,∠ABC=60°,∠ADC =30°,AD=2,BD=3,求CD的长.36.(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABD和等边△ACE,连结BE、CD,试猜想BE与CD的大小关系,并证明你的结论;(2)如图2,四边形ABCD中,AB=4,BC=3,AD=CD,∠ABC=30°,∠ADC=60°,求BD的长;(3)如图3,四边形ABCD中,AB=4,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长.37.如图,已知等腰直角三角形ABC中,AC=BC,把AB绕点B逆时针旋转一定角度到点D.连接AD、DC.使得∠DAC=∠BDC,当DC=时,求线段AC的长.38.请阅读下列材料:问题:如图1,在等边△ABC内有一点P,且P A=2,PB=,PC=1,求∠BPC.李明同学的思路是:将△BPC绕点B逆时针旋转60°,得到△BP′A(如图2),连接P′P.由旋转的性质知△BP′P是三角形;P′A=PC=1,∠BP′P=,P′P=PB=;在△AP′P中,∵P′P2+P′A2=()2+12=4=P A2;∴△AP′P是三角形;∴∠AP′P=°;∴∠BPC=∠BP′A=∠BP′P+∠AP′P=.问题得到解决.(1)将李明的思路补充完整;(2)请你参考李明同学的思路,探究并解决下列问题:如图3,等腰直角三角形ABC中,∠CAB=90°,P是△ABC内一点,且P A=1,PB=3,PC=,求∠CP A的度数.39.已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;(2)如图2,∠ABC=α,∠ACD=β,BC=6,BD=8.①若α=30°,β=60°,AB的长为;②若改变α、β的大小,但α+β=90°,求△ABC的面积.40.几何探究在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD 的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上时,求证:BD=CE.(2)如图2,若点D在线段CB的延长线上,∠BCE=α,∠BAC=β.则α、β之间有怎样的数量关系?写出你的理由.(3)如图3,当点D在线段BC上,∠BAC=90°,BC=4,求S△DCE最大值.手拉手biubiubiu参考答案与试题解析一.填空题(共18小题)1.已知△ABC中,∠ABC=45°,AB=7,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为.【分析】显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.【解答】解:以AB为腰作等腰Rt△ABE,连接EC,∵△ADC为等腰Rt△,∴,∠EAB=∠DAC=45°,∴∠EAB+∠BAC=∠BAC+∠DAC,∴∠EAC=∠DAB,∴△EAC∽△BAD,∴,作EF⊥BC交BC延长线于F,∵∠ABC=45°,∠EBA=90°,∴∠EBF=45°,∴△EFB为等腰Rt△,∴EF=FB===7,∴EC==25,∴BD==.【点评】本题主要考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等重要知识点,有一定难度.正确作出辅助线是本题的难点.2.如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为7.【分析】以AB为边作等边三角形AEB,连接CE,如图所示,由三角形ABE与三角形ACD都为等边三角形,利用等边三角形的性质得到AE=AB,AD=AC,且∠EAB=∠DAC =60°,利用等式的性质得到夹角相等,利用SAS得到三角形EAC与三角形BAD全等,利用余弦定理求出EC的长就是BD的长.【解答】解:以AB为边作等边三角形AEB,连接CE,如图所示,∵△ABE与△ACD都为等边三角形,∴∠EAB=∠DAC=60°,AE=AB,∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,,∴△EAC≌△BAD(SAS),∴BD=EC,∵∠EBA=60°,∠ABC=60°,∴∠EBC=120°,在△EBC中,BC=5,EB=3,过点E做BC的垂线交BC于点F,易知∠EBF=60°,∠FEB=30°,∴EF=,FB=,FC=5+=,∴EC2=FC2+EF2=49∴BD=EC=7.故答案为:7.【点评】此题考查了全等三角形的判定与性质,等边三角形的性质,以及余弦定理,熟练掌握全等三角形的判定与性质是解本题的关键.3.四边形ABCD中,AC=BC,∠ACB=90°,∠ADB=30°,AD=,CD=14,则BD=10.【分析】过C作CE⊥BD于E,过A作AF⊥BD于F,作CG作AF于G,证明△ACG ≌△BCE(AAS),得出AG=BE,CG=CE,证出四边形CEFG是正方形,得出CE=EF =GF,由直角三角形的性质得出AF=AD=3,DF=AF=3,设GF=CE=EF=x,则DE=x+3,在Rt△CDE中,由勾股定理得出方程,解方程得出GF=EF=,得出BE=AG=GF﹣AF=,即可得出答案.【解答】解:过C作CE⊥BD于E,过A作AF⊥BD于F,作CG作AF于G,如图所示:则四边形CEFG是矩形,∴∠ECG=90°=∠ACB,∴∠ACG=∠BCE,在△ACG和△BCE中,,∴△ACG≌△BCE(AAS),∴AG=BE,CG=CE,∴四边形CEFG是正方形,∴CE=EF=GF,∵∠ADB=30°,AD=,∴AF=AD=3,DF=AF=3,设GF=CE=EF=x,则DE=x+3,在Rt△CDE中,由勾股定理得:x2+(x+3)2=142,解得:x=(负值舍去),∴GF=EF=,∴BE=AG=GF﹣AF=,∴BD=BE+EF+DF=++3=10;故答案为:.【点评】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、正方形的判定与性质、勾股定理等知识;熟练掌握正方形的判定与性质,证明三角形全等是解题的关键.4.已知在四边形ABCD中,AB=AC,∠ABC=∠ADC=60°,连接BD,若CD=2,AB =2,则BD的长度为.【分析】根据等边三角形的判定定理得到△ABC是等边三角形,求得∠BAC=60°,过C作CE⊥AD与E,解直角三角形得到DE=CD=1,求得CE=DE=,根据直角三角形的性质得到∠CAD=30°,求得∠ACE=60°,∠BAD=90°,得到∠ACD=90°,根据勾股定理即可得到结论.【解答】解:∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,过C作CE⊥AD与E,∴∠AEC=∠CED=90°,∵∠ADC=60°,∴∠DCE=30°,∵CD=2,∴DE=CD=1,∴CE=DE=,∵AC=AB=2,∴CE=AC,∴∠CAD=30°,∴∠ACE=60°,∠BAD=90°,∴∠ACD=90°,∴AD=2CD=4,∴BD===2.故答案为:2.【点评】本题考查了直角三角形的判定和性质,等边三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.5.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=,BC=,连接AC、BD,若AC⊥AB,则BD的长度为2.【分析】过A作AE⊥AD,使AE=AD,连接CE,DE,过C作CF⊥AD于F,得到△ADE是等腰直角三角形,证明△DAB≌△EAC得:EC=BD,在Rt△DCE中,利用勾股定理求EC的长,于是得到结论.【解答】解:过A作AE⊥AD,使AE=AD,连接CE,DE,过C作CF⊥AD于F,则△ADE是等腰直角三角形,∵∠ADC=45°,∴△CDF是等腰直角三角形,∴CF=DF=CD=1,∵AC⊥AB,∠ABC=45°,∴△ABC是等腰直角三角形,∴AC=BC=,∴AF==2,∴AD=3,∴DE=AD=3,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE,(SAS),∴CE=BD,∵∠ADE=∠ADC=45°,∴∠CDE=90°,∴CE==2,∴BD=CE=2.故答案为:2.【点评】本题考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.6.如图,四边形ABCD中,∠ABC=∠ACD=∠ADC=45°,△DBC的面积为8,则BC 长为4.【分析】如图,作DH⊥BC交BC的延长线于H,取CD的中点O,连接OA,OB.证明A,C,B,D四点共圆,利用全等三角形的性质证明BC=DH,即可解决问题.【解答】解:如图,作DH⊥BC交BC的延长线于H,取CD的中点O,连接OA,OB.∵DH⊥BH,∴∠DHC=90°,∵∠DAC=90°,CO=OD,∴OA=OD=OC=OH,∴A,C,H,D四点共圆,∵AC=AD,∴∠CHA=∠AHD=45°,(没有学习四点共圆,可以这样证明:过点A作AM⊥DH于M,过点A作AN⊥BH于N,证明△AMD≌△ANC,推出AM=AN,推出AH平分∠MHN 即可)∵∠ABC=45°,∴∠BAH=90°,∴BA=AH,∵∠BAH=∠CAD=90°,∴∠BAC=∠HAD,∵AC=AD,AB=AH,∴△BAC≌△HAD(SAS),∴BC=DH,∴S△BCD=×BC×DH=×BC2=16,∴BC=4或﹣4(舍弃),故答案为4.【点评】本题考查旋转变换,等腰直角三角形的性质,全等三角形的判定和性质鞥知识,解题的关键是学会添加常用辅助线,利用辅助圆解决问题,属于中考填空题中的压轴题.7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC =.【分析】如图,作DE⊥DC交AC于E,连接BE交AD于O.利用全等三角形的性质证明BE=AC=5,BE⊥AC即可解决问题.【解答】解:如图,作DE⊥DC交AC于E,连接BE交AD于O.∵DA=DB,∠DAB=45°,∴∠DAB=∠DBA=45°,∴∠ADB=90°,∵∠DCE=45°,DE⊥DC,∴DC=DE,∵∠CDE=∠ADB=90°,∴∠CDA=∠EDB,∵DC=DE,DA=DB,∴△CDA≌△EDB(SAS),∴AC=BE=5,∠CAD=∠EBD,∵∠AOE=∠BOD,∴∠AEO=∠BDO=90°,∴BE⊥AC,∴S△ABC=•AC•BE=,故答案为.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,全等三角形的判定和性质,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.8.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC 的内部有一点P,P A=8,PB=4,PC=4,则线段AB的长为4.【分析】将△ABP绕点A逆时针旋转120°,得到△ACD,连接PD,过点A作AH⊥PD 于H,利用等腰三角形的性质及通过解直角三角形求出AH,PH,DH,PD的长,利用勾股定理的逆定理证明△PDC为直角三角形,再证△DMC∽△HMA,其对应边相等,可推出AM=CM=AC,HM=DM=HD=2,在Rt△DMC中,通过勾股定理求出CM的长,可推出AB=AC=2CM=4.【解答】解:如图,将△ABP绕点A逆时针旋转120°,得到△ACD,连接PD,过点A 作AH⊥PD于H,则△ABP≌△ACD,∠P AD=120°,∴P A=DA=8,PB=DC=4,∠APH=∠ADH=30°,∴AH=AP=4,∴PH=DH==4,∴PD=2PH=8,在△PDC中,PD2+CD2=(8)2+42=208,PC2=(4)2=208,∴PD2+CD2=PC2,∴△PDC为直角三角形,且∠PDC=90°,∴∠AHD=∠PDC,∴AH∥DC,∴△DMC∽△HMA,∵DC=AH=4,∴AM=CM=AC,HM=DM=HD=2,∴在Rt△DMC中,CM===2,∴AB=AC=2CM=4,故答案为:4.【点评】本题考查了旋转的性质,等腰三角形的性质,解直角三角形,相似三角形的判定与性质,勾股定理等,解题关键是能够通过勾股定理的逆定理证明△DMC为直角三角形.9.如图,在△ABC中,∠ABC=60°,=,D为△ABC外一点,连接AD、CD.若∠ADC=30°,AC=AD,则的值为.【分析】将△ABD绕A顺时针旋转120°得△ACQ,连BQ,则△ABD≌△AQC,依据旋转的性质以及勾股定理即可得到BD的长,进而得出的值.【解答】解:如图所示,将△ABD绕A顺时针旋转120°得△ACQ,连BQ,则∠BAQ=∠DAC=120°,BA=QA,∴∠ABQ=30°,∠QBC=60°+30°=90°,设BC=2,AB=3,过A作AE⊥BQ于E,则BQ=2BE=2cos30°×AB=2×,∴Rt△BCQ中,CQ=,∴BD=CQ=,∴.故答案为:.【点评】本题主要考查了旋转的性质以及勾股定理的运用,解决问题的关键是利用旋转变换构造直角三角形.10.如图,△ABC、△CDE是两个直角三角板,其中∠ECD=∠ACB=90°,∠CED=45°,∠CAB=30°,若AB=DE=2,将直角三角板CDE绕点C旋转一周,则|AD﹣BE|的最大值为﹣1.【分析】如图,在CA取一点J,使得CJ=CB,连接DJ.利用全等三角形的性质证明BE=DJ,推出|AD﹣BE|=|AD﹣DJ|≤AJ,求出AJ即可解决问题.【解答】解:如图,在CA取一点J,使得CJ=CB,连接DJ.在Rt△ACB中,AB=2,∠CAB=30°,∠ACB=90°,∴CB=CJ=AB=1,AC=BC=,∵∠ECD=∠BCJ=90°,∴∠DCJ=∠ECB,∵CD=CE,CJ=CB,∴△DCJ≌△ECB(SAS),∴DJ=BE,∴|AD﹣BE|=|AD﹣DJ|,∵|AD﹣DJ|≤AJ,∴|AD﹣BE|≤﹣1,∴|AD﹣BE|的最大值为﹣1.故答案为﹣1.【点评】本题考查旋转的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题.11.如图,点D为等边△ABC外一点,∠ADC=60°,连接BD,若AD=8,△BCD的面积为,则BD的长为.【分析】将△BCD顺时针方向旋转60°至△ACE,连接DE,过点E作EF⊥AD,交AD 的延长线于点F,由设DF=a,则EF=a,DE=CE=2a,三角形面积可求出EF长,由勾股定理可求出AE的长,则BD可求出.【解答】解:将△BCD顺时针方向旋转60°至△ACE,连接DE,过点E作EF⊥AD,交AD的延长线于点F,∴CD=CE,∠ECD=60°,∴△CDE为等边三角形,∴∠CDE=∠CED=∠ECD=60°,∵∠ADC=60°,∴∠ADC=∠ECD,∴AD∥CE,∴S△ACE=S△CDE,∵将△BCD顺时针方向旋转60°至△ACE,∴S△BCD=S△ACE,∴S△CDE=S△BCD=,∵∠ADC=∠CDE=60°,∴∠EDF=60°,在Rt△FDE中,设DF=a,则EF=a,DE=CE=2a,∴S△CDE=,解得:a=,∴EF=,∵AD=8,∴AF=8+=,∴AE===,∴BD=AE=.故答案为:.【点评】本题考查了旋转的性质,等边三角形的判定与性质,勾股定理,平行线的判定,三角形的面积等知识,熟练掌握旋转的性质是解题的关键.12.如图,△ABC中,∠ABC=45°,AB=2,BC=6,AD⊥AC,AD=AC,连接BD,则BD的长为2.【分析】如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN的延长线于E,易证明△ADN≌△CAM,四边形MNEB是矩形,在Rt△EBD中求出BE,ED即可.【解答】解:如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN 的延长线于E.∵∠E=∠ENM=∠NMB=90°,∴四边形MNEB是矩形,∴BM=EN,EB=MN,∵∠DAC=90°,∴∠DAN+∠MAC=90°,∵∠MAC+∠ACM=90°,∴∠DAN=∠ACM,在△ADN和△CAM中,,∴△ADN≌△CAM(AAS),∴AM=DN,AN=CM.在Rt△ABM中,∵AB=2,∠ABM=45°,∴BM=AM=2,MC=BC﹣BM=4,在Rt△BDE中,∵EB=MN=6,ED=4,∴BD===2.【点评】本题考查了旋转的性质,全等三角形的判定和性质、矩形的判定和性质、勾股定理等知识,添加辅助线构造全等三角形是解题的关键.13.如图,在△ABC中,∠ABC=60°,AB=3,BC=12,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为15.【分析】以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP ⊥BE于P,根据等腰三角形的性质、余弦的概念求出BE,根据旋转变换的性质得到∠DEB=90°,根据勾股定理计算即可.【解答】解:以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE于P,则∠BAE=120°,AB=AE,DE=BC,∴∠ABE=∠AEB=30°,∴BP=AB•cos∠ABP=,∠DEB=90°,∴BE=2BP=9,在Rt△BED中,BD==15,故答案为:15.【点评】本题考查的是勾股定理、直角三角形的性质、等腰三角形的性质,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.14.如图,△ABC为等腰直角三角形,∠ACB=90°,∠APC=165°,P A=3,PC=,则PB=.【分析】将△ACP绕着点C逆时针旋转90°得到△BCP′,连接PP′,可得△CPP′是等腰直角三角形,进而求出∠PP′B=120°,PP′=2,再作辅助线,构造直角三角形利用勾股定理可求出答案.【解答】解:将△ACP绕着点C逆时针旋转90°得到△BCP′,连接PP′,过点P作PD⊥BP′,交BP′的延长线于点D,如图所示:由旋转可知,CP=CP′,∠∠PCP′=90°,∠APC=∠BP′C=165°,∴∠CPP′=∠CP′P=45°,PP′=PC=2,∴∠PP′B=∠CP′B﹣∠CP′P=165°﹣45°=120°∴∠PP′D=180°﹣120°=60°,在Rt△PP′D中,P′D=PP′=1,PD==,∴BD=BP′+P′D=3+1=4,在Rt△BPD中,由勾股定理得:BP==,故答案为.【点评】考查旋转的性质,等腰直角三角形的性质、直角三角形的性质、勾股定理等知识,旋转的应用巧妙的将问题转化到一个三角形中,再依据特殊的边角关系求出答案是一个很好的方法.15.如图,在等腰直角三角形ABC中,已知∠ACB=90°,P是△ABC内一点,使P A=11,PB=7,PC=6,则∠BPC=135°.【分析】根据旋转的性质得到CE=CP=6,AE=BP=7,∠PCE=90°,求得∠CEP=∠CPE=45°,由勾股定理可得到PE=6,根据勾股定理的逆定理得到△PEA是直角三角形,求得∠PEA=90°,根据全等三角形的性质即可得到结论.【解答】解:如图,将△CPB绕点C旋转90°得△CEA,连接PE,∴△CPB≌△CEA,∴CE=CP=6,AE=BP=7,∠PCE=90°,∴∠CEP=∠CPE=45°,在Rt△PCE中,由勾股定理可得,PE=6,在△PEA中,PE2=(6)2=72,AE2=72=49,P A2=112=121,∵PE2+AE2=AP2,∴△PEA是直角三角形∴∠PEA=90°,∴∠CEA=135°,又∵△CPB≌△CEA,∴∠BPC=∠CEA=135°.故答案为135°【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,熟练掌握旋转的性质是解题的关键.16.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3;⑤S△AOC+S△AOB═6+.其中正确的结论是①②③⑤.【分析】证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;由△OBO′是等边三角形,可知结论②正确;在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=6+4,故结论④错误;如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″,计算可得结论⑤正确.【解答】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,又∵OB=O′B,AB=BC,∴△BO′A≌△BOC,又∵∠OBO′=60°,∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;如图①,连接OO′,∵OB=O′B,且∠OBO′=60°,∴△OBO′是等边三角形,∴OO′=OB=4.故结论②正确;∵△BO′A≌△BOC,∴O′A=5.在△AOO′中,三边长为3,4,5,这是一组勾股数,∴△AOO′是直角三角形,∠AOO′=90°,∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=×3×4+×42=6+4,故结论④错误;如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=×3×4+×32=6+,故结论⑤正确.综上所述,正确的结论为:①②③⑤.故答案为:①②③⑤.【点评】本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数3、4、5所构成的三角形是直角三角形,这是本题的要点.在判定结论⑤时,将△AOB向不同方向旋转,体现了结论①﹣结论④解题思路的拓展应用.17.等边△ABC的边长为2,三角形外部有一点D,CD=2,连接AD、BD,若∠ADC =30°,则BD的长为2.【分析】将AD绕点A顺时针旋转60°到AE,连接BE,DE,延长DC交AE于点F,由旋转的性质和等边三角形的性质可得DF=AF,AD=2AF,由勾股定理可求AF=2,AD=4,由全等三角形的性质可得BE=CD=2,∠BEA=∠CDA=30°,由勾股定理可求BD的长.【解答】解:如图,将AD绕点A顺时针旋转60°到AE,连接BE,DE,延长DC交AE 于点F,∵旋转∴AE=AD,∠DAE=60°,∴△ADE是等边三角形,∴AD=DE=AE,∠ADE=60°,又∵∠ADC=30°,∴DF平分∠ADE,且AD=DE,∴DF⊥AE,且∠ADF=30°,∴DF=AF,AD=2AF,在Rt△AFC中,AC2=AF2+CF2,∴28=AF2+(AF﹣2)2,∴AF=2,AF=﹣(不合题意)∴AD=2AF=4=DE,∵△ABC是等边三角形∴AB=AC,∠BAC=60°,∴∠BAC=∠DAE∴∠BAE=∠DAC,且AB=AC,AE=AD,∴△BAE≌△CAD(SAS)∴BE=CD=2,∠BEA=∠CDA=30°,∴∠BED=∠BEA+∠AED=90°∴BD==2故答案为:2【点评】本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识,综合运用这些性质进行推理是本题的关键.18.如图,在四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,∠BAD的平分线AE与DC边相交于点E,连接BE,AC,若AC=7,△BCE的周长为16,则线段BC 的长为6.【分析】把△ABC绕点A逆时针旋转90°得到△ADK,连接CK,作KH⊥CD于H,则AC=AK=7,∠CAK=90°,∠ADK=∠ABC,DK=BC=x,CK=14,根据∠BAD =90°,∠BCD=30°,可得∠ABC+∠ADC=240°,所以∠ADK+∠ADC=240°,即∠CDK=120°,因为DH=x,HK=x,CD=16﹣x,在Rt△KHC中,由勾股定理即可得出x的值,从而求得BC的长.【解答】解:如图,把△ABC绕点A逆时针旋转90°得到△ADK,连接CK,作KH⊥CD于H,则AC=AK=7,∠CAK=90°,∠ADK=∠ABC,DK=BC=x,∴CK=,∵∠BAD=90°,∠BCD=30°,∴∠ABC+∠ADC=360°﹣30°﹣90°=240°,∴∠ADK+∠ADC=240°,∴∠CDK=120°,即∠KDH=60°,∴DH=x,HK=x,∵AB=AD,∠BAE=∠DAE,AE=AE,∴△ABE≌△ADE(SAS),∴BE=ED,∵△BCE的周长为16,∴BC+CE+BE=BC+CE+ED=BC+CD=DK+CD=16,∴CD=16﹣x,CH=16﹣x+x=16﹣,在Rt△KHC中,,解得:x=6或x=10(舍去),∴BC的长为6.故答案为:6.【点评】本题考查图形的旋转,三角形全等的判定和性质,直角三角形的性质.解题的关键是掌握图形旋转的性质.二.解答题(共22小题)19.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:已知△ABC如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)●类比探究:如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么数量关系?说明理由.●灵活运用:如图3,已知△ABC中,AB=,BC=3,∠ABC=45°,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.【分析】(1)根据题意画出相应图形,如图所示,(分别以点A,B为圆心,AB长为半径画弧,两弧的交点即为点D,△ABD为等边三角形,△ACE同理可得),由三角形ABD 与三角形ACE都为等边三角形,利用等边三角形的性质得到AD=AB,AE=AC,且∠BAD=∠CAE=60°,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形AEB全等,利用全等三角形的对应边相等得到CD=BE;(2)CE=BG,理由为:由四边形ABDE与四边形ACFG都为正方形,利用正方形的性质得到AD=AB,AE=AC,且∠BAD=∠CAE=90°,利用等式的性质得到夹角相等,利用SAS得到三角形ACE与三角形ABG全等,利用全等三角形的对应边相等得到CE=BG;(3)以AB为边向外作等腰直角三角形ABG,连接CG,在等腰三角形ABG中,利用勾股定理求出BG的长,进而得到三角形BCG为直角三角形,利用勾股定理求出CG的长,由三角形ACG与三角形ABE都为等腰直角三角形,利用等腰直角三角形的性质得到AG =AB,AE=AC,且∠BAG=∠CAE=90°,利用等式的性质得到夹角相等,利用SAS 得到三角形ACG与三角形ABE全等,利用全等三角形的对应边相等得到CG=BE,即可求出BE的长.【解答】解:(1)作图,如图所示:。
初中数学专题一 旋转中的几何模型(手拉手模型、对角互补模型)(解析版)

专题一旋转中的几何模型模型一 “手拉手”模型模型特征:两个等边三角形或等腰直角三角形或正方形共顶点.模型说明:如图1,△ABE,△ACF都是等边三角形,可证△AEC≌△ABF.如图2,△ABD,△ACE都是等腰直角三角形,可证△ADC≌△ABE.如图3,四边形ABEF,四边形ACHD都是正方形,可证△ABD≌△AFC.图1 图2 图3等腰图形有旋转,辩清共点旋转边,关注三边旋转角,全等思考边角边。
1【问题提出】(1)如图①,△ABC,△ADE均为等边三角形,点D,E分别在边AB,AC上.将△ADE绕点A沿顺时针方向旋转,连结BD,CE.在图②中证明△ADB≅△AEC.[学以致用](2)在(1)的条件下,当点D,E,C在同一条直线上时,∠EDB的大小为度.[拓展延伸](3)在(1)的条件下,连结CD.若BC=6,AD=4直接写出△DBC的面积S的取值范围.【思路点拨】(1)根据“手拉手”模型,证明△ADB≅△AEC即可;(2)分“当点E在线段CD上”和“当点E在线段CD的延长线上”两种情况,再根据“手拉手”模型中的结论即可求得∠EDB的大小;(3)分别求出△DBC的面积最大值和最小值即可得到结论【详解】(1)∵ABC,ADE均为等边三角形,∴AD=AE,AB=AC,∴∠DAE-∠BAE=∠BAC-∠BAE,即∠BAD=∠CAE在△ADB和△AEC中,AD=AE∠BAD=∠CAE AB=AC∴ABD ≅ACE (SAS );(2)当D ,E ,C 在同一条直线上时,分两种情况:①当点E 在线段CD 上时,如图,∵△ADE 是等边三角形,∴∠ADE =∠AED =60°,∴∠AEC =180°-∠AED =120°,由(1)可知,△ADB ≅△AEC ,∴∠ADB =∠AEC =120°,∴∠EDB =∠ADB -∠ADE =120°-60°=60°②当点E 在线段CD 的延长线上时,如图,∵△ADE 是等边三角形,∴∠ADE =∠AED =60°∴∠ADC =180°-∠ADE =120°,由(1)可知,△ADB ≅△AEC∴∠ADB =∠AEC =60°,∴∠EDB =∠ADB +∠ADE =60°+60°=120°综上所述,∠EDB 的大小为60°或120°(3)过点A 作AF ⊥BC 于点F ,当点D 在线段AF 上时,点D 到BC 的距离最短,此时,点D 到BC 的距离为线段DF 的长,如图:∵ΔABC 是等边三角形,AF ⊥BC ,BC =6∴AB =BC =6,BF =12BC =3∴AF =AB 2-BF 2=62-32=33∴DF =33-4此时S .DBC =12BC ⋅DF =12×6×(33-4)=93-12;当D 在线段FA 的延长线上时,点D 到BC 的距离最大,此时点D 到BC 的距离为线段DF 的长,如图,∵ΔABC 是等边三角形,AF ⊥BC ,BC =6∴AB =BC =6,BF =12BC =3,∴AF =AB 2-BF 2=62-32=33∵AD =4∴DF =AF +AD =33+4此时,S .DBC =12BC ⋅DF =12×6×(33+4)=93+12;综上所述,△DBC 的面积S 取值是93-12≤5≤93+12【点评】 利用“手拉手”模型,构造对应边“拉手线”组成的两个三角形全等是解题关键2已知正方形ABCD 和等腰直角三角形BEF ,BE =EF ,∠BEF =90°,按图1放置,使点F 在BC 上,取DF 的中点G ,连接EG ,CG .(1)探索EG,CG的数量关系和位置关系并证明;(2)将图(1)中△BEF绕点B顺时针旋转45°,再连接DF,取DF中点G(见图2),(1)中的结论是否仍然成立?证明你的结论;(3)将图(1)中△BEF绕点B顺时针转动任意角度(旋转角在0°到90°之间),再连接DF,取DF中点G(见图3),(1)中的结论是否仍然成立?证明你的结论.【思路点拨】(1)首先证明B、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG= GF=CG,得到∠EGF=2∠EDG,∠CGF=2∠CDG,从而证得∠EGC=90°;(2)首先证明△FEG≌△DHG,然后证明△ECH为等腰直角三角形.可以证得:EG=CG且EG⊥CG;(3)首先证明:△BEC≌△FEH,即可证得:△ECH为等腰直角三角形,从而得到:EG=CG且EG⊥CG.【解题过程】解:(1)EG=CG且EG⊥CG.证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.∴∠EGF=2∠EDG,∠CGF=2∠CDG.∴∠EGF+∠CGF=2∠EDC=90°,即∠EGC=90°,∴EG⊥CG.(2)仍然成立,证明如下:如图②,延长EG交CD于点H.∵BE⊥EF,∴EF∥CD,∴∠1=∠2.又∵∠3=∠4,FG=DG,∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,∴△HFG≌△CDG,∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,∴HE=EC,∠BEC=∠FEH,∴∠BEF=∠HEC=90°,∴△ECH为等腰直角三角形.又∵CG=GH,∴EG=CG且EG⊥CG.针对训练11已知ΔABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF,CF,AF.(1)问题发现:如图1,当点E在线段AD上时,且∠AFC=35°,则∠FAC的度数是;(2)结论证明:如图2,当点E 在线段AD 的延长线上时,请判断∠AFC 和∠FAC 的数量关系,并证明你的结论;(3)拓展延伸:若点E 在直线AD 上运动,若存在一个位置,使得ΔACF 是等腰直角三角形,请直接写出此时∠EBC 的度数.【答案】(1)55°;(2)∠AFC +∠FAC =90°,见解析;(3)15°或75°【解析】(1)55°,理由:∵ΔABC 是等边三角形,∴AB =AC =BC ,∠ABC =∠BAC =∠ACB =60°,∵AB =AC ,AD ⊥BC ,∴∠BAD =30°,∵将BE 绕点B 顺时针方向旋转60°得到BF ,∴BE =BF ,∠EBF =60°,∴∠EBF =∠ABC ,在△ADC 和△BDA 中,AB =BC∠ABE =∠FBC BE =BF,∴ΔABE ≌ΔCBF SAS ,∴∠BAE =∠BCF =30°,∴∠ACF =90°,∴∠AFC +∠FAC =90°;∵∠AFC =35°,∴∠FAC =55°;(2)结论:∠AFC +∠FAC =90°,理由如下:∵ΔABC 是等边三角形,∴AB =AC =BC ,∠ABC =∠BAC =∠ACB =60°,∵AB =AC ,AD ⊥BC ,∴∠BAD =30°,∵将BE 绕点B 顺时针方向旋转60°得到BF ,∴BE =BF ,∠EBF =60°,∴∠EBF =∠ABC ,在△ADC 和△BDA 中,AB =BC∠ABE =∠FBC BE =BF,∴ΔABE ≌ΔCBF SAS ,∴∠BAE =∠BCF =30°,∴∠ACF =90°,∴∠AFC +∠FAC =90°;(3)∠EBC =15°或75°分两种情况:①点E 在点A 的下方时,如图:∵ΔACF 是等腰直角三角形,∴AC =CF ,由(2)得ΔABE ≌ΔCBF ,∴CF =AE ,∴AC =AE =AB ,∴∠ABE =180°-30°2=75°,∴∠EBC =∠ABE -∠ABC =75°-60°=15°;②点E 在和点A 的上方时,如图:同理可得∠EBC =∠ABE +∠ABC =75°.2已知四边形ABCD 是正方形,将线段CD 绕点C 逆时针旋转α(0°<α<90°),得到线段CE ,联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F .(1)如图,当BE =CE 时,求旋转角α的度数;(2)当旋转角α的大小发生变化时,∠BEF 的度数是否发生变化?如果变化,请用含α的代数式表示;如果不变,请求出∠BEF 的度数;(3)联结AF ,求证:DE =2AF .【答案】(1)30°;(2)不变;45°;(3)见解析【解析】(1)证明:在正方形ABCD 中, BC =CD .由旋转知,CE=CD,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形,∴∠BCE=60°.又∵∠BCD=90°,∴α=∠DCE=30°.(2)∠BEF的度数不发生变化.在△CED中,CE=CD,∴∠CED=∠CDE=180°-α2=90°-α2,在△CEB中,CE=CB,∠BCE=90°-α,∴∠CEB=∠CBE=180°-∠BCE2=45°+α2,∴∠BEF=180°-∠CED-∠CEB=45°.(3)过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于点H,过点C作CI⊥DF于点I易知四边形AGFH是平行四边形,又∵BF⊥DF,∴平行四边形AGFH是矩形.∵∠BAD=∠BGF=90°,∠BPF=∠APD,∴∠ABG=∠ADH.又∵∠AGB=∠AHD=90°,AB=AD,∴△ABG≌△ADH.∴AG=AH,∴矩形AGFH是正方形.∴∠AFH=∠FAH=45°,∴AH=AF∵∠DAH+∠ADH=∠CDI+∠ADH=90°∴∠DAH=∠CDI又∵∠AHD=∠DIC=90°,AD=DC,∴△AHD≌△DIC∴AH=DI,∵DE=2DI,∴DE=2AH=2AF模型二 对角互补模型对角互补模型的特征:外观呈现四边形,且对角和为180°。
手拉手模型-含答案

手拉手模型一.填空题(共18小题)1.已知△ABC中,∠ABC=45°,AB=7,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为.2.如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为.3.四边形ABCD中,AC=BC,∠ACB=90°,∠ADB=30°,AD=,CD=14,则BD=.4.已知在四边形ABCD中,AB=AC,∠ABC=∠ADC=60°,连接BD,若CD=2,AB =2,则BD的长度为.5.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=,BC=,连接AC、BD,若AC⊥AB,则BD的长度为.6.如图,四边形ABCD中,∠ABC=∠ACD=∠ADC=45°,△DBC的面积为8,则BC 长为.7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC =.8.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC 的内部有一点P,P A=8,PB=4,PC=4,则线段AB的长为.9.如图,在△ABC中,∠ABC=60°,=,D为△ABC外一点,连接AD、CD.若∠ADC=30°,AC=AD,则的值为.10.如图,△ABC、△CDE是两个直角三角板,其中∠ECD=∠ACB=90°,∠CED=45°,∠CAB=30°,若AB=DE=2,将直角三角板CDE绕点C旋转一周,则|AD﹣BE|的最大值为.11.如图,点D为等边△ABC外一点,∠ADC=60°,连接BD,若AD=8,△BCD的面积为,则BD的长为.12.如图,△ABC中,∠ABC=45°,AB=2,BC=6,AD⊥AC,AD=AC,连接BD,则BD的长为.13.如图,在△ABC中,∠ABC=60°,AB=3,BC=12,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为.14.如图,△ABC为等腰直角三角形,∠ACB=90°,∠APC=165°,P A=3,PC=,则PB=.15.如图,在等腰直角三角形ABC中,已知∠ACB=90°,P是△ABC内一点,使P A=11,PB=7,PC=6,则∠BPC=.16.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3;⑤S△AOC+S△AOB═6+.其中正确的结论是.17.等边△ABC的边长为2,三角形外部有一点D,CD=2,连接AD、BD,若∠ADC =30°,则BD的长为.18.如图,在四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,∠BAD的平分线AE与DC边相交于点E,连接BE,AC,若AC=7,△BCE的周长为16,则线段BC 的长为.二.解答题(共22小题)19.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:已知△ABC如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)●类比探究:如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么数量关系?说明理由.●灵活运用:如图3,已知△ABC中,AB=,BC=3,∠ABC=45°,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.20.将图形中的三角形绕某一点作适当旋转,可帮助解决很多几何问题.(1)如图1,直角△ABC中,AB=AC,∠BAC=90°,D为BC边上的一点,将△ABD 绕点A逆时针旋转90°至△ACF,作AE平分∠DAF交BC于E,请证明:BD2+CE2=DE2;(2)如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是64cm2,则AC长是cm;(3)如图3,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC=30°,AD=2,BD=3,求CD的长.21.直线m∥n,点A、B分别在直线m,n上(点A在点B的右侧),点P在直线m上,AP=AB,连接BP,将线段BP绕点B顺时针旋转60°得到BC,连接AC交直线n于点E,连接PC,且△ABE为等边三角形.(1)如图①,当点P在A的右侧时,请直接写出∠ABP与∠EBC的数量关系是,AP与EC的数量关系是.(2)如图②,当点P在A的左侧时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.(3)如图②,当点P在A的左侧时,若△PBC的面积为,求线段AC的长.22.某校八年级数学兴趣小组在研究等腰直角三角形与图形变换时,作了如下研究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为腰作等腰直角三角形DAF,使∠DAF=90°,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①CF与BC的位置关系为;②CF,DC,BC之间的数量关系为(直接写出结论);(2)数学思考如图2,当点D在线段CB的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,将△DAF沿线段DF翻折,使点A与点E重合,连接CE,若已知4CD=BC,AC=2,请求出线段CE的长.23.在等腰△ADC和等腰△BEC中,∠ADC=∠BEC=90°,BC<CD,将△BEC绕点C 逆时针旋转,连接AB,点O为线段AB的中点,连接DO,EO.(1)如图1,当点B旋转到CD边上时,请直接写出线段DO与EO的位置关系和数量关系;(2)如图2,当点B旋转到AC边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由;(3)若BC=4,CD=2,在△BEC绕点C逆时针旋转的过程中,当∠ACB=60°时,请直接写出线段OD的长.24.如图1,在Rt△ABC中,AB=AC,D、E是斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF.(1)试说明:△AED≌△AFD;(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.25.已知正方形ABCD,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.(1)如图1,求证:①AE=CF;②AE⊥CF.(2)若BE=2,①如图2,点E在正方形内,连接EC,若∠AEB=135°,EC=5,求AE的长;②如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,求AE的长.26.(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=a,S=a2.(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;②求∠ADB的度数.③若AD=2,BD=4,求△ABC的面积.(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.①求∠EAF的度数;②若CD=5,BD=2,求BC的长.27.【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB、CD所在直线夹角(锐角)为;(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角.【运用拓广】运用所形成的结论解决问题:(3)如图③,四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD =,求AD的长.28.已知△AOB和△MON都是等腰直角三角形(OA<OM=ON),∠AOB=∠MON=90°.(1)如图1:连AM,BN,求证:△AOM≌△BON;(2)若将△MON绕点O顺时针旋转,①如图2,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;②当点A,M,N在同一条直线上时,若OB=4,ON=3,请直接写出线段BN的长.29.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由;(3)如图②,若∠ADC=90°,AD=5,AC=13,求BE2的值.30.(1)【操作发现】如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD =40°,连接AC,BD交于点M.①的值为;②∠AMB的度数为.(2)【类比探究】如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.计算的值及∠AMB的度数;(3)【实际应用】在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.31.△ABC中,BC=8,以AC为边向外作等边△ACD.(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;(2)如图②,若∠ABC=60°,AB=4,求BD的长.32.阅读下列材料:问题:如图1,在正方形ABCD内有一点P,P A=,PB=,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连接PP′.请你参考小明同学的思路,解决下列问题:(1)图2中∠BPC的度数为;(2)如图3,若在正六边形ABCDEF内有一点P,且P A=,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.33.(1)如图,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,问:BE与CD有什么数量关系?请说明理由;(2)如图2,已知△ABC,以AB、AC为边向外作正方向ABFD和正方形ACGE,连接BE,CD,则BE和CD之间的数量关系是;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,四边形ADBC中,∠ACB=45°,AC=40,BC=60,AB、CD是对角线,AB ⊥AD,AB=AD,求CD的长;(4)探究:①在图1中,当∠ACB=30°时,请直接写出DC、BC、AC之间的数量关系;②在图2中,当∠ACB=45°时,请直接写出DC、BC、AC之间的数量关系.34.(1)如图1,已知△ABC,以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,BD=2,∠ABC=∠ACB=∠ADB=45°,求CD的长;(3)如图3,四边形ABCD中,∠BAC=90°,∠ADB=∠ABC=α,tanα=,BD=5,AD=12,求CD的长.35.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:操作发现:(1)如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)类比探究:(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.灵活运用:(3)如图3,在四边形ABCD中,AC,BD是对角线,AB=BC,∠ABC=60°,∠ADC =30°,AD=2,BD=3,求CD的长.36.(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABD和等边△ACE,连结BE、CD,试猜想BE与CD的大小关系,并证明你的结论;(2)如图2,四边形ABCD中,AB=4,BC=3,AD=CD,∠ABC=30°,∠ADC=60°,求BD的长;(3)如图3,四边形ABCD中,AB=4,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长.37.如图,已知等腰直角三角形ABC中,AC=BC,把AB绕点B逆时针旋转一定角度到点D.连接AD、DC.使得∠DAC=∠BDC,当DC=时,求线段AC的长.38.请阅读下列材料:问题:如图1,在等边△ABC内有一点P,且P A=2,PB=,PC=1,求∠BPC.李明同学的思路是:将△BPC绕点B逆时针旋转60°,得到△BP′A(如图2),连接P′P.由旋转的性质知△BP′P是三角形;P′A=PC=1,∠BP′P=,P′P=PB=;在△AP′P中,∵P′P2+P′A2=()2+12=4=P A2;∴△AP′P是三角形;∴∠AP′P=°;∴∠BPC=∠BP′A=∠BP′P+∠AP′P=.问题得到解决.(1)将李明的思路补充完整;(2)请你参考李明同学的思路,探究并解决下列问题:如图3,等腰直角三角形ABC中,∠CAB=90°,P是△ABC内一点,且P A=1,PB=3,PC=,求∠CP A的度数.39.已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;(2)如图2,∠ABC=α,∠ACD=β,BC=6,BD=8.①若α=30°,β=60°,AB的长为;②若改变α、β的大小,但α+β=90°,求△ABC的面积.40.几何探究在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD 的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上时,求证:BD=CE.(2)如图2,若点D在线段CB的延长线上,∠BCE=α,∠BAC=β.则α、β之间有怎样的数量关系?写出你的理由.(3)如图3,当点D在线段BC上,∠BAC=90°,BC=4,求S△DCE最大值.手拉手biubiubiu参考答案与试题解析一.填空题(共18小题)1.已知△ABC中,∠ABC=45°,AB=7,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为.【分析】显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.【解答】解:以AB为腰作等腰Rt△ABE,连接EC,∵△ADC为等腰Rt△,∴,∠EAB=∠DAC=45°,∴∠EAB+∠BAC=∠BAC+∠DAC,∴∠EAC=∠DAB,∴△EAC∽△BAD,∴,作EF⊥BC交BC延长线于F,∵∠ABC=45°,∠EBA=90°,∴∠EBF=45°,∴△EFB为等腰Rt△,∴EF=FB===7,∴EC==25,∴BD==.【点评】本题主要考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等重要知识点,有一定难度.正确作出辅助线是本题的难点.2.如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为7.【分析】以AB为边作等边三角形AEB,连接CE,如图所示,由三角形ABE与三角形ACD都为等边三角形,利用等边三角形的性质得到AE=AB,AD=AC,且∠EAB=∠DAC =60°,利用等式的性质得到夹角相等,利用SAS得到三角形EAC与三角形BAD全等,利用余弦定理求出EC的长就是BD的长.【解答】解:以AB为边作等边三角形AEB,连接CE,如图所示,∵△ABE与△ACD都为等边三角形,∴∠EAB=∠DAC=60°,AE=AB,∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,,∴△EAC≌△BAD(SAS),∴BD=EC,∵∠EBA=60°,∠ABC=60°,∴∠EBC=120°,在△EBC中,BC=5,EB=3,过点E做BC的垂线交BC于点F,易知∠EBF=60°,∠FEB=30°,∴EF=,FB=,FC=5+=,∴EC2=FC2+EF2=49∴BD=EC=7.故答案为:7.【点评】此题考查了全等三角形的判定与性质,等边三角形的性质,以及余弦定理,熟练掌握全等三角形的判定与性质是解本题的关键.3.四边形ABCD中,AC=BC,∠ACB=90°,∠ADB=30°,AD=,CD=14,则BD=10.【分析】过C作CE⊥BD于E,过A作AF⊥BD于F,作CG作AF于G,证明△ACG ≌△BCE(AAS),得出AG=BE,CG=CE,证出四边形CEFG是正方形,得出CE=EF =GF,由直角三角形的性质得出AF=AD=3,DF=AF=3,设GF=CE=EF=x,则DE=x+3,在Rt△CDE中,由勾股定理得出方程,解方程得出GF=EF=,得出BE=AG=GF﹣AF=,即可得出答案.【解答】解:过C作CE⊥BD于E,过A作AF⊥BD于F,作CG作AF于G,如图所示:则四边形CEFG是矩形,∴∠ECG=90°=∠ACB,∴∠ACG=∠BCE,在△ACG和△BCE中,,∴△ACG≌△BCE(AAS),∴AG=BE,CG=CE,∴四边形CEFG是正方形,∴CE=EF=GF,∵∠ADB=30°,AD=,∴AF=AD=3,DF=AF=3,设GF=CE=EF=x,则DE=x+3,在Rt△CDE中,由勾股定理得:x2+(x+3)2=142,解得:x=(负值舍去),∴GF=EF=,∴BE=AG=GF﹣AF=,∴BD=BE+EF+DF=++3=10;故答案为:.【点评】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、正方形的判定与性质、勾股定理等知识;熟练掌握正方形的判定与性质,证明三角形全等是解题的关键.4.已知在四边形ABCD中,AB=AC,∠ABC=∠ADC=60°,连接BD,若CD=2,AB =2,则BD的长度为.【分析】根据等边三角形的判定定理得到△ABC是等边三角形,求得∠BAC=60°,过C作CE⊥AD与E,解直角三角形得到DE=CD=1,求得CE=DE=,根据直角三角形的性质得到∠CAD=30°,求得∠ACE=60°,∠BAD=90°,得到∠ACD=90°,根据勾股定理即可得到结论.【解答】解:∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,过C作CE⊥AD与E,∴∠AEC=∠CED=90°,∵∠ADC=60°,∴∠DCE=30°,∵CD=2,∴DE=CD=1,∴CE=DE=,∵AC=AB=2,∴CE=AC,∴∠CAD=30°,∴∠ACE=60°,∠BAD=90°,∴∠ACD=90°,∴AD=2CD=4,∴BD===2.故答案为:2.【点评】本题考查了直角三角形的判定和性质,等边三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.5.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=,BC=,连接AC、BD,若AC⊥AB,则BD的长度为2.【分析】过A作AE⊥AD,使AE=AD,连接CE,DE,过C作CF⊥AD于F,得到△ADE是等腰直角三角形,证明△DAB≌△EAC得:EC=BD,在Rt△DCE中,利用勾股定理求EC的长,于是得到结论.【解答】解:过A作AE⊥AD,使AE=AD,连接CE,DE,过C作CF⊥AD于F,则△ADE是等腰直角三角形,∵∠ADC=45°,∴△CDF是等腰直角三角形,∴CF=DF=CD=1,∵AC⊥AB,∠ABC=45°,∴△ABC是等腰直角三角形,∴AC=BC=,∴AF==2,∴AD=3,∴DE=AD=3,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE,(SAS),∴CE=BD,∵∠ADE=∠ADC=45°,∴∠CDE=90°,∴CE==2,∴BD=CE=2.故答案为:2.【点评】本题考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.6.如图,四边形ABCD中,∠ABC=∠ACD=∠ADC=45°,△DBC的面积为8,则BC 长为4.【分析】如图,作DH⊥BC交BC的延长线于H,取CD的中点O,连接OA,OB.证明A,C,B,D四点共圆,利用全等三角形的性质证明BC=DH,即可解决问题.【解答】解:如图,作DH⊥BC交BC的延长线于H,取CD的中点O,连接OA,OB.∵DH⊥BH,∴∠DHC=90°,∵∠DAC=90°,CO=OD,∴OA=OD=OC=OH,∴A,C,H,D四点共圆,∵AC=AD,∴∠CHA=∠AHD=45°,(没有学习四点共圆,可以这样证明:过点A作AM⊥DH于M,过点A作AN⊥BH于N,证明△AMD≌△ANC,推出AM=AN,推出AH平分∠MHN 即可)∵∠ABC=45°,∴∠BAH=90°,∴BA=AH,∵∠BAH=∠CAD=90°,∴∠BAC=∠HAD,∵AC=AD,AB=AH,∴△BAC≌△HAD(SAS),∴BC=DH,∴S△BCD=×BC×DH=×BC2=16,∴BC=4或﹣4(舍弃),故答案为4.【点评】本题考查旋转变换,等腰直角三角形的性质,全等三角形的判定和性质鞥知识,解题的关键是学会添加常用辅助线,利用辅助圆解决问题,属于中考填空题中的压轴题.7.如图,D为△ABC内一点,且AD=BD,若∠ACD=∠DAB=45°,AC=5,则S△ABC =.【分析】如图,作DE⊥DC交AC于E,连接BE交AD于O.利用全等三角形的性质证明BE=AC=5,BE⊥AC即可解决问题.【解答】解:如图,作DE⊥DC交AC于E,连接BE交AD于O.∵DA=DB,∠DAB=45°,∴∠DAB=∠DBA=45°,∴∠ADB=90°,∵∠DCE=45°,DE⊥DC,∴DC=DE,∵∠CDE=∠ADB=90°,∴∠CDA=∠EDB,∵DC=DE,DA=DB,∴△CDA≌△EDB(SAS),∴AC=BE=5,∠CAD=∠EBD,∵∠AOE=∠BOD,∴∠AEO=∠BDO=90°,∴BE⊥AC,∴S△ABC=•AC•BE=,故答案为.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,全等三角形的判定和性质,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.8.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC 的内部有一点P,P A=8,PB=4,PC=4,则线段AB的长为4.【分析】将△ABP绕点A逆时针旋转120°,得到△ACD,连接PD,过点A作AH⊥PD 于H,利用等腰三角形的性质及通过解直角三角形求出AH,PH,DH,PD的长,利用勾股定理的逆定理证明△PDC为直角三角形,再证△DMC∽△HMA,其对应边相等,可推出AM=CM=AC,HM=DM=HD=2,在Rt△DMC中,通过勾股定理求出CM的长,可推出AB=AC=2CM=4.【解答】解:如图,将△ABP绕点A逆时针旋转120°,得到△ACD,连接PD,过点A 作AH⊥PD于H,则△ABP≌△ACD,∠P AD=120°,∴P A=DA=8,PB=DC=4,∠APH=∠ADH=30°,∴AH=AP=4,∴PH=DH==4,∴PD=2PH=8,在△PDC中,PD2+CD2=(8)2+42=208,PC2=(4)2=208,∴PD2+CD2=PC2,∴△PDC为直角三角形,且∠PDC=90°,∴∠AHD=∠PDC,∴AH∥DC,∴△DMC∽△HMA,∵DC=AH=4,∴AM=CM=AC,HM=DM=HD=2,∴在Rt△DMC中,CM===2,∴AB=AC=2CM=4,故答案为:4.【点评】本题考查了旋转的性质,等腰三角形的性质,解直角三角形,相似三角形的判定与性质,勾股定理等,解题关键是能够通过勾股定理的逆定理证明△DMC为直角三角形.9.如图,在△ABC中,∠ABC=60°,=,D为△ABC外一点,连接AD、CD.若∠ADC=30°,AC=AD,则的值为.【分析】将△ABD绕A顺时针旋转120°得△ACQ,连BQ,则△ABD≌△AQC,依据旋转的性质以及勾股定理即可得到BD的长,进而得出的值.【解答】解:如图所示,将△ABD绕A顺时针旋转120°得△ACQ,连BQ,则∠BAQ=∠DAC=120°,BA=QA,∴∠ABQ=30°,∠QBC=60°+30°=90°,设BC=2,AB=3,过A作AE⊥BQ于E,则BQ=2BE=2cos30°×AB=2×,∴Rt△BCQ中,CQ=,∴BD=CQ=,∴.故答案为:.【点评】本题主要考查了旋转的性质以及勾股定理的运用,解决问题的关键是利用旋转变换构造直角三角形.10.如图,△ABC、△CDE是两个直角三角板,其中∠ECD=∠ACB=90°,∠CED=45°,∠CAB=30°,若AB=DE=2,将直角三角板CDE绕点C旋转一周,则|AD﹣BE|的最大值为﹣1.【分析】如图,在CA取一点J,使得CJ=CB,连接DJ.利用全等三角形的性质证明BE=DJ,推出|AD﹣BE|=|AD﹣DJ|≤AJ,求出AJ即可解决问题.【解答】解:如图,在CA取一点J,使得CJ=CB,连接DJ.在Rt△ACB中,AB=2,∠CAB=30°,∠ACB=90°,∴CB=CJ=AB=1,AC=BC=,∵∠ECD=∠BCJ=90°,∴∠DCJ=∠ECB,∵CD=CE,CJ=CB,∴△DCJ≌△ECB(SAS),∴DJ=BE,∴|AD﹣BE|=|AD﹣DJ|,∵|AD﹣DJ|≤AJ,∴|AD﹣BE|≤﹣1,∴|AD﹣BE|的最大值为﹣1.故答案为﹣1.【点评】本题考查旋转的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题.11.如图,点D为等边△ABC外一点,∠ADC=60°,连接BD,若AD=8,△BCD的面积为,则BD的长为.【分析】将△BCD顺时针方向旋转60°至△ACE,连接DE,过点E作EF⊥AD,交AD 的延长线于点F,由设DF=a,则EF=a,DE=CE=2a,三角形面积可求出EF长,由勾股定理可求出AE的长,则BD可求出.【解答】解:将△BCD顺时针方向旋转60°至△ACE,连接DE,过点E作EF⊥AD,交AD的延长线于点F,∴CD=CE,∠ECD=60°,∴△CDE为等边三角形,∴∠CDE=∠CED=∠ECD=60°,∵∠ADC=60°,∴∠ADC=∠ECD,∴AD∥CE,∴S△ACE=S△CDE,∵将△BCD顺时针方向旋转60°至△ACE,∴S△BCD=S△ACE,∴S△CDE=S△BCD=,∵∠ADC=∠CDE=60°,∴∠EDF=60°,在Rt△FDE中,设DF=a,则EF=a,DE=CE=2a,∴S△CDE=,解得:a=,∴EF=,∵AD=8,∴AF=8+=,∴AE===,∴BD=AE=.故答案为:.【点评】本题考查了旋转的性质,等边三角形的判定与性质,勾股定理,平行线的判定,三角形的面积等知识,熟练掌握旋转的性质是解题的关键.12.如图,△ABC中,∠ABC=45°,AB=2,BC=6,AD⊥AC,AD=AC,连接BD,则BD的长为2.【分析】如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN的延长线于E,易证明△ADN≌△CAM,四边形MNEB是矩形,在Rt△EBD中求出BE,ED即可.【解答】解:如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN 的延长线于E.∵∠E=∠ENM=∠NMB=90°,∴四边形MNEB是矩形,∴BM=EN,EB=MN,∵∠DAC=90°,∴∠DAN+∠MAC=90°,∵∠MAC+∠ACM=90°,∴∠DAN=∠ACM,在△ADN和△CAM中,,∴△ADN≌△CAM(AAS),∴AM=DN,AN=CM.在Rt△ABM中,∵AB=2,∠ABM=45°,∴BM=AM=2,MC=BC﹣BM=4,在Rt△BDE中,∵EB=MN=6,ED=4,∴BD===2.【点评】本题考查了旋转的性质,全等三角形的判定和性质、矩形的判定和性质、勾股定理等知识,添加辅助线构造全等三角形是解题的关键.13.如图,在△ABC中,∠ABC=60°,AB=3,BC=12,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为15.【分析】以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP ⊥BE于P,根据等腰三角形的性质、余弦的概念求出BE,根据旋转变换的性质得到∠DEB=90°,根据勾股定理计算即可.【解答】解:以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE于P,则∠BAE=120°,AB=AE,DE=BC,∴∠ABE=∠AEB=30°,∴BP=AB•cos∠ABP=,∠DEB=90°,∴BE=2BP=9,在Rt△BED中,BD==15,故答案为:15.【点评】本题考查的是勾股定理、直角三角形的性质、等腰三角形的性质,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.14.如图,△ABC为等腰直角三角形,∠ACB=90°,∠APC=165°,P A=3,PC=,则PB=.【分析】将△ACP绕着点C逆时针旋转90°得到△BCP′,连接PP′,可得△CPP′是等腰直角三角形,进而求出∠PP′B=120°,PP′=2,再作辅助线,构造直角三角形利用勾股定理可求出答案.【解答】解:将△ACP绕着点C逆时针旋转90°得到△BCP′,连接PP′,过点P作PD⊥BP′,交BP′的延长线于点D,如图所示:由旋转可知,CP=CP′,∠∠PCP′=90°,∠APC=∠BP′C=165°,∴∠CPP′=∠CP′P=45°,PP′=PC=2,∴∠PP′B=∠CP′B﹣∠CP′P=165°﹣45°=120°∴∠PP′D=180°﹣120°=60°,在Rt△PP′D中,P′D=PP′=1,PD==,∴BD=BP′+P′D=3+1=4,在Rt△BPD中,由勾股定理得:BP==,故答案为.【点评】考查旋转的性质,等腰直角三角形的性质、直角三角形的性质、勾股定理等知识,旋转的应用巧妙的将问题转化到一个三角形中,再依据特殊的边角关系求出答案是一个很好的方法.15.如图,在等腰直角三角形ABC中,已知∠ACB=90°,P是△ABC内一点,使P A=11,PB=7,PC=6,则∠BPC=135°.【分析】根据旋转的性质得到CE=CP=6,AE=BP=7,∠PCE=90°,求得∠CEP=∠CPE=45°,由勾股定理可得到PE=6,根据勾股定理的逆定理得到△PEA是直角三角形,求得∠PEA=90°,根据全等三角形的性质即可得到结论.【解答】解:如图,将△CPB绕点C旋转90°得△CEA,连接PE,∴△CPB≌△CEA,∴CE=CP=6,AE=BP=7,∠PCE=90°,∴∠CEP=∠CPE=45°,在Rt△PCE中,由勾股定理可得,PE=6,在△PEA中,PE2=(6)2=72,AE2=72=49,P A2=112=121,∵PE2+AE2=AP2,∴△PEA是直角三角形∴∠PEA=90°,∴∠CEA=135°,又∵△CPB≌△CEA,∴∠BPC=∠CEA=135°.故答案为135°【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,熟练掌握旋转的性质是解题的关键.16.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3;⑤S△AOC+S△AOB═6+.其中正确的结论是①②③⑤.【分析】证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;由△OBO′是等边三角形,可知结论②正确;在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=6+4,故结论④错误;如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″,计算可得结论⑤正确.【解答】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,又∵OB=O′B,AB=BC,∴△BO′A≌△BOC,又∵∠OBO′=60°,∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;如图①,连接OO′,∵OB=O′B,且∠OBO′=60°,∴△OBO′是等边三角形,∴OO′=OB=4.故结论②正确;∵△BO′A≌△BOC,∴O′A=5.在△AOO′中,三边长为3,4,5,这是一组勾股数,∴△AOO′是直角三角形,∠AOO′=90°,∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=×3×4+×42=6+4,故结论④错误;如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=×3×4+×32=6+,故结论⑤正确.综上所述,正确的结论为:①②③⑤.故答案为:①②③⑤.【点评】本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数3、4、5所构成的三角形是直角三角形,这是本题的要点.在判定结论⑤时,将△AOB向不同方向旋转,体现了结论①﹣结论④解题思路的拓展应用.17.等边△ABC的边长为2,三角形外部有一点D,CD=2,连接AD、BD,若∠ADC =30°,则BD的长为2.【分析】将AD绕点A顺时针旋转60°到AE,连接BE,DE,延长DC交AE于点F,由旋转的性质和等边三角形的性质可得DF=AF,AD=2AF,由勾股定理可求AF=2,AD=4,由全等三角形的性质可得BE=CD=2,∠BEA=∠CDA=30°,由勾股定理可求BD的长.【解答】解:如图,将AD绕点A顺时针旋转60°到AE,连接BE,DE,延长DC交AE 于点F,∵旋转∴AE=AD,∠DAE=60°,∴△ADE是等边三角形,∴AD=DE=AE,∠ADE=60°,又∵∠ADC=30°,∴DF平分∠ADE,且AD=DE,∴DF⊥AE,且∠ADF=30°,∴DF=AF,AD=2AF,在Rt△AFC中,AC2=AF2+CF2,∴28=AF2+(AF﹣2)2,∴AF=2,AF=﹣(不合题意)∴AD=2AF=4=DE,∵△ABC是等边三角形∴AB=AC,∠BAC=60°,∴∠BAC=∠DAE∴∠BAE=∠DAC,且AB=AC,AE=AD,∴△BAE≌△CAD(SAS)∴BE=CD=2,∠BEA=∠CDA=30°,∴∠BED=∠BEA+∠AED=90°∴BD==2故答案为:2【点评】本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识,综合运用这些性质进行推理是本题的关键.18.如图,在四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,∠BAD的平分线AE与DC边相交于点E,连接BE,AC,若AC=7,△BCE的周长为16,则线段BC 的长为6.【分析】把△ABC绕点A逆时针旋转90°得到△ADK,连接CK,作KH⊥CD于H,则AC=AK=7,∠CAK=90°,∠ADK=∠ABC,DK=BC=x,CK=14,根据∠BAD =90°,∠BCD=30°,可得∠ABC+∠ADC=240°,所以∠ADK+∠ADC=240°,即∠CDK=120°,因为DH=x,HK=x,CD=16﹣x,在Rt△KHC中,由勾股定理即可得出x的值,从而求得BC的长.【解答】解:如图,把△ABC绕点A逆时针旋转90°得到△ADK,连接CK,作KH⊥CD于H,则AC=AK=7,∠CAK=90°,∠ADK=∠ABC,DK=BC=x,∴CK=,∵∠BAD=90°,∠BCD=30°,∴∠ABC+∠ADC=360°﹣30°﹣90°=240°,∴∠ADK+∠ADC=240°,∴∠CDK=120°,即∠KDH=60°,∴DH=x,HK=x,∵AB=AD,∠BAE=∠DAE,AE=AE,∴△ABE≌△ADE(SAS),∴BE=ED,∵△BCE的周长为16,∴BC+CE+BE=BC+CE+ED=BC+CD=DK+CD=16,∴CD=16﹣x,CH=16﹣x+x=16﹣,在Rt△KHC中,,解得:x=6或x=10(舍去),∴BC的长为6.故答案为:6.【点评】本题考查图形的旋转,三角形全等的判定和性质,直角三角形的性质.解题的关键是掌握图形旋转的性质.二.解答题(共22小题)19.某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:已知△ABC如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图并证明BE=CD.(要求:尺规作图,不写作法但保留作图痕迹)●类比探究:如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么数量关系?说明理由.●灵活运用:如图3,已知△ABC中,AB=,BC=3,∠ABC=45°,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.【分析】(1)根据题意画出相应图形,如图所示,(分别以点A,B为圆心,AB长为半径画弧,两弧的交点即为点D,△ABD为等边三角形,△ACE同理可得),由三角形ABD 与三角形ACE都为等边三角形,利用等边三角形的性质得到AD=AB,AE=AC,且∠BAD=∠CAE=60°,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形AEB全等,利用全等三角形的对应边相等得到CD=BE;(2)CE=BG,理由为:由四边形ABDE与四边形ACFG都为正方形,利用正方形的性质得到AD=AB,AE=AC,且∠BAD=∠CAE=90°,利用等式的性质得到夹角相等,利用SAS得到三角形ACE与三角形ABG全等,利用全等三角形的对应边相等得到CE=BG;(3)以AB为边向外作等腰直角三角形ABG,连接CG,在等腰三角形ABG中,利用勾股定理求出BG的长,进而得到三角形BCG为直角三角形,利用勾股定理求出CG的长,由三角形ACG与三角形ABE都为等腰直角三角形,利用等腰直角三角形的性质得到AG =AB,AE=AC,且∠BAG=∠CAE=90°,利用等式的性质得到夹角相等,利用SAS 得到三角形ACG与三角形ABE全等,利用全等三角形的对应边相等得到CG=BE,即可求出BE的长.【解答】解:(1)作图,如图所示:。
八下数学专题突破:勾股定理(手拉手模型)(人教版)
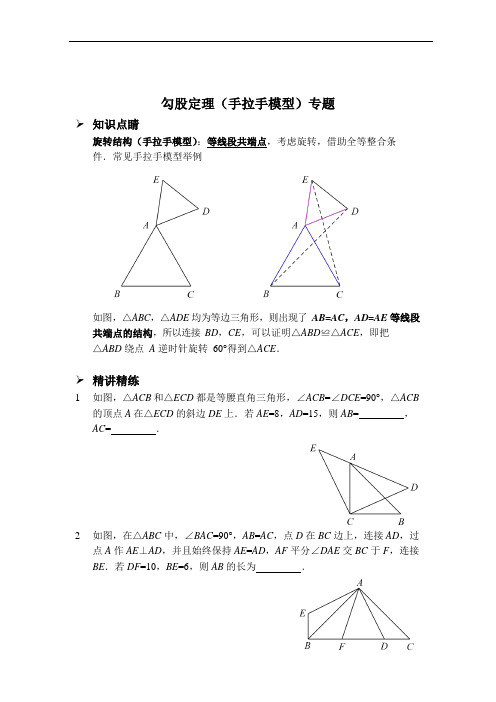
勾股定理(手拉手模型)专题➢知识点睛旋转结构(手拉手模型):等线段共端点,考虑旋转,借助全等整合条件.常见手拉手模型举例如图,△ABC,△ADE 均为等边三角形,则出现了AB=AC,AD=AE 等线段共端点的结构,所以连接BD,CE,可以证明△ABD≌△ACE,即把△ABD 绕点 A 逆时针旋转60°得到△ACE.➢精讲精练1.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠DCE=90°,△ACB的顶点A 在△ECD 的斜边DE 上.若AE=8,AD=15,则AB= ,AC= .2.如图,在△ABC 中,∠BAC=90°,AB=AC,点D 在BC 边上,连接AD,过点A 作AE⊥AD,并且始终保持AE=AD,AF 平分∠DAE 交BC 于F,连接BE.若DF=10,BE=6,则AB 的长为.117 3. 如图,已知 CA =CB ,CF =CE ,∠ACB =∠FCE =90°,且 A ,F ,E 三点共线, AE 与 CB 交于点 D .(1) 求证:AF 2+AE 2=AB 2; (2) 若 AC = ,BE =3,则 CE =.4. 如图,E 是正方形 ABCD 对角线 CA 的延长线上任意一点,以线段 AE 为边作一个正方形 AEFG ,线段 GB 与线段 ED ,AD 分别交于点 H ,M .(1) 求证:ED =GB ;(2) 判断 ED 与 GB 的位置关系,并说明理由; (3) 若 AB =2,AE = ,则 GB =.225.(1)如图1,O 是等边△ABC 内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO 绕点B 顺时针旋转后得到△BCD,连接OD.①旋转角是度;②线段OD 的长为;③求∠BDC 的度数.(2)如图2 所示,O 是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,∠AOB=135°,OA=1,OB=2,求OC 的长.小明同学借用了图1 的方法,将△BAO 绕点B 顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.36.如图,△ABC 是等腰直角三角形,∠BAC=90°,点D 为直线BC 上的动点(不与点B,C 重合),连接AD,将线段AD 绕点A 逆时针旋转90°,得到线段AE,连接DE.(1)如图1,当点D 在线段BC 上时,请直接写出线段DB,DC,DE 之间的数量关系:.(2)如图2,当点D 在BC 延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由.(3)如图3,当点D 在CB 延长线上时,若∠DAB=30°,BD=2,请直接写出AB 的长.47.如图,在Rt△ABC 中,∠ACB=90°,AC=BC,CD⊥AB 于点D,点E 是直线AC 上一动点,连接DE,过点D 作FD⊥ED,交直线BC 于点F.(1)如图1,当点E 在线段AC 上时,①求证:△CDE≌△BDF;②直接写出BF2,CF2,DF2 之间的数量关系:.(2)如图2,当点E 在线段AC 的延长线上时,判断(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)若动点E 满足EA1,直接写出DF的值:.AC 2 DC58.某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD 中,AB=6,将三角板放在正方形ABCD 上,使三角板的直角顶点与D 点重合,三角板的一边交AB 于点P,另一边交BC 的延长线于点Q.(1)求证:DP=DQ;(2)如图2,小明在图1 的基础上作∠PDQ 的平分线DE 交BC 于点E,连接P E,他发现PE 和QE 存在一定的数量关系,请猜测他的结论并予以证明.(3)如图3,固定三角板直角顶点在D 点不动,转动三角板,使三角板的一边交AB 的延长线于点P,另一边交BC 的延长线于点Q,仍作∠PDQ 的平分线DE 交BC 延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP 的面积(直接写出答案即可).6。
手拉手模型

手拉手模型(等线段共端点模型)1、定义:两个顶角相等且共顶点的等腰三角形形成的图形。
2、四个固定结论:判断左右:将等腰三角形顶角(头)朝上,正对读者,读者左边为着手顶点,右边为右手顶点,如图1、图2(1)经典线段相等:左拉左=右拉右找经典全等:包含A.经典线段B.两对等腰(等线段共端点)(2)共顶点旋转模型(证明基本思想“SAS”)核心导角:∠A=∠C则得出∠B=∠D,(八字图模型)核心图形:AB`=AC`,AB=AC ∠B`AC=∠BAC以上给出了连续变化的图形,图中两个阴影部分的三角形全等,注意利用三角形全等性质进项转化边或转化角3、利用旋转思想构造辅助线(1)根据相等的边找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角画出旋转后的三角形4、旋转前后具有以下性质(1)对应线段和对应角分别相等(2)对应点位置的排列次序相同(3)任意两条对应线段的夹角都等于旋转角例题讲解:A类1:在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD,证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)BH平分∠AHC;解题思路:1:出现共顶点的等边三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;2:如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H.问(1)△ADG≌△CDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分∠AHE?等边三角形要得到哪些结论?要联想到什么模型?等腰直角三角形要得到哪些结论?要联想到什么模型?解题思路:1:出现共顶点的等腰直角三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;3:如图,分别以△ABC 的边AB、AC 同时向外作等腰直角三角形,其中 AB =AE ,AC =AD,∠BAE =∠CAD=90°,点G为BC中点,点F 为BE 中点,点H 为CD中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理(手拉手模型)专题
知识点睛
旋转结构(手拉手模型):等线段共端点,考虑旋转,借助全等整合条件.常见手拉手模型举例
如图,△ABC,△ADE均为等边三角形,则出现了AB=AC,AD=AE等线段共端点的结构,所以连接BD,CE,可以证明△ABD≌△ACE,即把
△ABD绕点A逆时针旋转60°得到△ACE.
精讲精练
1.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,△ACB
的顶点A在△ECD的斜边DE上.若AE=8,AD=15,则AB=_________,AC=_________.
2.如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC边上,连接AD,过
点A作AE⊥AD,并且始终保持AE=AD,AF平分∠DAE交BC于F,连接BE.若DF=10,BE=6,则AB的长为_________.
3.如图,已知CA=CB,CF=CE,∠ACB=∠FCE=90°,且A,F,E三点共线,
AE与CB交于点D.
(1)求证:AF2+AE2=AB2;
(2)若AC=17,BE=3,则CE=_________.
4.如图,E是正方形ABCD对角线CA的延长线上任意一点,以线段AE为边
作一个正方形AEFG,线段GB与线段ED,AD分别交于点H,M.
(1)求证:ED=GB;
(2)判断ED与GB的位置关系,并说明理由;
(3)若AB=2,AE=2,则GB=___________.
5.(1)如图1,O是等边△ABC内一点,连接OA,OB,OC,且OA=3,OB=4,
OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.
①旋转角是__________度;
②线段OD的长为__________;
③求∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,∠AOB=135°,OA=1,OB=2,求OC的长.
小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.
6.如图,△ABC是等腰直角三角形,∠BAC=90°,点D为直线BC上的动点(不
与点B,C重合),连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接DE.
(1)如图1,当点D在线段BC上时,请直接写出线段DB,DC,DE之间的数量关系:________________.
(2)如图2,当点D在BC延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由.
(3)如图3,当点D在CB延长线上时,若∠DAB=30°,BD=2,请直接写出AB的长.
7.如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E是直线
AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.
(1)如图1,当点E在线段AC上时,
①求证:△CDE≌△BDF;
②直接写出BF2,CF2,DF2之间的数量关系:___________.
(2)如图2,当点E在线段AC的延长线上时,判断(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)若动点E满足
1
2
EA
AC ,直接写出
DF
DC的值:___________.
8.某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,
AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:DP=DQ;
(2)如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明.(3)如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积(直接写出答案即可).。
