函数与导函数图像(最新整理)
高中函数图像大全汇总

指数函数概念:一般地,函数y=a^x( a> 0,且a≠ 1)叫做指数函数,其中x 是自变量,函数的定义域是R。
1,否则不能为指数函数。
注意:⒈指数函数对外形要求严格,前系数要为⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:a 互为倒数时,两个函数关于y 轴对称,但这规律: 1. 当两个指数函数中的两个函数都不具有奇偶性。
2.当 a> 1 时,底数越大,图像上升的越快,在y 轴的右侧,图像越靠近y 轴;当 0< a< 1 时,底数越小,图像下降的越快,在y 轴的左侧,图像越靠近y 轴。
在 y 轴右边“底大图高”;在y 轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a> 1 时,图像在 R 上是增函数;当 0< a<1 时,图像在 R 上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数不同,指数也不同时,则需要引入中间量进行比较;4.对多个数进行比较,可用0 或 1 作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在 f(X) 后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数 y=a x在定义域 (-∞, +∞ )上是单调函数,所以它存在反函数,我们把指数函数 y=a x(a> 0, a≠1)的反函数称为对数函数,并记为y=log a x(a >0, a≠ 1).因为指数函数 y=a x的定义域为 (-∞, +∞ ),值域为 (0, +∞ ),所以对数函数y=log a x 的定义域为 (0, +∞ ),值域为 (- ∞, +∞ ).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x.据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a>0,a≠1)的性质,我们在同一直角坐标系中作出函数y=log 2x,y=log 10x, y=log 10x,y=log 1x,y=log1x 的草图210由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a> 0,a ≠1) 的图像的特征和性质 .见下表 .a> 1a< 1图象(1)x >0性(2) 当 x=1 时, y=0质(3) 当 x> 1 时, y> 0(3) 当 x> 1 时, y< 00< x< 1 时, y< 00< x<1 时, y> 0(4)在 (0,+∞ )上是增函数(4) 在 (0,+∞ )上是减函数补设 y1=log a x y2=log b x 其中 a> 1, b> 1(或 0< a<1 0< b<1)充当 x> 1 时“底大图低”即若 a> b 则 y1> y2性当 0< x< 1 时“底大图高”即若 a> b,则 y1> y2质比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断 .(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论 .(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较 .(4)若底数、真数都不相同,则常借助1、0、 -1 等中间量进行比较 .3.指数函数与对数函数对比名称一般形式定义域 值域 函 数 值 变 化 情 况单调性图像指数函数 对数函数y=a x (a > 0, a ≠ 1)y=log a x(a > 0, a ≠ 1)(-∞, +∞ ) (0, +∞ ) (0, +∞ ) (-∞, +∞ )当 a >1 时,当 a > 1 时1( x0)0( x 1) a x1( x 0) log a x0( x 1)1( x0)0( x1)当 0<a < 1 时, 当 0< a < 1 时,1( x0)0( x 1)a x1( x 0) log a x0(x 1) 1( x0)0(x1)当 a > 1 时, a x 是增函数; 当 a >1 时, log a x 是增函数; 当 0<a < 1 时, a x 是减函数 .当 0<a < 1 时, log a x 是减函数 .y=a x 的图像与 y=log a x 的图像 关于直线 y=x 对称 .幂函数幂函数的图像与性质幂函数 y x n 随着 n 的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握y x n,当 n 2 , 1,1 , 1, 3 的图像和性质,列表如下.2 3从中可以归纳出以下结论:① 它们都过点 1,1 ,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.② a1 , 1 ,1,2 ,3 时,幂函数图像过原点且在 0 ,3 2③ a1 , 1,2 时,幂函数图像不过原点且在 0 ,2④任何两个幂函数最多有三个公共点 .上是增函数.上是减函数.y x n奇函数 偶函数 非奇非偶函数y y y n1x x x O O Oy y y0n 1O x O x O xy y yn0x x O O x O定义域R R R奇偶性奇奇奇非奇非偶奇在第Ⅰ象限的增减在第Ⅰ象限在第Ⅰ象限在第Ⅰ象限在第Ⅰ象限在第Ⅰ象限性单调递增单调递增单调递增单调递增单调递减幂函数y x(xR,是常数)的图像在第一象限的分布规律是:①所有幂函数y x(x R,是常数)的图像都过点(1,1);1,2,3,1时函数y x的图像都过原点(0,0) ;②当2③当1时,y x的的图像在第一象限是第一象限的平分线(如c2);④当2,3 时,y x的的图像在第一象限是“凹型”曲线(如c 1 )1凸型”曲线(如c3)⑤当 2 时,yx的的图像在第一象限是“⑥当1时,y x的的图像不过原点(0,0),且在第一象限是“下滑”曲线(如c4)当0时,幂函数y x有下列性质:(1)图象都通过点(0,0), (1,1) ;(2)在第一象限内都是增函数;(3)在第一象限内,1时,图象是向下凸的;0 1时,图象是向上凸的;(4)在第一象限内,过点(1,1)后,图象向右上方无限伸展。
高中函数图像大全

高中必考函数大全指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数不同,指数也不同时,则需要引入中间量进行比较;4.对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x(a>0,a≠1)的反函数称为对数函数,并记为y=log a x(a>0,a≠1).因为指数函数y=a x的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a>0,a≠1)的性质,我们在同一直角坐标系中作出函数y=log 2x ,y=log 10x ,y=log 10x,y=log 21x,y=log 101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a >0,a ≠1)的图像的特征和性质.见下表. 图 象 a >1a <1性 (1)x >0(2)当x=1时,y=0质(3)当x>1时,y>00<x<1时,y<0 (3)当x>1时,y<0 0<x<1时,y>0(4)在(0,+∞)上是增函数(4)在(0,+∞)上是减函数补充性质设y1=log a x y2=log b x其中a>1,b>1(或0<a<1 0<b<1)当x>1时“底大图低”即若a>b则y1>y2当0<x<1时“底大图高”即若a>b,则y1>y2比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断.(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称指数函数对数函数一般形式y=a x(a>0,a≠1) y=log a x(a>0,a≠1)定义域(-∞,+∞) (0,+∞)值域(0,+∞) (-∞,+∞)函数值变化情况当a>1时,⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1xxxa x当0<a<1时,⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1xxxa x当a>1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0logxxxxa当0<a<1时,⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0logxxxxa单调性当a>1时,a x是增函数;当0<a<1时,a x是减函数. 当a>1时,log a x是增函数;当0<a<1时,log a x是减函数.图像y=a x的图像与y=log a x的图像关于直线y=x对称.幂函数幂函数的图像与性质幂函数ny x=随着n的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握ny x=,当112,1,,,323n=±±±的图像和性质,列表如下.从中可以归纳出以下结论:①它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.② 11,,1,2,332a =时,幂函数图像过原点且在[)0,+∞上是增函数.③ 1,1,22a =---时,幂函数图像不过原点且在()0,+∞上是减函数.④ 任何两个幂函数最多有三个公共点.n y x =奇函数偶函数非奇非偶函数1n >01n <<0n <定义域 R R R奇偶性奇奇奇非奇非奇OxyOxyOxyOxyOxyOx yOxyOxyOxy偶在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递减幂函数y x α=(x ∈R ,α是常数)的图像在第一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(; ②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y x α=有下列性质: (1)图象都通过点)1,1(),0,0(;(2)在第一象限内都是增函数;(3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的;(4)在第一象限内,过点)1,1(后,图象向右上方无限伸展。
常用导数图像

常用导数图像导数在微积分中起着至关重要的作用,它描述了一个函数在某一点处的变化率。
导数的图像可以帮助我们更直观地理解函数的斜率和变化趋势。
在本文中,将介绍几种常用函数的导数图像,包括线性函数、平方函数、正弦函数和指数函数等。
线性函数首先,让我们来看一下线性函数的导数图像。
对于函数f(f)=ff+f,其中f和f是常数,其导数f′(f)=f恒为常数。
这意味着线性函数的导数图像是一条水平直线,斜率恒定为f。
图中横轴表示自变量f,纵轴表示导数f′(f)。
例如,对于f(f)=2f+3,其导数图像将是一条斜率为2的水平直线。
平方函数接下来,我们来探讨平方函数的导数图像。
考虑函数f(f)=f2,其导数f′(f)=2f。
平方函数的导数图像是一条抛物线,斜率随着f的取值而变化。
当f=0时,斜率为0,在原点处达到极小值。
随着f增大,斜率也逐渐增大。
因此,平方函数的导数图像呈现出逐渐增大的趋势。
正弦函数现在我们转向正弦函数的导数图像。
正弦函数f(f)=fff(f)的导数f′(f)=fff(f)。
正弦函数的导数图像是一个周期性变化的曲线,代表着正弦函数的斜率随着f的变化而变化。
在导数图像中,我们可以观察到正弦函数的斜率在不同的f值处出现正弦曲线的特征。
指数函数最后,我们来看一下指数函数的导数图像。
指数函数f(f)=f f的导数f′(f)=f f。
指数函数的导数图像是一条逐渐增长的曲线,斜率随着f的增大而增大。
指数函数是增长最快的函数之一,因此其导数图像呈现出急剧增长的态势。
通过以上几种函数的导数图像,我们可以更好地理解导数在函数变化中的作用。
导数图像提供了直观的信息,帮助我们分析函数的斜率和变化趋势。
深入研究导数图像有助于我们更好地掌握微积分的重要概念,为解决实际问题提供了有力的工具。
以上为常用导数图像的简要介绍,希望能够帮助读者更好地理解函数的变化规律。
以上为常用导数图像文档,供参考。
常用函数图像
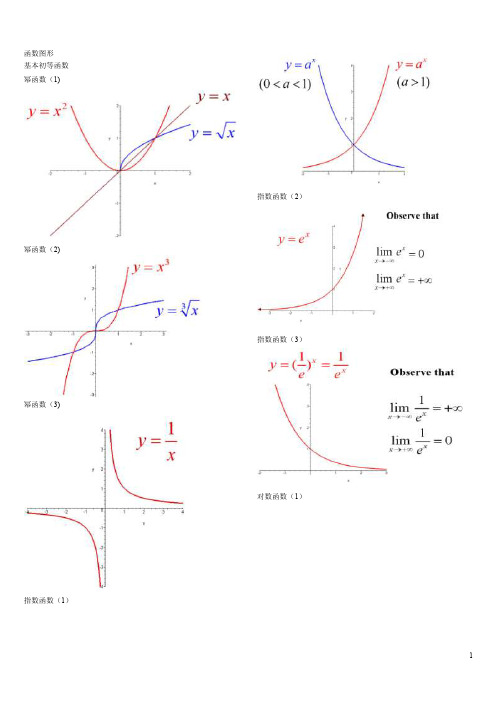
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
高中函数图像大全

指数函数之吉白夕凡创作概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不克不及为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1.当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4.指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数分歧,指数也分歧时,则需要引入中间量进行比较;4.对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=ax在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=ax(a>0,a≠1)的反函数称为对数函数,并记为y=logax(a>0,a≠1).因为指数函数y=ax的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=logax的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=logax(a >0,a≠1)的性质,我们在同一直角坐标系中作出函数y=log2x ,y=log10x ,y=log10x,y=log 21x,y=log 101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=logax(a >0,a≠1)的图像的特征和性质.见下表.图 象a >1a <1性 质(1)x >0(2)当x=1时,y=0 (3)当x >1时,y >0 0<x <1时,y <0 (3)当x >1时,y <0 0<x <1时,y >0 (4)在(0,+∞)上是增函数 (4)在(0,+∞)上是减函数弥补 性质设y1=logax y2=logbx 其中a >1,b >1(或0<a <1 0<b <1) 当x >1时“底大图低”即若a >b 则y1>y2当0<x <1时“底大图高”即若a >b ,则y1>y2比较对数大小的经常使用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断. (2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论. (3)若底数分歧、真数相同,则可用换底公式化为同底再进行比较. (4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较. 3.指数函数与对数函数对比名称 指数函数 对数函数 一般形式 y=ax(a >0,a ≠1)y=logax(a >0,a ≠1)定义域 (-∞,+∞) (0,+∞) 值域(0,+∞)(-∞,+∞)幂函数幂函数的图像与性质幂函数n y x =随着n 的分歧,定义域、值域都会发生变更,可以采纳按性质和图像分类记忆的方法.熟练掌握n y x =,当112,1,,,323n =±±±的图像和性质,列表如下.从中可以归纳出以下结论:① 它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.② 11,,1,2,332a =时,幂函数图像过原点且在[)0,+∞上是增函数. ③ 1,1,22a =---时,幂函数图像不过原点且在()0,+∞上是减函数.④何两个幂函数最多有三个公共点.定义域 R R R奇偶性奇 奇 奇 非奇非偶 奇 在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减ny x =奇函数 偶函数 非奇非偶函数1n >01n <<0n <Oxy OxyOxyOx yOxyOxy OxyOxyOxy幂函数y x α=(x ∈R ,α是常数)的图像在第一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(; ②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y x α=有下列性质:(1)图象都通过点)1,1(),0,0(; (2)在第一象限内都是增函数;(3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的; (4)(在第一象限内,过点)1,1(后,图象向右上方无限伸展。
函数图像总结

函数图像总结函数图像总结函数图像总结一基本函数图像1y=kx(x≠0)2y=kx+b(k≠0)3y4yax2bxc(a0)5yxa6yxk(k0)xk(k0)7yax(a 0,a1)x8ylogax(a0,a1)二抽象图像平移f(x)f(x+1)f(x)f(x-1)f(x)f(x)+1f(x)f(x)-1f(x)f(2x)f(x)2f(x) f(x)f(2x+2)y=f(-x)变成y=f(-x+2)练习:cosxcos2xcos2xcos(2x+4)cosxcos2x+4三图像的变换1f(x)f(|x|)保留y轴右边的,左边关于右边y轴对称2f(x)|f(x)|保留x轴上方的,下方关于x轴对称3f(x)f(-x)y轴对称4f(x)-f(x)x轴对称5f(x)-f(-x)原点对称6f(x)f(|x+1|)先根据1方法变成f(|x|),在向左平移一个单位得到f(|x+1|)7f(x)f(|x|+1)先向左平移一个单位得到f(x+1),再根据1方法变成f(|x|+1)8f(x)与f1(x)的图象关于直线yx对称联想点(x,y),(y,x)9f(x)与f(2ax)的图象关于点(a,0)对称egf(x)= 2x与g(x)=-2x关于对称一、函数yf(x)与函数yf(x)的图象关系函数yf(x)的图象是由yf(x)的图象经沿y轴翻折180°而得到的(即关于y轴对称)。
注意它与函数yf(x)满足f(x)f(x)的图象是不同的,前者代表两个函数,后者表示函数yf(x)本身是关于y轴对称的。
(二)伸缩变换及其应用:函数yaf(bx)的图像可以看作是由函数yf(x)的图像先将横坐标伸长(|b|<1)或缩短(|b|>1)到原来的1倍,再把纵坐标伸长(|a|>1)或缩短(|a|<1)到原来的|a|倍即可得到。
如:|b|1的图像x1要求:1会画y=|x+1|y=-2会画f(x)=lg|x|以及f(x)=|lgx|3会画f(x)=|lg|x+1||以及f(x)=x2-4|x|+5f(x)=|x2-2x-3|二1由图像可知f(x+1)为偶函数对称轴为2由图像可知f(x+1)为奇函数关于点(,)对称Eg、对a,bR,记max{a,b}=(A)0(B) a,ab,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是b,a<b13(C)(D)3901(选讲)1、yf(x)绕原点顺时针方向旋转;yf(x)12、yf(x);yf (x)绕原点逆时针方向旋转9000yQP(a,b)(yf(x)yQ1xP1(b,a)(yf1(x))P(a,b)(yf(x)0P1(b,a)1(yf(x))0(乙)x(甲)(图五)0说明:关于绕原点旋转180的变换实际上就是关于原点对称的问题。
(完整版)高中数学常见函数图像

高中数学常见函数图像1.2.对数函数:3.幂函数:定义形如αxy=(x∈R)的函数称为幂函数,其中x是自变量,α是常数.图像性质过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x轴与y轴.4.函数sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =; 当22xk ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数 奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
高中函数图像大全汇总
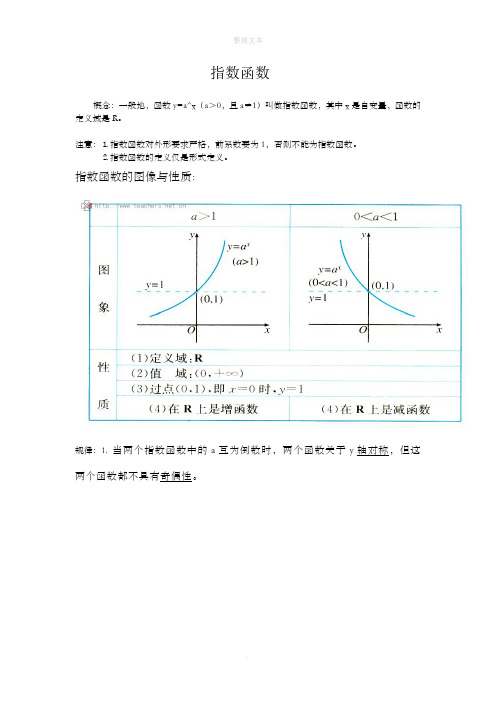
指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1. 当底数相同时,则利用指数函数的单调性进行比较;2. 当底数中含有字母时要注意分类讨论;3. 当底数不同,指数也不同时,则需要引入中间量进行比较;4. 对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x 在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x (a >0,a ≠1)的反函数称为对数函数,并记为y=log a x(a >0,a ≠1).因为指数函数y=a x 的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x 的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a >0,a ≠1)的性质,我们在同一直角坐标系中作出函数 y=log 2x ,y=log 10x ,y=log 10x,y=log 21x,y=log 101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a>0,a ≠1)的图像的特征和性质.见下表.图象a>1a<1性质(1)x>0(2)当x=1时,y=0(3)当x>1时,y>00<x<1时,y<0(3)当x>1时,y<00<x<1时,y>0 (4)在(0,+∞)上是增函数(4)在(0,+∞)上是减函数补充性质设y1=log a x y2=log b x其中a>1,b>1(或0<a<1 0<b<1)当x>1时“底大图低”即若a>b则y1>y2当0<x<1时“底大图高”即若a>b,则y1>y2比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断.(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比幂函数幂函数的图像与性质幂函数ny x=随着n的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握ny x=,当112,1,,,323n=±±±的图像和性质,列表如下.从中可以归纳出以下结论:①它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.②11,,1,2,332a=时,幂函数图像过原点且在[)0,+∞上是增函数.③1,1,22a=---时,幂函数图像不过原点且在()0,+∞上是减函数.④任何两个幂函数最多有三个公共点.ny x=奇函数偶函数非奇非偶函数1n>01n<<n<定义域R R R奇偶性奇奇奇非奇非偶奇在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减O xyO xyO xyO xyO xyO xyO xyO xyO xy=(x∈R,α是常数)的图像在第幂函数y xα一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(;②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y x α=有下列性质:(1)图象都通过点)1,1(),0,0(;(2)在第一象限内都是增函数;(3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的; (4)在第一象限内,过点)1,1(后,图象向右上方无限伸展。
经典数学函数图像(大全)

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线,其一般形式为 y = mx + b,其中 m是斜率,b 是 y 轴截距。
当 m > 0 时,直线向上倾斜;当 m < 0 时,直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线,其一般形式为 y = ax^2 + bx + c,其中 a、b、c 是常数。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线,余弦函数图像与正弦函数图像相似,但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线,其一般形式为 y = a^x,其中 a 是底数,x 是指数。
当 a > 1 时,曲线上升;当 0 < a < 1 时,曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线,其一般形式为 y =log_a(x),其中 a 是底数,x 是真数。
当 a > 1 时,曲线上升;当0 < a < 1 时,曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线,而双曲正切函数图像是一条周期性振荡的曲线。
7. 幂函数图像幂函数图像是一条上升或下降的曲线,其一般形式为 y = x^n,其中 n 是指数。
当 n > 0 时,曲线上升;当 n < 0 时,曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线,其一般形式为 y = k/x,其中 k是常数。
当 k > 0 时,曲线位于第一和第三象限;当 k < 0 时,曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数,包括反正弦函数、反余弦函数和反正切函数。
人教版 八年级下册课件19.1.2函数的图像(共16张PPT)

例2、下面的图象反映的过程是:小明从家里出发去菜地浇水,又去玉米 地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.
y/千米
锄草
2
1.1 浇水
0 15 25 37 55
80
根据图象回答下列问题:
时间x/分钟
1、菜地离小明家多远?小明走到菜地用了多少时间?
从纵坐标看:菜地离小明家1.1千米.
从横坐标看:小明走到菜地用了15分钟. 2、小明给菜地浇水用了多少时间?
从横坐标看:小明给菜地浇水用了10分钟(即25-15)
y/千米
锄草
2
1.1 浇水
0 15 25 37 55
80
时间x/分钟
3、菜地离玉米地多远?小明从菜地走到玉米地用了 多少时间? 从纵坐标看:菜地离玉米地0.9千米.
从横坐标看:小明从菜地用到玉米地用了12分钟. 4、小明给玉米地锄草用了多少时间?
第二步: 描点
y6 x
•
第三步: 连线
• •• •
归纳二:函数图象的画法:
1、列表 列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围), 并取值要适当,以便画图.
2、描点 建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值 对应的各点
3、连线 按照横坐标从小到大的顺序把描出的点用
面积s与边长x的函数关系式为:
s = x2 (x>0) 你知道为什么“x>0” ?
从式子s = x2来看,边长x越大,面积s也越大。 能不能用图象直观的反映出来呢?
画函数的图象:S = x2(x>0)
1、列表: x 0 0.5 1 1.5 2 2.5 3 …
s 0 0.25 1 2.25 4 6.25 9 …
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题三 函数与导函数图像
1.函数的导函数的图象如图所示,则函数的图象可能()y f x =()'y f x =()y f x =是( )
A. B.
C. D.
2.函数的图象如图所示,则其导函数的
()y f x =()'y f x =图象可能是( )
A. B.
C. D.
3.在R 上可导的函数的图象如图示, 为函数的导数,则关于的()f x ()f x '()f x x 不等式的解集为( )
()0x f x ⋅'<
A.
B. ()(),10,1-∞-⋃()()1,01,-⋃+∞
C.
D. ()()2,11,2--⋃()()
,22,-∞-⋃+∞4.已知函数的导函数的图象如图所示,则的图象可能是( )
y =f(x)y =f(x)
A. B. C. D.
5.如图是函数y =f (x )的导函数的图像,则下面判断正确的是( )
()'f x
A. 在区间(-2,1)上f (x )是增函数
B. 在(1,3)上f (x )是减函数
C. 在(4,5)上f (x )是增函数
D. 当x =4时,f (x )取极大值
6.函数的导函数的部分图象为( )
()cos sin f x x x x =⋅-
K O K
t O K t O t
O K
t
A B C D
7.如图是函数的导函数的图象,给出下列命题:
()y f x =()'y f x =①-2是函数的极值点; ②1是函数的极值点;
()y f x =()y f x =③的图象在处切线的斜率小于零;
()y
f x =0x =④函数在区间上单调递增.
()y f x =()2,2-则正确命题的序号是( )
A. ①③
B. ②④
C. ②③
D. ①④
8.如图是函数的导函数的图象,对此图象,有如下结论:
()y f x =()y f x '=
①在区间(-2,1)内是增函数;
()f x ②在区间(1,3)内是减函数;
()f x ③在时,取得极大值;
2x =()f x ④在时,取得极小值。
3x =()f x 其中正确的是 .
9.已知函数y =f (x )的图像是下列四个图像之一,且其导函数y =f ′(x )的图像如图所示,则该函数的图像是________.
参考答案1.D
2.D
3.A
4.D
5.C
6.D
7.D
8.③
9.②
4。
