MATLAB-第四章
matlab入门经典教程--第四章数值计算

m a t l a b入门经典教程--第四章数值计算-CAL-FENGHAI.-(YICAI)-Company One1第四章数值计算4.1引言本章将花较大的篇幅讨论若干常见数值计算问题:线性分析、一元和多元函数分析、微积分、数据分析、以及常微分方程(初值和边值问题)求解等。
但与一般数值计算教科书不同,本章的讨论重点是:如何利用现有的世界顶级数值计算资源MATLAB。
至于数学描述,本章将遵循“最低限度自封闭”的原则处理,以最简明的方式阐述理论数学、数值数学和MATLAB计算指令之间的内在联系及区别。
对于那些熟悉其他高级语言(如FORTRAN,Pascal,C++)的读者来说,通过本章,MATLAB卓越的数组处理能力、浩瀚而灵活的M函数指令、丰富而友善的图形显示指令将使他们体验到解题视野的豁然开朗,感受到摆脱烦琐编程后的眉眼舒展。
对于那些经过大学基本数学教程的读者来说,通过本章,MATLAB精良完善的计算指令,自然易读的程序将使他们感悟“教程”数学的基础地位和局限性,看到从“理想化”简单算例通向科学研究和工程设计实际问题的一条途径。
对于那些熟悉MATLAB基本指令的读者来说,通过本章,围绕基本数值问题展开的内容将使他们体会到各别指令的运用场合和内在关系,获得综合运用不同指令解决具体问题的思路和借鉴。
由于MATLAB的基本运算单元是数组,所以本章内容将从矩阵分析、线性代数的数值计算开始。
然后再介绍函数零点、极值的求取,数值微积分,数理统计和分析,拟合和插值,Fourier分析,和一般常微分方程初值、边值问题。
本章的最后讨论稀疏矩阵的处理,因为这只有在大型问题中,才须特别处理。
从总体上讲,本章各节之间没有依从关系,即读者没有必要从头到尾系统阅读本章内容。
读者完全可以根据需要阅读有关节次。
除特别说明外,每节中的例题指令是独立完整的,因此读者可以很容易地在自己机器上实践。
MATLAB从版升级到版后,本章内容的变化如下:MATLAB从版起,其矩阵和特征值计算指令不再以LINPACK和EISPACK库为基础,而建筑在计算速度更快、运行更可靠的LAPACK和ARPACK程序库的新基础上。
MATLAB-第4章

v
i 1
n
2 i
。
max { vi } 。
1 ≤i ≤n
设 A 是一个 m ×n 的矩阵,矩阵的 3 种常用范数如下。 1-范数: A 1 max { aij } 。
1 ≤ j ≤n i 1 m
2-范数: A 2 1 ,其中 λ 1 为 A'A 最大特征值。 ∞-范数: A max { aij } 。
【例4.6】先建立5 × 5矩阵A,然后将A的第一行元素乘以1, 第二行乘以2,…,第五行乘以5。 用一个对角矩阵左乘一个矩阵时,相当于用对角阵的第一个 元素乘以该矩阵的第一行,用对角阵的第二个元素乘以该 矩阵的第二行……依此类推,因此,只需按要求构造一个 对角矩阵D,并用D左乘A即可。命令如下: A=[1:5;2:6;3:7;4:8;5:9] D=diag(1:5); D*A %用D左乘A,对A的每行乘以一个指定常数
(2)构造对角矩阵 设V为具有m个元素的向量,diag(V,k)的功能是产生一个 n × n(n = m + k|)对角阵,其第k条对角线的元素即为 向量V的元素。 例如: diag(1:3,-1) ans = 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 省略k时,相当于k为0,其主对角线元素即为向量V的元素。
2.矩阵的秩与迹 (1)矩阵的秩 rank(A) (2)矩阵的迹 矩阵的迹即矩阵的对角线元素之和。 trace(A)。
3.向量和矩阵的范数
设向量 V = (v1 ,v2 ,…,vn ),向量的 3 种常用范数如下。 1-范数: V 2-范数: V ? -范数: V
1
vi 。
i 1
n
2
3.矩阵的转置 所谓转置,即把源矩阵的第一行变成目标矩阵第一列,第二 行变成第二列……依此类推。显然,一个m行n列的矩阵 经过转置运算后,变成一个n行m列的矩阵。MATLAB中, 转置运算符是单撇号(')。
Matlab学习教程 第四章(4)上机练习

第4章图形处理功能1 内容简介基本内容主要包括:(1)二维图形(2)三维图形(3)图形处理的基本技术2 达到的目标(1)掌握二维图形的绘制。
(2)掌握三维图形的绘制。
(3)掌握图形处理的基本技术3 具体内容3.1 二维图形3.1.1 基本绘图命令(1)当plot函数仅有一个输入变量例4-1y=[5 2 3 8 5]; %y 行矩阵plot(y) %一条线例4-2y=[5 2 3 8 5;2 4 3 1 5;1 1 1 1 1]; %y 矩阵plot(y) %5条线,等于矩阵的列数(2)当plot函数有两个输人变量例4-3x=0:0.01*pi:pi;y=sin(x).*cos(x);plot(x,y)例4-3x=0:0.01*pi:pi;y=[sin(x);cos(x); sin(x).*cos(x)];plot(x,y)例4-4x1=0:0.01*pi:pi;x2=pi:0.01*pi:2*pi;x=[x1' x2'];y=[sin(x1') cos(x2')];plot(x,y)例4-5x1=1:5;x2=6:10;y1=x1;y2=2*x2;plot([x1;x2],[y1;y2])%plot([x1' x2'],[y1' y2'])(3)当plot函数有三个输入变量时MATLAB语言中提供的对曲线的线型、颜色以及标识的控制符如表4.l所示。
例4-6 绘制带有显示属性设置的二维图形。
x=0.5*pi: 0.1*pi:2*pi;y=sin(x);z=cos(x);plot (x, y, '--ko', x, z, '-. r*')3.1.2 特殊的二维图形函数(1)特殊坐标系的二维图形函数(a)对数坐标例4-7 绘制X坐标为对数坐标的二维图形。
x=0.5*pi: 0.1*pi:2*pi;y=sin(x);semilogx (x, y, '-ro')(b)极坐标例4-8绘制极坐标下的二维图形。
第4章 MATLAB绘图ppt课件

其中x1—y1对应一条曲线,x2—y2对应 另一条曲线。横坐标的标度相同,纵坐 标有两个,左纵坐标用于x1—y1数据对, 右纵坐标用于x2—y2数据对。
精品课件
目录 17
例4.4 用不同标度在同一坐标内绘制曲线 y1=e-0.5xsin(2πx)
及曲线y2=1.5e-0.1xsin(x)。 程序如下:
x1=(0:12)/2;
y3=2*exp(-0.5*x1).*sin(2*pi*x1);
plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');
目录
精品课件
16
4.双纵坐标函数plotyy
plotyy函数是MATLAB 5.X新增的函数。 它能把函数值具有不同量纲、不同数量 级的两个函数绘制在同一坐标中。调用 格式为:
plot(x,y) 其中x和y为长度相同的向量,分别用于存储x坐
标和y坐标数据。条件是元素个数能对应。
精品课件
目录 4
例4.1 在0≤X≤2区间内,绘制 曲线y=2e-0.5xsin(2πx)。
程序如下:>> x=0:pi/100:2*pi;
y=2*exp(-0.5*x).*sin(2*pi*x); plot(x,y)
可搭配使用,如选项“ro” 表示绘制红色的圆划线,“y-”表
示黄色的实划线。
精品课件
14
例 用不同线型和颜色在同一坐标内绘制曲 线y=sinx,y=cosx的图像。
程序如下:
x=linspace(0,2*pi,100); plot(x,sin(x),‘kh’,x,cos(x),‘gp’) %正、余弦曲
matlab课后习题答案第四章
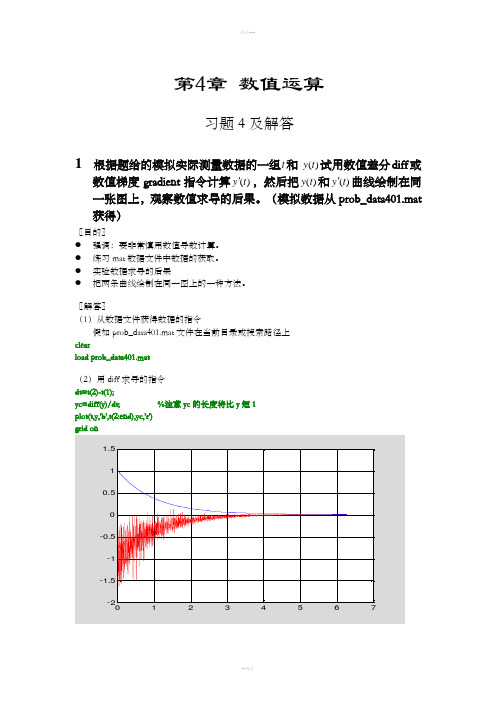
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
第4章 MATLAB程序流程控制

第4章 MATLAB程序流程控制
2.switch语句 switch语句根据表达式的取值不同,分别执行不 同的语句,其语句格式为:
第4章 MATLAB程序流程控制
(3) 多分支if语句: if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else 语句组n end
第4章 MATLAB程序流程控制
第4章 MATLAB程序流程控制
例4-4 输入一个字符,若为大写字母,则输出其对应 的小写字母;若为小写字母,则输出其对应的大写 字母;若为数字字符则输出其对应的数值,若为其 他字符则原样输出。
age is 17>> >> fprintf('age is %d\n',17); age is 17
第4章 MATLAB程序流程控制
例4-2 求一元二次方程ax2 +bx+c=0的根。 程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); delta=b*b-4*a*c; x=[(-b+sqrt(delta))/(2*a),(-b-sqrt(delta))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
M文件的扩展名为.mFra bibliotek第4章 MATLAB程序流程控制
1.建立新的M文件 为建立新的M文件,启动MATLAB编辑器有3种方法。 ① 在MATLAB主窗口选择“主页”选项卡,在“文件” 命令组中单击“新建脚本”命令按钮。 ② 在MATLAB命令行窗口输入命令: edit 文件名 启动MATLAB编辑器后,输入M文件的内容并存盘。 ③ 在命令历史窗口选中一些命令(按住Ctrl可同时选 择多条命令),然后从右键快捷菜单中选择“创建 脚本”命令,将会启动MATLAB编辑器,并在编辑 区中加入所选中的命令。
MATLAB数学实验 第四章 函数和方程

2 ( y f ( c , x )) i i i 0 n
• 当f关于c是线性函数,问题转化为一个线性方程组求解。 • 如果f关于c是非线性函数,问题转化为函数极值问题
3387/1943*x^2-7637646031980105/4503599627370496*x+4886217849135065/4503599627370496
• >> vpa(fun,5) ans = 1.7432*x^2-1.6959*x+1.0850
• >> xi=-0.2:0.01:0.3; • >> yi=polyval(p,xi); • >> plot(x,y,‘ro’,xi,yi)%拟合效果作图
c= lsqnonlin (Fun,c0) non-linear least squares problems.
使用迭代法搜索最优参数c. 其中Fun是以参数c(可 以是向量)为自变量的函数,表示误差向量yf(c,x)(x, y为数据),c0为参数c的近似初值(与c同 维向量),具体使请看帮助文件。
c=lsqcurvefit(Fun2,c0, x, y) 从外部输入数据, 这里Fun2为两变量c和x的函数 f(c, x)
的调用格式
x= -3 y= -2.7183
• (3) • >> fun3=inline('100*(v(2)-v(1)^2)^2+(1-v(1))^2','v') fun3 = Inline function: fun3(v) = 100*(v(2)-v(1)^2)^2+(1-v(1))^2 • >> [v,fv]=fminsearch(fun3,[1 1]) v= 1 1 fv = 0
第四章_MATLAB的数值计算功能

第四章MATLAB 的数值计算功能Chapter 4: Numerical computation of MATLAB数值计算是MATLAB最基本、最重要的功能,是MATLAB最具代表性的特点。
MATLAB在数值计算过程中以数组和矩阵为基础。
数组是MATLAB运算中的重要数据组织形式。
前面章节对数组、矩阵的特征及其创建与基本运算规则等相关知识已作了较详尽的介绍,本章重点介绍常用的数值计算方法。
一、多项式(Polynomial)`多项式在众多学科的计算中具有重要的作用,许多方程和定理都是多项式的形式。
MATLAB提供了标准多项式运算的函数,如多项式的求根、求值和微分,还提供了一些用于更高级运算的函数,如曲线拟合和多项式展开等。
1.多项式的表达与创建(Expression and Creating of polynomial)(1) 多项式的表达(expression of polynomial)_Matlab用行矢量表达多项式系数(Coefficient)和根,系数矢量中各元素按变量的降幂顺序排列,如多项式为:P(x)=a0x n+a1x n-1+a2x n-2…a n-1x+a n则其系数矢量(V ector of coefficient)为:P=[a0 a1… a n-1 a n]如将根矢量(V ector of root)表示为:ar=[ ar1 ar2… ar n]则根矢量与系数矢量之间关系为:(x-ar1)(x- ar2) … (x- ar n)= a0x n+a1x n-1+a2x n-2…a n-1x+a n(2)多项式的创建(polynomial creating)a,系数矢量的直接输入法利用poly2sym函数直接输入多项式的系数矢量,就可方便的建立符号形式的多项式。
例1:创建给定的多项式x3-4x2+3x+2poly2sym([1 -4 3 2])ans =x^3-4*x^2+3*x+2也可以用poly2str.求一个方阵对应的符号形式的多项式。
matlab第4章

行向量元素为按降幂排列的多项式系数。
1.多项式乘法函数 conv ( )
格式:C= conv (A, B) %求多项式A和B的乘积
A、B是两个多项式的系数向量,按降幂排列。 conv( ) 把两个多项式相乘合并成一个多项式。
2
p1 2s 3;
2
p2 s 2 4
3 2
A (2s 3)(s 4) 2s 3s 8s 12
x:操作点处的状态向量
u:操作点处的输入向量
x,u缺省值为0。
20
( s 1)(s 2 2s 6) 2 【例4.4】 求传递函数 G(s) 2 s (s 3)(s 3 2s 2 3s 4)
的分子和分母多项式,并求传递函数的特征 根。
21
% num 分子多项式 % conv( ) 采用嵌套形式
G (s)
5s 3 s 3 6 s 2 11s 6
13
3.部分分式展开函数residue ( ) 功能:对两个多项式的比进行部分展开。 格式:[r, p, k]=residue(b, a) 求B(s)/A(s)的部分分式展开式 向量b和a是按s降幂排列的多项式系数。
14
B( s) bn s n bn1s n1 ...b0 F ( s) A( s) an s n an1s n1 ...a0
38
2.并联 G(s)=G1(s)+G2(s) 模型并联函数 parallel 格式:[num, den]=parallel(num1, den1, num2, den2) num1, den1:G1(s) 的分子、分母多项式 num2, den2:G2(s)的分子、分母多项式 num, den:G(s) 的分子、分母多项式
第4章 MATLAB编程基础

(3)使用C-MEX文件:在必须使用for或 while循环体时,为了提高执行效率,可以将 循环部分的代码转化为C-MEX文件。 (4)尽量使用函数文件:在MATLAB中,函 数文件的效率一般比脚本文件的效率要高, 这是由于函数文件有自己的工作空间,执行 一次后仅保存程序运行必需的变量,并将函 数编译成伪代码,下次调用时提高了效率。
例:根据用户要求找出数组x中的最大值、最 小值或所有元素的和。
t=[0:100];x=exp(-t).*sin(t); %给定数组x require=input('Type min,max,or sum.','s') %用户输入要求 require=lower(require); switch require case 'min' %分支判断通过比较字符串完 成 minimum=min(x) case 'max' maximum=max(x) case 'sum' total=sum(x) otherwise disp('You have not entered a proper requirement') end
例:利用for循环求1!+2!+3!+ +5!的值
sum=0; for i=1:5 pdr=1; for k=1:i pdr=pdr*k; end sum=sum+pdr; end
e x 1 x x 2 2 x3 6 例:找出近似级数 中误差大于1%之前的最大的x值(精确到小数点后两
垂直条形图 水平条形图
误差条形图 y轴对数刻度 坐标
commet stairs
rose compass
第四章MATLAB的可视化功能

第四章MATLAB的可视化功能MATLAB是一种高级计算机语言和环境,非常适合进行科学计算和数据可视化。
它具有丰富的绘图和可视化功能,能够帮助用户更好地理解和展示数据。
MATLAB的可视化功能很强大,可以通过简单的命令和函数来创建各种类型的图表。
以下是MATLAB的一些主要可视化功能:2.散点图:散点图用于显示两个变量之间的关系,可以在二维空间中绘制离散的数据点。
MATLAB提供了多种散点图的选项,可以调整点的大小、形状和颜色。
3.条形图:条形图用于比较不同类别之间的数值大小,常用于展示离散数据。
MATLAB可以生成水平或垂直的条形图,用户可以自定义条的宽度、颜色和填充。
5.曲线图:曲线图用于显示连续数据的变化趋势,可以绘制平滑的曲线并描绘出趋势。
MATLAB可以创建简单的曲线图,还可以进行数据拟合和曲线平滑处理。
7.3D图形:MATLAB可以创建三维图形来显示数据的分布和关系,如三维线形图、散点图和曲面图。
用户可以旋转、缩放和平移图形,以查看不同角度和视角的数据。
8.动态可视化:MATLAB还支持动态可视化,可以通过对数据进行实时更新和交互来展示数据的变化。
用户可以创建动画、交互式图形和图表,并添加控件和输入。
MATLAB还提供了许多其他的可视化功能,如绘制轮廓图、热图、雷达图、网格图、直方图等。
用户可以使用MATLAB的绘图函数和工具箱,轻松地创建专业、高质量的图形和可视化效果。
除了绘图功能,MATLAB还提供了一些数据导入和处理的工具,可以轻松从文件、数据库或其他数据源中导入数据,并进行处理和清洗。
用户还可以使用MATLAB的统计函数和工具进行数据分析和可视化。
综上所述,MATLAB的可视化功能非常强大,可以帮助用户更好地理解和展示数据。
无论是进行科学研究、数据分析还是学术教学,MATLAB 的可视化功能都能提供有力的支持。
matlab第四章课后答案

%Exerc ise 1(1)r oots([1 11])%Exer cise1(2)roots([3 0 -4 0 2 -1])%Exerc ise 1(3)p=zero s(1,24);p([1 17 1822])=[5 -6 8 -5];ro ots(p)%E xerci se 1(4)p1=[2 3];p2=conv(p1,p1);p3=co nv(p1, p2);p3(end)=p3(en d)-4; %原p3最后一个分量-4r oots(p3)%Exer cise2fun=inli ne('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzer o(fun,2)%Exer cise3fun=inli ne('x^4-2^x');fplot(fun,[-2 2]);gr id on;fze ro(fu n,-1),fzer o(fun,1),f minbn d(fun,0.5,1.5)%Exe rcise 4fu n=inl ine('x*sin(1/x)','x');fp lot(f un, [-0.10.1]);x=z eros(1,10);fori=1:10, x(i)=fz ero(f un,(i-0.5)*0.01);end;x=[x,-x]%Ex ercis e 5f un=in line('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fso lve(f un,[0 0 0])%E xerci se 6fun=@(x)[x(1)-0.7*si n(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolv e(fun,[0.5 0.5])%E xerci se 7clear; clo se; t=0:p i/100:2*pi;x1=2+sqr t(5)*cos(t); y1=3-2*x1+sq rt(5)*sin(t);x2=3+s qrt(2)*cos(t);y2=6*sin(t);pl ot(x1,y1,x2,y2); gri d on; %作图发现4个解的大致位置,然后分别求解y1=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsol ve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fso lve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exerc ise 8(1)c lear;fun=inlin e('x.^2.*(x.^2-x-2)');fp lot(f un,[-2 2]);grid on;%作图观察x(1)=-2;x(2)=fminb nd(fu n,-1,-0.5);x(4)=fmi nbnd(fun,1,2);fun2=inlin e('-x.^2.*(x.^2-x-2)');x(3)=f minbn d(fun2,-0.5,0.5);x(5)=2feval(fun,x)%答案: 以上x(2)(4)是局部极小,x(1)(3)(5)是局部极大,从最后一句知道x(1)全局最大, x(4)最小。
《MATLAB程序设计》第4章数组及应用

0x0012FF68 a[0] 0x0012FF6C a[1] 0x0012FF70 a[2] 0x0012FF74 a[3]
数组元素
0x0012FF78 a[4]
0x0012FF7C a[5]
8
一维数组在内存中的存储形式
说明:
(1)数组名a表示内存首地址,是地址常量。
(2)数组a中每个数组元素占的内存空间根据 数组类型确定,整个数组占的内存为:数组元 素个数乘以每个元素所占内存空间如: int a[10]; 4×10=40 float b[20]; 4×20=80 double c[5]; 8×5=40 char d[8]; 1×8=8
第4章 数组
教学内容
数组的定义及应用
字符串处理函数
几个常用算法:排序算法(选择排序、
冒泡排序)
1
第4章 数组
重点、难点
数组的定义及应用
常用算法的设计(选择排序、
冒泡排序)
2
第4章 数组
教学目标
熟练掌握数组的定义及应用
掌握字符数组的定义及应用
掌握常用的字符串处理函数
熟练掌握几个常用算法:排序
算法(选择排序、冒泡排序)
分析:所谓转置就是将矩阵的行列互换,即将 a矩阵 的a[i][j]元素变成b矩阵的b[j][i]。
24
#include <iostream> using namespace std; int main() { int a[3][4] ={{1,2,3,4},{3,4,5,6},{5,6,7,8}}; int b[4][3],i,j; for(i=0;i<3;i++) //输出二维数组a[3][4] { for(j=0;j<4;j++) cout<<a[i][j]<<" "; cout<<endl; } for(i=0;i<4;i++) //将矩阵a转置给矩阵b for(j=0;j<3;j++) b[i][j]=a[j][i]; for(i=0;i<4;i++) //输出二维数组b[4][3] { for(j=0;j<3;j++) cout<<b[i][j]<<" "; cout<<endl; } return 0;}
第4章MATLAB程序设计

例 求一个值n,使n!最大但小于1050。 MATLAB程序如下: %初始化 r=1;k=1; 执行后结果如下: %做循环 The 41!Is while r<1e50 3.345253e+049 r=r*k; k=k+1; end k=k-1;r=r/k;k=k-1; % 输出结果 disp(['The',num2str(k),'!is',num2str(r)])
4.2.3 循环结构 for 循环:可完成指定次重复的循环,且在循环开 始之前,就知道代码重复的次数。
while 循环:while语句可完成不定次重复的循 环,与for语句不同,每次循环前要先判断条件 是否满足,再决定循环是否进行。
例 利用rand函数产生10个随机数,然后利用嵌套 for循环进行从小到大排序。
2 1.5 1 0.5 0 150 100 50
然后通过调用函数fun计算出z, 并利用mesh绘制出网格线。 编写的脚本文件如下: % 坐标系准备 x=[0:.02:2]; y=[-2:.02:0]; % 调用函数计算函数值 z=fun(x,y); % 绘图 figure mesh(z)
150 100 50
4.3.2 函数的调用 函数调用的一般格式如下: [输出实参表] = 函数名(输入实参表) 要注意的是,函数调用时各实参出现的顺 序、个数,应与函数定义时形参的顺序、 个数一致,否则会出错。函数调用时,先 将实参传递给相应的形参,从而实现参数 传递,然后再执行函数的功能。
例 对于函数
z ( x 1)2 ( y 1)2
fprintf函数中,format字符中常常会使用到一些特 殊字符来灵活的实现一些显示功能 format string 结果 %d %e %f %g 把值作为整数来处理 用科学记数法来显示数据 用于格式化浮点数,并显示这个 数 用科学记数格式,或浮点数格式, 根据那个表示的数位短,显示那 个 转到新的一行
第4章 MATLAB 绘图

4.图例标注
菜单Insert---legend 命令legend('string1','string2',...)
4.1.6 一个图形窗口多个子图的绘制
subplot(m,n,i)把图形窗口分为m*n个子图,并在第i个子图 中画图 例 4-11 在同一坐标系中画出两个函数,y=cos2x,y=sinxsin6x 的图形,自变量的范围为0≤ x ≤π,函数y=cos2x用红色星号,函数 y=sinxsin6x用蓝色实线,并加图名、坐标轴、图形、图例标注 解 MATLAB命令为: x=0:pi/50:pi; y1=cos(2*x);y2=sin(x).*sin(6*x); plot(x,y1,'r*',x,y2,'b-'),grid on title(‘曲线y1=cos(2x)曲线y2=sin(x)sin(6x)') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=sin(x)sin(6x)') legend('y1=cos(2x)','y2=sin(x)sin(6x)')
group 8 6 4 2 0 10 30 20
stack
1
2
3
4 stack
5
6
0
1
2
3
4 stack
5
6
8 6 5 4 3 2 1 0 10 20 30 6 4 2 0
其它特殊绘图略(见教科书 )
1
2
3
4
5
6
4.3 三维曲线绘图
第四章Matlab语言数据结构1

例3:将二进制按每3位转为十进制数 clc,clear
Xfram=[0 1 1 1 1 1]; Xfram_re=reshape(Xfram,3,2);
%每3位转为十进制数
NumTrans=zeros(1,2);%放转换后的十进制数
for i=1:2
NumTrans(i)=bin2dec(num2str(Xfram_re(:,i)'));
Thank you for your cooperation
4.1.2 结构和单元阵列
在工程和管理系统中,常常需要分层次地 把一些有一定联系但不同类型、不同规模 的数据组织起来成为一个变量。 如:要为一个班的学生建立一套student管 理档案,记录每个学生的三个项目:姓名 (字符串)、出生日期(字符串)、四门 课(高数,英语,马列,体育)的成绩 (数组)。
单元型:cell
结构型:struct Jave类 函数句柄型
§4.1 Matlab语言的数据结构
MATLAB的数据类型
array char numeric double sparse cell struct user- object -
storage
各种数据类型的层次关系
常用基本数据类型 double(双精度数值) char(字符) storage(存储型):只用于内存的有效存储 sparse(稀疏数据):专门用于处理稀疏矩阵 cell(单元数组):
结构阵列的数据索引举例
clc,clear ='John'; student.birthday='1985.06.15'; student.score=[85,85,87,97]; student(2).name=' Alice '; student(2).birthday=' 1986.01.20 '; student(2).score=[77,71,75,76]; ans = 85 85 ans = 77 71 87 97 75 76
第四章 MATLAB程序设计

第二节 选择结构
2.1 if 语句
在MATLAB中,if 语句有三种格式
1、单分支if 语句
语句格式为: if 条件 语句组 end 当逻辑表达式的值为真时,执行该结 构中的执行语句,执行完之后继续向 下进行;若为假,则跳过结构中的内 容,向下执行。
实例分析
例4.4 当x是整数矩阵时,输出x的值。
程序3:
x=input('输入x='); y=cos(x+1)+sqrt(x*x+1);
u=cos(x+1);
v= sqrt(x*x+1); y=u+v end if x~=10
if x~=10
y=x*sqrt(x+sqrt(x));
end
y
y=x*sqrt(x+sqrt(x))
end
第二节 选择结构
if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else if-elseif的执行方式为:如果逻辑表达式1 的值为真,则执行语句1;如果为假,则判 语句组m+1 断逻辑表达式2,如果为真,则执行语句2, end 否则向下执行。
3、多分支if语句
实例分析
y
实例分析
例4.11 求
ye
0.5 x
sin( x
6
)
定积分。
a=0;b=3*pi;n=1000; h=(b-a)/n; x=a:h:b; f=exp(-0.5*x).*sin(x+pi/6);
for i=1:n
s(i)= (f(i)+f(i+1))*h/2; end s=sum(s)
matlab(第四章 函数和方程)

4.1 预备知识:零点
非线性方程(组)f (x) = 0, x=(x1, x2, …, xn), f=(f1, f2, …, fm) • 数值方法主要是综合运用线性方程组和非线性方程求 解方法,常用的方法是Newton法、拟Newton法、最 小二乘法等。
4.1 预备知识:极值
设x为标量或向量,y=f(x)是xD上的标量值函数。
如果对于包含x=a的某个邻域 ,有 f(a)f(x) (f(a)f(x))对任意x成立, 则称a为f(x)的一个局 部极小(大)值点。 如果对任意xD,有f(a)f(x)(f(a)f(x))成立, 则称a为f(x)在区域D上的一个全局极小(大)值点。
4.1 预备知识:极值
4.1 预备知识:最次代数方程 (n次多项式方程) 1. 代数学基本定理可知,n次方程在复数 域上有n个根; 2. n<=4,有求根公式; n>=5无求根公式,只能借助数值解法;
代数方程的解法
• 远在公元前1700年的古巴比伦人就已有关于一、 二次方程的解法。《九章算术》(公元前50~100年) 其中“方程术”有联立一次方程组的一般解法。 • 1535年意大利数学家坦特格里亚(TorTaglia)发现 了三次方程的解法,卡当(H· Cardano)从他那里改 进了这种解法,于1545年在其名著《大术》中公 布了三次方程的公式解,称为卡当算法。
4.2 多项式MATLAB指令
• 多项式
y=polyval(p,x) 求得多项式p在x处的值y,x可以是一个 或多个点 p3=conv(p1,p2) 返回多项式p1和p2的乘积 [p3,r]=deconv(p1,p2) p3返回多项式p1除以p2的商,r返 回余项 x=roots(p) 求得多项式p的所有复根. p=polyfit(x,y,k)用k次多项式拟合向量数据(x, y),返回多 项式的降幂系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 变量的作用域
tips:尽量不使用全局变量! tips
第四章 MATLAB的编程基础
三、函数相关知识
4 函数的参数传递
按值传递机制
第四章 MATLAB的编程基础
三、函数相关知识
4 函数的参数传递
按值传递机制:当一个函数调用发生时, 按值传递机制:当一个函数调用发生时, MATLAB 将会复制实参生成一个副本,然后 将会复制实参生成一个副本, 把它们传递给函数。这次复制是非常重要的, 把它们传递给函数。这次复制是非常重要的, 因为它意味着虽然函数修改了输入参数, 因为它意味着虽然函数修改了输入参数,但 它并没有影响到调用者的原值。 它并没有影响到调用者的原值。 防止了因函数修改变量而导致的严重错误。 防止了因函数修改变量而导致的严重错误。
while 表达式 循环体 end
例:使用while循环计算1+2+3+…+100 使用while循环计算1+2+3+…+100 while循环计算
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构
clear sum=0; i=0; while i<100 i=i+1; sum=sum+i; end sum
第四章 MATLAB的编程基础
三、函数相关知识
4 函数的参数传递 sample.m function out = sample(a, b)
fprintf('In Sample,before compute: a = %f, b = %f \n',a,b);
第四章 MATLAB的编程基础
二、其他流程控制语句 1 . break 和 continue语句 * break语句用于立即跳出含该 语句用于立即跳出含该break语 语句用于立即跳出含该 语 句的循环语句。 句的循环语句。 * continue语句用于提前结束当前循环。 语句用于提前结束当前循环。 语句用于提前结束当前循环
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 2 选择结构 • if语句 if 表达式 程序模块1 程序模块 else 程序模块2 程序模块 end
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 2 选择结构 • if语句
if 表达式 程序模块 end
第四章 MATLAB的编程基础
第四章 MATLAB的编程基础
二、其他流程控制语句 2. return语句 * 用于终止当前命令的执行。 用于终止当前命令的执行。 在任何地方遇到return时程序立即终止。 时程序立即终止。 在任何地方遇到 时程序立即终止
第四章 MATLAB的编程基础
二、其他流程控制语句 3 try-catch语句 * * * 用于实现异常处理机制。 用于实现异常处理机制。 需要检测的程序必须放在try语句块中执行。 语句块中执行。 需要检测的程序必须放在 语句块中执行 异常由catch语句捕获并处理。 语句捕获并处理。 异常由 语句捕获并处理
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 1 顺序结构
程序模块1 程序模块1 模块 程序模块2 程序模块2
只需将程序语句顺序排列即可
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 2 选择结构 成立 不成立
条件
程序模块1 程序模块 程序模块2 程序模块
选择结构由两种语句结构实现: 选择结构由两种语句结构实现: if语句 switch语句
clear 第四章 MATLAB的编程基础 n=input('输入n= '); if n>=90 r='A' elseif n>=80 r='B' elseif n>=70 r='C' elseif n>=60 r='D' else r='E' End
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 2 选择结构 • switch语句
3 变量的作用域
例如: 例如: >> global Gvar (!!) func1.m function y=func1(x) global Gvar; y=x; Gvar=x*10 func2.m function y=func2(x) global Gvar; y=x; Gvar=x*100
第四章 MATLAB的编程基础
第四章 MATLAB的编程基础
二、其他流程控制语句
3 try-catch语句
* 用于实现异常处理机制。 用于实现异常处理机制。 书例5-5(page90)try-catch应用实例。 * 需要检测的程序段必须放在 需要检测的程序段必须放在try语句块中 语句块中 clear; 。 执行。 执行 N=input('please input N='); * 异常由 异常由catch语句捕获并处理。 语句捕获并处理。 语句捕获并处理 A=magic(3); A_N=A(N,N)
第四章 MATLAB的编程基础
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 3 循环结构
条件
程序模块 不成立
பைடு நூலகம்
成立
循环结构可以由两种语句结构实现: for语句 while语句
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 3 循环结构 • for语句
for 循环变量=起始值:步长:终止值 循环变量=起始值:步长: 循环体 end
2 私有函数 指存放在private子目录中的函数。 private 注意: 私有函数只能由其父目录中的函数调用; 在函数调用时优先于其他路径上的函数。 调用次序: 子函数->私有函数->搜索路径中的函数。
第四章 MATLAB的编程基础
三、函数相关知识
2 私有函数 Private Directories You can create your own private directories simply by creating subdirectories called private using the standard procedures for creating directories or folders on your computer. Do not place these private directories on your path.
第四章 MATLAB的编程基础
二、其他流程控制语句 3 try-catch语句 书例5-5(page90)try-catch应用实例。
clear; * 用于实现异常处理机制。 用于实现异常处理机制。 N=input('please input N='); A=magic(3); * 需要检测的程序段必须放在 需要检测的程序段必须放在try语句块中 语句块中 try 执行。 执行。 A_N=A(N,N) * 异常由 异常由catch语句捕获并处理。 语句捕获并处理。 语句捕获并处理 catch A_end=A(end,end) lasterr end
第四章 MATLAB的编程基础
二、其他流程控制语句
1 break 和 continue语句
* break语句用于立即跳出含该 语句用于立即跳出含该break语句的循环语句。 语句的循环语句。 语句用于立即跳出含该 语句的循环语句 for ii = 1:5; * continue语句用于提前结束当前循环。 continue语句用于提前结束当前循环 语句用于提前结束当前循环。 if ii == 3; break; end fprintf('ii = %d \n', ii); end disp('End of loop!');
例:使用for结构计算1+2+3+…+100 使用for结构计算1+2+3+…+100 for结构计算
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构
clear sum=0; for i=1:1:100 sum=sum+i; end sum
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 3 循环结构 • while语句
第四章 MATLAB的编程基础
二、其他流程控制语句
1 break 和 continue语句
for ii 语句用于立即跳出含该 = 1:5; * break语句用于立即跳出含该 语句用于立即跳出含该break语句的循环语句。 语句的循环语句。 语句的循环语句 * continue语句用于提前结束当前循环。 continue语句用于提前结束当前循环 语句用于提前结束当前循环。 if ii == 3; continue; end fprintf('ii = %d \n', ii); end disp('End of loop!');
第四章 MATLAB的编程基础
一、MATLAB的三种控制结构 2 选择结构 switch 表达式 • switch语句
case 数值1 程序模块1; case 数值2 程序模块2; …… case 数值n 程序模块n; otherwise 程序模块n+1 end
书例5-2(page86): 书例 ( ): 将百分制的学生成绩转换为五级制的成绩输出。 将百分制的学生成绩转换为五级制的成绩输出。 clear clear n=input('输入 输入n= '); 输入 n=input('输入 输入n= '); 输入 panduan= fix(n/10) switch fix(n/10) switch panduan case {10,9} case {10,9} r='A' r='A' case 8 case 8 r='B' r='B' case 7 case 7 r='C' r='C' case 6 case 6 r='D' r='D' otherwise otherwise r='E' r='E' end end
