matlab仿真第四章解读
matlab实验报告第四章

第四章N=21时:M4-3程序如下:N=input('N=');W=blackman(N);wc=0.4*pi;alpha=(N-1)/2;k=0:N-1;hd=(wc/pi)*sinc((wc/pi)*(k-alpha));h=hd.*W';omega=linspace(0,pi,512);mag=freqz(h,[1],omega);magdb=20*log10(abs(mag));plot(omega/pi,magdb);grid; N=51时:axis([0 1 -100 5]);set(gca,'ytick',[-80 -75 -60 -40 -20 0]);结论:滤波器的长度增加,即N增加时,通阻带的震荡波纹数量随之增加,波纹宽度变窄,过渡带变窄。
但最小阻带衰减不变,即最小阻带衰减与N无关。
m4-6(b)程序如下:wp=input('wp=');ws=input('ws=');N=61;alpha=(N-1)/2;dw=ws-wp;wc=(ws+wp)/2;h1=sinc((dw/pi).*((0:29)-alpha)/2)*(wc/pi).*sinc((wc/pi).*((0:29)-alpha));h2=wc/pi;h3=sinc((dw/pi).*((31:60)-alpha)/2)*(wc/pi).*sinc((wc/pi).*((31:60)-alpha));h=[h1 h2 h3];omega=linspace(0,pi,512); (1)ΔΩ=0.1*pi时,As= -36db: mag=freqz(h,[1],omega);magdb=20*log10(abs(mag));plot(omega/pi,magdb);grid;axis([0 1 -100 5]);(2)ΔΩ=0.3*pi时,As= -48db: (3)ΔΩ=0.5*pi时,As= -52db:可见:随着过渡带的增宽,阻带衰减值增加。
第四章 根轨迹法 matlab simulink与控制系统仿真 第三版 课件

KG
( 1 s
1)(
2 2
s
2
2 1
2s
1)…
s (T1s 1)(T22s 2 2 2T2s 1)…
f
(s zi )
K
* G
i 1 q
(s pi )
i 1
(4-5)
12
K
G
为前向通道增益,K
* G
为前向通道根轨迹增益
KG*
KG
1
2…
2
T1 T22…
(4-6)
l
(s z j)
H
(s)
③闭环系统的极点与开环系统的极点、
零点以及开环根轨迹增益 K * 有关。
根轨迹法的任务是在已知开环零、极点 分布的情况下,如何通过图解法求出闭 环极点。
16
三、根轨迹方程
• 闭环特征方程
D(s)=1+G(s)H(s)=0
(4-11)
闭环极点就是闭环特征方程的解,也称为特征根。
• 根轨迹方程
G(s)H(s)=-1
53
⑤渐近线
a
1.5
j11.5 21
j11 2
a
(2k 1) 21
π
⑥求分离点坐标d 1 1 1
d1.5j1 d1.5j1 d1 d1 2.12,d2 0.12 (舍去)
54
此系统根轨迹如图4-15所示。
图4-15
55
八、分离角与会合角
所谓分离角是指根轨迹离开分离点处的切
线与实轴正方向的夹角。
47
例4-5根轨迹的起始角和终止角
图4-13
48
七、根轨迹的分离点坐标d
• 定义:几条(两条或两条以上)根轨迹
电机与拖动基础及MATLAB仿真习题答案(第四章)

电机与拖动基础及MATLAB仿真习题答案(第四章)4-14 ⼀台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=87.5%,求电动机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-15 ⼀台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-16 已知⼀台直流电机极对数p=2,槽数Z 和换向⽚数K 均等于22,采⽤单叠绕组。
试求:(1)绕组各节距;(2)并联⽀路数。
解:(1)第⼀节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第⼆节距415y 12=-=-=y y(2)并联⽀路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,⽓隙每极磁通Φ=2.1×10-2Wb ,试求:(1)采⽤单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持⽀路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联⽀路对数a=p=3,电磁转矩 m N I a pN T a ?==Φ=38.1310021.0314.3240032π如果把电枢绕组改为单波绕组, 保持⽀路电流a i 的数值不变,则电磁转矩也不变,仍为 13.369m N ?,因为⽆论是叠绕组还是波绕组,所有导体产⽣的电磁转矩的⽅向是⼀致的, 保持⽀路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
也可以⽤计算的⽅法: 单叠绕组时并联⽀路数为6,⽀路电流 A I i a a 6106==改为单波绕组, 保持⽀路电流a i 的数值不变,仍为A 610,⽽并联⽀路数为2 (a=1), 电枢电流A i I a a 3102== 电磁转矩 m N T ?==38.13310021.0114.324003。
matlab数值分析第四章

4、现在可以选择两个点中的任何一 个,或者也可以选靠近它们的其他点。 再这样执行两步,区间不断缩小并达
到图4-6所示的情形。这是算法快接
近收敛时出现的典型情况,函数的图 形看上去非常像一条直线,而割线交
点或IQI算法得到的点远比区间二分
点快得多的收敛过程。再经过几步操 作,使函数值改变正负号的区间 长 度变得非常小(相对于原始的长度), 同时算法停止,将最后得到的b作为 结果返回。 图4-6
(1)m x J ( x) ( )2m m0 m!(m 1) 2
α=0时,
(1)m x J 0 ( x) ( )2 m m 0 m !(m 1) 2
上式中Γ(z)为Γ函数(它可视为阶乘函数向非整型自变 量的推广)。
下图是0阶、1阶和2阶的贝塞尔函数Jα(x)的图像α=(0,1,2) 第一类贝塞尔函数的形状大致与按速率 1 x 衰减的正弦或 余弦函数类似,但它们的零点并不是周期性的,另外随着x 的增加,零点的间隔会越来越接近周期性。
图4-2
• 函数fzerotx有两个输入参数: 第一个参数指定要计算零解的函数F(x), 第二个参数指定初始的搜索区间[a,b]。 以另一个函数为参数的函数,fzerotx也是MATLAB函 数的函数的例子,ezpot是另外一个例子。本书的其他 章—第6章,数值积分;第7章,常微分方程;甚至第9 章,随机数—中介绍的名字含“tx”和“gui”的M文 件也是函数的函数。 • 一个函数作为参数传递给另一个函数,可采用的方式 有以下几种: 函数句柄, 内嵌对象, 匿名函数。
在图4-2中,用‘x’标记了上述解对应的点(ξ,J0(ξ))。
在MATLAB第6版中,可以使用feval对函数参数求值。表达式 feval(F,x,...) 等价于F(x,...) 它们的区别在于,使用feval时,允许F作为一个被传递来的参 数。在MATLAB第7版中,feval就不再需要了。 fzerotx程序开始的一段注释内容如下:
matlab讲义第四章

图4.11 函数PEAKS的带洞孔曲面图
MATLAB的surf也有两个同种函数:surfc,它画出具有 基本等值线的曲面图。surfl,它画出一个有亮度的曲面 图。例如:
» [X,Y,Z]=peaks(30); » surfc(X,Y,Z) % surf plot with contour plot » grid,xlabel('x-axis'),ylabel('yaxis'),zlabel('z-axis') » title('SURFC of PEAKS')
图4.3 正弦曲线图
利用在x-y平面的矩形网格点上的z轴坐标值,MATLAB 定义了一个网格曲面。MATLAB通过将邻接的点用直线连接起 来形成网状曲面 ,其结果好象在数据点有结点的鱼网。例 如,用MATLAB的函数peaks可以画一个简单的曲面。 » [X,Y,Z]=peaks(30); » mesh(X,Y,Z) » grid on » xlabel('x-axis'),ylabel('y-axis'),zlabel('zaxis') » title('MESH of PEAKS')
图4.4 函数PEAKS的网格图
在显示器上要注意到线的颜色与网格的高度有关。一般情况下, 函数mesh有可选的参量来控制绘图中所用的颜色。关于MATLAB如何 使用、改变颜色在下面讨论。在任何情况下,由于颜色用于增加图 形有效的第四维,这样使用的颜色被称做伪彩色。 上图所示,网格线条之间的区域是不透明的。MATLAB命令 hidden控制网格图的这个特性。例如,用MATLAB的函数sphere产生 两个球面如下: » [X,Y,Z]=sphere(12); » subplot(1,2,1) » mesh(X,Y,Z),title('Opaque') » hidden on; » axis off; » subplot(1,2,2),title('Transparent'); » mesh(X,Y,Z); » hidden off; » axis off;
控制系统仿真及MATLAB语言--第四章 连续系统的离散化方法

t2 0.2, y2 y1 1 0.1y1 0.9 0.91 0.819 t10 1.0, y10 y9 1 0.1y9 0.4628
t3 0.3, y3 y2 1 0.1y2 0.8191 0.1 0.819 0.7519
状态方程的四阶龙格-库塔公式如下:
h xk +1 xk (K 1 2K 2 2K 3 K 4 ) 6 K 1 Axk Bu (tk ) K 2 A(xk h K 1 ) Bu (tk h ) 2 2 K A (x h K ) Bu (t h ) k 2 k 3 2 2 K A(x hK ) Bu (t h) k 3 k 4 y k +1 Cxk +1
41常微分方程的数值解法数值求解的基本概念设微分方程为则求解方程中函数xt问题的常微分方程初值问题所谓数值求解就是要在时间区间ab中取若干离散点求出微分方程在这些时刻的近似值这种方法的几何意义就是把ftx在区间tk1内的曲边面积用矩形面积近似代替
第四章 连续系统的离散化方法
4.1
常微分方程的数值解法
h xk 1 xk h f k ( ftk ' f xk ' f k ) 2!
f 'tk f 'xk 等各阶导数不易计算,用下式中 ki的线性组合代替
xk 1 xk h ai ki
i 1
r
线性组合
r为精度阶次,ai为待定系数,由精度确定;ki用下 式表示 i 1
ki f (tk b1h, xk hb2 k j ) , i 2,3
将 f tk b1h,xk hb2k1 在点 tk , xk 展成Taylor级数
数字语音处理及MATLAB仿真.rar-第四章

定义 可得
yi (n) X n (e ji )e jin
x(m)w(n-m)也应当是宽度为N有限时宽的。现在在频
域内L个角频率上对 X n (e j )进行取样,根据这些取样所 恢复出的时间信号应该是x(m)w(n-m)进行周期延拓的
结果,延拓周期等于L。为使恢复的时域信号不产生
混叠,要求L N,故频域最小取样数为窗宽 SRf=N。
24
数字语音处理及MATLAB仿真 张雪英编著
在,为:
X (ej ) x(m)ejm
(4.8)
m
W (ej ) w(m)ejm
(4.9)
m
当n固定时,序列w(n-m)的傅里叶变换为:
w(n m)ejm W (ej )ejn
m
(4.10)
10
数字语音处理及MATLAB仿真 张雪英编著
值决定于窗口序列的长度N和形状。
22
数字语音处理及MATLAB仿真 张雪英编著
若使用哈明窗,W (ej ) 的近似带宽为
B 2FS (Hz) N
(4.20)
j
X n (e
)的采样率为2B
4Fs
N
( 采样/秒)
若使用矩形窗, W(e j )的近似带宽为
B Fs (Hz) N
X n (e j )的采样率为
数字语音处理及MATLAB仿真 张雪英编著
第四章 语音信号的短时时域分析
1 4.1 概述 2 4.2 傅里叶变换的解释 3 4.3 滤波器的解释 4 4.4 短时谱的时域及频域采样率 5 4.5 短时综合的滤波器组相加法
1
数字语音处理及MATLAB仿真 张雪英编著
Matlab 系统辨识 仿真 CH3,CH4,CH6程序注释与剖析
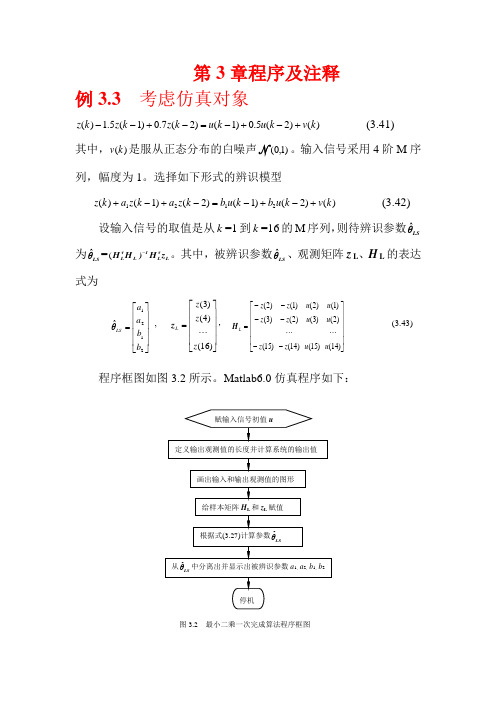
第3章程序及注释例3.3 考虑仿真对象)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (3.41) 其中,)(k v 是服从正态分布的白噪声N )1,0(。
输入信号采用4阶M 序列,幅度为1。
选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (3.42)设输入信号的取值是从k =1到k =16的M 序列,则待辨识参数LSθˆ为LS θˆ=L τL 1L τL z H )H H -(。
其中,被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H (3.43) 程序框图如图3.2所示。
Matlab6.0仿真程序如下:%二阶系统的最小二乘一次完成算法辨识程序,在光盘中的文件名:FLch3LSeg1.mu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16,步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on %画出输出观测值z的径线图形,并显示坐标网格u,z %显示输入信号和输出观测信号%L=14 %数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9) u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11)u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13)u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵H L赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15); z(16)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示θˆLS%Display Parametersa1=c(1), a2=c(2), b1=c(3),b2=c(4) %从θˆ中分离出并显示a1、a2、b1、LSb2%End程序运行结果:>>u =[ -1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]z =[ 0,0,0.5000,0.2500,0.5250,2.1125,4.3012,6.4731,6.1988,3.2670,-0.9386,-3.1949,-4.6352,6.2165,-5.5800,-2.5185]HL =0 0 1.0000 -1.0000-0.5000 0 -1.0000 1.0000-0.2500 -0.5000 1.0000 -1.0000-0.5250 -0.2500 1.0000 1.0000-2.1125 -0.5250 1.0000 1.0000-4.3012 -2.1125 1.0000 1.0000-6.4731 -4.3012 -1.0000 1.0000-6.1988 -6.4731 -1.0000 -1.0000-3.2670 -6.1988 -1.0000 -1.00000.9386 -3.2670 1.0000 -1.00003.1949 0.9386 -1.0000 1.00004.6352 3.1949 -1.0000 -1.00006.2165 4.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000ZL =[ 0.5000,0.2500,0.5250,2.1125,4.3012,6.4731,6.1988,3.2670,-0.9386,-3.1949,-4.6352,-6.2165,-5.5800,-2.5185]Tc =[ -1.5000,0.7000,1.0000,0.5000]Ta1 = -1.5000a2 = 0.7000b1 = 1.0000b2 =0.5000>>-11-1010-10010从仿真结果表3.1可以看出,由于所用的输出观测值没有任何噪声成分,所以辨识结果也无任何误差。
Matlab第四章详细讲解

v11 v21 V = v12 v22
λ 1 v11 A .v1 = λ 1 v1 = λ 1 v12
λ 2 v 21 A.v 2 = λ 2 v 2 = λ 2 v 22
A .v1
A .v 2
a11 a12 v11 v21 a11v11 + a12v12 a11v21 + a12v22 A*V = v v = a v + a v a v + a v a21 a22 12 22 21 11 22 12 21 21 22 22
2 − at
f ( t ) = (sin
t )e
−b=fzero(fun ,x0 ,option,p1,p2)
%(1)使用字符串表示被处理函数 P1=0.1;P2=0.5;
%按泛函指令要求,这里参数必须用P1,P2表示
y_C='sin(x).^2.*exp(-P1*x)-P2*abs(x)';
1、求函数的零点 (1)字符串表达式 q=quad(fun,a,b) 2、数值积分 (2)内联函数 3、解微分方程 q=quadl(fun,a,b) (3)“M函数文件”的函数句柄
[t,y]=ode45(fun ,tspan,y0)
4.3.1 求函数的零点
例:求以下函数的零点。
零点初始 猜测值
向函数fun传 递的参数
4.4 多项式和卷积
4、多项式的根
功能:计算多 项式P的根。
R=roots(P)
p1 x + p2 x
n
n −1
+ ... + pn x + p
-27 ];
MATLAB仿真课件--第4章

if(n2>0) disp('the system is unstable') disp('the unstable pole are:') disp(p(jj)) else disp('the system is stable') end %判断系统是否为最小相位系 统 if(n1>0) disp('the system is a nonminimal phase one') else disp('the syetem is a minimal phase one') end %绘制零极点图 pzmap(p,z)
1)直接求根判定系统稳定性 直接求根判定系统稳定性 the system is stable the system is a minimal phase one p= -1.9474 + 5.0282i -1.9474 - 5.0282i -4.2998 -2.8752 + 2.8324i -2.8752 - 2.8324i -0.0550 z= -2.1667 + 2.1538i -2.1667 - 2.1538i -1.0000
n2=length(jj); %判断系统是否稳定 if(n2>0) disp('the system is unstable') disp('the unstable pole are:') disp(p(jj)) else disp('the system is stable') end %判断系统是否为最小相位系统 if(n1>0) disp('the system is a nonminimal phase one') else disp('the syetem is a minimal phase one') end pzmap(p,z) %绘制零极点图 p,z
MATLAB仿真应用_第4章(1)

数长度)设定为8bit、16bit、32bit时,分频比分别
为28、216、232。
第4章 电子线路仿真试验
图4-10 计数器参数设置对话框
第4章 电子线路仿真试验 表4-12 Counter(计数器)的主要参数
发时,采集到并保持的正弦信号的样值。
(3)示波器通道3显示了仅在方波信号过零的下降沿触 发时,采集到并保持的正弦信号的样值。 (4)示波器通道4显示了在方波信号过零的上升或下降 沿触发时,采集到并保持的正弦信号的样值。
第4章 电子线路仿真试验 简而言之,触发电路是一个采样保持电路,采样 的时刻取决于触发信号的形状和触发方式的设定。
第4章 电子线路仿真试验
图4-1 信号合并的仿真系统框图
第4章 电子线路仿真试验
图4-2 信号合并的系统仿真结果
第4章 电子线路仿真试验 表4-1~表4-5分别给出了信号合并仿真系统中各个 模块的主要参数。
第4章 电子线路仿真试验
表4-1 Merge(信号合并器)的主要参数
第4章 电子线路仿真试验
图4-3 信号微积分运算的仿真系统框图
第4章 电子线路仿真试验
图4-4 信号微积分运算的仿真结果
第4章 电子线路仿真试验 微分和积分的模块都来自Simulink\Continuous库 中,微分模块不需要设置,积分模块的参设置如表 4-6所示。
第4章 电子线路仿真试验 表4-6 Integrator(积分器)的主要参数
第4章 电子线路仿真试验 积分模块有两种工作模式:简单积分方式(本例)和重 置积分方式。当设定的触发信号到来时,模块输出重置为初 始条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典控制理论CAD 现代控制理论CAD
控制系统稳定性分析
系统稳定性是系统能够成立和运行的首要条件
经典控制理论
对于连续系统,如果闭环极点全部在S平面左半平面, 则系统是稳定的。对于离散系统,如果系统全部极点都位于Z平 面的单位圆内,则系统是稳定的。 劳斯判据、胡尔维茨判据、奈奎斯特稳定性判据
控制工具箱
1.6 系统设计函数 Pole placement
place acker - MIMO pole placement. - SISO pole placement.
For example
LQR design
lqr, dlqr - Linear-quadratic (LQ) state-feedback regulator. lqry - LQ regulator with output weighting.
Outline 控制工具箱
控制系统
稳定性分析
经典控制理论CAD
现代控制理论CAD
控制工具箱
早期的控制系统分析过程复杂而耗时,如想得到一个系 统的冲激响应曲线,首先需要编写一个求解微分方程的 子程序,然后将已经获得的系统模型输入计算机,通过 计算机的运算获得冲激响应的响应数据,然后再编写一 个绘图程序,将数据绘制成可供工程分析的响应曲线。
Outline
控制工具箱
控制系统
稳定性分析
经典控制理论CAD 现代控制理论CAD
经典控制理论CAD
3.1 控制系统固有特性分析
1、时域分析 时域分析:是指典型输入信号作用下,通过过渡过程曲线来分 析和评价控制系统的性能。
MATLAB实现:
step——Step response of continuous system(dstep) impulse—impulse response of continuous system(dimpulse) initial—Initial condition response of state-space models. lsim——Simulate time response of continuous system to arbitrary inputs
经典控制理论CAD
3.1 控制系统固有特性分析
2、频域分析 bode( )函数的用法 bode(SYS): draws the Bode plot of the SYS (created with either TF, ZPKor SS). The frequency range and number of points are chosen automatically. bode(SYS,W):uses the user-supplied vector W of frequencies, in radian/second, at which the Bode response is to be evaluated. [m,p,w]=bode(SYS):return the response magnitudes and phases in degrees (along with the frequency vector W if unspecified). No plot is drawn on the screen.
minreal
ss2ss ctrbf obsvf
- Minimal realization and pole/zero cancellation.
- State coordinate transformation. -decomposition into the controllable and
uncontrollable subspaces.
Matrix equation solvers.
lyap dlyap care dare - Solve continuous Lyapunov equations. - Solve discrete Lyapunov equations. - Solve continuous algebraic Riccati equations. - Solve discrete algebraic Riccati equations.
经典控制理论CAD
3.1 控制系统固有特性分析
1、时域分析 step( )函数的用法 y=step(num,den,t):其中num和den分别为系统传递函数描 述中的分子和分母多项式系数,t为选定的仿真时间向量,一 般可以由t=0:step:end等步长地产生出来。该函数返回值y为 系统在仿真时刻各个输出所组成的矩阵。 [y,x,t]=step(A,B,C,D,iu):其中A,B,C,D为系统的状态空 间描述矩阵,iu用来指明输入变量的序号。x为系统返回的状 态轨迹。
控制工具箱
1.2 系统模型的连接 System interconnections.
append - Group LTI systems by appending inputs and outputs.
parallel
series feedback cloop
- Generalized parallel connection.
lqrd
kalman kalmd
- Discrete LQ regulator for continuous plant.
- Kalman estimator. - Discrete Kalman estimator for continuous plant.
For example
Outline
控制工具箱
- Generalized series connection. - Feedback connection of two systems. -unit feedback connection
控制工具箱
1.3 模型降阶与实现 Model reductions and realizations
balreal modred - Gramian-based input/output balancing. - Model state reduction.
经典控制理论CAD
3.1 控制系统固有特性分析
1、时域分析
For example
已知开环系统的传递函数为:
20 G (s) 4 s 8s 3 36 s 2 40 s
试求该系统在单位负反馈下的阶跃响应曲线和最大超调量。
经典控制理论CAD
3.1 控制系统固有特性分析
2、频域分析 频域分析:通常将频率特性用曲线的形式进行表示,包括对数 频率特性曲线和幅相频率特性曲线。
-decomposition into the observable and unobservable subspaces.
For example
控制工具箱
1.4 模型属性函数 Model properties
ctrb obsv gram damp - Controllability matrix. - Observability matrix. - Controllability and observability gramians. - Natural frequency and damping of system .
控制系统仿真
Control System Simulation
电力学院自动化系 温素芳
wensf@
本课程内容
第一章
第二章
第三章 第四章 第五章
系统仿真概述 控制系统的数学描述 MATLAB/SIMULINK 控制系统CAD 数字仿真技术的综合应用
第四章
控制系统CAD
MATLAB实现:
bode——draws the Bode plot of the SYS (created with either TF, ZPK or SS ). nyquist—draws the Nyquist plot of the SYS. nichols—draws the Nichols plot of the SYS. dbode dnyquist dnichols
Model conversions. tf2ss - Transfer function to state space conversion. zp2tf - Zero/pole/gain to state space conversion. ss2zp - State space to zero/pole/gain conversion. c2d - Continuous to discrete conversion. d2c - Discrete to continuous conversion. d2d - Resample discrete-time model. residue - Conversion between Partial-fraction expansion and transfer function
nyquist
nichols margin allmargin
- Nyquist plot.
- Nichols plot. - Gain and phase margins. - All crossover frequencies and related gain/phase margins.
For example
控制工具箱
1.5 分析函数 root locus
pzmap - Pole-zero map.
rlocus - Evans root locus.
For example
sgrid -Generate s-plane grid lines for a root locus or pzmap.
zgrid -Generate z-plane grid lines for a root locus or pzmap.
