MATLAB simulink 通信系统建模与仿真 第四章部分习题答案
SIMULINK仿真
后面的每一列对应每一个输入端口,矩阵的第一行表示某 一时刻各输入端口的输入状态。另外,也可以把矩阵分开 来表示,即MATLAB默认的表示方法[t,u],其中t是一维 时间列向量,表示仿真时间,u是和t长度相等的n维列向 量(n表示输入端口的数量),表示状态值。例如,在命 令窗口中定义t和u:
条件执行子系统分为
1.使能子系统
使能子系统表示子系统在由控制信号控制时,控制信号由 负变正时子系统开始执行,直到控制信号再次变为负时结 束。控制信号可以是标量也可以是向量。
建立使能子系统的方法是:打开Simulink模块库中的Ports & Subsystems模块库,将Enable模块复制到子系统模型 中,则系统的图标发生了变化。
阵、结构和包含时间的结构3种选择。“Limit data points to last”用来限定保存到工作空间中 的数据的最大长度。 输出选项(Output options)有: ① Refine output(细化输出) ② Produce additional output(产生附加输出) ③ Produce specified output only(仅在指定 的时刻产生输出)
4.1 初识Simulink—— 一个简单的仿 真实例
在MATLAB的命令窗口输入Simulink,或单击MATLAB主 窗口工具栏上的“Simulink”命令按钮即可启动Simulink。 Simulink启动后会显示如图4.1所示的Simulink模块库浏览 器(Simulink Library Browser)窗口。
U (s)
Kp
Ki s
Kd s
MATLABSimulink模型建立与仿真指南

MATLABSimulink模型建立与仿真指南第一章:MATLAB与Simulink简介MATLAB是一种高级的数值计算和科学分析的编程语言,由MathWorks开发。
它提供了强大的数学函数库和绘图工具,使得用户可以进行复杂的数值计算和数据可视化。
Simulink是MATLAB的扩展,是一种用于建立和仿真动态系统的图形化环境。
在MATLAB中,用户可以通过命令行或脚本文件进行计算。
而在Simulink中,用户可以利用图形化界面来搭建系统模型,并进行仿真。
Simulink提供了丰富的预置模块库,用户只需将这些模块连接起来,即可构建复杂的系统模型。
第二章:Simulink模型的基本组成Simulink模型由多个部分组成,包括输入信号、输出信号和系统组件。
输入信号可以是手动输入的常数,也可以是来自其他模型的信号。
输出信号是用户对系统模型感兴趣的结果。
系统组件即模型中的各个模块,这些模块可以完成各种功能,如乘法、滤波、逻辑运算等。
第三章:模型建立与仿真流程1. 确定系统模型的目标和需求:在建立模型之前,需要明确系统模型的目标和需求。
这些可能包括系统的输入输出关系、稳定性要求、性能要求等。
2. 模型建立:根据系统的目标和需求,选择合适的系统组件,并将其连接起来,构建系统模型。
可根据需要进行参数设置,以适应不同的场景。
3. 仿真设置:在进行仿真之前,需要设置仿真参数。
这些包括仿真时间、仿真步长等。
仿真时间指定了仿真的时间范围,仿真步长指定了仿真的时间间隔。
4. 仿真运行:设置好仿真参数后,可以运行仿真。
Simulink将逐步模拟系统的行为,并输出仿真结果。
第四章:Simulink模型调试与优化在进行仿真时,可能会发现模型存在问题,如输出不符合预期、系统不稳定等。
这时需要对模型进行调试和优化。
1. 系统调试:可以通过数据观察、信号域分析等方法,定位系统问题。
更换输入信号、输出信号,或调整模型参数,可以帮助发现问题。
matlab语言与控制系统仿真参考答案第4章

4.5 控制系统的数学模型MATLAB 实训1.练习并掌握TF 模型、ZPK 模型、SS 模型的建立方法。
2.练习并掌握TF 模型、ZPK 模型、SS 模型间的转换方法。
3.练习并掌握求取多个模块串联、并联、反馈后总的模型的方法。
4.练习并掌握模型数据的还原方法。
1.写出以下系统的多项式模型,并将其转换为零极点模型;(1)2153173261552115.35291)(23452341++++++-+-=s s s s s s s s s s G >> n1=[91,-52,3.5,-11,52];d1=[1,15,26,73,31,215];sys1=tf(n1,d1)[z1,p1,k1]=tf2zp(n1,d1)sys1zp=zpk(z1,p1,k1)运行结果如下:Transfer function:91 s^4 - 52 s^3 + 3.5 s^2 - 11 s + 52-------------------------------------------s^5 + 15 s^4 + 26 s^3 + 73 s^2 + 31 s + 215z1 =0.7705 + 0.5468i0.7705 - 0.5468i-0.4848 + 0.6364i-0.4848 - 0.6364ip1 =-13.4656-1.3473 + 1.9525i-1.3473 - 1.9525i0.5801 - 1.5814ik1 =91Zero/pole/gain:91 (s^2 - 1.541s + 0.8927) (s^2 + 0.9697s + 0.6401)--------------------------------------------------------------------------(s+13.47) (s^2 - 1.16s + 2.837) (s^2 + 2.695s + 5.627)(2)21.311395.2251315239.5621.635.711017.38)(23456723452++-+-++++-+-=s s s s s s s s s s s s s G >> n2=[1,-38.7,101,-71.5,63.1,562.39];d2=[1,2,5,-31,51,-22.5,39,311.21];sys2=tf(n2,d2)[z2,p2,k2]=tf2zp(n2,d2)sys2zpkmx=zpk(z2,p2,k2)Transfer function:s^5 - 38.7 s^4 + 101 s^3 - 71.5 s^2 + 63.1 s + 562.4---------------------------------------------------------------------------s^7 + 2 s^6 + 5 s^5 - 31 s^4 + 51 s^3 - 22.5 s^2 + 39 s + 311.2z2 =35.94372.95890.5590 + 1.9214i0.5590 - 1.9214i-1.3206p2 =-2.5015 + 3.1531i-2.5015 - 3.1531i1.9492 + 1.0027i1.9492 - 1.0027i0.2072 - 1.7349i-1.3097k2 =1Zero/pole/gain:(s-35.94) (s-2.959) (s+1.321) (s^2 - 1.118s + 4.004)--------------------------------------------------------------------------------------------------(s+1.31) (s^2 - 3.898s + 4.805) (s^2 - 0.4143s + 3.053) (s^2 + 5.003s + 16.2)2.写出以下系统的零极点模型,并将其转换为多项式模型,并将其展开成为部分分式形式;(1))11.5)(9.4)(5.3)(6.2)(3.1()02.6)(5.0(36)(1+++++++=s s s s s s s s s G >> z=[-0.5;-6.02];>> p=[0;-1.3;-2.6;-3.5;-4.9;-5.11];>> k=36;>> sys=zpk(z,p,k)Zero/pole/gain:36 (s+0.5) (s+6.02)--------------------------------------------------s (s+1.3) (s+2.6) (s+3.5) (s+4.9) (s+5.11)>> [n,d]=zp2tf(z,p,k)n =0 0 0 0 36.0000 234.7200 108.3600d =1.0000 17.4100 116.1430 367.5889 544.8325 296.2114 0>> systfxs=tf(n,d)Transfer function:36 s^2 + 234.7 s + 108.4-------------------------------------------------------------------------------s^6 + 17.41 s^5 + 116.1 s^4 + 367.6 s^3 + 544.8 s^2 + 296.2 s>> [r,p,k]=residue(n,d);>> [r';p']ans =9.1407 -14.8730 17.4236 -14.7227 2.6656 0.3658-5.1100 -4.9000 -3.5000 -2.6000 -1.3000 0即部分分式分解结果为 s s s s s s s G 3658.03.16656.26.27227.145.34236.179.4873.1411.51407.9)(++++-+++-+=(2))6)(5)(4)(2()5.3)(3)(1(15.9)(22+-++-++=s s s s s s s s s G >> z=[-1;-3;3.5];>> p=[0;0;-2;-4;5;6];>> k=9.15;>> sys=zpk(z,p,k)Zero/pole/gain:9.15 (s+1) (s+3) (s-3.5)-------------------------------s^2 (s+2) (s+4) (s-5) (s-6)>> [n,d]=zp2tf(z,p,k)n =0 0 0 9.1500 4.5750 -100.6500 -96.0750d =1 -5 -28 92 240 0 0>> systfxs=tf(n,d)Transfer function:9.15 s^3 + 4.575 s^2 - 100.7 s - 96.08---------------------------------------------------s^6 - 5 s^5 - 28 s^4 + 92 s^3 + 240 s^2>> [r,p,k]=residue(n,d);>> [r';p']ans =0.5004 -0.4183 0.0715 0.1123 -0.2659 -0.40036.0000 5.0000 -4.0000 -2.0000 0 0即部分分式分解结果为 24003.02659.021123.040715.054183.065004.0)(s s s s s s s G --++++---= 3.已知系统的状态空间表达式,写出其SS 模型,并求其传递函数矩阵(传递函数模型),若状态空间表达式为⎩⎨⎧+=+=DuCx y Bu Ax x ,则传递函数矩阵表达式为: D B A sI C s G +-=-1)()(。
通信系统仿真课后答案

第3章采样和量化3-1答:输入:syms t wXf=fourier(5*cos(6*pi*t)+3*sin(8*pi*t))输出:Xf=pi*(5*dirac(w+6*pi)+3*i*dirac(w+8*pi)-3*i*dirac(w-8*pi)+5*dirac(w-6*pi))matlab程序:t=0:0.02:8;L=length(t);xt=5*cos(6*pi*t)+3*sin(8*pi*t);f1=fft(xt);fs=10;Ts=1/fs;t1=8:-0.02:0;f=1./t1;Pt=zeros(1,L);for i=1:8:LPt(i)=1;endXst=xt.*Pt;f2=fft(Xst);f3=fs*f1;f4=ifft(f3);subplot(2,2,1)plot(f,f1)axis([0 10 -1000 3000])xlabel('f');ylabel('x(f)');subplot(2,2,2)plot(f,f2)axis([0 10 -200 400])xlabel('f');ylabel('Xs(f)');subplot(2,2,3)plot(f,f3)axis([0 10 -2000 4000])xlabel('f');ylabel('Xr(f)');subplot(2,2,4)plot(t,f4)xlabel('t');ylabel('Xr(t)');axis([0 6 -50 50])510-1000010002000fx (f )510-2000200fX s (f )510-2000020004000fX r (f )0246tX r (t )3-2答:matlab 程序: t=0:0.02:8;L=length(t);xt=5*cos(6*pi*t)+3*sin(8*pi*t); f1=fft(xt); fs=7;Ts=1/fs; t1=8:-0.02:0; f=1./t1;Pt=zeros(1,L); for i=1:8:L Pt(i)=1; endXst=xt.*Pt; f2=fft(Xst); f3=fs*f1; f4=ifft(f3); subplot(2,2,1) plot(f,f1)axis([0 10 -1000 3000]) xlabel('f');ylabel('x(f)'); subplot(2,2,2) plot(f,f2)axis([0 10 -200 400]) xlabel('f');ylabel('Xs(f)'); subplot(2,2,3) plot(f,f3)axis([0 10 -2000 4000]) xlabel('f');ylabel('Xr(f)'); subplot(2,2,4) plot(t,f4)xlabel('t');ylabel('Xr(t)'); axis([0 6 -50 50])510-1000010002000fx (f )510-2000200fX s (f )510-2000020004000fX r (f )0246-5050tX r (t )3.5信号()5sin(10)x t t π=,(a )信号的动态范围为25.84,49.93,98.09,194.42 dB SNR =。
Matlab与控制系统仿真部分习题答案

【4.2】程序:num=[5,0];den=conv([1,1],conv([1,2],[1,3])); [numc,denc]=cloop(num,den);[z,p,k]=tf2zp(numc,denc);[A,B,C,D]=tf2ss(numc,denc);g_zp=zpk(z,p,k)g_tf=tf(numc,denc)g_ss=ss(A,B,C,D)运行结果:Zero/pole/gain:5 s----------------------------------(s+0.4432) (s^2 + 5.557s + 13.54)Transfer function:5 s----------------------s^3 + 6 s^2 + 16 s + 6a =x1 x2 x3x1 -6 -16 -6x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 5 0d =u1y1 0【4.3】程序:A=[0 0 0 -1;1 0 0 -2;0 1 0 -3;0 0 1 -4]; B=[0;0;0;1];C=[1 0 0 0];g_ss=ss(A,B,C,D)[num,den]=ss2tf(A,B,C,D);g_tf=tf(num,den)[z,p,k]=ss2zp(A,B,C,D);g_zpk=zpk(z,p,k)运行结果:a =x1 x2 x3 x4x1 0 0 0 -1x2 1 0 0 -2x3 0 1 0 -3x4 0 0 1 -4b =u1x1 0x2 0x3 0x4 1c =x1 x2 x3 x4y1 1 0 0 0d =u1y1 0Continuous-time model.Transfer function:-3.109e-015 s^3 - s^2 - 3.331e-015 s - 4.441e-016 -------------------------------------------------s^4 + 4 s^3 + 3 s^2 + 2 s + 1Zero/pole/gain:- s^2----------------------------------------------(s+0.6724) (s+3.234) (s^2 + 0.0936s + 0.4599)【5.1】(1)程序num=[0,10];den=conv([1,0],[1,7,17]); [numc,denc]=cloop(num,den,-1); G=tf(numc,denc)[y,t]=step(G);plot(t,y,'b-')C=dcgain(G);n=1;while y(n)<0.1*Cn=n+1;endm=1;while y(m)<0.9*Cm=m+1;endrisetime=t(m)-t(n)[Y,k]=max(y); percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettlingtime=t(i)运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10risetime =2.7312percentovershoot =-0.4399settlingtime =5.1372图:0123456700.10.20.30.40.50.60.70.80.91(2)程序k=[10,100,1000];t=linspace(1,20,200);num=1;den=conv([1,0],[1,7,17]);for j=1:3;s1=tf(num*k(j),den);sys=feedback(s1,1)y(:,j)=step(sys,t);endplot(t,y(:,1),'r',t,y(:,2),'b',t,y(:,3),'g')gtext('k=10');gtext('k=100');gtext('k=1000') 运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10Transfer function:100------------------------s^3 + 7 s^2 + 17 s + 100Transfer function:1000-------------------------s^3 + 7 s^2 + 17 s + 1000图:024681012141618200.20.40.60.811.21.41.61.8图:02468101214161820-3-2-1123422【6.1】程序:(1)num1=[1,1];den1=conv([1,0,0],conv([1,2],[1,4]));sys1=tf(num1,den1)rlocus(sys1)运行结果:-12-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(2)num2=[1,1];den2=conv([1,0],conv([1,-1],[1,4,16]));sys2=tf(num2,den2)rlocus(sys2)运行结果:-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(3)num3=[1,8];den3=conv([1,0,0],conv([1,3],conv([1,5],conv([1,7],[1,15])))); sys3=tf(num3,den3)rlocus(sys3)运行结果:-30-25-20-15-10-5051015-20-15-10-505101520Root LocusReal Axis I m a g i n a r y A x i s【6.3】程序:num=[1,2];den=conv([1,0],conv([1,4],conv([1,8],[1,2,5])));sys=tf(num,den)rlocus(sys)[k,poles]=rlocfind(sys)运行结果:Transfer function:s + 2---------------------------------------s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 sSelect a point in the graphics windowselected_point =0.0296 + 2.2826i k =135.8815poles =-7.3248-5.41040.0145 + 2.3021i0.0145 - 2.3021i -1.2939图:-20-15-10-5051015-15-10-551015Root LocusReal Axis I m a g i n a r y A x i s【7.3】程序(1)画波特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)bode(sys)grid图(1)-150-100-50050100M a g n i t u d e (d B)10-210-1100101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)程序(2)画奈奎斯特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)nyquist(sys)grid图(2)-16-14-12-10-8-6-4-20-300-200-100100200300Nyquist DiagramReal Axis I m a g i n a r y A x i s程序(3)画零极点图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)pzmap(sys1)gird图(3)P ole-Zero MapReal Axis I m a g i n a r y A x i s -12-10-8-6-4-20-1.5-1-0.50.511.5程序(4)计算相角裕量和幅值裕量num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)[gm,pm,wcg,wcp]=margin(sys)运行结果Transfer function:50---------------------3 s^3 + 31 s^2 + 10 sTransfer function:50--------------------------3 s^3 + 31 s^2 + 10 s + 50gm =2.0667pm =7.5615wcg =1.8257wcp =1.2645程序(5)绘制阶跃响应曲线num=[50];den=conv([1,0],conv([1,10],[3,1])); sys=tf(num,den)sys1=feedback(sys,1)step(sys1)图(5)00.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d e【7.4】程序如下:num=[300];den=conv([1,0,0],conv([0.2,1],[0.02,1]));sys=tf(num,den)margin(sys)grid波特图如下:-150-100-50050100M a g n i t u d e (d B )10-1100101102103-360-315-270-225-180P h a s e (d e g )Bode DiagramGm = Inf , P m = -78 deg (at 11 rad/sec)Frequency (rad/sec)【9.3】程序:A=[-2 2 -1;0 -2 0;1 -4 0];B=[0;0;1];C=[1,0,0];D=0;M=ctrb(A,B)m=rank(M)if m==3;disp('系统可控')elsedisp('系统不可控')endN=obsv(A,C)n=rank(N)if n==3;disp('系统可观')elsedisp('系统不可观') endsys=ss(A,B,C,D) [num,den]=ss2tf(A,B,C,D) sys1=tf(num,den)[z,p,k]=ss2zp(A,B,C,D)运行结果:M =0 -1 20 0 01 0 -1m =2系统不可控N =1 0 0-2 2 -13 -4 2n =2系统不可观a =x1 x2 x3x1 -2 2 -1x2 0 -2 0x3 1 -4 0b =u1x1 0x2 0x3 1c =x1 x2 x3y1 1 0 0d =u1y1 0 Continuous-time model.0 0 -1 -2den =1 4 5 2Transfer function:-s - 2---------------------s^3 + 4 s^2 + 5 s + 2z =-2p =-1-1-2k = -1【10.1】(1)程序:A=[0,1,0,0;0,5,0,0;0,0,-7,0;0,0,0,-8]; B=[0;1;0;1];C=[1,2,3,4];D=zeros(1,1);G_ss=ss(A,B,C,D)运行结果:a =x1 x2 x3 x4x1 0 1 0 0x2 0 5 0 0x3 0 0 -7 0x4 0 0 0 -8u1x1 0x2 1x3 0x4 1c =x1 x2 x3 x4y1 1 2 3 4d =u1y1 0(2):程序:[num1,den1]=ss2tf(A,B,C,D); p=roots(den1)i=0;for k=1:1:length(p)if real(p(k))>0i=i+1;endendif i>0disp('系统不稳定');elsedisp('系统稳定');end运行结果:p =5.0000-8.0000-7.0000系统不稳定(3)(4)程序:AA=[0,1,0;0,5,0;0,0,-8];BB=[0;1;1];P=[-1,-2,-8];K=acker(AA,BB,P);i=4;K(4)=0;Kpp=eig(A-B*K)sys1=tf(num1,den1);[y1,t]=step(sys1);plot(t,y1)hold onA_feedback=A-B*K;[num2,den2]=ss2tf(A_feedback,B,C,D); sys2=tf(num2,den2);[y2,t]=step(sys2);plot(t,y2,'r')gridgtext('反馈前')gtext('反馈后')运行结果:K =2 8 0 0pp =-8-2-1-7图形:01234560123456【13.1】程序:A=[0,1;0,0];B=[0;1];C=[1,0];D=zeros(1,1);G_ss=ss(A,B,C,D)M=ctrb(A,B);if rank(M)==2disp('系统完全能控'); elsedisp('系统不完全能控'); endS=[1,0];N=obsv(A,S);if rank(N)==2disp('(A,S)可观测'); elsedisp('(A,S)不可观测'); endR=1;Q=[1,0;0,0];[K,P,E]=Lqr(A,B,Q,R)A_new=A-B*K;G_new=ss(A_new,B,C,D);t=linspace(0,5,100)';y1=step(G_ss,t);y2=step(G_new,t);plot(t,y1,'r:',t,y2,'b-')gridgtext('反馈前')gtext('反馈后')运行结果:a =x1 x2x1 0 1x2 0 0b =u1x1 0x2 1c =x1 x2y1 1 0d =u1y1 0Continuous-time model. 系统完全能控(A,S)可观测K =1.0000 1.4142P =1.4142 1.00001.0000 1.4142E =-0.7071 + 0.7071i-0.7071 - 0.7071i图形:00.51 1.52 2.53 3.54 4.5502468101214。
matlab第四章课后作业解答

matlab第四章课后作业解答第四章习题解答1、求下列多项式的所有根,并进行验算。
(3)267235865x x x x-+-(4)4)32(3-+x 解:>> p=zeros(1,24); >> p(1)=5;p(17)=-6;p(18)=8;p(22)=-5; >> root=roots(p)root =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927>> polyval(p,root)ans =1.0e-012 *-0.07120.0459 - 0.0081i0.0459 + 0.0081i-0.0419 + 0.0444i-0.0419 - 0.0444i0.0509 + 0.0929i0.0509 - 0.0929i-0.2059 + 0.0009i-0.2059 - 0.0009i-0.0340 + 0.0145i-0.0340 - 0.0145i0.1342 + 0.0910i0.1342 - 0.0910i0.0025 + 0.0027i0.0025 - 0.0027i-0.0077 + 0.4643i-0.0077 - 0.4643i-0.3548 - 0.1466i-0.3548 + 0.1466i-0.0251-0.0073(4) >> p1=[2 3];>> p=conv(conv(p1,p1),p1)-[0 0 0 4]; >> root=roots(p)root =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063>> polyval(p,root)ans =1.0e-014 *-0.7105 - 0.6217i-0.7105 + 0.6217i6、求解下列方程组在区域1,0<<βα内的解-=+=.sin 2.0cos 7.0,cos 2.0sin 7.0βαββαα 解:以初值)5.0,5.0(),(00=βα进行求解>> fun=inline('[0.7*sin(x(1))+0.2*cos(x(2))-x(1),0.7*cos(x(1))-0.2*sin(x(2))-x(2)]');>> [x,f,h]=fsolve(fun,[0.5 0.5])Optimization terminated: first-order optimality is less than options.TolFun.x =0.5265 0.5079f =1.0e-007 *-0.1680 -0.2712h =1因而,该方程组的近似根为5079.0,5265.0==βα。
matlab课后习题答案第四章
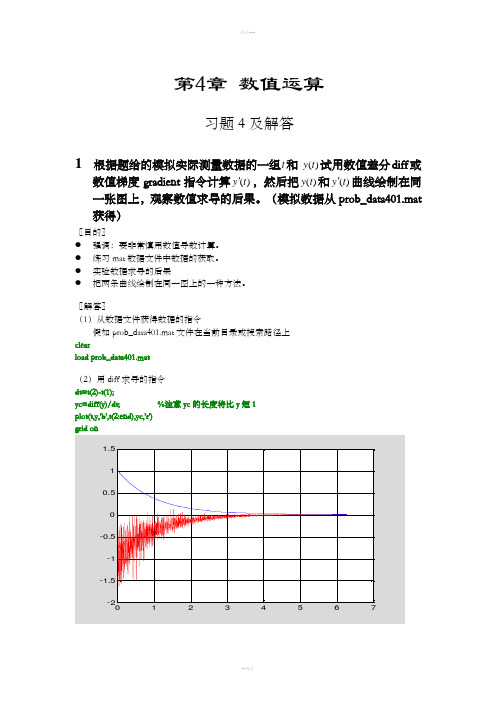
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
智慧树知到《数学建模与系统仿真》章节测试[完整答案]
![智慧树知到《数学建模与系统仿真》章节测试[完整答案]](https://img.taocdn.com/s3/m/4ec0dc8033d4b14e8524689f.png)
智慧树知到《数学建模与系统仿真》章节测试[完整答案]智慧树知到《数学建模与系统仿真》章节测试答案第一章单元测试1、数学模型是对于现实世界的一个特定对象,一个特定目的,根据特有的内在规律,做出一些必要的假设,运用适当的数学工具,得到一个数学结构.A:错B:对答案:【对】2、数学建模是利用数学方法解决实际问题的一种实践.即通过抽象、简化、假设、引进变量等处理过程后,将实际问题用数学方式表达,建立起数学模型,然后运用先进的数学方法及计算机技术进行求解,是对实际问题的完全解答和真实反映,结果真实可靠。
A:对B:错答案:【错】3、数学模型是用数学符号、数学公式、程序、图、表等刻画客观事物的本质属性与内在联系的理想化表述. 数学建模就是建立数学模型的全过程(包括表述、求解、解释、检验).A:对B:错答案:【对】4、数学模型(Mathematical Model):重过程;数学建模(Mathematical Modeling):重结果。
A:错B:对答案:【错】5、人口增长的Logistic模型,人口增长过程是先慢后快。
A:错B:对答案:【错】6、MATLAB的主要功能有A:符号计算B:绘图功能C:与其它程序语言交互的接口D:数值计算答案:【符号计算;绘图功能;与其它程序语言交互的接口;数值计算】7、Mathematica的基本功能有A:语言功能(Programing Language)B:符号运算(Algebric Computation)C:数值运算(Numeric Computation)D:图像处理(Graphics )答案:【语言功能(Programing Language);符号运算(Algebric Computation);数值运算(Numeric Computation);图像处理(Graphics )】8、数值计算是下列哪些软件的一个主要功能 A:MapleB:JavaC:MATLABD:Mathematica答案:【Maple;MATLAB;Mathematica】9、评阅数学建模论文的标准有:A:完全一致的结果B:表述的清晰性C:建模的创造性D:论文假设的合理性答案:【表述的清晰性;建模的创造性;论文假设的合理性】10、关于中国(全国)大学生数学建模竞赛(CUMCM)描述正确的是 A:2年举办一次B:一年举办一次C:开始于70年代初D:一年举办2次答案:【一年举办一次】第二章单元测试1、衡量一个模型的优劣在于它是否使用了高深的数学方法。
MATlab 仿真部分习题答案
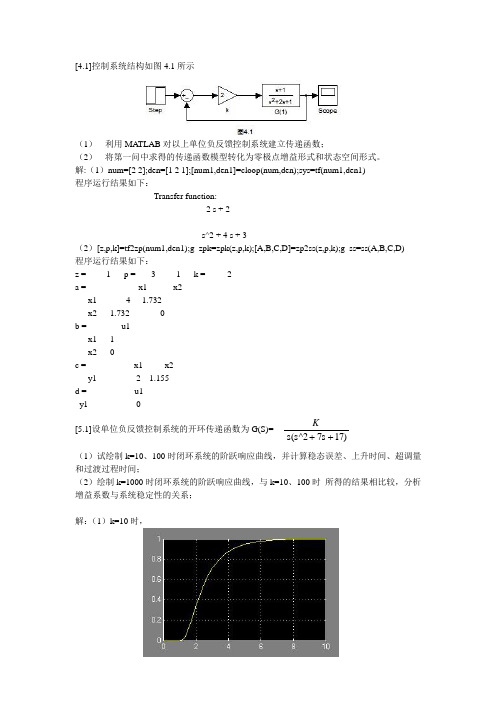
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
MATLAB仿真课后习题

第一章习题3.请指出以下的变量名(函数名、M文件名)中,哪些是合法的?Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解:合法的变量名有:Abc wu_20044.指令窗操作(1)求[12+2×(7-4)]÷32的运算结果解:>> [12+2*(7-4)]/3^2ans =2(2)输入矩阵A=[1,2,3;4,5,6;7,8,9],观察输出。
解:>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9(3)输入以下指令,观察运算结果;clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解:7.指令行编辑(1)依次键入以下字符并运行:y1=2*sin(0.3*pi)/(1+sqrt(5))解:>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键,实现指令回调和编辑,进行新的计算;y2=2*cos(0.3*pi)/(1+sqrt(5))解:>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中(3)的M脚本文件,并运行之。
解:第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。
解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02.要求在[0,2π]上产生50个等距采样数据的一维数组,试用两种不同的指令实现。
matlab第四章课后答案

%Exerc ise 1(1)r oots([1 11])%Exer cise1(2)roots([3 0 -4 0 2 -1])%Exerc ise 1(3)p=zero s(1,24);p([1 17 1822])=[5 -6 8 -5];ro ots(p)%E xerci se 1(4)p1=[2 3];p2=conv(p1,p1);p3=co nv(p1, p2);p3(end)=p3(en d)-4; %原p3最后一个分量-4r oots(p3)%Exer cise2fun=inli ne('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzer o(fun,2)%Exer cise3fun=inli ne('x^4-2^x');fplot(fun,[-2 2]);gr id on;fze ro(fu n,-1),fzer o(fun,1),f minbn d(fun,0.5,1.5)%Exe rcise 4fu n=inl ine('x*sin(1/x)','x');fp lot(f un, [-0.10.1]);x=z eros(1,10);fori=1:10, x(i)=fz ero(f un,(i-0.5)*0.01);end;x=[x,-x]%Ex ercis e 5f un=in line('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fso lve(f un,[0 0 0])%E xerci se 6fun=@(x)[x(1)-0.7*si n(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolv e(fun,[0.5 0.5])%E xerci se 7clear; clo se; t=0:p i/100:2*pi;x1=2+sqr t(5)*cos(t); y1=3-2*x1+sq rt(5)*sin(t);x2=3+s qrt(2)*cos(t);y2=6*sin(t);pl ot(x1,y1,x2,y2); gri d on; %作图发现4个解的大致位置,然后分别求解y1=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsol ve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fso lve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exerc ise 8(1)c lear;fun=inlin e('x.^2.*(x.^2-x-2)');fp lot(f un,[-2 2]);grid on;%作图观察x(1)=-2;x(2)=fminb nd(fu n,-1,-0.5);x(4)=fmi nbnd(fun,1,2);fun2=inlin e('-x.^2.*(x.^2-x-2)');x(3)=f minbn d(fun2,-0.5,0.5);x(5)=2feval(fun,x)%答案: 以上x(2)(4)是局部极小,x(1)(3)(5)是局部极大,从最后一句知道x(1)全局最大, x(4)最小。
MATLAB课后习题集附标准答案

第2章 MATLAB概论1、与其他计算机语言相比较,MATLAB语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MATLAB系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可.矚慫润厲钐瘗睞枥庑赖。
4、MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?聞創沟燴鐺險爱氇谴净。
答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。
5、如何启动M文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.酽锕极額閉镇桧猪訣锥。
6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。
7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.謀荞抟箧飆鐸怼类蒋薔。
Matlab与通信仿真实验报告册答案

Matlab 与通信仿真34.0000 22.0000 62.00001. 在Command Window 里面计算_7 8 914 5 6,计算:C = AxB,D =A + B,A C,C/B ; 12 3>> a=[1 2 3;4 5 6;7 8 9]; >> b=[7 8 9;4 5 6;1 2 3]; >> c=a*b c =18 24 30 5469 84 90114138>> d=a+b d =8 10 12 8 10 12 81012>> e=a\cWarning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.54 佃76e-018.(1) (3 5 8)- 5 10 ;>>(3+5+8)/5*10 ans=32>>sin(3*pi)/sqrt(9/5) ans=2.7384e-161 2 3(3)A= 4 5 6 ,B 78 9JMatlab 与通信仿真-50.0000-23.0000 -100.0000 28.0000 16.000056.0000>> f=c/bWarning: Matrix is singular to working precision.NaN NaN NaNNaN -Inf Inf NaNNaNNaN3 1.2 4(4) A= 7.5 6.6 3.1,求A :A, A ;(求矩阵的行列式)5.4 3.46.1 _>> a=[3 1.2 4;7.5 6.6 3.1;5.4 3.4 6.1]; >> a' ans =2.1555 0.4555 -1.6449 -2.1040-0.2393 1.5013 -0.7354-0.26980.7833>> det(a) ans =13.78803.0000 1.20004.0000>> inv (c )7.5000 6.6000 3.10005.4000 3.40006.1000Matlab 与通信仿真1 2 0 0 0(5) Z =『+2i 站如I 输入复数矩阵;§+6i 7 + 8i>> z=[1+2*i 3+4*i;5+6*i 7+8*i] 1.0000 + 2.0000i 3.0000 + 4.0000i 5.0000 + 6.0000i7.0000 + 8.0000i1 2川23 HI2.建立.m 文件,用for 循环语句生成5>5的矩阵A :* ..■fa ri H *RF弓 6 III>> a=zeros(5); for m=1:5for n=1:5 a(m,n)=m+n-1 end end1 0 0 0 0a = 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0直翻转得到矩阵 B 和C 。
matlab第四章部分课后答案

y=log(abs(b+c/x))
else
disp('input error');
end
a=input('a=');
b=input('b=');
c=input('c=');
x=input('0.5=<x<5.5=');
switchround(x)
case{1}
y=a*x^2+b*x+c
matlab第四章部分课后答案统计学第四章课后答案matlab第四章答案matlab课后习题答案matlab课后实验答案matlab第二版课后答案matlab刘卫国课后答案matlab课后答案matlab教程课后答案matlab张志涌课后答案
第四章
1.
A=input('输入四位整数A');Sign=1;cFra bibliotekse{2,3}
y=a*sin(b)^c+x
case{4,5}
y=log(abs(b+c/x))
otherwise
disp('input error');
end
3.
A=floor(rand(1,20)*89+10)
A =
11 76 49 92 51 47 85 56 28 69 84 11 70 43 84 54 73 48 37 26
A=D*1000+E*100+B*10+C
A=Sign*A;
2.
a=input('a=');
b=input('b=');
MATLAB仿真 课后习题
第一章习题3.请指出以下的变量名(函数名、M文件名)中,哪些是合法的?Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解:合法的变量名有:Abc wu_20044.指令窗操作(1)求[12+2×(7-4)]÷32的运算结果解:>> [12+2*(7-4)]/3^2ans =2(2)输入矩阵A=[1,2,3;4,5,6;7,8,9],观察输出。
解:>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9(3)输入以下指令,观察运算结果;clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解:7.指令行编辑(1)依次键入以下字符并运行:y1=2*sin(0.3*pi)/(1+sqrt(5))解:>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键,实现指令回调和编辑,进行新的计算;y2=2*cos(0.3*pi)/(1+sqrt(5))解:>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中(3)的M脚本文件,并运行之。
解:第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。
解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02.要求在[0,2π]上产生50个等距采样数据的一维数组,试用两种不同的指令实现。
MATLABSimulink系统仿真_习题答案

MATLABSimulink系统仿真_习题答案第12章 MATLAB Simulink系统仿真习题12⼀、选择题1.启动Simulink后,屏幕上出现的窗⼝是()。
AA.Simulink起始页B.Simulink Library Browser窗⼝C.Simulink Block Browser窗⼝D.Simulink模型编辑窗⼝2.模块的操作是在()窗⼝中进⾏的。
DA.Library Browser B.Model BrowserC.Block Editer D.模型编辑3.Integrator模块包含在()模块库中。
BA.Sources B.Continuous C.Sinks D.Math Operations 4.要在模型编辑窗⼝中复制模块,不正确的⽅法是()。
B A.单击要复制的模块,按住⿏标左键并同时按下Ctrl键,移动⿏标到适当位置放开⿏标B.单击要复制的模块,按住⿏标左键并同时按下Shift键,移动⿏标到适当位置放开⿏标C.在模型编辑窗⼝选择Edit→Copy命令和Edit→Paste命令D.右键单击要复制的模块,从快捷菜单中选择Copy命令和Paste命令5.已知仿真模型如图12-41(a)所⽰,⽰波器的输出结果如图12-41(b)所⽰。
(a)仿真模型(b )⽰波器输出结果图12-41 习题仿真模型及仿真结果则XY Graph 图形记录仪的输出结果是()。
CA .正弦曲线B .余弦曲线C .单位圆D .椭圆⼆、填空题1.Simulink (能/不能)脱离MATLAB 环境运⾏。
2.建⽴Simulink 仿真模型是在窗⼝进⾏的。
模型编辑窗⼝3.Simulink 仿真模型通常包括、系统模块和三种元素。
信号源(Source ),信宿(Sink )4.由控制信号控制执⾏的⼦系统称为,它分为、和。
条件执⾏⼦系统,使能⼦系统,触发⼦系统,使能加触发⼦系统。
5.为⼦系统定制参数设置对话框和图标,使⼦系统本⾝有⼀个独⽴的操作界⾯,这种操作称为⼦系统的。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^22-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
