材料热力学课件-期中考试题
材料热力学》试题

2. 已知纯钛α/β平衡相变温度为882℃,相变焓为
14.65kJ.mol-1,试求将βTi过冷到800℃时,β→α的相变 驱动力。
3.试用正规溶体模型计算一个IAB=16.7kJ.mol-1成分为XB
=0.4的二元固溶体,其发生Spinodal分解的上限温度
是多少?
4.试根据AI-Mg二元相图中Mg17Al12在Mg基固溶体(β)中的
《材料热力学》试题
2007级
一、计算题
1.已知液体锌的Cp(l)为
Cp(l)=29.66+4.81×10-3T J/mol.K 固体密排六方锌的Cp(l)为 Cp(l)=22.13+11.05×10-3T J/mol.K 锌的熔点692.6K,熔化热ΔH=6589.9J/mol,求固、 液相之间随温度变化自由能差值ΔG(T)。
(模型的建立、主要结论、适用对象)
3. 试画出如下共晶相图T2、T3、T5温度 下各相的自由能-成分曲线。
4. 试用摩尔自由能-成分图说明,为什么碳 素钢在淬火之后回火时,渗碳体的粒子越 细,其周围的铁素体中的含碳量越高?
三. 问答题
结合自己的研究课题,试述热力学
在材料中的应用。
谈谈本课程的学习体会以及对本课程
溶解度曲线数据(见下表),求Mg17Al12的生成自由能。 温度/℃ 400 11 350 8.2 300 6.1 250 4.3 200 2.9 150 1.7
溶解度(Al)/at.%
二、简答题
1. 用正规溶体近似解释二元合金固溶体的illiams近似和双亚点阵模型。
的建议。
材料热力学习题集

材料热力学习题集液态铅在1个大气压下的热容量Cp(l)称为Cp(L)= 32.43-3.10×10-3TJ/(mol·k),固态铅的热容量Cp(s)为Cp(S)= 23.56+9.75×10-3TJ/(mol·k)。
众所周知,当液态铅的熔点(600 K)固化成固体时,液态铅释放4811.60 J/mol的热量,并计算了当液态铅过冷到590K并固化成固体时的焓变化。
液态铅固态铅600Kb恒温相变c温升590Ka初始状态相变d最终状态?H示意图实施例1-2众所周知,锡在505K(熔点)时的熔化热为7070.96焦耳/摩尔,厘泊(L) = 34.69-9.20×10-3TJ/(摩尔·K)厘泊(S) = 18.49+26.36×10-3TJ/(摩尔·K)用于计算锡过冷至495 K时自动凝固的比例505K恒温,放热b相变c最终状态吸收热上升温度吸收热相变放热495Ka初始状态1摩尔液体d x摩尔固体(1-x)摩尔液体?H图例1-3铅的熔点为600K,凝固热为4811.6 J/mol,计算了铅在600K 凝固时的熵值变化(在一个大气压下)。
例1-4已知在1个大气压下液态铅的比热为32.43-3.10×10-3tj/(mol·k)CP(s)= 23.56+9.75×10-3tj/(mol·k)液态铅在其熔点(600K)固化成固体时释放4811.6 J/mol的热量。
计算了液态铅过冷到590K凝固时(在一个大气压下)熵值的变化。
1液态铅固态铅恒温相变600Kbc冷却温升590Ka初始相变d最终状态计算?S示意图实施例2-1已知液态锌的Cp(l)为Cp(L)= 29.66+4.81×10-3TJ/(mol·k),固态锌的Cp(s)为Cp(S)= 22.13+11.05×10-3TJ/(mol·k),锌的熔点为692.6K,熔化热δH = 6589.8J/mol,自由能差δG(δ的实施例2-2使用第一章中的数据计算铅在590 K(过冷10 K)凝固时的自由能变化δg(590 K),并将其与简单近似计算的结果(铅在590K 凝固时δH =-4811.6J/mol)进行比较可以从第一章的计算中看出:当铅在590K凝固时,焓变化δH =-4722.56J/mol;熵变化δs =-8.0j/(Mol·k)例2-3已知γ-铁、δ-铁和液态铁的Cp为Cp(γ)= 7.70+19.50×10-3 TJ/Mol·kcp(d)= 43.93j/Mol·k(1674 ~ 1809k)Cp(L)= 41.84j/Mol·k(L)G亚稳态?相的理论熔点?第一阶段?1673年?L1809G?g?GLT/K?阶段225y = 246.65t-34.138 tlnt+9.75?10t 20-32y/100015y = 14861.57t = 1793.82k 105005001000t,k 1500200025003000| 286K时199例4-1,α-Sn β-Sn的δh = 2092j/mol,锡的= 118.7,πα-Sn = 5.75g/mL,ψ计算100个大气压下相变温度的变化值例4-2在95.5℃单斜硫菱形硫中,δV = 0.01395毫升/克,δH = 13.05焦耳/克,找出压力对相变温度的影响例4-3固体锌的蒸气压与温度的关系为:lgp(ATM)=-6850/T-0.755 gt+8.36液态锌的蒸气压与温度的关系为:lgp(ATM)=-6620/T-1.255 LGT+9.46q:1)液态锌在1个大气压下的沸点;2)三点温度;3)1 ATM沸点下的汽化热;4)三相点的熔化热;5)固体锌和液体锌之间的δCp 例4-4锌在610 K时的蒸气压为10 mmHg,镉的计算蒸气压也为10-5 mmHg杜林定律:当相似物质具有相同的蒸汽压时,T1/T2 =常数例4-5碳在1个大气压和25℃下以石墨为稳定相,并试图找出在25℃下将石墨转化为金刚石所需的压力实施例5-1实验测得的镉-镁的摩尔体积如下表所示Cd-镁合金-5实施例5-2已知三元溶液的摩尔体积为VM = 7x1+10 x2+12x 3-2x1x2+3x1x2x 3(cm3/mol)339解决方案:虚拟机∠X1 = x2 = x3 = 1/3 =869 X1 = 1-X2-X3,因为X1+X2+X3 = 1经过取代,我们可以得到:实施例5-3在1075℃下实验测得的氧在银中的溶解度如下表所示,我们可以找出:1)氧在银中的溶解度是否符合西沃特定律,我们可以找出溶解度常数;2)1075℃时空气中氧在银中的溶解度实施例5-4将0.567 g尿素(CON2H4)溶解在500 g水中,测量该水溶液的冰点为-0.0351℃,并计算尿素的分子量。
材料热力学练习题

1、由5个粒子所组成的体系,其能级分别为0、ε、2ε及3ε,体系的总能量为3ε。
试分析5个粒子可能出现的分布方式;求出各种分布方式的微观状态数及总微观状态数。
2、有6个可别粒子,分布在4个不同的能级上(ε、2ε、3ε及4ε),总能量为10ε,各能级的简并度分别为2、2、2、1,计算各类分布的Ωj 及Ω总。
3、振动频率为ν的双原子分子的简谐振动服从量子化的能级规律。
有N 个分子组成玻耳兹曼分布的体系。
求在温度T 时,最低能级上分子数的计算式。
4、气体N 2的转动惯量I =1.394⨯10-46kg ⋅m 2,计算300K 时的Z J 。
5、已知NO 分子的Θυ=2696K ,试求300K 时的Z υ。
~J υ7、计算300K 时,1molHI 振动时对内能和熵的贡献。
8、在298K 及101.3kPa 条件下,1molN 2的Z t 等于多少?9、在300K 时,计算CO 按转动能级的分布,并画出分子在转动能级间的分布曲线。
10、计算H 2及CO 在1000K 时按振动能级的分布,并画出分子在振动能间的分布曲线;再求出分子占基态振动能级的几率。
11、已知HCl 在基态时的平均核间距为1.264⨯10-10m ,振动波数ν~=2990m -1。
计算298K 时的Θm S 。
12、证明1mol 理想气体在101.3kPa 压力下Z t =bLM 3/2(T /K )5/2 (b 为常数)13、计算1molO 2在25︒C 及101.3kPa 条件下的Θm G 、Θm S 及Θm H 。
设Θ0U 等于零。
14、已知300K 时金刚石的定容摩尔热容C V ,m =5.65J ⋅mol -1⋅K -1,求ΘE 及ν。
15.已知300K 时硼的定容摩尔热容C V ,m =10.46J ⋅mol -1⋅K -1,求(1) ΘD ;(2) 温度分别为30K 、50K 、100K 、700K 、1000K 时的C V ,m 值;(3) 作C V ,m 值− T 图形。
材料热力学 ppt课件

ppt课件
6
4.1 新相的形成和相变驱动力 4.2 马氏体相变热力学 4.3 珠光体转变(共析分解)热力学 4.4 脱溶分解热力学 4.5 调幅(Spinodal)分解热力学
ppt课件
7
4.1 新相的形成和相变驱动力
4.1.1 新相的形成
材料发生相变时,在形成新相前往往出现浓度起伏, 形成核胚再成为核心、长大。无论核胚是稳定相还是 亚稳相,只要符合热力学条件都可能成核长大。因此, 相变中可能出现一系列亚稳定的新相。
材料热力学
第四章 相变热力学 / 第五章 界面热力学
ppt课件
1
参考书目
徐祖耀 主编,材料热力学,高等教育出版社, 2009.
赵乃勤 主编,合金固态相变,中南大学出版社, 2008.
江伯鸿 编著,材料热力学,上海交通大学出版社, 1999.
徐瑞等 主编,材料热力学与动力学,哈尔滨工业 大学出版社,2003.
基本内容:
计算相变驱动力,以相变驱动力大小决定相 变的倾向,帮助判定相变机制,在能够估算临 界相变驱动力的条件下,可求得相变的临界温 度。相变驱动力与相变阻力的平衡。
ppt课件
5
相变的分类:
1. 按热力学分类:一级相变、二级相变…… 2. 按原子迁移特征分类(固态相变):扩散型
相变、无扩散型相变。 3. 按相变方式分类:形核-长大型相变(不连续
匀形核,因此所需的过冷度也小。
ppt课件
第四章 相变热力15 学
4.2 马氏体相变热力学
4.2.1 马氏体相变
高碳钢经淬火发生了马氏体相变,获得马氏体显 微组织,具有很高的硬度,但塑性较差。
马氏体相变是钢件热处理强化的主要手段,要求 高强度的钢都是通过淬火来实现。
大学材料科学专业《大学物理(下册)》期中考试试卷 附答案

大学材料科学专业《大学物理(下册)》期中考试试卷附答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、一束光线入射到单轴晶体后,成为两束光线,沿着不同方向折射.这样的现象称为双折射现象.其中一束折射光称为寻常光,它______________定律;另一束光线称为非常光,它___________定律。
2、一质量为0.2kg的弹簧振子, 周期为2s,此振动系统的劲度系数k为_______ N/m。
3、二质点的质量分别为、. 当它们之间的距离由a缩短到b时,万有引力所做的功为____________。
4、两根相互平行的“无限长”均匀带正电直线1、2,相距为d,其电荷线密度分别为和如图所示,则场强等于零的点与直线1的距离a为_____________ 。
5、四根辐条的金属轮子在均匀磁场中转动,转轴与平行,轮子和辐条都是导体,辐条长为R,轮子转速为n,则轮子中心O与轮边缘b之间的感应电动势为______________,电势最高点是在______________处。
6、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
7、两个相同的刚性容器,一个盛有氧气,一个盛氦气(均视为刚性分子理想气体)。
开始他们的压强和温度都相同,现将3J的热量传给氦气,使之升高一定的温度。
若使氧气也升高同样的温度,则应向氧气传递的热量为_________J。
8、一电子以0.99 c的速率运动(电子静止质量为9.11×10-31kg,则电子的总能量是__________J,电子的经典力学的动能与相对论动能之比是_____________。
材料热力学习题

材料热力学习题
1熟悉的条件、表达式及意义()。
2. 熟悉配分函数的条件、表达式及意义()。
3.三大分布是什么?,表达式?
4、热力学函数的微分表达式;热力学意义定律,第二定律;
5、固溶体中配置熵的计算;高分子模型中配置熵的计算;
6、分析铁基马氏体与有色金属中马氏体相变时的动力与阻力。
7、交互作用参数意义,各参数变化对其影响;
8、正规熔体及热函数表达式
9、在定压热容C p的经验表达式中,,试导出这时的焓(H)、熵(S)和Gibbs自由能(G)的表达式。
10、利用讨论偏析引起的自由能的变化。
《材料的热学》课件

解释能量转换与热能利用的科学原理。
热力学第二定律
1 热力学第二定律的表
述
在孤立系统中,不断增 加,不可逆过程不能自发 发生。
2 卡诺循环
理想的热机循环,能实现 最高效率的理论。
3 热力学第二定律的应
用
解释自然界中各种能量转 化的局限性。
热力学第三定律
1 熵的概念
研究系统无序程度的物理量。
的方向密切相关。
热力学循环
1 标准热力学循环
由一系列变化组成的最基本的热力学过程。
2 常见的热力学循环
卡诺循环、斯特林循环、奥托循环、布雷顿循环等。
结束语
1 热力学的理论与应用
为科学探索和工程实践提供了重要的基础。
2 热力学的未来发展
与材料科学、能源领域等关联紧密,将有更广阔的应用前景。
热量
能量的传递形式,使物体温度发生变化。
热力学功
系统与外界交换的能量。
热平衡与热传递
1 热平衡的条件
物体间热量的传递达到稳 定状态,没有净热量的交 换。
2 热平衡的稳定性
系统达到热平衡后,微小 扰动不会导致系统温度变 化。
3 热传递的方式
热传导、热对流、热辐射。
热力学第一定律
1 定与表述
能量守恒定律,能量既不能创造也不能消失,只能从一种形式转化为另一种形式。
《材料的热学》PPT课件
欢迎来到《材料的热学》PPT课件。本课程将为您介绍热力学的基本概念、定 律和参数,以及热平衡、热传递、热力学循环等内容,让您深入了解材料的 热学。
概述
• 热力学的基本概念 • 热力学的三大定律
热力学基本参数
温度
衡量物体热运动强度的物理量。
《热力学与统计物理学》期中考试答案

《热力学与统计物理学》期中考试答案1. 热力学第零定律:两物体同时与第三个物体热平衡时,这两个物体彼此之间也热平衡。
热力学第一定律:在一个热力学过程中,系统吸收的热量等于系统内能的增加和系统对外所做的功。
热力学第二定律:不可能从单一热源取热使之完全转化为功而不引起其它变化(不可能把热量从低温物体传到高温物体而不引起其它变化)。
热力学第三定律:不可能用有限的手续使系统温度达到绝对零度。
2. 卡诺循环包括以下四个准静态过程:(1)等温膨胀(2)绝热膨胀(3)等温压缩(4)绝热压缩 卡诺热机的效率 121T T −=η pV 图和TS 图分别见《热力学》教材第68页和第100页。
3. 设状态方程为),(T v p p =,那么)(()(2223)va b v RT d dv b v RT va dTb v R dv v p dT T p dp T v−−=⎥⎦⎤⎢⎣⎡−−+−=⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂=运用循环微分公式积分得 RT b v va p =−+)(2 利用级数展开公式,可得⎥⎦⎤⎢⎣⎡+++−+=−⎟⎟⎠⎞⎜⎜⎝⎛++++=L L 332233221)(11v b v b v RT a b RT v a v b v b v b RT pv 第二,第三,第四维里系数分别为: 32,,b D b C RTa b B ==−=4. 热力学第一定律: pdVdT C Q d V += 所以 ,又pdV dT C CdT V +=RT n pV ′=所以 RdT n VdP pdV ′=+,即R n Vdp pdV dT ′+=/)( 所以 pdV C C pdV C C R n Vdp C C p V V )()()(−=+−′=− 令 CC C C n V p −−=,则 0=+V dV n p dp ,所以 const pV n =对于,有const V p =2const pV =21,即21=n 而 R c c c n n c V V V 2)12(1+=−=−−=γγ5. (1)设想一可逆过程,水的熵变 K J T dT mc S /130537327311==Δ∫ (2)热源的熵变 K J TQ S /112137310018.410002−=××−=−=Δ 整个系统的熵变 K J S S S /18421=Δ+Δ=Δ(3)在0 ºC 与100 ºC 之间取彼此温差为无限小的无限多个热源,让水依次与这些温度递增的无限多个热源相接触,由0 ºC 吸热升温至100 ºC。
材料热力学11年试题

问答题1、简述热力学第一定律、热力学第二定律、热力学第三定律的内容及应用。
2、简述熵判据、亥姆赫兹函数判据和吉布斯函数判据的内容及使用条件3、请说明为什么纯金属(纯铁材料除外)加热的固态相变是由密排结构到疏排结构的变/link?url=TB3ynKTakLolx53PSt3lqIRlj9i0a7uxwlSvLchHRQzuXIqwFkc-ZsPauEoTMKUnLgq1B_IkWu-KihBIe8zx2YpCnkxGhYX9TYHlyKCPuSy室温下为铁磁性金属在超过居里温度将变为顺磁性,自发磁化消失物质由铁磁态变化到顺磁态的过程伴随着自由能的变化4、请说明为什么固相与气相或液相之间平衡时,相平衡温度T 与压力P 之间的关系是指数关系;而固相与液相之间平衡时,相平衡温度T 与压力P 之间的关系是直线关系5、对于一个二元体系A-B ,试简述相互作用能I AB 的意义,以及I AB 值对A-B 二元正规溶体体系吉布斯自由能-组分关系图形状以及A 、B 在溶体中微观存在状态的影响?T=0时i=0.自由能曲线倾斜的直线,0>i 自由能曲线向下的曲线i >0,自由能曲线向上的曲线T >0时i ≦0,向下凹曲线。
在绝大多数情况下,Gm-X 曲线都是单调向下弯曲的形状。
在i >0,T 不太高时,向上凸的曲线且两个拐点6、试简述多元体系中化学位和活度的意义,并说明为什么在一些固溶体中会发生上坡扩散的原因?7、试简述两相平衡条件的热力学条件、意义,对于两种或者两种以上物相存在的二元体系吉布斯自由能-组分关系图中如何确定相平衡条件啊和范围,以及上述方法的日力学原理;8、物相尺度影响其在溶体中的溶解度,晶体材料中出现晶界偏析的原因和热力学原理 P m GG G -=∆9简述固体热容的杜隆-普替定律,爱因斯坦,德拜模型中材料的热容随温度的变化规律,以及比较各自的优缺点杜隆-普替定律:温度较高Cv=3R 定值。
材料热力学习题及答案
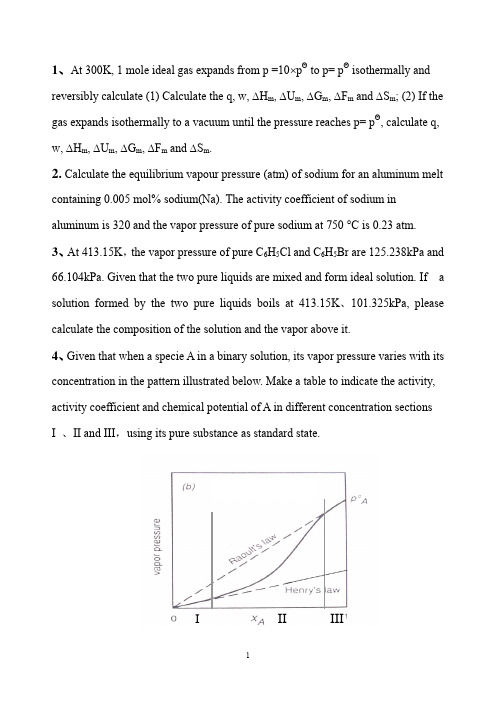
1、At 300K, 1 mole ideal gas expands from p =10⨯pΘ to p= pΘ isothermally and reversibly calculate (1) Calculate the q, w, ∆H m, ∆U m, ∆G m, ∆F m and ∆S m; (2) If the gas expands isothermally to a vacuum until the pressure reaches p= pΘ, calculate q, w, ∆H m, ∆U m, ∆G m, ∆F m and ∆S m.2. Calculate the equilibrium vapour pressure (atm) of sodium for an aluminum melt containing 0.005 mol% sodium(Na). The activity coefficient of sodium in aluminum is 320 and the vapor pressure of pure sodium at 750 °C is 0.23 atm.3、At 413.15K,the vapor pressure of pure C6H5Cl and C6H5Br are 125.238kPa and 66.104kPa. Given that the two pure liquids are mixed and form ideal solution. If a solution formed by the two pure liquids boils at 413.15K、101.325kPa, please calculate the composition of the solution and the vapor above it.4、Given that when a specie A in a binary solution, its vapor pressure varies with its concentration in the pattern illustrated below. Make a table to indicate the activity, activity coefficient and chemical potential of A in different concentration sectionsI 、II and III,using its pure substance as standard state.III III5、At 300K, the vapor pressure of liquid A and liquid B are 37.33kPa and 22.66kPa.When 2 moles of A and 2 moles of B are mixed to form a solution, the vapor pressure above the solution is 50.66kPa, and the molar fraction of A in the vapor is 0.60. Given that vapors can be taken as ideal gases. ①Calculate a A( R )and a B( R) in the solution, ②γA and γB , ③∆mix G , ④ If the solution is an ideal solution, what is the value of ∆mix G id ? ⑤ What is the value of ∆mix G ex of this solution?6、The variation, with composition, of G E for Fe-Mn alloys at 1863K is listedbelow:X Mn 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 G m E ,Joules 395703 925 1054 1100 1054925 703 395a 、Is the process to form Fe-Mn alloy at 1863K an exothermic one or an endothermic one ?b. Does the system exhibit regular solution behavior?c. Calculate E Feμ and EMn μ at X Mn = 0.6; d. Calculate m mix G ∆ atX Mn = 0.4; e. Calculate the partial pressures of Mn and Fe exerted by the alloy of X Mn = 0.27、Melts in the system Pb-Sn exhibit regular solution behavior. At 473︒C, a Pb =0.055 in a liquid solution of X Pb = 0.1. Calculate the value of PbSn ωfor the system and calculate the activity of Sn in the liquid solution of X Sn = 0.5 at 500︒C.8、With respect to the Ellingham diagram, answer the following questions:93.23ln 27.145390)(ln *+--=T Tatm pFe68.37ln 02.333440)(ln *+--=T Tatm p Mna) Explain the slope changes for the reaction 2Mg + O 2 = 2MgO; b) You want to heat up and a piece of silicon metal to 1600︒C, decide on a suitable crucible material;c) What is the value of ∆H Θ of formation of TiO 2 ? d) Find ∆G Θfor the reaction Fe + 0.5O 2 =FeO at 1200 ︒C;e) Find ∆G Θ for the reaction 3Mg + AlO 3 = 3MgO + 2A1 at 1500 ︒C; f) What is the equilibrium oxygen pressure when metallic titanium is in equilibrium with TiO 2 at 1000 ︒C?g) If you want to reduce pure TiO 2 to pure metallic titanium at 1000︒C using a CO/CO 2 gas mixture, what is the minimum CO/CO 2 ratio that can achieve such a reduction.9、Answer the following questions according to Ellingham diagram:① At what temperature(s) C can reduce SnO 2(s)、Cr 2O 3(s) and SiO 2(s) ? ② At what temperature, the decomposition pressure of CuO reaches 1.01325⨯105 Pa ?③ The temperature(s) at which Fe 3O 4 can be reduced to FeO by H 2 ? ④ ∆G Θ when Mg reduces Al 2O 3 at 1000︒C,⑤ At what temperature, for the reaction )(322)(3234S S O Cr O Cr =+,Pa 1019'2-(平)is p O ⑥ Calculate the ∆G when Fe reacts with O 2 at 10-5Pa and 10-10Pa respectivelyat1000︒C, and '(2平)O p as well. ⑦ Calculate the equilibrium constant of reaction 2)()(CO Mn CO MnO s s +=+ at1100︒C (CO CO p p K /2=)⑧ At what temperature, for reaction )(2)(2)(g s s O H Mn H MnO +=+, the(平))/(22O H H is 104/1 ? 10、The standard Gibbs free energy change for reaction I:Ni (s ) + 1/2 O2 == NiO (s )is -244560 + 98.53TlnT J/ mol , question: a) How much is the standard Gibbs free energy change for reaction II : 2Ni (s ) + O2 == 2 NiO (s )b) Calculate the equilibrium constants for reaction I and reaction II respectively at 1000︒ C.c) At 1000︒ C, when oxygen pressure is maintained at 10-4 atm, how much is theGibbs free energy change for reaction I ? Can reaction I proceed forward ? Is Ni stable under this condition ? Is NiO stable under this condition ? d) At 1000︒ C, how much should be the oxygen pressure if we want the Gibbs free energy change for reaction I to be 0, and how much should be the oxygen pressure if we want a Ni-NiO-O 2 system to be at equilibrium ?e) At 1000 C, what is the condition to prevent Ni from being oxidized ? and whatis the condition to reduce NiO ?11、Liquid FeO is reduced to metallic iron at 1600 °C with CO(gas) accordingto the following reaction:FeO(liquid) + CO(g) = Fe(liquid) + CO 2a) Calculate ∆G Θ at 1600 °C for this reactionb) Detennine the minimum CO/C02 ratio required to reduce pure liquid FeO topure metallic iron at 1600 °C.c) Determine the minimum CO/CO2 ratio required to reduce FeO dissolved in a liquid slag to metallic iron at 1600 °C. The metallic iron formed has a purity of 96 mole % iron. The activity of FeO in the liquid slag is 0.3.CO(g) at 1600 °C: ∆GΘ= -274.9 kJ/molCO2(g) at 1600 °C: ∆GΘ = -396.3 kJ/molFeO at 1600 °C: ∆GΘ = -144.6 kJ/molR= 8.314 J/ mol.K= 1.987 ca1/mol.K12、In an experiment, it was found that the Ar was not pure enough. So a setup was devised in an attempt to purify the Ar, as illustrated below. Ar which was at 2 atm was let to flow through a glass tube and the Cu powder pile in it. Given that the temperature in the glass tube is 600︒C and gas pressure is constant at 2 atm.. Calculate the purity of the outgoing Ar in percentage.Ellingham Diagram习题参考答案3.2 ΔG = -108.9 J/mol; ΔS = -21.42 J/(mol.K)3.6 (a ) 22.09/(.)S J mol K ∆=;(b) At 0︒C, ∆G =0; (c) ∆H = 5841.9 J;(d) ∆S =21.39J /(mol.K),∆G = 109.38 J/mol4.1 (a ) 2898.28J/mol; ( b ) No; ( c ) 345 J/mol; ( d ) 14939 atm; ( e ) 4921 J/mol 4.2 ( a ) 272.8K; ( b ) Pa P 610345⨯≈∆ ; ( c ) 249.46K 4.3 1202K4.4 P=5.73⨯10-6 atm 4.5 0.16P4.7 08.10430685ln +-=TP 4.8 ( a ) 1180K; ( b ) 695.3K; ( c ) 114.4kJ/mol; ( d ) 7123 J/mol; ( e ) 4.2J/mol 4.9 In the initial state: 4.06 mol %; in the final state: 5.3 mol% 4.10 ( a )348 kJ; ( b ) 2.3×10-3Pa ;( c ) “ solution not possible”; (d ) “solution not possible”5.1 atm p H 0005.0=5.2、atm p o 1221007.1-⨯= If the error in enthalpy is 500cal, the uncertainty in the pressure calculated is 28.6%, and if the error in enthalpy is -500cal, the uncertainty is -22.1%5.3、(a) T =462K; (b) T = 420K5.4 (a) atm P O 2621014.1-⨯=, (b) P O2 =2.28⨯10-10 atm., (c) The equilibrium oxygen pressureremains the same when the total pressure increases, which means a higher purity level of N 2 .5.5 (a) 略; (b) Pa atm P H 8.181013056.1800019.0)('2=⨯==; (c) 21.5L Ar is needed to bebubbled into the melt.5.6(a )l n K a1/T, 10-31/K=∆-=∆ooG kJ H 1000;50- 66.6kJ(b) Ja = 3 < Ka, the reaction will proceed from left to right, and the atmosphere willnot oxidize Ni.5.7 略5.8. (a) P SiO = 8.1⨯10-8 (atm) (b) ∆H o = 639500J; ∆So =334.9J/K (c ) PO2 =10-30 atm5.9 5.10.J H o72250=∆,the reaction is an endothermic one. )(106.08)(atm P g u -⨯=5.11. (a),166528J H o =∆ the reaction is an endothermic one.; (b) At 1168K, the equilibrium pressure of CO2 equals one atmosphere. 5.12 (a) 略 , (b) Mg CO P P =; (c) T = 2037 K 5.13 (a) 略; (b) 13109.2⨯=K ; (c) ppm 186.0 5.14 (a) 略; (b) kJ H 52.267=∆; (c) K T 1592= 5.15 (a) )(106.13atm -⨯≈; (b) )(1028.210)(2atm P g O H -⨯=5.16 (a) 97.9=K ; (b) atm x 14.4=; (c) if the temperature is increased, the fraction of water reacted will increase since the equilibria constant increases with increasing temperature.6.2 (a )1.287V;(b) When the water impure, the voltage will go higher; (c) 1.219V 6.4 (a) 145.3kJ;(b) The maximum work that could be derived is 702.36kJ;(c) In this case, the maximum work that could be derived is 696.56kJ. 6.5 (a) -6252J/mol; (b) 370.0)(=II Cd a ; (c) )(42.3mmHg P Cd =; 6.6 7.87⨯10-4 V 6.7 (a))(22g Cl Mg MgCl +=(b) Pa P Cl21'1086.82-⨯=; (c) 2.485V6.8 (a) Pa P O 11'2105.5-⨯=;(b) Anode:e NiNi 2+→Cathode:-→+2222/1O e O ; (c) 0.757V; (d) 0.261V6.10 (a) )(509.3V E o=;(b) 0.074kJ;(c) 4.1⨯106J;(d) Yes. In this case, the open circuit voltage is 3.648V;(e) In this case, to keep the temperature constant, 3.92⨯106J heat should beremoved from the battery per hour.6.11(a) TG CO Al C O Al o 26.3211008.12/322/36232-⨯=+=+Δ(b) The minimum voltage at which the electrolysis may be carried out at1250K is 1.172V .7.1 0.117 atm 7.5 ( a ) ,82.5 2.5 2.5B A B A B B T PV V V x x x x x ⎛⎫∂=+=--⎪∂⎝⎭ ,102.5 2.5 2.5A B A A B A T PV V V x x x x x ⎛⎫∂=+=-- ⎪∂⎝⎭( b) B A M x x V 5.2=7.7 2)1(736.0ln Sn Sn x --=γ7.8 The maximum solubility of MgF2 in liquid MgCl at 900 C is 19 mol% .7.9 ( a ) 1121K; ( b ) 1. 8 cal/K9.6Temperature(ºC ) Phase Composition Fraction1300 Liquid 0.59 0.64 α 0.06 0.36 β ---- 01000+Liquid 0.8 0.43 α 0.1 0.57 β ---- 01000-Liquid ---- 0α 0.1 0.65 β 0.95 0.359.8 Solution:(a) 90 mol%B is the composition of the first solid to form;10 mol % is the composition of the last liquid drop.(b) solid (60 mol%B is the composition) is about 77% ; liquid (15 mol%B is the composition) is 23%9.9 (a) 2900℃, α(12%) (b) 2300℃, liq(95%) (c) 8.2%α(composition is24% )+91.8%β(85%)习题参考答案1.ΔS m =19.1J/mol.K, ΔG m = -5740 J/mol, ΔF m = -5740 J/molIsothermally expands to a vacuum: w = 0, ΔH m =0 , ΔU m = 0,ΔS m =19.1J/mol.K, ΔG m = -5740 J/mol, ΔF m = -5740 J/mol2. 3.68 × 10-3 atm3、Pa x x Br H C Cl H C 406.0;594.05556==Pa p Pa p Br H C Cl H C 26838;744445556==4.5、JG J G J G a a ex mix id mix mix B A R B R A 5302)5(;6912)4(;1610)3(;788.1;62.1)2(;894.0;81.0)1()()(=∆-=∆-=∆====γγ 6. a endothermic one; b. Yes; c J J EMn E Fe 704;1584==μμd ;/9363mol J G m mix -=∆e Pa p Pa p Fe Mn 4;1198==7. J SnPb 4578-=ω; 418.0=Sn aPure Substance as Stand ard Statepq(b )I 、II 、IIIAAA AAA A AAAA x R T T p x k R T T p p R T T T 0'ln )(ln)(ln )()(γμμμμ+=+=+=*****III:I:II:AA AAAA a RT T p p RT T T ln )(ln )()('+=+=***μμμAA AA AA x RT T p p RT T T ln )(ln)()(*'*+=+=*μμμk A8. a) Mg boils and which makes o S ∆more negative, so the slope changes for larger; b) Firstly, we should avoid using metallic material for this purpose since the melting points of metals are mostly too low. Ceramic materials, usually composed of oxides and having high melting points can be chosen The material should not be reduced by pure silicon at 1600ºC. By examing Ellingham diagram, crucibles (坩埚) made of Al 2O 3 .c ) -890kJ /molO2;d ) -170kJ /molFeO; e) -30kJ; f) Pa 2110-; g)721063.0/⨯=pco p CO 9、⑨ 650ºC ,1220 ºC and 1520 ºC ; ⑩ 1480 ºC ;⑪ When the temperature is equal to or higher that 710 ºC ; ⑫ 2/100molO kJ G o -=∆ ⑬ 900 ºC; ⑭0,102/112,1010'25'2=∆=-=∆=--G Pa P molO kJ G Pa P O O , Pa p e O 10')(210-= ⑮ 510-=K ;⑯ 1220ºC10、a) -489120+197.06TlnT J/mol;b) 2.89×10-54 ; c) J G 749429=∆; Ni is stable under this condition, and NiO is not stable; d) Pa p e o 58')(21046.3⨯= e) from the calculation, we found that at 1000ºC,Pa p e o 58')(21046.3⨯=.So at 1000ºC, when theoxygen pressure is less than 3.46×1058Pa, Ni is stable and can not be oxidized, and NiO will be reduced to Ni under this condition.11. a) mol kJ G o /2.23=∆; b)43.42=⎪⎭⎫ ⎝⎛eCO COp p. This is the minimumCO/CO2 ratio required to reduce pure FeO to Fe at 1600ºC. c)2.142=⎪⎭⎫ ⎝⎛eCO CO p p . This is the minimum CO/CO2 ratio required to reduce FeO in a slag( 炉渣) to Fe in a metallic iron melt under the given conditions at 1600ºC.12.%100)1015.3%10⨯⨯-=(Ar。
SYU材料热力学复习题

材料热力学复习题一、填空:1、系统的平衡态是在(系统不受外界作用)的条件下,系统的(宏观物理性质)不随时间变化的状态。
2、逆卡诺循环是由两个(等温)过程、两个(等熵)过程所组成的。
3、G-T关系曲线反映了在(定压)条件下,G函数与温度T之间的关系。
4、dG=dU+PdV- TdS 成立的条件是(等温)。
5、亨利定律和拉乌尔定律分别从(溶质)和(溶剂)的角度描述了溶液的蒸气压。
6、液相或固相与其气相形成(相平衡)时的压强称为饱和蒸汽压。
7、表面能是指(产生单位表面面积所做的可逆功)。
8、两个组元的体系最多可以存在( 4 )相平衡。
9、二元系(组元设为i, j)中α,β和γ三相形成平衡的条件是( 3 )。
10、G-T 关系曲线反映了定压条件下,G 函数与温度T 之间的关系,其斜率的负值表示了体系的(熵)。
二、判断:1、闭口体系的绝热膨胀过程是等熵过程。
(×)2、在等压条件下,闭口体系的熵不变。
(×)3、闭口体系的可逆绝热过程是否为等熵过程。
(√)4、闭口体系的的自由能只能减少不能增加。
( )5、孤立系统的熵的变化不可能通过外界的加热来实现(√)。
6、闭口体系发生相变的方向不一定向着体系自由能减少的方向进行( )7、对于铁在一定温度、一定压力下的固——液平衡,若单一增大压力或提高温度,还有可能保持平衡( )。
8、体系发生相变,则体系的自由能减少。
( )9、三组元的体系中可能存在两相平衡。
( )10混合相的mol 自由能是构成它的两个相互平衡的相的mol 自由能之和( )11、混合相mol自由能绝对不是构成它的两个相互平衡的相mol自由能之和( )12、体系发生相变,则体系的自由能减少。
( )13、母相中形成新相,新相的mol自由能一定要低于原来母相的mol自由能( )14、在等温等压条件下,闭口体系发生平衡相变,则体系的自由能减少。
( )15对于一个体系的平衡相而言亚稳相由于摩尔自由能更高而不能够先出现( )三、简答:1、一个绝热开口体系的熵能减少吗?能增加吗?试举例说明。
材料热力学试题2009-2010-v1

2009-2010 年 秋 季学期研究生课程考试试题考 试 科 目:材料热力学与动力学 学生所在院(系):材料学院、航天学院学生所在学科:材料学、材料加工工程 (* 题签与答题纸一起上交)一、仔细阅读下列论述,判断正误,如果错误,请说明该论述违反了哪些热力学原理,并给出正确的论述。
(16分)(1) 纯金属中不存在空位时的吉布斯自由能最低。
(2) 可采用公切线法则确定晶界偏析(晶界相成分)。
(3) 材料变形过程的热力学流是扩散通量。
(4) 低压下不可能将石墨转变为金刚石。
二、(1)固态纯组元的G-T 曲线如下图所示,请判断哪条线正确,并解释原因。
(6分)(2)A-B 二元系中,固相和液相的摩尔自由能-成分曲线如下图所示。
请在自由能-成分曲线上,图示出体系成分为X*处,固相纯A 和液相纯B 混合后的吉布斯自由能的变化量∆G mix ,并说明原因。
(6分) (此题请直接答在题签上)三、简答题:(1) 请说明化学位和活度的物理意义。
(6分)(2) 简述Calphad 的三要素及其主要功能。
(6分)(3) 请解释Onsager 倒易关系、最小熵产生原理。
(6分)四、某些在平衡条件下固态互不混溶的二元系(I AB >0),通过高能球磨或高压扭转等剧烈塑性形变(应变量非常大)实现纳米化后,可发现两个组元的相互固溶度会显著提高。
试从热力学的角度解释该现象。
(8分)学院学号 姓名五、15克金和25克银混合后形成单相理想固溶体,问(1)金和银的摩尔分数各是多少?(2)固溶体总的混合熵是多少?(3)500o C 时,摩尔自由能变化为多少?(4)令纯金和纯银的自由能为零,那么500o C 时金和银的化学势各为多少?(5)在500o C 加入一个金原子,固溶体的自由能变化为多少?已知:金的原子量为197,银的原子量为108,气体常数R 为8.314J·mol -1·K -1. (15分)六、试通过如图所示的A-B 二元相图,判断A-B 固溶体的性质、溶体组元间的相互作用能。
材料热力学与动力学复习资料+课后习题

材料热力学与动力学(复习资料)一、 概念•热力学基本概念和基本定律1. 热0:一切互为热平衡的物体,具有相同的温度。
2. 热1: - 焓:恒压体系→吸收的热量=焓的增加→焓变等于等压热效应 - 变化的可能性→过程的方向;限度→平衡3. 热2:任何不受外界影响体系总是单向地趋向平衡状态→熵+自发过程+可逆过程→隔绝体系的熵值在平衡时为最大→熵增原理(隔离体系)→Gibbs 自由能:dG<0,自发进行(同T ,p : )4. 热3:- (H.W.Nernst ,1906): - (M .Plank ,1912):假定在绝对零度时,任何纯物质凝聚态的熵值为零S*(0K)=0 - (Lewis ,Gibson ,1920):对于过冷溶体或内部运动未达平衡的纯物质,即使在0K 时,其熵值也不等于零,而是存在所谓的“残余熵” - Final :在OK 时任何纯物质的完美晶体的熵值等于零• 单组元材料热力学1. 纯金属固态相变的体积效应- 除非特殊理由,所有纯金属加热固态相变都是由密排结构(fcc )向疏排结构(bcc )的转变→加热过程发生的相变要引起体积的膨胀→BCC 结构相在高温将变得比其他典型金属结构(如FCC 和HCP 结构)更稳定(除了Fe )- 热力学解释1→G :温度相同时,疏排结构的熵大于密排结构;疏排结构的焓大于密排结构→低温:H ;高温:TS - 热力学解释2→ Maxwell 方程: - α-Fe →γ-Fe :磁性转变自由能- Richard 规则:熔化熵-Trouton 规则:蒸发熵 (估算熔沸点)2. 晶体中平衡状态下的热空位- 实际金属晶体中空位随着温度升高浓度增加,大多数常用金属(Cu 、Al 、Pb 、W 、Ag …)在接近熔点时,其空位平衡浓度约为10-4;把高温时金属中存在的平衡空位通过淬火固定下来,形成过饱和空位状态,对金属中的许多物理过程(例如扩散、时效、回复、位错攀移等)产生重要影响3. 晶体的热容- Dulong-Petit :线性谐振动子+能量均分定律→适应于较高温度及室温附近,低温时与实验不符U Q W∆=-dH PV U d Q =+=)(δRd Q S Tδ=()d dH TdS G H d TS =--=00lim()lim()0p T T T GS T→→∂∆-=∆=∂()()V T T P V V S ∂∂=∂∂//()()()T T T V P V V S T V H ∂∂+∂∂=∂∂///RK mol J T H S mm m ≈⋅≈∆=∆/3.8/K mol J T H S b v v ⋅≈∆=∆/9.87/3V V VQ dU C RdT dT δ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭-Einstein(固体振动热容理论):晶体总共吸收了n 个声子,被分配到3N 个谐振子中;不适用于极低温度,无法说明在极低温度时定容热容的实验值与绝对温度的3次方成比例。
材料热力学习题集
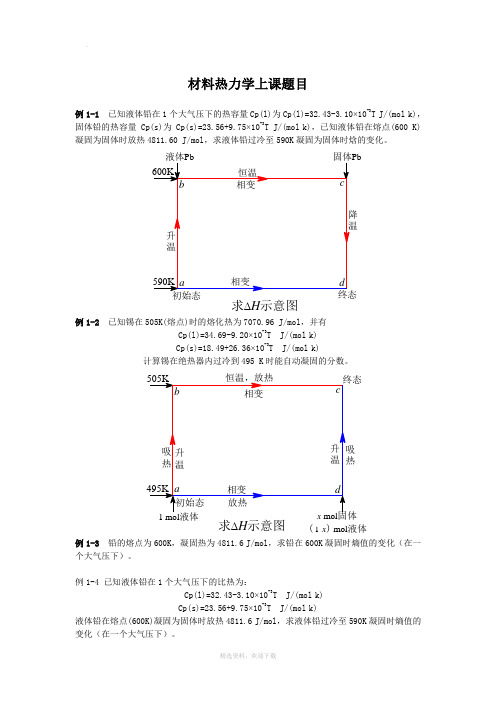
材料热力学上课题目例1-1 已知液体铅在1个大气压下的热容量Cp(l)为Cp(l)=32.43-3.10×10-3T J/(mol·k),固体铅的热容量Cp(s)为Cp(s)=23.56+9.75×10-3T J/(mol·k),已知液体铅在熔点(600 K)凝固为固体时放热4811.60 J/mol,求液体铅过冷至590K凝固为固体时焓的变化。
求∆H示意图例1-2已知锡在505K(熔点)时的熔化热为7070.96 J/mol,并有Cp(l)=34.69-9.20×10-3T J/(mol·k)Cp(s)=18.49+26.36×10-3T J/(mol·k)计算锡在绝热器内过冷到495 K时能自动凝固的分数。
求∆H示意图(1-x) mol液体例1-3铅的熔点为600K,凝固热为4811.6 J/mol,求铅在600K凝固时熵值的变化(在一个大气压下)。
例1-4 已知液体铅在1个大气压下的比热为:Cp(l)=32.43-3.10×10-3T J/(mol·k)Cp(s)=23.56+9.75×10-3T J/(mol·k)液体铅在熔点(600K)凝固为固体时放热4811.6 J/mol,求液体铅过冷至590K凝固时熵值的变化(在一个大气压下)。
Pb求∆S 示意图例题2-1 已知液体锌的Cp(l)为Cp(l)=29.66+4.81×10-3T J/(mol ·k), 固体锌的Cp(s)为 Cp(s)=22.13+11.05×10-3T J/(mol ·k),锌的熔点为692.6K ,熔化热ΔH =6589.8 J/mol ,求固、液相之间随温度变化的自由能差值ΔG(T)。
例题2-2 利用第一章的数据,求铅在590 K (过冷10 K )凝固时的自由能变化值ΔG(590 K),并与简易近似计算的结果进行比较(铅在熔点590 K 凝固时, ΔH =-4811.6 J/mol )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、反应的自由能变随温度变化的关系如下式:
G = -1,750,000 - 15.7T logT + 370T, J mol-1 (1)计算500 K时的反应S; ()计算500 K时的反应H;
(3)500 K时反应是否是自发的?
三、在286K,1atm,灰锡转变为白锡。 Cp = 21.6 + 18.210-3T, J mol-1 K-1 (适用于灰锡和白锡)
Hto = 2.1 J mol-1 (在286K下的转变热)。 (1)计算286K,1atm,相转变的自由能变G; (2)计算293K,1atm,相转变的自由能变G;
一、 1mol理想气体,求出下面4个依次变化条件下的 功W、热量Q、内能变化ΔU、焓变ΔH和ΔS及总的变 化。 (a)25℃, 1atm下,真空膨胀体积增大2倍; (b)等体积下,加热到125℃; (c)等温可逆膨胀体积增加到2倍; (d)最后等压条件下可逆冷却到25℃。 25℃, 1atm下,理想气体摩尔体积为22.414l。
1l atm 1.013102 J
二、 一封闭容器: (1)一半是1mol理想气体A,压力1atm ;另一半是 1mol理想气体B,压力1atm ;除去隔板,求ΔS 。 (2)一半是2mol理想气体,同样除去隔板,求ΔS 。 (3)两边都是气体A的情况下,与(1)相同求解。 (4)两边都是气体A的情况下,与(2)相同求解。
