2012年浙江省杭州市中考数学试题及答案
2012浙江杭州中考数学

2012年浙江省杭州市中考试题数学(满分120分,考试时间100分钟)一、选择题(本题有10个小题,每小题3分,共30分).1.(2012浙江杭州,1,3分)计算(2-3)+(-1)的结果是( )A.-2B.0C.1D.2【答案】A2.(2012浙江杭州,2,3分)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是( )A.内含B.内切C.外切D.外离【答案】B3.(2012浙江杭州,3,3分)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是( )A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球与摸到白球的可能性相等D.摸到红球比摸到白球的可能性大【答案】D4.(2012浙江杭州,4,3分)已知□ABCD中,∠B=4∠A,则∠C=( )A.18°B.36°C.72°D. 144°【答案】B5.(2012浙江杭州,5,3分)下列计算正确的是( )A.(-p2q)3=-p5q3B.(12a2b3c)÷(6ab2)=2abC.3m2÷(3m-1)= m-3m2D.(x2-4x)x-1=x-4【答案】D6.(2012浙江杭州,6,3分)如图是杭州市区人口的统计图,则根据统计图得出的下列判断中,正确的是( )A.其中有3个区的人口数都低于40万B.只有1个区的人口数超过百万C.上城区和下城区的人口数之和超过江干区的人口数D.杭州市区的人口总数已超过600万【答案】D7.(2012浙江杭州,7,3分)已知m=(3)×(-,则有( )A.5<m<6B. 4<m<5C.-5<m<-4D.-6<m<-5【答案】A8.(2012浙江杭州,8,3分)如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( )A.点B到AO的距离为sin54°B.点B到AO的距离为tan36°C.点A到OC的距离为sin36°sin54°D.点A到OC的距离为cos36°sin54°【答案】C9.(2012浙江杭州,9,3分)已知抛物线y=k(x+1)(x-3k)与x轴交于点A,B,与y轴交于点C,则能使△ABC 为等腰三角形的抛物线的条数是( )A.2B.3C.4D. 5【答案】B10.(2012浙江杭州,10,3分)已知关于x、y的方程组343x y ax y a+=-⎧⎨-=⎩,,其中-3≤a≤1,给出下列结论:①51xy=⎧⎨=-⎩,是方程组的解;②当a=-2时,x、y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解;④若x≤1,则1≤y≤4.其中正确的是( )A.①②B.②③C.②③④D.①③④【答案】C二、填空题(本题有6个小题,每小题4分,共24分).11.(2012浙江杭州,11,4分)数据1,1,1,3,4的平均数是;众数是 . 【答案】2,112.(2012浙江杭州,12,4分)化简216312mm--得;当m=-1时,原式的值为 .【答案】34+m ,113.(2012浙江杭州,13,4分)某企业向银行贷款1000万元,一年后归还银行1065.6多万元,则年利率高于 %. 【答案】6.5614.(2012浙江杭州,14,4a <0,若b =2-a ,则b 的取值范围是 . 【答案】32-<b <215.(2012浙江杭州,15,4分)已知一个底面为菱形的直棱柱,高为10cm ,体积为150cm 3,则这个棱柱的下底面积为 cm 2,若该棱柱的侧面展开图的面积为200 cm 2,记底面菱形的顶点依次为A ,B ,C ,D ,AE 是BC 边上的高,则CE 的长为 cm . 【答案】15,1或916.(2012浙江杭州,16,4分)如图,平面直角坐标系中有四个点,它们的横坐标均为整数.若在此平面内移动点A ,使得这四个点构成的四边形是轴对称图形,并且点A 的横坐标仍是整数,则移动后点A 的坐标为 .【答案】(1,1),(2,3),(0,2),(2,2)-----三、解答题(本题有7个小题,共66分).17.(2012浙江杭州,17,6分)化简:2[(m -1)m +m (m +1)][(m -1)m -m (m +1)].若m 是任意整数,请观察化简后的结果,你发现原式表示一个什么数? 【答案】原式=2222232()()2228m m m m m m m m m m m -++---=-⨯⋅=-观察38m -,则原式表示一个能被8整除的数18.(2012浙江杭州,18,8分)当k 分别取-1,1,2时,函数y =(k -1)x2-4x +5-k 都有最大值吗?请写出你的判断,并说明理由.若有,请求出最大值.【答案】k 只能-1,当1k =,函数为44y x =-+,是一次函数,一次函数无最值, 当2k =,函数为243y x x =-+,为二次函数,而此函数开口向上,则无最大值当1k =-,函数为2246y x x =--+,为二次函数,此函数开口向下,有最大值,变形为22(1)8y x =-++,则当1x =-时,m ax 8y =19.(2012浙江杭州,19,8分)如图是数轴的一部分,其单位长度为a .已知△ABC 中,AB =3a ,BC =4a ,AC =5a.(1)用直尺和圆规作出△ABC (要求:使点A 、C 在数轴上,保留作图痕迹,不必写出作法); (2)记△ABC 的外接圆的面积为S 圆,△ABC 的面积为S △,试说明S S圆>π.【答案】(1)如图(2)如图作外接圆由题可得,222(3)(4)(5)a a a +=, 222AB BC AC ∴+=,则A B C ∆为直角三角形,而=90ABC ∠ ,则A C为外接圆的直径2=62A B C A B B CS a∆⋅=,而2225=()24A C S aππ=圆2225254==624aS S aπππ∆>圆20.(2012浙江杭州,20,10分)有一组互不全等的三角形,它们的三边长均为整数,每个三角形有两条边的长分别为5和7. (1)请写出其中一个三角形的第三边的长; (2)设组中最多有n 个三角形,求n 的值;(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率. 【答案】(1)第三边长为6,(212<<边长中,任意整数边长即可);(2)设第三边长为L ,由三角形的性质可得7575L -<<+,即212L <<,而组中最多有n 个三角形=34567891011L ∴,,,,,,,,,则=9n ;(3)在这组三角形个数最多时,即=9n ,而要使三角形周长为偶数,且两条定边的和为12, 则第三边也必须为偶数, 则=46810L ,,,()49A P ∴=.21.(2012浙江杭州,21,10分)如图,在梯形ABCD 中,AD ∥BC ,AB =CD .分别以AB ,CD 为边向外侧作等边三角形ABE 和等边三角形DCF ,连接AF ,DE . (1)求证:AF =DE ; (2)若∠BAD =45°,AB =a ,△ABE 和△DCF 的面积之和等于梯形ABCD 的面积,求BC 的长.【答案】(1)在梯形A B C D 中,AD//BC ,A B C D =,BAD C D A ∴∠=∠而在正ABE ∆和正D C F ∆中,A B A E =,D C D F =且60BAE CDF ∠=∠=AE D F ∴=且EAD FD A ∠=∠且AD 公共()AED DFA SAS ∴∆≅∆ AF D E ∴=;(2)如图作BH AD ⊥,C K A D ⊥,则有B C H K = 45HAB KDC ∠=∠=AB ∴==,同理CD ==()=2A DBC H BS +⋅梯A B a =222)22=22a BC a a S ⨯+⋅+∴=梯而24AEB D C F S S a∆∆==而由题得A E B D C F S S S ∆∆+=梯22242a a +∴⨯=2BC ∴=22.(2012浙江杭州,22,12分)在平面直角坐标系中,反比例函数与二次函数y = k (x2+x -1)的图象交于点A (1,k )和点B (-1,-k ). (1)当k =-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y 随着x 的增大而增大,求k 应满足的条件以及x 的取值范围;(3)设二次函数的图象的顶点为Q ,当△ABQ 是以AB 为斜边的直角三角形时,求k 的值. 【答案】(1)当2k =-时,(1,2)A - A 在反比例函数图像上 ∴设反比例函数为y=xk ,代入A 点坐标可得2k =-2y x -∴=(2)要使得反比例函数与二次函数都是y 随着x 的增大而增大, 0k ∴<而对于二次函数2y kx kx k =+-,其对称轴为x =-21,要使二次函数满足上述条件,在0k <的情况下, 则x 必须在对称轴的左边, 即x <-21时,才能使得y 随着x 的增大而增大∴ 综上所述,则0k <,且x <-21(3)由(2)可得15(,)24Q k --ABQ ∆ 是以AB 为斜边的直角三角形A 点与B 点关于原点对称,所以原点O 平分A B 又 直角三角形中斜边上的中线是斜边的一半 O Q O A O B ∴== 作A D OC ⊥,QC OC ⊥O Q k =而OA ==(图为一种可能的情况)∴=,则k =k =-23.(2012浙江杭州,23,12分)如图,AE 切⊙O 于点E ,AT 交⊙O 于点M ,N ,线段OE 交AT 于点C ,OB ⊥AT于点B ,已知∠EAT =30°,AE MN(1)求∠COB 的度数; (2)求⊙O 的半径R ;(3)点F 在⊙O 上( FME 是劣弧),且EF =5,把△OBC 经过平移、旋转和相似变换后,使它的两个顶点分别与点E ,F 重合.在EF 的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点也在⊙O 上三角形吗?请你在图中画出这个三角形,并求出这个三角形与△OBC 的周长之比. 【答案】(1)O B A T ⊥ ,且A E C E ⊥∴在C A E ∆和C O B ∆中,90AEC CBO ∠=∠=而B C O A C E ∠=∠30COB A ∴∠=∠=;(2)AE = 30A ∠=3E C ∴= 连结O M在M O B ∆中,O M R =,2M N M B ==,OB ∴==而在C O B∆中,2BO C==O C B∴==又O C E C O M R+==3R∴=整理得2181150R R+-=(23)(5)R R+-=23R∴=-(不符合题意,舍去),或5R=则5R=(3)在E F同一侧,C O B∆经过平移、旋转和相思变换后这样的三角形有6个,如图,每小图2个顶点在圆上的三角形如图所示,延长E O交O于D,连结DF5E F=,直径10E D=,可得30FDE∠=FD∴=,则51015EFDC∆=++=+由(2)可得3COBC∆=+5E F DO BCCC∆∆∴==。
【推荐下载】2012浙江杭州中考数学真题及答案

2012浙Байду номын сангаас杭州中考数学真题及答案
1、计算(2-3)+(-1)的结果是()
A、-2B、0C、1D、2
2、若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是()
A、内含B、内切C、外切D、外离
3、一个不透明的盒子中装有2个红球和1个白球,他们除颜色外都相同。若从中
任意摸出一个球,则下列叙述正确的是()
A、摸到红球是必然事件B、摸到白球是不可能事件
C、摸到红球与摸到白球的可能性相等D、摸到红球比摸到白球的可能性大
4、已知平行四边形ABCD中,∠B=4∠A,则∠C=()
A、18°B、36°C、72°D、144°
1
[键入文字]
中考精华专题汇总:
2
[键入文字]
历年中考满分作文
中考后上国际高中
3
[键入文字]
历年上海中考试题
上海重点高中录取分数线
4
[键入文字]
中考数学试题及答案专题,阅读更多相关文章!
相关下载:
2012年浙江杭州中考数学真题及答案(1.16MB)
»去下载
5
[2015年中考必备]2012年中考数学卷精析版——浙江杭州卷
![[2015年中考必备]2012年中考数学卷精析版——浙江杭州卷](https://img.taocdn.com/s3/m/0c5698e4856a561252d36f7b.png)
2012年中考数学精析系列——杭州卷(本试卷满分120分,考试时间100分钟)一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确的答案.1.(2012浙江杭州3分)计算(2﹣3)+(﹣1)的结果是【】A.﹣2B.0C.1D.2【答案】A。
【考点】有理数的加减混合运算。
【分析】根据有理数的加减混合运算的法则进行计算即可得解:(2﹣3)+(﹣1)=﹣1+(﹣1)=﹣2。
故选A。
2.(2012浙江杭州3分)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是【】A.内含B.内切C.外切D.外离【答案】B。
【考点】圆与圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
因此,∵两圆的半径分别为2cm和6cm,圆心距为4cm.则d=6﹣2=4。
∴两圆内切。
故选B。
3.(2012浙江杭州3分)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是【】A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球比摸到白球的可能性相等D.摸到红球比摸到白球的可能性大【答案】D。
【考点】随机事件和可能性的大小。
【分析】利用随机事件的概念,以及个数最多的就得到可能性最大对选项分别分析即可:A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确。
;故选D。
4.(2012浙江杭州3分)已知平行四边形ABCD中,∠B=4∠A,则∠C=【】A.18°B.36°C.72°D.144°5.(2012浙江杭州3分)下列计算正确的是【】A.(﹣p2q)3=﹣p5q3B.(12a2b3c)÷(6ab2)=2abC.3m2÷(3m﹣1)=m﹣3m2D.(x2﹣4x)x﹣1=x﹣4【答案】D。
杭州市中考数学卷及答案

2012年浙江省杭州市中考数学试卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确的答案.1.(2012•杭州)计算(2﹣3)+(﹣1)的结果是()A.﹣2B.0C.1D.2考点:有理数的加减混合运算。
专题:计算题。
分析:根据有理数的加减混合运算的法则进行计算即可得解.解答:解:(2﹣3)+(﹣1),=﹣1+(﹣1),=﹣2.故选A.点评:本题主要考查了有理数的加减混合运算,是基础题比较简单.2.(2012•杭州)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是()A.内含B.内切C.外切D.外离考点:圆与圆的位置关系。
分析:两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d <R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.解答:解:∵两圆的半径分别为2cm和6cm,圆心距为4cm.则d=6﹣2=4,∴两圆内切.故选B.点评:本题主要考查两圆的位置关系.两圆的位置关系有:外离(d>R+r)、内含(d<R ﹣r)、相切(外切:d=R+r或内切:d=R﹣r)、相交(R﹣r<d<R+r).3.(2012•杭州)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球比摸到白球的可能性相等D.摸到红球比摸到白球的可能性大考点:可能性的大小;随机事件。
分析:利用随机事件的概念,以及个数最多的就得到可能性最大分别分析即可.解答:解:A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.摸到红球比摸到白球的可能性相等,根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确;故选:D.点评:此题主要考查了随机事件以及可能性大小,利用可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等得出是解题关键.4.(2012•杭州)已知平行四边形ABCD中,∠B=4∠A,则∠C=()A.18°B.36°C.72°D.144°考点:平行四边形的性质;平行线的性质。
2012杭州中考数学试题及答案

2012杭州中考数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 已知一个长方体的长、宽、高分别为8cm、6cm和5cm,其体积是多少立方厘米?A. 240B. 180C. 120D. 1003. 以下哪个表达式等价于 \(a^2 + b^2 = (a + b)^2\)?A. \(a^2 - 2ab + b^2\)B. \(a^2 + 2ab + b^2\)C. \(a^2 - b^2\)D. \(a^3 + b^3\)4. 如果一个数的60%是120,那么这个数是多少?A. 180B. 192C. 200D. 2205. 一个班级有48名学生,其中2/3是男生,那么这个班级有多少名女生?A. 16B. 24C. 32D. 406. 下列哪个数是无理数?A. 3.14B. \(\sqrt{2}\)C. 0.333...D. -57. 一个数的1/3加上它的1/4等于这个数的多少?A. 7/12B. 1/2C. 5/12D. 1/38. 一个圆的直径是14cm,那么它的半径是多少厘米?A. 7B. 14C. 28D. 219. 一个数的75%减去25等于50,这个数是多少?A. 100B. 80C. 120D. 20010. 下列哪个选项是正确的不等式?A. \(2 > 3\)B. \(5 \leq 5\)C. \(-1 < 1\)D. \(0 \geq -1\)二、填空题(每题4分,共20分)11. 一个数的1/2与它的1/3的差是1/6,这个数是________。
12. 一个长方体的长是10cm,宽是5cm,高是3cm,它的表面积是________平方厘米。
13. 一本书的价格是35元,打8折后的价格是________元。
14. 一个数的1/4加上它的1/5等于9/20,这个数是________。
15. 一个数的3倍减去15等于45,这个数是________。
2012杭州中考数学试题及答案

2012杭州中考数学试题及答案2012年杭州中考数学试题一、选择题(共10题,每题3分,共30分)1. 下列各数中,最大的数是()A. -3B. 0C. 3D. 52. 一个直角三角形的两条直角边分别是6和8,那么斜边的长度是()A. 10B. 12C. 14D. 163. 一个数的平方根是4,那么这个数是()A. 16B. -16C. 8D. -84. 一个圆的半径是5,那么这个圆的面积是()A. 25πB. 50πC. 100πD. 125π5. 一个数的倒数是2/3,那么这个数是()A. 3/2B. 2/3C. 3D. 1/26. 一个数列的前三项是1, 3, 6,那么这个数列的第四项是()A. 10B. 11C. 12D. 137. 如果一个角的补角是120°,那么这个角的度数是()A. 60°B. 30°C. 45°D. 90°8. 一个长方体的长、宽、高分别是2, 3, 4,那么这个长方体的体积是()A. 24B. 36C. 48D. 529. 一个分数的分子是7,分母是14,化简后的结果是()A. 1/2B. 3/7C. 5/8D. 7/1410. 如果一个方程的解是x=2,那么这个方程可以是()A. x+2=0B. x-2=0C. x^2-4=0D. x^2-4x=0二、填空题(共5题,每题3分,共15分)11. 一个数的立方是-27,那么这个数是______。
12. 一个数的绝对值是5,那么这个数可以是______或______。
13. 一个数的平方是25,那么这个数可以是______或______。
14. 一个数的平方根是2.5,那么这个数是______。
15. 如果一个三角形的内角和是180°,那么一个直角三角形的两个锐角的和是______。
三、解答题(共5题,每题5分,共25分)16. 计算下列表达式的值:(3x - 2) / (x^2 - 4),当x=-1。
2012年杭州市各类高中招生文化考试数学试题
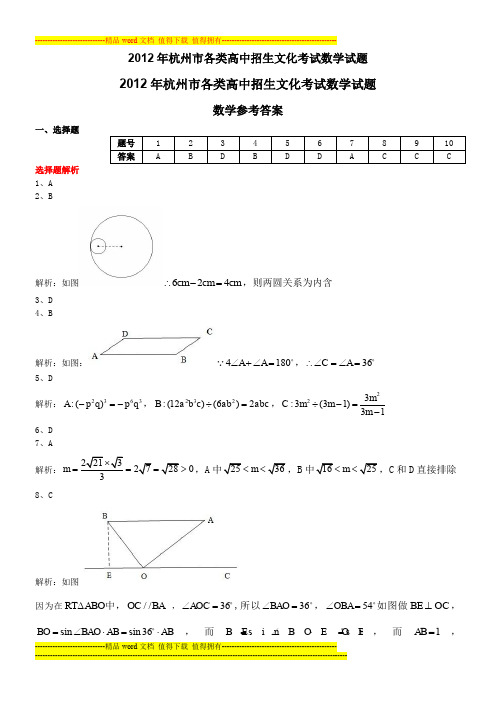
2012年杭州市各类高中招生文化考试数学试题2012年杭州市各类高中招生文化考试数学试题数学参考答案一、选择题选择题解析 1、A 2、B解析:如图624cm cm cm ∴-=,则两圆关系为内含3、D4、B解析:如图:4180A A ∠+∠=,36C A ∴∠=∠=5、D解析:2363:()A p q p q -=-,232:(12)(6)2B a b c ab abc ÷=,223:3(31)31m C m m m ÷-=-6、D7、A解析:0m ===>,A m <<,B m <<C 和D 直接排除 8、C解析:如图因为在RT ABO ∆中,//OC BA ,36AOC ∠=,所以36BAO ∠=,54OBA ∠=如图做BE OC ⊥,sin sin36BO BAO AB AB =∠⋅=⋅,而s i n s i n B E B O E O B O B =∠⋅=⋅,而1AB =,sin36sin54BE ∴=,即点A 到OC 的距离。
9、C解析:如图由所给的抛物线解析式可得A ,C 为定值(1,0)A -,(0,3)C -则AC =3(,0)B k , ⑴ 0k >,则可得①AC BC ==3k =②AC AB =,则有31k +=,可得k =, ③ ABBC =,则有31k +=34k =⑵ 0k <,B 只能在A 的左侧④只有AC AB =,则有31k --=k =10、C解析:对方程组进行化简可得211x a y a =+⎧⎨=-⎩①31a -≤≤,5213a ∴-≤+≤,仅从x 的取值范围可得知①错误②当2a =-时,33x y =-⎧⎨=⎩,则,x y 的值互为相反数,则②正确③当1a =时,30x y =⎧⎨=⎩,而方程43x y a +=-=,则,x y 也是此方程的解,则③正确⑤ 1x ≤,则211a +≤,则0a ≤,而题中所给31a -≤≤,则30a -≤≤,114a ≤-≤ 则14y ≤≤,选项④正确 二、填空题11、2,1; 12、43m +,1; 13、6.56; 14、22b ≤≤; 15、15,1或9; 16、(1,1),(2,3),(0,2),(2,2)-----填空题解析 11、(1)2,(2)112、(1)43m +,(2)1解析:原代数式=(4)(4)43(4)3m m m m +-+=-,代入1m =-得原式=113、6.56解析:设年利率为%x ,由题可得不等式1000(1%)1065.6x +≥,解得 6.56x ≥0> 则0a >,而要使得不等式的值小于0,则只有0a -,所以可得0a <<,可得222a --<,则22b -≤≤14、 (1)15,(2)1或9解析:由题意可知, V Sh =,代入可易得下底面积为215cm而2200cm 为总的侧面积,则每一条底边所在的侧面积为250cm ,因为高为10cm ,所以菱形底边长为5cm ,而底面积为215cm ,所以高3AE cm =① 如图,E 在菱形内部EC BC BE =-,4BE ==,所以1EC =② 如图,E 在菱形外部EC BC BE =+,9EC =解析:如图三、解答题17、解:原式=2222232()()2228m m m m m m m m m m m -++---=-⨯⋅=-观察38m -,则原式表示一个能被8整除的数18、 解:k 只能-1,当1k =,函数为44y x =-+,是一次函数,一次函数无最值, 当2k =,函数为243y x x =-+,为二次函数,而此函数开口向上, 则无最大值当1k =-,函数为2246y x x =--+,为二次函数,此函数开口向下,有最大值,变形为22(1)8y x =-++,则当1x =-时,max 8y =19、解:(1)作图略(2)如图作外接圆由题可得,222(3)(4)(5)a a a +=, 222AB BC AC ∴+=,则ABC ∆为直角三角形,而=90ABC ∠,则AC为外接圆的直径2=62ABC AB BC S a ∆⋅=,而2225=()24AC S aππ=圆 20、解:(1)第三边长为6,(212<<边长中,任意整数边长即可);(2)设第三边长为L ,由三角形的性质可得7575L -<<+,即212L <<,而组中最多有n 个三角形 =34567891011L ∴,,,,,,,,,则=9n ;(3)在这组三角形个数最多时,即=9n ,而要使三角形周长为偶数,且两条定边的和为12, 则第三边也必须为偶数, 则=46810L ,,,()49A P ∴=.21、解:(1)在梯形ABCD 中,AD//BC ,AB CD =,而在正ABE ∆和正DCF ∆中,AB AE =,DC DF =且60BAE CDF ∠=∠=AE DF ∴=且EAD FDA ∠=∠且AD 公共 AF DE ∴=;(2)如图作BH AD ⊥,CK AD⊥,则有BC HK =AB∴==,同理CD==而2AEB DCF S S ∆∆==而由题得AEB DCF S S S ∆∆+=梯22、解:(1)当2k =-时,(1,2)A -A 在反比例函数图像上∴设反比例函数为ky x =, 代入A 点坐标可得2k =-(2)要使得反比例函数与二次函数都是y 随着x 的增大而增大, 而对于二次函数2y kx kx k =+-,其对称轴为12x =-,要使二次函数满足上述条件,在0k <的情况下, 则x 必须在对称轴的左边,即12x <-时,才能使得y 随着x 的增大而增大∴ 综上所述,则0k <,且12x <-(3)由(2)可得15(,)24Q k --ABQ ∆是以AB 为斜边的直角三角形A 点与B 点关于原点对称,所以原点O 平分AB又直角三角形中斜边上的中线是斜边的一半作AD OC ⊥,QCOC ⊥而OA=(图为一种可能的情况)=,则k =k =23、解:(1)OB AT ⊥,且AE CE ⊥∴在CAE ∆和COB ∆中,90AEC CBO ∠=∠=而BCO ACE ∠=∠30COB A ∴∠=∠=;(2)3AE =30A ∠=连结OM在MOB ∆中,OM R =,2MNMB ==, 而在COB ∆中,BO == 又OC EC OM R +==整理得2181150R R +-=23R ∴=-(不符合题意,舍去),或5R = 则5R =(3)在EF 同一侧,COB ∆经过平移、旋转和相思变换后这样的三角形有6个,如图,每小图2个 顶点在圆上的三角形如图所示,延长EO 交O 于D ,连结DF5EF =,直径10ED =,可得30FDE∠=FD ∴=51015EFD C ∆=++=+ 由(2)可得3COB C∆=5EFD OBC C C ∆∆∴== 下面是“十个小故事大道理”不需要的朋友可以下载后编辑删除!!!谢谢!!!小故事1、《扁鹊的医术》魏文王问名医扁鹊说:“你们家兄弟三人,都精于医术,到底哪一位最好呢? 扁鹊答:“长兄最好,中兄次之,我最差。
2012年浙江杭州中考数学试题(含答案)

一、选择题(共8小题,每题3分,满分24分)1.-8的绝对值是()A.8B.18C.18-D.8-2.在平面直角坐标系中,点(3,-2)关于原点的对称点的坐标是()A.(3,2)B.(-3,-2)C.(-3,2)D.(-3,-2)3.计算(-a)2•a3的结果是()A.a5B.a6C.-a5D.-a64.如图是一个用相同的小立方体搭成的几何体的三视图,则组成这个几何体的小立方体的个数是()A.2 B.3 C.4 D.55.绿豆在相同条件下的发芽试验,结果如下表所示:则绿豆发芽的概率估计值是()A.0.96 B.0.95 C.0.94 D.0.906.已知一组数据:1,3,5,5,6,则这组数据的方差是()A.16 B.5 C.4 D.3.27.若⊙O1,⊙O2的半径分别是r1=2,r2=4,圆心距d=5,则这两个圆的位置关系是()A.内切B.相交C.外切D.外离8.在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是()A.(-2,3)B.(-1,4)C.(1,4)D.(4,3)二、填空题(每小题3分,满分30分)9.-5的相反数是.10.2x-x的取值范围是.2012年江苏宿迁中考数学试题(满分150分,考试时间120分钟)11.已知点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,若AC⊥BD,且AC≠BD,则四边形EFGH的形状是.(填“梯形”“矩形”或“菱形”)12.分解因式:ax2-ay2=.13.不等式组101(4)32xx->⎧⎪⎨+<⎪⎩的解集是.14.如图,SO,SA分别是圆锥的高和母线,若SA=12cm,∠ASO=30°,则这个圆锥的侧面积是cm2.第14题图第15题图第17题图15.如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C,D处,C E交AF于点G,若∠CEF=70°,则∠GF D=°.16.在平面直角坐标系中,若一条平行于x轴的直线l分别交双曲线6yx=-和2yx=于A,B两点,P是x轴上的任意一点,则△ABP的面积等于.17.如图,已知P是线段AB的黄金分割点,且P A>PB,若S1表示以P A为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1S2.(填“>”“=”或“<”)18.按照如下图所示的方法排列黑色小正方形地砖,则第14个图案中黑色小正方形地砖的块数是.三、解答题(共10小题,满分96分)19.(8分)计算:023(1)2cos30+-+︒20.(8分)解方程:1111x x+=+-21.(8分)求代数式(a+2b)(a-2b)+(a+2b)2-4ab的值,其中a=1,b=1 10;度数8 9 10 13 14 15天数 1 1 2 3 1 2(1)这10天用电量的众数是,中位数是,极差是;(2)求这个班级平均每天的用电量;(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.23.(10分)如图是使用测角仪测量一幅壁画高度的示意图,已知壁画AB的底端距离地面的高度BC=1m,在壁画的正前方点D处测得壁画顶端的仰角∠ADF=60°,底端的俯角∠BDF=30°,且点D距离地面的高度DE=2m,求壁画AB的高度.24.(10分)有四部不同的电影,分别记为A,B,C,D.(1)若甲从中随机选择一部观看,则恰好是电影A的概率是;(2)若甲从中随机选择一部观看,乙也从中随机选择一部观看,求甲、乙两人选择同一部电影的概率.25.(10分)学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h的速度走平路,共用了6h,问平路和坡路各有多远?26.(10分)如图,在四边形ABCD中,∠DAB=∠ABC=90°,CD与以AB为直径的半圆相切于点E,EF⊥AB于点F,EF交BD于点G,设AD=a,BC=b.(1)求CD的长度(用a,b表示);(2)求EG的长度(用a,b表示);(3)试判断EG与FG是否相等,并说明理由.27.(12分)(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=1 2∠ABC(0°<∠CBE<∠12ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处)连接DE′,求证:DE′=DE.(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=12∠ABC(0°<∠CBE<45°).求证:DE2=AD2+EC2.28.(12分)如图,在平面直角坐标系xOy中,已知直线l1:y=12x与直线l2:y=-x+6相交于点M,直线l2与x轴相交于点N.(1)求M,N的坐标.(2)矩形ABCD中,已知AB=1,B C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).(3)在(2)的条件下,当t为何值时,S的值最大?并求出最大值.2012年江苏宿迁中考数学参考答案19.320.x=021.代数式的值为222.(1)13度,13度,7度(2)12度(3)7200度23.AB=4m24.(1)14(2)1425.平路150千米,坡路120千米.26.(1)CD=a+b;(2)abEGa b=+;(3)EG FG=,理由略.27.证明略.28.(1)M(4,2),N(6,0);(2)2221(01)411()(14)2231349(45)4241(132)(56)21(7)(67)2t tt tS t t tt tt t⎧≤≤⎪⎪⎪-<≤⎪⎪⎪=-+-<≤⎨⎪⎪-<≤⎪⎪⎪-<≤⎪⎩(3)当13=3t时,S的值最大,最大值为116.1。
浙江省各市2012年中考数学分类解析 专题2:代数式和因式分解

浙江11市2012年中考数学试题分类解析汇编专题2:代数式和因式分解一、选择题1.(2012浙江杭州3分)下列计算正确的是【】A.(﹣p2q)3=﹣p5q3B.(12a2b3c)÷(6ab2)=2abC.3m2÷(3m﹣1)=m﹣3m2D.(x2﹣4x)x﹣1=x﹣4【答案】D。
【考点】整式的混合运算,积的乘方和幂的乘方,整式的乘法,同底数幂的乘法和除法。
【分析】根据整式的混合运算法则对各选项分别进行计算,即可判断:A、(﹣p2q)3=﹣p6q3,故本选项错误;B、12a2b3c)÷(6ab2)=2abc,故本选项错误;C、223m3m3m13m1÷=(﹣)(﹣),故本选项错误;D、(x2﹣4x)x﹣1=x﹣4,故本选项正确。
故选D。
2.(2012浙江湖州3分)计算2a-a,正确的结果是【】A.-2a3B.1 C.2 D.a【答案】D。
【考点】合并同类项。
【分析】根据合并同类项的运算法则计算作出判断:2a-a= a。
故选D。
3.(2012浙江湖州3分)要使分式1x有意义,x的取值范围满足【】A.x=0 B.x≠0 C.x>0 D.x<0 【答案】B。
【考点】分式有意义的条件。
【分析】根据分式分母不为0的条件,要使1x在实数范围内有意义,必须x≠0。
故选B。
4.(2012浙江嘉兴、舟山4分)若分式x1x+2-的值为0,则【】A.x=﹣2B.x=0C.x=1或2D.x=1【答案】D 。
【考点】分式的值为零的条件。
【分析】∵分式x 1x+2-的值为0,∴x 1=0x+2x+20-⎧⎪⎨⎪≠⎩,解得x=1。
故选D 。
5. (2012浙江丽水、金华3分)计算3a•(2b)的结果是【 】A .3abB .6aC .6abD .5ab【答案】C 。
【考点】单项式乘单项式。
【分析】根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可: 3a•(2b)=3·2a•b =6ab .故选C 。
2012年杭州市数学中考试卷

2012年杭州市数学中考试卷本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分.第1卷l 至4页,第Ⅱ卷5至12页.满分120分.考试时间120分钟.第1卷(选择题 共42分)注意事项:1.答第1卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后。
再选涂其它答案,不能答在试卷上。
3.考试结束,将本试卷和答题卡一并交回. 一、选择题(本题共14小题.每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的. 1.一3的绝对值是(A)3 (C)±3 (B) 3 (D)±132.2004年临沂市的国民生产总值为1012亿元,用科学记数法表示正确的是(A)1012×108元 (B)1.012×1110元 (C)1.0×1110元. (D)1.012×1210元.3.下列各式计算正确的是(A)527()a a =.(B)22122x x-= (C)236326a a a = (D)826a a a ÷=。
4.一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球,从中随机摸出一个,摸到黄球的概率是(A) 18 (B) 13 (C) 38 (D) 355.如图,将两根钢条'AA 、'BB 的中点O 连在一起,使'AA 、'BB 可以绕着点0自由转动,就做成了一个测量工件,则''A B 的长等于内槽宽AB ,那么判定△AOB ≅△''A OB 的理由是(A)边角边 (B)角边角 (C)边边边 (D)角角边6.已知两圆相交,其圆心距为6,大圆半径为8,则小圆半径r 的取值范围是 (A)r>2 (13)2<r<14 (C)l<r<8 (13)2<r<87.化简24()22a a a a a a---+ 的结果是 (A)一4 (B)4 (C)2a (13) 2a +48.如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD ,若BD =10,DF =4,则菱形ABCD 的边长为第5题图(A)4.(C)6. (D)9.9.小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm 幻灯片到屏幕的距离是1.5m ,幻灯片上小树的高度是10cm ,则屏幕上小树的高度是(A)50cm . (B)500cm . (C)60 cm . (D)600cm .10.多边形的内角中,锐角的个数最多有 (A)1个. (B)2个. (C)3个. (D)4个.11.如图,已知点A 的坐标为(1,0),点B 在直线y x =-上运动,当线段AB 最短时,点B 的坐标为(A)(0,0). (B)11(,)22-.(c) (D) 11(,)22-. 12.等腰三角形一腰上的高与另一腰的夹角为30。
【精品】浙江省杭州市中考数学试卷解析版

2012年浙江省杭州市中考数学试卷解析版一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确的答案.1.(2012•杭州)计算(2﹣3)+(﹣1)的结果是()A.﹣2 B.0 C.1 D.2有理数的加减混合运算。
考点:专计算题。
题:根据有理数的加减混合运算的法则进行计算即可得解.分析:解解:(2﹣3)+(﹣1),答:=﹣1+(﹣1),=﹣2.故选A.本题主要考查了有理数的加减混合运算,是基础题比较简单.点评:2.(2012•杭州)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是()A.内含B.内切C.外切D.外离考点:圆与圆的位置关系。
分析:两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d <R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.解答:解:∵两圆的半径分别为2cm和6cm,圆心距为4cm.则d=6﹣2=4,∴两圆内切.故选B.点评:本题主要考查两圆的位置关系.两圆的位置关系有:外离(d>R+r)、内含(d<R ﹣r)、相切(外切:d=R+r或内切:d=R﹣r)、相交(R﹣r<d<R+r).3.(2012•杭州)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球比摸到白球的可能性相等D.摸到红球比摸到白球的可能性大考点:可能性的大小;随机事件。
分析:利用随机事件的概念,以及个数最多的就得到可能性最大分别分析即可.解答:解:A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.摸到红球比摸到白球的可能性相等,根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确;故选:D.点评:此题主要考查了随机事件以及可能性大小,利用可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等得出是解题关键.4.(2012•杭州)已知平行四边形ABCD中,∠B=4∠A,则∠C=()A.18°B.36°C.72°D.144°考点:平行四边形的性质;平行线的性质。
浙江11市2012年中考数学试题分类解析汇编

浙江11市2012年中考数学试题分类解析汇编专题11:圆一、选择题1. (2012浙江杭州3分)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是【】A.内含B.内切C.外切D.外离2.(2012浙江湖州3分)如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是【】A.45°B.85°C.90°D.95°3. (2012浙江嘉兴、舟山4分)如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于【】A. 15°B.20°C. 30°D.70°4. (2012浙江嘉兴、舟山4分)已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为()A.15πcm2 b B.30πcm2C.60πcm2D.3cm25. (2012浙江宁波3分)如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b 满足的关系式是【】A.b=a B.b=5+1a2C.b=5a2D.b=2a6. (2012浙江衢州3分)如图,点A、B、C在⊙O上,∠ACB=30°,则sin∠AOB的值是【】A.B.C.D.7. (2012浙江衢州3分)用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是【】A.cm B.3cm C.4cm D.4cm8. (2012浙江绍兴4分)如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别是:甲:1、作OD的中垂线,交⊙O于B,C两点,2、连接AB,AC,△ABC即为所求的三角形乙:1、以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点。
2012-2017杭州中考数学

2012年省市中考数学试卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确的答案.1.(3分)(2012•)计算(2﹣3)+(﹣1)的结果是()A.﹣2 B.0C.1D.22.(3分)(2012•)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是()A.含B.切C.外切D.外离3.(3分)(2012•)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球比摸到白球的可能性相等D.摸到红球比摸到白球的可能性大4.(3分)(2012•)已知平行四边形ABCD中,∠B=4∠A,则∠C=()A.18°B.36°C.72°D.144°5.(3分)(2012•)下列计算正确的是()A.(﹣p2q)3=﹣p5q3B.(12a2b3c)÷(6ab2)=2abC.3m2÷(3m﹣1)=m﹣3m2D.(x2﹣4x)x﹣1=x﹣46.(3分)(2012•)如图是市区人口的统计图.则根据统计图得出的下列判断,正确的是()A.其中有3个区的人口数都低于40万B.只有1个区的人口数超过百万C.上城区与下城区的人口数之和超过江干区的人口数D.市区的人口数已超过600万7.(3分)(2012•)已知m=,则有()A.5<m<6 B.4<m<5 C.﹣5<m<﹣4 D.﹣6<m<﹣5 8.(3分)(2012•)如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则()A.点B到AO的距离为sin54°B.点B到AO的距离为tan36°C.点A到OC的距离为sin36°sin54°D.点A到OC的距离为cos36°sin54°9.(3分)(2012•)已知抛物线y=k(x+1)(x﹣)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是()A.2B.3C.4D.510.(3分)(2012•)已知关于x,y的方程组,其中﹣3≤a≤1,给出下列结论:①是方程组的解;②当a=﹣2时,x,y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④若x≤1,则1≤y≤4.其中正确的是()A.①②B.②③C.②③④D.①③④二、认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的容,尽量完整的填写答案.11.(4分)(2012•)数据1,1,1,3,4的平均数是;众数是.12.(4分)(2012•)化简得;当m=﹣1时,原式的值为.13.(4分)(2012•)某企业向银行贷款1000万元,一年后归还银行1065.6多万元,则年利率高于%.14.(4分)(2012•)已知(a﹣)<0,若b=2﹣a,则b的取值围是.15.(4分)(2012•)已知一个底面为菱形的直棱柱,高为10cm,体积为150cm3,则这个棱柱的下底面积为cm2;若该棱柱侧面展开图的面积为200cm2,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为cm.16.(4分)(2012•)如图,平面直角坐标系中有四个点,它们的横纵坐标均为整数.若在此平面直角坐标系移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横坐标仍是整数,则移动后点A的坐标为.三、全面答一答(本题有7个小题,共66分)解答应写出文字说明,证明过程或演算步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(6分)(2012•)化简:2[(m﹣1)m+m(m+1)][(m﹣1)m﹣m(m+1)].若m是任意整数,请观察化简后的结果,你发现原式表示一个什么数?18.(8分)(2012•)当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.19.(8分)(2012•)如图,是数轴的一部分,其单位长度为a,已知△ABC中,AB=3a,BC=4a,AC=5a.(1)用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法);(2)记△ABC的外接圆的面积为S圆,△ABC的面积为S△,试说明>π.20.(10分)(2012•)有一组互不全等的三角形,它们的边长均为整数,每个三角形有两条边的长分别为5和7.(1)请写出其中一个三角形的第三边的长;(2)设组中最多有n个三角形,求n的值;(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.21.(10分)(2013•鄂尔多斯)如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.(1)求证:AF=DE;(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.22.(12分)(2012•)在平面直角坐标系,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).(1)当k=﹣2时,求反比例函数的解析式;(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.23.(12分)(2012•)如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3,MN=2.(1)求∠COB的度数;(2)求⊙O的半径R;(3)点F在⊙O上(是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC 的周长之比.2013年省市中考数学试卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.(3分)(2013•)下列“表情图”中,属于轴对称图形的是()A.B.C.D.2.(3分)(2013•)下列计算正确的是()A.m3+m2=m5B.m3•m2=m6C.(1﹣m)(1+m)=m2﹣1 D.3.(3分)(2013•)在▱ABCD中,下列结论一定正确的是()A.AC⊥BD B.∠A+∠B=180°C. AB=AD D.∠A≠∠C4.(3分)(2013•)若a+b=3,a﹣b=7,则ab=()A.﹣10 B.﹣40 C.10 D.405.(3分)(2013•)根据2008~2012年市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是()A.2010~2012年市每年GDP增长率相同B.2012年市的GDP比2008年翻一番C.2010年市的GDP未达到5500亿元D.2008~2012年市的GDP逐年增长6.(3分)(2013•)如图,设k=(a>b>0),则有()A.k>2 B.1<k<2 C.D.7.(3分)(2013•)在一个圆中,给出下列命题,其中正确的是()A.若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直B.若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有4个公共点C.若两条弦所在直线不平行,则这两条弦可能在圆有公共点D.若两条弦平行,则这两条弦之间的距离一定小于圆的半径8.(3分)(2013•)如图是某几何体的三视图,则该几何体的体积是()A.B.C.D.9.(3分)(2013•)在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于()A.B.C.D.10.(3分)(2013•)给出下列命题及函数y=x,y=x2和y=的图象:①如果,那么0<a<1;②如果,那么a>1;③如果,那么﹣1<a<0;④如果时,那么a<﹣1.则()A.正确的命题是①④B.错误的命题是②③④C.正确的命题是①②D.错误的命题只有③二、认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的容,尽量完整地填写答案11.(4分)(2013•)32×3.14+3×(﹣9.42)= .12.(4分)(2013•)把7的平方根和立方根按从小到大的顺序排列为.13.(4分)(2013•)在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是(只需填上正确结论的序号)14.(4分)(2013•)市某4所高中近两年的最低录取分数线如下表(单位:分),设4所高中2011年和2012年的平均最低录取分数线分别为,,则= 分市某4所高中最低录取分数线统计表学校2011年2012年A中438 442B中435 442C中435 439D中435 43915.(4分)(2013•)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1﹣S2|= (平方单位)(2013•)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,(4分)16.QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)三、全面答一答(本题有7个小题,共66分)解答应写出文字说明,证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(6分)(2013•)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现了什么?请写出一条.18.(8分)(2013•)当x满足条件时,求出方程x2﹣2x﹣4=0的根.19.(8分)(2013•)如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.求证:△GAB是等腰三角形.20.(10分)(2013•)已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2=x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值围.21.(10分)(2013•)某班有50位学生,每位学生都有一个序号,将50编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1卡片.(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.22.(12分)(2013•)(1)先求解下列两题:①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数的图象经过点B,D,求k的值.(2)解题后,你发现以上两小题有什么共同点?请简单地写出.23.(12分)(2013•)如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形关于直线AC 成轴对称,设它们的面积和为S1.(1)求证:∠APE=∠CFP;(2)设四边形CMPF的面积为S2,CF=x,.①求y关于x的函数解析式和自变量x的取值围,并求出y的最大值;②当图中两块阴影部分图形关于点P成中心对称时,求y的值.2014年省市中考数学试卷一、仔细选一选(本题有10个小题,每小题3分,共30分)1.(3分)(2014•)3a•(﹣2a)2=()A.﹣12a3B.﹣6a2C.12a3D.6a22.(3分)(2014•)已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm23.(3分)(2014•)在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=()A.3sin40°B.3sin50°C.3tan40°D.3tan50°4.(3分)(2014•)已知边长为a的正方形的面积为8,则下列说法中,错误的是()A.a是无理数B.a是方程x2﹣8=0的一个解C.a是8的算术平方根D.a满足不等式组5.(3分)(2014•)下列命题中,正确的是()A.梯形的对角线相等B.菱形的对角线不相等C.矩形的对角线不能相互垂直D.平行四边形的对角线可以互相垂直6.(3分)(2014•)函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是()A.y=B.y=C.y=D.y=7.(3分)(2014•)若(+)•w=1,则w=()A.a+2(a≠﹣2)B.﹣a+2(a≠2)C.a﹣2(a≠2)D.﹣a﹣2(a≠±2)8.(3分)(2014•)已知2001年至2012年市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图.由图得出如下四个结论:①学校数量2007年~2012年比2001~2006年更稳定;②在校学生人数有两次连续下降,两次连续增长的变化过程;③2009年的大于1000;④2009~2012年,相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.其中,正确的结论是()A.①②③④B.①②③C.①②D.③④9.(3分)(2014•)让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或是3的倍数的概率等于()A.B.C.D.10.(3分)(2014•)已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC对称,点E与点F关于BD对称,AC与BD相交于点G,则()A.1+tan∠ADB=B.2BC=5CFC.∠AEB+22°=∠DEF D.4cos∠AGB=二、认真填一填(本题共6个小题,每小题4分,共24分)11.(4分)(2014•)2012年末统计,市常住人口是880.2万人,用科学记数法表示为人.12.(4分)(2014•)已知直线a∥b,若∠1=40°50′,则∠2= .13.(4分)(2014•)设实数x、y满足方程组,则x+y= .14.(4分)(2014•)已知市某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数是℃.15.(4分)(2014•)设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为.16.(4分)(2014•)点A,B,C都在半径为r的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H.若BH=AC,则∠ABC所对的弧长等于(长度单位).三、全面答一答(本题共7小题,共66分)解答应写出文字说明,证明过程或演算步骤,如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(6分)(2014•)一个布袋中装有只有颜色不同的a(a>12)个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).请补全该统计图并求出的值.18.(8分)(2014•)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.19.(8分)(2014•)设y=kx,是否存在实数k,使得代数式(x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)能化简为x4?若能,请求出所有满足条件的k的值;若不能,请说明理由.20.(10分)(2014•)把一条12个单位长度的线段分成三条线段,其中一条线段成为4个单位长度,另两条线段长都是单位长度的整数倍.(1)不同分段得到的三条线段能组成多少个不全等的三角形?用直尺和圆规作这些三角形(用给定的单位长度,不写作法,保留作图痕迹);(2)求出(1)中所作三角形外接圆的周长.21.(10分)(2014•)在直角坐标系中,设x轴为直线l,函数y=﹣x,y=x的图象分别是直线l1,l2,圆P(以点P为圆心,1为半径)与直线l,l1,l2中的两条相切.例如(,1)是其中一个圆P的圆心坐标.(1)写出其余满足条件的圆P的圆心坐标;(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.22.(12分)(2014•)菱形ABCD的对角线AC,BD相交于点O,AC=4,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,BP=x.(1)用含x的代数式分别表示S1,S2;(2)若S1=S2,求x的值.23.(12分)(2014•)复习课中,教师给出关于x的函数y=2kx2﹣(4k+1)x﹣k+1(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选出以下四条:①存在函数,其图象经过(1,0)点;②函数图象与坐标轴总有三个不同的交点;③当x>1时,不是y随x的增大而增大就是y随x的增大而减小;④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法.2015年省市中考数学试卷一、仔细选一选(每小题3分,共30分)1.(3分)(2015•)统计显示,2013年底市各类高中在校学生人数大约是11.4万人,将11.4万用科学记数法表示应为()A.11.4×102B.1.14×103C.1.14×104D.1.14×1052.(3分)(2015•)下列计算正确的是()A.23+26=29B.23﹣24=2﹣1C.23×23=29D.24÷22=223.(3分)(2015•)下列图形是中心对称图形的是()A.B.C.D.4.(3分)(2015•)下列各式的变形中,正确的是()A.(﹣x﹣y)(﹣x+y)=x2﹣y2B.﹣x=C.x2﹣4x+3=(x﹣2)2+1 D.x÷(x2+x)=+15.(3分)(2015•)圆接四边形ABCD中,已知∠A=70°,则∠C=()A.20°B.30°C.70°D.110°6.(3分)(2015•)若k<<k+1(k是整数),则k=()A.6B.7C.8D.97.(3分)(2015•)某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108B.54﹣x=20%(108+x)C.54+x=20%×162D.108﹣x=20%(54+x)8.(3分)(2015•)如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112ug/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是()A.①②③B.①②④C.①③④D.②③④9.(3分)(2015•)如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为()A.B.C.D.10.(3分)(2015•)设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则()A.a(x﹣x2)=d B.a(x2﹣x1)=d C.a(x1﹣x2)2=d D.a(x1+x2)2=d1二、认真填一填(每小题4分,共24分)11.(4分)(2015•)数据1,2,3,5,5的众数是,平均数是.12.(4分)(2015•)分解因式:m3n﹣4mn= .13.(4分)(2015•)函数y=x2+2x+1,当y=0时,x= ;当1<x<2时,y随x 的增大而(填写“增大”或“减小”).14.(4分)(2015•)如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA 为α度,则∠GFB为度(用关于α的代数式表示).15.(4分)(2015•)在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y=的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=的图象经过点Q,则k= .16.(4分)(2015•)如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD= .三、全面答一答(共66分)17.(6分)(2015•)市推行垃圾分类已经多年,但在剩余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾.如图是某一天收到的厨余垃圾的统计图.(1)试求出m的值;(2)市那天收到厨余垃圾约200吨,请计算其中混杂着的玻璃类垃圾的吨数.18.(8分)(2015•)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.(2015•)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,(8分)19.则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B 关于⊙O的反演点,求A′B′的长.20.(10分)(2015•)设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数).(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;(2)根据图象,写出你发现的一条结论;(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.21.(10分)(2015•)“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).22.(12分)(2015•)如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC 于点E.(1)若=,AE=2,求EC的长;(2)设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P.问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.23.(12分)(2015•)方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为r(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇;….请你帮助方成同学解决以下问题:(1)分别求出线段BC,CD所在直线的函数表达式;(2)当20<y<30时,求t的取值围;(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过h与乙相遇,问丙出发后多少时间与甲相遇?2016年省市中考数学试卷一、填空题(每题3分)1. =()A.2 B.3 C.4 D.52.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c 于点D,E,F,若=,则=()A. B. C. D.13.下列选项中,如图所示的圆柱的三视图画确的是()A.B. C.D.4.如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是()A.14℃,14℃B.15℃,15℃ C.14℃,15℃ D.15℃,14℃5.下列各式变形中,正确的是()A.x2•x3=x6 B. =|x|C.(x2﹣)÷x=x﹣1 D.x2﹣x+1=(x﹣)2+6.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为()A.518=2 B.518﹣x=2×106 C.518﹣x=2 D.518+x=27.设函数y=(k≠0,x>0)的图象如图所示,若z=,则z关于x的函数图象可能为()A. B.C. D.8.如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则()A.DE=EB B.DE=EB C.DE=DO D.DE=OB9.已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则()A.m2+2mn+n2=0 B.m2﹣2mn+n2=0 C.m2+2mn﹣n2=0 D.m2﹣2mn﹣n2=010.设a,b是实数,定义的一种运算如下:ab=(a+b)2﹣(a﹣b)2,则下列结论:①若ab=0,则a=0或b=0;②a(b+c)=ab+ac;③不存在实数a,b,满足ab=a2+5b2;④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,ab最大.其中正确的是()A.②③④ B.①③④ C.①②④ D.①②③二、填空题(每题4分)11.tan60°=.12.已知一包糖果共有5种颜色(糖果只有颜色差别),如图是这包糖果分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是.13.若整式x2+ky2(k为不等于零的常数)能在有理数围因式分解,则k的值可以是(写出一个即可).14.在菱形ABCD中,∠A=30°,在同一平面,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为.15.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为.16.已知关于x的方程=m的解满足(0<n<3),若y>1,则m的取值围是.三、解答题17.计算6÷(﹣),方方同学的计算过程如下,原式=6+6=﹣12+18=6.请你判断方方的计算过程是否正确,若不正确,请你写出正确的计算过程.18.某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?19.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.20.把一个足球垂直水平地面向上踢,时间为t (秒)时该足球距离地面的高度h (米)适用公式h =20t ﹣5t 2(0≤t ≤4).(1)当t =3时,求足球距离地面的高度; (2)当足球距离地面的高度为10米时,求t ;(3)若存在实数t 1,t 2(t 1≠t 2)当t =t 1或t 2时,足球距离地面的高度都为m (米),求m 的取值围.21.如图,已知四边形ABCD 和四边形DEFG 为正方形,点E 在线段DE 上,点A ,D ,G 在同一直线上,且AD =3,DE =1,连接AC ,CG ,AE ,并延长AE 交CG 于点H . (1)求sin ∠EAC 的值. (2)求线段AH 的长.22.已知函数y 1=ax 2+bx ,y 2=ax +b (ab ≠0).在同一平面直角坐标系中.(1)若函数y 1的图象过点(﹣1,0),函数y 2的图象过点(1,2),求a ,b 的值. (2)若函数y 2的图象经过y 1的顶点.①求证:2a +b =0;②当1<x <时,比较y 1,y 2的大小.23.在线段AB 的同侧作射线AM 和BN ,若∠MAB 与∠NBA 的平分线分别交射线BN ,AM 于点E ,F ,AE 和BF 交于点P .如图,点点同学发现当射线AM ,BN 交于点C ;且∠ACB =60°时,有以下两个结论:①∠APB =120°;②AF +BE =A B . 那么,当AM ∥BN 时:(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB 的度数,写出AF ,BE ,AB 长度之间的等量关系,并给予证明;(2)设点Q 为线段AE 上一点,QB =5,若AF +BE =16,四边形ABEF 的面积为32,求AQ的长.2017年省市中考数学试卷一.选择题1.(3分)﹣22=()A.﹣2 B.﹣4 C.2 D.42.(3分)太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为()A.1.5×108B.1.5×109C.0.15×109D.15×1073.(3分)如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则()A.B.C.D.4.(3分)|1+|+|1﹣|=()A.1 B.C.2 D.25.(3分)设x,y,c是实数,()A.若x=y,则x+c=y﹣c B.若x=y,则xc=ycC.若x=y,则D.若,则2x=3y6.(3分)若x+5>0,则()A.x+1<0 B.x﹣1<0 C.<﹣1 D.﹣2x<127.(3分)某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次.设参观人次的平均年增长率为x,则()A.10.8(1+x)=16.8 B.16.8(1﹣x)=10.8C.10.8(1+x)2=16.8 D.10.8[(1+x)+(1+x)2]=16.88.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则()A.l1:l2=1:2,S1:S2=1:2 B.l1:l2=1:4,S1:S2=1:2C.l1:l2=1:2,S1:S2=1:4 D.l1:l2=1:4,S1:S2=1:49.(3分)设直线x=1是函数y=ax2+bx+c(a,b,c是实数,且a<0)的图象的对称轴,()A.若m>1,则(m﹣1)a+b>0 B.若m>1,则(m﹣1)a+b<0C.若m<1,则(m﹣1)a+b>0 D.若m<1,则(m﹣1)a+b<010.(3分)如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则()A.x﹣y2=3 B.2x﹣y2=9 C.3x﹣y2=15 D.4x﹣y2=21二.填空题11.(4分)数据2,2,3,4,5的中位数是.12.(4分)如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB= .13.(4分)一个仅装有球的不透明布袋里共有3个球(只有颜色不同),其中2个是红球,1个是白球,从中任意摸出一个球,记下颜色后放回,搅匀,再任意摸出一个球,则两次摸出都是红球的概率是.14.(4分)若•|m|=,则m= .15.(4分)如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于.16.(4分)某水果点销售50千克香蕉,第一天售价为9元/千克,第二天降价6元/千克,第三天再降为3元/千克.三天全部售完,共计所得270元.若该店第二天销售香蕉t千克,则第三天销售香蕉千克.(用含t的代数式表示.)三.解答题17.(6分)为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).某校九年级50名学生跳高测试成绩的频数表组别(m)频数1.09~1.1981.19~1.29121.29~1.39A1.39~1.4910(1)求a的值,并把频数直方图补充完整;(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.18.(8分)在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)当﹣2<x≤3时,求y的取值围;(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.19.(8分)如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC 于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.20.(10分)在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)设矩形的相邻两边长分别为x,y.①求y关于x的函数表达式;②当y≥3时,求x的取值围;(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?21.(10分)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.。
2012年浙江省杭州市中考数学试卷-答案

浙江省杭州市2012年各类高中招生文化考试数学答案解析一、仔细选一选 1.【答案】A【解析】(23)(1)-+-1(1)=-+-2=-【提示】根据有理数的加减混合运算的法则进行计算即可得解. 【考点】有理数的加减混合运算. 2.【答案】B【解析】∵两圆的半径分别为2cm 和6cm ,圆心距为4cm.则624d =-=,∴两圆内切. 【提示】两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d R r >+则两圆相离,若d R r =+则两圆外切,若d R r =-则两圆内切,若R r d R r -<<+则两圆相交.本题可把半径的值代入,看符合哪一种情况. 【考点】圆与圆的位置关系. 3.【答案】D【解析】A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.摸到红球比摸到白球的可能性相等,根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确;【提示】利用随机事件的概念,以及个数最多的就得到可能性最大分别分析即可. 【考点】可能性的大小,随机事件. 4.【答案】B【解析】∵四边形ABCD 是平行四边形,∴C A ∠=∠,BC AD ∥,∴180A B ∠+∠=︒,∵4B A ∠=∠, ∴36A ∠=︒,∴36C A ∠=∠=︒【提示】关键平行四边形性质求出C A ∠=∠,BC AD ∥,推出180A B ∠+∠=︒,求出A ∠的度数,即可求出C ∠【考点】平行四边形的性质,平行线的性质. 5.【答案】D【解析】A.2363()p q p q -=-,故本选项错误;B.232)(()1262a b c ab abc ÷=,故本选项错误;AB︒,AO︒,∵sin54sin36AB︒︒=︒︒,故本选项正确;sin54sin36sin54sin36:由以上可知,选项错误;【提示】根据图形得出B到AO的距离是指BO的长,过AB︒,求出sin54下底面积,又由该棱柱侧面展开图的面积为2002cm ,即可求得底面菱形的周长与BC 边上的高AE 的长,由勾股定理求得BE 的长,继而求得CE 的长.【考点】菱形的性质,认识立体图形,几何体的展开图.16.【答案】()(112),2---,, 【解析】如图所示:1,12,2()()A A '''---,,故答案为:()(112),2---,,.【提示】根据轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,把A 进行移动可得到点的坐标,注意考虑全面. 【考点】利用轴对称设计图案. 三、全面答一答17.【答案】原式3(2)m =-,表示3个2m -相乘【解析】[][]2(1)(1)(1)(1)m m m m m m m m -++--+,2222()()2m m m m m m m m =-++---,38m =-,原式3(2)m =-,表示3个2m -相乘.【提示】根据单项式乘以多项式法则先计算括号里的乘法,再去括号合并同类项,即可算出结果. 【考点】整式的混合运算—化简求值.18.【答案】∵当开口向下时函数2(1)45y k x x k =--+-都有最大值 ∴10k -<解得1k <∴当1k =-时函数2(1)45y k x x k =--+-有最大值∴函数222462(1)8y x x x =--+=-++,故最大值为8.【提示】首先根据函数有最大值得到k 的取值范围,然后判断即可. 【考点】二次函数的最值. 19.【答案】(1)如图所示:)HB,AB )222a a +=,∴22a +m切O 于点E ,∴AEC OBC △∽△,又30A ∠=︒,∴30COB A ∠=∠=︒;点在圆上的三角形,如图所示:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.2012年浙江省杭州市中考数学试卷姓名班级一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确的答案.1.计算(2﹣3)+(﹣1)的结果是()A.﹣2B.0C.1D.22.若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是()A.内含B.内切C.外切D.外离3.一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球与摸到白球的可能性相等D.摸到红球比摸到白球的可能性大4.)已知平行四边形ABCD中,∠B=4∠A,则∠C=()A.18°B.36°C.72°D.144°5.下列计算正确的是()235323222A.(﹣pq)=﹣pq B.(12abc)÷(6ab)=2ab C.3m÷(3m﹣1)=m﹣3m2 1x4=x﹣.(x﹣4x)D )6.如图是杭州市区人口的统计图.则根据统计图得出的下列判断,正确的是(A.其中有3个区的人口数都低于40万B.只有1个区的人口数超过百万C.上城区与下城区的人口数之和超过江干区的人口数D.杭州市区的人口数已超过600万=,则有(.已知m)7A.5<m<6B.4<m<5C.﹣5<m<﹣4D.﹣6<m<﹣58.如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则();..A.点B到AO的距离为sin54°B.点B到AO的距离为tan36°C.点A到OC的距离为sin36°sin54°D.点A到OC的距离为cos36°sin54°﹣)与x轴交于点A,B,与y)(x轴交于点C,则能使△ABC为(9.已知抛物线y=kx+1等腰三角形的抛物线的条数是()A.2B.3C.4D.5的方程组,其中﹣3≤a≤1,给出下列结论:.已知关于10x,y①是方程组的解;②当a=﹣2时,x,y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④若x≤1,则1≤y≤4.其中正确的是()A.①②B.②③C.②③④D.①③④二、认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的内容,尽量完整的填写答案.11.数据1,1,1,3,4的平均数是;众数是..化简得;当m=﹣1时,原式的值为12 .13.某企业向银行贷款1000万元,一年后归还银行1065.6多万元,则年利率高于%.﹣)<0,若b=2﹣a,则b的取值范围是14.已知(a.315.已知一个底面为菱形的直棱柱,高为10cm,体积为150cm,则这个棱柱的下底面积为22cm;若该棱柱侧面展开图的面积为200cm,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为cm.16.如图,平面直角坐标系中有四个点,它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横坐标仍是整数,则移动后点A的坐标为.;..三、全面答一答(本题有7个小题,共66分)解答应写出文字说明,证明过程或演算步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.(6分)17.化简:2[(m﹣1)m+m(m+1)][(m﹣1)m﹣m(m+1)].若m是任意整数,请观察化简后的结果,你发现原式表示一个什么数?2都有最大值吗?请写出你kx+5﹣1)x﹣4kk分别取﹣1,1,2时,函数y=(﹣(8分)18.当的判断,并说明理由;若有,请求出最大值..=5a=4a,AC=3,已知△ABC中,ABa,BC其单位长度为(8分)19.如图,是数轴的一部分,a在数轴上,保留作图痕迹,不必写出作,CABC)用直尺和圆规作出△(要求:使点A(1 法);.>,试说明π,ABC的外接圆的面积为S△ABC的面积为S(2)记△△圆每个三角形有两条边的长分别分(10)20.有一组互不全等的三角形,它们的边长均为整数,为5和7.(1)请写出其中一个三角形的第三边的长;的值;n个三角形,求n(2)设组中最多有)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.(3为边向外侧作等边CD,BCAB=CD,分别以AB,中,分(10)21.如图,在梯形ABCDAD∥,连接AF,.DEDCF三角形ABE和等边三角形DE=;1()求证:AF的的面积,求的面积之和等于梯形△ABE,=,BAD2()若∠=45°ABa△和DCFABCDBC长.;..2,(11)的图象交于点A﹣反比例函数和二次函数y=k(x+x(12分)22.在平面直角坐标系中,).(﹣1,﹣kk)和点B 2时,求反比例函数的解析式;)当k=﹣(1的应满足的条件以及x随着x的增大而增大,求k(2)要使反比例函数和二次函数都是y 取值范围;k的值.是以AB为斜边的直角三角形时,求(3)设二次函数的图象的顶点为Q,当△ABQ于点AT,OB⊥,线段OE交AT于点C切⊙AEO于点E,AT交⊙O于点M,N23.如图,.=2,AEMN=3,B,已知∠EAT=30°的度数;)求∠COB(1 ;的半径R(2)求⊙O经过平移、旋转和相似变换后,使△,把OBC是劣弧),且EF(3)点F在⊙O=5上(它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.;..答案:1考点:有理数的加减混合运算。
专题:计算题。
分析:根据有理数的加减混合运算的法则进行计算即可得解.解答:解:(2﹣3)+(﹣1),=﹣1+(﹣1),=﹣2.故选A.点评:本题主要考查了有理数的加减混合运算,是基础题比较简单.2考点:圆与圆的位置关系。
分析:两圆的位置关系有5种:①外离;②外切;③相交;④内切;⑤内含.若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d<R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.解答:解:∵两圆的半径分别为2cm和6cm,圆心距为4cm.则d=6﹣2=4,∴两圆内切.故选B.点评:本题主要考查两圆的位置关系.两圆的位置关系有:外离(d>R+r)、内含(d<R﹣r)、相切(外切:d=R+r或内切:d=R﹣r)、相交(R﹣r<d<R+r).3考点:可能性的大小;随机事件。
分析:利用随机事件的概念,以及个数最多的就得到可能性最大分别分析即可.解答:解:A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.摸到红球比摸到白球的可能性相等,根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确;故选:D.点评:此题主要考查了随机事件以及可能性大小,利用可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等得出是解题关键.4考点:平行四边形的性质;平行线的性质。
专题:计算题。
分析:关键平行四边形性质求出∠C=∠A,BC∥AD,推出∠A+∠B=180°,求出∠A的度数,;. .即可求出∠C.解答:解:∵四边形ABCD是平行四边形,∴∠C=∠A,BC∥AD,∴∠A+∠B=180°,∵∠B=4∠A,∴∠A=36°,∴∠C=∠A=36°,故选B.点评:本题考查了平行四边形性质和平行线的性质的应用,主要考查学生运用平行四边形性质进行推理的能力,题目比较好,难度也不大.5考点:整式的混合运算;负整数指数幂。
分析:根据幂的乘方,积的乘方、整式的乘法、同底数幂的乘法和除法分别进行计算,即可判断.2363解答:解:A、(﹣pq)=﹣pq,故本选项错误;232B、12abc)÷(6ab)=2abc,故本选项错误;2,故本选项错误;=1)3、m÷(3m﹣C12﹣D、(x﹣4x)x=x﹣4,故本选项正确;故选D.点评:此题考查了整式的混合运算,用到的知识点是幂的乘方,积的乘方、整式的乘法、同底数幂的乘法和除法等,需熟练掌握运算法则,才不容易出错.6.考点:条形统计图。
分析:根据条形统计图可以看出每个区的人口数,根据每个区的人口数进行判断,可选出答案.解答:解:A、只有上城区人口数都低于40万,故此选项错误;B、萧山区、余杭区两个区的人口超过100万,故此选项错误;C、上城区与下城区的人口数之和低于江干区的人口数,故此选项错误;D、杭州市区的人口数已超过600万,故此选项正确;故选:D.点评:此题主要考查了条形统计图,关键是从图中获取正确信息,从条形统计图中很容易看出数据的大小,便于比较.7.考点:二次根式的乘除法;估算无理数的大小。
专题:推理填空题。
;..分析:()的范围5<m<6求出m的值,求出,即可得出选项.2解答:)2,(﹣)×解:m=(﹣,=3×,==,=2<,∵<<<65,∴即5<m<6,故选A.点评:<<6题考查了二次根式的乘法运算和估计无理数的大小的应用,注意:5,题本目比较好,难度不大.8.考点:解直角三角形;点到直线的距离;平行线的性质。
分析:根据图形得出B到AO的距离是指BO的长,过A作AD⊥OC于D,则AD的长是点A 到OC的距离,根据锐角三角形函数定义得出BO=ABsin36°,即可判断A、B;过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出AD=AOsin36°,AO=AB?sin54°,求出AD,即可判断C、D.解答:解:A、B到AO的距离是指BO的长,∵AB∥OC,∴∠BAO=∠AOC=36°,∵在Rt△BOA中,∠BOA=90°,AB=1,=,36°∴sin∴BO=ABsin36°=sin36°,故本选项错误;B、由以上可知,选项错误;C、过A作AD⊥OC于D,则AD的长是点A到OC的距离,∵∠BAO=36°,∠AOB=90°,∴∠ABO=54°,=,sin36°∵∴AD=AO?sin36°,=,sin∵54°;..∴AO=AB?sin54°,∴AD=AB?sin54°?sin36°=sin54°?sin36°,故本选项正确;D、由以上可知,选项错误;故选C.点评:本题考查了对解直角三角形和点到直线的距离的应用,解此题的关键是①找出点A到OC的距离和B到AO的距离,②熟练地运用锐角三角形函数的定义求出关系式,题目较好,但是一道比较容易出错的题目.9.考点:抛物线与x轴的交点。
