初中数学知识结构体系框架图
初中、小学数学知识结构图

初中、小学数学知识结构图一、小学数学知识结构图⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧可能性平均数、中位数、众数统计表、统计图统计与概率图形与位置旋转对称图形与变换表面积、体积球圆锥圆柱—正方体—长方体立体图形周长和面积圆—正方形——长方形—平行四边形梯形四边形四边形钝角三角形直角三角形锐角三角形三角形角直线、射线、线段平面图形空间与图形比例比比和比例单位之间的进率量单位体积(容积)单位、质长度单位、面积单位、常见的量方程用字母表示数式与方程混合运算的顺序运算定律则运算整数、小数、分数的四数的运算数因数、倍数、质数、合分数然数、小数、分数、百正数、负数、整数、自比较数的大小十进制计数法数的认识数与代数.3.2.1。
二、初中数学知识结构图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧锐角三角函数二次函数反比例函数一次函数函数分式方程分式的四则运算分式一元一次不等式一元二次方程二(三)元一次方程组一元一次方程整式方程乘法公式与因式分解整式的四则运算整式式与方程、不等式立方根—二次根式的四则运算—平方根无理数有理数的乘方有理数的四则运算整数与负数有理数实数的认识与运算数与代数.1⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧位似投影与视图旋转中心对称轴对称对称平移图形与变换平面直角坐标系弧长和扇形面积正多边形和圆置关系点、直线、圆和圆的位圆重心—特殊的平行四边形—平行四边形梯形四边形—多边形的内角和—多边形锐角三角函数相似三角形勾股定理与逆定理等腰三角形全等三角形与三角形有关的角与三角形有关的线段三角形角平分线系角的大小关系、位置关角的分类角平行线的性质平行线的判定平行线相交线直线、射线、线段平面图形空间与图形.2⎪⎪⎪⎩⎪⎪⎪⎨⎧随机事件的概率数据的波动数据的代表直方图调查统计统计与概率.3。
初中数学知识点及结构图
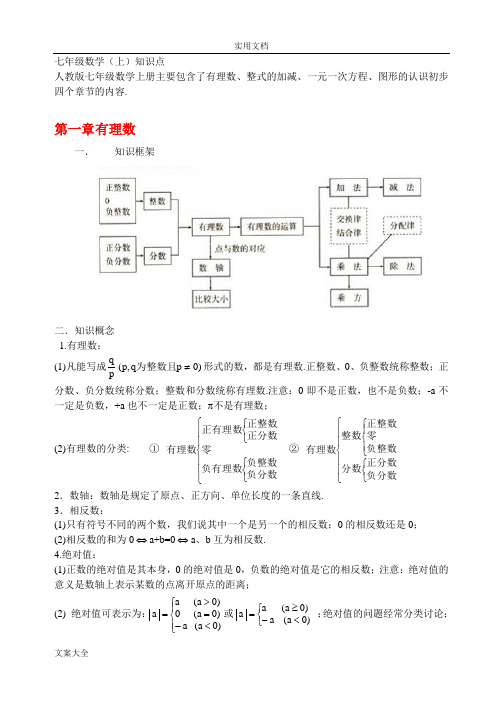
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识点及结构图

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识点框架图.

线段 高:高的作法及高的位置(可以在三角形的内部、边上、外部)
中位线:三角形的中位线平行于第三边且等于第三边的一半.
三角形
性质:线段垂直平分线上的点到线段两端点的距离相等; 中垂线 判定:到线段两端点的距离相等的点在线段的垂直平分线上.
外心:三角形三边垂直平分线的交点,到三个顶点的距离相等
性质 等腰三角形的两腰相等、两底角相等,具有三线合一性质,是轴对称图.形 等边三角形的三边上均有三线合一,三边相等,三角形等都6为0度.
单项式 单项式;多项式 单项式
混合运算:先乘方开方,再乘除,最后算加减;同级运算自左至右顺序计算;括号优先
乘法公式 平方差公式:(a b)(a b) a2 b2 完全平方公式:(a b)2 a2 2ab b2
分式的定义:分母中含可变字母
分式 分式有意义的条件:分母不为零
数与式
分式值为零的条件:分子为零,分母不为零
定义与解:
解法:代入消元法、加减消元法
二元一次方程(组)
方程
简单的三元一次方程组:
简单的二元二次方程组:
定义与判别式 ( △=b2 -4ac) 一元二次方程
解法:直接开平方法、配方法、求根公式法、因式分解法 .
定义与根(增根): 分式方程
解法:去分母化为整 式方程,解整式方程,验根 .
1. 行程问题:
’
1
60”;
余角与补角的性质:同角的余角(补角)相等,等角的余角(补角)相等,
角的位置关系:同位角、内错角、同旁内角、对顶角、邻补角
对顶角:对顶角相等 . 几何初步 相交线
垂线:定义,垂直的判定,垂线段最短 .
定义:在同一平面内,不相交的两条直线叫平行线 平行 线 性质:两直线平行,同位角相等、内错角相等、同旁内角互补;
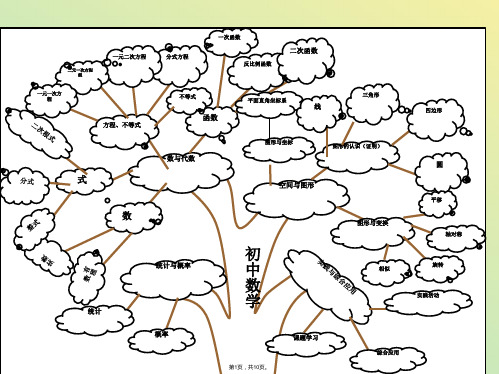
初中数学知识结构图思维导图(与“性质”相关文档)共10张PPT
法
公式
法
配方
法
直接
有一交点
( b,0)
2a
Δ=0
有两个等根
b x1= x2 = 2a
开平 方法
无交
Δ<0点Βιβλιοθήκη 关系 二次函数无实 根
解法
一元二次方程
应用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开向口上方向a<. 0.向a>下0.对置称轴在左y同轴右的异位半负轴半轴c=0.在原点
c<0.在
余角.补角
性质
等角的余角相等 等角的补角相等
和 为1800
相
定义 性质
等
一“放”二“靠” 三“推”四“画”
角的比较
角的比较与运算
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量
借助角研究平面内两条直 线的位置关系
相交线
图形认识初步
关系
相交线.平行线
判定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
性质
同位角相等 内错角相等
特
对应点与旋转中心所连线段的夹角=
征
旋转角
图形的 全等变 换
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其自身 重合
对称中心是对称点连线的中 点
对应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
直线.射线.线段
同旁内角互补
数学学霸整理:初中数学知识框架图,细致直...

数学学霸整理:初中数学知识框架图,细致直...
数学学霸整理:初中数学知识框架图,细致直观凸显重点,家里有孩子上初中,收藏下来暑假吃透了!
数学作为三大主科之一,也一直都是令同学们非常头疼的一门科目,尤其是初中数学。
初中数学是孩子数学学习的过渡阶段,承接小学,衔接高中,可以说初中数学是孩子为高中数学习打基础的时期。
小学的数学,知识内容浅,同学们通过刻苦努力就能取得好成绩。
进入初中后,随着课程的增多及学习内容的加深拓宽,尤其是数学从具体到抽象,静态到动态,由文字发展到符号、图形……学习内容发生了根本性的变化,同学们的认知结构也要发生变化。
数学这门学科说简单也简单,说难也难,对于基础好,思维能力强的学生而言,数学的学习就非常简单,但是对于思维能力不好,并且基础不扎实的学生来说,数学的学习就非常难。
尤其是初中阶段,数学的学习两极分化的情况更是明显。
初中数学的难度并不大,之所以一部分学生的成绩不理想,最主要的原因还是在基础方面吃了亏。
因此,老师今天就分享一位数学学霸整理的初中数学知识框架图,非常的全面,包含了3年的重点基础知识,家长们替孩子打印一份下来,趁着暑假的时间掌握好!
如果你觉得不错,欢迎留言……
#教育微头条##微头条名师团##知识分享#。
初中数学知识点框架图

初中数学知识点框架图数学是一门理论和实践相结合的科学,它涉及到许多不同的领域和知识点。
初中阶段是数学学习的基础阶段,学生将会接触到一系列的数学概念、原理和技巧。
下面是一个初中数学知识点的框架图,以帮助学生整理和理解数学知识的体系结构。
整数与有理数- 整数的概念:自然数、零、负数- 整数的运算:加法、减法、乘法、除法- 整数的性质:交换律、结合律、分配律等- 有理数的概念:正有理数、负有理数、零、分数- 有理数的比较:大小关系、绝对值、相反数等- 有理数的运算:加法、减法、乘法、除法- 有理数的性质:交换律、结合律、分配律等代数式与方程- 代数式的概念:字母、表达式、项、系数、指数等- 代数式的运算:加法、减法、乘法、除法- 代数式的化简:合并同类项、消去括号等- 一元一次方程:解的概念、方程的解法、实际问题的应用等- 一元一次方程的运算:加减法、乘除法、等式的性质等- 一元一次方程组:解的概念、方程组的解法、实际问题的应用等比例与变量- 比例的概念:比例关系、比例常数、比例的性质等- 比例的运算:比例的四则运算、比例的性质等- 百分数与分数:百分数的概念、百分数的转化、百分数的运算等- 比例与百分数的应用:物品折扣、人口增长、利润计算等- 变量的概念:未知数、代数式、函数等- 变量的运算:代数式的计算、代数式的化简、代入值等- 函数的概念:自变量、因变量、函数的图像等- 函数的运算:函数的四则运算、复合函数、反函数等几何与图形- 点、线、面的基本概念:点的坐标、线段、直线、射线、角、多边形等- 几何关系:相交、垂直、平行、全等、相似等- 三角形与四边形:三角形的分类、三角形的性质、四边形的分类、四边形的性质等- 圆的概念:半径、直径、圆周长、圆面积等- 测量与度量:长度、面积、体积、角度等- 坐标系与图形:直角坐标系、平面直角坐标系、点的坐标、图形的对称等数据与统计- 数据的收集和整理:样本、调查、图表、统计量等- 数据的表示与分析:频数、频率、直方图、折线图、饼图等- 数据的比较与推测:平均数、中位数、众数、范围、误差、抽样等数学思想与方法- 探究与证明:归纳法、演绎法、逆否命题、数学归纳法等- 问题解决与建模:问题解决的步骤、数学建模的过程等- 推理与判断:逻辑关系、命题关系、真值表等- 数学思维与技巧:分析能力、抽象能力、推理能力、创造能力等以上是初中数学知识点的框架图,涵盖了整数与有理数、代数式与方程、比例与变量、几何与图形、数据与统计以及数学思想与方法等多个方面的内容。
初中数学知识框架图
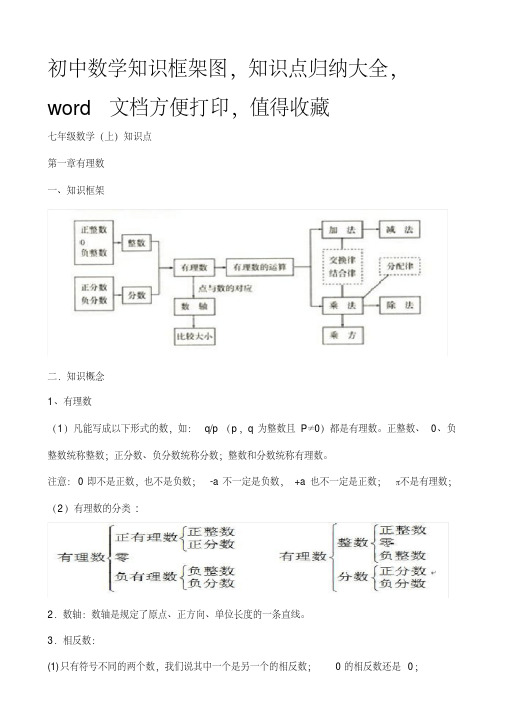
初中数学知识框架图,知识点归纳大全,word文档方便打印,值得收藏七年级数学(上)知识点第一章有理数一、知识框架二.知识概念1、有理数(1)凡能写成以下形式的数,如:q/p(p,q为整数且P≠0)都是有理数。
正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数。
注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;π不是有理数;(2)有理数的分类:2.数轴:数轴是规定了原点、正方向、单位长度的一条直线。
3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0,a+b=0 ,a、b互为相反数。
4、绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为或者:绝对值的问题经常讨论。
5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数>0,小数-大数<0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若a≠0,那么它的倒数是1/a;若ab=1,a、b互为倒数;若ab=-1,a、b互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);(3)乘法的分配律:a(b+c)=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,即a/0没有意义。
初中数学知识结构图思维导图(中考复习)
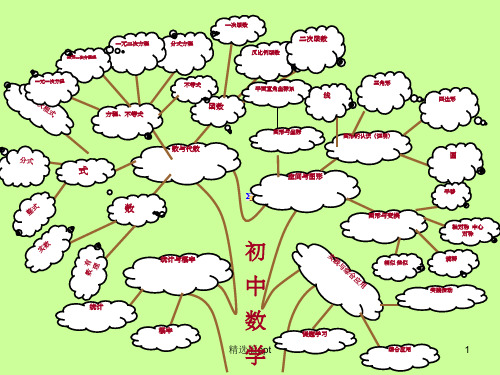
应用
坡度 仰.俯角 方位角
正弦
余弦
符号.几何意义. 特殊角的值
特殊值的运算
正切
精选版ppt
6
作对称轴 作一点到两点距离相等 等(外心)
作等腰三角形 作一点到三点距离相
翻折后与 另一图形重合
到两点距离相等的点
点到两点 的距离相 等
性质
判定
应用
垂直平分线
定义
对称点
关于轴对称
基本 图形
对称 轴
特征
要素
利用轴对称制作图案
法
直接
开平
有一交点
Δ=0
有两个等根
方法
( b,0)
b x1= x2 =
2a
2a
无交
Δ<0
点
关系 二次函数
无实 根
解法
一元二次方程
应用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开口上方a向<. 0.向a>下0.向对置称轴在左y同轴右的异位半 在轴 负半c=轴0.在原点
c<0.
解析
二次函数 与 一元二
动
应用
性质
特征
对应角相等, 周长的比=相似比 方
(1) aa0双非负
2
(2 ) a a (a 0 )
(3) a2 a
2
Y随 x的 增大 而增 大
b>0,图象在 一二三象限
y ox
y
b>0,图象在
o
x 一二四象限
b=0,图象在 一三象限
b<0,图象在 一三四象限
y
y
b=0,图象在
注意:过原点
二四象限
ox
ox
y
七年级数学知识点框架图

七年级数学知识点框架图
数学作为一个重要的学科,对于我们的学习和生活有着很大的影响。
而对于七年级的同学们来说,数学课程中有很多重要的知识点需要掌握。
为了帮助同学们更好地掌握这些知识点,今天我们来总结一下七年级常见的数学知识点框架图。
一、代数知识点框架图
1.代数式的概念
2.整式和分式的概念
3.代数式的加减法
4.代数式的乘法
5.代数式的除法
6.因式分解
7.整式乘除法
8.分式的乘法和除法
9.一元一次方程的概念
10.一元一次方程的计算
11.字母代数式的应用
二、几何知识点框架图
1.图形的基本概念
2.直线和线段的概念
3.角的概念
4.相交线与平行线
5.三角形的分类
6.三角形的性质
7.四边形的分类
8.平行四边形的性质
9.梯形和菱形的性质
10.圆的基本概念
11.圆的性质
三、数据统计知识点框架图
1.数据的呈现方式
2.数据的中心趋势
3.数据的离散程度
4.频数分布表的制作和分析
5.统计图的制作和分析
四、函数知识点框架图
1.函数的基本概念
2.函数的性质
3.函数的图像
4.一次函数和二次函数
5.函数的应用
以上内容是七年级数学课程中常见的知识点框架图,同学们可以根据这些知识点有目的地进行学习和复习。
在学习过程中,我们需要注意的是,这些知识点之间是相互关联的,所以我们要注意学习它们之间的联系和应用。
同时,还要多做练习,提高自己的数学素养,成为一个优秀的数学学习者。
初中数学知识点及结构图(新人教版)

1 -七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).2 -10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识点及结构图(新人教版)

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学各年级教材知识体系框架及教材各章节简介

初中数学各年级教材知识体系框架及教材各章节简介(一)体系框架(7~9年级)(二)体例结构各章基本结构如下:各节结构根据内容需要而确定,基本上包括以下部分:人教版数学七年级上各章节简介“第一章有理数”简介(新)本章是第三学段教科书的第一章,既承接前两个学段的内容,又为进一步学习打下基础。
本章主要内容是有理数的有关概念及其运算。
首先,从实例出发引入负数,接着引进关于有理数的一些概念,在此基础上,介绍有理数的运算。
本章教学时间约需19课时,具体安排如下:1.1 正数和负数约2课时1.2 有理数约4课时1.3 有理数的加减法约4课时1.4 有理数的乘除法约4课时1.5 有理数的乘方约3课时数学活动小结约2课时一、教科书内容和课程学习目标本章知识结构框图如下:引入负数是实际的需要,也是学习第三学段数学内容,特别是数与代数内容的需要。
引进数轴可以把有理数用数轴上的一个点直观地表示出来,从而可以直观地介绍相反数、绝对值,同时为用数轴引进有理数的加法法则与乘法法则作准备。
引入相反数的概念,一方面,可以加深对相反意义的量的认识,另一方面,可以为学习绝对值、有理数减法等作准备。
引入绝对值的的概念,可以加深对有理数的认识:一个有理数由符号与绝对值确定。
两个负数比较大小,有理数运算也要借助绝对值这个概念。
本章的重点是有理数的运算。
加法与乘法都是在介绍运算法则——着重是符号法则的基础上,进行基本运算,然后结合具体例子引入运算律,并运用运算律简化运算。
减法与除法,则是着重介绍如何向加法与乘法转化,从而利用加法与乘法的运算法则、运算律进行运算。
乘方是几个相同因数的乘积,也就可以利用乘法运算。
科学记数法与乘方有关,因而可进一步加以介绍。
近似数在实际问题中有广泛的应用,有必要在本章作进一步的认识。
利用计算器计算分两次安排,一次在加减乘除运算之后,一次在乘方运算之后。
学会了使用计算器进行有理数运算,较复杂的计算就可以用计算器完成。
