高三理科数学必修4练习答案
人教版高中数学必修4课后习题答案详解05042

第二章 平面向量2.1平面向量的实际背景及基本概念 练习(P77)1、略.2、AB u u u r,BA u u u r . 这两个向量的长度相等,但它们不等.3、2AB =u u u r , 2.5CD =u u u r ,3EF =u u u r,GH =u u u r4、(1)它们的终点相同; (2)它们的终点不同. 习题2.1 A 组(P77) 1、(2). 3、与DE u u u r 相等的向量有:,AF FC u u u r u u u r ;与EF u u u r相等的向量有:,BD DA u u u r u u u r ; 与FD u u u r相等的向量有:,CE EB u u u r u u u r .4、与a r 相等的向量有:,,CO QP SR u u u r u u u r u u r ;与b r 相等的向量有:,PM DO u u u u r u u u r; 与c r 相等的向量有:,,DC RQ ST u u u r u u u r u uu r5、AD =u u u r .6、(1)×; (2)√; (3)√; (4)×.习题2.1 B 组(P78)1、海拔和高度都不是向量.2、相等的向量共有24对. 模为1的向量有18对. 其中与AM u u u u r同向的共有6对,与AM u u u u r 反向的也有6对;与AD u u u r 同向的共有3对,与AD u u u r反向的也有6的向量共有4对;模为2的向量有2对 2.2平面向量的线性运算 练习(P84)1、图略.2、图略.3、(1)DA u u u r; (2)CB u u u r .4、(1)c r ; (2)f u r ; (3)f u r ; (4)g u r . 练习(P87)1、图略.2、DB u u u r ,CA u u u r ,AC u u u r ,AD u u u r ,BA u u u r. 3、图略. 练习(P90) 1、图略.2、57AC AB =u u u r u u u r ,27BC AB =-u u u r u u u r .说明:本题可先画一个示意图,根据图形容易得出正确答案. 值得注意的是BCuuu r与AB u u u r反向.3、(1)2b a =r r ; (2)74b a =-r r ; (3)12b a =-r r; (4)89b a =r r .4、(1)共线; (2)共线.5、(1)32a b -r r ; (2)111123a b -+r r; (3)2ya r . 6、图略.习题2.2 A 组(P91)1、(1)向东走20 km ; (2)向东走5 km ;(3)向东北走km ;(4)向西南走;(5)向西北走;(6)向东南走km. 2、飞机飞行的路程为700 km ;两次位移的合成是向北偏西53°方向飞行500 km.3、解:如右图所示:AB u u u r 表示船速,AD u u u r表示河水的流速,以AB 、AD 为邻边作□ABCD ,则 AC u u u r表示船实际航行的速度.在Rt △ABC 中,8AB =u u u r ,2AD =u u u r,所以AC ===u u u r 因为tan 4CAD ∠=,由计算器得76CAD ∠≈︒所以,实际航行的速度是km/h ,船航行的方向与河岸的夹角约为76°.4、(1)0r ; (2)AB u u u r ; (3)BA u u u r ; (4)0r ; (5)0r ; (6)CB u u u r ; (7)0r .5、略6、不一定构成三角形. 说明:结合向量加法的三角形法则,让学生理解,若三个非零向量的和为零向量,且这三个向量不共线时,则表示这三个向量的有向线段一定能构成三角形.7、略. 8、(1)略; (2)当a b ⊥r r 时,a b a b +=-r r r r9、(1)22a b --r r ; (2)102210a b c -+r r r ; (3)132a b +r r ; (4)2()x y b -r .10、14a b e +=r r u r ,124a b e e -=-+r r u r u u r ,1232310a b e e -=-+r r u r u u r . 11、如图所示,OC a =-u u u r r ,OD b =-u u u r r,DC b a =-u u u r r r ,BC a b =--u u u r r r .12、14AE b =u u u r r ,BC b a =-u u u r r r ,1()4DE b a =-u u u r r r ,34DB a =u u u r r,34EC b =u u u r r ,1()8DN b a =-u u u r r r ,11()48AN AM a b ==+u u u r u u u u r r r .13、证明:在ABC ∆中,,E F 分别是,AB BC 的中点,所以EF AC //且12EF AC =,即12EF AC =u u u r u u u r ;同理,12HG AC =u u u r u u u r,所以EF HG =u u u r u u u r .习题2.2 B 组(P92)1、丙地在甲地的北偏东45°方向,距甲地1400 km.2、不一定相等,可以验证在,a b r r不共线时它们不相等.3、证明:因为MN AN AM =-u u u u r u u u r u u u u r ,而13AN AC =u u u r u u u r ,13AM AB =u u u u r u u u r,所以1111()3333MN AC AB AC AB BC =-=-=u u u u r u u u r u u u r u u u r u u u r u u u r.4、(1)四边形ABCD 为平行四边形,证略 (2)四边形ABCD 为梯形.证明:∵13AD BC =u u u r u u u r,(第11题)(第12题)EHGFC AB丙(第1题)BC∴AD BC //且AD BC ≠ ∴四边形ABCD 为梯形.(3)四边形ABCD 为菱形.证明:∵AB DC =u u u r u u u r,∴AB DC //且AB DC =∴四边形ABCD 为平行四边形 又AB AD =u u u r u u u r∴四边形ABCD 为菱形.5、(1)通过作图可以发现四边形ABCD 为平行四边形.证明:因为OA OB BA -=u u u r u u u r u u u r ,OD OC CD -=u u u r u u u r u u u r而OA OC OB OD +=+u u u r u u u r u u u r u u u r所以OA OB OD OC -=-u u u r u u u r u u u r u u u r所以BA CD =u u u r u u u r,即∥.因此,四边形ABCD 为平行四边形.2.3平面向量的基本定理及坐标表示 练习(P100)1、(1)(3,6)a b +=r r ,(7,2)a b -=-r r ; (2)(1,11)a b +=r r ,(7,5)a b -=-r r;(3)(0,0)a b +=r r ,(4,6)a b -=r r ; (4)(3,4)a b +=r r ,(3,4)a b -=-r r. 2、24(6,8)a b -+=--r r ,43(12,5)a b +=r r.3、(1)(3,4)AB =u u u r ,(3,4)BA =--u u u r ; (2)(9,1)AB =-u u u r ,(9,1)BA =-u u u r; (3)(0,2)AB =u u u r ,(0,2)BA =-u u u r ; (4)(5,0)AB =u u u r ,(5,0)BA =-u u u r4、AB ∥CD . 证明:(1,1)AB =-u u u r ,(1,1)CD =-u u u r,所以AB CD =u u u r u u u r .所以AB ∥CD .5、(1)(3,2); (2)(1,4); (3)(4,5)-.6、10(,1)3或14(,1)3-7、解:设(,)P x y ,由点P 在线段AB 的延长线上,且32AP PB =u u u r u u u r ,得32AP PB =-u u u r u u ur(,)(2,3)(2,3)AP x y x y =-=--u u u r ,(4,3)(,)(4,3)PB x y x y =--=---u u u r(第4题(3))(第5题)∴3(2,3)(4,3)2x y x y --=---- ∴32(4)233(3)2x x y y ⎧-=--⎪⎪⎨⎪-=---⎪⎩∴815x y =⎧⎨=-⎩,所以点P 的坐标为(8,15)-.习题2.3 A 组(P101)1、(1)(2,1)-; (2)(0,8); (3)(1,2).说明:解题时可设(,)B x y ,利用向量坐标的定义解题.2、123(8,0)F F F ++=u u r u u r u u r3、解法一:(1,2)OA =--u u u r ,(53,6(1))(2,7)BC =---=u u u r而AD BC =u u u r u u u r ,(1,5)OD OA AD OA BC =+=+=u u u r u u u r u u u r u u u r u u u r. 所以点D 的坐标为(1,5).解法二:设(,)D x y ,则((1),(2))(1,2)AD x y x y =----=++u u u r,(53,6(1))(2,7)BC =---=u u u r由AD BC =u u u r u u u r 可得,1227x y +=⎧⎨+=⎩,解得点D 的坐标为(1,5).4、解:(1,1)OA =u u u r ,(2,4)AB =-u u u r.1(1,2)2AC AB ==-u u u r u u u r ,2(4,8)AD AB ==-u u u r u u u r ,1(1,2)2AE AB =-=-u u u r u u ur .(0,3)OC OA AC =+=u u u r u u u r u u u r,所以,点C 的坐标为(0,3); (3,9)OD OA AD =+=-u u u r u u u r u u u r,所以,点D 的坐标为(3,9)-; (2,1)OE OA AE =+=-u u u r u u u r u u u r,所以,点E 的坐标为(2,1)-. 5、由向量,a b r r 共线得(2,3)(,6)x λ=-,所以236x =-,解得4x =-.6、(4,4)AB =u u u r ,(8,8)CD =--u u u r ,2CD AB =-u u u r u u u r ,所以AB u u u r 与CD uuur 共线. 7、2(2,4)OA OA '==u u u r u u u r ,所以点A '的坐标为(2,4);3(3,9)OB OB '==-u u u r u u u r,所以点B '的坐标为(3,9)-; 故 (3,9)(2,4)(5,5)A B ''=--=-u u u u r 习题2.3 B 组(P101)1、(1,2)OA =u u u r ,(3,3)AB =u u u r.当1t =时,(4,5)OP OA AB OB =+==u u u r u u u r u u u r u u u r,所以(4,5)P ;当12t =时,13357(1,2)(,)(,)22222OP OA AB =+=+=u u u r u u u r u u u r ,所以57(,)22P ;当2t =-时,2(1,2)(6,6)(5,4)OP OA AB =-=-=--u u u r u u u r u u u r,所以(5,4)P --;当2t =时,2(1,2)(6,6)(7,8)OP OA AB =+=+=u u u r u u u r u u u r,所以(7,8)P .2、(1)因为(4,6)AB =--u u u r ,(1,1.5)AC =u u u r,所以4AB AC =-u u u r u u u r ,所以A 、B 、C 三点共线;(2)因为(1.5,2)PQ =-u u u r ,(6,8)PR =-u u u r ,所以4PR PQ =u u u r u u u r,所以P 、Q 、R 三点共线;(3)因为(8,4)EF =--u u u r ,(1,0.5)EG =--u u u r,所以8EF EG =u u u r u u u r ,所以E 、F 、G 三点共线.3、证明:假设10λ≠,则由11220e e λλ+=u r u u r r ,得2121e e λλ=-u r uu r .所以12,e e u r u u r 是共线向量,与已知12,e e u r u u r是平面内的一组基底矛盾,因此假设错误,10λ=. 同理20λ=. 综上120λλ==.4、(1)OP =u u u r (2)对于任意向量12OP xe ye =+u u u r u r u u r,,x y 都是唯一确定的,所以向量的坐标表示的规定合理.2.4平面向量的数量积 练习(P106)1、1cos ,86242p q p q p q ⋅=⋅⋅<>=⨯⨯=u r r u r r u r r .2、当0a b ⋅<r r 时,ABC ∆为钝角三角形;当0a b ⋅=r r时,ABC ∆为直角三角形.3、投影分别为0,-图略练习(P107)1、5a ==r ,b ==r 35427a b ⋅=-⨯+⨯=-r r .2、8a b ⋅=r r ,()()7a b a b +-=-r r r r ,()0a b c ⋅+=r r r ,2()49a b +=r r .3、1a b ⋅=r r ,a =r b =r 88θ≈︒.习题2.4 A 组(P108)1、a b ⋅=-r r 222()225a b a a b b +=+⋅+=-r r r r r r a b +=r r2、BC uuu r 与CA u u u r 的夹角为120°,20BC CA ⋅=-u u u r u u u r .3、a b +==r r ,a b -==r r .4、证法一:设a r 与b r 的夹角为θ.(1)当0λ=时,等式显然成立;(2)当0λ>时,a λr 与b r ,a r 与b λr 的夹角都为θ,所以 ()cos cos a b a b a b λλθλθ⋅==r r r r r r()cos a b a b λλθ⋅=r r r r()cos cos a b a b a b λλθλθ⋅==r r r r r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;(3)当0λ<时,a λr 与b r ,a r 与b λr 的夹角都为180θ︒-,则 ()cos(180)cos a b a b a b λλθλθ⋅=︒-=-r r r r r r()cos cos a b a b a b λλθλθ⋅==-r r r r r r()cos(180)cos a b a b a b λλθλθ⋅=︒-=-r r r r r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;综上所述,等式成立.证法二:设11(,)a x y =r ,22(,)b x y =r ,那么 11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+r r112212121212()(,)(,)()a b x y x y x x y y x x y y λλλλλ⋅=⋅=+=+r r11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;5、(1)直角三角形,B ∠为直角.证明:∵(1,4)(5,2)(6,6)BA =---=--u u u r ,(3,4)(5,2)(2,2)BC =-=-u u u r∴6(2)(6)20BA BC ⋅=-⨯-+-⨯=u u u r u u u r∴BA BC ⊥u u u r u u u r ,B ∠为直角,ABC ∆为直角三角形(2)直角三角形,A ∠为直角证明:∵(19,4)(2,3)(21,7)AB =---=u u u r ,(1,6)(2,3)(1,3)AC =-----=-u u u r∴2117(3)0AB AC ⋅=⨯+⨯-=u u u r u u u r∴AB AC ⊥u u u r u u u r ,A ∠为直角,ABC ∆为直角三角形(3)直角三角形,B ∠为直角证明:∵(2,5)(5,2)(3,3)BA =-=-u u u r ,(10,7)(5,2)(5,5)BC =-=u u u r∴35350BA BC ⋅=-⨯+⨯=u u u r u u u r∴BA BC ⊥u u u r u u u r ,B ∠为直角,ABC ∆为直角三角形6、135θ=︒.7、120θ=︒.22(23)(2)44361a b a b a a b b -+=-⋅-=r r r r r r r r ,于是可得6a b ⋅=-r r ,1cos 2a b a bθ⋅==-r r r r ,所以120θ=︒. 8、23cos 40θ=,55θ=︒. 9、证明:∵(5,2)(1,0)(4,2)AB =--=-u u u r ,(8,4)(5,2)(3,6)BC =--=u u u r , (8,4)(4,6)(4,2)DC =-=-u u u r∴AB DC =u u u r u u u r ,43(2)60AB BC ⋅=⨯+-⨯=u u u r u u u r∴,,,A B C D 为顶点的四边形是矩形.10、解:设(,)a x y =r ,则2292x y y x ⎧+=⎪⎨=⎪⎩,解得5x y ⎧=⎪⎪⎨⎪=⎪⎩5x y ⎧=-⎪⎪⎨⎪=⎪⎩.于是(55a =r或(55a =--r . 11、解:设与a r 垂直的单位向量(,)e x y =r ,则221420x y x y ⎧+=⎨+=⎩,解得5x y ⎧=⎪⎪⎨⎪=⎪⎩或5x y ⎧=-⎪⎪⎨⎪=⎪⎩.于是,55e =-r或(55e =-r . 习题2.4 B 组(P108)1、证法一:0()0()a b a c a b a c a b c a b c ⋅=⋅⇔⋅-⋅=⇔⋅-=⇔⊥-r r r r r r r r r r r r r r证法二:设11(,)a x y =r ,22(,)b x y =r ,33(,)c x y =r .先证()a b a c a b c ⋅=⋅⇒⊥-r r r r r r r1212a b x x y y ⋅=+r r ,1313a c x x y y ⋅=+r r由a b a c ⋅=⋅r r r r 得12121313x x y y x x y y +=+,即123123()()0x x x y y y -+-=而2323(,)b c x x y y -=--r r ,所以()0a b c ⋅-=r r r再证()a b c a b a c ⊥-⇒⋅=⋅r r r r r r r由()0a b c ⋅-=r r r 得 123123()()0x x x y y y -+-=,即12121313x x y y x x y y +=+,因此a b a c ⋅=⋅r r r r2、cos cos cos sin sin OA OB AOB OA OBαβαβ⋅∠==+u u u r u u u r u u u r u u u r . 3、证明:构造向量(,)u a b =r ,(,)v c d =r .cos ,u v u v u v ⋅=<>r r r r r r,所以,ac bd u v +=<>r r∴2222222222()()()cos ,()()ac bd a b c d u v a b c d +=++<>≤++r r 4、AB AC ⋅u u u r u u u r 的值只与弦AB 的长有关,与圆的半径无关.证明:取AB 的中点M ,连接CM ,则CM AB ⊥,12AM AB =u u u u r u u u r 又cos AB AC AB AC BAC ⋅=∠u u u r u u u r u u u r u u u r ,而AM BAC AC∠=u u u u r u u u r 所以212AB AC AB AM AB ⋅==u u u r u u u r u u u r u u u u r u u u r 5、(1)勾股定理:Rt ABC ∆中,90C ∠=︒,则222CA CB AB +=u u u r u u u r u u u r证明:∵AB CB CA =-u u u r u u u r u u u r ∴2222()2AB CB CA CB CA CB CA =-=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r u u u r .由90C ∠=︒,有CA CB ⊥,于是0CA CB ⋅=u u u r u u u r ∴222CA CB AB +=u u u r u u u r u u u r(2)菱形ABCD 中,求证:AC BD ⊥证明:∵AC AB AD =+u u u r u u u r u u u r ,,DB AB AD =-u u u r u u u r u u u r∴22()()AC DB AB AD AB AD AB AD ⋅=+⋅-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r .∵四边形ABCD 为菱形,∴AB AD =,所以220AB AD -=u u u r u u u r∴0AC DB ⋅=u u u r u u u r ,所以AC BD ⊥(3)长方形ABCD 中,求证:AC BD =证明:∵ 四边形ABCD 为长方形,所以AB AD ⊥,所以0AB AD ⋅=u u u r u u u r∴222222AB AB AD AD AB AB AD AD +⋅+=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r .∴22()()AB AD AB AD +=-u u u r u u u r u u u r u u u r ,所以22AC BD =u u u r u u u r ,所以AC BD =(4)正方形的对角线垂直平分. 综合以上(2)(3)的证明即可.2.5平面向量应用举例习题2.5 A 组(P113)(第4题)1、解:设(,)P x y ,11(,)R x y则1111(1,0)(,)(1,)RA x y x y =-=--u u u r ,(,)(1,0)(1,0)AP x y x =-=-u u u r由2RA AP =u u u r u u u r 得11(1,)2(1,)x y x y --=-,即11232x x y y =-+⎧⎨=-⎩ 代入直线l 的方程得2y x =. 所以,点P 的轨迹方程为2y x =.2、解:(1)易知,OFD ∆∽OBC ∆,12DF BC =, 所以23BO BF =. 2211()()3323AO BO BA BF a b a a a b =-=+=-+=+u u u r u u u r u u u r u u u r r r r r r r (2)因为1()2AE a b =+u u u r r r 所以23AO AE =u u u r u u u r ,因此,,A O E 三点共线,而且2AO OE = 同理可知:2,2BO CO OF OD ==,所以2AO BO CO OE OF OD === 3、解:(1)(2,7)B A v v v =-=-r u u r u u r ;(2)v r 在A v u u r 方向上的投影为135A Av v v ⋅=r u u r u u r . 4、解:设1F u u r ,2F u u r 的合力为F u r ,F u r 与1F u u r 的夹角为θ, 则31F =+u r ,30θ=︒; 331F =+u u r ,3F u u r 与1F u u r 的夹角为150°.习题2.5 B 组(P113)1、解:设0v u u r 在水平方向的速度大小为x v u u r ,竖直方向的速度的大小为y v u u r ,则0cos x v v θ=u u r u u r ,0sin y v v θ=u u r u u r .设在时刻t 时的上升高度为h ,抛掷距离为s ,则001sin ,()2cos h v t gt g s v t θθ⎧=-⎪⎨⎪=⎩u u r u u r 为重力加速度 所以,最大高度为220sin 2v g θu u r ,最大投掷距离为20sin 2v g θu u r .O DF E A B C (第2题) (第4题)2、解:设1v u r 与2v u u r 的夹角为θ,合速度为v r ,2v u u r 与v r 的夹角为α,行驶距离为d . 则1sin 10sin sin v v v θθα==u r r r ,0.5sin 20sin v d αθ==r . ∴120sin d v θ=r . 所以当90θ=︒,即船垂直于对岸行驶时所用时间最短.3、(1)(0,1)-解:设(,)P x y ,则(1,2)AP x y =--u u u r . (2,22)AB =-u u u r .将AB u u u r 绕点A 沿顺时针方向旋转4π到AP u u u r ,相当于沿逆时针方向旋转74π到AP u u u r ,于是7777(2cos 22sin ,2sin 22cos )(1,3)4444AP ππππ=+-=--u u u r 所以1123x y -=-⎧⎨-=-⎩,解得0,1x y ==- (2)32y x=- 解:设曲线C 上任一点P 的坐标为(,)x y ,OP u u u r 绕O 逆时针旋转4π后,点P 的坐标为(,)x y ''则cos sin 44sin cos 44x x y y x y ππππ⎧'=-⎪⎪⎨⎪'=+⎪⎩,即2()2()x x y y x y ⎧'=-⎪⎪⎨⎪'=+⎪⎩ 又因为223x y ''-=,所以2211()()322x y x y --+=,化简得32y x=- 第二章 复习参考题A 组(P118)1、(1)√; (2)√; (3)×; (4)×.2、(1)D ; (2)B ; (3)D ; (4)C ; (5)D ; (6)B .3、1()2AB a b =-u u u r r r ,1()2AD a b =+u u u r r r 4、略解:2133DE BA MA MB a b ==-=-+u u u r u u u r u u u r u u u r r r 2233AD a b =+u u u r r r ,1133BC a b =+u u u r r r 1133EF a b =--u u u r r r ,1233FA DC a b ==-u u u r u u u r r r1233CD a b =-+u u u r r r ,2133AB a b =-u u u r r r CE a b =-+u u u r r r 5、(1)(8,8)AB =-u u u r ,82AB =u u u r ;(2)(2,16)OC =-u u u r ,(8,8)OD =-u u u r ; (3)33OA OB ⋅=u u u r u u u r .6、AB u u u r 与CD u u u r 共线.证明:因为(1,1)AB =-u u u r ,(1,1)CD =-u u u r ,所以AB CD =u u u r u u u r . 所以AB u u u r 与CD u u u r 共线.7、(2,0)D -. 8、2n =. 9、1,0λμ=-=.10、34cos ,cos 0,cos 55A B C === 11、证明:2(2)22cos6010n m m n m m -⋅=⋅-=︒-=r u r u r r u r u r ,所以(2)n m m -⊥r u r u r .12、1λ=-. 13、13a b +=r r ,1a b -=r r . 14、519cos ,cos 820θβ== 第二章 复习参考题B 组(P119)1、(1)A ; (2)D ; (3)B ; (4)C ; (5)C ; (6)C ; (7)D .2、证明:先证a b a b a b ⊥⇒+=-r r r r r r .222()2a b a b a b a b+=+=++⋅r r r r r r r r ,222()2a b a b a b a b -=-=+-⋅r r r r r r r r .因为a b ⊥r r ,所以0a b ⋅=r r ,于是22a b a b a b +=+=-r r r r r r . 再证a b a b a b +=-⇒⊥r r r r r r .由于222a b a a b b +=+⋅+r r r r r r ,222a b a a b b -=-⋅+r r r r r r由a b a b +=-r r r r 可得0a b ⋅=,于是a b ⊥r所以a b a b a b +=-⇔⊥r r r r r r . 【几何意义是矩形的两条对角线相等】3、证明:先证a b c d =⇒⊥r r r u r22()()c d a b a b a b ⋅=+⋅-=-r u r r r r r r r(第6题)又a b =r r ,所以0c d ⋅=r u r ,所以c d ⊥r u r 再证c d a b ⊥⇒=r u r r r .由c d ⊥r u r 得0c d ⋅=r u r ,即22()()0a b a b a b +⋅-=-=r r r r r r所以a b =r r 【几何意义为菱形的对角线互相垂直,如图所示】4、12AD AB BC CD a b =++=+u u u r u u u r u u u r u u u r r r ,1142AE a b =+u u u r r r 而34EF a =u u u r r ,14EM a =u u u u r r ,所以1111(4242AM AE EM a b a =+=++=u u u u r u u u r u u u u r r r r 5、证明:如图所示,12OD OP OP =+u u u r u u u r u u u u r ,由于1230OP OP OP ++=u u u r u u u u r u u u r r ,所以3OP OD =-u u u r u u u r ,1OD =u u u r 所以11OD OP PD ==u u u r u u u r u u u r 所以1230OPP ∠=︒,同理可得1330OPP ∠=︒ 所以31260P PP ∠=︒,同理可得12360PP P ∠=︒,23160P P P ∠=︒,所以123PP P ∆为正三角形.6、连接AB .由对称性可知,AB 是SMN ∆的中位线,22MN AB b ==-u u u u r u u u r r 7、(18=(千米/时),沿与水流方向成60°的方向前进;(2)实际前进速度大小为沿与水流方向成903︒+的方向前进. 8、解:因为OA OB OB OC ⋅=⋅u u u r u u u r u u u r u u u r ,所以()0OB OA OC ⋅-=u u u r u u u r u u u r ,所以0OB CA ⋅=u u u r u u u r同理,0OA BC ⋅=u u u r u u u r ,0OC AB ⋅=u u u r u u u r ,所以点O 是ABC ∆的垂心.9、(1)2110200a x a y a y a x -+-=; (2)垂直;(3)当12210A B A B -=时,1l ∥2l ;当12120A A B B +=时,12l l ⊥,P 2(第5题)夹角θ的余弦cos θ=;(4)d =第三章 三角恒等变换3.1两角和与差的正弦、余弦和正切公式练习(P127)1、cos()cos cos sin sin 0cos 1sin sin 222πππαααααα-=+=⨯+⨯=. cos(2)cos2cos sin 2sin 1cos 0sin cos παπαπαααα-=+=⨯+⨯=.2、解:由3cos ,(,)52πααπ=-∈,得4sin 5α==;所以34cos()cos cos sin sin ()44455πππααα-=+=-=3、解:由15sin 17θ=,θ是第二象限角,得8cos 17θ===-;所以8115cos()cos cos sin sin 33317217πππθθθ-=+=-⨯+=.4、解:由23sin ,(,)32πααπ=-∈,得cos α==又由33cos ,(,2)42πββπ=∈,得sin β== 所以32cos()cos cos sin sin ((()43βαβαβα-=+=⨯+⨯-=. 练习(P131)1、(1; (2) (3 (4)22、解:由3cos ,(,)52πθθπ=-∈,得4sin 5θ==;所以413sin()sin cos cos sin ()333525πππθθθ+=+=⨯+-=. 3、解:由12sin 13θ=-,θ是第三象限角,得5cos 13θ===-; 所以5112cos()cos cos sin sin ()()66613213πππθθθ+=-=--⨯-=. 4、解:tan tan 314tan()241311tan tan 4παπαπα+++===--⨯-⋅. 5、(1)1; (2)12; (3)1; (4); (5)原式=1(cos34cos26sin34sin 26)cos(3426)cos602-︒︒-︒︒=-︒+︒=-︒=-; (6)原式=sin 20cos70cos20sin70(sin 20cos70cos20sin70)sin901-︒︒-︒︒=-︒︒+︒︒=-︒=-.6、(1)原式=cos cos sin sin cos()333x x x πππ-=+; (2)原式=1cos )2(sin cos cos sin )2sin()2666x x x x x πππ+=+=+; (3)原式=)2(sin cos cos sin )2sin()444x x x x x πππ=-=-; (4)原式=12(cos )cos sin sin ))2333x x x x x πππ=-=+. 7、解:由已知得3sin()cos cos()sin 5αβααβα---=, 即3sin[()]5αβα--=,3sin()5β-=所以3sin 5β=-. 又β是第三象限角, 于是4cos 5β===-. 因此55534sin()sin cos cos sin ()(()(444525210πππβββ+=+=-+-=. 练习(P135)1、解:因为812παπ<<,所以382αππ<<又由4cos 85α=-,得3sin 85α=-,3sin385tan 484cos 85ααα-===- 所以3424sinsin(2)2sin cos 2()()48885525αααα=⨯==⨯-⨯-=2222437cos cos(2)cos sin ()()48885525αααα=⨯=-=---=2232tan23162484tan tan(2)3482771tan 1()84αααα⨯=⨯===⨯=-- 2、解:由3sin()5απ-=,得3sin 5α=-,所以222316cos 1sin 1()525αα=-=--=所以2221637cos2cos sin ()25525ααα=-=--=3、解:由sin2sin αα=-且sin 0α≠可得1cos 2α=-,又由(,)2παπ∈,得sin α=,所以sin tan (2)cos ααα==-=4、解:由1tan 23α=,得22tan 11tan 3αα=-. 所以2tan 6tan 10αα+-=,所以tan 3α=-5、(1)11sin15cos15sin3024︒︒=︒=; (2)22cos sin cos 8842πππ-==;(3)原式=212tan 22.511tan 4521tan 22.522︒⋅=︒=-︒; (4)原式=cos45︒=. 习题3.1 A 组(P137)1、(1)333cos()cos cos sin sin 0cos (1)sin sin 222πππαααααα-=+=⨯+-⨯=-;(2)333sin()sin cos cos sin 1cos 0sin cos 222πππαααααα-=-=-⨯-⨯=-;(3)cos()cos cos sin sin 1cos 0sin cos παπαπαααα-=+=-⨯+⨯=-; (4)sin()sin cos cos sin 0cos (1)sin sin παπαπαααα-=-=⨯--⨯=.2、解:由3cos ,05ααπ=<<,得4sin 5α==,所以431cos()cos cos sin sin 666552πππααα-=+=⨯=.3、解:由2sin ,(,)32πααπ=∈,得cos α===又由33cos ,(,)42πββπ=-∈,得sin β===,所以32cos()cos cos sin sin ()(43αβαβαβ-=+=-+⨯=.4、解:由1cos 7α=,α是锐角,得sin α=== 因为,αβ是锐角,所以(0,)αβπ+∈, 又因为11cos()14αβ+=-,所以sin()αβ+===所以cos cos[()]cos()cos sin()sin βαβααβααβα=+-=+++1111()1472=-⨯= 5、解:由60150α︒<<︒,得9030180α︒<︒+<︒又由3sin(30)5α︒+=,得4cos(30)5α︒+=-所以cos cos[(30)30]cos(30)cos30sin(30)sin30αααα=︒+-︒=︒+︒+︒+︒431552=-+⨯=6、(1) (2) (3)2-7、解:由2sin ,(,)32πααπ=∈,得cos α===又由3cos 4β=-,β是第三象限角,得sin β==.所以cos()cos cos sin sin αβαβαβ+=-32()(43=--⨯=sin()sin cos cos sin αβαβαβ-=-23()((34=⨯--⨯=8、解:∵53sin ,cos 135A B ==且,A B 为ABC ∆的内角∴0,02A B ππ<<<<,124cos ,sin 135A B =±=当12cos 13A =-时,sin()sin cos cos sin AB A B A B +=+5312433()013513565=⨯+-⨯=-< A B π+>,不合题意,舍去∴124cos ,sin 135A B ==∴cos cos()(cos cos sin sin )C A B A B A B =-+=--1235416()13513565-⨯-⨯=- 9、解:由3sin ,(,)52πθθπ=∈,得4cos 5θ==-.∴sin 353tan ()cos 544θθθ==⨯-=-. ∴31tan tan 242tan()311tan tan 111()42θϕθϕθϕ-+++===--⋅--⨯. 31tan tan 42tan()2311tan tan 1()42θϕθϕθϕ----===-+⋅+-⨯. 10、解:∵tan ,tan αβ是22370x x +-=的两个实数根.∴3tan tan 2αβ+=-,7tan tan 2αβ⋅=-.∴3tan tan 12tan()71tan tan 31()2αβαβαβ-++===--⋅--.11、解:∵tan()3,tan()5αβαβ+=-=∴tan()tan()tan 2tan[()()]1tan()tan()αβαβααβαβαβαβ++-=++-=-+⋅-3541357+==--⨯tan()tan()tan 2tan[()()]1tan()tan()αβαββαβαβαβαβ+--=+--=++⋅-3511358-==-+⨯12、解:∵::2:3:6BD DC AD = ∴11tan ,tan 32BD DC AD AD αβ====∴tan tan tan tan()1tan tan BAC αβαβαβ+∠=+=-⋅1132111132+==-⨯ 又∵0180BAC ︒<∠<︒,∴45BAC ∠=︒ 13、(1))6x π+; (23sin()3x π-; (3)2sin()26x π+;(47sin()12x π-; (5; (6)12; (7)sin()αγ+; (8)cos()αγ--; (9) (10)tan()βα-.14、解:由sin 0.8,(0,)2παα=∈,得cos 0.6α===∴sin22sin cos 20.80.60.96ααα==⨯⨯= 2222cos2cos sin 0.60.80.28ααα=-=-=- 15、解:由cos 270ϕϕ=︒<<︒,得sin ϕ===∴sin 22sin cos 2((ϕϕϕ==⨯⨯=22221cos2cos sin ((3ϕϕϕ=-=-=-sin 2tan 2(3)cos 23ϕϕϕ==-=-16、解:设5sin sin 13B C ==,且090B ︒<<︒,所以12cos 13B =. ∴512120sin sin(1802)sin 22sin cos 21313169A B B B B =︒-===⨯⨯=2222125119cos cos(1802)cos2(cos sin )(()())1313169A B B B B =︒-=-=--=--=-(第12题)sin 120169120tan ()cos 169119119A A A ==⨯-=-17、解:22122tan 33tan 211tan 41()3βββ⨯===--,13tan tan 274tan(2)1131tan tan 2174αβαβαβ+++===-⋅-⨯. 18、解:1cos()cos sin()sin 3αββαββ+++=⇒1cos[()]3αββ+-=,即1cos 3α= 又3(,2)2παπ∈,所以sin α==∴1sin 22sin cos 2()339ααα==⨯-⨯=-222217cos2cos sin ()(39ααα=-=-=-∴78cos(2)cos2cos sin 2sin (444929218πππααα-+=-=-⨯--⨯=19、(1)1sin2α+; (2)cos2θ; (3)1sin 44x ; (4)tan2θ.习题3.1 B 组(P138) 1、略. 2、解:∵tan ,tan A B 是x 的方程2(1)10x p x +++=,即210x px p +++=的两个实根∴tan tan A B p +=-,tan tan 1A B p ⋅=+ ∴tan tan[()]tan()C A B A B π=-+=-+tan tan 11tan tan 1(1)A B pA B p +-=-=-=--⋅-+由于0C π<<,所以34C π=. 3、反应一般的规律的等式是(表述形式不唯一)223sin cos (30)sin cos(30)4αααα++︒++︒=(证明略) 本题是开放型问题,反映一般规律的等式的表述形式还可以是:223sin (30)cos sin(30)cos 4αααα-︒++-︒=223sin (15)cos (15)sin(15)cos(15)4αααα-︒++︒+-︒+︒=223sin cos sin cos 4αβαβ++=,其中30βα-=︒,等等思考过程要求从角,三角函数种类,式子结构形式三个方面寻找共同特点,从而作出归纳. 对认识三角函数式特点有帮助,证明过程也会促进推理能力、运算能力的提高.4、因为12PA PP =,则2222(cos()1)sin ()(cos cos )(sin sin )αβαβαβαβ+-++=-++ 即22cos()22cos cos 2sin sin αβαβαβ-+=-+ 所以cos()cos cos sin sin αβαβαβ+=-3.2简单的三角恒等变换 练习(P142)1、略.2、略.3、略.4、(1)1sin 42y x =. 最小正周期为2π,递增区间为[,],8282k k k Z ππππ-++∈,最大值为12;(2)cos 2y x =+. 最小正周期为2π,递增区间为[2,22],k k k Z ππππ++∈,最大值为3;(3)2sin(4)3y x π=+. 最小正周期为2π,递增区间为5[,],242242k k k Z ππππ-++∈,最大值为2.习题3.2 A 组( P143) 1、(1)略; (2)提示:左式通分后分子分母同乘以2; (3)略; (4)提示:用22sin cos ϕϕ+代替1,用2sin cos ϕϕ代替sin 2ϕ;(5)略; (6)提示:用22cos θ代替1cos2θ+;(7)提示:用22sin θ代替1cos2θ-,用22cos θ代替1cos2θ+; (8)略.2、由已知可有1sin cos cos sin 2αβαβ+=……①,1sin cos cos sin 3αβαβ-=……②(1)②×3-①×2可得sin cos 5cos sin αβαβ=(2)把(1)所得的两边同除以cos cos αβ得tan 5tan αβ= 注意:这里cos cos 0αβ≠隐含与①、②之中3、由已知可解得1tan 2θ=-. 于是2212()2tan 42tan 211tan 31()2θθθ⨯-===---- 1tan tan1142tan()1431tan tan 1()142πθπθπθ+-++===-⋅--⨯∴tan 24tan()4πθθ=-+4、由已知可解得sin x θ=,cos y θ=,于是2222sin cos 1x y θθ+=+=.5、()2sin(4)3f x x π=+,最小正周期是2π,递减区间为7[,],242242k k k Z ππππ++∈.习题3.2 B 组(P143) 1、略.2、由于762790+⨯=,所以sin76sin(9014)cos14m ︒=︒-︒=︒= 即22cos 71m ︒-=,得cos7︒=3、设存在锐角,αβ使223παβ+=,所以23απβ+=,tan()2αβ+又tantan 22αβ=,又因为tantan 2tan()21tantan 2αβαβαβ++=-,所以tantan tan()(1tan tan )3222αααβββ+=+-=由此可解得tan 1β=, 4πβ=,所以6πα=.经检验6πα=,4πβ=是符合题意的两锐角.4、线段AB 的中点M 的坐标为11((cos cos ),(sin sin ))22αβαβ++. 过M 作1MM 垂直于x 轴,交x 轴于1M ,111()()22MOM βαααβ∠=-+=+.在Rt OMA ∆中,cos cos 22OM OA βααβ--==. 在1Rt OM M ∆中,11cos cos cos22OM OM MOM αβαβ+-=∠=11sin sin cos22M M OM MOM αβαβ+-=∠=. 于是有 1(cos cos )cos cos222αβαβαβ+-+=, 1(sin sin )sin cos222αβαβαβ+-+= 5、当2x =时,22()sin cos 1f ααα=+=;当4x =时,4422222()sin cos (sin cos )2sin cos f ααααααα=+=+-211sin 22α=-,此时有1()12f α≤≤;当6x =时,662232222()sin cos (sin cos )3sin cos (sin cos )f ααααααααα=+=+-+231sin 24α=-,此时有1()14f α≤≤;由此猜想,当2,x k k N +=∈时,11()12k f α-≤≤6、(1)345(sin cos )5sin()55y x x x ϕ=+=+,其中34cos ,sin 55ϕϕ==所以,y 的最大值为5,最小值为﹣5;(2))y x ϕ+,其中cos ϕϕ==所以,y ;第三章 复习参考题A 组(P146)1、1665. 提示:()βαβα=+- 2、5665. 提示:5sin()sin[()]sin[()()]44ππαβπαββα+=-++=-+--3、1.4、(1)提示:把公式tan tan tan()1tan tan αβαβαβ++=-变形;(2; (3)2; (4) 提示:利用(1)的恒等式.5、(1)原式4sin(3010)4sin 20︒-︒==︒;(2)原式=sin10sin 40(sin 40cos10︒︒=︒ =2sin 40cos40sin801cos10cos10-︒︒-︒==-︒︒;(3)原式=tan 70cos101)tan 70cos10︒︒-=︒ =sin702sin10sin 20cos101cos70cos20cos70︒-︒-︒⋅︒⋅==-︒︒︒;(4)原式=sin50(1sin50︒⋅= 2cos50sin100sin501cos10cos10︒︒=︒⋅==︒︒6、(1)95; (2)2425;(3)223±. 提示:4422222sin cos (sin cos )2sin cos θθθθθθ+=+-;(4)1725.7、由已知可求得2cos cos 5αβ=,1sin sin 5αβ=,于是sin sin 1tan tan cos cos 2αβαβαβ==.8、(1)左边=222cos 214cos232(cos 22cos21)αααα-++=++22242(cos21)2(2cos )8cos ααα=+===右边(2)左边=2222sin cos 2sin cos (sin cos )2cos 2sin cos 2cos (cos sin )αααααααααααα+++=++sin cos 11tan 2cos 22αααα+==+=右边(3)左边=sin(2)2cos()sin sin[()]2cos()sin sin 2cos (cos sin )αβαβααβααβααααα+-+++-+=+ sin()cos cos()sin sin sin sin αβααβαβαα+-+===右边 (4)左边=222234cos22cos 212(cos 22cos21)34cos22cos 212(cos 22cos21)A A A A A A A A -+--+=++-++2224222(1cos2)(2sin )tan (1cos2)(2cos )A A A A A -===+=右边 9、(1)1sin 21cos2sin 2cos222)24y x x x x x π=+++=++++递减区间为5[,],88k k k Z ππππ++∈(222,最小值为22.10、2222()(cos sin )(cos sin )2sin cos cos2sin 22)4f x x x x x x x x x x π=+--=-+(1)最小正周期是π;(2)由[0,]2x π∈得52[,]444x πππ+∈,所以当24x ππ+=,即38x π=时,()f x 的最小值为2-()f x 取最小值时x 的集合为3{}8π.11、2()2sin 2sin cos 1cos2sin 22)14f x x x x x x x π=+=-+=-+(1)最小正周期是π21;(2)()f x 在[,]22ππ-上的图象如右图:12、()cos 2sin()6f x x x a x a π=++=++.(1)由21a +=得1a =-;(2)2{22,}3x k x k k Z πππ+∈≤≤.13、如图,设ABD α∠=,则CAE α∠=,2sin h AB α=,1cos hAC α=所以1212sin 2ABC h h S AB AC α∆=⋅⋅=,(0)2πα<<当22πα=,即4πα=时,ABC S ∆的最小值为12h h .第三章 复习参考题B 组(P147)1、解法一:由221sin cos 5sin cos 1αααα⎧-=⎪⎨⎪+=⎩,及0απ≤≤,可解得4sin 5α=,13cos sin 55αα=-=,所以24sin 225α=,7cos225α=-,sin(2)sin 2cos cos2sin 44450πππααα-=-=. 解法二:由1sin cos 5αα-= 得21(sin cos )25αα-=,24sin 225α=,所以249cos 2625α=. 又由1sin cos 5αα-=,得sin()4πα-=.因为[0,]απ∈,所以3[,]444πππα-∈-.而当[,0]44ππα-∈-时,sin()04πα-≤;当3[,]444πππα-∈时,sin()4πα->所以(0,)44ππα-∈,即(,)42ππα∈所以2(,)2παπ∈,7cos225α=-.sin(2)4πα-=2、把1cos cos 2αβ+=两边分别平方得221cos cos 2cos cos 4αβαβ++=把1sin sin 3αβ+=两边分别平方得221sin sin 2sin sin 9αβαβ++=(第13题)。
高中数学必修四习题答案

高中数学必修四习题答案高中数学必修四习题答案高中数学必修四是学生们在学习数学过程中必须掌握的一门课程。
而在学习过程中,习题是检验学生掌握程度的重要手段。
本文将为大家提供一些高中数学必修四习题的答案,帮助学生们更好地复习和巩固知识。
一、函数与导数1. 已知函数f(x) = 2x^3 - 3x^2 + 4x - 1,求f(x)的导函数f'(x)。
答案:f'(x) = 6x^2 - 6x + 42. 函数y = x^3 - 3x^2 + 2x + 1在点(1, 1)处的切线方程是什么?答案:切线方程为y = -2x + 33. 已知函数y = e^x + ln(x),求y的导函数。
答案:y' = e^x + 1/x二、三角函数1. 已知sinθ = 3/5,且θ是第二象限角,求cosθ的值。
答案:cosθ = -4/52. 已知tanα = 2/3,且α是第四象限角,求sinα的值。
答案:sinα = -2/√133. 已知cosβ = -1/2,且β是第三象限角,求tanβ的值。
答案:tanβ = √3三、概率与统计1. 有一袋中有4个红球和6个蓝球,从中不放回地抽取2个球,求抽到两个红球的概率。
答案:抽到两个红球的概率为4/92. 一批产品中有10%的次品,现从中随机抽取5个进行检验,求恰好有2个次品的概率。
答案:恰好有2个次品的概率为0.30243. 一组数据为5, 7, 9, 11, 13,求其平均数。
答案:平均数为9四、平面向量1. 已知向量a = (2, 3)和向量b = (4, 1),求向量a与向量b的数量积。
答案:a·b = 112. 已知向量a = (3, -1)和向量b = (2, 4),求向量a与向量b的叉积。
答案:a×b = 143. 已知向量a = (1, 2)和向量b = (3, 4),求向量a与向量b的夹角。
答案:夹角θ = arccos(11/√30)五、立体几何1. 已知正方体ABCD-A'B'C'D'的棱长为a,求其对角线AC的长度。
数学必修4习题答案

数学必修4习题答案数学必修4习题答案在学习数学必修4这门课程时,习题是非常重要的一部分。
通过做习题,我们可以巩固所学的知识,提高解题能力。
然而,有时候我们会遇到一些难以理解或者不会做的题目。
为了帮助大家更好地学习数学必修4,我整理了一些习题的答案,并解析了一些常见的题型。
1. 选择题选择题是数学必修4习题中常见的一种题型。
下面是一道选择题的答案和解析:题目:已知函数 f(x) = x^2 - 2x + 1,那么 f(3) 的值是多少?A. 4B. 5C. 6D. 7答案:B解析:将 x = 3 代入函数 f(x) 中,得到 f(3) = 3^2 - 2 * 3 + 1 = 9 - 6 + 1 = 4。
因此,选项 B 正确。
2. 解方程解方程是数学必修4习题中的重点内容之一。
下面是一道解方程的答案和解析:题目:解方程 2x + 5 = 17。
答案:x = 6解析:首先,我们需要将方程化简为一元一次方程。
将方程两边同时减去 5,得到 2x = 12。
然后,再将方程两边同时除以 2,得到 x = 6。
因此,方程的解为 x = 6。
3. 几何题几何题是数学必修4习题中的另一个重点。
下面是一道几何题的答案和解析:题目:已知直角三角形 ABC,其中∠C = 90°,AC = 5 cm,BC = 12 cm,求AB 的长度。
答案:AB = 13 cm解析:根据勾股定理,直角三角形的斜边的平方等于两直角边的平方和。
即AB^2 = AC^2 + BC^2 = 5^2 + 12^2 = 25 + 144 = 169。
因此,AB = √169 = 13 cm。
4. 统计题统计题在数学必修4习题中也是常见的一种题型。
下面是一道统计题的答案和解析:题目:某班级有 40 名学生,其中男生占总人数的 60%。
求该班级男生的人数。
答案:男生人数为 24 人解析:首先,我们需要计算男生人数占总人数的百分比。
男生人数占总人数的百分比为 60%。
数学必修4课后习题及答案

数学必修4课后习题及答案数学必修4课后习题及答案数学是一门抽象而又实用的学科,它贯穿于我们生活的方方面面。
而在学习数学的过程中,课后习题是不可或缺的一部分。
通过课后习题的练习,我们可以巩固所学的知识,培养逻辑思维能力,提高解决问题的能力。
本文将介绍数学必修4课后习题及答案,帮助大家更好地掌握数学知识。
第一章:函数与导数1. 已知函数$f(x)=2x^3-3x^2-12x+5$,求$f(x)$的导数。
答案:$f'(x)=6x^2-6x-12$2. 函数$y=x^3-3x^2+2x+5$的图像上是否存在切线?若存在,求出切线方程。
答案:存在切线,切线方程为$y=-3x+8$第二章:三角函数1. 求解方程$\sin^2 x - \cos^2 x = 1$。
答案:方程无解。
2. 求解方程$\sin 2x = \cos x$。
答案:方程的解为$x=\frac{\pi}{4}+2k\pi$,$x=\frac{3\pi}{4}+2k\pi$,其中$k$为整数。
第三章:数列与数学归纳法1. 求等差数列$\{a_n\}$的通项公式,已知$a_1=2$,$d=3$。
答案:$a_n=2+3(n-1)$2. 求等比数列$\{b_n\}$的通项公式,已知$b_1=2$,$q=2$。
答案:$b_n=2\cdot2^{n-1}$第四章:概率与统计1. 一枚硬币抛掷3次,求出现正面的次数为2次的概率。
答案:概率为$\frac{3}{8}$2. 一批产品中有10%的次品,从中随机抽取5个产品,求恰好有2个次品的概率。
答案:概率为$0.324$第五章:三角恒等变换1. 求证$\sin^2x+\cos^2x=1$。
答案:根据三角恒等变换,$\sin^2x+\cos^2x=1$成立。
2. 求证$\tan^2x+1=\sec^2x$。
答案:根据三角恒等变换,$\tan^2x+1=\sec^2x$成立。
通过以上习题的练习,我们可以更好地掌握数学必修4的知识点。
人教版高中数学必修4课后习题答案详解

第二章 平面向量2.1平面向量的实际背景及基本概念 练习(P77)1、略.2、AB ,BA . 这两个向量的长度相等,但它们不等.3、2AB =, 2.5CD =,3EF =,22GH =4、(1)它们的终点相同; (2)它们的终点不同. 习题 A 组(P77) 1、(2). 3、与DE 相等的向量有:,AF FC ;与EF 相等的向量有:,BD DA ; 与FD 相等的向量有:,CE EB .4、与a 相等的向量有:,,CO QP SR ;与b 相等的向量有:,PM DO ; 与c 相等的向量有:,,DC RQ ST5、33AD =. 6、(1)×; (2)√; (3)√; (4)×. 习题 B 组(P78)1、海拔和高度都不是向量.2、相等的向量共有24对. 模为1的向量有18对. 其中与AM 同向的共有6对,与AM 反向的也有6对;与AD同向的共有3对,与AD 反向的也有6对;模的向量共有4对;模为2的向量有2对2.2平面向量的线性运算 练习(P84)1、图略.2、图略.3、(1)DA ; (2)CB .4、(1)c ; (2)f ; (3)f ; (4)g . 练习(P87)1、图略.2、DB ,CA ,AC ,AD ,BA .3、图略. 练习(P90) 1、图略.2、57AC AB =,27BC AB =-.说明:本题可先画一个示意图,根据图形容易得出正确答案. 值得注意的是BC 与AB 反向.3、(1)2b a =; (2)74b a =-; (3)12b a =-; (4)89b a =.4、(1)共线; (2)共线.5、(1)32a b -; (2)111123a b -+; (3)2ya . 6、图略.习题 A 组(P91)1、(1)向东走20 km ; (2)向东走5 km; (3)向东北走km ;(4)向西南走;(5)向西北走;(6)向东南走 2、飞机飞行的路程为700 km ;两次位移的合成是向北偏西53°方向飞行500 km. 3、解:如右图所示:AB 表示船速,AD 表示河水的流速,以AB 、AD 为邻边作□ABCD ,则AC 表示船实际航行的速度.在Rt △ABC 中,8AB =,2AD =,所以228AC AB AD =+==因为tan4CAD ∠=,由计算器得76CAD ∠≈︒所以,实际航行的速度是km/h ,船航行的方向与河岸的夹角约为76°. 4、(1)0; (2)AB ; (3)BA ; (4)0; (5)0; (6)CB ; (7)0.5、略6、不一定构成三角形. 说明:结合向量加法的三角形法则,让学生理解,若三个非零向量的和为零向量,且这三个向量不共线时,则表示这三个向量的有向线段一定能构成三角形.7、略. 8、(1)略; (2)当a b ⊥时,a b a b +=-9、(1)22a b --; (2)102210a b c -+; (3)132a b +; (4)2()x y b -.10、14a b e +=,124a b e e -=-+,1232310a b e e -=-+. 11、如图所示,OC a =-,OD b =-,DC b a =-,BC a b =--.12、14AE b =,BC b a =-,1()4DE b a =-,34DB a =, 34EC b =,1()8DN b a =-,11()48AN AM a b ==+.13、证明:在ABC ∆中,,E F 分别是,AB BC 的中点,所以EF AC //且12EF AC =,即12EF AC =;同理,12HG AC =,所以EF HG =.习题 B 组(P92)1、丙地在甲地的北偏东45°方向,距甲地1400 km.2、不一定相等,可以验证在,a b 不共线时它们不相等.3、证明:因为MN AN AM =-,而13AN AC =,13AM AB =, 所以1111()3333MN AC AB AC AB BC =-=-=.4、(1)四边形ABCD 为平行四边形,证略 (2)四边形ABCD 为梯形.证明:∵13AD BC =,∴AD BC //且AD BC ≠ ∴四边形ABCD 为梯形. (3)四边形ABCD 为菱形.(第11题)(第12题)EHGFC AB丙乙(第1题)(第4题(2))BCD证明:∵AB DC =,∴AB DC //且AB DC =∴四边形ABCD 为平行四边形 又AB AD =∴四边形ABCD 为菱形.5、(1)通过作图可以发现四边形ABCD 为平行四边形. 证明:因为OA OB BA -=,OD OC CD -= 而OA OC OB OD +=+所以OA OB OD OC -=- 所以BA CD =,即∥.因此,四边形ABCD 为平行四边形. 2.3平面向量的基本定理及坐标表示 练习(P100)1、(1)(3,6)a b +=,(7,2)a b -=-; (2)(1,11)a b +=,(7,5)a b -=-; (3)(0,0)a b +=,(4,6)a b -=; (4)(3,4)a b +=,(3,4)a b -=-.2、24(6,8)a b -+=--,43(12,5)a b +=.3、(1)(3,4)AB =,(3,4)BA =--; (2)(9,1)AB =-,(9,1)BA =-; (3)(0,2)AB =,(0,2)BA =-; (4)(5,0)AB =,(5,0)BA =-4、AB ∥CD . 证明:(1,1)AB =-,(1,1)CD =-,所以AB CD =.所以AB ∥CD .5、(1)(3,2); (2)(1,4); (3)(4,5)-.6、10(,1)3或14(,1)3-7、解:设(,)P x y ,由点P 在线段AB 的延长线上,且32AP PB =,得32AP PB =-(,)(2,3)(2,3)AP x y x y =-=--,(4,3)(,)(4,3)PB x y x y =--=---∴3(2,3)(4,3)2x y x y --=---- ∴32(4)233(3)2x x y y ⎧-=--⎪⎪⎨⎪-=---⎪⎩(第4题(3))(第5题)∴815x y =⎧⎨=-⎩,所以点P 的坐标为(8,15)-.习题 A 组(P101)1、(1)(2,1)-; (2)(0,8); (3)(1,2).说明:解题时可设(,)B x y ,利用向量坐标的定义解题. 2、123(8,0)F F F ++=3、解法一:(1,2)OA =--,(53,6(1))(2,7)BC =---=而AD BC =,(1,5)OD OA AD OA BC =+=+=. 所以点D 的坐标为(1,5).解法二:设(,)D x y ,则((1),(2))(1,2)AD x y x y =----=++,(53,6(1))(2,7)BC =---=由AD BC =可得,1227x y +=⎧⎨+=⎩,解得点D 的坐标为(1,5).4、解:(1,1)OA =,(2,4)AB =-. 1(1,2)2AC AB ==-,2(4,8)AD AB ==-,1(1,2)2AE AB =-=-. (0,3)OC OA AC =+=,所以,点C 的坐标为(0,3); (3,9)OD OA AD =+=-,所以,点D 的坐标为(3,9)-; (2,1)OE OA AE =+=-,所以,点E 的坐标为(2,1)-. 5、由向量,a b 共线得(2,3)(,6)x λ=-,所以236x =-,解得4x =-. 6、(4,4)AB =,(8,8)CD =--,2CD AB =-,所以AB 与CD 共线. 7、2(2,4)OA OA '==,所以点A '的坐标为(2,4);3(3,9)OB OB '==-,所以点B '的坐标为(3,9)-; 故(3,9)(2,4)(5,5)A B ''=--=- 习题 B 组(P101)1、(1,2)OA =,(3,3)AB =.当1t =时,(4,5)OP OA AB OB =+==,所以(4,5)P ; 当12t =时,13357(1,2)(,)(,)22222OP OA AB =+=+=,所以57(,)22P ; 当2t =-时,2(1,2)(6,6)(5,4)OP OA AB =-=-=--,所以(5,4)P --; 当2t =时,2(1,2)(6,6)(7,8)OP OA AB =+=+=,所以(7,8)P .2、(1)因为(4,6)AB =--,(1,1.5)AC =,所以4AB AC =-,所以A 、B 、C 三点共线;(2)因为(1.5,2)PQ =-,(6,8)PR =-,所以4PR PQ =,所以P 、Q 、R 三点共线;(3)因为(8,4)EF =--,(1,0.5)EG =--,所以8EF EG =,所以E 、F 、G 三点共线.3、证明:假设10λ≠,则由11220e e λλ+=,得2121e e λλ=-. 所以12,e e 是共线向量,与已知12,e e 是平面内的一组基底矛盾, 因此假设错误,10λ=. 同理20λ=. 综上120λλ==.4、(1)19OP =(2)对于任意向量12OP xe ye =+,,x y 都是唯一确定的,所以向量的坐标表示的规定合理.2.4平面向量的数量积 练习(P106)1、1cos ,86242p q p q p q ⋅=⋅⋅<>=⨯⨯=. 2、当0a b ⋅<时,ABC ∆为钝角三角形;当0a b ⋅=时,ABC ∆为直角三角形.3、投影分别为0,-图略 练习(P107)1、2(3)5a =-=,252b =+=35427a b ⋅=-⨯+⨯=-.2、8a b ⋅=,()()7a b a b +-=-,()0a b c ⋅+=,2()49a b +=.3、1a b ⋅=,13a =,74b =,88θ≈︒. 习题 A 组(P108)1、63a b ⋅=-222()225a b a a b b +=+⋅+=-25a b +=- 2、BC 与CA 的夹角为120°,20BC CA ⋅=-.3、22223a b a a b b +=+⋅+=,22235a b a a b b -=-⋅+=. 4、证法一:设a 与b 的夹角为θ.(1)当0λ=时,等式显然成立;(2)当0λ>时,a λ与b ,a 与b λ的夹角都为θ,所以()cos cos a b a b a b λλθλθ⋅==()cos a b a b λλθ⋅=()cos cos a b a b a b λλθλθ⋅== 所以 ()()()a b a b a b λλλ⋅=⋅=⋅;(3)当0λ<时,a λ与b ,a 与b λ的夹角都为180θ︒-,则 ()cos(180)cos a b a b a b λλθλθ⋅=︒-=-()cos cos a b a b a b λλθλθ⋅==-()cos(180)cos a b a b a b λλθλθ⋅=︒-=- 所以 ()()()a b a b a b λλλ⋅=⋅=⋅; 综上所述,等式成立.证法二:设11(,)a x y =,22(,)b x y =,那么 11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+112212121212()(,)(,)()a b x y x y x x y y x x y y λλλλλ⋅=⋅=+=+11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+所以 ()()()a b a b a b λλλ⋅=⋅=⋅;5、(1)直角三角形,B ∠为直角.证明:∵(1,4)(5,2)(6,6)BA =---=--,(3,4)(5,2)(2,2)BC =-=-∴6(2)(6)20BA BC ⋅=-⨯-+-⨯=∴BA BC ⊥,B ∠为直角,ABC ∆为直角三角形(2)直角三角形,A ∠为直角证明:∵(19,4)(2,3)(21,7)AB =---=,(1,6)(2,3)(1,3)AC =-----=-∴2117(3)0AB AC ⋅=⨯+⨯-=∴AB AC ⊥,A ∠为直角,ABC ∆为直角三角形(3)直角三角形,B ∠为直角证明:∵(2,5)(5,2)(3,3)BA =-=-,(10,7)(5,2)(5,5)BC =-=∴35350BA BC ⋅=-⨯+⨯=∴BA BC ⊥,B ∠为直角,ABC ∆为直角三角形6、135θ=︒.7、120θ=︒.22(23)(2)44361a b a b a a b b -+=-⋅-=,于是可得6a b ⋅=-,1cos 2a ba bθ⋅==-,所以120θ=︒.8、23cos 40θ=,55θ=︒. 9、证明:∵(5,2)(1,0)(4,2)AB =--=-,(8,4)(5,2)(3,6)BC =--=,(8,4)(4,6)(4,2)DC =-=-∴AB DC =,43(2)60AB BC ⋅=⨯+-⨯= ∴,,,A B C D 为顶点的四边形是矩形.10、解:设(,)a x y =,则2292x y yx⎧+=⎪⎨=⎪⎩,解得5x y⎧=⎪⎪⎨⎪=⎪⎩5x y ⎧=⎪⎪⎨⎪=-⎪⎩.于是35(,55a =或35(55a =--. 11、解:设与a 垂直的单位向量(,)e x y =,则221420x y xy ⎧+=⎨+=⎩,解得5x y ⎧=⎪⎪⎨⎪=⎪⎩或5x y ⎧=-⎪⎪⎨⎪=⎪⎩.于是5(,55e =-或5(,55e =-. 习题 B 组(P108)1、证法一:0()0()a b a c a b a c a b c a b c ⋅=⋅⇔⋅-⋅=⇔⋅-=⇔⊥- 证法二:设11(,)a x y =,22(,)b x y =,33(,)c x y =.先证()a b a c a b c ⋅=⋅⇒⊥-1212a b x x y y ⋅=+,1313a c x x y y ⋅=+由a b a c ⋅=⋅得12121313x x y y x x y y +=+,即123123()()0x x x y y y -+-=而2323(,)b c x x y y -=--,所以()0a b c ⋅-= 再证()a b c a b a c ⊥-⇒⋅=⋅由()0a b c ⋅-=得 123123()()0x x x y y y -+-=, 即12121313x x y y x x y y +=+,因此a b a c ⋅=⋅2、cos cos cos sin sin OA OB AOB OA OBαβαβ⋅∠==+.3、证明:构造向量(,)u a b =,(,)v c d =.cos ,u v u v u v ⋅=<>,所以,ac bd u v +=<>∴2222222222()()()cos ,()()ac bd a b c d u v a b c d +=++<>≤++4、AB AC ⋅的值只与弦AB 的长有关,与圆的半径无关.证明:取AB 的中点M ,连接CM ,则CM AB ⊥,12AM AB =又cos AB AC AB AC BAC ⋅=∠,而AM BAC AC∠=所以212AB AC AB AM AB ⋅==5、(1)勾股定理:Rt ABC ∆中,90C ∠=︒,则222CA CB AB +=证明:∵AB CB CA =-∴2222()2AB CB CA CB CA CB CA =-=-⋅+. 由90C ∠=︒,有CA CB ⊥,于是0CA CB ⋅= ∴222CA CB AB +=(2)菱形ABCD 中,求证:AC BD ⊥证明:∵AC AB AD =+,,DB AB AD =-∴22()()AC DB AB AD AB AD AB AD ⋅=+⋅-=-.∵四边形ABCD 为菱形,∴AB AD =,所以220AB AD -= ∴0AC DB ⋅=,所以AC BD ⊥(3)长方形ABCD 中,求证:AC BD =证明:∵ 四边形ABCD 为长方形,所以AB AD ⊥,所以0AB AD ⋅=∴222222AB AB AD AD AB AB AD AD +⋅+=-⋅+.∴22()()AB AD AB AD +=-,所以22AC BD =,所以AC BD =(4)正方形的对角线垂直平分. 综合以上(2)(3)的证明即可. 2.5平面向量应用举例 习题 A 组(P113)1、解:设(,)P x y ,11(,)R x y则1111(1,0)(,)(1,)RA x y x y =-=--,(,)(1,0)(1,0)AP x y x =-=-由2RA AP =得11(1,)2(1,)x y x y --=-,即11232x x y y=-+⎧⎨=-⎩代入直线l 的方程得2y x =. 所以,点P 的轨迹方程为2y x =. 2、解:(1)易知,OFD ∆∽OBC ∆,12DF BC =, 所以23BO BF =.2211()()3323AO BO BA BF a b a a a b =-=+=-+=+(2)因为1()2AE a b =+所以23AO AE =,因此,,A O E 三点共线,而且2AOOE =同理可知:2,2BO CO OF OD ==,所以2AO BO COOE OF OD===3、解:(1)(2,7)B A v v v =-=-; (2)v 在A v 方向上的投影为135A Av v v ⋅=. 4、解:设1F ,2F 的合力为F ,F 与1F 的夹角为θ,则31F =+,30θ=︒; 331F =+,3F 与1F 的夹角为150°.习题 B 组(P113)1、解:设0v 在水平方向的速度大小为x v ,竖直方向的速度的大小为y v ,则0cos x v v θ=,0sin y v v θ=.设在时刻t 时的上升高度为h ,抛掷距离为s ,则001sin ,()2cos h v t gt g s v t θθ⎧=-⎪⎨⎪=⎩为重力加速度 所以,最大高度为220sin 2v gθ,最大投掷距离为20sin 2v gθ.2、解:设1v 与2v 的夹角为θ,合速度为v ,2v 与v 的夹角为α,行驶距离为d .则1sin 10sin sin v vvθθα==,0.5sin 20sin v d αθ==. ∴120sin d v θ=. 所以当90θ=︒,即船垂直于对岸行驶时所用时间最短. 3、(1)(0,1)-ODFEABC(第2题)(第4题)解:设(,)P x y ,则(1,2)AP x y =--. (2,22)AB =-.将AB 绕点A 沿顺时针方向旋转4π到AP ,相当于沿逆时针方向旋转74π到AP ,于是7777(2cos 22sin ,2sin 22cos )(1,3)4444AP ππππ=+-=--所以1123x y -=-⎧⎨-=-⎩,解得0,1x y ==-(2)32y x=-解:设曲线C 上任一点P 的坐标为(,)x y ,OP 绕O 逆时针旋转4π后,点P 的坐标为(,)x y ''则cos sin 44sin cos44x x y y x y ππππ⎧'=-⎪⎪⎨⎪'=+⎪⎩,即2()2()2x x y y x y ⎧'=-⎪⎪⎨⎪'=+⎪⎩又因为223x y ''-=,所以2211()()322x y x y --+=,化简得32y x=-第二章 复习参考题A 组(P118)1、(1)√; (2)√; (3)×; (4)×.2、(1)D ; (2)B ; (3)D ; (4)C ; (5)D ; (6)B .3、1()2AB a b =-,1()2AD a b =+4、略解:2133DE BA MA MB a b ==-=-+2233AD a b =+,1133BC a b =+1133EF a b =--,1233FA DC a b ==-1233CD a b =-+,2133AB a b =-CE a b =-+5、(1)(8,8)AB =-,82AB =;(2)(2,16)OC =-,(8,8)OD =-; (3)33OA OB ⋅=.(第4题)6、AB 与CD 共线.证明:因为(1,1)AB =-,(1,1)CD =-,所以AB CD =. 所以AB 与CD 共线. 7、(2,0)D -. 8、2n =. 9、1,0λμ=-=.10、34cos ,cos 0,cos 55A B C ===11、证明:2(2)22cos6010n m m n m m -⋅=⋅-=︒-=,所以(2)n m m -⊥.12、1λ=-. 13、13a b +=,1a b -=. 14、519cos ,cos 820θβ==第二章 复习参考题B 组(P119)1、(1)A ; (2)D ; (3)B ; (4)C ; (5)C ; (6)C ; (7)D .2、证明:先证a b a b a b ⊥⇒+=-.222()2a b a b a b a b+=+=++⋅,222()2a b a b a b a b -=-=+-⋅.因为a b ⊥,所以0a b ⋅=,于是22a b a b a b +=+=-. 再证a b a b a b +=-⇒⊥.由于222a b a a b b +=+⋅+,222a b a a b b -=-⋅+ 由a b a b +=-可得0a b ⋅=,于是a b ⊥所以a b a b a b +=-⇔⊥. 【几何意义是矩形的两条对角线相等】 3、证明:先证a b c d =⇒⊥22()()c d a b a b a b ⋅=+⋅-=- 又a b =,所以0c d ⋅=,所以c d ⊥ 再证c d a b ⊥⇒=.由c d ⊥得0c d ⋅=,即22()()0a b a b a b +⋅-=-=所以a b = 【几何意义为菱形的对角线互相垂直,如图所(第3题)(第6题)示】4、12AD AB BC CD a b =++=+,1142AE a b =+而34EF a =,14EM a =,所以1111(4242AM AE EM a b a =+=++=5、证明:如图所示,12OD OP OP =+,由于1230OP OP OP ++=,所以3OP OD =-,1OD = 所以11OD OP PD == 所以1230OPP ∠=︒,同理可得1330OPP ∠=︒所以31260P PP ∠=︒,同理可得12360PP P ∠=︒,23160P P P ∠=︒,所以123PP P ∆为正三角形.6、连接AB .由对称性可知,AB 是SMN ∆的中位线,222MN AB b a ==-. 7、(18=(千米/时), 沿与水流方向成60°的方向前进; (2)实际前进速度大小为 沿与水流方向成90︒+的方向前进. 8、解:因为OA OB OB OC ⋅=⋅,所以()0OB OA OC ⋅-=,所以0OB CA ⋅= 同理,0OA BC ⋅=,0OC AB ⋅=,所以点O 是ABC ∆的垂心. 9、(1)2110200a x a y a y a x -+-=; (2)垂直;(3)当12210A B A B -=时,1l ∥2l ;当12120A A B B +=时,12l l ⊥,夹角θ的余弦cos θ=;(4)d =P 2(第5题)第三章 三角恒等变换3.1两角和与差的正弦、余弦和正切公式 练习(P127)1、cos()cos cos sin sin 0cos 1sin sin 222πππαααααα-=+=⨯+⨯=.cos(2)cos2cos sin2sin 1cos 0sin cos παπαπαααα-=+=⨯+⨯=.2、解:由3cos ,(,)52πααπ=-∈,得4sin 5α==;所以34cos()cos cos sin sin ()44455πππααα-=+=-+=3、解:由15sin 17θ=,θ是第二象限角,得8cos 17θ===-;所以8115cos()cos cos sin sin 33317217πππθθθ-=+=-⨯+=. 4、解:由23sin ,(,)32πααπ=-∈,得cos α==又由33cos ,(,2)42πββπ=∈,得sin β==所以32cos()cos cos sin sin ((()43βαβαβα-=+=⨯+⨯-=. 练习(P131)1、(1; (2) (3(4)2 2、解:由3cos ,(,)52πθθπ=-∈,得4sin 5θ==;所以413sin()sin cos cos sin ()333525πππθθθ+=+=⨯+-=. 3、解:由12sin 13θ=-,θ是第三象限角,得5cos 13θ===-; 所以5112cos()cos cos sin sin ()()66613213πππθθθ+=-=--⨯-=. 4、解:tan tan 314tan()241311tan tan 4παπαπα+++===--⨯-⋅.5、(1)1; (2)12; (3)1; (4);(5)原式=1(cos34cos26sin34sin 26)cos(3426)cos602-︒︒-︒︒=-︒+︒=-︒=-;(6)原式=sin 20cos70cos20sin70(sin 20cos70cos20sin70)sin901-︒︒-︒︒=-︒︒+︒︒=-︒=-.6、(1)原式=cos cos sin sin cos()333x x x πππ-=+;(2)原式=1cos )2(sin cos cos sin )2sin()2666x x x x x πππ+=+=+;(3)原式=)2(sin cos cos sin )2sin()444x x x x x πππ=-=-;(4)原式=12(cos )cos sin sin )cos()2333x x x x x πππ=-=+.7、解:由已知得3sin()cos cos()sin 5αβααβα---=,即3sin[()]5αβα--=,3sin()5β-=所以3sin 5β=-. 又β是第三象限角,于是4cos 5β===-.因此55534sin()sin cos cos sin ()(()(44455πππβββ+=+=-+-=. 练习(P135)1、解:因为812παπ<<,所以382αππ<<又由4cos 85α=-,得3sin 85α=-,3sin385tan 484cos 85ααα-===- 所以3424sinsin(2)2sin cos 2()()48885525αααα=⨯==⨯-⨯-=2222437cos cos(2)cos sin ()()48885525αααα=⨯=-=---=2232tan23162484tan tan(2)3482771tan 1()84αααα⨯=⨯===⨯=-- 2、解:由3sin()5απ-=,得3sin 5α=-,所以222316cos 1sin 1()525αα=-=--=所以2221637cos2cos sin ()25525ααα=-=--=3、解:由sin2sin αα=-且sin 0α≠可得1cos 2α=-,又由(,)2παπ∈,得sin α=,所以sintan (2)cos ααα==-= 4、解:由1tan 23α=,得22tan 11tan 3αα=-. 所以2tan 6tan 10αα+-=,所以tan 3α=-5、(1)11sin15cos15sin3024︒︒=︒=; (2)22cos sin cos 88πππ-==;(3)原式=212tan 22.511tan 4521tan 22.522︒⋅=︒=-︒; (4)原式=cos45︒=. 习题 A 组(P137)1、(1)333cos()cos cos sin sin 0cos (1)sin sin 222πππαααααα-=+=⨯+-⨯=-;(2)333sin()sin cos cos sin 1cos 0sin cos 222πππαααααα-=-=-⨯-⨯=-;(3)cos()cos cos sin sin 1cos 0sin cos παπαπαααα-=+=-⨯+⨯=-; (4)sin()sin cos cos sin 0cos (1)sin sin παπαπαααα-=-=⨯--⨯=.2、解:由3cos ,05ααπ=<<,得4sin 5α==,所以431cos()cos cos sin sin 666552πππααα-=+=⨯=.3、解:由2sin ,(,)32πααπ=∈,得cos α===又由33cos ,(,)42πββπ=-∈,得sin β===,所以32cos()cos cos sin sin ()(43αβαβαβ-=+=-+⨯=.4、解:由1cos 7α=,α是锐角,得sin α=== 因为,αβ是锐角,所以(0,)αβπ+∈,又因为11cos()14αβ+=-,所以sin()αβ+===所以cos cos[()]cos()cos sin()sin βαβααβααβα=+-=+++1111()1472=-⨯= 5、解:由60150α︒<<︒,得9030180α︒<︒+<︒又由3sin(30)5α︒+=,得4cos(30)5α︒+=-所以cos cos[(30)30]cos(30)cos30sin(30)sin30αααα=︒+-︒=︒+︒+︒+︒431552=-+⨯=6、(1); (2) (3)2-7、解:由2sin ,(,)32πααπ=∈,得cos α===又由3cos 4β=-,β是第三象限角,得sin β==.所以cos()cos cos sin sin αβαβαβ+=-32()(43=--⨯=sin()sin cos cos sin αβαβαβ-=-23()((34=⨯--⨯=8、解:∵53sin ,cos 135A B ==且,A B 为ABC ∆的内角∴0,02A B ππ<<<<,124cos ,sin 135A B =±=当12cos 13A =-时,sin()sin cos cos sin AB A B A B +=+5312433()013513565=⨯+-⨯=-< A B π+>,不合题意,舍去∴124cos ,sin 135A B ==∴cos cos()(cos cos sin sin )C A B A B A B =-+=--1235416()13513565-⨯-⨯=- 9、解:由3sin ,(,)52πθθπ=∈,得4cos 5θ==-.∴sin 353tan ()cos 544θθθ==⨯-=-. ∴31tan tan 242tan()311tan tan 111()42θϕθϕθϕ-+++===--⋅--⨯. 31tan tan 42tan()2311tan tan 1()42θϕθϕθϕ----===-+⋅+-⨯. 10、解:∵tan ,tan αβ是22370x x +-=的两个实数根.∴3tan tan 2αβ+=-,7tan tan 2αβ⋅=-.∴3tan tan 12tan()71tan tan 31()2αβαβαβ-++===--⋅--.11、解:∵tan()3,tan()5αβαβ+=-=∴tan()tan()tan 2tan[()()]1tan()tan()αβαβααβαβαβαβ++-=++-=-+⋅-3541357+==--⨯tan()tan()tan 2tan[()()]1tan()tan()αβαββαβαβαβαβ+--=+--=++⋅-3511358-==-+⨯12、解:∵::2:3:6BD DC AD =∴11tan ,tan 32BD DC AD AD αβ====∴tan tan tan tan()1tan tan BAC αβαβαβ+∠=+=-⋅1132111132+==-⨯ 又∵0180BAC ︒<∠<︒,∴45BAC ∠=︒(第12题)13、(1))6x π+; (23sin()3x π-; (3)2sin()26x π+;(47sin()12x π-; (5)2; (6)12; (7)sin()αγ+; (8)cos()αγ--; (9) (10)tan()βα-.14、解:由sin 0.8,(0,)2παα=∈,得cos 0.6α===∴sin22sin cos 20.80.60.96ααα==⨯⨯= 2222cos2cos sin 0.60.80.28ααα=-=-=- 15、解:由cos 270ϕϕ=︒<<︒,得sin ϕ===∴sin 22sin cos 2((ϕϕϕ==⨯⨯=22221cos2cossin ((3ϕϕϕ=-=-=- sin 2tan 2(3)cos 23ϕϕϕ==-=-16、解:设5sin sin 13B C ==,且090B ︒<<︒,所以12cos 13B =. ∴512120sin sin(1802)sin 22sin cos 21313169A B B B B =︒-===⨯⨯=2222125119cos cos(1802)cos2(cos sin )(()())1313169A B B B B =︒-=-=--=--=-sin 120169120tan ()cos 169119119A A A ==⨯-=-17、解:22122tan 33tan 211tan 41()3βββ⨯===--,13tan tan 274tan(2)1131tan tan 2174αβαβαβ+++===-⋅-⨯. 18、解:1cos()cos sin()sin 3αββαββ+++=⇒1cos[()]3αββ+-=,即1cos 3α= 又3(,2)2παπ∈,所以sinα== ∴1sin 22sin cos 2(ααα==⨯⨯=222217cos2cos sin ()(39ααα=-=-=-∴7cos(2)cos2cos sin 2sin (4449πππααα+=-=-=19、(1)1sin2α+; (2)cos2θ; (3)1sin 44x ; (4)tan2θ.习题 B 组(P138) 1、略. 2、解:∵tan ,tan A B 是x 的方程2(1)10x p x +++=,即210x px p +++=的两个实根∴tan tan A B p +=-,tan tan 1A B p ⋅=+ ∴tan tan[()]tan()C A B A B π=-+=-+tan tan 11tan tan 1(1)A B pA B p +-=-=-=--⋅-+由于0C π<<,所以34C π=. 3、反应一般的规律的等式是(表述形式不唯一)223sin cos (30)sin cos(30)4αααα++︒++︒=(证明略) 本题是开放型问题,反映一般规律的等式的表述形式还可以是:223sin (30)cos sin(30)cos 4αααα-︒++-︒=223sin (15)cos (15)sin(15)cos(15)4αααα-︒++︒+-︒+︒=223sin cos sin cos 4αβαβ++=,其中30βα-=︒,等等思考过程要求从角,三角函数种类,式子结构形式三个方面寻找共同特点,从而作出归纳. 对认识三角函数式特点有帮助,证明过程也会促进推理能力、运算能力的提高.4、因为12PA PP =,则2222(cos()1)sin ()(cos cos )(sin sin )αβαβαβαβ+-++=-++ 即22cos()22cos cos 2sin sin αβαβαβ-+=-+ 所以cos()cos cos sin sin αβαβαβ+=-3.2简单的三角恒等变换 练习(P142)1、略.2、略.3、略.4、(1)1sin 42y x =. 最小正周期为2π,递增区间为[,],8282k k k Z ππππ-++∈,最大值为12;(2)cos 2y x =+. 最小正周期为2π,递增区间为[2,22],k k k Z ππππ++∈,最大值为3;(3)2sin(4)3y x π=+. 最小正周期为2π,递增区间为5[,],242242k k k Z ππππ-++∈,最大值为2.习题 A 组( P143) 1、(1)略; (2)提示:左式通分后分子分母同乘以2; (3)略; (4)提示:用22sin cos ϕϕ+代替1,用2sin cos ϕϕ代替sin 2ϕ;(5)略; (6)提示:用22cos θ代替1cos2θ+;(7)提示:用22sin θ代替1cos2θ-,用22cos θ代替1cos2θ+; (8)略.2、由已知可有1sin cos cos sin 2αβαβ+=……①,1sin cos cos sin 3αβαβ-=……②(1)②×3-①×2可得sin cos 5cos sin αβαβ=(2)把(1)所得的两边同除以cos cos αβ得tan 5tan αβ= 注意:这里cos cos 0αβ≠隐含与①、②之中3、由已知可解得1tan 2θ=-. 于是2212()2tan 42tan 211tan 31()2θθθ⨯-===---- 1tan tan1142tan()1431tan tan 1()142πθπθπθ+-++===-⋅--⨯ ∴tan 24tan()4πθθ=-+4、由已知可解得sin x θ=,cos y θ=,于是2222sin cos 1x y θθ+=+=.5、()2sin(4)3f x x π=+,最小正周期是2π,递减区间为7[,],242242k k k Z ππππ++∈.习题 B 组(P143) 1、略.2、由于762790+⨯=,所以sin76sin(9014)cos14m ︒=︒-︒=︒= 即22cos 71m ︒-=,得cos7︒=3、设存在锐角,αβ使223παβ+=,所以23απβ+=,tan()2αβ+又tantan 22αβ=,又因为tantan 2tan()21tantan 2αβαβαβ++=-,所以tantan tan()(1tan tan )3222αααβββ+=+-=由此可解得tan 1β=, 4πβ=,所以6πα=.经检验6πα=,4πβ=是符合题意的两锐角.4、线段AB 的中点M 的坐标为11((cos cos ),(sin sin ))22αβαβ++. 过M 作1MM 垂直于x 轴,交x 轴于1M ,111()()22MOM βαααβ∠=-+=+.在Rt OMA ∆中,cos cos 22OM OA βααβ--==. 在1Rt OM M ∆中,11cos cos cos22OM OM MOM αβαβ+-=∠=11sin sin cos22M M OM MOM αβαβ+-=∠=.于是有 1(cos cos )cos cos222αβαβαβ+-+=, 1(sin sin )sin cos222αβαβαβ+-+= 5、当2x =时,22()sin cos 1f ααα=+=;当4x =时,4422222()sin cos (sin cos )2sin cos f ααααααα=+=+-211sin 22α=-,此时有1()12f α≤≤;当6x =时,662232222()sin cos (sin cos )3sin cos (sin cos )f ααααααααα=+=+-+231sin 24α=-,此时有1()14f α≤≤;由此猜想,当2,x k k N +=∈时,11()12k f α-≤≤6、(1)345(sin cos )5sin()55y x x x ϕ=+=+,其中34cos ,sin 55ϕϕ==所以,y 的最大值为5,最小值为﹣5; (2))y x ϕ+,其中cos ϕϕ==所以,y ;第三章 复习参考题A 组(P146)(第4题)1、1665. 提示:()βαβα=+- 2、5665. 提示:5sin()sin[()]sin[()()]44ππαβπαββα+=-++=-+--3、1.4、(1)提示:把公式tan tan tan()1tan tan αβαβαβ++=-变形;(2; (3)2; (4)提示:利用(1)的恒等式.5、(1)原式4sin(3010)4sin 20︒-︒==︒;(2)原式=sin10sin 40(sin 40cos10︒︒=︒ =2sin 40cos40sin801cos10cos10-︒︒-︒==-︒︒;(3)原式=tan 70cos101)tan 70cos10︒︒=︒ =sin702sin10sin 20cos101cos70cos20cos70︒-︒-︒⋅︒⋅==-︒︒︒;(4)原式=sin50(1sin50︒⋅= 2cos50sin100sin501cos10cos10︒︒=︒⋅==︒︒6、(1)95; (2)2425;(3). 提示:4422222sin cos (sin cos )2sin cos θθθθθθ+=+-; (4)1725.7、由已知可求得2cos cos 5αβ=,1sin sin 5αβ=,于是sin sin 1tan tan cos cos 2αβαβαβ==. 8、(1)左边=222cos 214cos232(cos 22cos21)αααα-++=++22242(cos21)2(2cos )8cos ααα=+===右边(2)左边=2222sin cos 2sin cos (sin cos )2cos 2sin cos 2cos (cos sin )αααααααααααα+++=++sin cos 11tan 2cos 22αααα+==+=右边(3)左边=sin(2)2cos()sin sin[()]2cos()sin sin 2cos (cos sin )αβαβααβααβααααα+-+++-+=+sin()cos cos()sin sin sin sin αβααβαβαα+-+===右边(第12(2)题)(4)左边=222234cos22cos 212(cos 22cos21)34cos22cos 212(cos 22cos21)A A A A A A A A -+--+=++-++ 2224222(1cos2)(2sin )tan (1cos2)(2cos )A A A A A -===+=右边 9、(1)1sin 21cos2sin 2cos222)24y x x x x x π=+++=++++递减区间为5[,],88k k k Z ππππ++∈(222,最小值为22.10、2222()(cos sin )(cos sin )2sin cos cos2sin 22)4f x x x x x x x x x x π=+--=-=+(1)最小正周期是π;(2)由[0,]2x π∈得52[,]444x πππ+∈,所以当24x ππ+=,即38x π=时,()f x 的最小值为2-()f x 取最小值时x 的集合为3{}8π.11、2()2sin 2sin cos 1cos2sin 22)14f x x x x x x x π=+=-+=-+(1)最小正周期是π21;(2)()f x 在[,]22ππ-上的图象如右图:12、()3sin cos 2sin()6f x x x a x a π=++=++.(1)由21a +=得1a =-;(2)2{22,}3x k x k k Z πππ+∈≤≤.13、如图,设ABD α∠=,则CAE α∠=,2sin h AB α=,1cos hAC α=所以1212sin 2ABC h h S AB AC α∆=⋅⋅=,(0)2πα<<当22πα=,即4πα=时,ABC S ∆的最小值为12h h .第三章 复习参考题B 组(P147)1、解法一:由221sin cos 5sin cos 1αααα⎧-=⎪⎨⎪+=⎩,及0απ≤≤,可解得4sin 5α=, αh 1h 2l 2l 1BDE AC(第13题)13cos sin 55αα=-=,所以24sin 225α=,7cos225α=-,sin(2)sin 2cos cos2sin 44450πππααα-=-=. 解法二:由1sin cos 5αα-= 得21(sin cos )25αα-=,24sin 225α=,所以249cos 2625α=. 又由1sin cos 5αα-=,得sin()4πα-=.因为[0,]απ∈,所以3[,]444πππα-∈-.而当[,0]44ππα-∈-时,sin()04πα-≤;当3[,]444πππα-∈时,sin()4πα->所以(0,)44ππα-∈,即(,)42ππα∈所以2(,)2παπ∈,7cos225α=-.sin(2)4πα-=2、把1cos cos 2αβ+=两边分别平方得221cos cos 2cos cos 4αβαβ++=把1sin sin 3αβ+=两边分别平方得221sin sin 2sin sin 9αβαβ++=把所得两式相加,得1322(cos cos sin sin )36αβαβ++=,即1322cos()36αβ+-=,所以59cos()72αβ-=-3、由sin()sin 3παα++= 可得3sin 2αα=4sin()65πα+=-. 又02πα-<<,所以366πππα-<+<,于是3cos()65πα+=.所以cos cos[()]66ππαα=+-4、22sin 22sin 2sin cos 2sin 2sin cos (cos sin )sin 1tan cos sin 1cos x x x x x x x x x x x x x x +++==---1tan sin 2sin 2tan()1tan 4x x x x x π+==+-由177124x ππ<<得5234x πππ<+<,又3cos()45x π+=,所以4sin()45x π+=-,4tan()43x π+=-所以cos cos[()]cos()cos sin()sin 444444x x x x ππππππ=+-=+++=,sin 10x =-,7sin 22sin cos 25x x x ==, 所以2sin 22sin 281tan 75x x x +=--, 5、把已知代入222sin cos (sin cos )2sin cos 1θθθθθθ+=+-=,得22(2sin )2sin 1αβ-=.变形得2(1cos2)(1cos2)1αβ---=,2cos2cos2αβ=,224cos 24cos 2αβ= 本题从对比已知条件和所证等式开始,可发现应消去已知条件中含θ的三角函数.考虑sin cos θθ+,sin cos θθ这两者又有什么关系及得上解法. 5、6两题上述解法称为消去法6、()21cos22sin(2)16f x x x m x m π=+++=+++.由 [0,]2x π∈ 得72[,]666x πππ+∈,于是有216m ++=. 解得3m =.()2sin(2)4()6f x x x R π=++∈的最小值为242-+=,此时x 的取值集合由322()62x k k Z πππ+=+∈,求得为2()3x k k Z ππ=+∈7、设AP x =,AQ y =,BCP α∠=,DCQ β∠=,则tan 1x α=-,tan 1y β=- 于是2()tan()()x y x y xyαβ-++=+-又APQ ∆的周长为2,即2x y +,变形可得2()2xy x y =+- 于是2()tan()1()[2()2]x y x y x y αβ-++==+-+-.又02παβ<+<,所以4παβ+=,()24PCQ ππαβ∠=-+=.8、(1)由221sin cos 5sin cos 1ββββ⎧+=⎪⎨⎪+=⎩,可得225sin 5sin 120ββ--=解得4sin 5β=或3sin 5β=-(由(0,)βπ∈,舍去)所以13cos sin 55ββ=-=-,于是4tan 3β=-(2)根据所给条件,可求得仅由sin ,cos ,tan βββ表示的三角函数式的值,例如,sin()3πβ+,cos22β+,sin cos 2tan βββ-,sin cos 3sin 2cos ββββ-+,等等.。
人教版高中数学必修4课后习题答案详解

第二章 平面向量2.1平面向量的实际背景及基本概念 练习(P77)1、略.2、AB u u u r,BA u u u r . 这两个向量的长度相等,但它们不等.3、2AB =u u u r , 2.5CD =u u u r ,3EF =u u u r,GH =u u u r4、(1)它们的终点相同; (2)它们的终点不同. 习题2.1 A 组(P77) 1、(2). 3、与DE u u u r 相等的向量有:,AF FC u u u r u u u r ;与EF u u u r相等的向量有:,BD DA u u u r u u u r ; 与FD u u u r相等的向量有:,CE EB u u u r u u u r .4、与a r 相等的向量有:,,CO QP SR u u u r u u u r u u r ;与b r 相等的向量有:,PM DO u u u u r u u u r; 与c r 相等的向量有:,,DC RQ ST u u u r u u u r u uu r5、AD =u u u r .6、(1)×; (2)√; (3)√; (4)×.习题2.1 B 组(P78)1、海拔和高度都不是向量.2、相等的向量共有24对. 模为1的向量有18对. 其中与AM u u u u r同向的共有6对,与AM u u u u r 反向的也有6对;与AD u u u r 同向的共有3对,与AD u u u r反向的也有6的向量共有4对;模为2的向量有2对 2.2平面向量的线性运算 练习(P84)1、图略.2、图略.3、(1)DA u u u r; (2)CB u u u r .4、(1)c r ; (2)f u r ; (3)f u r ; (4)g u r . 练习(P87)1、图略.2、DB u u u r ,CA u u u r ,AC u u u r ,AD u u u r ,BA u u u r. 3、图略. 练习(P90) 1、图略.2、57AC AB =u u u r u u u r ,27BC AB =-u u u r u u u r .说明:本题可先画一个示意图,根据图形容易得出正确答案. 值得注意的是BCuuu r与AB u u u r反向.3、(1)2b a =r r ; (2)74b a =-r r ; (3)12b a =-r r; (4)89b a =r r .4、(1)共线; (2)共线.5、(1)32a b -r r ; (2)111123a b -+r r; (3)2ya r . 6、图略.习题2.2 A 组(P91)1、(1)向东走20 km ; (2)向东走5 km ;(3)向东北走km ;(4)向西南走;(5)向西北走;(6)向东南走km. 2、飞机飞行的路程为700 km ;两次位移的合成是向北偏西53°方向飞行500 km.3、解:如右图所示:AB u u u r 表示船速,AD u u u r表示河水的流速,以AB 、AD 为邻边作□ABCD ,则 AC u u u r表示船实际航行的速度.在Rt △ABC 中,8AB =u u u r ,2AD =u u u r,所以AC ===u u u r 因为tan 4CAD ∠=,由计算器得76CAD ∠≈︒所以,实际航行的速度是km/h ,船航行的方向与河岸的夹角约为76°.4、(1)0r ; (2)AB u u u r ; (3)BA u u u r ; (4)0r ; (5)0r ; (6)CB u u u r ; (7)0r .5、略6、不一定构成三角形. 说明:结合向量加法的三角形法则,让学生理解,若三个非零向量的和为零向量,且这三个向量不共线时,则表示这三个向量的有向线段一定能构成三角形.7、略. 8、(1)略; (2)当a b ⊥r r 时,a b a b +=-r r r r9、(1)22a b --r r ; (2)102210a b c -+r r r ; (3)132a b +r r ; (4)2()x y b -r .10、14a b e +=r r u r ,124a b e e -=-+r r u r u u r ,1232310a b e e -=-+r r u r u u r . 11、如图所示,OC a =-u u u r r ,OD b =-u u u r r,DC b a =-u u u r r r ,BC a b =--u u u r r r .12、14AE b =u u u r r ,BC b a =-u u u r r r ,1()4DE b a =-u u u r r r ,34DB a =u u u r r,34EC b =u u u r r ,1()8DN b a =-u u u r r r ,11()48AN AM a b ==+u u u r u u u u r r r .13、证明:在ABC ∆中,,E F 分别是,AB BC 的中点,所以EF AC //且12EF AC =,即12EF AC =u u u r u u u r ;同理,12HG AC =u u u r u u u r,所以EF HG =u u u r u u u r .习题2.2 B 组(P92)1、丙地在甲地的北偏东45°方向,距甲地1400 km.2、不一定相等,可以验证在,a b r r不共线时它们不相等.3、证明:因为MN AN AM =-u u u u r u u u r u u u u r ,而13AN AC =u u u r u u u r ,13AM AB =u u u u r u u u r,所以1111()3333MN AC AB AC AB BC =-=-=u u u u r u u u r u u u r u u u r u u u r u u u r.4、(1)四边形ABCD 为平行四边形,证略 (2)四边形ABCD 为梯形.证明:∵13AD BC =u u u r u u u r,(第11题)(第12题)EHGFC AB丙(第1题)BC∴AD BC //且AD BC ≠ ∴四边形ABCD 为梯形.(3)四边形ABCD 为菱形.证明:∵AB DC =u u u r u u u r,∴AB DC //且AB DC =∴四边形ABCD 为平行四边形 又AB AD =u u u r u u u r∴四边形ABCD 为菱形.5、(1)通过作图可以发现四边形ABCD 为平行四边形.证明:因为OA OB BA -=u u u r u u u r u u u r ,OD OC CD -=u u u r u u u r u u u r而OA OC OB OD +=+u u u r u u u r u u u r u u u r所以OA OB OD OC -=-u u u r u u u r u u u r u u u r所以BA CD =u u u r u u u r,即∥.因此,四边形ABCD 为平行四边形.2.3平面向量的基本定理及坐标表示 练习(P100)1、(1)(3,6)a b +=r r ,(7,2)a b -=-r r ; (2)(1,11)a b +=r r ,(7,5)a b -=-r r;(3)(0,0)a b +=r r ,(4,6)a b -=r r ; (4)(3,4)a b +=r r ,(3,4)a b -=-r r. 2、24(6,8)a b -+=--r r ,43(12,5)a b +=r r.3、(1)(3,4)AB =u u u r ,(3,4)BA =--u u u r ; (2)(9,1)AB =-u u u r ,(9,1)BA =-u u u r; (3)(0,2)AB =u u u r ,(0,2)BA =-u u u r ; (4)(5,0)AB =u u u r ,(5,0)BA =-u u u r4、AB ∥CD . 证明:(1,1)AB =-u u u r ,(1,1)CD =-u u u r,所以AB CD =u u u r u u u r .所以AB ∥CD .5、(1)(3,2); (2)(1,4); (3)(4,5)-.6、10(,1)3或14(,1)3-7、解:设(,)P x y ,由点P 在线段AB 的延长线上,且32AP PB =u u u r u u u r ,得32AP PB =-u u u r u u ur(,)(2,3)(2,3)AP x y x y =-=--u u u r ,(4,3)(,)(4,3)PB x y x y =--=---u u u r(第4题(3))(第5题)∴3(2,3)(4,3)2x y x y --=---- ∴32(4)233(3)2x x y y ⎧-=--⎪⎪⎨⎪-=---⎪⎩∴815x y =⎧⎨=-⎩,所以点P 的坐标为(8,15)-.习题2.3 A 组(P101)1、(1)(2,1)-; (2)(0,8); (3)(1,2).说明:解题时可设(,)B x y ,利用向量坐标的定义解题.2、123(8,0)F F F ++=u u r u u r u u r3、解法一:(1,2)OA =--u u u r ,(53,6(1))(2,7)BC =---=u u u r而AD BC =u u u r u u u r ,(1,5)OD OA AD OA BC =+=+=u u u r u u u r u u u r u u u r u u u r. 所以点D 的坐标为(1,5).解法二:设(,)D x y ,则((1),(2))(1,2)AD x y x y =----=++u u u r,(53,6(1))(2,7)BC =---=u u u r由AD BC =u u u r u u u r 可得,1227x y +=⎧⎨+=⎩,解得点D 的坐标为(1,5).4、解:(1,1)OA =u u u r ,(2,4)AB =-u u u r.1(1,2)2AC AB ==-u u u r u u u r ,2(4,8)AD AB ==-u u u r u u u r ,1(1,2)2AE AB =-=-u u u r u u ur .(0,3)OC OA AC =+=u u u r u u u r u u u r,所以,点C 的坐标为(0,3); (3,9)OD OA AD =+=-u u u r u u u r u u u r,所以,点D 的坐标为(3,9)-; (2,1)OE OA AE =+=-u u u r u u u r u u u r,所以,点E 的坐标为(2,1)-. 5、由向量,a b r r 共线得(2,3)(,6)x λ=-,所以236x =-,解得4x =-.6、(4,4)AB =u u u r ,(8,8)CD =--u u u r ,2CD AB =-u u u r u u u r ,所以AB u u u r 与CD uuur 共线. 7、2(2,4)OA OA '==u u u r u u u r ,所以点A '的坐标为(2,4);3(3,9)OB OB '==-u u u r u u u r,所以点B '的坐标为(3,9)-; 故 (3,9)(2,4)(5,5)A B ''=--=-u u u u r 习题2.3 B 组(P101)1、(1,2)OA =u u u r ,(3,3)AB =u u u r.当1t =时,(4,5)OP OA AB OB =+==u u u r u u u r u u u r u u u r,所以(4,5)P ;当12t =时,13357(1,2)(,)(,)22222OP OA AB =+=+=u u u r u u u r u u u r ,所以57(,)22P ;当2t =-时,2(1,2)(6,6)(5,4)OP OA AB =-=-=--u u u r u u u r u u u r,所以(5,4)P --;当2t =时,2(1,2)(6,6)(7,8)OP OA AB =+=+=u u u r u u u r u u u r,所以(7,8)P .2、(1)因为(4,6)AB =--u u u r ,(1,1.5)AC =u u u r,所以4AB AC =-u u u r u u u r ,所以A 、B 、C 三点共线;(2)因为(1.5,2)PQ =-u u u r ,(6,8)PR =-u u u r ,所以4PR PQ =u u u r u u u r,所以P 、Q 、R 三点共线;(3)因为(8,4)EF =--u u u r ,(1,0.5)EG =--u u u r,所以8EF EG =u u u r u u u r ,所以E 、F 、G 三点共线.3、证明:假设10λ≠,则由11220e e λλ+=u r u u r r ,得2121e e λλ=-u r uu r .所以12,e e u r u u r 是共线向量,与已知12,e e u r u u r是平面内的一组基底矛盾,因此假设错误,10λ=. 同理20λ=. 综上120λλ==.4、(1)OP =u u u r (2)对于任意向量12OP xe ye =+u u u r u r u u r,,x y 都是唯一确定的,所以向量的坐标表示的规定合理.2.4平面向量的数量积 练习(P106)1、1cos ,86242p q p q p q ⋅=⋅⋅<>=⨯⨯=u r r u r r u r r .2、当0a b ⋅<r r 时,ABC ∆为钝角三角形;当0a b ⋅=r r时,ABC ∆为直角三角形.3、投影分别为0,-图略练习(P107)1、5a ==r ,b ==r 35427a b ⋅=-⨯+⨯=-r r .2、8a b ⋅=r r ,()()7a b a b +-=-r r r r ,()0a b c ⋅+=r r r ,2()49a b +=r r .3、1a b ⋅=r r ,a =r b =r 88θ≈︒.习题2.4 A 组(P108)1、a b ⋅=-r r 222()225a b a a b b +=+⋅+=-r r r r r r a b +=r r2、BC uuu r 与CA u u u r 的夹角为120°,20BC CA ⋅=-u u u r u u u r .3、a b +==r r ,a b -==r r .4、证法一:设a r 与b r 的夹角为θ.(1)当0λ=时,等式显然成立;(2)当0λ>时,a λr 与b r ,a r 与b λr 的夹角都为θ,所以 ()cos cos a b a b a b λλθλθ⋅==r r r r r r()cos a b a b λλθ⋅=r r r r()cos cos a b a b a b λλθλθ⋅==r r r r r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;(3)当0λ<时,a λr 与b r ,a r 与b λr 的夹角都为180θ︒-,则 ()cos(180)cos a b a b a b λλθλθ⋅=︒-=-r r r r r r()cos cos a b a b a b λλθλθ⋅==-r r r r r r()cos(180)cos a b a b a b λλθλθ⋅=︒-=-r r r r r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;综上所述,等式成立.证法二:设11(,)a x y =r ,22(,)b x y =r ,那么 11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+r r112212121212()(,)(,)()a b x y x y x x y y x x y y λλλλλ⋅=⋅=+=+r r11221212()(,)(,)a b x y x y x x y y λλλλλ⋅=⋅=+r r所以 ()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r ;5、(1)直角三角形,B ∠为直角.证明:∵(1,4)(5,2)(6,6)BA =---=--u u u r ,(3,4)(5,2)(2,2)BC =-=-u u u r∴6(2)(6)20BA BC ⋅=-⨯-+-⨯=u u u r u u u r∴BA BC ⊥u u u r u u u r ,B ∠为直角,ABC ∆为直角三角形(2)直角三角形,A ∠为直角证明:∵(19,4)(2,3)(21,7)AB =---=u u u r ,(1,6)(2,3)(1,3)AC =-----=-u u u r∴2117(3)0AB AC ⋅=⨯+⨯-=u u u r u u u r∴AB AC ⊥u u u r u u u r ,A ∠为直角,ABC ∆为直角三角形(3)直角三角形,B ∠为直角证明:∵(2,5)(5,2)(3,3)BA =-=-u u u r ,(10,7)(5,2)(5,5)BC =-=u u u r∴35350BA BC ⋅=-⨯+⨯=u u u r u u u r∴BA BC ⊥u u u r u u u r ,B ∠为直角,ABC ∆为直角三角形6、135θ=︒.7、120θ=︒.22(23)(2)44361a b a b a a b b -+=-⋅-=r r r r r r r r ,于是可得6a b ⋅=-r r ,1cos 2a b a bθ⋅==-r r r r ,所以120θ=︒. 8、23cos 40θ=,55θ=︒. 9、证明:∵(5,2)(1,0)(4,2)AB =--=-u u u r ,(8,4)(5,2)(3,6)BC =--=u u u r , (8,4)(4,6)(4,2)DC =-=-u u u r∴AB DC =u u u r u u u r ,43(2)60AB BC ⋅=⨯+-⨯=u u u r u u u r∴,,,A B C D 为顶点的四边形是矩形.10、解:设(,)a x y =r ,则2292x y y x ⎧+=⎪⎨=⎪⎩,解得5x y ⎧=⎪⎪⎨⎪=⎪⎩5x y ⎧=-⎪⎪⎨⎪=⎪⎩.于是(55a =r或(55a =--r . 11、解:设与a r 垂直的单位向量(,)e x y =r ,则221420x y x y ⎧+=⎨+=⎩,解得5x y ⎧=⎪⎪⎨⎪=⎪⎩或5x y ⎧=-⎪⎪⎨⎪=⎪⎩.于是,55e =-r或(55e =-r . 习题2.4 B 组(P108)1、证法一:0()0()a b a c a b a c a b c a b c ⋅=⋅⇔⋅-⋅=⇔⋅-=⇔⊥-r r r r r r r r r r r r r r证法二:设11(,)a x y =r ,22(,)b x y =r ,33(,)c x y =r .先证()a b a c a b c ⋅=⋅⇒⊥-r r r r r r r1212a b x x y y ⋅=+r r ,1313a c x x y y ⋅=+r r由a b a c ⋅=⋅r r r r 得12121313x x y y x x y y +=+,即123123()()0x x x y y y -+-=而2323(,)b c x x y y -=--r r ,所以()0a b c ⋅-=r r r再证()a b c a b a c ⊥-⇒⋅=⋅r r r r r r r由()0a b c ⋅-=r r r 得 123123()()0x x x y y y -+-=,即12121313x x y y x x y y +=+,因此a b a c ⋅=⋅r r r r2、cos cos cos sin sin OA OB AOB OA OBαβαβ⋅∠==+u u u r u u u r u u u r u u u r . 3、证明:构造向量(,)u a b =r ,(,)v c d =r .cos ,u v u v u v ⋅=<>r r r r r r,所以,ac bd u v +=<>r r∴2222222222()()()cos ,()()ac bd a b c d u v a b c d +=++<>≤++r r 4、AB AC ⋅u u u r u u u r 的值只与弦AB 的长有关,与圆的半径无关.证明:取AB 的中点M ,连接CM ,则CM AB ⊥,12AM AB =u u u u r u u u r 又cos AB AC AB AC BAC ⋅=∠u u u r u u u r u u u r u u u r ,而AM BAC AC∠=u u u u r u u u r 所以212AB AC AB AM AB ⋅==u u u r u u u r u u u r u u u u r u u u r 5、(1)勾股定理:Rt ABC ∆中,90C ∠=︒,则222CA CB AB +=u u u r u u u r u u u r证明:∵AB CB CA =-u u u r u u u r u u u r ∴2222()2AB CB CA CB CA CB CA =-=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r u u u r .由90C ∠=︒,有CA CB ⊥,于是0CA CB ⋅=u u u r u u u r ∴222CA CB AB +=u u u r u u u r u u u r(2)菱形ABCD 中,求证:AC BD ⊥证明:∵AC AB AD =+u u u r u u u r u u u r ,,DB AB AD =-u u u r u u u r u u u r∴22()()AC DB AB AD AB AD AB AD ⋅=+⋅-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r .∵四边形ABCD 为菱形,∴AB AD =,所以220AB AD -=u u u r u u u r∴0AC DB ⋅=u u u r u u u r ,所以AC BD ⊥(3)长方形ABCD 中,求证:AC BD =证明:∵ 四边形ABCD 为长方形,所以AB AD ⊥,所以0AB AD ⋅=u u u r u u u r∴222222AB AB AD AD AB AB AD AD +⋅+=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r .∴22()()AB AD AB AD +=-u u u r u u u r u u u r u u u r ,所以22AC BD =u u u r u u u r ,所以AC BD =(4)正方形的对角线垂直平分. 综合以上(2)(3)的证明即可.2.5平面向量应用举例习题2.5 A 组(P113)(第4题)1、解:设(,)P x y ,11(,)R x y则1111(1,0)(,)(1,)RA x y x y =-=--u u u r ,(,)(1,0)(1,0)AP x y x =-=-u u u r由2RA AP =u u u r u u u r 得11(1,)2(1,)x y x y --=-,即11232x x y y =-+⎧⎨=-⎩ 代入直线l 的方程得2y x =. 所以,点P 的轨迹方程为2y x =.2、解:(1)易知,OFD ∆∽OBC ∆,12DF BC =, 所以23BO BF =. 2211()()3323AO BO BA BF a b a a a b =-=+=-+=+u u u r u u u r u u u r u u u r r r r r r r (2)因为1()2AE a b =+u u u r r r 所以23AO AE =u u u r u u u r ,因此,,A O E 三点共线,而且2AO OE = 同理可知:2,2BO CO OF OD ==,所以2AO BO CO OE OF OD === 3、解:(1)(2,7)B A v v v =-=-r u u r u u r ;(2)v r 在A v u u r 方向上的投影为135A Av v v ⋅=r u u r u u r . 4、解:设1F u u r ,2F u u r 的合力为F u r ,F u r 与1F u u r 的夹角为θ, 则31F =+u r ,30θ=︒; 331F =+u u r ,3F u u r 与1F u u r 的夹角为150°.习题2.5 B 组(P113)1、解:设0v u u r 在水平方向的速度大小为x v u u r ,竖直方向的速度的大小为y v u u r ,则0cos x v v θ=u u r u u r ,0sin y v v θ=u u r u u r .设在时刻t 时的上升高度为h ,抛掷距离为s ,则001sin ,()2cos h v t gt g s v t θθ⎧=-⎪⎨⎪=⎩u u r u u r 为重力加速度 所以,最大高度为220sin 2v g θu u r ,最大投掷距离为20sin 2v g θu u r .O DF E A B C (第2题) (第4题)2、解:设1v u r 与2v u u r 的夹角为θ,合速度为v r ,2v u u r 与v r 的夹角为α,行驶距离为d . 则1sin 10sin sin v v v θθα==u r r r ,0.5sin 20sin v d αθ==r . ∴120sin d v θ=r . 所以当90θ=︒,即船垂直于对岸行驶时所用时间最短.3、(1)(0,1)-解:设(,)P x y ,则(1,2)AP x y =--u u u r . (2,22)AB =-u u u r .将AB u u u r 绕点A 沿顺时针方向旋转4π到AP u u u r ,相当于沿逆时针方向旋转74π到AP u u u r ,于是7777(2cos 22sin ,2sin 22cos )(1,3)4444AP ππππ=+-=--u u u r 所以1123x y -=-⎧⎨-=-⎩,解得0,1x y ==- (2)32y x=- 解:设曲线C 上任一点P 的坐标为(,)x y ,OP u u u r 绕O 逆时针旋转4π后,点P 的坐标为(,)x y ''则cos sin 44sin cos 44x x y y x y ππππ⎧'=-⎪⎪⎨⎪'=+⎪⎩,即2()2()x x y y x y ⎧'=-⎪⎪⎨⎪'=+⎪⎩ 又因为223x y ''-=,所以2211()()322x y x y --+=,化简得32y x=- 第二章 复习参考题A 组(P118)1、(1)√; (2)√; (3)×; (4)×.2、(1)D ; (2)B ; (3)D ; (4)C ; (5)D ; (6)B .3、1()2AB a b =-u u u r r r ,1()2AD a b =+u u u r r r 4、略解:2133DE BA MA MB a b ==-=-+u u u r u u u r u u u r u u u r r r 2233AD a b =+u u u r r r ,1133BC a b =+u u u r r r 1133EF a b =--u u u r r r ,1233FA DC a b ==-u u u r u u u r r r1233CD a b =-+u u u r r r ,2133AB a b =-u u u r r r CE a b =-+u u u r r r 5、(1)(8,8)AB =-u u u r ,82AB =u u u r ;(2)(2,16)OC =-u u u r ,(8,8)OD =-u u u r ; (3)33OA OB ⋅=u u u r u u u r .6、AB u u u r 与CD u u u r 共线.证明:因为(1,1)AB =-u u u r ,(1,1)CD =-u u u r ,所以AB CD =u u u r u u u r . 所以AB u u u r 与CD u u u r 共线.7、(2,0)D -. 8、2n =. 9、1,0λμ=-=.10、34cos ,cos 0,cos 55A B C === 11、证明:2(2)22cos6010n m m n m m -⋅=⋅-=︒-=r u r u r r u r u r ,所以(2)n m m -⊥r u r u r .12、1λ=-. 13、13a b +=r r ,1a b -=r r . 14、519cos ,cos 820θβ== 第二章 复习参考题B 组(P119)1、(1)A ; (2)D ; (3)B ; (4)C ; (5)C ; (6)C ; (7)D .2、证明:先证a b a b a b ⊥⇒+=-r r r r r r .222()2a b a b a b a b+=+=++⋅r r r r r r r r ,222()2a b a b a b a b -=-=+-⋅r r r r r r r r .因为a b ⊥r r ,所以0a b ⋅=r r ,于是22a b a b a b +=+=-r r r r r r . 再证a b a b a b +=-⇒⊥r r r r r r .由于222a b a a b b +=+⋅+r r r r r r ,222a b a a b b -=-⋅+r r r r r r由a b a b +=-r r r r 可得0a b ⋅=,于是a b ⊥r所以a b a b a b +=-⇔⊥r r r r r r . 【几何意义是矩形的两条对角线相等】3、证明:先证a b c d =⇒⊥r r r u r22()()c d a b a b a b ⋅=+⋅-=-r u r r r r r r r(第6题)又a b =r r ,所以0c d ⋅=r u r ,所以c d ⊥r u r 再证c d a b ⊥⇒=r u r r r .由c d ⊥r u r 得0c d ⋅=r u r ,即22()()0a b a b a b +⋅-=-=r r r r r r所以a b =r r 【几何意义为菱形的对角线互相垂直,如图所示】4、12AD AB BC CD a b =++=+u u u r u u u r u u u r u u u r r r ,1142AE a b =+u u u r r r 而34EF a =u u u r r ,14EM a =u u u u r r ,所以1111(4242AM AE EM a b a =+=++=u u u u r u u u r u u u u r r r r 5、证明:如图所示,12OD OP OP =+u u u r u u u r u u u u r ,由于1230OP OP OP ++=u u u r u u u u r u u u r r ,所以3OP OD =-u u u r u u u r ,1OD =u u u r 所以11OD OP PD ==u u u r u u u r u u u r 所以1230OPP ∠=︒,同理可得1330OPP ∠=︒ 所以31260P PP ∠=︒,同理可得12360PP P ∠=︒,23160P P P ∠=︒,所以123PP P ∆为正三角形.6、连接AB .由对称性可知,AB 是SMN ∆的中位线,22MN AB b ==-u u u u r u u u r r 7、(18=(千米/时),沿与水流方向成60°的方向前进;(2)实际前进速度大小为沿与水流方向成903︒+的方向前进. 8、解:因为OA OB OB OC ⋅=⋅u u u r u u u r u u u r u u u r ,所以()0OB OA OC ⋅-=u u u r u u u r u u u r ,所以0OB CA ⋅=u u u r u u u r同理,0OA BC ⋅=u u u r u u u r ,0OC AB ⋅=u u u r u u u r ,所以点O 是ABC ∆的垂心.9、(1)2110200a x a y a y a x -+-=; (2)垂直;(3)当12210A B A B -=时,1l ∥2l ;当12120A A B B +=时,12l l ⊥,P 2(第5题)夹角θ的余弦cos θ=;(4)d =第三章 三角恒等变换3.1两角和与差的正弦、余弦和正切公式练习(P127)1、cos()cos cos sin sin 0cos 1sin sin 222πππαααααα-=+=⨯+⨯=. cos(2)cos2cos sin 2sin 1cos 0sin cos παπαπαααα-=+=⨯+⨯=.2、解:由3cos ,(,)52πααπ=-∈,得4sin 5α==;所以34cos()cos cos sin sin ()44455πππααα-=+=-=3、解:由15sin 17θ=,θ是第二象限角,得8cos 17θ===-;所以8115cos()cos cos sin sin 33317217πππθθθ-=+=-⨯+=.4、解:由23sin ,(,)32πααπ=-∈,得cos α==又由33cos ,(,2)42πββπ=∈,得sin β== 所以32cos()cos cos sin sin ((()43βαβαβα-=+=⨯+⨯-=. 练习(P131)1、(1; (2) (3 (4)22、解:由3cos ,(,)52πθθπ=-∈,得4sin 5θ==;所以413sin()sin cos cos sin ()333525πππθθθ+=+=⨯+-=. 3、解:由12sin 13θ=-,θ是第三象限角,得5cos 13θ===-; 所以5112cos()cos cos sin sin ()()66613213πππθθθ+=-=--⨯-=. 4、解:tan tan 314tan()241311tan tan 4παπαπα+++===--⨯-⋅. 5、(1)1; (2)12; (3)1; (4); (5)原式=1(cos34cos26sin34sin 26)cos(3426)cos602-︒︒-︒︒=-︒+︒=-︒=-; (6)原式=sin 20cos70cos20sin70(sin 20cos70cos20sin70)sin901-︒︒-︒︒=-︒︒+︒︒=-︒=-.6、(1)原式=cos cos sin sin cos()333x x x πππ-=+; (2)原式=1cos )2(sin cos cos sin )2sin()2666x x x x x πππ+=+=+; (3)原式=)2(sin cos cos sin )2sin()444x x x x x πππ=-=-; (4)原式=12(cos )cos sin sin ))2333x x x x x πππ=-=+. 7、解:由已知得3sin()cos cos()sin 5αβααβα---=, 即3sin[()]5αβα--=,3sin()5β-=所以3sin 5β=-. 又β是第三象限角, 于是4cos 5β===-. 因此55534sin()sin cos cos sin ()(()(444525210πππβββ+=+=-+-=. 练习(P135)1、解:因为812παπ<<,所以382αππ<<又由4cos 85α=-,得3sin 85α=-,3sin385tan 484cos 85ααα-===- 所以3424sinsin(2)2sin cos 2()()48885525αααα=⨯==⨯-⨯-=2222437cos cos(2)cos sin ()()48885525αααα=⨯=-=---=2232tan23162484tan tan(2)3482771tan 1()84αααα⨯=⨯===⨯=-- 2、解:由3sin()5απ-=,得3sin 5α=-,所以222316cos 1sin 1()525αα=-=--=所以2221637cos2cos sin ()25525ααα=-=--=3、解:由sin2sin αα=-且sin 0α≠可得1cos 2α=-,又由(,)2παπ∈,得sin α=,所以sin tan (2)cos ααα==-=4、解:由1tan 23α=,得22tan 11tan 3αα=-. 所以2tan 6tan 10αα+-=,所以tan 3α=-5、(1)11sin15cos15sin3024︒︒=︒=; (2)22cos sin cos 8842πππ-==;(3)原式=212tan 22.511tan 4521tan 22.522︒⋅=︒=-︒; (4)原式=cos45︒=. 习题3.1 A 组(P137)1、(1)333cos()cos cos sin sin 0cos (1)sin sin 222πππαααααα-=+=⨯+-⨯=-;(2)333sin()sin cos cos sin 1cos 0sin cos 222πππαααααα-=-=-⨯-⨯=-;(3)cos()cos cos sin sin 1cos 0sin cos παπαπαααα-=+=-⨯+⨯=-; (4)sin()sin cos cos sin 0cos (1)sin sin παπαπαααα-=-=⨯--⨯=.2、解:由3cos ,05ααπ=<<,得4sin 5α==,所以431cos()cos cos sin sin 666552πππααα-=+=⨯=.3、解:由2sin ,(,)32πααπ=∈,得cos α===又由33cos ,(,)42πββπ=-∈,得sin β===,所以32cos()cos cos sin sin ()(43αβαβαβ-=+=-+⨯=.4、解:由1cos 7α=,α是锐角,得sin α=== 因为,αβ是锐角,所以(0,)αβπ+∈, 又因为11cos()14αβ+=-,所以sin()αβ+===所以cos cos[()]cos()cos sin()sin βαβααβααβα=+-=+++1111()1472=-⨯= 5、解:由60150α︒<<︒,得9030180α︒<︒+<︒又由3sin(30)5α︒+=,得4cos(30)5α︒+=-所以cos cos[(30)30]cos(30)cos30sin(30)sin30αααα=︒+-︒=︒+︒+︒+︒431552=-+⨯=6、(1) (2) (3)2-7、解:由2sin ,(,)32πααπ=∈,得cos α===又由3cos 4β=-,β是第三象限角,得sin β==.所以cos()cos cos sin sin αβαβαβ+=-32()(43=--⨯=sin()sin cos cos sin αβαβαβ-=-23()((34=⨯--⨯=8、解:∵53sin ,cos 135A B ==且,A B 为ABC ∆的内角∴0,02A B ππ<<<<,124cos ,sin 135A B =±=当12cos 13A =-时,sin()sin cos cos sin AB A B A B +=+5312433()013513565=⨯+-⨯=-< A B π+>,不合题意,舍去∴124cos ,sin 135A B ==∴cos cos()(cos cos sin sin )C A B A B A B =-+=--1235416()13513565-⨯-⨯=- 9、解:由3sin ,(,)52πθθπ=∈,得4cos 5θ==-.∴sin 353tan ()cos 544θθθ==⨯-=-. ∴31tan tan 242tan()311tan tan 111()42θϕθϕθϕ-+++===--⋅--⨯. 31tan tan 42tan()2311tan tan 1()42θϕθϕθϕ----===-+⋅+-⨯. 10、解:∵tan ,tan αβ是22370x x +-=的两个实数根.∴3tan tan 2αβ+=-,7tan tan 2αβ⋅=-.∴3tan tan 12tan()71tan tan 31()2αβαβαβ-++===--⋅--.11、解:∵tan()3,tan()5αβαβ+=-=∴tan()tan()tan 2tan[()()]1tan()tan()αβαβααβαβαβαβ++-=++-=-+⋅-3541357+==--⨯tan()tan()tan 2tan[()()]1tan()tan()αβαββαβαβαβαβ+--=+--=++⋅-3511358-==-+⨯12、解:∵::2:3:6BD DC AD = ∴11tan ,tan 32BD DC AD AD αβ====∴tan tan tan tan()1tan tan BAC αβαβαβ+∠=+=-⋅1132111132+==-⨯ 又∵0180BAC ︒<∠<︒,∴45BAC ∠=︒ 13、(1))6x π+; (23sin()3x π-; (3)2sin()26x π+;(47sin()12x π-; (5; (6)12; (7)sin()αγ+; (8)cos()αγ--; (9) (10)tan()βα-.14、解:由sin 0.8,(0,)2παα=∈,得cos 0.6α===∴sin22sin cos 20.80.60.96ααα==⨯⨯= 2222cos2cos sin 0.60.80.28ααα=-=-=- 15、解:由cos 270ϕϕ=︒<<︒,得sin ϕ===∴sin 22sin cos 2((ϕϕϕ==⨯⨯=22221cos2cos sin ((3ϕϕϕ=-=-=-sin 2tan 2(3)cos 23ϕϕϕ==-=-16、解:设5sin sin 13B C ==,且090B ︒<<︒,所以12cos 13B =. ∴512120sin sin(1802)sin 22sin cos 21313169A B B B B =︒-===⨯⨯=2222125119cos cos(1802)cos2(cos sin )(()())1313169A B B B B =︒-=-=--=--=-(第12题)sin 120169120tan ()cos 169119119A A A ==⨯-=-17、解:22122tan 33tan 211tan 41()3βββ⨯===--,13tan tan 274tan(2)1131tan tan 2174αβαβαβ+++===-⋅-⨯. 18、解:1cos()cos sin()sin 3αββαββ+++=⇒1cos[()]3αββ+-=,即1cos 3α= 又3(,2)2παπ∈,所以sin α==∴1sin 22sin cos 2()339ααα==⨯-⨯=-222217cos2cos sin ()(39ααα=-=-=-∴78cos(2)cos2cos sin 2sin (444929218πππααα-+=-=-⨯--⨯=19、(1)1sin2α+; (2)cos2θ; (3)1sin 44x ; (4)tan2θ.习题3.1 B 组(P138) 1、略. 2、解:∵tan ,tan A B 是x 的方程2(1)10x p x +++=,即210x px p +++=的两个实根∴tan tan A B p +=-,tan tan 1A B p ⋅=+ ∴tan tan[()]tan()C A B A B π=-+=-+tan tan 11tan tan 1(1)A B pA B p +-=-=-=--⋅-+由于0C π<<,所以34C π=. 3、反应一般的规律的等式是(表述形式不唯一)223sin cos (30)sin cos(30)4αααα++︒++︒=(证明略) 本题是开放型问题,反映一般规律的等式的表述形式还可以是:223sin (30)cos sin(30)cos 4αααα-︒++-︒=223sin (15)cos (15)sin(15)cos(15)4αααα-︒++︒+-︒+︒=223sin cos sin cos 4αβαβ++=,其中30βα-=︒,等等思考过程要求从角,三角函数种类,式子结构形式三个方面寻找共同特点,从而作出归纳. 对认识三角函数式特点有帮助,证明过程也会促进推理能力、运算能力的提高.4、因为12PA PP =,则2222(cos()1)sin ()(cos cos )(sin sin )αβαβαβαβ+-++=-++ 即22cos()22cos cos 2sin sin αβαβαβ-+=-+ 所以cos()cos cos sin sin αβαβαβ+=-3.2简单的三角恒等变换 练习(P142)1、略.2、略.3、略.4、(1)1sin 42y x =. 最小正周期为2π,递增区间为[,],8282k k k Z ππππ-++∈,最大值为12;(2)cos 2y x =+. 最小正周期为2π,递增区间为[2,22],k k k Z ππππ++∈,最大值为3;(3)2sin(4)3y x π=+. 最小正周期为2π,递增区间为5[,],242242k k k Z ππππ-++∈,最大值为2.习题3.2 A 组( P143) 1、(1)略; (2)提示:左式通分后分子分母同乘以2; (3)略; (4)提示:用22sin cos ϕϕ+代替1,用2sin cos ϕϕ代替sin 2ϕ;(5)略; (6)提示:用22cos θ代替1cos2θ+;(7)提示:用22sin θ代替1cos2θ-,用22cos θ代替1cos2θ+; (8)略.2、由已知可有1sin cos cos sin 2αβαβ+=……①,1sin cos cos sin 3αβαβ-=……②(1)②×3-①×2可得sin cos 5cos sin αβαβ=(2)把(1)所得的两边同除以cos cos αβ得tan 5tan αβ= 注意:这里cos cos 0αβ≠隐含与①、②之中3、由已知可解得1tan 2θ=-. 于是2212()2tan 42tan 211tan 31()2θθθ⨯-===---- 1tan tan1142tan()1431tan tan 1()142πθπθπθ+-++===-⋅--⨯∴tan 24tan()4πθθ=-+4、由已知可解得sin x θ=,cos y θ=,于是2222sin cos 1x y θθ+=+=.5、()2sin(4)3f x x π=+,最小正周期是2π,递减区间为7[,],242242k k k Z ππππ++∈.习题3.2 B 组(P143) 1、略.2、由于762790+⨯=,所以sin76sin(9014)cos14m ︒=︒-︒=︒= 即22cos 71m ︒-=,得cos7︒=3、设存在锐角,αβ使223παβ+=,所以23απβ+=,tan()2αβ+又tantan 22αβ=,又因为tantan 2tan()21tantan 2αβαβαβ++=-,所以tantan tan()(1tan tan )3222αααβββ+=+-=由此可解得tan 1β=, 4πβ=,所以6πα=.经检验6πα=,4πβ=是符合题意的两锐角.4、线段AB 的中点M 的坐标为11((cos cos ),(sin sin ))22αβαβ++. 过M 作1MM 垂直于x 轴,交x 轴于1M ,111()()22MOM βαααβ∠=-+=+.在Rt OMA ∆中,cos cos 22OM OA βααβ--==. 在1Rt OM M ∆中,11cos cos cos22OM OM MOM αβαβ+-=∠=11sin sin cos22M M OM MOM αβαβ+-=∠=. 于是有 1(cos cos )cos cos222αβαβαβ+-+=, 1(sin sin )sin cos222αβαβαβ+-+= 5、当2x =时,22()sin cos 1f ααα=+=;当4x =时,4422222()sin cos (sin cos )2sin cos f ααααααα=+=+-211sin 22α=-,此时有1()12f α≤≤;当6x =时,662232222()sin cos (sin cos )3sin cos (sin cos )f ααααααααα=+=+-+231sin 24α=-,此时有1()14f α≤≤;由此猜想,当2,x k k N +=∈时,11()12k f α-≤≤6、(1)345(sin cos )5sin()55y x x x ϕ=+=+,其中34cos ,sin 55ϕϕ==所以,y 的最大值为5,最小值为﹣5;(2))y x ϕ+,其中cos ϕϕ==所以,y ;第三章 复习参考题A 组(P146)1、1665. 提示:()βαβα=+- 2、5665. 提示:5sin()sin[()]sin[()()]44ππαβπαββα+=-++=-+--3、1.4、(1)提示:把公式tan tan tan()1tan tan αβαβαβ++=-变形;(2; (3)2; (4) 提示:利用(1)的恒等式.5、(1)原式4sin(3010)4sin 20︒-︒==︒;(2)原式=sin10sin 40(sin 40cos10︒︒=︒ =2sin 40cos40sin801cos10cos10-︒︒-︒==-︒︒;(3)原式=tan 70cos101)tan 70cos10︒︒-=︒ =sin702sin10sin 20cos101cos70cos20cos70︒-︒-︒⋅︒⋅==-︒︒︒;(4)原式=sin50(1sin50︒⋅= 2cos50sin100sin501cos10cos10︒︒=︒⋅==︒︒6、(1)95; (2)2425;(3)223±. 提示:4422222sin cos (sin cos )2sin cos θθθθθθ+=+-;(4)1725.7、由已知可求得2cos cos 5αβ=,1sin sin 5αβ=,于是sin sin 1tan tan cos cos 2αβαβαβ==.8、(1)左边=222cos 214cos232(cos 22cos21)αααα-++=++22242(cos21)2(2cos )8cos ααα=+===右边(2)左边=2222sin cos 2sin cos (sin cos )2cos 2sin cos 2cos (cos sin )αααααααααααα+++=++sin cos 11tan 2cos 22αααα+==+=右边(3)左边=sin(2)2cos()sin sin[()]2cos()sin sin 2cos (cos sin )αβαβααβααβααααα+-+++-+=+ sin()cos cos()sin sin sin sin αβααβαβαα+-+===右边 (4)左边=222234cos22cos 212(cos 22cos21)34cos22cos 212(cos 22cos21)A A A A A A A A -+--+=++-++2224222(1cos2)(2sin )tan (1cos2)(2cos )A A A A A -===+=右边 9、(1)1sin 21cos2sin 2cos222)24y x x x x x π=+++=++++递减区间为5[,],88k k k Z ππππ++∈(222,最小值为22.10、2222()(cos sin )(cos sin )2sin cos cos2sin 22)4f x x x x x x x x x x π=+--=-+(1)最小正周期是π;(2)由[0,]2x π∈得52[,]444x πππ+∈,所以当24x ππ+=,即38x π=时,()f x 的最小值为2-()f x 取最小值时x 的集合为3{}8π.11、2()2sin 2sin cos 1cos2sin 22)14f x x x x x x x π=+=-+=-+(1)最小正周期是π21;(2)()f x 在[,]22ππ-上的图象如右图:12、()cos 2sin()6f x x x a x a π=++=++.(1)由21a +=得1a =-;(2)2{22,}3x k x k k Z πππ+∈≤≤.13、如图,设ABD α∠=,则CAE α∠=,2sin h AB α=,1cos hAC α=所以1212sin 2ABC h h S AB AC α∆=⋅⋅=,(0)2πα<<当22πα=,即4πα=时,ABC S ∆的最小值为12h h .第三章 复习参考题B 组(P147)1、解法一:由221sin cos 5sin cos 1αααα⎧-=⎪⎨⎪+=⎩,及0απ≤≤,可解得4sin 5α=,13cos sin 55αα=-=,所以24sin 225α=,7cos225α=-,sin(2)sin 2cos cos2sin 44450πππααα-=-=. 解法二:由1sin cos 5αα-= 得21(sin cos )25αα-=,24sin 225α=,所以249cos 2625α=. 又由1sin cos 5αα-=,得sin()4πα-=.因为[0,]απ∈,所以3[,]444πππα-∈-.而当[,0]44ππα-∈-时,sin()04πα-≤;当3[,]444πππα-∈时,sin()4πα->所以(0,)44ππα-∈,即(,)42ππα∈所以2(,)2παπ∈,7cos225α=-.sin(2)4πα-=2、把1cos cos 2αβ+=两边分别平方得221cos cos 2cos cos 4αβαβ++=把1sin sin 3αβ+=两边分别平方得221sin sin 2sin sin 9αβαβ++=(第13题)。
人教版高中数学必修4课后习题答案详细讲解

练习(第5页》1. 锐角是第一象限你第•象限你不一定是锐角;直角不膩于任何一个象限•不属于任何•个象限的角不一・定丛亢如:饨介迢第二象Wfft.第二绘限角不一定址钝介.说阴认识•说升广、-直角”•“mr和係限角”的区别埒联系.2•三•三• it.说明本題的II的足将终边相同的仰的符',;哦示应川到找他周期件何題匕题||联系实臥把教科筋中的除数360换戍毎个凡期的夭数7.利川了-M余”(这里余数是3)來确定7怡无氐7 k JjiU 也祁見川期•.这样的练习不难.町以II答.3•⑴第一魏探伽(2)第阿糾W伽(3)第二録限角$⑷第三簽限如.说明能作出结定的仰.并判定是第儿feRlfft・用略.4. ⑴305°・挖・第冋象Oh <2) 35鴛・第一象限伽⑶24『30'・第垛限处•说明能住给定范鬧内找出勺指定的角终边相同的角•并判定圧笫儿象瞅也・5. (1) «0|0 1303m 360°. AW引.-496*42\ —136°42‘・ 223。
叭(2) 〃|0= 225°M • 360°. W \、585°. - 225\ 135:说明用集合花示法和符号指定和终边柜同的介的集令•并在给定范田内找;l「j描定的角终边HI同的介. 练习C第9页)1. (1)令. (2)孕⑶攀说明能进行度U加度的换贰2. (!) 15°;<2) 210°€Ci) 54°.说明能进行瓶度9度的换◎・3. (I) {a | o= kK. it^Z}: (Z) ”!a=专十阪点€紂・说明川弧废;《丧示终边分别轴和y轴I:的"啲集舍.4. (I) cos 0. 75°・cos (L 75; (Z) tan L 2°"<^nni L 2$说明体会1诃数値不同的位的角对应的三角函数値町能不同•并进-步认识两种尬位制.注盘先用计算器求Jh函数血之前.耍先对il•算器中和的模式进行设證.如求cox«.75^i%•變将仰模人设比为"EG(用处制);求CON O.75之|條賞将巾校成设汽为RAIN丸懐制).r w5盲机说明通过分别込川佝加制和软度制下的孤氏公儿体会引人毎度制的必茨性・6. 如度数为1.2.说明进•少认沢弧直数的绝对備公式.匀題I. 1 (第9贡》A俎1. (I)95\第二彖服(2) «0\第一彖服(3) 236W.第三象Rh ⑷:iOO\第四象限.说明能任给定范附内找出习指定的角终边相同的角,并判定是第儿彖限角.2. S I cr A • |&)°・ itez}.说明将终边相I同的仰用集介表斥.3. ( I) {fl\p 60° + k - 360'• k^Z}.— 30O\ 60°;⑵ SI" -75+. 360°. «eZh 一75°. 285•:(3) SI” 一82十3()+・36(汽JtGZ). — 1(M'3()\ 255°30气⑷{p\p 475+• 3$(几翳幼-215% 115^⑸ }屮=90°+£・ 360°. &WZ). - 270°, 90°;<«)270° + 女• :<6(代JteZ}. - 90\ 270%(7){P\P IKO Q I - 360°, XZ}・ 1«0\ 18(f|(«)出|陰*任(几圧2}・-360°. 0°.说明川集伶衣〃湫和符号诸护孑出与能定角终边郴何的角的集合•并住绻定范IR内找出号指崔的角终边柏胡的角.5. (1> (:.说明14 为 <^< aV9O°・所以0°V 2a< 180\(2> I).说明冈为◎ • 360°0<90°十& • 360\ Jt€Z.所以k• 180'V号<45°十点• 1«()\ k"、半k为奇数时•;址第垛限伽臥为偶数时.号是第一象限角.6. 不等『1知址这是因为等于半轻长的弧所对的阀心角为】孤度•而零干半径氏的弦所对的弧比半径长.说明了解瓠度的槪念.说明能逬行麼吋加度的换算.& (1)— 210°; (2)600°;(3) 80.21\ (4) 3& 2°.说明能进行加度勺度的换算.9. 61°.说明町以先运用麵度制下的如氏公式求岀関心介的弧度数•卩術弧度换算为度・也町以K接运川血度制下的就尺公式.10. 11 CDL说明町以先将度换笫为匏度•再运川弧度制下的如氏公式•也可以M接运川角皮制卜的颅辰公式.1. <1)〈略)<2)设m子的阀心巾为0•山-7—52--------- =0.618.討(2兀一4〉0=0・ 618(2 穴一0).说明水題址一个数学实嘶动.Mil对“芙观的阳子"并没右给出标准.II的址止学生先占体验.然麻评运川所学知讲发现.大寥数血子之所以“芙观”是冈为射都満足舟Q・GI8(黄金分割比)的逍理.2. ⑴时针转了120\等于一竽弧喪)分针转了一14彳0°・筹于一&瓠度.(2)设经过八nin分针就9时针改合.川为两针31合的次数.因为分针旋转的如速朋为时什施转的如速度为矗5=盏(rad/min>-(計—希)用计算机或计算需作出函效戶誥的图象(如下页图)或汲格.从屮吋淸楚地介列时什'j分针每次1R 合所尙的吋间.因为HHI&E 转一夭所需的时何为24X60=1 440(min).所以等曲440. 川W22・故时fl 七分针一天内只会磴合22次.说明 通过时什与分针的旋转问題进…步地认识弧度的概念•并将何題引向深入•用南数思想进行 分析.在研究时针与分针一犬的亟合次数时.可利用计算器或计算机•从模拟的图形、衣格中的数 据.换数的解析式或图象等角度.不堆得到正确的结论.3・ 864\ 警• 15l ・27rna说明 通过W 轮的转动何题进一步地认识弧度的概念和弧长公式•当大垢轮转动•周时•小片轮转 动的加处器 X 360。
人教版高中数学必修4课后习题答案详解

第二章平面向量2.1 平面向量的实质背景及基本观点练习(P77)1、略.uuur uuur这两个向量的长度相等,但它们不等 .2、AB,BA .uuur uuur uuur uuur3、 AB2, CD 2.5 , EF3,GH 2 2.4、( 1)它们的终点同样;(2)它们的终点不一样 .习题 A 组(P77)1、( 2 )B45°O30°CAD.CA Buuur uuur uuuruuur uuur uuur3、与 DE 相等的向量有:AF , FC ;与 EF 相等的向量有: BD , DA ;uuur uuur uuur与 FD 相等的向量有: CE , EB .r uuur uuur uurr uuuur uuur4、与 a 相等的向量有:CO , QP, SR;与 b 相等的向量有: PM , DO ;r uuur uuur uuur与 c 相等的向量有: DC , RQ, STuuur 3 36、(1)×;(2)√;(3)√;(4)× .5、 AD.2习题 B 组(P78)1、海拔和高度都不是向量 .uuuur2、相等的向量共有24 对.模为 1的向量有 18对 . 此中与 AM 同向的共有 6uuuur uuur uuur对,与 AM 反向的也有 6 对;与 AD 同向的共有 3 对,与 AD 反向的也有 6 对;模为 2 的向量共有 4 对;模为 2 的向量有 2 对2.2 平面向量的线性运算 练习(P84)1、图略 .2、图略 .uuur uuur3、(1) DA ; (2) CB .r ururur 4、( 1) c ; ( 2) f ; (3) f ;( 4) g . 练习(P87) uuuruuur uuur1、图略 . uuur uuur3、图略 .2、DB ,CA , AC ,AD ,BA.练习(P90)1、图略 .5 uuur uuur 2 uuuruuur2、 ACAB ,BCAB .7 7uuur说明:此题可先画一个表示图,依据图形简单得出正确答案. 值得注意的是BCuuur与 AB 反向.rrr7rr1rr8r3、( 1) b2a ;(2) b4 a ;(3) ba ;(4) ba .294、( 1)共线;( 2)共线 .r r( 2)11r1rr6、图略 .5、( 1) 3a2b ;12 ab ;( 3) 2 ya .习题 A 组(P91)31、( 1)向东走 20 km ; (2)向东走 5 km ; (3)向东北走 10 2 km ;( 4)向西南走 5 2 km ;( 5)向西北走 10 2 km ;(6)向东南走 10 2 km.2、飞机飞翔的行程为 700 km ;两次位移的合成是向北偏西53°方向飞翔 500 km.uuur uuur3、解:如右图所示: AB 表示船速, AD 表示河水的流速,以 AB 、 AD 为邻边作 □ ABCD ,则uuurAC 表示船实质航行的速度 .uuur uuur在 Rt △ABC 中, AB 8 , AD 2 ,uuuruuur 2uuur 2222 17所以 ACAB AD82 因为 tan CAD4 ,由计算器得 CAD 76BCAD水流方向所以,实质航行的速度是 2 17 km/h ,船航行的方向与河岸的夹角约为 76°.r uuur uuur r r uuur4、(1) 0; (2) AB ; (3) BA ; (4)0 ; (5)0 ; (6)CB ; (7) r0 .5、略6、不必定组成三角形 . 说明:联合向量加法的三角形法例,让学生理解,若三个非零向量的和为零向量,且这三个向量不共线时,则表示这三个向量的有向线段必定能组成三角形 .7、略. 8、(1)略; r r r r r r(2)当 a b 时, a b a b9、(1) r r rr r ;r 1 r( 4)2( xr2a2b ; ( 2)10a 22b 10c (3)3a b ; y)b .r r ur r rur uur r r uruur 210、 a b 4e 1 , a be 1 4e 2 , 3a 2b3e 1 10e 2 .uuurr uuur r 11、如下图, OCa , ODb ,uuur r r uuur r rDCb a , BCa b .(第 11 题)uuur1ruuurr r uuur 1 r r uuur 3 r12、 AEb , BCb a , DE (b a) , DBa ,44 1 uuuur4uuur3ruuur1 r r uuur 1 r rEC b , DN8 (b a) , AN 4 AM (ab) .4813、证明:在ABC 中, E, F 分别是 AB, BC 的中点,所以 EF //AC 且EF 1AC ,(第 12 题)Guuur 1 uuur2D即 EF 2 AC ;1 uuuruuur同理, HG AC ,H2 uuur uuur所以 EFHG .E习题 B 组(P92) A(第 13 题)1、丙地在甲地的北偏东45°方向,距甲地 1400 km.乙2、不必定相等,能够考证在 r ra,b 不共线时它们不相等 .uuuur uuur uuuuruuur 1 uuur uuuur 1 uuur3、证明:因为 MN AN AM ,而 AN3 AC , AMAB ,1 uuur1 uuur1 uuur 3uuuur1 uuur uuur所以 MN3 AC3 AB 3 ( AC AB) 3 BC .甲4、( 1)四边形 ABCD 为平行四边形,证略(第 1 题)( 2)四边形 ABCD 为梯形 .Cuuur 1 uuur证明:∵ AD BC ,3∴ AD//BC 且 AD BC∴四边形 ABCD 为梯形 .DCFB丙BA( 3)四边形 ABCD 为菱形 .(第 4 题 (2))uuur uuurB证明:∵ AB DC ,∴ AB/ /DC 且 AB DC C A∴四边形 ABCD 为平行四边形uuur uuurD又 AB AD(第 4题 (3))∴四边形 ABCD 为菱形.M5、( 1)经过作图能够发现四边形ABCD 为平行四边形.uuur uuur uuur uuur uuur uuur证明:因为 OA OB BA,OD OC CDuuur uuur uuur uuur A D而OA OC OB ODuuur uuur uuur uuur B C 所以 OA OB OD OCuuur uuurO所以 BA CD ,即AB∥CD.所以,四边形 ABCD 为平行四边形.(第 5题)2.3 平面向量的基本定理及坐标表示练习(P100)r r r r r r r r1、( 1) a b(3,6) , a b(7,2) ;( 2) a b(1,11), a b(7,5);r r r r(4,6) ;r r r r(3,4) .( 3) a b(0,0) , a b(4) a b(3, 4) , a b r r r r(12,5) .2、 2a 4b( 6,8) , 4a3buuur(3, 4)uuur( 3,4) ;uuur(9,1)uuur(9,1)3、( 1) AB, BA(2) AB, BA;uuur(0, 2)uuur(0,2)uuur uuur(5,0)(3) AB, BA;(4) AB(5,0) , BA4、AB∥CD .uuur uuur(1,uuur uuur证明: AB(1, 1) , CD1) ,所以 ABCD.所以AB∥CD .5、(1)(3, 2);( 2) (1,4) ;(3)(4,5) .6、(10,1)或(14,1)33uuur3uuur uuur3 uuur7、解:设 P( x, y) ,由点P在线段AB的延伸线上,且AP2PB ,得 AP2PBuuur uuur( x, y) (2,3)( x(4,3)(x, y)(4x,3y) AP2, y 3) , PB3x23(4x)∴ ( x2, y3)x, 3 y)∴2(43( 32y3y)2x 8 ∴,所以点 P 的坐标为 (8, 15) .y15习题A 组(P101)1、( 1) ( 2,1) ;( 2) (0,8) ;( 3) (1,2) .说明:解题时可设 B(x, y) ,利用向量坐标的定义解题 .uur uur uur 2、 F 1 F 2 F 3(8,0)uuur ( 1, uuur (53,6 (1)) (2,7)3、解法一: OA 2),BCuuuruuur uuur uuuruuur uuur uuur (1,5) .所以点 D 的坐而 ADBC ,ODOAADOA BC标为 (1,5) .uuur ( x( 1), y ( 2)) ( x 1, y2) ,解法二:设 D( x, y) ,则 AD uuur (5 3,6 ( 1)) (2,7)BCuuur uuur1 2,解得点 D 的坐标为 (1,5) .由 ADBC 可得, xy 2 7uuur uuur2,4) .4、解: OA (1,1), AB (uuur 1 uuuruuuruuuruuur1 uuur(1, 2) .ACAB ( 1,2) , AD2 AB( 4,8) , AE2AB2uuur uuur uuur(0,3) ,所以,点 C 的坐标为 (0,3) ; OC OA ACuuur uuur uuur ( 3,9) ,所以,点 D 的坐标为 (3,9)OD OA AD;uuur uuur uuur(2, 1) ,所以,点 E 的坐标为 (2,1) .OE OA AE r r (2,3)(x,6),所以23,解得 x 4 .5、由向量 a,b 共线得x 6uuur (4, 4) uuur ( 8,uuur uuur uuuruuur 6、 AB , CD 8),CD 2AB ,所以 AB 与CD 共线 .uuuruuur(2, 4) ,所以点 A 的坐标为 (2, 4) ;7、 OA2OAuuur uuur ( 3,9)B 的坐标为( 3,9)OB 3OB ,所以点;故uuuur( 3,9) (2, 4) ( 5,5)A B 习题B 组(P101)uuur (1,2)uuur (3,3) . 1、 OA , AB当 tuuur uuur uuur uuur(4,5) ,所以 P(4,5) ; 1时, OP OA AB OB当 t1 uuur uuur1 uuur(1,2) 3 35 7 ) ,所以 5 , 7时, OPOAAB( , ) ( , P( ) ;222 2 2 2 2 2uuur uuuruuur( 5, 4) ,所以 P( 5, 4);当 t2时, OP OA 2AB(1,2) (6,6) 当 tuuur uuur uuur (7,8) ,所以 P(7,8) .2时, OP OA 2 AB (1,2) (6,6)uuur ( 4, 6) uuur uuur uuur2、(1)因为 AB , AC (1,1.5) ,所以 AB4AC ,所以 A 、B 、C 三 点共线;uuuruuuruuur uuur( 2)因为 PQ(1.5,2),PR(6, 8) ,所以 PR 4PQ ,所以 P 、Q 、R 三点共线;uuuruuur( 8,( 1, uuur uuur( 3)因为 EF4) ,EG 0.5) ,所以 EF 8EG ,所以 E 、F 、G三点共线 .uruur r ur uur3、证明:假定10 ,则由 1 e 12 e 2 0 ,得 e 12e 2 .1ur uurur uur 是平面内的一组基底矛盾 ,所以 e 1 ,e 2 是共线向量,与已知 e 1,e 2 所以假定错误,10 .同理 2 0 .综上 120 .uuuruuur ur uur4、(1) OP19 .( 2)关于随意愿量 OP xe 1 ye 2 , x, y 都是独一确定的,所以向量的坐标表示的规定合理 .2.4 平面向量的数目积 练习(P106)ur rur r ur r 8 6124 .1、 p q p q cos p, q2r rr rABC 为直角三角形 .2、当 a b 0 时,ABC 为钝角三角形;当 a b 0 时,3、投影分别为 3 2 , 0, 3 2 . 图略 练习(P107)r( 3)2 42r 52 22r r35427 .1、 a 5 , b29 , a br rr r rrr r rr r49 .2、 a b8 , (a b)(a b)7 , a (b c) 0 , (a b)2r r rr74,88 . 3、 a b 1, a13 , b习题 A 组(P108)r r r rr 2 r r r 2r r25 12 3.1、 a b6 3 , (a b)2 a2a b b25 12 3 , a buuur uuuruuur uuur 20 .2、 BC 与 CA 的夹角为 120°, BC CAr rr 2 r r r 2r rr 2 r r r 2 35 .3、 a ba 2ab b23 , a ba 2ab br r4、证法一:设 a 与 b 的夹角为 .( 1)当 0 时,等式明显建立;( 2)当r r rr时, a 与 b , a 与 b 的夹角都为 ,所以( r r r r r ra) b a b cosa b cos r rr r( a b)a b cosr r r r r r a ( b)ab cosa b cosr rr r r r所以 ( a) b(a b) a ( b) ;( 3)当r r r r180时, a 与 b , a 与 b 的夹角都为 ,则 (r r r r ) r r a) b a b cos(180 a b cosr r r r r r ( a b)a b cosa b cosr r r r )r r a ( b)ab cos(180a b cosr rr r r r 所以 ( a) b(a b) a ( b) ;综上所述,等式建立 .r r证法二:设 a (x 1, y 1 ) , b ( x 2 , y 2 ) ,r r那么 ( a) b ( x 1 , y 1 ) ( x 2 , y 2 ) x 1 x 2 y 1 y 2 r r( a b) ( x 1 , y 1 ) ( x 2, y 2 ) ( x 1 x 2 y 1 y 2 ) x 1x 2 y 1 y 2r r a ( b) (x 1, y 1 ) ( x 2 , y 2 ) x 1x 2 y 1 y 2所以 (r rr r r ra) b (a b)a ( b) ;5、( 1)直角三角形, B 为直角 .uuur( 1, 4)(5, 2) ( 6, 6)uuur(3, 4)(5, 2) ( 2, 2)证明:∵ BA , BCuuur uuur 6 ( 2) ( 6)2 0∴ BA BCuuur uuur B 为直角,ABC 为直角三角形∴ BABC , ( 2)直角三角形, A 为直角uuur (19,4) ( 2, 3) (21,7)uuur ( 1, 6) ( 2,3) (1, 3)证明:∵ AB , ACuuur uuur21 1 7 ( 3) 0∴ AB ACuuur uuur A 为直角,ABC 为直角三角形∴ ABAC ,( 3)直角三角形, B 为直角uuuruuur证明:∵ BA (2,5) (5, 2)( 3,3) , BC(10,7) (5, 2) (5,5)uuur uuur 3 5 3 5 0∴BA BCuuur uuur B 为直角,ABC 为直角三角形∴ BABC , 6、 135 . 7、120 .r r r r r 2 r r r 2 r r 6 ,(2a 3b)(2 a b)4a 4a b 3b 61 ,于是可得 a br r 1cosa b,所以 120 .r r2a b8、 cos23 , 55 .40uuuruuur9、证明:∵ AB(5, 2) (1,0) (4, 2) , BC(8, 4)(5, 2) (3,6) ,uuur(8, 4) (4,6) (4, 2)DCuuur uuur uuur uuur 4 3 ( 2) 6 0∴ AB DC ,AB BC∴ A, B,C , D 为极点的四边形是矩形 .r( x, y) ,10、解:设 ax 2y 2 9x 3 5x 3 5则y ,解得6 5 ,或 5 .x2y5 y6 55 5rr 3 5 , 6 5).于是 a (3 5 , 6 5) 或 a (5 55 5r r11、解:设与 a 垂直的单位向量 e (x, y) ,则 x2y 21x5或 x5,解得 5 5 . 4x2 y 0 y2 5 2 55 y 5r 5 ,r 5,2 5). 于是 e (2 5) 或 e (5555习题 B 组(P108)r r r r r rr rr r rr r r 1、证法一: a b a ca b a ca (b c)a(b c)rr r证法二:设 a( x 1 , y 1) , b (x 2 , y 2 ) , c ( x 3 , y 3 ) .r r r rr r r 先证 a b a ca(b c)r rr ra b x 1 x 2y 1 y 2 , a c x 1 x 3 y 1 y 3r r r r由a b a c得x 1 x 2 y 1 y 2 x 1 x 3 y 1 y 3,即x 1( x 2 x 3 ) y 1 ( y 2y 3 ) 0r rr r r而 b c ( x 2 x 3 , y 2y 3 ) ,所以 a (b c) 0rr r r r r r 再证 a(b c)a b a cr r r由 a (b c)0 得 x 1 (x 2x 3 ) y 1 ( y 2 y 3 )0 ,r rr r 即 x 1 x 2 y 1 y 2 x 1 x 3 y 1 y 3 ,所以 a ba cuuur uuur2、 cos AOBOA OB cos cos sinsin .uuur uuurOA OBr r (c, d) .3、证明:结构向量 u (a,b) , vr r r r r r,所以 acbda 2b 2c 2d 2 cos r ru v u v cos u,vu, v∴ (ac bd )2 (a 2 b 2 )(c 2d 2 ) cos 2 r r ( a 2 b 2 )( c 2 d 2 )u, vuuur uuur 4、 AB AC 的值只与弦 AB 的长相关,与圆的半径没关 .C证明:取 AB 的中点 M ,连结 CM ,则 CMuuuur 1 uuurAB,AM AB2uuuuruuur uuur uuur uuurBAC AM又AB AC AB AC cos BAC ,而uuurAC uuur uuur uuur uuuur1uuur 2所以 AB AC AB AM2ABuuur uuur 2uuur 25、( 1)勾股定理:Rt ABC中,C902,则 CA CB ABuuur uuur uuur证明:∵ AB CB CAuuur 2uuur uuur uuur 2uuur uuur uuur 2∴ AB(CB CA)2CB2CA CB CA .uuur uuur由 C 90 ,有 CA CB,于是CA CB 0uuur 2uuur2uuur2∴ CA CB AB(2)菱形ABCD中,求证:AC BDuuur uuur uuur uuur uuur uuur证明:∵ AC AB AD, DB AB AD ,uuur uuur uuur uuur uuur uuur uuur 2uuur 2∴ AC DB (AB AD) (AB AD)AB AD .∵四边形 ABCD 为菱形,∴ ABuuur 2uuur 2 AD ,所以AB AD0uuur uuurBD∴ AC DB 0,所以AC(3)长方形ABCD中,求证:AC BDuuur uuur 证明:∵ 四边形 ABCD 为长方形,所以 AB0AD ,所以AB ADuuur 2uuur uuur uuur 2uuur 2uuur uuur uuur 2.∴ AB2AB AD AD AB2AB AD ADuuur uuur uuur uuur uuur2uuur2BD ∴ (AB AD )2 (AB AD )2,所以 AC BD,所以 AC (4)正方形的对角线垂直均分. 综合以上( 2)( 3)的证明即可 .2.5 平面向量应用举例习题 A 组(P113)1、解:设 P(x, y) , R( x1 , y1)uuur uuur则 RA(1,0)(x1, y1 )(1x1,y1 ) ,AP(x, y)(1,0)( x1,0)uuur uuurx1,y1)2( x1, y) ,即x12x3由 RA2AP 得(1y12y代入直线 l 的方程得 y 2x . 所以,点 P 的轨迹方程为 y2x .A2、解:(1)易知, OFD ∽ OBC , DF1BC ,2BF .2DF所以 BOuuur uuur 32 uuurr 2 1 r rr1rrOuuurAOBOBABF a3 ( ba)a(a b)uuurr323BCr E(2)因为 AE1(ab)2(第 2 题) uuur 2 uuurAO 所以 AOAE ,所以 A,O, E 三点共线,并且23OE同理可知:BO2,CO2 ,所以AOBO CO 2r uur uurOFODOEOFOD3、解:(1) v v B v A( 2,7) ;uurr uurrv v A 13 . (2) v 在 v A 方向上的投影为uurv A5(第 4题)uuruur ur ur uur4、解:设 F 1 , F 2 的协力为 F , F 与 F 1 的夹角为 ,ur uur uur uur则 F 3 1, 30 ; F 3 3 1 , F 3 与 F 1 的夹角为 150°. 习题 B 组(P113)uuruuruur1、解:设 v 0 在水平方向的速度大小为v x ,竖直方向的速度的大小为v y ,uur uur uur uursin .则 v x v 0 cos , v y v 0设 在 时 刻 t时 的 上 升 高 度 为 h , 抛 掷 距 离 为 s, 则uur1gt,( g 为重力加快度 )hv 0 t sinuur2sv 0 t cosuur 2 uur 2v 0 sin2v 0 sin 2所以,最大高度为,最大扔掷距离为g.2guruur r uur r,行驶距离为 d .2、解:设 v 1 与 v 2 的夹角为 ,合速度为 v , v 2 与 v 的夹角为 ur r则 sin v 1 sin 10sin , d 0.5 v . d 1 .r r sin20sin ∴ r 20sinv v v所以当90 ,即船垂直于对岸行驶时所用时间最短 .3、( 1) (0, 1)uuur( x 1, y 2) . uuur2 2) .解:设 P( x, y) ,则 APAB(2,uuuruuur 7 将 AB 绕点 A 沿顺时针方向旋转到 AP ,相当于沿逆时针方向旋转到44uuur AP ,uuur7 2 7 7 2 7 (1,3)于是 AP( 2 cos2 sin, 2 sin2 cos )4444所以x1 1,解得 x0, y1y233( 2) y2 xuuur后,点 P 的坐解:设曲线 C 上任一点 P 的坐标为 ( x, y) , OP 绕 O 逆时针旋转4标为 (x , y )x x cosysin x2( x y)则44,即2yx siny cosy2y)4( x42又因为 x2y23,所以1( xy) 21( xy) 2 3 ,化简得 y32 22x第二章复习参照题 A 组( P118)1、( 1)√; (2)√;(3)×; (4)× .2、(1) D ;(2) B ;(3) D ;(4)C ;(5)D ;(6) B.uuur1rruuur 1 r r3、 AB(a b) , AD 2( a b)2uuur uuur uuur uuur2 r 1r4、略解: DEBAMA MBab3 3uuur 2 r2 ruuur1 r1 rAD ab , BC a b333 3uuur 1r1ruuuruuur 1 r 2rEFab , FA DC ab3333uuur 1r2ruuur 2r1rCDab , ABab33 3 3uuur r r CE abuuur (8, 8) uuur8 2 ;5、( 1) AB , AB(第 4题)uuur uuur( 8,8) ;uuur uuur(2) OC (2, 16) , OD (3) OA OB 33.uuur uuur6、AB与CD共线.uuur uuur uuur uuur uuur uuur 证明:因为 AB(1, 1) , CD(1, 1) ,所以 AB CD.所以 AB与CD 共线.7、D(2,0) .8、n 2 .9、1,0.30,cos C 410、cos A ,cos B55r ur ur r ur ur 21r ur ur11、证明:(2 n m) m2n m m 2cos600 ,所以 (2n m)m .12、 1 .r r r r1.14、cos5,cos19 13、a b13 , a b820第二章复习参照题B组(P119)1、(1) A;(2)D;(3)B;(4)C;(5)C;(6)C;(7)D .r r r r r r2、证明:先证a b a b a b .r r r r r 2r 2r ra b(a b)2a b2a b,r r r r r2r2r ra b( a b)2a b2ab .r r r r r r r 2r 2r r因为 a b ,所以 a b0 ,于是 a b a b a b .r r r r r r再证 a b a b a b .r r r 2r r r 2r r r 2r r r 2因为 a b a2a b b, a b a2a b br r r r r r r r由 a b a b 可得 a b0 ,于是 a br r r r r r所以 a b a b a b .【几何意义是矩形的两条对角线相等】r r r ur3、证明:先证a b c dr ur r r r r r2r 2c d(a b) (a b)a br r r ur r ur又 a b,所以 c d0 ,所以 c dr ur r r再证 c d a b .r ur r ur r r r r r 2r 20(第 3题)由 c d 得 c d0,即 ( a b) (a b) a br r所以 a b【几何意义为菱形的对角线相互垂直,如图所示】uuur uuur uuuruuur 1rr uuur1r1r4、 AD AB BCCDa b , AEa b P 3242uuur 3ruuuur 1 ruuuur uuuruuuur 1 r1 r1 r1 r r 而 EF4 a , EM4 a ,所以 AM AEEMa b a (a b)4 2 4 25、证明:如下图,uuur uuur uuuuruuur uuuur uuur rOD OP OP ,因为 OP OPOP0 ,12 1 23 Ouuuruuuruuur所以 OP 3 OD ,OD 1uuuruuur uuurP 1P 2所以 ODOP PD11所以 OPP 1 2 30 ,同理可得OPP 1330D(第 5题)所以3 1 260 ,同理可得1 2360, 23 160 ,所以123为P PPPP PP P PPP P正三角形 .6、连结 AB.uuuur uuur r rN.由对称性可知, AB 是 SMN 的中位线, MN 2AB 2b 2a7、( 1)实质行进速度大小为 42 (4 3) 2 8(千米/时),沿与水流方向成 60°的方向行进;( 2)实质行进速度大小为 4 2 千米/时,MBA沿与水流方向成 90arccos 6的方向行进 .OSuuur uuuruuur uuur 3uuur uuur uuur uuur uuur (第 6题)8、解:因为 OA OBOB OC ,所以 OB (OA OC ) 0 ,所以 OB CA uuur uuur0 , uuur uuur0 ,所以点 O 是 ABC 的垂心 .同理, OA BCOC AB9、( 1) a 2 x a 1 y a 1 y 0 a 2 x 0 0 ; (2)垂直;( 3)当 A 1B 2 A 2B 1 0时, l 1 ∥ l 2 ;当 A 1 A 2 B 1B 2 0时, l 1 l 2 ,夹角 的余弦 cosA 1A 2B 1B 2;A 1 2B 12A 22B 22Ax 0 By 0 C( 4) dA 2B 2第三章 三角恒等变换3.1 两角和与差的正弦、余弦和正切公式 练习(P127)1、 cos()coscossin sin0 cos1 sinsin .222cos(2) cos2 cossin2 sin 1 cos 0 sincos.2、解:由 cos3 , ( , ) ,得 sin 1cos 21 ( 3)24 ;525 5所以 cos()cos cossin sin 2 ( 3 ) 2 42 .4442 5 25 103、解:由 sin15 , 是第二象限角,得 cos 1 sin 21(15 )28 ;171717所以 cos() cos cossin sin8 1 153 8 15 3 .33317 2 172344、解:由 sin2 , ( ,3) ,得 cos1 sin 21 (2 )25 ;3 23 3 又由 cos3 , (3,2 ) ,得 sin1 cos21 (3)27 .4244所以cos()cos cossin sin3 (5 ) ( 7) ( 2) 3 5 2 7 .43 4 312练习(P131)1、( 1)6 2; (2)6 2; (3)62; (4)2 3.4442、解:由 cos3 , ( , ) ,得 sin 1 cos 21 ( 3)24 ;525 5所以 sin() sin coscos sin4 1 ( 3 ) 3 4 3 3 .3335 2 5 210 3、解:由 sin12 , 是第三象限角,得 cos 1 sin 21( 12) 25 ;131313所以cos()cos cossinsin 3 ( 5 ) 1 (12) 5 3 12 .666213 2 1326tantan3 14、解: tan()4 2 .41 tantan 1 3 145、( 1)1;(2)1;(3)1;(4)3 ;22( 5)原式 = (cos34 cos26sin34 sin 26 )cos(3426 )cos601 ;2(6)原式= sin20cos70 cos20 sin70 (sin 20 cos70 cos20 sin70 ) sin901 .6、( 1)原式 = cos cosx sinsin x cos( x) ;333( 2)原式 = 2(3sin x1cosx)2(sin x coscosxsin) 2sin( x) ;22666( 3)原式 = 2(2sin x2cos x) 2(sin x cos cos xsin 4) 2sin( x ) ;22 44( 4)原式 = 2 2( 1cos x3sin x)2 2(cos3 cosx sin sin x)2 2 cos(x) .22337、解:由已知得 sin()cos cos()sin3 ,5即 sin[()]3, sin()355所以 sin3. 又 是第三象限角,5于是 cos1 sin 21 (3) 2 4 .55因此sin(5 ) sin cos 5cos sin 5( 3 )( 2 ) ( 4 )(2 ) 7 2 .444 52 5 210练习(P135)31、解:因为 812 ,所以82443sin 335 又由 cos,得 sin1 (2, tan85)5 84 4 885cos85所以 sinsin(2) 2sin cos2 (3) ( 4)24 488 85525 coscos(2) cos 2 sin 28( 4 )2 ( 3 )2 7 48 85 5 252tan82 3 3 16 24tantan(2)432 774821 (21 tan8 )42、解:由 sin()3,得 sin3,所以 cos 21 sin 21 ( 3)2 16555 25所以 cos2cos 2sin 216 ( 3) 2 725 5 253、解:由 sin2sin 且 sin0 可得 cos1 ,2又 由( 2 , ),得sin1 cos 21 ( 1 )23, 所以2 2tansin 3 ( 2) 3 .cos24、解:由tan21 , 得 2tan1.所 以 tan 26tan1 0,所以3 1 tan 23tan3 105、(1)1sin30 1 ;(2)cos2sin2cos2 ;sin15 cos1582484 2( 3)原式 = 1 2tan 22.51 tan45 1 ;( 4)原式 = cos452 .2 1 tan 2 22.5 222习题A 组(P137)1、( 1) cos(3)cos3cossin3sin0 cos( 1) sinsin;222( 2) sin(3) sin3coscos3sin1 cos0 sincos ;222( 3) cos() cos cos sin sin1 cos 0 sincos ;( 4) sin( ) sin coscos sin0 cos( 1) sinsin .2、解:由 cos3,0,得 sin1 cos21 (3)24 ,55 5所以 cos() cos cos 6sinsin6 4 3 3 1 4 3 3 .65 25 2 103、解:由 sin2 , ( , ) ,得 cos1 sin 21( 2)25 ,3 233又由 cos3 , ( ,3) ,得 sin1 cos 21 ( 3) 27 ,4244所以cos() cos cossin sin5 ( 3 ) 2 ( 7 ) 3 5 2 7 .34 3 4 124、解:由 cos1 , 是锐角,得 sin1 cos21 (1)24 3777因为 , 是锐角,所以 (0, ) ,又因 为sin( )1 cos2 ()1 (所以 coscos[( )( 11) 1 5 314 7 14 5、解:由 60150 ,得 90cos()11 ,所以1411)25 3 1414] cos()cossin()sin4 3 17230 180又由 sin(30)3,得 cos(30)1 sin 2(30)1 (3)2455 5所以 coscos[(30 ) 30 ] cos(30)cos30 sin(30)sin304 3 3 1 4 3 35 252106、( 1)6 2 ;(2)24 6 ;(3) 2 3 .47、解:由 sin2 , (, ) ,得 cos 1 sin21 (2)25 .3233又由cos 3 ,是第三 象限角, 得4sin1cos 21 ( 3) 27 .4 4所以 cos() cos cossin sin5 ( 3 ) 2 ( 7 )3 4 3 4 3 52 712 sin() sincos cos sin2 ( 3) (5 ) ( 7 )3 4 3 46 35128、解:∵ sin A5 ,cos B3且 A, B 为 ABC 的内角13 5∴ 0 A,0 B, cos A12,sin B42135当 cos A12 时, sin( A B) sin AcosB cos Asin B 135 3 ( 12) 4 33 013 5 13565A B,不合题意,舍去∴ cos A12,sin B4135∴ cosCcos( A B)(cos AcosB sin Asin B)(123 5 4) 1613 5 13 5659、解:由 sin3 , ( , ) ,得 cos 1 sin21 (3)24 . 5255∴ tansin 3 ( 5 ) 3 . cos 5 44tantan 3 1 2∴ tan()43 21.1 tan tan1 ( )114 2tantan3 1tan()43 212 .1 tantan1 ( )4 210、解:∵ tan ,tan 是 2x 23x 7 0 的两个实数根 .∴ tantan3, tantan7 .22tantan3 1 ∴ tan( )21 tantan7.1 () 3211、解:∵ tan() 3,tan( ) 5∴ tan2tan[( )()]tan( ) tan()3 5 41 tan() tan( ) 1 3 57tan 2tan[()( )]tan() tan( ) 3511 tan() tan()1 3 5812、解:∵ BD : DC : AD2:3:6B∴ tanBD 1,tanDC 1AD3AD2D1 1tan tan∴ tan BAC tan(3 21)tantan1 111α3 2 AβC又∵ 0BAC180 ,∴ BAC45(第 12 题)13、( 1)6 5 sin( x) ;(2) 3sin( x) ;(3) x) ;(4) 27 x) ;3 2sin(2sin(62612(5)2;( 6) 1;(7)sin() ;( 8) cos();(9) 3 ; (10)22tan() .14、解:由 sin0.8,(0,) ,得 cos1 sin 21 0.820.62∴ sin22sin cos 2 0.8 0.6 0.96cos2 cos 2sin 20.620.820.2815、解:由 cos3,180270 ,得 sin1 cos 21( 3 ) 26333∴ sin 22sincos2 ( 6 ) ( 3)2 2333cos2cos 2sin 2(3 )2 ( 6 ) 2 13 3 3tan 2sin 2 2 2 (3)2 2cos2 316、解:设 sin Bsin C5,且0B 90 ,所以 cosB12 .1313∴ sin A sin(1802B) sin2 B 2sin Bcos B25 12 12013 13169cos A cos(1802B)cos2B(cos 2 Bsin 2 B)(( 12 )2 ( 5 )2 ) 11913 13169sin Atan Acos Atan 22tan 17、解: 1 tan 2120(169) 169 1192131 (1)2 3120 1193 ,tantan 21 3 7 41 . tan(2 )tan2141 tan 314718、解: cos()cossin()sin1cos[()]1,即 cos1333又( 3 ,2 ) ,所以 sin1 cos21 (1)22 2 233∴ sin 22sin cos2 ( 2 2 ) 14 23 39cos2cos 2sin 2( 1 )2( 2 2 ) 2733 9∴cos(2) cos2 cossin 2 sin7 2 4 2272 892(9 )184 44219、(1) 1 sin2;(2) cos2 ;(3) 1sin 4x ;(4) tan2 .4习题 B 组(P138)1、略.2、解:∵ tan A,tan B 是 x 的方程 x 2 p(x 1) 1 0 ,即 x 2px p 1 0 的两个实根∴ tan A tan B p , tan A tan B p 1∴ tan C tan[(A B)]tan(A B)tan A tan B p 1 tan A tan B11 ( p 1)因为 0 C,所以 C3 .43、反响一般的规律的等式是(表述形式不独一)sin 2cos 2 (30 )sincos(30 )3 (证明略)4 此题是开放型问题,反应一般规律的等式的表述形式还能够是:sin 2 (30 ) cos 2sin(30 )cos34sin 2 (15 ) cos 2 (15 ) sin( 15 )cos(15 ) 34 sin2cos2sincos3,此中30 ,等等4思虑过程要求从角,三角函数种类,式子结构形式三个方面找寻共同特色,进而作出概括 . 对认识三角函数式特色有帮助,证明过程也会促使推理能力、运算能力的提升 .4、因为 PAPP ,则 (cos() 1)2 sin 2 ()(coscos ) 2 (sinsin )21 2即 2 2cos() 2 2cos cos 2sin sin所以 cos() cos cossinsin3.2 简单的三角恒等变换 练习(P142)1、略.2、略 .3、略 .4、( 1) y1sin 4x . 最小正周期为,递加区间为 [8k , k ], k Z ,最222 82大值为 1;2( 2) y cosx 2 . 最小正周期为 2 ,递加区间为 [2k ,22k ], k Z ,最大值为 3;( 3) y 2sin(4 x) . 最小正周期 , 增区 [5k , k ], k Z ,最32242 24 2大 2.A ( P143)1、( 1)略;(2)提示:左式通分后分子分母同乘以2;( 3)略; ( 4)提示:用 sin 2 cos 2 取代 1,用 2sincos 取代 sin 2;( 5)略;( 6)提示:用 2cos 2 取代 1 cos2 ;( 7)提示:用 2sin 2 取代 1 cos2 ,用 2cos 2 取代 1 cos2 ; (8)略.2、由已知可有 sincoscos sin1⋯⋯①, sincoscos sin1⋯⋯②23(1)②× 3-①× 2 可得 sin cos 5cos sin(2)把( 1)所得的两 同除以 cos cos 得 tan5tan注意: 里 coscos0 含与①、②之中1. 于是 tan22tan2 (1) 4 3、由已知可解得tan221 tan 21 ( 1 ) 232tan tan1 11tan()42 141 tantan 1 ( ) 1 342∴ tan24tan()44、由已知可解得 x sin , ycos ,于是 x 2 y 2 sin 2cos 21.5、 f ( x) 2sin(4 x) ,最小正周期是 , 减区 [k , 7 k ], k Z .2 2423224B (P143)1、略.2、因为 76 2790 ,所以 sin76 sin(9014 ) cos14 m即 2cos 2 71 m ,得 cos7m 123、 存在 角,使22,所以23, tan(2)3 ,3tan tan又 tan tan23 ,又因 tan(2 ) 2,21 tan tan2所以 tantan tan()(1 tantan ) 33222由此可解得 tan1 ,4 ,所以.6经查验6 ,是切合题意的两锐角 .41(cos cos ), 1(sin sin)). 过M 作MM 1 垂4、线段 AB 的中点 M 的坐标为 (22直于 x 轴,交 x 轴于 M 1 , MOM 1 1 ()1 () .y22B在 Rt OMA 中, OMOA cos2 cos2.CMA在 Rt OM 1 M 中, OM 1 OM cos MOM 1cos 2 cos ,2M 1 M OM sin MOM 1sincos .OM 1x22于是有1cos ) coscos,(cos2 221(sinsin ) sin2cos2(第 4题)25、当 x2 时, f ( ) sin 2 cos 2 1 ;当 x 4 时, f ( ) sin 4cos 4(sin 2cos 2 )2 2sin 2 cos 21 1 sin 22 ,此时有 1≤ f ( )≤1;2 2当x 6时,f ( ) sin 6cos 6(sin 2 cos 2 )33sin 2 cos 2 (sin 2 cos 2 )1 3 sin 22 ,此时有 1≤ f ( )≤1;4 4 由此猜想,当 x2k,k N 时,k11 ≤ f ( ) ≤ 126、( 1) y 5( 3sin x4cosx) 5sin( x) ,此中 cos3,sin45 555所以, y 的最大值为 5,最小值为﹣ 5;( 2) ya 2b 2 sin( x) ,此中 cosa ,sin a 2ba 2b 2b 2所以, y 的最大值为a 2b 2 ,最小值为a 2b 2 ;第三章复习参照题 A 组( P146)。
高中数学必修4课后习题答案(2021年整理)

(完整)高中数学必修4课后习题答案(word版可编辑修改)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)高中数学必修4课后习题答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)高中数学必修4课后习题答案(word版可编辑修改)的全部内容。
高中数学必修4课后习题答案。
必修四数学课后习题答案

必修四数学课后习题答案必修四数学课后习题答案数学是一门重要的学科,对于培养学生的逻辑思维能力和解决问题的能力具有重要作用。
而数学课后习题则是巩固学习成果、提高解题能力的重要途径。
在必修四的数学课本中,有许多习题需要同学们进行思考和解答。
下面是一些常见习题的答案,供同学们参考。
一、函数与导数1. 函数f(x) = x^3 + 2x^2 - 3x + 1的导函数为f'(x) = 3x^2 + 4x - 3。
2. 函数f(x) = 2x^3 + 3x^2 - 4x + 1的导函数为f'(x) = 6x^2 + 6x - 4。
3. 函数f(x) = (x - 1)(x - 2)(x - 3)的导函数为f'(x) = 3(x - 1)(x - 2) + 2(x - 1)(x - 3) + (x - 2)(x - 3)。
4. 函数f(x) = 3x^4 - 4x^3 + 2x^2 - x + 1的导函数为f'(x) = 12x^3 - 12x^2 + 4x - 1。
二、三角函数与导数1. 函数f(x) = sin(x)的导函数为f'(x) = cos(x)。
2. 函数f(x) = cos(x)的导函数为f'(x) = -sin(x)。
3. 函数f(x) = tan(x)的导函数为f'(x) = sec^2(x)。
4. 函数f(x) = cot(x)的导函数为f'(x) = -csc^2(x)。
三、不定积分1. ∫(2x + 3)dx = x^2 + 3x + C。
2. ∫(3x^2 + 2x + 1)dx = x^3 + x^2 + x + C。
3. ∫(4x^3 - 2x^2 + 5x)dx = x^4/4 - 2x^3/3 + 5x^2/2 + C。
4. ∫(e^x + 1/x)dx = e^x + ln|x| + C。
四、定积分1. ∫[0, 1] (2x + 1)dx = [x^2 + x] [0, 1] = 1 + 1 = 2。
数学必修4课后习题答案

数学必修4课后习题答案数学必修4课后习题答案数学是一门理性而又美妙的学科,它贯穿于我们生活的方方面面。
而对于学习数学的学生来说,习题是巩固知识、培养思维能力的重要途径。
本文将为大家提供数学必修4课后习题的答案,希望能够帮助大家更好地理解和掌握这门学科。
1. 选择题1.1. A1.2. B1.3. C1.4. D1.5. B2. 填空题2.1. 162.2. 52.3. 22.4. 72.5. 13. 解答题3.1. 解:设正方形的边长为x,则正方形的面积为x^2。
根据题意,正方形的面积是边长的平方,所以x^2 = 64。
解得x = 8,所以正方形的边长为8。
3.2. 解:设圆的半径为r,则圆的周长为2πr。
根据题意,圆的周长是半径的2倍,所以2πr = 2r。
解得r = 0,所以圆的半径为0。
3.3. 解:设直角三角形的直角边分别为a和b,斜边为c。
根据勾股定理,有a^2 + b^2 = c^2。
根据题意,直角边的平方和等于斜边的平方,所以a^2 +b^2 = 25。
解得a = 3,b = 4,所以直角三角形的直角边分别为3和4。
通过以上题目的解答,我们可以看到数学必修4课后习题的答案。
但是,仅仅知道答案是不够的,更重要的是理解其中的思路和方法。
因此,在解答习题的同时,我们也要注重思考和探索,培养自己的数学思维能力。
数学必修4课后习题的答案只是一个参考,每个人的解答方法可能会有所不同。
因此,在学习数学的过程中,我们要多思考、多交流,不断提高自己的解题能力。
另外,数学的学习需要坚持和积累,不能仅仅停留在课堂上,更要注重自主学习和实践应用。
总之,数学必修4课后习题的答案只是一个开始,更重要的是我们能够通过解题的过程,理解数学的本质和思维方式。
希望大家在学习数学的过程中,能够保持好奇心和求知欲,不断挑战自己,取得更好的成绩。
数学的世界充满了无限可能,让我们一起探索和享受这个美妙的学科吧!。
高中数学必修四练习册(后含答案)
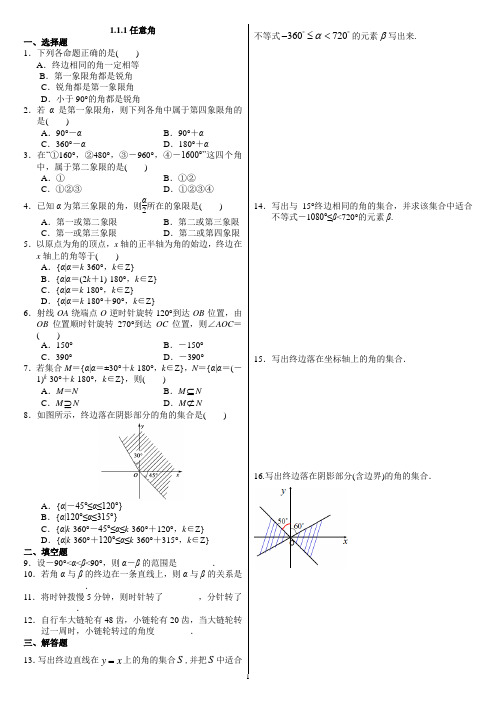
C.{α|α=k·180°,k∈Z}
D.{α|α=k·180°+90°,k∈Z}
6.射线 OA 绕端点 O 逆时针旋转 120°到达 OB 位置,由
OB 位置顺时针旋转 270°到达 OC 位置,则∠AOC=
()
A.150°
B.-150°
C.390°
D.-390°
7.若集合 M={α|α=±30°+k·180°,k∈Z},N={α|α=(-
D.α|α=2kπ+53π,k∈Z
3.已知集合 A={α|2kπ≤α≤(2k+1)π,k∈Z},B={α|-
4≤α≤4},则 A∩B=( )
A.
B.{α|0≤α≤π|
C.{α|-4≤α≤4|
D.{α|-4≤α≤-π 或 0≤α≤π}
4.一条弦的长等于半径,则这条弦所对的圆心角是____
弧度 ( )
1.1.1 任意角
一、选择题
1.下列各命题正确的是( )
A.终边相同的角一定相等
B.第一象限角都是锐角
C.锐角都是第一象限角
D.小于 90°的角都是锐角
2.若 α 是第一象限角,则下列各角中属于第四象限角的
是( )
A.90°-α
B.90°+α
C.360°-α
D.180°+α
3.在“①160°,②480°,③-960°,④-1600°”这四个角
A.sinα+cosα<0
B.tanα-sinα<0
π
π
π
A.π
B.2
C.3
D.4
5.如图中,圆的半径为 5,圆内阴影部分的面积是( )
175π A. 36
125π B. 18
75π C. 18
高中数学必修4习题和复习参考题及对应答案
高中数学必修4习题和复习参考题及对应答案A 组1、在0°~360°范围内,找出与下列各角终边相同的角,并指出它们是哪个象限的角: (1)-265°;(2)-1000°;(3)-843°10′;(4)3900°. 答案:(1)95°,第二象限; (2)80°,第一象限; (3)236°50′,第三象限; (4)300°,第四象限.说明:能在给定范围内找出与指定的角终边相同的角,并判定是第几象限角.2、写出终边在x 轴上的角的集合. 答案:S={α|α=k·180°,k ∈Z }.说明:将终边相同的角用集合表示.3、写出与下列各角终边相同的角的集合,并把集合中适合不等式-360°≤β<360°的元素β写出来:(1)60°;(2)-75°;(3)-824°30′;(4)475°;(5)90°;(6)270°;(7)180°;(8)0°.答案:(1){β|β=60°+k·360°,k ∈Z },-300°,60°; (2){β|β=-75°+k·360°,k ∈Z },-75°,285°; (3){β|β=-824°30′+k·360°,k ∈Z },-104°30′,255°30′; (4){β|β=475°+k·360°,k ∈Z },-245°,115°; (5){β|β=90°+k·360°,k ∈Z },-270°,90°; (6){β|β=270°+k·360°,k ∈Z },-90°,270°; (7){β|β=180°+k·360°,k ∈Z },-180°,180°; (8){β|β=k·360°,k ∈Z },-360°,0°. 说明:用集合表示法和符号语言写出与指定角终边相同的角的集合,并在给定范围内找出与指定的角终边相同的角.4、分别用角度和弧度写出第一、二、三、四象限角的集合. 答案: 象限 角度制弧度制一 {β|k·360°<β<90°+k·360°,k ∈Z } {|22,}2k k k πβπβπ<<+∈Z二 {β|90°+k·360°<β<180°+k·360°,k ∈Z }{|22,}2k k k πβπβππ+<<+∈Z三 {β|180°+k·360°<β<270°+k·360°,k ∈Z }3{|22,}2k k k πβππβπ+<<+∈Z 四{β|270°+k·360°<β<360°+k·360°,k ∈Z }3{|222,}2k k k πβπβππ+<<+∈Z 说明:用角度制和弧度制写出各象限角的集合.5、选择题:(1)已知α是锐角,那么2α是( ) A .第一象限角 B .第二象限角 C .小于180°的正角 D .第一或第二象限角 (2)已知α是第一象限角,那么2α是( )、 A .第一象限角 B .第二象限角 C .第一或第二象限角 D .第一或第三象限角 答案:(1)C 说明:因为0°<α<90°,所以0°<2α<180°. (2)D说明:因为k·360°<α<90°+k·360°,k ∈Z ,所以180451802k k α︒<<︒+︒,k ∈Z .当k 为奇数时,2α是第三象限角;当k 为偶数时,2α是第一象限角.6、一条弦的长等于半径,这条弦所对的圆心角等于1弧度吗?为什么?答案:不等于1弧度.这是因为等于半径长的弧所对的圆心角为1弧度,而等于半径长的弦所对的弧比半径长.说明:了解弧度的概念.7、把下列各角度化成弧度: (1)36°;(2)-150°;(3)1095°;(4)1440°.答案:(1)5π;(2)56π;(3)7312π-;(4)8π.说明:能进行度与弧度的换算.8、把下列各弧度化成度: (1)76π-;(2)103π-;(3)1.4;(4)23. 答案:(1)-210°;(2)-600°;(3)80.21°;(4)38.2°.说明:能进行弧度与度的换算.9、要在半径OA=100cm 的圆形金属板上截取一块扇形板,使其弧AB 的长为112cm ,求圆心角∠AOB 是多少度(可用计算器,精确到1°).答案:64°说明:可以先运用弧度制下的弧长公式求出圆心角的弧度数,再将弧度换算为度,也可以直接运用角度制下的弧长公式.10、已知弧长50cm 的弧所对圆心角为200°,求这条弧所在的圆的半径(可用计算器,精确到1cm ).答案:14cm .说明:可以先将度换算为弧度,再运用弧度制下的弧长公式,也可以直接运用角度制下的弧长公式.B 组1、每人准备一把扇子,然后与本小组其他同学的对比,从中选出一把展开后看上去形状较为美观的扇子,并用计算器算出它的面积S 1.(1)假设这把扇子是从一个圆面中剪下的,而剩余部分的面积为S 2,求S 1与S 2的比值;(2)要使S 1与S 2的比值为0.618,则扇子的圆心角应为几度(精确到10°)? 答案:(1)(略)(2)设扇子的圆心角为θ,由2122120.6181(2)2r S S r θπθ==-,可得θ=0.618(2π-θ),则θ=0.764π≈140°.说明:本题是一个数学实践活动.题目对“美观的扇子”并没有给出标准,目的是让学生先去体验,然后再运用所学知识发现,大多数扇子之所以“美观”是因为基本都满足:120.618S S =(黄金分割比)的道理.2、(1)时间经过4 h (时),时针、分针各转了多少度?各等于多少弧度?(2)有人说,钟的时针和分针一天内会重合24次、你认为这种说法是否正确?请说明理由.(提示:从午夜零时算起,假设分针走了t min 会与时针重合,一天内分针和时针会重合n 次,建立t 关于n 的函数关系式,并画出其图象,然后求出每次重合的时间.)答案:(1)时针转了-120°,等于23π-弧度;分针转了-1440°,等于-8π弧度 (2)设经过t min 分针就与时针重合,n 为两针重合的次数. 因为分针旋转的角速度为2(rad /min)6030ππ=, 时针旋转的角速度为2(rad/min)1260360ππ=⨯,所以()230360t n πππ-=,即72011t n =. 用计算机或计算器作出函数72011t n =的图象(如下页图)或表格,从中可清楚地看到时针与分针每次重合所需的时间.n u1 15. 981.82 16. 1047.3 17. 1112.7 18. 1178.2 19. 1243.6 20. 1309.1 21. 1374.5 22.1440.因为时针旋转一天所需的时间为24×60=1440(min ),所以720144011n ≤,于是n≤22.故时针与分针一天内只会重合22次.说明:通过时针与分针的旋转问题进一步地认识弧度的概念,并将问题引向深入,用函数思想进行分析.在研究时针与分针一天的重合次数时,可利用计算器或计算机,从模拟的图形、表格中的数据、函数的解析式或图象等角度,不难得到正确的结论.3、已知相互啮合的两个齿轮,大轮有48齿,小轮有20齿,当大轮转动一周时,小轮转动的角是__________度,即__________rad .如果大轮的转速为180r/min (转/分),小轮的半径为10.5cm ,那么小轮周上一点每1s 转过的弧长是__________.答案:864°,245π,151.2π cm . 说明:通过齿轮的转动问题进一步地认识弧度的概念和弧长公式.当大齿轮转动一周时,小齿轮转动的角是4824360864rad.205π⨯︒=︒= 由于大齿轮的转速为3r/s ,所以小齿轮周上一点每1s 转过的弧长是483210.5151.2(cm)20ππ⨯⨯⨯=. P20 习题1.2A 组1、用定义法、公式一以及计算器求下列角的三个三角函数值:(1)173π-;(2)214π;(3)236π-;(4)1500°. 答案:(1)31sin ,cos ,tan 322ααα===; (2)22sin ,cos ,tan 122ααα=-=-=; (3)133sin ,cos ,tan 223ααα===; (4)31sin ,cos ,tan 322ααα===. 说明:先利用公式一变形,再根据定义求值,非特殊角的三角函数值用计算器求.2、已知角α的终边上有一点的坐标是P (3a ,4a ),其中a≠0,求sinα,cosα,tanα的三角函数值.答案:当a >0时,434s i n ,c o s,t a n 553ααα===;当a <0时,434s i n ,c o s ,t a n 553ααα=-=-=-.说明:根据定义求三角函数值.3、计算:(1)6sin (-90°)+3sin0°-8sin270°+12cos180°; (2)10cos270°+4sin0°+9tan0°+15cos360°;(3)22322costantan sin cos sin 2446663ππππππ-+-++;(4)2423sincos tan 323πππ+-. 答案:(1)-10;(2)15;(3)32-;(4)94-.说明:求特殊角的三角函数值.4、化简:(1)asin0°+bcos90°+ctan180°;(2)-p 2cos180°+q 2sin90°-2pqcos0°;(3)223cos 2sincos sin 22a b ab ab ππππ-+-; (4)13tan 0cos sin cos sin 222m n p q r ππππ+---.答案:(1)0;(2)(p -q )2;(3)(a -b )2;(4)0.说明:利用特殊角的三角函数值化简.5、根据下列条件求函数3()sin()2sin()4cos 23cos()444f x x x x x πππ=++--++的值.(1)4x π=;(2)34x π=. 答案:(1)-2;(2)2.说明:转化为特殊角的三角函数的求值问题.6、确定下列三角函数值的符号: (1)sin186°; (2)tan505°; (3)sin7.6π; (4)23tan()4π-; (5)cos940°;(6)59cos()17π-. 答案:(1)负;(2)负;(3)负;(4)正;(5)负;(6)负. 说明:认识不同位置的角对应的三角函数值的符号.7、确定下列式子的符号: (1)tan125°·sin273°;(2)tan108cos305︒︒;(3)5411sin cos tan 456πππ;(4)511cos tan 662sin 3πππ. 答案:(1)正;(2)负;(3)负;(4)正.说明:认识不同位置的角对应的三角函数值的符号.8、求下列三角函数值(可用计算器):(1)67sin()12π-; (2)15tan()4π-;(3)cos398°13′; (4)tan766°15′. 答案:(1)0.9659;(2)1;(3)0.7857;(4)1.045.说明:可先运用公式一转化成锐角三角函数,然后再求出三角函数值.9、求证:(1)角θ为第二或第三象限角当且仅当sinθ·tanθ<0; (2)角θ为第三或第四象限角当且仅当cosθ·tanθ<0; (3)角θ为第一或第四象限角当且仅当sin 0tan θθ>;(4)角θ为第一或第三象限角当且仅当sinθ·cosθ>0.答案:(1)先证如果角θ为第二或第三象限角,那么sinθ·tanθ<0.当角θ为第二象限角时,sinθ>0,tanθ<0,则sinθ·tanθ<0;当角θ为第三象限角时,sinθ<0,tanθ>0,则sinθ·tanθ<0,所以如果角θ为第二或第三象限角,那么sinθ·tanθ<0.再证如果sinθ·tanθ<0,那么角θ为第二或第三象限角.因为sinθ·tanθ<0,即sinθ>0且tanθ<0,或sinθ<0且tanθ>0,当sinθ>0且tanθ<0时,角θ为第二象限角;当sinθ<0且tanθ>0时,角θ为第三象限角,所以如果sinθ·tanθ<0,那么角θ为第二或第三象限角.综上所述,原命题成立.(其他小题略)说明:以证明命题的形式,认识位于不同象限的角对应的三角函数值的符号.10、(1)已知3sin2α=-,且α为第四象限角,求cosα,tanα的值;(2)已知5cos13α=-,且α为第二象限角,求sinα,tanα的值;(3)已知3tan4α=-,求sinα,cosα的值;(4)已知cosα=0.68,求sinα,tanα的值(计算结果保留两个有效数字).答案:(1)1,3 2-;(2)1212,135-;(3)当α为第二象限角时,34 sin,cos55αα==-,当α为第四象限角时,34 sin,cos55αα=-=;(4)当α为第一象限角时,sinα=0.73,tanα=1.1,当α为第四象限角时,sinα=-0.73,tanα=-1.1.说明:要注意角α是第几象限角.11、已知1sin3x=-,求cosx,tanx的值.答案:当x为第三象限角时,222 cos,tan34x x=-=;当x为第四象限角时,222 cos,tan34 x x==-.说明:要分别对x是第三象限角和第四象限角进行讨论.12、已知3tan 3,2απαπ=<<,求cosα-sinα的值. 答案:1(31)2- 说明:角α是特殊角.13、求证: (1)2212sin cos 1tan 1tan cos sin x x xxx x--=+-;(2)tan 2α-sin 2α=tan 2α·sin 2α; (3)(cosβ-1)2+sin 2β=2-2cosβ; (4)sin 4x +cos 4x=1-2sin 2xcos 2x .答案:(1)2(cos sin )cos sin 1tan (cos sin )(cos sin )cos sin 1tan x x x x xx x x x x x x---===+-++左边; (2)222222222211cos sin sin (1)sin sin sin tan cos cos cos x x x xxx x xxx-=-===左边;(3)左边=1-2cosβ+cos 2β+sin 2β=2-2cosβ;(4)左边=(sin 2x +cos 2x )2-2sin 2x·cos 2x=1-2sin 2x·cos 2x .说明:还可以从右边变为左边,或对左右同时变形.可提倡一题多解,然后逐渐学会选择较为简单的方法.B 组1、化简(1+tan 2α)cos 2α. 答案:1说明:根据同角三角函数的基本关系,将原三角函数式转化为正余弦函数式.2、化简1sin 1sin 1sin 1sin αααα+---+,其中α为第二象限角. 答案:-2tanα说明:先变形,再根据同角三角函数的基本关系进行化简.3、已知tanα=2,求sin cos sin cos αααα+-的值.答案:3说明:先转化为正切函数式.4、从本节的例7可以看出,cos 1sin 1sin cos x xx x+=-就是sin 2x +cos 2x=1的一个变形.你能利用同角三角函数的基本关系推导出更多的关系式吗?答案:又如sin 4x +cos 4x=1-2sin 2x·cos 2x 也是sin 2x +cos 2x=1的一个变形;2211tan cos x x=+是sin 2x +cos 2x=1和sin tan cos xx x=的变形;等等. 说明:本题要求学生至少能写出每个同角关系式的一个变形.P29 习题1.3A 组1、将下列三角函数转化为锐角三角函数,并填在题中横线上: (1)cos210°=__________; (2)si n263°42′=__________; (3)cos()6π-=__________; (4)5sin()3π-=__________;(5)11cos()9π-=__________;(6)cos (-104°26′)=__________; (7)tan632°24′=__________; (8)17tan6π=__________. 答案:(1)-cos30°; (2)-sin83°42′ (3)cos 6π;(4)sin3π; (5)2cos 9π-;(6)-cos75°34′; (7)-tan87°36′; (8)tan6π-. 说明:利用诱导公式转化为锐角三角函数.2、用诱导公式求下列三角函数值: (1)17cos()4π-; (2)sin (-1574°); (3)sin (-2160°52′); (4)cos (-1751°36′); (5)cos1615°8′;(6)26sin()3π-.答案:(1)22;(2)-0.7193;(3)-0.0151;(4)0.6639;(5)-0.9964;(6)32 -说明:先利用诱导公式转化为锐角三角函数,再求值.3、化简:(1)sin(-1071°)·sin99°+sin(-171°)·sin(-261°);(2)1+sin(α-2π)·sin(π+α)-2cos2(-α).答案:(1)0;(2)-cos2α说明:先利用诱导公式转化为角α的三角函数,再进一步化简.4、求证:(1)sin(360°-α)=-sinα;(2)cos(360°-α)=cosα;(3)tan(360°-α)=-tanα.答案:(1)sin(360°-α)=sin(-α)=-sinα;(2)略;(3)略.说明:有的书也将这组恒等式列入诱导公式,但根据公式一可知,它和公式三等价,所以本教科书未将其列入诱导公式.B组1、计算:(1)sin420°·cos750°+sin(-330°)·cos(-660°);(2)tan675°+tan765°-tan(-330°)+tan(-690°);(3)252525sin cos tan() 634πππ++-.答案:(1)1;(2)0;(3)0.说明:先利用诱导公式转化为锐角三角函数,再求值.2、已知1sin()2πα+=-,计算:(1)sin(5π-α);(2)sin()2πα+; (3)3cos()2πα-; (4)tan()2πα-. 答案:(1)12; (2)3,,23,;2αα⎧⎪⎪⎨⎪-⎪⎩当为第一象限角当为第二象限角(3)12-; (4)3,,3,αα⎧⎪⎨-⎪⎩当为第一象限角当为第二象限角.说明:先用诱导公式将已知式和待求式都转化为角α的三角函数,然后再根据同角三角函数的基本关系得解. P46 习题1.4A 组1、画出下列函数的简图: (1)y=1-sinx ,x ∈[0,2π]; (2)y=3cosx +1,x ∈[0,2π]. 答案:(1)(2)说明:可以直接用“五点法”作出两个函数的图象;也可以先用“五点法”作出正弦、余弦函数的图象,再通过变换得到这两个函数的图象.2、求使下列函数取得最大值、最小值的自变量x 的集合,并分别写出最大值、最小值是什么.(1)11cos ,23y x x π=-∈R ; (2)3sin(2),4y x x π=+∈R ;(3)31cos(),226y x x π=--∈R ; (4)11sin(),223y x x π=+∈R .答案:(1)使y 取得最大值的集合是{x|x=6k +3,k ∈Z },最大值是32; 使y 取得最小值的集合是{x|x=6k ,k ∈Z },最大值是12; (2)使y 取得最大值的集合是{|,}8x x k k ππ=+∈Z ,最大值是3;使y 取得最小值的集合是3{|,}8x x k k ππ=-+∈Z ,最小值是-3; (3)使y 取得最大值的集合是{|2(21),}3x x k k ππ=++∈Z ,最大值是32; 使y 取得最小值的集合是{|4,}3x x k k ππ=+∈Z ,最小值是32-;(4)使y 取得最大值的集合是{|4,}3x x k k ππ=+∈Z ,最大值是12;使y 取得最小值的集合是5{|4,}3x x k k ππ=-+∈Z ,最小值是12-. 说明:利用正弦、余弦函数的最大值、最小值性质,研究所给函数的最大值、最小值性质.3、求下列函数的周期:(1)2sin 3y x =,x ∈R ; (2)1cos 42y x =,x ∈R . 答案:(1)3π;(2)2π说明:可直接由函数y=Asin (ωx +φ)和函数y=Acos (ωx +φ)的周期2T πω=得解.4、利用函数的单调性比较下列各组中两个三角函数值的大小: (1)sin103°15′与sin164°30′; (2)4744cos()cos()109ππ--与; (3)sin508°与sin144°;(4)cos760°与cos (-770°). 答案:(1)sin103°15′>sin164°130′; (2)4744cos()cos()109ππ->-; (3)sin508°<sin144°;(4)cos760°>cos (-770°).说明:解决这类问题的关键是利用诱导公式将它们转化到同一单调区间上研究.5、求下列函数的单调区间: (1)y=1+sinx ,x ∈R ; (2)y=-cosx ,x ∈R . 答案:(1)当[2,2]22x k k ππππ∈-++,k ∈Z 时,y=1+sinx 是增函数;当3[2,2]22x k k ππππ∈++,k ∈Z 时,y=1+sinx 是减函数. (2)当x ∈[(2k -1)π,2kπ],k ∈Z 时,y=-cosx 是减函数; 当x ∈[2kπ,(2k +1)π],k ∈Z 时,y=-cosx 是增函数.说明:利用正弦、余弦函数的单调性研究所给函数的单调性.6、求函数tan()26y x π=-++的定义域.答案:{|,}3x x k k ππ≠+∈Z .说明:可用换元法.7、求函数5tan(2),()3122k y x x k πππ=-≠+∈Z 的周期.答案:2π. 说明:可直接由函数y=Atan (ωx +φ)的周期T πω=得解.8、利用正切函数的单调性比较下列各组中两个函数值的大小: (1)13tan()tan()57ππ--与; (2)tan1519°与tan1493°; (3)93tan 6tan(5)1111ππ-与; (4)7tantan 86ππ与. 答案:(1)13tan()tan()57ππ->-;(2)tan1519°>tan1493°;(3)93tan 6tan(5)1111ππ>-;(4)7tantan 86ππ<. 说明:解决这类问题的关键是利用诱导公式将它们转化到同一单调区间上研究.9、根据正切函数的图象,写出使下列不等式成立的x 的集合: (1)1+tanx≥0;(2)tan 30x -≥. 答案:(1){|,}42x k x k k ππππ-+<+∈Z ≤;(2){|,}32x k x k k ππππ+<+∈Z ≤.说明:只需根据正切曲线写出结果,并不要求解三角方程或三角不等式.10、设函数f (x )(x ∈R )是以 2为最小正周期的周期函数,且x ∈[0,2]时f (x )=(x -1)2.求f (3),7()2f 的值.答案:由于f (x )以2为最小正周期,所以对任意x ∈R ,有f (x +2)=f (x ).于是:f (3)=f (1+2)=f (1)=(1-1)2=0;273331()(2)()(1)22224f f f =+==-=. 说明:利用周期函数的性质,将其他区间上的求值问题转化到区间[0,2]上的求值问题.11、容易知道,正弦函数y=sinx 是奇函数,正弦曲线关于原点对称,即原点是正弦曲线的对称中心.除原点外,正弦曲线还有其他对称中心吗?如果有,对称中心的坐标是什么?另外,正弦曲线是轴对称图形吗?如果是,对称轴的方程是什么?你能用已经学过的正弦函数性质解释上述现象吗? 对余弦函数和正切函数,讨论上述同样的问题.答案:由正弦函数的周期性可知,除原点外,正弦曲线还有其他对称中心,其对称中心坐标为(kπ,0),k ∈Z .正弦曲线是轴对称图形,其对称轴的方程是,2x k k ππ=+∈Z .由余弦函数和正切的周期性可知,余弦曲线的对称中心坐标为(,0)2k ππ+,k ∈Z ,对称轴的方程是x=kπ,k ∈Z ;正切曲线的对称中心坐标为(,0)2k π,k ∈Z ,正切曲线不是轴对称图形.说明:利用三角函数的图象和周期性研究其对称性.B 组1、根据正弦函数、余弦函数的图象,写出使下列不等式成立的x 的取值集合:(1)3sin ()2x x ∈R ≥; (2)22cos 0()x x +∈R ≥. 答案:(1)2{|22,}33x k x k k ππππ++∈Z ≤≤; (2)33{|22,}44x k x k k ππππ-++∈Z ≤≤. 说明:变形后直接根据正弦函数、余弦函数的图象写出结果,并不要求解三角方程或三角不等式.2、求函数3tan(2)4y x π=--的单调区间. 答案:单调递减区间5(,),2828k k k ππππ++∈Z . 说明:利用正切函数的单调区间求所给函数的单调区间.3、已知函数y=f (x )的图象如图所示,试回答下列问题:(1)求函数的周期;(2)画出函数y=f (x +1)的图象;(3)你能写出函数y=f (x )的解析式吗?答案:(1)2;(2)y=f (x +1)的图象如下;(3)y=|x -2k|,x ∈[2k -1,2k +1],k ∈Z .说明:可直接由函数y=f (x )的图象得到其周期.将函数y=f (x )的图象向左平行移动1个单位长度,就得到函数y=f (x +1)的图象.求函数y=f (x )的解析式难度较高,需要较强的抽象思维能力.可先求出定义域为一个周期的函数y=f (x ),x ∈[-1,1]的解析式为y=|x|,x ∈[-1,1],再根据函数y=f (x )的图象和周期性,得到函数y=f (x )的解析式为y=|x -2k|,x ∈[2k -1,2k +1],k ∈Z . P57 习题1.5A 组1、选择题:(1)为了得到函数1cos()3y x =+,x ∈R 的图象,只需把余弦曲线上所有的点( )A .向左平行移动3π个单位长度 B .向右平行移动3π个单位长度C .向左平行移动13个单位长度 D .向右平行移动13个单位长度(2)为了得到函数cos 5xy =,x ∈R 的图象,只需把余弦曲线上所有的点的( )、A .横坐标伸长到原来的5倍,纵坐标不变B .横坐标缩短到原来的15倍,纵坐标不变 C .纵坐标伸长到原来的5倍,横坐标不变 D .纵坐标缩短到原来的15倍,横坐标不变 (3)为了得到函数1cos 4y x =,x ∈R 的图象,只需把余弦曲线上所有的点的( ). A .横坐标伸长到原来的4倍,纵坐标不变B .横坐标缩短到原来的14倍,纵坐标不变 C .纵坐标伸长到原来的4倍,横坐标不变 D .纵坐标缩短到原来的14倍,横坐标不变 答案:(1)C ;(2)A ;(3)D .2、画出下列函数在长度为一个周期的闭区间上的简图(有条件的可用计算器或计算机作图检验):(1)14sin 2y x =,x ∈R ; (2)1cos32y x =,x ∈R ; (3)3sin(2)6y x π=+,x ∈R ; (4)112cos()24y x π=-,x ∈R .答案:(1)(2)(3)(4)说明:研究了参数A、ω、φ对函数图象的影响.3、不画图,直接写出下列函数的振幅、周期与初相,并说明这些函数的图象可由正弦曲线经过怎样的变化得到(注意定义域):(1)8sin()48xy π=-,x ∈[0,+∞);(2)1sin(3)37y x π=+,x ∈[0,+∞). 答案:(1)振幅是8,周期是8π,初相是8π-.先把正弦曲线向右平行移动8π个单位长度,得到函数1sin()8y x π=-,x ∈R 的图象;再把函数y 1的图象上所有点的横坐标伸长到原来的4倍(纵坐标不变),得到函数2sin()48x y π=-,x ∈R 的图象;再把函数y 2的图象上所有点的纵坐标伸长到原来的8倍(横坐标不变),得到函数38sin()48x y π=-,x ∈R 的图象;最后把函数y 3的图象在y 轴左侧的部分抹去,就得到函数8sin()48x y π=-,x ∈[0,+∞)的图象.(2)振幅是13,周期是23π,初相是7π.先把正弦曲线向左平行移动7π个单位长度,得到函数1sin()7y x π=+,x ∈R 的图象;再把函数y 1的图象上所有点的横坐标缩短到原来的13倍(纵坐标不变),得到函数2sin(3)7y x π=+,x ∈R 的图象;再把函数y 2的图象上所有点的纵坐标缩短到原来的13倍(横坐标不变),得到函数31sin(3)37y x π=+,x ∈R 的图象;最后把函数y 3的图象在y 轴左侧的部分抹去,就得到函数1sin(3)37y x π=+,x ∈[0,+∞)的图象.说明:了解简谐振动的物理量与函数解析式的关系,并认识函数y=Asin (ωx +φ)的图象与正弦曲线的关系.4、图 1.5-1的电流i (单位:A )随时间t (单位:s )变化的函数关系是5sin(100),[0,)3i t t ππ=+∈+∞.(1)求电流i 变化的周期、频率、振幅及其初相; (2)当t=0,1171,,,(:s)60015060060单位时,求电流i . 答案:(1)周期为150,频率为50,振幅为5,初相为3π.(2)t=0时,532i =;1600t =时,i=5;1150t =时,i=0;7600t =时,i=-5;160t =时,i=0.说明:了解简谐振动的物理量与函数解析式的关系,并求函数值.5、一根长为l cm 的线,一端固定,另一端悬挂一个小球.小球摆动时,离开平衡位置的位移s (单位:cm )与时间t (单位:s )的函数关系是3cos(),[0,)3g s t t l π=+∈+∞. (1)求小球摆动的周期;(2)已知g≈980cm/s 2,要使小球摆动的周期是1s ,线的长度l 应当是多少?(精确到0.1cm )答案:(1)2lgπ;(2)约24.8cm . 说明:了解简谐振的周期.B 组1、弹簧振子的振动是简谐运动.下表给出了振子在完成一次全振动的过程中的时间t 与位移s 之间的对应数据,根据这些数据求出这个振子的振动函数解析式. t 0t 02t 03t 0 4t 05t 06t 07t 08t 09t 0 10t 011t 012t 0s-20.0 -17.8 -10.10.110.3 17.7 20.0 17.7 10.30.1-10.1 -17.8 -20.0答案:根据已知数据作出散点图(如图).由散点图可知,振子的振动函数解析式为020sin()62x y t ππ=-,x ∈[0,+∞).说明:作出已知数据的散点图,然后选择一个函数模型来描述,并根据已知数据求出该函数模型.2、弹簧挂着的小球作上下运动,它在t 秒时相对于平衡位置的高度h 厘米由下列关系式确定:2sin()4h t π=+.以t 为横坐标,h 为纵坐标,作出这个函数在一个剧期的闭区间上的图象,并回答下列问题:(1)小球在开始振动时(即t=0)的位置在哪里?(2)小球的最高点和最低点与平衡位置的距离分别是多少? (3)经过多少时问小球往复运动一次? (4)每秒钟小球能往复振动多少次?答案:函数2sin()4h t π=+在[0,2π]上的图象为(1)小球在开始振动时的位置在(0,2); (2)最高点和最低点与平衡位置的距离都是2; (3)经过2π秒小球往复运动一次; (4)每秒钟小球能往复振动12π次. 说明:结合具体问题,了解解析式中各常数的实际意义.3、如图,点P 是半径为r cm 的砂轮边缘上的一个质点,它从初始位置P 0开始,按逆时针方向以角速度ω rad/s 做圆周运动.求点P 的纵坐标y 关于时间t 的函数关系,并求点P 的运动周期和频率.答案:点P的纵坐标关于时间t的函数关系式为y=rsin(ωt+φ),t∈[0,+∞);点P的运动周期和频率分别为2πω和2ωπ.说明:应用函数模型y=rsin(ωt+φ)解决实际问题.P65习题1.61、根据下列条件,求△ABC的内角A:(1)1sin2A=;(2)2cos2A=-;(3)tanA=1;(4)3 tan3A=-.答案:(1)30°或150°;(2)135°;(3)45°;(4)150°.说明:由角A是△ABC的内角,可知A∈(0°,180°).2、根据下列条件,求(0,2π)内的角x:(1)3sin2x=-;(2)sinx=-1;(3)cosx=0;(4)tanx=1.答案:(1)4533ππ或;(2)32π;(3)322ππ或;(4)544ππ或.说明:可让学生再变换角x的取值范围求解.3、天上有些恒星的亮度是会变化的.其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化、下图为一造父变星的亮度随时间的周期变化图、此变星的亮度变化的周期为多少天?最亮时是几等星?最暗时是几等星?答案:5.5天;约3.7等星;约4.4等星.说明:每个周期的图象不一定完全相同,表示视星等的坐标是由大到小.4、夏天是用电的高峰时期,特别是在晚上.为保证居民空调制冷用电,电力部门不得不对企事业拉闸限电,而到了0时以后,又出现电力过剩的情况.因此每天的用电也出现周期性的变化.为保证居民用电,电力部门提出了“消峰平谷”的想法,即提高晚上高峰时期的电价,同时降低后半夜低峰时期的电价,鼓励各单位在低峰时用电.请你调查你们地区每天的用电情况,制定一项“消峰平谷”的电价方案.答案:先收集每天的用电数据,然后作出用电量随时间变化的图象,根据图象制定“消峰平谷”的电价方案.说明:建立周期变化的模型解决实际问题.B组1、北京天安门广场的国旗每天是在日出时随太阳升起,在日落时降旗、请根据年鉴或其他的参考资料,统计过去一年不同时期的日出和日落时间.(1)在同一坐标系中,以日期为横轴,画出散点图,并用曲线去拟合这些数据,同时找到函数模型;(2)某同学准备在五一长假时去看升旗,他应当几点到达天安门广场?答案:略.说明:建立周期变化的函数模型,根据模型解决实际问题.2、一个城市所在的经度和纬度是如何影响日出和日落的时间的?收集其他有关的数据并提供理论证据支持你的结论.答案:略.说明:收集数据,建立周期变化的函数模型,根据模型提出个人意见.然后采取上网、查阅资料或走访专业人士的形式,获取这方面的信息,以此来说明自己的结论.P69复习参考题A 组1、写出与下列各角终边相同的角的集合S ,并且把S 中适合不等式-2π≤β≤4π的元素β写出来:(1)4π; (2)23π-;(3)125π; (4)0.答案:(1)79{|2,},,,4444k k ππππββπ=+∈-Z ;(2)22410{|2,},,,3333k k ββπππππ=-+∈-Z ;(3)128212{|2,},,,5555k k ββπππππ=+∈-Z ; (4){β|β=2kπ,k ∈Z },-2π,0,2π. 说明:用集合表示法和符号语言写出与指定角终边相同的角的集合,并在给定范围内找出与指定的角终边相同的角.2、在半径为15cm 的圆中,一扇形的弧含有54°,求这个扇形的周长与面积(π取3.14,计算结果保留两个有效数字).答案:周长约44cm ,面积约1.1×102cm 2.说明:可先将角度转化为弧度,再利用弧度制下的弧长和面积公式求解.3、确定下列三角函数值的符号: (1)sin4; (2)cos5; (3)tan8; (4)tan (-3). 答案:(1)负;(2)正;(3)负;(4)正.说明:将角的弧度数转化为含π的形式或度,再进行判断.4、已知1cos 4ϕ=,求sinφ,tanφ. 答案:当φ为第一象限角时,15sin ,tan 154ϕϕ==; 当φ为第四象限角时,15sin ,tan 154ϕϕ=-=-. 说明:先求sinφ的值,再求tanφ的值.5、已知sinx=2cosx ,求角x 的三个三角函数值. 答案:当x 为第一象限角时,tanx=2,525cos ,sin 55x x ==;当x 为第三象限角时,tanx=2,525cos ,sin 55x x =-=-. 说明:先求tanx 的值,再求另外两个函数的值.6、用cosα表示sin 4α-sin 2α+cos 2α.答案:cos 4α.说明:先将原式变形为sin 2α(sin 2α-1)+cos 2α,再用同角三角函数的基本关系变形.7、求证:(1)2(1-sinα)(1+cosα)=(1-sinα+cosα)2; (2)sin 2α+sin 2β-sin 2α·sin 2β+cos 2α·cos 2β=1. 答案:(1)左边=2-2sinα+2cosα-2sinαcosα=1+sin 2α+cos 2α-2sinα+2cosα-2sinαcosα =右边.(2)左边=sin 2α(1-sin 2β)+sin 2β+cos 2αcos 2β=cos 2β(sin 2α+cos 2α)+sin 2β =1=右边.说明:第(1)题可先将左右两边展开,再用同角三角函数的基本关系变形.8、已知tanα=3,计算: (1)4sin 2cos 5cos 3sin αααα-+;(2)sinαcosα; (3)(sinα+cosα)2. 答案:(1)57;(2)310;(3)85. 说明:第(2)题可由222sin tan 9cos ααα==,得21c o s10α=,所以23sin cos tan cos 10αααα==.或222s incs i n c10sin cos tan 131αααααααα====+++.9、先估计结果的符号,再进行计算. (1)252525sincos tan()634πππ++-; (2)sin2+cos3+tan4(可用计算器).答案:(1)0;(2)1.0771.说明:先根据各个角的位置比较它们的三角函数值的大小,再估计结果的符号.10、已知1sin()2πα+=-,计算:(1)cos(2π-α);(2)tan(α-7π).答案:(1)当α为第一象限角时,3 cos(2)2πα-=,当α为第二象限角时,3 cos(2)2πα-=-;(2)当α为第一象限角时,3 tan(7)3απ-=,当α为第二象限角时,3 tan(7)3απ-=-.说明:先用诱导公式转化为α的三角函数,再用同角三角函数的基本关系计算.11、先比较大小,再用计算器求值:(1)sin378°21′,tan1111°,cos642.5°;(2)sin(-879°),313t a n(),c o s()810ππ--;(3)sin3,cos(sin2).答案:(1)tan1111°=0.601,sin378°21′=0.315,cos642.5°=0.216;(2)sin(-879°)=-0.358,3313tan()0.414,cos()0.588 810ππ-=--=-;(3)sin3=0.141,cos(sin2)=0.614.说明:本题的要求是先估计各三角函数值的大小,再求值验证.12、设π<x<2π,填表:x 76π74πsinx -1cosx22-32tanx 3答案:x 76π54π43π32π74π116πsinx12-22-32--122-12-cosx32-22-12-2232tanx3313不存在-133-说明:熟悉各特殊角的三角函数值.13、下列各式能否成立,说明理由: (1)cos 2x=1.5;(2)3sin 4x π=-.答案:(1)因为cos 1.5x =,或cos 1.5x =-,而 1.51, 1.51>-<-,所以原式不能成立;(2)因为3sin 4x π=-,而3||14π-<,所以原式有可能成立.说明:利用正弦和余弦函数的最大值和最小值性质进行判断.14、求下列函数的最大值、最小值,并且求使函数取得最大、最小值的x 的集合: (1)sin 2xy π=+,x ∈R ;(2)y=3-2cosx ,x ∈R . 答案:(1)最大值为12π+,此时x 的集合为{|2,}2x x k k ππ=+∈Z ;最小值为12π-,此时x 的集合为{|2,}2x x k k ππ=-+∈Z ;(2)最大值为5,此时x 的集合为{x|x=(2k +1)π,k ∈Z }; 最小值为1,此时x 的集合为{x|x=2kπ,k ∈Z }.说明:利用正弦、余弦函数的最大值和最小值性质,研究所给函数的最大值和最小值性质.15、已知0≤x≤2π,求适合下列条件的角x 的集合: (1)y=sinx 和y=cosx 都是增函数; (2)y=sinx 和y=cosx 都是减函数;(3)y=sinx 是增函数,而y=cosx 是减函数; (4)y=sinx 是减函数,而y=cosx 是增函数.答案:(1)3{|2}2x x ππ≤≤; (2){|}2x x ππ≤≤;(3){|0}2x x π≤≤;(4)3{|}2x x ππ≤≤. 说明:利用函数图象分析.16、画出下列函数在长度为一个周期的闭区间上的简图: (1)1sin(3),;23y x x π=-∈R (2)2sin(),;4y x x π=-+∈R (3)1sin(2),;5y x x π=--∈R(4)3sin(),.63xy x π=-∈R 答案:(1)(2)(3)(4)说明:可要求学生在作出图象后,用计算机或计算器验证.17、(1)用描点法画出函数y=sinx ,[0,]2x π∈的图象.(2)如何根据第(1)小题并运用正弦函数的性质,得出函数y=sinx ,x ∈[0,2π]的图象?(3)如何根据第(2)小题并通过平行移动坐标轴,得出函数y=sin (x +φ)+k ,x ∈[0,2π]的图象?(其中φ,k 都是常数)答案:(1)x 0 18π9π 6π 29π 518π 3π 718π 49π 2π sinx0.170.340.500.640.770.870.940.981(2)由sin (π-x )=sinx ,可知函数y=sinx ,x ∈[0,π]的图象关于直线2x π=对称,据此可得函数y=sinx ,[,]2x ππ∈的图象;又由sin (2π-x )=-sinx ,可知函数y=sinx ,x ∈[0,2π]的图象关于点(π,0)对称,据此可得出函数y=sinx ,x ∈[π,2π]的图象.(3)先把y 轴向右(当φ>0时)或向左(当φ<0时)平行移动|φ|个单位长度,再把x 轴向下(当k >0时)或向上(当k <0时)平行移动|k|个单位长度,最后将图象向左或向右平行移动2π个单位长度,并擦去[0,2π]之外的部分,便得出函数y=sin (x +φ)+k ,x ∈[0,2π]的图象.说明:学会用不同的方法作函数图象.18、不通过画图,写出下列函数的振幅、周期、初相,并说明如何由正弦曲线得出它们的图象:(1)sin(5),;6y x x π=+∈R(2)12sin,.6y x x =∈R 答案:(1)振幅是1,周期是25π,初相是6π. 把正弦曲线向左平行移动6π个单位长度,可以得函数sin()6y x π=+,x ∈R 的图象;再把所得图象上所有点的横坐标缩短到原来的15倍(纵坐标不变),就可得出函数sin(5)6y x π=+,x ∈R 的图象.(2)振幅是2,周期是2π,初相是0.把正弦曲线上所有点的横坐标伸长到原来的6倍(纵坐标不变),得到函数1sin6y x =,x ∈R 的图象;再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),就可得到函数12sin()6y x =,x ∈R 的图象.说明:会根据解析式求各物理量,并理解如何由正弦曲线通过变换得到正弦函数的图象.。
必修4参考答案数学

必修4参考答案数学必修4参考答案数学数学是一门抽象而又实用的学科,它在我们的日常生活中起着重要的作用。
而必修4是高中数学课程中的一门重要课程,它涵盖了许多基础的数学知识和技巧。
下面将为大家提供一些必修4的参考答案,希望对大家的学习有所帮助。
第一章:集合与函数1. 集合的概念与表示方法- 集合是由一些确定的对象所组成的整体。
- 用大写字母表示集合,用小写字母表示集合中的元素。
- 集合可以通过列举法、描述法和图形法表示。
2. 集合的运算- 并集:将两个或多个集合中的所有元素放在一起,形成一个新的集合。
- 交集:两个或多个集合中共有的元素构成的集合。
- 差集:从一个集合中减去另一个集合中的元素所得到的集合。
- 补集:对于给定的全集,除去一个集合中的元素所得到的集合。
3. 函数的概念与表示方法- 函数是一种特殊的关系,它将一个集合的每个元素都对应到另一个集合中的唯一元素。
- 函数可以用映射图、映射表和函数式表示。
第二章:三角函数1. 弧度制与角度制的转换- 弧度制:弧长等于半径的角度制。
- 角度制:以度为单位来度量角的大小。
2. 三角函数的定义与性质- 正弦函数:在直角三角形中,对于一个锐角,其对边与斜边的比值。
- 余弦函数:在直角三角形中,对于一个锐角,其邻边与斜边的比值。
- 正切函数:在直角三角形中,对于一个锐角,其对边与邻边的比值。
3. 三角函数的图像与性质- 正弦函数的图像是一个周期性的波形,其最大值为1,最小值为-1。
- 余弦函数的图像也是一个周期性的波形,其最大值为1,最小值为-1。
- 正切函数的图像是一个周期性的波形,其在某些点上无定义。
第三章:解析几何1. 平面坐标系与直线方程- 平面直角坐标系:由两条相互垂直的直线所确定的坐标系。
- 直线的方程:直线可以用一般式、点斜式和两点式表示。
2. 圆的方程与性质- 圆的方程:圆可以用标准方程和一般方程表示。
- 圆的性质:圆的半径、直径、弦、弧等都有一些特殊的性质。
高中数学必修四答案

高中数学必修四答案第一章三角函数1.1 弧度制1.角度制和弧度制的转换关系:–弧度制 = 角度制× π / 180–角度制 = 弧度制× 180 / π2.弧度制下的等角弧长公式:–弧长 = 弧度制 × 半径1.2 三角函数的定义1.正弦函数:sin θ = 对边 / 斜边2.余弦函数:cos θ = 邻边 / 斜边3.正切函数:tan θ = 对边 / 邻边1.3 三角函数的性质1.基本性质:–正弦函数的值域为 [-1, 1]–余弦函数的值域为 [-1, 1]–正切函数的定义域为 R,其余的三角函数的定义域为 (-∞, ∞)2.周期性质:–正弦函数、余弦函数的周期为2π–正切函数的周期为π1.4 三角函数的图像1.正弦函数的图像:从 y = -sin x 推导其他形式的正弦函数图像2.余弦函数的图像:从 y = cos x 推导其他形式的余弦函数图像3.正切函数的图像:从 y = tan x 推导其他形式的正切函数图像第二章几何向量2.1 向量的概念和表示1.向量的定义:有大小和方向的量,通常用箭头表示2.向量的表示:–平行四边形法则:以原点为起点,以向量的终点为终点的有向线段表示向量–分量表示法:将向量投影到坐标轴上,用投影长度表示向量2.2 向量的线性运算1.向量的加法:–满足交换律:A + B = B + A–满足结合律:(A + B) + C = A + (B + C)2.向量的数乘:–定义:数乘一个向量等于扩大或缩小该向量的长度3.向量的减法:–定义:向量 A - 向量 B = 向量 A + (-1) × 向量 B 2.3 坐标系中的向量1.二维向量的表示:(x, y)2.三维向量的表示:(x, y, z)2.4 向量的数量积1.向量的数量积的定义:A · B = |A| × |B| × cos θ2.向量的数量积的性质:–结合律:(kA) · B = k(A · B) = A · (kB)–分配律:(A + B) · C = A · C + B · C– A · B = 0 的条件:向量 A 和向量 B 正交–向量 A 和向量 B 平行的条件:cos θ = 1 或 cos θ = -12.5 向量的向量积1.向量的向量积的定义:A × B = |A| × |B| × sin θ × n2.向量的向量积的性质:–反交换律:A × B = - (B × A)–结合律:(kA) × B = k(A × B) = A × (kB)–分配律:A × (B + C) = A × B + A × C第三章平面解析几何3.1 坐标系1.平面直角坐标系2.极坐标系3.2 平面直角坐标系下的方程1.直线的方程:–一般式:Ax + By + C = 0–点斜式:y - y1 = k(x - x1)–斜截式:y = kx + b–截距式:x / a + y / b = 12.圆的方程:–标准方程:(x - a)^2 + (y - b)^2 = r^2–一般方程:x^2 + y^2 + Dx + Ey + F = 0 3.3 极坐标系下的方程1.直线的极坐标方程:–ρ = cos θ / cos α2.圆的极坐标方程:–ρ = r3.4 平面解析几何的应用1.求点到直线的距离–利用距离公式:d = |Ax0 + By0 + C| / √(A^2 + B^2)2.求点到圆的距离–利用距离公式:d = |Ax0 + By0 + C| / √(A^2 + B^2) - r以上就是《高中数学必修四答案》的内容,希望对你有帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三理科数学必修4练习(辅导)答案
一、DCDBB ABDAC 二、11、3-;12、21
13
-
;13、12;14、2tan α-;15、③④;16、22sin(2)3y x π=+
三、17、解:由题意得13A b A b +=⎧⎨-+=-⎩,解得2
1A b =⎧⎨=-⎩
,∴2sin()1y x ωϕ=+-
由2sin()111272sin()1312πωϕπωϕ⎧⨯+-=⎪⎪⎨⎪⨯+-=-⎪⎩得sin()112
7sin()1
12
πωϕπωϕ⎧⨯+=⎪⎪⎨⎪⨯+=-⎪⎩,
又∵0,02ωϕπ>≤≤
∴122
73122
ππωϕππ
ωϕ⎧⨯+=⎪⎪⎨⎪⨯+=⎪⎩,∴2,3πωϕ==,∴函数的解析式是2sin(2)3y x π=+
18、解:
(1)2
2
()cos cos f x a b x x x m →→
=⋅=+-
2212cos 21sin(2)126
x x m x m π
=
++-=++- (2)∵6
3
x π
π
-
≤≤
,∴7266
6x π
π
π-
≤+
≤
,∴1sin(2)126
x π
-≤+≤ ∴()f x 的最小值是2
112
m -+-
又∵()f x 的最小值是4-,∴21142m -+-=-,∴2
92
m =
当sin(2)16
x π
+
=,
即26
2
x π
π
+=
,即6
x π=
时,()f x 取得最大值是95
1122
+-
=-。
19、解:(1)由sin()02
x π
+
≠得cos 0x ≠,∴,2
x k k Z π
π≠+
∈,
∴()f x 的定义域是{|,}2
x x k k Z π
π≠+
∈
(2
)1)
1cos 2sin 24()cos sin()2
f π
ααααπαα+-++=
=+ 22cos 2sin cos 2sin 2cos cos ααα
ααα
+=
=+
由3cos 5α=
,α为第四象限角得,4sin 5
α=- ∴432
()2sin 2cos 2()2555
f ααα=+=⨯-+⨯=-
20、解:(1)2
2
2
()(sin cos )2cos 12sin cos 2cos f x x x x x x x =++=++
sin 2cos 22)24
x x x π
=++=++
当sin(2)14
x π
+
=,即2,4
2
x k k Z π
π
π+
=+
∈,即,8
x k k Z π
π=+
∈时,
()f x 2,此时自变量x 的集合是{|,}8
x x k k Z π
π=+
∈
(2)由(1)知函数()f x 的最小正周期是π; 由222,2
4
2
k x k k Z π
π
π
ππ-
≤+
≤+
∈得5,8
8
k x k k Z π
π
ππ+
≤≤+
∈ ∴函数()f x 的单调递减区间是5[,]()8
8
k k k Z π
π
ππ+
+
∈ (3)把函数sin y x =图象上所有的点向左平移
4
π
个单位得到函数sin()4y x π=+
的图象,再把函数sin()4
y x π
=+的图象上的横坐标伸长到原来的2倍(纵坐
标不变)得到函数sin(2)4y x π
=+
的图象,
再把函数sin(2)4
y x π
=+的图象上
倍(横坐标不变)得到函数)4
y x π
=+的图
象,最后把函数)4
y x π
=+的图象上所有的点向上平移2个单位得到
函数)24
y x π
=
++的图象,。
