同济大学材料力学 7 梁变形共28页文档
合集下载
新编文档-材料力学第7章弯曲变形-精品文档

材料力学
出版社 理工分社
第7章 弯曲变形
页 退出
材料力学
出版社 理工分社
7.1概述 梁在载荷作用下,产生应力的同时也会发生变形。在许多工程问题中,梁不 仅要满足强度条件,同时还必须满足刚度条件,即梁的变形必须控制在工程 规定的许可范围之内,否则会影响正常工作。 例如,图7.1所示的齿轮轴,若弯曲变形过大,将影响齿轮的啮合和轴承的 配合,造成磨损不匀,产生噪声,降低寿命,还会影响加工精度。再比如, 桥式起重机大梁在起吊重物时,若变形过大,将使梁上小车行走困难,出现 爬坡现象,还会引起较严重的振动;管道变形过大,将影响管道内物料的正 常输送,出现积液、沉淀和法兰连接不密等现象;楼板梁变形过大,将使下 面的抹灰层开裂、脱落。因此,若变形超过允许范围,即使仍然是弹性的, 也被认为是一种失效。
挠度与转角是度量弯曲变形的两个基本量,二者都是梁截面位置x的函数。 在如图7.4所示的坐标系中,向上的挠度和逆时针的转角为正。
页 退出
材料力学
出版社 理工分社
纯弯曲情况下,弯矩与曲率间的关系为公式(7.1),即
横力弯曲时,梁截面上既有弯矩也有剪力。虽然式(a)只揭示了弯矩对弯曲 变形的影响,但对于跨度远大于截面高度的梁,剪力对弯曲变形的影响可以 忽略,所以式(a)也可作为横力弯曲变形的基本方程,此时1/ρ 为x的函数, 即
(6)求指定截面挠度和转角 自由端处,x=l,代入以上两式即得自由端B处的转角与挠度,分别为
页 退出
材料力学
出版社 理工分社
例7.2简支梁在左端支座处承受集中力偶作用,如图7.9所示。求梁的转角方
程和挠度方程,并确定
和
图7.9
页 退出
材料力学
解(1)计算简支梁的支反力,写出弯矩方程为 (2)建立挠曲线近似微分方程并积分 利用式(7.5)建立挠曲线近似微分方程,积分两次后得
出版社 理工分社
第7章 弯曲变形
页 退出
材料力学
出版社 理工分社
7.1概述 梁在载荷作用下,产生应力的同时也会发生变形。在许多工程问题中,梁不 仅要满足强度条件,同时还必须满足刚度条件,即梁的变形必须控制在工程 规定的许可范围之内,否则会影响正常工作。 例如,图7.1所示的齿轮轴,若弯曲变形过大,将影响齿轮的啮合和轴承的 配合,造成磨损不匀,产生噪声,降低寿命,还会影响加工精度。再比如, 桥式起重机大梁在起吊重物时,若变形过大,将使梁上小车行走困难,出现 爬坡现象,还会引起较严重的振动;管道变形过大,将影响管道内物料的正 常输送,出现积液、沉淀和法兰连接不密等现象;楼板梁变形过大,将使下 面的抹灰层开裂、脱落。因此,若变形超过允许范围,即使仍然是弹性的, 也被认为是一种失效。
挠度与转角是度量弯曲变形的两个基本量,二者都是梁截面位置x的函数。 在如图7.4所示的坐标系中,向上的挠度和逆时针的转角为正。
页 退出
材料力学
出版社 理工分社
纯弯曲情况下,弯矩与曲率间的关系为公式(7.1),即
横力弯曲时,梁截面上既有弯矩也有剪力。虽然式(a)只揭示了弯矩对弯曲 变形的影响,但对于跨度远大于截面高度的梁,剪力对弯曲变形的影响可以 忽略,所以式(a)也可作为横力弯曲变形的基本方程,此时1/ρ 为x的函数, 即
(6)求指定截面挠度和转角 自由端处,x=l,代入以上两式即得自由端B处的转角与挠度,分别为
页 退出
材料力学
出版社 理工分社
例7.2简支梁在左端支座处承受集中力偶作用,如图7.9所示。求梁的转角方
程和挠度方程,并确定
和
图7.9
页 退出
材料力学
解(1)计算简支梁的支反力,写出弯矩方程为 (2)建立挠曲线近似微分方程并积分 利用式(7.5)建立挠曲线近似微分方程,积分两次后得
材料力学 第7章 弯曲变形

M
Fx 挠曲轴近似微分方程: w ' ' EI 3 2 Fx Fx w Cx D w' ( x) C 6 EI 2EI
梁的弯矩方程: M ( x ) Fx
2、确定积分常数
FAy
A x
F L
B
X=0, w=0 X=L, w=0
M
Me L C=- ,D=0 6 EI
3、挠度方程、转角方程及B截面的转角
FAy
x
F L
B
M
3、挠度方程、转角方程及B截面的转角
Fx w' (x) 2EI 3 Fx w 6 EI
2
将 x=L 代入转角方程:
FL2 B 2 EI
例2:简支梁AB,弯曲刚 度 EI为常数,受力偶 M=FL作用,求w(x),
FAy
A x
F L
B
θ(x);
解:1、 建立挠曲轴微分方程并积分 A端约束反力 FAy=F
FA A a l
x
F D b
FB
B x
Fb 解:坐标系如图,求出反力。 FA l 分AD、DB两段分析:
y
Fa FB l
b AD段: 0 x a M x F x l b M x F x 则: EIw1 l
积分可得:
b M x F x EIw1 l
= 0
自由端:无位移边界条件。 位移连续与光滑条件 挠曲轴在B点连续且光滑 连续:wB左= wB右 光滑:左 = 右
F A B D
写出梁的挠曲轴方程的边界条件和连续条件。 例:
F A B C E D
思考: 1、 该梁可分几段积分? 2、 各边界和内部分界点有多少位移边界与连续条件? 分4段。 位移边界条件:A端:2个; C端:1个;D端:无。 位移连续条件:E:2个;B:1个;C:2个
工程力学(材料力学)8 弯曲变形与静不定梁

B
ql4 RBl3 0
8EI 3EI
q 约束反力为
B
RB
3 8
ql
RB
用变形比较法求解静不定梁的一般步骤:
(1)选择基本静定系,确定多余约束及反力。 (2)比较基本静定系与静不定梁在多余处的变形、确定 变形协调条件。 (3)计算各自的变形,利用叠加法列出补充方程。 (4)由平衡方程和补充方程求出多余反力,其后内力、 强度、刚度的计算与静定梁完全相同。
教学重点
• 梁弯曲变形的基本概念; • 挠曲线的近似微分方程; • 积分法和叠加法计算梁的变形; • 梁的刚度条件。
教学难点
• 挠曲线近似微分方程的推导过程; • 积分法和叠加法计算梁的变形; • 变形比较法求解静不定梁。
第一节 弯曲变形的基本概念
齿轮传动轴的弯曲变形
轧钢机(或压延机)的弯曲变形
例13-4 用叠加法求图示梁的 yC、A、B ,EI=常量。
M
P
解 运用叠加法
A
C
l/2
l/2
A
=
q
5ql4 Pl3 ml2
B
yC
384EI
48EI
16EI
A
ql3 24EI
Pl 2
16EI
ml 3EI
B
B
ql3 24EI
Pl2 16EI
ml 3EI
M
+
q
A
+
BA
B
二、梁的刚度条件
y max y,
A
max
A ql3
B
24EI
RA
q
A
θB
l
B θB RB
在梁跨中点 l /2 处有 最大挠度值
梁的变形
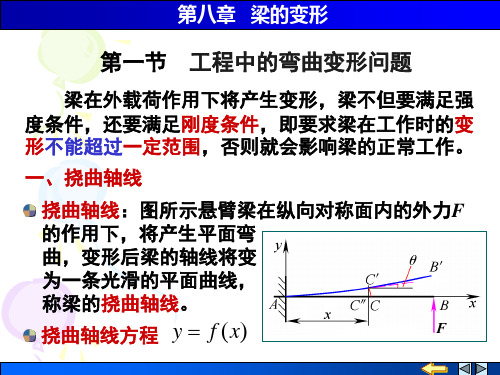
5ql 故有 yC = − (↓) 384 EI
4
ql θA = − (顺时针转动) 24
第八章 梁的变形
1 1 1 3 2 θ= ( qlx − qx ) + C EI 4 6 1 1 1 4 3 y= ( qlx − qx ) + Cx + D EI 12 24 边界条件: 边界条件: x = 0 时,y0 = 0 ; x = l 时,yl = 0 3 3 1 1 2 1 3 ql ql θ = ( qlx − qx − ) C=− EI 4 6 24 24EI 3 1 1 1 4 ql 3 D=0 y = ( qlx − qx − x) EI 12 24 24
第八章 梁的变形第二节 梁变形的基本方程来自一、挠曲轴线近似微分方程
M ( x) 1 = 梁任一截面的曲率 ρ ( x) EI y′′ 1 =± 曲线 y = f (x) 的曲率 ρ ( x) ′2 )3 / 2 (1 + y 二阶小量 y ′′ M ( x) =± 2 3/ 2 EI (1 + y ′ )
dy θ ≈ tan θ = y′ = dx
第八章 梁的变形
dy θ ≈ tan θ = y′ = dx
由此可知, 由此可知,只要知道梁的挠曲轴线方程 y = f (x) , 就可求出挠度和转角。 就可求出挠度和转角。 挠度和转角的正负号的 挠度和转角的正负号的规定 挠度: 轴正方向同向为 挠度:与y轴正方向同向为正,反之为负; 轴正方向同向为正 反之为 转角: 逆时针方向转动为正 反之为 转角:以逆时针方向转动为正,反之为负。 方向转动为
挠曲轴线 近似微分方程
M ( x) y′′ = ± EI
第八章 梁的变形 挠曲轴线 近似微分方程
4
ql θA = − (顺时针转动) 24
第八章 梁的变形
1 1 1 3 2 θ= ( qlx − qx ) + C EI 4 6 1 1 1 4 3 y= ( qlx − qx ) + Cx + D EI 12 24 边界条件: 边界条件: x = 0 时,y0 = 0 ; x = l 时,yl = 0 3 3 1 1 2 1 3 ql ql θ = ( qlx − qx − ) C=− EI 4 6 24 24EI 3 1 1 1 4 ql 3 D=0 y = ( qlx − qx − x) EI 12 24 24
第八章 梁的变形第二节 梁变形的基本方程来自一、挠曲轴线近似微分方程
M ( x) 1 = 梁任一截面的曲率 ρ ( x) EI y′′ 1 =± 曲线 y = f (x) 的曲率 ρ ( x) ′2 )3 / 2 (1 + y 二阶小量 y ′′ M ( x) =± 2 3/ 2 EI (1 + y ′ )
dy θ ≈ tan θ = y′ = dx
第八章 梁的变形
dy θ ≈ tan θ = y′ = dx
由此可知, 由此可知,只要知道梁的挠曲轴线方程 y = f (x) , 就可求出挠度和转角。 就可求出挠度和转角。 挠度和转角的正负号的 挠度和转角的正负号的规定 挠度: 轴正方向同向为 挠度:与y轴正方向同向为正,反之为负; 轴正方向同向为正 反之为 转角: 逆时针方向转动为正 反之为 转角:以逆时针方向转动为正,反之为负。 方向转动为
挠曲轴线 近似微分方程
M ( x) y′′ = ± EI
第八章 梁的变形 挠曲轴线 近似微分方程
同济大学材料力学第七章 弯曲应力PPT课件

截面上的最大拉应力和最大压应力。
y
F
150
A
L 2
B
L 2
Mmax
FL 4
16kNm
ym a x205 0 09.4 615.63mm
ym ax96.4mm
50
96.4
z
200
C
50
max
Mym ax IZ
24.09MPa
max
Mym ax IZ
15.12MPa
15
例题
长为2.5m的工字钢外伸梁,如图示,其外伸部分为0.5m,梁 上承受均布荷载,q=30kN/m,试选择工字钢型号。已知工字钢抗 弯强度[σ]=215MPa。
q30kNm
A
B
WZ
M max
61.2cm3
0.5m
FA46.9kN
31.9
2m FB28.1kN
查表 N0 12.6工字钢
WZ=77.5cm3
15
kN
28.1
13.16
kNm
16
3.75
例题
铸铁梁受荷载情况如图示。已知截面对形心轴
的惯性矩Iz=403×10-7m4,铸铁抗拉强度[σ+] =50MPa,抗压强度[σ-]=125MPa。试按正应力强
材料力学
讲授:顾志荣
1
标题添加
点击此处输入相 关文本内容
标题添加
点击此处输入相 关文本内容
总体概述
点击此处输入 相关文本内容
点击此处输入 相关文本内容
2
材料力学
第七章 弯曲应力
同济大学航空航天与力学学院 顾志荣
3
第七章 弯曲应力
一 基本概念与假设 二 梁的正应力强度计算 三 梁的剪应力强度计算 四 梁的合理设计
材料力学 积分法求梁的变形

一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
材料力学07(第七章 弯曲变形)

A a EI F=qa D a B a
3 3 3
B B×a Cq w
Cq
C
例:利用叠加原理求图示弯曲刚度为EI的中间铰梁铰 接点B处的挠度和B点右截面的转角以及D截面的挠度, 其中:F=2qa。
q F A a/2 a D EI B EI a C
解:可在铰接点处将梁分成图 a 和 b 所示两部分,并 可求得铰接点处的一对作用力与反作用力为:
qa4 qa4 qa4 6 EI 8EI 24EI
3
(向下)
2 3 qa 2a qa B B1 B 2
16EI
qa (顺时针) 3EI 12EI
(2)对图b,C截面的挠度和转角分别为:
qa4 wCq 8 EI
Cq
qa3 6 EI
F qa FB FB 2
A
F wB /2 wDF
直线
(a)
wB F/ 2 q F/ 2 wB B C
(b)
图a和b中分别给出了两部分的变形情况。 并且图b又可分解为图c所示两种载荷的组合。
q F/ 2
B
+
(c)
B
C
(1)对图b,可得其B截面的挠度和转角为:
qa wBFB 3EI 3 qa BFB 2 EI
原外伸梁C端的挠度和转角也可按叠加原理求得,即: 所以:
wC wCq B a
C B Cq
qa4 1 qa3 5qa4 wC a (向下) 8EI 12 EI 24EI qa qa qa C (顺时针) 6 EI 12EI 4 EI
C1 2l B1
wC1
wB1
Fl 3 wC1 3EI
3 3 3
B B×a Cq w
Cq
C
例:利用叠加原理求图示弯曲刚度为EI的中间铰梁铰 接点B处的挠度和B点右截面的转角以及D截面的挠度, 其中:F=2qa。
q F A a/2 a D EI B EI a C
解:可在铰接点处将梁分成图 a 和 b 所示两部分,并 可求得铰接点处的一对作用力与反作用力为:
qa4 qa4 qa4 6 EI 8EI 24EI
3
(向下)
2 3 qa 2a qa B B1 B 2
16EI
qa (顺时针) 3EI 12EI
(2)对图b,C截面的挠度和转角分别为:
qa4 wCq 8 EI
Cq
qa3 6 EI
F qa FB FB 2
A
F wB /2 wDF
直线
(a)
wB F/ 2 q F/ 2 wB B C
(b)
图a和b中分别给出了两部分的变形情况。 并且图b又可分解为图c所示两种载荷的组合。
q F/ 2
B
+
(c)
B
C
(1)对图b,可得其B截面的挠度和转角为:
qa wBFB 3EI 3 qa BFB 2 EI
原外伸梁C端的挠度和转角也可按叠加原理求得,即: 所以:
wC wCq B a
C B Cq
qa4 1 qa3 5qa4 wC a (向下) 8EI 12 EI 24EI qa qa qa C (顺时针) 6 EI 12EI 4 EI
C1 2l B1
wC1
wB1
Fl 3 wC1 3EI
材料力学 梁的变形

EIy ( x )
( M ( x)dx)dx C x C
1
2
3、根据弯曲梁变形的边界条件和连续条件确定积分常数。
PF A
C
B
D
P
边界条件: y A 0 连续条件:y C 左 =
第七章 弯曲变形 y
C右
yB 0
yD 0 D 0
C左 C右
(1)固定支座处:挠度等于零、转角等于零。
第七章 弯曲变形
4
3
A
练习题
第七章 弯曲变形
§7 —5 梁的刚度校核
一、梁的刚度条件
ymax y ymax ymax L L
max
其中[]称为许用转角;[δ /L]称为许用挠跨比。
二、刚度计算 、校核刚度: 、设计截面尺寸; 、确定外载荷。
一、前提条件:弹性、小变形。
二、叠加原理:各荷载同时作用下,梁任一截面的挠度或转角,等于
各荷载分别单独作用下同一梁同一截面挠度或转角的代数和。
B ( F1 , F2 , , Fn ) B1 ( F1 ) B 2 ( F2 ) Bn ( Fn )
第七章 弯曲变形
1 1 2 C1 FL ; C2 FL3 2 6
d)
确定挠曲线、转角方程
F 2 y x 2 Lx 2 EI
e) 自由端的挠度及转角
y
FL3 y ( L) 3EI
第七章 弯曲变形
FL2 ( L) 2 EI
x
F y ( x) 3Lx 2 x 3 6 EI
y Ba qa4 ; 8 EI
材料力学教程7弯曲变形

积分一次:
EIZ x EIZ f x M x dx C1
再次积分:
EIZ yx M x dx dx C1x C2
积分常数:需要利用边界条件和连续光滑条件来确定。
边界条件和连续光滑条件:梁上某些横截面处 位移为已知的条件。
第三节 用积分法求弯曲变形
例题1:求该悬臂梁的最大挠度和转角
y
d 2wy 0,M 0
dx 2
d 2 wy M dx 2 EI
d 2wy 0,M 0
dx 2
y
d 2 wy M dx 2 EI
d2y d2x
f (x)
M (x) EIZ
挠曲线近似微分方程
M x:梁的弯曲方程
d 2 y f (x) M (x) 挠曲线近似微分方程
d2x
EIZ
* 荷载叠加:将作用在梁上的荷载分解成单个
A 0 0
D1
D2
0 Pl
2
C1 C2 16
1
1 EIZ
( Pl2 16
Px2 4
)
2
1 EIZ
[
P 2
(x
l )2 2
1 4
Px2
Pl 2 16
]
1 Pl2x Px3
y1 EIZ ( 16
) 12
y2
1 EIZ
[
P 6
(x
l )3 2
1 12
Px3
Pl 2 x ] 16
x 0,x l,max
、ymax
Pl3 3EIZ
例题2:求该简支梁的最大挠度和转角
A
x
Amax
q
解:
建立坐标、 写弯矩方程
B
L
ym a x
材料力学第7章

积分一次: Fb 2 EIw1 x C1 2l 积分二次: Fb 3 EIw1 x C1 x D1 6l
11
CB段(a x l): 弯矩方程:
Fb M 2 x x F x a l
挠曲线近似微分方程:
Fb EIw2 x F x a l Fb 2 F 2 x x a C2 积分一次: EIw2 2l 2
ቤተ መጻሕፍቲ ባይዱ 1 x 0
Fab l b , B 2 6lEI
Fab l a B = 6lEI
Fl 3 Fl 3 Fl 3 2 EI 6 EI 3EI
7
wmax w x l
例题7.2:图示弯曲刚度为EI的简支梁,受集度为q的均布 荷载作用,试求梁的挠曲线方程和转角方程,并确定其最 大挠度和最大转角。 解:由平衡方程得支座反力 ql FA FB 2 建立坐标系,得梁的弯矩方程为 1 1 2 M x qlx qx 2 2 梁挠曲线近似微分方程
1 3 C ql , D 0 24
9
梁的转角方程
q w (4 x3 6lx 2 l 3 ) 24 EI
梁的挠曲线方程
(5)
qx w ( x3 2lx 2 l 3 ) 24 EI
最大转角
(6)
max
ql 3 A B 24 EI
2
最大挠度
M ( x) F l x
1
挠曲线近似微分方程
EIw M x F l x 2 两次积分,得 1 2 EIw Flx Fx C 2 1 1 3 2 EIw Flx Fx Cx D 2 6
材料力学第七章 梁的变形

EIy1=-Fx13/9+ 5Fa2x1/9 EIy2=-Fx23/9+F(x2-a )3/6+ 5Fa2x2/9
(0≤x1 ≤a)
( a ≤x2 ≤3a )
7. 求ymax , θmax
x 0,
max
A
5Fa2 9EI
()
x 1.367a,
ymax
0.4838 Fa3 EI
21
F
A
C
在如图所示的座标系下,顺时针转为正,反之为负。
转角方程 θ = θ(x)
平行于轴线方向的线位移忽略
7
挠度与转角的关系:
θ θ’
y
x y
小变形
θ =θ ′
tgθ ′ ≈ θ ′ = y′
y dy
dx
x
8
§7-2 直梁挠曲线近似微分方程
一、挠曲线近似微分方程
纯弯曲 k 1 M
EIz
(x)
F C yCF
42
例题4
怎样用叠加法确定C 和 yC ?
q
A
B
C
yC
l
l
C
2
2
43
A
B
l 2
q
C
yC
l
C
2
A
l 2
A
l 2
q
B
l 2
q
B
l 2
A
q
l
B
l
2
2
44
简单静不定梁(超静定梁)
一、静定梁
F Fl
A
B
C
l
l
2
2
qa
A
B
C
a
a
45
材料力学第7章 梁的变形

23
图7.15
图7.16
24
21
图7.14
22
第六节 用力法解简单超静定梁 前面几节分析的梁,如简支梁、悬臂梁、外伸 梁等,都是静定梁。在工程实际中,有时为了提高 强度或控制位移,常常采取增加约束的方式,使静 定梁变成了超静定梁或静不定梁(statically indeter minate beam),如图7.15所示。超静定梁的特点 是,独立未知力的数目大于独立静力平衡方程式的 数目,仅仅利用静力平衡条件不能求出全部的支座 反力和内力。超静定梁的基本求解方法与拉压超静 定问题相同,仍然是力法。本节将结合求梁变形的 叠加法,举例介绍简单超静定梁的求解。
1
图7.1
2
①挠度y。梁中任一横截面的形心C在垂直于 轴线方向的位移称为该截面处的挠度(deflection), 用y表示。显然,梁中不同横截面处的挠度一般是 不同的,可表示为
3
②转角θ。梁中任一横截面绕其中性轴转过的 角度,称为该截面的转角 (slope)。转角沿梁长度 方向的变化规律可用转角方上任一点的曲率 为
由式(a)和式(c)可得
7
在选取的坐标系下,根据弯矩M的正负号规定 可以看出:弯矩M的正负号与y″的正负号总是相反 的,如图7.2所示。因此,式(d)中应取负号,即
式(7.2)即为梁的挠曲线近似微分方程,适用 于理想线弹性材料制成的细长梁的小变形问题。
13
第五节 梁的刚度计算 一、梁的刚度计算 梁的刚度计算,通常是校核其变形是否超过许 用挠度[f]和许用转角[θ],可以表述为 式中,ymax和θmax为梁的最大挠度和最大转角。
14
在机械工程中,一般对梁的挠度和转角都进行 校核;而在土木工程中,通常只校核挠度,并且以 许用挠度与跨长的比值 作为校核的标准,即
图7.15
图7.16
24
21
图7.14
22
第六节 用力法解简单超静定梁 前面几节分析的梁,如简支梁、悬臂梁、外伸 梁等,都是静定梁。在工程实际中,有时为了提高 强度或控制位移,常常采取增加约束的方式,使静 定梁变成了超静定梁或静不定梁(statically indeter minate beam),如图7.15所示。超静定梁的特点 是,独立未知力的数目大于独立静力平衡方程式的 数目,仅仅利用静力平衡条件不能求出全部的支座 反力和内力。超静定梁的基本求解方法与拉压超静 定问题相同,仍然是力法。本节将结合求梁变形的 叠加法,举例介绍简单超静定梁的求解。
1
图7.1
2
①挠度y。梁中任一横截面的形心C在垂直于 轴线方向的位移称为该截面处的挠度(deflection), 用y表示。显然,梁中不同横截面处的挠度一般是 不同的,可表示为
3
②转角θ。梁中任一横截面绕其中性轴转过的 角度,称为该截面的转角 (slope)。转角沿梁长度 方向的变化规律可用转角方上任一点的曲率 为
由式(a)和式(c)可得
7
在选取的坐标系下,根据弯矩M的正负号规定 可以看出:弯矩M的正负号与y″的正负号总是相反 的,如图7.2所示。因此,式(d)中应取负号,即
式(7.2)即为梁的挠曲线近似微分方程,适用 于理想线弹性材料制成的细长梁的小变形问题。
13
第五节 梁的刚度计算 一、梁的刚度计算 梁的刚度计算,通常是校核其变形是否超过许 用挠度[f]和许用转角[θ],可以表述为 式中,ymax和θmax为梁的最大挠度和最大转角。
14
在机械工程中,一般对梁的挠度和转角都进行 校核;而在土木工程中,通常只校核挠度,并且以 许用挠度与跨长的比值 作为校核的标准,即
梁的变形 演示文稿
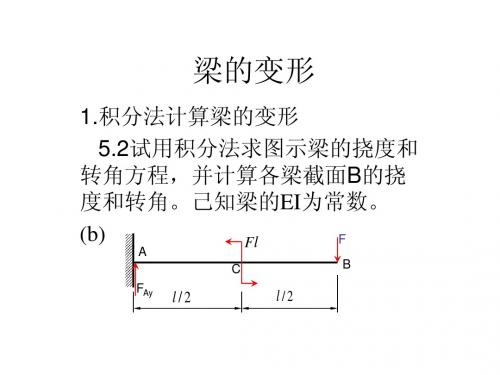
Fl 3 Fl 3 Fl 3 y(l ) = − =− 48EI 8EI 24 EI Fl 2 Fl 2 θ (l ) = − =0 2 EI 2 EI
如果采用迭加法求解 由F在B点引起的挠度与转角 3
Fl y1 (l ) = − ,(↓) 3EI
Fl 2 θ1 (l ) = − 2 EI
由Fl在B点引起的挠度与转角
3)边界条件和连续条件
边界条件:y1(0)=0, y2(l)=0 连续条件: y1(l)=y2(l) , y1’ (l)=y2’ (l) 由边界条件式(a)可得C2=0, Fal 2 Fl 2 (l + a) D1l D2 − − + + =0 6 EI 3EI EI EI 由连续条件式(b)得: (a) (b)
=−
Fa (2l + 3a ) (↵) 6 EI
梁的变形
1.积分法计算梁的变形 5.2试用积分法求图示梁的挠度和 转角方程,并计算各梁截面B的挠 B 度和转角。己知梁的EI为常数。 (b) F Fl
A C FAy B
l /2
l /2
解:1)求支反力 F =F,M =0 2)分段写弯矩方程并积分 AC段:(0 ≤x1 ≤l/2) CB段(l/2≤x2 ≤l) M1(x1)
Fl2 Fl2 θ(l) =θ1(l) +θ2 (l) =− + =0 2EI 2EI
5.2(d)
F B FBy C A
l
a
FAy
解:1)求支反力 F =F(l+a)/l, F =-Fa/l 2)分段列弯矩方程并积分 BC段(0≤x1 ≤l) CA段(l ≤x ≤l+a)
Ay By
2
M(x1)=FByx1=-Fax1/l EIy1’’(x1)= =-Fax1/l EIy1’ (x1)=-Fax12/(2l)+C1 EIy1(x1)=-Fax13/(6l)+C1x1+C2
如果采用迭加法求解 由F在B点引起的挠度与转角 3
Fl y1 (l ) = − ,(↓) 3EI
Fl 2 θ1 (l ) = − 2 EI
由Fl在B点引起的挠度与转角
3)边界条件和连续条件
边界条件:y1(0)=0, y2(l)=0 连续条件: y1(l)=y2(l) , y1’ (l)=y2’ (l) 由边界条件式(a)可得C2=0, Fal 2 Fl 2 (l + a) D1l D2 − − + + =0 6 EI 3EI EI EI 由连续条件式(b)得: (a) (b)
=−
Fa (2l + 3a ) (↵) 6 EI
梁的变形
1.积分法计算梁的变形 5.2试用积分法求图示梁的挠度和 转角方程,并计算各梁截面B的挠 B 度和转角。己知梁的EI为常数。 (b) F Fl
A C FAy B
l /2
l /2
解:1)求支反力 F =F,M =0 2)分段写弯矩方程并积分 AC段:(0 ≤x1 ≤l/2) CB段(l/2≤x2 ≤l) M1(x1)
Fl2 Fl2 θ(l) =θ1(l) +θ2 (l) =− + =0 2EI 2EI
5.2(d)
F B FBy C A
l
a
FAy
解:1)求支反力 F =F(l+a)/l, F =-Fa/l 2)分段列弯矩方程并积分 BC段(0≤x1 ≤l) CA段(l ≤x ≤l+a)
Ay By
2
M(x1)=FByx1=-Fax1/l EIy1’’(x1)= =-Fax1/l EIy1’ (x1)=-Fax12/(2l)+C1 EIy1(x1)=-Fax13/(6l)+C1x1+C2
