工程流体力学答案第二章 2
化工流体力学第二章习题解答精选全文

可编辑修改精选全文完整版习题2-2 一元流动用拉格朗日变数表示x =x (a,t ),p =p(a,t ),试证明:拉格朗日变数表示压力p 的当地变化率为:(,)(,)(,)(,)/p a t p a t x a t x a t t t a t ∂∂∂∂⎡⎤-⎢⎥∂∂∂∂⎣⎦证明:压力的导数为Dp p u p Dt t∂=+•∇∂ p 的当地变化率为p Dp u p t Dt ∂=-•∇∂ 式中:Dp Dt 用拉氏变数表示为(,)p a t t ∂∂ u 用拉氏变数表示为(,)x a t t∂∂ p ∇用拉氏变数表示为(,)p a t a a t ∂∂•∂∂ 所以有:(,)(,)(,)(,)/p p a t p a t x a t x a t t t t a t ∂∂∂∂∂⎡⎤=-⎢⎥∂∂∂∂∂⎣⎦习题2-3已知速度分布,t t x y u y u x e e -==++,求迹线方程。
解:x dx u y dt== 又t t y dy u x e e t -==++∂ 22t t d x dy x e e dt dt-∴==++ 积分可得:()()12121212t t t t t t t t x C e C e te te y C e C e te te ----=++-=+++如果t=0时,质点位置(,)a b ,则可得:12,22a b a bC C +-==2-4解:流线x ydxdyu u dx dy A Bt C∴==+可得:'Cy x C A Bt ∴=++上式为一直线轨线:()223'331(1)2(2)dxA Btdt x At Bt C dyCdt y Ct C y C y t C C C ∴=+=++==+-==+ 式2代入式(1)可得:()()2''3321(3)2y y x A C B C C C C =++++可见轨线为抛物线。
2-5解:Q AU =(1)等截面A=const , Q=const 所以:0x duuua u dt t x ∂∂==+=∂∂(2)变截面 A=A(x), ()x Qu A x ='22'3()()()()()x x u du u a u dt t xQ Q A x A x A x Q A x A x ∂∂==+∂∂⎛⎫=- ⎪⎝⎭=- 2-6解:22222211220.03750.0375d x d y d z a i j k dt dt dtt i t k=++=+ x=8时,t=12.9则加速度为0.1350.135a i k =+2-7解: 双曲正切函数()21tanh tanh 'cosh x xx x e e x x e e x ---==+2=tanh 1cosh UtlU t l θθθ∂=∂令 x x u u a u t x ∂∂=+∂∂其中:222222211cosh 2cosh 11cosh 2cosh u U x U U U t l l l U x U l l θθθθ∂=-∂=- tanh tanh tanh 22x x u U U u U x x l l θθθ∂⎡⎤==•-⎢⎥∂⎣⎦可得加速度计算:2222222211tanh tanh tanh cosh 2cosh 22111(1)22cosh tanh x x u u U x U U U a u U x t x l l l l U x Ut Ut l l l l θθθθθ∂∂⎡⎤=+==--•-⎢⎥∂∂⎣⎦⎡⎤⎢⎥⎢⎥=--⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(2)当x=L 时,其加速度为 222112cosh 2tanh U a Ut Ut l l l ⎡⎤⎢⎥⎢⎥=-⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦当a=0时,222222222110cosh 2tanh cosh 2tanh cosh cosh 2tanh 2sinh sinh 2Ut Ut l l Ut Ut l l θθθθθ-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭===或 其中:22sinh 2e e θθθ-⎛⎫-= ⎪⎝⎭(222100=52Ut ln 5e e e l θθθ-+-=±=±解得:所对应时间:(ln 52l t U =± 2-9流体质点的速度与质点到OX 轴的距离成正比,并且与OX 轴平行。
《工程流体力学》课后习题答案

pB 水 H B p A 水 H A Hg h pB p A 水 H A H B Hg h
pBA 水 H Hg h 9800 0.5 13.6 9800 0.5 71540 Pa 0.73at
2-10. 欲测输油管上 A、B 两点的压差,使用 U 形管压差计,内装水银,若读数 h=360mm, 油的相对密度 0.78,则 pA-pB=? 解:
p A 油hA pB 油hB Hg h p A pB Hg h 油 hB hA p A pB Hg h 油h 13.6 水 h 0.78 水 h 13.6 0.78 9800 360 10 3 45228.96 Pa 0.46at
题 2-4
4
2-5.
油罐内装相对密度 0.8 的油品,下有底水,为测 定油深及油面上的压力, 装置如图所示的 U 形管 水银压力计,测得各液面位置如图。试确定油面 高度 H 及液面压力 p0。 解:13.6×0.5-0.8=6mH2O 6-1.6=6-0.4-d 油 H H=(1.6-0.4)/d 油=1.5m P0=6-1.6mH2O=4.4mH2O=0.44at=4.312×104Pa (表压) 题 2-5 图
μ=νρ=0.4×10-4×890=3.56×10-2 Pa·s 1-8. 图示一平板在油面上作水平运动,已知运动速度 u=1m/s,板与固定边界 的距离δ=1,油的动力粘度μ=1.147Pa·s,由平板所带动的油层的运动 速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?
2
解: 1-9. 题
E
1-5.
1
p
1 4 108 Pa 9 2.5 10
工程流体力学 上册 李玉柱 课后答案第二章

第二章流体静力学2-1将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示),已 知L =30 cm , h =5cm ,试求汽车的加速度a 。
解:将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上,x 轴与加速度 的方向一致,则玻璃管装在作水平运动的汽车上时,单位质量液体的质量力和液 体的加速度分量分别为g x = 0, g y = 0, g z =- ga = a , a = 0, a = 0代入压力全微分公式得d p = -p (a d x + g d z )因为自由液面是等压面,即d p = 0,所以自由液面的微分式为a d x = -g d z 解得 a = g hL = % = 1.63m/s 22-2 一封闭水箱如图示,金属测压计测得的压强值为p =4.9kPa (相对压强), 测压计的中心比A 点高z =0.5m ,而A 点在液面以下h =1.5m 。
求液面的绝对压 强和相对压强。
解:由P 0 + p gh = p + p gz 得相对压强为P 0 = p + p g (z - h ) = 4.9 x 103 -1000 x 9.8 x 1 = -4.9kPa 绝对压强 p b = p 0 + p = (-4.9 + 98)kPa=93.1kPa积分得:z = -a x + c ,斜率为-ag g即 a ; g = h :L2-1图题27留2-3在装满水的锥台形容器盖上,加一力F=4kN。
容器的尺寸如图示,D = 2m, d=l m, h = 2m。
试求(1)A、B、A’、B’各点的相对压强;(2)容器底面上的总压力。
(1)p = — = —^5.09kP,由p = p +p gh得:0 A nd 2 4 0P A = P B = P0 = 5.09kPP = P = P + pgh = 5.09kP +1000 x 9.8 x 2P = 24.7 kPA' B‘0 a a a (2)容器底面上的总压力为P = P A A = 24.7kPa x兀D% = 77.6kN 2-4 一封闭容器水面的绝对压强p0=85kPa,中间玻璃管两端开口,当既无空气通过玻璃管进入容器、又无水进人玻璃管时,试求玻璃管应该伸入水面下的深度h。
工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
工程流体力学(闻建龙)课后答案(部分)

T
O( x)
A
y0 yc
h1
h2
hc
F
C
x
D
B
G
h3
yD
L
F ( yD y0 ) G 135792.72 (2.50185 1.1547) 9800 T 163324.84 L cos 2 2.3094 / 2 2
2 d2 752 v1 v2 2 23 12.94(m/s) 2 d1 100
v1d1 v2d2
y
对弯管的进、出口截面列伯努利方程
2 2 P1 v1 P2 v2 z1 z2 g 2g g 2g
x
P1
2 v2
2
v12
2g
1000 (232 12.942 ) 1.808 105 (Pa) 2
Q,v
平面图
α
y
0 (Q1v1 Q2v2 ) Qv cos 连续方程xFra bibliotekQ2 v2
Q Av Q1 Q2
Rx 0.173(kN) Q1=0.03(m 3 / s) 3 Q = 0.01(m / s) 2 Q1 : Q2=3 :1
作业解答
4-9 如图示,水流经弯管流入大气,已知d1=100mm,d2=75mm,v2=23m/s, 水的密度为1000kg/m3。不计水头损失,求弯管上所受的力F。 解:由连续性方程 2 2
h1
hc
工程流体力学 禹华谦 习题答案 第2章

第二章 流体静力学 2-1 作用于流体的外力有哪两种?答: 作用于流体的外力有质量力与表面力. 2-2 流体块表面上的压强有哪两项特性? 答: 流体块表面上的压强有以下两项特性1.法向应力的方向沿讨论流体块表面上某点的内法线方向,即压强沿垂直方向从外部指向表面。
2.静止流体中任一点处的压强大小与它所作用的表面方位无关。
2-3 什麽是绝对压强, 相对压强及真空度?答: 以绝对真空状态为基准计算的压强值叫绝对压强。
相对压强用于绝对压强大于大气压的场合,即一点处的相对压强指这点处的绝对压强高于大气压的部分.真空度用于绝对压强低于大气压的场合,即出现了真空的状态。
一点处的真空度指这点绝对压强小于大气压的那一部分.2-4 容器A 被部分抽成真空,容器下端接一玻璃管与水槽相通,玻管中水上升h=2m ,水的39800/N m γ=,求容器中心处的绝对压强p 和真空度v P ,当时当地大气压298000/a P N m =。
解:由a p h p =+γ,有2/784009800298000m N h p p a =⨯-=-=γ2/196007840098000m N p p p a v =-=-=2-5 以U 型管测量A 处水压强,h 1=0.15m ,h 2=0.3m ,水银的γ=N 3/m ,当时当地大气压强298000/a P N m =,求A 处绝对压强p 。
a解:由γ+p 水γ+1h 水银a p h =2,有-=a p p γ水-1h γ水银22/565463.013328015.0980098000m N h =⨯-⨯-=2-6 图中压差计上部有空气,h 1=0.6m ,h=0.45m ,h 2=1.8m ,求A 、B 两点压强差,工作介质水的39800/N m γ=。
解:设空气绝对压强为a p ,A ,B 两处绝对压强分别为B p p A ,,这里γ1h p p a A +=,γ)(2h h p p a b ++=,从而212/161709800)6.08.145.0()(m N h h h p p A B =-+=-+=-γ2-7 如图为一复式水银测压计,用以测量水箱中水的表面相对压强。
工程流体力学课后答案杨树人主编

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m Ng m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5. 用200L 汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC ,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC -1,弹性系数为14000kg/cm 2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E =E ’·g =14000×9.8×104PaΔp =0.18atdp pV dT T V dV ∂∂+∂∂=00V TVT V V T T ββ=∂∂⇒∂∂=00V p V p V V p p ββ-=∂∂⇒∂∂-= 所以,dp V dT V dp pVdT T V dV p T 00ββ-=∂∂+∂∂=从初始状态积分到最终状态得:LL L V p p E V T T V V dpV dT V dV T p pp T TT VV 4.21057.24.2200108.914000108.918.020*******.0)(1)(34400000000≈⨯-=⨯⨯⨯⨯⨯-⨯⨯=---=--=-⎰⎰⎰βββ即()kg V V M 32.13810004.220010007.0=-⨯⨯=∆-=ρ另解:设灌桶时每桶最多不超过V 升,则200=++p t dV dV VV dt V dV t t 2000061.0⨯=⋅⋅=βV dp V dV p p 18.0140001⨯-=⋅⋅-=β(1大气压=1Kg/cm 2) V =197.6升 dV t =2.41升 dV p =2.52×10-3升G =0.1976×700=138Kg =1352.4N 1-6.石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?()c S t St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν 1-7.相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/s μ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s 1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-9.如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa =2940Pap A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhgh hg + p A 表=0.1×13.6m H 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa =114268Pa ② 30c mH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-2 题2-32-2.水银压力计装置如图。
工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
第二章2-工程流体力学

五.一元流,二元流,三元流
一元流(one-dimensional flow):流体在一个方向流 动最为显著,其余两个方向的流动可忽略不计, 即流动流体的运动要素是一个空间坐标的函数。若 考虑流道(管道或渠道)中实际液体运动要素的断 面平均值, 则运动要素只是曲线坐标s的函数,这种流动属于一 元流动。 x u u ( x, t )
dr vdt
dx dy dz dt ux, y, z, t vx, y, z, t wx, y, z, t
初始时刻 t t0 时质点的坐标 a, b, c ,积 分得该质点的迹线方程。
二、流线(streamline)
• 流线:某一时刻处处与速度矢量相切的空间曲线-瞬时性, 。 • 任一时刻t,曲线上每一点处的切向量 d 都与该点的速度向量 相切。 r dxi dyj dzk v x, y, z, t • 流线微分方程:
ux ux ( x, y, z, t ) u y u y ( x, y, z, t )
p p( x, y, z, t )
uz uz ( x, y, z, t )
( x, y, z, t )
x, y, z ,t--欧拉变量,其中x,y,z与时间t有关。
欧拉法是常用的方法。
欧拉法中的加速度 -- 质点速度矢量对时间的变化率。
解:(1)流线方程的一般表达式为
将本题已知条件代入,则有: 积分得: (1+t)lnx = lny + lnC ' 当t= t0时,x=x0,y=y0 ,则有 故过A( x0,y0,z0 )点的流线方程为
(2)求迹线方程
代入本题已知条件有: 当t= t0时,x=x0代入上式得
工程流体力学课后答案 工程流体第2章 流体静力学
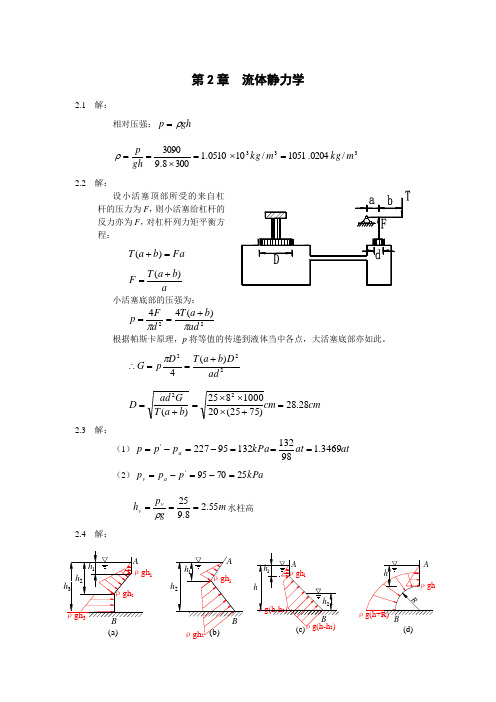
第2章 流体静力学2.1 解:相对压强:gh p ρ=333/0204.1051/100510.13008.93090m kg m kg gh p =⨯=⨯==ρ 2.2 解:设小活塞顶部所受的来自杠杆的压力为F ,则小活塞给杠杆的反力亦为F ,对杠杆列力矩平衡方程:Fa b a T =+)(a b a T F )(+=小活塞底部的压强为:22)(44ad b a T d F p ππ+==根据帕斯卡原理,p 将等值的传递到液体当中各点,大活塞底部亦如此。
222)(4ad D b a T D p G +==∴π cm cm b a T Gad D 28.28)7525(201000825)(22=+⨯⨯⨯=+=2.3 解:(1)at at kPa p p p a 3469.19813213295227'===-=-= (2)kPa p p p a v 257095'=-=-=m g p h v v 55.28.925===ρ水柱高 2.4 解:ρgh 2 ρgh 1ρgh 3ρgh 2ρgh 1h 2h 1 h 1 h 2h 3 (b)(a)BAA Bρg(h-h 2)ρg(h+R)ρghρg(h-h 2) ρgh 1Rhh 2h 1h(d)(c)B AAB2.5 解:1-1为等压面:gh p gH p a ρρ+=+0kPa m N m N m N H h g p p a 94.100/100940/)2.15.1(8.91000/108.9)('22240==-⨯⨯+⨯=-+=ρ kPa p 94.20=2.6 解: kPa gL p c 45.230sin 5.08.9sin =⨯⨯==αρ 2.7 解:如图所示,过1、2、3点的水平面是等压面。
)()()(322341121z z g z z g gh p z z g gh p B B A A ---++=--+ρρρρρ[])()()()(32212341z z g z z z z g h h g p p A B B A ---+-+-=-ρρρ[])()()()(3221234141z z g z z z z g z z g ---+-+-=ρρρ[]{}310)3262(8.0)1862()3253(6.13)5318(8.9-⨯---+-+-⨯=Pa 8085=2.8 解:gh gh p gh p p B B A A ρρρ+-=- ()gh h h g p p p B A B A ρρ+-=-=()[]gh h g p ρρ++-1=()[]31036.08.96.13136.08.9-⨯⨯⨯++-=34.6528kPa2.9 解:如图所示,A 、B 、C 点水平面是等压面。
(完整版)工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yuATmgddsinμθ==001.0145.04.062.22sin8.95sin⨯⨯⨯⨯==δθμuAmgsPa1047.0⋅=μ1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律yuddμτ=,定性绘出切应力沿y方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径0.9mm,长度20mm,涂料的粘度μ=0.02Pa.s。
工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
(完整版)工程流体力学课后习题答案1-3.doc

第一章 流体及其主要物理性质1-1. 轻柴油在温度 15oC 时相对密度为 0.83,求它的密度和重度。
水1000kg / m 3 相对密度: d解: 4oC 时9800 N / m3水水水0.83 所以,0.83水水0.83 1000 830kg / m 3 0.83 9800 8134 N / m 31-2.甘油在温度 0oC 时密度为 1.26g/cm 3 ,求以国际单位表示的密度和重度。
解: 1g / cm 3 1000kg / m 3g1.26g / cm 3 1260kg / m 3g 1260 9.8 12348N / m 31-3.水的体积弹性系数为 1.96×109N/m 2,问压强改变多少时,它的体积相对压缩 1%?解: E1(Pa)pdV VpdppV VV E 0.01E 1.96 10 7 Pa 19.6MPapV1-4.35 2时容积减少3容积 4m 的水,温度不变,当压强增加 10 N/m 1000cm ,求该水的体积压缩系数β p 和体积弹性系数 E 。
V V 1000 10 6解:4 91pp1052.5 10 PaE12.5 1 4 10 8 Pap10 91-5. 用 200L 汽油桶装相对密度为 0.70 的汽油,罐装时液面上压强为 1 个大气压,封闭后由于温度变化升高了 20oC ,此时汽油的蒸气压为 0.18 大气压。
若汽油的膨胀系数为 0.0006oC -1,弹性系数为 2。
试计算由于14000kg/cm 压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?4解: E =E ’· g =14000×9.8×10 PadVVdTVdpT pV V 0 VTVV V 0 V TTTppp Vp所以, dVVdTVdpT V 0dTp V 0dpTp从初始状态积分到最终状态得:V T pdVT V 0 dTp V 0 dpV 0T 0p 0即V V 0T (T T 0 )V 01( p p 0 )V 0E 1040.000620 0.18 9.8 2002009.8 104140002.4L2.57 10 3 L 2.4LMVV 0.7 1000200 2.4138.32kg 1000另解:设灌桶时每桶最多不超过 V 升,则V dV t dV p 200dV t tVdt 0.00061 20VdV ppV dp1 0.18V (1 大气压= 1Kg/cm 2)14000V =197.6 升dV t =2.41 升-3G =0.1976×700= 138Kg = 1352.4N1-6.石油相对密度 0.9,粘度 28cP ,求运动粘度为多少 m 2/s?解: 1cP 10 2 P1mPa s 10 3 Pa s1P 0.1Pa s28 10 3 3.1 10 5 m 2 / s 0.31St 31cSt0.9 10001-7.相对密度 0.89 的石油,温度 20oC 时的运动粘度为 40cSt ,求动力粘度为 多少?解: d-420.89ν= 40cSt =0.4St = 0.4 ×10 m/s水μ=νρ= 0.4 ×10-4 ×890= 3.56 × 10-2 Pa ·s1-8. 图示一平板在油面上作水平运动,已知运动速度 u=1m/s ,板与固定边界的距离δ =1,油的动力粘度μ= 1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:du 1.147 1 1.147 103 N / m 2dy 1 10 31-9. 如图所示活塞油缸,其直径D= 12cm,活塞直径 d= 11.96cm,活塞长度L=14cm,油的μ= 0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力 F=?解: A=π dL , μ= 0.65P=0.065 Pa · s , u=0.5m/s , y=(D-d)/2FA du0.065 3.14 11.96 10 2 14 10 2 0.510 28.55N dy 12 11.96 2第二章 流体静力学2-1. 如图所示的 U 形管中装有水银与水,试求:( 1) A 、 C 两点的绝对压力及表压各为多少?( 2) A 、 B 两点的高度差为多少?解:① p A 表 =γ h 水= 0.3mH 2O =0.03at = 0.3× 9800Pa =2940Pap A 绝= p a + p A 表 =(10+0.3)mH 2 O =1.03at = 10.3×9800Pa= 100940Pap C 表=γ hg h hg + p A 表= 0.1× 13.6mH 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝= p a + p C 表 =(10+1.66)mH 2O = 11.66 mH 2O =1.166at = 11.66×9800Pa =114268Pa ② 30c mH 2 = 2h = 30/13.6cm=2.2cmO 13.6h cmH O题 2-2题 2-32-2. 水银压力计装置如图。
工程流体力学 上册 李玉柱 课后答案第二章

第二章 流体静力学2-1 将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示),已知L =30 cm ,h =5cm ,试求汽车的加速度a 。
解:将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上,x 轴与加速度的方向一致,则玻璃管装在作水平运动的汽车上时,单位质量液体的质量力和液体的加速度分量分别为0,0,,0,0x y z x y z g g g ga a a a ===-===代入压力全微分公式得d (d d )p a x g z ρ=-+ 因为自由液面是等压面,即d 0p =,所以自由液面的微分式为d d a x g z =- 积分得:a z x c g =-+,斜率为a g -,即a g h L = 解得21.63m/s 6g a g h L ===2-2 一封闭水箱如图示,金属测压计测得的压强值为p =4.9kPa(相对压强),测压计的中心比A 点高z =0.5m ,而A 点在液面以下h =1.5m 。
求液面的绝对压强和相对压强。
解:由0p gh p gz ρρ+=+得相对压强为30() 4.91010009.81 4.9kPa p p g z h ρ=+-=⨯-⨯⨯=-绝对压强0( 4.998)kPa=93.1kPa abs a p p p =+=-+2-3 在装满水的锥台形容器盖上,加一力F =4kN 。
容器的尺寸如图示,D =2m ,d =l m ,h =2m 。
试求(1)A 、B 、A ’、B ’各点的相对压强;(2)容器底面上的总压力。
解:(1)a 20 5.09kP 4πd F A F p ==,由0p p gh ρ=+得: a 0B A 5.09kP P P P ===a a a 0B A kP 24.7P 29.81000kP 5.09ρgh P P P =⨯⨯+=+==''(2) 容器底面上的总压力为2'24.7kPa 77.6kN 4A D P p A π==⨯=2-4 一封闭容器水面的绝对压强p 0=85kPa ,中间玻璃管两端开口,当既无空气通过玻璃管进入容器、又无水进人玻璃管时,试求玻璃管应该伸入水面下的深度h 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[陈书2-8]容器中盛有密度不同的两种液体,问测压管A 及测压管B 的液面是否和容器中的液面O-O 齐平?为什么?若不齐平,则A 、B 测压管液面哪个高?
[解]依题意,容器内液体静止。
测压管A 与上层流体连通,且上层流体和测压管A 均与大气连通,故A 测压管的液面与液面O-O 齐平。
测压管B 与上下层流体连通,其根部的压强为:
a p gh gh p ++=2211ρρ
其中1h 为上层液体的厚度,2h 为液体分界面到B 管根部的垂向距离,a p 为大气压 因测压管B 与大气连通,其根部的压强又可表示为:
a p gh p +=2ρ
其中h 为B 管内气液界面到B 管根部的垂向距离 所以:gh gh gh 22211ρρρ=
+
212
1
22211h h h h h +=+=
ρρρρρ
由此可知:若21ρρ<,B 测压管的液面低于A 测压管的液面和O-O 面;若21ρρ>,B 测
压管的液面高A 测压管的液面和O-O 面;若21ρρ=,A 、B 测压管的液面和O-O 面三者平
齐。
又因为密度为1ρ的液体稳定在上层,故21ρρ<。
[陈书2-12]容器中有密度为1ρ和2ρ的两种液体,试绘出AB 面上的压强分布图。
[解]令上、下层液体的厚度分别为1h 和2h ,取垂直向下的方向为z 轴的正方向,并将原点设在自由表面上,可写出AB 表面上压强的表达式:
()⎩⎨⎧+≤<-++≤≤+=21121111 0
h h z h h z g gh p h z gz p p a
a ρρρ
整理得:
()⎩⎨⎧+≤<+-+≤≤+=211212111
h h z h gz gh p h z gz p p a a ρρρρ
A
C
B
P 012P g AC g BC
ρρ++01P g AC
ρ+/h m
/P Pa
[陈书2-24]直径D=1.2m ,L=2.5的油罐车,内装密度3
900m kg =ρ的石油,油面高度为h=1m ,以2
2s m a =的加速度水平运动。
试确定油罐车侧盖 A 和B 上所受到的油液的作用
力。
[解]取x 坐标水平向右,y 坐标垂直纸面向内,z 坐标垂直向上,原点定在油罐的中轴线上。
油液受到的体积力为:
a f x -= 0=y f g f z -=
由欧拉方程积分可得:gz ax p p C ρρ--=
根据题意及所选的坐标系,当h z x ==,0时,a p p = 故:gh p p C a ρ-=
gh p p a C ρ+=
所以:()ax z h g p p a ρρ--+=
因大气压的总体作用为零,故上式中可令0=a p 于是:()ax z h g p ρρ--=
左侧盖形心的坐标:0,2
=-
=z L
x 故该处的压强:2
L
a gh p L ρρ+=
左侧盖所受油液的作用力:N D p F L L 7.125234
2
==π(取2m 81.9=g ) 右侧盖形心的坐标:0,2
==
z L
x 故该处的压强:2
L
a gh p R ρρ-=
左侧盖所受油液的作用力:N D p F R R 1.74394
2
==π(取2m 81.9=g )
[陈书2-26]盛有水的圆筒形容器以角速度ω绕垂直轴作等速旋转,设原静水深为h ,容器半径为R ,试求当ω超过多少时可露出筒底?
解:非惯性坐标系中相对静止流体满足欧拉方程:()Zdz Ydy Xdx dp ++=ρ 等速旋转时液体所受的质量力为:
θωcos 2r X =,θωsin 2r Y =,g Z -=
将其代入欧拉方程,积分得:
C gz r p +⎪⎭
⎫ ⎝⎛-=2221ωρ
自由表面中心处r=0,a p p =(大气压),再令此处的z 坐标为:C z (令筒底处z=0),代入上式,得:
C gz p C a +-=ρ
所以:C a gz p C ρ+=
所以:C a gz p gz r p ρωρ++⎪⎭
⎫ ⎝⎛-=2
22
1
等压面的方程:
gz r gz p p C
a -=--222
1
ωρ
ρ 对于自由表面:a p p =,故自由表面的方程为:
gz r gz C
-=-222
1
ωρ
ρ 当筒底刚好露出时,0=C z ,所以自由面方程为:
2
221r g
z ω=
自由面与筒壁相交处的垂向坐标:2
221R g
H ω= 旋转后的水体体积:
4
2424222222422
2222
2
20
2244221212212R g
R g R g R g R g g R g
H g R g R dz gz
h R dz r H R V H
H ωπωπωπωωωπωπ
ω
πωπωπ
πππ=-=-
=
-=-=-=⎰⎰
将水视为不可压缩流体,根据质量守恒,旋转前后的水体体积应相等,所以:
h R R g
V 2424πωπ
==
所以:gh R
2
=
ω
[陈书2-39]在由贮水池引出的直径D=0.5m 的圆管中安装一蝶阀,h=10m ,蝶阀是一个与管道直径相同的圆板,它能绕通过中心的水平轴回转。
为不使该阀自行转动,问所需施加的力矩应为多大?
[解]将阀门的圆心定为坐标原点,z 轴垂直向上,则压强分布为:
()z h g p -=ρ
由于静水压导致阀门所受的总力矩为:
()⎰
⎰⎰⎰
⎰
⎰
⎰
----
-----=-⎪⎪⎭⎫ ⎝⎛-=-=-=-==2
2
2242
2
242
2
3
32
2
224
2
2
2
3
2
2
232
2
222
2cos sin 2cos sin 23cos 2cos sin 2cos sin 2cos sin sin 22ππππππππ
ππππθ
θθρθθθρθρθ
θθρθθθρθθθθρd gR d gR h gR d gR
d h gR d R h gR dz z R pz pzdA M R R R R
()14cos 8
1
162422cos sin 442
222
2
2
2-=+-=⎪⎪⎭⎫ ⎝
⎛-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭
⎫
⎝⎛-=----θθθσ
θσ
θσθσθi i i i i i i i e e e e e e e e
所以:()()m
N gR gR d gR d gR M .08.3044sin 414114cos 4
1
14cos 81242
24242
4==⎥⎥⎦
⎤⎢⎢⎣⎡-⎪⎭⎫
⎝⎛--=--=--=---⎰⎰
ρππθρθθρθθρππππππ
[陈书2-43]图示一储水设备,在C 点测得绝对压强为Pa 29430=p ,h=2m ,R=1m 。
求半球曲面AB 所受到液体的作用力。
[解]建立如图所示的坐标系,其中坐标原点取在球心,z 轴垂直向上。
以C 为参考点,容器内任意点的压强可表达为:
⎪⎭
⎫ ⎝⎛
+
-=2h z g p p C ρ
作用在曲面AB 上任意点处的压强均与表面垂直,即压力的作用线通过球心。
简单分析可知,曲面上水平方向的液体合压力为零,液体的曲面的总作用力仅体现在垂直方向,且合力方向向上,且合力作用线通过球心。
球面的外法线方向:
()
k j i n
θϕθϕθsin ,sin cos ,cos cos =
其中θ为纬度角,ϕ为经度角。
曲面AB 上的垂向总液体压力:
⎰
=2
2πθπrRd pn F z z
其中:θsin =z n ,θcos R r =
所以:⎰
=2
2
cos sin 2πθθθπd p R
F z
⎪
⎭
⎫
⎝⎛--=⎥
⎦⎤⎢⎣⎡⎪⎭⎫
⎝⎛+-=⎥⎦⎤⎢⎣
⎡⎪⎭⎫ ⎝⎛+-=⎰⎰⎰⎰⎰⎰
2020202202022
2cos sin 2cos sin cos sin 2cos sin 2cos sin 2cos sin 22ππππππθθθρθθθρθθθπθθθρθθθπθθθρπd h g d z g d p R d h z g d p R d h z g p R F C C C
z 将θsin R z =和2
1
cos sin 20=⎰πθθθd 代入上式,得:
⎪
⎭
⎫
⎝⎛--=⎪⎭⎫ ⎝⎛--=⎪⎭⎫
⎝⎛--=⎪
⎭⎫
⎝⎛--=⎰⎰gh gR p R gh gR p R gh d gR p R gh d gR p R F C C C C z ρρπρρπρθθθρπρθθθρπππ2132413121241cos sin 21241cos sin 212220222022
将Pa 29430=C p ,h=2m ,R=1m ,3m kg 1000=ρ和2
m 81.9=g 代入,得:
N 6.41102=z F。
