平面弯曲习题解答1
材料力学-习题集(含答案解析)

《材料力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《材料力学》(编号为06001)共有单选题,计算题,判断题,作图题等多种试题类型,其中,本习题集中有[判断题]等试题类型未进入。
一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关 (B)只与构件的形状尺寸有关(C)与二者都有关 (D)与二者都无关2.一直拉杆如图所示,在P力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中,图所示杆是轴向拉伸杆。
(A) P(C) (D)5.图示拉杆承受轴向拉力P的作用,斜截面m-m的面积为A,则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后,消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍,则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等,正负号相同(B)绝对值相等,正负号不同(C)绝对值不等,正负号相同(D)绝对值不等,正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内;(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上,各个截面上的。
第1节 平面弯曲的概念和实例

第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
第七章 直梁弯曲时的内力和应力
二、静定梁的基本形式 梁的支座形式:工程中常见的梁的支座有以下三 种形式。 1)固定铰支座:如图a所示,固定铰支座限制梁在 支承处任何方向的线位移,其支座反力可用两个正 交分量表示,即沿梁轴线方向的 FAx 和垂直于梁轴 线方向的FAy。
第七章 直梁弯曲时的内力和应力
第一节
平面弯曲的概念和实例
一、平面弯曲 弯曲变形:当杆件受到垂直于轴线的外力作用或 受到作用面平行于轴线的外力偶作用时,杆件的 轴线会由直线变为曲线,这种变形称弯曲变形。 梁:以弯曲变形为主的杆件称作梁。 直梁:工程中常见的轴线是直线的梁。 平面弯曲:若梁的外力及支 座反力都作用在纵向对称面 内,则梁弯曲时轴线将变成 此平面内的一条平面曲线, 该弯曲变形称为平面弯曲。
或
第七章 直梁弯曲时的内力和应力 2)活动铰支座:如图b所示,活动铰支座只能限制 梁在支承处垂直于支承面的线位移,支座反力可用 一个分量FRA表示。 3)固定端支座:如图c所示,固定端支座限制梁在 支承处的任何方向线位移和角位移,其支座反力有 两个正交力FAx、FAy和一个力偶分量MA。
或
MA
第七章 直梁弯曲时的内力和应力 静定梁的形式:根据梁的支座情况,工程中常见 的静定梁可以简化成以下三种形式。 1)简支梁:梁的支座一端是 固定铰支座,另一端是活 动铰支座。 2)外伸梁:梁的支座与简支 梁相同,只是梁的一端或 两端伸出在支座之外。 3)悬臂梁:梁的一端自由, 另一端是固定支座。
第七章 直梁弯曲时的Biblioteka 力和应力三、梁上载荷的简化
1)集中力:集中力作用在梁上的很小一段范围内, 可近似简化为作用于一点,如图所示的力F。单位 为牛顿(N)或千牛顿(kN)。 2)集中力偶:作用在微小梁段上的力偶,可近似 简化为作用于一点,如图所示的力偶M。单位为牛 顿· 米(N· m)或千牛顿· 米(KN· m)。 3)分布载荷:沿梁轴线方 向、在一定长度上连续分布 的力系,如图所示的均布载 荷q。其大小用载荷集度表 示,单位为牛顿/米(N/m) 或千牛/米(kN/m)。
材料力学第四章平面弯曲

得
∫ A ydA =0
M
dA
z
y z ζdA
My
横截面对中性轴 zdA 的面积矩为零, A 中性轴过形心。 E yzdA 0
A
y
Iyz =0——梁发生平面弯曲的条件
E I E 2 ∫ AσdA· z ∫ A y dA = Mz= y = ρ ρ 1 Mz = EIz —— 梁的弯曲刚度 中性层曲率公式 EI ρ z
y
m MB=-40kN· m MD=22.5kN· B M y B截面 上部受拉、下部受压 tBmax B t max 21.4MPa Iz B yt max 100mm B M y I z 186.6 106 m 4 B B c max 38.6MPa B c max yc max 180mm Iz
max
FQ S
* z max
Izd
d FQ 4 FQ 12 4 d 3 A d 64
3
d/2
z
max
四、薄壁圆环截面梁 中性轴处:
r0
z
max 2
FQ A
max
例 如图所示一T形截面。某截面上的剪力FQ=50kN,与y 轴重合。试求腹板的最大切应力,并画出腹板上的切应力分布图。
1
* FQ S z 1
I zd
4.13MPa
例 一矩形截面外伸梁,如图所示。现自梁中1、2、 3、4点处分别取四个单元体,试画出单元体上的应力,并 写出应力的表达式。
q
1 2 h/4 4 3
z l/4 b
l/4
l
解: (1)求支座反力:
FRA
FRB
1 l/4
工程力学习题册第八章 - 答案

第八章 直梁弯曲一、填空题1.工程中 发生弯曲 或以 弯曲变形 为主的杆件称为梁。
2.常见梁的力学模型有 简支梁 、 外伸梁 和 悬臂梁 。
3.平面弯曲变形的受力特点是 外力垂直于杆件的轴线,且外力和力偶都作用在梁的纵向对称面内 ;平面弯曲变形的变形特点是 梁的轴线由直线变成了在外力作用面内的一条曲线 ;发生平面弯曲变形的构件特征是 具有一个以上对称面的等截面直梁 。
4.作用在梁上的载荷有 集中力 、 集中力偶 和 分布载荷 。
5.梁弯曲时,横截面上的内力一般包括 剪力 和 弯矩 两个分量,其中对梁的强度影响较大的是 弯矩 。
6.在计算梁的内力时,当梁的长度大于横截面尺寸 五 倍以上时,可将剪力略去不计。
7.梁弯曲时,某一截面上的弯矩,在数值上等于 该截面左侧或右侧梁上各外力对截面形心的力矩 的代数和。
其正负号规定为:当梁弯曲成 凹面向上 时,截面上弯矩为正;当梁弯曲成凸面向上 时,截面上弯矩为负。
8.在集中力偶作用处,弯矩发生突变,突变值等于 集中力偶矩 。
9.横截面上弯矩为 常数 而剪力为 零 的平面弯曲变形称为 纯弯曲变形 。
10.梁纯弯曲变形实验中,横向线仍为直线,且仍与 梁轴线 正交,但两线不再 平行 ,相对倾斜角度θ。
纵向线变为 弧线 ,轴线以上的纵向线缩短,称为 缩短 区,此区梁的宽度 增大 ;轴线以下的纵向线伸长,称为 伸长 区,此区梁的宽度 减小 。
情况与轴向拉伸、压缩时的变形相似。
11.中性层与横截面的交线称为 中性轴 ,变形时梁的 所有横截面 均绕此线相对旋转。
12.在中性层凸出一侧的梁内各点,其正应力均为 正 值,即为 拉 应力。
13.根据弯曲强度条件可以解决 强度校核 、 截面选取 和 确定许可载荷 等三类问题。
14.产生最大正应力的截面又称为 危险截面 ,最大正应力所在的点称为 危险点 。
15.在截面积A 相同的条件下, 抗弯截面系数 越大,则梁的承载能力就越高。
平面弯曲习题解答1
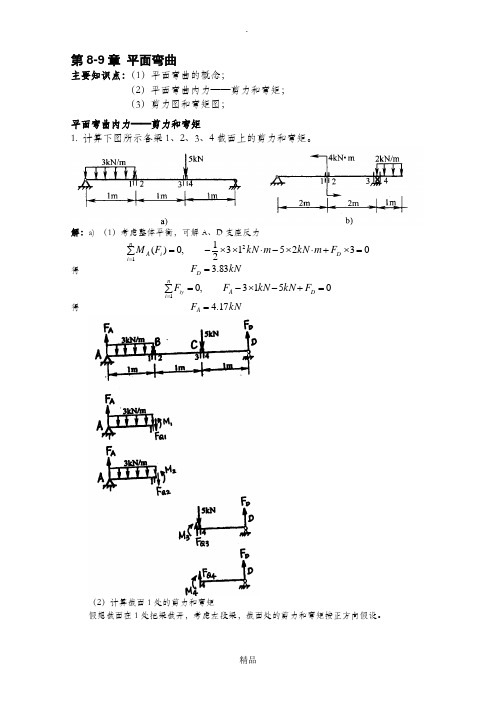
第8-9章 平面弯曲主要知识点:(1)平面弯曲的概念;(2)平面弯曲内力——剪力和弯矩; (3)剪力图和弯矩图; 平面弯曲内力——剪力和弯矩1. 计算下图所示各梁1、2、3、4截面上的剪力和弯矩。
解:a) (1)考虑整体平衡,可解A 、D 支座反力03251321,0)(21=⨯+⋅⨯-⋅⨯⨯-=∑=D ni i A F m kN m kN F M 得 kN F D 83.3=0513,01=+-⨯-=∑=D A ni iy F kN kN F F得 kN F A 17.4=(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,011=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.11=011321,0)(1121=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.21(3) 计算截面2处的剪力和弯矩假想截面2在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
013,021=-⨯-=∑=Q A ni iy F kN F F得 kN F Q 17.12=011321,0)(2221=+⨯-⋅⨯⨯-=∑=M F m kN F M Q ni i A 得 m kN M ⋅=67.22(4) 计算截面3处的剪力和弯矩假想截面在3处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
05,031=+-=∑=D Q ni iy F kN F F得 kN F Q 17.13=01,0)(31=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.33(5) 计算截面4处的剪力和弯矩假想截面在4处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。
0,041=+=∑=D Q ni iy F F F得 kN F Q 83.34-=01,0)(41=⨯+-=∑=D ni i C F M F M得 m kN M ⋅=83.34 将上述结果列表如下:b) (1)考虑整体平衡,可解A 、C 支座反力05.41244,0)(1=⋅⨯⨯-⨯+⋅=∑=m kN F m kN F M C ni i A得 kN F C 25.1=012,01=⨯-+=∑=kN F F F C A ni iy得 kNF A 75.0=(2)计算截面1处的剪力和弯矩假想截面在1处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。
《材料力学》第4章弯曲内力 课后答案

0 ; FS−C
= b F, a+b
M
− C
=
ba a+b
F
FS+C
=
−a a+b
F
,
M
+ C
=
ba a+b
F ; FSB
=
−A a+b
F
,MB
=
0
d解
图(d1), ∑ Fy
=
0,F
=
1 2
ql
,
∑
M
A
= 0,M A
=
− 3 ql 2 8
仿题 a 截面法得
FSA
=
1 2
ql
,MA
=
−
3 8
ql
2
;
FS−C
FS (x) = −F
⎜⎛ 0 < x < l ⎟⎞
⎝
2⎠
M (x) = −Fx ⎜⎛0 ≤ x ≤ l ⎟⎞
⎝
2⎠
FS (x) = F
⎜⎛ l < x < l ⎟⎞
⎝2
⎠
45
M (x) =
FA x +
FB
⎜⎛ ⎝
x
−
l 2
⎟⎞ ⎠
,
FB
= 2F
M (x) = Fx − Fl ⎜⎛ l ≤ x ≤ l ⎟⎞
( ) 解
∑MB
=
0 , FA
⋅l
+
ql 2
×
3l 4
− ql 2
=
0
, FA
=
5 ql 8
↑
( ) ∑ Fy
= 0 , FB
平面弯曲1(内力及内力图)
ΙΙ. ΙΙ. 梁的计算简图
一、载荷和约束力的类 型
1.集中力 2.集中力偶 3.分布力
F
m
q
二、梁的支座类型
1.固定铰支座
2.活动铰支座
3.固定端
三、梁的类型
1.简支梁
2.外伸梁 3.悬臂梁
约束力不超过三个, 以上三种梁统称为 : 静定梁(约束力不超过三个, 可由平衡方程求解。) 可由平衡方程求解。) 2
11
由外力写内力
力引起正剪力; 1.相对于横截面来说,左 段向上、右段向下的外 力引起正剪力; 相对于横截面来说, 段向上、 反之则反。 反之则反。
2.相对于横截面来说,左 、右段向上的外力引起 正弯矩; 相对于横截面来说, 正弯矩; 反之则反。 反之则反。
3.相对于横截面来说,外 力矩或外力偶,左段顺 时针转, 相对于横截面来说, 力矩或外力偶, 时针转, 反之则反。 右段逆时针转引起正弯 矩;反之则反。
3 .根据方程作图
Pa (a<x<l) l Pa (a ≤ x ≤ l ) M = FB ( l − x ) = (l − x ) l
Pa l
x
0
+
M
Pab l
8
例二、 作图示梁的剪力图和弯矩图,并标出控制点的数据。 例二、 作图示梁的剪力图和弯矩图,并标出控制点的数据。 解:
FA = FB = ql 2
18
例. 作图示梁的Fs、M图 作图示梁的F
y
解:
Fa Fa FA = (↓),FB = + F(↑) l l
x1
A
B
x2
C
FxBiblioteka axlAB段
Fa Fs = − l Fa M=− x l
工程力学习题库-弯曲变形

第8章 弯曲变形本章要点【概念】平面弯曲,剪力、弯矩符号规定,纯弯曲,中性轴,曲率,挠度,转角。
剪力、弯矩与荷载集度的关系;弯曲正应力的适用条件;提高梁的弯曲强度的措施;运用叠加法求弯曲变形的前提条件;截面上正应力分布规律、切应力分布规律。
【公式】 1. 弯曲正应力 变形几何关系:yερ=物理关系:Ey σρ=静力关系:0N AF dA σ==⎰,0y AM z dA σ==⎰,2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率:1MEIρ=弯曲正应力应力:,My Iσ=,max max z M W σ=弯曲变形的正应力强度条件:[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F bh F S S 2323max ==τ工字形梁弯曲切应力:dI S F y z z S ⋅⋅=*)(τ,A F dh F S S ==max τ圆形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F S 34max =τ弯曲切应力强度条件:[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程:()''EIw M x =-梁的转角方程:1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程:12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有()。
查看答案A 、平衡关系,物理关系,变形几何关系B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系D 、平衡关系, 物理关系,静力关系;2、 利用积分法求梁的变形,不需要用到下面那类条件()来确定积分常数。
查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上,各个截面上的()。
第四章 弯曲 (3)

极轴,q表示截面m–m的位置。
q
x
B
M (q ) Px P(R Rcosq ) PR(1 cosq ) (0 q )
FS (q ) P 1 Psinq (0 q )
N (q ) P q (0 q ) 2 Pcos
M图 R P
A
平面刚架 的内力图
刚结点:受力以后,刚节点处夹角保持不 变。刚节点能承受力与力矩。
平面刚架:是由在同一平面内,不同取向的杆件, 通过杆端相互刚性连结而组成的结构。 A 平面刚架的内力:剪力,弯矩,轴力。
C
B
弯矩图:画在各杆的受拉一側,不注明正、负号。 剪力和轴力图:可画在刚架轴线的任一側(通常正值画在 刚架的外側)。注明正、负号。
例 作图示刚架的弯矩图 解:求支反力 F
计算内力时, A 一般应先求支反力, 由于该图的A端为 一自由端,无需计 算支反力就可计算 弯矩,故此步骤可 省略。
x1
a x2
C
M图
1.5a
Fa Fa
B 作弯矩方程: 如图所示:AC段的坐标原点取在A端。 CB段的坐标原点取在C端。 (0 x1 a) AC: M x1 Fx1 CB: (0 x2 a) M x2 Fx2 作图: 注意:在绘制弯矩图时,我们规定为弯矩图画在杆件受拉的一侧, 即杆件弯曲变形凸入的一侧。由(a)(b)式可见:两段的弯矩方程均 为斜直线,故只要定出A、C、B三点处 的弯矩值即可作出弯矩图。
a q +
q
M x
–
qa2
=
=
2q M1
qa2 2qa2/2
–
x
+
q
+
工程力学习题及答案

1.力在平面上的投影(矢量)与力在坐标轴上的投影(代数量)均为代数量。
正确2.力对物体的作用是不会在产生外效应的同时产生内效应。
错误3.在静力学中,将受力物体视为刚体(D)A. 没有特别必要的理由B. 是因为物体本身就是刚体C. 是因为自然界中的物体都是刚体D. 是为了简化以便研究分析。
4.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确5.轴力图、扭矩图是内力图,弯矩图是外力图。
错误6.胡克定律表明,在材料的弹性变形范围内,应力和应变(A)A .成正比B .相等C .互为倒数 D. 成反比7.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体8.通常工程中,不允许构件发生(A)变形A.塑性B.弹性C.任何D.小9.圆轴扭转时,同一圆周上的切应力大小(A)A.全相同B.全不同C.部分相同D.部分不同10.杆件两端受到等值、反向且共线的两个外力作用时,一定产生轴向拉伸或压缩变形。
正确1.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体2.构件的许用应力是保证构件安全工作的(B)A.最低工作应力B.最高工作应力C.平均工作应力D.极限工作应力3.低碳钢等塑性材料的极限应力是材料的(A)A.屈服极限B.许用应力C.强度极限D.比例极限4.一个力作平行移动后,新点的附加力偶矩一定(B)A.存在B.存在且与平移距离有关C.不存在D.存在且与平移距离无关5.力矩不为零的条件是(A)A.作用力和力臂均不为零B.作用力和力臂均为零C. 作用力不为零D.力臂不为零6.构件抵抗变形的能力称为(B)A.强度B.刚度C.稳定性D.弹性7.工程实际计算中,认为切应力在构件的剪切面上分布不均匀。
错误8.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确9.圆轴扭转时,横截面上的正应力与截面直径成正比。
错误10.扭转时的内力是弯矩。
错误1.各力作用线互相平行的力系,都是平面平行力系。
国开建筑工程技术专科建筑力学各章节习题答案
整理时间:2020.06.20 国开学习系统各章节本章自测之习题答案第一章习题01.建筑力学在研究变形固体时,对变形固体做了什么假设?A. 连续性假设02.杆件的基本变形包括()B. 轴向拉压、剪切、扭转、弯曲03.杆件轴向伸长或缩短的变形称为()C. 轴向拉压04. 杆件轴线变为曲线的变形()B. 弯曲05.建筑力学的研究对象是()C. 杆件结构06.工程结构必需满足以下哪种条件?()D. 强度条件、刚度条件、稳定性条件07.一般认为以下哪种材料是不符合各向同性假设的?( D )A. 金属B. 玻璃C. 陶瓷D. 木材08.基于( D )假设,可假设构成变形固体的物质没有空隙地充满整个固体空间。
选择一项:A. 小变形假设B. 各向同性假设C. 均匀性假设D. 连续性假设09.基于( B )假设,可假设变形固体中各处的力学性能是相同的。
选择一项:A. 各向同性假设B. 均匀性假设C. 连续性假设D. 小变形假设10.基于( D )假设,可假设材料沿任意方向具有相同的力学性能。
选择一项:A. 小变形假设B. 均匀性假设C. 连续性假设D. 各向同性假设1.根据荷载的作用范围不同,荷载可分为( D )。
选择一项:A. 永久荷载和可变荷载B. 恒荷载和活荷载C. 静荷载和动荷载D. 集中荷载和分布荷载2.关于柔索约束,以下说法正确的是( A )。
选择一项:A. 只能承受拉力,不能承受压力和弯曲B. 只能承受压力,不能承受拉力和弯曲C. 既能承受拉力,又能承受压力和弯曲D. 只能承受压力,不能承受拉力3.关于光滑圆柱铰链约束,以下说法不正确的是( C )。
选择一项:A. 不能限制物体绕销钉轴线的相对转动B. 不能限制物体沿销钉轴线方向的相对滑动C. 能限制物体绕销钉轴线的相对转动D. 只限制两物体在垂直于销钉轴线的平面内任意方向的相对移动4.只限制物体向任何方向移动,不限制物体转动的支座为( D )。
选择一项:A. 可动铰支座B. 固定支座C. 定向支座D. 固定铰支座5.既限制物体沿任何方向运动,又限制物体转动的支座称为( B )。
平面弯曲的概念

2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
3-3纯弯曲时梁横截面上的正应力
3)纵向纤维的变形(伸长或缩短)与 它到中性层的距离有关,在横截面的同 一高度处,梁的纵向纤维的变形是相同 的,与它在横截面宽度上的位置无关。
2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
3-1 平面弯曲的概念
3、纵向对称平面:
工程上常见的梁,其横截面都具有一根 对称轴y。
纵向对称面—由对称轴和梁的轴线组成 的平面。
2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
3-1 平面弯曲的概念
4、平面弯曲: 梁由直线在纵向对称平面内变成曲线的弯
曲。 5、载荷分类:
作用在梁上的载荷一般可分为三种: 1)集中载荷(KN,N) 2)分布载荷(N/m) 3)集中力偶(N·m,KN·m)
2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
例
解: (1)求支座反力,画弯矩图。
RA 3kN RB 11kN
M B 4kN m
M c 3kN m
2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
2)CB段梁的剪力方程为:
Pa Q2 l
(a x2 l)
3)剪力图:见右图。
2008.9~2009.1
第三章 直梁的弯曲——《化工设备设计基础》
3-2 直梁弯曲时的内力分析
3、作弯矩图: 1)AC段梁的弯矩方程为:
M1
Pb l
x1
(0 x1 a)
2)CB段梁的弯矩方程为:
第06章弯曲变形题解
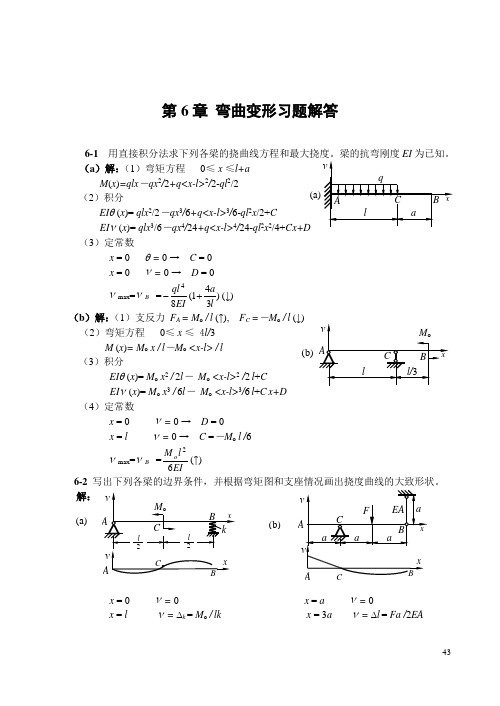
第6章 弯曲变形习题解答6-1 用直接积分法求下列各梁的挠曲线方程和最大挠度。
梁的抗弯刚度EI 为已知。
(a )解:(1)弯矩方程 0≤ x ≤l+aM (x )=qlx -qx 2/2+q<x-l>2/2-ql 2/2(2)积分 EI θ (x )= qlx 2/2-qx 3/6+q<x-l>3/6-ql 2x /2+CEI ν(x )= qlx 3/6-qx 4/24+q<x-l>4/24-ql 2x 2/4+Cx+D (3)定常数x = 0 θ = 0 → C = 0 x = 0 ν= 0 → D = 0νmax =ν B =)341(84laEI ql +-(↓)(b )解:(1)支反力 F A = M o / l (↑), F C =-M o / l (↓) (2)弯矩方程 0≤ x ≤ 4l/3M (x )= M o x / l -M o <x-l> / l (3)积分EI θ (x )= M o x 2 / 2l - M o <x-l>2 /2 l +CEI ν(x )= M o x 3 / 6l - M o <x-l>3/6 l +C x+D (4)定常数x = 0 ν= 0 → D = 0x = l ν= 0 → C =-M o l /6νmax =ν B =EIl M o 62(↑)6-2 写出下列各梁的边界条件,并根据弯矩图和支座情况画出挠度曲线的大致形状。
解:x = 0 ν= 0 x = a ν= 0x = l ν= ∆k = M o / lk x = 3a ν= ∆l = Fa /2EA(b) ν(b) (a)x = 0 θ = 0 x = 0 ν= 0 x = 0 ν=0 x = 3a ν= 0x = 0 ν= 0 x = 0 ν= 0 , θ = 0x =2a ν=0 x = 2a ν= 06-3 用叠加法求下列各梁C 截面的挠度和B 截面的转角。
第四章弯曲挠度3-Lu

C
q
B
( d)
C
wc1 (q)
c1 (q)
2 AB变形,BC不变形(刚化)。
ml c 2 (q ) B (q ) 3EI 2 1 3 qa 2 a qa 2 3 EI 3 EI 4 qa wc 2 (q) B (q) a 3 EI
A
qa2/2
B
(e)
AD : Fb( l 2 b 2 ) Fbx2 1 w1 6 EI 2 EIl
Fb( l 2 b 2 ) Fb 3 w1 x x 6 EIl 6 EIl
y
l
HOHAI UNIVERSITY
DB :
Fb( l 2 b 2 ) Fb 2 F 2 w x ( x a ) 2 2 6 EIl 2 EIl 2 EI
M x w EI z
—— 挠曲线近似微分方程
HOHAI UNIVERSITY
§4-9 用积分法计算梁的挠度与转角
对于等截面梁,EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M ( x)dx ]dx Cx D
θ p
A
y
C w C p θ
B x
1、挠度: 梁的截面形心在垂直于轴线方向的线位 移w。 w= w(x)——挠曲线方程(挠度方程)。向下为正.
2、转角:梁的截面绕中性轴转过的角度θ。
小变形时,θ≈tanθ=dw (x)/dx=w'(x)——转角方
程。顺时针为正。
HOHAI UNIVERSITY
§4-8 梁的挠曲线近似微分方程
B
x
工程力学第章弯曲强度答案(整理)

43 第7章弯曲强度7-1 直径为d 地圆截面梁,两端在对称面内承受力偶矩为M 地力偶作用,如图所示.若已知变形后中性层地曲率半径为ρ;材料地弹性模量为E .根据d 、ρ、E 可以求得梁所承受地力偶矩M .现在有4种答案,请判断哪一种是正确地.(A)M =E π d 习题7-1图(B) 64ρ M =64ρ (C) E π d4M =E π d (D)32ρM =32ρ E π d 3正确答案是A .7-2关于平面弯曲正应力公式地应用条件,有以下4种答案,请判断哪一种是正确地.(A)细长梁、弹性范围内加载;(B)弹性范围内加载、载荷加在对称面或主轴平面内;(C)细长梁、弹性范围内加载、载荷加在对称面或主轴平面内; (D)细长梁、载荷加在对称面或主轴平面内.正确答案是C _.7-3长度相同、承受同样地均布载荷q 作用地梁,有图中所示地4种支承方式,考虑,请判断哪一种支承方式最合理.l 5习题7-3图d . 7-4悬臂梁受力及截面尺寸如图所示.图中地尺寸单位为mm .求:梁地1-1截面上A 、−⎜ ⎟ A z B 两点地正应力.习题7-4图解:1. 计算梁地1-1截面上地弯矩:M =⎛1×103N ×1m+600N/m ×1m ×1m ⎞=−1300N ⋅m⎝2 ⎠2. 确定梁地1-1截面上A 、B 两点地正应力: A 点:⎛150×10−3m ⎞ 1300N ⋅m ×⎜−20×10−3m ⎟σ =M z y =⎝2⎠=2.54×106Pa =2.54MPa(拉应力) I zB 点:100×10-3m ×(150×10-3m )3121300N ⋅m ×⎜0.150m−0.04m ⎟⎛⎞σ=M z y =⎝2⎠=1.62×106Pa =1.62MPa(压应力)B 0.1m×(0.15m )3 127-5 简支梁如图所示.试求I-I 截面上A 、B 两点处地正应力,并画出该截面上地正应力 分布图. 习题7-5图A (a)A C B(b)F R AkN ⋅解:(1)求支座约束力F RA =3.64kN,F RB =4.36kN习题7-5解图(2)求I -I 截面地弯矩值(见习题7-5解图b )M I −I =3.64kN ⋅m(3)求所求点正应力σ=M I-I y AI z33I =bh 12=75×150 12=21.1×106mm 4 y A =(75−40)=35mm6∴σ=−3.64×10 ×35=−6.04MPa A 21.1×1066σ=3.64×10 ×75=12.94MPa B 21.1×1067-6加热炉炉前机械操作装置如图所示,图中地尺寸单位为mm .其操作臂由两根无缝 钢管所组成.外伸端装有夹具,夹具与所夹持钢料地总重F P =2200N ,平均分配到两根钢管上.求:梁内最大正应力(不考虑钢管自重).3习题7-6图解:1.计算最大弯矩:−33M max =−2200N ×2395×10m=−5.269×10N ⋅m2.确定最大正应力:σ=Mmax = M max,α= 66mm=0.611max32W σ=Mmax =2×πD32(1−α4)5.268N ⋅m108m m=24.71×106P a =24.71M P a max2W=π(1=08×10−3m ) 2×(1−0.6114) 327-7图示矩形截面简支梁,承受均布载荷q 作用.若已知q =2 kN/m ,l =3 m ,h =2b=240mm .试求:截面竖放(图c)和横放(图b)时梁内地最大正应力,并加以比较. 习题7-7图解:1.计算最大弯矩: ql22×103N/m ×(3m )2M max ===2.25×103N ⋅m882.确定最大正应力:3平放:σ =M max = 2.25×10N ⋅m ×6 =3.91×106Pa=3.91MPamax 2−3 −32hb6240×10 m ×(120×10 m )4 ⎝ ⎠ 竖放:σ=M max = 2.25×103N ⋅m ×6=1.95×106Pa=1.95MPamax 2−3 −32 bh 6120×10m ×(240×10 m )3.比较平放与竖放时地最大正应力:σmax (平放) () 3.91 ≈2.07-8圆截面外伸梁,图中尺寸单位为mm .已知F P =10kN ,q = M解:σ( )M max1 =32×30.65×10N ⋅m =113[σ] max 实= W 1π(140×10-3m )3σ( )M max2 = 32×20×103N ⋅m =100.3×106Pa=100.3MPa<[σ] max 空=⎡⎛⎞⎤ W 2π(140×10-3m )3⎢1− ⎢⎣ 100⎜140⎟⎥所以,梁地强度是安全地.7-9悬臂梁AB 受力如图所示,其中F P =10kN ,M =70kN ·m ,a =3m .梁横截面地形状及尺寸均示于图中(单位为mm),C 为截面形心,截面对中性轴地惯性矩I z =1.02×108mm 4,拉伸许用应力[σ]+=40MPa ,压缩许用应力[σ]-=120MPa .试校核梁地强度是否安全.解:画弯矩图如图所示:σ σ σ σ M (kN.m) C 截面30x+max =30×10N ⋅m ×96.4×10 m =28.35×106Pa=28.35MPa 1.02×108×10−12m 43−3 D 截面 -max =30×10N ⋅m ×153.6×10m =45.17×106Pa=45.17MPa 1.02×108×10−12m 43−3 +max =40×10N ⋅m ×153.6×10m =60.24×106Pa=60.24MPa>[σ] 1.02×108×10−12m 43−3- max =40×10N ⋅m ×96.4×10 m =37.8×106Pa=37.8MPa 1.02×108×10−12m 4所以,梁地强度不安全.7-10由No.10BC 连接,BC 杆在C 处用铰链悬挂[σ]=160MPa ,试求:M8max P习题7-10图解:画弯矩图如图所示:对于梁:M max =0.5qσ=M max ≤[σ], 0.5q ≤[σ] max WW[σ]W 160×106×49×10−6q ≤ ==15.68×103N/m=15.68kN/m 0.50.5对于杆: σ=F N ≤[σ],4F B =4×2.25q ≤[σ] maxA πd 2 πd 2πd 2×[σ] π×(20×10-3)2×160×106q ≤ ==22.34×103N/m=22.34kN/m4×2.254×2.25所以结构地许可载荷为[q ]=15.68kN/m7-11 图示外伸梁承受集中载荷F P 作用,尺寸如图所示.已知F P =20kN ,许用应力[σ]=160MPa ,试选择工字钢地号码. 习题7-11图解:M =F ×1m=20×103N ×1m=20×103N ⋅m σmax =M maxW≤[σ], F ×1m 20×103×1m W ≥ P ==0.125×10-3m 3=125cm 3[σ] 所以,选择No.16 工字钢. 160×106Pa7-12图示之AB 为简支梁,当载荷F P 直接作用在梁地跨度中点时,梁内最大弯曲正应力超过许用应力30%.为减小AB 梁内地最大正应力,在AB 梁配置一辅助梁CD ,CD 也可以 习题7-12图看作是简支梁.试求辅助梁地长度a .解:1.没有辅助梁时σmax=M max≤[σ], WF P l4 =1.30[σ] W σmax=M max≤[σ], WF P l(3−2a ) 2=[σ]W F P l (3−2a ) F P l2= 4=[σ]W 1.30×W 1.30×(3−2a )=3a =1.384m7-13一跳板左端铰接,中间为可移动支承.为使体重不同地跳水者站在跳板前端在跳板中所产生地最大弯矩M zmax 均相同,问距离a 应怎样变化? 习题7-13图解:最大弯矩发生在可移动简支点B 处.(见图a 、b )设不同体重分别为W ,W +ΔW ,则有,W (l −a )=(W +ΔW )(l −a −Δa ) ABW A整理后得 a 图 Δa = ΔW(W +ΔW )b 图(l −a ) 此即为相邻跳水者跳水时,可动点B 地调节距离Δa 与他们体重间地关系.7-14利用弯曲内力地知识,说明为何将标准双杠地尺寸设计成a=l /4.M MF习题7-14图解:双杠使用时,可视为外伸梁..A C Bb 图 若将a 地长度设计能达到下述情况为最经济、省工: M +=M −, max max即正负弯矩地绝对值相等,杠为等值杆.当a=l /4时,+ max− max=F P l /4(如图a,在中间面C ); =F P l /4(发生在图b 所示受力情况下地A 面或B 面).7-15图示二悬臂梁地截面均为矩形(b×h ),但(a)梁为钢质,(b)梁为木质.试写出危险截面上地最大拉应力与最大压应力地表达式,并注明其位置.二梁地弹性模量分别为E 、 E .P FP习题7-15图解:(1)两悬臂梁均为静定梁,故应力与材料弹性常数无关.(2)两悬臂梁均发生平面弯曲,危险面均在固定端处.σ σ σ σ 6 I 6I (3)钢梁: (4)木梁:+ max− max=6F P l bh 2 =6F P l bh 2(在固定端处顶边诸点) (在固定端处底边诸点) + max − max=6F P l hb 2=6F Pl hb 2(在固定端处后侧边诸点) (在固定端处前侧边诸点) 7-16T 形截面铸铁梁受力如图所示,其截面地I z=2.59×10−6m 4.试作该梁地内力图,求出梁内地最大拉应力和最大压应力,并指出它们地位置.画出危险截面上地正应力分布图.习题7-16图解:(1)求支座约束力F RA =37.5kN, F RB =112.5kN(2)作内力图,剪力图、弯矩图分别见习题7-16解图b 、c . (3)求所最大正应力和最小正应力E 、B 两截面分别发生最大正弯矩与最大负弯矩.所以,两个截面均有可能是危险截面.σ+=M E y2=14×10 ×142=76.8MPa (在E 截面下缘)z2.59×107σ−=M B y 2 =25×10 ×142=−137MPa (在B 截面下缘)z 2.59×107正应力分布图见图d.σ σ σ y m (a)AqEBD2m 1m50kN37.5kN⊕(b)⊕Ө1 62.5kN43.6MPa(d)(c)14kN·my 2⊕Ө25 kN·m 76.8MPa137MPa习题7-16解图7-17.在横放和竖放两种情况下,(a)比较许用弯曲力偶矩m O 绘出危险截面上地正应力分布图.解:(a)F R A2M (b) Өy 1(c)y 235y 1y 2σ习题7-17解图33(1)求支座约束力F RA=FRB=mOkN 5(2)作弯矩图见习题7-17解图b 所示. (3)竖放下地许用弯曲力偶矩m O由型钢表查得 从b 图中得:W =269.6×103 mm 3M =3m O由强度条件maxσmax =5 M maxW≤[σ] m ≤5W [σ]=5×269.6×10×160=71.89kN ⋅mO33(4)横放下地许用弯曲力偶矩m O由型钢表查得由强度条件W =30.61×103 mm 3m ≤5W [σ]=5×30.61×10 ×160=8.16kN ⋅mO33危险截面上地正应力分布图见图c.7-18制动装置地杠杆用直径d =30mm 地销钉支承在B 处.若杠杆地许用应力 [σ]=140MPa ,销钉地剪切许用应力[τ]=100MPa ,求许可载荷[F P1],[F P2].F P1F P2习题7-18图解:(1)求F P1 与F P2地关系4杠杠平衡时有:F P1×1000=F P2×250, (2)作弯矩图,如图 a 所示F P2 =4F P11000F(3σmax =M max W≤[σ]20×603 (20×303−)W = 1212=1.05×104mm 330 1000F p1W≤[σ] F ≤W [σ]=1.05×10×140=1.47kN P11000 1000∴F P2 ≤5.88kN(4)校核销钉地剪切强度剪切强度条件:F Q τmax = A≤[τ] 其中,F=5F=3.675mm 2 Q2P13 ∴τmax=3.675×10706.86=5.2MPa<[τ]则,销钉安全.(5)杠杆系统地许可载荷为[FP1]=1.47kN,[FP2]=5.88kN.上一章返回总目录下一章。
第3章 平面弯曲

2、弯曲变形;
3、剪切变形; 4、扭转变形; 三、弯曲的概念 1、一直杆在通过杆的轴线的一个纵向平面内,如果受到垂直于轴线的 外力(即横向力) 或力偶作用,杆的轴线就变成一条曲线,这种变形称为 弯曲变形。 2、纵向对称面:由横截面对称轴和梁的轴线组成的平面,称为纵向对 称面。 3、梁在变形时,它的轴线将弯曲成在纵向对称面内的一条曲线,这种 情况称为平面弯曲。
(1) 先求出支座反力
RA = RB =
ql 2
(2) 列出剪力方程和弯矩方程
1 ql - qx (0 < x < l) 2 1 1 M = qlx - qx 2 (0 x l) 2 2 Q=
(3) 作剪力图和弯矩图 1 Qmax = ql 2
由弯矩方程可知弯矩图是一抛物 线,故要定出几点(如5个点) 的M 值,才能近似地作出弯矩图。
二、剪力和弯矩方程 剪力图和弯矩图
AC段梁的弯矩方程为
M1 = Fb x1 l (0 x1 a)
a
1
F
b
2
A
x1
1 x2
C
2
B
CB段梁的弯矩方程为
Fa M2 = (l - x 2 ) l (a x 2 l)
l
M
Fab l
画出弯矩图
M max
Fab = l
x
3.2 直梁弯曲的内力分析
3.3 平面弯曲的应力计算
三个假设: (1 ) 梁在纯弯曲时, 横截面像直线 mn、m1n1 那样, 各自偏转一个角 度, 但仍然保持平面, 且垂直于梁 轴, 这就是平面截面假设。 (2 ) 纵向纤维的变形和它到中性 层的距离有关, 且沿宽度相等。 (3 ) 纵向纤维的变形只是简单的 拉伸或压缩, 它们之间没有相互 挤压, 因此, 梁的横截面上只能产 生拉应力或压应力。由于这些应 力都垂直于横截面, 故统称为正 应力。
材料力学-习题集(含答案)
《材料力学》课程习题集西南科技大学成人、网络教育学院 版权所有习题【说明】:本课程《材料力学》(编号为06001)共有单选题,计算题,判断题,作图题等多种试题类型,其中,本习题集中有[判断题]等试题类型未进入。
一、单选题1. 构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关 (C)与二者都有关(D)与二者都无关 2. 一直拉杆如图所示,在P 力作用下 。
(A) 横截面a 上的轴力最大(B) 横截面b 上的轴力最大 (C) 横截面c 上的轴力最大(D) 三个截面上的轴力一样大 3. 在杆件的某一截面上,各点的剪应力 。
(A)大小一定相等(B)方向一定平行 (C)均作用在同一平面内 (D)—定为零 4. 在下列杆件中,图 所示杆是轴向拉伸杆。
(A) (B)(C)(D) 5. 图示拉杆承受轴向拉力P 的作用,斜截面m-m 的面积为A ,则σ=P/A 为 。
(A)横截面上的正应力(B)斜截面上的剪应力 (C)斜截面上的正应力(D)斜截面上的应力 6. 解除外力后,消失的变形和遗留的变形 。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形 (C)分别称为塑性变形、弹性变形(D)通称为弹性变形 7. 一圆截面轴向拉、压杆若其直径增加—倍,则抗拉 。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍 (C)强度和刚度均是原来的2倍 (D)强度和刚度均是原来的4倍8. 图中接头处的挤压面积等于 。
P P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等,正负号相同(B)绝对值相等,正负号不同(C)绝对值不等,正负号相同(D)绝对值不等,正负号不同11.平面弯曲变形的特征是。
10-1平面弯曲

M
1
(+)
b
F
A
a
P1
C
P2
D
F
2
d
B
Y 0,
Fs 2 FB 0
A
1 c
B
P a P2b FB 1 F s2 l
(-)
l
M
F
0,
解得
M 2 FB d 0
M
(+)
2
F
s2
F
F
d B
B
P a P2b M 2 FB d 1 d l
求剪力和弯矩的简便方法
M图
FS max=ql
M max=ql 2 / 2
目录
例:图示简支梁C点受集中力作用。 试写出剪力和弯矩方程,并画 出剪力图和弯矩图。
a
F
b
A
FAY
C
l
B
FBY
解:1.求支座约束力
M =0
A
FBy=Fa/l FAy=Fb/l
目录
M =0
B
a
F
b
2.写出剪力和弯矩方程
A
FAY
x1
C x2
l
集中力 一段梁上 的外力情 况 F C 在C处有突变 集中力偶 M C
剪力图的特征
在C处无变化
C
弯矩图的特征
在C处有尖角 或
在C处有突变 M
微分关系绘制剪力图与弯矩图的方法:
根据载荷及约束力的作用位置,确 定控制面。 应用截面法确定控制面上的剪力和 弯矩数值。
建立FS一x和M一x坐标系,并将控制面 上的剪力和弯矩值标在相应的坐标系中。
应用平衡微分方程确定各段控制面 之间的剪力图和弯矩图的形状,进而画 出剪力图与弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)计算截面1处的剪力和弯矩假想截而在1处把梁截开,考虑左段梁,截而处的剪力和弯矩按正方向假设。
乞耳=0,F A -3xlkN —FQ 严0<=!第8-9章平面弯曲主要知识点:(1)平面弯曲的概念;(2) 平面弯曲内力——剪力和弯矩; (3) 剪力图和弯矩图;平面弯曲内力——剪力和弯矩 1.计算下图所示各梁1、2、3、4截面上的剪力和弯矩。
5kN 3kN/m 2 3114 一 Im -Lc 解:a )a ) (1)考虑整体平衡,可解A 、D 支座反力八(斥)=0, — = 3x1 叹 N ・/—5x2册•加+ 5x3 = 0i=i2F D =3.83kN 汰=0, F A -3xl£N-5kN+心=0 ;=iF A =4A7 kNA 3kWm得F ei = \A7kN得F A =0.75 kNf MM )= O,-异 xCkN ・ m-F Ql xl + M [ =0 2=1L得 M] =2HkN ・m (3) 计算截而2处的剪力和弯矩假想截而2在处把梁截开,考虑左段梁,截而处的剪力和弯矩按正方向假设。
土耳=0,F A —3X NN —F Q 2=O/=!得F Q 2=\ •门 kN门1乍为 M"・)= 0,-^x3xl 2^-/w-R.xl + Af 2=Or=l2得M2=26JkN ・m(4) 计算截而3处的剪力和弯站假想截而在3处把梁截开,考虑右段梁,截而处的剪力和弯矩按正方向假设。
左耳=0, F Q3-5kN +F D =Or=l得F Q3 = \AlkN£M C (£) = 0,-A/, + F D X 1 = 0J =I得M3 =3・83RN ・〃?(5) 计算截面4处的剪力和弯矩假想截而在4处把梁截开,考虑右段梁,截而处的剪力和弯矩按正方向假设。
士厲=0,心+你=01=1得伦4=-3・83kNfMc (£) = 0,-M 4 + F D X \=0.=1得M 4 = 323kN ・m±M A (斥) = 0,4kN ・〃z +耳 x4 — 2xlx4・5ZJV ・/ = 0 i=l得F c =\.25 kN为存=0, 心+件—2x1归V = 01=1(2)计算截面1处的剪力和弯矩假想截而在1处把梁截开,考虑左段梁,截而处的剪力和弯矩按正方向假设。
乞耳=0, F A-F Qi=O1=1 •得F Q] =0.75kN斥)= 0, -心x2 + M|=0l=i得M| =\.5kNm(3)计算截面2处的剪力和弯矩假想截而2在处把梁截开,考虑左段梁,截而处的剪力和弯矩按正方向假设。
土耳=0,代一伤2=0/=1得F Q2=0.15kN±M\(£) = 0, -F Q1x2 + 4kN-m + M2 =0(=i "得M2=—25kN・m(4)计算截面3处的剪力和弯站假想截而在3处把梁截开,考虑右段梁,截而处的剪力和弯矩按正方向假设。
£休=0, 甩+存-2x1册=0/=1得F Q3=0.75kNi >>工 (斥)= 0, — £x2xl*N・m = 0J=I• L得血=_\师5(5)计算截面4处的剪力和弯矩假想截而在4处把梁截开.考虑右段梁,截而处的剪力和弯矩按正方向假设。
22休=0,F —2x\kN = 0/=i得F Q 4= 2kN(斥) = 0, -M 4-|x2xl 2^-/n = 0J =IZ得M,=—\kN ・m截面 1 2 3 4 剪力(kN) 0.75 0.75 0.75 2 弯矩(kN-m)1.5-2.5-1-1剪力图和弯矩图2.建立图示梁的剪力方程和弯矩方程,2m(3)作剪力图和弯矩图弯矩图是两斜直线,在C 截而处有突变,突变量为MeM a pp 0 TcAy并画剪力图和弯矩图。
10kN(")解:a) (1)求支座反力—F B ・/ + M=O F B =^ 纽(好)=01=1-F A -/ + M =0 F A =—(2)求剪力方程和弯矩方程(分段建立方程)AC 段匸(、匸 MF Q (Q =入=y MM(x) = F A X = —X(OH)(0<x<a)CB 段MF Q (X ) = F A =〒M(x) = F a \l-x) = -^-(l-x) (a 恥)=¥ (0<x</)M T x(a <x< /)M (x)= <-十Q_Q (a<x<l)(/?)b) (1)求支座反力由整体平衡方程(见图8-2b):(斥)= 0, -你x2 + 10x3AW・m = 0, F B = \5kN2=1±M B(£)=0, - £\X2 + 10xl£N・m= 0 •F x= —5kN(2)'求剪力方程和弯矩方程梁上任取一截面(见图8-2b),到支座A的距离为斗由截而法得该截而的剪力方程和弯矩方程AB 段:F Q(x) = -5kN, M(x) = -5x, ( 0 < x < 2m )BC 段:FQ(x) = WkN, M(x) = -106-x),即M(x) = 10x-30, (2m<x<3m)lOkN(3)作剪力图和弯矩图:AB、BC段剪力都为常数,剪力图各为一水平直线。
AB、BC段弯矩方程是x的一次函数,弯矩图各为一斜直线。
两点可以确泄一条直线, 当x = 0 时,M(0) = 0;当x = 2m时,M(2) = —10£N・〃?:当x = 3m时,M ⑶=0,连A. B两点可得AB段弯矩图,连B、C两点可得BC段弯矩图.如图8・2b所示。
3・剪力和弯矩的正负号如何确定?梁在集中力、集中力偶及均布载荷作用下的剪力图和弯矩图有何特点?答:在汁算内力时,为了使考虑左段梁平衡与考虑右段梁平衡的结果一致,对剪力和弯矩的正负号作以下规定:剪力:使截而绕其内侧任一点有顺时针转趋势的剪力为正,反之为负。
弯矩:使受弯杆件下侧纤维受拉为正.使受弯杆件上侧纤维受拉为负。
或者使受弯杆件向下凸时为正,反之为负。
(1)当梁上有集中力作用时,剪力图在集中力作用处有突变,突变量是集中力的大小;弯矩图在集中力作用处产生尖角。
(2)当梁上有集中力偶作用时,剪力图在集中力偶作用处不变;弯矩图在集中力偶作用处有突变,突变量是集中力偶的大小。
(3) 梁的某一段内有均布载荷作用,则剪力©(X )是x 的一次函数,弯矩M(x)是x 的二 次函数。
剪力图为斜直线:若讥X)为正值,斜线向上倾斜:若讥切负值,斜线向下倾斜。
弯 矩图为二次抛物线,当g(x)为正值,弯矩图为凹曲线;当g(x)为负值,弯矩图为凸曲线。
4. 什么是剪力、弯矩和载荷集度的微分关系?如何利用微分关系作梁的剪力图和弯矩图?答:载荷集度水切、剪力①(X )和弯矩M(x)之间的微分关系如下:利用微分关系作梁的剪力图和弯矩图: 1. 无分布载荷作用的梁段(g=0)由于曝V = 0,因此q (x )=常数,即剪力图为水平直线。
而聲卫= ®(x)为常数, M(x)是x 的一次函数,即弯矩图为斜直线,其斜率由F Q (X )值确定。
(1) 当梁上仅有集中力作用时,剪力图在集中力作用处有突变,突变量是集中力的大小:弯矩图在集中力作用处产生尖角。
(2) 当梁上仅有集中力偶作用时,剪力图在集中力偶作用处不变:弯矩图在集中力偶作 用处有突变,突变量是集中力偶的大小。
2. 均布载荷作用的梁段(g(x)为常数)dF n (x)由于q(x) = q.因此—^― = ^,即F Q {X )是x 的一次函数• M (力是;v 的二次函数,所 以剪力图为斜宜线,其斜率由彳确左:弯矩图为二次抛物线。
当分布载荷向上(即00)时,〃 W q>0,弯矩图为凹曲线;反乙 当分布载荷向 dr5. 指岀下图所示各弯矩图的错误,画出正确的弯矩图。
k ——「一~a)b)解:a)弯矩图的斜率.起点错误,图8・5a 为正确的弯矩图;b)弯矩图应该是斜直线,图&5b 为正确的弯矩图;譽齐)兽5)dL下(即</<0)时,贵亠心,弯矩图为凸曲线。
图8-5 Fa0・5%2 d) 0・5%2c)解:c)弯矩图中间一段不为0,图8・5c为正确的弯矩图:d)弯矩图在支撑处没有突变,图8・5d为正确的弯矩图(设/>加)。
qM H HJ H H H屮)M0.5W0咖2图8-5d)6.利用剪力、弯矩与载荷集度的微分关系作图示各梁的剪力图和弯矩图。
/ ic H ・°小°斗° Jqa解:a)(1)求支座反力由整体平衡方程(见图8-6a):q JTHT—b)工耳=0, F —qci = 0,F.\ =2c/a/=!i (£) = 0,-qaxu-qax2・5u = 0, M A = -3・5qa 2(2) 作剪力图AC 段剪力图是水平线,大小为勿⑴CD 段剪力图也是水平线,大小为%, DB 是斜直线, 确建两个控制点F QD = qa ,①8=0,作剪力图如图&6a 所示。
(3) 作弯矩图AC 段与CD 段的弯矩图是斜直线,求出以下控制截而的弯矩M A =-3.5qa 2 , Me = — 1・5购2, M°=-0.5*2,可作这两段斜直线。
DB 段由于有均布载荷作用,弯矩图 是一段抛物线,如图8-6a所示。
b ) (1)求支座反力由整体平衡方程(见图8-6b ):±M A (£) = 0, -qx2axa + qa 2 +F 〃x3" = 0,得心=甞C=1/=!用8 人2也~ri %图 8-6a£ F\ = 0, F A -qx2a + F B = 0,r=l图8-6b(2)作剪力图CB段剪力图是水平线,大小为一年。
AC段剪力图是斜直线,确泄两个控制点佗° = 一半。
作剪力图如图8-6b所示。
(3)作弯矩图CB段的弯矩图是斜直线,求出以下控制截面的弯矩:M H=0,作出这段斜直线。
AC段由于有均布载荷作用,弯矩图是一段抛物线。
当剪力为0时(见图7-21所示D点), 弯矩岀现极值,即当x = |^时,M max(|«) = 1.389^\再求岀以下控制截而的弯矩:M A=0,M C =^qa2。
画弯矩图如图8-6b所示。
