二元一次方程组专项练习题59
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组.6.已知关于x,y的二元一次方程y=kx+b 的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:12.解二元一次方程组:;.15.解下列方程组:(1)(2).16.解下列方程组:(1)(2)二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.,得到一组新的方程,然后在用加减消元法消去未知数解:由题意得:,,∴2.解下列方程组(1)(2)(3)(4).故原方程组的解为故原方程组的解为)原方程组可化为.所以原方程组的解为,x=代入×﹣.所以原方程组的解为3.解方程组:解:原方程组可化为所以方程组的解为4.解方程组:)原方程组化为y=.所以原方程组的解为5.解方程组:解:即解得所以方程组的解为6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?的二元一次方程组,.y=x+y=y=x+7.解方程组:(1);(2).)原方程组可化为,∴方程组的解为;)原方程可化为即∴方程组的解为.8.解方程组:解:原方程组可化为则原方程组的解为9.解方程组:解:原方程变形为:y=解之得10.解下列方程组:(1)(2)),代入﹣=所以原方程组的解为)原方程组整理为所以原方程组的解为11.解方程组:(1)(2),解得∴原方程组可化为解得∴∴原方程组的解为12.解二元一次方程组:(1);(2).则方程组的解是;)此方程组通过化简可得:则方程组的解是.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.)把代入方程组得解得:.把代入方程组得解得:.∴方程组为则原方程组的解是14.x=y=∴原方程组的解为15.解下列方程组:(1);(2).)化简整理为故原方程组的解为,故原方程组的解为16.解下列方程组:(1)(2)∴原方程组的解为)原方程组可化为∴原方程组的解为。
二元一次方程组专项练习及答案

《二元一次方程组》专项练习及答案§二元一次方程组一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x 表示y ,则y= ,用y 表示x ,则x=3、已知方程(k 2-1)x 2+(k+1)x+(k-7)y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2(5-x)-3(y-2)=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若(4x-3)2+|2y+1|=0,则x+2= 。
7、方程组⎩⎨⎧==+b xy a y x 的一个解为⎩⎨⎧==32y x ,那么这个方程组的另一个解是 。
:8、若21=x 时,关于y x 、的二元一次方程组⎩⎨⎧=-=-212by x y ax 的解互为倒数,则=-b a 2 。
二、选择题1、方程2x-3y=5,xy=3,33=+yx ,3x-y+2z=0,62=+y x 中是二元一次方程的有( )个。
A、1 B、2 C、3 D、4 2、方程2x+y=9在正整数范围内的解有( )A 、1个B 、2个C 、3个D 、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是( )A 、10x+2y=4B 、4x-y=7C 、20x-4y=3D 、15x-3y=6 4、若是m y x 25与2214-++n m n y x 同类项,则n m -2的值为 ( )A 、1B 、-1C 、-3D 、以上答案都不对:5、在方程(k 2-4)x 2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k 值为( )A 、2B 、-2C 、2或-2D 、以上答案都不对. 6、若⎩⎨⎧-==12y x 是二元一次方程组的解,则这个方程组是( )A 、⎩⎨⎧=+=-5253y x y xB 、⎩⎨⎧=--=523x y x yC 、⎩⎨⎧=+=-152y x y xD 、⎩⎨⎧+==132y x y x7、在方程3)(3)(2=--+x y y x 中,用含x 的代数式表示y ,则 ( )A 、35-=x yB 、3--=x yC 、35+=x yD 、35--=x y 8、已知x=3-k,y=k+2,则y与x的关系是( )A、x+y=5 B、x+y=1 C、x-y=1 D、y=x-1 9、下列说法正确的是( )A、二元一次方程只有一个解)B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解 D、三元一次方程组一定由三个三元一次方程组成10、若方程组⎩⎨⎧=+=+16156653y x y x 的解也是方程3x+ky=10的解,则k的值是( =)A、k=6 = B、k=10 C、k=9 D、k=101 三、解答题1、解关于x 的方程)1(2)4)(1(+-=--x a x a a2、已知方程组⎩⎨⎧=+=+c y ax y x 27,试确定c a 、的值,使方程组:)(1)有一个解;(2)有无数解;(3)没有解3、关于y x 、的方程3623-=+k y kx ,对于任何k 的值都有相同的解,试求它的解。
(完整版)二元一次方程组练习题(含答案),推荐文档
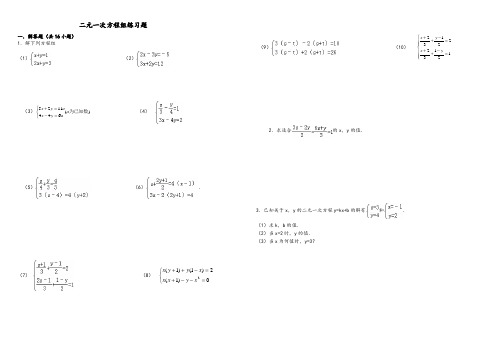
二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x ﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考解二元一次方程组.点:专题:计算题. 分析: 先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法. 解答:解:原方程组可化为, ①×4﹣②×3,得 7x=42, 解得x=6.把x=6代入①,得y=4. 所以方程组的解为.点评: ;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点: 解二元一次方程组. 专题: 计算题. 分析: 把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单. 解答:解:(1)原方程组化为,①+②得:6x=18, ∴x=3.代入①得:y=.所以原方程组的解为. 点评: 要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点: 解二元一次方程组. 专题: 计算题;换元法. 分析: 本题用加减消元法即可或运用换元法求解. 解答:解:,①﹣②,得s+t=4, ①+②,得s ﹣t=6, 即, 解得.所以方程组的解为.点评: 此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?考点: 解二元一次方程组. 专题: 计算题. 分析:(1)将两组x ,y 的值代入方程得出关于k 、b 的二元一次方程组,再运用加减消元法求出k 、b 的值.(2)将(1)中的k 、b 代入,再把x=2代入化简即可得出y 的值. (3)将(1)中的k 、b 和y=3代入方程化简即可得出x 的值.解答: 解:(1)依题意得:①﹣②得:2=4k , 所以k=, 所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x ﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a 、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.。
二元一次方程组练习题含答案

二元一次方程组专题训练1.⎩⎨⎧=-=+33651643y x y x 2. ⎩⎨⎧=+=-6251023x y x y ⎩⎨⎧=-=+19542023b a b a 1、 2、 3、 ⎩⎨⎧=-=+1572532y x y x4、⎩⎨⎧=+-=18435276t s t s 5、 ⎩⎨⎧=-=+574973p q q p 6、⎩⎨⎧=-=+42634y x y x7、⎩⎨⎧-=-=+22223n m n m 8、⎩⎨⎧=--=-495336y x y x 9、10、⎩⎨⎧=-=-y x y x 23532 11、⎩⎨⎧=-=+124532n m n m12、⎩⎨⎧=+=+10232556y x y x13、⎩⎨⎧=+=+2.54.22.35.12y x y x 14、⎪⎩⎪⎨⎧=-+-=+6)(3)1(26132y x x y x15、⎪⎩⎪⎨⎧=+--=-+-04235130423512y x y x 16、⎪⎩⎪⎨⎧=--=+-4323122y x y x yx17、⎪⎩⎪⎨⎧-=-++=-+52251230223x y x y x二元一次方程组练习题一、选择题:1.下列方程中,是二元一次方程的是( ) A .3x -2y=4z B .6xy+9=0 C .1x+4y=6 D .4x=2.下列方程组中,是二元一次方程组的是( )A .228423119...23754624x y x y a b xBCD x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩3.二元一次方程5a -11b=21 ( )A .有且只有一解B .有无数解C .无解D .有且只有两解4.方程y=1-x 与3x+2y=5的公共解是( )A .3333...2422x x x x B C D y y y y ==-==-⎧⎧⎧⎧⎨⎨⎨⎨===-=-⎩⎩⎩⎩5.若│x -2│+(3y+2)2=0,则的值是( )A .-1B .-2C .-3D .326.方程组43235x y kx y -=⎧⎨+=⎩的解与x 与y 的值相等,则k 等于( )7.下列各式,属于二元一次方程的个数有( )①xy+2x -y=7; ②4x+1=x -y ; ③1x+y=5; ④x=y ; ⑤x 2-y 2=2⑥6x -2y ⑦x+y+z=1 ⑧y (y -1)=2y 2-y 2+x A .1 B .2 C .3 D .48.某年级学生共有246人,其中男生人数y 比女生人数x 的2倍少2人,•则下面所列的方程组中符合题意的有( ) A .246246216246 (22222222)x y x y x y x y B C D y x x y y x y x +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨=-=+=+=+⎩⎩⎩⎩ 二、填空题9.已知方程2x+3y -4=0,用含x 的代数式表示y 为:y=_______;用含y 的代数式表示x 为:x=________. 10.在二元一次方程-12x+3y=2中,当x=4时,y=_______;当y=-1时,x=______.11.若x 3m -3-2y n -1=5是二元一次方程,则m=_____,n=______.12.已知2,3x y =-⎧⎨=⎩是方程x -ky=1的解,那么k=_______.13.已知│x -1│+(2y+1)2=0,且2x -ky=4,则k=_____.14.二元一次方程x+y=5的正整数解有______________. 15.以57x y =⎧⎨=⎩为解的一个二元一次方程是_________. 16.已知2316x mx y y x ny =-=⎧⎧⎨⎨=--=⎩⎩是方程组的解,则m=_______,n=______.三、解答题17.当y=-3时,二元一次方程3x+5y=-3和3y -2ax=a+2(关于x ,y 的方程)•有相同的解,求a 的值.18.如果(a -2)x+(b+1)y=13是关于x ,y 的二元一次方程,则a ,b 满足什么条件?19.二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x ,y 的值相等,求k .20.已知x,y是有理数,且(│x│-1)2+(2y+1)2=0,则x-y的值是多少?21.已知方程12x+3y=5,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩.22.根据题意列出方程组:(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,•问明明两种邮票各买了多少枚?(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;•若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?23.方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解?24.(开放题)是否存在整数m ,使关于x 的方程2x+9=2-(m -2)x 在整数范围内有解,你能找到几个m 的值?你能求出相应的x 的解吗?《二元一次方程组》单元测试题一、选择题(每题3分,共30分)1.下列方程组中,是二元一次方程组的是( ).(A ) 2311089x y x y ⎧+=⎨-=-⎩ (B )426xy x y =⎧⎨+=⎩ (C )21734x y y x -=⎧⎪⎨-=-⎪⎩(D )24795x y x y +=⎧⎨-=⎩2.二元一次方程组⎩⎨⎧==+xy y x 2,102的解是( )(A )⎩⎨⎧==;3,4y x (B )⎩⎨⎧==;6,3y x (C )⎩⎨⎧==;4,2y x (D )⎩⎨⎧==.2,4y x 3.根据图1所示的计算程序计算y 的值,若输入2=x , 则输出的y 值是( )(A )0 (B )2- (C )2 (D )44.如果2315a b 与114x x y a b ++-是同类项,则x ,y 的值是( )(A )⎩⎨⎧==31y x (B )⎩⎨⎧==22y x (C )⎩⎨⎧==21y x (D )⎩⎨⎧==32y x 5.已知12x y =⎧⎨=⎩ 是方程组120.ax y x by +=-⎧⎨-=⎩,的解,则a +b = ( ).(A )2 (B )-2 (C )4 (D )-46.如图2,AB ⊥BC ,∠ABD 的度数比∠DBC 的度数的两倍少15°,设∠ABD 和∠DBC 的度数分别为x 、y ,那么下面可以求出这两个角的度数的方程组是( )(A )9015x y x y +=⎧⎨=-⎩ (B )90215x y x y +=⎧⎨=-⎩(C )90152x y x y +=⎧⎨=-⎩ (D )290215x x y =⎧⎨=-⎩ADBC图2y °x °7.如果⎩⎨⎧-==23y x 是方程组⎪⎩⎪⎨⎧=+=+53121ny mx ny mx 的解,则一次函数y =mx +n 的解析式为( )(A )y =-x +2 (B )y =x -2 (C )y =-x -2(D )y =x +28.已知{21x y ==是二元一次方程组{81mx ny nx my +=-=的解,则2m -n 的算术平方根为( )(A )2± (B(C )2 (D )49.如果二元一次方程组⎩⎨⎧=+=-ay x ay x 3的解是二元一次方程0753=--y x 的一个解,那么a 的值是( )(A )3 (B )5 (C )7 (D )910.如图3,一次函数b ax y +=1和a bx y +=2(a ≠0,b ≠0)在同一坐标系的图象.则⎩⎨⎧+=+=a bx y b ax y 21的解⎩⎨⎧==n y mx 中( )o(A ) m >0,n >0 (B )m >0,n <0 (C ) m <0,n >0 (D )m <0,n <0 二、填空题(每小题4分,共20分)11.若关于x ,y 的二元一次方程组23-12-2x y k x y +=⎧⎨+=⎩的解满足x +y =1,则k 的取值范围是 .12.若直线7+=ax y 经过一次函数1234-=-=x y x y 和的交点,则a 的值 是 .13.已知2x -3y =1,用含x 的代数式表示y ,则y = , 当x =0时,y = .14.一个两位数的十位数字与个位数字的和为8,若把这个两位数加上18,正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数,则原来的两位数为_______.15.如图4,点A 的坐标可以看成是方程组 的解. 三、解答题16.解下列方程组(每小题6分,共12分)(1) ⎩⎨⎧-=--=-.2354,42y x y x (2)⎪⎩⎪⎨⎧=-+=+1323241y x x y17.已知⎩⎨⎧==34y x 是关于x ,y 的二元一次方程组⎩⎨⎧-=--=+21by x y ax 的解,求出a +b 的值.18.(8分)为了净化空气,美化环境,我市青羊区计划投资1.8万元种银杏和芙蓉树共80棵,已知某苗圃负责种活以上两种树苗的价格分别为:300元/棵,200元/棵,问可种银杏树和芙蓉树各多少棵?19.(10分)已知22012()x y +与20132--y x 的值互为相反数,求:(1)x 、y 的值; (2)20122013y x +的值.20.(本题12分)如图5,成都市某化工厂与A ,B 两地有公路和铁路相连.这家工厂从A 地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B 地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米).这两次运输共支出公路运费15000元,铁路运费97200元.请计算这批产品的销售款比原料费和运输费的和多多少元? (1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲: 1.5(2010)1.2(110120)x y x y ⎧+=⎪⎨+=⎪⎩乙: 1.5(2010)800010001.2(11012080001000x y x y ⎧⋅+⋅=⎪⎪⎨⎪⋅+⋅=⎪⎩根据甲、乙两名同学所列方程组,请你分别指出未知数x 、y 表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.甲:x 表示_____________________,y 表示________________________乙:x 表示_____________________,y 表示________________________(2)甲同学根据他所列方程组解得x =300.请你帮他解出y 的值,并解决该实际问题.答案:一、选择题1.D 解析:掌握判断二元一次方程的三个必需条件:①含有两个未知数;②含有未知数的项的次数是1;③等式两边都是整式.2.A 解析:二元一次方程组的三个必需条件:①含有两个未知数,②每个含未知数的项次数为1;③每个方程都是整式方程.3.B 解析:不加限制条件时,一个二元一次方程有无数个解.4.C 解析:用排除法,逐个代入验证.5.C 解析:利用非负数的性质.6.B7.C 解析:根据二元一次方程的定义来判定,•含有两个未知数且未知数的次数不超过1次的整式方程叫二元一次方程,注意⑧整理后是二元一次方程.8.B二、填空题9.424332x y--10.43-1011.43,2 解析:令3m-3=1,n-1=1,∴m=43,n=2.12.-1 解析:把2,3xy=-⎧⎨=⎩代入方程x-ky=1中,得-2-3k=1,∴k=-1.13.4 解析:由已知得x-1=0,2y+1=0,∴x=1,y=-12,把112xy=⎧⎪⎨=-⎪⎩代入方程2x-ky=4中,2+12k=4,∴k=1.14.解:12344321x x x xy y y y====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩解析:∵x+y=5,∴y=5-x,又∵x,y均为正整数,∴x为小于5的正整数.当x=1时,y=4;当x=2时,y=3;当x=3,y=2;当x=4时,y=1.∴x+y=5的正整数解为12344321x x x xy y y y====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩15.x+y=12 解析:以x与y的数量关系组建方程,如2x+y=17,2x-y=3等,此题答案不唯一.16.1 4 解析:将2316x mx yy x ny=-=⎧⎧⎨⎨=--=⎩⎩代入方程组中进行求解.三、解答题17.解:∵y=-3时,3x+5y=-3,∴3x+5×(-3)=-3,∴x=4,∵方程3x+5y=•-•3•和3x-2a x=a+2有相同的解,∴3×(-3)-2a×4=a+2,∴a=-119.18.解:∵(a-2)x+(b+1)y=13是关于x,y的二元一次方程,∴a-2≠0,b+1≠0,•∴a≠2,b≠-1解析:此题中,若要满足含有两个未知数,需使未知数的系数不{512+-=-=x y x y 为0.(•若系数为0,则该项就是0)19.解:由题意可知x=y ,∴4x+3y=7可化为4x+3x=7,∴x=1,y=1.将x=1,y=•1•代入kx+(k -1)y=3中得k+k -1=3, ∴k=2 解析:由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值. 20.解:由(│x │-1)2+(2y+1)2=0,可得│x │-1=0且2y+1=0,∴x=±1,y=-12.当x=1,y=-12时,x -y=1+12=32; 当x=-1,y=-12时,x -y=-1+12=-12.解析:任何有理数的平方都是非负数,且题中两非负数之和为0, 则这两非负数(│x │-1)2与(2y+1)2都等于0,从而得到│x │-1=0,2y+1=0.21.解:经验算41x y =⎧⎨=⎩是方程12x+3y=5的解,再写一个方程,如x -y=3. 22.(1)解:设0.8元的邮票买了x 枚,2元的邮票买了y 枚,根据题意得130.8220x y x y +=⎧⎨+=⎩.(2)解:设有x 只鸡,y 个笼,根据题意得415(1)y xy x +=⎧⎨-=⎩. 23.解:满足,不一定.解析:∵2528x y x y +=⎧⎨-=⎩的解既是方程x+y=25的解,也满足2x -y=8,•∴方程组的解一定满足其中的任一个方程,但方程2x -y=8的解有无数组,如x=10,y=12,不满足方程组2528x y x y +=⎧⎨-=⎩.24.解:存在,四组.∵原方程可变形为-mx=7,∴当m=1时,x=-7;m=-1时,x=7;m=•7时,x=-1;m=-7时x=1.参考答案一、1-5、DCDCB 6-10、BDCCA二、11.k=2; 12.-6; 13.213x -,31-; 14. 35;15.三、16.(1)x=0.5,y=5 (2)x=-3 , y=37-17.a+b=118.设银杏树为x ,芙蓉树为y.由题意可得:80, 30020018000.x yx y==⎧⎨+=⎩解得2060 xy=⎧⎨=⎩19.2 1120122013=+⇒⎩⎨⎧-==yxyx20.解:(1)甲:x表示产品的重量,y表示原料的重量乙:x表示产品销售额,y表示原料费甲方程组右边方框内的数分别为15000,97200,乙同甲(2)将x=300代入原方程组解得y=400 ∴产品销售额为300×8000=2400000元原料费为400×1000=400000元又∵运输费为15000+97200=112200元∴这批产品的销售款比原料费和运输费的和多2400000–(400000+112200)=1887800元。
二元一次方程组计算题50道(答案)

中 考 真 题 50 道中考真题之《二元一次方程组计算题》-----专项练习50题(有答案)1.(2012•德州)已知,则a+b 等于( )A. 3 B C. 2 D. 1 2.(2012菏泽)已知⎩⎨⎧==12y x 是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解,则n m -2的算术平方根为( )A .±2B .2C .2D . 43.(2012临沂)关于x 、y 的方程组3,x y m x my n -=⎧⎨+=⎩的解是1,1,x y =⎧⎨=⎩ 则m n -的值是( )A .5B .3C .2D .1 4.(2012•杭州)已知关于x ,y 的方程组,其中﹣3≤a≤1,给出下列结论:①是方程组的解;②当a=﹣2时,x ,y 的值互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a 的解; ④若x≤1,则1≤y≤4. 其中正确的是( )A .①②B .②③C .②③④D .①③④5. (2012广东湛江) 请写出一个二元一次方程组 ,使它的解是.6.(2012广东)若x ,y 为实数,且满足|x ﹣3|+=0,则()2012的值是 1 .7.(2012安顺)以方程组的解为坐标的点(x ,y )在第 象限.8.(2012•连云港)方程组的解为 .9.(2012•广州)解方程组.10.(2012广东)解方程组:.11.(2012•黔东南州)解方程组.12、(2012湖南常德)解方程组:⎩⎨⎧==+1-25y x y x13. (2011湖南益阳,2,4分)二元一次方程21-=x y 有无数多个解,下列四组值中不是..该方程的解的是 A .012x y =⎧⎪⎨=-⎪⎩B .11x y =⎧⎨=⎩C .10x y =⎧⎨=⎩D .11x y =-⎧⎨=-⎩14. (2011四川凉山州,3,4分)下列方程组中是二元一次方程组的是( )A .12xy x y =⎧⎨+=⎩B . 52313x y y x-=⎧⎪⎨+=⎪⎩ C .20135x z x y +=⎧⎪⎨-=⎪⎩ D .5723z x y =⎧⎪⎨+=⎪⎩15. (2011广东肇庆,4,3分)方程组⎩⎨⎧=+=-422y x y x 的解是A .⎩⎨⎧==21y xB .⎩⎨⎧==13y xC .⎩⎨⎧-==20y xD .⎩⎨⎧==02y x16. (2011山东东营,4,3分)方程组31x y x y +=⎧⎨-=-⎩,的解是①②A .12.x y =⎧⎨=⎩, B .12.x y =⎧⎨=-⎩, C .21.x y =⎧⎨=⎩, D .01.x y =⎧⎨=-⎩,17. (2011山东枣庄,6,3分)已知2,1x y =⎧⎨=⎩是二元一次方程组7,1ax by ax by +=⎧⎨-=⎩的解,则a b -的值为( ) A .-1 B .1 C .2 D .3 18. (2011安徽芜湖,13,5分)方程组237,38.x y x y +=⎧⎨-=⎩的解是 .19. (2011江西,12,3分)方程组257x y x y ì+=ïïíï-=ïî的解是 . 20. (2011福建泉州,12,4分)已知x 、y 满足方程组⎩⎨⎧=+=+,42,52y x y x 则x -y 的值为.21. (2011山东潍坊,15,3分)方程组524050x y x y --=⎧⎨+-=⎩的解是___________________.22. (2011江西南昌,12,3分)方程组257x y x y ì+=ïïíï-=ïî的解是 .23. (2011安徽芜湖,13,5分)方程组237,38.x y x y +=⎧⎨-=⎩的解是 .24. (2011湖北鄂州,7,3分)若关于x ,y 的二元一次方程组3133x y ax y +=+⎧⎨+=⎩的解满足2x y +<,则a 的取值范围为______.25. (2011湖南怀化,18,6分)解方程组:38.53 4.x y x y +=⎧⎨-=⎩26. (2011上海,20,10分)解方程组:222,230.x y x xy y -=⎧⎨--=⎩27.(2011湖北黄石,20,8分)解方程:)10553(4222=--+--y x y x 。
二元一次方程组练习题(含答案)

二元一次方程组练习题一.解答题(共16 小题)x2y11.解下列方程组32( 9)( 10)2x21y ( 1)( 2)312( 3)5x2 y11a(a为已知数 )( 4)4 x 4 y6a2.求适合的x,y的值.(5)(6).3.已知关于x, y 的二元一次方程y=kx+b 的解有和.( 1)求 k, b 的值.( 2)当 x=2 时, y 的值.( 3)当 x 为何值时, y=3?x( y 1) y(1 x)2(7)(8)x(x 1) y x 20..1.解下列方程组(1)(2);(9)(10);(3);(4)2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错(5).(6)了方程组中的b,而得解为.( 1)甲把 a 看成了什么,乙把 b 看成了什么?(2)求出原方程组的正确解.( 7)(8)word 版本..二元一次方程组解法练习题参精考选答案与试题解析故原方程组的解为.一.解答题(共 16 小题)( 2)①× 3﹣②×2得,﹣ 13y=﹣39,1.求适合的 x, y 的值.解得, y=3,把 y=3 代入①得,2x﹣3×3=﹣ 5,解得 x=2.考点:解二元一次方程组.故原方程组的解为.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出 y 的值,继而求出x 的值.( 3)原方程组可化为,解答:解:由题意得:,①+②得, 6x=36,x=6,①﹣②得, 8y=﹣ 4,由( 1)×2 得: 3x﹣ 2y=2( 3),由( 2)×3 得: 6x+y=3 ( 4),y=﹣.所以原方程组的解为.(3)×2得: 6x﹣ 4y=4( 5),(5)﹣( 4)得: y=﹣,( 4)原方程组可化为:,把 y 的值代入( 3)得: x=,①× 2+②得, x=,∴.把x=代入②得,3×﹣4y=6,y=﹣.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组所以原方程组的解为.(1)(2)(3)(4).考点:解二元一次方程组.分析:( 1)(2)用代入消元法或加减消元法均可;( 3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣ 2,解得 x=2,把x=2 代入①得, 2+y=1,解得 y=﹣ 1.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为 1 时,宜用代入法.3.解方程组:考解二元一次方程组.word 版本..点:专计算题.题:分先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.析:解答:解:原方程组可化为,考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4 ,①+②,得 s﹣t=6 ,①× 4﹣②× 3,得7x=42,解得 x=6.把 x=6 代入①,得y=4.所以方程组的解为.点;评:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于 x, y 的二元一次方程y=kx+b 的解有和.4.解方程组:( 1)求 k, b 的值.( 2)当 x=2 时, y 的值.( 3)当 x 为何值时, y=3?考点:解二元一次方程组.专题:计算题.考点:解二元一次方程组.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.专题:计算题.解答:分析:( 1)将两组 x, y的值代入方程得出关于k、 b 的二元一次方程组,再运用加减消元解:(1)原方程组化为,法求出 k、 b 的值.①+②得: 6x=18,∴x=3.代入①得: y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.( 2)将( 1)中的 k、b 代入,再把x=2 代入化简即可得出y 的值.( 3)将( 1)中的 k、b 和 y=3 代入方程化简即可得出x 的值.解答:解:( 1)依题意得:①﹣②得: 2=4k,所以 k=,所以 b=.5.解方程组:( 2)由 y= x+,word 版本.把x=2 代入,得 y= .(3)由 y= x+把y=3 代入,得 x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,( 2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①× 2﹣②得:y=﹣ 1,将 y=﹣ 1 代入①得:x=1.∴方程组的解为;( 2)原方程可化为,即,①× 2+②得:17x=51,x=3,将x=3 代入 x﹣4y=3 中得:y=0.∴方程组的解为..点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得 10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把 x=3 代入第一个方程,得4y=11,y=.word 版本..化和运用.解之得.11.解方程组:点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:( 1)运用代入法,把①代入②,可得出x, y 的值;( 2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y) +2y=﹣ 1,所以 y=﹣,把y=﹣代入③,得 x=4﹣ = .所以原方程组的解为.(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组( 1)需要先化简,再根据方程组的特点选择解法;方程组( 2)采用换元法较简单,设x+y=a, x﹣ y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设 x+y=a, x﹣ y=b,∴原方程组可化为,解得,∴∴原方程组的解为.( 2)原方程组整理为,点评:此题考查了学生的计算能力,解题时要细心.③× 2﹣④× 3,得 y= ﹣24,把 y=﹣ 24 代入④,得 x=60,12.解二元一次方程组:所以原方程组的解为( 1);.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强word 版本.(2).考点:解二元一次方程组.专题:计算题.分析:( 1)运用加减消元的方法,可求出x、 y 的值;( 2)先将方程组化简,然后运用加减消元的方法可求出x、 y 的值.解答:解:(1)将①× 2﹣②,得15x=30,x=2,把 x=2 代入第一个方程,得y=1.则方程组的解是;( 2)此方程组通过化简可得:,①﹣②得: y=7,把 y=7 代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把 a 看成了什么,乙把 b 看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:( 1)把甲乙求得方程组的解分别代入原方程组即可;( 2)把甲乙所求的解分别代入方程②和①,求出正确的a、 b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,.得,解得:.把代入方程组,得,解得:.∴甲把 a 看成﹣ 5;乙把 b 看成 6;( 2)∵正确的 a 是﹣ 2, b 是 8,∴方程组为,解得: x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由( 1) +( 2),并解得x=(3),把( 3)代入( 1),解得y=word 版本.∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①× 3,得 3x+3y=1500③,②﹣③,得x=350.把x=350 代入①,得 350+y=500,∴y=150.故原方程组的解为.( 2)化简整理为,①× 5,得 10x+15y=75③,②× 2,得 10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1 代入①,得 2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程..16.解下列方程组:( 1)( 2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①× 2﹣②得: x=1,将 x=1 代入①得:2+y=4,y=2.∴原方程组的解为;( 2)原方程组可化为,①× 2﹣②得:﹣y=﹣ 3,y=3.将 y=3 代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.word 版本。
二元一次方程组计算题60题

二元一次方程组计算题60题1.将方程组改写为标准形式:2x+9y=81,3x+y=34.2.将方程组改写为标准形式:9x+4y=35,8x+3y=30.3.将方程组改写为标准形式:7x+2y=52,7x+4y=62.4.将方程组改写为标准形式:4x+6y=54,9x+2y=87.5.将方程组改写为标准形式:2x+y=7,2x+5y=19.6.将方程组改写为标准形式:x+2y=21,3x+5y=56.7.将方程组改写为标准形式:5x+7y=52,5x+2y=22.8.将方程组改写为标准形式:5x+5y=65,7x+7y=203.9.将方程组改写为标准形式:8x+4y=56,x+4y=21.10.将方程组改写为标准形式:5x+7y=41,5x+8y=44.11.将方程组改写为标准形式:7x+5y=54,3x+4y=38.12.将方程组改写为标准形式:x+8y=15,4x+y=29.13.将方程组改写为标准形式:3x+6y=24,9x+5y=46.14.将方程组改写为标准形式:9x+2y=62,4x+3y=36.15.将方程组改写为标准形式:9x+4y=46,XXX。
16.将方程组改写为标准形式:9x+7y=135,4x+y=41.17.将方程组改写为标准形式:3x+8y=51,x+6y=27.18.将方程组改写为标准形式:9x+3y=99,4x+7y=95.19.将方程组改写为标准形式:9x+2y=38,3x+6y=18.20.将方程组改写为标准形式:5x+5y=45,7x+9y=69.21.将方程组改写为标准形式:8x+2y=28,7x+8y=62.22.将方程组改写为标准形式:x+6y=14,3x+3y=27.23.将方程组改写为标准形式:7x+4y=67,2x+8y=26.24.将方程组改写为标准形式:5x+4y=52,7x+6y=74.25.将方程组改写为标准形式:7x+y=9,4x+6y=16.26.将方程组改写为标准形式:6x+6y=48,XXX。
二元一次方程专项练习60题+解析答案

一元二次方程专练60题一.解答题(共60小题)1.解二元一次方程组.(1);(2).2.解下列方程组:(1);(2).3.解方程组:(1);(2).4.解方程组.(1);(2).5.解方程组:(1);(2).6.解下列方程组:(1);(2).7.解方程组:(1);(2).8.解二元一次方程组:(1);(2).9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).10.解方程组:(1);(2).11.解下列方程组:(1)(代入消元法);(2)(加减消元法).12.解下列方程组:(1);(2).13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).14.解下列方程组.(1);(2).15.解方程组:(1);(2).16.解下列方程组:(1);(2).17.解二元一次方程组:(1).(2).18.解方程组:(1);(2).19.解方程组:(1);(2).20.用适当的方法解下列方程组:(1)(2).21.解方程组:(1);(2).22.解二元一次方程组:(1);(2).23.解二元一次方程组:(1);(2).24.解方程组:(1);(2).25.解方程组:(1);(2).26.解方程组:(1);(2).27.解方程组:(1);(2).28.解方程组:(1);(2).29.解方程组:(1);(2).30.解方程组:(1);(2).31.解方程组:(1);(2).32.解方程组:(1);(2).33.用适当的方法解方程组:(1);(2).34.解下列方程组:(1);(2).35.解方程组:(1);(2).36.解方程组:(1);(2).37.解方程组:(1);38.解方程组:(1);(2).39.解方程组:(1);(2).40.解下列方程组:(1);41.解下列方程组:(1);(2).42.用加减消元法解方程:(1);(2).43.解二元一次方程组:(1);44.解方程组:(1);(2).45.解方程:(1);(2).46.用适当的方法解下列方程组:(1);47.解方程组:(1);(2).48.解方程组:(1);(2).49.解方程组:(1);(2).50.解方程组:(1);(2).51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.54.已知方程组和方程组的解相同求a、b的值.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b 的值.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.60.已知方程组和有相同的解,求a﹣2b的值.一元二次方程专练60题参考答案与试题解析一.解答题(共60小题)1.解二元一次方程组.(1);(2).【解答】解:(1)①+②,得4x=12,∴x=3.把x=3代入②,得3+2y=3,解得y=0所以原方程组的解为;(2),②化简得:2(x﹣2)﹣3(y﹣2)=6,即2x﹣3y=4③,①+③得:3x=18,解得:x=6,将x=6代入①得:6+3y=14,解得:y=,∴原方程组的解为:.2.解下列方程组:(1);(2).【解答】解:(1),由①得,3x+2y=12③,②×③﹣③×2,得5y=60,解得y=12,将y=12代入③,得3x+24=12,解得x=﹣4,∴原方程组的解为;(2),由①得x+1=5y+10,∴x=5y+9③,由②得6x﹣15﹣12y﹣16=5,整理,得6x﹣12y=36,∴x﹣2y=6④,将③代入④,得5y+9﹣2y=6,解得y=﹣1,将y=﹣1代入③,得x=﹣5+9=4,∴原方程组的解为.3.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x+4x=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②,得6x=24,解得x=4,把x=4代入②,得y=5,故原方程组的解为.4.解方程组.(1);(2).【解答】解:(1),①﹣②得:9y=18,解得:y=2,把y=2代入①中得:3x+10=5,解得:x=﹣,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:24u+27v=36③,③﹣②得:2v=22,解得:v=11,把v=11代入①中得:8u+99=12,解得:u=﹣,∴原方程组的解为:.5.解方程组:(1);(2).【解答】解:(1),①×2﹣②得:5x=﹣5,解得:x=﹣1,将x=﹣1代入①得:﹣3﹣y=﹣4,解得:y=1,故原方程组的解为;(2),①×5+②×3得:19x=19,解得:x=1,将x=1代入①得:2+3y=8,解得:y=2,故原方程组的解为.6.解下列方程组:(1);(2).【解答】解:(1),把②代入①得,6y﹣7﹣y=13,解得y=4;把y=4代入②得,x=6×4﹣7=17,故方程组的解为;(2),①×3﹣②×2得,6x+15y﹣6x﹣4y=24﹣10,解得y=,把y=代入②得,3x+2×=5,解得x=,故方程组的解为.7.解方程组:(1);(2).【解答】解:(1),①+②×2,得11x=33,解得:x=3,把x=3代入①,得9+2y=7,解得:y=﹣1,所以方程组的解是;(2)整理得:,①×2+②,得5x=15,解得:x=3,把x=3代入①,得3+2y=7,解得:y=2,所以方程组的解是.8.解二元一次方程组:(1);(2).【解答】解:(1),①﹣②×2,得7y=﹣14,解得y=﹣2,将y=﹣2代入①,得2x﹣2=2,解得x=2,∴原方程组的解为;(2),由①得,3x+4y=36③,由②得3x﹣2y=9④,③﹣④,得6y=27,解得y=,将y=代入④,得3x﹣9=9,解得x=6,∴原方程组的解为.9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).【解答】解:(1),由②,得y=5﹣3x③,把③代入①,得3x+2(5﹣3x)=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②×2,得7x=21,解得x=3,把x=3代入②,得y=5,故原方程组的解为.10.解方程组:(1);(2).【解答】解:(1),①×4得:8x﹣4y=20③,②+③得:11x=22,解得:x=2,把x=2代入①得:4﹣y=5,解得:y=﹣1,故原方程组的解是:;(2),整理得:,①+②得:8y=24,解得:y=3,把y=3代入②得:x+15=10,解得:x=﹣5,故原方程组的解是:.11.解下列方程组:(1)(代入消元法);(2)(加减消元法).【解答】解:(1),由①得:x=1+2y③,把③代入②,得4(1+2 y)+3y=26,解得:y=2,把y=2代入③,得x=1+2×2=5,所以;(2),由①+②,得7x=21,解得:x=3,把x=3代入①,得2×3+3y=3,解得:y=﹣1,所以.12.解下列方程组:(1);(2).【解答】解:(1)将原方程组化简整理得:,②×4得:8x+20y=28③,③﹣①得:27y=27,解得:y=1,把y=1代入②中得:2x+5=7,解得:x=1,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:9x﹣12y=﹣21③,②×4得:8x+12y=4④,③+④得:17x=﹣17,解得:x=﹣1,把x=﹣1代入②中得:﹣2+3y=1,解得:y=1,∴原方程组的解为:.13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).【解答】解:(1),把①代入②得:4x+3(2x﹣2)=5,解得x=,把x=代入①得:y=2×﹣2=,∴方程组的解为;(2),①×3得:3x+9y=﹣3③,③﹣②得:11y=﹣11,解得:y=﹣1,把y=﹣1代入①得:x﹣3=﹣1,解得:x=2,∴方程组的解为.14.解下列方程组.(1);(2).【解答】解:(1),由①+②得,5x=﹣5,解得x=﹣1,将x=﹣1代入①,得﹣2+5y=8,解得y=2,∴方程组的解为;(2),由①×3,②×2得:,由③+④得,13x=26,解得:x=2,把x=2代入①,得y=4,所以方程组的解为:.15.解方程组:(1);(2).【解答】解:(1),由①得,x=1+2y③,把③代入②,得3(1+2y)﹣y=3,解得y=0,把y=0代入③,得x=1,所以原方程组的解为:;(2)原方程组可化为,①+②得,4x=24,解得x=6,①﹣②得,6y=﹣6,解得y=﹣1,所以原方程组的解为:.16.解下列方程组:(1);(2).【解答】解:(1),①+②,得2x=12,解得x=6,将x=6代入①,得6﹣y=5,解得y=1,∴原方程组的解为;(2)原方程组化为,①﹣②,得25y=10,解得y=,将y=代入①,得5x+6=6,解得x=0,∴原方程组的解为.17.解二元一次方程组:(1).(2).【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:6+2y=0,解得y=﹣3.∴方程组的解是.(2),①×2+②×3得:13x=65,解得x=5.把x=5代入①得:10+3y=16,解得y=2.∴方程组的解是.18.解方程组:(1);(2).【解答】解:(1)对于方程组,①×2得:4x﹣10y=24③,②﹣③得:﹣13y=26,∴y=﹣2,将y=﹣2代入①得:x=1,∴原方程组的解为:.(2)对于方程组,将①代入②得:2×2y+y=5,∴y=1,将y=1代入①得:x=2,∴原方程组的解为:.19.解方程组:(1);(2).【解答】解:(1),①+②得4x=8,∴x=2,把x=2代入①得2+2y=3,,∴原方程组的解是.(2),整理得:,由①得:s=﹣2t③,把③代入②得:t=﹣2;把t=﹣2 代入③得:s=4,∴原方程组的解是.20.用适当的方法解下列方程组:(1)(2).【解答】解:(1),①+②得:6x=18,解得:x=3,把x=3代入①得:y=﹣4,则方程组的解为;(2),把①代入②得:4x﹣14=2,解得:x=4,把x=4代入①得:y=3,则方程组的解为.21.解方程组:(1);(2).【解答】解:(1),原方程可化为:,①+②×5得:46y=46,∴y=1,将y=1代入①得:x=7,∴原方程组得解为:;(2),原方程可化为:,①×4+②得:19x=57,∴x=3,将x=3代入①得:y=0,∴原方程组得解为:.22.解二元一次方程组:(1);(2).【解答】解:(1),②﹣①,得y=1,把y=1代入①,得x=2,故原方程组的解为;(2)原方程组整理,得,②﹣①×2,得7y=7,解得y=1,把y=1代入①,得x=5.故原方程组的解为.23.解二元一次方程组:(1);(2).【解答】解:(1),由②得y=13﹣2x③,把③代入①,得4x﹣3(13﹣2x)=11,解得x=5,把x=5代入③,得y=3,∴这个方程组的解是;(2),①×2﹣②×3,得﹣19y=19,解得y=﹣1.把y=﹣1代入①,得3x+2=5,解得x=1,∴这个方程组的解为.24.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x﹣8(x﹣3)=14,解得x=2,把x=2代入①,得y=﹣1,故原方程组的解为;(2),①×2﹣②,得7x=35,解得x=5,把x=5代入①,得y=0,故原方程组的解为.25.解方程组:(1);(2).【解答】解:(1),由①+②得:4x=8,解得:x=2,将x=2代入①得:2﹣2y=1,解得:y=,∴方程组的解为:;(2),由①可得:x=3﹣2y③,将③代入②得:3(3﹣2y)﹣4y=4,解得:y=,将y=代入③得:x=3﹣2×,解得:x=2,∴原方程组的解为:.26.解方程组:(1);(2).【解答】解:(1),①×2得:4x﹣2y=0③,②+③得:5x=5,解得:x=1,把x=1代入①中得:y=2,∴原方程组的解为:.(2),②×2,8x﹣2y=6③,①+③得:11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,∴原方程组的解为:.27.解方程组:(1);(2).【解答】解:(1),①+②,得7x=35,解得:x=5,把x=5代入①,得10﹣3y=﹣2,解得:y=4,所以方程组的解是;(2),①+②×2,得11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,所以方程组的解是.28.解方程组:(1);(2).【解答】解:(1),把②代入①得y﹣9+3y=7,解得y=4,把y=4代入②得x=4﹣9=﹣5,所以方程组的解为;(2),①×2+②得10x+3x=34+5,解得x=3,把x=3代入②得9+4y=5,解得y=﹣1,所以方程组的解为.29.解方程组:(1);(2).【解答】解:(1),①+②得:4x=8,解得:x=2,把x=2代入①得:2+2y=﹣1,解得:,∴方程组的解为;(2),由②得:y=2x﹣2,把y=2x﹣2代入①得:4x﹣3(2x﹣2)=5,解得:,把代入y=2x﹣2得:,∴方程组的解为.30.解方程组:(1);(2).【解答】解:(1),将①代入②,可得:3x+2x+3=18,解得x=3,把x=3代入①,可得:y=9,∴原方程组的解是.(2),①×2﹣②,可得7y=35,解得y=5,把y=5代入①,可得:x=0,∴原方程组的解是.31.解方程组:(1);(2).【解答】解:(1),把①代入②得:3x+2(2x﹣1)=5,解得:x=1,把x=1代入①得:y=2﹣1=1,故原方程组的解是:;(2),①+②得:3m=6,解得:m=2,把m=2代入①得:2+3n=5,解得:n=1,故原方程组的解是:.32.解方程组:(1);(2).【解答】解:(1)把②代入①中,得3x+2(2x﹣8)=5.解得x=3.把x=3代入②中,得y=2×3﹣8解得y=﹣2.∴这个方程组的解为;(2)①﹣②,得﹣4y=8.解得y=﹣2.把y=﹣2代入①中,得2x+2=10.解得x=4.∴这个方程组的解为.33.用适当的方法解方程组:(1);(2).【解答】解:(1),②﹣①×3得:x=1,把x=1代入①中,解得:y=1,∴这个方程组的解为;(2)方程组整理为:,②×2+①得:5x=30,解得:x=6,把x=6代入②中,解得:y=9,∴这个方程组的解为.34.解下列方程组:(1);(2).【解答】解:(1),将①代入②,得:3x﹣2(2x+1)=2,解得:x=﹣4,把x=﹣4代入①得:y=﹣7,∴方程组的解为:;(2)①×2+②,得:5x=10,解得:x=2,把x=2代入①,得:4+y=1,解得:y=﹣3,∴方程组的解为:.35.解方程组:(1);(2).【解答】解:(1),①+②得,7x=14,解得x=2,把x=2代入①得,3×2+7y=9,解得y=,∴方程组的解是;(2),①×3得,15x+6y=12③,②×2得,16x+6y=14④,④﹣③得,x=2,把x=2代入①得,y=﹣3,∴方程组的解是.36.解方程组:(1);(2).【解答】解:(1),②﹣①得:y=2,把y=2代入①得:,∴方程组的解为:;(2),由③得:y=3﹣2x,把y=3﹣2x代入④得:3x﹣5(3﹣2x)=11,3x﹣15+10x=11,13x=26,x=2,把x=2代入y=3﹣2x得:y=﹣1,∴方程组的解为:.37.解方程组:(1);(2).【解答】解:(1),①×3得:3x﹣15y=0③,②﹣③得:17y=17,解得:y=1,把y=1代入①得:x﹣5=0,解得:x=5,∴原方程组的解为:;(2),把①代入②得:y﹣13﹣6y=7,解得:y=﹣4,把y=﹣4代入①得:x=﹣4﹣13=﹣17,∴原方程组的解为:.38.解方程组:(1);(2).【解答】解:(1),①+②得:5x=25,解得:x=5,把x=5代入①得:5﹣3y=10,解得:y=﹣,故原方程组的解是:;(2),由①得:3x﹣2y=8③,②+③得:6x=12,解得:x=2,把x=2代入②得:6+2y=4,解得:y=﹣1,故原方程组的解是:.39.解方程组:(1);(2).【解答】解:(1),①+②得:3x=12,解得:x=4,把x=4代入①得:4﹣y=2,解得:y=2,则方程组的解为;(2)方程组整理得:,①×4﹣②×3得:﹣7x=﹣14,解得:x=2,把x=2代入①得:4﹣3y=1,解得:y=1,则方程组的解为.40.解下列方程组:(1);(2).【解答】解:(1),由①,得x=y+3③,把③代入②,得3y+9﹣8y=14,解得y=﹣1,把y=﹣1代入①,得x=2,故原方程组的解为;(2),①×2+②,得11x=11,解得x=1,把x=1代入①,得x=﹣2,故原方程组的解为.41.解下列方程组:(1);(2).【解答】解:(1),②代入①,可得x+2x﹣1=2,解得,x=1,将x=1代入②,可得y=1,故方程组的解为.(2),②﹣①,可得,解得,x=3,将x=3代入①,可得y=2,故方程组的解为.42.用加减消元法解方程:(1);(2).【解答】解:(1),①﹣②得:12y=﹣36,即y=﹣3,把y=﹣3代入①得:x=,则方程组的解为;(2)方程组整理得:,①﹣②得:4y=28,即y=7,把y=7代入①得:x=5,则方程组的解为.43.解二元一次方程组:(1);(2).【解答】解:(1)方程整理得,由①+②得:5a+5b=﹣5,即a+b=﹣1③,由①﹣③×2得:b=1,把b=1代入③得:a+1=﹣1,解得a=﹣2,∴方程组的解是.(2),由②得:x=3y﹣2③,把③代入①得:9(3y﹣2)﹣7y﹣12=0,解得y=,把y=代入③得x=﹣2=,∴方程组的解是.44.解方程组:(1);(2).【解答】解:(1),解:①+②得3x=33,解得x=11,把x=11代入①得y=14,∴方程组的解是;(2),解:原方程组可化为,①﹣②得6x=6,解得x=1,把x=1代入①得,∴方程组的解是.45.解方程:(1);(2).【解答】解:(1),①代入②得,2x+(3x+1)=﹣9,解得:x=﹣2,将x=﹣2代入①得,y=﹣5,∴方程组的解为:;(2),①×2+②得,6x+x=14,解得:x=2,将x=2代入①得6﹣2y=5,解得:,∴方程组的解为:.46.用适当的方法解下列方程组:(1);(2).【解答】解:(1),由①﹣②×2得:3y﹣(﹣2y)=1﹣5×2,解得:,将代入②得:,解得:,∴原方程组的解为;(2),由①×2+②得:7x=14,解得:x=2,把x=2代入①得:2×2+y=2,解得:y=﹣2,∴原方程组的解为.47.解方程组:(1);(2).【解答】解:(1),①×3+②得:7y=28,解得:y=4,将y=4代入①得:x=1,∴方程组的解为:;(2)整理得:,①+②×5得:23y=23,解得y=1,把y=1代入①得:5x﹣2=﹣12,解得x=﹣2,∴方程组的解为.48.解方程组:(1);(2).【解答】解:(1),①+②得,2x=6,解得:x=3,把x=3代入①得y=﹣1,∴方程组的解为;(2),①×2,得10x+4y=50③,③﹣②,得7x=35,解得:x=5,把x=5代入①得,25+2y=25,解得:y=0,所以方程组的解为.49.解方程组:(1);(2).【解答】解:(1),整理得:,由①﹣②得:4y=28,解得:y=7,把y=7代入①得:3x﹣7=8,解得:x=5,∴原方程组的解为:;(2),由②﹣①得:5x=15,解得:x=3,把x=3代入①得:y﹣2×3=0,解得:y=6,∴原方程组的解为.50.解方程组:(1);(2).【解答】解:(1),②×3得:15x+3y=21③,①+③得:19x=38,解得:x=2,把x=2代入②得:10+y=7,解得:y=﹣3,故原方程组的解是:;(2),①×2得:2x﹣4y=16③,②+③得:5x=10,解得:x=2,把x=2代入①得:2﹣2y=8,解得:y=﹣3,故原方程组的解是:.51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.【解答】解:(1)由①得x﹣y=1③,将③代入②得:4×1﹣y=0,解得y=4,把y=4代入①得:x﹣4﹣1=0,解得x=5,故原方程组的解是:;(2),整理得:,把③代入④得:2×2+1+15y=50,解得y=3,把y=3代入①得:3x﹣3﹣2=0,解得x=,故原方程组的解是:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.【解答】解:,①×2﹣②×3得:y=4﹣m,把y=4﹣m代入②得:x=2m﹣6,代入x+y=﹣10得:4﹣m+2m﹣6=﹣10,解得:m=﹣8,则原式=(m﹣1)2=81.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.【解答】解:(1)将x=,y=﹣2代入方程组得:,解得:,将x=3,y=﹣7代入方程组得:,解得:,则甲把a错看成了1;乙把b错看成了1;(2)根据(1)得正确的a=2,b=3,则方程组为,解得:.54.已知方程组和方程组的解相同求a、b的值.【解答】解:方程组的解为,由于方程组和方程组的解相同,所以,解得.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b的值.【解答】解:由题意,是bx+y=12的解得5b+2=12,解得b=2.又是x+ay=5的解得3+2a=5,解得a=1,∴5a﹣2b=5×1﹣2×2=1.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.【解答】解:(1)根据题中的新定义化简得:,解得:;(2)根据题中的新定义得:原式=2×(﹣1)+(﹣4)×1=﹣2﹣4=﹣6.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.【解答】解:(1)由题意,将代入bx﹣4y=4,得4b﹣4=4,∴b=2,将代入ax+3y=9,得3a+6=9,∴a=1;(2),①×2﹣②,得y=1.4,将y=1.4代入①得,x=4.8,∴方程组的解为.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.【解答】解:∵6※15=270,8※10=360,∴,解得:,∴﹣2※1=﹣100+4﹣(﹣2)×1=﹣94.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.【解答】解:(1)两方程组化简可得,,∵两方程组同解,∴①×2+②得:7x=21,解得:x=3,把x=3代入①式得:y=1,∴两个方程组的相同解为;(2)把代入方程组可得:①﹣②式得:2a=﹣4,解得:a=﹣2,把a=﹣2代入②式得:b=﹣5,∴(3a﹣b)2023=(﹣6+5)2023=﹣1.60.已知方程组和有相同的解,求a﹣2b的值.【解答】解:联立得:,①×2+②得:11x=11,解得:x=1,把x=1代入②得:y=﹣2,把代入,得,解得:,则a﹣2b=14﹣4=10.。
二元一次方程组的解法精选练习题(含答案)

二元一次方程组的解法精选练习题(含答案)二元一次方程组的解法精选练题一.解答题(共16小题)1.求适合以下方程组的x,y的值。
2.解下列方程组:3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和。
1)求k,b的值。
2)当x=2时,y的值。
3)当x为何值时,y=3?7.解方程组:8.解方程组:9.解方程组:10.解下列方程组:11.解方程组:12.解二元一次方程组:13.在解方程组时。
而得解为。
时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b。
1)甲把a看成了什么,乙把b看成了什么?2)求出原方程组的正确解。
14.15.解下列方程组:16.解下列方程组:参考答案与试题解析一.解答题(共16小题)1.求适合以下方程组的x,y的值。
解析:通过加减消元法或代入法,将两个方程组合并,并解出未知数的值。
解答:由第一个方程式可得:y = x - 1将y代入第二个方程式可得:x^2 + (x - 1)^2 = 10化简得:2x^2 - 2x - 9 = 0解得:x = (2 ± √40) / 4代入第一个方程式得:y = (1 ± √40) / 4因此,方程组的解为:(2 + √40) / 4,(1 + √40) / 4 或 (2 - √40) / 4,(1 - √40) / 4.2.解下列方程组:解析:采用加减消元法或代入法,将未知数的值求出。
解答:1)将第二个方程式代入第一个方程式,得到:2x + 3(2x - 1) = 7解得:x = 1将x代入第一个方程式得:y = -1因此,方程组的解为:1,-1.2)将第一个方程式代入第二个方程式,得到:3(2 - y) - 2y = 1解得:y = 5 / 7将y代入第一个方程式得:x = 8 / 7因此,方程组的解为:8 / 7,5 / 7.3.解方程组:解析:通过加减消元法或代入法,将未知数的值求出。
二元一次方程组计算题专项训练+

二元一次方程组计算题专项训练一、用代入法解下列方程组(1)⎩⎨⎧=+=-5253y x y x (2) ⎩⎨⎧=--=523x y x y二、用加减法解下列方程组(1)⎩⎨⎧-=+-=-53412911y x y x (2)⎩⎨⎧=+=-524753y x y x三、用适当的方法解下列方程组:1、⎩⎨⎧=+=+16156653y x y x2、{3x y 304x 3y 17--=+=(3)⎪⎩⎪⎨⎧=-=+2.03.05.0523151y x y x 4、x 2y+2=02y+22x536⎧⎪⎨⎪⎩---=7⎪⎩⎪⎨⎧=+=+=+634323x z z y y x 8 234x y y z z x +=⎧⎪+=⎨⎪+=⎩四、解答题1、如果1032162312=--+--b a b a y x 是一个二元一次方程,那么数a = b =2、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为多少3、若方程组322,543x y k x y k +=⎧⎨+=+⎩的解之和为x+y=-5,求k 的值,并解此方程组.4、已知方程组4234ax by x y -=⎧⎨+=⎩与2432ax by x y +=⎧⎨-=⎩的解相同,那么a=b=5、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =17的一组解,那么m 的值是多少6、一个星期天,小明和小文同解一个二元一次方程组{ax+by=16bx+ay=1 ① ②小明把方程①抄错,求得的解为{x=1y=3-,小文把方程②抄错,求得的解为{x=3y=2,求原方程组的解。
二元一次方程组解法练习题精选(含答案)

个人精心创作,质量一流,各级通用,希望能得到您的认可。
谢谢!二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为. (1)甲把a 看成了什么,乙把b 看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1); (2).16.解下列方程组:(1)(2)17.方程组2528x y x y +=⎧⎨-=⎩的解是否满足2x -y=8?满足2x -y=8的一对x ,y 的值是否是方程组2528x y x y +=⎧⎨-=⎩的解?二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.解二元一次方程组.考点:分先把两方程变形(去分母),得到一组新的方程,然后在用加减消析:元法消去未知数x,求出y的值,继而求出x的值.解解:由题意得:,答:由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.点评:2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.析:解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b 的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b 的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然评:后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.评:。
二元一次方程组练习的题目100道

二元一次方程组练习题100道(卷一)(范围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( )5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解,那么m 的值为m ≠-5 …………( )8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………( ) 9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( ) 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( ) 11、若|a +5|=5,a +b =1则32-的值为b a ………()12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 二、选择:13、任何一个二元一次方程都有( ) (A )一个解; (B )两个解; (C )三个解; (D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( )(A )5个 (B )6个 (C )7个 (D )8个15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数,那么a 的取值范围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( )(A )2; (B )-1; (C )1; (D )-2;17、在下列方程中,只有一个解的是( ) (A )⎩⎨⎧=+=+0331y x y x(B )⎩⎨⎧-=+=+2330y x y x(C )⎩⎨⎧=-=+4331y x y x(D )⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7 (C )10x +2y =4 (D )20x -4y =3 19、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114yx y x (B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14(B )a =3,b =-7 (C )a =-1,b =9(D )a =-3,b =14 21、若5x -6y =0,且xy ≠0,则yx yx 3545--的值等于( )(A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解 (B )有唯一一个解 (C )有无数多个解 (D )不能确定23、若|3x +y +5|+|2x -2y -2|=0,则2x 2-3xy 的值是( )(A )14 (B )-4 (C )-12 (D )12 24、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4(C )21=k ,b =4 (D )21-=k ,b =-4 三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______ 若x 、y 都是正整数,那么这个方程的解为___________; 26、方程2x +3y =10中,当3x -6=0时,y =_________;27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________; 28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解,则⎩⎨⎧==______________b a ; 29、方程|a |+|b |=2的自然数解是_____________; 30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+my x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______;33、若4x +3y +5=0,则3(8y -x )-5(x +6y -2)的值等于_________;34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________; 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、已知a -3b =2a +b -15=1,则代数式a 2-4ab +b 2+3的值为__________;四、解方程组37、⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm ; 38、)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+; 39、⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x ; 40、⎪⎩⎪⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x ; 41、⎪⎪⎩⎪⎪⎨⎧++=++=+=+6253)23(22)32(32523233y x y x yx y x ; 42、⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x ; 43、⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x ; 44、⎪⎩⎪⎨⎧=+=+=+101216x z z y y x ;45、⎪⎩⎪⎨⎧=-+=+-=-+35351343z y x z y x z y x ; 46、⎪⎪⎨⎧=+-==30325:3:7:4:z y x z x y x ;五、解答题:47x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎨==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
