工业机器人工业机器人课件第二章 数学基础
合集下载
工业机器人技术基础课件(最全)ppt课件

右图就处于a)的奇异状态,直角下示教会报警。
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
直角坐标系
Never Stop Improving
— 6—
1 机器人工坐业标系机器人坐标系
机器人系统 关节坐标系
两者关系???
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
— 2—
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
1 机器人坐标系
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
在分析机器人时会牵涉诸多坐标系,一些是操作者不须关心的,另外一些却是和工艺相 关的。常见的坐标系有: 关节坐标系 基座坐标系 工具坐标系 用户坐标系
Never Stop Improving
px a
p
py
b
1pz
c w
— 12 —
2 机器人位姿变换
坐标轴方向的描述:
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
i、j、k分别是直角坐标系中x、y、Z坐标轴的单位向量。若用齐次坐标来描述x、y、z轴的方向, 则
基坐标系
Never Stop Improving
— 7—
1 机器人工坐业标系机器人坐标系
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
用户坐标系(工件坐标系):
用于描述各个物体或工位的方位的需要。用户常常在自
z
己关心的平面建立自己的坐标系,以方便示教。
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
直角坐标系
Never Stop Improving
— 6—
1 机器人工坐业标系机器人坐标系
机器人系统 关节坐标系
两者关系???
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
— 2—
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
1 机器人坐标系
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
在分析机器人时会牵涉诸多坐标系,一些是操作者不须关心的,另外一些却是和工艺相 关的。常见的坐标系有: 关节坐标系 基座坐标系 工具坐标系 用户坐标系
Never Stop Improving
px a
p
py
b
1pz
c w
— 12 —
2 机器人位姿变换
坐标轴方向的描述:
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
i、j、k分别是直角坐标系中x、y、Z坐标轴的单位向量。若用齐次坐标来描述x、y、z轴的方向, 则
基坐标系
Never Stop Improving
— 7—
1 机器人工坐业标系机器人坐标系
变频器 | PLC | HMI | 伺服驱动器 | 电机 | 大传动 | 新能源
用户坐标系(工件坐标系):
用于描述各个物体或工位的方位的需要。用户常常在自
z
己关心的平面建立自己的坐标系,以方便示教。
《工业机器人技术基础》单元2 工业机器人的基本原理

对机器人的运动进行有效的实时控制
2.5 机器人动力学
2.5.2 机器人动力学方程
重复定位精度(mm) ±0.2-0.5 ±0.5 ±0.2-0.3 ±0.08-0.1 ±0.2-0.5
±0.02-0.03 ±0.06-0.08 ±0.06-0.1
2.2 工业机器人性能指标
2.2.2 其他技术参数
2 工作空间
2.2 工业机器人性能指标
2.2.2 其他技术参数
3 最大工作速度 有的厂家指工业机器人主要自由度上最大的稳定速度,有的厂家 指手臂末端最大的合成速度,对此通常都会在技术参数中加以说明。
2.3 工业机器人位姿描述与坐标变换
2.3.1 坐标系
● 2 柱面坐标系
2.3 工业机器人位姿描述与坐标变换
2.3.1 坐标系
● 3 球面坐标系
2.3 工业机器人位姿描述与坐标变换
2.3.2 工业机器人坐标系
1 基坐标系 2 关节坐标系 3 工件坐标系 4 工具坐标系 5 大地坐标系 6 用户坐标系
2.2.1 工业机器人自由度 4 关节机器人的自由度
(1)SCARA型关节 机器人
2.2 工业机器人性能指标
2.2.1 工业机器人自由度
4 关节机器人的自由度 (2)六轴关节机器人
2.2 工业机器人性能指标
2.2.1 工业机器人自由度
5 并联机器人的自由度
2.2 工业机器人性能指标
2.2.2 其他技术参数
2.4 机器人运动学
2.4.2 机器人运动方程 2 PUMA560机器人运动方程
2.5 机器人动力学
2.5.1 机器人动力学概述
机器人的动力学正问题:已知机器人各关节执行器的驱动力或力矩,求解机器人 各关节的位置、速度、加速度
2.5 机器人动力学
2.5.2 机器人动力学方程
重复定位精度(mm) ±0.2-0.5 ±0.5 ±0.2-0.3 ±0.08-0.1 ±0.2-0.5
±0.02-0.03 ±0.06-0.08 ±0.06-0.1
2.2 工业机器人性能指标
2.2.2 其他技术参数
2 工作空间
2.2 工业机器人性能指标
2.2.2 其他技术参数
3 最大工作速度 有的厂家指工业机器人主要自由度上最大的稳定速度,有的厂家 指手臂末端最大的合成速度,对此通常都会在技术参数中加以说明。
2.3 工业机器人位姿描述与坐标变换
2.3.1 坐标系
● 2 柱面坐标系
2.3 工业机器人位姿描述与坐标变换
2.3.1 坐标系
● 3 球面坐标系
2.3 工业机器人位姿描述与坐标变换
2.3.2 工业机器人坐标系
1 基坐标系 2 关节坐标系 3 工件坐标系 4 工具坐标系 5 大地坐标系 6 用户坐标系
2.2.1 工业机器人自由度 4 关节机器人的自由度
(1)SCARA型关节 机器人
2.2 工业机器人性能指标
2.2.1 工业机器人自由度
4 关节机器人的自由度 (2)六轴关节机器人
2.2 工业机器人性能指标
2.2.1 工业机器人自由度
5 并联机器人的自由度
2.2 工业机器人性能指标
2.2.2 其他技术参数
2.4 机器人运动学
2.4.2 机器人运动方程 2 PUMA560机器人运动方程
2.5 机器人动力学
2.5.1 机器人动力学概述
机器人的动力学正问题:已知机器人各关节执行器的驱动力或力矩,求解机器人 各关节的位置、速度、加速度
工业机器人技术基础-第2版-课件--第1章-工业机器人概论-
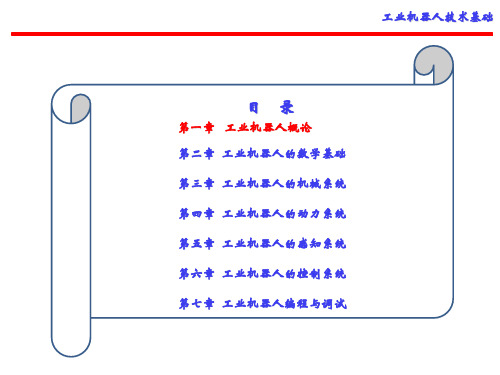
实际作业tact time最大缩 监视ROBOT的姿势、负荷, 设置面积A4尺寸,重量约
特
短15%幅度。附加功能:附 依据实际调整伺服增益/滤
加轴控制、追踪机能、
波。
8kg的新设计小型控制器。 搭载独自开发的5节闭连结
点 Ethernet等提升目标。
冲突检知机能,支持原点 机构及64bitCPU;
参 最大合成速度:5.5m/s 数 最大可搬重量:3.5kg
随着工业机器人的应用越来越广泛,我国也在积极推动我国机器人产业的发展。尤其是进入 “十三.五”以来,国家出台的《机器人产业发展规划(2016-2020)》对机器人产业进行了全面 规划,要求行业、企业搞好系列化、通用化、模块化设计,积极推进工业机器人产业化进程。
第1章 工业机器人概论
工业机器人技术基础
第1章 工业机器人概论
工业机器人技术基础
工业机器人在我国发展概况
中国的机器人产业应走什么道路,如何建立自己的发展模式,确实值得探讨。中国工程院在 2003年12月完成并公开的《我国制造业焊接生产现状与发展战略研究总结报告》中认为,我国应 从“美国模式”着手,在条件成熟后逐步向“日本模式”靠近。
目前,我国基本掌握了工业机器人的结构设计和制造、控制系统硬件和软件、运动学和轨迹规划等技术, 形成了机器人部分关键元器件的规模化生产能力。一些公司开发出的喷漆、弧焊、点焊、装配、搬运等机器人 已经在多家企业的自动化生产线上获得规模应用,弧焊机器人也已广泛应用在汽车制造厂的焊装线上。总体来 看,在技术开发和工程应用水平与国外相比还有一定的差距。主要表现在以下几个方面:
迅猛。由此可见,未来工业机器人的应用依托汽车产业,并迅速向各行业延伸。对于
机器人行业来讲,这是一个非常积极的信号。
《工业机器人技术基础》(第2章)

k 1
只有当左边矩阵的列数等于右边矩阵的行数时,两个矩阵才能相乘,否则 AB 没有意义。
矩阵乘法一般不满足交换律,即一般情况下, AB BA。根据矩阵乘法定义, 矩阵乘法满足下列性质(假定以下运算都能进行)。
2.1
工业机器人的数学基础
2.1.1 矩阵概述
1.矩阵的定义
由 m n 个数 aij (i 1 ,2 , ,m ;j 1 ,2 , ,n) 排成的 m 行 n 列数表,并用括号括起来,即
a11 a12
a21
a22
am1 am2
a1n a11 a12
a2n
或
a21
a22
amn
am1
am 2
a1n
a2
n
amn
称为 m 行 n 列矩阵,简称 m n 矩阵。通常用大写字母 A,B ,C , 表示矩阵, aij 表示矩阵中第 i 行、第 j 列的元素,这个元素可以是实数,也可以是虚数。 一个 m n 矩阵可以简记为 A Amn (aij )mn 。
1 0
0
A diag(1 ,2 ,
,n
)
பைடு நூலகம்
0
2
0
0 0
n
8)数量矩阵
主对角线元素相同的对角矩阵,称为数量矩阵,记为
0
0
A
0
0
0 0
9)单位矩阵 主对角线元素全为 1 的数量矩阵,称为单位矩阵,n 阶单位矩阵简记为 En 或 E ,即
只有当左边矩阵的列数等于右边矩阵的行数时,两个矩阵才能相乘,否则 AB 没有意义。
矩阵乘法一般不满足交换律,即一般情况下, AB BA。根据矩阵乘法定义, 矩阵乘法满足下列性质(假定以下运算都能进行)。
2.1
工业机器人的数学基础
2.1.1 矩阵概述
1.矩阵的定义
由 m n 个数 aij (i 1 ,2 , ,m ;j 1 ,2 , ,n) 排成的 m 行 n 列数表,并用括号括起来,即
a11 a12
a21
a22
am1 am2
a1n a11 a12
a2n
或
a21
a22
amn
am1
am 2
a1n
a2
n
amn
称为 m 行 n 列矩阵,简称 m n 矩阵。通常用大写字母 A,B ,C , 表示矩阵, aij 表示矩阵中第 i 行、第 j 列的元素,这个元素可以是实数,也可以是虚数。 一个 m n 矩阵可以简记为 A Amn (aij )mn 。
1 0
0
A diag(1 ,2 ,
,n
)
பைடு நூலகம்
0
2
0
0 0
n
8)数量矩阵
主对角线元素相同的对角矩阵,称为数量矩阵,记为
0
0
A
0
0
0 0
9)单位矩阵 主对角线元素全为 1 的数量矩阵,称为单位矩阵,n 阶单位矩阵简记为 En 或 E ,即
第2章工业机器人运动学PPT课件

图2-6 点的平移变换
第2章 工业机器人运动学
(2.8)
记为: a′=Trans(Δx, Δy, Δz)a 其中,Trans(Δx, Δy,Δz)称为平移算子,Δx、Δy、Δz分别 表示沿X、Y、Z轴的移动量。 即:
(2.9)
第2章 工业机器人运动学
注: ① 算子左乘: 表示点的平移是相对固定坐标系进行的坐 标变换。 ② 算子右乘: 表示点的平移是相对动坐标系进行的坐标 变换。 ③ 该公式亦适用于坐标系的平移变换、 物体的平移变换, 如机器人手部的平移变换。
图 2-11 连杆的关系参数连杆可以由四个参数来描述,其中两个是连杆 尺寸, 两个表示连杆与相邻连杆的连接关系。
确定连杆的运动类型, 同时根据关节变量即可设计关节 运动副,从而进行整个机器人的结构设计。
已知各个关节变量的值, 便可从基座固定坐标系通过连 杆坐标系的传递, 推导出手部坐标系的位姿形态。
图 2-12 SCARA装配机器人的坐标系
第2章 工业机器人运动学
该机器人的参数如表2.2所示。
连杆 连杆1 连杆2 连杆3
表2.2 SCARA装配机器人连杆参数
转角(变量)θ θ1
两连杆间距离d 连杆长度a
d1=0
a1=l1=100
当α=60°, β=60°, γ=45°时, 矢量为
第2章 工业机器人运动学
4. 动坐标系位姿的描述就是用位姿矩阵对动坐标系原点位
置和坐标系各坐标轴方向的描述。该位姿矩阵为(4×4)的方 阵。如上述直角坐标系可描述为:
(2.4)
第2章 工业机器人运动学
5. 机器人的每一个连杆均可视为一个刚体, 若给定了刚体
αn
扭角
连杆n两关节轴线之间的扭 角,尺寸参数
工业机器人技术基础(最全)最新精选PPT课件

第一关节 动力学方程
第二关节 动力学方
程
4 机器人工动业力机学 器人基础知识
动力学——动力学的部署 将经(正向,逆向?)动力学计算出的力矩, 以前馈的方式,加入到伺服的电流控制环路
4 机器人工动业力机学 器人基础知识
动力学 ——动力学控制器的评价指标 控制性能的好坏主要通过位置跟踪偏差,速度跟踪偏差以及
z
0
z
0
z
0
o
1
? ?
对刚体Q位姿的描述就是对固连于刚体Q`的坐标系O`X`Y`Z`位姿
的描述。
3 机器人运动 学
运动学:机器人运动学的研究对象是机器人各关节位置和机器人 末端位姿之间的关系
机器人运动学包含两个基本问题:
1末.已端知的机位器姿人;各关节的位置,求机器人 2各.已关知节机的器位人置末. 端的位姿,求机器人
关节坐标系下的坐标值均为机器人关节的绝对位 置,方便用户调试点位时观察机器人的绝对位置,避 免机器人出现极限位置或奇异位置
关节坐标系
1 机器人工坐业标机器人基础知识
系
直角坐标系:
直角坐标系,包括很多种,但我们常常狭隘 的将基座坐标系称为直角坐标系。
机器 人末 端
直角坐标系的Z轴即第一轴的Z轴,X轴
时间。
25mm
300m m
25mm
5 机器人工性业能机指器人基础知识
标
机器人性能指标 测量工具:Compugauge机器人性能测试系统,价格约80万人民币
(Dynalog ,美国公司,一直从事机器人性能研究)
位姿准确度和位姿重复性; 多方位位姿准确度变动; 距离准确度和距离重复性; 位置稳定时间和位置超调量; 互换性; 轨迹准确度和轨迹重复性; 拐角偏差; 轨迹速度特性; 最小定位时间; 静态柔顺性; 摆动偏差;
第二关节 动力学方
程
4 机器人工动业力机学 器人基础知识
动力学——动力学的部署 将经(正向,逆向?)动力学计算出的力矩, 以前馈的方式,加入到伺服的电流控制环路
4 机器人工动业力机学 器人基础知识
动力学 ——动力学控制器的评价指标 控制性能的好坏主要通过位置跟踪偏差,速度跟踪偏差以及
z
0
z
0
z
0
o
1
? ?
对刚体Q位姿的描述就是对固连于刚体Q`的坐标系O`X`Y`Z`位姿
的描述。
3 机器人运动 学
运动学:机器人运动学的研究对象是机器人各关节位置和机器人 末端位姿之间的关系
机器人运动学包含两个基本问题:
1末.已端知的机位器姿人;各关节的位置,求机器人 2各.已关知节机的器位人置末. 端的位姿,求机器人
关节坐标系下的坐标值均为机器人关节的绝对位 置,方便用户调试点位时观察机器人的绝对位置,避 免机器人出现极限位置或奇异位置
关节坐标系
1 机器人工坐业标机器人基础知识
系
直角坐标系:
直角坐标系,包括很多种,但我们常常狭隘 的将基座坐标系称为直角坐标系。
机器 人末 端
直角坐标系的Z轴即第一轴的Z轴,X轴
时间。
25mm
300m m
25mm
5 机器人工性业能机指器人基础知识
标
机器人性能指标 测量工具:Compugauge机器人性能测试系统,价格约80万人民币
(Dynalog ,美国公司,一直从事机器人性能研究)
位姿准确度和位姿重复性; 多方位位姿准确度变动; 距离准确度和距离重复性; 位置稳定时间和位置超调量; 互换性; 轨迹准确度和轨迹重复性; 拐角偏差; 轨迹速度特性; 最小定位时间; 静态柔顺性; 摆动偏差;
(完整版)工业机器人技术基础课件(最全)

p
py
b
1pz
c w
2 机器人位姿 变换
坐标轴方向的描述:
i、j、k分别是直角坐标系中x、y、Z坐标轴的单位向量。若用齐次坐标 来描述x、y、z轴的方向,则
X 1 0 0 0T Y 0 1 0 0T Z 0 0 1 0T
1.已知机器人各关节的位置,求机器人 末端的位姿; 2.已知机器人末端的位姿,求机器人 各关节的位置.
3学机器人工运业动机器人基础知识
为什么要研究运动学:机器人的运动无非有两种:PTP(点到点) 及CP(连续运动)
3学机器人工运业动机器人基础知识
运动学的实用方式:
位置反 馈
3 机器人运动
学
D-H参数:
关节 坐标
系
两个关节轴线沿公垂线的距离an,称为连杆长度;另一个是 垂直于an的平面内两个轴线的夹角αn,称为连杆扭角,这两 个参数为连杆的尺寸参数;是沿关节n轴线两个公垂线的距离,
刚体的姿态可由动坐标系的坐标轴方向来表示。 令n、o、a分别为X′、y ′、z ′坐标轴的单位 方向矢量,每个单位方向矢量在固定坐标系上的 分量为动坐标系各坐标轴的方向余弦,用齐次坐 标形式的(4×1)列阵分别表示为:
2 机器人位姿 变换
刚体的位姿可用下面(4×4)矩
阵来描述:
nx ox ax xo
a)4、6轴共线附件,即5轴角度0附件。 b)2、3、5轴关节坐标系原点接近共线,即 已经到达工作范围边界。
c) 5轴关节坐标系原点在Z轴正上方附近。
右图就处于a)的奇异状态,直角下示 教会报警。
直角坐标系
1 系
机器人工坐业标机器人坐标系
工业机器人概述ppt课件

22
③内撑式机械夹持器
内撑式机械夹持器采用四连 杆机构传递撑紧力,如图8-13 所示。
其撑紧方向与上述两种方式 的外夹式相反。钳爪3从工件内 孔撑紧工件,为使撑紧后能准 确地用内孔定位,多采用三个 钳爪(图中只画了两个)。
图8-13 内撑连杆杠杆式夹持器 1-驱动器 2-杆 3-钳爪
直角坐标型工业机器人 圆柱坐标型工业机器人 球坐标型工业机器人 多关节型工业机器人 平面关节型工业机器人
8
1)按操作机构坐标形式分类
①直角坐标型工业机器人
运动部分由三个相互垂直的直 线 移 动 组 成 如 图 8-3 所 示 , 其 工 作空间图形为长方体。各个轴向 的移动距离,可在各个坐标轴上 直接读出,直观性强;易于位置 和姿态的编程计算,定位精度最 高,控制无耦合,结构简单。
图8-l 工业机器人
2
综合上述定义 ,工业机器人有以下三个重要特性: 1) 是一种机械装置,可搬运材料、零件、工具或完成多
种操作和动作功能,即具是有通用性。 2) 可以再编程并具有多样程序流程,这为人-机联系提供
了可能,也使具有独立的柔软性。 3) 有一个自动控别系统,可以在无人的参与下,自动完
成操作作业和动作。
确定一个工业机器人操作机位置时所 需要的独立运动参数的数目称为工业机器 人的运动自由度。
自由度数取决于作业目标所要求的动 作。对于进行二维平面作业需三个自由度; 若要具有随意的位姿,则至少需要六个自 由度;而对于回避障碍作业的工业机器人 则需要有比六个自由度更多的冗余自由度。
工业机器人操作机常采用回转副或移
图8-7 平面关节型工业机器人
13
2)按控制方式分类 ① 点位控制工业机器人
采用点到点的控制方式,它只在目标点处准确控制工 业机器人手部的位姿,完成预定的操作要求,而不对点与 点之间的运动过程进行严格的控制。
③内撑式机械夹持器
内撑式机械夹持器采用四连 杆机构传递撑紧力,如图8-13 所示。
其撑紧方向与上述两种方式 的外夹式相反。钳爪3从工件内 孔撑紧工件,为使撑紧后能准 确地用内孔定位,多采用三个 钳爪(图中只画了两个)。
图8-13 内撑连杆杠杆式夹持器 1-驱动器 2-杆 3-钳爪
直角坐标型工业机器人 圆柱坐标型工业机器人 球坐标型工业机器人 多关节型工业机器人 平面关节型工业机器人
8
1)按操作机构坐标形式分类
①直角坐标型工业机器人
运动部分由三个相互垂直的直 线 移 动 组 成 如 图 8-3 所 示 , 其 工 作空间图形为长方体。各个轴向 的移动距离,可在各个坐标轴上 直接读出,直观性强;易于位置 和姿态的编程计算,定位精度最 高,控制无耦合,结构简单。
图8-l 工业机器人
2
综合上述定义 ,工业机器人有以下三个重要特性: 1) 是一种机械装置,可搬运材料、零件、工具或完成多
种操作和动作功能,即具是有通用性。 2) 可以再编程并具有多样程序流程,这为人-机联系提供
了可能,也使具有独立的柔软性。 3) 有一个自动控别系统,可以在无人的参与下,自动完
成操作作业和动作。
确定一个工业机器人操作机位置时所 需要的独立运动参数的数目称为工业机器 人的运动自由度。
自由度数取决于作业目标所要求的动 作。对于进行二维平面作业需三个自由度; 若要具有随意的位姿,则至少需要六个自 由度;而对于回避障碍作业的工业机器人 则需要有比六个自由度更多的冗余自由度。
工业机器人操作机常采用回转副或移
图8-7 平面关节型工业机器人
13
2)按控制方式分类 ① 点位控制工业机器人
采用点到点的控制方式,它只在目标点处准确控制工 业机器人手部的位姿,完成预定的操作要求,而不对点与 点之间的运动过程进行严格的控制。
工业机器人第二章 工业机器人运动学PPT课件

0T 0T 6A 1A 2A 3A 4A 5A 6
Z0 Z2
Z1
Z2 Z1 Z0
Z4 Z3
Z6 Z5
反向运动学
❖ 反向求解
——在已知手部要达到的目标位姿的情况下求 出各关节变量,以驱动各关节马达,使手部位 姿得到满足。
❖ 机器人运动学逆解问题求解存在若干问题:
解可能不存在; 存在多重解; 求解方法的多样性—分离变量法/直接求解法。
Z2 c2 0 0s2 01 0Y3 0
Z1
s2
0
0
0 1 0
00c2
0
X3
0
0Z2
d2 X2 1
0
1
Y2
A2
A3
A6 Rot (Zz3 5 ,6 )TranZs4 (0,0, H
Z6
X4
Y4
Z3
Z5
Z4
A4
c6
s5Rco6tX3(
s6
Yc3 5s6
z3 ,csZ654 4s)6
Xb
XP-Lcαcβ
Yb = YP-L(sαcγ +cαsβsγ)
(5)
Zb
ZP-L(sαsγ -cαsβcγ)
分析该机构特点,得Xa≡L, Yb≡L, Zc≡L,可建立该机构的位姿约束方程:
XP-Lsβ-L = 0
YP-L(sαcγ +cαsβsγ) -L= 0
(6)
ZP-L(cαsγ +sαsβcγ) -L= 0
A3
s
3
0
c 3 0
0
0
0
1
0
0
1 00 0 1 0
0
0
0
1
0
0
Z0 Z2
Z1
Z2 Z1 Z0
Z4 Z3
Z6 Z5
反向运动学
❖ 反向求解
——在已知手部要达到的目标位姿的情况下求 出各关节变量,以驱动各关节马达,使手部位 姿得到满足。
❖ 机器人运动学逆解问题求解存在若干问题:
解可能不存在; 存在多重解; 求解方法的多样性—分离变量法/直接求解法。
Z2 c2 0 0s2 01 0Y3 0
Z1
s2
0
0
0 1 0
00c2
0
X3
0
0Z2
d2 X2 1
0
1
Y2
A2
A3
A6 Rot (Zz3 5 ,6 )TranZs4 (0,0, H
Z6
X4
Y4
Z3
Z5
Z4
A4
c6
s5Rco6tX3(
s6
Yc3 5s6
z3 ,csZ654 4s)6
Xb
XP-Lcαcβ
Yb = YP-L(sαcγ +cαsβsγ)
(5)
Zb
ZP-L(sαsγ -cαsβcγ)
分析该机构特点,得Xa≡L, Yb≡L, Zc≡L,可建立该机构的位姿约束方程:
XP-Lsβ-L = 0
YP-L(sαcγ +cαsβsγ) -L= 0
(6)
ZP-L(cαsγ +sαsβcγ) -L= 0
A3
s
3
0
c 3 0
0
0
0
1
0
0
1 00 0 1 0
0
0
0
1
0
0
工业机器人工业机器人第二章数学基础
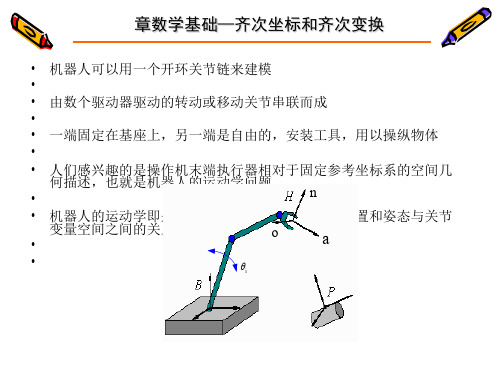
二、方位的描述(旋转矩阵)
为了规定空间某刚体B的方位,设置一直角坐标系{B}与此刚体固接 。用坐标系{B}的三个单位主矢量xB,yB,zB相对于参考坐标系{A}的 方向余弦组成的3×3矩阵
r11 r12 r13
BAR AxB AyB AzB r21 r22 r23
r31 r32 r33
Ap
坐标系{B} 的原点与{A}的原点既
不重合,两者的方位又不同时,用位
置矢量ApB。描述{B}的坐标原点相对
yC
于{A}
的位置,用旋转矩阵
B A
R
描述
Bp xB {B}相对于{A} 的方位,则任一点p在 坐标系{A} 和{B}的描述Ap和Bp具有
xC 如下变换关系
xA ApB。zC
zB
ApBARBpApB。
坐标的关系如下px px,py py,pz pz
可以看出,直角坐标系Oxyz原点的齐次坐标为(0,0,0,α)。 α为 非零实数。齐次坐标(1,0,0,0)T表示Ox轴的无穷远点,同理齐次坐 标(0,1,0,())T和(0,0,1,0) T分别指向Oy轴和0z轴的无穷远点,三 维空间的位置矢量的齐次坐标表达并不是惟一的。但若将ω取为1,则位 置矢量变换后的齐次坐标和矢量的实际坐标就相同了。在机器人学的应 用中ω总是取为1。
AxB• AxB = AyB • AyB = AzB • AzB =1 AxB• AyB = AyB • AzB = AzB • AxB =0
可见,旋转矩阵 是正交的,并且满足条件
A B
R
BAR1BART, BAR1
上标T表示转置 ,• 为行列式符号 。 对应于轴x,y或z作转角为θ的旋转变换,其旋转矩阵分别为
机器人的数学基础ppt课件

P''' 0
1
01
1
-1 0 02 3
;
〔2-14〕 〔2-15〕 〔2-16〕
12
Robotics 数学根底
上述计算方法非常繁琐,可以经过一系列计算得到上述 结果。将式〔2-14〕〔2-15〕〔2-16〕联写为如下方式:
Px
Py
R33
Pz
Pu
Pv
Pw
R3x3为二者之间的关系矩阵,我们令:
0 0 1 0 3 2
0 0 0 1 1 1
R(y,90)
0
1 0 0;;; 7 ;;;7
1 0 0 0 2 3
0
0 0 1
1
1
;
27
Robotics 数学根底
2.3 齐次坐标变换—相对变换
举例阐明: 例1:动坐标系∑0′起始位置与固定参考坐标系∑0重合,动坐标 系∑0′做如下运动:①R(Z,90º) ②R〔y,90º〕 ③Trans(4, -3, 7),求合成矩阵
• [1 0 0 0]T—指向无穷远处的OX轴 • [0 1 0 0]T—指向无穷远处的OY轴 • [0 0 1 0]T—指向无穷远处的OZ轴 • 这样,利用齐次坐标不仅可以规定点的位置,还可
以用来规定矢量的方向。第四个元素非零时,代表点 的位置;第四个元素为零时,代表方向。
; 23
Robotics 数学根底
s0c
0 0 1
将上式1增0广0为0 齐次式:c 0s0
cs00
R (x,)0 0c s cs0 0R (y,)0 s1 0c0 0 0R (z,)s0
c
0
00 10
00 0 1
0 001
工业机器人运动学1

*
手部位姿矢量为从固定参考坐标系OXYZ原点指向手部坐标系{B}原点的矢量p。手部的位姿可由(4×4)矩阵表示:
*
例:手部抓握物体Q,物体为边长2个单位的正立方体,写出表达该手部位姿的矩阵式。
*
解:
因为物体Q形心与手部坐标系0`X`y`z`的坐标原点0’相重合,所以手部位置的(4x1)列阵为:
工业机器人 PTP 运动和 CP 运动
运动轨迹规划
*
1955年Denavit和Hartenberg提出了一种采用矩阵代数的系统而广义的方法,来描述机器人手臂杆件相对于固定参考坐标系的空间几何关系,这种方法是标准、通用的。
这种方法使用4×4齐次变换矩阵来描述两个相邻的机械刚性构件间的空间关系,把正向运动学问题简化为寻求等价的4×4齐次变换矩阵,此矩阵把手部坐标系的空间位移与参考坐标系联系起来。并且该矩阵还可用于推导手臂运动的动力学方程。而逆向运动学问题可采用几种方法来求解。最常用的是矩阵代数、迭代或几何方法。
*
推导如下: 因A点是绕Z轴旋转的, 所以把A与A′投影到XOY平面内, 设OA=r, 则有
同时有
其中, α′=α+θ, 即
*
所以
所以
由于Z坐标不变, 因此有
*
写成矩阵形式为
记为:
A′=Rot(z, θ)A
其中, 绕Z轴旋转算子左乘是相对于固定坐标系,即
*
同理:
工业机器人反向运动学是工业机器人控制的基础,而正向运动学又是反向运动学的基础。
*
运动学正问题
How do I
put my
hand here?
Where is
my hand?
工业机器人技术基础 项目二 工业机器人数学基础

1
0
−1
可见,旋转矩阵 是正交的,并且满足条件:
= , = 1
2.1.1 位姿描述
3.位姿描述
前面已经说明了任一点相对于参考坐标系的位置和姿态的表示方法,
现在进一步说明物体B在空间中的位姿描述。首先在物体B上建立一
个 坐标系, 的坐标系原点选择通常是B的特征点,例如物体的
∙ ∙ ∙
∙ ∙ ∙ =
∙ ∙ ∙
11 12 13
21 22 23 =
31 32 33
=
为旋转矩阵,A为参考坐标系 ,B为与物体固连的坐标系 。
2.1.1 位姿描述
有9个元素,其中有3个元素相互独立。
,
,
是
的三个单位
向量,三者之间存在两两垂直的关系,所以这 9个元素满足6个约束条
件(即正交条件):
∙ = ∙ = ∙
=
൜ ∙ ∙
= =∙=
3.平移变换是坐标系
平移矢量
BORG平移到
即:
=
+
4.旋转变换是 旋转矩阵 到 描述和Bp具有如下变换关系: =
5.复合变换就是进行平移变换后再进行旋转变换
2.2工业机器人的机器人运动学基础
2.2 工业机器人的机器人运动学基础
学
转矩阵 描述 相对于的 方位。对于任一点p在两坐标系 和 中的描述
和Bp具有以下变换关系:Ap= + BORG
21机器人课件.pptx

1]T
• 所以,坐标系{B}的(4×4)矩阵表达式为
2.手部位置和姿态的表示
机器人手部的位置和姿态也可以用固连于手 部的坐标系{B}的位姿来表示,如图2-6所示。
坐标系{B}可以这样来确定: 取手部的中心点为原点OB: 关节轴为ZB轴, ZB铀的单 位方向矢量O称为接近矢 量,指向朝外;二手指的连 线为yB后轴,yB轴的单位方 向矢量。称为姿态矢量,指 向可任意选定,xB轴与yB后 铀及ZB轴垂直,X后轴的单 位方向矢量n为法向矢量, 且n=o×a,指向符合右手 法则。
第二章 工业机器人运动学
1、齐次坐标及对象物的描述 2、齐次变换及运算 3、工业机器人连杆参数及其 齐次变换矩阵 4、工业机器人运动学方程
机器人实际上可认为是由一系列关节连接 起来的连杆所组成。我们把坐标系固连在机器 的每个连杆关节上,可以用齐次变换来描述这些 坐标系之间的相对位置和方向。齐次变换具有 较直观的几何意义,而且可描述各杆件之间的关 系,所以常用于解决运动学问题。
§2-1齐次坐标及对象物的描述
一、点的位置描述 在选定的直角坐标系{A}中,空间任一
点P的位置可用3×1的位置矢量Ap表示,其 左上标代表选定的参考坐标系:
式中PX,PY,PZ是点P在坐标系{A}中的三个位 置坐标分量,如图2-1所示。
二、齐次坐标 如用四个数组成的(4×1)列阵
表示三维空间直角坐标系{A}中点p,则列阵[Px Py Pz 1]T称为三维空间点P的齐次坐标。
手部的位置矢量为固定参考系原点指向手部坐标系{B}
原点的矢量p,手部的方向矢量为n、o、a。于是手部
的位姿可用(4X4)矩阵表示为
五、目标物齐次矩阵表示
如图2.8所示,楔块Q在图( a )的情况下,其 位置和姿态可用6个点描述,矩阵表达式为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用旋转矩阵BAR 描述{B}相对于{A} 的方位。同一点p在两个坐标系{A} 和{B}中的描述Ap和Bp具有如下变换关系:
A pBAR Bp
上式为坐标旋转方程。
zB
zA
Bp
xA
xB
可以类似用
B A
R
描述{A} 相对于{B}的方位。
yB
B A
R
和
A B
R
都是正交矩阵,两者互逆。根据正交
矩阵的性质有:
yA
B A
R
BAR
1
BART
§ 2.2 坐标变换
三、复合变换
yB yA
Ap
坐标系{B} 的原点与{A}的原点既
不重合,两者的方位又不同时,用位
yC
置矢量ApB。描述{B}的坐标原点相对
于{A}
的位置,用旋转矩阵
B A
R
描述
Bp xB {B}相对于{A} 的方位,则任一点p在 坐标系{A} 和{B}的描述Ap和Bp具有如
t22 t32 t42
t23 t33 t43
t24 t34 t44
T11 T21
T12
T22
在机器人系统的运动分析中,齐次变换矩阵写成以下形式
T
R33 O13
P31
I11
旋转矩阵33
O13
位置矢量31
1
若三维空间的位置矢量P表示成齐次坐标,即P=(px py pz 1) T, 那么利用变换矩阵的概念,对纯转动,3 3旋转矩阵可扩展成4 4 齐次变换矩阵
0
04
4
1
1
1 1
1
1
0 1 0 0 0 0 2 2 0 0 0 0 0 0 4 4
0 0 0 1 1 1
1
11
1
1
1
1
11
1
§ 2.4 物体的变换及逆变换
(a) 变换前的坐标系
(b) 变换后的坐标系
图2.8 对楔形物体的变换
§ 2.4 物体的变换及逆变换
物体位置描述
我们可以用描述空间一点的变换方法来描述物体在 空间的位置和方向。例如,图2.8(a)所示物体可由固定该 物体的坐标系内的六个点来表示。我们可对上述楔形物 体的六个点变换如下:
0 0 1 4 1 1 1 1 1 1 4 4 6 6 4 4
1 0 0 0 0 0
• 齐次变换的逆变换
B p CBT Cp A p ABT Bp ABT CBT Cp
CAT ABT CBT
§ 2.4 物体的变换及逆变换
• 齐次变换的逆变换
定义复合变换 :
CAT ABT CBT
A B
R
0
A
pBo 1
B C
R
0
B
pCo 1
AxB•
Ay B
= AyB • AzB = AzB • AxB =0
可见,旋转矩阵
A B
R
是正交的,并且满足条件
R A 1
B
BART
,
A B
R
1
上标T表示转置 ,• 为行列式符号 。 对应于轴x,y或z作转角为θ的旋转变换,其旋转矩阵分别为
1 0 0
c 0 s
c s 0
A B
R
=I(单位矩阵);
当表示方位时,上式中的位置矢量ApB。 =0 。
§ 2.2 坐标变换
空间中任意点p在不同坐标系中的描述是不同的。为了阐明从一个
坐标系到另一个坐标系的描述关系,需要讨论变换问题。
一、坐标平移
设坐标系{A} 与{B}具有相同的方位,但 {B}坐标系的原点与 {A}
的原点不重合。 用位置矢量ApB。描述它相对于{A} 的位置,称ApB。为
对于直角坐标系{A},空间任一点p的位置可用3×1的列矢量Ap(位置 矢量)表示:
px
pA
py
pz
其中px,py,pz是点p 在坐标系{A}中的三个坐标 分量。 Ap的上标A代表参考 坐标系{A} 。
§ 2.1 刚体位姿描述
二、方位的描述(旋转矩阵)
为了规定空间某刚体B的方位,设置一直角坐标系{B}与此刚体固接
nx ox ax 0c s 0 0nx ny nz 0
CRot(z, )C 1 ny oy ay 0s c 0 0ox oy oz 0
n0z
oz 0
az 0
0 0 1 0
0 0
0 0
0 1
a0x
ay 0
az 0
0 1
xC 下变换关系
xA ApB。zC
zB
A pBAR Bp ApB。
zA
§ 2.3 齐次坐标变换
齐次坐标是用n +1维坐标来描述n维空间中的位置,其第n +1个分量
(元素)称为比例因子。引入齐次坐标不仅对坐标变换的数学表达带来方
便,而且具有坐标值缩放功能;对三维空间位置矢量P=(px,py,pz),
A B
R
CBR
0
A B
R
B
pCo 1
ApBo
§ 2.4 物体的变换及逆变换
变换方程初步 必须建立机器人各连杆之间,机器人与周围环境之间的
运动关系,用于描述机器人的操作。要规定各种坐标系来描 述机器人与环境的相对位姿关系。在下图 (a)中,位姿关系 可用相应的齐次变换来描述,机器人控制和规划的目标与其 他变换之间的关系可用空间尺寸链(有向变换图)来表示, 如图 (b)所示 。
其齐次坐标可以表示为P=(ω px, ω py, ω pz) T,实际坐标和齐次坐标
的关系如下
px
px
,
py
p y
,
pz
pz
可以看出,直角坐标系Oxyz原点的齐次坐标为(0,0,0,α)。 α为 非零实数。齐次坐标(1,0,0,0)T表示Ox轴的无穷远点,同理齐次坐标 (0,1,0,())T和(0,0,1,0) T分别指向Oy轴和0z轴的无穷远点,三维 空间的位置矢量的齐次坐标表达并不是惟一的。但若将ω取为1,则位置
§ 2.3 齐次坐标变换
(a)
图a表示u绕z轴旋转90°至v,再绕 y轴旋转90°至w
(b)
图b表示u绕y轴旋转90°至v,再绕 z轴旋转90°至w1
§ 2.3 齐次坐标变换
把旋转变换与平移变换结合起来,变换结果如下图所示 。
上图表示u绕z轴旋转90°至v,再绕y轴旋转90°至w,再进行 平移变换4i-3j+7k的结果
bx by bz
§ 2.3 齐次坐标变换
1 0
0 0
cos 0 sin 0
cos sin 0 0
Tx,
0 0
cos sin
sin cos
0, 0Ty,Fra bibliotek
0
sin
1 0
0 c os
0, 0
Tz ,
sin 0
矢量变换后的齐次坐标和矢量的实际坐标就相同了。在机器人学的应用 中ω总是取为1。
§ 2.3 齐次坐标变换
齐次变换矩阵是4 4矩阵,它能把一个以齐次坐标表示的位置矢量 由一个坐标系映射到另一个坐标系。齐次变换矩阵T写成以下形式
t11 t12 t13 t14
T t21 tt3411
某一坐标系{B}相固接。 {B}的坐标原点一般选在物体B的特征点上,如
质心或对称中心等。相对参考系 {A},坐标系{B}的原点位置和坐标轴
的方位,分别由位置矢量ApB。和旋转矩阵BAR 描述 ,这样刚体B的位姿
可由坐标系{B}来描述,即:
B A R B
A pB。
当表示位置时,上式中的旋转矩阵
4 4齐次变换矩阵把在O uvw 坐标系中用齐次坐标表示的矢量映 射到Oxyz参考坐标系中去,即
Pˆxyz TPˆuvw
nx ox ax px
T ny
nz 0
oy oz 0
ay az 0
py pz 1
n 0
o 0
a 0
p
1
§ 2.4 物体的变换及逆变换
基本齐次变换阵可以相乘以求得合成齐次变换阵,可是矩阵乘法是不 可交换的,必须注意这些矩阵的相乘次序。也就是说:若动坐标系O uvw绕 (或沿)Oxyz系(固定坐标系)主轴转动(或平移)则用相应的基本齐次阵左乘 齐次变换矩阵;若动坐标系O uvw绕(或沿)它自己的主轴(运动坐标系)转 动(或平移),则用相应的基本齐次旋转(或平移)矩阵右乘齐次变换矩阵。
变量空间之间的关系
n
o
a
i
刚体参考点的位置和刚体的姿态统称为刚体的位姿,其描述方法较多 ,如齐次变换法、矢量法、旋量法等等。本章采用齐次变换法,其优点在 于它将运动、变换和映射与矩阵运算联系起来。
§ 2.1 刚体位姿描述
为了描述机器人本身的各个连杆之间、机器人和环境(操作对象和障 碍物)之间的运动关系,通常将它们都看成刚体,研究各刚体之间的运 动关系。 一、位置的描述(位置矢量)
fx fxvers c
fx
fxvers
f z s
fx
fzvers 0
fz s
f y fxvers fz s f y f yvers c f y fzvers fxs
A pBAR Bp
上式为坐标旋转方程。
zB
zA
Bp
xA
xB
可以类似用
B A
R
描述{A} 相对于{B}的方位。
yB
B A
R
和
A B
R
都是正交矩阵,两者互逆。根据正交
矩阵的性质有:
yA
B A
R
BAR
1
BART
§ 2.2 坐标变换
三、复合变换
yB yA
Ap
坐标系{B} 的原点与{A}的原点既
不重合,两者的方位又不同时,用位
yC
置矢量ApB。描述{B}的坐标原点相对
于{A}
的位置,用旋转矩阵
B A
R
描述
Bp xB {B}相对于{A} 的方位,则任一点p在 坐标系{A} 和{B}的描述Ap和Bp具有如
t22 t32 t42
t23 t33 t43
t24 t34 t44
T11 T21
T12
T22
在机器人系统的运动分析中,齐次变换矩阵写成以下形式
T
R33 O13
P31
I11
旋转矩阵33
O13
位置矢量31
1
若三维空间的位置矢量P表示成齐次坐标,即P=(px py pz 1) T, 那么利用变换矩阵的概念,对纯转动,3 3旋转矩阵可扩展成4 4 齐次变换矩阵
0
04
4
1
1
1 1
1
1
0 1 0 0 0 0 2 2 0 0 0 0 0 0 4 4
0 0 0 1 1 1
1
11
1
1
1
1
11
1
§ 2.4 物体的变换及逆变换
(a) 变换前的坐标系
(b) 变换后的坐标系
图2.8 对楔形物体的变换
§ 2.4 物体的变换及逆变换
物体位置描述
我们可以用描述空间一点的变换方法来描述物体在 空间的位置和方向。例如,图2.8(a)所示物体可由固定该 物体的坐标系内的六个点来表示。我们可对上述楔形物 体的六个点变换如下:
0 0 1 4 1 1 1 1 1 1 4 4 6 6 4 4
1 0 0 0 0 0
• 齐次变换的逆变换
B p CBT Cp A p ABT Bp ABT CBT Cp
CAT ABT CBT
§ 2.4 物体的变换及逆变换
• 齐次变换的逆变换
定义复合变换 :
CAT ABT CBT
A B
R
0
A
pBo 1
B C
R
0
B
pCo 1
AxB•
Ay B
= AyB • AzB = AzB • AxB =0
可见,旋转矩阵
A B
R
是正交的,并且满足条件
R A 1
B
BART
,
A B
R
1
上标T表示转置 ,• 为行列式符号 。 对应于轴x,y或z作转角为θ的旋转变换,其旋转矩阵分别为
1 0 0
c 0 s
c s 0
A B
R
=I(单位矩阵);
当表示方位时,上式中的位置矢量ApB。 =0 。
§ 2.2 坐标变换
空间中任意点p在不同坐标系中的描述是不同的。为了阐明从一个
坐标系到另一个坐标系的描述关系,需要讨论变换问题。
一、坐标平移
设坐标系{A} 与{B}具有相同的方位,但 {B}坐标系的原点与 {A}
的原点不重合。 用位置矢量ApB。描述它相对于{A} 的位置,称ApB。为
对于直角坐标系{A},空间任一点p的位置可用3×1的列矢量Ap(位置 矢量)表示:
px
pA
py
pz
其中px,py,pz是点p 在坐标系{A}中的三个坐标 分量。 Ap的上标A代表参考 坐标系{A} 。
§ 2.1 刚体位姿描述
二、方位的描述(旋转矩阵)
为了规定空间某刚体B的方位,设置一直角坐标系{B}与此刚体固接
nx ox ax 0c s 0 0nx ny nz 0
CRot(z, )C 1 ny oy ay 0s c 0 0ox oy oz 0
n0z
oz 0
az 0
0 0 1 0
0 0
0 0
0 1
a0x
ay 0
az 0
0 1
xC 下变换关系
xA ApB。zC
zB
A pBAR Bp ApB。
zA
§ 2.3 齐次坐标变换
齐次坐标是用n +1维坐标来描述n维空间中的位置,其第n +1个分量
(元素)称为比例因子。引入齐次坐标不仅对坐标变换的数学表达带来方
便,而且具有坐标值缩放功能;对三维空间位置矢量P=(px,py,pz),
A B
R
CBR
0
A B
R
B
pCo 1
ApBo
§ 2.4 物体的变换及逆变换
变换方程初步 必须建立机器人各连杆之间,机器人与周围环境之间的
运动关系,用于描述机器人的操作。要规定各种坐标系来描 述机器人与环境的相对位姿关系。在下图 (a)中,位姿关系 可用相应的齐次变换来描述,机器人控制和规划的目标与其 他变换之间的关系可用空间尺寸链(有向变换图)来表示, 如图 (b)所示 。
其齐次坐标可以表示为P=(ω px, ω py, ω pz) T,实际坐标和齐次坐标
的关系如下
px
px
,
py
p y
,
pz
pz
可以看出,直角坐标系Oxyz原点的齐次坐标为(0,0,0,α)。 α为 非零实数。齐次坐标(1,0,0,0)T表示Ox轴的无穷远点,同理齐次坐标 (0,1,0,())T和(0,0,1,0) T分别指向Oy轴和0z轴的无穷远点,三维 空间的位置矢量的齐次坐标表达并不是惟一的。但若将ω取为1,则位置
§ 2.3 齐次坐标变换
(a)
图a表示u绕z轴旋转90°至v,再绕 y轴旋转90°至w
(b)
图b表示u绕y轴旋转90°至v,再绕 z轴旋转90°至w1
§ 2.3 齐次坐标变换
把旋转变换与平移变换结合起来,变换结果如下图所示 。
上图表示u绕z轴旋转90°至v,再绕y轴旋转90°至w,再进行 平移变换4i-3j+7k的结果
bx by bz
§ 2.3 齐次坐标变换
1 0
0 0
cos 0 sin 0
cos sin 0 0
Tx,
0 0
cos sin
sin cos
0, 0Ty,Fra bibliotek
0
sin
1 0
0 c os
0, 0
Tz ,
sin 0
矢量变换后的齐次坐标和矢量的实际坐标就相同了。在机器人学的应用 中ω总是取为1。
§ 2.3 齐次坐标变换
齐次变换矩阵是4 4矩阵,它能把一个以齐次坐标表示的位置矢量 由一个坐标系映射到另一个坐标系。齐次变换矩阵T写成以下形式
t11 t12 t13 t14
T t21 tt3411
某一坐标系{B}相固接。 {B}的坐标原点一般选在物体B的特征点上,如
质心或对称中心等。相对参考系 {A},坐标系{B}的原点位置和坐标轴
的方位,分别由位置矢量ApB。和旋转矩阵BAR 描述 ,这样刚体B的位姿
可由坐标系{B}来描述,即:
B A R B
A pB。
当表示位置时,上式中的旋转矩阵
4 4齐次变换矩阵把在O uvw 坐标系中用齐次坐标表示的矢量映 射到Oxyz参考坐标系中去,即
Pˆxyz TPˆuvw
nx ox ax px
T ny
nz 0
oy oz 0
ay az 0
py pz 1
n 0
o 0
a 0
p
1
§ 2.4 物体的变换及逆变换
基本齐次变换阵可以相乘以求得合成齐次变换阵,可是矩阵乘法是不 可交换的,必须注意这些矩阵的相乘次序。也就是说:若动坐标系O uvw绕 (或沿)Oxyz系(固定坐标系)主轴转动(或平移)则用相应的基本齐次阵左乘 齐次变换矩阵;若动坐标系O uvw绕(或沿)它自己的主轴(运动坐标系)转 动(或平移),则用相应的基本齐次旋转(或平移)矩阵右乘齐次变换矩阵。
变量空间之间的关系
n
o
a
i
刚体参考点的位置和刚体的姿态统称为刚体的位姿,其描述方法较多 ,如齐次变换法、矢量法、旋量法等等。本章采用齐次变换法,其优点在 于它将运动、变换和映射与矩阵运算联系起来。
§ 2.1 刚体位姿描述
为了描述机器人本身的各个连杆之间、机器人和环境(操作对象和障 碍物)之间的运动关系,通常将它们都看成刚体,研究各刚体之间的运 动关系。 一、位置的描述(位置矢量)
fx fxvers c
fx
fxvers
f z s
fx
fzvers 0
fz s
f y fxvers fz s f y f yvers c f y fzvers fxs
