MATLAB基础及其应用教程-周开利-邓春晖课后答案
Matlab编程与应用习题和一些参考答案

Matlab编程与应用习题和一些参考答案Matlab 上机实验一、二3.求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+-+-=-+=++-=--+41025695842475412743w z y x w z x w z y x w z y x >> a=[3 4 -7 -12;5 -7 4 2;1 0 8 -5;-6 5 -2 10];>> b=[4;4;9;4];>> c=a\b4.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=81272956313841A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=793183262345B ,求C1=A*B’;C2=A’*B;C3=A.*B,并求上述所有方阵的逆阵。
>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];>> B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7];>> C1=A*B'>> C2=A'*B>> C3=A.*B>> inv(C1)>> inv(C2)>> inv(C3)5.设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y ,把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线。
>> x=linspace(0,2*pi,101);>> y=cos(x)*(0.5+(1+x.^2)\3*sin(x));>> plot(x,y,'r')6.产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
(mean var )a=randn(8,6)mean(a)var(a)k=mean(a)k1=mean(k)i=ones(8,6)i1=i*k1i2=a-i1i3=i2.*i2g=mean(i3)g2=mean(g)10.利用帮助查找limit 函数的用法,并自己编写,验证几个函数极限的例子。
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章
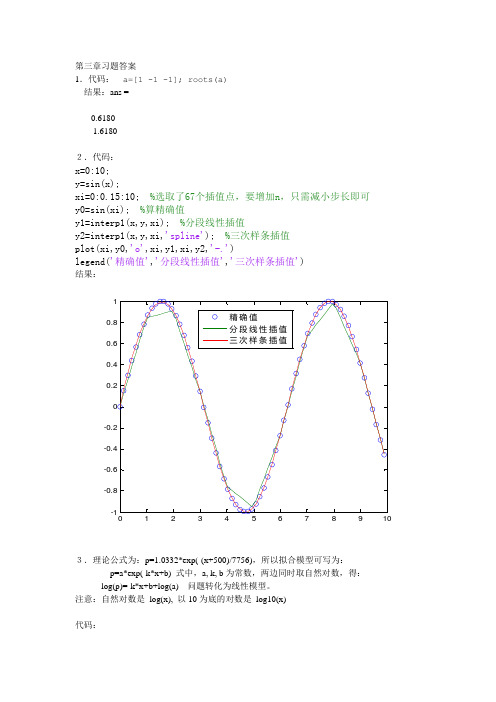
第三章习题答案1.代码:a=[1 -1 -1]; roots(a)结果:ans =-0.61801.61802.代码:x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点,要增加n,只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果:3.理论公式为:p=1.0332*exp(-(x+500)/7756),所以拟合模型可写为:p=a*exp(-k*x+b) 式中,a, k, b为常数,两边同时取自然对数,得:log(p)=-k*x+b+log(a)问题转化为线性模型。
注意:自然对数是log(x), 以10为底的对数是log10(x)代码:clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点,比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果:0200400600800100012001400160018002000从图像上,都符合得很好,但很难看出差异。
Matlab编程与应用习题和一些参考答案

n=rand(1,10) for j=1:10
for i=j+1:10 if n(j)<n(i) a=n(j); n(j)=n(i); n(i)=a; end
end end disp('重新排列后:') n
9.建立一个字符串向量,然后对该向量做如下处理: (1) 取第 1~5 个字符组成的子字符串。 (2) 将字符串倒过来重新排列。 (3) 统计字符串中小写字母的个数。
>> a='abcdef123456'; >> subch=a(1:5) subch = abcde >> revch=a(end:-1:1) revch = 654321fedcba>> k=find(a>='a'&a<='z'); >> a(k)=a(k)-('a'-'A'); >> char(a)
>> z=0:0.01:10;
>> x=z.*sin(3*z);
>> y=z.*cos(3*z);
>> plot3(x,y,z)
12.设 z x e2 (x2 y2 ) ,画出定义域 x=[-2,2],y=[-2,2]内的曲面图。
>> [x,y]=meshgrid([-2:0.1:2]); >> z=x.^2.*exp(-x.^2-y.^2); >> mesh(x,y,z) 13.设 z=0.05x-0.05y+0.1; 画出 z 的曲面(平面)图。 >> [X,Y]=meshgrid(1:10:200,1:10:200); >> Z=0.05*X-0.05*Y+0.1; >> surf(X,Y,Z)
matlab基础与应用教程课后答案

exp(-0.3*a).*sin(a+0.3)
3.x=[2,4;-0.45,5];
log(x+sqrt(1+x.*x))/2
4. A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0];
(1)A*B
ans =
129
432
4197
7
-407
-1052
end display(sqrt(s*6)) 向量运算
n=input('input n:'); k=1:n; display(sqrt(sum(1./k.^2)*6)) 4. y=0;k=0; while y<3
k=k+1; y=y+1/(2*k-1); end display([k-1,y-1/(2*k-1)]) 5. x0=0;x=1;k=0; a=input('a='); b=input('b='); while abs(x-x0)>=1e-5 && k<500 x0=x; x=a/(b+x0); k=k+1; end display([k,x]); display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);
1. P=pascal(5);H=hilb(5); Dp=det(P);Dh=det(H);
Kp=cond(P);Kh=cond(H); P 矩阵的性能更好,因为 Kp 较小 2. A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3] B=[3,pi/2,45;32,-76,sqrt(37);5,72,4.5e-4;exp(2),0,97] A1=diag(A);B1=diag(B); A2=triu(A);B2=triu(B); A3=tril(A);B3=tril(B); rA=rank(A);rB=rank(B);
MATLAB及其应用课后习题解答

5
“MATLAB 及其应用”课程作业
图 4- 2 画出函数图像
第5章
1. 已知椭圆的长、短轴 a 4, b 2 ,用“小红点线”画如下图所示的椭圆
x a cos t 。 y b sin t
(提示:参量 t ;点的大小;axis equal) 答 : 运 行 :clf; a=4;b=2;t=0:pi/80:2*pi;x=a*cos(t);y=b*sin(t);plot(x,y,’r’,’markersize’,15);axis equal;xlabel(‘x’);ylabel(‘y’);shg;结果如图 5-1 所示:
1
“MATLAB 及其应用”课程作业
a5=sin(sym(pi/4)+exp(sym(0.7+pi/3))); a6=sin(sym(pi/4)+sym(exp(0.7+pi/3))); a7=sin(sym(pi/4+exp(0.7+pi/3))); a8=sym(sin(pi/4+exp(0.7+pi/3))); da2 = vpa(a1-a2,30) da3 = vpa(a1-a3,30) da4 = vpa(a1-a4,30) da5 = vpa(a1-a5,30) da6 = vpa(a1-a6,30) da7 = vpa(a1-a7,30) da8 = vpa(a1-a8,30) 结果如图 2-2 所示: 只有 a2 是精准的,观察可知,这是由 于 sym('Num')和 sym(Num)的区别带来 图 2- 2 vpa 观察误差 的前者以字符串的形式传给符号运算内 核,可以保留完整的精度;而后者经过浮点数运算之后再转换为符号类型,存在精度损 失。 3.在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是独立自由变量。 sym('sin(w*t)') , sym('a*exp(-X)' ) , sym('z*exp(j*th)') 答:分别为 w,a,z,具体图 2-3 所示。
MATLAB基础及其应用教程周开利邓春晖课后答案

第三章习题及参考答案解答:>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答:取n=5,m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11,m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答:>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.');>> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较,都合理,误差也相近。
matlab课后习题答案

第2章 MATLAB 矩阵运算基础2.1 在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a ? >> a=[5 7 3;4 9 1]2.5 计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
>> a=[5 3 5;3 7 4;7 9 8]; >> b=[2 4 2;6 7 9;8 3 6];>> a+bans =7 7 7 9 14 13 15 12 142.6 求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i]; >> x’ans =4.0000 - 8.0000i 3.0000 - 2.0000i 3.0000 -5.0000i 7.0000 +6.0000i 2.0000 +7.0000i 9.0000 - 4.0000i 1.0000 - 4.0000i 3.0000 + 9.0000i 7.0000 + 5.0000i 4.0000 - 4.0000i2.7 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8]; >> a.*b ans =12 36 3 8 42 402.9 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;-0.5118 4.0427 1.33182.10 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
matlab基础与应用教程课后答案

matlab基础与应用教程课后答案【篇一:matlab教程基本应用练习题及解答】txt>要求:将每题的答案(命令行和运行结果、图片或m文件的文件名及具体内容)直接拷贝插入到各题的下方:(1)若为命令行,要求将提示符“”一起拷入,并在右侧用“%”注明命令行的每条命令的作用;(2)若为多个运行结果,拷入后要求解释每个结果具体对应题目中的哪个要求,也在右侧用“%”注明;(3)如果为m文件,除了将文件名和此文件的具体内容全部拷入外,再将所有原始m文件和本练习题电子版放在一个以“专业班级+本人姓名+学号”命名的文件夹内一起上传。
ans =1 0 00 1 00 0 1ans =0 0 00 0 0ans =1 1 11 1 11 1 11 1 120+40*rand(1,10) %生成10个在区间[20,60]上均匀分布的随机数。
ans =44.617351.677556.872549.528327.050636.228257.418856.676236 .410855.7460二.1)计算向量(2,4,6,8)的最大值,最小值,平均值,中值,排序,总和值; max([2,4,6,8])%最大值ans =8min([2,4,6,8])% 最小值ans =2mean([2,4,6,8])% 平均值ans =5median([2,4,6,8])% 中值ans =5sort([2,4,6,8])% 排序ans =2 4 6 8sum([2,4,6,8])% 总和值ans =202)在行向量(2,4,6,8)和(1,3,5,7)之间实施加减乘除及幂运算; a=[2 4 6 8];b=[1 3 5 7];a+b%加ans =3 7 11 15a-b%减ans =1 1 1 1a.*b%乘ans =2 12 30 56a./b%除ans =2.0000 1.3333 1.2000 1.1429a.^b%幂ans =2 64 7776 20971523)在向量(1,3,5)与标量2之间实施加减乘除及幂运算。
matlab课后习题答案1到6章

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等?答:(2)(3)答:(4)答:即逆左乘3.(1)答:5])(2)答:(3)答:(4)答:(5)答:(6)将含有12个元素的向量x转换成34⨯矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符。
答:char(49);4.下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0,0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0,0]L4的值为[4, 5, 6]6.当A=[34, NaN, Inf, -Inf, -pi, eps, 0]时,分析下列函数的执行结果:all(A),any(A),isnan(A),isinf(A),isfinite(A)。
答:all(A)的值为0any(A) 的值为1isnan(A) 的值为[ 0, 1, 0, 0, 0, 0, 0]isinf(A) 的值为[ 0, 0, 1, 1, 0, 0, 0]isfinite(A) 的值为[1, 0, 0, 0, 1, 1, 1]7.用结构体矩阵来存储5名学生的基本情况数据,每名学生的数据包括学号、姓名、专业和6门课程的成绩。
MATLAB基础及其应用教程-周开利-邓春晖课后标准答案
MATLAB基础及其应⽤教程-周开利-邓春晖课后标准答案MATLAB基础及其应⽤教程-周开利-邓春晖课后答案————————————————————————————————作者:————————————————————————————————⽇期:第三章习题及参考答案解答:>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答:取n=5,m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on >> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值⽅法与精确值之差取n=11,m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on分段线性和三次样条插值⽅法与精确值之差解答:>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.'); >> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合⽅法相⽐较,都合理,误差也相近。
matlab课后答案完整版

ones表示1矩阵zeros表示0矩阵ones(4)表示4x4的1矩阵zeros(4)表示4x4的0矩阵zeros(4,5)表示4x5的矩阵eye(10,10)表示10x10的单位矩阵rand(4,5)表示4x5的伴随矩阵det(a)表示计算a的行列式inv(a)表示计算a的逆矩阵Jordan(a)表示求a矩阵的约当标准块rank(a)表示求矩阵a的秩[v,d]=eig(a)对角矩阵b=a’表示求a矩阵的转置矩阵sqrt表示求平方根exp表示自然指数函数log自然对数函数abs绝对值第一章一、5(1)b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12];>> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112(2)a=50:1:100二、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =2、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)3、x=[2 4;-0.45 5];y=log(x+sqrt(1+x.^2))/2y = 4、a*b表示a矩阵和b矩阵相乘a.*b表示a矩阵和b矩阵单个元素相乘A(m,n)表示取a矩阵第m行,第n列A(m,:)表示取a矩阵第m行的全部元素A(:,n)表示取a矩阵的第n列全部元素A./B表示a矩阵除以b矩阵的对应元素,B.\A等价于A./BA.^B表示两个矩阵对应元素进行乘方运算A.^2表示a中的每个元素的平方A^2表示A*A例:x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量(如y=2).底数也可以是标量(如x=2)5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =d=c+a*b/(a+b)d =第二章二、4、(1)y=0;k=0;>> while y<3k=k+1;y=y+1/(2*k-1);end>> display([k-1,y-1/(2*k-1)])ans =第三章二1(1)x=0:pi/10:2*pi;>> y=x-x.^3/6;>> plot(x,y)(2)x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)(3)x=-8:0.01:8;y=sqrt((64-x.^2)/2);plot(x,y)(4)t=0:0.1:8*pi; >> x=t.*sin(t);>> y=t.*cos(t); >> plot(x,y)x=0:pi/100:2*pi;y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x);plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} ');>> xlabel('variable x');>> ylabel('variable y');>> text(1.5,0.5,'曲线y1=e^(-0.5x)');>> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}');>> legend('y1','y2')variable xvariabley2、(1)y1=2*x-0.5;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2);>> t1=t(k)t1 =>> z=sin(3.*(t1)).*cos(t1) z =>> plot(t,x,t,y,'k:',t1,z,'bp');(2)subplot(1,2,1);>> scatter(x1,y1,10);>> title('y=2x-0.5');>> subplot(1,2,2);>> scatter(x,y,10)3、subplot(1,2,1);x=0:0.01:pi;y=sin(1./x);plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])4、t=0:pi:2*pi;y=1./(1+exp(-t));subplot(2,2,1);%图形窗口的分割bar(t,'group'); %绘制柱形图(分组)subplot(2,2,2);barh(t,'stack'); %绘制柱形图(堆积)subplot(2,2,3);loglog(t,y); %函数使用全对数坐标,x,y均采用常用对数刻度subplot(2,2,4);semilogy(t,y); %函数使用半对数坐标,y轴为常用对数刻度,x轴仍为线性刻度101010101010105、(1)theta=linspace(-pi,pi,100);ro=5.*cos(theta)+4;polar(theta,ro);(2)x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x));polar(x,r);2706、(1)t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t);>> y=exp((-t)/20).*sin(t);>> z=t;>> plot3(x,y,z);(2)t=0:0.01:1;x=t;>> y=t.^2;>> z=t.^3;>> plot3(x,y,z);7、x=-30:0.1:0;>> y=0:0.1:30;>> [x,y]=meshgrid(x,y);>>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2 );>> meshc(x,y,z);绘制曲面图和等高线8、x=linspace(-3,3,100);>> y=linspace(-3,3,100);>> [x y]=meshgrid(x,y); %可以将向量转化为矩阵>> fxy=-5./(1+x.^2+y.^2);>> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN;>>surf(x,y,fxy) %绘制三维曲面图9、u=linspace(1,10,100);v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;第五章二1、a=rand(1,30000);mean(a) %求平均数 ans = >>b=std(a) %求标准差 b =>> c=max(a) c =>> d=min(a) d =size(find(a>0.5))/size(a)ans =2、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500];>> ww=interp1(h,w,hh,'spline')ww =3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.')5、(1)、(2) p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.46561.2400(3) a=[-1,4,3;2,1,5;0,5,6]; >>y1=polyval(p,a) %以矩阵a 的每一个元素为自变量 y1 =-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a) %以矩阵a 为自变量 y2 =391 2084 3273502 2693 4207720 3775 5892 6、(1)z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根z =第八章二、2t=0:pi/20:2*pi;x=sin(t);y=cos(t);x1=sin(7*t);y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2);set(gca,'xtick',-1:0.1:1);title('篮筐')3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2;h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3) ;text(5,2.4,'y=exp(-0.2*x).*cos(x)+2'); 4、t=-pi:pi/100:pi;x=cos(t);y=sin(t);z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串(空格也算)subch =Beijing>> k=find(ch>='a'&ch<='z'); 找到所有的小写字母的位置>> ch(k)=ch(k)-('a'-'A'); 将小写字母变成大写字母>> char(ch)ans =WELCOME TO BEIJING>> length(k) 统计小写字母的个数ans =14例:已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0;>> n=100;>> for i=1:100;y=y+(-1)^(i-1)/i;end>> disp(y)绘制二维曲线图x=0:pi/100:2*pi;>> y1=0.2*exp(-0.5*x).*cos(4*pi*x);>> y2=1.5*exp(-0.5*x).*cos(pi*x);>> plotyy(x,y1,x,y2);绘制三维图像例:x=sint+tcosty=cost-tsintz=tt=0:pi/10:10*pi;x=sin(t)+t.*cos(t);y=cos(t)-t.*sin(t);z=t;plot3(x,y,z);axis([-30 30 -30 30 0 35]); 坐标轴的最大值与最小值title('line in 3-D space'); 图形的题目>> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加网格线xz三维例]2/,0[],,0[,cossin22ππ∈∈+=yxyxz[x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/ 2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]);t=0:pi/20:2*pi;subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲面图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维网格图多项式求导例:f(x)=1/x^2+5p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注:c=conv(a,b) 表示a多项式与b 多项式乘积[p,r]=deconv(a,b) 表示a多项式与b 多项式相除其中p为商向量r为余数向量p=polyder(p) 表示求p的导数p=poleder(p,q) 表示求p乘以q的导数[p,q]=poleder(p,q) 表示p除以q的导数多项式求根例:f(x)=2x^4-12x^3+3x^2+5p=[2,-12,3,0,5];>> x=roots(p);>> p=[2,-12,3,0,5];x=roots(p) 求方程f(x)=0的根x =5.72460.8997>> g=poly(x) 已知多项式的根求多项式g =符号求导x=a(t-tsint)y=b(1-cost) 求y对x的一阶导数syms x y a b t;>> f21=a*(t-sin(t));>> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y对x的一阶导数ans =b*sin(t)/a/(1-cos(t))注:diff(f1,x,2) 表示f1对x的二阶导数diff(f3,x)表示z对x的偏导diff(f3,y)表示z对y的偏导求不定积分int(f) 求f的不定积分f1=int(f,a,b) 求f在a,b之间的定积分eval(f1)计算积分值符号求极限syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h趋向于0ans =cos(x) 例2f=sym('(1+t/x)^x');limit(f,inf) f 趋向于无穷 ans = exp(t) 例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正无穷ans = 1/2 大小写ch='Welcome to Beijing'; subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a'); >> char(ch)ans =welcome to beijing>> length(k)ans =2课堂习题2一、求方程组⎪⎩⎪⎨⎧=-+=++=-+234326454510243z y x z y x z y x 的解,用三种方法。
MATLAB 课后部分答案

P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m,程序如下:function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入:mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件,程序如下:clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件,程序如下:clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件,程序如下:clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件,程序如下:clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件,程序如下:clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件,程序如下:clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件,程序如下:function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入:>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件,程序如下:function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目(偶数).% sqnr=输入信号量化噪声比(偶数)。
matlab课后习题与答案

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等?答:不相等。
(2)A./B和B.\A的值是否相等?答:相等。
(3)A/B和B\A的值是否相等?答:不相等。
(4)A/B和B\A所代表的数学含义是什么?答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵的逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8) 求一个ASCII 码所对应的字符。
答:char(49);4. 下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5. 已知23100.7780414565532503269.5454 3.14A -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦完成下列操作:(1) 取出A 的前3行构成矩阵B ,前两列构成矩阵C ,右下角32⨯子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
matlab基础与应用部分习题答案

matlab基础与应用部分习题答案作业一4、写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1,3,5列元素赋给矩阵B。
>>M=[0:1:48];>> A=reshape(M,7,7) A =0 7 14 21 28 1 8 15 2229 2 9 16 23 30 3 10 1724 31 4 11 18 25 32 5 1219 26 33 6 13 20 27 34>> B=A(2:5,1:2:5) B =1 15 292 16 303 17 314 18 32(2)删除矩阵A的第七行元素。
>> A(7,:)=[] A =0 7 14 21 28 1 8 15 2229 2 9 16 23 30 3 10 1724 31 4 11 18 25 32 5 1219 26 33 (3)将矩阵A的每个元素值加30。
>> A=A+30 A=30 37 44 51 58 31 38 45 52 59 32 39 46 53 60 35 42 36 43 3744 38 45 39 46 40 47 41 48 35 42 36 4337 44 38 45 39 46 40 47 65 72 66 73 67 7433 40 47 54 61 68 75 34 41 48 55 62 69 7635 42 49 56 63 70 77 (4求矩阵A的大小和维素。
sizeA = size(A) dA = ndims(A)sizeA =6 7 dA =2(5)将向量t的0元素用机器零来代替。
>> t=[1 2 3 4 0 5]; t =1 2 3 4 0 5>> find(t==0)ans =5>> t(5)=eps t =1.00002.00003.00004.0000 0.0000 (6)将含有12个元素的向量x转换成3*4矩阵。
matlab基础与应用部分习题答案

作业一4、写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1,3,5列元素赋给矩阵B。
>> M=[0:1:48];>> A=reshape(M,7,7)A =0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 476 13 20 27 34 41 48>> B=A(2:5,1:2:5)B =1 15 292 16 303 17 314 18 32(2)删除矩阵A的第七行元素。
>> A(7,:)=[]A =0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 47(3)将矩阵A的每个元素值加30。
>> A=A+30A =30 37 44 51 58 65 7231 38 45 52 59 66 7332 39 46 53 60 67 7433 40 47 54 61 68 7534 41 48 55 62 69 7635 42 49 56 63 70 77(4求矩阵A的大小和维素。
sizeA = size(A)dA = ndims(A)sizeA =6 7dA =2(5)将向量t的0元素用机器零来代替。
>> t=[1 2 3 4 0 5];t =1 2 3 4 0 5>> find(t==0)ans =5>> t(5)=epst =1.00002.00003.00004.0000 0.00005.0000(6)将含有12个元素的向量x转换成3*4矩阵。
>> x=[0:11]x =0 1 2 3 4 5 6 7 8 9 10 11 >> y=reshape(x,3,4)y =0 3 6 91 4 7 102 5 8 11(7)求一个字符串的ASCII。
MatLab语言及应用--习题及参考答案

MatLab语言及应用--习题1.产生一个1x10的随机矩阵,大小位于(-5 5),并且按照从大到小的顺序排列好!1.A = [21 2 3; 4 35 6; 7 8 49];B = [3; 2; 1];设求AB、BTA、A-1与A-1B,求A2、A的2次数幂,并求矩阵A的秩、转置和行列式。
2.请产生一个100*5的矩阵,矩阵的每一行都是[1 2 3 4 5]4. 请修改下面的程序,让他们没有for循环语句!A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend5.a=[1 2 3 4 5],b=a(1)*a(5)+a(2)*a(4)+a(3)*a(3)+a(4)*a(2)+a(5)*a(1).试用MATLAB中最简单的方法计算b,注意最简单。
6. 求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3x +8z- 5w=9-6x+5y-2z+10w=-8求系数矩阵的秩;求出方程组的解。
7.设 y=cos[0.5+((3sinx)/(1+x^2))]把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线;8. 设f(x)=x^5-4x^4+3x^2+2x+6取x=[-2,8]之间函数的值(取100个点),画出 曲线,看它有几个零点。
9. 在[-10,10;-10,10]范围内画出函数的三维图形。
10.编写一个函数,使其能够产生如下的分段函数:⎪⎩⎪⎨⎧≤≤<-≤=x x x x x x f 65.0620.251.525.0)(,,,,并调用此函数,绘制曲线2)()(范围的2],[0在+•+=x f x f x 。
(10分)11.将一个屏幕分4幅,选择合适的步长在右上幅与左下幅绘制出下列函数的图形。
matlab基础教程课后答案

matlab基础教程课后答案【篇一:matlab基础练习题及答案】xt>1.4 matlab操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?答:在matlab操作桌面上有五个窗口。
在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口。
在独立窗口的desktop菜单中选择dock...项就可以将独立的窗口重新放置到桌面上。
1.5 如何启动m文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,m文件编辑/调试器将被启动。
在命令窗口中键入edit命令时也可以启动m文件编辑/调试器。
1.6 存储在工作空间中的数组能编辑吗?如何操作?1.7 命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到m文件中。
1.8 如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?答:当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的set path菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
1.9 在matlab中有几种获得帮助的途径?答:(1)帮助浏览器:选择view菜单中的help菜单项或选择help菜单中的matlab help菜单项可以打开帮助浏览器。
(2)help命令:在命令窗口键入“help” 命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息。
