图 论
离散数学——图论

提示:反证法。
设有两个连通分支,这两个分支至多是完 全图。由此得到图中点与边之间的数量关系。
§8.3欧拉图
欧拉图产生的背景就是前面的七桥问题。
定义:图G的回路,若它通过G中的每条边一 次,这样的回路称为欧拉回路。具有欧拉回 路的图称为欧拉图。
定义欧拉通路:通过图G中每条边一次的通 路(非回路)称为欧拉通路。
基本通路:通路中没有重复的点。
简单回路和基本回路。
基本通路一定是简单通路,但反之简单通路 不一定是基本通路。基本回路必是简单回路。
定理:一个有向(n,m)图中任何基本通路长 度≤n-1。任何基本回路的长度≤n。 任一通路中如果删去所有回路,必得基本通 路。 任一回路中如删去其中间的所有回路,必得 基本回路。
例1:教材121页。
结点次数
引出次数:有向图中以结点v为起点的边的条数称为 v的引出次数,记 deg(v) 引入次数:有向图中以结点v为终点的边的条数称为 v的引出次数,记 deg(v)
结点次数:有向图中引出次数和引入次数之和称为 结点次数;无向图中与结点v相关联的边的条数称为 V的次数。统一为记deg(v)。
图论的发展
图论的产生和发展经历了二百多年的历史, 从1736年到19世纪中叶是图论发展的第一阶 段。 第二阶段大体是从19世纪中叶到1936年,主 要研究一些游戏问题:迷宫问题、博弈问题、 棋盘上马的行走线路问题。
一些图论中的著名问题如四色问题(1852年)和哈密 尔顿环游世界问题(1856年)也大量出现。同时出现 了以图为工具去解决其它领域中一些问题的成果。
有向连通图
(图论)图的基本概念--第一章

证明 设G=<V,E>为任意一图,令
V1={v|v∈V∧d(v)为奇数} V2={v|v∈V∧d(v)为偶数} 则V1∪V2=V,V1∩V2= ,由握手定理可知
2m d (v) d (v) d (v)
vV
vV1
vV2
由于2m和 d (v) ,所以 d (v) 为偶数,
举例
NG(v1) = {v2,v5} NG(v1) = {v1,v2,v5} IG(v1) = {e1,e2,e3}
Г+D(d ) = {c} Г-D(d ) = {a,c} ND(d ) = {a,c} ND(d ) = {a,c,d}
简单图与多重图
定义1.3 在无向图中,关联一对顶点的无向边如果多于1条,则 称这些边为平行边,平行边的条数称为重数。 在有向图中,关联一对顶点的有向边如果多于1条,并且这些 边的始点和终点相同(也就是它们的方向相同),则称这些边 为平行边。 含平行边的图称为多重图。 既不含平行边也不含环的图称为简单图。
无向图和有向图
定义1 一个无向图是一个有序的二元组<V,E>,记作G,其中 (1)V≠称为顶点集,其元素称为顶点或结点。 (2)E称为边集,它是无序积V&V的多重子集,其元素称为无向 边,简称边。
定义2 一个有向图是一个有序的二元组<V,E>,记作D,其中 (1)V≠称为顶点集,其元素称为顶点或结点。 (2)E为边集,它是笛卡儿积V×V的多重子集,其元素称为有向 边,简称边。
vV2
vV1
但因V1中顶点度数为奇数, 所以|V1|必为偶数。
问题研究
问题:在一个部门的25个人中间,由于意见不同,是否可能每 个人恰好与其他5个人意见一致?
图论讲义1图路树

7. 连通性 图中两点的连通:如果在图 G 中 u,v 两点有路相通,则称顶点 u,v 在图 G 中连通。 连通图(connected graph):图 G 中任二顶点都连通。 图的连通分支(connected branch, component):若图 G 的顶点集 V(G)可划分为若干非空子集
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
3
(8) 完全图(complete graph)
(9) 图的顶点数(图的阶)ν 、边数 ε
(10) 顶点 v 的度(degree):d(v) = 顶点 v 所关联的边的数目(环边计两次)。
(11) 图 G 的最大度: ∆(G) = max{dG (v) | v ∈V (G)}
图 G 的最小度:δ (G) = min{dG (v) | v ∈V (G)}
证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
第五章 图论

图论可应用于多个领域,如信息论,控制论, 运筹学,运输网络,集合论等(如用关系图来 描述一个关系)。
计算机领域,其可应用于人工智能,操作系统, 计算机制图,数据结构)
§1
图论基本概念
1-1 图的实例 问题1、哥尼斯堡桥问题
A C B D C B A D
问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点?
同理,结点间按别的对应方式,便都不存在一一对应
关系。
所以G1,G2不同构。
两图同构有必要条件:
(1)结点数相同; (2)边数同; (3)次数相同的结点数目相等。
1-5 多重图与带权图
1.5.1 多重图 定义11、一个结点对对应多条边,称为多重边。
包含多重边的图称为多重图,否则,成为简单图。
如:
如:基本通路:p1,p2,p3.
简单通路:p1,p2,p3,p5,p6. p4,p7既不是基本通路,也不是简单通路。
定义3、起始结点和终止结点相同的通路称为回路。 各边全不同的回路称为简单回路,各点全不同 的回路称为基本回路。
例2、上例中,1到1的回路有: c1: (1,1,),c2: (1,2,1),c3: (1,2,3,1), 1 2
例2、设有四个城市c1,c2,c3,c4;其中c1与c2间, c1与c4间,c2与c3间有高速公路直接相连,用图表 示该事实。 解:G=<V,E>,其中:V={c1,c2,c3,c4}, E={l1,l2,l3}={(c1,c2),(c1,c4),(c2,c3)} 例3、有四个程序p1,p2,p3,p4,其间调用关系为p1 p2, p1 p4,p2 p3,用图表示该事实。 解:G=<V,E>,V={p1,p2,p3,p4}, E={l1,l2,l3}={(p1,p2),(p1,p4),(p2,p3)}
图论4-6-平面图ppt课件
证明 假设K3,3图是平面图。
在K3,3中任取三个结点,其中必有两个结点不 邻接,故每个面的次数都不小于4, 由4r≤2e,r≤e/2,即 v-e+e/2≥v-e+r=2, v-e/2≥2, 2v- e ≥ 4, 2v4≥e。
在K3,3中有6个结点9条边, 2v-4=2×6-4=8<9,与 2v-4≥e 矛盾, 故 K3,3不是平面图。
整理后得: e≤3v – 6
本定理的用途:判定某图是非平面图。
说明:这是简单 图是平面图的必 要条件。 •图论4-6-平面图
例如:K5中e=10,v=5,3v-6=9,从而e>3v-6, 所以K5不是平面图。
定理4.6.3的条件不是充分的。如K3,3图满 足定理4-6.3的条件(v=6,e=9,3v-6=12, e≤3v-6成立),但K3,3不是平面图。 证明K3,3图不是平面图。
例如图
deg(r1)=3 deg(r2)=3 deg(r3)=5 deg(r4)=4 deg(r5)=3
deg(r1)+deg(r2)+deg(r3)+deg(r4)+deg(r5)
=18
•图论4-6-平面图
3.定理4-6.1 设G为一有限平面图,面的次数之 和等于其边数的两倍。 证明思路:任一条边或者是两个面的共同边界 (贡献2次),或者是一个面的重复边(贡献2次)
•图论4-6-平面图
一、平面图 1、定义4-6.1 如果无向图G=<V,E>的所有结点和边 可以在一个平面上图示出来,而使各边仅在顶点处 相交。无向图G称为平面图,否则称G为非平面图。
有些图形从表面看有几条边是相交的,但是不 能就此肯定它不是平面图,例如,下面左图表面看 有几条边相交,但如把它画成右图,则可看出它是 一个平面图。
图论详细讲解

称为它为有向图,记作D =(V,A),其中V 表 示有向图D的点集合,A表示有向图D的弧集
• 1.图的基本概念与基本定理
例如.图8.4是一个无向图G=(V,E)
其中V={v1,v2,v3,v4}
E={[v1,v2],[v2,v1],[v2,v3],
[v3,v4],[v1,v4],[v2,v4],
图论详细讲解
•
引言
图论是应用非常广泛的运筹学分支,它
已经广泛地应用于物理学控制论,信息论, 工程技术,交通运输,经济管理,电子计算 机等各项领域。对于科学研究,市场和社会 生活中的许多问题,可以同图论的理论和方 法来加以解决。例如,各种通信线路的架设 ,输油管道的铺设,铁路或者公路交通网络 的合理布局等问题,都可以应用图论的方法 ,简便、快捷地加以解决。
边的两个端点是相同的,那么称为这条边是环,
如图8.4中的边[v,v3]是环。如果两个端点之间
有两个端点之间有两条以上的边,那么称为它
们为多重边,如图8.4中的边[v1,v2] ,[v2,v1]
。一个无环,无多重边的图标为简单图,一个 无环,有多重边的图标图称为多重图。
• 1.图的基本概念与基本定理
• 1.图的基本概念与基本定理
综上所述,图论中的图是由点和点与点 之间的线所组成的。通常,我们把点与点之 间不带箭头的线叫做边,带箭头的线叫做弧 。
如果一个图是由点和边所构成的,那么
,称为为无向图,记作G =(V,E),其中V表 示图G的点集合,E表示图G的边集合。连接 点vi,vj V的边记作[vi,vj],或者[vj,vi]。
•
引言
•C
•A
•B
•D
•图8.1 b
图论的发展及其在现实生活中的几个应用

图论的发展及其在生活中的应用数学与应用数学张佳丽指导教师刘秀丽摘要E要介绍了图论的起源与发展及其生活中的若干应用,如:渡河问题、旅游推销员问题、最小生成树问题、四色问题、安排问题、中国邮递员问题。
同时也涉及到了几种在图论中应用比较广泛的方法,如:最邻近法、求最小生成树的方法、求最优路线的方法等。
关键词图论生活问题应用Graph Theory Development and the Application in LifeMathematics and applied mathematics ZhangJialiTutor LiuXiuliAbstractThis papermainly introduces the origin and development of graph theory and its several applications in our life, such as:crossing river problem traveling salesman problem,minimum spanning tree problem, fourcolor problem • arrangement problem» Chinese postman problem. It alsoresearchesseveral methodsthat are more widely applied in graph theory.for example:the method of most neighboringjhe method of solving theminimum spanning tree, the method of the best route, and so on.Key wordsgraph theorylifeproblemapplication引言图论是一门古老的学科,是数学中有广泛应用的一个分支,与其他的数学分支,如群论、矩阵论、概率论、拓扑学、数分析等有着密切的联系.图论中以图为研究对象,图形中我们用点表示对象,两点之间的连线表示对象之间的某种特定的关系.事实上,任何一个包含了二元关系的系统都可以用图论来模拟.而且,图论能把纷杂的信息变的有序、直观、清晰.山于我们感兴趣的是两对象之间是否有某种特定关系,所以图形中两点间连接与否尤为重要,而图形的位置、大小、形状及连接线的曲直长短则无关紧要.图论在自然科学、社会科学等各个领域都有广泛的应用.随着科学的发展,以及生产管理、军事、交通运输等方面提出了大量实际的需要,图论的理论及其应用研究得到飞速发展。
离散数学图论

图的同构
对于两个图G和G,如果它们的顶点之间存在一一对应关系,而 且这种关系保持了两顶点间的邻接关系(在有向图中,还保 持了边的方向)和边的重数,则这两个图是同构的。
同构的图除了点和边的名称不同外,实际上代表同样的组织结 构。 由于图形的顶点位置和连线长度都可任意选择,同一个图可能 画出不同的形状来,因而引出图同构的概念。 如下面两个图同构:
32
Zhengjin,Central South University
33
8.3 图的矩阵表示
定义 1 设 G=<V,E> 是无向图,且无平行边,其中 V={v1,v2,…,vn}, 定义一个nn的矩阵A,其中各元素aij为:
1 如果<vi,vj>E aij=
0 如果<vi,vj>E
称这样的矩阵为图 G 的邻接矩阵。(即若两点间有边相连,则对应 的为1,无边相连,则对应的为0)
Zhengjin,Central South University
23
Zhengjin,Central South University
24
Zhengjin,Central South University
25
Zhengjin,Central South University
26
Zhengjin,Central South University
连通图
定义3 设G=<V,E>,且vi,vjV.如果存在从vi到vj的路径,则 称从vi可达vj. (因vi 可看作长度为 0的路径,即从vi可达vi, 即任何顶点都是自己可达)。
定义4 在无向图中,如果任何两个顶点都可达,则称之为连通图。 如果G的子图是连通图,称之为连通子图。 一个无向图如果不是连通图,就是由若干个连通子图构成。 定义5 在有向图G中,如果在任两个顶点中,存在从一个顶点到 另一个顶点的路径,则称图 G为单向连通的。如果在 G中,任 何两个顶点都互相可达,则称G为强连通的。如果它的基础图 (底图)是连通的,则称之为弱连通的。 显然,强连通的,也是单向连通的,也是弱连通的。
集合论与图论基础题

集合论与图论基础题在数学中,集合论和图论是两个重要的分支。
集合论研究元素的归类和组织,而图论研究元素之间的关系和连接。
本文将通过一些基础题目来介绍集合论和图论的基本概念和应用。
1. 集合论1.1. 基本概念在集合论中,我们首先需要了解集合的概念及其相关术语。
一个集合是由一些确定的元素组成的整体。
通常用大写字母表示集合,而集合中的元素用小写字母表示。
例如,集合A={1, 2, 3}表示一个包含元素1、2和3的集合。
1.2. 集合的运算在集合论中,还有一些常见的集合运算:并集、交集和补集。
- 并集(Union):将两个或多个集合中的元素合并成一个集合。
记作A∪B,表示包含了属于集合A或集合B的所有元素。
- 交集(Intersection):将两个或多个集合中共有的元素取出来,形成一个新的集合。
记作A∩B,表示包含了同时属于集合A和集合B的所有元素。
- 补集(Complement):给定一个全集U和一个集合A,A对于U 的补集是指在U中但不在集合A中的元素组成的集合。
记作A'或者A^c,表示不属于A的所有元素。
1.3. 集合的关系在集合论中,还可以通过比较集合的元素来描述集合之间的关系。
- 包含关系:如果集合A中的所有元素都属于集合B,我们称集合A是集合B的子集,记作A⊆B。
- 相等关系:如果两个集合A和B具有相同的元素,互相包含对方的所有元素,我们称它们相等,记作A=B。
- 真子集:如果集合A是集合B的子集,但集合A和集合B不相等,我们称集合A是集合B的真子集,记作A⊂B。
2. 图论2.1. 基本概念图是由一些顶点和连接这些顶点的边组成的数学结构。
图论研究顶点和边之间的关系及其相关性质。
2.2. 有向图与无向图图可以分为有向图和无向图两种类型。
- 有向图:图中的边有方向,连接顶点A和顶点B的边从A指向B,记作(A, B)。
- 无向图:图中的边没有方向,连接顶点A和顶点B的边可以从A到B,也可以从B到A,不加箭头表示。
5.图论

注意:在无向图中,无向边(a,b)是从顶点a到顶点b的 线段,无方向.在有向图中,有向边<a,b>是有方向的, 且箭头必须从a指向b.也常用e=<vi,vj>表示边.有时 用G泛指无向图或有向图,而D只能表示有向图. 几个概念: 设G=<V,E>为一无向图或有向图, (1)若V,E都是有穷集合,则称G是有限图. (2)若|V|=n,则称G为n阶图.(此处|V|表示V中元素个 数;这里n≥1) (3)若E=,则称G为零图(仅包含孤立结点的图).特别 的,若此时又有|V|=1,则称G为平凡图(只有一个结点 的图).
第三部分 图论
在计算机科学领域,如开关理论,逻辑设 计,形式语言,操作系统,编译程序,数据结 构和信息检索等,都以图论为工具来解决实 际问题和理论问题,图论有着广泛的应用. 图论的内容十分丰富,涉及面也比较广, 本部分所涉及的只是图论中最基本的,但在 实际中经常用到的知识.
第7章 图的基本概念
7.1 无向图和有向图
定义 一个无向图G是一个二元组<V,E>, 即 G=<V,E>,其中
(1)V是一个非空的集合(在图的运算中,有时产生 顶点集合为的结果,因而规定顶点集为的图 是无意义的),称为G的顶点集,V中元素称为顶 点或结点. (2)E是无序积V&V的一个多重子集(元素可重复出 现的集合为多重集),E中元素称为无向边,也简 称边. 在一个图G=<V,E>中,为了表示V和E分别为G的顶 点集和边集,常将V记成V(G),E记成E(G).
在上图中,(2),(3)均为(1)的子图,(3)是生成图,(2) 是顶点集{v1,v2}的导出子图,也是边子集{e4,e5}的 导出子图.(3)是边子集{e1,e3,e4}的导出子图. (5),(6)是(4)的子图,(5)是生成子图,也是边子集 {e1,e2}的导出子图.(6)边子集{e1}的导出子图.
图论

Graphs/图论
二、 图的术语/Graph Terminology 定义 相邻和关联: 在无向图G中,若e=(a,b) ∈E, 则称a与b相邻/adjacent,或边e关联a、b /incident或联结a、b/connect。a、b称为边e 的端点或结束顶点/endpoint. 在有向图G中,若e=(a,b)∈E,即 箭头由a到b,称a相邻到b,或a关联或联 结b。a称为e的起点/initial vertex,b称为e的 终点/terminal or end vertex。
v V
d(v)= d(v)+ d(v)= 2m
d(v)=2m- d(v)
vV2 vV1 vV2
vV1 vV2
d(v)是偶数,从而 d(v)也为偶数,
vV1
即奇数顶点的个数必为偶数,得结论成立.
8/7/2016 9:51 PM Discrete Math. , QingTai Wu 20
A
C
D
图1
8/7/2016 9:51 PM
B
2
Discrete Math. , QingTai Wu
图论的产生与发展史概述
Graphs/图论
当时那里的居民热衷于一个难题:一个散步者能否 从河岸或小岛出发,通过每一座桥,而且仅仅通过 一次回到原地?这个问题似乎不难,谁都愿意试一 试,但谁也回答不出来。 欧拉是一个数学家,头脑比较冷静。千百人的失 败使他猜想,也许了样的走法根本不存在。1736年, 欧拉证明了他的猜想,并在圣彼得堡科学院作了一次 报告。 为了证明这个问题没有解,欧拉将每一块陆地用 一个点来代表,将每一座桥用联结相应的两个点的一 条线来代替,从而得到了一个如图2所示的一个 “图”。于是七桥问题就变成了如下的一笔画问题: 能否笔不离开纸,把图2的“图”一笔画成,使每条 8/7/2016 9:51 PM Discrete Math. , QingTai Wu 3 线只画一次
图论及图的基本介绍

第四篇图论
什么是图论
定义
✓图论(Graph Theory)是数学的一个分支。
它以图为研究对象。
✓图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系;用点表示事物,用连接两点的线表示相应两个事物间的关系。
✓从一般意义而言,它描述了客观世界中的拓扑结构。
什么是图论
人们常称1736年是图论历史元年,因为在这一年瑞士数学家欧拉(Euler)发表了图论的首篇论文——《哥尼斯堡七桥问题无解》,所以人们普遍认为欧拉是图论的创始人。
1936年,匈牙利数学家寇尼格(Konig)出版了图论的第一部专著《有限图与无限图理论》,这是图论发展史上的重要的里程碑,它标志着图论将进入突飞猛进发展的新阶段。
哥尼斯堡七桥问题
18 世纪在哥尼斯堡城( 今俄罗斯加里宁格勒) 的普莱格尔河上有7 座桥,将河中的两个岛和河岸连结,如图所示。
城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7 座桥,而每座桥只许通过一次,最后仍回到起始地点。
这就是著名的哥尼斯堡七桥问题。
图论的应用
计算机科学、物理学、化学、运筹学、信息论、控制论、网络通讯、社会科学以及经济管理、军事、国防、工农业生产等方面都得到广泛的应用。
1936年,匈牙利数学家寇尼格(Konig)出版了图论的第一部专著《有限图与无限图理论》,这是图论发展史上的重要的里程碑,它标志着图论将进入突飞猛进发展的新阶段。
图论的知识体系概图
第十章图的基本概念
本章各节间的关系概图
图的基本概念在计算机科学技术相关领域的应用。
第七章 图论

• 对于有向图 G中的任意结点 u,v 和w,结点间的距离有以下 的性质: ① du,v≥0 ② du,u=0 ③ du,v+dv,w≥du,w • 注:一般来说, du,v不一定等于dv,u • 定义D=max du,v为图的直径 • 关于有向图两个结点间的距离可以很容易的推广到无向图 中
【例】如右图所示是一个图,其中 v1e1v2e3v3e4v2e3v3e7v5是一条从v1到v5的路 v1e1v2e3v3e4v2e5v4e8v5是一条从v1到v5的迹 v1e1v2e3v3e7v5是一条从v1到v5的通路 v3e3v2e5v4e8v5e6v2e4v3是一个回路 v3e3v2e5v4e8v5e7v3是一个圈
• 定义 7-1.9 设图 G=V,E 与图 G′=V′,E′ ,如果存 在一一对应的映射g: vi→vi′且e=(vi,vj)是G的一条 边当且仅当e′=(vi′,vj′)是G′的一条边,则称G与G′同 构,记为G≌G′.
• 通俗的讲两个图同构当且仅当两个图的结点和边存在着一 一对应,且保持关联关系
• 如果一对结点间的边多于一条,则称这些边为平行边
• 定义 7-1.4 含有平行边的任何一个图称为多重图
• 不含平行边和环的图称为简单图
• 定义 7-1.5 简单图G=<V,E>中, 若每一对结点都有 边相连,则称该图为完全图。
• n个结点的无向完全图记为Kn
• 定理7-1.4 • 定义7-1.6 给定一个图G,由G中所有结点和所有 能使G成为完全图的添加边组成的图,称为图G的 相对于完全图的补图,简称为G的补图,记为 G 。
1 n个结点的无向完全图Kn的边数为2 n(n 1)
• 定义7-1.7 设图G=<V,E>, 如果有图G′=<V′,E′>, 且 E′ E, V′ V, 则称G′为G的子图
图论
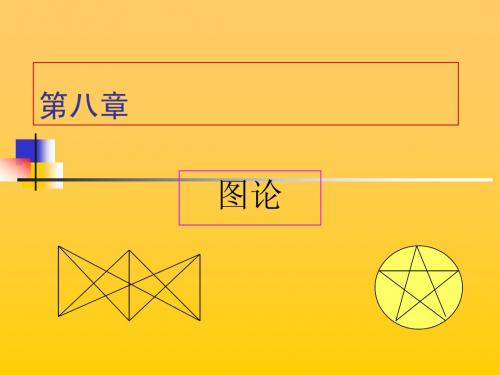
补图
定义1:设G是简单图,H是一个以V(G)为顶 点集的图,且两个顶点在H中邻接当且仅当它 在G中不邻接,则称H为G的补图,记为H= G
G G K5
定义2:由G的所有结点和为使G变成完全图, 所需要添加的那些边组成的图, 称之为G的补 图.
图的同构
例:图G如右图
2 1 3
3
3 4 5
3
4
3 2
2 1
4 5
2 1
2 5
(1) (2) (3) 则(1)是G的生成子图,是由边 (2,3),(2,4),(2,5),(1,2),(1,5)导出的子图,但不是点导 出子图。 (2)是由边(2,3),(2,4),(2,1)导出的子图。 (3)是由点{2,3,5}导出的子图,也是由边(2,3),(2,5) 导出的子图。 (4)既不是点导出的子图,又不是边导出的子图,是G 的子图。
2
5 7
3
一. 图的概念
设A,B为两个非空集合,记 AB={<a,b>|aA∧bB}(笛卡儿积) A&B={(a,b) |aA∧bB}(无序对集合) 定义1:一个无向图G定义为一个二元组<V,E>,记做 作G=<V,E>,其中 A (1)V是一个非空集合,称为G e1 e e5 2 的顶点集,它的元素称为顶点; G : B e6 D (2)EV&V,称为G的边集, e3 e 4 C e7 其元素称为边, V&V中的元素可以在 V(G)={A,B,C,D} E中出现不止一次。 注1:以下,用分别V(G),E(G)表示图G 的顶点集和边集。 注2:只讨论V(G)和E(G)有限的情形。 注3:在保持图的顶点和边的关系不变的情况下,图 形的位置、大小、形状都是无关紧要的。
《应用数学基础》(陈冲)教学课件 第八章 图 论

第八章 图 论
目录
ONTENTS
1 图的基本概念 2 图的矩阵表示 3 图的连通性
01 图的基本 概念
1.1 图的定义
在某计算机网络中,两台计算机之间通过网络线连接起来,如图 8-1 所示.顶点表示每台计 算机的位置,边表示网络连线.这类图在绘制时,可用圆圈(或实心点)来表示顶点,对图的 所有顶点标以名称:v1 ,v2 ,v3 ,v4 ;用直线或曲线来表示边,同时对图的所有边标以名称:e1 , e2 , e3 , e4 , e5 ,如图 8-2 所示.
该定理之所以称为握手定理,因为它有非常直观而形象的解释:假定有若干个人握手,每握
一次手,需要 2 只手来完成.此时有人用自己的右手握自己的左手,也算一次握手.参加握手的 手的总数目(包含重复的)恰好等于握手次数的 2 倍.这里用到了图论模型解决实际问题:把每 个人看成一个顶点,某两人握一次手,则在相应顶点之间连上一条边;如果某人与自己握手,则
设 G (V ,E) 是有向图, v V ,称以 v 为终点的边数为 v 的入度,记为 d (v) ;称以 v 为起 点的边数为 v 的出度,记为 d (v) .
若 d(v) 是奇数,就称 v 为奇点;若 d(v) 是偶数,就称 v 为偶点.度为 1 的点称为悬和是边数的 2 倍,这是图的一般性质.下面给出的定理是 Euler 在 1936 年提出 的,常称为握手定理,是图论中的基本定理.
定理 1(握手定理) 设 G (V ,E) 是图,G 中所有顶点度数之和 d (v) 等于 G 中边数 m 的 vV
两倍,即
d(v) 2m .
vV
1.2 顶点的度
在图 8-3 中,由于 e3 (v2 ,v3 ) ,则点 v2 与点 v3 邻接,点 v2 与边 e3 关联,点 v3 与边 e3 关联; 由于边 e1 和边 e3 有共同的顶点 v2 ,则边 e1 和边 e3 邻接; v5 为孤立点.
图论简介

v1
e1 e6 e4
v5
e2
v2 e3
e5 v3
v4
V 例1、(2) 有向图 D V , E , v1 , v2 , v3 , v4 , v5
E v1 , v2 , v3 , v2 , v3 , v2 , v3 , v4 , v2 , v4 , v4 , v5 , v5 , v4 , v5 , v5
第七章 图的基本概念
第一节 无向图及有向图
内容:有向图,无向图的基本概念。
重点:1、有向图,无向图的定义,
2、图中顶点,边,关联与相邻,顶点 度数等基本概念, 3、各顶点度数与边数的关系
d (v ) 2m 及推论,
i 1 i
n
内容:有向图,无向图的基本概念。
重点:4、简单图,完全图,子图,
n 1的初级通路。
6、性质。 定理:在一个 n 阶图中,若 vi 到自身存在回路,
则从 vi 到自身存在长度小于等于 n 的回路。
推论:在一个 n 阶图中,若 vi 到自身存在一个
简单回路,则从vi 到自身存在长度小于等于 n
的初级回路。
6、性质。 由以上定理可知,在 n 阶图中, 任何一条初级通路的长度 n 1 任何一条初级回路的长度 n
补图的概念, 5、图的同构的定义。
一、图的概念。
1、定义。 无序积 A & B (a, b) a A b B 无向图 G V , E
E V & V , E 中元素为无向边,简称边。
有向图 D V , E
E V V , E 中元素为有向边,简称边。
一、图的概念。
如例1的(1)中,
v1
图论
图论任课教师:王磊基础教学部数学教研室图论发展史图论在现代科学技术中有着广泛的应用,如:网络设计、计算机科学、信息科学、密码学、DNA 的基因谱的确定和计数、工业生产和企业管理中的优化方法等都广泛的应用了图论及其算法。
首先我们通过图的发展过程来了解一下图论所研究的内容。
图论起源于1736年的一个游戏----哥尼斯城堡七桥问题。
七桥问题C包含两个要素:对象(陆地)及对象间的二元关系(是否有桥连接)C转化A DEuler1736年B A DB图论中讨论的图问题:是否能从四块陆地中的任一块开始,通过每座桥恰好一次再回到起点?转化是否能从任意一个顶点开始,通过每条边恰好一次再回到起点?问题一:四色问题四色问题是世界近代三大数学难题之一。
四色问题的内容是:任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。
它的提出来自英国。
1852年,毕业于伦敦大学的弗南西斯·格思里发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家都被着上不同的颜色。
”进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。
后来美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。
1950年,有人从22国推进到35国。
1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国。
1976年6月,美国伊利诺大学哈肯与阿佩尔在两台不同的电子计算机上,用了1200个小时,作了100亿判断,终于完成了四色定理的证明,轰动了世界。
然而,真正数学上的严格证明仍然没有得到!数学家仍为此努力,并由此产生了多个不同的图论分支。
问题二:Hamilton问题Hamilton问题源于1856年,英国数学家H amilton 设计了一个名为周游世界的游戏:他用一个正十二面体的二十个端点表示世界上的二十座大城市(见图),要求游戏者找一条沿着十二面体的棱通过每个端点恰好一次的行走路线。
(课件)图论讲义

3
(8) 完全图(complete graph)
(9) 图的顶点数(图的阶)ν 、边数 ε
(10) 顶点 v 的度(degree):d(v) = 顶点 v 所关联的边的数目(环边计两次)。
(11) 图 G 的最大度: ∆(G) = max{dG (v) | v ∈V (G)}
图 G 的最小度:δ (G) = min{dG (v) | v ∈V (G)}
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
和 Y。
(2)否则,设 u′ 是 P 与 Q 的最后一个公共顶点,因 P 的 (u, u′) 段和 Q 的 (u, u′) 段都是 u 到 u′ 的最短路,故这两段长度相等。
假如 P,Q 的奇偶性相同,则 P 的 (u′, v1) 段和 Q 的 (u′, v2 ) 段奇偶性相同,这两段与边 e 构成一个奇圈,与定理条件矛盾。可见 P,Q 的奇偶性不同,从而 v1, v2 分属于 X 和 Y。
这便证明了 G 是一个二部图。 证毕。
7. 连通性 图中两点的连通:如果在图 G 中 u,v 两点有路相通,则称顶点 u,v 在图 G 中连通。 连通图(connected graph):图 G 中任二顶点都连通。 图的连通分支(connected branch, component):若图 G 的顶点集 V(G)可划分为若干非空子集
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例
• 图中的结点重排次 序为v5v2v1v3v6v4,得 另一个邻接矩阵
0 0 1 A 1G 0 1 1 0 1 0 1 1 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 1 1 0 1 0 0 1 1 0
• 在邻接矩阵A1G中,如果先交换第1、3行, 而后交换第1、3列;接着交换第3、4行, 再交换第3、4列;接着交换第5、6行,再 交换第5、6列;接着交换第4、5行,再交 换第4、5列。那么就能由邻接矩阵A1G得到 邻接矩阵AG。
例题
• 试写出下图所示图G的所有结点的邻接点、 所有边的邻接边,并指出所有的孤立结点 v3 v4 v5 和环。
e4 v2 e5 e1 e6 e2 v6 v1 e3 e7
分析
• 根据定义,如果两个结点间有边相连, 那么它们互为邻接点;如果两条边有公共 结点,那么它们互为邻接边。 • 需要注意的是,只要当一个结点处有环 时,它才是自己的邻接点;由于一条边有 两个端点,在计算邻接边时要把这两个端 点都算上,例如e2和e4都是e1的邻接边。 所有边都是自己的邻接边。
图的操作
• 定义 设图G = <V, E>。 1. 设e∈E,用G-e表示从G中去掉边e得到的图,称为 删除边e。又设EE,用G-E表示从G中删除E中 所有边得到的图,称为删除E。 2. 设v∈V,用G-v表示从G中去掉结点v及v关联的所 有边得到的图,称为删除结点v。又设VV,用GV 表示从G中删除V中所有结点及关联的所有边得 到的图,称为删除V。 3. 设e = (u, v)∈E,用G\e表示从G中删除e,将e的两 个端点u, v用一个新的结点w代替,使w关联除e外 的u和v关联的一切边,称为边e的收缩。一个图G 可以收缩为图H,是指H可以从G经过若干次边的收
钻石与足球烯
• 足球烯应用在超导、太阳能电池、护肤品 • 数学领先其他科学100年
奥秘尚未解开的“妖怪”
• 何为妖怪,指这种性质的图很难设计出来, 它是无桥三次正则图,每个顶点处关联了 三条边;它的围长不小于5,它的边色数是 4,删除三条边不会使它破裂成两个有边图。 • 通路? • 双覆盖?
更多妖怪
– 若边e与无序结点对(u,v)相对应,则称e为无向 A D 边(Undirected Edge),记为e = (u, v) = (v, u), B E 这时称u、v是边e的两个端点(End point)。
C F
– 若边e与有序结点对<u, v>相对应,则称e为有向 边(Directed Point)(或弧),记为e = <u, v>,这时 称u为e的始点(Initial Point)(或弧尾),v为e的终 点(terminal Point)(或弧头),统称为e的端点。
1 2
七桥问题
欧拉
游戏博弈问题 树 四色猜想 高速数字计算机
3
4 5
七桥问题
• 如何不重复的走完七座桥?
游戏博弈问题
数据结构中的树
四色问题
• 可否用四种颜色标示所有的地图?
高速计算
第一章 图
1 2 图的基本概念 图的表示、分类 图的性质 通路与回路 图的连通性
3
4 5
6
图的应用
第一章学习要求
• 形式化:对于一个图G,如果将其记为
– G = <V, E>,并写出V和E的集合表示 – 称为图的集合表示。
• 图形化:用小圆圈表示V中的结点,
– 用由u指向v的有向线段表示有向边<u, v> – 无向线段表示无向边(u, v), – 称为图的图形表示。
图论的艰苦
• 从许多实例中,我们发现图论最吸引人的特色是 它蕴含着大量强有力的思想、漂亮的图形和巧妙 的论证,即使是非常困难的尚未解决的问题也易 于表达。 • 问题外表的简单朴素和本质上的难以解决,使每 个搞图论的人在图论面前必须谨慎严肃地思考问 题。常常是貌似简单的问题,即使幸运地得出证 明,证明中包含的细节也十分之繁琐,并且往往 运用了极艰苦的计算。
B
C
E
F
基本思想
• 用图形表示一组对象,其中有些对象对 是有联系的。 对于这种图形,我们感兴趣的只是有多 少个点和哪些结点之间有线连接,至于连 线的长短曲直和结点的位置却无关紧要, 只要求每一条线都起始于一个点,而终止 于另一个点。
•
图的定义
• 一个图(Graph)是一个序偶<V, E>,记为G = <V, E>,其中:
图 论
第一节 课程概述
陕西科技大学 电气与信息工程学院 研究生课程 齐勇
• 任课教师
– 齐勇(qiyong@) – 电信学院计算机系办公室312#
教材与参考书
• 教材
– 《图论》,王树禾,科学出版社
• 参考书
– 《图论引导》,Douglas B. West,机器工业出版社
教学周历
例
v2
• 试写出下图所示图G的邻接矩阵。 • 分析 首先将图中的6个结点 6,v1 解 若结点排序为v1v2v3v4v5v 则其邻接矩阵 v4 v5 v6 排序,然后利用定义写出其邻 v1 v2 v3 接矩阵。初学时可先在矩阵的 v1 0 1 0 0 1 1 0 11 00 0 1 1 0 v2 1 0 0 行与列前分别按结点排序标上 v5 v3 0 1 1 1 0 1 1 0 0 0 1 0 结点,若第i行前的结点到第j 0 1 1 1 0 1 v4 0 A 0 1 0 1 1 列前的结点有边相连,则在邻 G v5 1 0 0 0 0 1 1 0 1 1 1 0 接矩阵的第i行第j列元素为1, v6 1 0 1 1 0 01 1 0 1 0 1 否则为0。若结点排序为 1 0 1 1 1 0 v1v2v3v4v5v6,则可标记如下:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 图的基本概念 树、生成树、最优树、有序二元树、追捕问题 平面图、Euler公式、灌木生长算法 匹配理论、图的因式分解 着色问题、四色证明、Ramsey数 Euler图、Hamilton图、邮递员问题 有向图、强弱连通、循环赛 最大流、2F算法、Dinic分层算法、网络流 连通度、边数最少的k连通图 图的线性空间与矩阵 图论中的NPC问题及算法分析 习题课与考试
Hamilton旅行游戏
• 货郎担问题
– TSP(Traveling Salesman Problem)
– 假设有一个旅行商人要拜访n个城市,他必须 选择所要走的路径,路经的限制是每个城市只 能拜访一次,而且最后要回到原来出发的城市。 路径的选择目标是要求得的路径路程为所有路 径之中的最小值。
– NPC问题
• (1)V = {v1, v2, …, vn}是有限非空集合,vi称为 结点(Nodal Point),简称点(Point),V称为结点 集(Nodal Set)。
• (2)E是有限集合,称为边集(Frontier Set)。E 中的每个元素都有V中的结点对与之对应,称之 为边(Edge)。
图的表示
v6
v3
v4
•
说明
由定义可看出,图G = <V, E>的邻接矩阵依赖 于V中元素的次序。对于V中各元素不同的排序, 可得到同一图G的不同邻接矩阵。但是,G的任 何一个邻接矩阵可以从G的另一邻接矩阵中通过 交换某些行和相应的列而得到,其交换过程与将 一个排序中的结点交换位置变为另一个排序是一 致的。如果我们略去由结点排序不同而引起的邻 接矩阵的不同,则图与邻接矩阵之间是一一对应 的。因此,我们略去这种由于V中元素的次序而 引起的邻接矩阵的任意性,只选V中元素的任一 种次序所得出的邻接矩阵,作为图G的邻接矩阵。
两种描述方法的优缺点
• 用集合描述图的优点是精确,但抽象不易 理解; • 用图形表示图的优点是形象直观,但当图 中的结点和边的数目较大时,使用这种方 法是很不方便的,甚至是不可能的。
图的矩阵表示
• 我们在学习中常常需要分析图并在图上 执行各种过程和算法,也许必须用计算机 来执行这些算法,因此必须把图的结点和 边传输给计算机,由于集合与图形都不适 合计算机处理,所以要找到一种新的表示 图的方法,这就是图的矩阵表示。 • 由于矩阵的行和列有固定的次序,因此 在用矩阵表示图时,先要将图的结点进行 排序,若不具体说明排序,则默认为书写 集合V时结点的顺序。
北京 长春
成都
上海 武汉
•
假设有4台计算机,分别标记为A、B、C 和D,在计算机A和B、C和D以及B和C之间 有信息流。这种情形可用下图表示,通常 称这种图为通信网络;和一组工作,这群人中的 某些人能够做这组工作中的某些工作。例 如,有3个人A、B和C,3件工作D、E和F, 假设A只能做工作D, B能做工作E和F, C能 做工作D和E。则这种情形可用下图表示, 其中,在人和这个人能够做的工作之间画 A D 有线。
定义: 邻接点与邻接边
• 在图G = <V, E>中,若两个结点vi和vj是边e的端点,则称 vi与vj互为邻接点(Adjacent Point),否则vi与vj称为不邻接 的; • 具有公共结点的两条边称为邻接边(Adjacent Edge); • 两个端点相同的边称为环(Ring)或自回路(Self-Loop); • 图中不与任何结点相邻接的结点称为孤立结点(Isolated Point); • 仅由孤立结点组成的图称为零图(Null Graph); • 仅含一个结点的零图称为平凡图(Trivial Graph); • 含有n个结点,m条边的图,称为(n, m)图。
次序与邻接矩阵
• 设图G = <V, E>,其中V = {v1, v2, …, vn}, 并假定结点已经有了从v1到vn的次序,则n 阶方阵AG = (aij)nxn称为G的邻接矩阵 (Adjacency Matrix),其中
