学而思十二级奥数体系
奥数1-6年级课表及学费 (学而思)
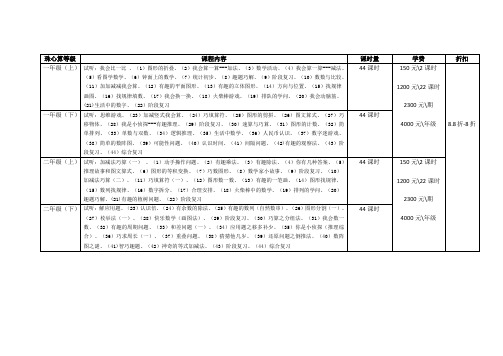
三年级(上)
试听:加法与减法 、(1)乘法与除法、(2)归总问题、(3)数字迷之加减法竖式、(4)周期问题(一)、(5)等量代换之常用解题方法、(6)枚举法、(7)和差问题、(8)多笔画问题、(9)图形数列找规律、(10)平均数问题、(11)巧求周长(二)、(12)和差倍问题(一)、(13)图形面积、(14)逻辑推理之对应型、真假型问题、(15)多位数除法、(16)乘除法巧算、(17)巧填算符(二)、(18)年龄问题、(19)周期问题(二)、(20)奇偶性分析、(21)最短路线、(22)综合复习
44课时
200元2课时
1800元\22课时
2800元\期
4800元\年级
六年级(下)
试听:小升初热点应用题盘点(一)(23)五大模型——蝴蝶模型、燕尾模型、(24)平面几何常用技巧、(25)立体几何常用技巧、(26)整除综合之整除判别方法、(27)余数综合之余数问题解题技巧、(28)数论综合之代数思想与枚举验证、(29)比例类行程问题之柳卡图、(30)小升初热点应用题盘点(二)(31)数论之质合、因倍、余数综合、(32)数论之最值、计数、行程综合(一)、(33)数论之最值、计数、行程综合(二)、(34)曲线型面积解题思路、(35)行程问题常用思想之图解法、综合分析、(36)行程问题常用思想之比例思想、代数思想、(37)小升初计算高频考点汇总与方法总结(一)、(38)小升初计数高频考点汇总与方法总结(二)、(39)小升初数论高频考点汇总与方法总结(一)、(40)小升初数论高频考点汇总与方法总结(二)、(41)小升初行程高频考点汇总与方法总结(一)、(42)第05讲小升初行程高频考点汇总与方法总结(二)、(43)小升初应用题高频考点汇总与方法总结(一)、(44)小升初应用题高频考点汇总与方法总结(二)、
学而思课程体系介绍

学而思课程体系介绍学而思是一家致力于提供优质教育资源和服务的教育机构,在教育行业具有广泛的影响力和较高的知名度。
学而思的课程体系是其成功的关键之一,它涵盖了丰富多样的学科和领域,并采用了先进的教育理念和教学方法,为学生的全面发展提供了保障。
一、课程种类及内容学而思的课程种类包括学科课程、兴趣课程和素质拓展课程等。
学科课程涵盖了语文、数学、英语、物理、化学、生物、地理、历史等主要学科,通过系统、规范的教学内容和方法,帮助学生扎实掌握学科知识和解题技巧。
兴趣课程则包括音乐、体育、美术、舞蹈等丰富多样的选修课,旨在培养学生的兴趣爱好和综合能力。
素质拓展课程则注重学生个人品质的培养,包括礼仪、演讲、领导力等课程,旨在提高学生的综合素质和社交能力。
在学科课程方面,学而思采用科学系统的教学内容和方法,通过分级、分类、归纳总结等方式,帮助学生建立扎实的学科基础。
课程内容与教材紧密对应,教师精选了一系列精彩的案例和实例,以更具体、形象的方式展示和解释知识点,帮助学生更好地理解与记忆。
同时,学而思还注重培养学生的自主学习能力,激发学生的学习兴趣和求知欲望,帮助他们形成自主、合作学习和独立思考的良好习惯。
二、教学方法与特点学而思的教学方法主要包括示范讲解、互动讨论、实践演练等。
示范讲解是指教师通过举例和案例的方式,结合多媒体教学辅助工具,演示知识和技能的运用过程,为学生树立学习的榜样和目标。
互动讨论是指教师和学生之间的积极互动,通过提问、讨论、答疑等方式,培养学生的思考能力和问题解决能力。
实践演练是指学生在教师指导下进行实际操作和练习,巩固和应用所学知识。
在教学特点方面,学而思的课程注重形成性评价,即通过课堂小测、作业、讲评等方式,及时了解学生的学习进度和掌握情况,并针对性地进行反馈和辅导。
学而思还非常重视作业的质量和规范,鼓励学生按时完成作业,并提供详细的批改和讲解,帮助学生发现和改正存在的问题,提高学习效果和思考能力。
学而思秘籍和奥数精讲

学而思秘籍和奥数精讲学而思秘籍和奥数精讲是当前备受瞩目的两门课程,尤其是在家庭教育领域中,备受青睐。
这两门课程都是针对小学生或者中学生的数学学习,而且都是由专业老师讲授,其教学质量和效果备受认可。
下面,我们详细介绍这两门课程的特点和优势。
1.学而思秘籍学而思秘籍是全球领先的K12在线个性化学习服务平台,也是目前市场上最受欢迎的一款学科提高辅导软件之一。
它不仅覆盖了各年龄段的学生,而且根据学生的个性化需求和学习特点进行量身定制课程。
学而思秘籍针对的是各学科的学习辅导及全面素质提升,以英语、语文、数学、美术等为主要科目。
学而思秘籍有以下优势:①以一对一个性化诊断,及时发现学生的学习问题,并针对性地布置题目,帮助学生克服不足。
②融合AI技术,通过智能诊断系统,进行数据分析,为家长和教师提供更加全面的学生学习数据。
③配有科学的学习路径,合理规划每一个知识点,让学生把复杂的学科内容变成小块的简单内容。
2.奥数精讲奥数精讲是一门针对小学低年级和高年级的课程,强调数学逻辑训练,注重启发学生的思维能力,创造多种多样的解题方法,让学生在学习中找到乐趣,从而慢慢地学会独立思考。
它有以下优势:①讲座方式生动有趣,采用多种互动方式,提高学生的参与度和兴趣。
②教材系统化,由易到难,分阶段教授,更容易让学生掌握知识点。
③严格的教学标准,多次复习,确保学生的知识储备和掌握度。
通过以上对学而思秘籍和奥数精讲的介绍,可以看出它们都是针对学生的个性化需求进行设计的,不仅注重知识点的讲解,同时强调了学生的思维能力和逻辑思维训练。
由于这样的优势,学而思秘籍和奥数精讲因而备受人们的追捧。
在这里,我们建议家长在为孩子选择适合的辅导课程时,一定要根据孩子的特点和兴趣综合考虑,以达到最大的效果。
奥数机构20排名

以下是奥数机构民间版20:1 学⽽思师资⼒量:A机构资质:正规资源指标:A++规模指标:A++企业成长性:B+班级体系:集训队-超A班-超常班-尖⼦班-提⾼班点评:沪上规模⼩奥机构,上市公司,市场服务意识强,但⽼师多以年轻⼤学⽣担纲,名师流失⾃⽴门户较多,适合打基础。
2 四季师资⼒量:A+机构资质:正规资源指标:A++规模指标:A+企业成长性:A班级体系:创新班-实验班-⾦牌班-精英班点评:沪上⽼牌培训机构,市场份额较⼤。
但⽬前名师流失严重,教学质量不断下降。
杯赛亚太杯主办⽅。
3 新东⽅泡泡师资⼒量:B+机构资质:正规资源指标:A++规模指标:A++企业成长性:B+班级体系:思维训练班+专项提⾼班点评:有很强的品牌知名度和规模,奥数体系⼀直在完善中。
4 昂⽴少⼉师资⼒量:B机构资质:正规资源指标:A++规模指标:A+企业成长性:B+班级体系:数理资优-竞赛培训-数学精品-思维拓展点评:沪上本⼟综合实⼒派,但奥数兼职⽼师为主。
5 新贝师资⼒量:B机构资质:正规资源指标:A++规模指标:A+企业成长性:B+班级体系:考证班-奥数提⾼班点评:市场营销强悍,各种杯赛关键字均为其买断的。
奥数兼职⽼师为主,没有标准化的体系,围绕着杯赛⼀直在做⽂章。
6 新⾈师资⼒量:A+机构资质:正规资源指标:A++规模指标:A企业成长性:A+班级体系:光明顶-竞赛班-精英班-提⾼班-基础班点评:浦东地区⽼牌培训机构,浦东地区市场份额较⼤。
传背后有⼤资⾦⼊驻,近期将向全市发展。
7 尚品师资⼒量:B++机构资质:正规资源指标:A+规模指标:A企业成长性:B++班级体系:精英班-提⾼班-基础班点评:沪上⽼牌机构,上海⾛美杯举办⽅,资源渠道丰富,若不是近年教师流失⾮常严重,值得关注!8 乐在四季师资⼒量:B+机构资质:正规资源指标:A++规模指标:A企业成长性:B++班级体系:⾦牌班-精英班-优等⽣班点评:闵⾏区业数就放在其校区可见其资源渠道的实⼒,稍微⽋缺的就是师资⼒量。
学而思想奥数全能版目录

第一专题:计算专题共34讲【强化篇17讲竞赛篇17讲】一、计算竞赛篇共17讲竞赛1-加减法巧算之凑整与组合思想之竞赛篇(第1讲)竞赛2-乘除法巧算之提取公因式与组合思想之竞赛篇(第2讲)竞赛3-四则混合巧算只综合技巧之竞赛篇(第3讲)竞赛4-定义新运算之速算与巧算之竞赛篇(第4讲)竞赛5-数列求和与公式技巧之竞赛篇(第5讲)竞赛6-多位计算与归纳思想之竞赛篇(第6讲)竞赛7-小数计算与换元思想之竞赛篇(第7讲)竞赛8-数表计算与代数公式应用之竞赛篇(第8讲)竞赛9-循环小数互化与错位相减技巧之竞赛篇(第9讲)竞赛10-分数(繁分数)计算综合与比例转化之竞赛篇(第10讲)竞赛11-比较与估算综合技巧之竞赛篇(第11讲)竞赛12-分数计算之拆分、裂项与通项归纳之竞赛篇(第12讲)竞赛13-分数计算之换元与缩放之竞赛篇(第13讲)竞赛14-定义新运算之复杂运算与抽象运算之竞赛篇(第14讲)竞赛15-四大杯赛中的计算综合思想之竞赛篇(第15讲)竞赛16-计算综合之复杂分数裂项计算综合之复杂整数裂项之竞赛篇(第16讲) 竞赛17-计算综合之复杂公式与复杂换元计算之竞赛篇(第17讲)二、计算强化篇共17讲第一讲加减法巧算之凑整与组合思想(第18讲)第二讲乘除法巧算之提取公因式与组合思想(第19讲)第三讲四则混合巧算只综合技巧(第20讲)第四讲定义新运算之速算与巧算(第21讲)第五讲数列求和与公式技巧(第22讲)第六讲多位计算与归纳思想(第23讲)第七讲小数计算与换元思想(第24讲)第八讲数表计算与代数公式应用(第25讲)第九讲循环小数互化与错位相减技巧(第26讲)第十讲分数(繁分数)计算综合与比例转化(第27讲)第十一讲比较与估算综合技巧(第28讲)第十二讲分数计算之拆分、裂项与通项归纳(第29讲)第十三讲分数计算之换元与缩放(第30讲)第十四讲定义新运算之复杂运算与抽象运算(第31讲)第十五讲四大杯赛中的计算综合思想(第32讲)第十六讲计算综合之复杂分数裂项与整数裂项(第33讲)第十七讲计算综合之复杂公式与复杂换元计算(第34讲)第二专题数论专题计算专题共38讲【强化篇19讲竞赛篇19讲】一、数论竞赛篇第一讲奇偶数的性质与应用之竞赛篇(第35讲)第二讲有趣余数之性质与周期之竞赛篇(第36讲)第三讲整数分拆之分类与计数之竞赛篇(第37讲)第四讲整数分拆之最值与应用之竞赛篇(第38讲)第五讲数的整除之性质与求法之竞赛篇(第39讲)第六讲数的整除之代数思想与运用之竞赛篇(第40讲)第七讲数的整除之四大判断法综合运用之竞赛篇(第41讲)第八讲质数、合数与两大约数定理之竞赛篇(第42讲)第九讲因数与倍数之最大公因数与最小公倍数之竞赛篇(第43讲)第十讲因数与倍数之综合应用之竞赛(第44讲)第十一讲完全平方数之竞赛篇(第45讲)第十二讲带余除法之竞赛篇(第46讲)第十三讲同余问题之竞赛篇(第47讲)第十四讲中国剩余定理之竞赛篇(第48讲)第十五讲进制与位值原理之竞赛篇(第49讲)第十六讲四大杯赛的数论综合思想之竞赛篇(第50讲)第十七讲数论综合之整除相关问题之竞赛篇(第51讲)第十八讲数论综合之余数相关问题之竞赛篇(第52讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第53讲) 二、数论强化篇第一讲奇偶数的性质与应用(第54讲)第二讲有趣余数之性质与周期(第55讲)第三讲整数分拆之分类与计数(第56讲)第四讲整数分拆之最值与应用(第57讲)第五讲数的整除之性质与求法(第58讲)第六讲数的整除之代数思想与运用(第59讲)第七讲数的整除之四大判断法综合运用(第60讲)第八讲质数、合数与两大约数定理(第61讲)第九讲因数与倍数之最大公因数与最小公倍数(第62讲)第十讲因数与倍数之综合应用(第63讲)第十一讲完全平方数(第64讲)第十二讲带余除法(第65讲)第十三讲同余问题(第66讲)第十四讲中国剩余定理(第67讲)第十五讲进制与位值原理(第68讲)第十六讲四大杯赛中的数论综合思想(第69讲)第十七讲数论综合之整除相关问题(第70讲)第十八讲数论综合之余数相关问题(第71讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第72讲) 第三专题行程专题计算专题共30讲【强化篇15讲竞赛篇15讲】一、行程竞赛篇第一讲基础行程之竞赛篇(第73讲)第二讲简单相遇、追及之竞赛篇(第74讲)第三讲复杂相遇、追及之竞赛篇(第75讲)第四讲猎狗追兔之竞赛篇(第76讲)第五讲火车过桥之竞赛篇(第77讲)第六讲多次相遇之竞赛篇(第78讲)第七讲多人行程之竞赛篇(第79讲)第八讲流水行船之竞赛篇(第80讲)第九讲简单环形之竞赛篇(第81讲) 第十讲复杂环形之竞赛篇(第82讲) 第十一讲接送问题之竞赛篇(第83讲) 第十二讲间隔发车之竞赛篇(第84讲) 第十三讲电梯问题之竞赛篇(第85讲) 第十四讲变速变道之竞赛篇(第86讲) 第十五讲综合行程之竞赛篇(第87讲) 二、行程强化篇第一讲基础行程(第88讲)第二讲简单相遇、追及(第89讲)第三讲复杂相遇、追及(第90讲)第四讲猎狗追兔(第91讲)第五讲火车过桥(第92讲)第六讲多次相遇(第93讲)第七讲多次行程(第94讲)第八讲流水行船(第95讲)第九讲简单环形(第96讲)第十讲复杂环形(第97讲)第十一讲接送问题(第98讲)第十二讲间隔发车(第99讲)第十三讲电梯问题(第100讲)第十四讲变速变道(第101讲)第十五讲综合行程(第102讲)第四专题应用题专题共16讲一应用题1和差倍问题(第103讲)盈亏问题(第104讲)二应用题2还原问题(第105讲)鸡兔同笼(第106讲)三应用题3年龄问题(第107讲)周期问题(第108讲)四应用题4平均数问题(第109讲)统筹与规划问题(第110讲)五应用题5分数百分数问题(第111讲)牛吃草(第112讲)六应用题6比和比例(第113讲)工程问题(第114讲)七应用题7经济问题(第115讲)浓度问题(第116讲)八应用题8方程解复杂应用题(第117讲)应用题综合(第118讲)第五专题:几何专题计算专题共4讲【5级2讲6级2讲】一、几何专题能力进阶五级:五大模型及常用思维与方法第一讲五大模型(第119讲)第二讲常用思维与方法(第120讲)二、几何专题能力进阶六级:曲线型与立体几何第一讲曲线型(第121讲)第二讲立体几何(第122讲)。
学而思小学奥数知识点梳理(大纲视图)精编版

植 四、 典型应用题
1. 树问题
①开放型与封闭型 ②间隔与株数的关系 阵 2. 方 问题 外层边长数-2=内层边长数 (外层边长数-1)×4=外周长数 外层边长数 2-中空边长数 2=实面积数 车 桥 3. 列 过 问题 ①车长+桥长=速度×时间 ②③列车车车长长与甲甲人++车车或长长骑乙乙车==速速人度度或和差另××一追相列及遇车时时上间间的司机的相遇及追及问题 车长=速度和×相遇时间 车长=速度差×追及时间 龄 4. 年 问题
概述
一、 计算
1. 四则混合运算繁分数 ⑴ 运算顺序 ⑵ 分数、小数混合运算技巧
①一般而言: 加减运算中,能化成有限小数的统一以小数形式;
② 乘除运算中,统一以分数形式。
⑶带分数与假分数的互化 ⑷繁分数的化简 2. 简便计算 ⑴凑整思想 ⑵基准数思想 ⑶裂项与拆分 ⑷提取公因数 ⑸商不变性质 ⑹改变运算顺序
六、 计数问题
类枚举 1. 加法原理:分 排 2. 乘法原理: 列组合 容斥 3. 原理:
① 总 量数 =A+B+C-(AB+AC+BC)+ABC ② 常 总 量 用: 数 =A+B-AB
抽屉 4. 原理:
5. 握手至问多题至少问题
在 广泛 图形计数中应用 ① 角、线段、三角形,
② ③
长正方方形形、梯形、平行四边形
3.
路流程水行差船=速度差×追及时间 顺逆水水速速度度==船船速速+-水水速速
4. 船水多速速次相==((遇顺顺水水速速度度+-逆逆水水速速度度))÷÷22
线环型型路路程程:: 甲甲乙乙共共行行全全程程数数==相相遇遇次次数数×2-1
5. 环其形中跑甲道共行路程=单在单个全程所行路程×共行全程数
学而思初中数学课程规划

学而思初中数学课程规划初中数学的学习不同于小学小学是课内知识过于简单,课外的奥数较难,而且整个社会没有统一的教材,基本上都是各自研发,比如学而思的十二级体系。
而初中最终目标是中考,有明确的方向性,同时有统一规划的课本,知识体系非常完整。
因此整个初中的学习更适合在一个合理而科学的体系下学习,唯一不同就在于不同的孩子可以选择不同的进度和难度。
初中班型设置介绍初一年级:基础班,提高班,尖子班,竞赛班,联赛班初二年级:基础班,提高班,尖子班,竞赛班,联赛班初三年级:基础班,提高班,尖子班,目标班联赛班走联赛体系,一年半学完初中数学知识;竞赛班走竞赛体系,两年学完初中数学知识;基础班,提高班,尖子班走领先中考培优体系,两年半学完初中数学知识。
到初三不再设竞赛班和联赛班,统一回归到目标班,冲击中考。
2015年学而思初中教学体系体系联赛体系竞赛体系领先中考培优体系班型定位数学超常发展冲击竞赛一等奖中考满分兼顾竞赛同步提高冲击中考满分学制设计一年半学完初中内容两年学完初中内容两年半学完初中内容课程容量每节课的课程容量与难度比竞赛班大1.2-1.5倍每节课的容量与难度比尖子班大1.5-1.8倍每节课的容量是校内课程的3-5倍难度比校内课程高1.5-2倍适合学生课内知识掌握非常扎实,发展方向为冲击初中数学联赛,希望在数学方面有独特发展,例如未来参加IMO或CMO比赛,高中数学联赛冲击一等奖。
课内知识学习轻松,在保证中考路径的同时兼顾拔高与竞赛。
未来目标为冲击中考满分,同时参加一些数学竞赛,激发兴趣,锻炼思维。
从课内知识上夯实基础、同步提高,同时拓宽视野,系统化学习,目标冲击中考满分入学体系10次课学完初一----预备班选拔考试----联赛竞赛预备班----参加入学选拔考试----通过后选择联赛体系---开始学习10次课学完初一----预备班选拔考试----联赛竞赛预备班----参加入学选拔考试----通过后选择竞赛体系---开始学习10次课学完初一----入学测试题----领先中考培优体系---开始学习班次安排联赛1班、联赛2班竞赛班基础班、提高班、尖子班,初三加开目标班走竞赛路线的孩子。
学而思小学奥数知识点梳理(大纲设计视图)

学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③连除的性质④同级运算移项的性质⑤增减括号的性质⑥变式提取公因数形如:3.估算求某式的整数部分:扩缩法4.比较大小①通分a. 通分母b. 通分子②跟“中介”比③利用倒数性质若,则c>b>a.。
形如:,则。
5.定义新运算6.特殊数列求和运用相关公式:①②③④⑤⑥⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n二、数论1.奇偶性问题奇奇=偶奇×奇=奇奇偶=奇奇×偶=偶偶偶=偶偶×偶=偶2.位值原则形如:=100a+10b+c3.数的整除特征:整除数特征2 末尾是0、2、4、6、83 各数位上数字的和是3的倍数5 末尾是0或59 各数位上数字的和是9的倍数11 奇数位上数字的和与偶数位上数字的和,两者之差是11的倍数4和25 末两位数是4(或25)的倍数8和125 末三位数是8(或125)的倍数7、11、13 末三位数与前几位数的差是7(或11或13)的倍数4.整除性质①如果c|a、c|b,那么c|(a b)。
学而思小学奥数知识点梳理大纲视图

学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③连除的性质④同级运算移项的性质⑤增减括号的性质⑥变式提取公因数形如:3.估算求某式的整数部分:扩缩法4.比较大小①通分a. 通分母b. 通分子②跟“中介”比③利用倒数性质若,则c>b>a.。
形如:,则。
5.定义新运算6.特殊数列求和运用相关公式:①②③④⑤⑥⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n二、数论1.奇偶性问题奇奇=偶奇×奇=奇奇偶=奇奇×偶=偶偶偶=偶偶×偶=偶2.位值原则形如:=100a+10b+c3.数的整除特征:整除数特征2 末尾是0、2、4、6、83 各数位上数字的和是3的倍数5 末尾是0或59 各数位上数字的和是9的倍数11 奇数位上数字的和与偶数位上数字的和,两者之差是11的倍数4和25 末两位数是4(或25)的倍数8和125 末三位数是8(或125)的倍数7、11、13 末三位数与前几位数的差是7(或11或13)的倍数4.整除性质①如果c|a、c|b,那么c|(a b)。
学而思课程体系介绍

学而思课程体系介绍学而思是中国领先的教育培训机构之一,致力于为学生提供全面优质的教育资源和服务。
学而思的课程体系涵盖了小学、初中和高中阶段的多个学科,旨在帮助学生全面提升学业能力,并培养其终身学习的能力和兴趣。
一、小学部课程体系学而思小学部的课程体系以培养学生的学习兴趣和学习方法为核心,注重提高学生的语文、数学、英语等基础学科能力。
为了更好地满足不同学生的需求,学而思还开设了少儿编程、美术、音乐等丰富多彩的课程,旨在培养学生的创造力和综合素养。
在语文课程方面,学而思注重培养学生的阅读理解和写作能力。
通过精心设计的课程和有趣的教学活动,学而思帮助学生提高阅读速度和理解能力,同时激发学生的写作兴趣和表达能力。
在数学课程方面,学而思注重培养学生的数学思维和解题能力。
学而思的数学课程注重理论与实践结合,注重培养学生的逻辑思维和问题解决能力。
在英语课程方面,学而思注重培养学生的听说读写能力。
学而思的英语课程注重自然拼读,通过英语角、英语游戏等活动,提高学生的英语口语表达能力和沟通能力。
二、初中部课程体系学而思初中部的课程体系以提高学生的学科能力和学习方法为目标,注重打牢学科基础。
学而思的初中课程团队由一支经验丰富、专业素质高的教师组成,他们擅长引导学生培养科学思维和学习方法,帮助学生实现全面发展。
在语文、数学、英语等基础学科方面,学而思为初中生提供了系统的课程体系。
学而思的初中课程注重通过提高学生的学科素养,全面提高学生的学习能力和学科成绩。
此外,学而思还为初中生提供了辅导班、寒暑假培训等多样化的学习机会。
学而思的辅导班根据学生的实际情况和需求,帮助学生解决学习中的问题,同时提供适合学生的学习资源和指导。
三、高中部课程体系学而思高中部的课程体系以高考复习和出国留学为目标,注重提高学生的学科水平和综合素质。
学而思的高中课程团队由一支高水平的教师组成,他们熟悉高考考点和出国留学要求,具备丰富的教学经验。
学而思的高中课程注重提高学生的英语水平和数学思维能力,同时注重培养学生的科学研究和创新能力。
学而思教育奥数速成班

学而思教育奥数速成专题1. 333 (1234234517181920)+++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 2.57191232348910+++=⨯⨯⨯⨯⨯⨯ .3.234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++4. 132435911⨯+⨯+⨯+⨯5. 22222222(246100)(13599)12391098321+++⋅⋅⋅+-+++⋅⋅⋅++++⋅⋅⋅+++++⋅⋅⋅+++6. 221234876624688766++⨯=________.7.5717191155234345891091011⨯++++⨯⨯⨯⨯⨯⨯⨯⨯ ()8. 22222223992131991⨯⨯⨯=---9.()()()()()()()()11111111111102020=+=+=+=+=+10. 1111111111(1)()(1)()2424624624++⨯++-+++⨯+11. 11111111111111111111234523456234562345⎛⎫⎛⎫⎛⎫⎛⎫++++⨯++++-+++++⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭12. 某学生将1.23乘以一个数a 时,把1.23 误看成1.23,使乘积比正确结果减少0.3.则正确结果该是多少?13. 1232343458910⨯⨯+⨯⨯+⨯⨯++⨯⨯ 14. 111111212312100++++++++++ 15.12349223234234523410+++++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 16. 22222211111131517191111131+++++=------ .17. 已知1.08 1.2 2.310.8÷÷=÷□,其中□表示的数是 。
18. 2221111112131991⎛⎫⎛⎫⎛⎫+⨯+⨯⨯+ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭19. ()2314159263141592531415927-⨯=________;20. ()20078.58.5 1.5 1.5101600.3-⨯-⨯÷÷-=⎡⎤⎣⎦ .21. 11111111111111(1)()(1)()23423452345234+++⨯+++-++++⨯++22. 纯循环小数0.abc写成最简分数时,分子和分母的和是58,则三位数_________abc =23. 学校买来篮球、足球、排球共49个,其中篮球的个数是足球的3倍.排球比足球多4个.问学校买来的篮球、足球、排球各多少个?24. 爸爸15年前的年龄相当于儿子12年后的年龄,当爸爸的年龄是儿子的4倍时,爸爸多少岁?25.小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?26.六个自然数的平均数是7,其中前四个数的平均数是8,第4个数是11,求后三个数的平均数?27.李明的妈妈去超市买洗衣粉,雕牌和碧浪的单价分别为8元和10元,李妈妈带的钱买雕牌洗衣粉比买碧浪洗衣粉可多买3袋,并且没有剩余的钱.问:李妈妈带了多少钱?28.幼儿园将一筐苹果分给小朋友,如果全部分给大班的小朋友,每人分5个,则余下10个。
最新学而思奥数知识点总结最新

学而思小学奥数知识点梳理概述一、 计算1. 四则混合运算繁分数⑴ 运算顺序⑵ 分数、小数混合运算技巧一般而言:① 加减运算中,能化成有限小数的统一以小数形式;② 乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2. 简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序① 运算定律的综合运用② 连减的性质③ 连除的性质④ 同级运算移项的性质⑤ 增减括号的性质⑥ 变式提取公因数形如:1212......(......)n n a b a b a b a a a b ÷±÷±±÷=±±±÷3. 估算求某式的整数部分:扩缩法4. 比较大小① 通分a. 通分母b. 通分子② 跟“中介”比③ 利用倒数性质 若111a b c>>,则c>b>a.。
形如:312123m m m n n n >>,则312123n n n m m m <<。
5. 定义新运算6. 特殊数列求和运用相关公式:①()21321+=++n n n ②()()612121222++=+++n n n n ③()21n a n n n n =+=+④()()412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc⑥()()b a b a b a -+=-22 ⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n 2二、 数论1. 奇偶性问题奇±奇=偶 奇×奇=奇奇±偶=奇 奇×偶=偶偶±偶=偶 偶×偶=偶2. 位值原则 形如:abc =100a+10b+c4. 整除性质① 如果c|a 、c|b ,那么c|(a ±b)。
学而思十二级课程体系

《小学数学智力开发课程》十二级体系1、什么是十二级体系?“十二级体系”,即“小学数学智力开发课程十二级体系”。
是学而思教育专家团队经过7年的积累和沉淀,在2010年推出的全国唯一的完整的奥数学系知识体系。
其包括“优秀儿童智力开发体系”、“超常儿童培养体系”两个结构统一的部分。
为了培养孩子品质全面提升,十二级体系中加入了二十四项品格教育,将采取“分阶段、分年级”的方式,使品格教育符合孩子的认知规律,从而取得良好的学习效果。
一年级孝顺、勇敢、勤奋、谦虚二年级自律、自信、主动、同情心三年级诚信、专注、坚持、忠诚四年级反思、行动、感恩、坚韧五年级学习、热忱、乐观、责任六年级宽容、目标、信念、全力以赴《超常儿童培养课程》封面《优秀儿童智力开发课程》封面各年级阶段品格培养目标年级划分(一年两级,既相互联系又相对独立)注:由于体系详细内容属教研宝贵成果,暂不对外公布,请见谅!2、为什么要建立十二级体系?(1)我们每年培训无数金牌选手的培训教材需要沉淀;(2)近几年尤其是09年和10年杯赛及小升初的现状有了新的变化;(3)当前缺乏完整而优质的教材体系,数学的教学效果需要在分层的基础上实现标准化。
3、谁来创立主导十二级体系?在全国著名数学教育家,超常教育的卓越实践者陶晓永教授指导下,在众多华杯赛等全国顶级赛事的主试委员们的关心下,由一批全部来自清华北大等顶尖学府、拥有辉煌竞赛及培训战绩的学而思教育核心教研团队经过长时间的充分酝酿及反复调研,最终推出这套《超常儿童培养体系》及《优秀儿童智力开发体系》。
编委会成员:王伟张瑞祥林博季云英周清赵永明陈晨张旷昊张超月申强张剑肖京园曹岚李春芳吴昊庄文辉吴旭谷运增张邦鑫韩涛孙凯赵璞铮杨巍田芳宇张嘉荆晨伟况雯董博聪王雪婷戴宁震荣谢玉才兰海赵元红周斌姜付加王磊张宇鹏何晓燕4、在哪些班级展开?在学而思小学数学课程全面展开。
其中,"优秀儿童智力开发体系"将在现有的基础班、提高班、尖子班推行;"超常儿童培养体系"将在竞赛班、竞赛123班推行。
学而思超难奥数题之数论专题综合拼数感

1
测试题
1.请你将1 、 2 、3 、……、 2 0 0 6 这 2 0 0 6 个数重新排成一列,使得:第1 个数能被第 2 个数 整除,前 2 个数的和能被第 3 个数整除,前 3 个数的和能被第 4 个数整除,……,前 2 0 0 4 个数的和能被第 2 0 0 5 个数整除,前 2 0 0 5 个数的和能被最后一个数整除。
显 然 368 x a 2b 最 多 能 取 到 368 2 1 2 0 365 , 最 少 能 取 到
3 6 8 2 1 2 2 2 2 3 2 7 9 ,即 279
365 m
,由于 m 是整数,所以10 m 13 ,
28
28
这时可以分类讨论,按照 m 13 , m 12 ……依次分析,显然当 m 13 时
x a 2b 4 , m x 最多能取到13 3 16 ,(此时 a 1 , b 0 ),而当 m 12 时
x a 2b 32 ,此时 x 能取到最大值 23,那么 m x 也就能取得到 23 12 35 ,
号是多少?
【例 3】(第四届“华杯赛”总决赛) 小华玩某种游戏,每局可随意玩若干次,每次的得分是 8、a、0 这三个自然数中的一个,每 局各次的得分的总和叫做这一局的总积分。小华曾得到过这样的总积分:103、104、105、 106、107、108、109、110,又知道他不可能得到“83 分”这个总积分。问 a 是多少?
当 m 1 2 时,显然不可能取到更大的值。所以 m x 的最大值为 35。
奥数体系1-12级

工程问题
十级(上)
寒假班
面对各大杯赛的难度,十级重点学习钟表问题、余数与同余、方程与比例、复杂行程等必考奥数专题,掌握数学思想引导,集中
训练希望杯、走美杯、华杯赛等竞赛真题,为各位同学的杯赛考试打好基础,为六年级十一级奥数做好准备。
时钟问题
十级(下)春季班
不定方程
六年级
十一级(上)暑期班十一级开始,重点进行第一轮奥数系统总结与复习,50%的六年级新知识点+50%总结拔高内容,对计算、数论、行程、应用题、
几何、方程六大专题进行系统梳理,同时为年前迎春杯、中环杯等区域性杯赛备战。
概率的应用
十一级(下)
秋季班
数论发散
十二级(上)
寒假班
十二级的寒假、春季班会结合最新题型及经典题型,有的放矢地进行学习冲刺,并加入新初一实验班分班考试的精选内容与初中数学的衔接内容,达到重点中学实验班入学考试水平,并为初中
学习打下坚实基础。
四级(下)春季班求周长、逻辑推理等。通过四级学习,可为春季即将举行的学而思杯及仁华入学等活动进行必考知识储备
三年级
五级(上)
暑期班
在四级学习了巧算、两个量之间的和差关系、图形认知等之后,学生随之进入一个思维方式塑造的黄金时期,从五级的暑期班开始,继续学习多个量之间的和差关系(年龄问题)等。并在五级秋季班中接受高年级重要知识点的启蒙,如,通过和差倍的综合运用,六级开始接触行程问题初步等相关专题。
归一问题
五级(下)
秋季班
和差倍问题
六级(上)
寒假班
从六级开始,除了讲解一些经典奥数专题,如,等差数列综合应用、盈亏问题、鸡兔同笼、行程初步等,开始穿插讲解一些杯赛及仁华考试真题。从此,更加注重知识点的应用。在学和练的过程中,为更高级别奥数专题的学习打下坚实基础。速算巧算:
学而思课程体系介绍

学而思课程体系介绍
学而思(Xueersi)是中国一家知名的教育培训机构,成立于2001年。
学而思的课程体系是以K12教育为核心,涵盖了学前教育、小学、初中和高中的各个阶段。
学而思的课程体系主要包括以下几个方面:
1. 学前教育:学而思提供学前教育课程,帮助幼儿建立良好的学习基础,包括启蒙认知、语言表达、数学逻辑等方面的培养。
2. 小学阶段:学而思的小学课程主要针对小学一年级到六年级的学生,涵盖了语文、数学、英语等学科的学习内容。
课程旨在提高学生的学科知识水平,并培养他们的学习方法和解决问题的能力。
3. 初中阶段:学而思的初中课程主要面向初中一年级到九年级的学生,包括语文、数学、英语、物理、化学、生物等学科。
该阶段的课程注重培养学生的学科知识和思维能力,帮助他们适应中学学习的要求。
4. 高中阶段:学而思的高中课程主要面向高中一年级到三年级的学生,包括语文、数学、英语、物理、化学、生物、地理、历史、政治等学科。
高中阶段的课程更加注重对学科知识的深入理解和应用能力的培养,为学生的高考和大学入学做准备。
学而思的课程体系在教学上注重个性化教育,提供小班教学、一对一辅导等多种教学方式,以满足不同学生的需求。
同时,学而思还结合了现代科技手段,开发了在线学习平台和教育App,为学生提供在线学习资源和个性化学习辅导。
总之,学而思的课程体系致力于提供全面的K12教育解决方案,帮助学生提高学习成绩,培养综合素质和学习能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行程问题:
多人行程二次相遇多次相遇火车过桥流水行船环形跑道简单的相遇
基本行程问题钟面行程走走停停接送问题发出问题电梯行程猎狗追兔平均速度数论问题:
数的整除约数倍数余数问题质数合数奇偶分析
中国剩余定理位置原理完全平方数整数拆分进位置
几何问题:
巧求周长几何的五大模型勾股定理与弦图圆与扇形立体图形的表面积体积立体图形染色计数其它直线型几何问题格点与面积
计数问题:
加法原理乘法原理排列组合枚举法标数法捆绑法插板法排除法对应法树形图法归纳法整体法递推法容斥原理几何图形计数
应用题:
分数百分数应用题工程问题鸡兔同笼问题盈亏问题年龄问题植树问题牛吃草问题经济利润问题浓度问题比例问题还原问题列方程解应用题
计数问题:
数学计算公式繁分数的计算分数裂项与整数裂项换元法凑整找规律比较与估算循环小数化分数拆分通项归纳定义新运算
奥数杂题:
逻辑推理数阵图与数字谜抽屉原理操作与策略不定方程最值问题染色问题。
