第三部分习题答案

合集下载

汽车构造(第三版)习题册参考答案

第一章汽车总体构造第一节汽车分类及结构一、填空1.动力、四个、四个、载运人员、货物2.乘用车、商用车辆3. 94. 115.客车、半挂牵引车、货车6.发动机、底盘、电气设备、车身7.发电机、蓄电池8.驾驶室、货厢9.滚动阻力、空气阻力、上坡阻力、加速阻力 10.ϕF ＝ϕN二、简答1.发动机是为汽车行使提供动力的装置。

其作用是使燃料燃烧产生动力，然后通过底盘的传动系驱动车轮使汽车行驶。

2.底盘作用是支承、安装汽车发动机及其各部件、总成，形成汽车的整体造型，并接受发动机的动力，使汽车产生运动，保证正常行驶。

3.一是发动机要有足够的功率；二是驱动轮与路面间要有足够的附着力。

第二节汽车识别代码和技术参数一、名词解释1.汽车完全装备好的质量，包括润滑油、燃料、随车工具、备胎等所有装置的质量。

2.汽车满载时的总质量。

3.汽车最前端至前轴中心的距离。

4.汽车最后端至后轴中心的距离。

5.汽车满载时，最低点至地面的距离。

最小离地间隙越大，汽车越容易越过障碍物，但重心偏高，降低了稳定性。

6.汽车转向时，汽车外侧转向轮的中心平面在车辆支承平面上的轨迹圆半径。

转向盘转到极限位置时的转弯半径为最小转弯半径。

7.汽车在道路上行驶时每百公里平均燃料消耗量。

二、简答1.（1）第一部分：世界制造厂识别代码（WMI）（2）第二部分：车辆说明部分（VDS）（3）第三部分：检验位（4）第四部分：车辆指示部分（VIS）2.（1）除挂车和摩托车外，标牌应固定在门铰链柱、门锁柱或与门锁柱接合的门边之一的柱子上，接近于驾驶员座位的地方；如果没有这样的地方可利用，则固定在仪表板的左侧。

如果那里也不能利用，则固定在车门内侧靠近驾驶员座位的地方。

（2）标牌的位置应当是除了外面的车门外，不移动车辆的任何零件就可以容易读出的地方。

（3）我国轿车的VIN码大多可以在仪表板左侧、风挡玻璃下面找到。

（4）美国规定应安装在仪表板左侧，在车外透过挡风玻璃可以清楚地看到而便于检查。

3静力学第三章习题答案

第三章部分习题解答3-10 AB ,AC 和DE 三杆连接如图所示。

杆DE 上有一插销H 套在杆AC 的导槽内。

试求在水平杆DE 的一端有一铅垂力F 作用时，杆AB 所受的力。

设DE BC HE DH DB AD ===,,，杆重不计。

解：假设杆AB ，DE 长为2a 。

取整体为研究对象，受力如右图所示，列平衡方程：∑=0C M02=⋅a F By0=By F取杆DE 为研究对象，受力如图所示，列平衡方程：∑=0HM0=⋅-⋅a F a F DyF F Dy =∑=0B M 02=⋅-⋅a F a F DxF F Dx 2=取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0y F0=++By Dy Ay F F FF F Ay -=(与假设方向相反)∑=0A M02=⋅+⋅a F a F Bx DxF F Bx -=(与假设方向相反) ∑=0B M02=⋅-⋅-a F a F Dx AxF F Ax -=(与假设方向相反)3-12AD AC AB ,,和BC 四杆连接如图所示。

在水平杆AB 上作用有铅垂向下的力F 。

接触面和各铰链均为光滑的，杆重不计，试求证不论力F 的位置如何，杆AC 总是受到大小等于F 的压力。

解：取整体为研究对象，受力如图所示，列平衡方程：∑=0C M0=⋅-⋅x F b F DF bx F D =F CF C yF DF CxF CyF BxF ByF DxF DyF HyF BxF ByF DyF DxF Ax F Ay取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0A M0=⋅-⋅x F b F BF bx F B =杆AB 为二力杆，假设其受压。

取杆AB 和AD 构成的组合体为研究对象，受力如图所示，列平衡方程：∑=0E M02)2(2)(=⋅--⋅+⋅+bF x b F b F F AC D B解得F F AC =，命题得证。

注意：销钉A 和C 联接三个物体。

化工原理习题第三部分蒸馏答案

第三部分蒸馏一、填空题1、均相液体混合物2、 5.07%3、挥发度。

4、精馏段和提馏段5、拉乌尔定律6、泡点温度，简称泡点7、露点温度，简称露点8、饱和蒸气压9、难易程度 10、全回流 11、最小回流比 12、进料热状况参数 13、越少14、逐渐降低 15. 冷液, 最远 , 最少 16、部分冷凝和部分汽化增加 17. 1333.3 18. 沸点, 易.19、普通精馏分离，萃取精馏或恒沸精馏分离20. 液相，提高 21. 单效蒸发和多效蒸发 22、蒸馏 , 改变状态参数 23、挥发度v v A=p A/x A v B=p B/x B24、相对挥发度。

：α=v A/v B=（p A/x A）/（p B/x B）=y A x B/y B x A25、平衡 , 大于；相同，大于 26、多次部分汽化和多次部分冷凝, 混合物中各组分挥发度的差异，塔顶液相回流和塔底产生上升蒸汽 ,由上至下逐级降低；27、低于,塔顶易挥发组分浓度高于塔底，相应沸点较低；原因之二是：存在压降使塔底压力高于塔顶，塔底沸点较高。

28、理论板 29、再沸器，冷凝器 30、R/R+1， x/R+1。

31、D进料量和进料热状况 32、（1）温度低于泡点的冷液体；（2）泡点下的饱和液体；（3）温度介于泡点和露点的气液混合物；（4）露点下的饱和蒸汽；（5）温度高于露点的过热蒸汽。

33、最少为N。

34、减少，增加，增加，增加，增大。

min变大。

36、愈大，先减小后增大的过程。

37、拉乌尔定律。

38、35、xD逐渐降低，逐渐升高。

39. 1 40. 变大，减小，不变，增加 41、0.77（塔板从上往下数），0.35（塔板从下往上数）。

42、逐渐升高，减小 43、增大，变大。

44、 8m 。

45、y = x, T > t。

46、减少，增大；上移，增多，减少。

47. 增加，增加。

48. 蒸馏 ; 泡点。

49. 饱和液体线。

50. 66.7 kmol/h 。

大学物理第三章部分课后习题答案

大学物理第三章部分课后习题答案3-1半径为R、质量为M的均匀薄圆盘上，挖去一个直径为R的圆孔，孔的中心在求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。

分析：用补偿法（负质量法）求解，由平行轴定理求其挖去部分的转动惯量，用原圆盘转动惯量减去挖去部分的转动惯量即得。

注意对同一轴而言。

解：没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为：1R处，2J11MR2①2由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：1MRMR3J2Jcmd2()2()2MR2②2424232由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：JJ1J213MR2323-2如题图3-2所示，一根均匀细铁丝，质量为M，长度为L，在其中点O处弯成120角，放在某Oy平面内，求铁丝对O某轴、Oy轴、Oz轴的转动惯量。

分析：取微元，由转动惯量的定义求积分可得解：（1）对某轴的转动惯量为：L20J某rdm(lin600)22M1dlML2L32（2）对y轴的转动惯量为：L1ML2M5Jy()2(lin300)2dlML20322L96（3）对Z轴的转动惯量为：1ML1Jz2()2ML2322122题图3-23-3电风扇开启电源后经过5达到额定转速，此时角速度为每秒5转，关闭电源后经过16风扇停止转动，已知风扇转动惯量为0.5kgm，且摩擦力矩Mf和电磁力矩M均为常量，求电机的电磁力矩M。

分析：Mf，M为常量，开启电源5内是匀加速转动，关闭电源16内是匀减速转动，可得相应加速度，由转动定律求得电磁力矩M。

解：由定轴转动定律得：MMfJ1，即52520.54.12Nm5163-4飞轮的质量为60kg，直径为0.5m，转速为1000r/min，现要求在5内使其制动，求制动力F，假定闸瓦与飞轮之间的摩擦系数0.4，飞轮的质量全部分布在轮的外周上，MJ1MfJ1J20.5尺寸如题图3-4所示。

分析：分别考虑两个研究对象：闸瓦和杆。

第三部分无损检测习题及答案(最终版)

第一篇超声探伤习题一、是非题1.由于机械波是由机械振动产生的，所以波动频率等于振动频率。

( )2.频率相同的纵波，在水中的波长大干在钢中的波长。

( )3.既然水波能在水面传播，那么超声表面波也能沿液体表面传播。

( )4.材料的声阻抗越大，超声波传播时衰减越大。

( )5.当钢中的气隙（如裂纹）厚度一定时，超声波频率增加，反射波也随着增加。

( )6.探头频率越高，声束扩散角越小。

( )7.超声被波长越长，声柬扩散角就越大，发现小缺陷的能力就越强。

( )8.因为近场区内有多个声压为零的点，所虹探伤时近场区缺陷往往会漏检。

( )9.面积相同．频率相同的圆晶片和方晶片，超声场的近场长度一样。

( )10.同声场理想大平面与平底孔回波声压的地值随频率的提高而减小。

( )11.C型显示能展现工件中缺陷的长度和宽度，但不能屣现深度。

( )12.通用A VG曲线采用的距离是以近场长度为单位的归一化距离，适用于不同规格的探头。

( )13.由于水中只能传播纵波，所以水浸探头只能进行纵波探伤。

( )14.测定“始波宽度时，应将仪器的灵敏度谓至最大。

( )15.为提高分辨力，在满足探伤灵敏度要求下，仪器的发射强度应尽量调得低些。

( )16.软保护膜探头可减小粗糙表面对探伤的影响。

( )17.串列法探伤适用于擒捌垂直于探测面的平面缺陷。

( )18.“灵敏”意味着发现小缺陷的能力，因此超声探伤灵敏度越高越好。

( )19.半波高度法用来测量小于声柬截面的虢陷尺寸。

( )20.采用当量法确定的缺陷尺寸～般小于缺陷的实际尺寸。

( )21.超声波撵伤焊缝时，裂纹类缺粥的反射波幅一般都很高。

( )22.焊缝探伤所用斜探头，当楔块底而前部磨损较大，其K值将变小。

( )23.横渡探伤选掸斜探头K值时，随投厚的增加，K值柑应减小。

( )24.铝焊缝探伤应选用较高频率的横被专用探头。

( )25.裂纹探防时，裂垃的回波出较尖锐，探头转动时，波揠惋鞘失。

数字通信原理第二版课后习题答案第3章

=sin（2000πt）+sin（4000πt）
故上边带信号为 SUSB(t)=1/2m(t) coswct-1/2m’(t)sinwct
10
《通信原理》习题第三章
=1/2cos(12000πt)+1/2cos(14000πt)
下边带信号为
SLSB(t)=1/2m(t) coswct+1/2m’(t) sinwct =1/2cos(8000πt)+1/2cos(6000πt) 其频谱如图 3-2 所示。
ω (t ) = 2*106 π + 2000π sin 2000π t
故最大频偏（2）调频指数
∆f = 10* mf = 2000π = 10 kHZ 2π
∆f 103 = 10* 3 = 10 fm 10
故已调信号的最大相移 ∆θ = 10 rad 。（3）因为 FM 波与 PM 波的带宽形式相同，即 BFM = 2(1 + m f ) f m ，所以已调信号的带宽为
《通信原理》习题第三章
第三章习题
习题 3.1 设一个载波的表达式为 c(t ) = 5cos1000π t ，基带调制信号的表达式为： m(t)=1+ cos 200π t 。试求出振幅调制时已调信号的频谱，并画出此频谱图。解：
s(t ) = m(t )c(t ) = (1 + cos 200πt )5 cos(1000πt )
因为调制信号为余弦波，设
B = 2(1 + m f ) f m ∆f = 1000 kHZ = 100 m'2 (t ) =
2
，故
m' (t ) = 0,
m2 1 ≤ 2 2
则：载波频率为边带频率为因此

（完整版）财务管理第三章习题及答案

（完整版）财务管理第三章习题及答案第三章财务分析⼀、单项选择题1、下列经济业务会使企业的速动⽐率提⾼的是( )。

A、销售库存商品B、收回应收账款C、购买短期债券D、⽤固定资产对外进⾏长期投资2、下列财务⽐率中，可以反映企业偿债能⼒的是( )。

A、平均收款期B、销售利润率C、市盈率D、已获利息倍数3、下列不属于偿债能⼒分析指标的是（）。

A、资产负债率B、现⾦⽐率C、产权⽐率D、安全边际4、下列财务⽐率中综合性最强、最具有代表性的指标是（）。

A 、资产周转率B、净值报酬率C 、资产负债率D 、资产净利率5、流动⽐率⼩于1时，赊购原材料若⼲，将会( )。

A、增⼤流动⽐率B、降低流动⽐率C、降低营运资⾦D、增⼤营运资⾦6、在计算速动⽐率时，要把存货从流动资产中剔除的原因，不包括( )A、可能存在部分存货已经损坏但尚未处理的情况B、部分存货已抵押给债权⼈C、可能存在成本与合理市价相差悬殊的存货估价问题D、存货可能采⽤不同的计价⽅法7、不影响应收账款周转率指标利⽤价值的因素是( )。

A、销售折让与折扣的波动B、季节性经营引起的销售额波动C、⼤量使⽤分期付款结算⽅式D、⼤量使⽤现⾦结算的销售8、ABC公司⽆优先股，去年每股盈余为4元，每股发放股利2元，保留盈余在过去⼀年中增加了500万元。

年底每股账⾯价值为30元，负债总额为5000万元，则该公司的资产负债率为( )。

A、30%B、33%C、40%D、44%9、在杜邦财务体系中，假设其他情况相同，下列说法中错误的是( )A、权益乘数⼤则财务风险⼤B、权益乘数⼤则权益净利率⼤C、权益乘数等于资产权益率的倒数D、权益乘数⼤则资产净利率⼤10、下列公式中不正确的是( )。

A、股利⽀付率+留存盈利⽐率=1B、股利⽀付率×股利保障倍数=1C、变动成本率+边际贡献率=1D、资产负债率×产权⽐率=111、市净率指标的计算不涉及的参数是( )。

A、年末普通股股数B、年末普通股权益C、年末普通股股本D、每股市价12、⼀般认为，流动⽐率保持在( )以上时，资产的流动性较好。

会计课后习题答案(第三章)

答案: 正确
19 企业计提当年盈余公积的基数，不包括年初未分配利润。
答案: 正确
20 年度终了，“利润分配”账户所属的各明细账户中，除“未分配利润”明细账户可能有余额外，其他明细账户均无余额。
答案: 正确
21 得利与损失是与企业日常活动直接关联的经济利益总流入或总流出。
答案: 错误
8 下列支出不得列入成本费用的是。
A: 支付给金融机构的手续费
答案: 制造费用
10 “应付职工薪酬”账户可设置、、、、和“非货币性福利”等明细分类账户。
答案: 工资社会保险费职工福利工会经费职工教育经费
11 .直接生产工人的薪酬费用应计入账户，车间技术及管理人员薪酬费用应计入账户，销售机构人员的薪酬费用计入账户，行政管理人员薪酬费用计入账户。
答案: 正确
15 企业按职工工资总额一定比例计提的工会经费及职工教育经费应记入管理费用。
答案: 错误
16 企业专设销售机构的固定资产修理费用应计入销售费用。
答案: 正确
17 “生产成本”账户若有余额应在借方，反映期末自制半成品的实际生产成本。
答案: 错误
18 企业当年可供分配的利润包括当年实现的净利润和年初未分配利润。
B: 制造费用
C: 本年利润
D: 管理费用
E: 利润分配
答案: B, D
5 工业企业以下收入中应记入其他业务收入的有。
A: 销售产品
B: 销售材料
C: 固定资产盘盈
D: 固定资产出租收入
E: 处置固定资产净收益
答案: B, D
6 工业企业以下各项应记入营业外支出的是。

政治经济学练习及答案(3)

第3章资本的生产过程国家开放大学经济管理教学部王社荣第一部分学习要求重点掌握：1．名词：劳动力商品，价值增殖过程，资本，剩余价值，可变资本，不变资本，工资2．劳动力成为商品与货币转化为资本；3．价值形成过程与价值增殖过程；4．不变资本与可变资本；5．剩余价值率；6．工资的本质。

掌握：1．名词：劳动过程，劳动资料，劳动对象，必要劳动，剩余劳动, 剩余价值率，绝对剩余价值生产，相对剩余价值生产，超额剩余价值2．绝对剩余价值与相对剩余价值；3．超额剩余价值。

了解：1．资本的原始积累；2．绝对剩余价值与相对剩余价值的关系；3．相对剩余价值生产的三阶段。

第二部分习题练习一、单项选择题（下列每小题给出的选项中，只有一个选项是符合题目要求的。

）1．资本原始积累之所以表现为"原始"的过程，是因为这一过程发生在（）A．原始社会B．资本主义生产方式完全确立之前C．资本主义生产方式完全确立之后D．垄断资本主义阶段2．小商品生产是指（）A．基本上是以一家一户为单位的自给自足的生产B．生产条件很差和熟练程度很低的生产C．生产资料公有制下的以个人劳动为基础的商品生产D．个人占有生产资料并主要以个人劳动为基础的商品生产3．资本原始积累是指（）A．原始社会的积累B．个人最初的财富积累C．前资本主义初始资本的形成D．剩余价值的资本化4．资本总公式是（）A．G-W-GB．G-W-G′C．W-G-WD．W-G-W′5．资本总公式的矛盾是（）A．等价交换和价值增殖的矛盾B．G'>GC．剩余价值既不在流通领域产生，又离不开流通领域D．劳动与资本的不等价交换6．货币转化为资本的前提是（）A．劳动者一无所有B．劳动者有人身自由C．劳动力成为商品D．带来剩余价值7．劳动力商品的价值是（）A．父母为养育儿女所耗费的劳动B．劳动力所创造的价值C．维持劳动力再生产所必需的生活资料的价值D．资本家支付的工资8．劳动力商品使用价值的特殊性在于它被使用时（）A．能把自身价值转移到新产品中去B．把全部使用价值消费掉C．只能创造出自身的价值D．能创造比自身价值更大的价值9．劳动对象和劳动资料的总和称为（）A．生产要素B．生产工具C．生产资料D．物质资料10．以生产资料形式存在的那部分资本，所以叫不变资本，是因为（）A．它的价值不会转移到新产品中去B．它的价值会转移到新产品中去，但价值量不发生变化C．它在资本的价值形成和价值增殖过程中不起任何作用D．它的实物形态不发生任何变化11．资本的不同部分按其在剩余价值生产中的不同作用，可分为（）A．固定资本和流动资本B．不变资本和可变资本C．生产资本和流通资本D．生产资本和商品资本12．不变资本和可变资本的区分，是根据资本不同部分（）A．在剩余价值生产过程中的不同作用B．在使用价值生产中所起的不同作用C．在劳动过程中的不同作用D．在价值周转方式上的不同13．剩余价值来源于（）A．工人的剩余劳动B．资本家或工人的节俭C．先进技术在生产中的运用D．资本家在市场上的贱卖贵买14．资本主义生产过程中所产生的剩余价值是（）A．工人全部劳动的产物B．工人必要劳动的产物C．工人无酬劳动的产物D．工人有酬劳动的产物15．资本主义生产过程的特点是（）A．劳动过程和价值增殖过程的统一B．劳动过程和价值形成过程的统一C．劳动过程和劳动力价值转移过程的统一D．劳动过程和生产资料价值转移过程的统一16．在资本主义价值增殖过程中（）A．具体劳动转移生产资料的价值，抽象劳动创造出大于劳动力价值的新价值B．具体劳动转移生产资料的价值，抽象劳动创造出相当于劳动力价值的新价值C．具体劳动创造出新价值，抽象劳动转移生产资料价值D．具体劳动创造出新的价值，抽象劳动创造出新的使用价值17．价值增殖过程不过是超过一定点而延长了的价值形成过程，这个"一定点"就是指（）A．工人转移旧价值的时间B．工人创造新价值的时间C．工人生产使用价值的时间D．工人再生产劳动力价值的时间18．剩余价值与可变资本的比率称为（）A．剩余价值率B．年剩余价值率C．平均利润率D．利润率19．进入汽车修配厂修理的汽车是（）A．运输工具B．劳动对象C．劳动资料D．生产要素20．剩余价值率是指（）A．剩余价值与可变资本的比率B．剩余价值与全部预付资本的比率C．剩余价值总额和社会总资本的比率D．剩余价值与不变资本的比率21．生产资料是指（）A．劳动资料和劳动对象之和B．劳动资料和劳动工具之和C．劳动对象和生产工具之和D．劳动资料和劳动手段之和22．劳动过程的简单要素是（）A．劳动者的劳动、劳动工具、劳动资料B．劳动者的劳动、劳动对象、劳动资料C．劳动者的劳动、生产资料、劳动对象D．劳动者的劳动、生产资料、劳动工具23．在资本主义生产中，工人新创造的全部价值是（）A．商品的价值B．劳动力自身的价值C．剩余价值D．劳动力自身价值和剩余价值24．可变资本是（）A．资本家为购买原材料支付的货币B．资本家为购买生产资料支付的货币C．资本家为购买劳动力支付的货币D．资本家为购买生产工具支付的货币25．相对剩余价值生产的第一阶段是（）A．简单协作B．工场手工业C．机器大工业D．自动化体系和机器人的出现26．绝对剩余价值生产假定（）A．工作日长度可变B．工作日长度不变C．劳动生产率不变D．劳动生产率可变27．相对剩余价值生产假定（）A．工作日长度可变B．工作日长度不变C．劳动生产率不变D．劳动生产率可变28．绝对剩余价值生产是（）A．在必要劳动时间不变的条件下延长工作日取得的B．在工作日不变的条件下缩短必要劳动时间取得的C．个别企业提高劳动生产率的结果D．各个资本家追求超额剩余价值的必然结果29．相对剩余价值的获得是（）A．个别企业提高劳动生产率的结果B．加大劳动强度的结果C．延长工作日的结果D．社会劳动生产率提高的结果30．绝对剩余价值生产和相对剩余价值生产都是依靠（）A．延长工作日获得的B．提高劳动生产率获得的C．缩短工人的必要劳动时间获得的D．延长工人的剩余劳动时间获得的31．在不延长工作日的情况下来提高剥削程度的剩余价值生产方法，属于（）A．绝对剩余价值生产B．相对剩余价值生产C．超额剩余价值生产D．价值增殖32．单个资本家提高劳动生产率的直接目的是获取（）A．绝对剩余价值B．相对剩余价值C．超额剩余价值D．劳动力价值33．工资实质是（）A．劳动的价值或价格的转化形式B．劳动的价值的货币表现C．对劳动者的全部劳动所付的报酬D．劳动力价值或价格的转化形式二、多项选择题（下列每小题给出的选项中，至少有两个选项是符合题目要求的。

概率论与数理统计(理工类,第四版)吴赣昌主编课后习题答案第三章

第三章多维随机变量及其分布3.1 二维随机变量及其分布习题1设(X,Y)的分布律为X\Y12311/61/91/1821/3a1/9求a.分析：dsfsd1f6d54654646解答：由分布律性质∑i⋅jPij=1,可知1/6+1/9+1/18+1/3+a+1/9=1,解得a=2/9.习题2(1)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(1)P{a<X≤b,Y≤c};解答：P{a<X≤b,Y≤c}=F(b,c)-F(a,c).习题2(2)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(2)P{0<Y≤b};解答：P{0<Y≤b}=F(+∞,b)-F(+∞,0).习题2(3)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(3)P{X>a,Y≤b}.解答：P{X>a,Y≤b}=F(+∞,b)-F(a,b).习题3(1)3.设二维离散型随机变量的联合分布如下表：试求：(1)P{12<X<32,0<Y<4;解答：P{12<X<23,0<Y<4P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=14+0+0=14.习题3(2)3.设二维离散型随机变量的联合分布如下表：试求：(2)P{1≤X≤2,3≤Y≤4};解答：P{1≤X≤2,3≤Y≤4}=P{X=1,Y=3}+P{X=1,Y=4}+P{X=2,Y=3}+P{X=2,Y=4}=0+116+0+14=516.习题3(3)3.设二维离散型随机变量的联合分布如下表：试求：(3)F(2,3).解答：F(2,3)=P(1,1)+P(1,2)+P(1,3)+P(2,1)+P(2,2)+P(2,3)=14+0+0+116+14+0=916.习题4设X,Y为随机变量，且P{X≥0,Y≥0}=37,P{X≥0}=P{Y≥0}=47,求P{max{X,Y}≥0}.解答：P{max{X,Y}≥0}=P{X,Y至少一个大于等于0}=P{X≥0}+P{Y≥0}-P{X≥0,Y≥0}=47+47-37=57.习题5(X,Y)只取下列数值中的值：(0,0),(-1,1),(-1,13),(2,0)且相应概率依次为16,13,112,512,请列出(X,Y)的概率分布表，并写出关于Y的边缘分布.解答：(1)因为所给的一组概率实数显然均大于零，且有16+13+112+512=1,故所给的一组实数必是某二维随机变量(X,Y)的联合概率分布. 因(X,Y)只取上述四组可能值，故事件：{X=-1,Y=0},{X=0,Y=13,{X=0,Y=1},{X=2,Y=13,{X=2,Y=1}均为不可能事件，其概率必为零. 因而得到下表：Y01/31pk7/121/121/3习题6设随机向量(X,Y)服从二维正态分布N(0,0,102,102,0),其概率密度为f(x,y)=1200πex2+y2200,求P{X≤Y}.解答：由于P{X≤Y}+P{X>Y}=1，且由正态分布图形的对称性，知P{X≤Y}=P{X>Y},故P{X≤Y}=12.习题7设随机变量(X,Y)的概率密度为f(x,y)={k(6-x-y),0<x<2,2<y<40,其它, (1)确定常数k;(2)求P{X<1,Y<3};(3)求P{X<1.5};(4)求P{X+Y≤4}.解答：如图所示(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数k.∫02∫24k(6-x-y)dydx=k∫02(6-2x)dx=8k=1,所以k=18.(2)P{X<1,Y<3}=∫01dx∫2318(6-x-y)dy=38.(3)P{X<1.5}=∫01.5dx∫2418(6-x-y)dy=2732.(4)P{X+Y≤4}=∫02dx∫24-x18(6-x-y)dy=23.习题8已知X和Y的联合密度为f(x,y)={cxy,0≤x≤1,0≤y≤10,其它,试求：(1)常数c;(2)X和Y的联合分布函数F(x,y).解答：(1)由于1=∫-∞+∞∫-∞+∞f(x,y)dxdy=c∫01∫01xydxdy=c4,c=4.(2)当x≤0或y≤0时，显然F(x,y)=0;当x≥1,y≥1时，显然F(x,y)=1;设0≤x≤1,0≤y≤1,有F(x,y)=∫-∞x∫-∞yf(u,v)dudv=4∫0xudu∫0yvdv=x2y2.设0≤x≤1,y>1,有F(x,y)=P{X≤1,Y≤y}=4∫0xudu∫01ydy=x2.最后，设x>1,0≤y≤1,有F(x,y)=P{X≤1,Y≤y}=4∫01xdx∫0yvdv=y2.函数F(x,y)在平面各区域的表达式F(x,y)={0,x≤0或y≤0x2,0≤x≤1,y>1x2y2,0≤x≤1,0≤y≤1.y2,x>习题9设二维随机变量(X,Y)的概率密度为f(x,y)={4.8y(2-x),0≤x≤1,x≤y≤10,其它,求边缘概率密度fY(y).解答：fX(x)=∫-∞+∞f(x,y)dy={∫0x4.8y(2-x)dy,0≤x≤10,其它={2.4x2(2-x),0≤x≤10,其它.fY(y)=∫-∞+∞f(x,y)dx={∫0y4.8y(2-x)dx,0≤y≤10,其它={2.4y(4y-y2),0≤y≤10,其它.习题10设(X,Y)在曲线y=x2,y=x所围成的区域G里服从均匀分布，求联合分布密度和边缘分布密度. 解答：区域G的面积A=∫01(x-x2)dx=16,由题设知(X,Y)的联合分布密度为f(x,y)={6,0≤x≤1,x2≤y≤x0,其它,从而fX(x)=∫-∞+∞f(x,y)dy=6∫x2xdy=6(x-x2),0≤x≤1,即fX(x)={6(x-x2),0≤x≤10,其它,fY(y)=∫-∞+∞f(x,y)dx=6∫yydx=6(y-y),0≤y≤1,即fY(y)={6(y-y),0≤y≤10,其它.3.2 条件分布与随机变量的独立性习题1二维随机变量(X,Y)的分布律为从而(X,Y)的联合概率分布为P{X≤a,∣X∣≤a}=P{X≤a}⋅P{∣X∣≤a},而事件{∣X∣≤a}⊂{X≤a},故由上式有P{∣X∣≤a}==P{X≤a}⋅P{∣X∣≤a},⇒P{∣X∣≤a}(1-P{X≤a})=0⇒P{∣X≤a∣}=0或1=P{X≤a}⋅(∀a>0)但当a>0时，两者均不成立，出现矛盾，故X与∣X∣不独立.习题9设X和Y是两个相互独立的随机变量，X在(0,1)上服从均匀分布，Y的概率密度为fY(y)={12e-y2,y>00,y≤0,(1)求X与Y的联合概率密度；(2)设有a的二次方程a2+2Xa+Y=0,求它有实根的概率.解答：(1)由题设易知fX(x)={1,0<x<10,其它,又X,Y相互独立，故X与Y的联合概率密度为f(x,y)=fX(x)⋅fY(y)={12e-y2,0<x<1,y>00,其它;(2)因{a有实根}={判别式Δ2=4X2-4Y≥0}={X2≥Y},故如图所示得到：P{a有实根}=P{X2≥Y}=∫∫x2>yf(x,y)dxdy=∫01dx∫0x212e-y2dy=-∫01e-x22dx=1-[∫-∞1e-x22dx-∫-∞0e-x22dx]=1-2π[12π∫-∞1e-x22dx-12π∫-∞0e-x22dx]=1-2π[Φ(1)-Φ(0),又Φ(1)=0.8413,Φ(0)=0.5,于是Φ(1)-Φ(0)=0.3413,所以P{a有实根}=1-2π[Φ(1)-Φ(0)]≈1-2.51×0.3413=0.1433.3.3 二维随机变量函数的分布习题1设随机变量X和Y相互独立，且都等可能地取1,2,3为值，求随机变量U=max{X,Y}和V=min{X,Y}的联合分布.解答：由于U≥V,可见P{U=i,V=j}=0(i<j).此外，有P{U=V=i}=P{X=Y=i}=1/9(i=1,2,3),P{U=i,V=j}=P{X=i,Y=j}+P{X=j,Y=i}=2/9(i>j),于是，随机变量U和V的联合概率分布为=∫01dy∫y2y12dx=14,P{U=1,V=1}=1-P{U=0,V=0}-P{U=0,V=1}-P{U=1,V=0}=1/2,即U\V01011/401/41/2习题4设(X,Y)的联合分布密度为f(x,y)=12πe-x2+y22,Z=X2+Y2,求Z的分布密度.解答：FZ(z)=P{Z≤z}=P{X2+Y2≤z}.当z<0时，FZ(z)=P(∅)=0;当z≥0时，FZ(z)=P{X2+Y2≤z2}=∫∫x2+y2≤z2f(x,y)dxdy=12π∫∫x2+y2≤z2e-x2+y22dxdy=12π∫02πdθ∫0ze-ρ22ρdρ=∫0ze-ρ22ρdρ=1-e-z22.故Z的分布函数为FZ(z)={1-e-z22,z≥00,z<0.Z的分布密度为fZ(z)={ze-z22,z>00,z≤0.习题5设随机变量(X,Y)的概率密度为f(x,y)={12(x+y)e-(x+y),x>0,y>00,其它,(1)问X和Y是否相互独立？(2)求Z=X+Y的概率密度.解答：(1)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞12(x+y)e-(x+y)dy,x>00,x≤0\under2line令x+y=t{∫x+∞12te-tdt=12(x+1)e-x,x>00,x≤0,由对称性知fY(y)={12(y+1)e-y,y>00,y≤0,显然f(x,y)≠fX(x)fY(y),x>0,y>0,所以X与Y不独立.(2)用卷积公式求fZ(z)=∫-∞+∞f(x,z-x)dx.当{x>0z-x>0即{x>0x<z时，f(x,z-x)≠0,所以当z≤0时，fZ(z)=0;当z>0时，fZ(z)=∫0z12xe-xdx=12z2e-z.于是，Z=X+Y的概率密度为fZ(z)={12z2e-z,z>00,z≤0.习题6设随机变量X,Y相互独立，若X服从(0,1)上的均匀分布，Y服从参数1的指数分布，求随机变量Z=X+Y的概率密度.解答：据题意，X,Y的概率密度分布为fX(x)={1,0<x<10,其它,fY(y)={e-y,y≥00,y<0,由卷积公式得Z=X+Y的概率密度为fZ(z)=∫-∞+∞fX(x)fY(z-x)dx=∫-∞+∞fX(z-y)fY(y)dy=∫0+∞fX(z-y)e-ydy.由0<z-y<1得z-1<y<z,可见：当z≤0时，有fX(z-y)=0,故fZ(z)=∫0+∞0⋅e-ydy=0;当z>0时，fZ(z)=∫0+∞fX(z-y)e-ydy=∫max(0,z-1)ze-ydy=e-max(0,z-1)-e-z,即fZ(z)={0,z≤01-e-z,0<z≤1e1-z-e-z,z>1.习题7设随机变量(X,Y)的概率密度为f(x,y)={be-(x+y),0<x<1,0<y<+∞,0,其它.（1）试确定常数b；（2）求边缘概率密度fX(x),fY(y)；（3）求函数U=max{X,Y}的分布函数.解答：（1）由∫-∞+∞∫-∞+∞f(x,y)dxdy=1，确定常数b.∫01dx∫0+∞be-xe-ydy=b(1-e-1)=1，所以b=11-e-1，从而f(x,y)={11-e-1e-(x+y),0<x<1,0<y<+∞,0,其它.（2）由边缘概率密度的定义得fX(x)={∫0+∞11-e-1e-(x+y)dy=e-x1-e-x,0<x<1,0,其它，fY(x)={∫0111-e-1e-(x+y)dx=e-y,0<y<+∞,0,其它（3）因为f(x,y)=fX(x)fY(y)，所以X与Y独立，故FU(u)=P{max{X,Y}≤u}=P{X≤u,Y≤u}=FX(u)F Y(u)，其中FX(x)=∫0xe-t1-e-1dt=1-e-x1-e-1,0<x<1，所以FX(x)={0,x≤0,1-e-x1-e-1,0<x<1,1,x≥1.同理FY(y)={∫0ye-tdt=1-e-y,0<y<+∞,0,y≤0，因此FU(u)={0,u<0,(1-e-u)21-e-1,0≤u<1,1-e-u,u≥1.习题8设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成，L1和L2的寿命分别为X与Y,其概率密度分别为ϕ1(x)={αe-αx,x>00,x≤0,ϕ2(y)={βe-βy,y>00,y≤0,其中α>0,β>0,α≠β,试求系统L的寿命Z的概率密度.解答：设Z=min{X,Y},则F(z)=P{Z≥z}=P{min(X,Y)≤z}=1-P{min(X,Y)>z}=1-P{X≥z,Y≥z}=1-[1P{X<z}][1-P{Y<z}]=1-[1-F1{z}][1-F2{z}]由于F1(z)={∫0zαe-αxdx=1-e-αz,z≥00,z<0,F2(z)={1-e-βz,z≥00,z<0,故F(z)={1-e-(α+β)z,z≥00,z<0,从而ϕ(z)={(α+β)e-(α+β)z,z>00,z≤0.习题9设随机变量X,Y相互独立，且服从同一分布，试证明：P{a<min{X,Y}≤b}=[P{X>a}]2-[P{X>b}]2.解答：设min{X,Y}=Z,则P{a<min{X,Y}≤b}=FZ(b)-FZ(a),FZ(z)=P{min{X,Y}≤z}=1-P{min{X,Y}>z}=1-P{X>z,Y>z}=1-P{X>z}P{Y>z}=1-[P{X>z}]2,代入得P{a<min{X,Y}≤b}=1-[P{X>b}]2-(1-[P{X>a}]2)=[P{X>a}]2-[P{X>b}]2.证毕.复习总结与总习题解答习题1在一箱子中装有12只开关，其中2只是次品，在其中取两次，每次任取一只，考虑两种试验：(1)放回抽样；(2)不放回抽样.我们定义随机变量X,Y如下：X={0,若第一次取出的是正品1,若第一次取出的是次品, Y={0,若第二次取出的是正品1,若第二次取出的是次品,试分别就(1),(2)两种情况，写出X和Y的联合分布律.解答：(1)有放回抽样，(X,Y)分布律如下：P{X=0,Y=0}=10×1012×12=2536; P{X=1,Y=0}=2×1012×12=536,P{X=0,Y=1}=10×212×12=536, P{X=1,Y=1}=2×212×12=136,(2)不放回抽样，(X,Y)的分布律如下：P{X=0,Y=0}=10×912×11=4566, P{X=0,Y=1}=10×212×11=1066,P{X=1,Y=1}=2×112×11=166,习题2假设随机变量Y服从参数为1的指数分布，随机变量Xk={0,若Y≤k1,若Y>k(k=1,2),求(X1,X2)的联合分布率与边缘分布率.解答：因为Y服从参数为1的指数分布，X1={0,若Y≤11,若Y>1, 所以有P{X1=1}=P{Y>1}=∫1+∞e-ydy=e-1,P{X1=0}=1-e-1,同理P{X2=1}=P{Y>2}=∫2+∞e-ydy=e-2,P{X2=0}=1-e-2,因为P{X1=1,X2=1}=P{Y>2}=e-2，P{X1=1,X2=0}=P{X1=1}-P{X1=1,X2=1}=e-1-e-2,P{X1=0,X2=0}=P{Y≤1}=1-e-1,P{X1=0,X2=1}=P{X1=0}-P{X1=0,X2=0}=0,故(X1,X2)联合分布率与边缘分布率如下表所示：习题3在元旦茶话会上，每人发给一袋水果，内装3只橘子，2只苹果，3只香蕉. 今从袋中随机抽出4只，以X记橘子数，Y记苹果数，求(X,Y)的联合分布.解答：X可取值为0,1,2,3,Y可取值0,1,2.P{X=0,Y=0}=P{∅}=0,P{X=0,Y=1}=C30C21C33/C84=2/70,P{X=0,Y=2}=C30C22C32/C84=3/70,P{X=1,Y=0}=C31C20C33/C84=3/70,P{X=1,Y=1}=C31C21C32/C84=18/70,P{X=1,Y=2}=C31C22C31/C84=9/70,P{X=2,Y=0}=C32C20C32/C84=9/70,P{X=2,Y=1}=C32C21C31/C84=18/70,P{X=2,Y=2}=C32C22C30/C84=3/70,P{X=3,Y=0}=C33C20C31/C84=3/70,P{X=3,Y=1}=C33C21C30/C84=2/70,P{X=3,Y=2}=P{∅}=0,所以，(X,Y)的联合分布如下：习题4设随机变量X与Y相互独立，下表列出了二维随机变量(X,Y)的联合分布律及关于X与Y解答：由题设X与Y相互独立，即有pij=pi⋅p⋅j(i=1,2;j=1,2,3), p⋅1-p21=p11=16-18=124,又由独立性，有p11=p1⋅p⋅1=p1⋅16故p1⋅=14.从而p13=14-124-18, 又由p12=p1⋅p⋅2, 即18=14⋅p⋅2.从而p⋅2=12. 类似的有p⋅3=13,p13=14,p2⋅=34.将上述数值填入表中有习题5设随机变量(X,Y)的联合分布如下表：求：(1)a值；(2)(X,Y)的联合分布函数F(x,y)；(3)(X,Y)关于X,Y的边缘分布函数FX(x)与FY(y).解答：(1)\because由分布律的性质可知∑i⋅jPij=1, 故14+14+16+a=1,∴a=13.(2)因F(x,y)=P{X≤x,Y≤y}①当x<1或y<-1时，F(x,y)=0;②当1≤x<2,-1≤y<0时，F(x,y)=P{X=1,Y=-1}=1/4;③当x≥2,-1≤y<0时，F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}=5/12;④当1≤x<2,y>0时，F(x,y)=P{X=1,Y=-1}+P{X=1,Y=0}=1/2;⑤当x≥2,y≥0时，F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}+P{X=1,Y=0}+P{X=2,Y=0}=1;综上所述，得(X,Y)联合分布函数为F(x,y)={0,x<1或y<-11/4,1≤x<2,-1≤y<05/12,x≥2,-1≤y<01/2,1≤x<2,y≥01,x≥2,y≥0.(3)由FX(x)=P{X≤x,Y<+∞}=∑xi<x∑j=1+∞pij, 得(X,Y)关于X的边缘分布函数为：FX(x)={0,x<114+14,1≤x<214+14+16+13,x≥2={0,x<11/2,1≤x<21,x≥2,同理，由FY(y)=P{X<+∞,Y≤y}=∑yi≤y∑i=1+∞Pij, 得(X,Y)关于Y的边缘分布函数为FY(y)={0,y<-12/12,-1≤y<01,y≥0.习题6设随机变量(X,Y)的联合概率密度为f(x,y)={c(R-x2+y2),x2+y2<R0,x2+y2≥R,求：(1)常数c; (2)P{X2+Y2≤r2}(r<R).解答：(1)因为1=∫-∞+∞∫-∞+∞f(x,y)dydx=∫∫x2+y2<Rc(R-x2+y)dxdy=∫02π∫0Rc(R-ρ)ρdρdθ=cπR33,所以有c=3πR3.(2)P{X2+Y2≤r2}=∫∫x2+y2<r23πR3[R-x2+y2]dxdy=∫02π∫0r3πR3(R-ρ)ρdρdθ=3r2R2(1-2r3R).习题7设f(x,y)={1,0≤x≤2,max(0,x-1)≤y≤min(1,x)0,其它,求fX(x)和fY(y).解答：max(0,x-1)={0,x<1x-1,x≥1, min(1,x)={x,x<11,x≥1,所以，f(x,y)有意义的区域(如图)可分为{0≤x≤1,0≤y≤x},{1≤x≤2,1-x≤y≤1},即f(x,y)={1,0≤x≤1,0≤y≤x1,1≤x≤2,x-1≤y≤1,0,其它所以fX(x)={∫0xdy=x,0≤x<1∫x-11dy=2-x,1≤x≤20,其它,fY(y)={∫yy+1dx=1,0≤y≤10,其它.习题8若(X,Y)的分布律为则α,β应满足的条件是¯, 若X与Y独立，则α=¯,β=¯.解答：应填α+β=13;29;19.由分布律的性质可知∑i⋅jpij=1, 故16+19+118+13+α+β=1,即α+β=13.又因X与Y相互独立，故P{X=i,Y=j}=P{X=i}P{Y=j}, 从而α=P{X=2,Y=2}=P{X=i}P{Y=j},=(19+α)(14+α+β)=(19+α)(13+13)=29,β=P{X=3,Y=2}=P{X=3}P{Y=2}=(118+β)(13+α+β)=(118+β)(13+13)，∴β=19.习题9设二维随机变量(X,Y)的概率密度函数为f(x,y)={ce-(2x+y),x>0,y>00,其它,(1)确定常数c; (2)求X,Y的边缘概率密度函数；(3)求联合分布函数F(x,y); (4)求P{Y≤X};(5)求条件概率密度函数fX∣Y(x∣y); (6)求P{X<2∣Y<1}.解答：(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1求常数c.∫0+∞∫0+∞ce-(2x+y)dxdy=c⋅(-12e-2x)\vline0+∞⋅(-e-y)∣0+∞=c2=1,所以c=2.(2)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞2e-2xe-ydy,x>00,x≤0={2e-2x,x>00,x≤0,fY(y)=∫-∞+∞f(x,y)dx={∫0+∞2e-2xe-ydx,y>00,其它={e-y,y>00,y≤0.(3)F(x,y)=∫-∞x∫-∞yf(u,v)dvdu={∫0x∫0y2e-2ue-vdvdu,x>0,y>00,其它={(1-e-2x)(1-e-y),x>0,y>00,其它.(4)P{Y≤X}=∫0+∞dx∫0x2e-2xe-ydy=∫0+∞2e-2x(1-e-x)dx=13.(5)当y>0时，fX∣Y(x∣y)=f(x,y)fY(y)={2e-2xe-ye-y,x>00,x≤0={2e-2x,x>00,x≤0.(6)P{X<2∣Y<1}=P{X<2,Y<1}P{Y<1}=F(2,1)∫01e-ydy=(1-e-1)(1-e-4)1-e-1=1-e-4.习题10设随机变量X以概率1取值为0, 而Y是任意的随机变量，证明X与Y相互独立.解答：因为X的分布函数为F(x)={0,当x<0时1,当x≥0时, 设Y的分布函数为FY(y),(X,Y)的分布函数为F(x,y)，则当x<0时，对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{∅∩(Y≤y)}=P{∅}=0=FX(x)FY(y);当x≥0时，对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{S∩(Y≤y)}=P{Y≤y}=Fy(y)=FX(x)FY(y),依定义，由F(x,y)=FX(x)FY(y)知，X与Y独立.习题11设连续型随机变量(X,Y)的两个分量X和Y相互独立，且服从同一分布，试证P{X≤Y}=1/2. 解答：因为X,Y独立，所以f(x,y)=fX(x)fY(y).P{X≤Y}=∫∫x≤yf(x,y)dxdy=∫∫x≤yfX(x)fY(y)dxdy=∫-∞+∞[fY(y)∫-∞yfX(x)dx]dy=∫-∞+∞[fY(y)FY(y)]dy=∫-∞+∞FY(y)dFY(y)=F2(y)2∣-∞+∞=12,也可以利用对称性来证，因为X,Y独立同分布，所以有P{X≤Y}=P{Y≤X},而P{X≤Y}+P{X≥Y}=1, 故P{X≤Y}=1/12.习题12设二维随机变量(X,Y)的联合分布律为若X与Y相互独立，求参数a,b,c的值.解答：关于X的边缘分布为由于X与Y独立，则有p22=p2⋅p⋅2 得b=(b+19)(b+49) ①p12=p1⋅p⋅2 得19=(a+19)(b+49) ②由式①得b=29, 代入式②得a=118. 由分布律的性质，有a+b+c+19+19+13=1,代入a=118,b=29, 得c=16.易验证，所求a,b,c的值，对任意的i和j均满足pij=pi⋅×p⋅j.因此，所求a,b,c的值为a=118,b=29,c=16.习题13已知随机变量X1和X2的概率分布为且P{X1X2=0}=1.(1)求X1和X2的联合分布律；(2)问X1和X2是否独立？解答：(1)本题是已知了X1与X2的边缘分布律，再根据条件P{X1X2=0}=1, 求出联合分布. 列表如下：P{X1=1,X2=1}=0,P{X1=-1,X2=1}=0.再由p⋅1=p-11+p11+p01, 得p01=12, p-10=p-1⋅=p-11=14,p10=p1⋅-p11=14,从而得p00=0.(2)由于p-10=14≠p-1⋅⋅p⋅0=14⋅12=18, 所以知X1与X2不独立.习题14设(X,Y)的联合密度函数为f(x,y)={1πR2,x2+y2≤R20,其它,(1)求X与Y的边缘概率密度；(2)求条件概率密度，并问X与Y是否独立？解答：(1)当x<-R或x>R时，fX(x)=∫-∞+∞f(x,y)dy=∫-∞+∞0dy=0;当-R≤x≤R时，fX(x)=∫-∞+∞f(x,y)dy=1πR2∫-R2-x2R2-x2dy=2πR2R2-x2.于是fX(x)={2R2-x2πR2,-R≤x≤R0,其它.由于X和Y的地位平等，同法可得Y的边缘概率密度是：fY(y)={2R2-y2πR2,-R≤y≤R0,其它.(2)fX∣Y(x∣y)=f(x,y)fY(y)注意在y处x值位于∣x∣≤R2-y2这个范围内，f(x,y)才有非零值，故在此范围内，有fX∣Y(x∣y)=1πR22πR2⋅R2-y2=12R2-y2,即Y=y时X的条件概率密度为fX∣Y(x∣y)={12R2-y2,∣x∣≤R2-y20,其它.同法可得X=x时Y的条件概率密度为fY∣X(y∣x)={12R2-x2,∣y∣≤R2-x20,其它.由于条件概率密度与边缘概率密度不相等，所以X与Y不独立.习题15设(X,Y)的分布律如下表所示X\Y -112-12 1/102/103/102/101/101/10求：(1)Z=X+Y; (2)Z=max{X,Y}的分布律.解答：与一维离散型随机变量函数的分布律的计算类似，本质上是利用事件及其概率的运算法则. 注意，Z的相同值的概率要合并.概率(X,Y)X+YXYX/Ymax{X,Y}1/102/103/102/101/101/10(-1,-1)(-1,1)(-1,2)(2,-1)(2,1)(2,2)-2011341-1-2-2241-1-1/2-221-112222于是(1)习题16设(X,Y)的概率密度为f(x,y)={1,0<x<1,0<y<2(1-x)0,其他，求Z=X+Y的概率密度.解答：先求Z的分布函数Fz(z)，再求概率密度fz(z)=dFz(z)dz.如右图所示.当z<0时，Fz(z)=P{X+Y≤z}=0;当0≤z<1时，Fz(z)=P{X+Y≤z}=∫∫x+y≤zf(x,y)dxdy=∫0zdx∫0z-x1dy=∫0z(z-x)dx=z2-12x2∣0z=12z2；当1≤z<2时，Fz(z)=∫02-zdx∫0z-xdy+∫2-z1dx∫02(1-x)dy=z(2-z)-12(2-z)2+(z-1)2；当z≥2时，∫∫Df(x,y)dxdy=∫01dx∫02(1-x)dy=1.综上所述Fz(z)={0,z<012z2,0≤z<1z(2-z)-12(2-z)2+(z-1)2,1≤z<21,z≥2，故fz(z)={z,0≤z<12-z,1≤z<20,其它.习题17设二维随机变量(X,Y)的概率密度为f(x,y)={2e-(x+2y),x>0,y>00,其它,求随机变量Z=X+2Y的分布函数.解答：按定义FZ(Z)=P{x+2y≤z},当z≤0时，FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫∫x+2y≤z0dxdy=0.当z>0时，FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫0zdx∫0(z-x)/22e-(x+2y)dy=∫0ze-x⋅(1-ex-z)dx=∫0z(e-x-e-z)dx=[-e-x]∣0z-ze-z=1-e-z-ze-z,故分布函数为FZ(Z)={0,z≤01-e-z-ze-z,z>0.习题18设随机变量X与Y相互独立，其概率密度函数分别为fX(x)={1,0≤x≤10,其它, fY(y)={Ae-y,y>00,y≤0,求：(1)常数A; (2)随机变量Z=2X+Y的概率密度函数.解答：(1)1=∫-∞+∞fY(y)dy=∫0+∞A⋅e-ydy=A.(2)因X与Y相互独立，故(X,Y)的联合概率密度为f(x,y)={e-y,0≤x≤1,y>00,其它.于是当z<0时，有F(z)=P{Z≤z}=P{2X+Y≤z}=0;当0≤z≤2时，有F(z)=P{2X+Y≤z}=∫0z/2dx∫0z-2xe-ydy=∫0z/2(1-e2x-z)dx;当z>2时，有F(z)=P{2X+Y≤2}=∫01dx∫0z-2xe-ydy=∫01(1-e2x-z)dx.利用分布函数法求得Z=2X+Y的概率密度函数为fZ(z)={0,z<0(1-e-z)/2,0≤z<2(e2-1)e-z/2,z≥2.习题19设随机变量X,Y相互独立，若X与Y分别服从区间(0,1)与(0,2)上的均匀分布，求U=max{X,Y}与V=min{X,Y}的概率密度.解答：由题设知，X与Y的概率密度分别为fX(x)={1,0<x<10,其它, fY(y)={1/2,0<y<20,其它,于是，①X与Y的分布函数分别为FX(x)={0,x≤0x,0≤x<11,x≥1, FY(y)={0,y<0y/2,0≤y<21,y≥2,从而U=max{X,Y}的分布函数为FU(u)=FX(u)FY(u)={0,u<0u2/2,0≤u<1u/2,1≤u<21,u≥2,故U=max{X,Y}的概率密度为fU(u)={u,0<u<11/2,1≤u<20,其它.②同理，由FV(v)=1-[1-FX(v)][1-FY)]=FX(v)+FY(v)-FX(v)FY(v)=FX(v)+FY(v)-FU(v),得V=min{X,Y}的分布函数为FV(v)={0,v<0v2(3-v),0≤v<11,v≥1,故V=min{X,Y}的概率密度为fV(v)={32-v,0<v<10,其它.注：(1)用卷积公式，主要的困难在于X与Y的概率密度为分段函数，故卷积需要分段计算；(2)先分别求出X,Y的分布函数FX(x)与FY(y), 然后求出FU(u)，再求导得fU(u); 同理先求出FV(v), 求导即得fV(v).。

《信息论与编码》第三章部分习题参考答案

第三章习题参考答案第三章习题参考答案3-1解：(1)判断唯一可译码的方法：①先用克劳夫特不等式判定是否满足该不等式；②若满足再利用码树，看码字是否都位于叶子结点上。

如果在叶节点上则一定是唯一可译码，如果不在叶节点上则只能用唯一可译码的定义来判断是不是。

可译码的定义来判断是不是。

其中C1,C2,C3,C6都是唯一可译码。

都是唯一可译码。

对于码C2和C4都满足craft 不等式。

但是不满足码树的条件。

就只能就只能举例来判断。

举例来判断。

对C5：61319225218ki i ---==+´=>å，不满足该不等式。

所以C5不是唯一可译码。

译码。

(2)判断即时码方法：定义：即时码接收端收到一个完整的码字后，就能立即译码。

特点：码集任何一个码不能是其他码的前缀，即时码必定是唯一可译码, 唯一可译码不一定是即时码。

唯一可译码不一定是即时码。

其中C1,C3,C6都是即时码。

都是即时码。

对C2：“0”是“01”的前缀，……，所以C2不是即时码。

不是即时码。

(1) 由平均码长61()i i i K p x k ==å得1236 3 1111712(3456) 241681111712(3456) 2416811152334 24162K bitK bit K bitK bit==´+´+´+++==´+´+´+++==´+´+´´=62111223366()()log () 2 /()266.7%3()294.1%178()294.1%178()280.0%52i i i H U p u p u H U K H U K H U K H U K h h h h ==-=============å比特符号3-7解：(1)信源消息的概率分布呈等比级数，按香农编码方法，其码长集合为自然数数列1, 2, 3, ···, i, ·, i, ····；对应的编码分别为：0, 10, 110, ···, 111…110 ( i 110 ( i –– 1个1), ·1), ····。

离散数学-第三部分代数结构练习题答案(课件模板)

《离散数学》第三部分----代数结构一、选择或填空1、设A={2,4,6}，A上的二元运算*定义为：a*b=max{a,b}，则在独异点<A,*>中，单位元是( )，零元是( )。

答：2，62、设A={3,6,9}，A上的二元运算*定义为：a*b=min{a,b}，则在独异点<A,*>中，单位元是( )，零元是( )；答：9，33、设〈G,*〉是一个群，则(1) 若a,b,x∈G，a*x=b，则x=( )；(2) 若a,b,x∈G，a*x=a*b，则x=( )。

答：（1）a*-1 b （2）b4、设a是12阶群的生成元，则a2是( )阶元素，a3是( )阶元素。

答：6,45、代数系统<G,*>是一个群，则G的等幂元是( )。

答：单位元6、设a是10阶群的生成元，则a4是( )阶元素，a3是( )阶元素。

答：5，107、群<G,*>的等幂元是( )，有( )个。

答：单位元，18、素数阶群一定是( )群, 它的生成元是( )。

答：循环群，任一非单位元9、设〈G,*〉是一个群，a,b,c∈G，则(1) 若c*a=b，则c=( )；(2) 若c*a=b*a，则c=( )。

答：（1）b1-*a(2) b10、<H,,*>是<G,,*>的子群的充分必要条件是( )。

答：<H,,*>是群或∀ a，b ∈G，a*b∈H，a-1∈H 或∀ a,b ∈G，a*b-1∈H 11、群＜A,*＞的等幂元有( )个，是( )，零元有( )个。

答：1，单位元，012、在一个群〈G,*〉中，若G中的元素a的阶是k，则a-1的阶是( )。

答：k13、在自然数集N上，下列哪种运算是可结合的？（）(1) a*b=a-b (2) a*b=max{a,b} (3) a*b=a+2b (4) a*b=|a-b| 答：(2)14、任意一个具有2个或以上元的半群，它（）。

应用多元统计分析课后习题答案高惠璇三部分习题解答公开课一等奖优质课大赛微课获奖课件

(n＞p)为来自p维正态总体X样本.似然比统计量为
max
0
L(0,0 )
max
L(
,
0
)
分子
|
1
20
|n/ 2
exp
1 2
n
( X ( )
1
0 )01( X ( )
0 )
|
1
20
|n/ 2
exp
1 2
n
tr[01
1
( X ( )
0 )( X ( )
0 )]
第17页 17
第三章多元正态总体参数检查
Yr1
X BX
Y Γ BΓΓ
Y HY
(Yr
1
,,
Yn
)
H
22
Yn
由于Y1, …,Yr ,Yr+1 ,…,Yn互相独立,
故X′AX与X′BX互相独立.
第9页
9
第三章多元正态总体参数检查
3-3 设X～Np(μ,Σ),Σ＞0,A和B为p阶对称阵, 试证实 (X-μ)′A(X-μ)与(X-μ)′B(X-μ)互相独立
Np(μ,Σ)随机样本, X和Ax分别表示正态总体X样本均值向量和离差阵,则由性质1有
Tx2 n(n 1)( X ) Ax1( X )
~ T 2 ( p, n 1).
令 Y(i) CX (i) d (i 1,..., n)
其中C是p p非退化常数矩阵, d是p 1常向量。
则 Y(i) ~ N p (C d,CC) (i 1,2,..., n)
max L(
, 0 )
max L(, ) ,
分子当ˆ X达最大,且最大值
L( X
, 0 )

化工原理习题第三部分蒸馏答案（1）

化⼯原理习题第三部分蒸馏答案（1）第三部分蒸馏⼀、填空题1、蒸馏是⽤来分离均相液体混合物的单元操作。

2、含⼄醇12%（质量百分数）的⽔溶液，其⼄醇的摩尔分率为5.07%。

3、蒸馏操作是借助于液体混合物中各组分挥发度的差异⽽达到分离的⽬的。

4、进料板将精馏塔分为精馏段和提馏段。

5、理想溶液的⽓液相平衡关系遵循拉乌尔定律。

6、当⼀定组成的液体混合物在恒这⼀总压下，加热到某⼀温度，液体出现第⼀个⽓泡，此温度称为该液体在指定总压下的泡点温度，简称泡点。

7、在⼀定总压下准却⽓体混合物，当冷却到某⼀温度，产⽣第⼀个液滴，则此温度称为混合物在指定总压下的露点温度，简称露点。

8、理想溶液中各组分的挥发度等于其饱和蒸⽓压。

9、相对挥发度的⼤⼩反映了溶液⽤蒸馏分离的难易程度。

10、在精馏操作中，回流⽐的操作上限是全回流。

11、在精馏操作中，回流⽐的操作下限是最⼩回流⽐。

12、表⽰进料热状况对理论板数的影响的物理量为进料热状况参数。

13、q值越⼤，达到分离要求所需的理论板数越少。

14、精馏塔中温度由下⽽上沿塔⾼的变化趋势为逐渐降低。

15、当分离要求⼀定，回流⽐⼀定时，在五种进料状况中，冷液进料的q值最⼤，此时，提馏段操作线与平衡线之间的距离最远，分离所需的总理论板数最少。

16、精馏过程是利⽤部分冷凝和部分汽化的原理⽽进⾏的。

精馏设计中，回流⽐越⼤，所需理论板越少，操作能耗增加，随着回流⽐的逐渐增⼤，操作费和设备费的总和将呈现先降后升的变化过程。

17、精馏设计中，当回流⽐增⼤时所需理论板数减⼩（增⼤、减⼩），同时蒸馏釜中所需加热蒸汽消耗量增⼤（增⼤、减⼩），塔顶冷凝器中冷却介质消耗量减⼩（增⼤、减⼩），所需塔径增⼤（增⼤、减⼩）。

18、分离任务要求⼀定，当回流⽐⼀定时，在5种进料状况中,冷液体进料的q 值最⼤，提馏段操作线与平衡线之间的距离最远,分离所需的总理论板数最少。

19、相对挥发度α=1，表⽰不能⽤普通精馏分离分离，但能⽤萃取精馏或恒沸精馏分离。

流体与过程热力学第三版部分习题答案

5-12 针对摩尔比为9:1的甲烷(1)和乙烷(2)气体混合物，叙述其在400K，0.2MPa时摩尔㶲值的求解过程，同时列出必要的公式和数据(说明来源)等。

【解】根据题意已知：x1=0.9, x2=1-x1=0.1； T=400K, p=0.2MPa约定环境温度压力为：T0=298.15K, p0=0.1MPaa. 混合气体的㶲值可由式(1)计算：ε(T,p,x)=Σxi[εi(T,p)+RT0lnai]+(1-T0/T)ΔmixH(T,p,x) (1)其中ai为混合物中i组分的活度，此处可视作理想混合，即ai≈xi，且同时有ΔmixH(T,p,x)≈0，得到：ε(T,p,x)≈Σxi[εi(T,p)+RT0lnxi] (1')如果混合非理想，则需要用相应过量Gibbs自由能模型计算活度系数和混合焓变。

b. 纯组分的㶲值εi(T,p)由式(2)计算：εi(T,p)=εi(T0,p0)+Δεigi+(ΔHRi-T0ΔSRi ) (2)式中εi(T0,p0)为组分i的摩尔标准㶲εөi，而Δ代表(T0,p0)→(T,p)时的变化量。

根据题目条件，(T0,p0)和(T,p)这两个状态的剩余性质均可忽略，即在该状态下气体可视为理想气体，得：εi(T,p)≈εөi+Δεigi (2')如果压力较高或温度较低，可选择普遍化方法(如Lee-Kesler关联)求取剩余焓与熵。

c. 理想气体㶲的变化由式(3)计算：Δεigi=ΔHigi-T0ΔSigi =∫T0→T(1-T0/T)Cp,iigdT+RT0ln(p/p0) (3)Cp,iig为组分i的理想气体等压摩尔热容，可由教材附录B1查出。

d. 摩尔标准㶲εөi，可通过元素标准㶲和物质的标准生成Gibbs自由能计算得到：εө(CH4)=ΔfGө(CH4)+εө(C)+4εө(H)εө(C2H6)=ΔfGө(C2H6)+2εө(C)+6εө(H)C和H的元素标准㶲可从教材第五章表5/2-4或附录B9查出：εө(C)=410.515 kJ/mol; εө(H)=117.575 kJ/mol标准Gibbs生成自由能由教材附录B1查出：ΔfGө(CH4)=-50.87 kJ/mol; ΔfGө(C2H6)=-32.95 kJ/mol综上所述，可以求出该混合体系的摩尔㶲值。

移动通信(第三版)课后答案部分第三章习题

• 7. 某一移动通信系统，基站天线高度为 100m，天线增益为Gb ＝6dB，移动台天线高度为3m，天线增益Gm 为0dB。市区为中等起伏地，通信距离为10km，工作频段为450MHz，试求： • (1) 传播路径损耗中值； • (2) 若基站发射机送至天线的信号功率为10W，求移动台天线得到的信号功率中值。 •
由式(3 - 21)求第一菲涅尔区半径x1为
x1
d1d 3 10 10 3 47 .1m 3 3 15 10
P x d1 h1 d2 h2
T d 1 R h1 x P
d2
R h2
T
(a)
(b)
图 3 - 3 障碍物与余隙 (a) 负余隙； (b) 正余隙
•
(2) 由式(3 - 63)和式(3 - 64)可求得中等起伏地市区中接收信号的功率中值
2 PP PT GbGm Am ( f , d ) H b (hb , d ) H m (hm , f ) 4d PT L fs Gb Gm Am ( f , d ) H b (hb , d ) H m (hm , f ) PT Gb Gm LT 10 lg10 6 0 129 113dBW 83dBm
•
•
(2) 由式(3 - 63)和式(3 - 64)可求得中等起伏地市区中接收信号的功率中值
2 PP PT GbGm Am ( f , d ) H b (hb , d ) H m (hm , f ) 4d PT L fs Gb Gm Am ( f , d ) H b (hb , d ) H m (hm , f ) PT Gb Gm LT 10 lg10 6 0 138.5 122.5dBW 92.5dBm

C语言程序设计练习题第3部分答案

C程序设计语言练习题第三部分63.已知：int x; 则下面说明指针变量pb的语句是正确的。

A) int pb=&x; B)int *pb=x; C)int *pb=&x D)*pb=*x;64.有如下程序段：int *p,a,b=1;p=&a;*p=10;a=*p+b;执行该程序段后，a值是。

A) 12 B) 11 C) 10 D) 编译出错65.若有说明：int i,j=2,*p=&i；，则能完成i=j赋值功能的语句是。

A) i=*p; B) *p=*&j; C) i=&j; D) i=**p;66.已知：int a,*p=&a; 则为了得到变量a的值，下列错误的表达式为______。

A) *&p B) *p C) p[0] D) *&a67.已知static int a[2][3]={2,4,6,8,10,12};正确表示数组元素地址的是__。

A) *(a+1)B) a[1]+2 C) a[1]+3 D) a[0][0]68.已知int a[3][4],*p=*a; p+=6;那么*p和______的值相同。

A) *(a+6) B) *(&a[0]+6) C) *(a[1]+2)D) *(&a[0][0]+6)69.已知说明int (*p)[M]; 其中p是______。

A) M个指向整型变量的指针B) 指向M个整型变量的函数指针C) 一个指向具有M个整型元素的一维数组的指针D) 具有M个指针元素的一维指针数组，每个元素都只能指向整型变量70.若有定义和语句:int c[4][5], (*cp)[5]; cp=c;则对c数组元素的引用正确的是哪个？A)cp+1 B)*(cp+3) C)*(cp+1)+3 D)*(*cp+2)71.设有以下定义：int a[4][3]={1,2,3,4,5,6,7,8,9,10,11,12};int (*prt)[3]=a,*p=a[0];则下列能够正确表示数组元素a[1][2]的表达式是__________。

大学化学(第二版)部分习题参考答案

＝2×90.25 ＝180.50 kJ•mol-1 △rSmө(298.15K)＝∑vi Smө(生成物) -∑viSmө(反应物）＝2×210.76 –(191.5 + 205.14) ＝24.88 J•k-1•mol-1
-ΔrGm
2.303RT
T =1300℃ = 1300 + 273.15 = 1573.15K
ΔrGmө(298.15K) =ΔrHmө(298.15K) -T·ΔrSmө(298.15K) = -125.7 - 298.15×6.6×10-3 = -127.67kJ· -1 mol lgKө = -ΔrGmө(T) 2.303RT - (-127.67)
=
2.303×8.314×10-3×298.15
= 0.318(kJ· -1) mol
[P33:3题] 解题思路
解：查表可知： ΔfGmө (298.15K)/( kJ· -1) mol Sn(s) + O2(g) = SnO2(s) 0 0 -519.7
(1) 根据 ΔrGm(T)=ΔrGmө(T) + 2.303RTlgQ 计算.
当T=298.15K时，ΔrGmө(T) = △rGmө(298.15K)
ΔrGmө(T) ≈ △rHmө(298.15K) –T•△rSmө(298.15K) = 180.50 -1573.15×24.88×10-3 = 141.36 kJ•mol-1 lgKө = - △rGmө/ 2.303RT = -（141.36）/（2.303×8.314×10-3×1573.15） = - 4.69
ΔrGm(T) =
ΔrGmө(T)+2.303RT
lgQ
Sn(s)+O2(g)= SnO2(s)

弹性力学简明教程(第四版)第三章课后习题答案

③在 x=0，x=l 的次要边界上，面力可写成主矢、主矩形式： x=0 上 x=l 上
x向主矢：FN1 = y向主矢：FS1 = 主矩：M 1 =
h/2 -h/2
h/2
h / 2 h/2
f x dy 0, f y dy F ,
FN2 FS2
h/2
h / 2 h/2

h / 2
④在次要边界 x l 上，分布面力为
f x x l x x l f y x l xy
主矩：弹性体边界上的面力分布及在次要上面力的主矢和主矩如图所示
M'
x x l ydy h / 2 2blydy 0 h / 2
（3） cxy
3
将应力函数代入公式（2-24），得应力分量表达式
x 6cxy, y 0, xy yx 3cy 2
考察应力边界条件，主要边界,由公式（2-15）得
y
在
h h h f x y bh, f y y 0 2 2 2 主要边界，上边界上，面力为
在
y
h h h f x y bh, f y y 0 2 2 2 ，下边界上，面力为
面力的主矢、主矩为 x 向主矢
Fx
x x l dy h / 2 6clydy 0 h / 2
h/2 h / 2
h/2
h/2
y 向主矢：
Fy
h/2

y x l
dy
h/2
h/2
h / 2
ch 3cy dy 1 4
2
3
主矩：

结构力学教材习题第三章答案全解——哈工大老师提供

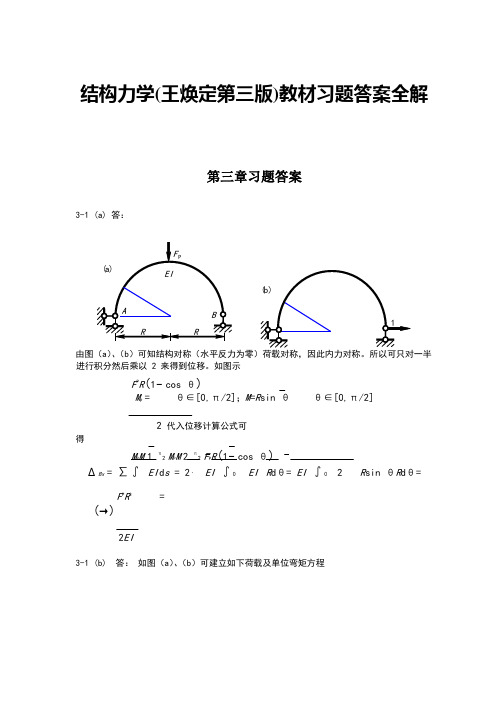
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答：由图（a）、（b）可知结构对称（水平反力为零）荷载对称，因此内力对称。

所以可只对一半进行积分然后乘以 2 来得到位移。

如图示F P R(1−cos θ)M P = θ∈[0,π/2]；M=R sin θθ∈[0,π/2]2 代入位移计算公式可得M P M 1 π2 M P M 2 π2 F P R(1−cos θ)∆Bx = ∑∫ EI d s = 2⋅EI ∫0 EI R dθ= EI ∫0 2 R sin θR dθ=F P R3 =(→)2EI3-1 (b) 答：如图（a）、（b）可建立如下荷载及单位弯矩方程pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R dθ= qEI 4 ∫0π2 (1−2cosθ+cos 2 θ)R dθqR 4 ⎡ θ 1 ⎡3π ⎡ qR 4= EI ×⎡θ−2sinθ+ 2 + 4sin2θ⎡⎡0 =⎡⎡ 4 − 2⎡⎡ 2EI (→)2 ⎡3-2 答：作M P 图和单位力弯矩图如下图：由此可得内力方程代入位移公式积分可得2 2 P 0s i n ( ) d (c o s ) (c o s )q M R q R M R θθ α α θ θ − == − = − ∫AqRBα θ( a θ( b )根据题意 EI (x ) = EI (l + x )2l 代入位移公式并积分（查积分表）可得M P M l2 q 0x 4∆Bx =∑∫ EI d x =∫0 6EI (l + x ) d x7 q 0l 4 ql 4= (ln 2− )× =(→)12 3EI EI3-3 答：分别作出荷载引起的轴力和单位力引起的轴力如下图所示：由此可得 C 点的竖向为移为：1 lM 图 x3 0 p x q M M xl= = xP M 图2 0 6q lABl q 05 83 8F NP F N1 F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =6 5kN× ×6 m+2× kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 8 8EA=×10−4 m当求CD 和CE 杆之间的夹角改变使：施加如图所示单位广义力并求作出F N2 图，则F∆=∑∫ F NP EA F N2 ds=∑ NP EA F N2 l2× kN×(−×5 m+(− kN)××6 m =EA=−×10−4 rad ( 夹角减小）3-4 （a）答：先作出M p和M 如右图所示。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第10章建立嵌入式系统开发环境10.2.5习题1．使用vi查看安装程序install.sh，对比install.sh中的语句与安装过程。

答：首先建立合适的安装目录，然后安装交叉编译工具软件，然后安装Linux内核，建立根文件系统，之后安装调试工具gdb和gdbserv，最后安装试验源代码及相关文档。

2．若使用上位机的com2口与下位机进行连接，应在minicom中如何设置？答：若使用上位机的com2口与下位机进行连接，应在minicom中选择“Serial port setup”进入串口配置界面。

输入“A”，将“Serial device”的值修改为“/dev/ttyS1”，表示连接的是上位机的com2口。

3．若下位机的IP地址为192.168.0.121，上位机的IP地址为202.201.33.15，请写出将上位机和下位机的IP地址配置在同一个网段的过程。

答：在上位机的终端命令窗口中键入下面的命令，可以将上位机和下位机的IP地址配置在同一个网段192.168.0.:ifconfig eth0 192.168.0.252 netmask 255.255.255.010.3.5习题1．在“vivi>”提示符状态下，使用help查看vivi命令的用法，比较与Linux命令的不同。

2．写出下位机软件系统的四个组成部分的功能。

答：下位机的软件系统由Bootloader系统内核、根文件系统和应用程序四部分组成。

Bootloader相当于PC机上的BIOS，在下位机加电时自动运行，执行硬件初始化和调用系统内核的功能。

Bootloader分为U-boot、Vivi、Blob、ARMBoot、RedBoot等多种，本实验使用实验箱自带光盘中的vivi。

系统内核就是运行在下位机上的操作系统内核，本实验使用实验箱自带光盘中的zImage，是ARM-Linux的内核，版本号为2.6。

根文件系统是Linux系统必不可少的一部分，用来管理下位机中的文件。

本实验使用实验箱自带光盘中的root.cramfs。

Cramfs是专门针对Flash设计的只读压缩的文件系统，其容量上限为256M，采用zlib压缩，文件系统类型可以是EXT2或EXT3，经常作为下位机的根文件系统。

应用程序是需要烧写到下位机，在下位机中运行的程序，在上位机中以压缩文件包的形式保存，本实验使用实验箱自带光盘中的yaffs.tar.bz2。

应用程序所使用的文件系统为Yaffs （Yet Another Flash File System），Yaffs是一种专门为Flash设计的嵌入式文件系统，运行速度快、占用内存小，提供写均衡、垃圾收集等底层功能。

3．查阅相关资料，了解下位机软件系统的四个组成部分的生成过程。

省略11.1.5习题1．Makefile是如何工作的？其中的宏定义分别是什么意思？答：makefile文件中语句的语法是Shell语句语法的子集，以“#”开头的语句为注释语句，内容一般分为两部分，前面部分由include和变量定义语句构成，include语句能够将另外一个文件的内容包含进来，变量定义语句定义后面部分要使用的变量。

前面部分的内容可以为空。

makefile的后面部分内容是文件的主要内容，由一些规则描述的语句块组成，make执行时将根据这些语句块的描述执行相应的命令或者程序。

其中常用的宏有：CC：指明采用的编译器；EXEC ：表示编译后生成的可执行文件名；OBJS：给出目标文件列表；CFLAGS：给出编译参数；LDFLAGS：给出连接参数；all:给出编译主入口；clean: 表示清除编译结果2．嵌入式开发的基本过程有哪几步？答：嵌入式开发的基本过程为：采用相应的编辑工具编写应用程序，然后在上位机编译调试应用程序，然后使用NFS将上位机上编译好的文件下载到下位机上运行。

11.2.6 习题1．在生产者-消费中实例中，加入一个新的线程用于处理键盘的输入，并在按键为ESC 时终止所有线程。

答：参考程序见“/labs/ Lab_2”文件夹中的“pth1.c”。

2．使用信号量控制方式编写多线程程序，设4个线程，其中两个线程负责从文件中读取数据到公共的缓冲区，另两个线程从缓冲区读取数据做不同的处理（加和乘运算）。

答：参考程序见“/labs/ Lab_2”文件夹中的“sem_example.c”。

3．线程的优先级的控制。

答：程序控制线程的优先级，一般是用pthread_attr_getschedpolicy来获取系统使用的调度策略，如果是SCHED_OTHER的话，表明当前策略不支持线程优先级的使用，否则可以。

当然所设定的优先级范围必须在最大和最小值之间，可以通过sched_get_priority_max和sched_get_priority_min来获取。

在系统允许使用线程优先级别的时候，使用下面两个函数pthread_attr_setschedparam、thread_attr_getschedparam来设置线程的优先级。

11.3.6 习题1．修改程序，编写一个简单的文件收、发程序，完成串口文件下载。

答：参考本次试验提供的用户程序，在receive函数中新建一个简单文件，读取串口字符写入文件即可，须注意发送和接收线程的互锁机制。

2．RS-232串行通信的数据格式是什么？答：开始前，线路处于空闲状态，送出连续“1”。

传送开始时首先发一个“0”作为起始位，然后传输字符的二进制编码。

每个字符的数据位长度可以约定为5-8位，一般采用ASCII 编码。

后面是奇偶校验位，根据约定，用奇偶校验位将所传字符中为“1”的位数凑成奇数个或偶数个，也可不要奇偶校验。

最后是停止位的“1”信号，停止位可以约定持续1 位、1.5 位或2 位的时间宽度。

至此一个字符传送完毕，线路又进入空闲，持续为“1”。

经过一段随机的时间后，下一个字符开始传送才又发出起始位。

3．串行通信最少需要几根线？分别如何连接？答：当通信距离较近时，通信双方可以直接连接。

最简单的情况，在通信中根本不需要RS-232C的控制联络信号，只需三根线（发送线、接收线、信号地线）便可实现全双工异步串行通信。

图1 最简单的串行通信连接方式图1中的2号线与3号线交叉连接是因为在直连方式时，把通信双方都当作数据终端设备看待，双方都可发也可收。

在这种方式下，通信双方的任何一方，只要请求发送RTS有效和数据终端准备好DTR有效就能开始发送和接收。

4．ARM的串口有几个？相应的寄存器是什么？答：S3C2410提供了三个通用异步串行通信接口，每个串口都有一个波特率发生器、接收寄存器、发送寄存器和一个控制单元，另外，还有两个16字节的FIFO寄存器作为发送和接收的缓冲装置。

在S3C2410中，对串口的控制是通过设置相应的控制寄存器来实现的，其常用的寄存器主要有以下几个：(1)ULCONn寄存器：主要用来设置串口工作模式，包括数据位长度、停止位个数，以及数据校验方式等。

S3C2410支持四种校验方式，分别是奇校验、偶校验、MARK校验和SPACE校验。

(2)UCONn寄存器：该寄存器涉及到中断模式控制、DMA模式控制，以及时钟的选择等。

(3)UTRSTATn寄存器：串口的状态寄存器，用于指示串口是否接收或发送完毕。

(4)UTXHn和URXHn寄存器：发送和接收寄存器。

(5)UBRDIVn寄存器：波特率设置寄存器，用于对时钟分频，产生需要的波特率。

5．终端如何处理特殊字符？答：在串口的参数配置结构struct termios中，通过设置c_cc数组成员来定义支持的特殊控制字符以及一些timeout参数。

c_cc 支持的常量名称有：VINTR 中断控制，对应键为CTRL+C；VQUIT 退出操作，对应键为CRTL+Z；VERASE 删除操作，对应键为Backspace （BS）；VKILL 删除行，对应键为CTRL+U；VEOF 位于文件结尾，对应键为CTRL+D；VEOL 位于行尾，对应键为Carriage return（CR）；VEOL2 位于第二行尾，对应键为Line feed（LF）；VMIN 指定了最少读取的字符数；VTIME 指定了读取每个字符的等待时间。

11.4.6习题1．修改用户程序，将三个电位器的多次转换的结果写入一个文件中。

答：参考程序见“/labs/ Lab_4”文件夹中的“main1.c”。

2．逐次逼近型的A/D转换器原理是什么？答：逐次逼近型A/D 转换器其工作原理是：将被测电压和由D/A转换生成的电压进行比较，用对分搜索的方法来逐次逼近被测电压。

它的实质是逐次把设定的SAR 寄存器中的数字量经D/A 转换后得到电压Vc 与待转换模拟电压V。

进行比较。

比较时，先从SAR 的最高位开始，逐次确定各位的数码应是“1”还是“0”，其工作过程如下：转换前，先将SAR 寄存器各位清零。

转换开始时，控制逻辑电路先设定SAR 寄存器的最高位为“1”，其余位为“0”，此试探值经D/A 转换成电压Vc，然后将Vc 与模拟输入电压Vx 比较。

如果Vx≥Vc，说明SAR 最高位的“1”应予保留；如果Vx<Vc，说明SAR 该位应予清零。

然后再对SAR 寄存器的次高位置“1”，依上述方法进行D/A 转换和比较。

如此重复上述过程，直至确定SAR 寄存器的最低位为止。

过程结束后，状态线改变状态，表明已完成一次转换。

最后，逐次逼近寄存器SAR 中的内容就是与输入模拟量V 相对应的二进制数字量。

3．A/D转换的重要指标包括哪些？答：A/D 转换的重要指标有；分辨率、精度、转换时间、电源灵敏度、量程、输出逻辑电平和工作温度范围等。

4．ARM的A/D功能的相关寄存器有哪几个，对应的地址是什么？答：与A/D相关的寄存器主要有A/D转换控制寄存器（ADCCON）和A/D转换数据寄存器ADCDAT0。

ADCCON的地址为0x58000000，ADCDAT0的地址为0x5800000C。

5．如何启动ARM 开始转换A/D，有几种方式？转换开始时ARM 是如何知道转换哪路通道的？如何判断转换结束？答：A/D转换的数据可以通过中断或查询的方式来访问，如果使用中断方式，全部的转换时间（从A/D转换的开始到数据读出）要更长。