MBA管理运筹学课后习题答案
管理运筹学课后习题答案

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法,它通过建立数学模型,寻找最优解来解决实际问题。
下面我们来讨论一些常见的线性规划习题。
1. 一家工厂生产两种产品A和B,每单位产品A需要3小时的加工时间和2小时的装配时间,每单位产品B需要2小时的加工时间和4小时的装配时间。
工厂每天有8小时的加工时间和10小时的装配时间。
已知产品A的利润为300元,产品B的利润为400元。
如何安排生产,使得利润最大化?解答:设生产产品A的数量为x,生产产品B的数量为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 300x + 400y约束条件:3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即生产4个产品A和1个产品B时,利润最大化,为2000元。
2. 一家超市有两种品牌的洗衣液,品牌A和品牌B。
品牌A每瓶售价20元,每瓶利润为5元;品牌B每瓶售价25元,每瓶利润为7元。
超市每天销售洗衣液的总利润不能超过100元,并且每天至少要销售10瓶洗衣液。
如何安排销售,使得利润最大化?解答:设销售品牌A的瓶数为x,销售品牌B的瓶数为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 5x + 7y约束条件:20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即销售5瓶品牌A和5瓶品牌B时,利润最大化,为60元。
二、排队论排队论是管理运筹学中研究排队系统的一种方法,它通过数学模型和概率统计来分析和优化排队系统。
下面我们来讨论一些常见的排队论习题。
1. 一家银行有两个窗口,每个窗口的服务时间服从指数分布,平均服务时间分别为3分钟和4分钟。
顾客到达的间隔时间也服从指数分布,平均间隔时间为2分钟。
如果顾客到达时,两个窗口都有空闲,顾客会随机选择一个窗口进行服务。
《管理运筹学》(第二版)课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0b,≥i决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0bAX,的解,称为可行解。
=X≥基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a x x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学第二版课后习题参考答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0 i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
表1—15 某极大化问题的单纯形表7.用大M 法求解如下线性规划。
s .t . ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≤++0,,101632182321321321321x x x x x x x x x x x x解:加入人工变量,进行人造基后的数学模型如下:s .t . ⎪⎪⎩⎪⎪⎨⎧=≥=+++=+++=+++)6,,2,1(0101632182632153214321 i x x x x x x x x x x x x x i列出单纯形表x为“第i电站向第j城市分配的电量”(i=1,2; j=1,2,3),建立模型如下:解:设ijs .t . ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥≤+≥+=+≤+≥+=++=++3,2,1;2,1,035027025032029045040023132313221221112111232221131211j i x x x x x x x x x x x x x x x x x ij10s .t . ⎪⎪⎪⎪⎩⎨=≥≤≤≤4,3,2,1,0,,101520)3()2()1()1(4)1(3)1(2i x x x x x x i i i 通过LINGO 软件计算得:44,12,0,20,10)2(1)2(1)1(3)1(2)1(1=====x x x x x . 10.某家具制造厂生产五种不同规格的家具。
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
? (3)由图2-1可知,最优解为B 点,最优解 x =12, x ??15 727图2-1 ;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解?x 1 ??0.2,函数值为3.6。
?x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
? (5)无穷多解。
?x ? (6)有唯一解 ??1? 203,函数值为 92 。
8 3x ? ??2 33.解: (1)标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??30 3x 1 ??2x 2 ??s 2 ??13 2x 1 ??2x 2 ??s 3 ??9 x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2 ??10 7x 1 ??6x 2 ??4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??70 2x 1????5x 2????5x 2??????50 3x 1????2x 2????2x 2??????s 2 ??30 x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4.解: 标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1 ??95x 1 ??2x 2 ??s 2 ??8x1, x2 , s1, s2 ≥0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》第二课后习题答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》第四版课后习题答案
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
当 c1 不变时 ,c2 在 负无穷 到 6.4 的范 围内变 化,最优 解不 变。 (5)约 束条件 1 的右 边值 在 780 000,1500 000 变化,对偶价格仍 为 0.057(其他同理) 。 (6)不能,因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ,理由
4.25 3.6
11.解: 设圆 桌和衣柜的生 产件数分 别为 x、y,所获 利润为 z,则 z=6x+10y.
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域.平移 6x+ 10y=0 ,如图
y0
2x y 800
x 350
得
即 C(350,100) .当直线 6x+ 10y=0 即 3x+ 5y=0 平移
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
管理运筹学课后答案
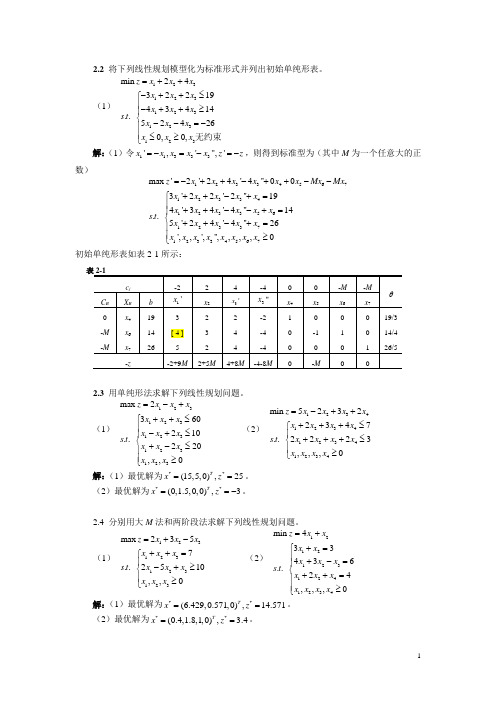
2.2 将下列线性规划模型化为标准形式并列出初始单纯形表。
(1)123123123123123min 243221943414..524260,0,z x x x x x x x x x s t x x x x x x =++-++≤⎧⎪-++≥⎪⎨--=-⎪⎪≤≥⎩无约束 解:(1)令11333','",'x x x x x z z =-=-=-,则得到标准型为(其中M 为一个任意大的正数)12334567123341233561233712334567max '2'24'4''003'22'2''194'34'4''14..5'24'4''26',,','',,,,0z x x x x x x Mx Mx x x x x x x x x x x x s t x x x x x x x x x x x x x =-++-++--++-+=⎧⎪++--+=⎪⎨++-+=⎪⎪≥⎩初始单纯形表如表2-1所示:表2-1c j-22 4-4 0 0 -M -M θC B X B b 1'xx 2 3'x3''xx 4 x 5 x 6 x 7 0 x 4 19 3 2 2 -2 1 0 0 0 19/3 -M x 6 14 [ 4 ] 3 4 -4 0 -1 1 0 14/4 -Mx 7 265 2 4-40 0 0 1 26/5 -z-2+9M2+5M4+8M -4-8M-M2.3 用单纯形法求解下列线性规划问题。
(1)123123123123123max 2360210..220,,0z x x x x x x x x x s t x x x x x x =-+++≤⎧⎪-+≤⎪⎨+-≤⎪⎪≥⎩ (2) 1234123412341234min 52322347..2223,,,0z x x x x x x x x s t x x x x x x x x =-+++++≤⎧⎪+++≤⎨⎪≥⎩解:(1)最优解为**(15,5,0),25T x z ==。
MBA管理运筹学课后部分作业答案

* f2(s2,x2) 0.5s2+ f 3 ( s2 )
3+x2+0.5s2+ f 3* ( s2 )
f 2* ( s2 )
s2 0 1 2 16 16.5 16.5 x2 0 1 2 3 17 17 15 4 17.5 15.5 16 5 16 16.5 17 6 17 17.5 16 15.5 15
变换标准型,找出最大元素为1000,用1000减 去各个元素得:
100 200 100 600 0
600 500 300 200 500
400 100 700 700
200 0 500 400
500 100 400 0 200 100 500 100 200 0
400 100
0 200 0 500 0
45+125 70+95
170
1
• • • •
顺序递推,得出结论 由表可知,当x1=1,x2=3,x3=1时各商场的增加额最大 最大值 f1*=170(万元) 即该公司应分配给甲、乙、丙3个商场以1,3,1个人员。这样增加额最大,为 170万元。 3
7-6 某厂生产一种机械设备。据市场调查,今后4个时期该 产品需求量依次为2、3、2、4台。该厂每期最大生产能力 为6台;每期固定生产费用为3万元(若不生产则为0), 单台成本1万元,每期贮存保养费为每台0.5万元。若第1期 初和第4期末均无库存,试确定各期产量,使总费用最少。 解:1. 建立模型 令k=1、2、3、4表示4个时期的序号 设Sk=第K时期初(或第k-1时期末的库存量) Xk——第k时期的产量 dk表第k时期的需求量,则状态转移方程为: Sk+1=Sk+Xk-dk 设:Uk(Sk,Xk)——第k时期生产费用; fk (Sk,Xk)——第k月初到第4月末的生产费用 * f k k,Xk)——第k月初到底4月末的最低生产费用 (S
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
管理运筹学第二版课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming, LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、LI标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;U标函数是决策者希望实现的LI标,为决策变量的线性函数表达式,有的LI标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现儿种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解:(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:LI标函数极大化,约束条件为等式,右端常数项^>0, 决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“事”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件AX=b, X>0的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使訂标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:基可行解5.用表格单纯形法求解如下线性规划。
max Z = 4Xj + x2+ 2x3 8Xj + 3X2 +x3 <26xj + x 2 + 兀3 § 8 飞°解:标准化max Z = 4x t + x2 + 2x38xj + 3X2+x3 + x4 = 2< + x2 + x3 +x5 = 8列出单纯形表故最优解为X* = (0Q2Q6V ,即M = 09x2 = 0內=2 ,此时最优值为Z(X*) = 4 •6.表1—15中给出了求极大化问题的单纯形表,问表中5<2,5心,〃为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以“代替基变量心;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》第四版课后习题答案
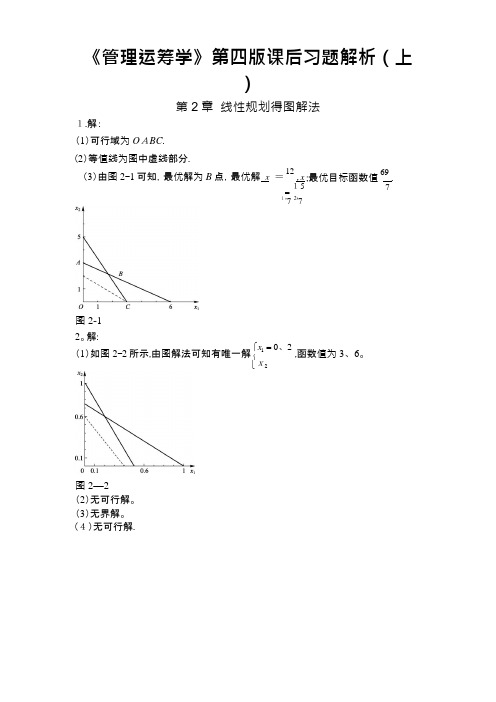
⎨ 《管理运筹学》第四版课后习题解析(上)第2章 线性规划得图解法1.解:(1)可行域为O ABC .(2)等值线为图中虚线部分.(3)由图2-1可知,最优解为B 点,最优解 x = 12, x = 15 1ﻩ7 2ﻩ7图2-1;最优目标函数值 69 . 72。
解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1= 0、2 ,函数值为3、6。
⎩x2图2—2(2)无可行解。
(3)无界解。
(4)无可行解.⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 20 3 ,函数值为 92 . 83ﻩx = ⎪⎩ 2 33。
解:(1)标准形式ma x f = 3x 1 + 2x2 + 0s1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 132x1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s1 + 0s23x1 - x 2 - s 1= 6 x 1 + 2x2+ s 2 = 10 7x 1- 6x 2 = 4x 1, x2 , s1, s 2 ≥ 0(3)标准形式m in f = x 1' - 2x2' + 2x 2'' + 0s 1 + 0s 2 -3x1 + 5x 2' - 5x 2'' + s 1 = 702x1' - 5x 2' + 5x2'' = 50 3x1' + 2x2' - 2x 2'' - s 2 = 30 x 1', x2' , x 2'' , s 1, s 2 ≥0 4.解:标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s23x 1 + 4x 2 + s 1= 95x 1 + 2x 2 + s2 = 8x 1, x 2 , s 1, s 2 ≥ 0≤ 松弛变量(0,0)最优解为 ﻮx 1 =1,x 2=3/2.5.解:标准形式mi n f = 11x1 + 8x 2 + 0s1 + 0s 2 + 0s 310x1 + 2x2 - s 1 = 203x 1 + 3x2 - s 2 = 184x 1 + 9x2 - s3 = 36x 1, x2 , s 1, s 2 , s 3 ≥ 0剩余变量(0, 0, 13)最优解为 x1=1,x 2=5。
管理运筹学(第三版)课后习题答案
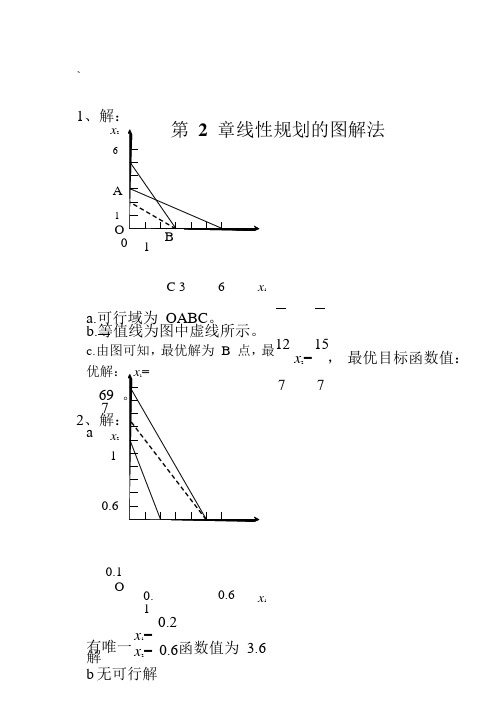
、1、解:x26A1O0 1第2章线性规划的图解法BC 3 6 x1a.可行域为OABC。
b.等值线为图中虚线所示。
c.由图可知,最优解为B 点,最优解:x1= 12 15x2= ,最优目标函数值:69 。
7 2、解:7 7a x210.60.1O0.1 x1= 0.20.6 x1有唯一解x2= 0.6函数值为 3.6b 无可行解c 无界解d 无可行解e 无穷多解f 有唯一解3、解:a 标准形式:x1x2==20383函数值为923maxf =3x1+2x2+0s1+0s2+ 0s3 x+91+=2x s30x+31x+21222 1+ s=x22+ s=139b 标准形式:x1x23s s, x2, s1, ,2 3≥0ma x f = −x x s s41− 63− 01− 02 3 −x−s= 6x12 1x + + =1 2x s2 2107 x1− 6x2= 4c 标准形式:x1, x2, , ss12= − +x'x'≥' −ma x f 2 −2x s s0 − 021−x +2x' −2 1' + =x s3 5 5 701 2 212x '− 5x '+ 5x '= 50 1 x '+ 312 x '− 222' − =2x s30 x ', x 2',x 2',, s 2 ≥ 024 、解:1 s 12z = x + x + +max 10 5 s s标准形式: 1 2 0 0x + 31x+ 514 2 1 + s = x 21+ s = x 22 9 8 2s 1= 2, s 2= 0x 1, x 2, , s s 12≥ 05 、解:f = x + x+ ++ min 11 8 s s s标准形式: 1 2 0 0 0x+ 101 x +2 1 − s = x 21− = 2 203 31x+413x s 2 2 − =9x s 18 36 s 1= 0, s 2= 0, s 3= 13 6 、解: b 1 ≤ c 1≤ 3c 2 ≤ c 2≤ 6x 1= 6 x 12 3 s s , x 2, s 1, , 2 3≥ 0 de x 2= 4 x 1∈ [ ]8x = 16 − 2x221f 变化。
管理运筹学课后习题解答

1 绪论1、运筹学的内涵答:本书将运筹学定义为:“通过构建、求解数学模型,规划、优化有限资源的合理利用,为科学决策提供量化依据的系统知识体系。
”2、运筹学的工作过程答:(1)提出和形成问题。
即要弄清问题的目标、可能的约束、可控变量、有关的参数以及搜索有关信息资料。
(2)建立模型。
即要把问题中的决策变量、参数和目标、约束之间的关系用一定的模型表示出来。
(3)求解模型。
根据模型的性质,选择相应的求解方法,求得最优或者满意解,解的精度要求可由决策者提出。
(4)解的检验和转译。
首先检查求解过程是否有误,然后再检查解是否反映客观实际。
如果所得之解不能较好地反映实际问题,必须返回第(1)步修改模型,重新求解;如果所得之解能较好地反映实际问题,也必须仔细将模型结论转译成现实结论。
(5)解的实施。
实施过程必须考虑解的应用范围及对各主要因素的敏感程度,向决策者讲清楚用法,以及在实施中可能产生的问题和修改的方法。
3、数学模型及其三要素答:数学模型可以简单的描述为:用字母、数字和运算符来精确地反映变量之间相互关系的式子或式子组。
数学模型由决策变量、约束条件和目标函数三个要素构成。
决策变量即问题中所求的未知的量,约束条件是决策所面临的限制条件,目标函数则是衡量决策效益的数量指标。
2 线性规划1、试述线性规划数学模型的组成部分及其特性答:线性规划数学模型由决策变量、约束条件和目标函数三个部分组成。
线性规划数学模型特征:(1) 用一组决策变量表示某一方案,这组决策变量均为非负的连续变量;(2) 存在一定数量(m )的约束条件,这些约束条件可以用关于决策变量的一组线性等式或者不等式来加以表示;(3) 有一个可以用决策变量加以表示的目标函数,而该函数是一个线性函数。
2、一家餐厅24小时全天候营业,在各时间段中所需要的服务员数量分别为:2:00~6:00 3人 6:00~10:00 9人 10:00~14:00 12人 14:00~18:00 5人 18:00~22:00 18人 22:00~ 2:00 4人设服务员在各时间段的开始时点上上班并连续工作八小时,问该餐厅至少配备多少服务员,才能满足各个时间段对人员的需要。
《管理运筹学》第四版课后习题答案
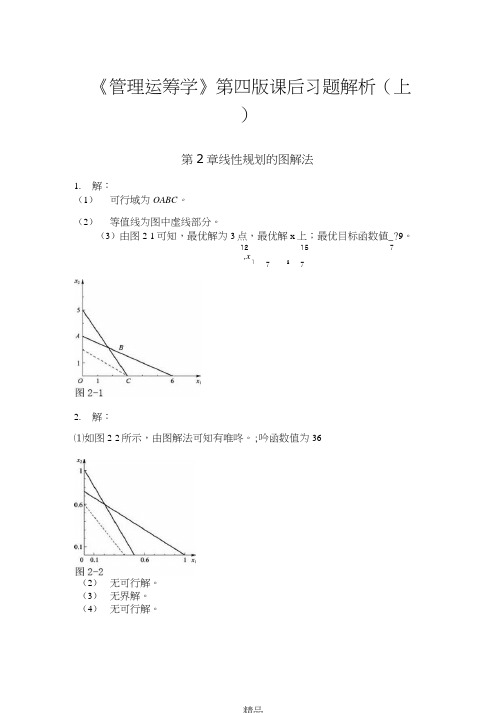
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为3点,最优解x上;最优目标函数値_?9。
12 15 7,x17 272.解:⑴如图2-2所示,由图解法可知有唯咚。
;吟函数值为36(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
x 20(62有唯一解J ,函数值珂翌~。
3.解:(1)标准形式max f3为2X20》0s2°Ss9禺2X2§303马2x,S?132x\2x?习9坷,屯,S2 »$0(2)标准形式min f4也6-v2 Os】0s23址x2勺 6画2X2s2107 X、 6 Ao4X\, X2 , q, S2 Mo(3)标准形式4.解: 标准形式0 S] 0 S23曲5 Ao5^2q702冯5X25X2503西 2 An 2X2S2禺,x?,X2,勺,S2 Mo30 max z3 禺4x z勺 95 禺 2 Ab s2 8 Aj, X2 , S2 $0松弛变量(0, 0)最优解为禺二1, X2=3/2O5.解:标准形式min f llAj 8X2 0勺0s210题 2 Ao L203羽3也184禺9疋S336禺,勺,S?,习$0x2,剩余变量(0,0,13)最优解为X1=1, X2=5O6.解:(1)最优解为禺二3, A2=7O(2) 1 q 3 o(3) 2 c2 6 o(5)最优解为^1=8, ^2=0o(6)不变化。
因为当斜率J最篇掣解不变,变化后斜率为】,所以iw q不变。
7.解:设x, y分别为甲、乙两种柜的日产量,目标函数z=200x +240y,线性约束条件:12 y x2120 f20作出可行域.n4y1 2x y6416即X0x0y0y2x y16z 仆 200 4 240 8 2720答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720 元.8.解:设需截第一种钢板x张,第二种钢板y张,所用钢板面积zm2.目标函数z二x + 2y, 线性约束条件:x y122x y15x 3y27x 0 x 3y 27y作出可行域,并做一组一组平行直线x+2y=t.解x y 12得£(9 / 2,15 / 2)答:应截第一种钢板4张,第二种钢板8张,能得所需三种规格的钢板,且使所用钢板的面积最小.9.解:设用甲种规格原料x张,乙种规格原料y张,所用原料的总面积是zm2,目标函数z=X 2 y23x + 2y r线性约束条件Xy作出可行域.作一组平等直线3x + 2y=t・解x 22 得C(4 / 3,1 / 3) 2xy3C不是整点,C不是最优解.在可行域内的整点中,点B(l, 1)使Z取得最小值. z 垠小=3X14-2X1=5,答:用甲种规格的原料1张,乙种原料的原料1张,可使所用原料的总面积最小为 5 m2.10.解:设租用大卡车x辆,农用车y辆,最低运费为z元.目标函数为z二960x + 360y.0 x 10线性约束条件是<y作出可行域,并作直线960x + 360y=0.208x 2.5 y 100即8x+3y=0,向上平移sly)\V>=X(T)+(T)-12-16x10由得最佳点为&108x 2.5y 100作直线960x +360y=0.即8x+3y=0,向上平移至过点B(10, 8)时,z=960x + 360y取到最小值.z 垠小=960X10+360X8=12480答:大卡车租10辆,农用车租8辆时运费最低,最低运费为12480元.11.解:设圆桌和衣柜的生产件数分别为X、y,所获利润为z,则z=6x + 10y.0. 18x0. 092x y800y720. 08x0. 28y56作出可行域.平移6x+10y=0 ,如2x7 y1400 即x x 0°y 02x y X即C(350, 100).当直线6x+10y二0 即3x+5y二0 平移800得350到2x7 y y1400100经过点C(350, 100)时,z=6x+10y 最大12.解:模型max z 500为400JV22X\ W3003也<5402x\ 2x\ W4401.2x\ 1. 5Ao W 300Aj, x2 ^0(1)x、 150 , x? 70 ,即目标函数最优值是103 000o(2)2, 4有剩余,分别是330, 15,均为松弛变量。
管理运筹学课后习题答案
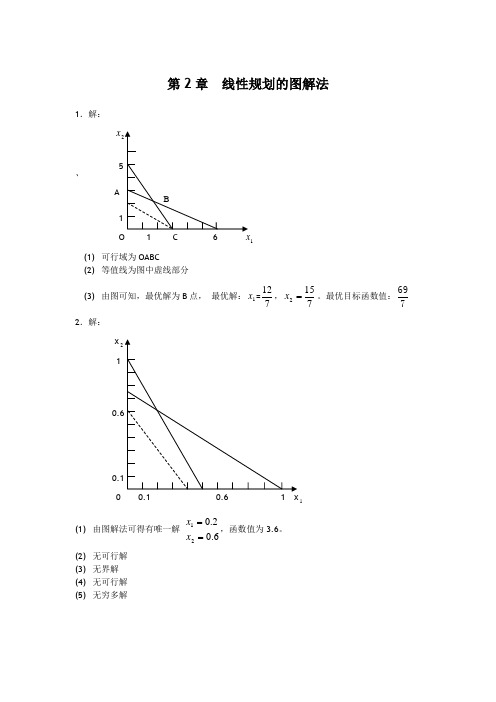
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 21(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
《管理运筹学》第四版课后习题答案
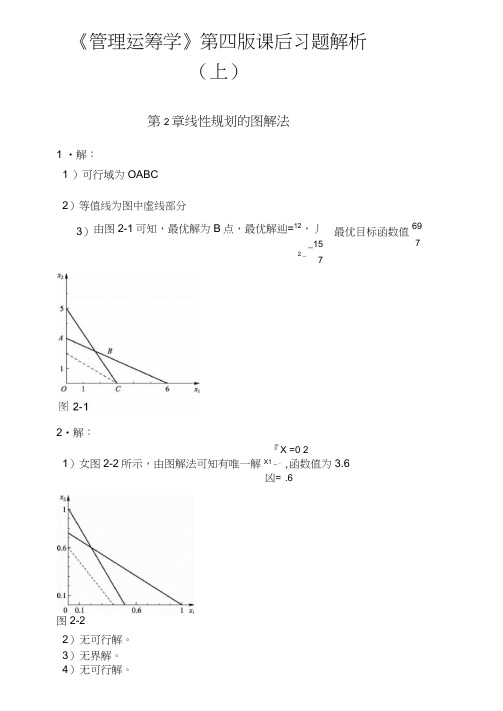
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1 •解:1 )可行域为OABC2)等值线为图中虚线部分2•解:『X =0 21)女图2-2所示,由图解法可知有唯一解X1 _ . ,函数值为3.6凶=°.6图2-22) 无可行解。
3) 无界解。
4) 无可行解。
3)由图2-1可知,最优解为B 点,最优解辿=12,丿 最优目标函数值 _152 _ 76975)无穷多解3•解:1)标准形式max f =3x i 2x 2 0s i - 0s 2 - 0s 39xi 2x 2 si =303x 1 亠2X 2 亠s =132x i 亠2x 2 亠S 3 =9x i , x 2 ,S 1, S 2, S 3》02) 标准形式min f =4x 1 亠6x 2 亠0$ 亠0s 23x i - X 2 - Si — 6x 1 2x 2 S 2 =i07x i -6x 2 =4x i , x , S i , S 2 A 03) 标准形式min f =xi —2X 2 亠2X 2 亠0s 1 亠0S 2-3x i 5x 2 -5x 2 S i =702x i -5x 2 5X 2: =503x i 2x 2 —2x 2 -S 2 =30x i , xl X 2: Si, S 2 A 0 4•解:标准形式max z =10x i ' 5x 2 ' 0s i 0S 23x 1 4x 2 Si =95xi 2x 2 S 2 =8x i , x , S i , S 2 A 06)有唯一解■: X 2=20 3,函数值为 83 92 3松弛变量0,0) 最优解为x i =1, X 2=3/2。
5•解:标准形式min f =11x i 8x 2 - 0s i - 0s 2 - 0S 310X 1 2X 2 -s 1 =203X I 亠 3X2 -S 2 =184X1 9X2 —S3 =36X 1, X 2 , S 1, S 2 , S3》0剩余变量0, 0, 13)最优解为X 1=1 , X 2=5。
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1. 什么是线性规划?线性规划的三要素是什么?答:线性规划(Lin ear Programmi ng , LF)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2. 求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3. 什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项 ' ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业 来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明 “遅 约束的左边取值大于右边规划值,出现剩余量。
4•试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关 系。
答:可行解:满足约束条件 扎—‘丸 的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5 •用表格单纯形法求解如下线性规划解:标准化1可行基:对应于基可行解的基,称为可行基。
基可行解SA] +S 21s.t.列出单纯形表/43/21/2[8]/83/2/6/8 1/8]5/4 /41/2/8 1/4/(1/83/4 13/2/(1/412 5故最优解为二「- 1,即—心I八,此时最优值为' 1士匚6.表1 —15中给出了求极大化问题的单纯形表,问表中1为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学课后答案

第一章第一章1. 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量(Decision Variable)是决策问题待定的量值,取值一般为非负;约束条件(Constraint Conditions)是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数(Objective Function)是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.(1)设立决策变量;(2)确定极值化的单一线性目标函数;(3)线性的约束条件:考虑到能力制约,保证能力需求量不能突破有效供给量;(4)非负约束。
3.(1)唯一最优解:只有一个最优点(2)多重最优解:无穷多个最优解(3)无界解:可行域无界,目标值无限增大(4)没有可行解:线性规划问题的可行域是空集无界解和没有可行解时,可能是建模时有错。
4. 线性规划的标准形式为:目标函数极大化,约束条件为等式,右端常数项bi≥0 , 决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
5. 可行解:满足约束条件AX =b,X≥0的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
6. 计算步骤:第一步,确定初始基可行解。
第二步,最优性检验与解的判别。
第三步,进行基变换。
第四步,进行函数迭代。
判断方式:唯一最优解:所有非基变量的检验数为负数,即σj< 0无穷多最优解:若所有非基变量的检验数σj≤ 0 ,且存在某个非基变量xNk 的检验数σk= 0 ,让其进基,目标函数的值仍然保持原值。
如果同时存在最小θ值,说明有离基变量,则该问题在两个顶点上同时达到最优,为无穷多最优解。
