管理运筹学课后习题答案
管理运筹学第三版课后答案

管理运筹学第三版课后答案【篇一:管理运筹学(第三版)课后习题答案】ss=txt>1、解:ax= 150 x= 7012目标函数最优值 103000b 1,3 使用完2,4 没用完 0,330,0,15c 50,0,200,0含义: 1 车间每增加 1 工时,总利润增加 50 元3 车间每增加 1 工时,总利润增加 200 元 2、4 车间每增加 1 工时,总利润不增加。
d 3 车间,因为增加的利润最大e 在 400 到正无穷的范围内变化,最优产品的组合不变f 不变因为在 [0,500]的范围内g 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条j 不发生变化允许增加的百分比与允许减少的百分比之和没有超出100% k 发生变化 2、解:a 4000 10000 62000b 约束条件 1:总投资额增加 1 个单位,风险系数则降低 0.057约束条件 2:年回报额增加 1 个单位,风险系数升高 2.167 c 约束条件 1 的松弛变量是 0,约束条件 2 的剩余变量是 0约束条件 3 为大于等于,故其剩余变量为 700000 d 当 c不变时,c在 3.75 到正无穷的范围内变化,最优解不变21当 c不变时, c在负无穷到 6.4 的范围内变化,最优解不变12e 约束条件 1 的右边值在 [780000,1500000]变化,对偶价格仍为0.057(其他同理)f 不能,理由见百分之一百法则二 3 、解:a 18000 3000 102000 153000b 总投资额的松弛变量为 0基金 b 的投资额的剩余变量为 0c 总投资额每增加 1 个单位,回报额增加 0.1基金 b 的投资额每增加 1 个单位,回报额下降 0.06 d c不变时, c 在负无穷到 10 的范围内变化,其最优解不变12c不变时, c在 2 到正无穷的范围内变化,其最优解不变21e 约束条件 1 的右边值在 300000 到正无穷的范围内变化,对偶价格仍为 0.1约束条件 2 的右边值在 0 到 1200000 的范围内变化,对偶价格仍为-0.06 + = 100% 故对偶价格不变900000 900000 f4、解:a x=1x= 1.52x= 03x= 1 最优目标函数 18.548.5b 约束条件 2 和 3 对偶价格为 2 和 3.5c 选择约束条件 3,最优目标函数值 22d 在负无穷到 5.5 的范围内变化,其最优解不变,但此时最优目标函数值变化e 在 0 到正无穷的范围内变化,其最优解不变,但此时最优目标函数值变化 5、解:a 约束条件 2 的右边值增加 1 个单位,目标函数值将增加 3.622b 才有可能大于零或生产2c 根据百分之一百法则判定,最优解不变15 65d + 100 % 根据百分之一百法则二,我们不能判定? 30 ? 9.189因为111.25 15其对偶价格是否有变化第 4 章线性规划在工商管理中的应用1、解:为了用最少的原材料得到 10 台锅炉,需要混合使用 14 种下料方4286398505479691180剩余758设按 14 种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7,x8,x9, x10,x11,x12,x13,x14,则可列出下面的数学模型: min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14 s.t. 2x1+x2+x3+x4 ≥ 80x2+3x5+2x6+2x7+x8+x9+x10≥ 350 x3+x6+2x8+x9+3x11+x12+x13≥ 420x4+x7+x9+2x10+x12+2x13+3x14 ≥ 10x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥ 0 用管理运筹学软件我们可以求得此问题的解为:x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0, x9=0,x10=0,x11=140,x12=0,x13=0,x14=3.333 最优值为 300。
《管理运筹学》第四版课后习题答案
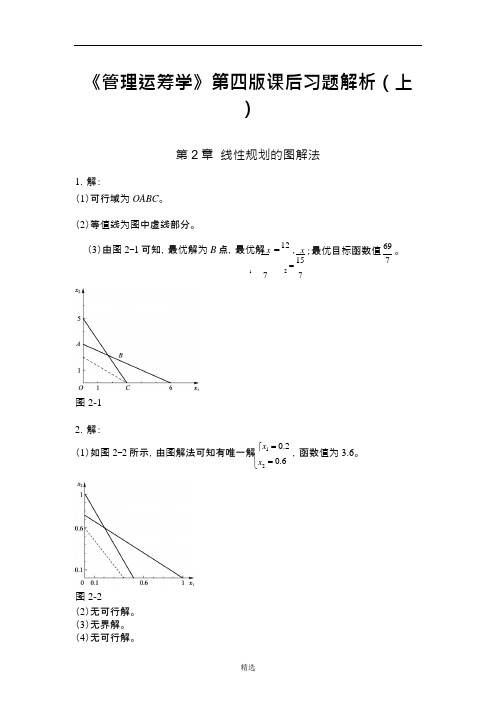
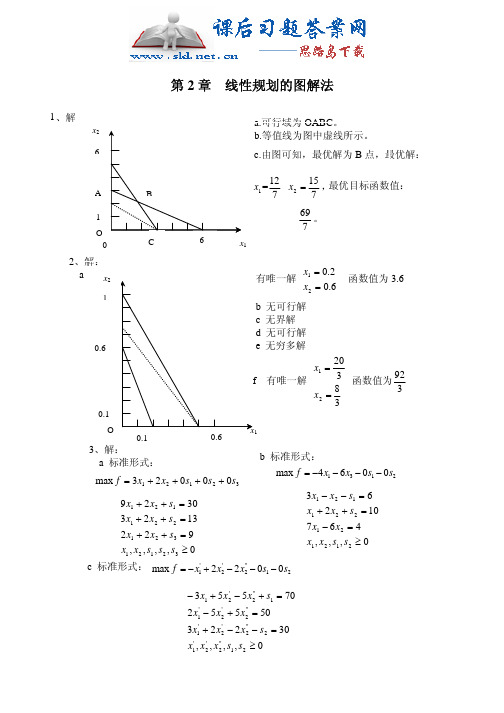
精选⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x = 15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 203 ,函数值为 92 。
8 3 x = ⎪⎩ 2 33.解: (1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
管理运筹学课后习题答案

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法,它通过建立数学模型,寻找最优解来解决实际问题。
下面我们来讨论一些常见的线性规划习题。
1. 一家工厂生产两种产品A和B,每单位产品A需要3小时的加工时间和2小时的装配时间,每单位产品B需要2小时的加工时间和4小时的装配时间。
工厂每天有8小时的加工时间和10小时的装配时间。
已知产品A的利润为300元,产品B的利润为400元。
如何安排生产,使得利润最大化?解答:设生产产品A的数量为x,生产产品B的数量为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 300x + 400y约束条件:3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即生产4个产品A和1个产品B时,利润最大化,为2000元。
2. 一家超市有两种品牌的洗衣液,品牌A和品牌B。
品牌A每瓶售价20元,每瓶利润为5元;品牌B每瓶售价25元,每瓶利润为7元。
超市每天销售洗衣液的总利润不能超过100元,并且每天至少要销售10瓶洗衣液。
如何安排销售,使得利润最大化?解答:设销售品牌A的瓶数为x,销售品牌B的瓶数为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 5x + 7y约束条件:20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即销售5瓶品牌A和5瓶品牌B时,利润最大化,为60元。
二、排队论排队论是管理运筹学中研究排队系统的一种方法,它通过数学模型和概率统计来分析和优化排队系统。
下面我们来讨论一些常见的排队论习题。
1. 一家银行有两个窗口,每个窗口的服务时间服从指数分布,平均服务时间分别为3分钟和4分钟。
顾客到达的间隔时间也服从指数分布,平均间隔时间为2分钟。
如果顾客到达时,两个窗口都有空闲,顾客会随机选择一个窗口进行服务。
《管理运筹学》课后习题答案
min f=25x11+20x12+30x21+24x22
s.t.x11+x12+x21+x22 2000
x11+x12=x21+x22
约束条件2:年回报额增加1个单位,风险系数升高2.167;
约束条件3:基金B的投资额增加1个单位,风险系数不变。
(3)约束条件1的松弛变量是0,表示投资额正好为1200000;约束条件2的剩余变量是0,表示投资回报率正好是60000;约束条件3的松弛变量为700000,表示投资B基金的投资额为370000。
总成本最小为264元,能比第一问节省:320-264=56元。
3.解:设生产A、B、C三种产品的数量分别为x1,x2,x3,则可建立下面的
数学模型:
max z=10 x1+12x2+14x3
s.t. x1+1.5x2+4x3 2000
2x1+1.2x2+x3 1000
x1 200
x2 250
x3 100
3.解:
(1).式:
4.解:
标准形式:
松弛变量(0,0)
最优解为 =1,x =3/2.
5.解:
标准形式:
剩余变量(0.0.13)
最优解为x1=1,x2=5.
6.解:
(1)最优解为x1=3,x2=7.
(2)
(3)
(4)
(5)最优解为x1=8,x2=0.
(6)不变化。因为当斜率 ,最优解不变,变化后斜率为1,所以最优解不变.
(5)约束条件1的右边值在300000到正无穷的范围内变化,对偶价格仍为0.1;
管理运筹学课后习题答案
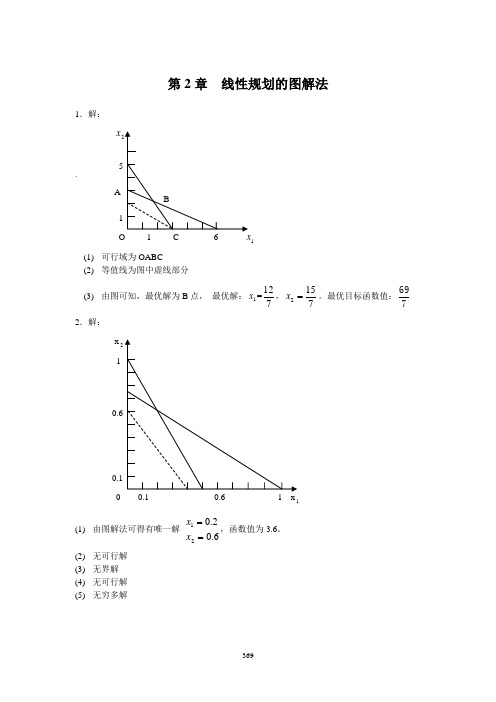
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
管理运筹学 第三版 (韩伯棠) 高等教育出版社 课后参考答案
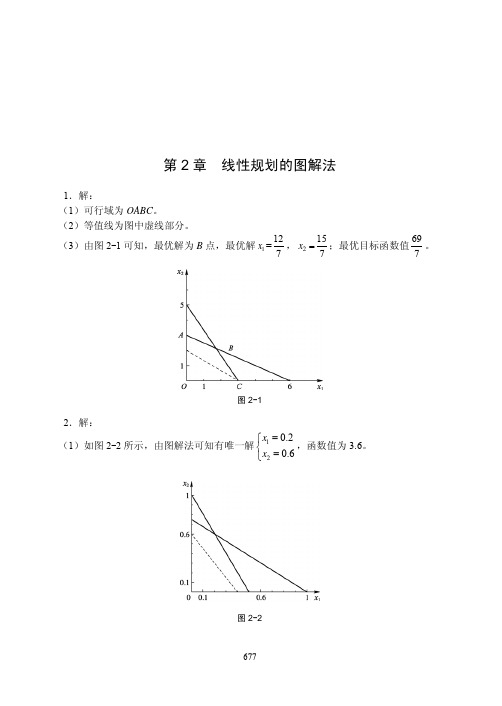
表 4-1 各种下料方式
1 2 3 4 5 6 7 8 9 10 11 12 13 14
2 640 mm
21110000000000
1 770 mm
01003221110000
1 650 mm
00100102103210
1 440 mm
00010010120123
min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14 s.t. 2x1+x2+x3+x4≥80
max z = 10x1 + 5x2 + 0s1 + 0s2 3x1 + 4x2 + s1 = 9 5x1 + 2x2 + s2 = 8 x1, x2, s1, s2 ≥ 0 松弛变量(0,0)
最优解为 x1 =1,x2=3/2。
5.解:
678
标准形式
min f = 11x1 + 8x2 + 0s1 + 0s2 + 0s3
1.解: (1) x1 = 150 , x2 = 70 ;目标函数最优值 103 000。 (2)1、3 车间的加工工时数已使用完;2、4 车间的加工工时数没用完;没用完的加工工时 数为 2 车间 330 小时,4 车间 15 小时。 (3)50,0,200,0。 含义:1 车间每增加 1 工时,总利润增加 50 元;3 车间每增加 1 工时,总利润增加 200 元; 2 车间与 4 车间每增加一个工时,总利润不增加。 (4)3 车间,因为增加的利润最大。 (5)在 400 到正无穷的范围内变化,最优产品的组合不变。
(2)这时付给临时工的工资总额为 80 元,一共需要安排 20 个临时工的班次。
《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000,10000。 回报率:60000
b 模型变为: max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后,用管理运筹学软件求解可得:总成本最小为 264 元。 安排如下:y1=8( 即在此时间段安排 8 个 3 小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56 元。
x2+x3+x4+x5+1 ≥ 3 x3+x4+x5+x6+2 ≥ 3 x4+x5+x6+x7+1 ≥ 6 x5+x6+x7+x8+2 ≥ 12 x6+x7+x8+x9+2 ≥ 12 x7+x8+x9+x10+1 ≥ 7 x8+x9+x10+x11+1 ≥ 7 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥ 0 用管理运筹学软件我们可以求得此问题的解为:
b、 这时付给临时工的工资总额为 80 元,一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
.解:标准化.列出单纯形表412b02[8]2 /80868 /641241/41/81/8]/8(1/4/(1/813/265/4/43/4(13/2/(1/4 0-1/23/21/222806-221-12-502故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学》-第四版课后习题答案.docx
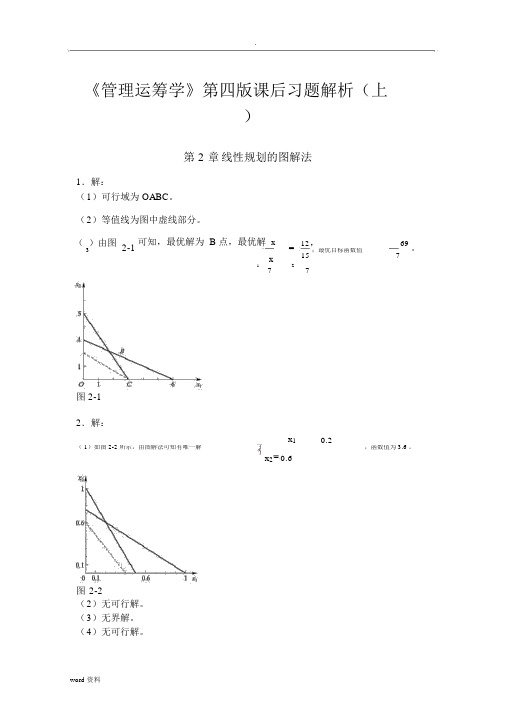
.《管理运筹学》第四版课后习题解析(上)第 2 章线性规划的图解法1.解:(1)可行域为 OABC。
(2)等值线为图中虚线部分。
()由图2-1可知,最优解为 B 点,最优解x=12,69。
315;最优目标函数值7x1277图 2-12.解:x10.2( 1)如图 2-2 所示,由图解法可知有唯一解,函数值为 3.6 。
x20.6图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
word 资料.( 5)无穷多解。
x2092( 6)有唯一解3,函数值为。
183x2 33.解:( 1)标准形式maxf 3 12x2010s20s3 x s9 x12x2s1303x12x2s2132 x12x2s39x1,x2, s1,s2,s3≥0( 2)标准形式min f4x16x20 s10s23x1x2s16x1 2 x2s2107 x16x24x1, x2, s1, s2≥0( 3)标准形式min f x12x22x20 s10s23x15x25x2s1702 x15x25x2503x1 2 x2 2 x2s230x1, x2, x2, s1 , s2≥ 04.解:标准形式max z10 x15x20 s10s2word 资料.3x14x2s195 x12x2s28x1, x2, s1, s2≥0word 资料.松弛变量( 0,0)最优解为 x 1 =1,x 2=3/2 。
5.解: 标准形式min f11x 18 x 20 s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4 x 19x 2s 336x 1, x 2 , s 1 , s 2 , s 3 ≥ 0剩余变量( 0, 0, 13 )最优解为 x 1=1,x 2=5。
6.解:( 1)最优解为 x 1=3,x 2=7。
( 2) 1 c 1 3 。
( 3) 2 c 26 。
( 4)x 16。
x 24。
( 5)最优解为 x 1=8,x 2=0。
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
《管理运筹学》第四版课后习题答案
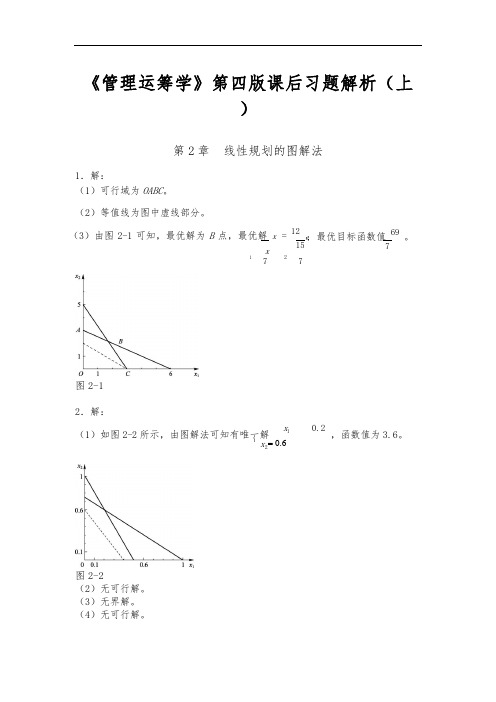
⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x=12, x15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 x 10.2,函数值为3.6。
x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
x(6)有唯一解 120 3,函数值为 92 。
8 3x2 33.解:(1)标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f4x 16x 20s 10s 23x 1x 2 s 16 x 12x 2s 210 7x 16x 2 4x 1,x 2, s 1, s 2 ≥ 0(3)标准形式min fx 12x 22x 20s 1 0s 23x 15x25x 2s 170 2x15x 25x 250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04.解: 标准形式max z10x 15x 20s 10s 23x 1 4x 2s915x1 2x 2 s2 8 x, x2 , s1, s2 ≥01≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
5.解: 标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
《管理运筹学》第四版课后习题答案
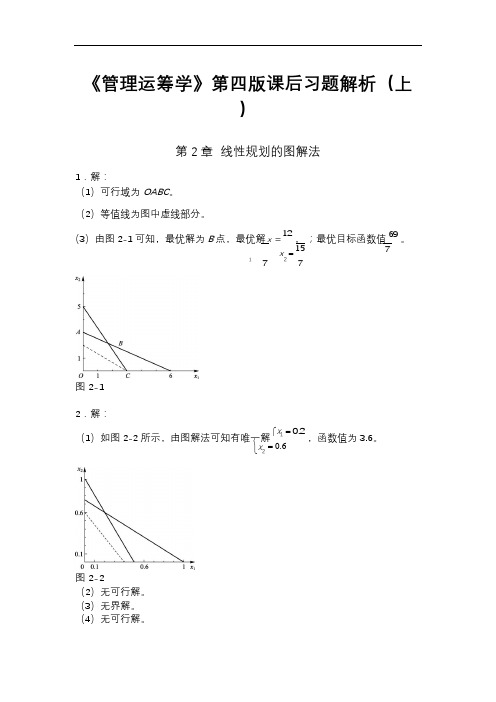
⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12 , x = 151727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解⎪1⎪203,函数值为 92 。
8 3x = ⎪⎩ 233.解:(1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 30 3x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 95x 1 + 2x 2 + s 2 = 8x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》(第二版)课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming, LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、LI标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;U标函数是决策者希望实现的LI标,为决策变量的线性函数表达式,有的LI标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现儿种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解:(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:LI标函数极大化,约束条件为等式,右端常数项^>0, 决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“事”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件AX=b, X>0的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使訂标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:基可行解5.用表格单纯形法求解如下线性规划。
max Z = 4Xj + x2+ 2x38Xj + 3X2 +x3 <26xj + x2 + 兀3 § 8 飞°解:标准化max Z = 4x t + x2 + 2x38xj + 3X2+x3 + x4 = 2< + x2 + x3 +x5 = 8故最优解为X* = (0Q2Q6V ,即M = 09x2 = 0內=2 ,此时最优值为Z(X*) = 4 •6.表1—15中给出了求极大化问题的单纯形表,问表中5<2,5心,〃为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以“代替基变量心;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》(第二版)课后习题参考答案(2020年7月整理).pdf

max Z = 2.7x1 + 3x2 + 4.5x3 + 2.5x4 + 3x5
3x1 + 4x2 + 6x3 + 2x4 + 3x5 3600
s.t.
42xx11
+ +
3x2 3x2
+ +
5x3 3x3
+ +
6x4 4x4
+ +
4x5 3x5
3950 2800
xi 0,i = 1,2,,5
通过 LINGO 软件计算得: x1 = 0, x2 = 38, x3 = 254, x4 = 0, x5 = 642, Z = 3181 .
11.某厂生产甲、乙、丙三种产品,分别经过 A,B,C 三种设备加工。已知生产
单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表 2—10 所示。
《管理运筹学》(第二版)课后习题参考答案
第 1 章 线性规划(复习思考题)
1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是 应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化 工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决 策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条 件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的 线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项 bi 0 , 决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业 来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束 的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件 AX = b,X 0 的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示: 5.用表格单纯形法求解如下线性规划。
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1. 什么是线性规划?线性规划的三要素是什么?答:线性规划(Lin ear Programmi ng , LF)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2. 求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3. 什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项 ' ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业 来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明 “遅 约束的左边取值大于右边规划值,出现剩余量。
4•试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关 系。
答:可行解:满足约束条件 扎—‘丸 的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5 •用表格单纯形法求解如下线性规划解:标准化1可行基:对应于基可行解的基,称为可行基。
基可行解SA] +S 21s.t.列出单纯形表/43/21/2[8]/83/2/6/8 1/8]5/4 /41/2/8 1/4/(1/83/4 13/2/(1/412 5故最优解为二「- 1,即—心I八,此时最优值为' 1士匚6.表1 —15中给出了求极大化问题的单纯形表,问表中1为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目标2:总产量不低于1.25万t;
目标3:小麦产量以0.5万t为宜;
目标4:大豆产量不少于0.2万t;
目标5:玉米产量不超过0.6万t;
目标6:农场现能提供5000t化肥;若不够,可在市场高价购买,但希望高价采购量愈少愈好。
试就该农场生产计划建立数学模型(各目标的重要性依次排列,目标1最重要)。
6.用x1,x2,x3分别代表I,II,III三种产品的产量,则有
(a)X*= (100/3, 200/3, 0)
(b)X*= (175/6, 275/6, 25)
(c) 6≤c1≤15
(d)4≤θ≤5
(e)该新产品值得安排生产
(f)X*= (95/3, 175/3, 10)
7.(a)用矿石M1为10t,M2为225t,总费用为1.14万元;
1< C1<2
C1=2
2< C1<
A点
AB线段
B点
BC线段
C点
3.某饲养场需饲养动物,设每头动物每天至少需700g蛋白质、30g矿物质、100mg维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表1-8所示。
表1-8
饲料
蛋白质/g
矿物质/g
维生素/mg
价格/元/kg
1
2
3
4
5
3
2
1
6
(c) minz=x1+x2(d) minz=3x12x2
(e) minz=3x1+9x2
2. (a)唯一最优解,z* =3,x1=1/2,x2=0;(b)无可行解;(c)有可行解,但max z无界;(d)无可行解;(c)无穷多最优解,z*=66;(f)唯一最优解,z*=
C1值
最优解
<C1<1
C1=1
12.埋设电缆的最优方案为总长6200m,故工程费用预算为6200(10+0.6×3+5)=104160元。
13.设
其数学模型为
14. a.如果x2=0,则x1=2。如果x1=0,则x2=4。
c.斜率= -2
d.x2=-2 x1+4
15. a.最优解:(x1,x2)=(2, 4),C=130
bc.
最优解X*=(6,2)Z*=130
18
1
0.5
0.2
2
0.5
0.5
1.0
0.2
2
0.8
0.2
0.7
0.4
0.3
0.8
要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
4.
(a)max=3y15y2+2y3
(b)max=15y1+20y25y3
(c)min=10y1-5y2+8y3
(d)max=y1+5y2
(e)max=y1+y2+y3
5.试述目标规划的数学模型同一般线性规划数学模型的相同和异同之点。
(答案参考教材)
二、判断题
1. (√)
2. (√)
3. (×)
4. (√)
5. (√)
三、计算题
1.用图解法求解下列线性规划问题,并指出各问题是具有唯一最优解、无穷多最优解、无界解或无可行解。
(a) minz=6x1+4x2(b) minz=4x1+8x2
5. (a)以x1,x2,x3分别代表甲、乙、丙产品产量,则有X*= (5, 0, 3),最大盈利z*=35
(b)产品甲的利润变化范围为[3,6]
(c)安排生产丁有利,新最优计划为安排生产产品丁15件,而x1=x2=x3=0
(d)购进原材料B15单位为宜s
(e)新计划为X*=(0, 0, 6),z*=30
表3-23
甲
乙
丙
A
B
15
21
18
25
22
16
11.友谊农场有3万亩(每亩等于666.66平方米)农田,欲种植玉米、大豆和小麦三种农作物。各种作物每亩需施化肥分别为0.12、0.20、0.15t。预计秋后玉米每亩收获500kg,售价为0.24元/kg,大豆每亩可收获200kg,售价为1.20元/kg,小麦每亩可收获300kg,售价为0.70元/kg。农场年初规划时考虑如下几个方面:
16. ac.
最优解X*=(3.33,3.33)Z*=133.33
17.a.所需要进行的决策是每一种产品应当生产多少。决策的约束条件是碾磨机、车床和磨工的可用时数以及产品3的潜在销量。总的绩效测度是利润,利润必须最大化。
(b)最优决策变为用矿石M1为142.8t,矿石M2为85.7t,总费用为1.13万元。
8.化肥的最佳调运方案见表3A-2:
表3A-2
甲
乙
丙
丁
供应量
A
B
C
5
4
2
0
3
3
7
8
3
需求量
6
6
3
3
9.增加一个假想需求部门丁,最优调拨方案见表3A-3,表中将A调拨给丁500件,表明玩具A有500件销不出去。
表3A-3
表3-22
B1
B2
B3
B4
B5
A1
A2
A3
10
20
30
15
40
35
20
15
40
20
30
55
40
30
25
试确定一个使总费用最低的调运方案。
3.18仓库总容量为300t,各地区需要量总计290t。仓库有30t装不满,各地区有20t需要不能满足。可虚设一库容20t的仓库A,来满足需要,相应虚设一地区B6来虚购仓库中未装进的30t糖。由此列出产销平衡表与单位运价见表3A-14。
《管理运筹学》作业题参考答案
一、简答题
1.试述线性规划数学模型的结构及各要素的特征。
2.求解线性规划问题时可能出现哪几种结果,哪些结果反映建模时有错误。
3.举例说明生产和生活中应用线性规划的方面,并对如何应用进行必要描述。
4.什么是资源的影子价格,同相应的市场价格之间有何区别,以及研究影子价格的意义。
甲
乙丙Biblioteka 丁可供量A
B
C
1500
500
500
500
1500
500
1000
2000
2000
销售量
1500
1500
1500
500
3.18.某糖厂每月最多生产糖270t,先运至A1,A2,A3三个仓库,然后再分别供应B1,B2,B3,B4,B5五个地区需要。已知各仓库容量分别为50,100,150(t),各地区的需要量分别为25,105,60,30,70(t)。已知从糖厂经由各仓库然后供应各地区的运费和储存费如表3-2所示。
表3A-14
B1
B2
B3
B4
B5
B6
供应
A1
A2
A3
A4
10
20
30
0
15
40
35
0
20
15
40
0
20
30
55
0
40
30
25
0
0
0
0
50
100
150
20
需求
25
105
60
30
70
30
10.有甲、乙、丙三个城市,每年分别需要煤炭320,250,350(万t),由A,B两个煤炭负责供应。已知煤矿年产量A为400万t,B为450万t,从两煤矿至各城市煤炭运价(元/t)如表3-23所示。由于需求大于产量,经协商平均,甲城市必要时可少供0 ~ 30万t,乙城市需求量须全部满足,丙城市需求量不少于270万t.。试求将甲、乙两矿煤炭全部分配出去,满足上述条件又使总运费为最低的调运方案。
