遗传算法作业
遗传算法(大作业)
遗传算法求最大值(大作业)09电子(2)班 郑周皓 E09610208 题目:函数]20)5()5(exp[999.0)10)5()5(exp(9.0),(22222-+--*++++*=y x y x y x f (x,y 在-10到10之间),利用遗传算法求函数的最大值及对应的位置。
要求: 种群数N=50,交叉位数n/2,即个体位数的一半,且位置自行设计,变异位数自定,x,y 分辨率为0.0001。
效果比较:交叉个数=20,28,36,44变异个数=1,5,10,15解:问题分析:对于本问题,只要能在区间[-10,,10]中找到函数值最大的点a,b,则函数f(x,y)的最大值也就可以求得。
于是,原问题转化为在区间[-10, 10]中寻找能使f(x,y)取最大值的点的问题。
显然, 对于这个问题, 任一点x ,y ∈[-10, 10]都是可能解, 而函数值f (x )= sinx/x 也就是衡量x 能否为最佳解的一种测度。
那么,用遗传算法的眼光来看, 区间[-10, 10]就是一个(解)空间,x 就是其中的个体对象, 函数值f (x )恰好就可以作为x 的适应度。
这样, 只要能给出个体x 的适当染色体编码, 该问题就可以用遗传算法来解决。
自变量x,y 可以抽象为个体的基因组,即用二进制编码表示x,y;函数值f(x,y)可以抽象为个体的适应度,函数值越小,适应度越高。
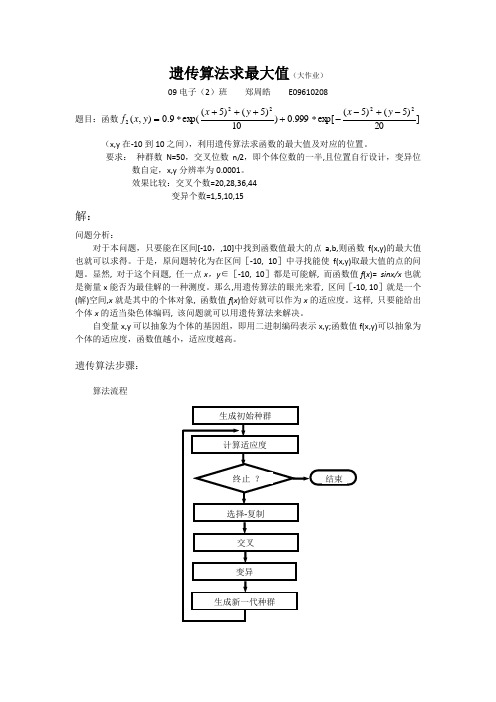
遗传算法步骤:算法流程第1步在论域空间U上定义一个适应度函数f(x),给定种群规模N,交叉率P c和变异率P m,代数T;取适度函数为f(x)=sinx/x,种群规模N=50,用popsize表示。
x,y的精度为0.0001 .交叉率(crossover rate):参加交叉运算的染色体个数占全体染色体总数的比例,记为Pc,取值范围一般为0.4~0.99,根据要求本例中选为20/50、28/50、36/50、44/50。
变异率(mutation rate):发生变异的基因位数所占全体染色体的基因总位数的比例,记为Pm,取值范围一般为0.0001~0.1,根据要求本例中选为1/50、5/50、10/50、15/50。
数学建模遗传算法例题

数学建模遗传算法例题数学建模中,遗传算法是一种基于进化思想的优化算法,可以应用于复杂的优化问题中。
本文将介绍一些遗传算法的例题,帮助读者更好地理解遗传算法的应用。
例题一:背包问题有一个体积为V的背包和n个物品,第i个物品的体积为vi,价值为wi。
求这个背包最多能装多少价值的物品。
遗传算法的解决步骤:1. 初始化种群:随机生成一定数量的个体作为初始种群。
2. 适应度函数:将每个个体代入适应度函数,计算其适应度值。
3. 选择:根据每个个体的适应度值,选择一定数量的个体进入下一代。
4. 交叉:对被选中的个体进行交叉操作,生成新的个体。
5. 变异:对新的个体进行变异操作,引入新的基因。
6. 重复以上步骤,直到符合终止条件。
在背包问题中,适应度函数可以定义为:背包中物品的总价值。
交叉操作可以选择单点交叉或多点交叉,变异操作可以选择随机变异或非随机变异。
例题二:旅行商问题有n个城市,旅行商需要依次经过这些城市,每个城市之间的距离已知。
求旅行商经过所有城市的最短路径。
遗传算法的解决步骤:1. 初始化种群:随机生成一定数量的个体作为初始种群,每个个体代表一种旅行路线。
2. 适应度函数:将每个个体代入适应度函数,计算其适应度值。
3. 选择:根据每个个体的适应度值,选择一定数量的个体进入下一代。
4. 交叉:对被选中的个体进行交叉操作,生成新的个体。
5. 变异:对新的个体进行变异操作,引入新的基因。
6. 重复以上步骤,直到符合终止条件。
在旅行商问题中,适应度函数可以定义为:旅行商经过所有城市的总距离。
交叉操作可以选择顺序交叉或部分映射交叉,变异操作可以选择交换或反转基因序列。
总结:遗传算法是一种强大的优化算法,可以应用于多种复杂的优化问题中。
在数学建模中,遗传算法的应用也越来越广泛。
本文介绍了背包问题和旅行商问题的遗传算法解决步骤,希望对读者有所帮助。
遗传算法 例题 详解

遗传算法例题详解遗传算法是一种模拟自然选择和遗传机制的优化方法,它模拟了生物进化的过程,通过模拟种群的遗传变异和适应度选择,寻找最优解。
下面我们以一个简单的例题来详细解释遗传算法的原理和应用。
假设我们要解决一个简单的优化问题,找到函数 f(x) = x^23x + 4 的最小值,其中 x 的取值范围在 [0, 5] 之间。
首先,我们需要定义遗传算法的基本要素:1. 个体表示,在这个例子中,个体可以用一个实数来表示,即x 的取值。
2. 适应度函数,即要优化的目标函数,对于这个例子就是 f(x) = x^2 3x + 4。
3. 遗传操作,包括选择、交叉和变异。
接下来,我们用遗传算法来解决这个优化问题:1. 初始化种群,随机生成一定数量的个体作为初始种群。
2. 评估适应度,计算每个个体的适应度,即计算函数 f(x) 的值。
3. 选择操作,根据个体的适应度来选择父代个体,适应度越高的个体被选中的概率越大。
4. 交叉操作,对选中的父代个体进行交叉操作,生成新的个体。
5. 变异操作,对新生成的个体进行变异操作,引入一定的随机性。
6. 重复步骤2-5,直到满足停止条件(如达到迭代次数或找到满意的解)。
通过不断地迭代选择、交叉和变异操作,种群中的个体将不断进化,最终找到函数的最小值对应的 x 值。
在上述例题中,遗传算法通过模拟自然选择和遗传机制,不断优化种群中个体的适应度,最终找到了函数 f(x) = x^2 3x + 4 的最小值对应的 x 值。
这个例子展示了遗传算法在优化问题中的应用,它能够有效地搜索解空间,找到全局最优解或者接近最优解的解。
遗传算法在实际应用中有着广泛的应用,如工程优化、机器学习、数据挖掘等领域。
遗传算法求解优化问题实例

遗传算法求解优化问题实例
一个常见的优化问题是旅行商问题(Traveling Salesman Problem,TSP)。
给定一组城市和每对城市之间的距离,旅行商问题要求找到一条经过所有城市一次且回到起点的最短路径。
以下是使用遗传算法求解TSP的实例:
1. 随机生成一个初始种群,种群中的每个个体表示一条路径。
每个个体由一个城市序列表示,例如[1, 2, 3, ..., n],其中n是城市的数量。
2. 计算种群中每个个体的适应度。
适应度可以定义为路径的总长度,即经过所有城市的距离之和。
3. 选择适应度较高的个体作为父代,进行交叉和变异操作以生成新的子代。
交叉操作可以是将两条路径的一部分交换,变异操作可以是随机改变路径中的一个或多个城市顺序。
4. 计算新生成的子代的适应度。
5. 重复步骤3和4,直到达到终止条件(例如达到最大迭代次数)。
6. 返回适应度最好的个体作为最优解,即最短路径。
遗传算法的优势在于可以在大规模问题中寻找较好的解,虽然不一定能找到最佳解,但可以得到相对较优的解。
基于改进的遗传算法在车间作业调度中的应用与研究

择 ” 可 以 保 证 精 英 个 体 遗 传 到 下 一 代 。 然 后 重 复 上述 操
结 构 和 交 叉 变 异 方 面 ,本 文 设 计 了一 种 新 的 选 择 和 交 叉 变 异算 子对 算 法 进 行 改 进 。
2表 示 T 件 ,3表 示 T 件 。 因 为 每 个 l 有 3道 工 序 , 丁件 所 以 ,每 个 工 件 在 一 个 染 色 体 中 刚 好 出 现 3次 。染 色 体 上 第 一 个 2表 示 T 件 2的 第 一 个 T 序 ,对 照 机 器 约 束 .该 _ 『 二 序 在 机 器 m。 加 T , 工件 2的 第 二 个 工 序 在 机 器 上 加 上 工 , 以 此 类 推 ,工 件 2的 第 三 个 工 序 在 机 器 m 上 加 工 . , 因 此 ,在基 于工 序 的 编码 方 法 下 ,每 个 个 体 都 对 应 问题 的
作 ,直 到新 种 群 的个 数 等 于 父 代 种 群 的 个 数 。选 择 操 作 流
程 如 1所 示 、
31编 码 方 法 .
编 码 是 问 题 解 的遗 传 基 因 表 示 ,也 就 是 把 一 个 问 题 的
可行 解 从 其 解 空 间转 化 到遗 传 算 法 所 能 处 理 的 搜 索 空 间 的 转 换 。它 是 应 用 遗 传 算 法 时要 解 决 的 首 要 问 题 ,也 是 应 用 成 功 与否 的关 键 步 骤 , 鉴 于 车 间 调 度 问题 的 约 束 性 ,编 码 技 术 必 须 考 虑 其 合 法 性 和 可 行 性 。 本 文 采 用 的 是 MI S O TU G n等 人 提 出 的基 于 1 序 的 编 码 方 法 ,染 色 体 是 由 昕 有 T e 一 件 的_ 排 序 组 成 的 .它 具 有 解 码 和 置 换 染 色 体 后 总 能 得 丁序
03第三章 遗传算法

第三章遗传算法习题与答案1.填空题(1)遗传算法的缩写是,它模拟了自然界中过程而提出,可以解决问题。
在遗传算法中,主要的步骤是、、。
(2)遗传算法的三个算子是、、。
解释:本题考查遗传算法的基础知识。
具体内容请参考课堂视频“第3章遗传算法”及其课件。
答案:(1)GA,生物进化,全局优化,编码,计算适应度函数,遗传算子(2)选择,交叉,变异2.对于编码长度为7的二进制编码,判断以下编码的合法性。
(1)[1020110](2)[1011001](3)[0110010](4)[0000000](5)[2134576]解释:本题考查遗传算法的二进制编码的合法性。
具体内容请参考课堂视频“第3章遗传算法”及其课件。
答案:(1)[1020110]不合法,不能出现“2”(2)[1011001]合法(3)[0110010]合法(4)[0000000]合法(5)[2134576]不合法,不能出现0、1以外的数字3.下图能够基本反映生物学遗传与优胜劣汰的过程。
理解该图,联想计算类问题求解,回答下列问题。
(1)下列说法正确的是_____。
(多选)A)任何一个生物个体的性状是由其染色体确定的,染色体是由基因及其有规律的排列所构成的,因此生物个体可由染色体来代表。
B)生物的繁殖过程是通过将父代染色体的基因复制到子代染色体中完成的,在复制过程中会发生基因重组或基因突变。
基因重组是指同源的两个染色体之间基因的交叉组合,简称为“杂交/交配”。
基因突变是指复制过程中基因信息的变异,简称“突变”。
C)不同染色体会产生不同生物个体的性状,其适应环境的能力也不同。
D)自然界体现的是“优胜劣汰,适者生存”的丛林法则。
不适应环境的生物个体将被淘汰,自然界生物的生存能力会越来越强。
解释:本题考核对生物遗传观点以及所给图片的理解。
具体内容请参考课堂视频“第3章遗传算法”及其课件。
答案:A、B、C、D关于生物遗传进化的基本观点如下:(1)生物的所有遗传信息都包含在其染色体中,染色体决定了生物的性状。
数学建模遗传算法例题

数学建模遗传算法例题数学建模是一种重要的实践活动,通过运用数学工具和方法对实际问题进行建模和求解。
而遗传算法则是一种基于生物进化原理的优化算法,能够通过模拟自然选择、交叉和变异等过程来搜索全局最优解。
在数学建模中,遗传算法也是一种常用的求解工具。
下面以一个简单的例题来介绍遗传算法在数学建模中的应用。
假设有一个机器人需要从起点出发沿着一条直线路径到达终点,并且需要尽量减少行驶路程。
此外,机器人有两种可选的行驶策略:一种是直行,另一种是先左转再右转。
由于机器人的行驶方向只能是水平或竖直,因此左转和右转的方向只有两种。
问题:如何确定机器人应该采用哪种行驶策略,并如何规划其行驶路径?解决此问题的一种方法是使用遗传算法。
具体步骤如下:1. 定义遗传算法的编码和解码方式因为机器人只有两种行驶策略,因此可以用一个二进制字符串来表示机器人的行驶方案。
例如,'01'表示机器人先左转再右转,“10”表示机器人直行。
因此,一个长度为N的二进制字符串可以代表机器人在N个路口的行驶方案。
2. 定义适应度函数适应度函数用于评估染色体的优劣程度。
在此例中,适应度函数应为机器人到达终点的路程长度。
因此,需要计算出每个染色体对应的机器人行驶方案下的总路程长度作为其适应度值。
3. 初始化种群初始化一个大小为M的随机种群,每个染色体为长度为N的二进制字符串。
4. 选择操作选择操作是指通过适应度函数对染色体进行选择,保留适应度较高的染色体,淘汰适应度较低的染色体。
在此例中,可以采用轮盘赌选择算法对染色体进行选择。
5. 交叉操作交叉操作是指将两个染色体的部分基因进行交换,产生新的后代染色体。
在此例中,可以采用单点交叉算法,即随机选择一个位置将两个染色体划分成两部分,然后交换这两部分,从而产生新的后代染色体。
6. 变异操作变异操作是指随机改变染色体中的一个基因,从而产生一个新的染色体。
在此例中,可以选择随机选择一个基因位置,将其取反,从而产生一个新的染色体。
遗传算法在车间作业调度上的应用

C ia hn ) A sr c:B sdo h te t a mo e o bs o c euigs se ti p p rdsu sstegn t bta t ae ntema ma cl dl f o h p sh d l y tm, hs a e模型的基础上以遗传算法为优化工具对问题进行求解着重介绍了生成可行调度的算法和对遗传算法的改进同时选择典型的jobshop调度问题ft06作为算法的试验对象最后分别给出了基本遗传算法和改进后的遗传算法的测试结果测试结果表明基本遗传算法在求解jobshop调度问题ft06时通常只能找到次优解而改进后的遗传算法在求解该问题时基本能找到最优解
so c eui rbe F 0 ) u ti GA ip o e n a s ay f dteb s rsl o i shd l g h p sh d l gp o l n m(T 6, t hs m rvme t nuu l i h et eut ft s ceui b c l n h n p o l I a oso ht h a ai f eov g o h p shd l g rbe e c n ,n l rbe t l h ws a te p c y o i rsli bso ceui o l i d f i ta dt l m. s t c t GA n nj n p ms s i e es ta ti G rvmet sfail a dmuhb t r h eov g o h p sh d l gpo l s S ht hs A i o e n es e n c et a GA i rsli bso ce ui rb m . o mp i b e tn n n j n e teftr i ci f p l gGA meh dt eo e o h p shd l gpo l sG p o e n. h ued et no pi to ors l bs o ceui rbe i A i rv met u r o a n vj n ms m
南京航空航天大学遗传算法大作业

end
end
end
popm_sel=popm_sel(1:nn,:);
[len_m len_index]=min(len_1);
popm_sel=[popm_sel;popm(len_index,:)];
nnper=randperm(nn);
A=popm_sel(nnper(1),:);
若所建的数学模型有显函数形式,需绘出该函数图像;要求尽可能发挥自己的想像力和创造力,提出新问题、新解法,若问题过于复杂,无法写出目标函数求解过程中的一些中间量,可略去其过程,论述清楚你所选择的其它辅助软件或工具的功能及其与智能算法程序的连接思想或方法即可;具体要求在大作业中有问题描述和理论分析、图像或曲线、结果输出、程序源代码等,并提交电子版,任何人的程序不得重复,否则按不及格论处!!!
for i=1:nn*Pc
[A,B]=cross(A,B);
popm_sel(nnper(1),:)=A;
popm_sel(nnper(2),:)=B;
end
for i=1:nn
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
figure(2);
plot_route(pos,R);
axis([-3 3 -3 3]);
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);
人工智能结课作业-遗传算法粒子群寻优蚁群算法解决TSP问题

⼈⼯智能结课作业-遗传算法粒⼦群寻优蚁群算法解决TSP问题代码已经发布到了github:如果帮到你了,希望给个star⿎励⼀下1 遗传算法1.1算法介绍遗传算法是模仿⾃然界⽣物进化机制发展起来的随机全局搜索和优化⽅法,它借鉴了达尔⽂的进化论和孟德尔的遗传学说。
其本质是⼀种⾼效、并⾏、全局搜索的⽅法,它能在搜索过程中⾃动获取和积累有关搜索空间的知识,并⾃适应的控制搜索过程以求得最优解。
遗传算法操作使⽤适者⽣存的原则,在潜在的解决⽅案种群中逐次产⽣⼀个近似最优解的⽅案,在遗传算法的每⼀代中,根据个体在问题域中的适应度值和从⾃然遗传学中借鉴来的再造⽅法进⾏个体选择,产⽣⼀个新的近似解。
这个过程导致种群中个体的进化,得到的新个体⽐原来个体更能适应环境,就像⾃然界中的改造⼀样。
遗传算法具体步骤:(1)初始化:设置进化代数计数器t=0、设置最⼤进化代数T、交叉概率、变异概率、随机⽣成M个个体作为初始种群P(2)个体评价:计算种群P中各个个体的适应度(3)选择运算:将选择算⼦作⽤于群体。
以个体适应度为基础,选择最优个体直接遗传到下⼀代或通过配对交叉产⽣新的个体再遗传到下⼀代(4)交叉运算:在交叉概率的控制下,对群体中的个体两两进⾏交叉(5)变异运算:在变异概率的控制下,对群体中的个体进⾏变异,即对某⼀个体的基因进⾏随机调整(6)经过选择、交叉、变异运算之后得到下⼀代群体P1。
重复以上(1)-(6),直到遗传代数为 T,以进化过程中所得到的具有最优适应度个体作为最优解输出,终⽌计算。
旅⾏推销员问题(Travelling Salesman Problem, TSP):有n个城市,⼀个推销员要从其中某⼀个城市出发,唯⼀⾛遍所有的城市,再回到他出发的城市,求最短的路线。
应⽤遗传算法求解TSP问题时需要进⾏⼀些约定,基因是⼀组城市序列,适应度是按照这个基因的城市顺序的距离和分之⼀。
1.2实验代码import randomimport mathimport matplotlib.pyplot as plt#读取数据f=open("test.txt")data=f.readlines()#将cities初始化为字典,防⽌下⾯被当成列表cities={}for line in data:#原始数据以\n换⾏,将其替换掉line=line.replace("\n","")#最后⼀⾏以EOF为标志,如果读到就证明读完了,退出循环if(line=="EOF"):break#空格分割城市编号和城市的坐标city=line.split("")map(int,city)#将城市数据添加到cities中cities[eval(city[0])]=[eval(city[1]),eval(city[2])]#计算适应度,也就是距离分之⼀,这⾥⽤伪欧⽒距离def calcfit(gene):sum=0#最后要回到初始城市所以从-1,也就是最后⼀个城市绕⼀圈到最后⼀个城市for i in range(-1,len(gene)-1):nowcity=gene[i]nextcity=gene[i+1]nowloc=cities[nowcity]nextloc=cities[nextcity]sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)return 1/sum#每个个体的类,⽅便根据基因计算适应度class Person:def__init__(self,gene):self.gene=geneself.fit=calcfit(gene)class Group:def__init__(self):self.GroupSize=100 #种群规模self.GeneSize=48 #基因数量,也就是城市数量self.initGroup()self.upDate()#初始化种群,随机⽣成若⼲个体def initGroup(self):self.group=[]i=0while(i<self.GroupSize):i+=1#gene如果在for以外⽣成只会shuffle⼀次gene=[i+1 for i in range(self.GeneSize)]random.shuffle(gene)tmpPerson=Person(gene)self.group.append(tmpPerson)#获取种群中适应度最⾼的个体def getBest(self):bestFit=self.group[0].fitbest=self.group[0]for person in self.group:if(person.fit>bestFit):bestFit=person.fitbest=personreturn best#计算种群中所有个体的平均距离def getAvg(self):sum=0for p in self.group:sum+=1/p.fitreturn sum/len(self.group)#根据适应度,使⽤轮盘赌返回⼀个个体,⽤于遗传交叉def getOne(self):#section的简称,区间sec=[0]sumsec=0for person in self.group:sumsec+=person.fitsec.append(sumsec)p=random.random()*sumsecfor i in range(len(sec)):if(p>sec[i] and p<sec[i+1]):#这⾥注意区间是⽐个体多⼀个0的return self.group[i]#更新种群相关信息def upDate(self):self.best=self.getBest()#遗传算法的类,定义了遗传、交叉、变异等操作class GA:def__init__(self):self.group=Group()self.pCross=0.35 #交叉率self.pChange=0.1 #变异率self.Gen=1 #代数#变异操作def change(self,gene):#把列表随机的⼀段取出然后再随机插⼊某个位置#length是取出基因的长度,postake是取出的位置,posins是插⼊的位置geneLenght=len(gene)index1 = random.randint(0, geneLenght - 1)index2 = random.randint(0, geneLenght - 1)newGene = gene[:] # 产⽣⼀个新的基因序列,以免变异的时候影响⽗种群 newGene[index1], newGene[index2] = newGene[index2], newGene[index1] return newGene#交叉操作def cross(self,p1,p2):geneLenght=len(p1.gene)index1 = random.randint(0, geneLenght - 1)index2 = random.randint(index1, geneLenght - 1)tempGene = p2.gene[index1:index2] # 交叉的基因⽚段newGene = []p1len = 0for g in p1.gene:if p1len == index1:newGene.extend(tempGene) # 插⼊基因⽚段p1len += 1if g not in tempGene:newGene.append(g)p1len += 1return newGene#获取下⼀代def nextGen(self):self.Gen+=1#nextGen代表下⼀代的所有基因nextGen=[]#将最优秀的基因直接传递给下⼀代nextGen.append(self.group.getBest().gene[:])while(len(nextGen)<self.group.GroupSize):pChange=random.random()pCross=random.random()p1=self.group.getOne()if(pCross<self.pCross):p2=self.group.getOne()newGene=self.cross(p1,p2)else:newGene=p1.gene[:]if(pChange<self.pChange):newGene=self.change(newGene)nextGen.append(newGene)self.group.group=[]for gene in nextGen:self.group.group.append(Person(gene))self.group.upDate()#打印当前种群的最优个体信息def showBest(self):print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg())) #n代表代数,遗传算法的⼊⼝def run(self,n):Gen=[] #代数dist=[] #每⼀代的最优距离avgDist=[] #每⼀代的平均距离#上⾯三个列表是为了画图i=1while(i<n):self.nextGen()self.showBest()i+=1Gen.append(i)dist.append(1/self.group.getBest().fit)avgDist.append(self.group.getAvg())#绘制进化曲线plt.plot(Gen,dist,'-r')plt.plot(Gen,avgDist,'-b')plt.show()ga=GA()ga.run(3000)print("进⾏3000代后最优解:",1/ga.group.getBest().fit)1.3实验结果下图是进⾏⼀次实验的结果截图,求出的最优解是11271为避免实验的偶然性,进⾏10次重复实验,并求平均值,结果如下。
智能计算作业 遗传算法

clc clear all close all %%画出函数图 figure(1); hold on ; lb=1;ub=2;%函数自变量范围
ezplot('sin(10*pi*X)/X',[lb,ub]);%画出函数曲线 xlabel('自变量/X') ylabel('函数值/Y') %%定义遗传算法参数 NIND=40;%种群大小 MAXGEN=20;%最大遗传代数 PRECI=20;%个体长度 GGAP=0.95;%代沟 px=0.7;%交叉概率 pm=0.01;%变异概率 trace=zeros(2,MAXGEN);%寻优结果的初始值 FieldD=[PRECI;lb;ub;1;0;1;1];%区域描述器 Chrom=crtbp(NIND,PRECI);%创建任意离散随机种群 %%优化 gen=0;%代计数器 X=bs2rv(Chrom,FieldD);%初始种群二进制到十进制转换 ObjV=sin(10*pi*X)./X;%计算目标函数值 while gen<MAXGEN FitnV=ranking(ObjV);%分配适应度 SelCh=select('sus',Chrom,FitnV,GGAP);%选择 SelCh=recombin('xovsp',SelCh,px);%重组 SelCh=mut(SelCh,FieldD);%变异 X=bs2rv(SelCh,FieldD);%子代个体的目标函数值 ObjVSel=sin(10*pi*X)./X;%计算子代的目标函数值 [Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel);%重插入子代到父代,得到新种群 X=bs2rv(Chrom,FieldD); gen=gen+1; %代数器增加
数学建模遗传算法例题

数学建模遗传算法例题数学建模是指通过数学模型来解决现实世界中的问题。
而遗传算法是一种基于演化论的优化方法,通过模拟自然界中的生物遗传进化过程来求解问题。
在数学建模中,遗传算法常常被用来寻找最优解或者优化模型参数。
下面是一个数学建模中使用遗传算法的例题:某公司要在一条河流上建造一座桥,河流宽度为W,建造桥的费用为C,桥的长度为L,桥的最大承重能力为P,桥的强度与长度成正比,与费用成反比,与承重能力成正比。
求出桥的最佳长度和费用。
解题思路:1. 建立数学模型:设桥的长度为x,费用为y,则桥的强度为k(x,y),承重能力为p(x,y)。
由题可知,强度与长度成正比,与费用成反比,与承重能力成正比,即:k(x,y) = k1*x/k2*yp(x,y) = p1*x/p2*y其中k1、k2、p1、p2为常数。
2. 确定适应度函数:适应度函数是遗传算法中非常重要的一部分,它用来评价染色体的优劣。
在本题中,适应度函数可以定义为:f(x,y) = 1/k(x,y) * p(x,y) / C其中,C为建造桥的费用。
3. 设计遗传算法流程:(1) 初始化种群:随机生成一批长度和费用的染色体,并计算其适应度。
(2) 选择操作:根据适应度函数选择优秀个体,并进行交叉和变异操作,得到新一代染色体群体。
(3) 计算适应度:计算新一代染色体的适应度。
(4) 终止条件:当符合一定的停止条件时,停止运行遗传算法。
(5) 输出结果:输出最优解。
4. 编写代码:在实际运用中,可以使用Python语言来实现遗传算法,并求解出桥的最佳长度和费用。
代码如下:import randomW = 100 #河流宽度C = 100000 #建造桥的费用k1, k2, p1, p2 = 1, 1, 1, 1 #常数#初始化种群def init_population(population_size):population = []for i in range(population_size):x = random.randint(1, W)y = random.randint(1, C)population.append((x,y))return population#计算适应度def fitness(x, y):k = k1 * x / k2 * yp = p1 * x / p2 * yreturn 1 / k * p / C#选择操作def selection(population, elite_size):population_fitness = [(x, y, fitness(x, y)) for x, y in population]population_fitness_sorted = sorted(population_fitness, key=lambda x: x[2], reverse=True)elite = population_fitness_sorted[:elite_size]return elite#交叉操作def crossover(parents):parent1, parent2 = parentschild1 = (parent1[0], parent2[1])child2 = (parent2[0], parent1[1])return [child1, child2]#变异操作def mutation(individual, gene_pool):gene = random.randint(0, 1)if gene == 0:x = random.choice(gene_pool)individual = (x, individual[1])else:y = random.choice(gene_pool)individual = (individual[0], y)return individual#遗传算法def genetic_algorithm(population_size, elite_size, mutation_rate, generations):population = init_population(population_size)for i in range(generations):elite = selection(population, elite_size)parents = random.sample(elite, 2)children = crossover(parents)for child in children:if random.uniform(0, 1) < mutation_rate:child = mutation(child, range(1, W+1))population.append(child)population = random.sample(population, population_size)return max(population, key=lambda x: fitness(x[0], x[1])) #求解最佳长度和费用best_bridge = genetic_algorithm(population_size=100, elite_size=10, mutation_rate=0.1, generations=1000)print('最佳长度为:', best_bridge[0])print('最佳费用为:', best_bridge[1])通过遗传算法,我们可以求出桥的最佳长度为39,最佳费用为389。
作业车间调度遗传算法python

作业车间调度是优化生产效率和资源利用的重要工作。
在实际工厂生产中,作业车间的调度问题往往十分复杂,需要考虑多个因素和约束条件。
为了解决这一问题,许多研究者提出了多种优化算法,其中遗传算法是一种常用且有效的方法之一。
一、遗传算法概述遗传算法是一种模拟自然选择和遗传机制的优化算法,其核心思想是通过模拟自然界的进化过程,利用交叉、变异、选择等操作不断迭代,最终找到最优解。
遗传算法广泛应用于组合优化、函数优化、机器学习等领域,其灵活性和高效性受到了广泛认可。
二、遗传算法在作业车间调度中的应用1.问题建模作业车间调度问题可以理解为将一组作业分配到多台设备上,并确定它们的顺序和时间安排,以最大化生产效率和资源利用率。
这一问题的复杂性体现在多个方面,例如设备之间的关系、作业的执行时间、优先级约束等。
2.遗传算法解决方案遗传算法作为一种全局搜索算法,能够有效地处理作业车间调度问题中的复杂约束条件和多目标优化。
通过编码、交叉、变异和选择等操作,遗传算法可以逐步优化作业的调度方案,找到最优解或较优解。
三、基于Python的作业车间调度遗传算法实现基于Python语言的遗传算法库有许多,例如DEAP、Pyevolve、GAlib等。
这些库提供了丰富的遗传算法工具和接口,使得作业车间调度问题的求解变得简单且高效。
1.问题建模针对具体的作业车间调度问题,首先需要将问题进行合理的数学建模,包括作业集合、设备集合、作业执行时间、约束条件等。
然后根据问题的具体性质选择适当的遗传算法编码方式和适应度函数。
2.遗传算法实现利用Python的遗传算法库进行实现,首先需要定义遗传算法的相关参数,如种裙大小、迭代次数、交叉概率、变异概率等。
然后通过编码、交叉、变异和选择等操作,逐步优化作业的调度方案,直至达到收敛或达到一定迭代次数。
3.结果评估与分析得到最终的调度方案后,需要对结果进行评估和分析。
可以比较遗传算法得到的调度方案与其他常规方法的效果,如贪婪算法、模拟退火算法等。
python实现遗传算法求函数最大值(人工智能作业)

python实现遗传算法求函数最⼤值(⼈⼯智能作业)题⽬:⽤遗传算法求函数f(a,b)=2a x sin(8PI x b) + b x cos(13PI x a)最⼤值,a:[-3,7],b:[-4:10]实现步骤:初始化种群计算种群中每个个体的适应值淘汰部分个体(这⾥是求最⼤值,f值存在正值,所以淘汰所有负值)轮盘算法对种群进⾏选择进⾏交配、变异,交叉点、变异点随机分析:为了⽅便,先将⾃变量范围调整为[0,10]、[0,14]有两个变量,种群中每个个体⽤⼀个列表表⽰,两个列表项,每项是⼀个⼆进制字符串(分别由a、b转化⽽来)种群之间交配时需要确定交叉点,先将个体染⾊体中的两个⼆进制字符串拼接,再确定⼀个随机数作为交叉点为了程序的数据每⼀步都⽐较清晰正确,我在select、crossover、mutation之后分别都进⾏了⼀次适应值的重新计算具体代码:import mathimport randomdef sum(list):total = 0.0for line in list:total += linereturn totaldef rand(a, b):number = random.uniform(a,b)return math.floor(number*100)/100PI = math.pidef fitness(x1,x2):return 2*(x1-3)*math.sin(8*PI*x2)+(x2-4)*math.cos(13*PI*x1)def todecimal(str):parta = str[0:4]partb = str[4:]numerical = int(parta,2)partb = partb[::-1]for i in range(len(partb)):numerical += int(partb[i])*math.pow(0.5,(i+1))return numericaldef tobinarystring(numerical):numa = math.floor(numerical)numb = numerical - numabina = bin(numa)bina = bina[2:]result = "0"*(4-len(bina))result += binafor i in range(7):numb *= 2result += str(math.floor(numb))numb = numb - math.floor(numb)return resultclass Population:def __init__(self):self.pop_size = 500 # 设定种群个体数为500self.population = [[]] # 种群个体的⼆进制字符串集合,每个个体的字符串由⼀个列表组成[x1,x2]self.individual_fitness = [] # 种群个体的适应度集合self.chrom_length = 22 # ⼀个染⾊体22位self.results = [[]] # 记录每⼀代最优个体,是⼀个三元组(value,x1_str,x2_str)self.pc = 0.6 # 交配概率self.pm = 0.01 # 变异概率self.distribution = [] # ⽤于种群选择时的轮盘def initial(self):for i in range(self.pop_size):x1 = rand(0,10)x2 = rand(0,14)x1_str = tobinarystring(x1)x2_str = tobinarystring(x2)self.population.append([x1_str,x2_str]) # 添加⼀个个体fitness_value = fitness(x1,x2)self.individual_fitness.append(fitness_value) # 记录该个体的适应度self.population = self.population[1:]self.results = self.results[1:]def eliminate(self):for i in range(self.pop_size):if self.individual_fitness[i]<0:self.individual_fitness[i] = 0.0def getbest(self):"取得当前种群中的⼀个最有个体加⼊results集合"index = self.individual_fitness.index(max(self.individual_fitness))x1_str = self.population[index][0]x2_str = self.population[index][1]value = self.individual_fitness[index]self.results.append((value,x1_str,x2_str,))def select(self):"轮盘算法,⽤随机数做个体选择,选择之后会更新individual_fitness对应的数值""第⼀步先要初始化轮盘""选出新种群之后更新individual_fitness"total = sum(self.individual_fitness)begin = 0for i in range(self.pop_size):temp = self.individual_fitness[i]/total+beginself.distribution.append(temp)begin = tempnew_population = []new_individual_fitness = []for i in range(self.pop_size):num = random.random() # ⽣成⼀个0~1之间的浮点数j = 0for j in range(self.pop_size):if self.distribution[j]<num:continueelse:breakindex = j if j!=0 else (self.pop_size-1)new_population.append(self.population[index])new_individual_fitness.append(self.individual_fitness[index])self.population = new_populationself.individual_fitness = new_individual_fitnessdef crossover(self):"选择好新种群之后要进⾏交配""注意这只是⼀次种群交配,种群每⼀次交配过程,会让每两个相邻的染⾊体进⾏信息交配"for i in range(self.pop_size-1):if random.random()<self.pc:cross_position = random.randint(1,self.chrom_length-1)i_x1x2_str = self.population[i][0]+self.population[i][1] # 拼接起第i个染⾊体的两个⼆进制字符串i1_x1x2_str = self.population[i+1][0]+self.population[i+1][1] # 拼接起第i+1个染⾊体的两个⼆进制字符串 str1_part1 = i_x1x2_str[:cross_position]str1_part2 = i_x1x2_str[cross_position:]str2_part1 = i1_x1x2_str[:cross_position]str2_part2 = i1_x1x2_str[cross_position:]str1 = str1_part1+str2_part2str2 = str2_part1+str1_part2self.population[i] = [str1[:11],str1[11:]]self.population[i+1] = [str2[:11],str2[11:]]"然后更新individual_fitness"for i in range(self.pop_size):x1_str = self.population[i][0]x2_str = self.population[i][1]x1 = todecimal(x1_str)x2 = todecimal(x2_str)self.individual_fitness[i] = fitness(x1,x2)def mutation(self):"个体基因变异"for i in range(self.pop_size):if random.random()<self.pm:x1x2_str = self.population[i][0]+self.population[i][1]pos = random.randint(0,self.chrom_length-1)bit = "1" if x1x2_str[pos]=="0" else "0"x1x2_str = x1x2_str[:pos]+bit+x1x2_str[pos+1:]self.population[i][0] = x1x2_str[:11]self.population[i][1] = x1x2_str[11:]"然后更新individual_fitness"for i in range(self.pop_size):x1_str = self.population[i][0]x2_str = self.population[i][1]x1 = todecimal(x1_str)x2 = todecimal(x2_str)self.individual_fitness[i] = fitness(x1, x2)def solving(self,times):"进⾏times次数的整个种群交配变异""先获得初代的最优个体"self.getbest()for i in range(times):"每⼀代的染⾊体个体和适应值,需要先淘汰,然后选择,再交配、变异,最后获取最优个体。
基于遗传算法求解作业车间调度问题【精品毕业设计】(完整版)

基于遗传算法求解作业车间调度问题【精品毕业设计】(完整版)基于遗传算法求解作业车间调度问题摘要作业车间调度问题(JSP)简单来说就是设备资源优化配置问题。
作业车间调度问题是计算机集成制造系统(CIMS)工程中的一个重要组成部分,它对企业的生产管理和控制系统有着重要的影响。
在当今的竞争环境下,如何利用计算机技术实现生产调度计划优化,快速调整资源配置,统筹安排生产进度,提高设备利用率已成为许多加工企业面临的重大课题。
近年来遗传算法得到了很大的发展,应用遗传算法来解决车间调度问题早有研究。
本文在已有算法基础上详细讨论了染色体编码方法并对其进行了改进。
在研究了作业车间调度问题数学模型和优化算法的基础上,将一种改进的自适应遗传算法应用在作业车间调度中。
该算法是将sigmoid函数的变形函数应用到自适应遗传算法中,并将作业车间调度问题中的完工时间大小作为算法的评价指标,实现了交叉率和变异率随着完工时间的非线性自适应调整,较好地克服了标准遗传算法在解决作业车间调度问题时的“早熟”和稳定性差的缺点,以及传统的线性自适应遗传算法收敛速度慢的缺点。
以改进的自适应遗传算法和混合遗传算法为调度算法,设计并实现了作业车间调度系统,详细介绍了各个模块的功能与操作。
最后根据改进的编码进行遗传算法的设计,本文提出了一种求解车间作业调度问题的改进的遗传算法,并给出仿真算例表明了该算法的有效性。
关键词:作业车间调度;遗传算法;改进染色体编码;生产周期Solving jopshop scheduling problem based ongenetic algorithmAbstractSimply speaking, the job shop scheduling problem(JSP) is the equipment resources optimization question. Job Shop Scheduling Problem as an important part of ComputerIntegratedManufacturing System (CIMS) engineering is indispensable, and has vital effect onproduction management and control system. In the competion ecvironment nowadays, how touse the assignments quickly and to plan production with due consideration for all concernedhas become a great subject for many manufactory.In recent years,the genetic algorithms obtained great development it was used to solve the job shop scheduling problem early.This paper discusses the chromosome code method in detail based on the genetic algorithms and make the improvement on it. Through the research on mathematics model of JSP and optimized algorithm, theimproved adaptive genetic algorithm (IAGA) obtained by applying the improved sigmoidfunction to adaptive genetic algorithm is proposed. And in IAGA for JSP, the fitness ofalgorithm is represented by completion time of jobs. Therefore, this algorithm making thecrossover and mutation probability adjusted adaptively and nonlinearly with the completiontime, can avoid such disadvantages as premature convergence, low convergence speed andlow stability. Experimental results demonstrate that the proposed genetic algorithm does notget stuck at a local optimum easily, and it is fast in convergence, simple to be implemented. the job shop scheduling system based on IAGA and GASH is designed andrealized, and the functions and operations of the system modules are introduced detailedly. In the end ,according to the code with improved carries on the genetic algorithms desing, this paper offer one improved genetic algorithms about soloving to the job shop scheduling problem, and the simulated example has indicated that this algorithm is valid.Keywords: jop shop scheduling; genetic algorithm;improvement chromosome code; production cycl目录摘要 .......................................................................................................................... . (I)Abstract............................................................................................................... ....................................... II 1绪论 . (1)1.1课题来源 (1)1.2作业车间调度问题表述 (1)1.3车间作业调度问题研究的假设条件及数学模型 (2)1.3.1车间作业调度问题研究的假设条件 (2)1.3.2 车间作业调度问题的数学模型 (3)1.4课题研究内容及结构安排 (4)2 遗传算法相关理论与实现技术 (6)2.1自然进化与遗传算法 (6)2.2基本遗传算法 (7)2.2.1遗传算法的基本思路 (7)2.2.2遗传算法的模式定理 (7)2.2.3 遗传算法的收敛性分析 (9)2.2.4基本遗传算法参数说明 (10)2.3遗传算法的优缺点 (11)2.3.1 遗传算法的优点 (11)2.3.2遗传算法的缺点 (11)2.4遗传算法的进展 (12)2.5小结 (15)3用遗传算法对具体问题的解决与探讨 (16)3.1 研究过程中的几个关键问题 (16)3.1.1设备死锁现象 (16)3.1.2参数编码 (16)3.1.3初始种群的生成 (19)3.1.4 个体的适应度函数 (20)3.1.5算法参数 (20)3.1.6 遗传算子的设计 (21)3.2遗传算法终止条件 (24)3.3 遗传算法解决车间调度问题的改进 (24)3.4 系统仿真 (24)3.5 小结 (29)结论 (30)致谢 (31)参考文献 (32)附录 (33)1 绪论1.1 课题来源随着加入WTO,市场竞争越来越激烈,对制造企业来说,为了能够在竞争中立于不败,降低成本是不得不面临的问题,而确保生产车间较高的生产能力和效率,是当务之急。
遗传算法及蚂蚁算法作业

(1)用遗传算法来做:第一步:确定决策变量及其约束条件s.t. -5<=x<=5第二步:建立优化模型第三步:确定编码方法,用长度为50位的二进制编码串来表示决策变量x第四步:确定解码方法第五步:确定个体评价方法个体的适应度取为每次迭代的最小值的绝对值加上目标函数值,即第六步:确定参数本题种群规模n=30,迭代次数ger=200,交叉概率pc=0.65,变异概率pm=0.05代码:clear all;close all;clc;tic;n=30;ger=200;pc=0.65;pm=0.05;% 生成初始种群v=init_population(n,50);[N,L]=size(v);disp(sprintf('Number of generations:%d',ger));disp(sprintf('Population size:%d',N)); disp(sprintf('Crossover probability:%.3f',pc)); disp(sprintf('Mutation probability:%.3f',pm));% 待优化问题xmin=-5;xmax=5;ymin=-5;ymax=5;f='-(2-exp(-(x.^2+y.^2)))';[x,y]=meshgrid(xmin:0.1:xmax,ymin:0.1:ymax);vxp=x;vyp=y;vzp=eval(f);figure(1);mesh(vxp,vyp,-vzp);hold on;grid on;% 计算适应度,并画出初始种群图形x=decode(v(:,1:25),xmin,xmax);y=decode(v(:,26:50),ymin,ymax);fit=eval(f);plot3(x,y,-fit,'k*');title('(a)染色体的初始位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 迭代前的初始化vmfit=[];vx=[];it=1; % 迭代计数器% 开始进化while it<=ger% Reproduction(Bi-classist Selection) vtemp=roulette(v,fit);% Crossoverv=crossover(vtemp,pc);% MutationM=rand(N,L)<=pm;%M(1,:)=zeros(1,L);v=v-2.*(v.*M)+M;% Resultsx=decode(v(:,1:25),xmin,xmax);y=decode(v(:,26:50),ymin,ymax);fit=eval(f);[sol,indb]=max(fit); % 每次迭代中最优目标函数值v(1,:)=v(indb,:);fit_mean=mean(fit); % 每次迭代中目标函数值的平均值vx=[vx sol];vmfit=[vmfit fit_mean];it=it+1;end%%%% 最后结果disp(sprintf('\n')); %空一行% 显示最优解及最优值disp(sprintf('Maximumfound[x,f(x)]:[%.4f,%.4f,%.4f]',x(indb),y(indb),-sol));% 图形显示最优结果figure(2);mesh(vxp,vyp,-vzp);hold on;grid on;plot3(x,y,-fit,'r*');title('染色体的最终位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 图形显示最优及平均函数值变化趋势figure(3);plot(-vx);%title('最优,平均函数值变化趋势');xlabel('Generations');ylabel('f(x)');hold on;plot(-vmfit,'r');hold off;runtime=toc运行结果:Maximum found[x,f(x)]:[0.0033,0.0017,1.0000](2)用蚁群算法来做代码:% Ant main programclear all;close all;clc;tic;Ant=100;xmin=-5;xmax=5;ymin=-5;ymax=5;tcl=0.05;f='-(2-exp(-(x.^2+y.^2)))'; % 待优化的目标函数[x,y]=meshgrid(xmin:tcl:xmax,ymin:tcl:ymax);vxp=x;vyp=y;vzp=eval(f);figure(1);mesh(vxp,vyp,-vzp);hold on;% 初始化蚂蚁位置for i=1:AntX(i,1)=(xmin+(xmax-xmin)*rand(1));X(i,2)=(ymin+(ymax-ymin)*rand(1));% T0----信息素,函数值越大,信息素浓度越大T0(i)=exp(-(X(i,1).^2+X(i,2).^2))-2;endplot3(X(:,1),X(:,2),-T0,'k*');grid on;title('蚂蚁的初始分布位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 开始寻优for i_ger=1:GerP0=0.2; % P0----全局转移选择因子P=0.8; % P ----信息素蒸发系数lamda=1/i_ger; % 转移步长参数[T_Best(i_ger),BestIndex]=max(T0);for j_g=1:Ant % 求取全局转移概率r=T0(BestIndex)-T0(j_g);Prob(i_ger,j_g)=r/T0(BestIndex);endfor j_g_tr=1:Antif Prob(i_ger,j_g_tr)<P0temp1=X(j_g_tr,1)+(2*rand(1)-1)*lamda;temp2=X(j_g_tr,2)+(2*rand(1)-1)*lamda;elsetemp1=X(j_g_tr,1)+(xmax-xmin)*(rand(1)-0.5);temp2=X(j_g_tr,2)+(ymax-ymin)*(rand(1)-0.5);endif temp1<xmintemp1=xmin;endif temp1>xmaxtemp1=xmax;endif temp2<ymintemp2=ymin;endif temp2>ymaxtemp2=ymax;endif-(2-exp(-(temp1.^2+temp2.^2)))>-(2-exp(-(X(j_g_tr,1).^2+X(j_g_tr,2).^2)))X(j_g_tr,1)=temp1;X(j_g_tr,2)=temp2;endend%信息素更新for t_t=1:AntT0(t_t)=(1-P)*T0(t_t)-(2-exp(-(X(t_t,1).^2+X(t_t,2).^2)));end[c_iter,i_iter]=max(T0);maxpoint_iter=[X(i_iter,1),X(i_iter,2)];max_local(i_ger)=-(2-exp(-(X(i_iter,1).^2+X(i_iter,2).^2)));%将每代全局最优解存到max_global矩阵中if i_ger>=2if max_local(i_ger)>max_global(i_ger-1)max_global(i_ger)=max_local(i_ger);elsemax_global(i_ger)=max_global(i_ger-1);endelsemax_global(i_ger)=max_local(i_ger);endend% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % %% %figure(2);mesh(vxp,vyp,-vzp);hold on;x=X(:,1);y=X(:,2);plot3(x,y,-eval(f),'b*');hold on;grid on;title('蚂蚁的最终分布位置');xlabel('x');ylabel('y');zlabel('f(x,y)');figure(3);plot(1:Ger,-max_global,'b-')hold on;title('最优函数值变化趋势');xlabel('iteration');ylabel('f(x)');grid on;[c_max,i_max]=max(T0);maxpoint=[X(i_max,1),X(i_max,2)]maxvalue=-(2-exp(-(X(i_max,1).^2+X(i_max,2).^2)))runtime=toc结果:maxvalue =1.0000题目2:利用蚁群算法求下面加权有向图中从A到G的最短路:解:第一步:初始化N只蚂蚁,也就是N条道路第二步:初始化运行参数,开始迭代第三步:在迭代步数范围之内,计算转移概率,如果小于全局转移概率就进行小范围的搜索,否则就进行大范围的搜索第四步:更新信息素,记录状态,准备进行下一次迭代第五步:转第三步第六步:输出结果代码:function shortroad_ant_main% Ant main programclear all;close all;clc;%清屏tic;%计时开始Ant=50;Ger=100;%运行参数初始化power=[0 5 3 100 100 100 100 100 100 100 100 100 100 100 100 100;100 0 100 1 3 6 100 100 100 100 100 100 100 100 100 100;100 100 0 100 8 7 6 100 100 100 100 100 100 100 100 100;100 100 100 0 100 100 100 6 8 100 100 100 100 100 100 100;100 100 100 100 0 100 100 3 5 100 100 100 100 100 100 100;100 100 100 100 100 0 100 100 3 3 100 100 100 100 100 100;100 100 100 100 100 100 0 100 8 4 100 100 100 100 100 100;100 100 100 100 100 100 100 0 100 100 2 2 100 100 100 100;100 100 100 100 100 100 100 100 0 100 100 1 2 100 100 100;100 100 100 100 100 100 100 100 100 0 100 3 3 100 100 100;100 100 100 100 100 100 100 100 100 100 0 100 100 3 5 100;100 100 100 100 100 100 100 100 100 100 100 0 100 5 2 100;100 100 100 100 100 100 100 100 100 100 100 100 0 6 6 100; 100 100 100 100 100 100 100 100 100 100 100 100 100 0 100 4; 100 100 100 100 100 100 100 100 100 100 100 100 100 100 0 3; 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 0];[PM PN]=size(power);% 初始化蚂蚁位置v=init_population(Ant,PN);v(:,1)=1;v(:,PN)=1;%始点和终点纳入路径%把距离当信息素浓度fit=short_road_fun(v,power);%距离越小越好,所以要和信息素浓度相对应。
遗传算法简单易懂的例子

遗传算法简单实例为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各个主要执行步骤。
例:求下述二元函数的最大值:(1) 个体编码遗传算法的运算对象是表示个体的符号串,所以必须把变量x1, x2 编码为一种符号串。
本题中,用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数,所以分别用3位无符号二进制整数来表示,将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型,表示一个可行解。
例如,基因型 X=101110 所对应的表现型是:x=[ 5,6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。
(2) 初始群体的产生遗传算法是对群体进行的进化操作,需要给其淮备一些表示起始搜索点的初始群体数据。
本例中,群体规模的大小取为4,即群体由4个个体组成,每个个体可通过随机方法产生。
如:011101,101011,011100,111001(3) 适应度汁算遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传机会的大小。
本例中,目标函数总取非负值,并且是以求函数最大值为优化目标,故可直接利用目标函数值作为个体的适应度。
(4) 选择运算选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。
一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。
本例中,我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。
其具体操作过程是:•先计算出群体中所有个体的适应度的总和fi ( i=1.2,…,M );•其次计算出每个个体的相对适应度的大小 fi / fi ,它即为每个个体被遗传到下一代群体中的概率,•每个概率值组成一个区域,全部概率值之和为1;•最后再产生一个0到1之间的随机数,依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。
(5) 交叉运算交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某两个个体之间的部分染色体。
遗传算法学习作业

遗传算法学习总结1.1 概述遗传算法是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的自适应概率性随机化迭代搜索算法。
1962年霍兰德(Holland)教授首次提出了GA算法的思想,它的基本思想是基于Darwin进化论和Mendel的遗传演说。
Darwin进化论最重要的是适者生存的原理,它认为每一代种群总是向着前进方向发展,越来越适应环境。
每一个个体都有继承前代的特性,但不是完全继承,会产生一些新特性。
最终只有适应环境的特征才能被保留下来。
Mendel遗传学说最重要的是基因遗传原理,它认为遗传以密码方式存在细胞中,并以基因形式包含在染色体内。
一条染色体中存在很多基因,每个基因有自己的位置并控制着外部特征;基因的产生和变异直接影响到个体的特性是否能适应环境。
经过存优去劣的自然淘汰,适应性高的基因结构得以保存下来。
遗传算法正是借用了仿真生物遗传学和自然选择机理,通过自然选择、遗传、变异等作用机制,实现各个个体的适应性的提高。
与自然界相似,遗传算法对求解问题的本身一无所知,从代表问题可能潜在解集的一个种群(population)开始,每一个种群则由经过基因(gene)编码(coding)的一定数目的个体(individual)构成。
每个个体实际上是染色体(chromosome)带有特征的实体。
把问题的解表示成染色体,并基于适应值来选择染色体,遗传算法所需要的仅是对算法所产生的每个染色体进行评价,使适应性好的染色体有更多的繁殖机会。
在算法中也就是以二进制编码的串。
并且,在执行遗传算法之前,给出一群染色体,也就是假设解。
然后,把这些假设解置于问题的“环境”中,也即在一个适应度函数中来评价。
并按适者生存的原则,从中选择出较适应环境的染色体进行复制,淘汰低适应度的个体,再通过交叉,变异过程产生更适应环境的新一代染色体群。
对这个新种群进行下一轮进化,直到最适合环境的值。
1.2遗传算法的基本原理和特点1.2.1 算法原理在遗传算法中,通过随机方式产生若干个所求解问题的数字编码,即染色体,形成初始种群;通过适应度函数给每个个体一个数值评价,淘汰低适应度的个体,选择高适应度的个体参加遗传操作,经过遗传操作后的个体集合形成下一代新的种群,再对这个新种群进行下一轮进化,这就是遗传算法的基本原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
遗传、蚁群算法作业1、利用遗传算法求出下面函数的极小值:z=2-exp[-(x2+y2)], x,y∈[-5,+5] 解:第一步确定决策变量及其约束条件:x,y∈[-5,+5]第二步建立优化模型:min z(x,y)=2-exp[-(x2+y2)]第三步确定编码方法。
用长度为50位的二进制编码串来表示决策变量x,y。
第四步确定解码方法。
解码时将50位长的二进制编码前25位转换为对应的十进制整数代码,记为x,后25位转换后记为y。
第五步确定个体评价方法。
第六步设计遗传算子。
选择运算用比例选择算子,交叉运算使用单点交叉算子,变异运算使用基本位变异算子。
第七步确定遗传算法的运行参数。
实现代码:% n ---- 种群规模% ger ---- 迭代次数% pc ---- 交叉概率% pm ---- 变异概率% v ---- 初始种群(规模为n)% f ---- 目标函数值% fit ---- 适应度向量% vx ---- 最优适应度值向量% vmfit ---- 平均适应度值向量clear all;close all;clc;tic;n=30;ger=200;pc=0.65;pm=0.05;% 生成初始种群v=init_population(n,50);[N,L]=size(v);disp(sprintf('Number of generations:%d',ger));disp(sprintf('Population size:%d',N));disp(sprintf('Crossover probability:%.3f',pc));disp(sprintf('Mutation probability:%.3f',pm));% 待优化问题xmin=-5;xmax=5;ymin=-5;ymax=5;f='-(2-exp(-(x.^2+y.^2)))';[x,y]=meshgrid(xmin:0.1:xmax,ymin:0.1:ymax); vxp=x;vyp=y;vzp=eval(f);figure(1);mesh(vxp,vyp,-vzp);hold on;grid on;% 计算适应度,并画出初始种群图形x=decode(v(:,1:25),xmin,xmax);y=decode(v(:,26:50),ymin,ymax);fit=eval(f);plot3(x,y,-fit,'k*');title('(a)染色体的初始位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 迭代前的初始化vmfit=[];vx=[];it=1; % 迭代计数器% 开始进化while it<=ger% Reproduction(Bi-classist Selection)vtemp=roulette(v,fit);% Crossoverv=crossover(vtemp,pc);% MutationM=rand(N,L)<=pm;%M(1,:)=zeros(1,L);v=v-2.*(v.*M)+M;% Resultsx=decode(v(:,1:25),xmin,xmax);y=decode(v(:,26:50),ymin,ymax);fit=eval(f);[sol,indb]=max(fit); % 每次迭代中最优目标函数值v(1,:)=v(indb,:);fit_mean=mean(fit); % 每次迭代中目标函数值的平均值 vx=[vx sol];vmfit=[vmfit fit_mean];it=it+1;end%%%% 最后结果disp(sprintf('\n')); %空一行% 显示最优解及最优值disp(sprintf('Maximumfound[x,f(x)]:[%.4f,%.4f,%.4f]',x(indb),y(indb),-sol));% 图形显示最优结果figure(2);mesh(vxp,vyp,-vzp);hold on;grid on;plot3(x,y,-fit,'r*');title('染色体的最终位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 图形显示最优及平均函数值变化趋势figure(3);plot(-vx);%title('最优,平均函数值变化趋势');xlabel('Generations');ylabel('f(x)');hold on;plot(-vmfit,'r');hold off;runtime=toc结果:Number of generations:200Population size:30Crossover probability:0.650Mutation probability:0.050Maximum found[x,f(x)]:[-0.0091,0.0099,1.0002] runtime =5.2720故最优解为x=-0.0091,y=0.0099,z=1.0002第八步结果分析图1 原始函数图形图2 染色体的最终位置图3 个体适应度的最大值和平均值2、利用蚁群算法求出下面函数的极小值:z=2-exp[-(x2+y2)], x,y [-5,+5]解:实现代码如下:% Ant main programclear all;close all;clc;tic;Ant=100;Ger=50;xmin=-5;xmax=5;ymin=-5;ymax=5;tcl=0.05;f='-(2-exp(-(x.^2+y.^2)))'; % 待优化的目标函数[x,y]=meshgrid(xmin:tcl:xmax,ymin:tcl:ymax);vxp=x;vyp=y;vzp=eval(f);figure(1);mesh(vxp,vyp,-vzp);hold on;% 初始化蚂蚁位置for i=1:AntX(i,1)=(xmin+(xmax-xmin)*rand(1));X(i,2)=(ymin+(ymax-ymin)*rand(1));% T0----信息素,函数值越大,信息素浓度越大T0(i)=exp(-(X(i,1).^2+X(i,2).^2))-2;endplot3(X(:,1),X(:,2),-T0,'k*');hold on;grid on;title('蚂蚁的初始分布位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 开始寻优for i_ger=1:GerP0=0.2; % P0----全局转移选择因子P=0.8; % P ----信息素蒸发系数lamda=1/i_ger; % 转移步长参数[T_Best(i_ger),BestIndex]=max(T0);for j_g=1:Ant % 求取全局转移概率r=T0(BestIndex)-T0(j_g);Prob(i_ger,j_g)=r/T0(BestIndex);endfor j_g_tr=1:Antif Prob(i_ger,j_g_tr)<P0temp1=X(j_g_tr,1)+(2*rand(1)-1)*lamda;temp2=X(j_g_tr,2)+(2*rand(1)-1)*lamda;elsetemp1=X(j_g_tr,1)+(xmax-xmin)*(rand(1)-0.5);temp2=X(j_g_tr,2)+(ymax-ymin)*(rand(1)-0.5);endif temp1<xmintemp1=xmin;endif temp1>xmaxtemp1=xmax;endif temp2<ymintemp2=ymin;endif temp2>ymaxtemp2=ymax;endif-(2-exp(-(temp1.^2+temp2.^2)))>-(2-exp(-(X(j_g_tr,1).^2+X(j_g_tr,2).^ 2)))X(j_g_tr,1)=temp1;X(j_g_tr,2)=temp2;endend%信息素更新for t_t=1:AntT0(t_t)=(1-P)*T0(t_t)-(2-exp(-(X(t_t,1).^2+X(t_t,2).^2))); end[c_iter,i_iter]=max(T0);maxpoint_iter=[X(i_iter,1),X(i_iter,2)];max_local(i_ger)=-(2-exp(-(X(i_iter,1).^2+X(i_iter,2).^2)));%将每代全局最优解存到max_global矩阵中if i_ger>=2if max_local(i_ger)>max_global(i_ger-1)max_global(i_ger)=max_local(i_ger);elsemax_global(i_ger)=max_global(i_ger-1);endelsemax_global(i_ger)=max_local(i_ger);endend% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % figure(2);mesh(vxp,vyp,-vzp);hold on;x=X(:,1);y=X(:,2);plot3(x,y,-eval(f),'b*');hold on;grid on;title('蚂蚁的最终分布位置');xlabel('x');ylabel('y');zlabel('f(x,y)');figure(3);plot(1:Ger,-max_global,'b-')hold on;title('最优函数值变化趋势');xlabel('iteration');ylabel('f(x)');grid on;[c_max,i_max]=max(T0);maxpoint=[X(i_max,1),X(i_max,2)]maxvalue=(2-exp(-(X(i_max,1).^2+X(i_max,2).^2))) runtime=toc结果:maxpoint = 0.0033 -0.0035maxvalue = 1.0000runtime = 0.9855图1 原始函数图形图2 染色体的最终位置图3 个体适应度的最大值和平均值3、利用蚁群算法求下面加权有向图中从A到G的最短路。
