《三角形的证明》复习课件PPT
合集下载
八年级 下册 数学 PPT课件 精品课件 第一章 三角形的证明 角平分线(二)

2. (巴中•中考)如图所示,是一块三角形的草坪,现
要在草坪上建一凉亭供大家休息,要使凉亭到草坪三
条边的距离相等,凉亭的位置应选在( )
A.△ABC 的三条中线的交点
A
B.△ABC 三边的中垂线的交点
C.△ABC 三条角平分线的交点
B
C
D.△ABC 三条高所在直线的交点
【解析】选C. 根据三角形三条角平分线的性质定理得.
合作交流 ⅰ、如图, 有两条公路相交于点A处,现计划 修建一个油库,要求到两条公路的距离相等, 你们该如何选择油库的位置?
A
合作交流
ⅱ、如图, 有两条公路相交于点A处,如果再增 加一条公路,与这两条公路都相交(不经过点A 处),现计划修建一个油库,那么如何选择油库 的位置才能保证油库到三条公路的距离相等?
你发现了什么?
三条折痕交于一点
新知探究
Ⅱ、如图,△ABC,用尺规作出三角形三个角的
角平分线。
A
你又发现了什么?
1、三个角的角平分线 交于一点;
B 2、交点到三条边的 距离相等。
P C
新知探究
Ⅲ、求证:三角形的三条角平分线相交于一点,并
且这一点到三条边的距离相等。
A
已知:如图,△ABC中,角平分线BM与角
两边距离相等的点,在这个角的平分线上)
即 ∠A的平分线经过点P
新知归纳
三角形三条角平分线定理: 三角形的三条角平分线交于一点,并且这一
点到三条边的距离相等。
情景引入
如图,三个城镇A、B、C之间有三条公路连
接,现要在三条公路围成的内部区域建一个加油
站,使加油站到三条公路的距离相等,你能确定
加油站的位置吗?
3.(曲靖·中考)在Rt△ABC中,∠C=90°,若BC
三角形的外角及常见结论的证明复习课件人教版八年级上册

4、如图,已知△ABC中,∠A沿着EF翻折到∠A’,
解:因为∠ADC是△ABD的外角. 说出下列图形中∠1和∠2的度数:
A
所以∠ADC=∠B+∠BAD=80°.
(1)位置关系:相邻和不相邻.
外角大于不相邻的任何一个内角.
所以∠ADC=∠B+∠BAD=80ห้องสมุดไป่ตู้.
探究1:三角形外角的性质 解:因为∠ADC是△ABD的外角. 如图,求证:∠BDC= ∠B+ ∠C+ ∠BAC
__36_0°_.
B
A
C
1
P
N3
2M
F
D
E
2 .如图,D 是△ABC 的BC边上一点,∠B =∠BAD, ∠ADC =80°, ∠BAC =70°,求:(1)∠B 的度数;(2)∠C 的度数.
解:因为∠ADC是△ABD的外角.
所以∠ADC=∠B+∠BAD=80°.
又因为∠B=∠BAD,
所以B 80 1 40, 在△ABC中: 2
.
80 ° ∠ACD = ∠A +∠B.
∠C=180º-40º-70º=70°. 1、如图,试求出∠A+∠B+∠C+∠D+∠E+∠F =____.
6、如图所示,已知△ABC ,∠CBD和∠BCE的角平分
60 ° 1 请用三种不同的方法证明该结论!
如图,求证:∠BDC= ∠B+ ∠C+ ∠BAC ∠1+ ∠2+ ∠3=?
∠B+∠BAC+∠C=180°, ∠C=180º-40º-70º=70°.
A
70°
40°
80°
B
D
C
课堂 小结
北师大版八年级数学下册第一章三角形的证明串讲课件

2.
【例5】用反证法证明
1. 等腰三角形的底角是锐角。 2. 求证:一个三角形中,如果两个角不相等, 那么它们所对的边也不相等。 3. 证明:三角形中至少有一个角不小于60°。
六.等腰三角形中的多解问题——分类讨论 【例6】 a) 等腰三角形的两边长分别是4和5,这个 三角形的周长是( ) b) 等腰三角形的两边长分别是4和8,这个 三角形的周长是( ) c) 等腰三角形一腰上的中线把该三角形的 周长分为12和15两部分,求该三角形各 边的长。 (8、8、11;10、10、7) d) 等腰三角形一腰上的高与另一腰的夹角 为30°则等腰三角形的顶角为( )°
【例2】
① 证明等边三角形的性质定理(略) ② 如图1, ABC中,AB=AC,点D是BC的中点, 点E在AD上,
a) 求证:BE=CE b) 如图2,若BE的延长线交AC于F点,且BF⊥AC, 垂足为F,∠BAC=45°,原题其它条件不变,求 证:△AEF≌△BCF
A 图1 图2 A
E B D C B
第一章 三角形的证明
八年级(下册)
点→线(两点定线)→角(两线)→(面)图→体
学习几何 基本规律
一个图(三角形、四边形---)形的定义,性质,判定
两个图形之间的关系:全等、相似、对称、位似----
两次翻折=一次平移
对称 旋转
全ቤተ መጻሕፍቲ ባይዱ变换
平移
形状大小都不变
• 图形变换
翻折
相似变换(形状不变大小变) 如:位似变换。
(2)求证:⊿CEF是等边三角形 M
E F
N
A
C
B
五.反证法
1. 定义:先假设命题的结论不成立,然后推导 出与定义、基本事实、已有定理或已知条件 相矛盾的结果,从而证明命题的结论一定成 立。这种证明方法称为反证法。 反证法——常用的间接证明法。步骤:
北师大版八年级下册数学《线段的垂直平分线》三角形的证明说课教学课件复习

三角形三条边的垂直平分线的性质:三角形三条边的垂直平分线 相交于一点,并且这一点到三个顶点的距离相等.
实践探究,交流新知
已知等腰三角形的底边和该边上的高,求作等腰三角形
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作 几个?所作出的三角形都全等吗? (2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几 个?所作出的三角形都全等吗? (3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?如 果能,能作几个?
. 39°
3.如图,在△ABC中,∠BAC是钝角. (1)画出边BC上的中线AD; (2)画出边BC上的高AH.
第1题
第2题
第3题
课堂小结,整体感知
1.课堂小结:请同学们回顾本节课所学的内容,有哪些收获? (1)三角形三条边的垂直平分线的性质 (2)尺规作线段的垂直平分线、等腰三角形
2.布置作业:
开放训练,体现应用
例1 (教材第22页例1)已知:如图,在△ABC中,AB=AC,O是△ABC内一点, 且OB=OC.求证:直线AO垂直平分线段BC.(解法不唯一)
证明:∵AB=AC, ∴点A为线段BC垂直平分线上的一点 ∵OB=OC, ∴点O为线段BC垂直平分线上的一点 ∴直线AO是线段BC的垂直平分线
课堂检测,巩固新知
解:(1)∵∠BAC=50°,AD平分∠BAC ∴∠EAD=1∠BAC=25°
2
∵DE⊥AB ∴∠AED=90° ∴∠EDA=90°-25°=65° (2)证明:∵DE⊥AB ∴∠AED=90°=∠ACB 又∵AD平分∠BAC ∴∠DAE=∠DAC 又∵AD=AD ∴△AED≌△ACD(AAS) ∴AE=AC ∵AD平分∠BAC ∴AD⊥CE,AD平分线段EC 即直线AD是线段CE的垂直平分线
实践探究,交流新知
已知等腰三角形的底边和该边上的高,求作等腰三角形
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作 几个?所作出的三角形都全等吗? (2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几 个?所作出的三角形都全等吗? (3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?如 果能,能作几个?
. 39°
3.如图,在△ABC中,∠BAC是钝角. (1)画出边BC上的中线AD; (2)画出边BC上的高AH.
第1题
第2题
第3题
课堂小结,整体感知
1.课堂小结:请同学们回顾本节课所学的内容,有哪些收获? (1)三角形三条边的垂直平分线的性质 (2)尺规作线段的垂直平分线、等腰三角形
2.布置作业:
开放训练,体现应用
例1 (教材第22页例1)已知:如图,在△ABC中,AB=AC,O是△ABC内一点, 且OB=OC.求证:直线AO垂直平分线段BC.(解法不唯一)
证明:∵AB=AC, ∴点A为线段BC垂直平分线上的一点 ∵OB=OC, ∴点O为线段BC垂直平分线上的一点 ∴直线AO是线段BC的垂直平分线
课堂检测,巩固新知
解:(1)∵∠BAC=50°,AD平分∠BAC ∴∠EAD=1∠BAC=25°
2
∵DE⊥AB ∴∠AED=90° ∴∠EDA=90°-25°=65° (2)证明:∵DE⊥AB ∴∠AED=90°=∠ACB 又∵AD平分∠BAC ∴∠DAE=∠DAC 又∵AD=AD ∴△AED≌△ACD(AAS) ∴AE=AC ∵AD平分∠BAC ∴AD⊥CE,AD平分线段EC 即直线AD是线段CE的垂直平分线
《三角形的认识》课件

建筑中的三角形应用
屋顶结构
许多建筑的屋顶采用三角形的设 计,以提供更好的承重和稳定性
。
钢架结构
在建筑中,钢架结构经常采用三角 形的设计,以增强结构的强度和稳 定性。
桥梁支撑
桥梁的支撑结构经常采用三角形的 设计,以分散重量并增强稳定性。
数学中的三角形应用
勾股定理
勾股定理是三角形的一个重要性 质,它描述了直角三角形三边的
《三角形的认识》 ppt课件
REPORTING
• 三角形的定义与性质 • 三角形的分类 • 三角形的面积与周长 • 三角形的应用 • 三角形的证明与定理
目录
PART 01
三角形的定义与性质
REPORTING
三角形的定义
总结词
三角形是由三条边和三个角构成 的平面图形。
详细描述
三角形是最简单的多边形之一, 由不在同一直线上的三条线段首 尾顺次连接形成的平面图形。
详细描述
三角形的边与角之间存在密切的关系,如等腰三角形的两腰相等,且对应的两个 底角也相等;直角三角形中有一个角为90度,且斜边与直角边的关系满足勾股定 理等。这些关系是三角形的重要性质,有助于解决各种几何问题。
PART 02
三角形的分类
REPORTING
按角度分类
01
02
03
锐角三角形
三个角都小于90度的三角 形。
边边边(SSS)证明方法
如果两个三角形有三条边分别相等,则这两 个三角形全等。
边角边(SAS)证明方法
如果两个三角形有两条边和夹角分别相等, 则这两个三角形全等。
角角边(AAS)证明方法
如果两个三角形有两个角和一条非夹角边分 别相等,则这两个三角形全等。
北师大版八年级下册数学《等腰三角形》三角形的证明说课教学课件复习(第3课时)

在一般三角形中,如果有两个角相等,那么它们所对的边有什么关系?
猜想:如果一个三角形有两个角相等,那么这两个角所对的边也相等.如何证明?
数学语言:已知:在△ABC中,∠B=∠C;求证:AB=AC 方法思考:①作高AD可以吗? ②作角平分线AD呢? ③作中线AD呢?
等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等,
∴△ABP≌△ACQ(SAS)
∴AP=AQ,∠BAP=∠CAQ
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°
∴△APQ是等边三角形
课堂检测,巩固新知
1.如图,一棵大树在一次强台风中离地面5米处折断倒下,倒下部分与地面成
30°夹角,这棵大树在折断前的高度为( B )
A.10米 B.15米 C.25米 D.30米 2.如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证 :△CEB为等边三角形.
开放训练,体现应用
例 2 (教材第11页例4)求证:如果等腰三角形的底角等于15°,那么腰上的高是
腰长的一半.
已知:如图,在△ABC中,AB=AC,∠B=15°,CD是腰AB上的高.
求证:CD=1AB.
2
证明:在△ABC中, ∵AB=AC,∠B=15° ∴∠B=∠ACB=15°(等边对等角) ∴∠DAC=∠B+∠ACB=30° ∵CD是腰AB上的高 ∴∠ADC=90° ∴CD=AC ∴CD=1AB
开放训练,体现应用
变式训练1 如图,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC 的平分线BD交边AC于点D.求证:△BCD为等腰三角形.
证明:∵∠BAC=75°,∠ACB=35° ∴∠ABC=180°-∠BAC-∠ACB=70° ∵BD平分∠ABC ∴∠DBC=∠ABC=35° ∴∠DBC=∠ACB=35° ∴DB=DC ∴△BCD为等腰三角形
猜想:如果一个三角形有两个角相等,那么这两个角所对的边也相等.如何证明?
数学语言:已知:在△ABC中,∠B=∠C;求证:AB=AC 方法思考:①作高AD可以吗? ②作角平分线AD呢? ③作中线AD呢?
等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等,
∴△ABP≌△ACQ(SAS)
∴AP=AQ,∠BAP=∠CAQ
∵∠BAC=∠BAP+∠PAC=60°
∴∠PAQ=∠CAQ+∠PAC=60°
∴△APQ是等边三角形
课堂检测,巩固新知
1.如图,一棵大树在一次强台风中离地面5米处折断倒下,倒下部分与地面成
30°夹角,这棵大树在折断前的高度为( B )
A.10米 B.15米 C.25米 D.30米 2.如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证 :△CEB为等边三角形.
开放训练,体现应用
例 2 (教材第11页例4)求证:如果等腰三角形的底角等于15°,那么腰上的高是
腰长的一半.
已知:如图,在△ABC中,AB=AC,∠B=15°,CD是腰AB上的高.
求证:CD=1AB.
2
证明:在△ABC中, ∵AB=AC,∠B=15° ∴∠B=∠ACB=15°(等边对等角) ∴∠DAC=∠B+∠ACB=30° ∵CD是腰AB上的高 ∴∠ADC=90° ∴CD=AC ∴CD=1AB
开放训练,体现应用
变式训练1 如图,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC 的平分线BD交边AC于点D.求证:△BCD为等腰三角形.
证明:∵∠BAC=75°,∠ACB=35° ∴∠ABC=180°-∠BAC-∠ACB=70° ∵BD平分∠ABC ∴∠DBC=∠ABC=35° ∴∠DBC=∠ACB=35° ∴DB=DC ∴△BCD为等腰三角形
北师大版八年级数学下册《直角三角形》三角形的证明PPT(第1课时)

获取新知
知识点二:直角三角形的边的关系
B
勾股定理 直角三角形两条直角边的平方
和等于斜边的平方.
A
C
关于勾股定理的证明,可以欣赏“16页的读一读”, 并可以上网搜索,诸如美国第二十任总统的证法、赵 爽弦图法等
勾股定理反过来,怎么叙述呢?
如果一个三角形两边的平方和等于第三边的平方,那 么这个三角形是直角三角形.
一项指标.现测得AB=4 cm,BC=3 cm,AD=13 cm,CD=12 cm, ∠ABC=90°,根据这些条件,能否得出∠ACD等于90°?请说明理由.
解:能.理由:在Rt△ABC中,
∵AB=4 cm,BC=3 cm,∠ABC=90°,
∴AC=
=5(cm).
在△ACD中,∵AD=13 cm,CD=12 cm,AC=5 cm,
你来给出完整的 证明过程吧,试 一试
例题讲解 例1 如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC 于点D,AE为∠BAC的平分线,求∠DAE的度数. 解:由题意可知, ∠BAC=180°-∠B-∠C=80°. ∵AE为∠BAC的平分线, ∴∠CAE=∠BAE= ∠BAC=40°. ∵AD⊥BC,∴∠ADC=90°. ∴∠CAD=90°-∠C=90°-70°=20°. ∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
原命题都存在逆命题 ,
但是互逆命题的真假 无法保证
如果一个定理的逆命题也是定理,那么这两个定理叫 做互逆定理,其中的一个定理叫做另一个定理的逆定理.
注意1:逆命题、互逆命题不一定是真命题, 但逆定理、互逆定理,一定是真命题.
注意2:不是所有的定理都有逆定理.
定理
“两直线平行,内错角相等”
《三角形内角和定理的证明》-完整版课件
∵ DE∥AB(所作)
A
F
E
B
D
C
本课小结:
谈谈 本节课你的收获!
来的图形上添画的线叫做辅助线。在 平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化 为一个平角或同旁内角互补,这种转 化思想是数学中的常用方法.
回顾与思考☞
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路; (5)依据思路,运用数学符号和数学语言条理清晰地 写出证明过程; (6)检查表达过程是否正确,完善.
思考
直角三角形的两锐角之和是多少度?
请说明你的结论.
A
由基本事实、定理直接得
出的真命题叫做推论
C
B
推论1: 直角三角形的两个锐角互余. 推论2: 有两个锐角互余的三角形是 直角三角形.
回顾 ☞
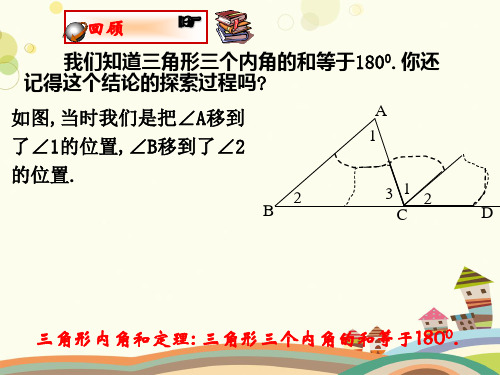
我们知道三角形三个内角的和等于1800.你还 记得这个结论的探索过程吗?
如图,当时我们是把∠A移到 了∠1的位置,∠B移到了∠2 的位置.
2 B
A 1
31 2
C
D
三角形内角和定理: 三角形三个内角的和等于1800.
例题讲解
已知:如图 △ABC.
A
E
求证:∠A+∠B+∠C=1800.
分析:延长BC到D,过点C作射 线CE∥AB,这样,就相当于把 B ∠A移到了∠1的位置,把∠B 移到了∠2的位置. 证明:作BC的延长线CD,过点C作CE∥AB,则
练习P81
补充完成下列证明,并填上推理的依据:
A
F
E
B
D
C
本课小结:
谈谈 本节课你的收获!
来的图形上添画的线叫做辅助线。在 平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化 为一个平角或同旁内角互补,这种转 化思想是数学中的常用方法.
回顾与思考☞
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路; (5)依据思路,运用数学符号和数学语言条理清晰地 写出证明过程; (6)检查表达过程是否正确,完善.
思考
直角三角形的两锐角之和是多少度?
请说明你的结论.
A
由基本事实、定理直接得
出的真命题叫做推论
C
B
推论1: 直角三角形的两个锐角互余. 推论2: 有两个锐角互余的三角形是 直角三角形.
回顾 ☞
我们知道三角形三个内角的和等于1800.你还 记得这个结论的探索过程吗?
如图,当时我们是把∠A移到 了∠1的位置,∠B移到了∠2 的位置.
2 B
A 1
31 2
C
D
三角形内角和定理: 三角形三个内角的和等于1800.
例题讲解
已知:如图 △ABC.
A
E
求证:∠A+∠B+∠C=1800.
分析:延长BC到D,过点C作射 线CE∥AB,这样,就相当于把 B ∠A移到了∠1的位置,把∠B 移到了∠2的位置. 证明:作BC的延长线CD,过点C作CE∥AB,则
练习P81
补充完成下列证明,并填上推理的依据:
北师大版八年级下册数学《等腰三角形》三角形的证明说课教学课件复习

即“等角对等边”.
实践探究,交流新知
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不
相等.你认为小明这个结论成立吗?如果成立,你能证明它吗?
证明:如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么
相等,要么不相等.假设AB=AC,那么根据“等边对等角”
定理可得∠C=∠B,但这与已知条件∠B≠∠C相矛盾,因
(3)若AD⊥BC,∠BAC=40°,则∠BAD=
20° .
(4)若BD=CD,则AD⊥BC,∠BAD= ∠CAD .
想一想:在等腰三角形中画出一些线段(比如角平分线、中线、高等),你能发
现其中一些相等的线段吗?能证明你的结论吗?
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
课件 课件
课件 课件
(2)归谬:从假设出发,通过推理得出矛盾;
(3)结论:说明假设不成立,从而得到原命题的结论正确.
开放训练,体现应用
例1 (教材第8页例2)已知:如图,AB=DC,BD=CA,BD与CA相交于
点E,求证:△AED是等腰三角形.
AB=DC,
证明:在△ABD和△DCA中,BD=CA,
AD=DA,
∴△ABD≌△DCA(SSS)
创设情境,导入新课
问题1:请同学们回顾一下,前面我们学习了等腰三角形的哪些性质?
(1)等腰三角形两底角相等,也就是“等边对等角”.
(2)“三线合一”.
(3)等腰三角形两腰上的高相等,两腰上的中线相等,两底角的平分线相等.
问题2:等腰三角形两底角相等,这个命题的条件和结论是什么?
实践探究,交流新知
实践探究,交流新知
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不
相等.你认为小明这个结论成立吗?如果成立,你能证明它吗?
证明:如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么
相等,要么不相等.假设AB=AC,那么根据“等边对等角”
定理可得∠C=∠B,但这与已知条件∠B≠∠C相矛盾,因
(3)若AD⊥BC,∠BAC=40°,则∠BAD=
20° .
(4)若BD=CD,则AD⊥BC,∠BAD= ∠CAD .
想一想:在等腰三角形中画出一些线段(比如角平分线、中线、高等),你能发
现其中一些相等的线段吗?能证明你的结论吗?
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
课件 课件
课件 课件
(2)归谬:从假设出发,通过推理得出矛盾;
(3)结论:说明假设不成立,从而得到原命题的结论正确.
开放训练,体现应用
例1 (教材第8页例2)已知:如图,AB=DC,BD=CA,BD与CA相交于
点E,求证:△AED是等腰三角形.
AB=DC,
证明:在△ABD和△DCA中,BD=CA,
AD=DA,
∴△ABD≌△DCA(SSS)
创设情境,导入新课
问题1:请同学们回顾一下,前面我们学习了等腰三角形的哪些性质?
(1)等腰三角形两底角相等,也就是“等边对等角”.
(2)“三线合一”.
(3)等腰三角形两腰上的高相等,两腰上的中线相等,两底角的平分线相等.
问题2:等腰三角形两底角相等,这个命题的条件和结论是什么?
实践探究,交流新知
三角形全等的证明ppt课件

∴AC=AD .
讲解新课
例2、已知:点D在AB上,点E在AC上,BE和CD交于 O点,AB=AC,∠B=∠C. 求证:BD=CE
证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴AD=AE
∵AB=AC
∴BD=CE
.
课
堂 如图,要证明△ACE≌ △BDF,根据给定的条件
E
的条件,不难发现图3是由图2平移而得。 利用AE=CF,可得:AF=CE
证明:∵AD∥BC(已知)
F
B
C
图3
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE 在△AFD 和△CEB 中
AD=CB(已知)
问:若求证∠D=∠B ,
如何证明?
∠A=∠C(已证)
∴ ∠B=∠D(全等三角形对应角相等)
D C
.
小结:四边形问题转化为三角形 问题解决。
问:此题添加辅助线,若连结BD行吗?A 在原有条件下,还能推出什么结论?
B
答:∠ABC=∠ADC,AB∥CD,AD∥BC
.
D C
归纳:二个三角形全等的判定方法
对应 相等 的元
素
两边一角 两角一边
两边及其 两边及其 两角及其 两角及其
写为“ASA”)
.
讲解新课:
例1、已知:如图,∠DAB=∠CAB,∠C=∠D 求证:AC=AD 证明:∵ ∠DAB=∠CAB,∠C=∠D
∴∠ABD=∠ACD (三角形内角和定理) 在△ACB和△ADB中
∠DAB=∠CAB AB=AB (共用边) ∠ABD=∠ACD
讲解新课
例2、已知:点D在AB上,点E在AC上,BE和CD交于 O点,AB=AC,∠B=∠C. 求证:BD=CE
证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴AD=AE
∵AB=AC
∴BD=CE
.
课
堂 如图,要证明△ACE≌ △BDF,根据给定的条件
E
的条件,不难发现图3是由图2平移而得。 利用AE=CF,可得:AF=CE
证明:∵AD∥BC(已知)
F
B
C
图3
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE 在△AFD 和△CEB 中
AD=CB(已知)
问:若求证∠D=∠B ,
如何证明?
∠A=∠C(已证)
∴ ∠B=∠D(全等三角形对应角相等)
D C
.
小结:四边形问题转化为三角形 问题解决。
问:此题添加辅助线,若连结BD行吗?A 在原有条件下,还能推出什么结论?
B
答:∠ABC=∠ADC,AB∥CD,AD∥BC
.
D C
归纳:二个三角形全等的判定方法
对应 相等 的元
素
两边一角 两角一边
两边及其 两边及其 两角及其 两角及其
写为“ASA”)
.
讲解新课:
例1、已知:如图,∠DAB=∠CAB,∠C=∠D 求证:AC=AD 证明:∵ ∠DAB=∠CAB,∠C=∠D
∴∠ABD=∠ACD (三角形内角和定理) 在△ACB和△ADB中
∠DAB=∠CAB AB=AB (共用边) ∠ABD=∠ACD
八年级 下册 数学 PPT课件 精品课件 第一章 三角形的证明 直角三角形(一)

范例讲解 例2、写出命题“如果两个有理数相等,那么它 们的平方相等”的逆命题,这两个命题都是真命 题吗? 解:其逆命题为“如果两个有理数的平方相等,
那么这两个有理数也相等” 原命题是真命题,而逆命题是假命题 训练题:写出下列命题的逆命题,并判断它们是真 命题还是假命题。 (1)两直线平行,同旁内角相等。 (2)如果a是偶数,b是偶数,那么a+b是偶数。 (3)在直角三角形中,如果一个锐角等于30˚,那 么它所对的直角边等于斜边的一半。 (4)等腰三角形的两腰相等。
∴这个三角形不是直角三角形
∴没有与60m长的南北边线垂直的边线
∴没有一条边线为东西向
ⅳ、观察下面两个命题:
直角三角形两条直角边的平方和等于斜边的 平方。
如果一个三角形两边的平方和等于第三边的 平方,那么这个三角形是直角三角形。
它们的条件和结论之间有什么关系?
合作交流 ⅴ、观察下面三组命题:
如果两个角是对顶角,那么它们相等, 如果两个角相等,那么它们是对顶角; 如果小明患了肺炎,那么他一定发烧, 如果小明发烧,那么他一定患了肺炎;
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形; (2)两直线平行,同旁内角互补; (3)如果ab=0,那么a=0 b=0
解:(1)多边形是四边形.原命题是真命题, 而逆命题是假命题.
(2)同旁内角互补,两直线平行. 原命题与逆命题同为真命题.
(3)如果a=0,b=0,那么ab=0. 原命题是假命题,而逆命题
是真命题.
1.(钦州·中考)如图是一张直角三角形的纸片, 两直角边AC=6 cm,BC=8 cm,现将△ABC折叠, 使点B与点A重合,折痕为DE,则BE的长为( ) (A)4 cm (B)5 cm
三角形内角和定理证明ppt课件

(1) ∠ACD是△ABC的
CD
(2)∵∠ +∠ ∠ +∠
∴∠ = ∠
+∠ =180°(三角形三个内角的和等于180° )
=180°(平角的定义)
+∠
(
)
推论:三角形的一个外角等于与它不相邻的两个内角的和.
公理、定理及由它们直接推出来的 结论(推论),以后可以直接运用. 9
练一练:
已知:如图,AD是△ABC的角平分线,E是BC延长 线上一点,∠EAC=∠B,求证:∠ADE=∠DAE
B
∠A+∠B+∠AOB=180°(三角形三个内角的和等于180°)
O
∴∠A+∠B=180°-∠AOB
在⊿COD中 同理可得
∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
C
D
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D( 等量代换)
8
A
议一议:
B
如图所示:把△ABC的边BC延长,得到∠ACD.
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
1
2 C
辅助线
D
6
A
E
你还有什么
不同的方法?
B
P
AC
Q
B
H
C
B
A
E
C
7
试一试:
已知:如图,AC、BD相交于点O, 求证:∠A+∠B=∠C+∠D.
A 证明:
在⊿AOB中
CD
(2)∵∠ +∠ ∠ +∠
∴∠ = ∠
+∠ =180°(三角形三个内角的和等于180° )
=180°(平角的定义)
+∠
(
)
推论:三角形的一个外角等于与它不相邻的两个内角的和.
公理、定理及由它们直接推出来的 结论(推论),以后可以直接运用. 9
练一练:
已知:如图,AD是△ABC的角平分线,E是BC延长 线上一点,∠EAC=∠B,求证:∠ADE=∠DAE
B
∠A+∠B+∠AOB=180°(三角形三个内角的和等于180°)
O
∴∠A+∠B=180°-∠AOB
在⊿COD中 同理可得
∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
C
D
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D( 等量代换)
8
A
议一议:
B
如图所示:把△ABC的边BC延长,得到∠ACD.
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
1
2 C
辅助线
D
6
A
E
你还有什么
不同的方法?
B
P
AC
Q
B
H
C
B
A
E
C
7
试一试:
已知:如图,AC、BD相交于点O, 求证:∠A+∠B=∠C+∠D.
A 证明:
在⊿AOB中
北师大版八年级数学下册《线段的垂直平分线》三角形的证明PPT课件(第2课时)

实践探究,交流新知
解:(1)已知三角形的一条边及这条边上的高,能作出三角形,并且能作出无 数多个,如图所示. (2)已知等腰三角形的底边,用尺规作出等腰三角形,这样的等腰三角形也有 无数多个. (3)如果等腰三角形的底边和底边上的高都一定,这样的等腰三角形应该只有 两个,它们是全等的,且分别位于已知底边的两侧,如图所示.
北师大版 八年级下册 第一章 三角形的证明
线段的垂直平分线(第2课时 )
前言
学习目标
1.会证明三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,并 解决相关的问题. 2.会用尺规作已知线段的垂直平分线,培养尺规作图的技能.
学习重点
掌握三角形三条边的垂直平分线的性质,能利用尺规作出符合条件的三角形.
(1)教材第26页随堂练习. (2)教材第26页习题1.8第1,2题.
同学们, 下课!
. 39°
3.如图,在△ABC中,∠BAC是钝角. (1)画出边BC上的中线AD; (2)画出边BC上的高AH.
第1题
第2题
第3题
课堂小结,整体感知
1.课堂小结:请同学们回顾本节课所学的内容,有哪些收获? (1)三角形三条边的垂直平分线的性质 (2)尺规作线段的垂直平分线、等腰三角形
2.布置作业:
学习难点
三角形三条边的垂直平分线性质的证明及应用.
创设情境,导入新课
1.问题提出: 利用尺规作三角形三条边的垂直平分线,当作图完成后你发现了什么? 2.问题探究: ①三角形三边的垂直平分线交于一点; ②这一点到三角形三个顶点的距离相等.
创设情境,导入新课
3.问题解决: 如图,剪一个三角形纸片,通过折叠找出每条边的垂直平分线,观察这 三条垂直平分线,上述结论是否成立? 4.问题思考: 以上结论都是通过眼睛观察得到的,那么该结论一定成立吗?我们还需 运用已学过的公理和定理进行推理证明,这样,此发现才更有意义.
人教版11章《三角形》全章复习(共25张PPT)

例5 如图,在锐角△ABC中,CD、BE 分别是AB、AC边上的高,且CD、BE 交于一点P,若∠A=50°,则∠BPC的 度数是(B)
A.150° B.130° C.120° D.100°
例6 如图所示,BE与CD相交于点A,CF为∠BCD 的平分线,EF为∠BED的平分线。 (1)试探求∠F与∠B、∠D间有何等量关系。
(2)根据你的猜想,当n=4时说明∠BO3C的 度数成立.
解:当n=4时,代入所猜想的公式得 ∠BO3C=(1/4)×180°+(3/4)×∠A。
另外,在△BO3C中由三角形内角和定理 得:
∠BO[3]C=180°-(∠O3BC+∠O3CB) =180°-(3/4)(∠ABC+∠ACB) =180°-(3/4)(180°-∠A) =(1/4)×180°+(3/4)∠A
解:(1)∠D+∠B=2∠F ∵EF平分∠BED,CF平分∠BCD ∴∠DEF=(1/2)DEB,∠FCD=(1/2)∠BCD 而∠EMC=∠D+(1/2)∠BED,
∠EMC=∠F+(1/2)∠BCD ∴∠D+(1/2)∠BED=∠F+(1/2)∠BCD ① 同理可得: ∠B+(1/2)∠BCD=∠F+(1/2)∠BED ②
11章《三角形》 章末复习
R·八年级上册
知识框架
回顾思考
1.本章的主要内容是: 三角形的概念, 三角形的三边关系定理, 三角形的三条重要线段(高、中线和角平分线), 三角形内角和定理。
三角形的外角,多边形的内、外角和定理,简单 的平面镶嵌。
三角形的稳定性和四边形的不稳定性。
2.经历三角形内角和等于180°的验证与证明过 程,初步体验对一个规律的发展到发现确认艰 辛历程。体会证明的重要性,初步接触辅助线 在几何研究中不 可或缺的作用。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点,连结AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD; (2)AB=BC+AD.
上册第一章复习 ┃ 考点攻略
[解析] 这个有趣的问题是勾股定理的典型应用,此问题看上 去是一个曲面上的路线问题,但实际上能通过圆柱的侧面展开而 转化为平面上的路线问题,值得注意的是,在剪开圆柱侧面时, 要从 A 开始并垂直于 AB 剪开,这样展开的侧面才是个矩形,才 能得到直角,再利用勾股定理解决此问题.
上册第一章复习 ┃ 知识归类 8.三线共点
三角形三条边的垂直平分线相交于 一点 三角形三个顶点的距离 相等 .
9.角平分线的性质定理及判定定理
,并且这一点到
性质定理:角平分线上的点到这个角两边的距离 相等 判定定理:在一个角的内部,且到角的两边 距离 点,在这个角的平分线上.
.
相等的
上册第一章复习 ┃ 知识归类
上册第一章复习 ┃ 知识归类 逆定理:如果三角形两边的平方和等于第三边的平方,那 么这个三角形是 直角 三角形. 7.线段的垂直平分线的性质定理及判定定理 性质定理:线段的垂直平分线上的点到这条线段两个端点 的距离 相等 . 判定定理:到一条线段两个端点距离相等的点,在这条线 段的 垂直平分线 上. [点拨] 线段的垂直平分线可以看作和线段两个端点距离相 等的所有点的集合.
∴△FDE≌△ADE(ASA),∴DF=DA.
∵CD=DF+CF,∴CD=AD+BC.
上册第一章复习 ┃ 考点攻略
方法技巧 “截长补短法”是解决这一类问题的一种特殊方法,利用此 种方法常可使思路豁然开朗.掌握好“截长补短法”对于更好的 理解数学中的化归思想有较大的帮助.
上册第一章复习 ┃ 习题讲析
上册第一章复习 ┃ 考点攻略
证明:在CD上截取CF=BC,如图S1-9, 在△FCE与△BCE中, ∴△FCE≌△BCE(SAS),
∴∠2=∠1.
∵AD∥BC,∴∠ADC+∠BCD=180°. 又∠ADE=∠CDE, 图S1-9
上册第一章复习 ┃ 考点攻略
∴∠DCE+∠CDE=90°, ∴∠2+∠3=90°,∠1+∠4=90°, ∴∠3=∠4. 在△FDE与△ADE中,
上册第一章复习 ┃ 考点攻略 ► 考点四 例4 等腰三角形的判别
已知:在△ABC中,∠A=90°,AB=AC,D为BC的
中点.
(1) 如图 S1- 4, E, F分别是 AB, AC上的点,且 BE= AF, 求证:△DEF为等腰直角三角形; (2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其 他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的
结论.
上册第一章复习 ┃ 考点攻略
图S1-5
[ 解析 ] 要证明△ DEF 为等腰三角形,需要证 DE = DF. 连接 AD,利用全等可得这一结论.至于在延长线上,可利用同样的 方法.
上册第一章复习 ┃ 考点攻略
解:(1)证明:连接AD,如图S1-6:
∵AB=AC,∠BAC=90°,D为BC的中点, ∴AD⊥BC,BD=AD, ∴∠B=∠DAC=45°, 又BE=AF,
为5∶7∶9的三部分,分别种植不同的农作物,请你设计一种方
案.
图S1-12
上册第一章复习 ┃ 习题讲析 解:如图S1-13所示,分别作∠ACB和∠ABC的平分线,相
交于点D,连接AD,则S△ADC∶S△ADB∶S△BDC=5∶7∶9.
图S1-13
上册第一章复习 ┃ 习题讲析
9. 如图 S1 - 14 ,在四边形 ABCD 中, AD∥BC , E 为 CD 的中
[注意] 角的平分线是在角的内部的一条射线,所以它的逆 定理必须加上“在角的内部”这个条件.
10.三角形三条角平分线的性质 三角形的三条角平分线相交于一点,并且这一点到三条边 的距离 相等 .
上册第一章复习 ┃ 考点攻略
┃考点攻略┃
► 考点一
例1
线段垂直平分线的性质的应用
如图 S1 - 1 ,在△ ABC 中, DE 垂直平分 AC 交 AB 于 E ,
上册第一章复习 ┃ 考点攻略
方法技巧 等腰三角形的应用体现在利用等腰三角形的性质与判定上, 尤 其是“三线合一”的性质用来对线段或角进行转化, 从而摆脱用全 等三角形证明线段相等或角相等的思维定势, 更简捷地说明两线段 或角相等.在中考中,等腰三角形常与其他知识结合,综合性强, 多以证明或计算题出现.
上册第一章复习 ┃ 考点攻略 ► 考点五 例5 角平分线与“截长补短”
如图 S1 - 8 , AD∥BC ,点 E 在线段 AB 上,∠ ADE =
∠CDE,∠DCE=∠ECB.
求证:CD=AD+BC.
图S1-8
上册第一章复习 ┃ 考点攻略
[解析] 结论是CD=AD+BC,可考虑用“截长补短法”中的 “截长”,即在 CD 上截取 CF = CB ,只要再证 DF = DA 即可,这 就转化为证明两线段相等的问题,从而达到简化问题的目的.
上册第一章复习 ┃ 习题讲析
3.在直角三角形中,一条直角边长为a,另一条边长为2a,
那么它的三个内角之比为( D )
A.1∶2∶3 B.2∶2∶1 C.1∶1∶2 D.以上都不对
上册第一章复习 ┃ 习题讲析
4.如图 S1 - 9,△ ABC中,∠ ACB= 90°, BA 的垂直平分 线交 CB 边于 D ,若 AB = 10 , AC = 5 ,则图中等于 60°的角的个 数为( D ) A.2 B.3 C.4 D.5
上册第一章复习 ┃ 考点攻略 ► 考点三 勾股定理的应用
2 例 3 如图 S1-3,已知圆柱体底面圆的半径为 ,高为 2, π AB,CD 分别是两底面圆的直径,AD,BC 是母线,若一只小虫从 A 点出发,从侧面爬行到 C 点,求小虫爬行的最短路线的长度(结 果保留根号).
上册第一章复习 ┃ 考点攻略
解:答案不惟一,命题一:在△ABC和△DEF中,B,E,C, F在同一直线上,AB=DE,AC = DF,BE=CF.求证:∠ABC =∠DEF.
命题二:在△ABC和△DEF中,B,E,C,F在同一直线上, AB=DE,∠ABC=∠DEF,BE=CF.求证:AC=DF.
下面证明命题一:
已知:如题图,在△ABC和△DEF中,B,E,C,F在同一
第一章复习 ┃ 知识归纳 3.用反证法证明的一般步骤
(1)假设命题的结论不成立;
(2)从这个假设出发,应用正确的推论方法,得出与定义、公理、 已证定理或已知条件相矛盾的结果; (3)由矛盾的结果判定假设不正确,从而肯定命题的结论正确. 4.等边三角形的判定 (1)有一个角等于60°的 等腰 三角形是等边三角形;
∠A=30°,∠ACB=80°,则∠BCE=________. 50°
上册第一章复习 ┃ 考点攻略
[解析] 根据线段垂直平分线的性质,线段垂直平分线上的 点到线段两端点的距离相等,所以 EA = EC , ∠ A = ∠ ACE = 30°,又∠ACB=80°,故∠BCE=80°—30°=50°.
∴△BDE≌△ADF(SAS),
∴ED=FD,∠BDE=∠ADF, ∴△DEF为等腰直角三角形.
图 S1-6
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,
上册第一章复习 ┃ 考点攻略 (2)若E,F分别是AB,CA延长线上的点,如图S1-7所示: 连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
直线上,AB=DE,AC = DF,BE=CF.
求证:∠ABC=∠DEF.
上册第一章复习 ┃ 考点攻略 证明:在△ABC和△DEF中, ∵BE=CF,∴BC=EF.
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS).
∴∠ABC=∠DEF.
上册第一章复习 ┃ 考点攻略
方法技巧 与全等三角形有关的开放型试题形式多样, 设计新颖, 能培养 同学们的逆向思维能力、 创新能力和综合运用知识的能力. 解答条 件开放型试题,需要执果索因,逆向推理,逐步探求结论成立的条 件.同时要注意挖掘图形中的隐含条件,如对顶角、公共角、公共 边等,然后合理选择全等三角形的知识解决.另外,要注意这类题 的答案往往不唯一,只要合理即可.
图S1-10
上册第一章复习 ┃ 习题讲析 5.如图S1-11,在Rt△ABC中,∠C=90°,∠B=15°, DE是AB的中垂线,垂足为D,交BC于点E,若BE=4,则AC= ________. 2
图S1-11
上册第一章复习 ┃ 习题讲析
6.若点P是△ABC内一点,PD⊥AB于D,PE⊥BC于E, PF⊥AC于F,且PD=PE=PF,则点P是△ABC的( C ) A.三条高的交点 B.三条中线的交点
上册第一章复习 ┃ 知识归类 (2)三个角相等的三角形是等边三角形;
(4)有两个角等于60°的三角形是等边三角形. 5.直角三角形的性质 在直角三角形中,如果一个锐角等于 30°,那么它所对的直 角边等于斜边的 一半 . 6.勾股定理及其逆定理 勾股定理:直角三角形两条直角边的平方和等于斜边的 平方 .
∴AD=BD,AD⊥BC,
∴∠DAC=∠ABD=45°,
∴∠DAF=∠DBE=135°. 又AF=BE, ∴△DAF≌△DBE(SAS),
图S1-7
上册第一章复习 ┃ 考点攻略
∴FD=ED,∠FDA=∠EDB,
∴∠ EDF = ∠ EDB + ∠ FDB = ∠ FDA + ∠ FDB = ∠ ADB = 90°, ∴△DEF仍为等腰直角三角形.
1.以下命题中,是真命题的是( D )
A.两条直线只有相交和平行两种位置关系
B.同位角相等
C.两边和一角对应相等的两个三角形全等
D.等腰三角形底边中点到两腰的距离相等
上册第一章复习 ┃ 习题讲析 2.下列说法中,正确的是( C )
