磁介质的磁化规律
合集下载
10磁介质的磁化和介质中的安培环路定理(45)
顺磁质
内部各点处的小分子电流相互抵消， 内部各点处的小分子电流相互抵消，表面上的小分子 电流方向相同没有抵消， 电流方向相同没有抵消，相当在表面上有一层表面电 流流过。 磁化电流）（或束缚电流） ）（或束缚电流 流流过。（磁化电流）（或束缚电流）, 记作 Is。
7
对顺磁质和铁磁质,磁化电流产生的磁场 对顺磁质和铁磁质 磁化电流产生的磁场 是加强磁介质内部原磁场的; 是加强磁介质内部原磁场的 对抗磁质,磁化电流产生的磁场 对抗磁质 磁化电流产生的磁场 是削弱磁介质内部原磁场的。 是削弱磁介质内部原磁场的。 的大小反映了磁化的强弱。 磁化电流 Is的大小反映了磁化的强弱。
r r r 发现磁介质中的磁场： 发现磁介质中的磁场：B = B + B′ 0
r r r B = B0 + B′
I 长直密绕螺线管
r 传导电流 I → B0
磁介质上有磁化电流， 磁介质上有磁化电流，
r 磁化电流 I′ → B′
2
实验发现：充各种磁介质， 实验发现：充各种磁介质，磁介质内的磁场 有的比真空时弱， 有的比真空时强。 有的比真空时弱， 有的比真空时强。
ab
ab
∴ B = µ 0 µ r H = µ 0 µ r nI
∴ H ab = ∑ I c = n abI , H = nI
2.管内真空中 管内真空中 作环路 abcda ; 在环路上应用介 质中的安培环路定理，同理有： 质中的安培环路定理，同理有：
H = nI 真空中 µr = 1 ∴ B = µ 0 H = µ 0 nI
6
三
磁介质的磁化
在外磁场作用下磁介质出现磁性或磁性 发生变化的现象称为磁化。 发生变化的现象称为磁化。
磁场中的磁介质
矩
e ev 电子电流 I 2r / v 2r ev evr 2 m IS r 2r 2
m en
I S
e L 2m e
角动量 L me vr
二、原子的磁矩
2.电子的量子轨道磁矩
h L m, m 0,1,2, 1.05 10 34 J S 2 e 24 一个可能的值 m 9.27 10 J / T 2m e
分子电流为
dI n a 2 dr cos i
n m dr cos
M dr cos M dr
dI M dr
三、磁介质的磁化
若 dr 选在磁介质表面，则 d I 为面束缚电流。
面束缚电流密度
dI M cos M r j dr
电流为i，半径为 a，分子磁 矩为 m ,任取一微小矢量 dr 2 a 元 dr ，它与外磁场 B 的夹角 m i 为，则与 dr 套住的分子电 流的中心都是位于以为 dr 轴、 以 a2 为底面积的斜柱体内。 i
m
B
三、磁介质的磁化
若单位体积内的分子数为n ，则与 dr 套连的总
2.磁化强度
单位体积内分子磁矩的矢量和称作磁介质的 磁化强度。 mi M V
单位 安每米（A/m）
3.实验规律
实验发现，在外磁场不是很强时，对所有磁 介质
r 1 M BB
0 r
三、磁介质的磁化
3.束缚电流与磁化强度之间的关系
以顺磁质为例 , 等效分子
电子的自旋磁矩（内禀磁矩） 电子自旋角动量 内禀磁矩
s 2
玻尔磁子
e e mB s 9.27 10 24 J / T me 2me
e ev 电子电流 I 2r / v 2r ev evr 2 m IS r 2r 2
m en
I S
e L 2m e
角动量 L me vr
二、原子的磁矩
2.电子的量子轨道磁矩
h L m, m 0,1,2, 1.05 10 34 J S 2 e 24 一个可能的值 m 9.27 10 J / T 2m e
分子电流为
dI n a 2 dr cos i
n m dr cos
M dr cos M dr
dI M dr
三、磁介质的磁化
若 dr 选在磁介质表面，则 d I 为面束缚电流。
面束缚电流密度
dI M cos M r j dr
电流为i，半径为 a，分子磁 矩为 m ,任取一微小矢量 dr 2 a 元 dr ，它与外磁场 B 的夹角 m i 为，则与 dr 套住的分子电 流的中心都是位于以为 dr 轴、 以 a2 为底面积的斜柱体内。 i
m
B
三、磁介质的磁化
若单位体积内的分子数为n ，则与 dr 套连的总
2.磁化强度
单位体积内分子磁矩的矢量和称作磁介质的 磁化强度。 mi M V
单位 安每米（A/m）
3.实验规律
实验发现，在外磁场不是很强时，对所有磁 介质
r 1 M BB
0 r
三、磁介质的磁化
3.束缚电流与磁化强度之间的关系
以顺磁质为例 , 等效分子
电子的自旋磁矩（内禀磁矩） 电子自旋角动量 内禀磁矩
s 2
玻尔磁子
e e mB s 9.27 10 24 J / T me 2me
大学物理(7.6.1)--磁介质及磁化微观机制
大学物理
B Bm
- H m Br
Q
O
Pﾢ
Hc - Bm
P
H
+ Hm
磁滞回线
I0 反ﾢﾢ向H反I0 ﾢ向ﾢﾢﾢ B ﾢ H � ﾢ ﾢ+ H反m向B ﾢ IB0 ﾢm�—ﾢ -H饱Hﾢm和ﾢ磁�B感ﾢB强但=度不- B按m 原路返
当反I0 向= 0反I0, ﾢ向Hﾢ = 0 时H回ﾢB =ﾢBr反ﾢ向0 B ﾢ B仍r—不剩按余原磁路感返强回度 反当向反 II00 =ﾢ向0ﾢ, H = 0H时ﾢ ﾢ BB=ﾢ-Br 当 H = HC 时 B = 0
等效磁i 矩
mv '
（结果是一样
的）
说明： 这种效应在顺磁质中也有，不过与分子固有磁矩的
转向效应相比弱得多。
理学院 物理系 ( 张建锋 )
大学物理
三、铁磁质
1. 磁滞回线（ hysteresis loop ）
测
Φ
B
=
Φ S
测 I0 H = nI0
由此可得到 B ~ H 曲线 ：
理学院 物理系 ( 张建锋 )
理学院 物理系 ( 张建锋 )
大学物理
第六讲 磁介质及磁化微观机制
理学院 物理系 ( 张建锋 )
大学物理
第六讲：磁介质及磁化微观机制
一、磁介质
。
1. 磁
v E=
介质
-
v E0 +
：是经磁化后能
Ev ﾢ
+ +
+
v E0
v Eﾢ=
v+ E0
er
<
v E0
够
影
响磁
Bv =
磁介质的磁化规律
• 影响铁磁质磁性的因素
– 温度，高过居里点铁磁性就消失，变为顺磁质。如纯铁的居 里点为1043K，镝的居里点为89K；
– 强烈震动会瓦解磁畴 – 尺寸影响磁畴结构性——介观尺度下有新现象 – 介观尺度：即介于宏观尺度与微观尺度之间，一般为0.1——
100nm
宏观铁磁体的尺寸减小到介观尺度
• 此时磁性材料不再是具有畴壁的多磁畴结构，而 是没有畴壁的单畴结构，单畴的临界尺度大约在 纳米级范围，例如铁的球形颗粒产生单畴的临界 直径为28nm，钴为240nm。
与螺绕环类比
H B M0
0
B和M方向一致为
B0H0M B0i'0M
The End
谢谢您的聆听！
期待您的指正！
4 磁滞损耗
• 铁磁质在交变磁场下反复磁化时，由于磁滞 效应，磁体要发热而散失热量，这种能量损 失称为磁滞损耗。
• 可以证明：B－H图中磁滞回线所包围的“面 积”代表在一个反复磁化的循环过程中单位 体积的铁芯内损耗的能量
• 磁滞回线越胖，曲线下面积越大，损耗越大； • 磁滞回线越瘦，曲线下面积越小，损耗越小 • 证明 ，计算电源要抵抗感应电动势做功
导率为 r 的磁介质.当两圆筒
通有相反方向的电流 I时，
I
试 求（1）磁介质中任意点
r
P 的磁感应强度的大小;
d
（2）圆柱体外面一点Q 的磁感强度.
I
R
r
25
解 rdR
Hdl I 2πdHI
l
BH0rI
2πd
d R
HdlII0
I
l
r
2πdH0, H0
d
BH0
同理可求 dr, B0
I
R
– 温度，高过居里点铁磁性就消失，变为顺磁质。如纯铁的居 里点为1043K，镝的居里点为89K；
– 强烈震动会瓦解磁畴 – 尺寸影响磁畴结构性——介观尺度下有新现象 – 介观尺度：即介于宏观尺度与微观尺度之间，一般为0.1——
100nm
宏观铁磁体的尺寸减小到介观尺度
• 此时磁性材料不再是具有畴壁的多磁畴结构，而 是没有畴壁的单畴结构，单畴的临界尺度大约在 纳米级范围，例如铁的球形颗粒产生单畴的临界 直径为28nm，钴为240nm。
与螺绕环类比
H B M0
0
B和M方向一致为
B0H0M B0i'0M
The End
谢谢您的聆听！
期待您的指正！
4 磁滞损耗
• 铁磁质在交变磁场下反复磁化时，由于磁滞 效应，磁体要发热而散失热量，这种能量损 失称为磁滞损耗。
• 可以证明：B－H图中磁滞回线所包围的“面 积”代表在一个反复磁化的循环过程中单位 体积的铁芯内损耗的能量
• 磁滞回线越胖，曲线下面积越大，损耗越大； • 磁滞回线越瘦，曲线下面积越小，损耗越小 • 证明 ，计算电源要抵抗感应电动势做功
导率为 r 的磁介质.当两圆筒
通有相反方向的电流 I时，
I
试 求（1）磁介质中任意点
r
P 的磁感应强度的大小;
d
（2）圆柱体外面一点Q 的磁感强度.
I
R
r
25
解 rdR
Hdl I 2πdHI
l
BH0rI
2πd
d R
HdlII0
I
l
r
2πdH0, H0
d
BH0
同理可求 dr, B0
I
R
磁介质的磁化规律和机理-PPT精品文档
磁介质的磁化规律和机理
张炜
磁介质的分类
磁介质大体分为3类:
顺磁质 抗磁质 铁磁质
r m 1
磁 质 :m 0 r 1 r 1 顺 磁 质 :m 0 r 1 r 1 抗 2 3 铁 磁 质 : 0 1 (10 ~10 ) m r
c
R
C
Hc
O
R'
C'
Hபைடு நூலகம்
S'
局部的小磁滞回线
局部的小磁滞回线到处可以产生
B
H
去磁过程
B
H
d N SB dt 电 源 抵 抗 感 应 电 动 势 作 功 ： d d A I 0 d t I 0 d t I0d dt H dA N S d B S lH d B V H d B N /l 单 位 体 积 铁 芯 ， 电 源 作 功 为 ： dA da H dB V a
B0
抗磁质的磁化机制
每个分子无固有磁矩;(相互抵消) 在外场作用下,感生磁矩都与外场方向相反. 顺磁质: 抗磁效应比顺磁效应小被掩盖. 0 B B
0 0
+
V
-
+
V
-
m
f
m
0
f
超导体的迈斯纳效应
超导体的基本特性： 在低于特定温度Tc(转变温度),电阻为零; 完全抗磁(迈斯纳效应). 抗磁效应机制: 表面的超导电流产生的附加磁场将体内磁场完全 抵消.
i B
M B
I0
0
H
H nI 0
起始磁化曲线
饱和磁化强度Ms
B M H 0
张炜
磁介质的分类
磁介质大体分为3类:
顺磁质 抗磁质 铁磁质
r m 1
磁 质 :m 0 r 1 r 1 顺 磁 质 :m 0 r 1 r 1 抗 2 3 铁 磁 质 : 0 1 (10 ~10 ) m r
c
R
C
Hc
O
R'
C'
Hபைடு நூலகம்
S'
局部的小磁滞回线
局部的小磁滞回线到处可以产生
B
H
去磁过程
B
H
d N SB dt 电 源 抵 抗 感 应 电 动 势 作 功 ： d d A I 0 d t I 0 d t I0d dt H dA N S d B S lH d B V H d B N /l 单 位 体 积 铁 芯 ， 电 源 作 功 为 ： dA da H dB V a
B0
抗磁质的磁化机制
每个分子无固有磁矩;(相互抵消) 在外场作用下,感生磁矩都与外场方向相反. 顺磁质: 抗磁效应比顺磁效应小被掩盖. 0 B B
0 0
+
V
-
+
V
-
m
f
m
0
f
超导体的迈斯纳效应
超导体的基本特性： 在低于特定温度Tc(转变温度),电阻为零; 完全抗磁(迈斯纳效应). 抗磁效应机制: 表面的超导电流产生的附加磁场将体内磁场完全 抵消.
i B
M B
I0
0
H
H nI 0
起始磁化曲线
饱和磁化强度Ms
B M H 0
磁介质的磁化
得M到c重os要=关M系t是M磁t=化i 强或度者沿M介质n 表i面' 的切向分量，
介质表面磁化电流密度只决定于磁化强度沿该
表面的切向分量，与法向分量无关，只存在于介
质表面附近磁化强度有切向分量的地方。 7
四、有L B磁d介l 质磁0存场( i在强I0时度i 的矢i 安量Ii培) H环=L路(B0B0定M理M )
它与外壁之间充满均匀磁介质，电流从芯流过再沿
外壁流回。求介质中磁场分布及与导体
相邻的介质表面的束缚电流。
解
LH dl I L
H I 2πr
I
I
B
0rH 0r
H
B
M
,
0
I 2πr
j'
（R1<r<R2 )
M沿圆en切线j方' 向Men
j' (r 1)
磁介质内表面的
I 2πR
方向与轴平行
B1
即
S en
BdS
(B2
B1
B1)
(-enS) B2 (enS) 0
0 或B1n=B2n，表示从一种介质过
渡到另一种介质时，磁感应强度的法向分量不变。
10
在 介 质 分 界 面 处 作 一 矩 形 的 回 路 abcda ， 使 两
长边分别处于两种介质 中，与界面平行，短边很
小，取切向单位矢量
磁化强度矢量表征宏观磁性，定义 为单位体积内分子磁矩的矢量和
M
=
m
式中 m 是体积 内的分子磁矩或分子
感生磁矩的矢量和。
如果磁介质中各处的磁化强度的大小和方向都
一致，就称均匀磁化。在国际单位制中, 磁场强
度和磁化强度的单位都是Am-1 (安培/米)。3Βιβλιοθήκη 二、磁化的磁介质内的磁感应强度
磁介质的磁化及有磁介质存在时的磁场
2013/4/17
磁化强度矢量M和B的关系
磁介质磁化达到平衡后，一般说来，磁化
强度矢量M应由总磁感应强度B确定
BB
M和B之间的关系
0
B'
磁介质的磁化规律（通常由实验确定）
磁介质种类繁多，结构性质各异，磁介质中M
和B的关系很难归纳成一个统一的形式
线性磁介质
M kmB
非线性磁介质：
km
m 0
均与介 质性质 有关
M与介M质表n 面i'或磁M化t 电i' 流的面关磁化系电流密度
证明
在介质表面取闭合回路
穿过回路的磁化电流
I' i'l
b
b
a
M t dl
c
M=0
d
a
M dl a M dl b M dl c M dl d M dl
L
bc、da<< dl
M tl i' l M t i' 得证
以“分子电流”模型取代磁荷模型，从根 本上揭示了物质极化与磁化的内在联系
其实在安培时代，对于物质的分子、原子 结构的认识还很肤浅，电子尚未发现，所 谓“分子”泛指介质的微观基本单元
继续
2013/4/17
“磁荷”模型要点
磁荷有正、负，同号相斥，异号相吸 磁荷遵循磁的库仑定律（类似于电库仑定律） 定义磁场强度 H为单位点磁荷所受的磁场力 把磁介质分子看作磁偶极子 认为磁化是大量分子磁偶极子规则取向使正、负
附加场反过来要影响原来空间的 磁场分布。
各向同性的磁介质只有介质表面 处，分子电流未被抵销，形成磁 化电流
2013/4/17
磁化电流与传导电流
传导电流
磁介质的磁化
对于各向同性的顺磁质和抗磁质，存在 M m H，
表示对于各向同性的顺磁质和抗磁质，磁化强度与磁
场强度成正比。式中m 称为磁介质的磁化率。 B 0 (1 m )H ，r=1+m 称为磁介质的相对磁导率。
B 0 r H H
= 0 r 称为磁介质的绝对磁导率。 顺磁质m>0，r>1；抗磁质m<0，r<1；铁磁质m 和r都很大，都是H 的非单值函数，r>>1 。
具有强烈磁性的物质称为铁磁质(ferromagnet)，如 铁、钴、镍和它们的合金，稀土钴合金，钕—铁—硼 以及各种铁氧体等都属于此类。
铁磁晶体原子间存在交换作用，使相邻原子磁矩自 发彼此平行排列，抵御分子热运动的破坏作用。
分子磁矩为零时，电子在外磁场作用下产生一种附 加磁性。磁化强度方向总与外磁场方向相反，为抗磁 性 (diamagnetism) 。 具 有 这 种 磁 性 的 物 质 称 为 抗 磁 质，如汞、铜、铋、氢、氯、银、锌和铅等。
Mcos=Mt是磁化强度沿介质表面的切向分量，
得到重要关系Mt=i 或者 M n¸ i '。
介质表面磁化电流密度只决定于磁化强度沿该
表面的切向分量，与法向分量无关，只存在于介
质表面附近磁化强度有切向分量的地方。
四、有磁介质存在时的安培环路定理
¸ ¸ Bdl
L
¸ H dl
L
0( I0i Ii)
§2-7 磁介质的磁化
一、物质磁性的概述 磁介质(magnetic medium)是能够对磁场产生影响的
物质。由原子分子构成的物质都属于磁介质。
可以用电结构解释磁性。原子中每个电子同时参与 绕核的轨道运动和自旋两种运动，对应轨道磁矩和自 旋磁矩。整个原子的磁矩是它所包含的所有电子的轨 道磁矩和自旋磁矩的矢量和。
第15章磁介质
第15章磁介质一、物质的磁化1、磁介质中的磁场设真空中的磁感应强度为的磁场中，放进了某种磁介质，在磁场和磁介质的相互作用下，磁介质产生了附加磁场，这时磁场中任意一点处的磁感应强度2、磁导率由于磁介质产生了附加磁场磁介质中的磁场不再等于原来真空中的磁场，定义和的比值为相对磁导率：介质中的磁导率：式中为真空中的磁导率3、三种磁介质（1）顺磁质：顺磁质产生的与方向相同，且。
略大于1（2）抗磁质：抗磁质产生的与方向相反，且。
略小于1（3）铁磁质：铁磁质产生的与方向相同，且。
远大于1二、磁化强度1、磁化强度定义为单位体积中分子磁矩的矢量和即：2、磁化强度与分子面电流密度的关系：式中为磁介质外法线方向上的单位矢量。
3、磁化强度的环流即磁化强度对闭合回路的线积分等于通过回路所包围面积内的总分子电流三、磁介质中的安培环路定律1、安培环流定律在有磁介质条件下的应用即：2、磁场强度定义为：3、磁介质中的安培环路定律：4、应用磁介质中的安培环路定律的注意点：（1）的环流只与传导电流有关，与介质（或分子电流）无关。
（2）的本身（）既有传导电流也与分子电流有关。
既描写了传导电流磁场的性质也描写了介质对磁场的影响。
（3）要应用磁介质中的安培环路定律来计算磁场强度时，传导电流和磁介质的分布都必须具有特殊的对称性。
5、磁介质中的几个参量间的关系：（1）磁化率（2）与的关系（3）与等之间的关系四、磁场的边界条件（界面上无传导电流）ေ、壁介蔨分界面伤边磁感应强度的法向分量连廭，即Ҩ2、磁介谨分界面两龹的磁场强嚦纄切向分量连续，即：Ƞ3 磃感应线的折射定律ā＊怎义如图15-1所示）五、铁磁物贩q、磁畴：电子ꇪ旋磁矩取向相同的對区域。
2、磁化曲线（图55-2中曲线）ေ磁导率曲线（图15-2中??曲线）4、磁滞回线ေ图17耩3）图中乺矫끽嚛㠂5、铁磁质与非铁㳁质的主要区别：铁磁物质产生的附加磁场错误!未定义书签。
的比原来真空中的磁场大得多。
6、磁介质及其磁化特性
二、磁介质的分类
(1)顺磁质 r 1, 0 , B与B0同向 B B0 , ,
如：空气、氧、铝、铬、铂等。 实验表明，磁介质可分为三类：
如：水、氢、铜、铅、水银等。 (3)铁磁质 r 1, 0 , B与B0同向 B B0 , , 且r 不是常数它与B0 及磁化过程有关 : 铁、 , ,如 钴、镍等。 顺磁质、抗磁质对磁场的影响很小，称为弱磁 性物质。而铁磁质能显著增强磁场，故称为强磁性 物质。
假定在磁化场为零时铁 B 磁质处于未磁化的状态，当 Bm H逐渐增加时，B先是缓慢 c 增加(oa段)，然后经过一段 b 急剧的增加(ab段)之后，又 a 逐渐缓慢下来(bc段)，最后 O 当H很大时，B逐渐趋于饱 和(cs段)。
s
H
从未磁化到饱和磁化的这段曲线os，叫做 铁磁质的的起始磁化曲线；饱和值Bm称为饱和 磁感应强度。
大
0 I 小 dl 0 I小l小 方向 B小 弧 2 4 R 2 小 弧 4 R
方向
B
又 I 大 / I 小 l小 / l 大
BO B大 B小 0
P.27.6、如图，半径为R的带电圆盘，电荷面密度 为 ，圆盘以角速度 绕过盘心并垂直盘面的轴旋 转，则中心O处的磁感应强度大小为（A） （A）0R/2 （B） 0 R/4 （C） 0 R/6 （D） 0 R/8 解：任取一细环(如图) 其 周长为2 r，宽为dr 面积为 dS 2π rdr O r dB 电量为 dq σ dS σ 2π rdr r+dr 以转动时相当于圆电流
P34.5、如图所示，一根半径为R1 的长直圆柱形 铜导线(r=1)，外包一层相对磁导率为 r的圆筒状 顺磁质，顺磁质的外半径为R2，导线内有电流I从 纸面向里的方向流动，且电流I均匀分布在导线的 横截面上，求空间的磁感应强度和磁场强度。 I 解： j 2 πR1 磁场分布具有轴对称性 I
磁介质的磁化规律
2 起始磁化曲线：Ms、 Bs分别为饱和磁化强 度和饱和磁感应强度
M H
,
0r
B H
B 0(H M ) 0M
3 磁滞回线
当外磁场由 Hm 逐渐减小时，这种 B 的变化落后于H的变 化的现象，叫做磁滞 现象 ，简称磁滞.
由于磁滞，H 0 时，磁感强度 B 0 ，Br 叫做剩余磁感强 度(剩磁).
v L
mr
2v
i e ev e T 2 r 2
mvl
e 2m
v L
电子自旋磁矩
mvS
e m
v S
与角动量方向相反
若所有电子的总角动量为零，抗磁
所有电子的总角动量不为零 ，顺磁
• 考虑电子轨道运动，设电子角速度平行于外 磁场
– 求无外磁场时的角速度 0(电子只受库仑力）
➢对于各向同性线性磁介质
v
v
M mH
vv
v H
v B
v M
v
0
磁化率
v
v
B 0H 0M 0(1 m )H 0rH
➢B和M的关系为
v B
0r
v M
1
v M
相 对 磁 导 率
➢各向同性线性磁介质 m
km
m 0, 1, | m | 很小 M和B同向，顺磁质
• 对各向异性磁介质 m会因方位不同而不同，是
二阶张量
– 如铁磁质 M与H不成正比关系，甚至也不是单值关系 – M与H为非线性单值关系时，虽仍可用上述关系式定
义，但它们都不是恒量，而是H的函数，且m >>1，
M H
,
0r
B H
B 0(H M ) 0M
3 磁滞回线
当外磁场由 Hm 逐渐减小时，这种 B 的变化落后于H的变 化的现象，叫做磁滞 现象 ，简称磁滞.
由于磁滞，H 0 时，磁感强度 B 0 ，Br 叫做剩余磁感强 度(剩磁).
v L
mr
2v
i e ev e T 2 r 2
mvl
e 2m
v L
电子自旋磁矩
mvS
e m
v S
与角动量方向相反
若所有电子的总角动量为零，抗磁
所有电子的总角动量不为零 ，顺磁
• 考虑电子轨道运动，设电子角速度平行于外 磁场
– 求无外磁场时的角速度 0(电子只受库仑力）
➢对于各向同性线性磁介质
v
v
M mH
vv
v H
v B
v M
v
0
磁化率
v
v
B 0H 0M 0(1 m )H 0rH
➢B和M的关系为
v B
0r
v M
1
v M
相 对 磁 导 率
➢各向同性线性磁介质 m
km
m 0, 1, | m | 很小 M和B同向，顺磁质
• 对各向异性磁介质 m会因方位不同而不同，是
二阶张量
– 如铁磁质 M与H不成正比关系，甚至也不是单值关系 – M与H为非线性单值关系时，虽仍可用上述关系式定
义，但它们都不是恒量，而是H的函数，且m >>1，
第三节 介质的磁化规律.
第六章磁介质§3 介质的磁化规律（P605）1. 一环形铁芯横截面的直径为 4.0毫米 ,环的平均半径R= 15毫米 ,环上密绕着200匝线圈(见附图),当线圈导线通有25毫安的电流时,铁芯的(相对)磁导率μ=300,求通过铁芯横截面的磁通量Φ。
解：2.一铁环中心线的周长为 30厘米，横截面积为 1.0厘米 2，在环上紧密地绕有300匝表面绝缘的导线。
当导线中通有电流32毫安时，通过环的横截面的磁通量为2.0x10-6韦伯。
求：(1)铁环内部磁感强度的大小B；(2)铁环内部磁场强度的大小H；（3）铁的磁化率Χm和（相对）磁导率μ（4）铁环的磁化强度的大小M。
解：3.一螺绕环由表面绝缘的导线在铁环上密绕而成,每厘米绕有10匝;当导线中的电流为2.0安时,测得铁环内的磁感强度为1.0特斯拉。
求：（1）铁环内的磁场强度H；（2）铁环的磁极化强度J；（3）铁环的（相对）磁导率μ。
解：4.一无穷长圆柱形直导线外包一层磁导率为μ的圆筒形磁介质，导线半径为R1，磁介质的外半径为R2（见附图），导线内有电流I通过。
（1）求介质内，外的磁场强度和磁感应强度的分布，并画H-r，B-r曲线；（2）介质内，外表面的磁化面电流密度i’；（3）从磁荷观点来看，介质表面有无磁荷？解：5. 若§1习题6磁介质的磁导率μ=200，B=2.0特斯拉，求两空穴中心的H。
解：6. 一抗磁质小球的质量为 0.10克。
密度为ρ= 9.8克 /厘米3，磁化率为Χm=-1.82x10-4。
放在一个半径R= 10厘米的圆线圈的轴线上距圆心为l= 10厘米处（见附图）。
圈中载有电流I=100安。
求电流作用在这抗磁质小球上力的大小和方向。
[提示：参看§2习题13。
]解：7.附图是某种铁磁材料的起始磁化曲线，试根据这曲线求出最大磁导率μM，并绘制响应的μ-H曲线。
解：8. 附表中列出某种磁性材料的H和B的实验数据，（1）画出这种材料的起始磁化曲线；（2）求出表中所列出的各点处材料的（相对）磁导率μ；（3）求最大磁导率μM。
04磁介质的磁化和介质中的安培环路定理
解： 由螺线管的磁场分布 可知，管内的场各处均匀
R
r
a Bb
一致，管外的场为零；
H
1、介质内部
作 abcda 矩形回路。
d Ic
回路内的传导电流代数和为： I c n ab I
在环路上应用介质中的环路定理：
H dl H dl H dl H dl H dl
有半径为 R2的无限长同轴圆柱面，该面也通有电流 I，
圆柱面外为真空，在R1<r<R2区域内，充满相对介质常 数为 r2的 磁介质，且r2 >r1。求B和 H的分布?
解：根据轴对称性，以轴上一点为圆心在
垂直于轴的平面内取圆为安培回路：
r R1
H1
2rH1
I
2R12
I
R12
磁介质的磁化 磁介质中的高斯定 理和安培环路定理
1
一、磁介质的磁化现象
凡是能与磁场发生相互作用的物质叫磁介质。
磁场中放入磁介质
磁介质发生磁化
出现磁化电流
产生附加磁场
磁介质内部的总场强 B B0 B
在各向同性均匀介质中：
r 称为相对磁导率。
B内
r B0
磁介质的分类：
介质中的磁感 应强度是真空
美国在 磁谱仪中，将采用超导磁铁产生强磁场，
2003 年再次送入地球轨道，观察暗物质和反物质。
高温超导现已达到 -153°C。
11
L
对各B向同性的磁介质
dl
L 0r
I0内
B r B0
B
定义:磁场强度
H
0r
08磁介质的磁化和介质中的安培环路定理
0
磁力线为闭合曲线， 磁力线为闭合曲线，穿过任何一个闭合曲面的 磁通量为零。 磁通量为零。
v v B⋅ dS = 0 ∫
s
三、磁介质中的安培环路定理 1、磁介质中的安培环路定理
r r 在真空中的安培环路定理中： 在真空中的安培环路定理中： B0 ⋅ dl = µ 0 ∑ I ∫
3
r r 在介质中： 在介质中： ∫ B ⋅ dl = µ 0 ∑ ( I + I ′)
磁介质的磁化 磁介质中的高斯定 理和安培环路定理
1
一、磁介质的磁化现象 凡是能与磁场发生相互作用的物质叫磁介质。 凡是能与磁场发生相互作用的物质叫磁介质。 磁场中放入磁介质 磁介质发生磁化 产生附加磁场 r r r 磁介质内部的总场强 B = B0 + B′ 出现磁化电流
r r r B 在各向同性均匀介质中： 在各向同性均匀介质中： B = µ r B0 即 r = µ r B0
H = nI
H = nI 真空中 µ = 1 ∴ B = µ 0 H = µ 0 nI
8
r r r r H ⋅ dl = ∫da H ⋅ dl = 0
a
B
∴ H ab = ∑ I c = n abI ,
∴ B = µ 0 µ r H = µ 0 µ r nI
2、管内真空中 、 作环路 abcda ; 在环路上应用介 质中的安培环路定理，同理有： 质中的安培环路定理，同理有：
4
r r H ⋅ dl = ∑I ∫
L L
r r H ⋅ dl = ∑I ∫
L L
----磁介质中的环路定理 磁介质中的环路定理
物理意义：磁场强度沿闭合路径的线积分， 物理意义：磁场强度沿闭合路径的线积分，等于环路 所包围的传导电流的代数和。 所包围的传导电流的代数和。 2、明确几点： 明确几点：
磁力线为闭合曲线， 磁力线为闭合曲线，穿过任何一个闭合曲面的 磁通量为零。 磁通量为零。
v v B⋅ dS = 0 ∫
s
三、磁介质中的安培环路定理 1、磁介质中的安培环路定理
r r 在真空中的安培环路定理中： 在真空中的安培环路定理中： B0 ⋅ dl = µ 0 ∑ I ∫
3
r r 在介质中： 在介质中： ∫ B ⋅ dl = µ 0 ∑ ( I + I ′)
磁介质的磁化 磁介质中的高斯定 理和安培环路定理
1
一、磁介质的磁化现象 凡是能与磁场发生相互作用的物质叫磁介质。 凡是能与磁场发生相互作用的物质叫磁介质。 磁场中放入磁介质 磁介质发生磁化 产生附加磁场 r r r 磁介质内部的总场强 B = B0 + B′ 出现磁化电流
r r r B 在各向同性均匀介质中： 在各向同性均匀介质中： B = µ r B0 即 r = µ r B0
H = nI
H = nI 真空中 µ = 1 ∴ B = µ 0 H = µ 0 nI
8
r r r r H ⋅ dl = ∫da H ⋅ dl = 0
a
B
∴ H ab = ∑ I c = n abI ,
∴ B = µ 0 µ r H = µ 0 µ r nI
2、管内真空中 、 作环路 abcda ; 在环路上应用介 质中的安培环路定理，同理有： 质中的安培环路定理，同理有：
4
r r H ⋅ dl = ∑I ∫
L L
r r H ⋅ dl = ∑I ∫
L L
----磁介质中的环路定理 磁介质中的环路定理
物理意义：磁场强度沿闭合路径的线积分， 物理意义：磁场强度沿闭合路径的线积分，等于环路 所包围的传导电流的代数和。 所包围的传导电流的代数和。 2、明确几点： 明确几点：
大学物理第15章磁介质的磁化
pm
B
旋及绕核的轨道运动，对应有轨道
磁矩和自旋磁矩。
I
用等效的分子电流的磁效应来
表示各个电子对外界磁效应的总合，
称为分子固有磁矩。
顺磁质： Pm
未加外磁场时:
V内，
Pm
0
抗磁质： Pm 0
类比：电介质的微观图象
不显磁性
有极分子、无极分子。
2). 顺磁质的磁化
加外磁场时: M Pm B
2）有剩磁，去磁要有矫顽力Hc 3）具有使铁磁质性质消失的“居里点”。
装置如图所示：将悬挂着的镍片移近永久 磁铁，即被吸住，说明镍片在室温下具有 铁磁性。用酒精灯加热镍片，当镍片的温 度升高到超过一定温度时，镍片不再被吸 引，在重力作用下摆回平衡位置，说明镍 片的铁磁性消失，变为顺磁性。移去酒精 灯，稍待片刻，镍片温度下降到居里点以 下恢复铁磁性，又被磁铁吸住。
2r3
0
d
l
0
H 0 B 0 (R2 r)
15.3 铁磁质
一 磁化规律
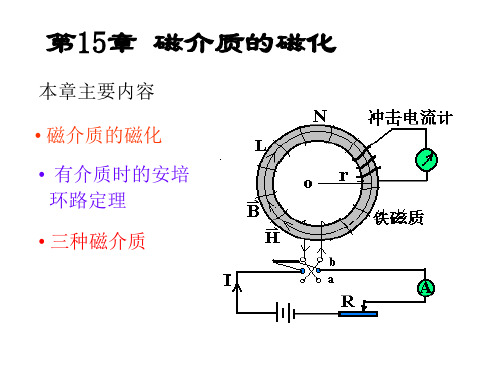
装置：螺绕环; 铁磁质
原理:励磁电流 I; H NI
用安培定理得H
2R
冲击电流计测量B
B r oH
铁磁质的 r 非线性；
起始磁化曲线；
磁饱和现象
B, r
B~H
r ~ H
H
起始磁化曲线；
饱和磁感应强度B S
磁滞回线--不可逆过程
式中N为螺绕环上线圈的总匝数。由对称性可知，在所取圆形 回路上各点的磁场强度的大小相等，方向都沿切线。
H 2r NI
当环内充满均匀介质时
H NI nI
2r
B H 0rH
B 0rnI
例：如图所示，一半径为R1的无限长圆柱体（导体 ≈0）中均
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
外圆柱面内一点到轴的垂直距离是 I I I
r1，以r1为半径作一圆，取此圆为积 分回路，根据安培环路定理有Biblioteka Hdl H
2r1 0
dl
I
H I
2r1
B
0 H
0
I
2 r1
（2）设在圆柱体内一点到轴的垂直距离是r2，则
以r2为半径作一圆，根据安培环路定理有
H
d
l
H
2r2
0
d
l
H
2r2＝I
r 2 2
迈斯纳效应：完全抗磁性
处于迈斯纳态的超导体会表现出完美抗磁性，或超抗磁性，意思是 超导体深处（离表面好几个穿透深度的地方）的总磁场非常接近零。 亦即是它们的磁化率 = −1。抗磁性体的定义为能产生自发磁化的 物料，且磁化方向与外加场直接相反。然而，超导体中抗磁性的基 本来源与一般材料的非常不同。在一般材料中，抗磁性是原子核旁 电子的轨道自旋，与外加磁场间电磁感应的直接结果。在超导体中， 完全抗磁性的原因是表面的超导电流所引起的，电流的流动方向与
的基本物理量。
例1 在均匀密绕的螺绕环内充满均匀的顺磁介质，
已知螺绕环中的传导电流为I ，单位长度内匝数 n ，环
的横截面半径比环的平均半径小得多，磁介质的相对磁 导率为 。求环内的磁场强度和磁感应强度。
解：在环内任取一点，
过该点作一和环同心、 半径为 的圆r形回路。
r
H dl NI
式中 为N螺绕环上线圈
进动 pm
L e
进动
pm
e
L
pm
pm
B0
进动 B0
可以证明：不论电子原来 的磁矩与磁场方向之 间的夹角是何值，在外磁场 B0中，电子角动量 L进 动这的种转等向 效总 圆是 电和 流的磁磁力矩矩的M方的向方永向远构与成右B0手的螺方旋向关相系反。。
磁矩，附用加符磁号矩：p因m表进示动。而产生的等效磁矩称为附加
M p Pm B sin
B
式中是质子自旋轴和磁场的夹角。在磁力矩
的作用下，质子以磁场为轴线作进动，在dt时间内
转角度d，角动量的增量为
dLp Lp sind
又因角动量的时间变化率等于力矩，即
Mp
dLp dt
或dLp
M pdt
所以 Lp sind＝PmB sindt
从而可求得质子在磁场中的进动角速度
定义
H
B为磁M场强度
0
(
B
M ) dl
0
I
有磁介质时的
则 H dl I
安培环路定理
磁介质中的安培环路定理：磁场强度沿任意
闭合路径的线积分等于穿过该路径的所有传导电流的 代数和，而与磁化电流无关。
H
B
M
0
B 0H 0M
实验证明：对于各向同性的介质，在磁介质中
任意一点磁化强度和磁场强度成正比。
R2
＝I
r2 2
R2
式中
I
r是22 该环路所包围的电流部分，由1 此得 1 R 2
1
H＝
Ir2
2R
2
1
B
0 H
0
Ir2
2 R12
（3）在圆柱面外取一点，它到轴的垂直距离 是r3，以r3为半径作一圆，根据安培环路定理,考
虑到环路 H中所 d包l围的电H流02的r代3 d数l和为0零，所以得
即 H 0
外加场相反（迈斯纳效应）；抗磁性并非只由轨道自旋所引起。
一个实验：在一个浅平的锡盘中，放入一个体积很小磁性很强的永久磁 铁，然后把温度降低，使锡出现超导性。这时可以看到，小磁铁竟然离 开锡盘表面，飘然升起，与锡盘保持一定距离后，便悬空不动了。这是 由于超导体的完全抗磁性，使小磁铁的磁力线无法穿透超导体，磁场发 生畸变，便产生了一个向上的浮力。进一步的研究表明：处于超导态的 物体，外加磁场之所以无法穿透它的内部，是因为在超导体的表面感生 一个无损耗的抗磁超导电流，这一电流产生的磁场，恰巧抵消了超导体 内部的磁场。这一发现非常有意义，在此之后，人们用迈斯纳效应来判 别物质是否具有超导性。
介质，在圆柱面上通有相反方向的电流I。试求（1） 圆柱体外圆柱面内一点的磁场；（2）圆柱体内一点磁 场；（3）圆柱面外一点的磁场。
解 （1）当两个无限长的同轴圆柱
体和圆柱面中有电流通过时，它们 所激发的磁场是轴对称分布的，而
R1 R2
磁介质亦呈轴对称分布，因而不会 r3
r2 r1
改变场的这种对称分布。设圆柱体
抗磁质的磁化：抗磁材料在外磁场的作用下，磁体内任意体 积元中大量分子或原子的附加磁矩的矢量和 有一定的量 值，结果在磁体内激发一个和外磁场方向相反的附加磁场， 这就是抗磁性的起源。它是一切磁介质所共有的性质 。
顺磁质的磁化：在顺磁体内任意取一体积元，其中各分子磁 矩的矢量和 将有一定的量值，因而在宏观上呈现出一个与外 磁场同向的附加磁场，这就是顺磁性的起源。它是一切磁介 质所共有的性质 。
例3 试求磁距为 pm=1.4×10-26A·m2，自旋角动量为 Lp=0.53×10-34kg·m2/s 的 质 子 , 在 磁 感 应 强 度 B 为 0.50T的均匀磁场中进动角速度.
解 质子带正电,它的 自旋磁距与自旋角动 量的方向相同,如图所 示.质子在磁场中受到 的磁力矩为
d
LP
dLP
M mH
式中 只m 与磁介质的性质有关，称为磁介质的
磁化率，是一个纯数。如果磁介质是均匀的，它
是一个常量；如果磁介质是不均匀的，它是空间
位置的函数。
m 0 顺磁质 m 0 抗磁质
B
0
H
0
M
M mH
B 0 (1 m )H
令 1 m
相对
磁导
率
B 0H
是反值映得磁注场意性：质的H为基研本究物介理质量中，的磁才B场r是提反供映方磁便场而性不质
的总匝数。由对称性可知，在所取圆形回路上各
点的磁感应强度的大小相等，方向都沿切线。
解： H d l NI
H 2r NI H NI nI 2r
r
当环内是真空时 B0 0H
当环内充满均匀介质时
B 0H
B
B0
, L
0
L0
例2 如图所示，一半径为R1的无限长圆柱体（导体
≈ 1 ）中均匀地通有电流I，在它外面有半径为R2的无 限长同轴圆柱面，两者之间充满着磁导率为的均匀磁
或 B0
二. 抗磁性和迈斯纳效应
电子的进动：在外磁场 B0的作用下，分子或原 子中和每个电子相联系的磁矩都受到磁力矩的作用， 由于分子或原子中的电子以一定的角动量作高速转动， 这时，每个电子除了保持环绕原子核的运动和电子本 身的自旋以外，还要附加电子磁矩以外磁场方向为轴 线的转动，称为电子的进动。
p
d
dt
PmB sin Lp sin