八年级数学经典压轴题:平行四边形
【常考压轴题】平行四边形存在性问题—2023-2024学年八年级数学下册(浙教版) (解析版)

平行四边形存在性问题【知识储备】①平行四边形是中心对称图形②中心对称图形的性质:对称中心平分中心对称图形内通过该点的任意线段,且使中心对称图形的面积被平分③中点公式: 类型一 几何背景下的平行四边形存在性问题【典题练习】1.(2023•河北二模)如图,在四边形ABCD 中,∠A =∠B =90°,AD =8cm ,BC =6cm ,点P 从点D 出发,以1cm /s 的速度向点A 运动,点M 从点B 同时出发,以相同的速度向点C 运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P 的运动时间为t (单位:s ),下列结论正确的是( )A .当t =3s 时,四边形ABMP 为矩形B .当t =4s 时,四边形CDPM 为平行四边形C .当CD =PM 时,t =3sD .当CD =PM 时,t =3s 或5s【分析】根据题意,表示出DP ,BM ,AP 和CM 的长,当四边形ABMP 为矩形时,根据AP =BM ,列方程求解即可;当四边形CDPM 为平行四边形,根据DP =CM ,列方程求解即可;当CD =PM 时,分两种情况:①四边形CDPM 是平行四边形,②四边形CDPM 是等腰梯形,分别列方程求解即可.【解答】解:根据题意,可得DP =t cm ,BM =t cm ,∵AD =8cm ,BC =6cm ,∴AP =(8﹣t )cm ,CM =(6﹣t )cm ,当四边形ABMP 为矩形时,AP =BM ,即8﹣t =t ,解得t =4,故A 选项不符合题意;当四边形CDPM 为平行四边形,DP =CM ,)2,2),(),,(21212211y y x x P y x B y x A ++坐标为(,则其中点若即t=6﹣t,解得t=3,故B选项不符合题意;当CD=PM时,分两种情况:①四边形CDPM是平行四边形,此时CM=PD,即6﹣t=t,解得t=3,②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示:则∠MGP=∠CHD=90°,∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD,∵AG=AP+GP=8﹣t+,又∵BM=t,∴8﹣t+=t,解得t=5,综上,当CD=PM时,t=3s或5s,故C选项不符合题意,D选项符合题意,故选:D.2.(2023春•盱眙县期末)如图,在▱ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动.点Q在BC边上以每秒4cm的速度从点C出发,在CB之间往返运动.两个点同时出发,当点P到达点D时停止(同时点Q也停止运动),设运动时间为t秒.当5<t<10时,运动时间t为何值时,以P、D、Q、B为顶点的四边形是平行四边形()A.B.8C.4或D.或8【分析】根据P的速度为每秒1cm,可得AP=t cm,从而得到PD=(10﹣t)cm,由四边形ABCD为平行四边形可得出PD∥BQ,结合平行四边形的判定定理可得出当PD=BQ时以P、D、Q、B四点组成的四边形为平行四边形,当5<t<10时,分两种情况考虑,在每种情况中由PD=BQ即可列出关于t的一元一次方程,解之即可得出结论.【解答】解:∵四边形ABCD为平行四边形,∴PD∥BQ.若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.当5<t≤时,AP=t cm,PD=(10﹣t)cm,CQ=(4t﹣20)cm,BQ=(30﹣4t)cm,∴10﹣t=30﹣4t,解得:t=;当<t≤10时,AP=t cm,PD=(10﹣t)cm,BQ=(4t﹣30)cm,∴10﹣t=4t﹣30,解得:t=8综上所述:当运动时间为秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.故选:D.3.(2022春•曹县期中)如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F 运动:点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q 也同时停止运动,当点P运动()秒时,以点P、Q、E、F为顶点的四边形是平行四边形.A.2B.3C.3或5D.4或5【分析】由平行四边形的性质可得AD∥BC,AD=BC,由平行线的性质可得BF=DF=12cm,可得AD =AF+DF=18cm=BC,由平行四边形的性质可得PF=EQ,列出方程可求解.【解答】解:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC∴∠ADB=∠MBC,且∠FBM=∠MBC∠ADB=∠FBM∴BF=DF=12cm∴AD=AF+DF=18cm=BC,∵点E是BC的中点∴EC=BC=9cm,∵以点P、Q、E、F为顶点的四边形是平行四边形∴PF=EQ∴6﹣t=9﹣2t,或6﹣t=2t﹣9∴t=3或5故选:C.4.(2023春•大竹县校级期末)如图,平行四边形ABCD的对角线AC,BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.若点E,F同时运动,设运动时间为t秒,当t=时,四边形AECF是平行四边形.【分析】先根据平行四边形的性质求出OB的长,从而得到OE的长,再由平行四边形的性质得到OE=OF进而得到关于t的方程,解方程即可.【解答】解:由题意得OE=OB﹣BE=OB﹣t,OF=2t,∵四边形ABCD是平行四边形,BD=12cm,∴OB=OD=6cm,∴OE=6﹣t,∵四边形AECF是平行四边形,∴OE=OF,∴6﹣t=2t,∴t=2,∴当t=2时,四边形AECF是平行四边形,故答案为:2.5.(2023秋•红山区校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度向点C运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点P运动到点C时,点Q随之停止运动,设运动的时间t(秒).(1)求DQ、PC的代数表达式;(2)当t为何值时,四边形PQDC是平行四边形;(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.【分析】(1)根据题意,写出代数表达式即可;(2)根据平行四边形的性质知DQ=CP,分当P从B运动到C时,当P从C运动到B时,两种情况进行求解即可;(3)分PQ=QD、PQ=PD、QD=PD三种情况讨论求出t值即可.【解答】解:(1)根据题意,DQ=(16﹣t)cm,PC=(21﹣2t)cm;(2)∵四边形PQDC是平行四边形,∴DQ=CP,当P从B运动到C时,∵DQ=AD﹣AQ=16﹣t,CP=21﹣2t,∴16﹣t=21﹣2t,解得:t=5,∴当t=5秒时,四边形PQDC是平行四边形;(3)当PQ=PD时,作PH⊥AD于H,则HQ=HD,∵cm,AH=BP,∴,∴.当PQ=QD时,QH=AH﹣AQ=BP﹣AQ=2t﹣t=t cm,QD=(16﹣t)cm,∵QD2=PQ2=t2+122,∴(16﹣t)2=122+t2,解得.当QD=PD时,DH=AD﹣AH=AD﹣BP=16﹣2t,∵QD2=PD2=PH2+HD2=122+16﹣2t)2,∴(16﹣t)2=122+(16﹣2t)2,即3t2﹣32t+144=0,∵Δ=(﹣32)2﹣4×3×144=﹣704<0,∴方程无实根,综上可知,当秒或秒时,△PQD是等腰三角形.6.(2023春•和平区校级月考)已知▱ABCD中,一动点P在AD边上,以每秒1cm的速度从点A向点D 运动.(1)如图1,运动过程中,若BP平分∠ABC,且满足AB=BP,求∠ABC的度数.(2)如图2,在(1)的条件下,连结CP并延长,与AB的延长线交于点F,连结DF,若CD=2cm,直接写出:△DPF的面积为cm2.(3)如图3,另一动点Q在BC边上,以每秒4cm的速度从点C出发,在BC间往返运动,两个点同时出发,当点P停止运动时Q点也停止,设运动时间为t(t>0),若AD=12cm,则t=秒时,以P、D、Q、B为顶点的四边形是平行四边形.【分析】(1)可证AB=AP,从而可证AB=BP=AP,即可求解;(2)设边CD上的高为h1,边BC上的高为h2,,可得S△DPF=S△P AB,即可求解;(3)当PD=BQ时,四边形PDBQ是平行四边形,进行分类讨论:①当12﹣t=12﹣4t时,②当12﹣t =24﹣4t时,③当12﹣t=4t﹣12时,④当12﹣t=4t﹣24时,⑤当12﹣t=36﹣4t时,⑥当12﹣t=4t﹣36时,即可求解.【解答】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠APB=∠CBP,∵BP平分∠ABC,∴∠ABP=∠CBP,∴∠ABP=∠APB,∴AB=AP,∵AB=BP,∴AB=BP=AP,∴△ABP是等边三角形,∴∠ABP=60°,∴∠ABC=120°.(2)如图,设边CD上的高为h1,边BC上的高为h2,,∵四边形ABCD是平行四边形,∴S△CDF=•CD=S▱ABCD,S△PBC=h2•BC=S▱ABCD,∴S△PBC=S△CDF=S▱ABCD,∴S△PCD+S△DPF=S▱ABCD,∴S△P AB+S△PCD=S▱ABCD,∴S△PCD+S△DPF=S△P AB+S△PCD,∴S△DPF=S△P AB,∵△ABP是等边三角形,∴S△DPF=S△P AB==3,故答案为:;(3)∵PD∥BQ,∴当PD=BQ时,四边形PDBQ是平行四边形,∵(s),∴0≤t<12,①当12﹣t=12﹣4t时,解得:t=0(不合题意,舍去);此时当P与A重合,Q与C重合;②当12﹣t=24﹣4t时,解得:t=4;③当12﹣t=4t﹣12时,解得:t=4.8;④当12﹣t=4t﹣24时,解得:t=7.2;⑤当12﹣t=36﹣4t时,解得:t=8;⑥当12﹣t=4t﹣36时,解得:t=9.6;综上所述:t为4秒或4.8秒或7.2秒或8秒或9.6秒.类型二“三定一动”求平行四边形的顶点坐标当平面直角坐标系中有3个定点,找第4个点形成平行四边形时:①设第4个点的坐标②以3个定点组成的3条线段为对角线分类讨论③以中心对称图形的性质为等量关系列式求解例,如图所示,平面直角坐标系内有A、B、C三点,在平面内找第4个点,构成平行四边形;【典题练习】7.(2022春•西双版纳期末)在平面直角坐标系中,点A、B、C的坐标分别是A(0,1),B(1,0),C(3,1),若以A,B,C,D为顶点的四边形是平行四边形,那么点D的坐标是.【分析】分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时;由平行四边形的性质容易得出点D的坐标.【解答】解:分三种情况:①BC为对角线时,点D的坐标为(4,0);②AB为对角线时,点D的坐标为(﹣2,0)③AC为对角线时,点D的坐标为(2,2)综上所述,点D的坐标是(﹣2,0)或(4,0)或(2,2);故答案为:(4,0)或(﹣2,0)或(2,2).8.(2018春•大邑县期末)如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;(2)在图中作出△ABC关于y轴的对称图形△A2B2C2;(3)若以点A,B,C,D为顶点的四边形为平行四边形时,请直接写出满足条件的点D的坐标.【分析】(1)根据关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)根据关于y轴对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可得到△A2B2C2;(3)分别以AB、BC、AC为对角线画平行四边形可得到D点坐标.【解答】解:(1)如图,△A11C1为所作;(2如图,△A2B2C2为所作;(3)满足条件的点D的坐标为(2,2)或(﹣4,﹣2)或(﹣6,4).9.(2023春•凤山县期末)如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,且OA,OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C,过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求直线AB的解析式;(2)若△ABC的面积为15,求点C的坐标;(3)在(2)的条件下,在坐标平面内是否存在点P,使以O,C,E,P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【分析】(1)根据绝对值和完全平方式的非负性得出OA和OB的值,然后确定A点和B点的坐标,用待定系数法求出直线AB的解析式即可;(2)根据△ABC的面积为15,得出AC的长,确定C点的坐标即可;(3)分情况根据平行四边形的性质分别求出P点的坐标即可.【解答】解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,∴A(﹣8,0),B(0,6),设直线AB的解析式为y=kx+b,代入A点和B点的坐标得,解得,∴直线AB的解析式为y=;(2)∵△ABC的面积为15,∴AC•OB=15,即AC×6=15,∴AC=5,∵OA=8,∴OC=OA﹣AC=8﹣5=3,即C(﹣3,0);(3)存在,∵D点在直线AB上,设D(a,a+6),∵BC平分∠ABO,∴CD=OC,即=3,解得a=﹣,∴D(﹣,),设直线DE的解析式为y=sx+t,∴,解得,∴直线DE的解析式为y=﹣x﹣4,∴E(0,﹣4),设点P的坐标为(m,n),①以CE为对角线时,此时以O,C,E,P为顶点的四边形是矩形,∵O(0,0),C(﹣3,0),E(0,﹣4),∴P(﹣3,﹣4);②以OE为对角线时,由平行四边形对角线互相平分可知,,解得,即P'(3,﹣4);③以OC为对角线时,由平行四边形对角线互相平分可知,,解得,即P''(﹣3,4);综上所述,符合条件的P点坐标为(﹣3,﹣4)或(3,﹣4)或(﹣3,4).类型三“两定两动”求平行四边形的顶点坐标当坐标系中有2个定点,且另外两个动点均在特殊的位置上时,方法策略同类型二。
八年级初二数学数学平行四边形试题含答案

(3)连接AF、DF,当△ADF是等腰三角形时,求t的值.
8.已知四边形ABCD是正方形,将线段CD绕点C逆时针旋转 ( ),得到线段CE,联结BE、CE、DE. 过点B作BF⊥DE交线段DE的延长线于F.
(1)如图,当BE=CE时,求旋转角 的度数;
(1)求证:CG平分∠DCB;
(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;
(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.
5.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF.
10.如图1,点 为正方形 的边 上一点, ,且 ,连接 ,过点 作 垂直于 的延长线于点 .
(1)求 的度数;
(2)如图2,连接 交 于 ,交 于 ,试证明: .
【参考答案】***试卷处理标记,请不要删除
一、解答题
1.(1)见解析;(2)
【分析】
(1)根据题意先证明四边形ABCD是平行四边形,再由AB=AD可得平行四边形ABCD是菱形;
(2)①当AE=3.5时,平行四边形CEDF是矩形.过A作AM⊥BC于M,求出BM=1.5,根据平行四边形的性质得到∠CDA=∠B=60°,DC=AB=3,BC=AD=5,求出DE=1.5=BM,证明△MBA≌△EDC(SAS),得到∠CED=∠AMB=90°,推出四边形CEDF是矩形;
②根据四边形CEDFCEDF是菱形,得到CD⊥EF,DG=CG=1212CD=1.5,求出∠DEG=30°,得到DE=2DG=3,即可求出AE=AD-DE=5-3=2.
2020-2021备战中考数学压轴题专题复习——平行四边形的综合含答案

2020-2021备战中考数学压轴题专题复习——平行四边形的综合含答案一、平行四边形1.如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.(1)求证:AD=EC;(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形即可;(2)由∠BAC=90°,AD是边BC上的中线,得AD=BD=CD,即可证明.【详解】(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AD是边BC上的中线,∴BD=DC,∴AE=DC,又∵AE∥BC,∴四边形ADCE是平行四边形.(2) 证明:∵∠BAC=90°,AD是边BC上的中线.∴AD=CD∵四边形ADCE是平行四边形,∴四边形ADCE是菱形.【点睛】本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条件灵活应用平行四边形的判定方法是证明的关键.2.如图(1)在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G 交AD于F(1)求证:AF=DE;(2)连接DG,若DG平分∠EGF,如图(2),求证:点E是CD中点;(3)在(2)的条件下,连接CG,如图(3),求证:CG=CD.【答案】(1)见解析;(2)见解析;(3)CG=CD,见解析.【解析】【分析】(1)证明△BAF≌△ADE(ASA)即可解决问题.(2)过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.想办法证明AF=DF,即可解决问题.(3)延长AE,BC交于点P,由(2)知DE=CD,利用直角三角形斜边中线的性质,只要证明BC=CP即可.【详解】(1)证明:如图1中,在正方形ABCD中,AB=AD,∠BAD=∠D=90o,∴∠2+∠3=90°又∵BF⊥AE,∴∠AGB=90°∴∠1+∠2=90°,∴∠1=∠3在△BAF与△ADE中,∠1=∠3 BA=AD ∠BAF=∠D,∴△BAF≌△ADE(ASA)∴AF=DE.(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.由(1)得∠1=∠3,∠BGA=∠AND=90°,AB=AD ∴△BAG≌△ADN(AAS)∴AG=DN,又DG平分∠EGF,DM⊥GF,DN⊥GE,∴DM=DN,∴DM=AG,又∠AFG=∠DFM,∠AGF=∠DMF∴△AFG≌△DFM(AAS),∴AF=DF=DE=12AD=12CD,即点E是CD的中点.(3)延长AE,BC交于点P,由(2)知DE=CD,∠ADE=∠ECP=90°,∠DEA=∠CEP,∴△ADE≌△PCE(ASA)∴AE=PE,又CE∥AB,∴BC=PC,在Rt△BGP中,∵BC=PC,∴CG=12BP=BC,∴CG=CD.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,角平分线的性质定理,直角三角形斜边中线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.3.(1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD 于点E ,交BC 于点F ,连接BE 、DF ,且BE 平分∠ABD .①求证:四边形BFDE 是菱形;②直接写出∠EBF 的度数;(2)把(1)中菱形BFDE 进行分离研究,如图②,点G 、I 分别在BF 、BE 边上,且BG=BI ,连接GD ,H 为GD 的中点,连接FH 并延长,交ED 于点J ,连接IJ 、IH 、IF 、IG.试探究线段IH 与FH 之间满足的关系,并说明理由;(3)把(1)中矩形ABCD 进行特殊化探究,如图③,当矩形ABCD 满足AB=AD 时,点E 是对角线AC 上一点,连接DE 、EF 、DF ,使△DEF 是等腰直角三角形,DF 交AC 于点G.请直接写出线段AG 、GE 、EC 三者之间满足的数量关系.【答案】(1)①详见解析;②60°.(2)IH =3FH ;(3)EG 2=AG 2+CE 2.【解析】【分析】(1)①由△DOE ≌△BOF ,推出EO =OF ,∵OB =OD ,推出四边形EBFD 是平行四边形,再证明EB =ED 即可.②先证明∠ABD =2∠ADB ,推出∠ADB =30°,延长即可解决问题.(2)IH =3FH .只要证明△IJF 是等边三角形即可.(3)结论:EG 2=AG 2+CE 2.如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,先证明△DEG ≌△DEM ,再证明△ECM 是直角三角形即可解决问题.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE 和△BOF 中,EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB =ED ,∴四边形EBFD 是菱形.②∵BE 平分∠ABD ,∴∠ABE =∠EBD ,∵EB =ED ,∴∠EBD =∠EDB ,∴∠ABD =2∠ADB ,∵∠ABD +∠ADB =90°,∴∠ADB =30°,∠ABD =60°,∴∠ABE =∠EBO =∠OBF =30°,∴∠EBF =60°.(2)结论:IH=3FH .理由:如图2中,延长BE 到M ,使得EM =EJ ,连接MJ .∵四边形EBFD 是菱形,∠B =60°,∴EB =BF =ED ,DE ∥BF ,∴∠JDH =∠FGH ,在△DHJ 和△GHF 中,DHG GHF DH GHJDH FGH ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DHJ ≌△GHF ,∴DJ =FG ,JH =HF ,∴EJ =BG =EM =BI ,∴BE =IM =BF ,∵∠MEJ =∠B =60°,∴△MEJ 是等边三角形,∴MJ =EM =NI ,∠M =∠B =60°在△BIF 和△MJI 中,BI MJ B M BF IM ⎧⎪∠∠⎨⎪⎩===,∴△BIF ≌△MJI ,∴IJ =IF ,∠BFI =∠MIJ ,∵HJ =HF ,∴IH ⊥JF ,∵∠BFI +∠BIF =120°,∴∠MIJ +∠BIF =120°,∴∠JIF =60°,∴△JIF 是等边三角形,在Rt △IHF 中,∵∠IHF =90°,∠IFH =60°,∴∠FIH =30°,∴IH=3FH .(3)结论:EG 2=AG 2+CE 2.理由:如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,∵∠FAD +∠DEF =90°,∴AFED 四点共圆,∴∠EDF =∠DAE =45°,∠ADC =90°,∴∠ADF +∠EDC =45°,∵∠ADF =∠CDM ,∴∠CDM +∠CDE =45°=∠EDG ,在△DEM 和△DEG 中,DE DE EDG EDM DG DM ⎧⎪∠∠⎨⎪⎩=== , ∴△DEG ≌△DEM ,∴GE =EM ,∵∠DCM =∠DAG =∠ACD =45°,AG =CM ,∴∠ECM =90°∴EC 2+CM 2=EM 2,∵EG =EM ,AG =CM ,∴GE 2=AG 2+CE 2.【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.4.如图,在平行四边形ABCD 中,AD ⊥DB ,垂足为点D ,将平行四边形ABCD 折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度5.已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).【答案】(1)见解析;(2)△APE、△APF、△CPF、△PGH.【解析】【分析】(1)由三角形中位线定理得出EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,推出EF∥GH,EF=GH,证得四边形EGHF是平行四边形,证得EF⊥AP,推出EF⊥EG,即可得出结论;(2)由△APE与△BPE的底AE=BE,又等高,得出S△APE=S△BPE,由△APE与△APF的底EP=FP,又等高,得出S△APE=S△APF,由△APF与△CPF的底AF=CF,又等高,得出S△APF=S△CPF,证得△PGH底边GH上的高等于△AEF底边EF上高的一半,推出S△PGH=12S△AEF=S△APF,即可得出结果.【详解】(1)证明:∵E、F、G、H分别是AB、AC、PB、PC的中点,∴EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,∴EF∥GH,EF=GH,∴四边形EGHF是平行四边形,∵AB=AC,∴AD⊥BC,∴EF⊥AP,∵EG∥AP,∴EF⊥EG,∴平行四边形EGHF是矩形;(2)∵PE是△APB的中线,∴△APE与△BPE的底AE=BE,又等高,∴S△APE=S△BPE,∵AP是△AEF的中线,∴△APE与△APF的底EP=FP,又等高,∴S△APE=S△APF,∴S△APF=S△BPE,∵PF是△APC的中线,∴△APF与△CPF的底AF=CF,又等高,∴S△APF=S△CPF,∴S△CPF=S△BPE,∵EF∥GH∥BC,E、F、G、H分别是AB、AC、PB、PC的中点,∴△AEF底边EF上的高等于△ABC底边BC上高的一半,△PGH底边GH上的高等于△PBC 底边BC上高的一半,∴△PGH底边GH上的高等于△AEF底边EF上高的一半,∵GH=EF,∴S△PGH=12S△AEF=S△APF,综上所述,与△BPE面积相等的三角形为:△APE、△APF、△CPF、△PGH.【点睛】本题考查了矩形的判定与性质、平行四边形的判定、三角形中位线定理、平行线的性质、三角形面积的计算等知识,熟练掌握三角形中位线定理是解决问题的关键.6.如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=13x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.(1)求边EF的长;(2)将正方形EFGH沿射线FB10个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).①当点F1移动到点B时,求t的值;②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积.【答案】(1)EF=15;(2)①10;②120;【解析】【分析】(1)根据已知点E(30,0),点D(0,40),求出直线DE的直线解析式y=-43x+40,可求出P点坐标,进而求出F点坐标即可;(2)①易求B(0,5),当点F1移动到点B时,1010=10;②F点移动到F'10t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,NFNF'=13,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,43MHEM'=,t=4,S=12×(12+454)×11=10238;当点G运动到直线DE上时,在Rt△F'PK中,PKF K'=13,PK=t-3,F'K=3t-9,在Rt△PKG'中,PKKG'=31539tt--+=43,t=7,S=15×(15-7)=120.【详解】(1)设直线DE的直线解析式y=kx+b,将点E(30,0),点D(0,40),∴30040k bb+=⎧⎨=⎩,∴4340kb⎧=-⎪⎨⎪=⎩,∴y=﹣43x+40,直线AB与直线DE的交点P(21,12),由题意知F(30,15),∴EF=15;(2)①易求B(0,5),∴BF=10,∴当点F 1移动到点B 时,t =101010÷=10; ②当点H 运动到直线DE 上时,F 点移动到F'的距离是10t ,在Rt △F'NF 中,NF NF '=13, ∴FN =t ,F'N =3t ,∵MH'=FN =t ,EM =NG'=15﹣F'N =15﹣3t ,在Rt △DMH'中,43MH EM '=, ∴41533t t =-, ∴t =4, ∴EM =3,MH'=4,∴S =1451023(12)11248⨯+⨯=; 当点G 运动到直线DE 上时,F 点移动到F'10,∵PF =10∴PF'10t ﹣10,在Rt △F'PK 中,13PK F K =', ∴PK =t ﹣3,F'K =3t ﹣9,在Rt △PKG'中,PK KG '=31539t t --+=43, ∴t =7,∴S =15×(15﹣7)=120.【点睛】本题考查一次函数图象及性质,正方形的性质;掌握待定系数法求函数解析式,利用三角形的正切值求边的关系,利用勾股定理在直角三角形中建立边之间的联系,准确确定阴影部分的面积是解题的关键.7.如图所示,矩形ABCD 中,点E 在CB 的延长线上,使CE =AC ,连接AE ,点F 是AE 的中点,连接BF 、DF ,求证:BF ⊥DF .【答案】见解析.【解析】【分析】延长BF ,交DA 的延长线于点M ,连接BD ,进而求证△AFM ≌△EFB ,得AM =BE ,FB =FM ,即可求得BC +BE =AD +AM ,进而求得BD =BM ,根据等腰三角形三线合一的性质即可求证BF ⊥DF .【详解】延长BF ,交DA 的延长线于点M ,连接BD .∵四边形ABCD 是矩形,∴MD ∥BC ,∴∠AMF =∠EBF ,∠E =∠MAF ,又FA =FE ,∴△AFM ≌△EFB ,∴AM =BE ,FB =FM .∵矩形ABCD 中,∴AC =BD ,AD =BC ,∴BC +BE =AD +AM ,即CE =MD .∵CE =AC ,∴AC =CE = BD =DM .∵FB =FM ,∴BF ⊥DF .【点睛】本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB =DM 是解题的关键.8.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.9.问题情境在四边形ABCD 中,BA =BC ,DC ⊥AC ,过点D 作DE ∥AB 交BC 的延长线于点E ,M 是边AD 的中点,连接MB ,ME.特例探究(1)如图1,当∠ABC =90°时,写出线段MB 与ME 的数量关系,位置关系;(2)如图2,当∠ABC =120°时,试探究线段MB 与ME 的数量关系,并证明你的结论; 拓展延伸(3)如图3,当∠ABC =α时,请直接用含α的式子表示线段MB 与ME 之间的数量关系.【答案】(1)MB =ME ,MB ⊥ME ;(2)ME =3MB .证明见解析;(3)ME =MB·tan 2α. 【解析】【分析】(1)如图1中,连接CM .只要证明△MBE 是等腰直角三角形即可;(2)结论:EM=3MB .只要证明△EBM 是直角三角形,且∠MEB=30°即可; (3)结论:EM=BM•tan2α.证明方法类似; 【详解】(1) 如图1中,连接CM .∵∠ACD=90°,AM=MD ,∴MC=MA=MD ,∵BA=BC ,∴BM 垂直平分AC ,∵∠ABC=90°,BA=BC ,∴∠MBE=12∠ABC=45°,∠ACB=∠DCE=45°, ∵AB ∥DE ,∴∠ABE+∠DEC=180°,∴∠DEC=90°,∴∠DCE=∠CDE=45°,∴EC=ED ,∵MC=MD ,∴EM 垂直平分线段CD ,EM 平分∠DEC ,∴∠MEC=45°,∴△BME 是等腰直角三角形,∴BM=ME ,BM ⊥EM .故答案为BM=ME ,BM ⊥EM .(2)ME =3MB .证明如下:连接CM ,如解图所示.∵DC ⊥AC ,M 是边AD 的中点,∴MC =MA =MD .∵BA =BC ,∴BM 垂直平分AC .∵∠ABC =120°,BA =BC ,∴∠MBE =12∠ABC =60°,∠BAC =∠BCA =30°,∠DCE =60°. ∵AB ∥DE ,∴∠ABE +∠DEC =180°,∴∠DEC =60°,∴∠DCE =∠DEC =60°,∴△CDE 是等边三角形,∴EC =ED .∵MC =MD ,∴EM 垂直平分CD ,EM 平分∠DEC , ∴∠MEC =12∠DEC =30°, ∴∠MBE +∠MEB =90°,即∠BME =90°.在Rt △BME 中,∵∠MEB =30°,∴ME 3.(3) 如图3中,结论:EM=BM•tan 2.理由:同法可证:BM ⊥EM ,BM 平分∠ABC ,所以EM=BM•tan 2. 【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.10.在矩形纸片ABCD 中,AB=6,BC=8,现将纸片折叠,使点D 与点B 重合,折痕为EF ,连接DF .(1)说明△BEF 是等腰三角形;(2)求折痕EF 的长.【答案】(1)见解析;(2).【解析】【分析】 (1)根据折叠得出∠DEF =∠BEF ,根据矩形的性质得出AD ∥BC ,求出∠DEF =∠BFE ,求出∠BEF =∠BFE 即可;(2)过E 作EM ⊥BC 于M ,则四边形ABME 是矩形,根据矩形的性质得出EM =AB =6,AE =BM ,根据折叠得出DE =BE ,根据勾股定理求出DE 、在Rt △EMF 中,由勾股定理求出即可.【详解】(1)∵现将纸片折叠,使点D 与点B 重合,折痕为EF ,∴∠DEF =∠BEF .∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠DEF =∠BFE ,∴∠BEF =∠BFE ,∴BE =BF ,即△BEF 是等腰三角形;(2)过E 作EM ⊥BC 于M ,则四边形ABME 是矩形,所以EM =AB =6,AE =BM .∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE==DE=BF,AE=8﹣DE=8﹣==BM,∴FM=﹣=.在Rt△EMF中,由勾股定理得:EF==.故答案为:.【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点,能熟记折叠的性质是解答此题的关键.11.如图,抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣32)两点,与x轴交于另一点B.(1)求经过A,B,C三点的抛物线的解析式;(2)过点C作CE∥x轴交抛物线于点E,写出点E的坐标,并求AC、BE的交点F的坐标(3)若抛物线的顶点为D,连结DC、DE,四边形CDEF是否为菱形?若是,请证明;若不是,请说明理由.【答案】(1)y=12x2+x﹣32;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。
八年级平行四边形压轴题

八年级平行四边形压轴题一、选择题(每题3分,共15分)1. 在平行四边形ABCD中,对角线AC与BD相交于点O,若AC = 8,BD = 10,AB = 6,则△OAB的周长为()- A. 12.- B. 15.- C. 20.- D. 16.- 解析:- 因为平行四边形对角线互相平分,所以OA = 1/2AC = 4,OB = 1/2BD = 5。
- 又已知AB = 6,所以△OAB的周长为OA+OB + AB=4 + 5+6 = 15。
答案为B。
2. 平行四边形ABCD中,∠A:∠B = 2:1,则∠C的度数为()- A. 60°.- B. 120°.- C. 45°.- D. 30°.- 解析:- 因为平行四边形邻角互补,即∠A+∠B = 180°,又∠A:∠B = 2:1,设∠B=x,则∠A = 2x,所以2x+x=180°,解得x = 60°。
- ∠A = 120°,平行四边形对角相等,所以∠C=∠A = 120°。
答案为B。
3. 下列条件中,不能判定四边形ABCD是平行四边形的是()- A. AB = CD,AD = BC.- B. AB∥CD,AB = CD.- C. AB = CD,AD∥BC.- D. AB∥CD,AD∥BC.- 解析:- 根据平行四边形的判定定理,A选项两组对边分别相等可判定是平行四边形;B 选项一组对边平行且相等可判定是平行四边形;D选项两组对边分别平行可判定是平行四边形。
- C选项一组对边相等,另一组对边平行,不能判定是平行四边形,答案为C。
4. 平行四边形ABCD的周长为36cm,AB = 8cm,则BC的长为()- A. 10cm.- B. 16cm.- C. 14cm.- D. 28cm.- 解析:- 平行四边形的周长等于两组对边之和,即2(AB + BC)=36,已知AB = 8cm,代入可得2(8 + BC)=36,16+2BC = 36,2BC = 20,BC = 10cm。
最新北师大版八年级下册数学期末复习压轴题练习试题以及答案

最新北师大版八年级下册数学期末复习压轴题练习试题以及答案八年级下册数学期末压轴题1.在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.1) 证明四边形ABCD是平行四边形;2) 若AB=3cm,BC=5cm,AE=1/3 AB,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,使△BEP为等腰三角形?2.△XXX的XXX在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与XXX重合,且DF=EF.1) 观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系;2) 将△DEF沿直线m向左平移到图(2)的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△XXX能否通过旋转重合?请证明你的猜想.3.在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.1) 观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;2) 当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;3) 当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)4.图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.1) 操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连结AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;2) 操作:若将图1中的△C′DE绕点C按顺时针方向任意旋转一个角度,连结AD,BE,如图3;在图3中,线段BE 与AD之间具有怎样的大小关系?证明你的结论;3) 根据上面的操作过程,请你猜想当为多少度时,线段AD的长度最大?是多少?当为多少度时,线段AD的长度最小?是多少?(不要求证明)之间的数量关系,并说明理由;2)证明你所得到的猜想;3)若平行四边形ABCD的周长为20且a+b+c+d=10求平行四边形ABCD的面积.5、在△ACB和△AED中,已知AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE。
经典平行四边形压轴题

1.如图,已知以△ABC 的三边为边在BC 的同侧作等边△ABD 、△BCE 、△ACF ,请回答下列问题: (1)四边形ADEF 是什么四边形?写出理由。
(2)当△ABC 满足什么条件时,四边形ADEF 是菱形?(3)当△ABC 满足什么条件时,以A 、D 、E 、F 为顶点的四边形不存在?2.(2009临沂)数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=o,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.ADFCGE B图1ADF C GE B 图2 ADFC GE B图3A G D BFE 图ADCBFEG图3.(2009年铁岭市)ABC △是等边三角形,点D 是射线BC 上的一个动点(点D 不与点B C 、重合),ADE △是以AD 为边的等边三角形,过点E 作BC 的平行线,分别交射线AB AC 、于点F G 、,连接BE . (1)如图(a )所示,当点D 在线段BC 上时. ①求证:AEB ADC △≌△;②探究四边形BCGE 是怎样特殊的四边形?并说明理由;(2)如图(b )所示,当点D 在BC 的延长线上时,直接写出(1)中的两个结论是否成立? (3)在(2)的情况下,当点D 运动到什么位置时,四边形BCGE 是菱形?并说明理由.4.(2009年日照市)已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG . (1)求证:EG =CG ;(2)将图①中△BEF 绕B 点逆时针旋转45º,如图②所示,取DF 中点G ,连接EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)D 第24题图① DDE第24题图②E第24题图③5(2009江西)如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①当点N 在线段AD 上时(如图2),PMN △的形状是否发生改变?若不变,求出PMN △的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由6.如图1,△ABC 是等腰直角三角形,四边形ADEF 是正方形,D 、F 分别在AB 、AC 边上,此时BD =CF ,BD ⊥CF 成立.(1)当正方形ADEF 绕点A 逆时针旋转θ(0°<θ<90°)时,如图2,BD =CF 成立吗?若成立,请证明;若不成立,请说明理由.(2)当正方形ADEF 绕点A 逆时针旋转45°时,如图3,延长BD 交CF 于点G . ①求证:BD ⊥CF ; ②当AB =4,AD =时,求线段BG 的长.A D EBF C图4(备AD E BF C图5(备ADE BF C图1 图2A D EB FC PNM 图3AD E BFCP N M321GEFD CBA(第25题)E FDCBA(第25题)EFD CBA(第25题)7.探究问题:⑴方法感悟: 如图①,在正方形ABCD 中,点E ,F 分别为DC ,BC 边上的点,且满足∠EAF=45°,连接EF ,求证DE+BF=EF .感悟解题方法,并完成下列填空:将△ADE 绕点A 顺时针旋转90°得到△ABG ,此时AB 与AD 重合,由旋转可得: AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°, ∴∠ABG+∠ABF=90°+90°=180°, 因此,点G ,B ,F 在同一条直线上.∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°. ∵∠1=∠2, ∴∠1+∠3=45°. 即∠GAF=∠_________. 又AG=AE ,AF=AF ∴△GAF ≌_______.∴_________=EF ,故DE+BF=EF .⑵方法迁移: 如图②,将ABC Rt ∆沿斜边翻折得到△ADC ,点E ,F 分别为DC ,BC 边上的点,且∠EAF=21∠DAB .试猜想DE ,BF ,EF 之间有何数量关系,并证明你的猜想. ⑶问题拓展:如图③,在四边形ABCD 中,AB=AD ,E ,F 分别为DC,BC 上的点,满足DAB EAF ∠=∠21,试猜想当∠B 与∠D 满足什么关系时,可使得DE+BF=EF .请直接写出你的猜想(不必说明理由).。
备战中考数学—平行四边形的综合压轴题专题复习含答案

备战中考数学—平行四边形的综合压轴题专题复习含答案一、平行四边形1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG⊥BE.过点O作OM⊥BE于点M,ON⊥AG于点N,与(2)同理,可以证明△AON≌△BOM,可得OMHN为正方形,所以HO平分∠BHG,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M 沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为多少(用含x的代数式表示);(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.【答案】(1)P点坐标为(x,3﹣x).(2)S的最大值为,此时x=2.(3)x=,或x=,或x=.【解析】试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.(3)本题要分类讨论:①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN 的长,联立CN的表达式即可求出x的值.试题解析:(1)过点P作PQ⊥BC于点Q,有题意可得:PQ∥AB,∴△CQP∽△CBA,∴∴解得:QP=x,∴PM=3﹣x,由题意可知,C(0,3),M(x,0),N(4﹣x,3),P点坐标为(x,3﹣x).(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,NC边上的高为,其中,0≤x≤4.∴S=(4﹣x)×x=(﹣x2+4x)=﹣(x﹣2)2+.∴S的最大值为,此时x=2.(3)延长MP交CB于Q,则有PQ⊥BC.①若NP=CP,∵PQ⊥BC,∴NQ=CQ=x.∴3x=4,∴x=.②若CP=CN,则CN=4﹣x,PQ=x,CP=x,4﹣x=x,∴x=;③若CN=NP,则CN=4﹣x.∵PQ=x,NQ=4﹣2x,∵在Rt△PNQ中,PN2=NQ2+PQ2,∴(4﹣x)2=(4﹣2x)2+(x)2,∴x=.综上所述,x=,或x=,或x=.考点:二次函数综合题.3.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.【解析】试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=AE,利用三角形全等证出AE=AF,而DM=AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN 是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性质.4.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.(1)如图①,当点D落在BC边上时,求点D的坐标;(2)如图②,当点D落在线段BE上时,AD与BC交于点H.①求证△ADB≌△AOB;②求点H的坐标.(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).【答案】(1)D(1,3);(2)①详见解析;②H(175,3);(3)30334-≤S 30334+【解析】【分析】(1)如图①,在Rt△ACD中求出CD即可解决问题;(2)①根据HL证明即可;②,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,根据AH2=HC2+AC2,构建方程求出m即可解决问题;(3)如图③中,当点D在线段BK上时,△DEK的面积最小,当点D在BA的延长线上时,△D′E′K的面积最大,求出面积的最小值以及最大值即可解决问题;【详解】(1)如图①中,∵A(5,0),B(0,3),∴OA=5,OB=3,∵四边形AOBC是矩形,∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°,∵矩形ADEF是由矩形AOBC旋转得到,∴AD=AO=5,在Rt△ADC中,CD=22=4,AD AC∴BD=BC-CD=1,∴D(1,3).(2)①如图②中,由四边形ADEF是矩形,得到∠ADE=90°,∵点D在线段BE上,∴∠ADB=90°,由(1)可知,AD=AO,又AB=AB,∠AOB=90°,∴Rt△ADB≌Rt△AOB(HL).②如图②中,由△ADB≌△AOB,得到∠BAD=∠BAO,又在矩形AOBC中,OA∥BC,∴∠CBA=∠OAB,∴∠BAD=∠CBA,∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,∵AH2=HC2+AC2,∴m2=32+(5-m)2,∴m=17,5∴BH=175,∴H(175,3).(3)如图③中,当点D在线段BK上时,△DEK的面积最小,最小值=12•DE•DK=12×3×(5-342)=303344-,当点D在BA的延长线上时,△D′E′K的面积最大,最大面积=12×D′E′×KD′=12×3×(5+342)=303344+.综上所述,303344-≤S≤303344+.【点睛】本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建方程解决问题.5.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.6.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.7.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E ,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。
初中八年级 平行四边形 拔高题 综合题 压轴题(含答案)

初中八年级平行四边形拔高题综合题压轴题(含答案)题目一已知平行四边形ABCD中,AB = 6cm,BC = 8cm,过点B作平行于AD的直线与AC交于点E,连接DE交BC的延长线于点F。
求EF的长度。
答案一连接DE并延长交BC于点G,根据平行四边形的性质,我们知道AG || DE。
所以AG || BF。
由此可得∆BFG与∆BCD为三角形对应边平行,则根据平行线截断比定理可知:$\frac{{BE}}{{BD}} = \frac{{FG}}{{GC}}$又已知$BE = BC + CE$,$CE = BD$,$BC = 8$,代入得:$\frac{{8+BD}}{{BD}} = \frac{{FG}}{{GC}}$整理可得:$\frac{{BD}}{{FG}} = \frac{{GC}}{{8+BD}}$ 由于$FG = GD$,所以:$\frac{{BD}}{{FG}} = \frac{{BD}}{{GD}} = 1$ 代入可得:$\frac{{1}}{{1}} = \frac{{GC}}{{8+BD}}$整理得:$BD = GC - 8$题目中已知BC=8,所以GC=16。
代入可得:$BD = 16 - 8 = 8$所以EF的长度等于BD,即EF=8cm。
题目二平行四边形PQRS中,已知PR = 5cm,PQ = 6cm,PS = 7cm。
点A在PS上,且PA的长度是PS的一半。
连接AQ并延长交QR 的延长线于点B,连接RP交QA的延长线于点C。
求BC的长度。
答案二设PS的长度为2x,则PA = x。
由平行四边形的性质可知AQ || RB,所以根据平行线截断比定理:$\frac{{RP}}{{PC}} = \frac{{AQ}}{{CQ}}$代入已知条件,得:$\frac{{2x + 6}}{{PC}} = \frac{{4}}{{2x - 6}}$ 整理可得:$(2x + 6)(2x - 6) = 4PC$解方程得:$x = 3$所以PA = 3cm。
专题05 平行四边形选填题压轴训练(原卷版)八年级数学下学期期中考试压轴题专练(人教版)

专题05 平行四边形选填题压轴训练(原卷版)一.选择题(共25小题)1.平行四边形一边长是10cm,那么它的两条对角线的长度可以是()A.8cm和6cm B.8cm和8cm C.8cm和12cm D.8cm和16cm2.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,且∠ACD=30°,DE∥BC交AC于点E,BF⊥CD于点F,连接EF.若AC=2,则EF的长是()A.2B.C.1D.3.如图,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E,O,F.下列结论正确的个数有()①四边形AFCE为菱形;②△ABF≌△CDE;③当F为BC中点时,∠ACD=90°.A.0个B.1个C.2个D.3个4.如图,在平行四边形ABCD中,N是CD的中点,AB=2BC,BN=m,AN=n,则CD的长为()A.+n B.m+C.D.5.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是P A、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形()A.AD=3B.AD=4C.AD=5D.AD=66.已知矩形ABCD,一条直线将该矩形分割成两个多边形,则所得任一多边形的内角和度数不可能是()A.180°B.360°C.540°D.720°7.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为()A.24B.24C.12D.128.如图,正方形ABCD的边长为3,点P为对角线AC上任意一点,PE⊥BC,PQ⊥AB,垂足分别是E,Q,则PE+PQ 的值是()A.B.3C.D.9.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是()A.3.5B.5.5C.6.5D.3.5或6.510.如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使四边形AECF是平行四边形,则添加的条件不能是()A.AE=CF B.BE=FD C.BF=DE D.∠1=∠211.如图,在▱ABCD中,BC=6,∠A=135°,S▱ABCD=12.若点E、F分别在边BC、AD上,且AF=CE,∠EFD=30°,则AF的长为()A.﹣1B.2﹣1C.6﹣6D.4﹣212.如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是()A.1B.2C.3D.413.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有()A.4个B.3个C.2个D.1个14.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为()A.2﹣2B.2C.3﹣1D.215.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=MF,④ME+MF=MB.其中正确结论的有()A.4个B.3个C.2个D.1个16.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,点B的横坐标为,则矩形AOBC的面积为()A.B.5C.D.317.如图,P为菱形ABCD内一动点,连接P A,PB,PD,∠APD=∠BAD=60°,AB=2,则PB+PD的最大值为()A.B.C.D.18.如图,在矩形ABCD中,AB=1,AD=,O是对角线的交点,过C作CE⊥BD于点E,EC的延长线与∠BAD的平分线相交于点H,AH与BC交于点F.给出下列四个结论:①AF=FH;②BF=BO;③AC=CH;④BE =3DE.其中正确结论有()A.1个B.2个C.3个D.4个19.如图,在平行四边形ABCD中,AD=2AB,作CE⊥AB于点E,点F是AD的中点,连接CF,EF.关于下列四个结论:①∠BCF=∠DCF;②∠FEC=∠FCE;③∠AEF=∠CFD;④S△CEF=S△BCE,则所有正确结论的序号是()A.①②③④B.①②③C.②③④D.③④20.如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是()A.2B.4C.D.221.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,④CF=BD=2,其中正确的是()A.①②③B.②③④C.①②④D.①③④22.如图,在正方形ABCD中,AB=4,AC与BD相交于点O,N是AO的中点,点M在BC边上,且BM=3,P 为对角线BD上一点,当对角线BD平分∠NPM时,PM﹣PN值为()A.1B.C.2D.23.矩形OABC在平面直角坐标系中的位置如图所示,已知B(2,2),点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作PD⊥PC,交x轴于点D.下列结论:①OA=BC=2;②当点D运动到OA的中点处时,PC2+PD2=7;③在运动过程中,∠CDP是一个定值;④当△ODP为等腰三角形时,点D的坐标为(,0).其中正确结论的个数是()A.1个B.2个C.3个D.4个24.在平面直角坐标系中,点B,C的坐标分别为B(﹣,﹣),C(,).任意一点A都满足|AB﹣AC|=2.作∠BAC的内角平分线AE,过点B作AE的垂线交AE于点F,已知当点A在平面内运动时,点F与坐标原点O的距离为()A.B.C.D.125.如图,正方形ABCD的边长为,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是()①∠DAE=∠DEA;②∠DMC=45°;③;④若MH=2,则S△CMD=A.1个B.2个C.3个D.4个二.填空题(共20小题)26.在平面直角坐标系中,已知三点O(0,0),A(1,﹣2),B(3,1),若以A、B、C、O为顶点的四边形是平行四边形,则点C的坐标为.27.如图,矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF的延长线交CD于点H.过F作MN ∥DC,交AD于M,交BC于N.若AB=6,则CH的长为.28.如图,在平行四边形ABCD中,∠ABC=135°,AD=4,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为.29.如图,等边△AOB,点C是边AO所在直线上的动点,点D是x轴上的动点,在矩形CDEF中,CD=6,DE =,则OF的最小值为.30.正方形ABCD中,点E、F分别在边BC、CD上,AE⊥BF于点G,过点F作AE的平行线,交AD于点M,交BC的延长线于点N,CN=3DM,AM=,则FG的长为.31.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q 同时出发秒后其中一个新四边形为平行四边形.32.如图,四边形ABCD是边长为4的菱形,∠C=60°,点P是射线CE上的动点,线段AP的垂直平分线MN 交AD于点F,连接PF,若△DPF是等腰三角形,则PF的长为.33.如图,在平行四边形ABCD中,∠B=60°,AB=6,BC=4,点E为边AB上的一个动点,连接ED并延长至点F,使得DE=2DF,以EC、EF为邻边构造平行四边形EFGC,连接EG,则EG的最小值为.34.如图是一个边长大于16cm的正方形,以距离正方形的四个顶点8cm处沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积.35.如图,菱形ABCD的顶点B、C在x轴上(B在C的左侧),顶点A、D在x轴上方,对角线BD的长是,点E(﹣2,0)为BC的中点,点P在菱形ABCD的边上运动,当点F(0,6)到EP所在直线的距离取得最大值时,点P恰好落在AB的中点处,则菱形ABCD的边长等于.36.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列四种说法:①CE⊥FG;②四边形ABGF是菱形;③BC=2EG;④∠DFC=∠EFG.正确的有.(填序号)37.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC =4,则BC2+DF2的值为.38.如图,△ABC中,∠BAC=90°,AB=BC=a,点D在边AC上运动(不与点A,C重合),以BD为边作正方形BDEF,使点A在正方形BDEF内,连接EC,则下列结论:①△BCD≌△ECD;②当CD=2AD时,∠ADE=30°;③点F到直线AB的距离为a;④△CDE面积的最大值是a2.其中正确的结论是(填写所有正确结论的序号)39.如图,正方形ABCD的对角线BD上有一点E,且BE=3DE,点F在AB的延长线上,连接EF,过点E作EG ⊥EF,交BC的延长线于点G,连接GF并延长,交DB的延长线于点P,若AB=4,BF=1,则线段EP的长是.40.在▱ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:①对于任意的点E,四边形BEDF都是平行四边形;②当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;③当AB<AD时,至少存在一个点E,使得四边形BEDF是菱形;④当∠ADB=45°时,至少存在一个点E,使得四边形BEDF是正方形.所有正确说法的序号是.41.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为.42.如图,在△ABC中,BC=12,AC=16,∠C=90°,M是AC边上的中点,N是BC边上任意一点,且2CN<BC,若点C关于直线MN的对称点C'恰好落在△ABC的中位线上,则CN=.43.如图,在矩形OAHC中,OC=8,OA=12,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动,动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM,CN,MN,设运动时间为t(秒)(0<t<10).则t=时,△CMN为直角三角形.44.如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为.45.已知正方形ABCD的边长为1,P为射线AD上的动点(不与点A重合),点A关于直线BP的对称点为E,连接PE,BE,CE,DE.当△CDE是等腰三角形时,AP的值为.。
2020-2021学年 苏科版八年级数学下册 中心对称图形平行四边形压轴题复习(二)

中心对称图形——平行四边形压轴题复习(二)1.如图,四边形ABCD是平行四边形,E、F分别为边AB、CD的中点,连接DE、DB、BF.(1)求证:∠DEB=∠BFD;(2)若∠ADB=90°,证明:四边形BFDE是菱形.2.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.(1)求证:四边形DEBF是平行四边形;(2)当DE=DF时,求四边形DEBF的面积S四边形DEBF.3.如图1,在正方形ABCD中,点E在AD的延长线上,P是对角线BD上的一点,且点P位于AE的垂直平分线上,PE交CD于点F.(1)猜测PC和PE有什么大小及位置关系,并给出证明.(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系.并说明理由.4.如图,在Rt△ABC中,∠BAC=90°,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC,AE分别交于点O,E,连接EC.(1)求证:四边形ADCE是菱形;(2)若AB=AO,OD=1,则菱形ADCE的周长为.5.如图,四边形ABCD是平行四边形,AC,BD相交于点O,∠1=∠2.它是一个矩形吗?为什么?6.如图,在矩形ABCD中,F是CD的中点,连接AF交BC延长线于点E.求证:BC=EC.7.如图,四边形ABCD为矩形,连接对角线AC,分别作∠BAC、∠BCA、∠ACD、∠DAC的角平分线AE、CE、CF、AF.(1)当AB=BC时,求证:四边形AECF是菱形;(2)设AB=4,BC=3,分别作EM⊥AC于点M,FN⊥AC于点N,求MN的长;(3)分别作EG⊥BC于点G,FH⊥CD于点H,当GC=3,HC=4时,求矩形ABCD的面积.8.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD 边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求DF的长.9.已知P是正方形ABCD边BC上一点,连接AP,作PE⊥AP,且∠DCE=45°.若PE 和CE交于E点,连接AE交CD于F.(1)求证:EP=AP;(2)若正方形的边长为4,CF=3,求CE的长.10.已知在△ABC中,AD平分∠BAC,交BC于点D,点E在边AC上AB=AE,过点E 作EF∥BC,交AD于点F,连接BF.(1)如图1,求证:四边形BDEF是菱形;(2)如图2,当AB=BC时,在不添加辅助线的情况下,请直接写出图中度数等于∠BAD 的2倍的所有的角.11.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB 上,EF⊥AB,OG∥EF.(1)OE AE(填<、=、>);(2)求证:四边形OEFG是矩形;(3)若AD=10,EF=4,求OE和BG的长.12.已知,如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.(1)求证:四边形ABEF是菱形;(2)若AE=12,BF=16,CE=5,求四边形ABCD的面积.13.如图,菱形ABCD中,E为AB边上的一点,F为BC延长线上的一点,且∠BED+∠F =180°求证:DE=DF.14.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.15.如图,在平行四边形ABCD中,线段AC的垂直平分线交AC于O,分别交BC,AD 于E,F,连接AE,CF.(1)证明:四边形AECF是菱形;(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=2,求四边形AECF的面积.参考答案1.(1)证明:∵四边形ABCD是平行四边形,∴DC=AB且DC∥AB,∵E,F分别为边AB、CD上的中点,∴DF=DC,BE=AB,且DF∥BE,∴DF=BE且DF∥BE,∴四边形BFDE是平行四边形,∴∠DEB=∠BFD;(2)证明:∵E为边AB的中点,∴AE=BE,∵∠ADB=90°,∴△ADB为直角三角形∴DE=AB=BE,由(1)得,四边形BFDE是平行四边形,∴平行四边形BFDE是菱形.2.(1)证明:∵四边形ABCD是矩形,∴DC∥AB,∴∠FDO=∠EBO,∵O是BD的中点,∴DO=BO,在△DFO和△BEO中,,∴△DFO≌△BEO(ASA),∴DF=BE,∵DC∥AB(即DF∥BE),∴四边形DEBF是平行四边形;(2)解:∵四边形ABCD是矩形,∴∠A=90°,∵AB=8,AD=6,∴BD===10,∵四边形DEBF是平行四边形,DE=DF,∴四边形DEBF是菱形,∴DE=BE,设DE=BE=x,在Rt△DAE中,AD2+AE2=DE2,即62+(8﹣x)2=x2,解得:x=,即BE=,∴四边形DEBF的面积S四边形DEBF=BE×AD=×6=.3.解:(1)PC=PE,PC⊥PE证明∵点P位于AE的垂直平分线上,∴PA=PE,∵四边形ABCD是正方形,∴AB=AC,∠ADB=∠CDB,∵PD=PD,∴△ABP≌△CBP(SAS)∴PA=PC,∴PC=PE,∵四边形ABCD是正方形,∴AD=CD,∠ADP=∠CBP,∵PB=PB,∴△ADP≌△CDP(SAS),∴∠PAD=∠PCD,∵PA=PE,∴∠PAD=∠E,∴∠PCD=∠E,∵∠PFC=∠DFE,∴△CPF∽△EDF,∴∠CPF=∠FDE,∵四边形ABCD是正方形,,∴∠ADC=90°,∴∠FDE=90°,∴∠CPF=90°,∴PC⊥PE.(2)PA=CE.理由如下:证明:∵点P位于AE的垂直平分线上,∴PA=PE,∵四边形ABCD是菱形,∴AB=AC,∠ADB=∠CDB,∵PD=PD,∴△ABP≌△CBP,∴PA=PC∴PC=PE,∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CBP,∵PB=PB,∴△ADP≌△CDP,∴∠PAD=∠PCD,∵PA=PE,∴∠PAD=∠PED,∴∠PCD=∠PED,∵∠PFC=∠DFE,∴△CPF∽△EDF,∴∠CPF=∠EDF,∵四边形ABCD是菱形,∠ABC=120°∴∠ADC=∠ABC=120°∴∠EDF=180°﹣∠ADC=60°∴∠CPF=60°∵PE=PC∴△PCE是等边三角形∴CE=PE∴AP=CE.4.(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE为平行四边形,∴AE=BD,∵AD是边BC上的中线,∴BD=CD,∴AE=CD,∴四边形ADCE是平行四边形,又∵∠BAC=90°,AD是边BC上的中线,∴AD=BC=CD,∴平行四边形ADCE是菱形;(2)解:∵四边形ADCE是菱形,∴AD=AE=CE=CD,AC⊥DE,OA=OC,∵BD=CD,∴OD是△ABC的中位线,∴AB=2OD=2,∴AO=AB=2,∴AD===,∴菱形ADCE的周长=4AD=4,故答案为:4.5.解:四边形ABCD是矩形.理由如下:证明:如图,∵四边形ABCD是平行四边形,∴OC=AC,OB=BD.又∵∠1=∠2,∴OB=OC,∴BD=AC,∴▱ABCD是矩形.6.证明:∵四边形ABCD是矩形,∴AD∥BE,AD=BC,∴∠ADF=∠ECF,∠DAF=∠CEF,∵F是CD的中点,∴DF=CF,∴在△ADF和△ECF中,∴△ADF≌△ECF(AAS).∴AD=EC,而AD=BC∴BC=EC.7.解:(1)∵四边形ABCD为矩形,∴AB∥CD,∴∠BAC=∠DCA,∵AE平分∠BAC,CF平分∠ACD,∴∠EAC=∠FCA,∴AE∥CF,同理,AF∥CE,∴四边形AECF是平行四边形,∵AB=BC,∴∠BAC=∠ACB,∵AE平分∠BAC,CE平分∠ACB,∴∠EAC=∠ECA,∴AE=CE,∴四边形AECF是菱形;(2)过E作EH⊥BC于点H,EG⊥AB于点G,∵∠B=90°,∴四边形BHEG为矩形,∵AE平分∠BAC,CE平分∠ACB,∴EM=EG=EH,∴四边形BHEG是正方形,∴BG=BH,∵EM=EG=EH,AE=AE,CE=CE,∴Rt△AEG≌Rt△AEM(HL),Rt△CEH≌Rt△CEM(HL),∴AM=AG,CM=CH,∵AB=4,BC=3,∴AC=5,设AM=AG=x,CM=CH=y,BH=BG=z,则,解得,,∴AM=3,CM=2,∵由(1)知四边形AECF是平行四边形,∴AF=CE,AF∥CE,∴∠FAN=∠ECM,∵∠ANF=∠CME=90°,∴△ANF≌△CME(AAS),∴AN=CM=2,∴MN=AM﹣AN=3﹣2=1;(3)过E作EK⊥AB于点K,EL⊥AC于点L,如图,∵矩形ABCD中AB∥CD,∴∠BAC=∠ACD,∵AE、CF分别平分∠BAC和∠ACD,∴∠KAE=∠HCF,∵四边形AECF是平行四边形,∴AE=CF,∵∠AKE=∠CHF=90°,∴△AEK≌△CHF(AAS),∴AK=CH=4,∵AE平分∠BAC,CE平分∠ACB,∴EK=EL=EG,∵AE=AE,CE=CE,∴Rt△AEK≌Rt△AEL(HL),Rt△CEG≌Rt△CEL(HL),∴AK=AL=4,CG=CL=3,∴AC=AL+CL=4+3=7,∵EK=EG,∠EKB=∠B=∠EGB=90°,∴四边形BGEK为正方形,∴BG=BK,∴矩形ABCD的面积=AB•BC=24.8.(1)证明:∵四边形ABCD是矩形,O是BD的中点,∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,∴∠OBE=∠ODF,∴△BOE≌△DOF(ASA),∴EO=FO,∴四边形BEDF是平行四边形;(2)解:当四边形BEDF是菱形时,BD⊥EF,设BE=x,则DE=x,AE=6﹣x,在Rt△ADE中,DE2=AD2+AE2,∴x2=42+(6﹣x)2,解得:x=,∵DF=.9(1)证明:连接AC,过P点作PG⊥BC交AC于G点,∵四边形ABCD是正方形,∴∠ACB=45°,∠BCD=90°,∵PG⊥BC,∴∠GPC=90°,∴∠PGC=45°,∴PG=PC,∵∠DCE=45°,∴∠AGP=∠ECP=90°+45°=135°,∵AP⊥PE,∴∠APE=∠GPC=90°,∴∠APG=∠EPC=90°﹣∠GPE,在△PAG和△PEC中∴△PAG≌△PEC(ASA),∴PE=PA;(2)解:延长CB到Q,使BQ=DF,过E作EH⊥BC,EH交BC延长线于H,连接AQ,PF,∵四边形ABCD是正方形,∴∠D=∠DAB=∠ABC=90°,AD=AB,∴∠ABQ=∠D=90°,在△ABQ和△ADF中∴△ABQ≌△ADF(SAS),∴AQ=AF,∠DAF=∠QAB,∵∠APE=90°,AP=PE,∴∠PAE=∠AEP=45°,∴∠AQP=∠QAB+∠BAP=∠DAF+∠BAP=∠DAB﹣∠PAE=90°﹣45°=45°=∠PAE,在△QAP和△FAP中∴△QAP≌△FAP(SAS),∴QP=PE,∵EH⊥BC,∠ABP=90°,∠APE=90°,∴∠ABP=∠H=90°,∠APB=∠PEH=90°﹣∠EPH,在△PEH和△APB中∴△PEH≌△APB(AAS),∴BP=EH,∵∠H=90°,∠DCE=45°,∴∠ECH=45°=∠CEH,∴CH=EH=BP,设EH=CH=BP=x,∴PC=4﹣x,PF=BQ+BP=DF+BP=4﹣3+x=1+x,在Rt△PCF中,由勾股定理得:(1+x)2=(4﹣x)2+32,解之得:x=,即CH=EH=,∴在Rt△CHE中,由勾股定理得:CE=CH=.10.解:(1)证明:∵AD平分∠BAC,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),∴DB=DE,∠BDA=∠EDA.∵EF∥BC,∴∠EFD=∠BDA,∴∠EFD=∠EDF,∴EF=ED,∴EF=BD,∵EF∥BD,∴四边形BDEF为菱形.(2)∵AD平分∠BAC,∴∠BAC=2∠BAD,∵AB=BC,∴∠BAC=∠BCA=2∠BAD,∵EF∥BC,∴∠FEC=∠BCA=2∠BAD,∵∠ABF=∠AEF,∴∠ABF=2∠BAD.所以图中度数等于∠BAD的2倍的所有的角:∠BAC,∠BCA,∠ABF,∠AEF.11.(1)解:∵四边形ABCD是菱形,∴AC⊥BD,∵E是AD的中点,∴OE=AD=AE,故答案为:=;(2)证明:∵四边形ABCD是菱形,∴OB=OD,∵E是AD的中点,∴OE是△ABD的中位线,∴OE∥FG,∵OG∥EF,∴四边形OEFG是平行四边形,∵EF⊥AB,∴∠EFG=90°,∴平行四边形OEFG是矩形;(3)解:∵四边形ABCD是菱形,∴BD⊥AC,AB=AD=10,∴∠AOD=90°,∵E是AD的中点,∴OE=AE=AD=5;由(1)知,四边形OEFG是矩形,∴FG=OE=5,∵AE=5,EF=4,∴AF===3,∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.12.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AFB=∠FBE,∵BF平分∠ABC,∴∠ABF=∠EBF,∴∠AFB=∠ABF,∴AF=AB,∵AE⊥BF,∴∠AOB=∠EOB=90°,OB=OB,∠ABO=∠EBO,∴△ABO≌△EBO(ASA),∴AB=BE,∴AF=BE,又AF∥BE,∴四边形ABEF是平行四边形,∵AB=BE,∴平行四边形ABEF是菱形.(2)如图,作AG⊥BC于点G,∵四边形ABEF是菱形,OA=OE=AE=6,OB=OF=BF=8,∴AB==10,BE=10,设BG=x,则EG=BE﹣BG=10﹣x,∴在Rt△ABG和Rt△AEG中,根据勾股定理,得AG2=AB2﹣BG2=AE2﹣EG2即102﹣x2=122﹣(10﹣x)2解得x=,∴AG==.∴四边形ABCD的面积为:BC•AG=15×=144.13.解:如图,过点D作DN⊥AB于N,DM⊥BC于F,∵四边形ABCD是菱形,∴AB=BC,∵S菱形ABCD=AB×DN=BC×DM,∴DN=DM,∵∠BED+∠F=180°,∠BED+∠AED=180°,∴∠F=∠AED,又∵∠DNE=∠DMF,∴△DNE≌△DMF(AAS)∴DE=DF.14.(1)证明:连接MN,如图1所示:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠B=90°,∴∠EAM=∠FCN,AC===5,∵M,N分别是AD,BC的中点,∴AM=DM=BN=CN,AM∥BN,∴四边形ABNM是平行四边形,又∵∠B=90°,∴四边形ABNM是矩形,∴MN=AB=3,在△AME和△CNF中,,∴△AME≌△CNF(SAS),∴EM=FN,∠AEM=∠CFN,∴∠MEF=∠NFE,∴EM∥FN,∴四边形EMFN是平行四边形,又∵AE=CF=1,∴EF=AC﹣AE﹣CF=3,∴MN=EF,∴四边形EMFN为矩形.(2)解:连接MN,作MH⊥BC于H,如图2所示:则四边形ABHM是矩形,∴MH=AB=3,BH=AM=x,∴HN=BC﹣BH﹣CN=4﹣2x,∵四边形EMFN为矩形,AE=CF=0.5,∴MN=EF=AC﹣AE﹣CF=4,在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,∴x=2﹣.15.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠OAF=∠OCE,∵EF是线段AC的垂直平分线,∴OA=OC,EF⊥AC,在△AOF和△COE中,,∴△AOF≌△COE(ASA),∴AF=CE,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形;(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,∴CE=AE=2,OA=OC,OB=OD,∵AC⊥AB,∴EF∥AB,∴∠OEC=∠B=30°,∴OC=CE=1,OE=OC=,∴AC=2OC=2,EF=2OE=2,∴四边形AECF的面积=AC×EF=×2×2=2.。
初二数学:平行四边形知识点总结及压轴题练习(附答案解析)

A C BD 初二平行四边形所有知识点总结和常考题知识点:1、平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
2、平行四边形的性质:⑴平行四边形的对边相等;⑵平行四边形的对角相等:⑶平行四边形的对角线互相平分。
3平行四边形的判定:⑴.两组对边分别相等的四边形是平行四边形; ⑵对角线互相平分的四边形是平行四边形;⑶两组对角分别相等的四边形是平行四边形; ⑷一组对边平行且相等的四边形是平行四边形。
4、矩形的定义:有一个角是直角的平行四边形。
5、矩形的性质:⑴矩形的四个角都是直角;⑵矩形的对角线相等。
6、矩形判定定理:⑴ 有三个角是直角的四边形是矩形;⑵对角线相等的平行四边形是矩形。
7、中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
(连接三角形两边中点的线段叫做三角形的中位线。
)8、菱形的定义 :有一组邻边相等的平行四边形。
9、菱形的性质:⑴菱形的四条边都相等;⑵菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
S 菱形=1/2×ab (a 、b 为两条对角线长)10、菱形的判定定理:⑴四条边相等的四边形是菱形。
⑵对角线互相垂直的平行四边形是菱形。
11、正方形定义:一个角是直角的菱形或邻边相等的矩形。
12正方形判定定理:⑴ 邻边相等的矩形是正方形。
⑵有一个角是直角的菱形是正方形。
(矩形+菱形=正方形)常考题:一.选择题(共14小题)1.矩形具有而菱形不具有的性质是( )A .两组对边分别平行B .对角线相等C .对角线互相平分D .两组对角分别相等2.平行四边形ABCD 中,AC 、BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形4.顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形5.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)6.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.117.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.168.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°9.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.1010.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.1711.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.812.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.1913.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF ⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣414.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°二.填空题(共13小题)15.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.16.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.17.如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.18.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD 和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为.19.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是.20.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.21.如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是.22.如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.23.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.24.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C (0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为.25.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标.26.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.27.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.三.解答题(共13小题)28.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.29.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.30.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.31.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.32.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.33.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.34.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?35.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.36.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:(1)△AEH≌△CGF;(2)四边形EFGH是菱形.37.如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.(1)求证:△ABD≌△EBD;(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.38.如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.39.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.40.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.初二平行四边形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2013•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分 D.两组对角分别相等【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.(2014•河池)平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD【分析】根据对角线相等的平行四边形是矩形判断.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B、是对角线相等,可推出平行四边形ABCD是矩形,故正确;C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D、无法判断.故选B.【点评】本题主要考查的是矩形的判定定理.但需要注意的是本题的知识点是关于各个图形的性质以及判定.3.(2008•扬州)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;C、有一个角是直角的平行四边形是矩形,故C选项正确;D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;综上所述,符合题意是D选项;故选:D.【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.4.(2011•张家界)顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【分析】顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.【解答】解:连接BD,已知任意四边形ABCD,E、F、G、H分别是各边中点.∵在△ABD中,E、H是AB、AD中点,∴EH∥BD,EH=BD.∵在△BCD中,G、F是DC、BC中点,∴GF∥BD,GF=BD,∴EH=GF,EH∥GF,∴四边形EFGH为平行四边形.故选:A.【点评】本题三角形的中位线的性质考查了平行四边形的判定:三角形的中位线平行于第三边,且等于第三边的一半.5.(2006•南京)在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).【解答】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),∵AB在x轴上,∴点C与点D的纵坐标相等,都为3,又∵D点相对于A点横坐标移动了2﹣0=2,∴C点横坐标为2+5=7,∴即顶点C的坐标(7,3).故选:C.【点评】本题主要是对平行四边形的性质与点的坐标的表示及平行线的性质和互为余(补)角的等知识的直接考查.同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合,但本题对学生能力的要求并不高.6.(2014•河南)如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【分析】利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO==5,∴BD=2BO=10,故选:C.【点评】本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.7.(2013•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.16【分析】在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD 沿EF翻折点B恰好落在AD边的B′处,所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等边三角形,由此可得出∠A′B′E=90°﹣60°=30°,根据直角三角形的性质得出A′B′=AB=2,然后根据矩形的面积公式列式计算即可得解.【解答】解:在矩形ABCD中,∵AD∥BC,∴∠DEF=∠EFB=60°,∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中,∵∠DEF=∠EFB=∠EB′F=60°∴△EFB′是等边三角形,Rt△A′EB′中,∵∠A′B′E=90°﹣60°=30°,∴B′E=2A′E,而A′E=2,∴B′E=4,∴A′B′=2,即AB=2,∵AE=2,DE=6,∴AD=AE+DE=2+6=8,∴矩形ABCD的面积=AB•AD=2×8=16.故选D.【点评】本题考查了矩形的性质,翻折变换的性质,两直线平行,同旁内角互补,两直线平行,内错角相等的性质,解直角三角形,作辅助线构造直角三角形并熟记性质是解题的关键.8.(2013•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°【分析】连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.【解答】解:如图,连接BF,在菱形ABCD中,∠BAC=∠BAD=×80°=40°,∠BCF=∠DCF,BC=DC,∠ABC=180°﹣∠BAD=180°﹣80°=100°,∵EF是线段AB的垂直平分线,∴AF=BF,∠ABF=∠BAC=40°,∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CDF=∠CBF=60°.故选:B.【点评】本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,综合性强,但难度不大,熟记各性质是解题的关键.9.(2015•河南)如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.10【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.【解答】解:连结EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO===4,∴AE=2AO=8.故选C.【点评】本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.10.(2013•凉山州)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.17【分析】根据菱形得出AB=BC,得出等边三角形ABC,求出AC,长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.【解答】解:∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,故选C.【点评】本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.11.(2013•泰安)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC 的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.8【分析】由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF 为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD 与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF 与三角形ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.故选:B【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.12.(2013•菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.19【分析】由图可得,S1的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=;然后,分别算出S1、S2的面积,即可解答.【解答】解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=x,x=CD,∴AC=2CD,CD==2,∴EC2=22+22,即EC=;∴S2的面积为EC2==8;∵S1的边长为3,S1的面积为3×3=9,∴S1+S2=8+9=17.故选:B.【点评】本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.13.(2013•连云港)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣4【分析】根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE 的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的倍计算即可得解.【解答】解:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4,∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=BE=×(4﹣4)=4﹣2.故选:C.【点评】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的判定与性质,根据角的度数的相等求出相等的角,再求出DE=AD是解题的关键,也是本题的难点.14.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE 相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.【解答】解:∵四边形ABCD是正方形,∴AB=AD,又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,∴∠ABE=∠AEB,∠BAE=90°+60°=150°,∴∠ABE=(180°﹣150°)÷2=15°,又∵∠BAC=45°,∴∠BFC=45°+15°=60°.故选:C.【点评】本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.二.填空题(共13小题)15.(2008•恩施州)已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为24cm2.【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半即:6×8÷2=24cm2.故答案为:24.【点评】此题主要考查菱形的面积等于两条对角线的积的一半.16.(2015•梅州)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD 的周长等于20.【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.【解答】解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,故答案为:20.【点评】本题考查了平行四边形的性质,解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB.17.(2013•厦门)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米.【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF 是△OAB的中位线即可得出EF的长度.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC+BD=24厘米,∴OA+OB=12cm,∵△OAB的周长是18厘米,∴AB=6cm,∵点E,F分别是线段AO,BO的中点,∴EF是△OAB的中位线,∴EF=AB=3cm.故答案为:3.【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.18.(2007•临夏州)如图,矩形ABCD的对角线AC和BD相交于点O,过点O 的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为3.【分析】根据矩形是中心对称图形寻找思路:△AOE≌△COF,图中阴影部分的面积就是△BCD的面积.【解答】解:∵四边形ABCD是矩形,∴OA=OC,∠AEO=∠CFO;又∵∠AOE=∠COF,在△AOE和△COF中,,∴△AOE≌△COF,∴S△AOE =S△COF,∴图中阴影部分的面积就是△BCD的面积.S△BCD=BC×CD=×2×3=3.故答案为:3.【点评】此题主要考查了矩形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为矩形面积的一半,是解决问题的关键.19.(2014•宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B 的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是(5,4).【分析】利用菱形的性质以及勾股定理得出DO的长,进而求出C点坐标.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D 在y轴上,∴AB=5,∴DO=4,∴点C的坐标是:(5,4).故答案为:(5,4).【点评】此题主要考查了菱形的性质以及坐标与图形的性质,得出DO的长是解题关键.20.(2015•黄冈)如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.【分析】根据正方形的性质得出∠BAE=∠DAE,再利用SAS证明△ABE与△ADE 全等,再利用三角形的内角和解答即可.【解答】解:∵正方形ABCD,∴AB=AD,∠BAE=∠DAE,在△ABE与△ADE中,,∴△ABE≌△ADE(SAS),∴∠AEB=∠AED,∠ABE=∠ADE,∵∠CBF=20°,∴∠ABE=70°,∴∠AED=∠AEB=180°﹣45°﹣70°=65°,故答案为:65【点评】此题考查正方形的性质,关键是根据正方形的性质得出∠BAE=∠DAE,再利用全等三角形的判定和性质解答.21.(2013•十堰)如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是1.【分析】根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.【解答】解:∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE=CD,即D为CE中点,∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,∵EF=,∴CE==2,∴AB=1,故答案为:1.【点评】本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.22.(2013•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF ⊥CD于F,∠B=60°,则菱形的面积为.【分析】根据已知条件解直角三角形ABE可求出AE的长,再由菱形的面积等于底×高计算即可.【解答】解:∵菱形ABCD的边长为4,∴AB=BC=4,∵AE⊥BC于E,∠B=60°,∴sinB==,∴AE=2,∴菱形的面积=4×2=8,故答案为8.【点评】本题考查了菱形的性质:四边相等以及特殊角的三角函数值和菱形面积公式的运用.23.(2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是11.【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.【解答】解:∵BD⊥CD,BD=4,CD=3,∴BC===5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=6,∴四边形EFGH的周长=6+5=11.故答案为:11.【点评】本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.24.(2015•攀枝花)如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).【分析】由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.【解答】解:∵四边形OABC是矩形,∴∠OCB=90°,OC=4,BC=OA=10,∵D为OA的中点,∴OD=AD=5,①当PO=PD时,点P在OD得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,PC==3,∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3;分两种情况:当E在D的左侧时,如图2所示:OE=5﹣3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故答案为:(2.5,4),或(3,4),或(2,4),或(8,4).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.25.(2013•阜新)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D 的坐标(3,2),(﹣5,2),(1,﹣2).【分析】首先根据题意画出图形,分别以BC,AB,AC为对角线作平行四边形,即可求得答案.【解答】解:如图:以A,B,C为顶点的平行四边形的第四个顶点D的坐标分别为:(3,2),(﹣5,2),(1,﹣2).故答案为:(3,2),(﹣5,2),(1,﹣2).【点评】此题考查了平行四边形的性质.注意坐标与图形的关系.26.(2014•丹东)如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.【分析】延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF 是等边三角形,再利用菱形的边长为4求出时间t的值.。
人教备战中考数学压轴题之平行四边形(备战中考题型整理,突破提升)附详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C 关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.(1)求∠FDP的度数;(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)连接AC,若正方形的边长为2,请直接写出△ACC′的面积最大值.【答案】(1)45°;(2)BP+DP2AP,证明详见解析;(32﹣1.【解析】【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=12∠ADC=45°;(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;(3)先作高线C'G,确定△ACC′的面积中底边AC为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C'D,∠CDE=∠C'DE,在正方形ABCD中,AD=CD,∠ADC=90°,∴AD=C'D,∵F是AC'的中点,∴DF⊥AC',∠ADF=∠C'DF,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠PAP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP=90°∴∠APD=45°,∴∠P'=45°,∴AP=AP',在△BAP和△DAP'中,∵BA DABAP DAP AP AP'=⎧⎪∠=∠⎨='⎪⎩,∴△BAP≌△DAP'(SAS),∴BP=DP',∴DP+BP=PP'=2AP;(3)如图,过C'作C'G⊥AC于G,则S△AC'C=12AC•C'G,Rt△ABC中,AB=BC2,∴AC22(2)(2)2+=,即AC为定值,当C'G最大值,△AC'C的面积最大,连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,∵CD =C 'D =2,OD =12AC =1, ∴C 'G =2﹣1,∴S △AC 'C =112(21)2122AC C G '•=⨯-=-. 【点睛】 本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.2.如图,四边形ABCD 中,∠BCD =∠D =90°,E 是边AB 的中点.已知AD =1,AB =2. (1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域;(2)当∠B =70°时,求∠AEC 的度数;(3)当△ACE 为直角三角形时,求边BC 的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2117+. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-,则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD=AE=1,∴∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,∴∠AEC=70°+35°=105°.(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,则在△ABH中,∠B=60°,∠AHB=90°,AB=2,得BH=1,于是BC=2.②当∠CAE=90°时,易知△CDA∽△BCA,又2224AC BC AB x=-=-,则2241174AD CA xxAC CB x-±=⇒=⇒=-(舍负)易知∠ACE<90°,所以边BC的长为117+.综上所述:边BC的长为2或1172+.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.3.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E 是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.【答案】(1)见解析;(2)S平行四边形ADBC273【解析】【分析】(1)在Rt△ABC中,E为AB的中点,则CE=12AB,BE=12AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD//BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,求出BC,AC即可解决问题;【详解】解:(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°,在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,∵E为AB的中点,∴AE=BE,又∵∠AEF=∠BEC,∴△AEF≌△BEC,在△ABC中,∠ACB=90°,E为AB的中点,∴CE=12AB,BE=12AB,∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,∴四边形BCFD是平行四边形;(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,∴BC=AF=3,AC=33,∴S平行四边形BCFD=3×33=93,S△ACF=12×3×33=93,S平行四边形ADBC=2732.【点睛】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.4.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度5.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;(2)如图②,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=27,当CF=1时,请直接写出BE的长.【答案】(1)CA=CE+CF.(2)CF-CE=43AC.(3)BE的值为3或5或1.【解析】【分析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵7,∴22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.6.如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC过点P 作PE⊥PC交直线AB于E.(1)求证:PC=PE;(2)延长AP交直线CD于点F.①如图2,若点F是CD的中点,求△APE的面积;②若ΔAPE的面积是21625,则DF的长为(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ,MQ,过点P作PN∥CD交EC于点N,连接QN,若PQ=5,MN=723,则△MNQ的面积是【答案】(1)略;(2)①8,②4或9;(3)5 6【解析】【分析】(1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;(2)作出△ADP和△DFP的高,由面积法容易求出这个高的值.从而得到△PAE的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;(3)根据已经条件证出△MNQ是直角三角形,计算直角边乘积的一半可得其面积.【详解】(1) 证明:∵点P在对角线BD上,∴△ADP ≌△CDP ,∴AP=CP , ∠DAP =∠DCP ,∵PE ⊥PC ,∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP =90°-∠DCP ,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;(2)①如图2,过点P 分别作PH ⊥AD,PG ⊥CD,垂足分别为H 、G.延长GP 交AB 于点M.∵四边形ABCD 是正方形,P 在对角线上,∴四边形HPGD 是正方形,∴PH=PG,PM ⊥AB,设PH=PG=a,∵F 是CD 中点,AD =6,则FD=3,ADF S=9, ∵ADF S=ADP DFP S S +=1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4,又∵PA=PE,∴AM=EM,AE=4,∵APE S =1144822EA MP ⨯=⨯⨯=, ②设HP =b,由①可得AE=2b,MP=6-b,∴APE S =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或,∵ADF S =ADP DFP S S +=1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯,∴当b=2.4时,DF=4;当b =3.6时,DF =9,即DF 的长为4或9;(3)如图,∵E 、Q 关于BP 对称,PN ∥CD,∴∠1=∠2,∠2+∠3=∠BDC=45°,∴∠1+∠4=45°,∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC,∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC,∴∠6+∠7=90°,∴△MNQ 是直角三角形,设EM=a,NC=b 列方程组222252372 a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56, ∴MNQ 56S =, 【点睛】本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.要注意运用数形结合思想.7.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【答案】(1)AG2=GE2+GF2(2)【解析】试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+x)2,解得x=,推出BN=,再根据BG=BN÷cos30°即可解决问题.试题解析:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,MN=x,在Rt△ABN中,∵AB2=AN2+BN2,∴1=x2+(2x+x)2,解得x=,∴BN=,∴BG=BN÷cos30°=.考点:1、正方形的性质,2、矩形的判定和性质,3、勾股定理,4、直角三角形30度的性质8.(问题发现)(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为;(拓展探究)(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;(解决问题)(3)如图(3)在正方形ABCD中,AB=2,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.【答案】(1)AC垂直平分BD;(2)四边形FMAN是矩形,理由见解析;(3)16+8或16﹣8【解析】【分析】(1)依据点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,即可得出AC 垂直平分BD;(2)根据Rt△ABC中,点F为斜边BC的中点,可得AF=CF=BF,再根据等腰三角形ABD 和等腰三角形ACE,即可得到AD=DB,AE=CE,进而得出∠AMF=∠MAN=∠ANF=90°,即可判定四边形AMFN是矩形;(3)分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,②以点A为旋转中心将正方形ABCD顺时针旋转60°,分别依据旋转的性质以及勾股定理,即可得到结论.【详解】(1)∵AB=AD,CB=CD,∴点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,∴AC垂直平分BD,故答案为:AC垂直平分BD;(2)四边形FMAN是矩形.理由:如图2,连接AF,∵Rt△ABC中,点F为斜边BC的中点,∴AF=CF=BF,又∵等腰三角形ABD和等腰三角形ACE,∴AD=DB,AE=CE,∴由(1)可得,DF⊥AB,EF⊥AC,又∵∠BAC=90°,∴∠AMF=∠MAN=∠ANF=90°,∴四边形AMFN是矩形;(3)BD′的平方为16+8或16﹣8.分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,如图所示:过D'作D'E⊥AB,交BA的延长线于E,由旋转可得,∠DAD'=60°,∴∠EAD'=30°,∵AB=2=AD',∴D'E=AD'=,AE=,∴BE=2+,∴Rt△BD'E中,BD'2=D'E2+BE2=()2+(2+)2=16+8②以点A为旋转中心将正方形ABCD顺时针旋转60°,如图所示:过B作BF⊥AD'于F,旋转可得,∠DAD'=60°,∴∠BAD'=30°,∵AB=2=AD',∴BF=AB=,AF=,∴D'F=2﹣,∴Rt△BD'F中,BD'2=BF2+D'F2=()2+(2-)2=16﹣8综上所述,BD′平方的长度为16+8或16﹣8.【点睛】本题属于四边形综合题,主要考查了正方形的性质,矩形的判定,旋转的性质,线段垂直平分线的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理进行计算求解.解题时注意:有三个角是直角的四边形是矩形.9.如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC ,∠ACB=∠DCF=90°,BC=FC ,所以△ABC ≌△DFC ,从而△ABC 与△DFC 的面积相等;(2)延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q .得到四边形ACDE ,BCFG 均为正方形,AC=CD ,BC=CF ,∠ACP=∠DCQ .所以△APC ≌△DQC . 于是AP=DQ .又因为S △ABC =12BC•AP ,S △DFC =12FC•DQ ,所以S △ABC =S △DFC ; (3)根据(2)得图中阴影部分的面积和是△ABC 的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC 的面积最大,当△ABC 是直角三角形,即∠C 是90度时,阴影部分的面积和最大.所以S 阴影部分面积和=3S △ABC =3×12×3×4=18. (1)证明:在△ABC 与△DFC 中, ∵{AC DCACB DCF BC FC∠∠===,∴△ABC ≌△DFC .∴△ABC 与△DFC 的面积相等;(2)解:成立.理由如下:如图,延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q . ∴∠APC=∠DQC=90°.∵四边形ACDE ,BCFG 均为正方形,∴AC=CD ,BC=CF ,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ .∴{APC DQCACP DCQ AC CD∠∠∠∠===,△APC ≌△DQC (AAS ),∴AP=DQ .又∵S△ABC=12BC•AP,S△DFC=12FC•DQ,∴S△ABC=S△DFC;(3)解:根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.∴S阴影部分面积和=3S△ABC=3×12×3×4=18.考点:四边形综合题10.如图1,在菱形ABCD中,ABC=60°,若点E在AB的延长线上,EF∥AD,EF=BE,点P是DE的中点,连接FP并延长交AD于点G.(1)过D作DH AB,垂足为H,若DH=,BE=AB,求DG的长;(2)连接CP,求证:CP FP;(3)如图2,在菱形ABCD中,ABC=60°,若点E在CB的延长线上运动,点F在AB的延长线上运动,且BE=BF,连接DE,点P为DE的中点,连接FP、CP,那么第(2)问的结论成立吗?若成立,求出的值;若不成立,请说明理由.【答案】(1)1;(2)见解析;(3).【解析】试题分析:(1)根据菱形得出DA∥BC,CD=CB,∠CDG=∠CBA=60°,则∠DAH=∠ABC=60°,根据DH⊥AB得出∠DHA=90°,根据Rt△ADH的正弦值得出AD的长度,然后得出BE的长度,然后证明△PDG≌△PEF,得出DG=EF,根据EF∥AD,AD∥BC 得出EF∥BC,则说明△BEF为正三角形,从而得出DG的长度;(2)连接CG、CF,根据△PDG≌△PEF得出PG=PF,然后证明△CDG≌△CBF,从而得到CG=CF,根据PG=PF得出垂直;(3)过D作EF的平行线,交FP延长于点G,连接CG、CF证△PEF≌△PDG,然后证明△CDG≌△CBF,从而得出∠GCE=120°,根据Rt△CPF求出比值.试题解析:(1)解:∵四边形ABCD为菱形∴DA∥BC CD="CB" ∠CDG=∠CBA=60°∴∠DAH=∠ABC=60°∵DH⊥AB ∴∠DHA=90°在Rt△ADH中 sin∠DAH=∴AD=∴BE=AB=×4=1 ∵EF∥AD ∴∠PDG=∠PEB ∵P为DE的中点∴PD=PE∵∠DPG=∠EPF ∴△PDG≌△PEF ∴DG=EF ∵EF∥AD AD∥BC ∴EF∥BC∴∠FEB=∠CBA=60°∵BE=EF ∴△BEF为正三角形∴EF=BE=1 ∴DG=EF=1、证明:连接CG、CF由(1)知△PDG≌△PEF ∴PG=PF在△CDG与△CBF中易证:∠CDG=∠CBF=60° CD=CB BF=EF=DG ∴△CDG≌△CBF∴CG=CF ∵PG=PF ∴CP⊥GF(3)如图:CP⊥GF仍成立理由如下:过D作EF的平行线,交FP延长于点G连接CG、CF证△PEF≌△PDG ∴DG=EF=BF ∵DG∥EF ∴∠GDP=∠EFP ∵DA∥BC∴∠ADP=∠PEC∴∠GDP-∠ADP=∠EFP-∠PEC ∴∠GDA=∠BEF=60°∴∠CDG=∠ADC+∠GDA=120°∵∠CBF=180°-∠EBF=120°∴∠CBF=∠CDG ∵CD=BC DG=BF ∴△CDG≌△CBF∴CG=CF ∠DCG=∠FCE ∵PG=PF ∴CP⊥PF ∠GCP=∠FCP∵∠DCP=180-∠ABC=120°∴∠DCG+∠GCE=120°∴∠FCE+∠GCE=120°即∠GCE=120°∴∠FCP=∠GCE=60°在Rt△CPF中 tan∠FCP=tan60°==考点:三角形全等的证明与性质.。
八年级几何综合:四边形压轴题综合训练1(50道真题)含解析

几何综合压轴题专题1.如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;(3)观察两图,你还可得出和DE相关的什么结论?请说明理由.(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.2.在Rt△AEB中,∠AEB=90°,以斜边AB为边向Rt△AEB形外作正方形ABCD,若正方形ABCD的对角线交于点O(如图1).(1)求证:EO平分∠AEB;(2)猜想线段OE与EB、EA之间的数量关系为(直接写出结果,不要写出证明过程);(3)过点C作CF⊥EB于F,过点D作DH⊥EA于H,CF和DH的反向延长线交于点G(如图2),求证:四边形EFGH为正方形.3.定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);(2)下列说法正确的有;(填写所有正确结论的序号)①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;②在①的条件下,连接BD,若BD=,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.4.如图1,在正方形ABCD中,点E是边AB上的一个动点(点E与点A,B不重合),连接CE,过点B作BF ⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,连接EF、CF,若CE=8,求四边形BEFC的面积;(3)如图3,当点E运动到AB中点时,连接DG,求证:DC=DG.5.【问题情境】课外兴趣小组活动时,老师提出了如下问题:(1)如图1,Rt△ABC中,∠C=90o,若AC=12,BC=5,点M是斜边AB上一动点,求线段CM的最小值.在组内经过合作交流,得到了如下的解决方法:根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:当CM⊥AB时,线段CM取得最小值.请你根据小明的思路求出这个最小值.【思维运用】(2)如图2,在Rt△ABC中,∠C=90°,AC=4,BC=3,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥BC于点E,求线段DE的最小值.【问题拓展】(3)如图3,AB=6,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上.∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离的最小值为.(直接写出结果,不需要写过程)6.如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处(1)求CE的长;(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.7.如图,在正方形ABCD中,E是CD边上一动点,DF⊥BE交BE的延长线于F.(1)如图(1),若BE平分∠DBC时,①直接写出∠FDC的度数;②延长DF交BC的延长线于点H,补全图形,探究BE与DF的数量关系,并证明你的结论;(2)如图(2),过点C作CG⊥BE于点G,猜想线段BF,CG,DF之间的数量关系,并证明你的猜想.8.如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.(1)求证:HE=HG;(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求的值;9.如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)(1)当t为何值时,四边形ABQP是平行四边形?(2)当t=3时四边形OQCD的面积为多少?(3)是否存在t的值,使△AQP为等腰三角形?若存在,请直接写出t的值;若不存在,请说明理由.10.平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.11.如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、∠ACD的平分线于点E、F.(1)猜想与证明,试猜想线段OE与OF的关系,并说明理由.(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.(3)若AC边上存在一点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.12.我们定义:对角线互相垂直的四边形叫做垂美四边形.(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.①求证:四边形BCGE是垂美四边形;②若AC=4,AB=5,求GE的长.13.问题发现:如图1,在Rt△ABC中,AB=AC,D为BC边所在直线上的一动点(不与点B、C重合),连结AD,以AD为边作Rt△ADE,且AD=AE,根据∠BAC+∠CAD=∠CAD+∠DAE,得到∠BAD=∠CAE,结合AB =AC,AD=AE得出△BAD≌△CAE,发现线段BD与CE的数量关系为BD=CE,位置关系为BD⊥CE;(1)探究证明:如图2,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,且点D在BC边上滑动(点D不与点B,C重合),连接EC.①则线段BC,DC,EC之间满足的等量关系式为;②求证:BD2+CD2=2AD2;(2)拓展延伸:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=13cm,CD=5cm,求AD 的长.14.如图,在四边形ABCD中,AB∥CD,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.(1)求证:点P也是BC的中点;(2)若CB⊥AB,且DP=,CD=,AB=4,求AP的长;(3)在(2)的条件下,若线段AE上有一点Q,使得△ABQ是等腰三角形,求AQ的长.15.如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.(1)求证:BP=CQ;(2)若BP=PC,求AN的长;(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.16.如图,Rt△ABC中,AB=AC,D为BC的中点,∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F 两点(1)求证:△DEF是等腰直角三角形;(2)求证:BE+CF=AC;(3)若BC的长为16,求四边形AEDF的面积.17.如图,正方形ABCD的边长为a,射线AM是∠BAD外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=BE,CF与AD相交于点G,连结EC、EF、EG.(1)求证:CE=EF;(2)求△AEG的周长(用含a的代数式表示);(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大.18.如图所示,四边形ABCD是正方形,M是AB延长线上一点,直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)求证:∠ADE=∠FEM;(2)如图(1),当点E在AB边的中点位置时,猜想DE与EF的数量关系,并证明你的猜想;(3)如图(2),当点E在AB边(除两端点)上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.19.在平面直角坐标系中,已知A(﹣4,0),B(4,0),点C,D在x轴上方,且四边形ABCD的面积为32,(1)若四边形ABCD是菱形,求点D的坐标.(2)若四边形ABCD是平行四边形,如图1,点E,F分别为CD,BC的中点,且AE⊥EF,求AE+2EF的值.(3)若四边形ABCD是矩形,如图2,点M为对角线AC上的动点,N为边AB上的动点,求BM+MN的最小值.20.(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合),连接AD,过点A作AE⊥AD,并满足AE=AD,连接CE.则线段BD和线段CE的数量关系是,位置关系是.(2)探索:如图2,当D点为BC边上一点(不与点B,C重合),Rt△ABC与Rt△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;(3)拓展:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=3,CD=1,请直接写出线段AD的长.21.我们定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如图(1),△ABC与△ADE都是等腰三角形,其中∠BAC=∠DAE,则△ABD≌△ACE(SAS)(1)熟悉模型:如图(2),已知△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,求证:BD=CE;(2)运用模型:如图(3),P为等边△ABC内一点,且PA:PB:PC=3:4:5,求∠APB的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以BP为边构造等边△BPM,这样就有两个等边三角形共顶点B,然后连结CM,通过转化的思想求出了∠APB的度数,则∠APB的度数为度;(3)深化模型:如图(4),在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求BD的长.22.在△ABC方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.(1)图1中线段AB的长是;请判断△ABC的形状,并说明理由.(2)请在图2中画出△DEF,使DE,EF,DF三边的长分别为,,.(3)如图3,以图1中△ABC的AB,AC为边作正方形ABPR和正方形ACQD,连接RD,求△RAD的面积.23.有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;(2)如图2,已知△ABC,点C在AB的垂直平分线上,E在边AB上,D是△ABC内一点,连接ED,CD,∠AED=60°,∠BCD=30°,若四边形BCDE是邻余四边形,BC是邻余线.①ED与BC有什么位置关系?说明理由.②判断△ABC形状,说明理由.24.在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB =8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.请你回答:(1)在图①中,中线AD的取值范围是.(2)应用上述方法,解决下面问题①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.25.如图,在平行四边形ABCD中,AB⊥AC,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC、AD于点E、F,已知AB=1,,连接BF.(1)如图①,在旋转的过程中,请写出线段AF与EC的数量关系,并证明;(2)如图②,当α=45°时,请写出线段BF与DF的数量关系,并证明;(3)如图③,当α=90°时,求△BOF的面积.26.如图,△ABC中,AB=AC,∠BAC=120°,已知AB1C1≌△ABC,BC与B1C1相交于点D,AC与B1C1相交于点E,AB1与BC相交于点F.(1)如图1,观察并猜想CE和B1F有怎样的数量关系?并说明理由.(2)筝形的定义:两组邻边分别相等的四边形叫做筝形.如图1,证明四边形AFDE是筝形.(3)如图2,若∠CAC1=30°,B1C1=3,其他条件不变,求C1E的长度.27.综合与实践(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.请写出∠AEB的度数及线段AD,BE之间的数量关系,并说明理由.(2)类比探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE 中DE边上的高,连接BE.填空:①∠AEB的度数为;②线段CM,AE,BE之间的数量关系为.(3)拓展延伸在(2)的条件下,若BE=4,CM=3,则四边形ABEC的面积为.28.如图,正方形OABC的边长为8,P为OA上一点,OP=2,Q为OC边上的一个动点,分别以OP\PQ为边在正方形OABC内部作等边三角形OPD和等边三角形PQE.(1)证明:DE=OQ;(2)直线ED与OC交于点F,点Q在运动过程中.①∠EFC的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;②连结AE,求AE的最小值.29.如图,已知正方形ABCD,AB=8,点E是射线DC上一个动点(点E与点D不重合),连接AE,BE,以BE为边在线段AD的右侧作正方形BEFG,连结CG.(1)当点E在线段DC上时,求证:△BAE≌△BCG;(2)在(1)的条件下,若CE=2,求CG的长;(3)连接CF,当△CFG为等腰三角形时,求DE的长.30.已知:如图,在△ABC中,∠ACB=90°,AC=CB=8cm,F是AB边上的中点,将∠AFC绕点F顺时针旋转,旋转角为α(0°≤α≤90°)得到∠A'FC',∠A'FC'的两边分别与AC、BC边相交于点D,E两点,连结DE.(1)求证:△ADF≌△CEF;(2)求∠EDF的度数;(3)当△EFB变成等腰直角三角形时,求CE的长;(4)在此运动变化的过程中,四边形CDFE的面积是否保持不变?试说明理由.31.我们把对角线互相垂直的四边形叫做垂直四边形.(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.32.(1)观察猜想如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则△ADB和△EAC是否全等?(填是或否),线段AB、AC、BD、CE之间的数量关系为.(2)问题解决如图②,在Rt△ABC中,∠ABC=90°,AC=6,AB=6,以AC为直角边向外作等腰Rt△DAC,连接BD,求BD的长.(3)拓展延伸如图③,在四边形ABCD中,∠ABC=∠ADC=90°,AB=5,AD=,DC=DA,CG⊥BD于点G,求CG的长,33.如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.(1)求证:DG=BC;(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.34.阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=,AB=2,求GE的长.35.勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.(1)连接BI、CE,求证:△ABI≌△AEC;(2)过点B作AC的垂线,交AC于点M,交IH于点N.①试说明四边形AMNI与正方形ABDE的面积相等;②请直接写出图中与正方形BCFG的面积相等的四边形.(3)由第(2)题可得:正方形ABDE的面积+正方形BCFG的面积=的面积,即在Rt△ABC中,AB2+BC2=.36.在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.37.阅读下面材料,完成相应任务:全等四边形能够完全重合的两个四边形叫做全等四边形.由此可知,全等四边形的对应边相等,对应角相等;反之,四条边分别相等、四个角也分别相等的两个四边形全等.在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.根据探究三角形全等条件的经验容易发现,满足1个、2个、3个、4个条件时,两个四边形不一定全等.在探究“满足5个条件的四边形ABCD和四边形A'B'C'D'是否全等”时,智慧小组的同学提出如下命题:①若AB=A'B',∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D',则四边形ABCD≌四边形A'B'C'D';②若AB=A'B',BC=B'C',CD=C'D',AD=A'D',∠A=∠A',则四边形ABCD≌四边形A'B'C'D'.(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是命题(填“真”或“假”).(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.(3)小颖经过探究又提出了一个新的命题:“若AB=A′B′,BC=B'C',CD=C'D',,,则四边形ABCD≌四边形A'B'C'D'”请在横线上填写两个关于“角”的条件,使该命题为真命题.38.(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点,若∠AMN=90°,求证:△AMN为等腰三角形.下面给出此问题一种证明的思路,你可以按这一思路继续完成证明,也可以选择另外的方法证明此结论.证明:在AB边上截取AE=MC,连接ME,在正方形ABCD中,∠B=∠BCD=90°,AB=BC∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB.(下面请你连接AN,完成余下的证明过程)(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,试探究△AMN是何种特殊三角形,并证明探究结论.(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,试猜想:当∠AMN的大小为多少时,(1)中的结论仍然成立?39.(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).40.我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.例如:某三角形三边长分别是2,4,,因为,所以这个三角形是奇异三角形.(1)根据定义:“等边三角形是奇异三角形”这个命题是命题(填“真”或“假”);(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;(3)如图,以AB为斜边分别在AB的两侧做直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE =AD,CB=CE.①求证:△ACE是奇异三角形;②当△ACE是直角三角形时,求∠DBC的度数.41.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为,点C的坐标为;请直接写出点N纵坐标n的取值范围是;(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN:=+1,=﹣1)42.我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方.即如果一个直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么a2+b2=c2.(1)直接填空:如图①,若a=3,b=4,则c=;若a+b=4,c=3,则直角三角形的面积是.(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明a2+b2=c2.(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?43.在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:问题初探:(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为;问题再探:(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.成果运用(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是.44.如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G.(l)判断四边形EFDG的形状是(不必证明);(2)现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;(3)如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.45.如图1,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD、BE.(Ⅰ)求证:CE=AD;(Ⅱ)如图2,当点D是AB中点时,连接CD.(i)四边形BECD是什么特殊四边形?说明你的理由;(ii)当∠A=°时,四边形BECD是正方形.(直接写出答案)46.已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P 在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒(1)当t为何值时,四边形PODB是平行四边形?(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.(3)在线段PB上有一点M,且PM=5,当P运动秒时,四边形OAMP的周长最小,并画图标出点M 的位置.47.(1)如图①,在正方形ABCD中,E、F分别是BC、CD边上的点,BE=CF,连接AF,DE交于点G.求证:AF⊥DE且AF=DE.(2)如图②,若点E、F分别在CB、DC的延长线上,且BE=CF,(1)中的结论是否成立?如果成立,请说明理由.(3)如图③,在图②的基础上连接AE、EF,H、M、N、P分别是AE、EF、FD、DA的中点,请直接写出四边形HMNP的形状.48.已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.(1)如图1,求证:CM+CN=BC;(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.(4)如图3,若AB=1,直接写出BE+AE的最小值.49.如图①所示,▱ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:(1)公园的面积为km2;(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.50.定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”(1)①如图1,在不完全矩形ABCD中,∠ABC=90°,若AB=3,BC=4,则BD=:②如图2,在平面直角坐标系中,A(0.4),B(6,0),若整点M使得四边形AOBM是不完全矩形,则点M的坐标是;(整点指横坐标、纵坐标都为整数的点)(2)如图3,在正方形ABCD中,点E,F分别是AD,AB上的点,且CF⊥BE,求证:四边形BCEF是不完全矩形.。
八年级下册数学压轴题(含答案)

八年级下册数学压轴题(含答案)四边形AOBC的对角线互相平分,且相等,故为菱形;又因为OC经过翻折后落在AB上,且AC与x轴垂直,故OC垂直于AB,故AO=OC=OB=BC,故AOBC是一个菱形;3)设点P的坐标为(x,y),则BPC为直角三角形,且BP=PC,又因为BP在y轴下方,故y<0,且BP与BC垂直,故BP的斜率为-2;设BP的解析式为y=-2x+b,且B点坐标为(0,-5),则有b=-5;又因为BP=PC,故PC的解析式为y=2x+b,且C点坐标为(a,0),代入得a=5;又因为XXX在BC下方,故y<0,代入得y=-2x-5;代入BP的解析式得x=5/3,代入得y=-25/3;故存在点P(5/3,-25/3),使△BCP为等腰直角三角形。
题目:在平面直角坐标系中,已知点A(0,0),B(5,0),C(0,5√2),D从A出发沿AC方向以1m/s的速度向C匀速运动,同时点E从B出发沿BA方向以√2m/s的速度向A匀速运动。
当其中一个点到达终点时,另一个点也随之停止运动。
设点D,E运动的时间是t(0<t≤10)秒。
过点E作EF⊥BC于点F,连接DE,DF。
1)求BE和CD的长度。
2)试说明,无论t为何值,四边形ADEF都是平行四边形。
3)当t为何值时,△DEF为直角三角形?请说明理由。
解法:1)由题意可知,BE=√2t,CD=t,故BE=√2t,CD=t。
2)如图所示,由题意可得,∠C=90°,∠A=45°,故∠B=45°。
又因为EF⊥BC,所以∠EFB=90°,∠FEB=45°,所以BE=EF。
又因为AE=√2t,DE=CD,所以DE=√2t。
因此,四边形ADEF的对角线相等,且相互平分,所以ADEF是平行四边形。
3)如图所示,当EF⊥BC时,由勾股定理可知,DE²=DF²+EF²,即(√2t)²=(t+BE)²+(5√2-BF)²。
八年级下册平行四边形压轴题专题专练

八年级下册平行四边形压轴题专题专练学校:___________姓名:___________班级:___________一、解答题(本大题共20小题,共160.0分)1.如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;的值.(2)设▱ABCD的面积为S,四边形AEDF的面积为T,求ST2.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE//BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE.(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请说明理由.3.已知:如图,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为AB的中点,N为DC的中点.求证:∠PMN=∠PNM.4.如图所示,在四边形ABCD中,AB∥CD,AD∥BC,点E,F在对角线AC上,且AE=CF,请你分别以E,F为一端点,和图中已标字母的某点连成两条相等的新线段(只需证明一组线段相等即可).(1)连接______;(2)结论:______=______;(3)证明:5.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.,求AB的长.(2)若GB=3,BC=6,BF=326.(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB、AD、DC之间的等量关系为______;(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.7.如图,点O为▱ABCD的对角线AC,BD的交点,∠BCO=90∘,∠BOC=60∘,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.(1)求线段EF的长.(2)若△OAE的面积为S1,△OCF的面积为S2,S1+S2的值是否发生变化?若不变,求出这个定值;若变化,请说明随着DE的增大,S1+S2的值是如何发生变化的.8.如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.9.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE//AC交直线AB于点E,DF//AB交直线AC于点F.(1)当点D在边BC上时,如图 ①,求证:DE+DF=AC;(2)当点D在BC的延长线上时,如图 ②;当点D在BC的反向延长线上时,如图 ③,请分别写出这两个图中DE、DF、AC之间的数量关系(不需要证明);(3)若AC=6,DE=4,则DF= .10.如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;(2)当点P运动的时间为3秒时,求此时四边形ADEC的周长是多少?211.如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.(1)用含字母a,b的代数式表示矩形中空白部分的面积;(2)当a=3,b=2时,求矩形中空白部分的面积.12.已知在△ACD中,P是CD的中点,B是AD延长线上的一点,连结BC,AP.(1)如图1,若∠ACB=90°,∠CAD=60°,BD=AC,AP=√3,求BC的长.(2)过点D作DE∥AC,交AP延长线于点E,如图2所示,若∠CAD=60°,BD=AC,求证:BC=2AP.(3)如图3,若∠CAD=45°,是否存在实数m,当BD=mAC时,BC=2AP?若存在,请直接写出m的值;若不存在,请说明理由.13.如图,在平面直角坐标系xOy中,一次函数y=﹣2x+3的图象与x轴、y轴分别交于A、B两点,E(1,1)为平面内一点.(1)点E是否在一次函数y=﹣2x+3的图象上?说明理由;x+b的图象经过E点,与x轴交于C点.(2)一次函数y=﹣13①求BC的长;②求证:AB平分∠OBC;③正比例函数y=kx的图象与一次函数y=﹣2x+3的图象交于P点,O、P到一次函x+b的图象的距离相等,直接写出符合条件的k值.数y=﹣1314.如图1.在Rt△ABC中,∠A=90°,AB=AC,点D、E分别在边AB、AC上,AD=AE.连接DC,点M、P、N分别为DE、DC、BC的中点.(1)图1中,线段PM与PN的数量关系是____,位置关系是____;(2)把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,判断△PMN的形状,并说明理由;(3)把△ADE绕点A在平面内自由旋转,若DE=2,BC=6,请直接写出△PMN 面积的最大值.15.如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M.(1)求证:BE=AD;(2)直接用含α的式子表示∠AMB的度数为______.(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,直接写出答案即可.16.在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.(1)当点E恰好在AC上时,如图1,求∠ADE的大小;(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.17.我们定义:如图 ①,在△ABC中,把AB绕点A顺时针旋转α(0∘<α<180∘)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180∘时,我们称△AB'C'是△ABC的“旋补三角形”,△AB'C'的边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.特例感知(1)在图 ② ③中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”. ①如图 ②,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC; ②如图 ③,当∠BAC=90∘,BC=8时,AD长为 .(提示:直角三角形斜边上的中线等于斜边的一半)猜想论证(2)在图 ①中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.18.将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB'C',如图①,我们将这种变换记为[θ,n].(1)如图①,对△ABC作变换[40°,√7]得△AB'C',则S△AB'C':S△ABC=______;直线BC与直线B'C'所夹的锐角为______度;(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得△AB'C',使点B、C、C'在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=2,对△ABC作变换[θ,n]得△AB'C',使点B、C、B'在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.19.如图,在长方形纸片ABCD中,翻折∠B,∠D,使BC,AD都恰好落在AC上,F,H分别是B,D落在AC上的两点,E,G分别是折痕CE,AG与AB,CD的交点.(1)求证:四边形AECG是平行四边形;(2)若AB=4 cm,BC=3 cm,求线段EF的长.20.如图1,已知Rt△ABC≌Rt△DCE,∠B=∠D=90°,BC=2AB.(1)若AB=2,求点B到AC的距离;(2)当Rt△DCE绕点C顺时针旋转,连AE,取AE中点H,连BH,DH,如图2,求证:BH⊥DH;(3)在(2)的条件下,若AB=2,P是DE中点,连接PH,当Rt△DCE绕点C顺时针旋转的过程中,直接写出PH的取值范围.答案和解析1.【答案】解:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ABC+∠BAD=180°,∵AF∥BE,∴∠EBA+∠BAF=180°,∴∠CBE=∠DAF,同理得∠BCE=∠ADF,在△BCE和△ADF中,∵{∠CBE=∠DAF BC=AD∠BCE=∠ADF,∴△BCE≌△ADF(ASA);(2)∵点E在▱ABCD内部,∴S△BEC+S△AED=12S▱ABCD,由(1)知:△BCE≌△ADF,∴S△BCE=S△ADF,∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=12S▱ABCD,∵▱ABCD的面积为S,四边形AEDF的面积为T,∴S T =S12S=2.【解析】此题主要考查了平行四边形的性质以及全等三角形的判定与性质,熟练利用三角形和平行四边形边的关系得出面积关系是解题关键.(1)根据ASA证明:△BCE≌△ADF;(2)根据点E在▱ABCD内部,可知:S△BEC+S△AED=12S▱ABCD,可得结论.2.【答案】(1)证明:∵AB=AC,∴∠B=∠ACB.又∵AD 是BC 边上的中线,∴AD ⊥BC .即∠ADB =90∘.∵AE //BC ,∴∠EAC =ACB .∴∠B =∠EAC .∵CE ⊥AE ,∴∠CEA =90∘.∴∠ADB =∠CEA .又∵AB =CA ,∴△ABD ≌△CAE (AAS ).(2)解:DE //AB 且DE =AB .理由如下:∵△ABD ≌△CAE ,∴AE =BD .又∵AE //BD ,∴四边形ABDE 是平行四边形.∴DE //AB 且DE =AB .【解析】略3.【答案】解:∵在四边形ABCD 中,P 是对角线BD 的中点,M ,N 分别是AB ,CD 的中点,∴NP ,PM 分别是△CDB 与△DAB 的中位线,∴PN =12BC ,PM =12AD ,PN ∥BC ,PM ∥AD ,∴∠NPD =∠DBC ,∠MPB =∠ADB ,∵AD=BC,∴PN=PM,故△NMP是等腰三角形.∴∠PMN=∠PNM.【解析】根据中位线定理和已知,易证明△NMP是等腰三角形和PN∥BC,PM∥AD,进而得到∠NPD=∠DBC,∠MPB=∠ADB,根据等腰三角形的性质即可得到结论.此题主要考查了三角形中位线定理,以及等腰三角形的判定与性质,熟练掌握等腰三角形的性质是解题的关键.4.【答案】BE,DF BE DF【解析】解:连接BE,DF,∵在四边形ABCD中,AB∥CD,AD∥BC,∴AB=CD,∠BAE=∠DCF,又∵AE=CF,∴△ABE≌△CDF.∴BE=DF.此题的答案不唯一.可以连接BE,DF或连接BF,DE.根据平行四边形的性质和已知条件证明全等三角形,从而证明BE=DF或BF=DE.此题是一道开放性试题.能够根据平行四边形是中心对称图形,发现怎样连接所得的两条线段一定相等.5.【答案】解:(1)∵E是AC的中点,∴AE=CE,∵AB∥CD,∴∠AFE=∠CDE,在△AEF和△CED中,∵{∠AFE=∠CDE ∠AEF=∠CED AE=CE,∴△AEF≌△CED(AAS),∴AF=CD,又AB ∥CD ,即AF ∥CD ,∴四边形AFCD 是平行四边形;(2)∵AB ∥CD ,∴△GBF ∽△GCD ,∴GB GC =BF CD ,即33+6=32CD ,解得:CD =92,∵四边形AFCD 是平行四边形,∴AF =CD =92,∴AB =AF +BF =92+32=6.【解析】本题主要考查平行四边形的判定与性质,解题的关键是掌握全等三角形、相似三角形及平行四边形的判定与性质.(1)由E 是AC 的中点知AE =CE ,由AB ∥CD 知∠AFE =∠CDE ,据此根据“AAS ”即可证△AEF ≌△CED ,从而得AF =CD ,结合AB ∥CD 即可得证;(2)证△GBF ∽△GCD 得GB GC =BF CD ,据此求得CD =92,由AF =CD 及AB =AF +BF 可得答案.6.【答案】解:(1)AD =AB +DC ;(2)AB =AF +CF ,证明:如图②,延长AE 交DF 的延长线于点G ,∵E 是BC 的中点,∴CE =BE ,∵AB ∥DC ,∴∠BAE =∠G ,在△AEB 和△GEC 中,{∠BAE =∠G ∠AEB =∠GEC BE =CE,∴△AEB ≌△GEC ,∴AB =GC ,∵AE 是∠BAF 的平分线,∴∠BAG =∠FAG ,∵AB ∥CD ,∴∠BAG =∠G ,∴∠FAG =∠G ,∴FA =FG ,∴AB =CG =AF +CF ;(3)AB =23(CF +DF ),证明:如图③,延长AE 交CF 的延长线于点G ,∵AB ∥CF ,∴△AEB ∽△GEC ,∴AB CG =BE EC =23,即AB =23CG ,∵AB ∥CF ,∴∠A =∠G ,∵∠EDF =∠BAE ,∴∠FDG =∠G ,∴FD =FG ,∴AB =23CG =23(CF +DF ).【解析】解:(1)如图①,延长AE交DC的延长线于点F,∵AB∥DC,∴∠BAF=∠F,∵E是BC的中点,∴CE=BE,在△AEB和△FEC中,{∠BAF=∠F∠AEB=∠FEC BE=CE,∴△AEB≌△FEC,∴AB=FC,∵AE是∠BAD的平分线,∴∠DAF=∠BAF,∴∠DAF=∠F,∴DF=AD,∴AD=DC+CF=DC+AB,故答案为:AD=AB+DC;(2)见答案;(3)见答案.【分析】(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明;(3)延长AE交CF的延长线于点G,根据相似三角形的判定定理得到△AEB∽△GEC,根据相似三角形的性质得到AB=23CG,计算即可.本题考查的是全等三角形的判定和性质、相似三角形的判定和性质,正确作出辅助性、灵活运用相关的性质定理和判定定理是解题的关键.7.【答案】解:(1)∵四边形ABCD是平行四边形,∴OD=OB.∵DE=OF,∴EF=OD=12BD=4.(2)S 1+S 2的值不变.理由如下:连接AF .∵四边形ABCD 是平行四边形,∴AO =OC .∴S △AOF =S △COF .∵DE =OF ,∴S △ADE =S △AOF =S △COF .∴S 1+S 2=S △AEF =S △AOD .∵∠BCO =90∘,∠BOC =60∘,∴∠DAC =90∘,∠AOD =60∘.∴AO =12OD =2.在Rt △AOD 中,AD =√OD 2−AO 2=2√3.∴S 1+S 2=S △AOD =12AD ⋅AO =12×2√3×2=2√3.【解析】略8.【答案】(1)证明:∵∠A =∠F ,∴DE ∥BC ,∵∠1=∠2,且∠1=∠DMF ,∴∠DMF =∠2,∴DB ∥EC ,则四边形BCED 为平行四边形;(2)解:∵BN 平分∠DBC ,∴∠DBN =∠CBN ,∵EC∥DB,∴∠CNB=∠DBN,∴∠CNB=∠CBN,∴CN=BC=DE=2.【解析】(1)由已知角相等,利用对顶角相等,等量代换得到同位角相等,进而得出DB与EC平行,再由内错角相等两直线平行得到DE与BC平行,即可得证;(2)由角平分线得到一对角相等,再由两直线平行内错角相等,等量代换得到一对角相等,再利用等角对等边得到CN=BC,再由平行四边形对边相等即可确定出所求.此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.9.【答案】(1)证明:∵DF//AB,DE//AC,∴四边形AEDF是平行四边形,∴AF=DE,∵DF//AB,∴∠FDC=∠B,又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=CF,∴DE+DF=AF+CF=AC.(2)题图 ②中,AC+DF=DE;题图 ③中,AC+DE=DF.(3)2或10.【解析】略10.【答案】(1)证明:连接CD 交AE 于F ,∵四边形PCOD 是平行四边形,∴CF =DF ,OF =PF ,∵PE =AO ,∴AF =EF ,又CF =DF ,∴四边形ADEC 为平行四边形;(2)解:当点P 运动的时间为32秒时,OP =32,OC =3, 则OE =92,由勾股定理得,AC =√OA 2+OC 2=3√2,CE =√OC 2+OE 2=32√13, ∵四边形ADEC 为平行四边形,∴周长为(3√2+32√13)×2=6√2+3√13.【解析】(1)连接CD 交AE 于F ,根据平行四边形的性质得到CF =DP ,OF =PF ,根据题意得到AF =EF ,又CF =DP ,根据平行四边形的判定定理证明即可;(2)根据题意计算出OC 、OP 的长,根据勾股定理求出AC 、CE ,根据平行四边形的周长公式计算即可.本题考查的是平行四边形的性质和判定、勾股定理的应用,掌握对角线互相平分的四边形是平行四边形是解题的关键,注意坐标与图形的关系的应用.11.【答案】解:(1)S =ab -a -b +1;(2)当a =3,b =2时,S =6-3-2+1=2;【解析】(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;(2)将a =3,b =2代入(1)中即可;本题考查阴影部分面积,平行四边形面积,代数式求值;能够准确求出阴影部分面积是解题的关键.12.【答案】解:(1)∵∠ACB=90°,∠CAD=60°,∴AB=ACcos60∘=2AC,∵BD=AC,∴AD=AC,∴△ADC是等边三角形,∴∠ACD=60°,∵P是CD的中点,∴AP⊥CD,在Rt△APC中,AP=√3,∴AC=APsin60∘=2,∴BC=AC×tan60°=2√3,(2)证明:连接BE,∵DE∥AC,∴∠CAP=∠DEP,在△CPA和△DPE中{∠CAP=∠DEP ∠CPA=∠EPD CP=DP,∴△CPA≌△DPE(AAS),∴AP=EP=12AE,DE=AC,∵BD=AC,∴BD=DE,又∵DE∥AC,∴∠BDE=∠CAD=60°,∴△BDE是等边三角形,∴BD=BE,∠EBD=60°,∵BD=AC,∴AC=BE,在△CAB和△EBA中{AC=BE∠CAB=∠EBA AB=BA,∴△CAB≌△EBA(SAS),∴AE=BC,∴BC=2AP,(3)存在这样的m,m=√2.理由如下:作DE∥AC交AP延长线于E,连接BE,由(2)同理可得DE=AC,∠EDB=∠CAD=45°,AE=2AP,当BD=√2AC时,∴BD=√2DE,∵∠EDB=45°,作BF⊥DE于F,∴BD=√2DF,∴DE=DF,∴点E,F重合,∴∠BED=90°,∴∠EBD=∠EDB=45°,∴BE=DE=AC,同(2)可证:△CAB≌△EBA(SAS),∴BC=AE=2AP,∴存在m=√2,使得BC=2AP【解析】(1)证△ADC是等边三角形,P为CD中点,通过等边三角形三线合一,得到AP⊥CD,解三角形即可;(2)借助中点和平行,可证得△CPA≌△DPE,得出AP=EP=12AE,DE=AC,再证明△CPA≌△DPE,即可得出结论;(3)由(2)总结的解题方法延伸到图3中,类比解决问题.本题主要考查了等边三角形的判定与性质,三角形全等的判定与性质,三角形函数的计算等知识,构造出全等三角形是解决(2)的关键,类比(2)来解决(3)是解决几何题常用的方法,体现了变中不变的思想.13.【答案】解:(1)在,理由如下:∵在y =﹣2x +3中,当x =1时,y =-2×1+3=1, ∴点E 在一次函数y =-2x +3的图象上;(2)①∵一次函数y =-13x +b 的图象经过E 点,∴1=-13+b ,∴b =43,∴y =-13x +43,当y =0时,x =4,∴点C (4,0),∴OC =4,∵一次函数y =-2x +3的图象与x 轴、y 轴分别交于A 、B 两点,∴点A (32,0),点B (0,3),∴OB =3,OA =32,∴BC =√OB 2+OC 2=√16+9=5;②如图,取点D (0,-2),连接AD ,∴BD =BO +OD =5=BC ,∵AO =32,∴AC =4-32=52,AD =√AO 2+OD 2=√4+94=52, ∴AD =AC ,在△ABD 和△ABC 中,{AB =AB AD =AC BD =BC,∴△ABD ≌△ABC (SSS ),∴∠ABD =∠ABC ,∴AB 平分∠OBC ;③当点O ,点P 在直线AB 的同侧时,∵O 、P 到一次函数y =-13x +43的图象的距离相等, ∴OP 与直线y =-13x +43平行,∴k =-13,当点O ,点P 在直线AB 的异侧时,过点O 作OH ⊥CE 于H ,过点P 作PQ ⊥CE 于Q ,直线y =kx 交CE 于F ,∵O 、P 到一次函数y =-13x +43的图象的距离相等,∴OH =PQ ,又∵∠PFQ =∠OFH ,∠PQF =∠OHF ,∴△PQF ≌△OHF (AAS ),∴PF =OF ,∵直线y =kx 的图象与直线y =-2x +3的图象交于P 点,∴{y =kx y =−2x +3, ∴{x =3k+2y =3k k+2, ∴点P (3k+2,3k k+2),∴点F 坐标为[32(k+2),3k 2(k+2)],∵点F 在一次函数y =-13x +43上,∴3k 2(k+2)=-13×32(k+2)+43, ∴k =13,经检验k 的值是此分式方程的根,综上所述:k =-13或13.【解析】本题是一次函数的综合题,考查了一次函数的性质,全等三角形的判定和性质,勾股定理,利用分类讨论思想解决问题是本题的关键.(1)将点E 坐标代入解析式可求解;(2)①分别求出点B ,点C 坐标,由勾股定理可求解;②由“SSS ”可证△ABD ≌△ABC ,可得∠ABD =∠ABC ,可得结论;③分两种情况讨论,全等三角形的性质和平行线的性质可求解.14.【答案】解:(1)PM =PN ;PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由:如图2,连接BD ,CE ,由旋转知,∠BAD =∠CAE ,∵AB =AC ,AD =AE ,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,BD =CE ,利用三角形的中位线得,PN =12BD ,PM =12CE ,∴PM =PN ,∴△PMN 是等腰三角形,利用三角形的中位线得,PM // CE ,∴∠DPM =∠DCE ,利用三角形的中位线得,PN // BD ,∴∠PNC =∠DBC ,∵∠DPN =∠DCB +∠PNC =∠DCB +∠DBC ,∴∠MPN =∠DPM +∠DPN =∠DCE +∠DCB +∠DBC=∠BCE +∠DBC =∠ACB +∠ACE +∠DBC=∠ACB +∠ABD +∠DBC =∠ACB +∠ABC ,∵∠BAC =90°,∴∠ACB +∠ABC =90°,∴∠MPN =90°,∴△PMN 是等腰直角三角形;(3)如图3,同(2)的方法得,△PMN 是等腰直角三角形,∴MN 最大时,△PMN 的面积最大,∴DE // BC 且DE 在顶点A 上面,∴MN 最大=AM +AN ,连接AM ,AN ,在△ADE 中,DE =2,∠DAE =90°,∴AM =1,在Rt △ABC 中,BC =6,AN =3,∴MN 最大=1+3=4,∴S △PMN 最大=12PM 2=12×12MN 2=14×42=4.【解析】【分析】此题是几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质,解(1)的关键是判断出PM =12CE ,PN =12BD ,解(2)的关键是判断出△ABD ≌△ACE ,解(3)的关键是判断出MN 最大时,△PMN 的面积最大,是一道中考常考题.(1)利用三角形的中位线得出PM =12CE ,PN =12BD ,进而判断出BD =CE ,即可得出结论,再利用三角形的中位线得出PM ∥CE 得出∠DPM =∠DCA ,最后用互余即可得出结论;(2)连接BD ,CE ,先判断出△ABD ≌△ACE ,得出BD =CE ,同(1)的方法得出PM =12BD ,PN =12BD ,即可得出PM =PN ,同(1)的方法即可得出结论;(3)先判断出MN 最大时,△PMN 的面积最大,进而求出AN ,AM ,即可得出MN 最大=AM +AN ,最后用面积公式即可得出结论.【解答】解:(1)∵点P ,N 是BC ,CD 的中点,∴PN ∥BD ,PN =12BD ,∵点P ,M 是CD ,DE 的中点,∴PM ∥CE ,PM =12CE ,∵AB =AC ,AD =AE ,∴BD =CE ,∴PM =PN ,∵PN ∥BD ,∴∠DPN =∠ADC ,∵PM ∥CE ,∠DPM =∠DCA ,∵∠BAC =90°,∴∠ADC +∠ACD =90°,∴∠MPN =∠DPM +∠DPN =∠DCA +∠ADC =90°,∴PM ⊥PN ,故答案为:PM =PN ,PM ⊥PN ,(2)见答案;(3)见答案. 15.【答案】α【解析】(1)证明:如图1,∵∠ACB =∠DCE =α,∴∠ACD =∠BCE ,在△ACD 和△BCE 中,{CA=CB∠ACD=∠BCE CD=CE,∴△ACD≌△BCE(SAS),∴BE=AD;(2)解:如图1,∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠BAC+∠ABC=180°-α,∴∠BAM+∠ABM=180°-α,∴∠AMB=180°-(180°-α)=α;(2)△CPQ为等腰直角三角形,理由如下:如图2,由(1)可得,BE=AD,∵AD,BE的中点分别为点P、Q,∴AP=BQ,∵△ACD≌△BCE,∴∠CAP=∠CBQ,在△ACP和△BCQ中,{CA=CB∠CAP=∠CBQ AP=BQ,∴△ACP≌△BCQ(SAS),∴CP=CQ,∠ACP=∠BCQ,又∵∠ACP+∠PCB=90°,∴∠BCQ+∠PCB=90°,∴∠PCQ=90°,∴△CPQ为等腰直角三角形.(1)由“SAS”可证△ACD≌△BCE,可得BE=AD;(2)由三角形内角和定理可求解;(3)由“SAS”可证△ACP≌△BCQ,可得CP=CQ,∠ACP=∠BCQ,可得结论.本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,灵活运用这些性质解决问题是解题的关键.16.【答案】(1)解:如图1,∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,∵CA=CD,∴∠CAD=∠CDA=1(180°-30°)=75°,2∴∠ADE=90°-75°=15°;(2)证明:连接AD,如图2,∵点F是边AC中点,∴BF=1AC,2∵∠ACB=30°,∠ABC=90°,∴AB=1AC,2∴BF=AB,∵△ABC绕点C顺时针旋转60°得到△DEC,∴∠BCE=∠ACD=60°,CB=CE,DE=AB,∴DE=BF,△ACD和△BCE为等边三角形,∴BE=CB,∵点F为△ACD的边AC的中点,∴DF⊥AC,则∠DFC=∠ABC=90°,∠FDC=∠ACB=30°,DC=AC,∴△CFD≌△ABC(AAS),∴DF=BC,∴DF=BE,而BF=DE,∴四边形BEDF是平行四边形.【解析】本题考查了旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.(1)如图1,利用旋转的性质得CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,再根据等腰三角形的性质和三角形内角和计算出∠CAD,从而利用互余计算出∠ADE的度数;AC,利用含30度的直角三(2)如图2,利用直角三角形斜边上的中线性质得到BF=12AC,则BF=AB,再根据旋转的性质得到∠BCE=∠ACD=60°,角形三边的关系得到AB=12CB=CE,DE=AB,从而得到DE=BF,△ACD和△BCE为等边三角形,接着证明△CFD≌△ABC得到DF=BC,然后根据平行四边形的判定方法得到结论.17.【答案】解: (1) ①1. ②4.2BC.(2)猜想:AD=12证明:如图,延长AD至E,使DE=AD,连接B'E,C'E.∵AD是△ABC的“旋补中线”,∴B'D=C'D,∴四边形AB'EC'是平行四边形,∴EC'//B'A,EC'=B'A,∴∠AC'E+∠B'AC'=180∘.由旋补三角形的定义可知∠B'AC'+∠BAC=180∘,B'A=BA,AC=AC',∴∠AC'E=∠BAC,EC'=BA,∴△AC'E≌△CAB,∴AE=CB.∵AD=1AE,2∴AD=1BC.2【解析】略18.【答案】解:(1)7;40;(2)如图②中,∵四边形ABB'C'是矩形,∴∠BAC'=90°.∴θ=∠CAC'=∠BAC'-∠BAC=90°-30°=60°.在Rt△ABB'中,∠ABB'=90°,∠BAB'=60°,∴n=AB′=2;AB(3)如图③中,∵四边形ABB'C'是平行四边形,∴AC'∥BB',又∵∠BAC=36°,∴θ=∠CAC'=∠ACB=72°∴∠C'AB'=∠AB'B=∠BAC=36°,∴θ=∠BAB'=72°,又∵∠B=∠B,∴△ABC∽△B'BA,∴AB2=CB•B'B=CB•(BC+CB′),∵CB'=AC=AB=B'C',BC=2,∴AB2=2•(2+AB)∴AB=1+√5或1-√5(舍),∵AB>0,∴B 'C '=AB =1+√5,∴n =B′C′BC =√5+12.【解析】解:(1)如图①中,设直线BC 与直线B 'C '的交点为H ,AB '交BH 于O .∵△ABC ∽△AB 'C ',AB :AB '=√7,∴S △ABC :S △AB 'C '=7,∵∠B =∠B ',∠AOB =∠HOB ',∴∠OHB =∠BAO =40°,故答案为:7,40;(2)见答案;(3)见答案.【分析】(1)根据变换[40°,√7]的定义,即可解决问题.(2)想办法求出∠CAC ',以及AC′AC 的值即可.(3)想办法求出∠BAB ',以及B′C′BC 的值即可本题考查四边形综合题、相似三角形的性质、一元二次方程、变换[θ,n ]的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型. 19.【答案】(1)证明:由翻折的性质可得∠GAH =12∠DAC ,∠ECF =12∠ACB .∵四边形ABCD 是长方形,∴DA //BC ,AB //CD ,∠B =90∘.∴∠DAC =∠ACB .∴∠GAH =∠ECF .∴AG //CE .又∵AE //CG ,∴四边形AECG 是平行四边形.(2)解:由翻折的性质可得BC =CF =3 cm ,BE =EF ,∠B =∠CFE =90∘.在Rt △ABC 中,根据勾股定理得AC =5 cm ,∴AF =2 cm .设EF =BE =x cm ,则AE =(4-x )cm ,在Rt △AEF 中,根据勾股定理得AE 2=AF 2+EF 2,即(4−x)2=22+x 2.解得x =32.∴线段EF 的长为32 cm .【解析】略20.【答案】解:(1)在Rt △ABC 中,∵AB =2,BC =2AB =4,∴AC =√AB 2+BC 2=√22+42=2√5,设点B 到AC 的距离为h ,则S △ABC =12AB ·BC =12AC ·h , ∴2×4=2√5h , ∴h =4√55, 即点B 到AC 的距离为4√55. (2)证明:延长BH 到F 点,使HF =BH ,连FE ,延长BC 、FE 交于点G ,连BD 、DF . ∵HF =BH ,∠EHF =∠AHB ,EH =AH ,∴△EHF ≌△AHB ,∴EF=AB,∠FEH=∠BAH,∴EF∥AB,由Rt△ABC≌Rt△DCE可得CD=AB,∴EF=CD,∵EF∥AB,∴∠ABC=∠FGC=90°,∵∠CDE=90°,∠CKD=∠EKG,∠BCD=∠CDE+∠CKD,∠DEF=∠FGC+∠EKG,∴∠BCD=∠DEF,又∵EF=CD,BC=DE,∴△BCD≌△DEF,∴DB=DF,∵HF=BH,∴DH⊥BH;(3)√5−1⩽PH⩽√5+1.【解析】【分析】本题考查了旋转的性质、全等三角形的判定和性质、等腰三角形的性质、三角形的面积、勾股定理、三角形中位线的性质、三角形三边关系,解题关键是掌握旋转的概念和性质. (1)在Rt△ABC中由勾股定理可以求出AC,再由三角形的面积公式列式可以求出点B 到AC的距离;(2)延长BH到F点,使HF=BH,连FE,延长BC、FE交于点G,连BD、DF.先证明△EHF≌△AHB,得出EF=AB,EF∥AB,进而证明∠BCD=∠DEF,再证明△BCD≌△DEF,得出DB=DF,由等腰三角形的三线合一即可证明结论;AD,根据三角形三边关系可知:当Rt△DCE (3)连AD,由三角形中位线的性质可得PH=12绕点C顺时针旋转的过程中,点D运动到AC的延长线上时,有AD=AC+CD,此时线段AD最长,PH也最长;当Rt△DCE绕点C顺时针旋转的过程中,点D运动到线段AC上时,有AD =AC -CD ,此时线段AD 最短,PH 也最短;据此可以求出PH 的取值范围.【解答】解:(1)见答案;(2)见答案;(3)如下图1,连AD ,∵P 是DE 中点,H 是AE 中点,∴PH =12AD ,由题意得:AC =2√5,CD =AB =2,在△ACD 中,AD < AC +CD ,当Rt △DCE 绕点C 顺时针旋转的过程中,点D 运动到AC 的延长线上时(如下图2),有AD =AC +CD ,此时线段AD 最长,PH 也最长,所以PH 的最大值=12AD =12(AC +CD )=12(2√5+2)=√5+1;当Rt △DCE 绕点C 顺时针旋转的过程中,点D 运动到线段AC 上时(如上图3),有AD =AC -CD ,此时线段AD 最短,PH 也最短,所以PH 的最小值=12AD =12(AC -CD )=12(2√5-2)=√5−1,因此PH 的取值范围为√5−1⩽PH ⩽√5+1.故答案为√5−1⩽PH ⩽√5+1.。
浙教版八年级(下)数学期末特殊平行四边形压轴题专项汇编(3)(含详解)

浙教版八年级(下)数学期末特殊平行四边形压轴题专项汇编(3)(含详解)1.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.(1)如图2,取AB的中点H,连接HE,求证:AE=EF.(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.2.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(2)当t为何值时,△DEF为直角三角形?请说明理由.3.定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)如图1,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF 是准矩形;(2)如图2,准矩形ABCD中,M、N分别AD、BC边上的中点,若AC=2MN,求AB2、BC2、CD2、AD2之间的关系.4.如图,以△ABC的各边为边长,在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.(1)求证:△BDE≌△BAC;(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;②求证:四边形ADEG是平行四边形;(3)当△ABC满足什么条件时,四边形ADEG是正方形?请说明理由.5.已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.(1)若点G在点B的右边.试探索:EH﹣BG的值是否为定值,若是,请求出定值;若不是,请说明理由.(2)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数.6.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.7.已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD 的边AB、BC、DA上.(1)如图1,四边形EFGH 为正方形,AE =2,求GC 的长.(2)如图2,四边形EFGH 为菱形,设BF =x ,△GFC 的面积为S ,且S 与x 满足函数关系S =621x .在自变量x 的取值范围内,是否存在x ,使菱形EFGH 的面积最大?若存在,求x 的值,若不存在,请说明理由.8.如图,正方形ABCD 的对角线相交于点O ,∠CAB 的平分线分别交BD 、BC 于E 、F ,作BH ⊥AF 于点H ,分别交AC 、CD 于点G 、P ,连接GE 、GF . (1)求证:△OAE ≌△OBG .(2)试问:四边形BFGE 是否为菱形?若是,请证明;若不是,请说明理由.9.已知,如图,O 为正方形对角线的交点,BE 平分∠DBC ,交DC 于点E ,延长BC 到点F ,使CF =CE ,连接DF ,交BE 的延长线于点G ,连接OG . (1)求证:△BCE ≌△DCF .(2)判断OG与BF有什么关系,证明你的结论.(3)若DF2=8﹣42,求正方形ABCD的面积?10.如图,四边形ABCD、BEFG均为正方形,(1)如图1,连接AG、CE,试判断AG和CE的数量关系和位置关系并证明;(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.(3)在(2)的条件下,过A作AN⊥MB交MB的延长线于点N,请求出线段CM与BN的数量关系.参考答案与解析1.(1)证明:取AB的中点H,连接EH;如图1所示∵四边形ABCD是正方形,AE⊥EF;∴∠1+∠AEB =90°,∠2+∠AEB =90° ∴∠1=∠2,∵BH =BE ,∠BHE =45°,且∠FCG =45°, ∴∠AHE =∠ECF =135°,AH =CE , 在△AHE 和△ECF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠ECF AHE CEAH 21, ∴△AHE ≌△ECF (ASA ), ∴AE =EF ;(2)解:AE =EF 成立,理由如下:如图2,延长BA 到M ,使AM =CE , ∵∠AEF =90°, ∴∠FEG +∠AEB =90°. ∵∠BAE +∠AEB =90°, ∴∠BAE =∠FEG , ∴∠MAE =∠CEF . ∵AB =BC , ∴AB +AM =BC +CE , 即BM =BE . ∴∠M =45°, ∴∠M =∠FCE . 在△AME 与△ECF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠ECF M CEAM CEF MAE , ∴△AME ≌△ECF (ASA ), ∴AE =EF .2.(1)证明:能.理由如下:在△DFC 中,∠DFC =90°,∠C =30°,DC =4t , ∴DF =2t , 又∵AE =2t , ∴AE =DF ,∵AB ⊥BC ,DF ⊥BC , ∴AE ∥DF , 又∵AE =DF ,∴四边形AEFD 为平行四边形, 当AE =AD 时,四边形AEFD 为菱形,即60﹣4t =2t ,解得t =10.∴当t =10秒时,四边形AEFD 为菱形.(2)①当∠DEF =90°时,由(1)知四边形AEFD 为平行四边形, ∴EF ∥AD ,∴∠ADE =∠DEF =90°, ∵∠A =60°, ∴∠AED =30°, ∴AD=21AE =t , 又AD =60﹣4t ,即60﹣4t =t ,解得t =12;②当∠EDF =90°时,四边形EBFD 为矩形,在Rt △AED 中∠A =60°,则∠ADE =30°, ∴AD =2AE ,即60﹣4t =4t ,解得t=215. ③若∠EFD =90°,则E 与B 重合,D 与A 重合,此种情况不存在. 综上所述,当t=215或12秒时,△DEF 为直角三角形.3.(1)证明:∵四边形ABCD 是正方形, ∴AB =BC ∠A =∠ABC =90°, ∴∠EAF +∠EBC =90°, ∵BE ⊥CF ,∴∠EBC +∠BCF =90°, ∴∠EBF =∠BCF , ∴△ABE ≌△BCF , ∴BE =CF ,∴四边形BCEF 是准矩形;(2)解:连接AN 、DN ,过点C 作CE ∥BD ,过点B 作BE ∥DC , 则四边形BECD 为平行四边形,连接DE ,则D 、N 、E 三点共线,过点B 作BF ⊥CE 于F ,过点D 作DG ⊥EC 交EC 延长线于点G ,如图2所示: ∵四边形BECD 为平行四边形, ∴BE =DC ,BE ∥DC ,ED =2DN , ∴∠BEF =∠DCG , 在△BEF 和△DCG 中,⎪⎩=DC BE ∴△BEF ≌△DCG (AAS ), ∴BF =DG ,EF =CG ,在Rt △BFC 中,BC 2=BF 2+FC 2=BF 2+(EC ﹣EF )2,在Rt △DEG 中,DE 2=DG 2+EG 2=DG 2+(EC +CG )2=BF 2+(EC +EF )2, ∴BC 2+DE 2=2BF 2+2EC 2+2EF 2=2(BF 2+EF 2)+2EC 2=2BE 2+2EC 2=2BD 2+2CD 2, ∴BC 2+4DN 2=2BD 2+2CD 2,∴DN 2=41(2BD 2+2CD 2﹣BC 2) 同理:AN 2=41(2AB 2+2AC 2﹣BC 2),MN 2=41(2AN 2+2DN 2﹣AD 2)=41(BD 2+CD 221-BC 2+AB 2+AC 221-BC 2﹣AD 2)=41(AC 2+CD 221-BC 2+AB 2+AC 221-BC 2﹣AD 2)21=AC 2+41(AB 2+CD 2﹣BC 2﹣AD 2),∵AC 2=MN ,∴MN 221=AC 2, ∴MN 2=MN 2+41(AB 2+CD 2﹣BC 2﹣AD 2),即:41(AB 2+CD 2﹣BC 2﹣AD 2)=0,∴AB 2+CD 2=BC 2+AD 2.4.(1)证明:∵四边形ABDI 、四边形BCFE 、四边形ACHG 都是正方形, ∴AC =AG ,AB =BD ,BC =BE ,∠GAC =∠EBC =∠DBA =90°. ∴∠ABC =∠EBD (同为∠EBA 的余角). 在△BDE 和△BAC 中,⎪BE⎩=BC∴△BDE≌△BAC(SAS),(2)①解:∵△BDE≌△BAC,∠ADB=45°,∴∠EDA=α﹣45°,∵∠DAG=360°﹣45°﹣90°﹣α=225°﹣α,②证明:∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).(3)解:结论:当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.理由:由①知,当∠DAG=90°时,∠BAC=135°.∵四边形ABDI是正方形,=AB.∴AD2又∵四边形ACHG是正方形,∴AC=AG,=AB.∴AC2=AB时,四边形ADEG是正方形.∴当∠BAC=135°且AC25.解:(1)EH﹣BG的值是定值,∵EH⊥AB,∴∠GHE=90°,∴∠GEH+∠EGH=90°,又∠AGD+∠EGH=90°,∴∠GEH=∠AGD,∵四边形ABCD与四边形DGEF都是正方形,∴∠DAG=90°,DG=GE,∴∠DAG=∠GHE,在△DAG和△GHE中,⎪DG⎩=GE∴△DAG≌△GHE(AAS);∴AG=EH,又AG=AB+BG,AB=4,∴EH=AB+BG,∴EH﹣BG=AB=4;(2)(I)当点G在点B的左侧时,如图1,同(1)可证得:△DAG≌△GHE,∴GH=DA=AB,EH=AG,∴BH=AG=EH,又∠GHE=90°,∴△BHE是等腰直角三角形,∴∠EBH=45°;(II)如图2,当点G在点B的右侧时,由△DAG≌△GHE.∴GH=DA=AB,EH=AG,∴AG=BH,又EH=AG,∴EH=HB,又∠GHE=90°,∴△BHE是等腰直角三角形,∴∠EBH=45°;(III)当点G与点B重合时,如图3,同理△DAG≌△GHE,∴GH=DA=AB,EH=AG=AB,∴△GHE(即△BHE)是等腰直角三角形,∴∠EBH=45°综上,在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°.6.解:(1)∵MN∥BC,∴∠3=∠2,又∵CF平分∠GCO,∴∠1=∠2,∴∠1=∠3,∴FO=CO,同理:EO=CO,∴EO=FO.(2)当点O运动到AC的中点时,四边形AECF是矩形.∵当点O运动到AC的中点时,AO=CO,∴四边形AECF 是平行四边形,由(1)可知,FO =CO ,∴AO =CO =EO =FO ,∴AO +CO =EO +FO ,即AC =EF ,∴四边形AECF 是矩形.(3)当点O 运动到AC 的中点时,且△ABC 满足∠ACB 为直角的直角三角形时,四边形AECF 是正方形.∵由(2)知,当点O 运动到AC 的中点时,四边形AECF 是矩形,∵MN ∥BC ,∴∠AOE =∠ACB∵∠ACB =90°,∴∠AOE =90°,∴AC ⊥EF ,∴四边形AECF 是正方形.7.解:(1)如图1,过点G 作GM ⊥BC ,垂足为M .由矩形ABCD 可知:∠A =∠B =90°,由正方形EFGH 可知:∠HEF =90°,EH =EF ,∴∠1+∠2=90°,又∠1+∠3=90°,∴∠3=∠2,∴△AEH ≌△BFE .∴BF =AE =2,同理可证:△MGF ≌△BFE ,∴GM =BF =2,FM =BE =8﹣2=6,∴CM =BC ﹣BF ﹣FM =12﹣2﹣6=4,在Rt △CMG 中,由勾股定理得:CG=524222=+;(2)如图2,过点G 作GM ⊥BC ,垂足为M ,连接HF ,由矩形ABCD 得:AD ∥BC ,∴∠AHF =∠HFM ,由菱形EFGH 得:EH ∥FG ,EH =FG ,∴∠EHF =∠HFM ,∴∠AHE =∠GFM ,又∠A =∠M =90°,EH =FG ,∴△MGF ≌△AEH ,∴GM =AE ,又 BF =x ,∴S △GFC 21=FC•GM 21=(12﹣x )•GM =621-x , ∴GM =1,∴AE =GM =1,BE =8﹣1=7,∵H 在边AD 上,∴菱形边长EH 的最大值14511222=+=,即EH =EF 145=, 此时BF =x ()6496181452==--=, ∴0≤x ≤64,∵EH =EF ,由勾股定理得:AH 2222248171x x EH +=-+=-=,∴S 菱形EFGH =BM •AB ﹣2⨯⨯217x ﹣2248121x +⨯⨯⨯=8(x +FM )﹣7x ﹣FM =x +7248x +, ∴当x 最大时,菱形EFGH 的面积最大,即当x =64时,菱形EFGH 的面积最大.8.(1)证明:∵四边形ABCD 是正方形,∴OA =OB ,∠AOE =∠BOG =90°.∵BH ⊥AF ,∴∠AHG =∠AHB =90°,∴∠GAH +∠AGH =90°=∠OBG +∠AGH ,∴∠GAH =∠OBG ,即∠OAE =∠OBG .在△OAE 与△OBG 中,⎪⎩⎪⎨⎧∠=∠=∠=∠BOG AOE OBOA OBG OAE , ∴△OAE ≌△OBG (ASA );(2)解:四边形BFGE 为菱形;理由如下:在△AHG 与△AHB 中,⎪⎩⎪⎨⎧∠=∠=∠=∠AHB AHG AHAH BAH GAH , ∴△AHG ≌△AHB (ASA ),∴GH =BH ,∴AF 是线段BG 的垂直平分线,∴EG =EB ,FG =FB .∵∠BEF =∠BAE +∠ABE =67.5°,∠BFE =90°﹣∠BAF =67.5°, ∴∠BEF =∠BFE ,∴EB =FB ,∴EG =EB =FB =FG ,∴四边形BFGE 是菱形;9.(1)证明:∵四边形ABCD 是正方形,∴BC =DC ,∠BCE =∠DCF =90°,在△BCE 和△DCF 中,⎪⎩⎪⎨⎧=∠=∠=CF CE DCF BCE DC BC ,∴△BCE ≌△DCF (SAS );(2)OG ∥BF 且OG=21BF , 理由:如图,∵BD 是正方形ABCD 的对角线,∴∠CDB =∠CBD =45°,∵BE 平分∠DBC ,∴∠2=∠3=21∠CBD =22.5°, 由(1)知,△BCE ≌△DCF ,∴∠CDF =∠3=22.5°,∴∠BDF =∠CDB +∠CDF =67.5°,∴∠F =180°﹣∠CBD ﹣∠BDF =67.5°=∠BDF ,∴BD =BF ,而BE 是∠CBD 的平分线,∴DG =GF ,∵O 为正方形ABCD 的中心,∴DO =OB ,∴OG 是△DBF 的中位线,∴OG ∥BF 且OG=21BF ; (3)设BC =x ,则DC =x ,BD=2x ,由(2)知△BGD ≌△BGF , ∴BF =BD ,∴CF =(2-1)x ,∵DF 2=DC 2+CF 2,∴x 2+[(2-1)x ]2=8﹣42,解得x 2=2,∴正方形ABCD 的面积是2.10.解:(1)AG =EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB =BE ,∠ABG =90°,AB =BC ,∠ABC =90°,在△ABG 和△BEC 中,⎪⎩⎪⎨⎧=∠=∠=BC BA EBC ABC BE BG ,∴△ABG ≌△BEC (SAS ),∴CE =AG ,∠BCE =∠BAG ,延长CE 交AG 于点M ,∴∠BEC =∠AEM ,∴∠ABC =∠AME =90°,∴AG =EC ,AG ⊥EC ;(2)∠EMB 的度数不发生变化,∠EMB 的度数为45°理由为: 过B 作BP ⊥EC ,BH ⊥AM ,在△ABG 和△CEB 中,⎪⎩⎪⎨⎧=∠=∠=EB BG EBC ABG BC AB ,∴△ABG ≌△CEB (SAS ),∴S △ABG =S △EBC ,AG =EC ,∴21EC •BP=21AG •BH , ∴BP =BH ,∴MB 为∠EMG 的平分线,∵∠AMC =∠ABC =90°,∴∠EMB=21∠EMG=21×90°=45°;(3)CM=2BN ,理由为:在NA 上截取NQ =NB ,连接BQ , ∴△BNQ 为等腰直角三角形,即BQ=2BN ,∵∠AMN =45°,∠N =90°,∴△AMN 为等腰直角三角形,即AN =MN ,∴MN ﹣BN =AN ﹣NQ ,即AQ =BM ,∵∠MBC +∠ABN =90°,∠BAN +∠ABN =90°,∴∠MBC =∠BAN ,在△ABQ 和△BCM 中,⎪⎩⎪⎨⎧=∠=∠=BCAB MBC BAN BMAQ ,∴△ABQ ≌△BCM (SAS ),∴CM =BQ ,则CM=2BN .故答案为:CM=2BN。
期末难点特训(三)与平行四边形有关的压轴题-【微专题】八年级数学下册常考点微专题提分精练

八下期末难点特训(三)与平行四边形有关的压轴题1. (1)问题背景:如图1,点E ,F 分别在正方形ABCD 的边BC ,CD 上,BE =DF ,M 为AF 的中点,求证:①∠BAE =∠DAF ;②AE =2DM .(2)变式关联:如图2,点E 在正方形ABCD 内,点F 在直线BC 的上方,BE =DF ,BE ⊥DF ,M 为AF 的中点,求证:①CE ⊥CF ;②AE =2DM .(3)拓展应用:如图3,正方形ABCD 的边长为2,E 在线段BC 上,F 在线段BD 上,BE =DF ,直接写出()2AE AF +的最小值.2. 已知:正方形ABCD 中,点E 在对角线BD 上,连接CE ,作EF CE ⊥交AB 于点F .(1)如图(1),求证:CE EF =;(2)如图(2),作EM BD ⊥交AD 于点M ,连接BM ,求证:BM =;(3)如图(3),延长CE 交DA 于点N ,若BE =6AN =,则CE =_________.3. 已知,在菱形ABCD 中,120ABC ∠=︒,6AB =,E 、F 分别为AD 、CD 上一点.(1)如图1,若60EBF ∠=︒,求证:AE DF =;(2)如图2,E 为AD 中点,1DF =,线段EG 交BC 于G ,FH 交AB 于H ,60EOF ∠=︒,若BH x =,CG y =.①求y 与x 之间的函数关系式;②若6x y +=,则HF =______.4. (1)问题背景:如图1,E 是正方形ABCD 的边AD 上的一点,过点C 作CB CD ⊥交AB 的延长线于F 求证:CE CF =;(2)尝试探究:如图2,在(1)的条件下,连接DB 、EF 交于M ,请探究DM 、BM 与BF 之间的数量关系,并证明你的结论.(3)拓展应用:如图3,在(2)的条件下,DB 和CE 交于点N ,连接CM 并延长交AB 于点P ,已知DE =,15DME ∠=︒,直接写出PB 的长________.5. 正方形ABCD 的边长为4.(1)如图1,点E 在AB 上,连接DE ,作AF D E ⊥于点F ,CG DE ⊥于点G .①求证:DF CG =;②如图2,对角线AC ,BD 交于点O ,连接OF ,若3AE =,求OF 的长;(2)如图3,点K 在CB 的延长线上,2BK =,点N 在BC 的延长线上,4CN =,点P 在BC 上,连接AP ,在AP 的右侧作PQ AP ⊥,PQ AP =,连接KQ .点P 从点B 沿BN 方向运动,当点P 运动到BC 中点时,设KQ 的中点为1M ,当点P 运动到N 点时,设KQ 的中点为2M ,直接写出12M M 的长为________.6. 如图,已知四边形ABCD ,∠A =∠C =90°,BD 是四边形ABCD 的对角线,O 是BD 的中点,BF 是∠ABE 的角平分线交AD 于点F ,DE 是∠ADC 的角平分线交BC 于点E ,连接FO 并延长交DE 于点G .(1)求∠ABC +∠ADC 的度数;(2)求证:FO =OG ;(3)当BC =CD ,∠BDA =∠MDC =22.5°时,求证:DM =2AB7. 如图,已知在ABC 和ADE 中,AB AC =.(1)如图1,若90BAC ∠=︒,=90DAE ∠︒,AD AE =,4AC =,3CE =,连接CD ,求线段CD 的长;(2)如图2,若60BAC DAB ∠=∠=︒,AD AB =,E 、F 分别为BC AB 、边上的动点,CF 与AE 相交于点M ,BCF CAE ≌,连接DM ,点N 是DM 的中点,证明:2AM CM AN +=;(3)在(2)的条件下,G 是AC 的中点,1AC =,连接GE ,H 是ABC 所在平面内一点,连接HE HG 、,HGE 和CGE 关于直线GE 成轴对称图形,连接HD ,求HD 的最小值.8. 在□ABCD 中,对角线AC AB =,且AC AB ⊥,E 为CD 边上一动点,连接BE 交AC 于点F ,M 为线段BE 上一动点,连接AM .(1)如图1,若8AB =,2CF =,M 为BF 的中点,求AM 的长;(2)如图2,若M 在线段BF 上,45AME ∠=︒,作CN AM ∥交BE 于点N ,连接AN ,求证:AN AB =;(3)如图3,若M 在线段EF 上,将△ABM 沿着AM 翻折至同一平面内,得到AB M ' ,点B 的对应点为点B '.当30ABE ∠=︒,90BMB '∠=︒时,请直接写出B M EM AM'-的值.9. 在菱形ABCD 中,点E 、F 分别为BC 、CD 边上的点,连接AC 、AF 、EF .(1)如图1,EF 与AC 交于点G ,若CE CF =,5AF =,6EF =,求AG 的长;(2)如图2,若60ABC ∠=︒,DAF EFC ∠=∠,求证:BE CF =;(3)如图3,在(2)的条件下,将BEF △沿BF 翻折至同一平面内,得到BE F ' ,连接CE '与BF 交于点O ,记CEF △、CE F ' 、BCF △的面积分别为1S 、2S 、3S ,当O 为BF 中点时,请直接写出3213S S S -的值.10. 在菱形ABCD 中,60ABC ∠=︒,E 为对角线BD 上一动点,连接AE .(1)如图1,点F 为DE 的中点,连接AF ,若BE AE =,求FAD ∠的度数;(2)如图2,BEM △是等边三角形,连接DM ,H 为DM 的中点,连接AH ,猜想线段AH 与AE 之间的数量关系,并证明.(3)在(2)的条件下,N 为AD 的中点,连接AM ,以AM 为边作等边 AMP ,连接PN ,若AD =PN 的最小值.11. 问题解决:如图1,在矩形ABCD 中,点,E F 分别在,AB BC 边上,,DE AF DE AF =⊥于点G .(1)求证:四边形ABCD 是正方形;(2)延长CB 到点H ,使得BH AE =,判断AHF △的形状,并说明理由.类比迁移:如图2,在菱形ABCD 中,点,E F 分别在,AB BC 边上,DE 与AF 相交于点G ,,60,6,2DE AF AED AE BF =∠=︒==,求DE 的长.12. 矩形ABCD 中,将矩形沿AE 、AG 翻折,点B 的对应点为点F ,点D 的对应点为点Q ,A 、F 、Q 三点在同一直线上.(1)如图1,求EAG ∠的度数;(2)如图2,当AB BC =时,连接BD ,交AE 、AG 于点M 、N ,若3BM =,4DN =,求MN 的长度;(3)如图3,当8AB =,9AD =时,连接EG ,45GEC ∠=︒,求BE 的长.13. 如图,正方形ABCD 中,6AB =,点E 在CD 边上运动(不与点C 、D 重合).过点B 作AE 的平行线交DC 的延长线于点F ,过点D 作AE 的垂线DN 分别交于AE ,BF 于点M 、N .(1)求证:四边形ABFE 是平行四边形;(2)若13DE DC =,求线段MN 的长;(3)点E 在CD 边上运动过程中,CND ∠的大小是否改变?若不变,求出该值,若改变请说明理由.14. (1)如图1,在正方形ABCD 中,AE ,DF 相交于点O 且AE ⊥DF .则AE 和DF 的数量关系为 .(2)如图2,在正方形ABCD 中,E ,F ,G 分别是边AD ,BC ,CD 上的点,BG ⊥EF ,垂足为H .求证:EF =BG .(3)如图3,在正方形ABCD中,E,F,M分别是边AD,BC,AB上的点,AE =2,BF=4,BM=1,将正方形沿EF折叠,点M的对应点与CD边上的点N重合,求CN的长度.15. 已知:在边长为6的正方形ABCD中,点P为对角线BD上一点,且BP .将三角板的直角顶点与点P重合,一条直角边与直线BC交于点E,另一条直角边与射线BA交于点F(点F不与点B重合),将三角板绕点P旋转.(1)如图,当点E、F在线段BC、AB上时,求证:PE=PF;(2)当∠FPB=60°时,求△BEP的面积;(3)当△BEP为等腰三角形时,直接写出线段BF的长.16. 已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D 不与B、C重合).以AD为边作正方形ADEF,连接CF.=-.(1)如图①,当点D在线段BC上时,求证:CF BC CD(2)如图②和③,当点D在线段BC的延长线上或反向延长线上时,其它条件不变,请判断CF、BC、CD三条线段之间的关系,并证明之;(3)如图③,若连接正方形ADEF对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.17. 在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB 于E.(1)如图1,连接CE,求证:△BCE是等边三角形;(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.18. 在菱形ABCD中,∠BAD=60°.(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC 的中点,连接DQ,MQ,求证:DM=2DQ.八下期末难点特训(三)与平行四边形有关的压轴题【1题答案】【答案】(1)①见解析;②见解析;(2)①见解析;②见解析;(3)8【解析】【分析】(1)问题情景:①证明△ABE≌△ADF(SAS),由全等三角形的性质得出∠BAE=∠DAF;②由全等三角形的性质得出AE=AF,由直角三角形的性质可得出结论;(2)变式关联:①延长BE交DF于G,BG交CD于H,证明△CBE≌△CDF (SAS),由全等三角形的性质得出∠BCE=∠DCF,则可得出结论;②延长DM到N,使DM=MN,连接AN,证明△AMN≌△FMD(SAS),由全等三角形的性质得出AN=DF,证明△ABE≌△DAN(SAS),由全等三角形的性质得出AE=DN=2DM;(3)拓展应用:过点D作DP⊥DF,且使PD=AB,连接PF,PA,过点P作PQ⊥AD,交AD的延长线于点Q,证明△ABE≌△PDF(SAS),由全等三角形的性质得出AE=PF,AF+AE=AF+PF≥AP,即当A,F,P三点共线时,AE+AF的最小值为AP,求出2AP则可得出答案.【详解】解:(1)问题情景:①证明:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADF=90°,∵BE=DF,∴△ABE≌△ADF(SAS),∴∠BAE=∠DAF;②证明:∵△ABE≌△ADF,∴AE=AF,∵M为AF的中点,AF,∴DM=12∴AE=AF=2DM;(2)变式关联:①证明:延长BE交DF于G,BG交CD于H,∵四边形ABCD为正方形,∴∠BCD=90°,CD=CB,∵BE⊥DF,∴∠BGD=∠BCD=90°,∵∠BHD=∠CBE+∠BCD,∠BHD=∠BGD+∠CDF,∴∠CBE+∠BCD=∠BGD+∠CDF,∴∠CBE=∠CDF,又∵BE=DF,∴△CBE≌△CDF(SAS),∴∠BCE=∠DCF,∵∠BCD=90°,∴∠ECF=∠ECD+∠DCF=∠ECD+∠BCE=90°,∴CE⊥CF;②延长DM到N,使DM=MN,连接AN,∵M为AF的中点,∴AM=MF,∵MD=MN,∠AMN=∠FMD,∴△AMN≌△FMD(SAS),∴AN=DF,∵△CBE ≌△CDF ,∴BE =DF =AN ,∠NAM =∠DFM ,∴AN ∥DF ,∴∠DAN +∠ADF =180°,∵四边形ABCD 为正方形,∴∠BAD =90°,AB =DA ,∵∠BGD =90°,∴∠ABE +∠ADF =180°,∴∠ABE =∠DAN ,∴△ABE ≌△DAN (SAS),∴AE =DN =2DM ;(3)拓展应用:过点D 作DP ⊥DF ,且使PD =AB ,连接PF ,PA ,过点P 作PQ ⊥AD ,交AD 的延长线于点Q ,∴△ABE ≌△PDF (SAS),∴AE =PF ,∵∠ADB =45°,∴∠PDQ =45°,DQ =PQ ,∴AF +AE =AF +PF ≥AP ,即当A ,F ,P 三点共线时,AE +AF 的最小值为AP ,∵AD =AB =DP =2,∴PQ =DQ ,∴(2222228AP AQ QP =+=++=+∴()2AE AF +的最小值为.【点睛】本题属于四边形综合题,考查了正方形的性质,直角三角形的性质,全等三角形的判定和性质,等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.【2题答案】【答案】(1)见解析(2)见解析(3)【解析】【分析】(1)过点E 作EH ⊥BC 于H ,EG ⊥AB 于G ,由“ASA ”可证△ECH =△EFG ,可得CE =EF ;(2)过点E 作EH ⊥BC 于H ,交AD 于Q ,EG ⊥AB 于G ,交CD 于P ,由正方形的性质和矩形的性质可证△CEF 是等腰直角三角形,从而得到CF =,再证得四边形AGPD 是矩形,四边形DQHC 是矩形,四边形DQEP 是矩形,从而得到DQ =QM =GF =AG ,由“SAS ”可证△ABM ≌△BCF ,可得BM =CF ,可得结论;(3)过点E 作GE ⊥AB 于点G ,EQ ⊥AD 于点Q ,可得△EGB 是等腰直角三角形,进而得到BG =EG =7,再根据四边形AGEQ 是矩形,可得AQ =EG =7,从而得到QN =1,再由勾股定理列出方程可求EF 的长.【小问1详解】证明:如图,过点E 作EH ⊥BC 于H ,EG ⊥AB 于G ,∵四边形ABCD 是正方形,∴∠ABD =∠CBD =45°,∵EG ⊥AB ,EH ⊥BC ,∠ABC =90°,∴四边形FGBH 是正方形,∴GE=EH,∠GEH=90°,∴∠CEF=∠GEH=90°,∴∠CEH=∠GEF=90°-∠HEF,在△ECH和△EFG中,∵∠CEH=∠GEF,EH=EG,∠EHC=∠EGF=90°,∴△ECH≌△EFG(ASA),∴CE=EF;【小问2详解】证明:如图,过点E作EH⊥BC于H,交AD于Q,EG⊥AB于G,交CD于P,∵四边形ABCD是正方形,∴AD∥BC,CD∥AB,∴PG⊥CD,QH⊥AD,∵CE=EF,CE⊥EF,∴△CEF是等腰直角三角形,∴CF ,∵PG⊥AB,QH⊥AD,∴∠A=∠ADC=∠DCB=∠ABC=90°,∴四边形AGPD是矩形,四边形DQHC是矩形,四边形DQEP是矩形,∴DQ=CH,DP=AG,∵∠ADB=∠CDB=45°,EQ⊥AD,EP⊥CD,∴EP=EQ,∴四边形DPEQ是正方形,∴DQ=DP=PE=QE=CH=AG,∵△ECH≌△EFG,∴GF=CH=DQ,∵ME⊥BD,∠ADB=45°,∴△DEM是等腰直角三角形,∵EQ⊥AD,∴DQ=QM,∴DQ=QM=GF=AG,∴DM=AF,∵AD=AB,∴AM=BF,又∵AB=BC,∠A=∠CBF=90°,∴△ABM≌△BCF(SAS),∴BM=CF,∴BM=;【小问3详解】解:如图,过点E作GE⊥AB于点G,EQ⊥AD于点Q,由(2)得:AG=GF=QE,∵EG⊥AB,∠ABD=45°,∴△EGB是等腰直角三角形,∵BE=,∴BG=EG=7,∵EQ⊥AD,EG⊥AB,∠A=90°,∴四边形AGEQ是矩形,∴AQ=EG=7,∵AN =6,∴QN =1,∵22222NF EN EF AN AF =+=+,222EN QE QN =+,222EF EG GF =+,∴222364149GF GF GF +=+++,∴27GF =,∴249756EF =+=,∴EF CE ==.故答案为:.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,矩形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.【3题答案】【答案】(1)证明见解析(2)①4y x =+;②【解析】【分析】(1)连接DB ,由菱形的性质得出∠ABD =∠BDC =60°,60,A C ∠=∠=︒证出△ABD 为等边三角形, AB =BD ,证明△ABE ≌△DBF (ASA ),由全等三角形的性质可得出结论;(2)①过点B 作,BM EG BN HF ∥∥交EG 于点I ,证明四边形BMEG 为平行四边形,由平行四边形的性质得出BG =EM =6-y ,得出AM =y -3,同理DN =1+x ,由(1)得AM =DN ,得出y -3=x +1,则可得出答案; ②过点D 作DM ⊥AB 于点M ,过点F 作FN ⊥AB 于点N ,由题意求出x =1,y =5,得出BH =1,CG =5,由直角三角形的性质求出AM =3,由勾股定理求出答案即可.【小问1详解】证明:如图1,连接DB ,∵四边形ABCD 为菱形,∠ABC =120°,∴∠ABD =∠BDC =60°,,,AB CD AD BC ∥∥60,A C ∴∠=∠=︒∴△ABD 为等边三角形,∴AB =BD ,∵∠EBF =60°,∴∠ABE =∠DBF ,在△ABE 和△DBF 中, ,ABE DBF AB BD A BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE ≌△DBF (ASA ),∴AE =DF ;【小问2详解】解:①如图2,过点B 作,BM EG BN HF ∥∥交EG 于点I ,∵,AD BC BM EG ∥∥,∴四边形BMEG 为平行四边形,而6,,,AB BC CD AD CG y BH x ====== ∴BG =EM =6-y ,∵E 是AD的中点,∴3,AE DE ==∴AM =y -3, 同理DN =1+x ,∵BN HF ∥,∴∠EOF =∠EIN =60°,∵BM EG ∥,∴∠MBN =∠EIN =60°,由(1)得,AM =DN ,∴y -3=x +1,∴y =x +4;②如图3,过点D 作DM ⊥AB 于点M ,过点F 作FN ⊥AB 于点N ,由①知y =x +4,又∵x +y =6,∴x =1,y =5,∴BH =1,CG =5,∵DM ⊥AB ,AB CD ∥,∴DM ⊥CD ,∴四边形MDFN 为矩形,∴DM =NF ,DF =MN =1,∵∠A =60°,AD =6,∴AM =12AD =3,∴DM ==,∵AB =6,∴NH =AB -AM -MN -BH =6-3-1-1=1,∴HF ===,故答案为:.【点睛】本题属于四边形综合题,考查了菱形的性质,矩形的判定与性质,等边三角形的判定与性质,直角三角形的性质,全等三角形的判定和性质,勾股定理,二次根式的化简等知识,解题的关键是熟练掌握菱形的性质.【4题答案】【答案】(1)证明见解析;(2)DM=BMBF;(3【解析】【分析】(1)由“ASA”可证△CDE≌△CBF,可得CE=CF;(2)由“AAS”可证△DME≌△HMF,可得DM=MH,可得结论;(3)由直角三角形的性质可得AFAE,可求AB的长,由勾股定理可求PF的长,即可求解.【详解】(1)证明:在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,∴∠CBF=180°−∠ABC=90°,∵CF⊥CE,∴∠ECF=90°,∴∠DCB=∠ECF=90°,∴∠DCE=∠BCF,在△CDE和△CBF中,D CBF DC BCDCE BCF ∠∠⎧⎪⎨⎪∠∠⎩===∴△CDE≌△CBF(ASA),∴CE=CF;(2)DM=BMBF,理由如下:如图,过点F作FH⊥AF,交DB的延长线于H,∵△CDE≌△CBF,∴DE=BF,∵四边形ABCD是正方形,∴∠ABD=∠CBD=45°,∴∠FBH=45°,∵FH⊥AB,∴∠FBH=∠H=45°,∴BF=FH=DE,∴BH BF,∵∠EDM=∠H=45°,∠EMD=∠HMF,DE=FH,∴△DME≌△HMF(AAS),∴DM=MH,EM=MF,∴DM=MB+BH=MB BF;(3)连接EP,∵∠DME=15°,∠ABD=45°,∴∠AFE=30°,∴AF,∴AB+BF AB−DE),∴AB +=-+,∴AB =,∴AE =,AF =,∵EC =CF ,∠ECF =90°,EM =MF ,∴CP 是EF 的垂直平分线,∴EP =PF ,∵PE 2=AE 2+AP 2,∴PF 2=24+(−PF )2,∴PF =,∴PB +,【点睛】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的性质等知识,灵活运用这些性质解决问题是解题的关键.【5题答案】【答案】(1)①见解析;(2)【解析】【分析】(1)①证明△ADF ≌△DCG ,即可求证;②连接OG ,由①得:△ADF ≌△DCG ,可得AF =DG ,可证得△AOF ≌△DOG ,从而得到OG =OF ,∠DOG =∠AOF ,进而得到△FOG 为等腰直角三角形,可得到OF FG =,再由1122ADE S AE AD AF DE =⨯=⨯ ,求出125DG AF ==,从而得到165DF =,进而得到FG = 45,即可求解;(2)取CK 的中点Y ,连接MY ,CQ ,可得12YM CQ =,从而得到点M 的运动轨迹为线段YM ,然后分别计算出当点P 运动到BC 中点时,当点P 运动到N 点时,YM 1,YM 2的长, 即可求解.【小问1详解】①证明:在正方形ABCD 中,AD =CD ,∠DAB =∠ADC =90°,∴∠ADF +∠CDG =90°,∵AF D E ⊥,CG DE ⊥,∴∠AFD =∠CGD =90°,∴∠ADF +∠DAF =90°,∴∠DAF =∠CDG ,∴△ADF ≌△DCG ,∴DF =CG ;②解:如图,连接OG ,在正方形ABCD 中,OA =OD ,∠BAO =∠ADO =45°,∠AOD =∠BAD =90°,∴∠DAF +∠EAF =90°,∠EAF +∠OAF =∠ODG +∠ADF =45°,由①得:△ADF ≌△DCG ,∴AF =DG ,∵AF ⊥DE ,∴∠AFD =90°,∴∠ADF +∠DAF =90°,∴∠ADF =∠EAF ,∴∠OAF =∠ODG ,在△AOF 和△DOG 中,∵AF =DG ,∠OAF =∠ODG ,OA =OD ,∴△AOF ≌△DOG ,∴OG=OF,∠DOG=∠AOF,∴∠FOG=∠AOF+∠AOG=∠DOG+∠AOG=∠AOD=90°,∴△FOG为等腰直角三角形,∴FG==,∴OF FG=,在Rt AED△中,AD=4,AE=3,∠DAE=90°,∴5DE=,∵AF⊥DE,∴1122ADES AE AD AF DE=⨯=⨯,∴125 DG AF==,∴165 DF=,∴FG=DF-DG=45,∴OF==;【小问2详解】解:如图,取CK的中点Y,连接MY,CQ,∵点M为KQ的中点,∴12YM CQ=,YM∥CQ,∴点M的运动轨迹为线段YM,如图,当点P运动到BC中点,即BP=CP=2时,过点Q作QJ⊥CN于点J,在正方形ABCD中,∠ABC=90°,∴∠BAP+∠APB=90°,∵AP⊥PQ,∴∠APQ=90°,∴∠APB+∠QPJ=90°,∴∠BAP=∠QPJ,∵∠PJQ=∠ABP=90°,AP=PQ,∴△ABP≌△PJQ,∴QJ=BP=2,PJ=AB=4,∴CJ=2,∴CQ==YM=∴1如图,当点P运动到N点,即BP=BC+CN=8时,过点Q作QL⊥CN交CN延长线于点L,同理:△ABP≌△PLQ,∴QL=BP=8,PL=AB=4,∴CL=8,∴CQ ==,∴2YM =,∴12M M 的长为21YM YM -==.故答案为:【点睛】本题主要考查了全等三角形的判定和性质,正方形的性质,三角形中位线定理,勾股定理等知识,熟练掌握全等三角形的判定和性质,正方形的性质,三角形中位线定理,勾股定理等知识是解题的关键.【6题答案】【答案】(1)180°(2)见解析(3)见解析【解析】【分析】(1)在四边形ABCD 中,内角和为360°,因为∠A =∠C =90°,所以∠ABC +∠ADC =180°;(2)由(1)可知,∠ABF +∠CBF +∠ADE +∠CDE =180°,根据BF 、DE 分别是∠ABE 、∠ADC 的角平分线,得到∠ABF +∠ADE =90°,由∠ABF +∠AFB =90°,得∠ADE =∠AFB ,求出BF ∥ED ,所以∠BFG =∠FGD ,得证BFO ∆≌DOG ∆,由此得出结论;(3)证法一:过D 点作CD 的垂线,延长BA 相交于点N ,过B 点作BK 垂直DN ,易证BCD BKD ∆≅∆,所以BK =CD ,可证∆≅∆BAD NAD ,所以2=NB AB ,由22.5∠=∠=∠=︒ABK KDA MDC ,可证∆≅∆BKN MCD ,所以2==MD BN AB ;证法二:延长DM ,延长DC ,过B 点作MD 的垂线,垂足为N ,交DC 的延长线于点L ,可得∆≅∆BAD BND ,所以=AB NB ,再由∆≅∆LND BND 得=NB NL ,所以2=BL AB ,易证LBC MDC ∠=∠,则∆≅∆LCB MCD ,所以2==BL MD AB .【小问1详解】解:∵四边形ABCD 的内角和为360°,∠A =∠C =90°,∴∠ABC +∠ADC =180°.【小问2详解】证明:由(1)可知,∠ABF +∠CBF+∠ADE +∠CDE =180°,∵BF 、DE 分别是∠ABE 、∠ADC 的角平分线∴∠ABF =∠CBF ;∠ADE =∠CDE ,∴2∠ABF +2∠ADE =180°,∴∠ABF +∠ADE =90°,又∵∠ABF +∠AFB =90°,∴∠ADE =∠AFB ,∴BF ∥ED ,∴∠BFG =∠FGD .在BFO ∆和DOG ∆中BFO DGO BO ODBOF DOG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴∆≅∆BFO DOG ,∴OF OG =;【小问3详解】证法一:过D 点作CD 的垂线,延长BA 相交于点N ,过B 点作BK 垂直DN,∴四边形BCDK 是矩形,∵BC=CD ,∴四边形BCDK 是正方形,∴BCD BKD ∆≅∆,∴BK =CD ,∵∠BDA =∠MDC =22.5°,∠BDK =45°,∴∠ADN =22.5°=∠BDA ,在△BAD 和△NAD 中ADB ADN AD AD BAD NAD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴∆≅∆BAD NAD (ASA )∴2=NB AB ,∵22.5∠=∠=∠=︒ABK KDA MDC ,在△BKN 和△MCD 中22.5ABK MDC BK CD BKN MCD ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴∆≅∆BKN MCD (ASA )∴2==MD BN AB ;解法二:延长DM ,延长DC ,过B 点作MD 的垂线,垂足为N ,交DC 的延长线于点L .∵BC=CD ,∠BCD =90°,∴∠CBD =∠BDC =45°,∵∠BDA =∠MDC =22.5°,∴∠BDM =22.5°,在△BAD 和△BND 中ADB BDN BD BDBAD BND ∠=∠⎧⎪=⎨⎪∠=∠⎩,BAD BND ∴∆≅∆(ASA ),AB NB ∴=,在△LND 和△BND 中90BND LDN ND ND BDN LDN ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,LND BND ∴∆≅∆(ASA ),NB NL ∴=,2BL AB ∴=,∴LBC MDC ∠=∠,在△LCB 和△MCD 中BCL BCD BC CD LBC MDC ∠=∠⎧⎪=⎨⎪∠=∠⎩,LCB MCD ∴∆≅∆(ASA ),2BL MD AB ∴==.【点睛】本题考查了全等三角形的性质与判定,正方形的性质与判定,第(2)问作出辅助线构造全等三角形是解题的关键.【7题答案】【答案】(1(2)证明见解析(312-【解析】【分析】(1)先证明45ABC ACB ∠=∠=︒,BAD CAE ∠=∠,再证明BAD CAE ≌,得到45ABD ACE ∠=∠=︒,3BD CE ==,则90CBD ∠=︒,求出BC =CD =;(2)如图所示,延长DA 到Q 使得AD AQ =,延长ME 到H 使得MH MC =,连接QM QC CH ,,,先求出60CAQ ∠=︒,再由已知条件得到AD AB AC AQ ===,即可证明ABC ACQ △,△都是等边三角形,得到60ACB ACQ CQ AC ==︒=∠∠,,由全等三角形的性质得到CAE BCF ∠=∠,即可证明60CMH ∠=︒,推出MCH △是等边三角形,则60CM HM CH MCH ===︒,∠,证明QCM ACH △≌△得到QM AH =,再证明AN 是DMQ △的中位线,得到2QM AN =,即可证明2AM CM AN +=;(3)如图所示,连接AH CH ,,DH DG ,,根据轴对称的性质得到CG HG =,则12AG CG HG ===,由三角形三边的关系得到HD DG HG ≤-,则当D G H 、、三点共线时,HD 最小,最小值为12DG -,过点G 作GT AD ⊥交DA延长线于T ,求出14AT =,TG =54DT =,即可求出DG =,则12HD =-最小值.【小问1详解】解:如图所示,连接BD ,∵90BAC ∠=︒,=90DAE ∠︒,AB AC =,∴BAC BAE DAE BAE ∠-∠=∠-∠,45ABC ACB ∠=∠=︒,∴BAD CAE ∠=∠,又∵AD AE =,∴()SAS BAD CAE ≌△△,∴45ABD ACE ∠=∠=︒,3BD CE ==,∴90CBD ∠=︒,∵4AC =,∴BC ==,∴CD ==【小问2详解】证明:如图所示,延长DA 到Q 使得AD AQ =,延长ME 到H 使得MH MC =,连接QM QC CH ,,,∵60BAC DAB ∠=∠=︒,∴60CAQ ∠=︒,∵AD AB =,AB AC =,∴AD AB AC AQ ===,∴ABC ACQ △,△都是等边三角形,∴60ACB ACQ CQ AC ==︒=∠∠,,∵BCF CAE ≌,∴CAE BCF ∠=∠,∴60CMH CAE ACM BCF ACM ACB =+=+==︒∠∠∠∠∠∠,∴MCH △是等边三角形,∴60CM HM CH MCH ===︒,∠,∴MCH ACM ACQ ACM +=+∠∠∠∠,即QCM ACH =∠∠,∴()SAS QCM ACH △≌△,∴QM AH =,∵N 是DM 的中点,AD AQ =,∴AN 是DMQ △的中位线,∴2QM AN =,∴2AH AN =,即2AM MH AN +=,∴2AM CM AN +=;【小问3详解】解:如图所示,连接AH CH ,,DH DG ,,∵HGE 和CGE 关于直线GE 成轴对称图形,∴CG HG =,∵G 是AC 的中点,∴1122AG CG HG AC ====,∴HD DG HG ≤-,∴当D G H 、、三点共线时,HD 最小,最小值为12DG HG DG -=-,过点G 作GT AD ⊥交DA 延长线于T ,∵60BAC DAB ∠=∠=︒,∴60GAT =︒∠,∴30AGT =︒∠,∴1124AT AG ==,∴TG ==,54DT AD AT =+=,∴DG ==,∴12HD =-最小值.【点睛】本题主要考查了等边三角形的性质与判定,全等三角形的性质与判定,三角形中位线定理,勾股定理,含30度角的直角三角形的性质,轴对称图形的性质,三角形三边的关系,正确作出辅助线是解题的关键.【8题答案】【答案】(1)5;(2)证明过程见解析;(3)'B M EM AM-=.【解析】【分析】(1)先根据已知条件求出AF 的长度,再用勾股定理求出BF 的长度,最后根据直角三角形斜边中线定理求出AM 的长度即可;(2)过点A 作AG ⊥AM ,交BE 于点G ,连接CG ,先证出△ABM 和△ACG 全等,再证出BG ⊥CG ,再证出△ACG 和△ANG 全等,得到AC =AN ,即可得到结论;(3)根据已知条件使用勾股定理、等腰直角三角形的性质和直角三角形30°所对的直角边等于斜边的一半,用含有字母的代数式表示出NF 、AN 、MN 、AB 、AM 的长度,然后表示出BM 、EM 的长度,最后求出答案即可.【小问1详解】∵8AC AB ==,2CF =,∴826AF AC CF =-=-=,∵AC AB ⊥,∴在Rt ABF 中由勾股定理得:10BF ===,∵M 为BF 的中点,∴1110522AM BF ==⨯=.【小问2详解】作AG AM ⊥交BE 于点G ,连接CG ,∵AC AB ⊥,AG AM ⊥,∴1+3=90∠∠︒,2390∠+∠=︒,∴12∠=∠.∵45AME ∠=︒,∴AMG 为等腰直角三角形,∴AM AG =.在ABM 和ACG 中,∵12AB AC AM AG =⎧⎪∠=∠⎨⎪=⎩,∴ABM ≌ACG (SAS ),∴45∠=∠.∵67∠=∠,∴90CGF BAF ∠=∠=︒,∵//CN AM ,∴845AME ∠=∠=︒,∴CNG △为等腰直角三角形,∴GN CG =,∵45AGM ∠=︒,∴9135∠=︒,∴3609135AGC CGN ∠=︒-∠-∠=︒.在ACG 和ANG 中,∵9AG AG AGC CG NG =⎧⎪∠=∠⎨⎪=⎩,∴ACG ≌ANG (SAS ),∴AC AN =,∴AN AB =.【小问3详解】'B M EM AM-=.解析:作AN BE ⊥于点N ,设FN a =,∵130∠=︒,90BMB '∠=︒,∴根据折叠知2690245∠=∠=︒÷=︒,又AN ⊥BE ,∴5360∠=∠=︒,430∠=︒,∴22AF FN a ==,在Rt △AFN 中根据勾股定理得AN ==,∴AN MN ==,同理AM ==,2AB AN ==,同理3BN a ==,'3B M BM BN NM a ==+=+.∵2222BE BF EF AF FC AC AB =+=+===,∴()26BM EM BM BE BM BM BE a -=--=-=-,∴'B M EM AM -==.【点睛】本题考查了等腰直角三角形的判定和性质、直角三角形斜边中线定理、直角三角形30°所对的直角边等于斜边的一半、勾股定理、全等三角形的判定和性质;考查的内容比较多,按照阶梯难度逐级上升,熟练掌握那些定理并能画出辅助线是解决本题的关键.【9题答案】【答案】(1)4(2)证明见解析 (3)16【解析】【分析】(1)根据等腰三角形三线合一可知AG EF ⊥,EG FG =,可得132FG EF ==,根据勾股定理即可求出AG 的长;(2)在AD 上截取DH DF =,连接FH ,则AH CF =,因为60ABC ∠=︒,所以120AHF ECF ∠=∠=︒,则可证AHF △≌FCE △(ASA ),所以CE HF DF ==,又因为BC =CD ,所以BE CF =;(3)延长CE '交AB 于点I ,连接FI ,则△BOI ≌△FOC ,所以BI =CF ,又因为BI ∥CF ,所以四边形ACFI 是平行形,BFI BFC S S =△△,由BOI FOI S S =△△,''BOE FOE S S =△△,设''BE I FE I S S x ==△△,则32''CFI CE F FE I S S S S S x -=-==△△△,1'''2BCF BEF BIF BE F BE I FE I S S S S S S S x =-=-=+=△△△△△△,代入计算可得321136-=S S S .【小问1详解】解:∵在菱形ABCD 中,AC 平分BCD ∠,CE CF = ,∴AG EF ⊥,EG FG =.∵6EF =,∴116322FG EF ==⨯=在Rt AFG 中,90AGF ∠=︒,5AF =,∴4AG ===.【小问2详解】证明:在AD 上截取DH DF =,连接FH .∵在菱形ABCD 中,DA DC =,∴DA DH DC DF -=-,即AH CF =.∵60ABC ∠=︒,∴60D ABC ∠=∠=︒.∴DFH 为等边三角形.∴60DHF ∠=︒.∴180********AHF DHF ∠=︒-∠=︒-︒=︒.∵//AD BC ,∴180********BCD D ∠=︒-∠=︒-︒=︒.∴AHF ECF ∠=∠.在AHF △和FCE △中,∵DAF EFC AH FC AHF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴AHF △≌FCE △(ASA ).∴CE HF DF ==.∵BC DC =,∴BC CE DC DF -=-,即BE CF =.【小问3详解】321136-=S S S.解析:延长CE '交AB 于点I ,连接FI .∵AB ∥CD ,∴∠ABF =∠BFC ,∵点O 是BF 的中点,∴BO =FO ,∵∠BOI =∠FOC ,∴△BOI ≌△FOC ,∴BI =FC ,∴四边形ACFI 是平行形,∴BFI BFC S S =△△,∵BOI FOI S S =△△,''BOE FOE S S =△△,∴''BE I FE I S S x ==△△.∴3BCF CFI S S S ==△△.∴32''CFI CE F FE I S S S S S x -=-==△△△.∵BEF △沿BF 翻折至同一平面内得到BE F ' ,∴'BEF BE F S S =△△,∴1'''2BCF BEF BIF BE F BE I FE I S S S S S S S x=-=-=+=△△△△△△∴32113326S S x S x -==⨯.【点睛】本题考查了菱形,熟练运用菱形的性质,结合三角形的相关知识(等腰三角形、等边三角形、全等三角形等)是解题的关键.【10题答案】【答案】(1)30°;(2)AE=2AH,证明见解析;(3【解析】【分析】(1)根据菱形的性质以及等腰三角形的性质可得∠ABD=∠ADB=30°,∠EAD=∠BAD−∠BAE=90°,根据直角三角形斜边上的中线得AF=DF,即可得∠FAD=∠ADB=30°;(2)延长DA至F点,使得AF=DA,连接AM,CE,FM,证明△AMB≌△CEB (SAS),根据全等三角形的性质得AM=CE,∠MAB=∠ECB,可得出∠FAM=∠ECA,再证△FAM≌△ACE(SAS),可得MF=AE,根据三角形中位线定理即可得出结论;(3)连接NC、PC、NP,证明△AMB≌△APC(SAS),可得PC=BM=BE,∠PCA=∠BMA=30°,根据等边三角形的性质得CN⊥AD,∠ACN=∠DCN=30°,则∠PCN=∠PCA+∠ACN=60°,在点E运动过程中,当NP⊥PC时,PN 长度最短,根据含30°角的直角三角形的性质即可求解.【小问1详解】解:∵四边形ABCD为菱形,∠ABC=60°,∴AB=AD,∠ABD=∠ADB=30°,∠BAD=120°,∵BE=AE,∴∠ABE=∠BAE=30°,∴∠EAD=∠BAD−∠BAE=90°,∵点F为DE的中点,DE,∴AF=DF=12∴∠FAD=∠ADB=30°;【小问2详解】AE=2AH,证明:延长DA至F点,使得AF=DA,连接AM,CE,FM,∵∠ABC=60°,AB=BC,∴△ABC是等边三角形,∴∠ACB=60°,∵△BEM是等边三角形,∴∠ABM十∠ABE=∠ABE+∠EBC=60°,MB=BE,∴∠ABM=∠EBC,∴△AMB≌△CEB(SAS),∴AM=CE,∠MAB=∠ECB,∵AD=DC,且∠ADC=∠ABC=60°,∴△ADC为等边三角形,∴AD=AC,∵AD=AF,∴AF=AC,∵∠FAB=180°−∠BAD=60°,∴∠FAB=∠ACB=60°,∴∠FAM=∠FAB−∠MAB=∠ACB−∠ECB=∠ECA,∴△FAM≌△ACE(SAS),∴MF=AE,∵FA=AD,H为DM的中点,MF,∴AH=12∴AE=MF=2AH;【小问3详解】连接NC、PC、NP,∵△AMP为等边三角形,∴∠MAP=60°,AM=AP,∵四边形ABCD为菱形,∠ABC=60°,∴AB=BC=CD=AD,∴△ABC为等边三角形,△ADC为等边三角形,∴∠BAC=60°,AB=AC=CD,∠ACD=60°,∴∠MAB=∠MAP−∠BAP=∠BAC−∠BAP=∠PAC,∴△AMB≌△APC(SAS),∴PC=BM=BE,∠PCA=∠BMA=30°,∵AC=CD,N为AD的中点,∴CN⊥AD,∠ACN=∠DCN=30°,∴∠PCN=∠PCA+∠ACN=60°,在点E运动过程中,当NP⊥PC时,PN长度最短,∵AD=,∴DN=12AD,∴NC DN=3,∵∠PCN=60°,NP⊥PC,∴∠PNC=30°,∴PC=12NC=32,∴PN PC PN.【点睛】本题是四边形综合题,考查了菱形的性质,等边三角形的判定和性质,直角三角形的性质,全等三角形的判定和性质等,添加恰当辅助线构造全等三角形是解题的关键.【11题答案】【答案】问题解决:(1)见解析;(2)等腰三角形,理由见解析;类比迁移:8【解析】【分析】问题解决:(1)证明矩形ABCD 是正方形,则只需证明一组邻边相等即可.结合DE AF ⊥和=90DAE ∠︒可知BAF ADG ∠=∠,再利用矩形的边角性质即可证明ABF DAE ≌,即AB AD =,即可求解;(2)由(1)中结论可知AE BF =,再结合已知BH AE =,即可证明ABH DAE △≌△,从而求得AHF △是等腰三角形;类比迁移:由前面问题的结论想到延长CB 到点H ,使得6BH AE ==,结合菱形的性质,可以得到ABH DAE ∆∆≌,再结合已知60AED ∠=︒可得等边AHF ∆,最后利用线段BF 长度即可求解.【详解】解:问题解决:(1)证明:如图1,∵四边形ABCD 是矩形,90ABC DAB ∴∠=∠=︒.90BAF GAD ∴∠+∠=︒.,90DE AF ADG GAD ⊥∴∠+∠= .BAF ADG ∴∠=∠.又,,AF DE ABF DAE AB AD =∴∴= ≌.∴矩形ABCD 是正方形.(2)AHF △是等腰三角形.理由如下:,90,AB AD ABH DAE BH AE =∠=∠=︒= ,,ABH DAE AH DE ∴∴= ≌.又,DE AF AH AF =∴= ,即AHF △是等腰三角形.类比迁移:如图2,延长CB 到点H ,使得6BH AE ==,连接AH .∵四边形ABCD 是菱形,,,AD BC AB AD ABH BAD ∴=∴∠=∠∥.,BH AE ABH DAE =∴∆ ≌.,60AH DE AHB DEA ∴=∠=∠=︒.又,DE AF AH AF =∴= .60,AHB AHF ∠=︒∴ 是等边三角形,AH HF ∴=,628DE AH HF HB BF ∴===+=+=.【点睛】本题考查正方形的证明、菱形的性质、三角形全等的判断与性质等问题,属于中档难度的几何综合题.理解题意并灵活运用,做出辅助线构造三角形全等是解题的关键.【12题答案】【答案】(1)45°(2)5(3)4【解析】【分析】(1)由折叠的性质得()290EAQ GAQ ∠+∠=︒,则45EAG EAQ GAQ ∠=∠+∠=︒;(2)连接MF ,NF ,BF ,DF ,由折叠的性质知AE 垂直平分BF ,AG 垂直平分DF ,则3BM MF ==,4DN NF ==,再求出90MFN ∠=︒,利用勾股定理可得答案;(3)设BE x =,则9EC x =-,()891DG CD GC x x =-=--=-,1QF =,过点G 作GH 垂直EF 交EF 的延长线于H ,证明四边形FQGH 是矩形,求出EH ,在Rt GHE 中,利用勾股定理列方程求解可得答案.【小问1详解】解:由折叠的性质可知:BAE QAE ∠=∠,DAG QAG ∠=∠,四边形ABCD 是矩形,90BAD ∴∠=︒,90BAE QAE DAG QAG ∴∠+∠+∠+∠=︒,()290EAQ GAQ ∴∠+∠=︒,45EAG EAQ GAQ ∴∠=∠+∠=︒;【小问2详解】如图,连接MF ,NF ,BF ,DF ,若AB BC =,则四边形ABCD 是正方形,由题意可知点Q 与点F 重合,由折叠的性质可知:点B 与点F 关于AE 对称,点D 与点F 关于AG 对称,AE ∴垂直平分BF ,AG 垂直平分DF ,3BM MF ∴==,4DN NF ==,BD 为正方形ABCD 的对角线,1452MBE MFE ABC ∴∠=∠=∠=︒,1452NDG NFG ADC ∠=∠=∠=︒,18090MFN MFE NFG ∴∠=︒-∠-∠=︒,在Rt MFN 中,由勾股定理得:5MN ==.【小问3详解】设BE x =,由题意可知:45GEC ∠=︒,90ECG ∠=︒,180EGC GEC ECG ∴∠=︒-∠-∠ 1804590=︒-︒-︒ 45=︒,GEC EGC ∴∠=∠,EC CG ∴=,ECG ∴ 是等腰直角三角形,在矩形ABCD 中,9BC AD ==,8CD AB ==,BE x = ,9EC GC BC BE x ∴==-=-,()891DG CD GC x x =-=--=-,)9EG x ∴==-,由折叠的性质可知:BE EF x ==,1DG QG x ==-,90AFE ABE ∠=∠=︒,90AQG ADG ∠=∠=︒,9AQ AD ==,8AF AB ==,1QF AQ AF ∴=-=,如图,过点G 作GH 垂直EF 交EF 的延长线于H ,则90FHG HFQ FQG ∠=∠=∠=︒,∴四边形FQGH 是矩形,1FH QG x ∴==-,1GH QF ==,121EH EF FH x x x ∴=+=+-=-,在Rt GHE 中,由勾股定理得:222GH EH EG +=,即)2221(21)9]x x +-=-,整理得:()()2040x x +-=,解得4x =或20(x =-舍去),4BE ∴=.【点睛】本题是四边形综合题,主要考查了翻折的性质,矩形的判定和性质,正方形的性质,轴对称的性质,等腰直角三角形的性质,勾股定理等知识,熟练掌握翻折的性质是解题的关键,同时注意方程思想的运用.【13题答案】【答案】(1)见解析 (2)MN = (3)点E 在CD 边上运动过程中,CND ∠的大小不改变,且45CND ∠=︒【解析】【分析】(1)根据正方形的性质,得出AB CD ,再根据AE BF ∥,即可证明四边形ABFE 是平行四边形;(2)根据正方形的性质,结合勾股定理,求出AE =,再根据平行四边形的面积求出EF 的长即可;(3)在DN 上截取DG =BN ,连接CG ,根据“SAS ”证明DGC BNC ≌,得出CG =NC ,DCG BCN ∠=∠,说明△GCN 为等腰直角三角形,即可得出结果.【小问1详解】证明:∵四边形ABCD 为正方形,∴AB CD ,即AB EF ∥,∵AE BF ∥,∴四边形ABFE 是平行四边形.【小问2详解】解:∵四边形ABCD 为正方形,∴6AB BC CD AD ====,90ABC BCD CDA DAB ∠=∠=∠=∠=︒,∵123DE DC ==,∴在Rt △ADE 中根据勾股定理得:AE ===,∵ABFE S AB BC AE MN =⨯=⨯ ,∴AB BC MN AE ⨯===【小问3详解】解:点E 在CD 边上运动过程中,CND ∠的大小不改变;在DN 上截取DG =BN ,连接CG ,如图所示:∵DN ⊥AE ,∴90DME ∠=︒,∵AE BF ∥,∴90DNF DME ∠=∠=︒,∴90F NDF ∠+∠=︒,∵18090BCF BCD ∠=︒-∠=︒,∴90F FBC ∠+∠=︒,∴NDF FBC ∠=∠,∵在△DGC 和△BNC 中DC BC CDG CBN DG BN =⎧⎪∠=∠⎨⎪=⎩,∴DGC BNC ≌(SAS ),∴CG =NC ,DCG BCN ∠=∠,∴90BCN BCG BCG DCG ∠+∠=∠+∠=︒,∴190452CND CGN ∠=∠=⨯︒=︒.【点睛】本题主要考查了正方形的性质,平行四边形的判定,全等三角形的判定和性质,勾股定理,平行四边形的面积,作出辅助线,构造全等三角形,是解题的关键.【14题答案】【答案】(1)AE =DF ;(2)见解析;(3)CN 的长度为3【解析】【分析】(1)证明∠BAE =∠ADF ,则△ABE ≌△DAF (AAS ),即可求解;(2)由正方形的性质得出∠CBG =∠MEF ,证明△BCG ≌△EMF (ASA ),即可求解;(3)证明△EHF ≌△MGN (ASA ),则NG =HF ,而AE =2,BF =4,故NG =HF =4-2=2,进而求解.【详解】解:(1)∵∠DAO +∠BAE =90°,∠DAO +∠ADF =90°,∴∠BAE =∠ADF ,在△ABE 和△DAF 中,BAE ADF ABE DAF AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DAF (AAS ),∴AE =DF ,故答案为:AE =DF ;(2)如图1,过点E 作EM ⊥BC 于点M ,则四边形ABME 为矩形,则AB =EM ,在正方形ABCD 中,AB =BC ,∴EM =BC ,∵EM ⊥BC ,∴∠MEF +∠EFM =90°,∵BG ⊥EF ,∴∠CBG +∠EFM =90°,。
平行四边形压轴题20道

平行四边形压轴题20道平行四边形是初中数学中一个重要的概念,其在几何中的应用非常广泛。
下面是 20 道有关平行四边形的初中奥数题,其中包括一些难题和压轴题。
1. 一个平行四边形的对角线相交于一点,那么这个点的坐标是多少?2. 一个三角形的三个顶点坐标都是公理,那么这个三角形是不是平行四边形?3. 一个矩形的对角线相等,并且矩形的两条边长之和等于第三边的长,那么这个矩形的周长是多少?4. 已知平行四边形的一边长为 3,另一边长为 5,那么这个平行四边形的对角线长是多少?5. 已知三角形的两边长分别为 3 和 5,那么这个三角形的第三边长是多少?6. 一个矩形的对角线相交于一点,那么这个点的坐标是多少?7. 已知平行四边形的一边长为 4,另一边长为 6,那么这个平行四边形的周长是多少?8. 已知三角形的两边长分别为 4 和 5,那么这个三角形的第三边长是多少?9. 一个平行四边形的对角线相等,并且平行于另外两条对角线,那么这个平行四边形的面积是多少?10. 已知矩形的一边长为 3,另一边长为 5,那么这个矩形的对角线长是多少?11. 一个矩形的对角线相交于一点,那么这个点的坐标是多少?12. 已知平行四边形的一边长为 3,另一边长为 4,那么这个平行四边形的周长是多少?13. 已知三角形的两边长分别为 3 和 4,那么这个三角形的第三边长是多少?14. 一个矩形的对角线相交于一点,那么这个点的坐标是多少?15. 已知平行四边形的一边长为 3,另一边长为 4,那么这个平行四边形的面积是多少?16. 已知三角形的两边长分别为 3 和 4,那么这个三角形的面积是多少?17. 一个矩形的对角线相等,并且平行于另外两条对角线,那么这个矩形的面积是多少?18. 已知矩形的一边长为 4,另一边长为 6,那么这个矩形的周长是多少?19. 一个矩形的对角线相交于一点,那么这个点的坐标是多少?20. 已知平行四边形的一边长为 4,另一边长为 6,那么这个平行四边形的周长是多少?以上 20 道平行四边形的初中奥数题,有些难度较高,需要学生有一定的几何思想和解题能力。
2020-2021备战中考数学压轴题专题平行四边形的经典综合题附答案
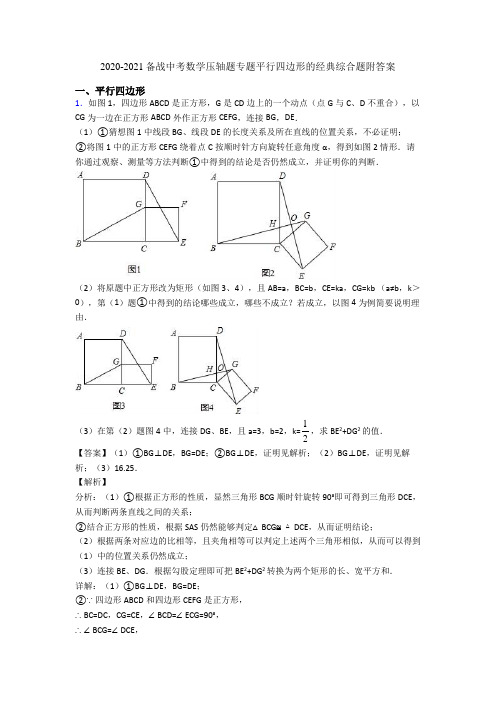
2020-2021备战中考数学压轴题专题平行四边形的经典综合题附答案一、平行四边形1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=12,求BE2+DG2的值.【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.【解析】分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.详解:(1)①BG⊥DE,BG=DE;②∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE,∴BG=DE,∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(2)∵AB=a,BC=b,CE=ka,CG=kb,∴BC CG b==,DC CE a又∵∠BCG=∠DCE,∴△BCG∽△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(3)连接BE、DG.根据题意,得AB=3,BC=2,CE=1.5,CG=1,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.2.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到到B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′(2)若AB = 8,DE = 3,点P为线段AC上任意一点,PG⊥AE于G,PH⊥BC于H.求PG + PH的值.【答案】(1)证明见解析;(2).【解析】【分析】(1)由折叠的性质知,,,,则由得到;(2)由,可得,又由,即可求得的长,然后在中,利用勾股定理即可求得的长,再过点作于,由角平分线的性质,可得,易证得四边形是矩形,继而可求得答案.【详解】(1)四边形为矩形,,,又,;(2),,,,在中,,过点作于,,,,,,,、、共线,,四边形是矩形,,.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作法,注意数形结合思想的应用.3.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.【答案】(1)证明见解析;(2)133. 【解析】分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点, ∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD , ∴∠OBE=∠ODF , 在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ), ∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF , 设BE=x ,则 DE=x ,AE=6-x , 在Rt △ADE 中,DE 2=AD 2+AE 2, ∴x 2=42+(6-x )2, 解得:x= 133, ∵22AD AB +13∴OB=1213 ∵BD ⊥EF ,∴22BE OB -213∴413点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键4.如图,在正方形ABCD 中,E 是边AB 上的一动点,点F 在边BC 的延长线上,且CF AE =,连接DE ,DF ,EF . FH 平分EFB ∠交BD 于点H .(1)求证:DE DF ⊥; (2)求证:DH DF =:(3)过点H 作HM EF ⊥于点M ,用等式表示线段AB ,HM 与EF 之间的数量关系,并证明.【答案】(1)详见解析;(2)详见解析;(3)22EF AB HM =-,证明详见解析. 【解析】 【分析】(1)根据正方形性质, CF AE =得到DE DF ⊥.(2)由AED CFD △△≌,得DE DF =.由90ABC ∠=︒,BD 平分ABC ∠, 得45DBF ∠=︒.因为FH 平分EFB ∠,所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.(3)过点H 作HN BC ⊥于点N ,由正方形ABCD 性质,得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥,,得HM HN =.因为4590HBN HNB ∠=︒∠=︒,,所以22sin 45HNBH HN HM ===︒.由22cos 45DFEF DF DH ===︒,得22EF AB HM =-.【详解】(1)证明:∵四边形ABCD 是正方形, ∴AD CD =,90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒. ∵CF AE =。
