(完整版)初二数学经典难题(带答案及解析)

合集下载

初二数学经典难题(带答案与解析)

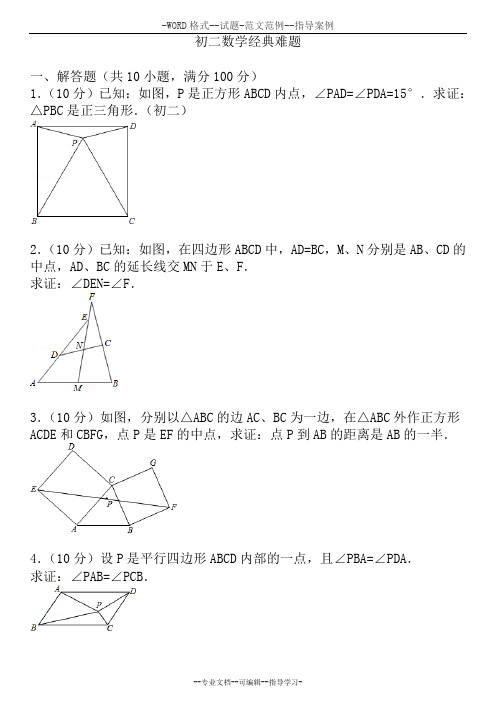
-WORD格式--试题-范文范例--指导案例初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ 与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•河南）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值范围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•福州）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN 于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•河南）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值范围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•福州）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初二数学经典难题(带答案与解析)

10．（ 10 分）（2007?福州）如图，已知直线 y= x 与双曲线
交于 A，
B 两点，且点 A 的横坐标为 4．
（ 1）求 k 的值；
（ 2）若双曲线
上一点 C的纵坐标为 8，求△ AOC的面积；
（ 3）过原点 O的另一条直线 l 交双曲线
于 P点 A， B，P， Q为顶点组成的四边形面积为 24，求点 P 的坐标．
考正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边点：三角形的判定。 1097743 专证明题。题：分在正方形内做△ DGC 与△ ADP全等，根据全等三角形的性质求出△ PDG 析：为等边，三角形，根据 SAS证出△ DGC≌△ PGC，推出 DC=PC，推出
PB=DC=P，C 根据等边三角形的判定求出即可．解证明：答： ∵正方形 ABCD，
-WORD格式 -- 试题 - 范文范例 -- 指导案例
初二数学经典难题一、解答题（共 10 小题，满分 100 分） 1．（ 10 分）已知：如图， P 是正方形 ABCD内点，∠ PAD=∠PDA=15°．求证： △PBC是正三角形．（初二）
2．（ 10 分）已知：如图，在四边形 ABCD中， AD=BC， M、 N 分别是 AB、CD的中点， AD、 BC的延长线交 MN于 E、 F．求证：∠ DEN=∠F．
-- 专业文档 -- 可编辑 -- 指导学习 -
-WORD格式 -- 试题 - 范文范例 -- 指导案例
-- 专业文档 -- 可编辑 -- 指导学习 -
-WORD格式 -- 试题 - 范文范例 -- 指导案例
初二数学经典难题参考答案与试题解析
一、解答题（共 10 小题，满分 100 分） 1．（ 10 分）已知：如图， P 是正方形 ABCD内点，∠ PAD=∠PDA=15°．求证： △PBC是正三角形．（初二）

(完整版)初中数学经典难题(含答案)

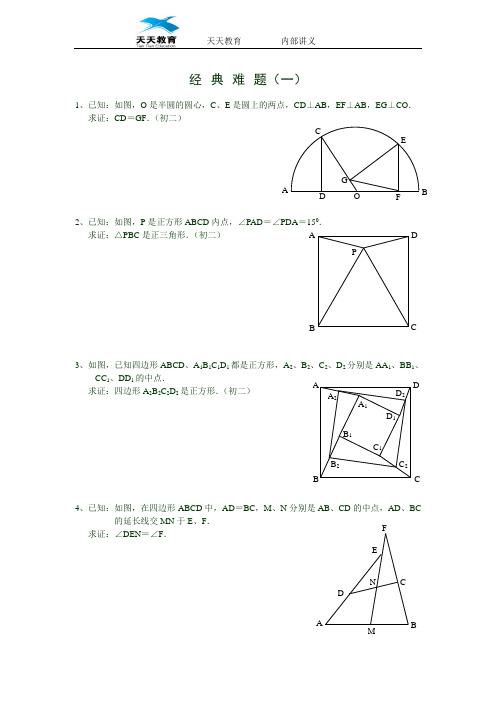
经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知：△ABC 中，H 为垂心（各边高线的交点），O （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）D AF D E C B E DA CB F A E PC B A OD BFAECP1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．APCBACBPDEDCB AA CBPD经典难题（一）1、2、3、4、经典难题（二）1、2、4、经典难题（三）1、3、4、1、2、3、4、证明：过D 作DQ ⊥AE ，DG ⊥CF,并连接DF 和DE ，如右图所示则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线，∴∠DPA=∠DPC1、2、3、3、4、。

(完整版)初二数学经典难题(带答案及解析)

初中数学经典难题(含答案)

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．经典难题（一）1、2、3、4、经典难题（二）1、2、4、经典难题（三）1、3、4、1、2、3、4、证明：过D 作DQ ⊥AE ，DG ⊥CF,并连接DF 和DE ，如右图所示则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线，∴∠DPA=∠DPC1、2、3、3、4、。

初二数学经典难题(带答案与解析)

初二数学经典难题(带答案与解析)1. 一位农夫要过一条河，他只有一艘小船，船只能支持他和一件物品的重量。

他需要把他自己，一只狼，一只绵羊和一束青菜都安全地运送到对岸。

但是，他不能让狼和绵羊在船上单独相处，因为狼会吃掉绵羊，而他也不能把青菜留在对岸，因为狼会吃掉青菜。

请问，农夫应该如何安全地将这些物品都运送到对岸？答案:农夫的运输过程，可以分为3个阶段:第一次船过去，农夫把绵羊放在岸边，然后把狼和青菜带到对岸。

第二次船会回来，这一次农夫只带绵羊回对岸，留下狼和青菜。

第三次船过去，农夫把青菜放在岸边，把狼带到对岸，然后返回把绵羊也带到对岸。

解析:这是一个相当著名的数学难题，考验玩家的逻辑思维和解决问题的能力。

农夫需要分别带着“绵羊、狼、青菜”三个物品过河，但是船只能支撑一人和一样物品的质量。

如果让“狼”单独和“绵羊”在一起，绵羊就会被吃掉，如果让“青菜”单独和“狼”在一起，青菜就会被吃掉。

怎么办呢？我们需要一步一步来想象这个过程。

首先，农夫需要把狼在非常安全的状态下到对岸。

所以，他需要先把绵羊放在岸边，然后带上狼和青菜一起过河。

这样，在对岸靠岸后，他可以先把青菜放在岸边，回来把狼送过去，并且把青菜留在对岸。

最后再回到原来的岸边，带上绵羊将其送往对岸即可。

这样，农夫就能够安全地将三个物品都运送到了对岸，而他没有违反任何规则。

这个问题是一个“二进制数学问题”，要求玩家发挥他们的逻辑思维和判断能力，找出最好的解决方案。

2. 一支队伍从A地出发向北行走360英里后到达B地，并停留了5天。

然后他们又向北行走280英里，到达C地，他们在C地停留了10天。

然后他们又向北行走400英里，到达D地。

他们在D地停留了15天，然后再向北前进60英里就到达他们的终点E地。

请问他们总共行走的距离以及他们在路途上平均每天行走的距离是多少？答案:他们总共行走的距离是: 1100 英里。

他们在路途上平均每天行走的距离是: 22 英里。

初二数学各类经典难题(含答案)

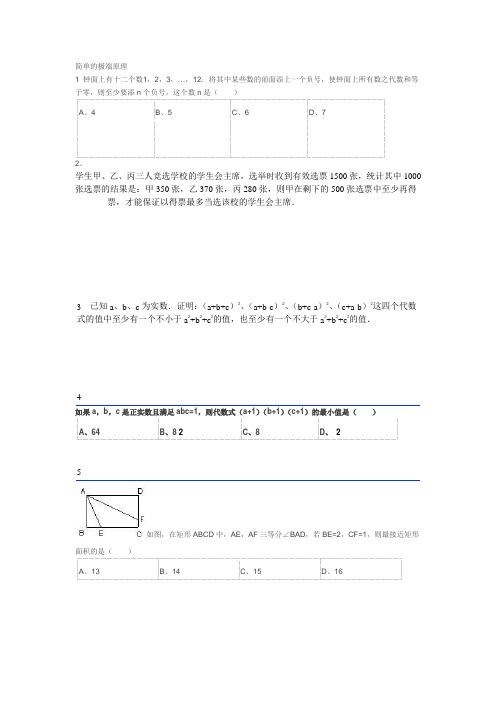
简单的极端原理1 钟面上有十二个数1，2，3，…，12．将其中某些数的前面添上一个负号，使钟面上所有数之代数和等于零，则至少要添n个负号，这个数n是（）A、4B、5C、6D、72、学生甲、乙、丙三人竞选学校的学生会主席，选举时收到有效选票1500张，统计其中1000张选票的结果是：甲350张，乙370张，丙280张，则甲在剩下的500张选票中至少再得票，才能保证以得票最多当选该校的学生会主席．3 已知a、b、c为实数．证明：（a+b+c）2、（a+b-c）2、（b+c-a）2、（c+a-b）2这四个代数式的值中至少有一个不小于a2+b2+c2的值，也至少有一个不大于a2+b2+c2的值．4如果a，b，c是正实数且满足abc=1，则代数式（a+1）（b+1）（c+1）的最小值是（）A、64B、8 2C、8D、25如图，在矩形ABCD中，AE，AF三等分∠BAD，若BE=2，CF=1，则最接近矩形面积的是（）A、13B、14C、15D、166.正方形A 1B 1C 1O ，A 2B 2C 2C 1，A 3B 3C 3C 2， …按如图所示的方式放置．点A 1，A 2，A 3， …和点C 1，C2，C 3，…分别在直线y=kx+b(k ＞0)和x 轴上，已知点B 1(1，1)，B 2(3，2)，则Bn 的坐标是_________．7（2005•烟台）（1）如图1，以△ABC 的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ，连接EG ，试判断△ABC 与△AEG 面积之间的关系，并说明理由．（2）园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是a 平方米，内圈的所有三角形的面积之和是b 平方米，这条小路一共占地多少平方米．yxO C1 B2A2C3B1A3B3A1 C8 已知，如图，等边三角形ABC中，AB=4，点P为AB边上的任意一点（点P可以与点A 重合，但不与点B重合），过点P作PE⊥BC，垂足为E，过点E作EF⊥AC，垂足为F，过点F作FQ⊥AB，垂足为Q，设BP=x，AQ=y．（1）写出y与x之间的函数关系式；（2）当BP的长等于多少时，点P与点Q重合．9（2001•苏州）如图，L甲、L乙分别是甲、乙两弹簧的长ycm与所挂物体质量xkg之间函数关系的图象，设甲弹簧每挂1kg物体伸长的长度为k甲cm，乙弹簧每挂1kg物体伸长的长度为k乙cm，则k甲与k乙的关系是（）A、k甲＞k乙B、k甲=k乙C、k甲＜k乙D、不能确定10 如图，在平面直角坐标系中，直线y=- x + 3 交x轴于A点，交y轴于B点，点C是线段AB 的中点，连接OC，然后将直线OC绕点C顺时针旋转30°交x轴于点D，再过D点作直线DC1∥OC，交AB与点C1，然后过C1点继续作直线D1C1∥OC，交x轴于点D1，并不断重复以上步骤，记△OCD的面积为S1，△DC1D1的面积为S2，依次类推，后面的三角形面积分别是S3，S4…，那么S1= ，若S=S1+S2+S3+…+S n，当n无限大时，S的值无限接近于．11 如图，正方形ABCD和正方形CGEF（CG＞BC），连接AE，取线段AE的中点M．证明：FM⊥MD，且FM=MD．解答：证明：如图，过点E作AD的平行线分别交DM、DC的延长线于N、H，连接DF、FN．∴∠ADC=∠H，∠3=∠4．∵AM=ME，∠1=∠2，∴△AMD≌△EMN∴DM=NM，AD=EN．∵ABCD和CGEF是正方形，∴AD=DC，FC=FE，∠ADC=∠FCG=∠CFE=90°，∠5=∠6=90°-∠NEG=∠NEF，DC=AD=NE．又∵∠H=90°，∴∠DCF+∠7=∠5+∠7=90°∴∠DCF=∠5=∠NEF∵FC=FE，∴△DCF≌△NEF．∴FD=FN，∠DFC=∠NEF．∵∠CFE=90°，∴∠DFN=90°，即△DFN为等腰直角三角形．又DM=MN，∴FM⊥MD，MF=MD．点评：本题考查了正方形各边相等且各内角为直角的性质，考查了全等三角形的判定和对应边、对应角相等的性质，本题中求证△DCF≌△NEF是解题的关键．。

初中数学经典难题(含问题详解)

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A PC D B A FG C EBO D D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF经典难题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）E1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，l ＝PA ＋PB ＋PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA＝200，求∠BED 的度数．经典难题（一）1、2、3、4、经典难题（二）1、2、3、4、经典难题（三）1、2、3、4、经典难题（四）2、3、4、证明：过D 作DQ ⊥AE ，DG ⊥CF,并连接DF 和DE ，如右图所示则S △ADE =21S ABCD =S △DFC∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线，∴∠DPA=∠DPC经典难题（五）2、3、3、4、。

(完整版)初二数学八年级各种经典难题例题(含答案)非常经典

1 已知一个等腰三角形两内角的度数之比为1: 4 ，则这个等腰三角形顶角的度数为（）A ． 20B ．120C ． 20 或120D ． 361．一个凸多边形的每一个内角都等于 150°，则这个凸多边形所有对角线的条数总共有（）A ．42 条B ．54 条C ．66 条D ．78 条3、若直线 y = k x +1 与 y = k x - 4 的交点在 x 轴上，那么 k 1 等于（） 1 2 2A .4 B. - 4 C. 1 41 1 D. - 1 4 （竞赛）1 正实数 x , y 满足 xy = 1,那么 x 4 + 4 y 4的最小值为:( ) 15(A) (B) (C)1 (D) 2 8(竞赛）在△ABC 中，若∠A ＞∠B ，则边长 a 与 c 的大小关系是（）A 、a ＞cB 、c ＞aC 、a ＞1/2cD 、c ＞1/2a16. 如图，直线 y=kx+6 与 x 轴 y 轴分别交于点 E ，F.点 E的坐标为(-8，0)，点 A 的坐标为(-6，0).(1)求 k 的值；(2) 若点 P(x ，y)是第二象限内的直线上的一个动点，当点 P 运动过程中，试写出△OPA 的面积 S 与 x 的函数关系式，并写出自变量 x 的取值范围；27(3) 探究：当 P 运动到什么位置时，△OPA 的面积为，并说明理由.8 2k⎝ ⎭ 6、已知，如图，△ABC 中，∠BAC=90°，AB=AC,D 为 AC 上一点，且∠BDC=124°，延长 BA 到点 E ，使 AE=AD,BD 的延长线交 CE 于点 F ，求∠E 的度数。

7.正方形 ABCD 的边长为 4，将此正方形置于平面直角坐标系中，使 AB 边落在 X 轴的正半轴上，且 A 点的坐标是（1，0）。

4 8 ①直线 y=3x-3经过点 C ，且与 x 轴交与点 E ，求四边形 AECD 的面积；②若直线l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线l 的解析式， ③若直线l 经过点 F ⎛- 3 .0⎫ 且与直线 y=3x 平行,将②中直线l 沿着 y 轴向上平移 2 个单位1 2 ⎪ 3交 x 轴于点 M ,交直线l 1 于点 N ,求∆NMF 的面积.（竞赛奥数）如图，在△ABC 中，已知∠C=60°，AC＞BC，又△ABC′、△BCA′、△CAB′都是△ABC 形外的等边三角形，而点D 在AC 上，且BC=DC（1）证明：△C′BD≌△B′DC；（2）证明：△AC′D≌△DB′A；3x + 4 与x 轴相交于点A，与直线y = 3x 相交于点P．9.已知如图，直线y =-3①求点P 的坐标．②请判断∆OPA 的形状并说明理由．③动点E 从原点O 出发，以每秒1 个单位的速度沿着O→P→A 的路线向点A 匀速运动（E 不与点O、A 重合），过点E 分别作EF⊥x 轴于F，EB⊥y 轴于B．设运动t 秒时，矩形EBOF 与△OPA 重叠部分的面积为S．求：S 与t 之间的函数关系式．yPEBO F A x16多边形内角和公式等于（n －2）×180根据题意即（n －2）×180=150n,求得n=12，多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12，则这个多边形所有对角线的条数共有 54 条因为两直线交点在x 轴上，则k1 和k2 必然不为0，且交点处x=-1/k1=4/k2,所以k1：k2=-1：41/x^4+1/4y^4=(y^4+x^4)/x^4y^4因为xy=1所以x^4y^4=1所以原式=y^4+x^4因为(x^2-y^2)^2>0且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于0所以y^4+x^4 大于或等于x^2y^2 即1所以 y^4+x^4 的最小值为 1竞赛解：在△ABC 中，∵∠A＞∠B，∴a＞b，∵a+b＞c，∴2a＞a+b＞c，∴a＞12c．故选C．1、y=kx+6 过点E（-8,0）则-8K+6＝0K＝3/42、因点E（-8,0）则OE＝8直线解析式Y＝3X/4+6当X＝0 时，Y＝6,则点F（0,6）因点A（0,6），则A、F 重合OA＝6设点P（X，Y）则点P 对于Y 轴的高为｜X｜当P 在第二象限时，｜X｜＝-XS＝OA×｜X｜/2＝-6X/2＝-3X3、S＝3｜X｜当S＝278 时278＝±3XX1＝278/3,X2＝-278/3 Y1＝3X1/4+6＝3/4×278/3+6＝151/2 Y2＝3X2/4+6＝-3/4×278/3+6＝-127/2点 P1（278/3,151/2），P2（-278/3,-127/2）6解：在△ABD 和△ACE 中，∵AB=AC，∠DAB=∠CAE=90°AD=AE，∴△ABD≌△ACE（SAS），∴∠E=∠ADB．∵∠ADB=180°-∠BDC=180°-124°=56°，∴∠E=56°．7（1）由题意知边长已经告诉，易求四边形的面积；（2）由第一问求出E 点的坐标，设出F 点，根据直线l 经过点E 且将正方形ABCD 分成面积相等的两部分，其实是两个直角梯形，根据梯形面积公式，可求出F 点坐标，从而解出直线l 的解析式．解：（1）由已知条件正方形ABCD 的边长是4，∴四边形ABCD 的面积为：4×4=16；（2）由第一问知直线y=4/3x-8/3 与x 轴交于点E，∴E（2，0），设F（m，4），直线l 经过点E 且将正方形ABCD 分成面积相等的两部分，由图知是两个直角梯形，∴S 梯形AEFD=S 梯形EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB)∴m=4，∵F（4，4），E（2，0），∴直线 l 的解析式为：y=2x-4竞赛奥数(1) 先证△ABC≌△C1BD：∵AB=C1B, ∠ABC=∠C1BD (因为都是60°+∠ABD), BD=BC。

初二数学经典难题(带答案及解析)

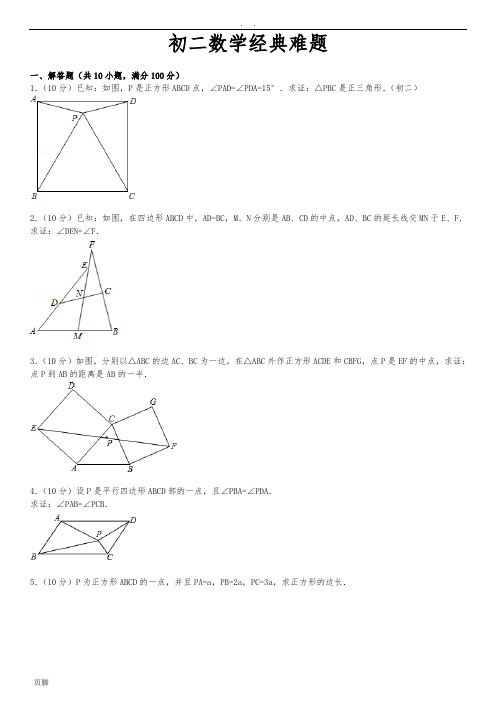
. .初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC 上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•河南）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值范围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•福州）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初中数学难题精选(附答案)

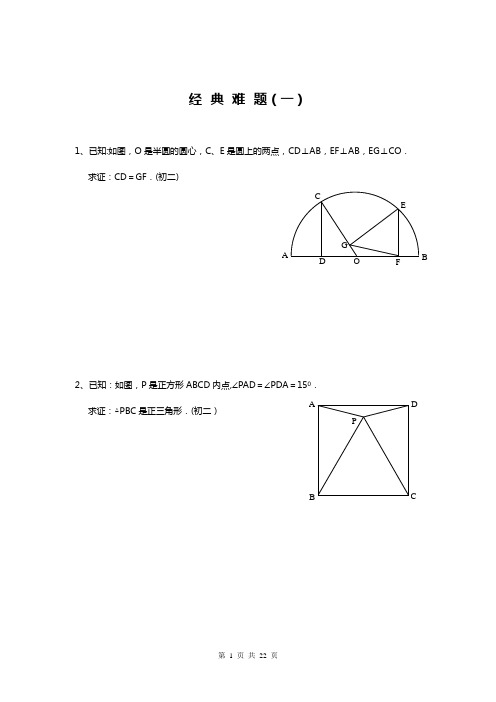
经典难题（一）1、已知:如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．(初二)2、已知：如图，P 是正方形ABCD 内点,∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．(初二）APCDB AFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知:如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．D 2 C 2B 2A 2 D 1C 1B 1CBDA A 1B经典难题（二)1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1)求证:AH＝2OM;（2)若∠BAC＝600，求证：AH＝AO．(初二)2、设MN是圆O外一直线，过O作OA⊥MN于A，自A及D、E，直线EB及CD分别交MN于P、Q．求证:AP＝AQ．（初二）F3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE,设P 、Q ．求证：AP ＝AQ ．（初二）4、如图,分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题(三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二)2、如图，四边形ABCD 为正方形，DE ∥AC,且CE ＝CA,直线EC 交DA 延长线于F ．求证:AE ＝AF ．（初二）3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．4、如图，PC切圆O于C，AC为圆的直径，B、D．求证:AB＝DC，BC＝AD．（初三)经典难题(四）1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．求：∠APB的度数．（初二)2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD为圆内接凸四边形,求证：AB·CD＋AD·BC＝AC·BD．(4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ,且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．FP DE CBAA2、已知：P是边长为1的正方形ABCD内的一点,求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点,并且PA＝a，PB＝2a，PC＝3a4、如图,△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点,∠DCA＝300,∠EBA ＝200，求∠BED的度数．经典难题（一）1。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题：证明题。

分析：在正方形内做△DGC与△ADP全等，根据全等三角形的性质求出△PDG为等边，三角形，根据SAS证出△DGC≌△PGC，推出DC=PC，推出PB=DC=PC，根据等边三角形的判定求出即可．解答：证明：∵正方形ABCD，∴AB=CD，∠BAD=∠CDA=90°，∵∠PAD=∠PDA=15°，∴PA=PD，∠PAB=∠PDC=75°，在正方形内做△DGC与△ADP全等，∴DP=DG，∠ADP=∠GDC=∠DAP=∠DCG=15°，∴∠PDG=90°﹣15°﹣15°=60°，∴△PDG为等边三角形（有一个角等于60度的等腰三角形是等边三角形），∴DP=DG=PG，∵∠DGC=180°﹣15°﹣15°=150°，∴∠PGC=360°﹣150°﹣60°=150°=∠DGC，在△DGC和△PGC中，∴△DGC≌△PGC，∴PC=AD=DC，和∠DCG=∠PCG=15°，同理PB=AB=DC=PC，∠PCB=90°﹣15°﹣15°=60°，∴△PBC是正三角形．点评：本题考查了正方形的性质，等边三角形的性质和判定，全等三角形的性质和判定等知识点的应用，关键是正确作出辅助线，又是难点，题型较好，但有一定的难度，对学生提出了较高的要求．2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN 于E、F．求证：∠DEN=∠F．考点：三角形中位线定理。

专题：证明题。

分析：连接AC，作GN∥AD交AC于G，连接MG，根据中位线定理证明MG∥BC，且GM=BC，根据AD=BC 证明GM=GN，可得∠GNM=∠GMN，根据平行线性质可得：∠GMF=∠F，∠GNM=∠DEN从而得出∠DEN=∠F．解答：证明：连接AC，作GN∥AD交AC于G，连接MG．∵N是CD的中点，且NG∥AD，∴NG=AD，G是AC的中点，又∴M是AB的中点，∴MG∥BC，且MG=BC．∵AD=BC，∴NG=GM，△GNM为等腰三角形，∴∠GNM=∠GMN，∵GM∥BF，∴∠GMF=∠F，∵GN∥AD，∴∠GNM=∠DEN，∴∠DEN=∠F．点评：此题主要考查平行线性质，以及三角形中位线定理，关键是证明△GNM为等腰三角形．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．考点：梯形中位线定理；全等三角形的判定与性质。

专题：证明题。

分析：分别过E，F，C，P作AB的垂线，垂足依次为R，S，T，Q，则PQ=（ER+FS），易证Rt△AER≌Rt△CAT，则ER=AT，FS=BT，ER+FS=A T+BT=AB，即可得证．解答：解：分别过E，F，C，P作AB的垂线，垂足依次为R，S，T，Q，则ER∥PQ∥FS，∵P是EF的中点，∴Q为RS的中点，∴PQ为梯形EFSR的中位线，∴PQ=（ER+FS），∵AE=AC（正方形的边长相等），∠AER=∠CA T（同角的余角相等），∠R=∠A TC=90°，∴Rt△AER≌Rt△CAT（AAS），同理Rt△BFS≌Rt△CBT，∴ER=AT，FS=BT，∴ER+FS=AT+BT=AB，∴PQ=AB．点评：此题综合考查了梯形中位线定理、全等三角形的判定以及正方形的性质等知识点，辅助线的作法很关键．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．考点：四点共圆；平行四边形的性质。

专题：证明题。

分析：根据已知作过P点平行于AD的直线，并选一点E，使PE=AD=BC，利用AD∥EP，AD∥BC，进而得出∠ABP=∠ADP=∠AEP，得出AEBP共圆，即可得出答案．解答：证明：作过P点平行于AD的直线，并选一点E，使PE=AD=BC，∵AD∥EP，AD∥BC．∴四边形AEPD是平行四边形，四边形PEBC是平行四边形，∴AE∥DP，BE∥PC，∴∠ABP=∠ADP=∠AEP，∴AEBP共圆（一边所对两角相等）．∴∠BAP=∠BEP=∠BCP，∴∠PAB=∠PCB．点评：此题主要考查了四点共圆的性质以及平行四边形的性质，熟练利用四点共圆的性质得出是解题关键．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．考点：正方形的性质；勾股定理；等腰直角三角形；旋转的性质。

专题：综合题。

分析：把△ABP顺时针旋转90°得到△BEC，根据勾股定理得到PE=2a，再根据勾股定理逆定理证明△PEC是直角三角形，从而得到∠BEC=135°，过点C作CF⊥BE于点F，△CEF是等腰直角三角形，然后再根据勾股定理求出BC的长度，即可得到正方形的边长．解答：解：如图所示，把△ABP顺时针旋转90°得到△BEC，∴△APB≌△CEB，∴BE=PB=2a，∴PE==2a，在△PEC中，PC2=PE2+CE2=9a2，∴△PEC是直角三角形，∴∠PEC=90°，∴∠BEC=45°+90°=135°，过点C作CF⊥BE于点F，则△CEF是等腰直角三角形，∴CF=EF=CE=a，在Rt△BFC中，BC===a，即正方形的边长为a．点评：本题考查了正方形的性质，旋转变化的性质，等腰直角三角形的性质，勾股定理以及逆定理的应用，作出辅助线构造出直角三角形是解题的关键．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．考点：分式方程的应用。

分析：设小水管进水速度为x，则大水管进水速度为4x，一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分可列方程求解．解答：解：设小水管进水速度为x立方米/分，则大水管进水速度为4x立方米/分．由题意得：解之得：经检验得：是原方程解．∴小口径水管速度为立方米/分，大口径水管速度为立方米/分．点评：本题考查理解题意的能力，设出速度以时间做为等量关系列方程求解．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．考点：反比例函数综合题。

专题：压轴题。

分析：（1）正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），设出正比例函数和反比例函数的解析式，运用待定系数法可求它们解析式；（2）因为P（﹣1，﹣2）为双曲线Y=上的一点，所以△OBQ、△OAP面积为1，依据反比例函数的图象和性质，点Q在双曲线上，即符合条件的点存在，是正比例函数和反比例函数的图象的交点；（3）因为四边形OPCQ是平行四边形，所以OP=CQ，OQ=PC，而点P（﹣1，﹣2）是定点，所以OP的长也是定长，所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值．解答：解：（1）设正比例函数解析式为y=kx，将点M（﹣2，﹣1）坐标代入得k=，所以正比例函数解析式为y=x，同样可得，反比例函数解析式为；（2）当点Q在直线OM上运动时，设点Q的坐标为Q（m，m），于是S△OBQ=|OB×BQ|=×m×m=m2，而S△OAP=|（﹣1）×（﹣2）|=1，所以有，m2=1，解得m=±2，所以点Q的坐标为Q1（2，1）和Q2（﹣2，﹣1）；（3）因为四边形OPCQ是平行四边形，所以OP=CQ，OQ=PC，而点P（﹣1，﹣2）是定点，所以OP的长也是定长，所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值，（8分）因为点Q在第一象限中双曲线上，所以可设点Q的坐标为Q（n，），由勾股定理可得OQ2=n2+=（n﹣）2+4，所以当（n﹣）2=0即n﹣=0时，OQ2有最小值4，又因为OQ为正值，所以OQ与OQ2同时取得最小值，所以OQ有最小值2，由勾股定理得OP=，所以平行四边形OPCQ周长的最小值是2（OP+OQ）=2（+2）=2+4．（10分）点评：此题难度稍大，考查一次函数反比例函数二次函数的图形和性质，综合性比较强．要注意对各个知识点的灵活应用．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．考点：二次函数综合题。