逐次逼近法(1)(优选.)
第六章 逐次逼近法lz
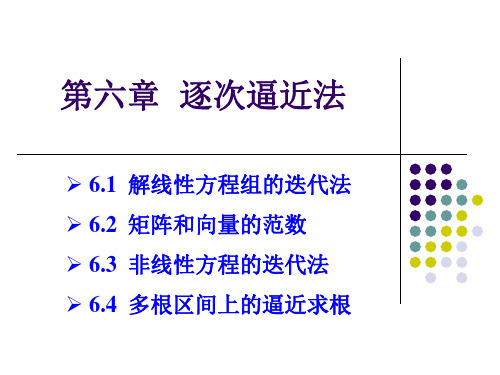
x1 x 2 x3
( k 1)
0 0 1 2 x1 0.1 0 0 0.1 0 ( 1 0 2 x 2 0 0 0.2 1 1 0 x3
L+U
(k )
(k )
第六章 逐次逼近法
第一节
解线性方程组的迭代法
二、Jacobi迭代法
1.解线性方程组的迭代法:将联立方程组的求解归结为重
复计算一组彼此独立的线性表达式,从而简化问题。 考察一般形式的线性方程组: aij x j bi
j 1 n
(i=1~n)
a11 x1 a12 x2 ... a1n xn b1 a21 x1 a22 x2 ... a2 n xn b2 a 0 ii ... ... ... ... an1 x1 an 2 x2 ... ann xn bn
7.2 8.3 ) 4.2
据此可以建立迭代公式如下:
x1 x 2 x3
( k 1)
0 0.1 0.2 x1 0.72 0.1 0 0.2 x2 0.83 0.2 0.2 0 x3 0.42
解线性方程组的迭代法
二、Jacobi迭代法
(k=0~+∞)
(k 1) (k ) ( k ) 1 1 x D (L U ) x D b BJ x f J
(k ) (k ) * * 若x x ,即: x x lim
k
(k+1) ( k ) 对x =BJ x f J 两边取极限:x*=BJ x* f J
1 x [b a x ] a
常用降维动态规划

常用降维动态规划1 逐次逼近动态规划(DPSA)逐次逼近动态规划是求解多维问题的有效方法之一,它的基本思想是把带有若干决策变量的问题分解成仅带有1个决策变量的若干个子问题,每个子问题比原来的总问题具有较少的状态变量,从而大大节省状态存储量及计算工作量,便于计算机求解。
对于多库联调优化问题,在确定初始可行调度线后采用DPSA求解的过程如下:(1)先假定第2个到最后一个水库的调度过程全部固定,对第1个水库进行优化,这时相当于单库优化调度,可以通过常规动态规划找到第1个水库的最优调度过程,此时其它水库仅进行简单的水务计算即可。
计算完成后用最优结果替代初始解中第1个水库的调度过程。
(2)假定第1个,第3个到最后一个水库的调度过程全部固定,求第2个水库的最优过程,这也相当于单库优化调度,同样通过常规动态规划找到第2个水库的最优调度过程。
并将其最优结果替代初始解中第2个水库的调度过程。
(3)依次类推,直至最后一个水库计算完成。
此时初始可行解依次被各次的单库最优结果替代,一轮计算完成。
(4)以上一轮最优结果为基础,重新依次计算单个电站的最优过程,并替换总体最优结果,反复轮流优选,直至收敛。
DPSA的思想是通过减少每次参与计算的电站数目,达到降维效果,其搜索结果精度与初始状态序列有关,因此它不能保证在所有情况下都收敛到真正的总体最优解,求解过程中可以从多个不同的初始状态(库群初始调度过程)开始,求得多个最优值,然后选择最好的结果。
2 增量动态规划(DDDP)DDDP是用逐次逼近方法寻优,每次寻优只在某个状态序列附近的小范围内,用动态规划法进行搜索。
其搜索流程是先根据一般经验或常规方法获得初始状态序列作为初始调度线,然后在该初始状态序列的上下各变动一个小范围,这个变动范围成为增量,形成一个带状“廊道”,接着在该廊道内用常规的动态规划寻优,可求得一条新的更接近于最优的状态序列。
这样就完成了一轮寻优,然后在新的状态序列上下再变动一个增量,并进行寻优。
逐步逼近法介绍

逐步逼近法介绍逐步逼近法介绍也称逐级逼近。
一种宏观上的数学分析方法数学猜想中有不少是世界上著名难题,对于这些数学难题,人们常常设法先证明它的一种减弱命题,然后一步一步地向它逐渐逼近。
例如,对于哥德巴赫猜想的研究就是采用这样的步骤,自1742年提出后,许多数学家陆续作出了越来越接近最后解决(假定以偶数(1+1)来表示)的成果:1920年挪威数学家布克龙证明了偶数=9+9;1924年德国数学家马哈证明了偶数=7+7;1932年英国数学家爱斯特曼证明了偶数=6+6;1938年苏联数学家布赫斯塔勃证明了偶数=5+5;1940年布赫斯塔勃又证明了偶数=4+4;1950年苏联数学家维诺格拉多夫证明了偶数=3+3;1957年中国数学家王元证明了奇数=2+3;1962年中国数学家潘承洞证明了偶数=1+5;1962年中国数学家王元、潘承洞证明了奇数=1+4;1965年布赫斯塔勃、维诺格拉多夫和明比科都证明了偶数=1+3;1966年中国数学家陈景润证明了奇数=1+2目前距哥德巴赫猜想最终得证只剩一步之遥。
一种解题方法与上述宏观上的方法类似,在解决具体问题时,在以下情况下:1、没有现成的公式可用,如高级方程或微分议程2、有现成的公式但求解过程非常复杂3、不要求精确求解,只要求在一定范围内控制误差这时,可用逐级逼近方式求解。
具体方法是:在已经被确定的函数单调区间内,先将假定的解代入方程,然后根据方程的误差反过来修正解,直到方程的误差降至设定的范围。
上述方法在求解某些问题时也被称作逐级叠代法(实际上逐级叠代法是逐级逼近法的一种应用)。
一种电路理论或电路结构基于前述的理论方法,在电子电路中,也存有逐级逼近式电路。
典型应用就是逐级逼近式ADC(也称作逐级比较式ADC),这种电路的原理是:1、电路核心部分由DAC、时钟、计数器、比较器组成;2、计数器对时钟信号计数,可实现加/减双向;3、计数计数的加/减控制信号由比较器产生;4、比较器产生加/减指令的依据是比较输入电压和DAC输出电压的结果而定,DAC输出电压高于输入电压时,输出减指令,DAC输出电压低于输入电压时,输出加指令。
第四章逐次逼近法

(k )
( D L)1 b
令 BG ( D L)1U , fG ( D L) 1 b
则
x ( k 1) BG x ( k ) fG (k 0,1,)
3.1.2 迭代法的收敛性
考虑如下问题: ① 如何判断迭代过程是否收敛呢? ② 迭代格式收敛的充要条件、充分条件是什么? ③ 决定迭代收敛速度的因素是什么? 设某种迭代格式为
x
( k 1)
BJ x
(k )
f J (k 0,1,)
由 A D L U , 得 (D - L)x Ux b 从而
x D - L Ux D - L b
1 1
则Gauss-Seidel迭代法可以写成
x
( k 1)
( D L) Ux
则
A D L U
由 A D L U , 得 Dx ( L U ) x b 从而
x D1 L U x D1b
则Jacobi迭代法可写成为:
x
( k 1)
D
1
L U x
k
D 1b
k 0, 1, 2,
令 BJ = D 1 L U , f J D 1b, 则
定理 3.2
(k ) 迭代法 x ( k 1) Bx f 对任意 x ( 0 ) 和 f
均收敛的充要条件为: ( B) 1。
定理 3.3 (充分条件) 若 || B || 1 ,则迭代法收敛, 且有 证明
|| x
(k )
x ||
*
(1) (0) || B || (k ) ( k 1) x x || x x || 1 B 1 || B ||
逐次逼近比较式DVM示例解析

举例:设被测电压Ux = 3.285V ,逐次逼近寄存器和D/A变换器都为6位,基准电压Uref = 10V 。
解:最后输出010101,显示3.281V
过程:
首先因为是6位的,所以先将10V分成64份(二进制数111111即为十进制64),即10/64,接下来就可以开始计算了。
1)100000,即32,所以第一个比较电压是32*10/64=5V,显然Ux<5V,所
以最高位为0(表示去码);
2)010000(注意:之前确定的位要保留),即16,所以第二个比较电压是2.5V,
由于Ux>2.5V,所以第二位为1(表示留码);
3)011000,即24,所以第三个比较电压是24*10/64=3.75V,同上,第三位取
0;
4)010100,即20,所以第四个比较电压是20*10/64=3.125V,同上,第四位
取1;
5)010110,即22,所以第五个比较电压是22*10/64=3.4375V,同上,第五位
取0;
6)010101,即21,所以第六个比较电压是21*10/64=3.28125,同上,第六位
取1。
综上可知,输出010101,显示3.281V。
由于D/A变换器输出的基准电压是量化的,因此经变换后显示的数值3.281V比实际电压值低0.004V,这就是A/D变换的量化误差。
减小量化误差的方法是增加比较次数,即增加逐次比较式A/D变换器的位数。
(正好复习时也有疑问,百度上却没有明确的解析,自己明白后就做了这个,希望对大家有帮助!
——1103子夜)。
逐次逼近法(1)

设 Ax = b为一线性方程组 , A为非奇异矩阵 , x为其精确解
若常数项 b 存在误差 δ b , 则解也应存在误差 δ x
即有
A( x + δ x ) = b + δ b
--------(15)
Aδ x = δ b
所以 又因为 可得
δ x = A −1δ b
n× n
.
则称 A 为矩阵 A的范数 .
对于复空间 C n×n中的矩阵范数可以类似 定义
例2.
设 n阶方阵 A = ( aij ) n× n
类似向量的 2-范数 --------(5)
设 A
F
n n 2 = ∑ ∑ a ij i = 1 j =1
1
2
不难验证其满足定义2的4个条件
cond ( A )1 = A 1 ⋅ A cond ( A) ∞ = A
∞
−1 1 −1 ∞
T
⋅ A
1 cond ( A) 2 = A 2 ⋅ A 2 = λmax ( A A) λ min ( AT A) T λ max ( A A) = λmin ( AT A)
−1
根据定义7的定义,(18)式和(22)式可表示为
--------(8)
对于给定的向量范数 ⋅ υ 和矩阵范数 ⋅ µ , Ax ≤ A xυ
--------(9)
若 ∀x ∈ R n , A ∈ R n × n , 都有
υ µ
则称所给的向量范数 ⋅ υ 和矩阵范数 ⋅ µ 相容 .
由(8)式,可知算子范数和其对应的向量范数是相容的
根据向量的常用范数可以得到常用的矩阵算子范数
−1 −1
图4.21逐次逼近式AD转换器原理框图

A/D转换器A/D转换器是用来通过一定的电路将模拟量转变为数字量。
模拟量可以是电压、电流等电信号,也可以是压力、温度、湿度、位移、声音等非电信号。
但在A/D转换前,输入到A/D 转换器的输入信号必须经各种传感器把各种物理量转换成电压信号。
A/D转换后,输出数字信号可以有8位、10位、12位和16位等。
AD转换器的工作原理主要介绍3种:逐次逼近法双积分法电压频率转化法1 逐次逼近法:逐次逼近式A/D是比较常见的一种A/D转换电路,转换的时间为微秒级。
采用逐次逼近法的A/D转换器是由一个比较器、D/A转换器、缓冲寄存器及控制逻辑电路组成,如图4.21所示。
基本原理是从高位到低位逐位试探比较,好像用天平称物体,从重到轻逐级增减砝码进行试探。
图4.21 逐次逼近式A/D转换器原理框图逐次逼近式A/D转换器原理框图逐次逼近法转换过程是:初始化时将逐次逼近寄存器各位清零;转换开始时,先将逐次逼近寄存器最高位置1,送入D/A转换器,经D/A转换后生成的模拟量送入比较器,称为Vo,与送入比较器的待转换的模拟量Vi进行比较,若V,该位1被保留,否则被清除。
然后再置逐次逼近寄存器次高位为1,将寄存器中新的数字量送D/A转换器,输出的Vo再与Vi比较,若VoVi,该位1被保留,否则被清除。
重复此过程,直至逼近寄存器最低位。
转换结束后,将逐次逼近寄存器中的数字量送入缓冲寄存器,得到数字量的输出。
逐次逼近的操作过程是在一个控制电路的控制下进行的。
2双积分法:采用双积分法的A/D转换器由电子开关、积分器、比较器和控制逻辑等部件组成。
如图4.22所示。
基本原理是将输入电压变换成与其平均值成正比的时间间隔,再把此时间间隔转换成数字量,属于间接转换。
图4.22 双积分式A/D转换的原理框图双积分法A/D转换的过程是:先将开关接通待转换的模拟量Vi,Vi采样输入到积分器,积分器从零开始进行固定时间T的正向积分,时间T到后,开关再接通与Vi极性相反的基准电压VREF,将VREF输入到积分器,进行反向积分,直到输出为0V时停止积分。
矩阵 逐次逼近法

第三章 逐次逼近法1.1内容提要1、一元迭代法x n+1=φ(x n )收敛条件为:1)映内性x ∈[a,b],φ(x) ∈[a,b] 2)压缩性∣φ(x) -φ(y)∣≤L ∣x-y ∣其中L <1,此时φ为压缩算子,在不断的迭代中,就可以得到最终的不动点集。
由微分中值定理,如果∣φ’∣≤L <1,显然它一定满足压缩性条件。
2、多元迭代法x n+1=φ(x n )收敛条件为:1)映内性x n ∈Ω,φ(x n ) ∈Ω 2)压缩性ρ(▽φ)<1,其中▽φ为x n 处的梯度矩阵,此时φ为压缩算子,在不断的迭代中,就可以得到最终的不动点集。
3、当φ(x )= Bx+f 时,收敛条件为,ρ(B )<1,此时x n+1= Bx n +f ,在不断的迭代中,就可以得到线性方程组的解。
4、线性方程组的迭代解法,先作矩阵变换 U L D A --= Jacobi 迭代公式的矩阵形式 f Bxb Dx U L Dx nn n +=++=--+111)(Gauss-Seidel 迭代公式的矩阵形式 f Bx b L D Ux L D x n n n +=-+-=--+111)()( 超松弛迭代法公式的矩阵形式f Bxb L D x U D L D xkk k +=-++--=--+ωωωωω111)(])1[()(三种迭代方法当1)(<B ρ时都收敛。
5、线性方程组的迭代解法,如果A 严格对角占优,则Jacob 法和Gauss-Seidel 法都收敛。
6、线性方程组的迭代解法,如果A 不可约对角占优,则Gauss-Seidel 法收敛。
7、Newton 迭代法,单根为二阶收敛 2211'''21lim)(2)(lim---∞→+∞→--=-==--k k k k k k k k x x x x f f c x x ξξαα8、Newton 法迭代时,遇到重根,迭代变成线性收敛,如果知道重数m , )()('1k k k k x f x f m x x -=+仍为二阶收敛 9、弦割法)()())((111--+---=k k k k k k k x f x f x x x f x x 的收敛阶为1.618,分半法的收敛速度为(b-a )/2n-110、Aitken 加速公式11211112)(),(),(+----+-+--+---+---===k k k k k k k k k k k x x x x x x x x x x x ϕϕ1.2 典型例题分析1、证明如果A 严格对角占优,则Jacob 法和Gauss-Seidel 法都收敛。
逐次逼近式ad转换原理

一、逐次逼近式AD转换器与计数式A/D转换类似,只是数字量由“逐次逼近寄存器SAR”产生。
SAR使用“对分搜索法”产生数字量,以8位数字量为例,SAR首先产生8位数字量的一半,即10000000B,试探模拟量Vi的大小,若Vo>Vi,清除最高位,若Vo<Vi,保留最高位。
在最高位确定后,SAR又以对分搜索法确定次高位,即以低7位的一半y1000000B(y为已确定位) 试探模拟量Vi的大小。
在bit6确定后,SAR以对分搜索法确定bit5位,即以低6位的一半yy100000B(y为已确定位) 试探模拟量的大小。
重复这一过程,直到最低位bit0被确定,转换结束。
转换过程:(1)首先发出“启动信号”信号S。
当S由高变低时,“逐次逼近寄存器SAR”清0,DAC输出Vo=0,“比较器”输出1。
当S变为高电平时,“控制电路”使SAR开始工作。
(2)SAR首先产生8位数字量的一半,即10000000B,试探模拟量的Vi大小,若Vo>Vi,“控制电路”清除最高位,若Vo<Vi,保留最高位。
(3)在最高位确定后,SAR又以对分搜索法确定次高位,即以低7位的一半y1000000B(y 为已确定位) 试探模拟量Vi的大小。
在bit6确定后,SAR以对分搜索法确定bit5位,即以低6位的一半yy100000B(y为已确定位) 试探模拟量Vi的大小。
重复这一过程,直到最低位bit0被确定。
(4)在最低位bit0确定后,转换结束,“控制电路”发出“转换结束”信号EOC。
该信号的下降沿把SAR的输出锁存在“缓冲寄存器”里,从而得到数字量输出。
从转换过程可以看出:启动信号为负脉冲有效。
转换结束信号为低电平。
我觉得,这有点像数学中的二分法,如给一个数a,先用8'b1000000(设为b)与a相比较,如果a大于b,则保留最高位1,即原来的范围变成了0-7'b1111111(第8位已确认)。
第6章 逐次逼近法

第六章 逐次逼近法 §1 线性方程组解的误差分析 因为线性方程组涉及到矩阵和向量,为了对线性方程组的近似解进行误差估计,以及后面研究迭代法解线性方程组的收敛性,需要对向量和矩阵引进范数的概念。
一、向量和矩阵的范数 1.向量的范数定义 1 如果向量空间nR 上的某个非负实值函数()N =x x 满足条件:(1)正定性:0≥x ,当且仅当=0x 时0=x ;(2)齐次性:c c =x x ,c 为任意实数; (3)三角不等式:+≤+x y x y 。
则称⋅为n R 上的一个向量范数。
n 维向量空间12{|(,,,),,1,2,,}nn i R x x x x R i n ==∈= x x上常用的三种范数:(1)向量的2—范数:2=x;(2)向量的∞—范数:1max i i nx ∞≤≤=x; (3)向量的1—范数:∑==ni ix x 11。
例1 设(1,2,3,4)T=--x ,则2141max 4,123410.i i x ∞≤≤=====++-+-=x xx后面我们研究迭代法解线性方程组时,需要讨论算法的收敛性。
为此,先给出算法产生的迭代点列收敛的概念。
定义2 设()()()1(,,)k k k nnx x R =∈ x,***1(,,)nnx x R =∈ x ,若),,2,1(,lim *)(n i x xik ik ==∞→,则称点列(){}k x 收敛于*x ,并记作()*lim k k →∞=x x。
由定义可知:()*lim k k →∞=xx ()*lim k k ∞→∞⇔-=0xx,()*lim k k →∞=xx ()*1lim k k →∞⇔-=0x x ,()*lim k k →∞=xx ()*2lim k k →∞⇔-=0xx。
2.矩阵的范数定义 3 如果矩阵空间nn R⨯上的某个非负实值函数()N =A A 满足以下条件:(1) 正定性:0≥A ,且0=⇔=0A A ;(2)齐次性:c c =A A ,c 为任意实数; (3)三角不等式:+≤+A B A B ; 则称()N A 为nn R⨯上的一个矩阵范数。
数学中的逐步逼近法

§5.4
逐步逼近法
为了叙述方便,先引入一个概念和两个符号。 如果对于一个固定的整数 n > 0,当自然数 m的素因数不 超 过 n 个 时 , 称 m 为 素 因 数不超 过 n 个的殆 素 数 。例 如 , 15=3× 5, 21=3× 7都是不超过 2 的殆素数; 30是素因数不 超过3的殆素数。 如果对于每个充分大的偶数都可表示为两个素因数分别 不超过a与b的殆素数之和时,记为a+b。 如果对于每一个充分大的偶数都可表示为一个素数与一 个素因数不超过c的殆素数之和时,记为(1+c)。
§5.4
逐步逼近法
逐步逼近法在解决问题的过程中,使后一 步比前一步更接近探索目标,其一般有三种结 果:(1)通过有限步逐步逼近最终达到目标; (2)通过无限逼近的极限,最终达到目标; (3)不能最终达到目标,但可以通过多次的 逼近,取得对目标的接近而达到一定的要求。 逐步逼近法也是一种化归方法。基本上可 分为两类:一类是问题序列的逐步逼近法,另 一类是问题解序列逐步逼近法。
§5.4
逐步逼近法
再估计 n2:又C92 1 35 个 ,最接近37,故 n2 9 即通过移动,把剩下的直线中的9条变为一个直线束, 则交点的个数又减少 35 个。再调整使交点的个数减 少2个即可。 2 C 因为 3 1 2 个, 故 n3 3,即把剩下的14条直线
中的3条变为一个直线束,而其余11条直线位置不变。 这样,经过调整后的100条直线就恰好只有1988个交 点。
因为 bk1 , bk2 ,
, bkn 经过有限次相邻元素的对换,
, bn),使每次
总可以换成 bn , bn1 , , b1(或 b1 , b2 , 不增(或不减)。 Sn 故,不等式 得证。
第6章 逐次逼近法

赣南师范学院数学与计算机科学学院
• 迭代矩阵 记
A D L U
0 a11 D 0 ann
0 0 a21 0 L 0 a ann 1 0 n1
a1n 0 a12 0 U 0 an 1n 0 0
赣南师范学院数学与计算机科学学院
( k 1) x1 x ( k 1) 2 ( k 1) xn
格式很简单:
1 (k ) (k ) (a12 x2 a1n xn b1 ) a11 1 (k ) (k ) (k ) (a21 x1 a23 x3 a1n xn b2 ) a22 1 (k ) (k ) (an1 x1 an n 1 xn 1 bn ) ann
赣南师范学院数学与计算机科学学院
2 1 1 A 1 1 1 1 1 2
1、Jacobi迭代
0 1/ 2 1/ 2 B D 1 ( L U ) 1 0 1 1/ 2 1/ 2 0
特征值为
5 I B 0 4
Ps ( )
,则
Ps ( ) I G I ( D L) 1U ( D L) 1 ( D L) U
A D L U 为对角占优阵,则 1 时 ( D L) U (D L) U 0 即 Ps ( ) 0
证明:
G D1 ( L U ) aij G max 1 aij aii i j i aii j i aij G 1 max 1 i i j aii
② A为列对角占优阵,则AT为行对角占优阵,有
毕卡逐次逼近法

毕卡逐次逼近法在定理证明中的应用邹添杰 05级数学与应用数学基地班指导老师:尹小玲2006年8月摘要 本文用毕卡逐次逼近法及数学分析知识,证明“隐函数存在定理”和一阶方程初值问题解的非局部存在性定理。
一·毕卡逐次逼近法证明隐函数存在定理 定理1· 设),(y x F 满足下列条件: (I )y ,F F x 在b y y a x x D ≤-≤-00,:上连续; (II )0),(00=y x F (通常称为初始条件) (III )对D y x ∈∀),(,恒有0),(y ≠y x F ; (IV )在D 上),(),(y x y x F y x F 条件满对Lipchitz y :即对D 上任意两点),(),(21y x y x ,,不等式 212y 2x 1y 1x ),(),(),(),(y y L y x F y x F y x F y x F --≤ (1)恒成立,L 是与),(1y x 和),(2y x 无关的正常数(常数Lipchitz )。
则在区间0),(0=上y x F h x x ≤-唯一确定一个隐函数)(x y ϕ=,满足)(00x y ϕ=。
这个函数在h x x ≤-0上连续可微。
其中},min{Mba h = ……(2) ),(),(maxyx ),(y x F y x F M D y x ∈= (3)证明:若0),(=y x F 在h x x ≤-0上能唯一确定可导的隐函数)(x y ϕ=,则有0))(,(=x y x F ,方程两边对x 求导,得0·'=+y F F y X 。
由0≠y F ,得 ),(),(y x 'y x F y x F y =-。
因此,0),(=y x F 在h x x ≤-0上能确定唯一可导的隐函数)()(00x y x y ϕϕ=且=,等价于初值问题),(),(0))(,(y x '00{y x F y x F y x y x F =-= ……(*)在h x x ≤-0上有唯一解)()(00x y x y ϕϕ=且=。
逐次逼近型AD原理及应用
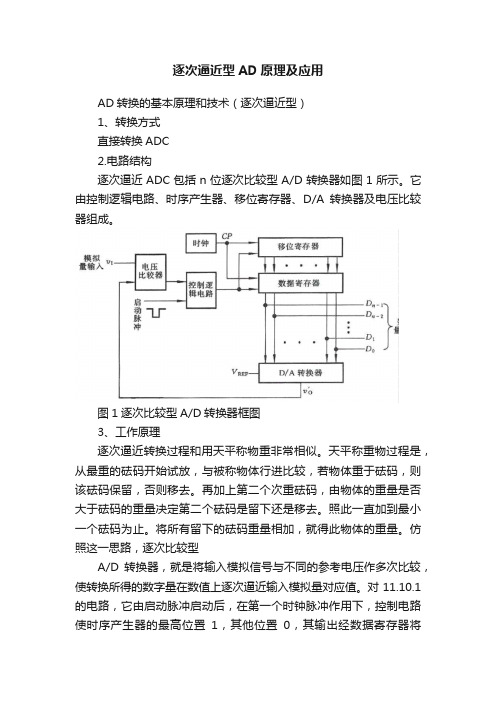
逐次逼近型AD原理及应用AD转换的基本原理和技术(逐次逼近型)1、转换方式直接转换ADC2.电路结构逐次逼近ADC包括n位逐次比较型A/D转换器如图1所示。
它由控制逻辑电路、时序产生器、移位寄存器、D/A转换器及电压比较器组成。
图1逐次比较型A/D转换器框图3、工作原理逐次逼近转换过程和用天平称物重非常相似。
天平称重物过程是,从最重的砝码开始试放,与被称物体行进比较,若物体重于砝码,则该砝码保留,否则移去。
再加上第二个次重砝码,由物体的重量是否大于砝码的重量决定第二个砝码是留下还是移去。
照此一直加到最小一个砝码为止。
将所有留下的砝码重量相加,就得此物体的重量。
仿照这一思路,逐次比较型A/D转换器,就是将输入模拟信号与不同的参考电压作多次比较,使转换所得的数字量在数值上逐次逼近输入模拟量对应值。
对11.10.1的电路,它由启动脉冲启动后,在第一个时钟脉冲作用下,控制电路使时序产生器的最高位置1,其他位置0,其输出经数据寄存器将1000……0,送入D/A转换器。
输入电压首先与D/A器输出电压(VREF/2)相比较,如v1≥VREF/2,比较器输出为1,若vI 设图11.10.1电路为8位A/D转换器,输入模拟量vA=6.84V,D/A转换器基准电压VREF=10V。
根据逐次比较D/A转换器的工作原理,可画出在转换过程中CP、启动脉冲、D7~D0及D/A转换器输出电压vO的波形,如图11.10.2所示。
由图11.10.2可见,当启动脉冲低电平到来后转换开始,在第一个CP作用下,数据寄存器将D7~D0=10000000送入D/A转换器,其输出电压v0=5V,vA与v0比较,vA>v0存1;第二个CP到来时,寄存器输出D7~D0=11000000,v0为7.5V,vA再与7.5V比较,因vA<7.5V,所以D6存0;输入第三个CP时,D7~D0=10100000,v0=6.25V;vA再与v0比较,……如此重复比较下去,经8个时钟周期,转换结束。
计算方法(三)逐次逼近法

(3-3)
称为迭代法,也称迭代过程或迭代格式. 如果对任意 其中
x
(k )
x
(0)
,都有当
(k ) (k )
k
(k ) T
时,x
*
(k )
x 。
*
( x1 , x 2 , , x n ) ,
x ( x1 , x 2 , , x n )
* * *
T
称该迭代法收敛,否则称迭代法发散.
0 a 21 a 22 a n1 a nn
a 12 a 11 0 an2 a nn
a 1n a 11 a 2n a 22 0
x1 (k ) x2 x (k ) n
k
*
lim B
k
k 1
ε
(0)
0
(0)
x
(0)
x
是一个非零的常向量,因此
k 1
k
lim B
O n n
(零矩阵)
定理 3.1
k
lim ε
(k )
0
(即
k
( xi
k
(k )
* x i , i 1, 2 , , n )
的充要条件是 定理 3.2 迭代法
(1 )
1 . 768939
(5)
x1
(5)
2 . 999843 ,
x
x2
( k 1)
(5)
2 . 000072 , x 3
(k )
1 . 000061 。
逐次逼近原理构成数据采集系统电力配电知识

逐次靠近原理构成数据采集系统 - 电力配电学问电力系统中的电量信号都是在时间和数值上连续变化的信号,因此,都属于模拟信号。
而微机继电爱护装置是对数字信号进行处理,故必需把模拟信号转变为计算机能够处理的数字信号。
数字信号是在时间上离散、在数值上量化的一种信号。
模拟信号→数字信号,需要对模拟信号进行预处理。
包括信号幅度的变换、利用模拟低通滤波器滤除信号中频率大于采样频率一半的信号、采样保持等环节。
经过预处理的信号才能输入到A/D转换芯片,进行模拟信号到数字信号的变换。
框图(组成):电压形成回路、模拟滤波器ALF、采样保持器S/H、多路开关MPX、A/D转换。
图1 逐次靠近原理构成数据采集系统组成框图一、电压形成回路1. 信号来源:微机爱护与传统爱护一样,它的输入信号来自被爱护线路或设备的电流互感器、电压互感器的二次侧。
2. 使用前提:互感器的二次侧的电流或电压一般数值较大,变化范围也较大,不适应模数转换器的工作要求,需要使用各种中间变换器来实现变换。
3. 中间变换器::电流变换器Tam;电压变换器TVm;电抗变换器TXm。
4. 输入变换及电压形成回路的原理:将电流互感器TA、电压互感器TV的二次电流、电压输出转化为计算机能识别的弱电信号,一般输出信号为±5V或± 10V,具体由A/D芯片打算。
电流变换:一般接受电流变换器并在其二次侧并电阻以取得所需电压,转变电阻值可以转变输出范围的大小;也可以接受电抗变换器。
◆电流变换接受电抗变换器的优缺点:优点:由于铁芯带气隙而不易饱和,线性范围大,且有移相作用;缺点:会抑制直流重量,放大高频重量。
◆电流变换接受电流变换器的优缺点:优点:只要铁芯不饱和,其二次电流及并联电阻上电压的波形基本保持与一次电流波形相同且同相,即它的变换可使原信息不失真;缺点:在非周期重量的作用下简洁饱和,线性度较差,动态范围小。
补充说明:电压形成回路除了电量变换作用外,还起着屏蔽和隔离作用,使得微机电路在电气上与强电部分隔离,从而阻挡来自强电系统的干扰。
逐步逼近法介绍

逐步逼近法介绍逐步逼近法介绍也称逐级逼近。
一种宏观上的数学分析方法数学猜想中有不少是世界上著名难题,对于这些数学难题,人们常常设法先证明它的一种减弱命题,然后一步一步地向它逐渐逼近。
例如,对于哥德巴赫猜想的研究就是采用这样的步骤,自1742年提出后,许多数学家陆续作出了越来越接近最后解决(假定以偶数(1+1)来表示)的成果:1920年挪威数学家布克龙证明了偶数=9+9;1924年德国数学家马哈证明了偶数=7+7;1932年英国数学家爱斯特曼证明了偶数=6+6;1938年苏联数学家布赫斯塔勃证明了偶数=5+5;1940年布赫斯塔勃又证明了偶数=4+4;1950年苏联数学家维诺格拉多夫证明了偶数=3+3;1957年中国数学家王元证明了奇数=2+3;1962年中国数学家潘承洞证明了偶数=1+5;1962年中国数学家王元、潘承洞证明了奇数=1+4;1965年布赫斯塔勃、维诺格拉多夫和明比科都证明了偶数=1+3;1966年中国数学家陈景润证明了奇数=1+2目前距哥德巴赫猜想最终得证只剩一步之遥。
一种解题方法与上述宏观上的方法类似,在解决具体问题时,在以下情况下:1、没有现成的公式可用,如高级方程或微分议程2、有现成的公式但求解过程非常复杂3、不要求精确求解,只要求在一定范围内控制误差这时,可用逐级逼近方式求解。
具体方法是:在已经被确定的函数单调区间内,先将假定的解代入方程,然后根据方程的误差反过来修正解,直到方程的误差降至设定的范围。
上述方法在求解某些问题时也被称作逐级叠代法(实际上逐级叠代法是逐级逼近法的一种应用)。
一种电路理论或电路结构基于前述的理论方法,在电子电路中,也存有逐级逼近式电路。
典型应用就是逐级逼近式ADC(也称作逐级比较式ADC),这种电路的原理是:1、电路核心部分由DAC、时钟、计数器、比较器组成;2、计数器对时钟信号计数,可实现加/减双向;3、计数计数的加/减控制信号由比较器产生;4、比较器产生加/减指令的依据是比较输入电压和DAC输出电压的结果而定,DAC输出电压高于输入电压时,输出减指令,DAC输出电压低于输入电压时,输出加指令。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: A的F − 范数为
∑ ∑ A F
=
n i=1
n
a
2 ij
j=1
12
类似于向量的2-范数
但 A F 并不是从属于 x 2的算子范数
考虑单位矩阵 I
IF = n
I
υ
=
max x≠0
Ix υ
x
υ
= max x υ x≠0
x
υ
=
1
因此
A
F
是不从属于任意向量范数
⋅
的矩阵范数
υ
故而矩阵范数和算子范数并不完全是一回事
第六章 逐次逼近法
第六章 逐次逼近法
§6.1 基本概念 §6.2 线性方程组的迭代法 §6.3 非线性方程组的迭代法 §6.4 矩阵特征值问题的数值算法 §6.5 迭代法的加速
本章要点
本章主要介绍线性方程组的迭代法、非线性方程组 的数值方法 主要方法
基本迭代法、G-J迭代法、G-S迭代法、 Newton迭代法、SOR方法和Aitken加速方法
§6.1 基本概念
二维向量和三维向量都可以度量其大小和长度 高维向量的"长度"能否定义呢? "范数"是对向量和矩阵的一种度量,实际上是二维 和三维向量长度概念的一种推广 数域: 数的集合,对加法和乘法封闭 线性空间: 可简化为向量的集合,对向量的加法和
数量乘法封闭, 也称为向量空间
一、向量和矩阵的范数
0
−1 1
=
2 0 1
0 9 −1
1
−1 2
特征方程为
det( λI
−
AT A)
=
λ−2 0 −1
0
λ −9 1
−1 1 λ−2
=
0
可得 AT A的特征值为 λ1 = 9.1428 , λ2 = 2.9211 , λ3 = 0.9361
λmax ( AT A) = 9.1428 A 2 = λmax ( AT A) = 3.0237
定理1. 设 ⋅ 是R n×n上的一种算子范数 , B ∈ R n×n ,
若B满足 B < 1, 则I + B非奇异 ,且
证明略
(I + B)−1 < 1 1− B
--------(14)
推论:设 A ∈ R n×n可逆, 且 A−1 ≤ α , C ∈ R n×n , A − C ≤ β ,
且αβ < 1,则C可逆,且 C −1 ≤ α (摄动定理 ) 1− αβ
≤ 1−
1 A − 1δA
(19)式化为 A(I + A−1δA)δx = −δA ⋅ x
δx = −( I + A−1δA)−1 A−1δA ⋅ x --------(21)
δx ≤ (I + A−1δA)−1 ⋅ A−1 ⋅ δA ⋅ x
δx x
A−1 ⋅ δA ≤ 1 − A−1δA
A−1 ⋅ δA ≤ 1 − A−1 ⋅ δA
在向量空间 Rn (C n )中, 设x = ( x1 , x2 ,L , xn )T 常用的向量 x的范数有
x 2 = ( x1 2 + x2 2 + L + xn 2 )1 2 --------(1) x的2 − 范数或欧氏范数
x 1 = x1 + x2 + L + xn
--------(2)
1=
max
1≤ j≤n
i =1
aij
= max{2,5,2} = 5 1≤ j≤n
n
∑ A
=
∞
max
1≤i≤n
j=1
aij
= max{3,4,2} = 4 1≤i≤n
由于
A 2 = λmax ( AT A)
因此先求 AT A的特征值
AT A
=
1 2 0
−1 2 −1
0 1 1
⋅
1
−1 0
2 2 1
δx ≤ A ⋅ A−1 ⋅ δb
x
b
相对误差
--------(17) --------(18)
(18)式表明,由常数项产生的误差,最多可将解的 相对误差放大 A ⋅ A−1 倍
2.系数矩阵A的扰动对方程组解的影响 若系数矩阵 A存在误差 δA,则解也应存在误差 δx
( A + δA)( x + δx) = b
x1
p
+
x2
p
+L +
xn
p
) 1 p ≤ (n max 1≤i≤n
= n 1 p max 1≤i≤n
xi
→ max 1≤i≤n
xi
(p → ∞)
xi p ) 1 p
x p → x ∞ ( p → ∞时 ),
所以
x
也是
∞
x
的特例
p
且 x∞≤ x2≤ x1
例1.求下列向量的各种常用范数 x = (1,4,3,−1)T
若常数项 b存在误差 δb,则解也应存在误差 δx
即有
A(x + δx) = b + δb
--------(15)
所以
Aδx = δb
δx = A−1δb
δx = A−1δb ≤ A−1 ⋅ δb
--------(16)
又因为 可得
b = Ax ≤ A ⋅ x 1≤ A xb
(16)和(17)两式相乘,得
二、误差分析简介
定义6. 对于线性方程组 Ax = b,如果系数矩阵 A或 常数项 b的元素的微小变化 ,就会引起方程组解的 巨大变化 ,则称该方程组是 "病态"的, A为"病态"矩 阵.否则称为 "良态 "的.
1.常数项b的扰动对方程组解的影响
设Ax = b为一线性方程组 , A为非奇异矩阵 , x为其精确解
显然 A 2 = λmax ( AT A) = ρ( AT A)
对于某种向量范数 x υ 和算子范数 A υ ,
Ax υ ≤ A υ x υ
而
Ax υ = λx υ = λ ⋅ x υ
因此
λ ⋅ xυ≤ Aυ xυ
即
λ ≤ Aυ
所以
ρ(A) ≤ A υ
即矩阵A的谱半径不超过矩阵的 任何一种算子范数
x的 1 − 范数
x
∞
=
max
1≤i≤n
xi
--------(3) x的∞ − 范数或最大范数
x p = ( x1 p + x2 p + L + xn p ) 1 p
--------(4)
x的p − 范数 , p ≥ 1
显然
x 1和
x2
是
x
在p
p
=
1和p
=
2时的特例
并且由于
max
1≤i ≤n
xi
≤(
δA ⋅ x + Aδx + δA ⋅δx = 0
( A + δA)δx = −δA ⋅ x
--------(19)
在上式能直接使用范数吗?
( A + δA) = A(I + A−1δA)
如果假设
A−1δA < 1
--------(20)
则由定理1.,可知 I + A−1δA非奇异
且
( I + A−1δA)−1
解: x 1 = x1 + x2 + L + x4 = 9 x 2 = ( x1 2 + x2 2 + L + x4 2 )1 2 = 27 = 3 3
x
∞
=
max
1≤i≤4
xi
=4
定义2. 对于空间 R n×n中任意一个矩阵 A, 若存在唯一一个实数 A ∈ R与A对应,且满足
(1) (正定性 ) A ≥ 0,且∀A ∈ R n×n , A = 0 ⇔ A = 0; (2) (齐次性 ) α A = α ⋅ A ,∀A ∈ R n×n ,α ∈ R ; (3) (三角不等式 ) A + B ≤ A + B ,∀A, B ∈ R n×n . (4) AB ≤ A ⋅ B ,∀A, B ∈ R n×n . 则称 A 为矩阵 A的范数 . 对于复空间 C n×n中的矩阵范数可以类似 定义
A F = tr( AT A) = 2 + 9 + 2 = 3.6056
A1
A∞
A2
A F
容易计算
计算较复杂 不是从属范数
对矩阵元素的 变化比较敏感
较少使用
性质较好
使用最广泛
定义5. 设A ∈ R n×n的特征值为 λ1 , λ2 ,L , λn , 称 ρ( A) = max{ λ1 , λ2 ,L , λn } --------(13) 为矩阵 A的谱半径
例2. 设n阶方阵 A = (aij )n×n
∑ ∑ 设
A F
=
n i=1
n
a
2 ij
j =1
12
类似向量的 2-范数 --------(5)
不难验证其满足定义2的4个条件
因此 A F 是一种矩阵范数 称为Frobenius范数,简称F-范数
( ) ( ) 而且可以验证 A F = tr( AT A) 1 2 = tr( AAT ) 1 2
定义1. 对于 n维向量空间 Rn中任意一个向量 x, 若存在唯一一个实数 x ∈ R与x对应,且满足
(1) (正定性 ) x ≥ 0,且∀x ∈ R n , x = 0 ⇔ x = 0; (2) (齐次性 ) α x = α ⋅ x ,∀x ∈ Rn ,α ∈ R; (3) (三角不等式 ) x + y ≤ x + y ,∀x, y ∈ R n . 则称 x 为向量 x的范数 . 对于复线性空间C n中的向量范数可以类似定义
