第三章、逐次逼近法
第三章第三节拱桥计算2
悬链线拱轴线与三铰拱压力线存在近似波形的自然偏离， 据此道理，三铰拱压力线基础上根据实际情况再叠加一个正弦 波形调整拱轴线，用逐次逼近法使弹压砼收缩产生的不利弯矩 为最小。
九、考虑几何非线性的拱桥计算简介
➢ 在线弹性条件下，一般拱桥内力与变形计算结果 和实际不会产生太大误差，随着拱桥跨度增大， 这种由于非线性引起的误差会增大；
（1）假载法调整内力 （2）用临时铰调整内力 （3）改变拱轴线调整内力
（1）假载法调整内力
所谓假载法调整内力，就是在计算跨径、 计算矢高和拱圈厚度保持不变的情况下，通 过改变拱轴系数的数值来改变拱轴线形状， m调整幅度一般为半级或一级。
( y1/4 相差0.01为一级) f
（1）假载法调整内力
实腹拱的内力调整
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时，常常 出现拱脚负弯矩或拱顶正弯矩过大的情况， 为了减小它们，可从设计、施工方面采取 措施调整拱圈内力。
（1）假载法调整内力 （2）用临时铰调整内力 （3）改变拱轴线调整内力
八、主拱内力调整
• 悬链线无铰拱在最不利荷载组合时，常常 出现拱脚负弯矩或拱顶正弯矩过大的情况， 为了减小它们，可从设计、施工方面采取 措施调整拱圈内力。
三、拱桥内力计算
（一）手算法计算拱桥内力 1、等截面悬链线拱恒载内力计算 2、等截面悬链线拱活载内力计算 3、等截面悬链线拱其它内力计算
（二）有限元法计算简介 （三）拱在横向力及偏心荷载作用下的计算 （四）拱上建筑计算 （五）内力调整 （六）考虑几何非线性的拱桥计算简介
四、拱在横向水平力及偏心荷载作用下的计算
• 调整前：
简述逐次逼近法的工作原理
简述逐次逼近法的工作原理
逐次逼近法是一种数值计算方法，用于求解近似解的近似值。
其主要工作原理如下：
1. 初始化：选择一个初始值作为近似解的初始近似值。
2. 迭代过程：根据某种规则进行迭代，每次迭代都会产生一个较接近真实解的近似值。
3. 收敛判断：判断近似解是否足够接近真实解。
如果接近程度满足预定的收敛准则，则输出近似解；否则返回第2步进行下一次迭代。
4. 输出结果：输出满足收敛准则的近似解作为最终结果。
逐次逼近法的核心思想是不断迭代，通过每一次迭代对近似解进行修正，逐渐接近真实解。
在迭代过程中，常用的方法有不动点迭代法、Newton-Raphson迭代法等等。
这些方法在每一步迭代中通过一定的数学计算方式来更新近似解，并不断逼近真实解。
逐次逼近法的优点是易于实现和理解，适用于一些求解复杂方程或函数的数值解问题。
然而，它的收敛速度可能很慢，对于某些问题可能无法得到满意的解。
因此，在应用中需要根据具体问题选择合适的迭代方法，以提高计算效率和准确性。
常微分方程考研讲义第三章-一阶微分方程解的存在定理
第三章一阶微分方程解的存在定理[教学目标]1.理解解的存在唯一性定理的条件、结论及证明思路，掌握逐次逼近法，熟练近似解的误差估计式。
2.了解解的延拓定理及延拓条件。
3.理解解对初值的连续性、可微性定理的条件和结论。
[教学重难点] 解的存在唯一性定理的证明，解对初值的连续性、可微性定理的证明。
[教学方法] 讲授，实践。
[教学时间] 12学时[教学内容] 解的存在唯一性定理的条件、结论及证明思路，解的延拓概念及延拓条件，解对初值的连续性、可微性定理及其证明。
[考核目标]1.理解解的存在唯一性定理的条件、结论，能用逐次逼近法解简单的问题。
2.熟练近似解的误差估计式，解对初值的连续性及可微性公式。
3.利用解的存在唯一性定理、解的延拓定理及延拓条件能证明有关方程的某些性质。
§1 解的存在性唯一性定理和逐步逼近法微分方程来源于生产实践际，研究微分方程的目的就在于掌握它所反映的客观规律，能动解释所出现的各种现象并预测未来的可能情况。
在第二章介绍了一阶微分方程初等解法的几种类型，但是，大量的一阶方程一般是不能用初等解法求出其通解。
而实际问题中所需要的往往是要求满足某种初始条件的解。
因此初值问题的研究就显得十分重要，从前面我们也了解到初值问题的解不一定是唯一的。
他必须满足一定的条件才能保证初值问题解的存在性与唯一性，而讨论初值问题解的存在性与唯一性在常微分方程占有很重要的地位，是近代常微分方程定性理论，稳定性理论以及其他理论的基础。
例如方程dydx=过点(0,0)的解就是不唯一，易知0y =是方程过(0,0)的解，此外，容易验证，2y x =或更一般地，函数20 0() c<1x cy x c x ≤≤⎧=⎨-≤⎩ 都是方程过点(0,0)而且定义在区间01x ≤≤上的解，其中c 是满足01c <<的任一数。
解的存在唯一性定理能够很好地解释上述问题，它明确地肯定了方程的解在一定条件下的存在性和唯一性。
逐次插值逼近法
'(0 ) k
2
2 ( ( k ) (0 ) '(0 ) k )
k
将其作为新的
这是一个插值法与充分下降条件 组合起来的线性搜索方法.
,
这个方法开始时,令 1, 如果 x k (即后退),一直到
xk d k
d k 不可接受，则减少
可接受为止.
f ( xk ) k g k d k
T
f ( x k ) (1 ) k g k d k
T
0
b c a [b,c]称为可接受区间
Wolfe准则
用下面的条件代替
g k 1 d k g k d k , ( ,1)
T T
曲率条件
即
'( k 1 ) g ( xk k d k ) d k
停止迭代， 步3 若检验准则 ( k ) (0) (1 ) k '(0) 成立， 输出 ; 否则，令a k 1 : k , b k 1 b k .若 b k 1 m ax ,
k
转步4； 否则，令 步4
k 1 : t k , k : k 1, 转步2；
T
f ( xk k d k ) f ( xk ) (1 ) k g k d k
T
( k ) (0) k '(0)
( k ) (0) (1 ) k '(0)
Goldstein准则算法
步1 选取初始数据.给出初始搜索区间 [ a 0 , b0 ], 给出初始点
k , x k 1 : x k k d k
k
第四章逐次逼近法
(k )
( D L)1 b
令 BG ( D L)1U , fG ( D L) 1 b
则
x ( k 1) BG x ( k ) fG （k 0,1,）
3.1.2 迭代法的收敛性
考虑如下问题： ① 如何判断迭代过程是否收敛呢？ ② 迭代格式收敛的充要条件、充分条件是什么？ ③ 决定迭代收敛速度的因素是什么？ 设某种迭代格式为
x
( k 1)
BJ x
(k )
f J （k 0,1,）
由 A D L U , 得 (D - L)x Ux b 从而
x D - L Ux D - L b
1 1
则Gauss-Seidel迭代法可以写成
x
( k 1)
( D L) Ux
则
A D L U
由 A D L U , 得 Dx ( L U ) x b 从而
x D1 L U x D1b
则Jacobi迭代法可写成为：
x
( k 1)
D
1
L U x
k
D 1b
k 0, 1, 2,
令 BJ = D 1 L U , f J D 1b, 则
定理 3.2
(k ) 迭代法 x ( k 1) Bx f 对任意 x ( 0 ) 和 f
均收敛的充要条件为： ( B) 1。
定理 3.3 （充分条件） 若 || B || 1 ，则迭代法收敛， 且有 证明
|| x
(k )
x ||
*
(1) (0) || B || (k ) ( k 1) x x || x x || 1 B 1 || B ||
第三章、逐次逼近法
第三章 逐次逼近法1.1内容提要1、一元迭代法x n+1=φ(x n )收敛条件为：1）映内性x ∈[a,b]，φ(x) ∈[a,b] 2）压缩性∣φ(x) -φ(y)∣≤L ∣x-y ∣其中L ＜1，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。
由微分中值定理，如果∣φ’∣≤L ＜1，显然它一定满足压缩性条件。
2、多元迭代法x n+1=φ(x n )收敛条件为：1）映内性x n ∈Ω，φ(x n ) ∈Ω 2）压缩性ρ（▽φ）＜1，其中▽φ为x n 处的梯度矩阵，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。
3、当φ(x )= Bx+f 时，收敛条件为，ρ（B ）＜1，此时x n+1= Bx n +f ，在不断的迭代中，就可以得到线性方程组的解。
4、线性方程组的迭代解法，先作矩阵变换 U L D A --=Jacobi 迭代公式的矩阵形式 f Bx b D x U L D x n n n +=++=--+111)(Gauss-Seidel 迭代公式的矩阵形式 f Bx b L D Ux L D x n n n +=-+-=--+111)()(超松弛迭代法公式的矩阵形式f Bx b L D x U D L D x k k k +=-++--=--+ωωωωω111)(])1[()(三种迭代方法当1)(<B ρ时都收敛。
5、线性方程组的迭代解法，如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。
6、线性方程组的迭代解法，如果A 不可约对角占优，则Gauss-Seidel 法收敛。
7、Newton 迭代法，单根为二阶收敛 2211'''21lim)(2)(lim---∞→+∞→--=-==--k k k k k k k k x x x x f f c x x ξξαα8、Newton 法迭代时，遇到重根，迭代变成线性收敛，如果知道重数m ， )()('1k k k k x f x f m x x -=+仍为二阶收敛 9、弦割法)()())((111--+---=k k k k k k k x f x f x x x f x x 的收敛阶为1.618，分半法的收敛速度为（b-a ）/2n-110、Aitken 加速公式11211112)(),(),(+----+-+--+---+---===k k k k k k k k k k k x x x x x x x x x x x ϕϕ1.2 典型例题分析1、证明如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。
第三章第四节 电力系统低频减载
第四节电力系统低频减载一、概述1）事故情况下，系统可能产生严重的有功缺额，因而导致系统频率大幅度下降。
2）所缺功率已经大大超过系统热备用容量，只能在系统频率降到某值以下，采取切除相应用户的办法来减少系统的有功缺额，使系统频率保持在事故允许的限额之内。
3）这种办法称为按频率自动减负荷。
中文简拼为“ZPJH”，英文为UFLS（Under Frequency Load Shedding）。
二、系统频率的事故限额（1）系统频率降低使厂用机械的出力大为下降，有时可能形成恶性循环，直至频率雪崩。
（2）系统频率降低使励磁机等的转速也相应降低，当励磁电流一定时，发送的无功功率会随着频率的降低而减少，可能造成系统稳定的破坏。
发生在局部的或某个厂的有功电源方面的事故可能演变成整个电力系统的灾难。
（3）电力系统频率变化对用户的不利影响主要表现在以下几个方面：①频率变化将引起异步电动机转速的变化，有这些电动机驱动的纺织、造纸等机械产品的质量将受到影响，甚至出现残、次品。
②系统频率降低将使电动机的转速和功率降低，导致传动机械的出力降低。
③国防部门和工业使用的测量、控制等电子设备将因为频率的波动而影响准确性和工作性能，频率过低时甚至无法工作。
“电力工业技术管理法规”中规定的频率偏差范围为±0.2~±0.5Hz。
（4）汽轮机对频率的限制。
频率下降会危及汽轮机叶片的安全。
因为一般汽轮机叶片的设计都要求其自然频率充分躲开它的额定转速及其倍率值。
系统频率下降时有可能因机械共振造成过大的振动应力而使叶片损伤。
容量在300MW 以上的大型汽轮发电机组对频率的变化尤为敏感。
例如我国进口的某350MW机组，频率为48.5Hz时，要求发瞬时信号，频率为47.5Hz时要求30s跳闸，频率为47Hz时，要求0s跳闸。
进口的某600MW机组，当频率降至47.5Hz时，要求9s跳闸。
（5）频率升高对大机组的影响。
电力系统因故障被解列成几个部分时，有的区域因有功严重缺额而造成频率下降，但有的区域却因有功过剩而造成频率升高，从而危及大机组的安全运行。
第三章数据采集系统基本原理
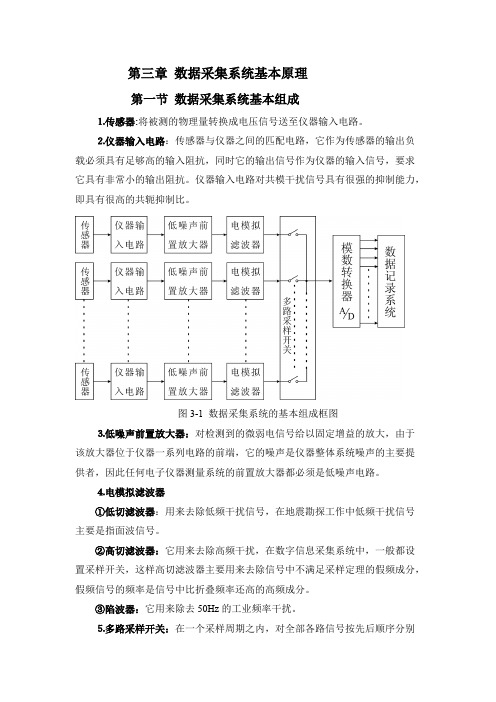
第三章数据采集系统基本原理第一节数据采集系统基本组成⒈传感器:将被测的物理量转换成电压信号送至仪器输入电路。
⒉仪器输入电路：传感器与仪器之间的匹配电路，它作为传感器的输出负载必须具有足够高的输入阻抗，同时它的输出信号作为仪器的输入信号，要求它具有非常小的输出阻抗。
仪器输入电路对共模干扰信号具有很强的抑制能力，即具有很高的共轭抑制比。
图3-1 数据采集系统的基本组成框图⒊低噪声前置放大器：对检测到的微弱电信号给以固定增益的放大，由于该放大器位于仪器一系列电路的前端，它的噪声是仪器整体系统噪声的主要提供者，因此任何电子仪器测量系统的前置放大器都必须是低噪声电路。
⒋电模拟滤波器①低切滤波器：用来去除低频干扰信号，在地震勘探工作中低频干扰信号主要是指面波信号。
②高切滤波器：它用来去除高频干扰，在数字信息采集系统中，一般都设置采样开关，这样高切滤波器主要用来去除信号中不满足采样定理的假频成分，假频信号的频率是信号中比折叠频率还高的高频成分。
③陷波器：它用来除去50Hz的工业频率干扰。
⒌多路采样开关：在一个采样周期之内，对全部各路信号按先后顺序分别采样一次，将多路系统转换为单路系统，实现多路合一；同时将连续的模拟信号转换为离散的模拟子样脉冲。
⒍模数转换器：则将每一个子样脉冲电压转换为二进制代码。
⒎数据记录系统：将二进制代码按照国际专业技术组织的规定，进行编排和编码，编排主要是将一定长度的二进制数据编排成便于计算机数据处理的字节形式；编码则是为了数据写读的方便，针对数码“1”和“0”对磁带剩余磁通的变化方式所作出的规定。
第二节 输入电路和低噪声前置放大器一、差动放大器输入电路A 1和A 2的输出分别为V 1和V 2，它们可表示为，2111i W FOi W FOV R R V RR V ⋅-⋅⎪⎪⎭⎫ ⎝⎛+=1221i W FOi W FO V R R V RR V ⋅-⋅⎪⎪⎭⎫ ⎝⎛+=放大器A 3具备输入平衡条件，它的输出V 0表示为()()2121021i i fFW FO f FV V R R R R V V R R V -⋅⋅⎪⎪⎭⎫ ⎝⎛+-=-⋅-=闭环增益为： fF W FO i i F R R R R V V V K ⎪⎪⎭⎫ ⎝⎛+-=-=21210由于该电路具有很高的输入阻抗和共模抑制比，许多数字地震仪的输入电路都采用了该形式的电路。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 逐次逼近法1.1内容提要1、一元迭代法x n+1=φ(x n )收敛条件为：1）映内性x ∈[a,b]，φ(x) ∈[a,b] 2）压缩性∣φ(x) -φ(y)∣≤L ∣x-y ∣其中L ＜1，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。
由微分中值定理，如果∣φ’∣≤L ＜1，显然它一定满足压缩性条件。
2、多元迭代法x n+1=φ(x n )收敛条件为：1）映内性x n ∈Ω，φ(x n ) ∈Ω 2）压缩性ρ（▽φ）＜1，其中▽φ为x n 处的梯度矩阵，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。
3、当φ(x )= Bx+f 时，收敛条件为，ρ（B ）＜1，此时x n+1= Bx n +f ，在不断的迭代中，就可以得到线性方程组的解。
4、线性方程组的迭代解法，先作矩阵变换 U L D A --= Jacobi 迭代公式的矩阵形式 f Bx b D x U L D x n n n +=++=--+111)(Gauss-Seidel 迭代公式的矩阵形式 f Bx b L D Ux L D x n n n +=-+-=--+111)()(超松弛迭代法公式的矩阵形式f Bxb L D x U D L D xkk k +=-++--=--+ωωωωω111)(])1[()(三种迭代方法当1)(<B ρ时都收敛。
5、线性方程组的迭代解法，如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。
6、线性方程组的迭代解法，如果A 不可约对角占优，则Gauss-Seidel 法收敛。
7、Newton 迭代法，单根为二阶收敛 2211'''21lim)(2)(lim---∞→+∞→--=-==--k k k k k k k k x x x x f f c x x ξξαα8、Newton 法迭代时，遇到重根，迭代变成线性收敛，如果知道重数m ， )()('1k k k k x f x f m x x -=+仍为二阶收敛 9、弦割法)()())((111--+---=k k k k k k k x f x f x x x f x x 的收敛阶为1.618，分半法的收敛速度为（b-a ）/2n-110、Aitken 加速公式11211112)(),(),(+----+-+--+---+---===k k k k k k k k k k k x x x x x x x x x x x ϕϕ1.2 典型例题分析1、证明如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。
证明：首先证Jacob 法收敛，因为A 严格对角占优，则),...,2,1(,,1n i a a nij j ij ii =>∑≠-，于是),...,2,1(,11,1n i a a nij j ij ii=<∑≠-，从而1)(1<+∞-U L D，这又有1))((1<+-U L Dρ，因此Jacob 迭代法收敛。
再证G-S 法收敛，因为1)(1<+∞-U L D，由定理1.6，)(1U L DI ++-非奇异，而0)det()det()det())(det())(det(1111≠==++=++----A DA D U L D DU L DI ，所以0)d e t (≠A ，从而严格对角占优矩阵一定可逆。
在G-S 法中，0)det(1≠=-∏=ni ii a L D ，从而0))det((1≠--L D ，求矩阵特征值时，))(det())det()))(()det(())(det(111=---=---=-----U L D L D U L D L D U L D I λλλ只能是0))(det(=--U L D λ，因为A 严格对角占优，),...,2,1(,,1n i a a nij j ij ii =>∑≠-，如果1≥λ，两边乘∑∑∑∑∑+---+---≠-+>+=>ni j ij i j ij n i j ij i j ij n ij j ij ii a a a a a a 111111,1,λλλλλλ那么，这说明矩阵U L D --)(λ仍然严格对角占优，前面已证明，该行列式不能为0，这是一个矛盾。
因此，只能是1<λ，而这恰好说明Gauss-Seidel 迭代法收敛。
2、证明：如果A 的对角元非零，超松弛迭代法收敛的必要条件是20<<ω证明：令])1[()(1U D L D L ωωωω+--=-，如果超松弛迭代法收敛，应该有1)(<ωρL∏∏∏===--=-=-=+--=ni inni iinn i ii dd U D L D L 11111)1()1()())1det(())det(()det(λωωωωωω而11,1)max (1)1(,1max )(1111<-<≤=-=-<=≤≤==≤≤∏∏ωλλωλωλρωni ni ni i nni ini ni L ，所以，从而必须满足20<<ω。
3、分析方程2x -3x +4x -5x +6x -7x +8x -9x +10x =10是否有实根，确定根所在的区间，写出求根的Newton 迭代公式,并确定迭代的初始点。
解：0)ln()1()(,0)2(,0)1(,10)1()(102'102>-=><--=∑∑==i ix f f f ix f xi i xi i 显然令因此该方程在[1,2]有且仅有一个实根，Newton 迭代公式为(1-=+n n x x )10)1(102--∑=nx i i i/（)ln()1(102i inx i i∑=-），x 0=1.5 即可 4、由求a 的Newton 迭代公式 ,...,2,1,0,0),(211=>+=+k x x a x x k kk k证明：对一切,...,,,121x x a x k k 并且有≥≥ 是递减序列。
证明：首先，如果{}∞=>10,0k k x x 则迭代序列中的x k >0 ，于是 ,...2,1,0,,1.2.21)(2111=≥=≥+=++k a x x a a x x a ax a x k k k k k k 所以。
又因为k=1开始，为递减序列所以，于是1221,1))(1(21)1(21++≥=+≤+=≥k k kkk k x x a a xa x x a x5、若f(x)在零点ξ的某个邻域中有二阶连续导数，并且f ’(ξ)≠0，试证：由Newton 迭代法产生的x k (k=0,1,2,…)有)(2)(lim '''2211ξξf f x x x x k k k k k -=-----∞→证明：由Taylor 公式，得证。
，，由于，整理得到）式变为）后，（）代替（用（）（）（迭代公式整理可以得到由）（）（,)(2)()(!2)())(()()(23440))(()(30))(()(2)(!2)())(()()(1)(!2)())(()()(111111'''2211221''11'1111'1212'2221''212'2122''22'2ξξξξξξ ----------------------------------=---+-+=-----=-+----=-+---+-+=--------+-+=k k k k x k k x k k k k k k x k k k k k k k k k k k k k k k x k k k k k k x k k k x x f f x x x x x x f x x x f x f x f x x x f x f x x x f x f Newton x x f x x x f x f x f x x f x x x f x f x f6、证明：A ∈C n*n ,对任意范数有，)(lim A Akkk ρ=∞→证明：首先存在某种范数 )()()()(*A A A AA kkkkkρρερρ=+≤≤，而 所以))(/1)(()()(*A A A AA kkkkkρερερρ+=+≤≤，取)(A kρε= 得到)(2)(*A AA kkk ρρ≤≤ ，对不等式同时取极限即得到 )(lim*A Akkk ρ=∞→再根据范数的等价性*2*1kkk Ac AA c ≤≤ 对不等式同时取极限即得到对任意范数有结果 )(limA Akkk ρ=∞→7、确定常数p,q,r ，使如下迭代法收敛到52213,kkk k x ra x qa px x a ++=+，该方法至少几阶？解：根据定理3.6，一个迭代格式，在根附近它的p-1阶导数为零，就至少有p 阶收敛速度速度。
附近，至少有三阶收敛，此时该迭代格式在根立即可以解出：右端求函数和导数值对数值和各阶导数，令为根，在此处求函，那么如果它收敛到由迭代格式91,95)(,0)(,0)(,)(,)(3"3'3333522-=======++=r q p x a a a a a x a xra xqa px x ϕϕϕϕϕ1.3 习题解答1、 判断正误、选择和填空：1）、对于迭代过程，x n+1=φ(x n )，若迭代函数在x * 的邻域有连续的二阶导数，且1)(*'<x φ，则迭代过程为超线性收敛。
（不正确），x n+1=φ(x n )的迭代收敛条件有两条，1）映内性x n ∈[a,b]，φ(x n ) ∈[a,b] 2）压缩性1)(*'<≤L x φ。
更不能保证有超线性收敛，例如：，它只有线性收敛速度但是满足，迭代收敛，并有根023)(311)(,38197.0)1(31)(*21212112**21limlim>=--=--<=+==-++∞→+++∞→+xxx x x x x x x x x x x x k kk k k kk k k k k k k ϕϕ2） 用Newton 迭代法求任何非线性方程 均局部平方收敛。
（不正确）3） 若线性方程组Ax=b 的系数矩阵A 为严格对角占优，则Jacobi 迭代法和G-S 迭代法都收敛。
（正确） 4） 解非线性方程f(x)=0的弦解法迭代具有（局部超线性敛速 1.618）。
（A ） 局部平方收敛；（B ）局部超线性收敛；（C ）线性收敛5） 任给初始向量x (0)及右端向量f ，迭代法x (k+1)=Bx (k)+f 收敛于方程组Ax=b 的精确解x *的充要条件是（1)(<B ρ）。