习题课(刚体)
合集下载
大学物理刚体力学习题讲解
(A) 只有(1)是正确的．
（B）
(B) (1) 、(2)正确，(3) 、(4) 错误． (C) (1)、(2) 、(3) 都正确，(4)错误． (D) (1) 、(2) 、(3) 、(4) 都正确．
M=L×F |M|=|L|×|F|sinθ
2. 一轻绳绕在有水平轴的定滑轮上，滑轮的转动惯量为J，绳下
4. 一作定轴转动的物体，对转轴的转动惯量J＝ 3.0 kg·m2，角速度0＝6.0 rad/s．现对物体加一 恒定的制动力矩M ＝－12 N·m，当物体的角速度 减慢到＝2.0 rad/s时，物体已转过了角度 ＝
4.0rad
M=Jβ
2as=v`2-v2 2βθ= 2 -02
5. 质量为m1， m2 （ m1 > m2） 的两物体，通过一定滑轮用绳
6. 一长为1 m的均匀直棒可绕过 其一端且与棒垂直的水平光滑固 定轴转动．抬起另一端使棒向上 与水平面成60°，然后无初转速 地将棒释放．已知棒对轴的转动
惯量为1/3ml3，其中m和l分别为
棒的质量和长度．求： (1) 放手时棒的角加速度； (2) 棒转到水平位置时的角
加速度．
l m g
O 60°
端挂一物体．物体所受重力为P，滑轮的角加速度为．若将物体
去掉而以与P相等的力直接向下拉绳子，滑轮的角加速度将
(A) 不变． (B) 变小．
(C) 变大． (D) 如何变化无法判断．
［ C］
①物体状态at=rβ （P-atm）r=Jβ ②拉力情况下Pr=Jβ
挂重物时，mg－T= ma =mRβ, TR =J, P=mg
5. 解：由人和转台系统的角动量守恒
J11 + J22 = 0 其中 J1＝75×4 kg·m2 =300 kg·m2，1=v/r =0.5 rad / s J2＝3000 kg•m2
静力学-刚体系统平衡习题课2
p
FGy
G
3、再研究AG杆，求出 FGy
0 FGy
刚体系平衡求解
1、研究对象
2、受力分析
3、平衡条件 4、列方程、求解 尽量一个方程解一个未知量！
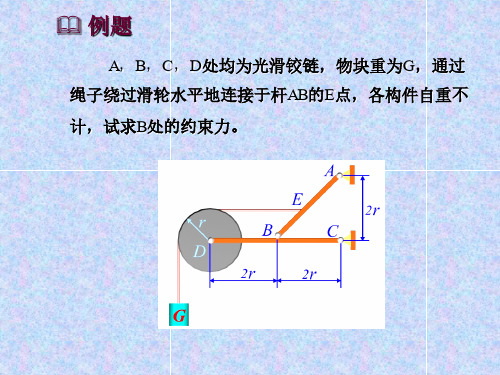
例：已知 F，求 AG 杆上的约束力。
A
a
C
F
2a E
a
B
a
a
a
D
a
解：1、研究AG杆， 画受力图. H
A
F
FDx FGx
G
O
FDy
D
M
D
(F ) 0
FGxa Fa 0
G
FGy
FGx F FDx 2F
G
M
(F ) 0
FDxa F 2a 0
A
a D
F
2a E
x
FDy
D
FGx F FGy 3F
FGy 3F
[AG]:
Fy 0
FDy 3F
FGy
G
A C a D a G
F
2a a
B E a H
研究图示构件，画受力图 B C
FDx D
a 2a
E a
H
O
a
O
FCG FDy
方法3 A
F
FDx FGx
求出
FDy
p
FH
FDy
D
M F
y
0 FDy
13 G G F A sin 45 8
D A
K C B Ⅰ
2. [DEC] 受力分析如图所示
列平衡方程
E
Ⅱ
M
其中
刚体习题课资料
6、一飞轮以角速度0绕轴旋转，飞轮对轴的转
动惯量为J1，另一静止飞轮突然被啮合到同一个
轴上，该飞轮对轴的转动惯量为前者的两倍。啮 (1/3).0 合后整个系统的角速度
利用J1o=(J1+2J1)
一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量m1 和 m2 的物体 (m1< m2)，如图所示.绳与轮 之间无相对滑动，某时刻滑轮沿逆时针方 向转动，则绳的张力
（A）
2v 3L
4v （B） 5L 8v （D） 9 L
L
6v （C） 7L
以顺时针为转动正方向 两小球与细杆组成的系统 对竖直固定轴角动量守恒
m
v
o
m
o
v
L
由
及
Lmv+Lmv=2mL2+J
J= mL2/3
可知正确答案为 [ C ]
作业：P19.5
人：m=75kg，转台：J=3000kgm2, R=2m，初始，系 统静止；人沿转台边缘行走，v=1m/s,在转台上行走一 周所用的时间？ 解： 人和转台系统，外力矩为0，角动量守恒
0 mRv J1
2 2 T mR 2 2 1 2 (1 ) J
v 2 R
40 s 11
5.如图所示,一均匀 细杆长为 l ,质量为 m,平放在摩擦系数 为 m 的水平桌面上, 设开始时杆以角速 度 0 绕过中心 o 且 垂直与桌面的轴转 动,试求:
0
1 1 2 Md J 2 J12 2 26．动能定理 2 Nhomakorabea1
7．机械能守恒
1 1 2 2 mgh c1 J1 mgh c 2 J 2 2 2
8．刚体的角动量（动量矩）：
大学物理第三章刚体力学基础习题答案
方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞，系统机械能守恒： 2 2 2 1 1 2 2 又： J M 2l Ml 12 3 6mu M 3m u 联立可得： v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后，经过t1时间到达了额定 转速，此时相应的角速度为 0。当关闭电源后，经 过t2时间风扇停转。已知风扇转子的转动惯量为 J， 并假定摩擦力矩和电机的电磁力矩均为常量，试根据 已知量推算电机的电磁力矩。 解： 设电机的电磁力矩为M，摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得： a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
物理学 第四版 马文蔚 习题课ppt
J＝1/3 mR2
（a）（b）两图中的细棒和小球均相同，系统可绕o 轴在竖直面内自由转动系统从水平位置静止释放，转动 到竖直位置所需时间分别为ta和tb，则：
( A) ta tb , ( B) ta tb , ( C) ta tb , (D) 无法判定
判断两种情况下小球绕轴转动的角加速度
P
一子弹水平地射穿两个前后并排放在光滑水平桌面上的 木块。木块质量分别为m1和m2，测得子弹穿过两木块 的时间分别为Δt1和Δt2，已知子弹在木块中受的阻力为 恒力F。求子弹穿过后两木块各以多大的速度运动。 两个木块受到子弹给它们的力均为F
木块1 木块2
还是角动量守恒
2.质量为m，半径为R的均匀圆盘，可在 水平桌面上绕中心轴转动，若盘与桌面 间的摩擦系数为μ，则盘转动时所受摩擦 力矩Mf = 。
μ
μ
μ
μ
补充专题：刚体平衡问题
μ
补充专题：刚体平衡问题
平衡要求： 合力为零 ∑F＝0 μ 对任意点，合力矩为零 ∑M＝0
补充专题：刚体平衡问题
∑M
μ
若对刚体某轴的合外力矩为零 则对其他轴的合外力矩也为零 学会聪明地选轴
补充专题：刚体平衡问题
μ
题：刚体平衡问题
角动量守恒
（B）
两个匀质圆盘A和B的密度分别为rA和rB ，若rA＞ rB，但两圆盘的质量与厚度相同，如两盘对通过盘心垂 直于盘面轴的转动惯量各为JA和JB，则
(A) JA＞JB． (C) JA＝JB． (B) JB＞JA． (D) JA、JB哪个大，不能确定．
（B）
厚度相同，质量相同，密度大的半径小
μ
补充专题：刚体平衡问题
μ
补充专题：刚体平衡问题
（a）（b）两图中的细棒和小球均相同，系统可绕o 轴在竖直面内自由转动系统从水平位置静止释放，转动 到竖直位置所需时间分别为ta和tb，则：
( A) ta tb , ( B) ta tb , ( C) ta tb , (D) 无法判定
判断两种情况下小球绕轴转动的角加速度
P
一子弹水平地射穿两个前后并排放在光滑水平桌面上的 木块。木块质量分别为m1和m2，测得子弹穿过两木块 的时间分别为Δt1和Δt2，已知子弹在木块中受的阻力为 恒力F。求子弹穿过后两木块各以多大的速度运动。 两个木块受到子弹给它们的力均为F
木块1 木块2
还是角动量守恒
2.质量为m，半径为R的均匀圆盘，可在 水平桌面上绕中心轴转动，若盘与桌面 间的摩擦系数为μ，则盘转动时所受摩擦 力矩Mf = 。
μ
μ
μ
μ
补充专题：刚体平衡问题
μ
补充专题：刚体平衡问题
平衡要求： 合力为零 ∑F＝0 μ 对任意点，合力矩为零 ∑M＝0
补充专题：刚体平衡问题
∑M
μ
若对刚体某轴的合外力矩为零 则对其他轴的合外力矩也为零 学会聪明地选轴
补充专题：刚体平衡问题
μ
题：刚体平衡问题
角动量守恒
（B）
两个匀质圆盘A和B的密度分别为rA和rB ，若rA＞ rB，但两圆盘的质量与厚度相同，如两盘对通过盘心垂 直于盘面轴的转动惯量各为JA和JB，则
(A) JA＞JB． (C) JA＝JB． (B) JB＞JA． (D) JA、JB哪个大，不能确定．
（B）
厚度相同，质量相同，密度大的半径小
μ
补充专题：刚体平衡问题
μ
补充专题：刚体平衡问题
《大学物理期末复习》刚体转动习题课李明明 -
有一只小虫以速率 垂直v0落在距点O为 l/4 处，并背离点
O向细杆的端点A爬行。设小虫与细杆的质量均为m。问： 欲使细杆以恒定的角速度转动，小虫应以多大速率向细杆 端点爬行?
O
l/4
解 虫与杆的碰撞前 后，系统角动量守恒
mv0
l 4
1 12
ml
2
m( l )2 4
12 v0
7l
12 v0 c
2 2n2
J1
m( l1 2
)2
m( l1 2
)2
J2
m( l2 2
)2
m( l2 2
)2
J0
m l12n1 2 n2
l
2 2
n2
n1
将转台、砝码、人看作一个系统22，(J(0J＋0＋过程中人作的功W等于系统动能
之增量 将J0代入W式，得
W
E 12 (J J ) k ) n1 = 2 (J0＋
0 t 2 02 2
0
0t
1 2
t 2
18：
已知：1
20 ,60转变2
30 ,
22 12 2 , 6.54(rad / s)
19：
2 1 t, t 4.8(s)
已知：5s内，由1 40，变2 10，求： ？，t ? 0
0
t,
0 t0
2
02
2, N
2
62.5
（3）、从t=0到t=10s内所转过的角度：
0t
1 2
t 2
3. 解：根据转动定律：
已知：M = -k
M=J =Jd (3) 10＝0t＋ / dt = -k
d k dt
J
0 / 2 1 d t k d t
O向细杆的端点A爬行。设小虫与细杆的质量均为m。问： 欲使细杆以恒定的角速度转动，小虫应以多大速率向细杆 端点爬行?
O
l/4
解 虫与杆的碰撞前 后，系统角动量守恒
mv0
l 4
1 12
ml
2
m( l )2 4
12 v0
7l
12 v0 c
2 2n2
J1
m( l1 2
)2
m( l1 2
)2
J2
m( l2 2
)2
m( l2 2
)2
J0
m l12n1 2 n2
l
2 2
n2
n1
将转台、砝码、人看作一个系统22，(J(0J＋0＋过程中人作的功W等于系统动能
之增量 将J0代入W式，得
W
E 12 (J J ) k ) n1 = 2 (J0＋
0 t 2 02 2
0
0t
1 2
t 2
18：
已知：1
20 ,60转变2
30 ,
22 12 2 , 6.54(rad / s)
19：
2 1 t, t 4.8(s)
已知：5s内，由1 40，变2 10，求： ？，t ? 0
0
t,
0 t0
2
02
2, N
2
62.5
（3）、从t=0到t=10s内所转过的角度：
0t
1 2
t 2
3. 解：根据转动定律：
已知：M = -k
M=J =Jd (3) 10＝0t＋ / dt = -k
d k dt
J
0 / 2 1 d t k d t
高中物理奥林匹克竞赛专题--刚体-习题课(共12张PPT)
解:
设碰后棒开始转动的角速度为 , 滑块m2可视为质点, 碰撞瞬时忽略摩擦阻 力矩, 则m1、m2系统对o轴的角动量守恒, 取逆时针转动的方向为正方向, 由角动量 守恒定律, 有 碰后棒在转动过程中受到的摩擦阻力矩为
o
m1
m v1 2 v2
l
1 2 m2 v1l m2 v 2 l m1l 3
使 L 方向改变,而大小不变.
M L
自转轴将在水平面内逆时针方向(俯视)回转
质点力学、刚体力学有关公式对照表
质点的运动 速度 加速度 质量 刚体的定轴转动 角速度
d r dt
2
dr v dt dv a dt
角加速度 转动惯量
ddt
d dt
d 2 dt 2
m 力 F 运动定律 F ma 动量 p mv 角动量 L r p
动量定理
力矩
转动定律 动量 角动量
M r F
J r 2 dm
M J p mi vi
L J
dmv F dt
2 mg R 2 2 M f dM f r dr mgR 2 0 R 3
(2)求圆盘停止转动的时间有两种解法
dr r
o
R
解1 用转动定律 2 1 2 d M f mgR J mR 3 2 dt
3R dt d 4g
t
0
3R 0 dt d 4g 0
l
A
m1 1 M f gxdx m1 gl 0 l 2
1 m2 v1l m2 v 2 l m1l 2 3
大学物理课后习题及答案刚体
题：一汽车发动机曲轴的转速在s 12内由13min r 102.1-⋅⨯均匀的增加到13min r 107.2-⋅⨯。
（1）求曲轴转动的角加速度；（2）在此时间内，曲轴转了多少转题解：（1）由于角速度2n （n 为单位时间内的转数），根据角加速度的定义t d d ωα=，在匀变速转动中角加速度为()200s rad 1.132-⋅=-=-=tn n t πωωα （2）发动机曲轴转过的角度为()t n n t t t 0020221+=+=+=πωωαωθ在12 s 内曲轴转过的圈数为圈390220=+==t n n N πθ 题：某种电动机启动后转速随时间变化的关系为)1(0τωωt e --=，式中10s rad 0.9-⋅=ω，s 0.2=τ。
求：（1）s 0.6=t 时的转速；（2）角加速度随时间变化的规律；（3）启动后s 0.6内转过的圈数。
题解：（1）根据题意中转速随时间的变化关系，将t s 代入，即得100s 6.895.01--==⎪⎪⎭⎫ ⎝⎛-=ωωωτt e（2）角加速度随时间变化的规律为220s 5.4d d ---===tt e e t ττωωα （3）t = s 时转过的角度为rad 9.36d 1d 60060=⎪⎪⎭⎫ ⎝⎛-==⎰⎰-s t s t et τωωθ 则t = s 时电动机转过的圈数圈87.52==πθN 题：如图所示，一通风机的转动部分以初角速度0ω绕其轴转动，空气的阻力矩与角速度成正比，比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ，问：（1）经过多少时间后其转动角速度减少为初角速度的一半（2）在此时间内共转过多少转题解：（1）通风机叶片所受的阻力矩为ωM C -=，由转动定律αM J =，可得叶片的角加速度为J C t ωωα-==d d （1）根据初始条件对式（1）积分，有⎰⎰-=ωωω00d d d t t J C t 由于C 和J 均为常量，得t J C e -=0ωω 当角速度由0021ωω→时，转动所需的时间为 2ln CJ t = （2）根据初始条件对式（2）积分，有⎰⎰-=t t J C t e 000d d ωθθ即CJ 20ωθ= 在时间t 内所转过的圈数为CJ N πωπθ420== 题：一燃气轮机在试车时，燃气作用在涡轮上的力矩为m N 1003.23⋅⨯，涡轮的转动惯量为2m kg 0.25⋅。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
选出正确答案.
5
2. 一个半径为R的水平圆盘转台,可绕通过其中心的 竖直固定光滑轴转动,转动惯量为J,开始时转台以匀 角速度0转动,此时有一个质量为m的人站在转台中 心,随后此人沿半径方向向外跑去,当人到达转台边 缘时转台的角速度为[ ]
(A)
J
J mR2
0
(B)
(J
J m)R2
0
(C)
J mR2
O
解：这个问题可分为三个阶段
进行分析。第一阶段是棒自由
摆落的过程。对棒＋地球：除
C
重力外，其余内力与外力都不
作功，所以机械能守恒。
9
取棒在竖直位置时质心所在处为重力势能零点，用
表示棒这时的角速度，则
mg l 1 J 2＝1 1 ml 2 2
22
23
（1）
第二阶段是碰撞过程。因碰撞时间极短，产生的冲力 极大，物体所受地面的摩擦力可以忽略。对棒＋物体， 系统所受的对转轴O的合外力矩为零，故系统对轴O 的角动量守恒。用v表示物体碰撞后的速度，则
过多少时间才停止转动？
d r R
e
dr
解：由于摩擦力不是集中作用于一点，而是分布在整个圆盘与
桌子的接触面上，力矩的计算要用积分法。在图中，把圆盘分
成许多环形质元，每个质元的质量dm=rddre，所受到的阻力
矩是rdmg 。此处e是盘的厚度。
习题课
（刚体的转动）
课件公共邮箱：physics-fanghm@
密
码：0901－06
1
第五章 刚体的转动 总结
1、描述刚体转动的物理量
角位移 角速度
d
d
dt
角加速度 d
dt
与线量的关系
v r
a r
an
v2 r
r 2
2、刚体定轴转动定律
M J J d (Fv mav m dvv)
mgh 1 1 ml 2 2
23 把式（5）代入上式，所求结果为
h l 3s 6sl
2
（6）
12
补充2 一质量为m，半径为R，高h = R的圆柱体，可绕oo’轴线
转动。在圆柱体侧面上开有一与水平成 =450角的螺旋槽，放
一质量也为m的小球于槽中。开始时小球由静止从圆柱顶端A受
重力作用滑下，圆柱体同时发生转动。设各摩擦均不计，试求
0
(D) 0
6
3. 光滑的水平桌面上有一长为2L,质量为m的匀质细 杆,可绕过杆的中点并且垂直于杆的竖直光滑固定轴 自由转动,起初杆静止,两个质量均为m的小球各自沿 桌面正对这杆的一端在垂直于杆长的方向上以相同 的速率v相向运动,当两个小球同时与杆的两端发生 完全非弹性碰撞后就与杆粘在一起转动,则这一系统 碰撞后的转动角速度为[ ]
(A) 2v/3L (B) 4v/5L (C) 6v/7L (D) 2v/7L
7
4向. ）一,刚设体此以时每刚分体钟上6一0圈点绕的z位轴置匀矢速为转动r（
沿z轴 正方
3i 4 j 5k ,
单位为10-2m ,若以10-2m/s为速度单位,则此时刻P点速
度为[ ]
(A) v 94.2i 125.6 j 157.0k
mgh 1 J 2 1 m(u cos R )2 1 m(u sin )2 R
2
2
2
将J 1 mR 2和h R代 入 解 得 2g , u 3gR
2
3R
B
o
m
X
u
13
补充3 一半径为R，质量为m匀质圆盘，平放在粗糙的
水平桌面上。设盘与桌面间摩擦系数为，令圆盘最初 以角速度0绕通过中心且垂直盘面的轴旋转，问它经
0 v2 2as
（4）
由上述四式联合求解，即得
3gl 3 2gs
l
（5）
11
当′取正值时棒向左摆，其条件为
3gl 3 2gs 0 ，亦即l > 6 s；
当′取负值时棒向右摆，其条件为
3gl 3 2gs 0，亦即l < 6 s
棒的质心C上升的最大高度与第一阶段情况相似，对棒 ＋地球：由机械能守恒定律求得：
1 ml 2 mvl 1 ml 2
3
3
（2）
10
式中′可正可负，是棒在碰撞后的角速度。 ′取正值，
表示碰后棒向左摆；反之，表示棒向右摆。
第三阶段是碰撞后物体的滑行过程和棒的上升过程。
对物体：物体作匀减速直线运动，加速度由牛顿第二
定律求得为
mg ma
（3）
由匀减速直线运动的公式得
当小球滑落到圆柱体底部B时，小球相对圆柱体的速度和圆柱体
的角速度。
解小：球设相对圆圆柱柱体体沿的图运示速方度向为转动u的。角则速小度球为相ω对， 于地面的速度水平分量为：u cos R
o
R
A
h 对小球圆柱体：系统对定轴的角动量守恒：
J mR(u cos R ) 0
对小球＋圆柱体＋地球：系统的机械能守恒：
dt
dt
2
力矩
M rF
大小：M F r sin
方向：右手法则 转动惯量：
J Δmiri2
J r2dm
3、刚体定轴转动的动能定理
A
M d
1 2
J22
1 2
J12
(A
Fdr
1 2
mv22
1 2
mv12
)
力矩的功 A Md
刚体定轴转动动能 1 J 2
2
3
4、刚体定轴转动角动量定理
8
补充1 一匀质细棒长为 l ，质量为m，可绕通过其端
点O的水平轴转动，如图所示。当棒从水平位置自由
释放后，它在竖直位置上与放在地面上的物体相撞。
该物体的质量也为m ，它与地面的摩擦系数为。相
撞后，物体沿地面滑行一距离s而停止。求相撞后棒
的质心C离地面的最大高度h，并说明棒在碰撞后将向
左摆或向右摆的条件。
LZ miviri miri2 JZ
i
M dL dt
i
dp
(F )
dt
Mdt L2 L1 J2 J1
当 M 0
L J 常量
(
Fdt
p2
p1)
(F
0,
p
常矢量)
4
1. 两个力作用在一个有固定转轴的刚体上, (1) 这两个力都平行于轴作用时,它们对轴的合力 矩一定是零. (2) 这两个力都垂直于轴作用时,它们对轴的合力 矩可能是零. (3) 当这两个力的合力为零时,它们对轴的合力矩 也一定是零. (4) 当这两个力对轴的合力矩为零时,它们的合力 也一定是零.
(B) v 25.1i 18.8 j (C) v 25.1i 18.8 j
(D) v 31.4k
5. 飞轮作加速转动,轮边缘一点的运动方程s=0.1t3(SI),
飞轮半径2m,当该点速率v=30m/s时.其切向加速度为
___6_m__/_s2___,法向加速度为___4_5_0_m__/s_2___.
5
2. 一个半径为R的水平圆盘转台,可绕通过其中心的 竖直固定光滑轴转动,转动惯量为J,开始时转台以匀 角速度0转动,此时有一个质量为m的人站在转台中 心,随后此人沿半径方向向外跑去,当人到达转台边 缘时转台的角速度为[ ]
(A)
J
J mR2
0
(B)
(J
J m)R2
0
(C)
J mR2
O
解：这个问题可分为三个阶段
进行分析。第一阶段是棒自由
摆落的过程。对棒＋地球：除
C
重力外，其余内力与外力都不
作功，所以机械能守恒。
9
取棒在竖直位置时质心所在处为重力势能零点，用
表示棒这时的角速度，则
mg l 1 J 2＝1 1 ml 2 2
22
23
（1）
第二阶段是碰撞过程。因碰撞时间极短，产生的冲力 极大，物体所受地面的摩擦力可以忽略。对棒＋物体， 系统所受的对转轴O的合外力矩为零，故系统对轴O 的角动量守恒。用v表示物体碰撞后的速度，则
过多少时间才停止转动？
d r R
e
dr
解：由于摩擦力不是集中作用于一点，而是分布在整个圆盘与
桌子的接触面上，力矩的计算要用积分法。在图中，把圆盘分
成许多环形质元，每个质元的质量dm=rddre，所受到的阻力
矩是rdmg 。此处e是盘的厚度。
习题课
（刚体的转动）
课件公共邮箱：physics-fanghm@
密
码：0901－06
1
第五章 刚体的转动 总结
1、描述刚体转动的物理量
角位移 角速度
d
d
dt
角加速度 d
dt
与线量的关系
v r
a r
an
v2 r
r 2
2、刚体定轴转动定律
M J J d (Fv mav m dvv)
mgh 1 1 ml 2 2
23 把式（5）代入上式，所求结果为
h l 3s 6sl
2
（6）
12
补充2 一质量为m，半径为R，高h = R的圆柱体，可绕oo’轴线
转动。在圆柱体侧面上开有一与水平成 =450角的螺旋槽，放
一质量也为m的小球于槽中。开始时小球由静止从圆柱顶端A受
重力作用滑下，圆柱体同时发生转动。设各摩擦均不计，试求
0
(D) 0
6
3. 光滑的水平桌面上有一长为2L,质量为m的匀质细 杆,可绕过杆的中点并且垂直于杆的竖直光滑固定轴 自由转动,起初杆静止,两个质量均为m的小球各自沿 桌面正对这杆的一端在垂直于杆长的方向上以相同 的速率v相向运动,当两个小球同时与杆的两端发生 完全非弹性碰撞后就与杆粘在一起转动,则这一系统 碰撞后的转动角速度为[ ]
(A) 2v/3L (B) 4v/5L (C) 6v/7L (D) 2v/7L
7
4向. ）一,刚设体此以时每刚分体钟上6一0圈点绕的z位轴置匀矢速为转动r（
沿z轴 正方
3i 4 j 5k ,
单位为10-2m ,若以10-2m/s为速度单位,则此时刻P点速
度为[ ]
(A) v 94.2i 125.6 j 157.0k
mgh 1 J 2 1 m(u cos R )2 1 m(u sin )2 R
2
2
2
将J 1 mR 2和h R代 入 解 得 2g , u 3gR
2
3R
B
o
m
X
u
13
补充3 一半径为R，质量为m匀质圆盘，平放在粗糙的
水平桌面上。设盘与桌面间摩擦系数为，令圆盘最初 以角速度0绕通过中心且垂直盘面的轴旋转，问它经
0 v2 2as
（4）
由上述四式联合求解，即得
3gl 3 2gs
l
（5）
11
当′取正值时棒向左摆，其条件为
3gl 3 2gs 0 ，亦即l > 6 s；
当′取负值时棒向右摆，其条件为
3gl 3 2gs 0，亦即l < 6 s
棒的质心C上升的最大高度与第一阶段情况相似，对棒 ＋地球：由机械能守恒定律求得：
1 ml 2 mvl 1 ml 2
3
3
（2）
10
式中′可正可负，是棒在碰撞后的角速度。 ′取正值，
表示碰后棒向左摆；反之，表示棒向右摆。
第三阶段是碰撞后物体的滑行过程和棒的上升过程。
对物体：物体作匀减速直线运动，加速度由牛顿第二
定律求得为
mg ma
（3）
由匀减速直线运动的公式得
当小球滑落到圆柱体底部B时，小球相对圆柱体的速度和圆柱体
的角速度。
解小：球设相对圆圆柱柱体体沿的图运示速方度向为转动u的。角则速小度球为相ω对， 于地面的速度水平分量为：u cos R
o
R
A
h 对小球圆柱体：系统对定轴的角动量守恒：
J mR(u cos R ) 0
对小球＋圆柱体＋地球：系统的机械能守恒：
dt
dt
2
力矩
M rF
大小：M F r sin
方向：右手法则 转动惯量：
J Δmiri2
J r2dm
3、刚体定轴转动的动能定理
A
M d
1 2
J22
1 2
J12
(A
Fdr
1 2
mv22
1 2
mv12
)
力矩的功 A Md
刚体定轴转动动能 1 J 2
2
3
4、刚体定轴转动角动量定理
8
补充1 一匀质细棒长为 l ，质量为m，可绕通过其端
点O的水平轴转动，如图所示。当棒从水平位置自由
释放后，它在竖直位置上与放在地面上的物体相撞。
该物体的质量也为m ，它与地面的摩擦系数为。相
撞后，物体沿地面滑行一距离s而停止。求相撞后棒
的质心C离地面的最大高度h，并说明棒在碰撞后将向
左摆或向右摆的条件。
LZ miviri miri2 JZ
i
M dL dt
i
dp
(F )
dt
Mdt L2 L1 J2 J1
当 M 0
L J 常量
(
Fdt
p2
p1)
(F
0,
p
常矢量)
4
1. 两个力作用在一个有固定转轴的刚体上, (1) 这两个力都平行于轴作用时,它们对轴的合力 矩一定是零. (2) 这两个力都垂直于轴作用时,它们对轴的合力 矩可能是零. (3) 当这两个力的合力为零时,它们对轴的合力矩 也一定是零. (4) 当这两个力对轴的合力矩为零时,它们的合力 也一定是零.
(B) v 25.1i 18.8 j (C) v 25.1i 18.8 j
(D) v 31.4k
5. 飞轮作加速转动,轮边缘一点的运动方程s=0.1t3(SI),
飞轮半径2m,当该点速率v=30m/s时.其切向加速度为
___6_m__/_s2___,法向加速度为___4_5_0_m__/s_2___.