09-习题课(一)
合集下载
原子核物理习题课1 (1)
习题一：1. 试谈谈你对“格拉肖蛇”的理解。
物质科学体系——从“格拉肖蛇”蛇头到蛇尾，物质空间尺度依次减小，同时，“格拉肖蛇”首尾相衔，表明物理学中研究最大对象和最小对象的两个分支 宇宙学和粒子物理学就奇妙地衔接在一起，这并不意味着天体物理把粒子物理吞没，而是指在足够小和足够大的尺度下，两者具有统一的理论，即弱、电、强和引力相互作用“合四为一”。
2. 试论述中微子超光速实验测量原理。
意大利格兰萨索国家实验室下属的一个名为OPERA的实验装置接收了来自著名的欧洲核子研究中心的中微子,两地相距730公里,中微子“跑”过这段距离的时间比光速还快了60纳秒。
3. 试论述希格斯粒子对标准模型和超统一模型的作用。
杨振宁和米尔斯提出的杨-米尔斯非阿贝尔规范场理论，逐步构建完成了现代的标准模型理论。
但是杨-米尔斯方法无论应用到弱还是强相互作用中所遇到的主要障碍就是质量问题，由于规范理论规范对称性禁止规范玻色子带有任何质量，然而这一禁忌却与实验中的观测不相符合。
希格斯提出通过希格斯场产生对称性破缺，同时在现实世界留下了一个自旋为零的希格斯粒子，也称希格斯玻色子（Higgs boson ）或“上帝粒子”。
可以说，希格斯粒子是整个标准模型的基石，也是标准模型中最后一种未被发现的粒子。
如果希格斯粒子不存在，将使整个标准模型失去效力。
4. 试绘出各层次物质的德布罗意波长变化曲线。
λ=p h =p 341062.6-⨯m=nm p251062.6-⨯以λ为纵坐标，p 为横坐标绘制曲线，λ与p 成反比关系。
5. 谈谈爱因斯坦质能方程（式1-1）的理解。
爱因斯坦狭义相对论中“质能关系式”进行质量能量转换：2E mc =，他是通过比例系数c 2将质量和能量联系起来，这也就表明物质质量和能量有一定对应关系。
6. 试绘出物质质量随运动速率变化（式1-2）的曲线。
提示：以速度υ运动着的物质的质量m 和它的静止质量0m之间有着关系：m =，当物质运动速率与光速可比拟时，必须要考虑相对论效应。
充要条件(习题课)
若x B成立的一个充分不必要条件是x A, 试求实数m的取值范围
2．求证：关于x的方程ax2+bx+c=0有一个根为-1的 充要条件是a-b+c=0.
小结：充要条件的证明一般分两步：证充分性即 证A =>B，证必要性即证B=>A一定要使题目与证明 中的叙述一致 本题的难点是分清：充分和必要二个命题
学例2
“cos2α=
1 (2009· 湖北卷)“sinα= ”是 2 1 2
”的 ( A )
A.充分而不必要条件
B.B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 若sinα=
1 2α=1-2× , 则 cos2 α =1-2sin 2
1 1 但当sinα=- 时，也有cos2α= ，故选A. 2 2
充要条件(习题课)
知识回顾
1.若A=>B且B推不出A，则A是B的充分不必要条件
2.若A推不出B且B=>A，则A是B的必要不充分条件 3.若A=>B且B=>A，则A是B的充要条件 4.若A推不出B且B推不出A，则A既不是B的充分条件， 也不是B的必要条件.
练习一
1.已知p 是q 的必要而不充分条件，那么┐ p 是┐q的 ___ 2.若A是B的必要而不充分条件，C是B的充要条件，D 是C的充分而不必要条件，那么D是A的________ 3. 关于 x 的不等式：｜ x｜+｜x-1｜＞m 的解集为 R 的 充要条件是( ) (A)m＜0 (D)m≤1 答案： (1)充分不必要条件 (2)充分不必要条件 (3)C (B)m≤0 (C)m＜1
2.搞清①A是B的充分条件与A是B的充分非必 要条件之间的区别与联系；②A是B的必要条件与A 是B的必要非充分条件之间的区别与联系是非常重 要的,否则容易在这一点上出错误.
大学物理习题课1
v0
v 0 与水平方向夹角
19．如图所示，小球沿固定的光滑的 1/4圆弧从A点由静止开始下滑，圆弧半 径为R，则小球在A点处的切向加速度 at =______________________，小球 在B点处的法向加速度 an =_______________________．
θ
A R
B
三．计算题
t 0 .96 0 mg , t 0 .20 1 9 .8 0 .96 1s
此后合力为 第2秒内冲量
I
t 0 .96 mg
t 0 .96 0 .14 1 9 .8 dt
2 1
1 t 0 .412 dt
2
1 2
t
2 2 1
(B)
(C)
a g sin
a g
a 4 g (1 cos ) g sin
2 2 2 2
(D) ． ［ ］ 4. 将细绳绕在一个具有水平光滑轴的飞轮边缘上，现 在在绳端挂一质量为m的重物，飞轮的角加速度 为 ．如果以拉力2mg代替重物拉绳时，飞轮的角加 速度将 (A) 小于 ． (B) 大于 ，小于2 ． (C) 大于2 ． (D) 等于2 ．［ ］
二．填空题 13．如图所示，质量为m的小球系在劲度系数为k 的轻弹簧一端，弹簧的另一端固定在O点．开始时弹 簧在水平位置A，处于自然状态，原长为l0．小球由 位置A释放，下落到O点正下方位置B时，弹簧的长度 为l，则小球到达B点时的速度大小为v＝____
O l0 A k l m
O′
P
B m
Q R
R
F
F Ft
2 n
2
s 2 as 1 R
v 0 与水平方向夹角
19．如图所示，小球沿固定的光滑的 1/4圆弧从A点由静止开始下滑，圆弧半 径为R，则小球在A点处的切向加速度 at =______________________，小球 在B点处的法向加速度 an =_______________________．
θ
A R
B
三．计算题
t 0 .96 0 mg , t 0 .20 1 9 .8 0 .96 1s
此后合力为 第2秒内冲量
I
t 0 .96 mg
t 0 .96 0 .14 1 9 .8 dt
2 1
1 t 0 .412 dt
2
1 2
t
2 2 1
(B)
(C)
a g sin
a g
a 4 g (1 cos ) g sin
2 2 2 2
(D) ． ［ ］ 4. 将细绳绕在一个具有水平光滑轴的飞轮边缘上，现 在在绳端挂一质量为m的重物，飞轮的角加速度 为 ．如果以拉力2mg代替重物拉绳时，飞轮的角加 速度将 (A) 小于 ． (B) 大于 ，小于2 ． (C) 大于2 ． (D) 等于2 ．［ ］
二．填空题 13．如图所示，质量为m的小球系在劲度系数为k 的轻弹簧一端，弹簧的另一端固定在O点．开始时弹 簧在水平位置A，处于自然状态，原长为l0．小球由 位置A释放，下落到O点正下方位置B时，弹簧的长度 为l，则小球到达B点时的速度大小为v＝____
O l0 A k l m
O′
P
B m
Q R
R
F
F Ft
2 n
2
s 2 as 1 R
9、多元函数微分习题课(1)
2z 其中f 具有二阶连续偏导数， z = f (e x sin y , x 2 + y 2 ), 其中 具有二阶连续偏导数，求 4、 设 、 xy z = e x sin yf1′ + 2 xf 2′ 解 x
2z ′′ ′′ ′′ = f11e 2 x sin y cos y + 2e x ( y sin y + x cos y ) f12 + 4 xyf 22 + f1′e x cos y xy
x0 y0 z0 . 6abc
u=xyz（x>0，y>0，z>0）在条件( 于是问题转化为求函数 u=xyz（x>0，y>0，z>0）在条件(1)下的 最大值问题. 最大值问题. F(x,y,z)=xyz＋ x,y,z)=xyz 令 F(x,y,z)=xyz＋λ( a
x + b y + c z 1 )，解方程组
2、 由方程 xyz + 、
x 2 + y 2 + z 2 = 2 所确定的函数 z=z(x, y)
在点（ 在点（1,0,－1）处的全微分 dz = dx － ） [利用全微分 由方程得 利用全微分] 利用全微分 因此，在点 因此，在点(1,0,-1)处 处
2dy
1 x + y +z
2 2 2
yzdx + xzdy + xydz +
在曲面上， 因 P0 在曲面上，即 a x 0 + b y 0 + c z 0 = 1 ，
(2)
a b c x+ y+ z =1 将它代入( 可化切平面方程为， 将它代入(2)式，可化切平面方程为， x0 y0 z0
129964189620781250习题课-1
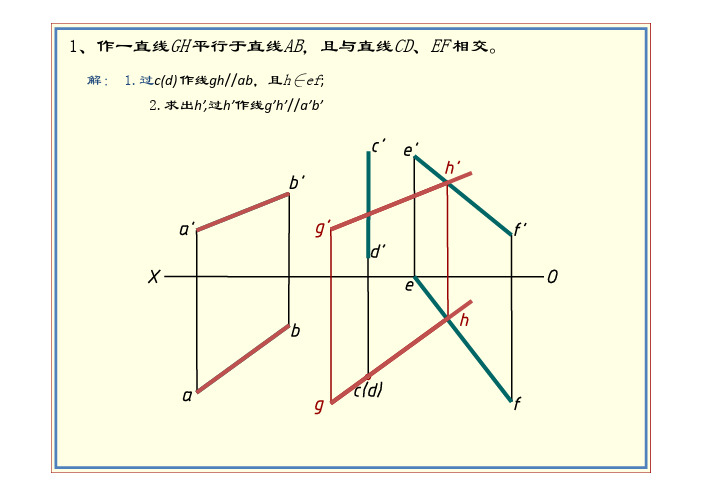
1、作一直线GH平行于直线AB，且与直线CD、EF相交。
解： 1.过c(d)作线gh//ab，且h∈ef;1过且2.求出h’,过h’作线g’h’//a’b’2、作一直线，使它与直线AB及CD均相交，且平行于OX轴。
解： 1.过c(d)作线ef//OX轴，且e∈ab;1过轴且2.求出e’,过e’作线e’f’// OX轴3、求作一直线MN ，使它与直线AB 平行，并与直线CD 相交于点K ，且CK :KD ＝1:2。
分析： 1.求出交点K 。
2.过交点K 求作AB解： 1.k’ 与c’(d’)重影。
2.用定比概念求k 。
的平行线MN 。
4.过k 作mn //ab 。
3.过k ’作m ’n ’//a’b’4、过点K作直线KF与直线CD正交。
解：CD是一般位置线，利用直角投影定理，过点K可作水平线KF、正平线KF均为所求;15、已知直线AB 与CD 垂直相交，求作c'd'。
空间分析：AB 为侧平线，故CD 为侧垂线。
解法一：2.CD 为侧垂线,故c’d’//OX 轴。
1.利用定比概念求出交点K 。
6、在直观图上标出各平面的位置（用相应的大写字母），在投影图上标出指定平面的其他两个投影。
并写出指定平面的名称。
一般位置平面面是面是水平面正平面面是铅垂面面是面是侧平面正垂面面是面是侧平面面是水平面7、已知下列平面上平面图形的一个投影，画出另一个投影。
解: 用面上取点、线的方法，即可完成水平投影。
8、作图判断直线AB 是否属于给定的平面。
解：1.在△ACD 上取线DI a’b’ d’1’ ab 不d1）,故AB 不属于ACD ；2.判断AB 与DI 两面投影是否平行（//,//）,△。
不属于9、求作五边形平面的水平投影。
解：三角形ABC可确定该平面，求出该平面上的点D、E的水平投影即可。
10、判别三条平行直线是否属于同一平面。
解：任取两直线组成一个平面，判别第三条直线是否属于该平面。
不属于答:11、给定一平面⊿ABC，作属于该平面的水平线，该线在H面上方，且距H面10mm；作属于该平面的正平线，该线在V面前方，且距V面；线，线，15mm。
09大学物理复习波动方程
n2 n1
时
r 2dn2 t 2dn2 2
第十四章 波动光学
n3 n2 n1
r 2dn2 2 t 2dn2
时
n2 n1
n1 n2 n3
波动光学习题课选讲例题 等厚干涉 1）干涉条纹为光程差相同的点的轨迹，即厚度 相等的点的轨迹 k 1 d 2n 2）厚度线性增长条纹等间距，厚度非线性增长 条纹不等间距 3）条纹的动态变化分析（ n, , 变化时） 4）半波损失需具体问题具体分析
波动光学习题课选讲例题
物理学教程 （第二版）
例 如图两同相的相干点光源 S1和 S 2 ，发出波 长为 的光，A 是连线中垂线上的一点， S1 与A 间插 入厚度为 的薄片，求 1）两光源发出的光在 A 点的 相位差；2）已知 500 nm , n 1.5 , A为第四级 明纹中心, 求薄片厚度 e 的大小.
1）相位差和光程差的关系
nr
2 π
第十四章 波动光学
光程差
光在真空中波长
波动光学习题课选讲例题
物理学教程 （第二版）
2） 透镜不引起附加的光程差
3）光由光疏媒质射向光密媒质而在界面上反射时， 发生半波损失，这损失相当于 2 的光程. 三 薄膜干涉 入射光在薄膜上表面由于反射和折射而“分振幅”， 在上下表面反射的光为相干光. n1 当光线垂直入射时 i 0 当 当
若在牛顿环装置的透镜和平板玻璃板间充满
某种折射率大于透镜折射率而小于平板玻璃的某种液
体，则从入射光方向所观察到的牛顿环的环心是
（1）暗斑 （2）明斑 （3）半明半暗的斑 （4）干涉现象消失
n1
n2
n1 n2 n3
第8章线性变换的可对角化问题习题课(09-10第二学期)
i 量， = 1, 2,
线性无关.
推论 8.2.6：设 A 是数域 K 上的 n × n 方阵，如 果 A 的特征多项式在 K 中有 n 个不同的根，则 A 可 对角化。
高等代数与解析几何
定理 8.2.7
n 阶矩阵 A = ( aij ) ∈ M n ( K ) 属于特征
k
值 λ0 的线性无关特征向量有 k 个,那么 A 的特征多项式 必有因子 (λ − λ0 ) .
α1 , α 2 ,
由W 的基α1 , α2 ,
高等代数与解析几何
, α r , α r +1 ,
,α n
由于 σ (αi ), i = 1, 2,
, r 仍属于W ,所以 σ (α i ) 可
, αr 线性表示,设
σ (α1 ) = a11α1 + a21α 2 + σ (α 2 ) = a12α1 + a22α 2 + V 的一个基 α 1 , α 2 ,
, α n ，使得 σ (α i ) = λiα i ，这里
λi ∈ K , i = 1, 2,
, n.
定义 8.3.1 设 V 是数域 K 上的线性空间， λ 是 K 中
σ 的一个数， 是V 的一个线性变换. 如果存在 V 的非零
+ an ,r +1α n
由此知 σ 在 V 的一个基 α1 , α 2 , 的矩阵为
, α r , α r +1 ,
,α n 下
高等代数与解析几何
⎛ a11 ⎜ ⎜ ⎜ ar 1 A=⎜ ⎜ 0 ⎜ ⎜ ⎜ 0 ⎝
a1r arr 0 0
a1,r +1 ar , r + 1 ar +1,r +1 an , r + 1
静力学习题课(1)
F4=8 （ N ）， F5=10 （ N ）， 则 该 力 系 简 化 的 最 后 结 果
为
。
答案：-40N·m，顺时针方向
受力分析题
1、请画出 横梁AB、立柱AE、整体的受力分析图
受力分析题
2、请画出物体D、轮O、杆AB的受力图
计算题
图示电动机用螺栓A，B固定在角架上，自重不计。角架用螺 栓C，D固定在墙上。若M=20kN·m，a=0.3m，b=0.6m，求螺 栓A，B，件、活动铰支座；柔索约束，光滑接触面约束；固定铰支座， 固定端约束
2、平面任意力系向一点的简化，需要将力系中各力都
到
作用面内任意选定的一点上，该点称为
。
答案：平行移动；简化中心
填空题
3、
是作用在刚体平面内上的两个力偶等效的充分
必要条件。
答案：力偶矩相同
4、对于给定的任意力系，其主矢与简化
。但在一
般情况下，简化中心的位置不同时，对应的力系的
。
答案：中心位置无关；主矩则不同
填空题
图示结构受矩为 M=10KN.m 的力偶作用。若 a=1m，各杆自重不计。则固定铰支座 D 的反
力的大小为
，方向
。
答案：10KN；水平向右
已知平面平行力系的五个力分别为 F1=10（N），F2=4（N），F3=8（N），
1、解锯弓
（1）取梁锯弓画受力图如图所示。（2）建直角坐标系，列平衡方程：
解得：
FBA=5.18kN FD=-2.44kN(↓) FC=-1.18kN(↑)
2、解锯床转盘
（1）取锯床转盘画受力图如图所示。（2）建直角坐标系，列平衡方程：
解得 ：
FOX=5kN （→）FOy=1.34kN(↑) M=500N·m( )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 h( x ) = 0 − 1〈 x〈3 其他
计算
f ( x ) ∗ h( x )
y
并作图
y
y
-3
-2
-1
1
2
3
x
-3
-2
-1
0
1
2
3
x
X-3
-3
-2
x X+1
-1 0
1
2
3
x
第一步
翻 转
第二步 平 移
17
第三步 乘 积
习 题 一 解 答
y y
求面积） 第四步 积 分（求面积）
y
?
X-3
f(x)*h(x)
3 2 1
-3
-2
-1
1
2
3
4
5
6
x
19
傅里叶光学
习 题 一 解 答
x x − a / 2 1 x 1．7 求证： rect + rect ． 求证： ∗ comb = 1 b a − b a a
分析
0<x<a
y
x a2 − x2 1 1 f ( x ) Λh ( x ) = a − × x × = 2 2 a 2a
a/2
1
-a -3
-2
-1
1
2
3
a
x
25
习 题 一 解 答
• 同理
a2 − x2 2a h ( x ) Λf ( x ) = (a − x) 2 2a
可见， 可见，求相关不满足交换律
点的矩形函数， （1）第一项是宽度为 、中心在 点的矩形函数， ）第一项是宽度为b、中心在0点的矩形函数 第二项是宽度为（ － ）、中心在a/2处的矩形函数 ）、中心在 处的矩形函数， 第二项是宽度为（a－b）、中心在 处的矩形函数， 由图可见，两者相加得到一个宽度为a的矩形函数 的矩形函数。 由图可见，两者相加得到一个宽度为 的矩形函数。 （2）Comb函数由间隔为 的一系列δ函数组成 ） 函数由间隔为a的一系列 函数组成 函数由间隔为 的一系列 1 a x b/2 a－b/2 -2a -a 1 0 a x 2a
傅里叶光学
习 题 一 解 答
1．1 给定函数 f (x) = rect (x+2) + rect (x-2) ． 画出以下函数图形： 画出以下函数图形： f(x) （1） f (x) ）
1 x -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
（2）f (x) sgn (x) ）
f(x) 1 -6 -5 -4 -3 -2 -1 x 0 1 2 3 4 5 6
−a ≤ x ≤0 −≤x≤a
26
习 题 一 解 答 1.10 求函数的傅立叶变换
1 1) H ( x) = 0 x>0 x<0
∞ 0
∫
∞
0
e
− ax
1 dx = a
(a > 0)
解：F [ H ( x)] = ∫
1 exp(− j 2πux)dx = j 2πu
∞
2) sgn( x)
解：F [sgn( x)] = ∫ sgn( x) ⋅ exp(− j 2πux)dx
∞
x− y =ξ
y = x −ξ
dy = dξ
左边= 所以 左边 = =
∫ ∫
−∞
+∞ ∞
f ( x − ξ ) ⋅ h(ξ )(−dξ )
h (ξ ) ⋅ f ( x − ξ ) d ξ
−∞
h( x) ∗ f ( x) =右边 右边
得证
15
习 题 一 解 答 证明 3) f ( x / b) ∗ h( x / b) = b g ( x / b)
a −b x− ∞ 2 − na = ∑ rect ( a −∞
21
习 题 一 解 答
1.8 求下列卷积，并画出图形 求下列卷积，
• 1)
f ( x) = rect ( x) ∗ rect ( x) = Λ(x)
h( x) = rect ( x) ∗ [rect ( x) ∗ δ ( x − 2)] = rect ( x) ∗ rect ( x) ∗ δ ( x − 2)
（3）两者卷积的结果是 ，如图所示 ）两者卷积的结果是1， 1 -2a 0 a 2a x
20
-a
习 题 一 解 答
注意卷积性质
f ( x) ∗ comb( x) = ∫ f (ξ )comb( x − ξ )dξ = ∑ f ( x − n)
−∞ −∞ ∞ ∞
a−b a−b x− x− ∞ 1 x 2 ) ∗ comb( ) = rect ( 2 ) ∗ δ ( x − na ) rect ( ∑ a a a a −∞
1
傅里叶光学
习 题 一 解 答
f (x) = rect (x+2) + rect (x-2)
x x （3） f (x / 2) = rect + 2 + rect − 2 ） 2 2
x+4 x−4 = rect + rect 2 2
5
傅里叶光学
习 题 一 解 答
= 4 A 2 cos 2 (2 π f 0 x )
f (x) = Aexp（j2πf0 x） （ ） （3） | f (x) + f *(x) | 2 ）
= 2 A 2 [cos( 4 π f 0 x ) + 1 ]
f(x) 4A2
Y
x -1/2f0 0 1/2f0
习 题 一 解 答
f ( x − x0 ) ∗ h( x) = ∫ f (ξ ) ⋅ h[ x − (ξ + x0 )]dξ
−∞ ∞
= ∫ f (ξ ) ⋅ h[(x − x0 ) − ξ ]dξ
∞ −∞
Q f ( x ) ∗ h( x ) = g ( x ) ∴ ∫ f (ξ ) ⋅ h( x − ξ )dξ = g ( x)
= A2
f(x) A2
x
4
傅里叶光学
习 题 一 解 答
f (x) = Aexp（j2πf0 x） （ ） （2） f (x) + f *(x) ）
＝ A [exp
( j 2 π f 0 x ) + exp (−
f(x)
Y
j 2 π f 0 x )]
= 2 A cos(2 πf 0 x )
2A x -1/f0 0 1/f0
g(x) 1
……
……
x
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
• 4)
1 H ( x) ∗ H ( x)其中H ( x) = 0
x>0 x<0
x H ( x) ∗ H ( x) = 0
x≥0 其它
23
习 题 一 解 答
x/a 0≤x≤a
1.9 已知函数 求下列互相关函数 （1）f (x) h (x) （2）h (x) f (x)
0<x-3<3 x+1<0或x-3>3
1 2 1 g ( x) = 3 − × ( x − 3) × ( x − 3) = − x 2 + 2 x 2 3 3
g(x)=0
18
习 题 一 解 答
综上： 综上：
1 −1 < x < 2 ( x + 1) 2 3 3 2< x<3 f ( x ) ∗ h( x ) = 1 2 − x + 2 x 3< x <6 3 0 x > 6或x < −1
习 题 一 解 答 1.4 画出函数的图形
• 1） f1 ( x) = 1 comb x • rect x
a a
2 1
5a
f(x)
……
-3a -2a -a
∞
……
a 2a 3a x
f ( x) • comb( x) = ∑ f (n)δ ( x − n)
6
习 题 一 解 答
1.3 画出下列函数的图形 • 1）f ( x) = rect ( x / 4) − rect ( x / 2)
f(x) 1 x -3 -2 -1
0
1
2
3
7
习 题 一 解 答
1.3 画出下列函数的图形 • 2） g ( x ) = 2Λ ( x / 2) − Λ ( x)
g(x) 2 1
-2
-1
1
2
x
8
习 题 一 解 答
1.3 画出下列函数的图形 • 3）h( x) = 2Λ ( x / 2) − 2Λ ( x )
h(x) 2 1
-2
-1
1
2
x
9
习 题 一 解 答
1.3 画出下列函数的图形 • 4）
p ( x) = Λ ( x) step( x)
h(x) 2 1
-2
-1
1
2
x
10
-3 -2 -1 0
?
2 3 x -3 -2
x X+1
1
X-3
-1
0
1
2
x X+1
3
x
-3
-2
-1
0
X-3
1
2
3
x X+1
x
0<x+1<3 x-3<0且x+1>3
-1<x<2 2<x<3 3<x<6 x<-1或x>6
计算
f ( x ) ∗ h( x )
y
并作图
y
y
-3
-2
-1
1
2
3
x
-3
-2
-1
0
1
2
3
x
X-3
-3
-2
x X+1
-1 0
1
2
3
x
第一步
翻 转
第二步 平 移
17
第三步 乘 积
习 题 一 解 答
y y
求面积） 第四步 积 分（求面积）
y
?
X-3
f(x)*h(x)
3 2 1
-3
-2
-1
1
2
3
4
5
6
x
19
傅里叶光学
习 题 一 解 答
x x − a / 2 1 x 1．7 求证： rect + rect ． 求证： ∗ comb = 1 b a − b a a
分析
0<x<a
y
x a2 − x2 1 1 f ( x ) Λh ( x ) = a − × x × = 2 2 a 2a
a/2
1
-a -3
-2
-1
1
2
3
a
x
25
习 题 一 解 答
• 同理
a2 − x2 2a h ( x ) Λf ( x ) = (a − x) 2 2a
可见， 可见，求相关不满足交换律
点的矩形函数， （1）第一项是宽度为 、中心在 点的矩形函数， ）第一项是宽度为b、中心在0点的矩形函数 第二项是宽度为（ － ）、中心在a/2处的矩形函数 ）、中心在 处的矩形函数， 第二项是宽度为（a－b）、中心在 处的矩形函数， 由图可见，两者相加得到一个宽度为a的矩形函数 的矩形函数。 由图可见，两者相加得到一个宽度为 的矩形函数。 （2）Comb函数由间隔为 的一系列δ函数组成 ） 函数由间隔为a的一系列 函数组成 函数由间隔为 的一系列 1 a x b/2 a－b/2 -2a -a 1 0 a x 2a
傅里叶光学
习 题 一 解 答
1．1 给定函数 f (x) = rect (x+2) + rect (x-2) ． 画出以下函数图形： 画出以下函数图形： f(x) （1） f (x) ）
1 x -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
（2）f (x) sgn (x) ）
f(x) 1 -6 -5 -4 -3 -2 -1 x 0 1 2 3 4 5 6
−a ≤ x ≤0 −≤x≤a
26
习 题 一 解 答 1.10 求函数的傅立叶变换
1 1) H ( x) = 0 x>0 x<0
∞ 0
∫
∞
0
e
− ax
1 dx = a
(a > 0)
解：F [ H ( x)] = ∫
1 exp(− j 2πux)dx = j 2πu
∞
2) sgn( x)
解：F [sgn( x)] = ∫ sgn( x) ⋅ exp(− j 2πux)dx
∞
x− y =ξ
y = x −ξ
dy = dξ
左边= 所以 左边 = =
∫ ∫
−∞
+∞ ∞
f ( x − ξ ) ⋅ h(ξ )(−dξ )
h (ξ ) ⋅ f ( x − ξ ) d ξ
−∞
h( x) ∗ f ( x) =右边 右边
得证
15
习 题 一 解 答 证明 3) f ( x / b) ∗ h( x / b) = b g ( x / b)
a −b x− ∞ 2 − na = ∑ rect ( a −∞
21
习 题 一 解 答
1.8 求下列卷积，并画出图形 求下列卷积，
• 1)
f ( x) = rect ( x) ∗ rect ( x) = Λ(x)
h( x) = rect ( x) ∗ [rect ( x) ∗ δ ( x − 2)] = rect ( x) ∗ rect ( x) ∗ δ ( x − 2)
（3）两者卷积的结果是 ，如图所示 ）两者卷积的结果是1， 1 -2a 0 a 2a x
20
-a
习 题 一 解 答
注意卷积性质
f ( x) ∗ comb( x) = ∫ f (ξ )comb( x − ξ )dξ = ∑ f ( x − n)
−∞ −∞ ∞ ∞
a−b a−b x− x− ∞ 1 x 2 ) ∗ comb( ) = rect ( 2 ) ∗ δ ( x − na ) rect ( ∑ a a a a −∞
1
傅里叶光学
习 题 一 解 答
f (x) = rect (x+2) + rect (x-2)
x x （3） f (x / 2) = rect + 2 + rect − 2 ） 2 2
x+4 x−4 = rect + rect 2 2
5
傅里叶光学
习 题 一 解 答
= 4 A 2 cos 2 (2 π f 0 x )
f (x) = Aexp（j2πf0 x） （ ） （3） | f (x) + f *(x) | 2 ）
= 2 A 2 [cos( 4 π f 0 x ) + 1 ]
f(x) 4A2
Y
x -1/2f0 0 1/2f0
习 题 一 解 答
f ( x − x0 ) ∗ h( x) = ∫ f (ξ ) ⋅ h[ x − (ξ + x0 )]dξ
−∞ ∞
= ∫ f (ξ ) ⋅ h[(x − x0 ) − ξ ]dξ
∞ −∞
Q f ( x ) ∗ h( x ) = g ( x ) ∴ ∫ f (ξ ) ⋅ h( x − ξ )dξ = g ( x)
= A2
f(x) A2
x
4
傅里叶光学
习 题 一 解 答
f (x) = Aexp（j2πf0 x） （ ） （2） f (x) + f *(x) ）
＝ A [exp
( j 2 π f 0 x ) + exp (−
f(x)
Y
j 2 π f 0 x )]
= 2 A cos(2 πf 0 x )
2A x -1/f0 0 1/f0
g(x) 1
……
……
x
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
• 4)
1 H ( x) ∗ H ( x)其中H ( x) = 0
x>0 x<0
x H ( x) ∗ H ( x) = 0
x≥0 其它
23
习 题 一 解 答
x/a 0≤x≤a
1.9 已知函数 求下列互相关函数 （1）f (x) h (x) （2）h (x) f (x)
0<x-3<3 x+1<0或x-3>3
1 2 1 g ( x) = 3 − × ( x − 3) × ( x − 3) = − x 2 + 2 x 2 3 3
g(x)=0
18
习 题 一 解 答
综上： 综上：
1 −1 < x < 2 ( x + 1) 2 3 3 2< x<3 f ( x ) ∗ h( x ) = 1 2 − x + 2 x 3< x <6 3 0 x > 6或x < −1
习 题 一 解 答 1.4 画出函数的图形
• 1） f1 ( x) = 1 comb x • rect x
a a
2 1
5a
f(x)
……
-3a -2a -a
∞
……
a 2a 3a x
f ( x) • comb( x) = ∑ f (n)δ ( x − n)
6
习 题 一 解 答
1.3 画出下列函数的图形 • 1）f ( x) = rect ( x / 4) − rect ( x / 2)
f(x) 1 x -3 -2 -1
0
1
2
3
7
习 题 一 解 答
1.3 画出下列函数的图形 • 2） g ( x ) = 2Λ ( x / 2) − Λ ( x)
g(x) 2 1
-2
-1
1
2
x
8
习 题 一 解 答
1.3 画出下列函数的图形 • 3）h( x) = 2Λ ( x / 2) − 2Λ ( x )
h(x) 2 1
-2
-1
1
2
x
9
习 题 一 解 答
1.3 画出下列函数的图形 • 4）
p ( x) = Λ ( x) step( x)
h(x) 2 1
-2
-1
1
2
x
10
-3 -2 -1 0
?
2 3 x -3 -2
x X+1
1
X-3
-1
0
1
2
x X+1
3
x
-3
-2
-1
0
X-3
1
2
3
x X+1
x
0<x+1<3 x-3<0且x+1>3
-1<x<2 2<x<3 3<x<6 x<-1或x>6