怀化市2014上期高三二模成绩(文科)排名(1)

合集下载

2014届高三二模学生成绩

编号姓名性别班级考号选科语文排名数学排名英语21王艳卿女29031400108理科11041501117 19陈浩祥男29031400936理科10961352122 13许建辉男29031401448理科101151274130 14陈语捷女29031401456理科118.5210122106 2蔡咏池男29031401431理科104.5911611129 20叶秀谦男29031400323理科103.5111313123.5 6陈佑宇男29031401435理科922911512110.5 18叶洁贤女29031401471理科109.551235110.5 7梁威镰男29031401440理科991810518105 15林晓茵女29031401462理科93269029109.5 3蔡梓图男29031401432理科92.5281012292.5 22孔婷婷女29031401527理科90.532962593 10刘伟豪男29031401445理科86391101478 12吴孟哲男29031401447理科73471101480 9梁卓恒男29031401443理科86391081674 17薛琦女29031401470理科9719118994 4陈国海男29031401433理科9521942764.5 1蔡林偌男29031401430理科9521843355 16林雅熹女29031401463理科104.59634190 8梁智宏男29031401441理科8738813590 5陈祈至男29031401434理科100.516683971.5 11刘学儒男29031401446理科8443534690.5 27钟洁雯女29031401474文科119.511217129 17梁楚冰女29031401461文科102131208131.5 6杨镇城男29031400185文科11231226108.5 21缪丽思女29031401466文科103.5111189107.5 13陈靖宜女29031401455文科1021310518120.5 16何嘉琪女29031401459文科93269824116 10尹康丞男29031401452文科71.54910518124.5 26郑汶珠女29031401473文科100.5166937104 11张键豪男29031401453文科94.523962587.5 14邓闵云女29031401457文科95.52010321115 4梁仲濠男29031401442文科1068793692.5 1黄冠程男29031401437文科88.535634197.5 18梁丽珍女29031400803文科92296839108 12布安萍女29031401454文科76441111384.5 28陈俊威男29031401526文科91311061784 8葉林男29031401450文科93.524912888.5 29高伟健男29031401436文科85.541853291 3李展辉男29031401439文科88.535693778 19刘泓滟女29031401464文科85.541883185 24许懿婷女29031401469文科90.532584495.5 5林奕材男29031401444文科7347902977.5 22伍慧琳女29031401467文科68.5506341102.5 2黄炜祺男29031401438文科75.545534692 25余晓芬女29031401472文科88.535285090.5 9殷智恒男29031401451文科9034354974 30杨炯辉男29031401449文科7446454863 23许婉仪女29031401468文科108.575844111.5 7姚子立男29031401520文科93.524833481 15关松雅女29031401458文科20刘静雯女29031401465文科排名历史排名地理排名物理排名化学排名总分排名9148114426691 7120714136272 2136313246263 1914421491618.54 313631324617.55 6123612966106 13127511613560.57 13841512965568 209613124105299 151041012410520.510 2710891241051811 26102111259506.512 4298121151448713 411118981547214 458016971644515 255819731944016 4888149617437.517 507017126843018 3347219617400.519 336318662038720 475020592134921 3141225722325.522 311611481633.51 111611433612.52 169781288567.53 18107413065664 810261297558.55 10101713245406 59510118145147 2110551279505.58 369510125104989 1186159823497.510 2796912011493.511 2311611201148512 178417131548313 3864241452480.514 3991121021847415 3587131101747016 30871311415462.517 42831812011438.518 3778199922435.519 2473211002141720 4485168126406.521 2268221021840422 29592511216391.523 3177201012038524 456723952536125 49982328026 1227827 40257.528。

2014届高三二模学生成绩

2014届高三二模学生成绩编号姓名性别班级考号选科语文排名数学排名英语21王艳卿女29031400108理科11041501117 19陈浩祥男29031400936理科10961352122 13许建辉男29031401448理科101151274130 14陈语捷女29031401456理科118.5210122106 2蔡咏池男29031401431理科104.5911611129 20叶秀谦男29031400323理科103.5111313123.5 6陈佑宇男29031401435理科922911512110.5 18叶洁贤女29031401471理科109.551235110.5 7梁威镰男29031401440理科991810518105 15林晓茵女29031401462理科93269029109.5 3蔡梓图男29031401432理科92.5281012292.5 22孔婷婷女29031401527理科90.532962593 10刘伟豪男29031401445理科86391101478 12吴孟哲男29031401447理科73471101480 9梁卓恒男29031401443理科86391081674 17薛琦女29031401470理科9719118994 4陈国海男29031401433理科9521942764.5 1蔡林偌男29031401430理科9521843355 16林雅熹女29031401463理科104.59634190 8梁智宏男29031401441理科8738813590 5陈祈至男29031401434理科100.516683971.5 11刘学儒男29031401446理科8443534690.5 27钟洁雯女29031401474文科119.511217129 17梁楚冰女29031401461文科102131208131.5 6杨镇城男29031400185文科11231226108.5 21缪丽思女29031401466文科103.5111189107.5 13陈靖宜女29031401455文科1021310518120.5 16何嘉琪女29031401459文科93269824116 10尹康丞男29031401452文科71.54910518124.5 26郑汶珠女29031401473文科100.5166937104 11张键豪男29031401453文科94.523962587.5 14邓闵云女29031401457文科95.52010321115 4梁仲濠男29031401442文科1068793692.5 1黄冠程男29031401437文科88.535634197.5 18梁丽珍女29031400803文科92296839108 12布安萍女29031401454文科76441111384.5 28陈俊威男29031401526文科91311061784 8葉林男29031401450文科93.524912888.5 29高伟健男29031401436文科85.541853291 3李展辉男29031401439文科88.535693778 19刘泓滟女29031401464文科85.541883185 24许懿婷女29031401469文科90.532584495.5 5林奕材男29031401444文科7347902977.5 22伍慧琳女29031401467文科68.5506341102.5 2黄炜祺男29031401438文科75.545534692 25余晓芬女29031401472文科88.535285090.5 9殷智恒男29031401451文科9034354974 30杨炯辉男29031401449文科7446454863 23许婉仪女29031401468文科108.575844111.5 7姚子立男29031401520文科93.524833481 15关松雅女29031401458文科20刘静雯女29031401465文科排名历史排名地理排名物理排名化学排名总分排名9148114426691 7120714136272 2136313246263 1914421491618.54 313631324617.55 6123612966106 13127511613560.57 13841512965568 209613124105299 151041012410520.510 2710891241051811 26102111259506.512 4298121151448713 411118981547214 458016971644515 255819731944016 4888149617437.517 507017126843018 3347219617400.519 336318662038720 475020592134921 3141225722325.522 311611481633.51 111611433612.52 169781288567.53 18107413065664 810261297558.55 10101713245406 59510118145147 2110551279505.58 369510125104989 1186159823497.510 2796912011493.511 2311611201148512 178417131548313 3864241452480.514 3991121021847415 3587131101747016 30871311415462.517 42831812011438.518 3778199922435.519 2473211002141720 4485168126406.521 2268221021840422 29592511216391.523 3177201012038524 456723952536125 49982328026 1227827 40257.528。

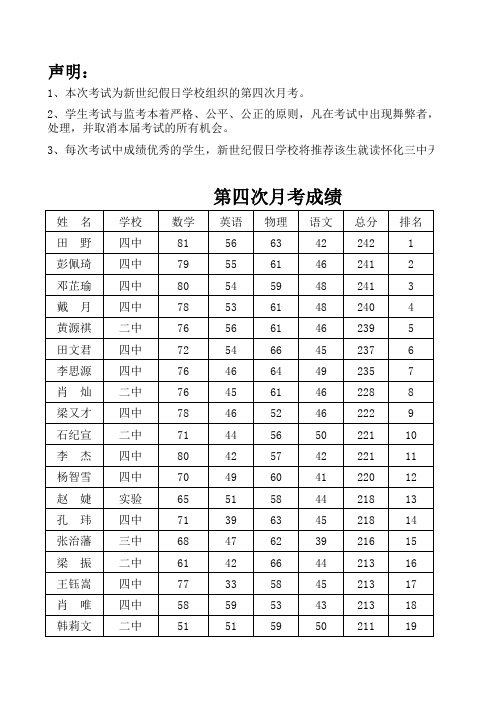
2014-4考试结果

182 181 181 181 181 180 180 179 179 179 178 178 178 178 177 177 175 173 173 173 172 172 171 171 170 170 170
74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
39 40 36 32 45 41 30 37 46 23 41 53 28 34 42 33 39 51 29 37 44 33 33 33 41 32 41
55 58 49 46 56 49 50 58 61 54 45 47 66 41 59 47 43 45 52 50 48 60 57 48 43 43 49
47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
刘湘君中方中兴学校佘雨婷张德仪彭嘉兴夏雨龙泓婷陈俐妃吕泳庆陈彩奕丁春红袁嘉敏王心蕾实验武陵实验三中二中四中三中四中二中实验中学三中
44 46 44 41 44 40 42 39 36 44 39 50 44 42 42 44 43 43 44 46 45 42 44 41
170 170 169 168 167 166 165 165 165 164 163 163 162 161 159 157 154 151 149 149 146 146 140 135
唐倩肖琪赵雯夏梦瑶罗葳瞿湘孙钰菲周楷傑周坚肖杰丹赵志明谢睿林李祎航唐岑陈佳敏夏慧琳刘建宏韩承誉张勇平肖新豪石雨昕杨芳丁芷若罗伟莙罗子毓黄鑫张颖楠

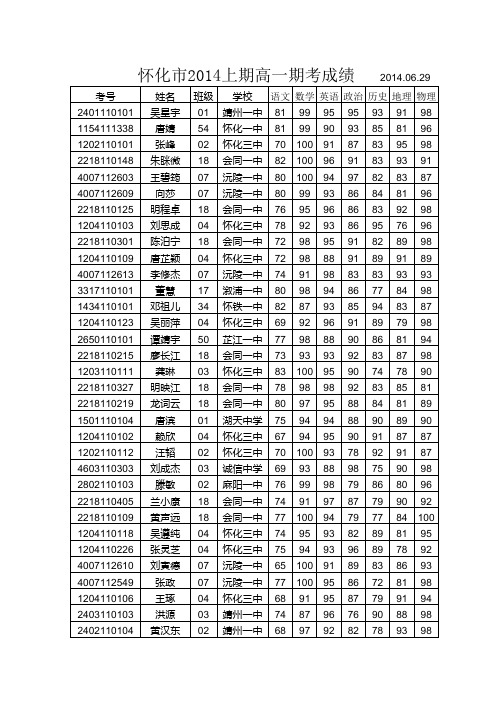
怀化市2014上期高一期考成绩

91 93 92 81 69 84 77 79 89 84 82 86 76 83 92 84 88 83 87 76 94 85 98 89 85 84 77 77 94 77 84 81 77 76 81
90 85 80 87 81 75 89 77 86 85 95 77 73 88 78 90 84 78 92 78 83 80 97 81 77 88 88 86 95 86 80 90 81 85 82
靖州一中新晃一中通道一中怀化三中会同一中怀化三中怀铁一中怀化三中怀化三中麻阳一中会同一中怀化三中怀化三中麻阳一中黔阳一中湖天中学湖天中学会同一中芷江一中湖天中学溆浦一中沅陵一中新晃一中湖天中学怀化三中怀化一中怀化三中湖天中学芙蓉中学怀化三中怀化三中怀化一中沅陵一中怀铁一中芷江一中
78 70 69 66 81 73 66 82 72 72 69 75 74 74 78 75 81 80 73 72 65 68 67 72 78 76 76 70 72 77 70 80 69 73 73
98 95 95 89 87 93 96 94 93 98 96 92 100 89 98 99 92 90 87 99 95 92 93 86 89 97 98 96 95 95 94 96 92 91 94
郁利芳杨璧宁金贻秋赵子杰梁卓怡刘一楠崔铃戴永强肖梓茜娄思敏黄翰林向昭颖龙彦洁张欢杨远健彭逸成芷怡于晨杨依锦胡连杰罗雨晨覃超罗淦方易铂胜米京万佳蓉姚源昊舒华峰李新科林璐彭琳凯韩慧萍张家华白文超杨惠晰
02 07 01 02 18 02 34 08 01 03 18 03 01 01 10 01 01 18 50 01 17 07 07 02 05 53 03 04 05 03 15 52 07 33 60

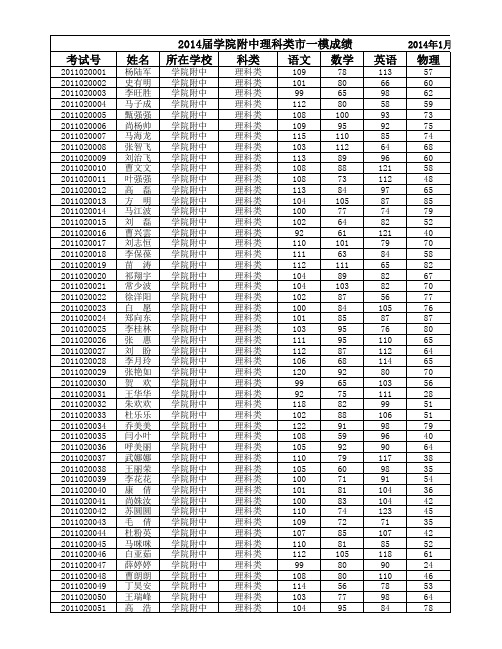
2014届全市高三第一次模拟成绩单

104 108 105 97 110 90 107 108 104 103 95 96 104 103 105 101 98 103 91 108 85 97 101 104 102 102 104 102 91 110 109 104 109 85 112 107 116 103 108 115 107 115 113 107 107 107 107 117 100 106 106 116 108 109 110 107 110 114
理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类理科类
考试号
2011020001 2011020002 2011020003 2011020004 2011020005 2011020006 2011020007 2011020008 2011020009 2011020010 2011020011 2011020012 2011020013 2011020014 2011020015 2011020016 2011020017 2011020018 2011020019 2011020020 2011020021 2011020022 2011020023 2011020024 2011020025 2011020026 2011020027 2011020028 2011020029 2011020030 2011020031 2011020032 2011020033 2011020034 2011020035 2011020036 2011020037 2011020038 2011020039 2011020040 2011020041 2011020042 2011020043 2011020044 2011020045 2011020046 2011020047 2011020048 2011020049 2011020050 2011020051 2011020052 2011020053 2011020054 2011020055

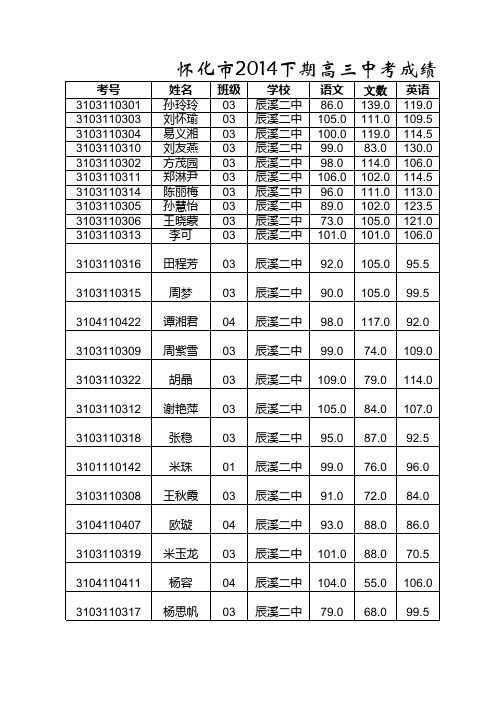
怀化市2014下期高三中考成绩(文科)(1)

王静张雪莲张钦诸丽敏曾双双朱珊蒲金玲张玲玲张子健李发顺魏雯伍艳华傅美源刘亚妮刘香孙福林戴梅菊米愿刘自有宋玉梅王艳丹张文宋叶宾黄科胡蝶汪淑丽谢雅群李霞孙靖张娅夏点何雪滢张琪瑞龚梦莲瞿芬芬张云娇王玉梅张莲莲赵鑫
04 05 03 02 02 03 07 02 02 02 01 05 01 01 01 05 01 05 02 01 01 04 01 01 02 02 01 01 02 05 01 04 05 07 01 01 07 05 02
45.5 54.0 75.5 87.0 62.5 57.5 85.0 48.0 55.0 49.0 75.5 52.5 71.5 59.5 59.5 76.5 59.0 62.5 59.0 43.0 58.5 58.5 87.5 78.5 60.0 69.0 62.5 58.5 48.0 60.0 77.0 43.5 66.0 55.5 62.5 45.0 50.0 49.0 70.0
3101110137 3104110420 3101110147 3105110505 3101110120 3101110121 3105110533 3103110324 3102110227 3102110234 3107110613 3102110209 3102110212 3105110549 3107110623 3105110519 3107110636 3107110603 3105110525 3101110134 3102110425 3101110111 3102110231 3104110402 3107110601 3105110518 3102110230 3101110105 3102110241 3101110117 3105110544 3105110543 3104110403 3107110614 3107110611 3105110531 3105110524 3105110539 3101110123

2014-2015学年湖南省怀化市高三(上)期中数学试卷和答案(文科)

2014-2015学年湖南省怀化市高三（上）期中数学试卷（文科）一、选择题：本大题共10小题，每小题5分，共计50分，在每小题给出的四个选项中，只有一项符合题目要求，请把正确答案的代号填在答题卡上. 1．（5分）已知全集U={0，1，2，3，4，5}集合A={1，2，3，5}，B={2，4}，则（∁U A）∪B为（）A．{0，2，4}B．{2，3，5}C．{1，2，4}D．{0，2，3，5}2．（5分）给定函数①y=x，②y=log x，③y=|x﹣1|，④y=2x，其中在区间（0，1）上单调递减的函数序号是（）A．①②B．②③C．③④D．①④3．（5分）“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件4．（5分）函数f（x）=1﹣2sin22x的最小正周期是（）A．B．πC．2πD．4π5．（5分）一个锥体的主视图和左视图如图所示，下面选项中，不可能是该锥体的俯视图的是（）A．B．C．D．6．（5分）运行如图的程序框图，则输出s的结果是（）A．B．C．D．7．（5分）已知=（λ，2），=（﹣3，5），且与的夹角为锐角，则λ的取值范围（）A．λ＜B．λ≥C．λ＜且λ≠﹣D．λ≤且λ≠﹣8．（5分）已知a≠0直线ax+（b+2）y+4=0与直线ax+（b﹣2）y﹣3=0互相垂直，则ab的最大值等于（）A．0 B．2 C．4 D．9．（5分）已知曲线y=在点P（1，4）处的切线与直线l平行且距离为，则直线l的方程为（）A．4x﹣y+9=0或4x﹣y+25=0 B．4x﹣y+9=0C．4x+y+9=0或4x+y﹣25=0 D．以上都不对10．（5分）已知函数，y=g（x）为k（x）=lnx+a+1在x=1处的切线方程，若方程f（x）﹣g（x）=0有且只有两个不相等的实数根，则实数a的取值范围是（）A．（﹣∞，1）B．（﹣∞，1]C．（0，1） D．[0，+∞）二、填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡上的相应横线上.11．（5分）已知x，y满足不等式组，则目标函数z=2x+y的最大值为．12．（5分）已知、均为单位向量，它们的夹角为60°，那么|+3|等于．13．（5分）．14．（5分）已知正项等比数列{a n}的公比q=2，若存在两项a m，a n，使得=4a1，则+的最小值为．15．（5分）定义在R上的函数f（x）满足f（x+6）=f（x）．当﹣3≤x＜﹣1时，当f（x）=﹣（x+2）2，当﹣1≤x＜3时．f（x）=x，则f（1）+f（2）+f（3）+…+f （2015）=．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.16．（12分）函数f（x）=Asin（ωx+φ）部分图象如图所示．（Ⅰ）求f（x）的最小正周期及解析式；（Ⅱ）设g（x）=f（x）﹣cos2x，求函数g（x）在区间上的最大值和最小值．17．（12分）已知向量，．（Ⅰ）若x，y∈R，且1≤x≤6，1≤y≤6，求满足的概率．（Ⅱ）若x，y分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时第一次、第二次出现的点数，求满足的概率．18．（12分）如图所示的长方体ABCD﹣A1B1C1D1中，底面ABCD是边长为2的正方形，O为AC与BD的交点，BB1=，M是线段B1D1的中点．（1）求证：BM∥平面D1AC；（2）求三棱锥D1﹣AB1C的体积．19．（13分）设数列{a n}的前n项和为S n，a1=1，且对任意正整数n，点（a n+1，S n）在直线2x+y﹣2=0上．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）是否存在实数λ，使得数列{S n+λ•n+}为等差数列？若存在，求出λ的值；若不存在，则说明理由．20．（13分）在平面直角坐标系xOy中，O为坐标原点，以O为圆心的圆与直线x﹣y﹣4=0相切．（Ⅰ）求圆O的方程；（Ⅱ）若直线l：y=kx+3与圆C交于A，B两点，在圆C上是否存在一点M，使得=+，若存在，求出此时直线l的斜率；若不存在，说明理由．21．（13分）已知函数f（x）=（x2﹣2x）•lnx+ax2+2．（Ⅰ）当a=﹣1时，求f（x）在（1，f（1））处的切线方程；（Ⅱ）当a=1时，设函数g（x）=f（x）﹣x﹣2，若，都有g（x）≤m恒成立，求m的取值范围．2014-2015学年湖南省怀化市高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共计50分，在每小题给出的四个选项中，只有一项符合题目要求，请把正确答案的代号填在答题卡上. 1．（5分）已知全集U={0，1，2，3，4，5}集合A={1，2，3，5}，B={2，4}，则（∁U A）∪B为（）A．{0，2，4}B．{2，3，5}C．{1，2，4}D．{0，2，3，5}【解答】解：∵全集U={0，1，2，3，4，5}，集合A={1，2，3，5}，∴∁U A={0，4}，∵B={2，4}，∴（∁U A）∪B={0，2，4}．故选：A．2．（5分）给定函数①y=x，②y=log x，③y=|x﹣1|，④y=2x，其中在区间（0，1）上单调递减的函数序号是（）A．①②B．②③C．③④D．①④【解答】解：选项①y=x在（0，+∞）上单调递增，不存在减区间，故错误；选项②y=log x，在（0，+∞）上单调递减，故正确；选项选项③y=|x﹣1|在（﹣∞，1）单调递减，故正确；选项④y=2x在R上单调递增，无递减区间，故错误．故选：B．3．（5分）“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：当α=时，cos2，反之，当时，可得⇒，k∈Z，或⇒，“”是“”的充分而不必要条件．故选：A．4．（5分）函数f（x）=1﹣2sin22x的最小正周期是（）A．B．πC．2πD．4π【解答】解：由题意可得：f（x）=cos4x，所以周期为T==．故选：A．5．（5分）一个锥体的主视图和左视图如图所示，下面选项中，不可能是该锥体的俯视图的是（）A．B．C．D．【解答】解：本题中给出了正视图与左视图，故可以根据正视图与俯视图长对正，左视图与俯视图宽相等来找出正确选项A中的视图满足三视图的作法规则；B中的视图满足三视图的作法规则；C中的视图不满足三视图的作法规则中的宽相等，故其为错误选项；D中的视图满足三视图的作法规则；故选：C．6．（5分）运行如图的程序框图，则输出s的结果是（）A．B．C．D．【解答】解：当n=2时，满足进入循环的条件，执行循环体后，S=，n=4；当n=4时，满足进入循环的条件，执行循环体后，S=，n=6；当n=6时，满足进入循环的条件，执行循环体后，S=，n=8；当n=8时，满足进入循环的条件，执行循环体后，S=，n=10；当n=10时，不满足进入循环的条件，故输出的S值为，故选：B．7．（5分）已知=（λ，2），=（﹣3，5），且与的夹角为锐角，则λ的取值范围（）A．λ＜B．λ≥C．λ＜且λ≠﹣D．λ≤且λ≠﹣【解答】解：由题意可得•＞0，且与不共线，即﹣3λ+10＞0，且，5λ≠2×（﹣3），解得λ＜且λ≠﹣，故选：C．8．（5分）已知a≠0直线ax+（b+2）y+4=0与直线ax+（b﹣2）y﹣3=0互相垂直，则ab的最大值等于（）A．0 B．2 C．4 D．【解答】解：解法一：若b=2，两直线方程为y=﹣x﹣1和x=，此时两直线相交但不垂直．若b=﹣2，两直线方程为x=﹣和y=x﹣，此时两直线相交但不垂直．所以当b≠±2时，两直线方程为y=﹣﹣和y=﹣，此时两直线的斜率分别为﹣、﹣，由﹣（﹣）=﹣1，求得a2+b2=4．因为a2+b2=4≥2ab，所以ab≤2，即ab的最大值等2，当且仅当a=b=时取等号．故选：B．解法二：∵已知a≠0，直线ax+（b+2）y+4=0与直线ax+（b﹣2）y﹣3=0互相垂直，∴a2+（b+2）•（b﹣2）=0，即a2+b2=4．因为a2+b2=4≥2ab，所以ab≤2，即ab的最大值等2，当且仅当a=b=时取等号．故选：B．9．（5分）已知曲线y=在点P（1，4）处的切线与直线l平行且距离为，则直线l的方程为（）A．4x﹣y+9=0或4x﹣y+25=0 B．4x﹣y+9=0C．4x+y+9=0或4x+y﹣25=0 D．以上都不对【解答】解：因为曲线y=，所以y′=﹣，所以在点P（1，4）处的切线的斜率为﹣4，方程为4x+y﹣8=0，与直线l平行且距离为的直线方程为4x+y+c=0，则=，所以c=9或﹣25，因此直线的方程为4x+y+9=0或4x+y﹣25=0，故选：C．10．（5分）已知函数，y=g（x）为k（x）=lnx+a+1在x=1处的切线方程，若方程f（x）﹣g（x）=0有且只有两个不相等的实数根，则实数a的取值范围是（）A．（﹣∞，1）B．（﹣∞，1]C．（0，1） D．[0，+∞）【解答】解：∵k（x）=lnx+a+1，∴k′（x）=，k（1）=a+1，∴k′（1）=1，∴k（x）=lnx+a+1在x=1处的切线方程为y﹣a﹣1=x﹣1，∴g（x）=x+a．函数的图象如图所示，当a＜1时，函数y=f（x）的图象与函数y=x+a的图象有两个交点，即方程f（x）=x+a有且只有两个不相等的实数根．所以实数a的取值范围是（﹣∞，1）．故选：A．二、填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡上的相应横线上.11．（5分）已知x，y满足不等式组，则目标函数z=2x+y的最大值为6．【解答】6解：作出不等式组对应的平面区域如图：（阴影部分）．由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，此时z最大．由，解得，即A（2，2），代入目标函数z=2x+y得z=2×2+2=6．即目标函数z=2x+y的最大值为6．故答案为：6．12．（5分）已知、均为单位向量，它们的夹角为60°，那么|+3|等于．【解答】解；∵，均为单位向量，∴||=1，||=1又∵两向量的夹角为60°，∴=||||cos60°=∴|+3|===故答案为13．（5分）[kπ+，kπ+]，k ∈z ．【解答】解：由于函数y=2sin （﹣2x ）=﹣2sin （2x ﹣），故本题即求y=2sin（2x ﹣）的减区间．令 2kπ+≤2x ﹣≤2kπ+，k ∈z ，求得 kπ+≤x ≤kπ+，k ∈z ，故y=2sin （2x ﹣）的减区间为[kπ+，kπ+]，k ∈z ，故答案为[kπ+，kπ+]，k ∈z ．14．（5分）已知正项等比数列{a n }的公比q=2，若存在两项a m ，a n ，使得=4a 1，则+的最小值为．【解答】解：正项等比数列{a n }的公比q=2， ∵存在两项am ，a n ，使得=4a 1，∴=4a 1，∵a 1≠0， ∴2m +n ﹣2=24， ∴m +n=6．则+=（m +n ）（）==，当且仅当n=2m=4时取等号．∴+的最小值为．故答案为：．15．（5分）定义在R 上的函数f （x ）满足f （x +6）=f （x ）．当﹣3≤x ＜﹣1时，当f （x ）=﹣（x +2）2，当﹣1≤x ＜3时．f （x ）=x ，则f （1）+f （2）+f （3）+…+f （2015）= 336 ．【解答】解：∵f （x +6）=f （x ）， ∴T=6，∵当﹣3≤x＜﹣1时，当f（x）=﹣（x+2）2，当﹣1≤x＜3时．f（x）=x，∴f（1）=1，f（2）=2f（3）=f（﹣3）=﹣1，f（4）=f（﹣2）=0，f（5）=f（﹣1）=﹣1，f（6）=f（0）=0，∴f（1）+f（2）+f（3）+f（4）+f（5）+f（6）=1；f（1）+f（2）+f（3）+…+f（2015）=335×1+f（1）+f（2）+f（3）+f（4）+f（5）=336故答案为：336．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.16．（12分）函数f（x）=Asin（ωx+φ）部分图象如图所示．（Ⅰ）求f（x）的最小正周期及解析式；（Ⅱ）设g（x）=f（x）﹣cos2x，求函数g（x）在区间上的最大值和最小值．【解答】解：（Ⅰ）由图可得A=1，，所以T=π．（2分）所以ω=2．当时，f（x）=1，可得，因为，所以．（5分）所以f（x）的解析式为．（6分）（Ⅱ）===．（10分）因为，所以．当，即时，g（x）有最大值，最大值为1；当，即x=0时，g（x）有最小值，最小值为．（13分）17．（12分）已知向量，．（Ⅰ）若x，y∈R，且1≤x≤6，1≤y≤6，求满足的概率．（Ⅱ）若x，y分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时第一次、第二次出现的点数，求满足的概率．【解答】解：（Ⅰ）用B表示事件“”，即x﹣2y＞0…（1分）试验的全部结果所构成的区域为{（x，y）|1≤x≤6，1≤y≤6}，…（3分）构成事件B的区域为{（x，y）|1≤x≤6，1≤y≤6，x﹣2y＞0}，如图所示…（5分）所以所求的概率为P（B）=…（6分）（Ⅱ）设（x，y）表示一个基本事件，则抛掷两次骰子的所有基本事件有（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），…，（6，5），（6，6），共36个．…（8分）用A表示事件“”，即x﹣2y=﹣1…（9分）则A包含的基本事件有（1，1），（3，2），（5，3），共3个…（10分）∴P（A）=…（12分）18．（12分）如图所示的长方体ABCD﹣A1B1C1D1中，底面ABCD是边长为2的正方形，O为AC与BD的交点，BB1=，M是线段B1D1的中点．（1）求证：BM∥平面D1AC；（2）求三棱锥D1﹣AB1C的体积．【解答】解：（Ⅰ）连接D1O，如图，∵O、M分别是BD、B1D1的中点，BD1D1B是矩形，∴四边形D1OBM是平行四边形，∴D1O∥BM．（2分）∵D1O⊂平面D1AC，BM⊄平面D1AC，∴BM∥平面D1AC．（4分）（Ⅱ）连接OB 1，∵正方形ABCD的边长为2，，∴，OB 1=2，D1O=2，则OB12+D1O2=B1D12，∴OB1⊥D1O．（6分）又∵在长方体ABCD﹣A1B1C1D1中，AC⊥BD，AC⊥D1D，且BD∩D1D=D，∴AC⊥平面BDD1B1，又D1O⊂平面BDD1B1，∴AC⊥D1O，又AC∩OB1=O，（10分）∴D1O⊥平面AB1C，即D1O为三棱锥D1﹣AB1C的高．（12分）∵，D1O=2∴．14（5分）19．（13分）设数列{a n}的前n项和为S n，a1=1，且对任意正整数n，点（a n+1，S n）在直线2x+y﹣2=0上．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）是否存在实数λ，使得数列{S n+λ•n+}为等差数列？若存在，求出λ的值；若不存在，则说明理由．【解答】解：（Ⅰ）∵点（a n+1，S n）在直线2x+y﹣2=0上，∴2a n+1+S n ﹣2=0．①n≥2时，2a n+s n﹣1﹣2=0．②①─②得2a n+1﹣2a n+a n=0，∴=（n≥2）．再由a1=1，可得a2=．∴{a n}是首项为1，公比为的等比数列，∴a n =．（Ⅱ）由（Ⅰ）可得s n==2﹣．若数列{S n+λ•n+}为等差数列，则s1+λ+，s2+2λ+，s3+3λ+成等差数列，∴2（s2+2λ+）=（s1+λ+）+（s3+3λ+），解得λ=2．又λ=2时，S n+λ•n+=2n+2，显然{2n+2}成等差数列，故存在实数λ=2，使得数列{S n+λ•n+}成等差数列．20．（13分）在平面直角坐标系xOy中，O为坐标原点，以O为圆心的圆与直线x﹣y﹣4=0相切．（Ⅰ）求圆O的方程；（Ⅱ）若直线l：y=kx+3与圆C交于A，B两点，在圆C上是否存在一点M，使得=+，若存在，求出此时直线l的斜率；若不存在，说明理由．【解答】解：（Ⅰ）设圆O的半径为r，圆心为（0，0），∵直线x﹣y﹣4=0与圆O相切，∴d=r==2，…（3分）∴圆O的方程为x2+y2=4；…（5分）（Ⅱ）在圆O上存在一点M，使得=+，理由为：法1：∵直线l：y=kx+3与圆O相交于A，B两点，∴圆心O到直线l的距离d=＜r=2，解得：k＞或k＜﹣，…（7分）假设存在点M，使得=+，∴四边形OAMB为菱形，…（8分）∴OM与AB互相垂直且平分，…（9分）∴圆心O到直线l：y=kx+3的距离d=|OM|=1，…（10分）即d==1，整理得：k2=8，…（11分）解得：k=±2，经验证满足条件，…（12分）则存在点M，使得=+；…（13分）法2：记OM与AB交于点C（x0，y0），∵直线l斜率为k，显然k≠0，∴OM直线方程为y=﹣x，…（7分）将直线l与直线OM联立得，解得；∴点M坐标为（，），…（9分）又点M在圆上，将M坐标代入圆方程得：+=4，解得：k2=8，…（11分）∴k=±2，经验证满足条件，…（12分）则存在点M，使得=+．…（13分）21．（13分）已知函数f（x）=（x2﹣2x）•lnx+ax2+2．（Ⅰ）当a=﹣1时，求f（x）在（1，f（1））处的切线方程；（Ⅱ）当a=1时，设函数g（x）=f（x）﹣x﹣2，若，都有g（x）≤m恒成立，求m的取值范围．【解答】解：（Ⅰ）当a=﹣1时，f（x）=（x2﹣2x）•lnx﹣x2+2，定义域（0，+∞），f'（x）=（2x﹣2）•lnx+（x﹣2）﹣2x，∴f'（1）=﹣3，又f（1）=1，则f（x）在（1，f（1））处的切线方程3x+y﹣4=0；（Ⅱ）当a=1时，g（x）=（x2﹣2x）•lnx+x2﹣x，若e﹣2＜x＜e，g（x）≤m，只需证明g（x）max≤m，g'（x）=（x﹣1）•（3+2lnx），令g'（x）=0，得x=1或．又∵e﹣2＜x＜e，∴函数g（x）在上单调递增，在上单调递减，在（1，e）上单调递增．又，g（e）=2e2﹣3e，∵，即，∴m≥2e2﹣3e．。

2014年高三期末考试成绩 (进班)

122 134 115 127 109 128 118 123 125 111 126 123 135 121 132 130 121 112 118 128 98 117 113 114 102 100 114 96 105 115 91 105 119 101 102 94 104 102 93 102
班总分年名班名名 3 629 1 1 4 5 1 31 16 17 13 24 6 2 20 9 10 8 36 22 11 32 25 14 15 20 27 30 17 28 26 33 6 29 23 42 19 35 12 37 33 39 38 40 41
111227010602 田若 111227010447 吴枕 111227010604 杨黎 111227010473 杨飞 111227010526 姚伟烨 111227010617 吴伟 111227010527 罗慧 111227010601 姚青青 111227010611 杨礼全 111227010536 姚淞允 111227010616 张绍术 111227010599 杨珍颖 111227010612 吴利民 111227010578 杨长岭 111227010567 张昌良 111227010606 杨文君 111227010570 杨祖慧 111227010605 吴佳桦 111227010600 刘通 111227010541 张成龙 111227010414 杨涛 111227010467 尹婧 111227010609 陈伊轲 111227010618 姚淼 111227010556 杨奕程 111227010569 吴钰欣 111227010539 姚炜 111227010621 张家愿 111227010472 蒲曾钱 111227010615 姚治栗 111227010572 杨咏雪 111227010610 张雪梅 111227010yhr 姚厚任 111227010537 吴明蔚 111227010573 金有士 111227010538 张家异 111227010574 杨晋 111227010577 杨铠源 111227010589 吴臻 111227010591 陈鹏

怀化2014高考分数线发布

怀化2014高考分数线发布
考试是笔杆上的战争，考生们个个都摩拳擦掌希望挤进1本的大门，高考频道将第一时间发布2014年xx各批次的高考分数线，请广大考生关注本网站。

参考历年怀化高考录取查询分数线（提示：怀化高考为统考，分数线为全省统一），详情如下：
高考网温馨提示：
冷门里也可“挖金子”
“哪个专业是热门专业，未来就业好?”当考生和家长为热门专业挤破头时，在招生办老师眼里，还有很多冷门专业是“闪闪发光的金子”。

“大家都喜欢挑名字好听的专业，其实不少工科、制造类就业前景都非常好。

”周长江说，比如广西大学资环学院的矿物资源工程专业，毕业生每年供不应求。

有些专业大家感觉冷门，如环境科学、统计学、学前教育、文化产业管理等，但实际上就业形势趋好。

考生社会阅历不丰富，对于就业状况了解少，考虑不全面，需要听取家长的意见。

但家长既要考虑到就业好，同时也要结合到考生的个性、兴趣爱好。

否则任何一个单方行动，都会留下遗憾。

湖南省怀化市高三文综第二次模拟考试试题

湖南省怀化市2013届高三文综第二次模拟考试试题注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整，笔迹清楚。

3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．作选做题时，考生按题目要求作答。

本试题卷共14页，如有缺页，考生须声明，否则后果自负。

2013年怀化市高三第二次模拟考试统一检测试卷文科综合命题：怀化三中张淑芳审题：市教科院王新建邱续发刘勇怀化三中李英怀铁一中唐玉怀化三中吴敏怀化五中曾劲松怀化一中贺显华王春华会同一中张自忠靖州一中张声健本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第42—48题为选考题，其它题为必考题。

考生作答时将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

第I卷本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

今年是巴拿马运河开通100周年。

1913年10月10日，巴拿马运河的最后一部分通道打开了，小船开始可以穿过运河，1914年8月15日巴拿马运河正式通航。

建有船闸的巴拿马运河开通，极大缩减了大西洋与太平洋间的航程。

读图，回答第1～2题。

1．运河上修建船闸，可以A．拦河蓄水，减轻洪涝B．抬高水位，利于发电C．克服水位落差，利于航行D．减慢水流速度，减少流量2. 影响该运河航运的自然条件主要为A．多暴雨和大雾B．全年高温炎热C．多飓风D．运输量大气候学上通常以候平均温度（每5日的平均气温）作为季节的划分标准：候温高于 22^C的时期为夏季，低于10°C为冬季，介于二者之间的为春季和秋季。

湖南省怀化市2014届高三第二次模拟考试文科数学试卷(带解析)

湖南省怀化市2014届高三第二次模拟考试文科数学试卷（带解析）1．复数11z i=+ 的模为（）A.12【答案】B 【解析】试题分析：111z i i=+=-，z ∴==，故选B.考点：1.复数的除法；2.复数的模2．设:f x x →是集合A 到集合B 的映射，若{}1,0,1A =-，则A B 为（）A.{}0B.{}1C.{}0,1D.{}1,0,1- 【答案】C 【解析】试题分析：根据映射的定义可得{}0,1B =，因此{}0,1A B =，故选C.考点：1.映射的定义；2.集合的运算 3．下列有关命题的说法中错误的是A.若“p q ∧”为真命题，则p 、q 均为真命题B.若命题:p “x R ∃∈，20x ≥”则命题p ⌝为“x R ∀∈，20x <”C.“2x >”是“0x ≥”的充分不必要条件D.“1sin 2x =”的必要不充分条件是“6x π=” 【答案】D【解析】试题分析：对于A 选项，若“p q ∧”为真命题，当且两个命题均为真命题，A 选项正确；对于B 选项，由特称命题的否定可知B 选项正确；对于C 选项，由集合的包含关系可知，20x x >⇒≥，但20x x >⇐>/，故命题C 正确；对于D 选项，1sin 26x x π=⇒=/，且1sin 26x x π=⇐=，因此“6x π=”是“1sin 2x =”的一个充分不必要条件，故D 选项正确.考点：1.复合命题；2.命题的否定；3.充分必要条件4．已知某几何体的三视图如图所示，若该几何体的体积为24，则正视图中a 的值为（） A.8 B.6 C.4 D.2【答案】B 【解析】试题分析：由三视图可知，该几何体是以底面是矩形的四棱锥，且底面积为3S a =,，三棱锥的高为4，因此四棱锥的体积为1143442433V S a a =⋅=⨯⨯==，解得6a =，故选B. 考点：1.三视图；2.空间几何体的体积5．已知a 、b 都是正实数，函数2x y ae b =+的图象过()0,1点，则11a b+的最小值是（）A.3+3-4 D.2 【答案】A 【解析】试题分析：由题意知21a b +=，()111122333a b a b a b a b b a ⎛⎫∴+=+⋅+=++≥++ ⎪⎝⎭11a b+的最小值是3+ A. 考点：基本不等式6．将函数()sin 2y x ϕ=+的图象沿x 轴向左平移6π个单位后，得到一个关于y 轴对称的图象，则ϕ的一个可能取值为（） A.3π B.6π C.3π- D.6π-【答案】B【解析】试题分析：将函数()sin 2y x ϕ=+的图象向左平移6π个单位后，得到的函数的解析式为()f x =sin 2sin 263x x ππϕϕ⎡⎤⎛⎫⎛⎫++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，由于函数()f x 的图象关于y 轴对称，则()0sin 3f πϕ⎛⎫=+ ⎪⎝⎭1=±，因此()32k k Z ππϕπ+=+∈，()6k k Z πϕπ∴=+∈，取0k =得到ϕ的一个取值为6π，故选B. 考点：1.三角函数图象变换；2.三角函数图象的对称性7．若1a =，2b =，且()a b a +⊥，则a 与b 的夹角是（） A.6π B.3π C.56π D.23π【答案】D【解析】试题分析：()()200a b a a b a a a b +⊥⇔+⋅=⇔+⋅=，即2c o s 0a a b θ+⋅⋅=（其中θ为a 与b 的夹角），即21112cos 0cos 2θθ+⨯⨯=⇒=-，由于0θπ≤≤，解得23πθ=，故选D.考点：平面向量数量积8．已知双曲线22214x y b-=的右焦点与抛物线212yx =的焦点重合,则该双曲线的焦点到其渐近线的距离为（）3 D.5 【答案】A 【解析】试题分析：抛物线212y x =的焦点坐标为()3,0，因此双曲线的右焦点的坐标也为()3,0，所以2243b +=，解得b =02x =20y ±=，因此双曲线的焦点到其渐近线的距离为d == A.考点：1.双曲线的几何性质；2.点到直线的距离9．一个算法的程序框图如图所示，其输出结果是（）A.0B.2C.12+1【答案】B 【解析】试题分析：12014n =≤不成立，执行第一次循环，sin4S π=，112n =+=；22014n =≤不成立，执行第二次循环，2sinsin44S ππ=+，213n =+=；32014n =≤不成立，执行第三次循环，23sin sin sin 444S πππ=++，314n =+=；依此类推，执行最后一次循环， 232014sin sin sin sin 4444S ππππ=++++，201412015n =+=； 20152014n =≤不成立，跳出循环体，输出232014s i n s i n s i n s i n 4444S ππππ=++++，下面来计算232014sin sin sin sin 4444S ππππ=++++，构造数列{}n a ，其中sin 4n n a π=，则数列{}n a 的周期为284T ππ==，而S 为数列{}n a 的前2014项和，易求得12380a a a a ++++=，由于20142518=⨯+，因此()()12251S a a a a a a a a a a a a a a a a =⨯++++++++++=+++++()23456sinsinsin sin sin sin 101444444ππππππ⎛=+++++=+++-= ⎝⎭，故选B.考点：1.算法与程序框图；2.三角函数的周期性10．设定义域为()0,+∞的单调函数()f x ，对任意的()0,x ∈+∞，都有()2l o g 3f f x x-=⎡⎤⎣⎦，若0x 是方程()()2f x f x '-=的一个解，则0x 可能存在的区间是（）A.()0,1B.()1,2C.()2,3D.()3,4 【答案】B 【解析】试题分析：由于函数()f x 在其定义域()0,+∞上单调，则存在唯一实数()0,c ∈+∞使得()3f c =，对任意的()0,x ∈+∞，都有()2log 3f f x x -=⎡⎤⎣⎦，则()()22log log f x x c f x x c -=⇒=+，由于()3f c =，因此2log 3c c +=，因为函数()2log g x x x =+在区间()0,+∞上单调递增，且()23g =，所以2c =，故()2log 2f x x =+，令()()()212l o g l n2h x f x f x x x '=--=-，则()h x 在区间()0,+∞上单调递增，且()10g <，()20g >，故()01,2x ∈，故选B. 考点：1.零点存在定理；2.函数的单调性11．在平面直角坐标系xOy 中，已知曲线1cos :sin x C y θθ=⎧⎨=⎩（θ为参数），将曲线1C 上的所有点的横坐标、纵坐标分别伸长为原来的、2倍后得到曲线2C 的直角坐标方程为 .【答案】22134x y +=. 【解析】试题分析：易得曲线1C 的普通方程为221x y +=，在曲线221x y +=，在曲线221x y +=上任取一点(),x y ''，经过坐标变换后对应的点坐标为(),x y ，则有322xxy y yy⎧'=⎪⎧'=⎪⎪⇒⎨⎨'=⎪⎩⎪'=⎪⎩，由于点(),x y''在曲线221x y+=，则有()()221x y''+=，于是有2212y⎛⎫+=⎪⎝⎭⎝⎭，化简后得22134x y+=，即曲线2C的方程为22134x y+=.考点：1.参数方程；2.坐标变换12．已知等比数列{}n a的公比2q=，其前4项和460S=，则2a= .【答案】8.【解析】试题分析：()()441141111215604112a q aS a aq--====⇒=--，21428a a q∴==⨯=.考点：等比数列的定义与求和13．一只昆虫在边长分别为5、12、13的三角形区域内随机爬行，则其到三角形顶点的距离小于2的地方的概率为 .【答案】15π.【解析】试题分析：如下图所示，易知三角形为直角三角形，昆虫爬行的区域是在三角形区域内到以各顶点为圆心，半径为2的圆在三角形区域内的部分，实际上就是三个扇形，将这三个扇形拼接起来就是一个半圆，其半径长为2，面积为21222Sππ'=⨯=，三角形的面积为1512302S=⨯⨯=，因此昆虫爬行时到三角形顶点的距离小于2的地方的概率为23015SPSππ'===.考点：几何概型14．已知实数x、y满足约束条件2025020x yx yy--≤⎧⎪+-≥⎨⎪-≤⎩，则2x yzx+=的最小值是 .【答案】73.【解析】试题分析：作出不等式组2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩所表示的可行域如下图所示，22x y y z x x +==+，令yk x=，则2z k =+，k 为原点与点(),x y 之间连线的斜率，直线20x y --=与直线25x y +=交于点()3,1A ，显然，直线OA 的倾斜角最小，且为锐角，此时k 取最大值，即max 13k =，因此，min 17233z =+=. 考点：1.线性规划；2.斜率15．已知()21211nn n x a x a x a x +=++++，n N *∈且122n n S a a na =+++，n N *∈，当3n =时，3S = ；当n N *∈时，1nii S==∑ .【答案】12；()121nn -⋅+.【解析】试题分析：在等式()21211nn n x a x a x a x +=++++两边求导得()111212n n n n x a a x na x --+=+++，令1x =得，11222n n n S a a na n -=+++=⋅，所以233212S =⨯=，011112222nn ii Sn -==⨯+⨯++⋅∑，令01112222n n T n -=⨯+⨯++⋅，则()11212122n n n T n n -=⨯++-⋅+⋅，下式-上式，得()()01101111222222222212n n n n n n n T n n n ---=----+⋅=⋅-+++=⋅--()()221121nnnn n =⋅--=-⋅+，()1121nn i i S n =∴=-⋅+∑.考点：1.导数；2.错位相减法求和16．某广告公司设计一个凸八边形的商标，它的中间是一个正方形，外面是四个腰长为1，顶角为2α的等腰三角形. （1）若角223πα=时，求该八边形的面积；（2）写出α的取值范围，当α取何值时该八边形的面积最大，并求出最大面积.【答案】（1）3（2）0,2πα⎛⎫∈ ⎪⎝⎭，当38πα=时，八边形的面积取最大值3+ 【解析】试题分析：（1）先利用223πα=结合余弦定理确定正方形的边长，然后将八边形分为一个正方形与四个等腰三角形求面积，最后将面积相加得到八边形的面积；（2）利用()20,απ∈得到角α的取值范围，利用正弦定理求出正方形的边长（利用含α的代数式表示），然后利用面积公式求出八边形的面积关于α的三角函数，结合降幂公式、辅助角公式将三角函数解析式进行化简，最后求出相应函数在区间0,2π⎛⎫⎪⎝⎭的最大值.（1）由题可得正方形边长为211211sin 3423S π=+⨯⨯⨯⨯= （2）显然02απ<<，所以02πα<<，()211cos 22sin 4sin 242sin 222S αααα-=+⨯⨯=⨯+224πα⎛⎫=+- ⎪⎝⎭，02πα<<，32444πππα-<-<，故sin 214πα⎛⎫<-≤ ⎪⎝⎭，max 2S ∴=+38πα=. 考点：1.三角形的面积；2.二倍角；3.辅助角公式；4.三角函数的最值17．2013年11月，青岛发生输油管道爆炸事故造成胶州湾局部污染．国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作，有关数据见表1（单位：人）海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响，随机选取了110只海豚进行了检测，并将有关数据整理为不完整的22⨯列联表，如表2. （1）求研究小组的总人数；（2）写出表2中A 、B 、C 、D 、E 的值，并判断有多大的把握认为海豚身体不健康与受到污染有关；（3）若从研究小组的环保专家和海洋生物专家中随机选2人撰写研究报告，求其中恰好有1人为环保专家的概率.附：①()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.②【答案】（1）12；（2）20A =，50B =，80C =，30D =，110E =，99%；（3）815. 【解析】试题分析：（1）先根据分层抽样列方程求出x 和y 的值，从而求出所抽取的总人数；（2）根据表中数据求出A 、B 、C 、D 、E 的值，然后根据独立性检验的基本思想求出犯错误的概率，从而得到相关性的把握；（3）利用列举法求出所有的基本事件数以及问题中涉及的事件所包含的基本事件数，最后利用古典概型的概率计算公式求出相应事件的概率.（1）由题意知6244872x y ==，解得2x =，4y =，所以总人数为24612++=；（2）由题意得3050A +=，1060B +=，30B C +=，10A D +=，110E =，解得20A =，50B =，80C =，30D =，110E =，()22110301050207.846 6.63550608030K ⨯⨯-⨯=≈>⨯⨯⨯，因此，大约有99%的把握认为海豚身体不健康与受到污染有关；（3）设所抽取的两名环保专家记为1a 、2a ，4名海洋专家记为1b 、2b 、3b 、4b ，则所有的基本事件有：()12,a a 、()11,a b 、()12,a b 、()13,a b 、()14,a b 、()21,a b 、()22,a b 、()23,a b 、()24,a b 、()12,b b 、()13,b b 、()14,b b 、()23,b b 、()24,b b 、()34,b b ，记事件A ：从研究小组的环保专家和海洋生物专家中随机选2人撰写研究报告求其中恰好有1人为环保专家，则事件A 所包含的基本事件有： ()11,a b 、()12,a b 、()13,a b 、()14,a b 、()21,a b 、()22,a b 、()23,a b 、()24,a b ，共8个，因此，()815P A =. 考点：1.分层抽样；2.独立性检验；3.古典概型18．如图，在直三棱柱111ABC A B C -中，AB AC ==90BAC ∠=，且异面直线1A B 与11B C 所成的角等于60.（1）求棱柱的高；（2）求11B C 与平面11A BC 所成的角的大小.【答案】（1（2）6π. 【解析】试题分析：（1）由11Rt A AB Rt A AC ∆≅∆得到11A B AC =，借助11//BC BC 异面直线1A B 与11B C 所成的角等于1A AC ∠，进而说明1A AC ∆为等边三角形，得出1A B 的长度后再利用勾股定理求出1BB 的长，从而得到棱柱的高；（2）连接1A B 交1AB 于点O ，利用直线与平面垂直的判定定理证明1B O ⊥平面11A BC ，然后连接1OC ，于是得到11B C O ∠即为直线11B C与平面11A BC 所成的角，最终在11Rt B C O ∆中计算相应的边长来求出11B C O ∠的大小. （1）11Rt A AB Rt A AC ∆≅∆，11A B AC ∴=又160A BC ∠=，1A BC ∴∆为正三角形，12A B ∴=，所以棱柱的高为1BB = （2）连接1AB ，11A BAB O =，OC 1B 1A 1CBA11BO A B ⊥，1B O AC ⊥，1B O ∴⊥平面11A BC ， 11B C O ∴∠即为所求，在11Rt B C O ∆中，11BO =，112B C =，116B C O π∴∠=.考点：1.异面直线所成的角；2.直线与平面所成的角19．已知数列{}n a 满足12a =，向量()2,1a =-，()12,nn n b a a +=+且a b ⊥.（1）求证数列2n n a ⎧⎫⎨⎬⎩⎭为等差数列，并求{}n a 通项公式；（2）设()21nn a b n n =+，若对任意n N *∈都有239n m mb ->成立，求实数m 的取值范围. 【答案】（1）2n n a n =⋅；（2）()1,4-. 【解析】试题分析：（1）先利用向量垂直结合向量坐标运算得到1122n n n a a ++=+，并在等式两边同时除以12n +得到11122n n n na a ++=+，结合定义证明数列2n n a ⎧⎫⎨⎬⎩⎭为等差数列，并确定其首项和公差，求出数列2n n a ⎧⎫⎨⎬⎩⎭的通项公式，进而求出数列{}n a 的通项公式；（2）先确定数列{}n b 的通项公式，将不等式239n m m b ->等价转化为()2min 39n m mb ->，利用作商法研究数列{}n b 的单调性，并确定数列{}n b 的最小项，解不等式()min n b >239m m-求出实数m 的取值范围. （1）因为a b ⊥，所以()1220nn n a a ++-=，即1122n n n a a ++=+，11122n nn na a ++∴=+，所以数列2n na ⎧⎫⎨⎬⎩⎭为等差数列，且()11122n n a a n n =+-⨯=，2nn a n ∴=⋅；（2）可知()221nn b n =+，令211212n n b n b n ++⎛⎫=> ⎪+⎝⎭，得22n n >⇒> 即当2n ≥，n N *∈，都有23n b b b <<<，而121429b b =>=，故()min 49n b =，从而23499m m -<，解得14m -<<. 考点：1.定义法证明等差数列；2.数列的单调性；3.数列不等式恒成立20．如图，椭圆()222210x y a b a b+=>>的长轴长为4，点A 、B 、C 为椭圆上的三个点，A 为椭圆的右端点，BC 过中心O ，且2BC AB =，3ABC S ∆=．（1）求椭圆的标准方程；（2）设P 、Q 是椭圆上位于直线AC 同侧的两个动点（异于A 、C ），且满足PBC QBA ∠=∠，试讨论直线BP 与直线BQ 斜率之间的关系，并求证直线PQ 的斜率为定值.【答案】（1）22143x y +=；（2）详见解析. 【解析】试题分析：（1）利用题中条件先得出a 的值，然后利用条件2BC AB =，3ABC S ∆=结合椭圆的对称性得到点B 的坐标，然后将点B 的坐标代入椭圆方程求出b 的值，从而确定椭圆的方程；（2）将条件PBC ∠= QBA ∠得到直线BP 与BQ 的斜率直线的关系（互为相反数），然后设直线BP 的方程为()312y k x -=-，将此直线的方程与椭圆方程联立，求出点P 的坐标，注意到直线BP 与BQ 的斜率之间的关系得到点Q 的坐标，最后再用斜率公式证明直线PQ 的斜率为定值.（1）2BC AB =，1322OAB ABC S S ∆∆∴==，又AOB ∆是等腰三角形，所以31,2B ⎛⎫ ⎪⎝⎭，把B 点代入椭圆方程22214x y b +=，求得23b =，所以椭圆方程为22143x y +=；（2）由题易得直线BP 、BQ 斜率均存在，又PBC QBA ∠=∠，所以BP BQ k k =-，设直线()3:12BP y k x -=-代入椭圆方程22143x y +=，化简得()2223348412302k x k k x k k ⎛⎫+--+--= ⎪⎝⎭，其一解为1，另一解为22412334P k k x k --=+，可求221263342P k k y k --=++，用k -代入得22412334Q k k x k +-=+，221263342Q k k y k -+=++， 12P Q PQ P Qy y k x x -∴==-为定值. 考点：1.椭圆的方程；2.直线与椭圆的位置关系；3.两点间连线的斜率 21．设函数()ln f x x ax =-.（1）当0a >时，求函数()f x 在区间[]1,e 内的最大值；（2）当1a =-时，方程()22mf x x =有唯一实数解，求正数m 的值.【答案】（1）详见解析；（2）12. 【解析】试题分析：（1）先求出导数方程()0f x '=的根，对此根与区间[]1,e 的位置关系进行分类讨论，确定函数在区间[]1,e 上的单调性，从而求出函数()f x 在区间[]1,e 上的最大值；（2）构造函数()()22g x x mf x =-，利用导数求出函数()g x的极值点22m x +=()g x 的单调性，得到()()2200g x g x '=⎧⎪⎨=⎪⎩，消去22x 并化简得到222ln 10x x +-=，通过构造函数()2ln 1h x x x =+-并利用导数研究函数()h x 的单调性并结合()10h =，1=，从而求出m 的值.（1）()11ax f x a x x-'=-=，0x >，令()0f x '=得1x a =. 因为10,x a ⎛⎫∈ ⎪⎝⎭时，()0f x '>，1,x a ⎛⎫∈+∞ ⎪⎝⎭时，()0f x '<，所以()f x 在10,a ⎛⎫ ⎪⎝⎭递增，在1,a ⎛⎫+∞ ⎪⎝⎭递减；①当101a<≤时，即1a ≥时，()f x 在[]1,e 上递减，所以1x =时()f x 取最大值()1f a =-； ②当11e a <<时，即11a e <<时，()f x 在11,a ⎛⎫ ⎪⎝⎭递增，在1,e a ⎛⎫⎪⎝⎭递减，所以1x a=时，()f x 取最大值1ln 1f a a ⎛⎫=-- ⎪⎝⎭； ③当1e a ≥即10a e<≤时，()f x 在()1,e 递增，所以x e =时()f x 取最大值()1f e ae =-；（2）因为方程()22mf x x =有唯一实数解，即22ln 20x m x mx --=有唯一实数解，设()22ln 2g x x m x mx =--，则()2222x mx mg x x--'=，令()0g x '=，20x mx m --=，因为0m >，0x >，所以10x =<（舍去），2x = 当()20,x x ∈时，()0g x '<，()g x 在()20,x 上单调递减，当()2,x x ∈+∞时，()0g x '>，()g x 在()2,x +∞上单调递增，所以()g x 最小值为()2g x ，则()()2200g x g x =⎧⎪⎨'=⎪⎩，即2222222ln 200x m x mx x mx m ⎧--=⎨--=⎩，所以222ln 0m x mx m +-=，即222ln 10x x +-=，设()()2ln 10h x x x x =+->，()210h x x'=+> )0(1ln 2)(>-+=x x x x h ，()210h x x=+>恒成立，故()h x 在()0,+∞单调递增， ()0h x =至多有一解，又()10h =，所以21x =1=，解得12m =.考点：1.分类讨论；2.函数的最值；3.函数的零点。

怀化市2014上期高一期考成绩(副)

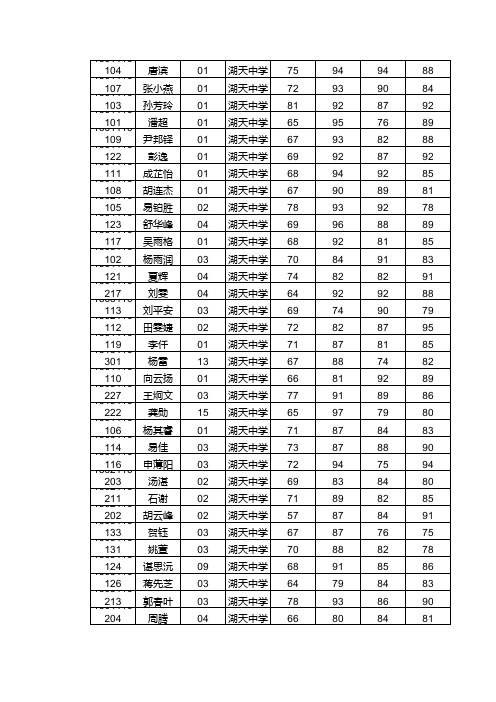
82 74 74 87 80 84 64 87 73 76 88 87 83 81 76 88 71 74 85 82 79 76 79 85 92 90 80 84 76 72 72 85 87
88 72 82 71 86 86 66 85 73 71 81 68 85 74 85 82 69 70 74 82 84 82 85 89 79 84 75 78 81 74 82 71 78
01 02 02 09 08 14 04 19 04 01 03 15 02 03 03 04 10 01 16 05 04 01 17 07 09 17 04 14 01 05 04 01 04
湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学湖天中学
94 90 87 76 82 87 92 89 92 88 81 91 82 92 90 87 81 74 92 89 79 84 88 75 84 82 84 76 82 85 84 86 84
88 84 92 89 88 92 85 81 78 89 85 83 91 88 79 95 85 82 89 86 80 83 90 94 80 85 91 75 780209 张胜男 1501110219 张康 1501110319 杨凇 1504110115 李佳琳 1505110127 向锦明 1501110132 毛浩然 1502110221 邬栩 1509110234 蒲丽淇 1504110208 蒋美玲 1502110120 谭林华 1503110207 蒋雅霖 1503110321 宋谋虓 1502110218 杨冉诗雨 1502110130 石磊 1504110214 张小钰 1503110135 马嘉 1512110125 贺志翔 1503110331 肖博文 1501110226 唐洋 1501110318 张楚东 1504110313 彭群群 1512110134 宋梦瑶 1503110215 张凌之 1501110210 陈彦东 1516110411 曾贵阳 1504110212 黄苑文 1507110302 颜慧琪 1502110332 覃佳宇 1508110205 彭馨莹 1504110118 聂宏运 1511110232 舒琴 1501110206 胡杨杰 1501110128 张若兰

2014年4月高三二模考试文科成绩

13 38 32 13 63 8 38 84 23 1 3 4 54 32 29 32 11 32 63 23 32 9 38 127 127 12 97 112 38 139 84 97 89 97 97 54 121 112 127 63 93 47 123 141 171 243 127 149 187 158 241 145 158 139 226 201
36 5 84 69 11 122 285 193 57 104 474 267 122 42 149 193 193 474 84 224 149 521 434 122 11 267 434 331 724 383 383 224 757 193 24 285 383 866 285 434 681 173 383 833 521 285 564 605 224 285 267 641 69 383 605 474
76 74 80 69 63 56 75 73 58 67 71 67 64 70 68 63 66 66 71 68 51 68 70 67 61 62 65 71 69 78 71 71 65 62 53 71 59 57 50 51 60 66 58 61 60 62 44 59 69 59 64 61 62 56 63 48
59 443 101 1165 153 240 240 240 739 2933 1165 918 38 2306 3621 153 739 578 1410 2306 918 1993 1410 918 739 1410 17 739 1165 59 2933 5537 918 2621 6654 1410 1410 739 1165 1703 1410 5320 2933 2621 918 5 443 1703 5537 2306 2306 3301 6562 2306 1410 1703

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

106 104 108 94 102 108 91 104 103 110 100 113 112 104 103 103 101 102 119 101 97 106 94 102 100 97 88 96 101 105 103 95 94 107 100 97 102 96 90 95 110 84 87 96 108 88 88
11 11 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12
1133 1133 1137 1133 1133 1133 1133 1133 1137 1137 1137 1212 1212 1213 1212 1212 1212 1212 1212 1212 1212 1212 1212 1212 1212 1212 1212 1213 1212 1212 1212 1212 1213 1213 1212 1212 1213 1212 1213 1213 1212 1212 1212 1212 1212 1212 1212
赵芳李佳王侦谭宇明夏之璐唐敏杨财英王赛迪徐艳琪覃美云肖芳菁丁玉林宋慧君阮荣玮田明杨利廖欢欢全俊杰毛昕冉夏雨李骓嶙贺进夏琪琳周可情梁艺凡张显桥向慧陈景周翔汪明静罗金滕诗茹蒋罗丹仇昭君王钦范雅萱张雨萍罗俊林邓思葭张慧粟玛丽米芃昕杨序袁张佳雨姚翔夏迪曾辉
1137110312 1127110314 1133110327 1133110302 1128110413 1137110421 1127110217 1133110416 1133110332 1128110334 1128110410 1133110313 1128110402 1127110304 1133110305 1137110423 1133110409 1133110411 1133110414 1137110329 1137110407 1133110405 1133110417 1133110325 1128110235 1133110415 1137110425 1133110403 1133110408 1133110406 1137110419 1133110427 1133110420 1137110422 1133110603 1133110418 1133110424 1137110430 1133110335 1133110429 1133110609 1133110432 1137110433 1137110601 1133110604 1133110435 1133110607
11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 1 1128 1127 1128 1127 1128 1127 1127 1128 1128 1127 1127 1133 1128 1127 1128 1128 1127 1127 1127 1128 1127 1127 1133 1128 1128 1133 1127 1127 1133 1133 1128 1128 1133 1133 1128 1137 1128 1128 1133 1133 1137 1127 1128 1133
78 101 104 90 92 95 114 89 77 91 92 85 60 91 85 75 77 79 79 72 69 82 90 62 90 59 88 62 82 85 55 98 53 54 66 54 65 72 68 86 51 79 64 61 55 90 51
11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11
怀化市2014上期高三二模成绩（文科）2014.
学校 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 班级 1127 1127 1128 1128 1127 1128 1128 1128 1128 1127 1128 1128 1127 1128 1127 1127 1127 1127 1127 1128 1128 1127 1127 1128 1127 1128 1128 1127 1127 1127 1128 1127 1128 1128 1127 1128 1127 1127 1127 1128 1127 1127 1127 1128 学籍号 1127110103 1127110108 1128110102 1128110113 1127110101 1128110104 1128110121 1128110105 1128110129 1127110114 1128110106 1128110122 1127110123 1128110112 1127110107 1127110116 1127110109 1127110135 1127110119 1128110115 1128110127 1127110206 1127110230 1128110117 1127110120 1128110110 1128110124 1127110111 1127110131 1127110132 1128110126 1127110201 1128110118 1128110125 1127110214 1128110213 1127110219 1127110205 1127110203 1128110301 1127110231 1127110220 1127110215 1128110128 学校怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中姓名杨倩向坤李亚萍田浩月杨洋唐杨杨湘平杨雯惠邱鹏文燕红夏禹李娜杨乐彭傲男陆丽奇杨港李叔忆王玉琴刘皇晏印梦琴郝洺成梦田烨青赵温也杨先贝刘桂芳杨静卢蓉肖继艳蒲书琴米桂芳尹琴怡杨灵芝黄艳红吴素米奠柳菁李文静彭建英田小香黄海涛梁宇峰杨莎陈金莲唐健惠语文 127 116 118 115 106 103 115 117 110 106 108 101 113 111 112 110 113 113 109 110 98 113 109 118 106 102 109 97 100 112 113 102 105 106 112 110 114 105 115 99 109 115 106 107 数学 112 118 110 115 124 117 104 111 111 114 116 121 116 101 109 109 101 104 96 86 117 93 99 93 121 99 102 98 109 81 93 85 74 79 103 90 95 94 79 63 70 97 89 85
李君婷李慧杨金容胡宏唐卉吴慧兰周怡如舒孝舟魏朗向新霖杨雅予粟海棠胡倩倩杨琼谌洁姚淑杨碧娟易兴梓周颖彭雨凌魏婧张玲向朝旭钟巧俊杨小艳何松景孙婕钧张弘艺瞿靓谭芳莲彭怡欣李芷宁陈皓梁佳慧彭柃源潘韵文徐文韬杨国俊赵欢向婕胡连田袁诗贵肖扬彭梦洁丁妹向晓春杨倩
怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中怀化一中
105 96 92 95 95 79 101 101 99 95 113 102 103 90 94 99 109 97 102 96 93 91 104 87 85 94 87 89 95 91 80 95 85 92 82 86 91 85 90 86 86 83 84 78 84 84 75
67 51 69 77 57 68 72 52 51 60 37 44 41 54 55 55 54 49 50 60 68 48 65 39 54 40 59 35 36 61 62 38 47 54 30 51 51 36 31 29 33 40 44 26 37 48 37
1137 1127 1133 1133 1128 1137 1127 1133 1133 1128 1128 1133 1128 1127 1133 1137 1133 1133 1133 1137 1137 1133 1133 1133 1128 1133 1137 1133 1133 1133 1137 1133 1133 1137 1133 1133 1133 1137 1133 1133 1133 1133 1137 1137 1133 1133 1133