自编自控教材习题解答(1).doc
自控第一章习题答案.doc

i -1水箱液im高度控制系统的3种原理方案如图2-i-i所示。
在运行中,希望液面高度H维持不变。
M w W解:(a) ⑶工作原理:当电位器电刷位于中点(对应电压为零)时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度H。
当液面升高时(H>Ho),浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到液面恢复给定高度Ho(H=Ho),电动机的停止转动。
反之,若液面降低(H〈H°),则通过自动控制作用,增大进水阀门开度,加大流入水量,直到液面恢复给定高度Ho(H=Ho) o被控对象:水箱;被控量:水箱的实际水位H;给定量:液位的希望值H。
;干扰量:用水量系统是按偏差调节的闭环控制系统。
系统方块图如图所示:工作原理:当流出水量匾变小时,液面的实际水位H升高(H>Ho),浮子也相应升高,通过杠杆调节阀门从而减小流入的水量Q.使液面逐渐降低,浮子位置也相应下降,直到液面恢复给定高度Ho(H=Ho)o反之,当流出水量Q2变大时,液面的实际水位H降低(IKHo),浮子也相应降低,通过杠杆调节阀门L,从而增大流入的水量Q,使液面逐渐升高,浮子位置也相应升高,直到液面恢复给定高度Ho(H=Ho)o被控对象:水箱;被控量:水箱的实际水位H;给定量:液位的希望值H。
;手排曷.田永昼m系统是按偏差调节的闭环控制系统。
系统方块图如图所示:(c)工作原理:当输出阀门12改变时,通过杠杆调节输入阀门L,改变输入流量Q,使液面高度维持不变(H=H。
)。
被控对象:水箱;被控量:水箱的实际水位H;给定量:液位的希望值H。
;干扰量:输出阀门b系统是按干扰补偿的开环控制系统。
系统方块图如图所示:I - 2仓库大门|'|动控制系统的原理如图 2 - I - 5所示。
自动控制原理习题答案详解

自动控制原理习题答案详解自动控制原理习题详解(上册)第一章习题解答1-2日常生活中反馈无处不在。
人的眼、耳、鼻和各种感觉、触觉器官都是起反馈作用的器官。
试以驾车行驶和伸手取物过程为例,说明人的眼、脑在其中所起的反馈和控制作用。
答:在驾车行驶和伸手取物过程的过程中,人眼和人脑的作用分别如同控制系统中的测量反馈装置和控制器。
在车辆在行驶过程中,司机需要观察道路和行人情况的变化,经大脑处理后,不断对驾驶动作进行调整,才能安全地到达目的地。
同样,人在取物的过程中,需要根据观察到的人手和所取物体间相对位置的变化,调整手的动作姿势,最终拿到物体。
可以想象蒙上双眼取物的困难程度,即使物体的方位已知。
1-3 水箱水位控制系统的原理图如图1-12所示,图中浮子杠杆机构的设计使得水位达到设定高度时,电位器中间抽头的电压输出为零。
描述图1-12所示水位调节系统的工作原理,指出系统中的被控对象、输出量、执行机构、测量装置、给定装置等。
图1-12 水箱水位控制系统原理图答:当实际水位和设定水位不相等时,电位器滑动端的电压不为零,假设实际水位比设定水位低,则电位器滑动端的电压大于零,误差信号大于零(0e >),经功率放大器放大后驱动电动机M 旋转,使进水阀门开度加大,当进水量大于出水量时(12Q Q >),水位开始上升,误差信号逐渐减小,直至实际水位与设定水位相等时,误差信号等于零,电机停止转动,此时,因为阀门开度仍较大,进水量大于出水量,水位会继续上升,导致实际水位比设定水位高,误差信号小于零,使电机反方向旋转,减小进水阀开度。
这样,经反复几次调整后,进水阀开度将被调整在一适当的位置,进水量等于出水量,水位维持在设定值上。
在图1-12所示水位控制系统中,被控对象是水箱,系统输出量水位高,执行机构是功率放大装置、电机和进水阀门,测量装置浮子杠杆机构,给定和比较装置由电位器来完成。
1-4 工作台位置液压控制系统如图1-13所示,该系统可以使工作台按照给定电位器设定的规律运动。
自编自控教材习题解答

自编自控教材习题解答第一章1-2 图1-17 是液位自动控制系统原理示意图。
图中SM为执行电动机。
试分析系统的工作原理,指出该系统参考输入、干扰量、被控对象、被控量、控制器,并画出系统的方框图。
图1-17 习题1-2 液位自动控制系统【解】系统参考输入:预期液位;被控对象:水箱;被控量:水箱液位;控制器:电动机减速器和控制阀门;干扰量:用水流量Q2。
系统的方块图如下1-3在过去,控制系统常常以人作为闭环控制系统的一部分,图1-18是人在回路中的水位控制示意图,试画出该控制系统的方框图。
图1-18 习题1-3 阀门控制系统【解】略1-4图1-19是仓库大门自动控制系统原理图。
试说明系统自动控制大门开闭的工作原理,并画出系统的方块图。
图1-19 习题1-4 仓库大门自动系统【解】1-5 图1-20为水温控制系统示意图。
冷水在热交换器中由通入的蒸汽加热,从而得到一定温度的热水。
冷水流量变化用流量计测量。
试绘制系统方块图,并说明为了保持热水温度为期望值,系统是如何工作的?指出该系统的参考输入、干扰量、被控对象和控制装置各是什么?图1-20 习题1-5 水温控制系统示意图【解】该系统的参考输入:给定温度;干扰量:冷水流量的变化;被控对象:热交换器;被控量:交换器的水温;控制装置:温度控制器,此时控制器的输出不仅与实际水温有关而且和冷水的流量有关,所以该系统不仅是反馈控制而是反馈+前馈的复合控制方式。
它的主要目的是一旦冷水流量增大或减少时,及时调整蒸汽流量,不用等到水温降低会升高后再调节,所以可提高系统对扰动的能力。
实际给定第二章2-2 若某系统在阶跃输入r(t)=1(t)时,零初始条件下的输出响应c(t)=1-e -2t +e -t ,试求系统的传递函数和脉冲响应。
【解】根据传递函数的定义,其传递函数为零初始条件下,输出信号的拉氏变换与输入信号拉氏变换之比,即()1111()()/()21C s G s R s s s s s ==-+++ 242(1)(2)s s s s ++=++ 2-3 设系统传递函数为342)(2++=s s s G初始条件0/)0(,1)0(=-=dt dc c 。
自动控制原理课后习题答案.docx
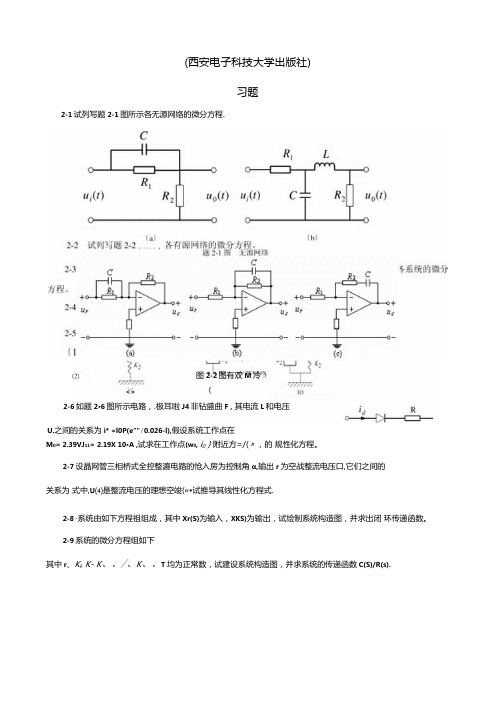
(西安电子科技大学出版社)习题2-1试列写题2-1图所示各无源网络的微分方程.M 0= 2.39VJ 11= 2.19X 10∙A ,试求在工作点(w 0, i 0}附近方=/(〃,的 规性化方程。
2-7设晶网管三相桥式全控整漉电路的怆入房为控制角α,输出r 为空战整流电压口,它们之间的 关系为 式中,U ⑷是整流电压的理想空竣(«•试推导其线性化方程式.2-8 ∙系统由如下方程祖组成,其中Xr(S)为输入,XKS)为输出,试绘制系统构造图,并求出闭 环传递函数。
2-9系统的微分方程组如下其中r 、K l . K- K 、、/、K 、、T 均为正常数,试建设系统构造图,并求系统的传递函数C(S)/R(s).图2-2图有双M 冷 ⑵(W <»U.之间的关系为i* =l0P(e""∕0.026-l),假设系统工作点在 2-6如题2∙6图所示电路,.极耳啦J4非钻盛曲F ,其电流L 和电压2-10试化简即2-10图所示的系统构造图.并求传递函数C(S)11R(S), K(S) C(S)/ C(S) R(S) 筑书规图所材 Gl C(S) G,卡G 5佛与函数 国S) C(S) G) 5 “七; Hl 弟统 £(S) M(S)2-16零初 设某 2-17 g (t) = 7-5e 6f . 咫2∙ 15图求系统 的传速函数, 始条件下的输出响试求该系统的传递 2-18系统的 W'> I 控制系统构造t f 1*1 2-16 W 系统构造图 R(S) ΛU) 2-15 E(S) C (Λ I I - L_rτ∏J ∙13图 系统G:" r ,(5) E(S)凤 F) R ⑸M ⑸松) ⅛4和脉冲响应函数, 单位脉冲响应为。
自控课后答案

2-1 什么是系统的数学模型?在自动控制系统中常见的数学模型形式有哪些? 用来描述系统因果关系的数学表达式,称为系统的数学模型。
常见的数学模型形式有:微分方程、传递函数、状态方程、传递矩阵、结构框图和信号流图。
2-2 简要说明用解析法编写自动控制系统动态微分方程的步骤。
2-3 什么是小偏差线性化?这种方法能够解决哪类问题?在非线性曲线(方程)中的某一个工作点附近,取工作点的一阶导数,作为直线的斜率,来线性化非线性曲线的方法。
2-4 什么是传递函数?定义传递函数的前提条件是什么?为什么要附加这个条件?传递函数有哪些特点?传递函数:在零初始条件下,输出量的拉氏变换与输入量的拉氏变换之比。
定义传递函数的前提条件:当初始条件为零。
为什么要附加这个条件:在零初始条件下,传递函数与微分方程一致。
传递函数有哪些特点:1.传递函数是复变量S 的有理真分式,具有复变函数的所有性质;n m ≤且所有系数均为实数。
2.传递函数是一种有系统参数表示输出量与输入量之间关系的表达式,它只取决于系统或元件的结构和参数,而与输入量的形式无关,也不反映系统内部的任何信息。
3.传递函数与微分方程有相通性。
4.传递函数)(s W 的拉氏反变换是系统的单位脉冲响应。
2-5 列写出传递函数三种常用的表达形式。
并说明什么是系统的阶数、零点、极点和放大倍数。
nn n n mm m m a s a s a s a b s b s b s b s W ++++++++=----11101110)(ΛΛ ()()∏∏==++=nj jmi i s T s T K s W 1111)( 其中nma b K =()()∏∏==++=nj jmi i g p s z s K s W 11)( 其中0a b K g =传递函数分母S 的最高阶次即为系统的阶数,i z -为系统的零点,j p -为系统的极点。
K 为传递函数的放大倍数,g K 为传递函数的根轨迹放大倍数。
自编自控教材习题解答

自控习题及解答第五章5-1问答题:(1) 在Bode 图中采用对数坐标的优点是什么? (2) 如何定义分贝?(3) 截止频率是如何定义的? (4) 如何定义相位裕度(PM )? (5) 如何定义幅值裕度(GM )?(6) 伯德图上什么特征最能体现闭环系统阶跃响应的超调量? (7) 伯德图上什么特征最能体现闭环系统阶跃响应的上升时间? (8) 伯德图上的性能度量上,超前补偿的主要作用是什么? (9) 伯德图上的性能度量上,滞后补偿的主要作用是什么? (10) 怎样从伯德图上找出Ⅰ型系统的K v ?(11) 为什么我们在从奈奎斯特图上确定系统稳定时,要预先知道开环系统不稳定极点的数目?(12) 要求某控制系统能跟踪正弦波,它的频率范围是0≤ω≤450/rad s ,且幅值是5个单位,要求(正弦的)稳态误差不超过0.01,画出(描述)对应的性能函数G (s)。
5-1 设单位负反馈控制系统的开环传递函数为1()21G s s =+ 当下列输入信号作用在闭环系统上时,求系统的稳态输出C ss 。
(1)r(t)=sin2t(2)r(t)=sin(t+300)-2cos(2t -450) 【解】解: 由图可得闭环传递函数为系统稳定,其频率特性为由式(5-8)频率特性的意义,求出ω=2 rad/s 时频率特性的幅值和相角可得系统的稳态输出0()0.22sin(263.4)ss c t t =-由线性系统的叠加性,可得系统的稳态输出00()0.35sin(15)0.44sin(2108)ss c t t t =---5-2 若系统的单位阶跃响应为49()1 1.80.8t t h t e e --=-+(t ≥0)试求系统的频率特性。
5-3 作出下列传递函数的对数幅频特性L (ω)和相频特性φ(ω)。
(1)1()G s Ts=,T =10及T =0.1 (2)211()1T s G s T s +=+,T 1>T 2及T 1<T 2(3) 20()(101)G s s s =+,210(0.51()(0.11)s G s s s +=+(3)123()(1)(1)(1)KG sT s T s T s =+++,T 1>T 2>T 3【解】(1)频率特性为对数幅频表达式幅频特性,当10T =时,为过0.1c ω=,斜率为-20的直线。
自动控制第一章习题答案

自动控制第一章习题答案自动控制第一章习题答案自动控制是一门研究如何对动态系统进行控制的学科。
它涉及到数学、物理、工程等多个领域的知识,在现代工业和科学中扮演着重要的角色。
在学习自动控制的过程中,习题是检验理论掌握程度和加深理解的重要方式。
本文将为大家提供自动控制第一章习题的答案,帮助读者更好地理解和应用自动控制的基础知识。
1. 什么是自动控制?自动控制是指通过某种控制器对一个系统进行调节,以使系统的输出能够按照预定的要求进行变化。
它可以通过测量系统的输出信号,并与期望的输出信号进行比较,从而产生控制信号,使系统能够自动地调整自身的状态。
2. 什么是控制系统?控制系统是由若干个组成部分组成的整体,用于控制一个或多个物理过程或设备。
它包括输入、输出、控制器和被控对象等组成部分。
输入是指控制系统接收的外部信号,输出是指控制系统产生的控制信号,控制器是指用于处理输入信号并产生输出信号的设备,被控对象是指受到控制系统控制的物理过程或设备。
3. 什么是开环控制?开环控制是指控制器的输出信号不受被控对象的反馈信号影响的控制方式。
在开环控制中,控制器根据预先设定的输入信号生成输出信号,而不考虑被控对象的实际状态。
开环控制的优点是简单、快速,但缺点是对于被控对象的变化无法进行实时调整。
4. 什么是闭环控制?闭环控制是指控制器的输出信号受到被控对象的反馈信号影响的控制方式。
在闭环控制中,控制器根据被控对象的实际状态和预期状态之间的差异来生成输出信号。
闭环控制的优点是能够实时调整控制器的输出信号,使系统能够更加稳定和准确地达到预期状态。
5. 什么是负反馈?负反馈是指将被控对象的输出信号与期望的输出信号进行比较,并将比较结果作为控制器的输入信号的一种控制方式。
负反馈控制的目的是通过调整控制器的输出信号,使被控对象的输出信号逐渐趋近于期望的输出信号。
负反馈控制能够有效地抑制系统中的干扰和噪声,提高系统的稳定性和准确性。
6. 什么是正反馈?正反馈是指将被控对象的输出信号与期望的输出信号进行比较,并将比较结果作为控制器的输入信号的一种控制方式。
自编自控教材习题解答

自控习题及解答第六章6-1 问答题(1)系统的非线性通常分为哪两大类?在数学上分别有什么特征? (2)典型的本质非线性特性有哪几种? (3)什么叫描述函数?如何求取描述函数?(4)如何应用描述函数法来分析一个非线性控制系统?(5)什么是相平面?什么是相轨迹?在相平面上有时间信息吗?是以什么方式来表示的? (6)什么叫相平面的奇点?在数学上应满足什么条件?几何解释是什么? (7)说出对非线性系统进行相平面分析的一般步骤。
6-2 某单位负反馈控制系统的开环传递函数为3)(+=s Ks G 若校正装置为sas s G c +=)( 试确定a 和K 的取值,使系统阶跃响应的稳态误差为零,超调量为5%,调节时间为1秒(Δ=2%)。
答案: K =5,a =6.46-3 某单位负反馈系统的开环传递函数为)4)(2()(++=s s s Ks G若引入的校正装置为4.16)2.2(53.7)(++=s s s G c试确定K 的取值,使系统具有n ω=0.5和=ξ0.5的主导极点,且K v ≥2.7。
答案 K=226-4 某控制系统如图6-43所示,为了使系统对阶跃输入响应有合适的稳态误差,我们先选取控制器参数K 2=4。
试确定参数K 1的取值,使系统的相角裕度为600,并求出此时的阶跃响应的峰值时间和超调量。
图6-43 习题6-2 图6-5 设有单位反馈的火炮指挥仪伺服系统,其开环传递函数为)15.0)(12.0()(++=s s s Ks G若要求系统最大输出速度为120/s ,输出位置的容许误差小于20,试求:(1)满足上述指标的最小K 值,计算该K 值下系统的相角裕度和幅值裕度; (2)在前向通路中串联超前校正网络108.014.0)(++=s s s G c计算校正后系统的相角裕度和幅值裕度,说明超前校正对系统动态性能的影响。
6-6 设单位反馈系统的开环传递函数)1()(+=s s Ks G试设计一串联超前校正装置,使系统满足如下指标:(1)相角裕度γ≥450;(2)在单位斜坡输入下的稳态误差e ss (∞)<1/15rad 。
(完整版)自动控制原理习题及答案.doc
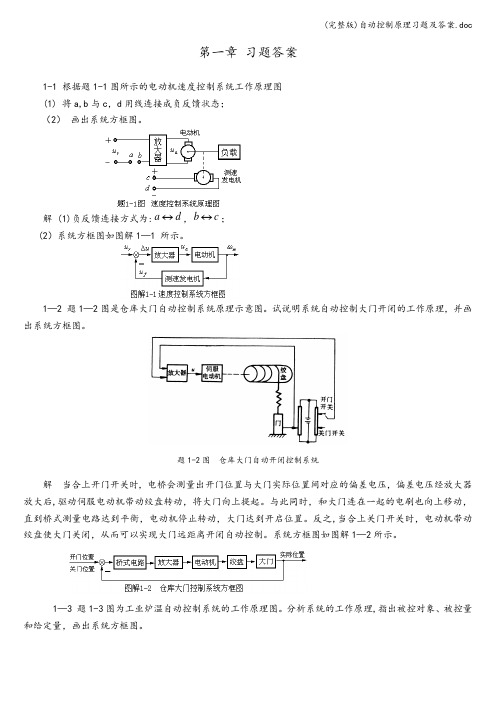
第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1—1 所示。
1—2 题1—2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1—2所示。
1—3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C,热电偶的输出电压f u 正好等于给定电压r u .此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值.这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程: 控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
自动控制理论第一章习题答案.doc

第一章自动控制概论思考题1、什么是自动控制?他对人类活动有什么意义?所谓自动控制就是在没有人直接参与的情况下,通过控制装置使被控制对彖或生产过程自动地按照预定的规律运行,使Z达到预期的状态或性能要求。
自动控制是人类在认识世界和发明创新的过程屮发展起來的一门重要的科学技术。
依靠它,人类可以从笨重、重复性的劳动中解放出來,从事更富创造性的工作。
2、什么是反馈?什么是负反馈?通常,我们把输出量送回到输入端并与输入信号比较的过程称为反馈。
若反馈的信号是与输入信号相减而使偏差值越来越小,则称为负反馈。
3、开环控制系统是怎样实现控制作用的?请举例说明。
开环控制系统:如果系统的输出端和输入端Z间不存在反馈回路,输出量对系统的控制作用没有影响,这样的系统称为开环控制系统。
例:原始的数控机床进给系统就是开环控制系统。
指令输入到计算机控制系统Z中,带动步进电机运动,使工作台移动,产生位移输出。
在口常生活中,许多控制系统都可以理解成开环控制系统,如电风扇的转速是由档位决定的,不能根据环境温度自动调节;洗衣机定时系统是由功能和时间决定,不能根据所洗衣物清洁程度自动调节。
4、闭环控制系统是怎样实现控制作用的?请举例说明。
闭环控制系统:闭环控制(亦称为反馈控制,Feedback Control)是指能对输出量与输入量进行比较,并且将它们的偏差作为控制手段,以保持两者Z间预定关系的系统。
如:自动调温空调,当环境温度高于设定温度时,空调制冷系统自动开启,调定室温到设定值。
5、对自动控制系统的基本要求是什么?对控制系统的基本要求是:系统的稳定性、响应的快速性、响应的准确性。
6、试叙述电冰箱中温度控制系统的温度控制过程。
电冰箱温度控制系统由感温管,温度调节,执行动作等系统组成。
冰箱没工作时,感温管内气体遇热就膨涨,触点就将两原来断开的接触点靠在一起了。
冰箱在工作时,由于冰箱内制冷系统在给冰箱不段的输入冷气,就越来越冷,随着温度不短降低,感温管内的气体缩小,气垫就将断点段开,然而就将冰箱停止工作!7、试叙述骑自行车时的闭环控制过程。
自动控制课后习题答案

1n=3,根轨迹有3条分支,且均趋于无穷远处;
2实轴上的根轨迹:[-50,0],( 00];
3渐进线: , ;
4分离点:
求解得: , (舍去);
作出根轨迹如图所示:
(2)临界开环增益 为根轨迹与虚轴交点对应的开环增益。
令 ,代入 ,并令其实部、虚部分别为零,即
,
解得: (舍去)
(3)系统处于临界阻尼比 ,相应闭环根位于分离点处,即要求分离点d对应的K值。将s=d=-21.3代入幅值条件:
(2)系统的脉冲响应
2-10试简化图2-9中的系统结构图,并求传递函数C(s)/R(s )和C(s)/N(s)。
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示
2-12 试用梅逊增益公式求图2-8中各系统信号流图的传递函 数C(s)/R(s)。
其中,T1、T2和K2为正常数。若要求r(t)=1+ t时,c?
分析:先求出系统的误差传递函数,再利用稳态误差计算公式,根据题目要求确定参数。
解:对方程组进行拉普拉斯变换,可得
按照上面三个公式画出系统的结构图如下:
定义误差函数
所以
令 ,可得 ,因此,当 时,满足条件。
可见,当 第一次为0时, ,所以
根据调节时间 的定义: ,即
,得
所以:
3-5设图3-3是简化的飞行控制系统结构图,试选择参数K1和Kt,使系统ωn=6、ζ=1。
分析:求出系统传递函数,如果可化为典型二阶环节形式,则可与标准二阶环节相对照,从而确定相应参数。
解 对结构图进行化简如图所示。
自动控制原理课后习题及答案

第一章 绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答:1开环系统(1) 优点:结构简单,成本低,工作稳定;用于系统输入信号及扰动作用能预先知道时,可得到满意的效果;(2) 缺点:不能自动调节被控量的偏差;因此系统元器件参数变化,外来未知扰动存在时,控制精度差;2 闭环系统⑴优点:不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高;它是一种按偏差调节的控制系统;在实际中应用广泛;⑵缺点:主要缺点是被控量可能出现波动,严重时系统无法工作;1-2 什么叫反馈为什么闭环控制系统常采用负反馈试举例说明之;解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈;闭环控制系统常采用负反馈;由1-1中的描述的闭环系统的优点所证明;例如,一个温度控制系统通过热电阻或热电偶检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值;1-3 试判断下列微分方程所描述的系统属于何种类型线性,非线性,定常,时变122()()()234()56()d y t dy t du t y t u t dt dt dt ++=+ 2()2()y t u t =+3()()2()4()dy t du t ty t u t dt dt +=+ 4()2()()sin dy t y t u t t dt ω+= 522()()()2()3()d y t dy t y t y t u t dt dt ++=62()()2()dy t y t u t dt +=7()()2()35()du t y t u t u t dtdt =++⎰解答: 1线性定常 2非线性定常 3线性时变 4线性时变 5非线性定常 6非线性定常7线性定常1-4 如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量;控制的目的是保持水位为一定的高度;试说明该系统的工作原理并画出其方框图;题1-4图 水位自动控制系统解答:1 方框图如下:⑵工作原理:系统的控制是保持水箱水位高度不变;水箱是被控对象,水箱的水位是被控量,出水流量Q2的大小对应的水位高度是给定量;当水箱水位高于给定水位,通过浮子连杆机构使阀门关小,进入流量减小,水位降低,当水箱水位低于给定水位时,通过浮子连杆机构使流入管道中的阀门开大,进入流量增加,水位升高到给定水位;1-5 图1-5是液位系统的控制任务是保持液位高度不变;水箱是被控对象,水箱液位是被控量,电位器设定电压时表征液位的希望值Cr 是给定量;题1-5图 液位自动控制系统解答:1 液位自动控制系统方框图:2当电位器电刷位于中点位置对应Ur 时,电动机不动,控制阀门有一定的开度,使水箱中流入水量与流出水量相等;从而液面保持在希望高度上;一旦流入水量或流出水量发生变化,例如当液面升高时,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一事实上的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液位流量减少;此时,水箱液面下降,浮子位置相应下降,直到电位器电刷回到中点位置,系统重新处于平衡状态,液面恢复给定高度;反之,若水箱液位下降,则系统会自动增大阀门开度,加大流入量,使液位升到给定的高度;1-6题图1-6是仓库大门自动控制系统的示意图,试说明该系统的工作原理,并画出其方框图;题1-6图仓库大门自动控制系统示意图解答:(1)仓库大门自动控制系统方框图:2工作原理:控制系统的控制任务是通过开门开关控制仓库大门的开启与关闭;开门开关或关门开关合上时,对应电位器上的电压,为给定电压,即给定量;仓库大门处于开启或关闭位置与检测电位器上的电压相对应,门的位置是被控量;当大门所处的位置对应电位器上的电压与开门或关门开关合上时对应电位器上的电压相同时,电动机不动,控制绞盘处于一定的位置,大门保持在希望的位置上,如果仓库大门原来处于关门位置,当开门开关合上时,关门开关对应打开,两个电位器的电位差通过放大器放大后控制电动机转动,电动机带动绞盘转动将仓库大门提升,直到仓库大门处于希望的开门位置,此时放大器的输入为0,放大器的输出也可能为0;电动机绞盘不动,大门保持在希望的开门位置不变;反之,则关闭仓库大门;1-7题图1-7是温湿度控制系统示意图;试说明该系统的工作原理,并画出其方框图;题1-7图温湿度控制系统示意图解答:1方框图:2被控对象为温度和湿度设定,控制任务是控制喷淋量的大小来控制湿度,通过控制蒸汽量的大小来控制温度;被控量为温度和湿度,设定温度和设定湿度为给定量;第二章 控制系统的数学模型2-2 试求图示两极RC 网络的传递函数U c S /U r S;该网络是否等效于两个RC 网络的串联解答:故所给网络与两个RC 网络的串联不等效;2-4 某可控硅整流器的输出电压U d =KU 2Φcos α式中K 为常数,U 2Φ为整流变压器副边相电压有效值,α为可控硅的控制角,设在α在α0附近作微小变化,试将U d 与α的线性化;解答:.202002020cos (sin )()...sin sin )d u ku ku ku ku φφφφαααααααα=--+∆=-⋅∆=-d d 线性化方程:u 即u (2-9系统的微分方程组为式中1T 、2T 、1K 、2K 、3K 均为正的常数,系统地输入量为()r t ,输出量为()c t ,试画出动态结构图,并求出传递函数()()C s R s ; 解答:2-12 简化图示的动态结构图,并求传递函数()()C s R s ; 解答:ab c d e2-13 简化图示动态结构图,并求传递函数()()C s R s ;解答: a bcde(d)f第三章 时域分析法3-1 已知一阶系统的传递函数今欲采用负方馈的方法将过渡过程时间s t 减小为原来的倍,并保证总的放大倍数不变,试选择H K 和0K 的值;题3-1图解答:闭环传递函数:10()0.2110s s θ=+由结构图知:00010()10110()0.21()0.21101110HHh HK k G S k K s K G S s k S K θ+===+++++由00101011011010100.910H H H k k k k k ⎧⎪⎪⎨⎪⎪⎩⎧⎪⎨⎪⎩=++===3-2已知系统如题3-2图所示,试分析参数b 对输出阶跃过渡过程的影响;题3-2 图解答:系统的闭环传递函数为:由此可以得出:b 的大小影响一阶系统的时间常数,它越大,系统的时间常数越大,系统的调节时间,上升时间都会增大;3-3 设温度计可用1(1)Ts +描述其特性;现用温度计测量盛在容器内的水温,发现1分钟可指示98%的实际水温值;如果容器水温依10℃/min 的速度线性变化,问温度计的稳态指示误差是多少解答:本系统是个开环传递函数 系统的闭环传递函数为:系统的传递函数:1()1G s Ts =+则题目的误差传递函数为:3-4 设一单位反馈系统的开环传递函数试分别求110K s -=和120K s -=时系统的阻尼比ζ、无阻尼自振频率n w 、单位阶跃响应的超调量p σ%和峰值时间p t ,并讨论K 的大小对动态性能的影响;解答:开环传递函数为3-8 设控制系统闭环传递函数试在s 平面上给出满足下列各要求的闭环特征根可能位于的区域: 1. 10.707,2n ζω>≥≥ 2. 0.50,42n ζω≥>≥≥ 3. 0.7070.5,2n ζω≥≥≤解答:欠阻尼二阶系统的特征根:1. 由0.7071,arccos ζβζ<<=,得045β︒︒<≤,由于对称关系,在实轴的下半部还有;2. 由00.5,arccos ζβζ<≤=,得6090β︒︒≤<,由于对称关系,在实轴的下半部还有;3. 由0.50.707,arccos ζβζ≤≤=,得出4560β︒︒≤≤,由于对称关系,在实轴的下半部还有;则闭环特征根可能位于的区域表示如下:1. 2. 3.3-10 设单位反馈系统开环传递函数分别为: 1.[]()(1)(0.21)G s K s s s =-+2. ()(1)[(1)(0.21)]G s K s s s s =+-+ 试确定使系统稳定的K 值;解答:1.系统的特征多项式为:()D s 中存在特征多项式中存在负项,所以K 无论取什么值,系统都不会稳定;2.系统的特征多项式为:32()0.20.8(1)D s s s k s k =++-+ 劳斯阵列为:3s k-12s k 0s k系统要稳定 则有 0.60.800.80k k ⎧⎪⎨⎪⎩->>所以系统稳定的K 的范围为43k >3-14 已知单位反馈系统开环传递函数如下: 1.]()10(0.11)(0.51)G s s s =++2.2()7(1)(4)(22)G s s s s s s ⎡⎤=++++⎣⎦ 3.2()8(0.51)(0.11)G s s s s ⎡⎤=++⎣⎦ 解答:1.系统的闭环特征多项式为: 可以判定系统是稳定的.则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11111ss p e k ==+当()1()r t t t =⋅时, 1ss ve k ==∞当2()1()r t t t =⋅时, 2ss ae k ==∞2.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于一型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==∞+ 当()1()r t t t =⋅时,187ss v e k ==当2()1()r t t t =⋅时, 20ss ae k ==3.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==+ 当()1()r t t t =⋅时, 10ss v e k ==当2()1()r t t t =⋅时, 214ss a e k ==第四章 根轨迹法4-2 已知单位反馈系统的开环传递函数,绘出当开环增益1K 变化时系统的根轨迹图,并加以简要说明;1.1()(1)(3)K G s s s s =++2.12()(4)(420)K G s s s s s =+++解答:1 开环极点: p1=0,p2=-1,p3=-3实轴上的根轨迹区间: -∞,-3,-1,0 渐进线:分离点:111013d d d ++=++解得d1、2=-,;d2=-不在根轨迹上,舍去; 与虚轴交点:特征方程321()430D s s s s K =+++= 将s =j ω代入后得解之得 ω= 112K =当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4-21所示;2 开环极点:p1=0,p2=-4,p3、4=-2±j4实轴上的根轨迹区间:-4,0 渐进线:分离点:)8018368(2341++++-=s s s s K 由01=ds dK解得 s1、2=-2,624,3j s ±-= 分离点可由a 、b 、c 条件之一进行判定:a .∠Gs 3=-129o+51o -90o+90o=-180o,满足相角条件;b .100)80368()(62234313>=+++-=+-=j s s s s s s KK 1在变化范围 )0[∞→ 内;c .由于开环极点对于σ=-2直线左右对称,就有闭环根轨迹必定也是对于σ=-2直线左右对称,故s3在根轨迹上;与虚轴交点: 特征方程Routh 表s 4 1 36 K 1 s 3 8 80 s 2 26 K 1 s 80-8K1/26 s 0 K 1由 80-8k1/26=0和26s2+ k1=0,解得k1=260,102,1j s ±= ;当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4-22所示;4-3 设单位反馈系统的开环传递函数为(1) 试绘制系统根轨迹的大致图形,并对系统的稳定性进行分析;、(2) 若增加一个零点1z =-,试问根轨迹有何变化,对系统的稳定性有何影响解答1 K 1>0时,根轨迹中的两个分支始终位于s 右半平面,系统不稳定;2 增加一个零点z=-1之后,根轨迹左移,根轨迹中的三个分支始终位于s 左半平面,系统稳定;4-4 设系统的开环传递函数为12(2)()()(2)K s G s H s s s s a +=++,绘制下列条件下的常规根轨迹;11a =; 2 1.185a = 33a =解答: 11=a实轴上的根轨迹区间: -∞,-1,-1,0 渐进线:分离点:22231+++-=s as s s K解得01=ds dK只取253+-=d ;与虚轴交点:特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式:得出与虚轴的交点系统的根轨迹如下图: 2185.1=a 零点为2-=z极点为0,43.01j p ±-=实轴上的根轨迹区间: -∞,-1,-1,0 渐进线:分离点:22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式:得出与虚轴的交点系统的根轨迹如下图: 33=a 零点为2-=z极点为0,41.11j p ±-=实轴上的根轨迹区间: -∞,-1,-1,0 渐进线:分离点:22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式:得出与虚轴的交点系统的根轨迹如下图:4-8 根据下列正反馈回路的开环传递函数,绘出其根轨迹的大致形状;1()()1()()12K G s H s s s =++ 2()()1()()12K G s H s s s s =++3()()()12()()13(4)K s G s H s s s s s +=+++解答:1 2 34-15 设单位反馈系统的开环传递函数为确定a 值,使根轨迹图分别具有:0、1、2个分离点,画出这三种情况的根轨迹;解答:首先求出分离点:分离点:321s s K s a +=-+ 解得2122(31)20()dK s a s as ds s a +++=-=+得出分离点1,2d =当119a <<时,上面的方程有一对共轭的复根当911<>a a 或时,上面的方程有两个不等的负实根当119a a ==或时,上面的方程有两个相等的实根1当1=a 时 系统的根轨迹为:可以看出无分离点 ,故排除2当91=a 时 系统的根轨迹为:可以看出系统由一个分离点 3当1>a 时 比如3=a 时系统的根轨迹为:可以看出系统由无分离点 4当91<a 时 比如201=a 时系统的根轨迹为: 可以看出系统由两个分离点 5当191<<a 时 比如21=a 时系统的根轨迹为:可以看出系统由无分离点 第五章 频域分析法5-1设单位反馈控制系统开环传递函4()1G s s =+,当将()sin(260)2cos(45)r t t t =+--作用于闭环系统时,求其稳态输出;解答:开环传递函数14)(+=s s G 闭环传递函数54)(+=Φs s闭环频率特性54)()()(+==Φωωωωαj e M j j当ω=2时,M2=,α2=; 当ω=1时,M1=,α1=; 则闭环系统的稳态输出:5-2 试求110()4G s s =+24()(21)G s s s =+3(1)()(1,)1K s G s K T Ts ττ+=>>+的实频特性()X ω、虚频特性()Y ω、幅频特性()A ω、相频特性()ϕω;解答:⑴4arctan 222216101610164016)4(10410)(wj e w w w j w w jw jw jw G -+=+-+=+-=+=则21640)(w w X +=,21610)(w ww Y +-=⑵)21arctan 180(2331444448)12(4)(wj ew w w w j w w w jw jw jw G ++=+-+-=+=则 w w w w X +-=348)( , w w w Y +-=344)(⑶)]arctan()[arctan(222222222111)(1)1(1)1()(wT w j e w T w k w T w T k j w T Tw k jTw w j k jw G -++=+-+++=++=τττττ则2221)1()(w T Tw k w X ++=τ,221)()(w T wT k w Y +-=τ 5-4 绘制下列传递函数的对数幅频渐近线和相频特性曲线;14()(21)(81)G s s s =++ 2()242()(0.4)(40)s G s s s +=++ 3228(0.1)()(1)(425)s G s s s s s s +=++++ 4210(0.4)()(0.1)s G s s s +=+解答:1转折频率为21,8121==w w2 3 45-10 设单位负反馈系统开环传递函数; 110()(0.51)(0.021)G s s s s =++,21()as G s s +=试确定使相角裕量等于45的α值; 2 3()(0.011)KG s s =+,试确定使相角裕量等于45的K 值;32()(100)KG s s s s =++,,试确定使幅值裕量为20dB 的开环增益K 值;解答:1由题意可得:解得: ⎩⎨⎧==84.019.1αc w2由题意可得:解得: ⎩⎨⎧==83.2100k w c3由题意可得:解得: ⎩⎨⎧==1010k w g5-13 设单位反馈系统开环传递函数 试计算系统的相角裕量和幅值裕量;解答:由18002.0arctan 5.0arctan 90)(-=---=g g g w w w γ所以幅值裕量)(14dB h =故16102.0arctan 5.0arctan 90)(-=---=c c c w w w ϕ所以相角裕量19161180)(=-=c w γ系统的幅频特性曲线的渐近线: 系统的幅相特性曲线:第六章 控制系统的综合与校正6-1 试回答下列问题:1 进行校正的目的是什么为什么不能用改变系统开环增益的办法来实现答:进行校正的目的是达到性能指标;增大系统的开环增益在某些情况下可以改善系统的稳态性能,但是系统的动态性能将变坏,甚至有可能不稳定;2 什么情况下采用串联超前校正它为什么能改善系统的性能答:串联超前校正主要用于系统的稳态性能已符合要求,而动态性能有待改善的场合;串联超前校正是利用校正装置的相位超前特性来增加系统的橡胶稳定裕量,利用校正装置幅频特性曲线的正斜率段来增加系统的穿越频率,从而改善系统的平稳性和快速性;(3)什么情况下采用串联滞后校正它主要能改善系统哪方面的性能答:串联滞后校正主要是用于改善系统的稳态精度的场合,也可以用来提高系统的稳定性,但要以牺牲快速性为代价;滞后校正是利用其在高频段造成的幅值衰减,使系统的相位裕量增加,由于相位裕量的增加,使系统有裕量允许增加开环增益,从而改善稳态精度,同时高频幅值的衰减,使得系统的抗干扰能力得到提高;思考题:1. 串联校正装置为什么一般都安装在误差信号的后面,而不是系统股有部分的后面2. 如果1型系统在校正后希望成为2型系统,但又不影响其稳定性,应采用哪种校正规律6-3 设系统结构如图6-3图所示,其开环传递函数0()(1)KG s s s =+;若要求系统开环截至频率 4.4c ω≥rad/s,相角裕量045γ≥,在单位斜坡函数输入信号作用下,稳态误差0.1ss e ≤,试求无源超前网络参数;解答:1由10.1ss e K =≤可得:10K ≥,取10K =2原系统 3.16c ω= rad/s,017.6γ=,不能满足动态性能指标;3选' 4.4c ω=rad/s,由'0()10lg c L ωα=-即'21020lg10lg cαω=-可得:3.75α=那么0.12T == 无源超前校正网络:10.531()10.121c Ts s G s Ts s α++==++(4) 可以得校正后系统的'51.8γ=,满足性能指标的要求;6-4 设单位反馈系统开环传递函数()()()010.51KG s s s s =++;要求采用串联滞后校正网络,使校正后系统的速度误差系数5(1)v K s =,相角裕量40γ≥;解答: ⑴由00lim ()v s K sG s K→==可得:5K =2 原系统 2.15c ω=,22.2γ=-不满足动态要求3 确定新的'c ω由''1804012(90arctan arctan 0.5)c c ωω-++=---可解得:'0.46c ω=⑷由020lg 20lg (')c b G j ω=-得:0.092b =取'111510cbT ω⎛⎫= ⎪⎝⎭='15c ω得:118T =校正网络为:1111()11181c Tbs s G s Ts s ++=≈++校正后系统的相角裕量'42γ=,故校正后的系统满足性能指标的要求;第七章 非线性控制系统7-1 三个非线性系统的非线性环节一样,线性部分分别为1.2()(0.11)G s s s =+ 2.2()(1)G s s s =+ 3. 2(1.51)()(1)(0.11)s G s s s s +=++ 解答:用描述函数法分析非线性系统时,要求线性部分具有较好的低通滤波性能即是说低频信号容易通过,高频信号不容易通过; 从上图可以看出:系统2的分析准确度高;7-2 一个非线性系统,非线性环节是一个斜率1N -的饱和特性;当不考虑饱和因素时,闭环系统是稳定的;问该系统有没有可能产生自振荡解答:饱和特性的负倒描述函数如下:当1k =时,1()N A -曲线的起点为复平面上的(1,0)j -点; 对于最小相位系统有:闭环系统稳定说明系统的奈氏曲线在实轴(,1)-∞-段没有交点,因此,当存在1k =的饱和特性时,该系统不可能产生自激振荡7-4 判断图中各系统是否稳定,1()N A -与()G j ω的交点是否为自振点;图中P为()G s的右极点个数;解答:首先标出各图的稳定区用阴影部分表示abc da1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;b1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;c 交点,a c为自激振荡点,交点b不时自激振荡点;d 闭环系统不稳定;e 交点a不是自激振荡点;f 交点a是自激振荡点7-5 非线性系统如图所示,试确定其自振振幅和频率;题7-5图解答:由题可得下图:由1()()G j N A ω-=得1()()N A G j ω-=即:()()10*412j j j A ωωωπ++=- 320ωω-=得:ω=2403A ωπ-=-得:24020 2.1233A ππω===振幅为203π7-6非线性系统如图所示,试用描述函数法分析当10K =时,系统地稳定性,并求K 的临界稳定值;题7-6图解答:由题可得下图:K 的临界稳定值为:010653K == 所以,当06K <<时,()G j ω曲线不包围1()N A -曲线,系统闭环稳定;第八章 线性离散系统8-1 求函数()x t 的Z 变换;1.()1at x t e -=- 2. ()sin x t t t ω=3. ()sin x t t t ω=4. 2()atx t t e -=解答:1. (1)()1(1)()aT aT aT z e z z X z z z e z z e ----=-=----2.2222(1)sin sin ()()2cos 1(2cos 1)Tz z T d z T X z Tz dz z z T z z T ωωωω-=-=-+-+Z 域微分定理3.22222(cos )cos ()2cos 12cos aT aT aT aT aT aT aTze ze T z ze T X z z e ze T z ze T e ωωωω-----==-+-+复数位移定理4.23(1)()4(1)aT aT aT Tze ze X z ze +=-复数位移定理8-2 已知()X s ,试求对应的()X z ;1.3()(1)(2)s X z s s +=++ 2.2()(1)s X z s s =+3.21()s X z s += 4. 21()(1)s e X z s s --=+解答:1. ()321()12(1)2s X s s s s s +==-++++ 2. 2111()1(1)(1)s X s s s s s s s ===-+++ 3. 22111()s X s s s s +==+4. ()()221111()111s s e X s e s s s s s --⎡⎤⎢⎥⎢⎥⎣⎦-==--+++()1211(1)T T Tzz z X z z z z e z --⎛⎫⎡⎤⎪⎢⎥⎪⎢⎥⎣⎦⎝⎭=--+---()121(1)1(1)1()T T T T z z z e T T e z z e ----⎛⎫⎡⎤⎪⎢⎥ ⎪⎣⎦⎝⎭-+++-+=--负偏移定理8-3 已知()X z ,试求()X nT ;1. ()()()1012zX z z z =--2. ()()()20.80.1z X z z z =--3. ()2(1)1.250.25z z X z z z -=-+解答:1. ()()()1012zX z z z =--=10()21zz z z ---2. ()()()20.80.1z X z z z =--81770.80.1z zz z =---3.()2(1)1.250.25z zX zz z-=-+(1)(0.25)(1)z zz z-=--(0.25)zz=-8-6 已知系统的结构如图所示,1T s=,试求系统的闭环脉冲传递函数()zφ;解答:211111 ()*(1)1(1)TsTseG s es s ss s s--⎛⎫⎪⎪⎝⎭-==--+++思考题:1. 在单位阶跃输入作用下,试求上题所给系统的输出()c t;2. 系统结构如上题,试求当输入为()1()r t t=、t、2t时的稳态误差;。
《自动控制原理》习题及解答

自动控制原理习题及解答1. 引言自动控制原理是控制工程中最基础的一门课程,是研究系统的建模、分析和设计的基础。
通过习题的练习和解答,可以加深对自动控制原理的理解和掌握。
本文档将提供一些常见的自动控制原理习题及其解答,希望对学习者有所帮助。
2. 习题2.1 系统建模习题1:一个质量为m的弹簧振子的运动方程可以表示为:$$m\\frac{d^2x(t)}{dt^2} + c\\frac{dx(t)}{dt} + kx(t) = 0$$其中,m(m)为振子的位移,m为阻尼系数,m为弹性系数。
请利用拉普拉斯变换求解该系统的传递函数。
解答:对原方程两边进行拉普拉斯变换得:mm2m(m)+mmm(m)+mm(m)=0整理后可得传递函数:$$\\frac{X(s)}{F(s)} = \\frac{1}{ms^2 + cs + k}$$其中,m(m)为输出的拉普拉斯变换,m(m)为输入的拉普拉斯变换。
2.2 系统分析习题2:有一个开环传递函数为$G(s) =\\frac{3}{s(s+2)(s+5)}$的系统,求该系统的阻尼比和自然频率。
解答:该系统的传递函数可以表示为:$$G(s) = \\frac{3}{s(s+2)(s+5)}$$根据传递函数的形式可以得知,该系统是一个三阶系统,有三个极点。
通过对传递函数进行因式分解可以得到:$$G(s) = \\frac{A}{s} + \\frac{B}{s+2} + \\frac{C}{s+5}$$将上述表达式通分并整理后可得:$$G(s) = \\frac{3s^2 + 16s + 5}{s(s+2)(s+5)}$$通过对比系数可以得到:$$A = 1, B = -\\frac{2}{3}, C = \\frac{5}{3}$$根据阻尼比和自然频率的定义,可以得到:$$\\zeta = \\frac{c}{2\\sqrt{mk}}, \\omega_n =\\sqrt{\\frac{k}{m}}$$其中,m为系统的阻尼系数,m为系统的弹性系数,m为系统的质量。
自控习题答案

自控习题答案自控习题答案自控是一种重要的能力,它可以帮助我们更好地管理自己的行为和情绪,从而实现个人目标。
为了提高自控能力,我们可以通过练习自控习题来锻炼自己。
下面是一些常见的自控习题及其答案,希望对大家有所帮助。
1. 你正在看一部电影,突然收到一个重要的工作邮件,你会怎么做?答案:首先,先停下来冷静一下,评估邮件的重要性和紧急性。
如果邮件确实需要立即回复或处理,可以先暂停电影,专注地处理邮件。
如果邮件不是很紧急,可以先将其标记为未读,继续享受电影,等到合适的时候再回复邮件。
2. 你正在减肥,朋友请你吃一块蛋糕,你会怎么做?答案:首先,要感谢朋友的邀请,表达自己的理解。
然后,可以委婉地拒绝朋友的邀请,告诉他们自己正在减肥,希望他们能够理解。
可以提议改为一起喝茶或者散步,以保持社交互动的同时不影响自己的减肥计划。
3. 你正在学习,突然手机收到一条消息,你会怎么做?答案:首先,要克制住对消息的好奇心,不要立即打开手机查看。
可以先将手机调至静音或者将其放在远离自己的地方,以避免分心。
然后,专注地继续学习,直到完成当前的任务或者学习计划。
等到合适的时候再查看手机,回复消息。
4. 你正在做一项重要的任务,突然感到疲倦,你会怎么做?答案:首先,要意识到疲倦是正常的,不要因此感到沮丧或者焦虑。
可以先休息一会儿,做一些放松的活动,如散步或者听音乐,以提高精神状态。
如果疲倦感仍然存在,可以考虑调整任务的安排,将一些重要的工作留到精神状态较好的时候再完成。
5. 你正在购物,看到一件心仪已久的衣服,但是超出了自己的预算,你会怎么做?答案:首先,要冷静地评估自己的实际需求和经济状况。
如果购买该衣服会对自己的财务状况造成较大的影响,可以先放弃购买,寻找其他更经济实惠的选择。
如果真的很喜欢该衣服,可以考虑等到打折或者促销时再购买,以节约开支。
以上是一些常见的自控习题及其答案。
通过这些习题的练习,我们可以逐渐提高自己的自控能力,更好地管理自己的行为和情绪。
自控原理习题答案(全)

第一章 习题答案1-11-21-3 闭环控制系统主要由被控对象,给定装置,比较、放大装置,执行装置,测量和变送装置,校正装置等组成。
被控对象:指要进行控制的设备和过程。
给定装置:设定与被控量相对应给定量的装置。
比较、放大装置:对给定量与测量值进行运算,并将偏差量进行放大的装置。
执行装置:直接作用于控制对象的传动装置和调节机构。
测量和变送装置:检测被控量并进行转换用以和给定量比较的装置。
校正装置:用以改善原系统控制性能的装置。
题1-4 答:(图略)题1-5 答:该系统是随动系统。
(图略) 题1-6 答:(图略)第二章习题答案题2-1 解:(1)F(s)=12s 1+-Ts T(2)F(s)=0.5)421(2+-s s(3)F(s)=428+⋅s es sπ (4)F(s)=25)1(12+++s s(5)F(s)=32412ss s ++ 题2-2 解:(1) f(t)=1+cost+5sint(2) f(t)=e -4t(cost-4sint) (3) f(t)=t t t te e e 101091811811----- (4) f(t)= -t t tte e e ----+-3118195214 (5) f(t)= -t te e t 4181312123--+++ 题2-3 解:a)dtduu C R dt du R R c c r 22111=++)( b)r c c u CR dt du R R u C R dt du R R 1r 12112111+=++)( c) r r r c c c u dtdu C R C R dtu d C C R R u dtdu C R C R C R dtu d C C R R +++=++++)()(1211222121122111222121 题2-4 解:a) G(s)=1)(212++s T T sT (T 1=R 1C, T 2=R 2C )b) G(s)=1)(1212+++s T T s T (T 1=R 1C, T 2=R 2C )c) G(s)= 1)(1)(32122131221+++++++s T T T s T T s T T s T T (T 1=R 1C 1, T 2=R 1C 2, T 3=R 2C 1, T 4=R 2C 2 ) 题2-5 解:(图略) 题2-6 解:33)(+=Φs s 题2-7 解:a) ksf ms s +-=Φ21)(b) )()()(1))(1)(()(21221s G s G s G s G s G s +++=Φc) )()(1)())()(()(31321s G s G s G s G s G s ++=Φd) )()()()(1))()()(323121s G s G s G s G s G s G s -+-=Φe) G(s)=[G 1(s)- G 2(s)]G 3(s)f) )()()()()()()()()()(1)()()()()(43213243214321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +-++=Φg) )()()()()()()()(1)()()()(43213212321s G s G s G s G s G s G s G s G s G s G s G s -+-=Φ题2-8 解:102310)1()()(k k s s T Ts k k s R s C ⋅++++⋅=1023101)1()()(k k s s T Ts k k s N s C ⋅++++⋅=1023102)1()()(k k s s T Ts s T k k s N s C ⋅++++⋅⋅⋅= 题2-9 解:)()()()(1)()()(4321111s G s G s G s G s G s R s C +=)()()()(1)()()(4321222s G s G s G s G s G s R s C +=)()()()(1)()()()()(432142121s G s G s G s G s G s G s G s R s C +=)()()()(1)()()(4321412s G s G s G s G s G s R s C +=题2-10 解:(1)3212321)()(k k k s k k k s R s C +=3212032143)()()(k k k s s G k k k s k k s N s C +⋅+=(2) 2140)(k k sk s G ⋅-= 题2-11 解:122212211111)()1()()(z z s T s T T C s T T s T k k s s m m d e L ⋅++⋅+++⋅=ΘΘ (T 1=R 1C, T 2=R 2C, T d =L a /R a , T m =GD 2R a /375C e C m )第三章 习题答案3-1. s T 15=(取5%误差带) 3-2. 1.0=H K K=2 3-3.当系统参数为:2.0=ξ,15-=s n ω时,指标计算为:%7.52%222.0114.32.01===-⨯---e eξξπσs t ns 352.033=⨯==ξωs t n p 641.02.01514.3122=-⨯=-=ξωπ当系统参数为:0.1=ξ,15-=s n ω时,系统为临界阻尼状态,系统无超调,此时有:st ns 95.057.10.145.67.145.6=-⨯=-=ωξ3-4.当110-=s K 时,代入上式得:110-=s n ω,5.0=ξ,此时的性能指标为:%3.16%225.0114.35.01===-⨯---e eξξπσs t ns 6.0105.033=⨯==ξωs t n p 36.05.011014.3122=-⨯=-=ξωπ当120-=s K 时,代入上式得:11.14-=s n ω,35.0=ξ,此时的性能指标为:%5.30%2235.0114.335.01===-⨯---e eξξπσs t ns 6.01.1435.033=⨯==ξω由本题计算的结果可知:当系统的开环放大倍数增大时,其阻尼比减小,系统相对稳定性变差,系统峰值时间变短,超调量增大,响应变快,但由于振荡加剧,调节时间不一定短,本题中的调节时间一样大。
自动控制原理习题集及其解答

自动控制原理习题及其解答第一章(略) 第二章例2-1 弹簧,阻尼器串并联系统如图2-1示,系统为无质量模型,试建立系统的运动方程。
解:(1) 设输入为y r ,输出为y 0。
弹簧与阻尼器并联平行移动。
(2) 列写原始方程式,由于无质量按受力平衡方程,各处任何时刻,均满足∑=0F ,则对于A 点有021=-+K K f F F F其中,F f 为阻尼摩擦力,F K 1,F K 2为弹性恢复力。
(3) 写中间变量关系式220110)()(y K F Y Y K F dty y d f F K r K r f =-=-⋅=(4) 消中间变量得 020110y K y K y K dtdy f dt dy f r r=-+- (5) 化标准形 r r Ky dtdyT y dt dy T +=+00 其中:215K K T +=为时间常数,单位[秒]。
211K K K K +=为传递函数,无量纲。
例2-2 已知单摆系统的运动如图2-2示。
(1) 写出运动方程式 (2) 求取线性化方程 解:(1)设输入外作用力为零,输出为摆角θ ,摆球质量为m 。
(2)由牛顿定律写原始方程。
h mg dtd l m --=θθsin )(22其中,l 为摆长,l θ 为运动弧长,h 为空气阻力。
(3)写中间变量关系式)(dtd lh θα= 式中,α为空气阻力系数dtd l θ为运动线速度。
(4)消中间变量得运动方程式0sin 22=++θθθmg dt d al dtd ml (2-1)此方程为二阶非线性齐次方程。
(5)线性化由前可知,在θ =0的附近,非线性函数sin θ ≈θ ,故代入式(2-1)可得线性化方程为022=++θθθmg dt d al dtd ml 例2-3 已知机械旋转系统如图2-3所示,试列出系统运动方程。
解:(1)设输入量作用力矩M f ,输出为旋转角速度ω 。
(2)列写运动方程式f M f dtd J+-=ωω式中, f ω为阻尼力矩,其大小与转速成正比。
(完整版)自动控制原理课后习题答案

(完整版)自动控制原理课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
1-2 自动控制系统通常有哪些环节组成各个环节分别的作用是什么解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
自编自控教材习题解答

自控习题及解答第八章8-1 问答题(1)什么叫信号的采样?(2)对连续时间信号进行采样,应满足什么条件才能不丢失信息? (3)什么叫保持器?保持器的功能是什么? (4)z 反变换有哪几种方法?各有什么优点? (5)什么叫差分?差分有哪几种?主要有什么区别? (6)脉冲传递函数是如何来描述采样系统的?(7)如何采用变换域劳斯判据来确定离散控制系统的稳定性? 8-2 求下列函数的z 变换 (a )()ate t te-=(b )2()e t t = (c )()1ate t e-=-(d )()cos e t t ω=8-3 求下列函数的z 反变换,T =1s (a )()()()zE z z a z b =--(b )(1)()(1)()T Tz e E z z z e ---=-- (c )22561()710z z E z z z ++=-+(d )()()()aT aTzE z z e z e --=-- 8-4 试确定下列函数的终值。
(a )11()(1)Tz E z z --=- (b )2()(2)(1)z E z z z =-+8-5 带有采样开关的RC 电路如图8-33所示,已知输入电压100tr u e -=V ,求电路的采样输出电压()c u kT 。
图8-33 题8-4的RC 电路8-6 求图8-34中系统的脉冲传递函数,假定图中采样开关是同步的。
(a )(b )(c )(d )图8-34 题8-5的离散控制系统8-7 已知采样控制系统的特征方式为322460z z z +++=,判断系统是否稳定。
8-8 求图8-35所示系统的开环脉冲传递函数()G z 和闭环脉冲传递函数()z Φ,其中T =1s 。
图8-35 题8-7的离散控制系统8-9 已知系统结构如图8-36所示,T =1s 。
(a )当K =8时,分析系统的稳定性;(b )求K 的临界稳定值。
图8-36 题8-8的离散控制系统8-10 已知系统结构如图8-36所示,其中K =1,T =0.1s ,输入为()1()u t t t =+,试用静态误差系数法求稳态误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自控习题及解答第二章2-2 若某系统在阶跃输入r(t)=1(t)时,零初始条件下的输出响应c(t)=1-e -2t +e -t ,试求系统的传递函数和脉冲响应。
【解】根据传递函数的定义,其传递函数为零初始条件下,输出信号的拉氏变换与输入信号拉氏变换之比,即()1111()()/()21C s G s R s s s s s==-+++ 242(1)(2)s s s s ++=++2-3 设系统传递函数为342)(2++=s s s G初始条件0/)0(,1)0(=-=dt dc c 。
求单位阶跃输入r (t)=1(t)时,系统的输出响应c (t)。
【解】系统传递函数与微分方程是一一对应的,故通过传递函数先求出微分方程,然后通过拉氏变换的方法求解微分方程。
系统对应的微分方程为 4()3()2()c c t c t r t ++=&&&在给定的非零初始条件下,进行拉氏变换22(43)()(0)(0)4(0)s s C s sc c c s++---=& 整理后2221()(43)(43)s C s s s s s s +=-++++部分分式展开后,拉氏反变换111223242/35/25/6()[()][][](43)(43)13255326t t s c t L C s L L s s s s s s s s e e -----+==-=-+++++++=-+2-4 在图2-48中,已知G (s) 和H (s)两方框对应的微分方程分别为()2()5()4()3()6()c t c t e t b t b t c t +=+=&&图2-48 习题2-4系统结构框图且初始条件为零,试求传递函数C (s)/R (s)。
【解】求出每个方框的传递函数,利用反馈等效的方法求C(s)/R(s)。
根据定义可得5()2G s s =+,6()43H s s =+ 255()5()25(43)10075(2)56()1()()(2)(43)30411361(2)(43)C s G s s s s R s G s H s s s s s s s +++====+++++++++2-5 图2-49是由电阻、电容和运算法放大器组成的无源网络和有源网络,试列写以V in (t)为输入量,V out (t)为输出量的传递函数。
(a) (b )(c) (d)图2-49 习题2-5电路图【解】(a) 1211211,1R Z R Z C s RC s C s===+P 22112121211()1()11Z C s RC s G s R Z Z R C C s RC s C s +===+++++(b ) 21122211R Z R Z R Cs R Cs ===+P 2222111211()1R Z R Cs R G s Z R R R Cs +=-==-+gRC(c) 32321123232321()(1)1()1()1R R R R Cs Cs Z R Z R R Cs R R Cs R R Cs++==+==++++P 323232211132(1)()11()()1R R Cs R R Cs R Z R Cs G s Z R R R R Cs ++++=-=-=-++g(d) 本题和(b)、(c)做法图通,因为反馈通路有接地的部分。
根据理想运放的假定,负端输入为虚地和虚开。
设R 2和R 3中间节点的电压为V ,则有122301/in out V V R R V V V V R R Cs ⎧=-⎪⎪⎨--⎪=+⎪⎩ 由此,得2123311()in out R V V R V V Cs R R R ⎧=-⎪⎪⎨⎪++=⎪⎩ 在两式中消去V ,可得到V in 与V out 的关系式232311()out in V R R R R Cs V R =-++ 2-6设弹簧特性由下式描述1.165.12y F =其中,F 是弹簧力,y 是变性位移。
若弹簧在变性位移0.25附近做微小变化,试推导△F 的线性化方程。
【解】001.1,,12.65 1.1(0.25)12.11y y y y y F F F dF F y F y ydy=∆=-∆=-∆=∆∆=⨯⨯∆=∆2-7 试简化图2-50中的系统结构图,并求传递函数C (s)/R (s)和C (s)/N (s)。
图2-50 习题2-7结构图【解】 (1)求C(s)/R(s), 由于N(s)=0,所以很简单1212122()()1G GC sR s G G H G H=++(2) 求C(s)/N(s),等效反馈内回路和相关串联通路,有下列图化简移动相加点后,1223121221()()1G G G GC sN s G G H G H++=++2-8 已知系统结构图如图2- 51所示,试通过结构图等效变换求系统的传递函数C(s)/R(s)。
(c) (d))(sC)(sN11222()()()1()()G s H s G sG s H s+2322()()1()()G s G sG s H s+11()()G s H s)(3sG)(sC)(sN222()1()()G sG s H s+)(2sG)(sH)(sR)(sC)(1sG)(sG)(sH)(sR)(sC)(sB10(e)(f)(g)图2-51 习题2-8 结构图【解】(a)121234()()1()()G G C s R s G G G G +=++-, (b) 122212()()1()G G G C s R s G H H +=+-)(2s G )(s H )(s R )(s C )(1s G )(s G )(s H )(s R )(s C )(s B 10)(3s G )(1s H )(s R )(s C )(1s G )(2s H )(2s G )(2s H )(3s G )(1s H )(s R )(s C )(1s G )(2s G )(3s G )(s H )(s (s C )(1s G )(2s G©()10(1)()1C s GH R s H GH-=+-,(d)122()()1G G C s R s G H-=+(e)1323133()()1G G G G C s R s G G G H+=++ 2-9 图2-52介绍了一种非常灵活的电路结构,它的传递函数可以化为两个二阶或一个四阶系统。
通过选择R a , R b , R c , R d 的不同值,电路可以实现低通、高通或带阻滤波器功能。
(a ) 证明如果R a =R ,R b =R c =R d =∞,则从V in , 到V out 的传递函数可以写成以下的低通滤波器的形式1222++=Ts s T AV V in out ξ 其中,212,,R RRC T R R A out ===ξ)(s C)(b) 若R a=R,R d=R1,R b=R c=∞,求出电路描述的传递函数inoutVV。
图2-52 习题2-9电路图2-10 画出图2-53中各系统结构图对应的信号流图,并用梅逊增益公式求各系统的传递函数C(s)/R(s)和C(s)/N(s)。
【解】(a) 信号流图如下132314241323()()1G G G G G G G GC sR s G G G G+++=++()1()C sN s=(b) 信号流图如下11G2G1R C1N3G41-1)(tuoC1R2RbRcRCRRinVdRRRoutVRaR112233441234112212343434,1,,,1,,1,i p G G p p G G p G G G G L G G L G G G G L L G G =-=-==-∆==-===-12341234121234341()()G G G G G G G G C s R s G G G G G G G G -+-=++ (c) 信号流图如下`求C(s)/R(s)112225345112,,L G G H L G G L G G p G G =-=-==,1231314511L L L L L G G ∆=---+∆=-12451225451245(1)()()1G G G G C s R s G G H G G G G G G HG G -=++-- 求C(s)/N(s)1122253451322145245,,,,1,1L G G H L G G L G G p G p G G G G G =-=-===∆=-∆=-23451225451245()(1)()()1G G G G C s N s G G H G G G G G G HG G +-=++-- 11G 2G 1R C1N3G 4G H-1-5G 134G G 1R C1E1-G G 1-111-1-2-11 试用梅逊增益公式求图2-54中各系统信号流图的的传递函数C (s)/R (s)。
【解】 (a) 四条回路,3,4不接触,两条前向通路,第二余项1+G 3123453123421231352352(1)()()1G G G G G G C s R s G G G G H G G G H G G H G G H ++=+++++(b) 三条回路,两条回路不接触,两条前向通路,两个余项匀不为112341232331223312312313(1)1(1)()()1G G G G f G G f G f C s R s G G f G f f G G f f G f f -+⨯-+=-+-+-© ()(1)()1C s abcd f ch agdR s ae ch aech+-+=--+)s)s)s。
