第十六届全国华罗庚金杯少年数学邀请赛总决

合集下载

第十六届“华罗庚金杯”少年数学邀请赛决赛试卷a(小学组)

2011年第十六届“华罗庚金杯”少年数学邀请赛决赛试卷A（小学组）一、填空题（每小题3分，共80分）1．（3分）1+3+5+7＝．2．（3分）工程队的8个人用30天完成了某项工程的，接着增加了4个人完成了其余的工程，那么完成这项工程共用了天．3．（3分）甲乙两人骑自行车同时从A地出发去B地，甲的车速是乙的车速的1.2倍．乙骑了5 千米后，自行车出现故障，耽误的时间可以骑全程的．排除故障后，乙的速度提高了60%，结果甲乙同时到达B地．那么A，B两地之间的距离为千米．4．（3分）在火车站的钟楼上装有一个电子报时钟，在圆形钟面的边界，每分钟的刻度处都有一个小彩灯，晚上9时35分20秒时，在分针与时针所夹的锐角内有个小彩灯．5．（3分）在边长为1厘米的正方形ABCD中，分别以A、B、C、D为圆心，1厘米为半径画四分之一圆，交点E、F、G、H，如图，则中间阴影部分的周长为厘米．（取圆周率π＝3.141）6．（3分）用40元钱购买单价分别为2元、5元和11元的三种练习本，每种至少买一本，而且钱恰好花完．则不同的购买方法有种．7．（3分）已知某个几何体的三视图如右图，根据图中标示的尺寸（单位：厘米），这个几何体的体积是（立方厘米）8．（3分）将自然数1～22分别填在下面的“□”内（每个“□”只能填一个数），在形成的11个分数中，分数值为整数的最多能有个二、解答下列各题（每题10分，共40分，要求写出简要过程）9．长方形ABCD的面积是2011平方厘米．梯形AFGE的顶点F在BC上，D 是腰EG的中点．试求梯形AFGE的面积．10．公交车的线路号是由数字显示器显示的三位数，其中每个数字是由横竖放置的七支荧光管显示，如图所示．某公交车的数字显示器有两支坏了的荧光管不亮，显示的线路号为“351”，则该公交车的线路号有哪些可能？11．设某年中有一个月里有三个星期日的日期为奇数，则这个月的20日可能是星期几？12．以[x]表示不超过x的最大整数，设自然数n满足[]+[]+[]+…+[]+[]＞2011，则n的最小值是多少？三、解答下列各题（每小题0分，共30分，要求写出详细过程）13．在如图的加法竖式中，不同的汉字代表不同的数字．问：满足要求的不同算式共有多少种？14．如图，两只蜘蛛同处在一个正方体的顶点A，而一只爬虫处在A的体对顶点G，假设蜘蛛和爬虫均以同样的速度沿正方体的棱移动，任何时候它们都知道彼此的位置，蜘蛛能预判爬虫的爬行方向，试给出一个两只蜘蛛必定捉住爬虫的方案．2011年第十六届“华罗庚金杯”少年数学邀请赛决赛试卷A（小学组）参考答案与试题解析一、填空题（每小题3分，共80分）1．（3分）1+3+5+7＝18．【分析】根据加法结合律和加法交换律进行计算．【解答】解：1+3+5+7＝1++3++5++7+＝（1+3+5+7）+（+++）＝16+2＝18故答案为：18．2．（3分）工程队的8个人用30天完成了某项工程的，接着增加了4个人完成了其余的工程，那么完成这项工程共用了70 天．【分析】把这项工程看作单位“1”，用“÷30÷8＝”求出1人1天的工作效率，则12个人工作效率和为×12＝，求出剩下的工作总量，然后根据：工作总量÷工作效率＝工作时间“求出后来用的时间，进而求出完成这项工程共用的时间．【解答】解：一个人的工作效率是÷30÷8＝，12个人的工作效率和为×12＝，共需：（1﹣）÷+30＝40+30＝70（天）答：一共用了70天．故答案为：70．3．（3分）甲乙两人骑自行车同时从A地出发去B地，甲的车速是乙的车速的1.2倍．乙骑了5 千米后，自行车出现故障，耽误的时间可以骑全程的．排除故障后，乙的速度提高了60%，结果甲乙同时到达B地．那么A，B两地之间的距离为45 千米．【分析】根据题意可知，甲乙的车速比是1.2：1＝6：5，所以所用时间比为5：6，不妨设甲用时5t，则乙原定时间为6t，乙因故障耽误的时间为×6t＝t，而最后全程用时5t，所以故障排除后，乙的提速使它节省了2t 的时间．提速后的速度与原来速度比为1.6：1＝8：5，所以时间比为5：8，节省了三份的时间，所以每份为t，所以这段路原计划用时t×8＝t，所以一开始的5千米原计划用时是6t﹣t＝t，所以A、B之间的距离为5×（6t÷t），然后计算即可．【解答】解：甲乙的车速比是1.2：1＝6：5，所以所用时间比为5：6；设甲用时5t，则乙原定时间为6t；乙因故障耽误的时间为×6t＝t，而最后全程用时5t，所以故障排除后，乙的提速使它节省了2t的时间．提速后的速度与原来速度比为1.6：1＝8：5，所以时间比为5：8，节省了三份的时间，所以每份为t，所以这段路原计划用时t×8＝t，所以一开始的5千米原计划用时是6t﹣t＝t，所以A、B之间的距离为：5×（6t÷t），＝5×9，＝45（千米）；故答案为：45．4．（3分）在火车站的钟楼上装有一个电子报时钟，在圆形钟面的边界，每分钟的刻度处都有一个小彩灯，晚上9时35分20秒时，在分针与时针所夹的锐角内有12 个小彩灯．【分析】先求出晚上9时35分20秒时针与分针所夹的角；再根据表盘共被分成60小格，每一大格所对角的度数为30°，每一小格所对角的度数为6°，即可求出晚上9时35分20秒时针与分针间隔的分钟的刻度，从而求出晚上9时35分20秒时，时针与分针所夹的角内装有的小彩灯个数．【解答】解：晚上9时35分20秒时，时针与分针所夹的角为：9×30°+35×0.5°+20×0.5°÷60﹣（7×30°+20×6°÷60）＝270°+17.5°+10°÷60﹣210°﹣2°＝（75）°（75）°÷6≈12（个）．故在分针与时针所夹的锐角内有12个小彩灯．故答案为：12．5．（3分）在边长为1厘米的正方形ABCD中，分别以A、B、C、D为圆心，1厘米为半径画四分之一圆，交点E、F、G、H，如图，则中间阴影部分的周长为 2.094 厘米．（取圆周率π＝3.141）【分析】如图所示：由题意很容易就可以得出△ABF为等边三角形，则弧为圆，同理弧也为圆，所以弧＝+﹣＝圆，同理其余三段也为圆，故周长＝圆，再据圆的周长公式即可得解．【解答】解：依题易知△ABF为等边三角形，故弧为圆，同理弧也为圆，所以弧＝+﹣＝圆，同理其余三段也为圆，故阴影部分的周长＝圆×4＝圆＝＝2.094（厘米）；答：中间阴影部分的周长为 2.094厘米．6．（3分）用40元钱购买单价分别为2元、5元和11元的三种练习本，每种至少买一本，而且钱恰好花完．则不同的购买方法有 5 种．【分析】每种先都减去1本，剩余40﹣2﹣5﹣11＝22元．然后根据剩余的钱数，分类解答，解决问题．【解答】解：每种先都减去1本，剩余40﹣2﹣5﹣11＝22元．如果再买2本11元的，恰好用完，计1种方法；如果再买1本11元的，剩余11元，可以买1本5元和3本2元，计1种方法；如果不再买11元的，22元最多买4本5元的，5元的本数可以是4，2，0，计3种方法．共有1+1+3＝5种方法．答：不同的购买方法有5种．7．（3分）已知某个几何体的三视图如右图，根据图中标示的尺寸（单位：厘米），这个几何体的体积是2666（立方厘米）【分析】由三视图可知，该几何体为四棱锥，分别确定底面积和高，利用锥体的体积公式求解即可．【解答】解：由三视图可知，该几何体为四棱锥，底面ABCD为边长为20cm 的正方体，OE⊥CD且E是CD的中点，所以棱锥的高OE＝20cm．所以四棱锥的体积为×202×20＝×400×20＝2666（cm3）．答：这个几何体的体积是2666cm3．故答案为：2666．8．（3分）将自然数1～22分别填在下面的“□”内（每个“□”只能填一个数），在形成的11个分数中，分数值为整数的最多能有10 个【分析】分值为整数，说明分母是分子的约数．大于11的质数13、17、19要想构成分值为整数的分数，只能做1的分子．然后写出这几个数即可．【解答】解：根据分析可知，22个数最多能构成的整数为：，，，，，，，，，．所以分数值为整数的最多能有10个．故答案为：10．二、解答下列各题（每题10分，共40分，要求写出简要过程）9．长方形ABCD的面积是2011平方厘米．梯形AFGE的顶点F在BC上，D 是腰EG的中点．试求梯形AFGE的面积．【分析】根据题意可连接DF，三角形ADF和长方形ABCD是同底等高的，因此可知三角形ADF的面积是长方形ABCD面积的一半，因为点D是EG的中点，AE平行与FG，所以三角形ADF也是梯形AFGE面积的一半，因为点D是线段EG的中点，所以三角形ADE和三角形DGF的面积就为梯形AFGE 面积的一半，即梯形的面积等于长方形的面积，据此解答即可．【解答】解：如图，连接DF．三角形ADF＝2011÷2＝1005.5（平方厘米），因为点D为EG的中点，所以三角形AED+三角形DFG＝1005.5（平方厘米），梯形AFGE的面积：1005.5+1005.5＝2011（平方厘米），答：梯形AFGE的面积是2011平方厘米．10．公交车的线路号是由数字显示器显示的三位数，其中每个数字是由横竖放置的七支荧光管显示，如图所示．某公交车的数字显示器有两支坏了的荧光管不亮，显示的线路号为“351”，则该公交车的线路号有哪些可能？【分析】显示的百位数字3有一处坏，可能是9，有两处坏可能是8；十位数字5，有一处坏，可能是6和9，有两处坏，可能是8；个位数字1，有一处坏可能是7，有两处坏可能是4；在不亮的灯管中可能应该都不亮，可能有一处该亮却没亮，可能有2处该亮却没亮，分三种可能情况，细致分析，即可得解．【解答】解：分三种情形考虑．第一种情形：线路号的数字中没有荧光管坏了．只有351 一个可能线路号．第二种情形：线路号的数字中有1 支荧光管坏了．坏在第一位数字上，可能的数字为9，线路号可能是951；坏在第二位数字上，可能的数字为6，9，线路号可能是361，391；坏在第三位数字上，可能的数字为7，线路号可能是357．第三种情形：线路号的数字中有2 支荧光管坏了．都坏在第一位数字上，可能的数字为8，线路号可能是851；都坏在第二位数字上，可能的数字为8，线路号可能是381；都坏在第三位数字上，可能的数字为4，线路号可能是354；坏在第一、二位数字上，第一位数字可能的数字为9，第二位数字可能的数字为6，9，线路号可能是961，991；坏在第一、三位数字上，第一位数字可能的数字为9，第三位数字可能的数字为7，线路号可能是957；坏在第二、三位数字上，第二位数字可能的数字为6，9，第三位数字可能的数字为7，线路号可能是367，397．所以可能的线路号有13 个：351，354，357，361，367，381，391，397，851，951，957，961，991．答：则该公交车的线路号有13种可能．11．设某年中有一个月里有三个星期日的日期为奇数，则这个月的20日可能是星期几？【分析】有三个星期日的日期为奇数，这三个星期日应是不相邻的．并且两个奇数周日之间应相隔14天．故可设第一个周日为x，那么第二个周日为x+14，则第三个周日为x+28，第三个周日的日期应不大于31．【解答】解：因为每个周日的间隔是7日，所以若一个月中有三个星期日为奇数，则这三个星期日必定不会是连续的，而是两个奇数周日间间隔14日，一个月最多31日，设第一个周日为x，那么第二个周日为x+14，则第三个周日为x+28，所以x+28≤31，解得x≤3；这样第一个星期日可以是1号或3号．如果第一个星期日是1号，那么该月的20号是星期五；如果第一个星期日是3号（此时本月有31天），那么该月的20号是星期三．故这个月的20日可能是星期五或星期三（此时本月有31天）．12．以[x]表示不超过x的最大整数，设自然数n满足[]+[]+[]+…+[]+[]＞2011，则n的最小值是多少？【分析】观察：[]＝0，[]＝0，…，[]＝0，前14个数的和为0 []＝1，[]＝[1]＝1，…，[]＝[1]＝1，这15个数都是1，之和为1×15＝15，[]＝2，[]＝[2]＝2，…，[]＝[2]＝2，这15个数都是2，之和为2×15＝30，…观察可以得到，规律是间隔15个增加1，（1+2+3+…+15）×15＝1800，（1+2+3+…+15+16）×15＝2040，2040＞2011，因此整数部分加到15，只是达到1800，继续往下到达整数部分是16，2011﹣1800＝211，211÷16＝13.1875，那么要取14个，即最少取到16，才能保证大于2011，则n最下值是：16×15+13＝253．【解答】解：（1+2+3+…+15）×15＝1800，（1+2+3+…+15+16）×15＝2040，2040＞2011，那么整数部分到16，2011﹣1800＝211，211÷16＝13.1875，即最少取到16，才能保证大于2011，则n最下值是：16×15+13＝253．答：自然数n的最小值是253．三、解答下列各题（每小题0分，共30分，要求写出详细过程）13．在如图的加法竖式中，不同的汉字代表不同的数字．问：满足要求的不同算式共有多少种？【分析】由于2+0+1+1＝4 且 0+1+2+3+4+6+7+8+9＝40，4≡40（mod 9），所以，九个不同的汉字代表的数字：0，1，2，3，4，6，7，8，9．易知：40﹣4＝36，36÷9＝4（次），说明此算式共发生四次进位．“4＝2+2＝1+1+2＝1+2+1”显然：①华＝1，“4＝2+2”无解②华＝1，“4＝1+1+2”有解，据此分析讨论即可解答问题．【解答】解：由于2+0+1+1＝4 且 0+1+2+3+4+6+7+8+9＝40，4≡40（mod 9），所以，九个不同的汉字代表的数字：0，1，2，3，4，6，7，8，9．易知：40﹣4＝36，36÷9＝4（次），说明此算式共发生四次进位．“4＝2+2＝1+1+2＝1+2+1”显然：①华＝1，“4＝2+2”无解②华＝1，“4＝1+1+2”有解A：28+937+1046＝2011，可组成算式36 种（6×6×1＝36）B：69+738+1204＝2011，可组成算式48 种（6×4×2＝48）C：79+628+1304＝2011，可组成算式48 种（6×4×2＝48）③华＝1，“4＝1+2+1”有解A：46+872+1093＝2011，可组成算式36 种（6×6×1＝36）B：98+673+1240＝2011，可组成算式72 种（6×6×2＝72）C：97+684+1230＝2011，可组成算式72 种（6×6×2＝72）总计：72×3+96＝216+96＝312（种）．答：一共有312种．14．如图，两只蜘蛛同处在一个正方体的顶点A，而一只爬虫处在A的体对顶点G，假设蜘蛛和爬虫均以同样的速度沿正方体的棱移动，任何时候它们都知道彼此的位置，蜘蛛能预判爬虫的爬行方向，试给出一个两只蜘蛛必定捉住爬虫的方案．【分析】根据题意，可假设一只蜘蛛先不动另一只蜘蛛去追击沿着棱去追击虫子，不论虫子如何逃跑，虫子和追击的蜘蛛始终能保持的最大距离为2个棱的长度，随着爬虫的移动，爬虫必然和等待的蜘蛛会出现最小距离为1个棱的长度，此时即可抓到虫子．【解答】解：其中一只蜘蛛先不动，控制正方体的其中一个面，我们定义这个面为A1面，另一只蜘蛛开始向A1面的相对的面爬行，我们定义这个相对的面为A2面；这时2只蜘蛛，每个蜘蛛控制一个面，不论虫子如何移动，必然会移动到A1面或者A2面；于是必然有一个蜘蛛和虫子处于一个面，这时处于一个面的蜘蛛（设追击的蜘蛛为B1）开始追击虫子，另一个面的蜘蛛则不动，不论虫子如何逃跑，虫子和追击的蜘蛛始终能保持的最大距离为2个棱的长度，随着爬虫的移动，爬虫必然和等待的蜘蛛会出现最小距离为1个棱的长度，这时等待的蜘蛛出击，必然能抓到虫子．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:54:16；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。

第十六届全国“华罗庚金杯”少年数学邀请赛初赛(清晰版)

第十六届全国“华罗庚金杯”少年数学邀请赛（2011年3月19日上午10：00～11：00）一、选择题（每小题10分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）1、若连续的四个自然数都是合数，那么这四个数之和的最小值是（）（A ）100 （B ）101 （C ）102 （D ）1032、用火柴棍摆放数字0～9的方式如下：现在，去掉“”的左下侧，就成了数字“”，我们称“”对应1；去掉“错误！链接无效。

”的上下两根和左下角一根，就成了数字“”，我们称“”对应3。

规定“错误！链接无效。

”对应0，按照这样的规则，可以对应出（）个不同的数字。

（A ）10 （B ）8 （C ）6 （D ）53、两数之和与两数之商都为6，那么这两数之积减这两数之差（大减小）等于（）（A ）2674 （B ）571 （C ）76 （D ）496 4、老师问学生：“昨天你们有几个人复习数学了？”张：“没有人。

”李：“一个人。

”王：“二个人。

”赵：“三个人。

”刘：“四个人。

”老师知道，他们昨天下午有人复习，也有人没复习，复习了的人都说真话，没复习的人说的都是假话。

那么，昨天这5个人中复习数学的有（）个人。

（A ）0 （B ）1 （C ）2 （D ）35、如右图所示，在7×7方格的格点上，有7只机器小蚂蚁，它们以相同的速度沿格线爬行到格点M 、N 、P 、Q （图中空心圆圈所表示的四个位置）中的某个点上聚会，所用时间总和最小的格点是（）（A ）M （B ）N （C ）P （D ）Q6、用若干台计算机同时录用一部书稿，计划若干小时完成。

如果增加3台计算机，只需原定时间的75％；如果减少3台计算机，则比原定时间多用65小时，那么原来完成录入这部书稿的时间是（）小时。

（A ）35（B ）310 （C ）65 （D ）611 二、填空题（每小题10分，满分40分）7、右图由4个正六边形组成，每个面积是6，以这4个正六边形的顶点为顶点，可以连接面积为4的等边三角形有个。

(完整版)第十六届华杯赛总决赛试题

第十六届华罗庚金杯少年数学邀请赛总决赛小学组一试2011年7月23日中国·惠州一. 填空题：（共3题，每题10分）1. 计算 313615176413900114009144736543++++++＝_________.2. 如右图所示，正方形ABCD 的面积为12，AE ＝ED ，且EF ＝2FC ，则三角形ABF 的面积等于_________.3. 某地区的气象记录表明，在一段时间内，全天下雨共1天；白天雨夜间晴或白天晴夜间雨共9天；6个夜间和7个白天晴朗。

则这段时间有_______天，其中全天天晴有_______天。

二. 解答题：（共3题，每题10分，写出解答过程）4. 已知a 是各位数字相同的两位数，b 是各位数字相同的两位数，c 是各位数字相同的四位数，且c b a =+2。

求所有满足条件的（a ，b ，c ）。

5. 纸板上写着100、200、400三个自然数，再写上两个自然数，然后从这五个数中选出若干个数（至少两个）做只有加、减法的四则运算，在一个四则运算式子中，选出的数只能出现一次，经过所有这样的运算，可以得到k 个不同的非零自然数。

那么k 最大是多少？6. 将1，2，3，4，5，6，7，8，9填入右图的圆圈中，每个圆圈恰填一个数，满足下列条件：1）正三角形各边上的数之和相等；2）正三角形各边上的数之平方和除以3的余数相等。

问：有多少种不同的填入方法？( 注意，经过旋转和轴对称反射，排列一致的，视为同一种填法 )总决赛小学组二试2011年7月23日中国·惠州一. 填空题：（共3题，每题10分）1. 某班共36人都买了铅笔，共买了50支，有人买了1支，有人买了2支，有人买了3支。

如果买1支的人数是其余人数的2倍，则买2支的人数是_________.2. 右图中，四边形ABCD 的对角线AC 与BD 相交于O ，E 为BC 的中点，三角形ABO 的面积为45，三角形ADO 的面积为18，三角形CDO 的面积为69。

第16届华杯赛决赛模拟题.答案版(终版)

第十六届华罗庚金杯少年数学邀请赛决赛——模拟试卷一、填空题（每小题10分，共80分）1. 计算：=+⨯++⨯+⨯125.0201131407725.040223201114 。

【分析】： 2。

2. 四位数中，数码0出现_ ____次。

【分析】一个数中出现3个0的有1000，2000，……, 9000.共9个。

一个数中出现2个0的有993243⨯⨯=个；只出现1个0的有39992187⨯⨯⨯=个。

因此，四位数中，数码0出现21872243392700+⨯+⨯=次。

3. 如图,每个正六边形的面积是1,则图中虚线围成的五边形的面积是_______.【分析】：整个图形的面积减去外面的8个小块的面积.整个图形一共有10个小正六边形.我们把外面8个小块编号为1,2,3,4,5,6,7,8.如图.1号和6号正好是小六边形的一半,面积都是0.5.2号和3号刚好可以凑成一个六边形,所以,面积是1.同样,7号和8好凑成一个六边形,面积是1.4号和5号是两个一样的小三角形,而正六边形可以分成6个这样的小三角形,所以,4号和5号的面积都是1/6.所求面积是: 10-0.5×2-1-1-1/6×2=6+2/3=6.7.4. “12345678910111213…484950”是一个位数很多的多位数，从中划去80个数字，使剩下的数字（顺序不变）组成一个首位不为0的多位数，则这个多位数最大为______，最小为___ ___。

【分析】：根据题意，由于共有941291+⨯=个数字，最后划去80个数字，还剩下11个数字，99997484950；10000123440。

，为得到最小值，留下小的数字。

5. 所有适合不等式187＜5n ＜720的自然数n 之和为。

【分析】：根据题意，n 可以是2到14中的任意自然数，于是：2＋3＋…＋14 = 104。

6. 请从2、3、5、7、9中选出4个不同的数字组成一个四位完全平方数，那么这个平方数是。

第十六届华罗庚金杯少年数学邀请赛总决赛

第十六届“华罗庚金杯”少年数学邀请赛总决赛华罗庚中学工作方案为确保第十六届“华罗庚金杯”少年数学邀请赛总决赛圆满成功，提高我校的办学知名度和办学成果，树立华罗庚中学良好的形象，展现华中人风采。

明确职责，各归其位，确保总决赛顺利开展，特制订本方案。

一、活动名称第十六届“华罗庚金杯”少年数学邀请赛总决赛二、活动宗旨弘扬华罗庚教授的爱国主义精神，学习华罗庚教授勤奋学习，献身科学的优秀品质三、参加单位及人数全国100个城市组队参赛，约1000余人四、时间与地点2011年7月22日至25日在我校举行五、主要工作（一）负责国内代表队接待工作（二）负责笔试考务工作（三）数学文化节活动六、工作领导小组组长：戴立波副组长：吴永丹、宋词、黄进添（协调）、姜前勇、涂光峰、张开河成员：戴辉、杨永强、范恩辉、蓝世剑、陈翰生、章智良、李京华、李茂恒、谢林海、石丽萍、侯粤春、杨元高、唐福东、韩建军、刘刚利、解凤英、张毅、刘卫忠、周淼淼、丁志勇、甄红、周铭耿、范碧珊、王文广、黄伟周、韩荣兰、闵庆田、张启龙、万金花、邓勇威、陈倬飞、邓亚军、张晓红、陈冠宁、邓勇威、黎润秋七、具体相关工作组（一）会务组组长：宋词组员：杨永强、李小艳、黄碧婷、莫永壮、范文静、罗丹、张涛、汤美娴、张秋君、董学凌主要职责：1、负责贵宾接待工作2、负责活动期间校内相关会议安排3、负责国内代表队派发相关资料（“华杯赛”活动指南、考务手册、文化节活动资料、学校宣传资料等）4、负责组织、安排国内参赛代表每天参加比赛及有关活动5、负责与市会务组联系、沟通协调6、负责车辆安排工作（二）考务组组长：黄进添组员：戴辉、杨永强、范恩辉、谢林海、陈翰生、李京华、丁志勇、甄红、张启龙、韩荣兰、熊伟、林惠琦、曾雨挺、戴慧婷主要职责：1、安排考务办公室、考场、报告厅、休息室、医疗室；2、培训、安排70名监考教师、考务工作人员；3、组织考试等工作。

（三）接待组1.惠州宾馆接待组：邓振武、刘素芬、熊晏樱、周玲、赵娟、2.金华悦酒店接待组：操瑞英、方惠灵、罗春霞、黄云霞、洪文洁3.学校接待组：北京、天津、石家庄、邯郸、郑州、洛阳、太原、呼和浩特、葫芦岛、营口、枣庄、青岛总负责人：吴永丹长春、吉林、辽源、哈尔滨、桂林、玉林、南宁、柳州、来宾、温州、慈溪、嘉兴、金华、上海、南京、徐州、金坛、盐城、合肥、蚌埠、马鞍山、福州、长沙、株洲、武汉、吉安、重庆、成都、邛崃、彭州、都江堰、贵阳、遵义、西宁、金昌、银川、乌鲁木齐、广州、江门、佛山、深圳、湛江、梅州、汕头、惠州总负责人：姜前勇（1）北京、天津负责人：章智良、谢凤英、北京接待员：陈婕、龙静瑶、李惠珠、刘鎏、邹银芬、天津接待员：向峰2）石家庄、邯郸、郑州、洛阳、太原、呼和浩特、葫芦岛、营口、枣庄、青岛负责人：张毅、张晓虹石家庄、邯郸接待员：温智勇郑州、洛阳接待员：邱惠茜太原、呼和浩特接待员：刘智皓葫芦岛、营口接待员：万金花枣庄、青岛接待员：宁婧（3）长春、吉林、辽源、哈尔滨、桂林、玉林、南宁、柳州、来宾、温州、慈溪、嘉兴、金华、上海、南京负责人：范碧珊、邓勇威长春接待员：朱春悠吉林、辽源、哈尔滨接待员：林夏桂林、玉林、南宁接待员：李淑媛柳州、来宾、温州接待员：张嘉玲慈溪、嘉兴、金华、上海接待员：张莹蓥南京接待员：陈颖颖（4）徐州、金坛、盐城、合肥、蚌埠、马鞍山、福州、长沙、株洲、武汉、吉安、重庆、成都、邛崃、彭州、都江堰负责人：刘刚利、邓亚军徐州、金坛、盐城接待员：刘蓓蓓合肥、蚌埠、马鞍山接待员：钟妙银福州、长沙、株洲、武汉接待员：杨谷吉安、重庆、成都接待员：何贝雅邛崃、彭州、都江堰接待员：周锦梅（5）贵阳、遵义、西宁、金昌、银川、乌鲁木齐、广州、江门、佛山、深圳、湛江、梅州、汕头、惠州负责人：杨元高、王文广贵阳、遵义、西宁接待员：林丽金昌、银川、乌鲁木齐接待员：白晶晶广州接待员：黄颖媛江门、佛山接待员：杨君深圳接待员：王慧斌湛江、梅州、汕头接待员：林丽红惠州接待员：吴珊珊主要职责：1、负责国内代表队参赛选手的接待工作（包括吃、住、行等活动）。

第十六届华赛杯小学组决赛试题及答案

第十六届华罗庚金杯少年数学邀请赛决赛试题（深圳赛区小学组）（时间: 2011年4月16日）一、填空（每题 10 分, 共80分）1．11122181819 .2320320192020⎛⎫⎛⎫⎛⎫++++++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2.甲车从A 出发驶向B,往返来回；乙车从B 同时出发驶向A,往返来回.两车第一次相遇后，甲车继续行驶4小时到达B ，乙车继续行驶1小时到达A. 若A,B 两地相距100千米，那么当甲车第一次到达B 时,乙车的位置距离A 千米。

3.每个铅字上刻有一个数码.如果印刷十二页书，所用的页码铅字要以下15个：1，2，3，4，5，6，7，8，9，1，0，1，1，1，2。

现要印刷一本新书，从库房领出页码铅字共2011个，排版完成后有剩余.那么，这本书最多有页.最少剩余个铅字.4. 一列数:8,3,1,4,.….., 从第三个开始,每个数都是最靠近它前两个数的和的个位数.那么第2011个数是 .5.编号从1到50的50个球排成一行,现在按照如下方法涂色:1)涂2个球；２）被涂色的２个球的编号之差大于2.如果一种涂法被涂色的两个球与另一种涂法被涂色的两个球至少有一个是不同号的,这两种涂法就称为”不同的”.那么不同的涂色方法有种.6. A，B两地相距100千米。

甲车从A到B要走m个小时，乙车从A 到B要走n个小时，m ,n是整数.现在甲车从A,乙车从B同时出发，相向而行，经过5小时在途中C点相遇。

若甲车已经走过路程的一半，那么C到A路程是千米。

7. 自然数b与175的最大公约数记为d. 如果176(111)51⨯-⨯+=⨯+，b d d则b = .8. 如右图. ABCD为平行四边形.AE=2EB.若三角形CEF的面积=1.那么，平行四边形ABCD的面积= .二、解答下列各题（每题10 分, 共40分, 要求写出简要过程）9．三位数的十位数字与个位数字的和等于百位数字的数,称为”好数”.共有多少个好数？10．在下列2n 个数中，最多能选出多少个数，使得被选出的数中任意两个数的比都不是2或12?2345213, 32, 32, 32, 32, 32,, 32.n -⨯⨯⨯⨯⨯⨯11 .一个四位数abcd 和它的反序数dcba 都是65 的倍数.求这个数.12. 用写有+1和-1的长方块放在10n方格中，使得每一列和每一行的数的乘积都是正的，n的最小值是多少？三、解答下列各题（每题15 分, 共30分, 要求写出详细过程）13. 十五个盒子，每个盒子装一个白球或一个黑球.，且白球不多于 12个.你可以任选三个盒子来提问：“这三个盒子中的球是否有白球？”并得到真实的回答. 那么你最少要问多少次，就能找出一个或更多的白球？14. 求与2001互质，且小于2001的所有自然数的和。

(华杯)16届初一总决赛试题答案讲解版

第十六届华罗庚金杯少年数学邀请赛总决赛初一组一试试题解答一、填空题（共3题，每题10分）1. 计算)]5(31[)41(2)32(|231|)1()2(22343-⨯-+-⨯-⎥⎦⎤⎢⎣⎡--÷---⨯-= 解： 3432228594(2)(1)|123|()8122832781146472()[13(5)]4⎡⎤-⨯---÷---⨯-÷--⎢⎥⎣⎦==+-⨯-+-⨯- 6459431.4784--==-⨯ 2. 正方形ABCD 的面积等于625平方厘米.如图，DE 与CF 相交于G.已知125ADE CDG S S ∆∆==平方厘米.△BFG 的面积是平方厘米.答：△BFG 的面积是50平方厘米.解：由于正方形ABCD 的面积等于625平方厘米.所以，边长25AB =厘米.由于125ADE S ∆=平方厘米，所以AE =10厘米.连接CE , 则1162531222CDE S ∆=⨯=（平方厘米）. 而已知125CDG S ∆=（平方厘米），则1252,312.55CDG CDE S DG DE S ∆∆===连接AG . 由221255055ADG ADE S S ∆∆==⨯=（平方厘米）但16252ADGCBG S S ∆∆+=⨯，而16252BFG CBG S S ∆∆+=⨯，比较可得 50BFG ADG S S ∆∆==（平方厘米）.3. 用长度分别为50,,2,1 的木条去摆三角形，每个三角形的三条边的长度分别为c b a ,,，c b a <<，问),,(c b a 最多有多少种不同的取法？答案：9500.解：利用三条边可以构成三角形的条件：任意的两个边的和大于第三边. 边长为1的木条不能与其它长度的木条构成三角形.三角形的最小边长为2时，边长为2的木条只能与差值为1的两个木条构成三角形，故有47对.三角形的最小边长为3时，边长为3的木条只能与差值为1，2的两个木条构成三角形，故有46+45对.三角形的最小边长为4时，边长为3的木条只能与差值为1，2，3的两个木条构成三角形，故有45+44+43对.......三角形的最小边长为k （)25≤k 时，边长k 为的木条只能与差值为1，2，3，⋯，1-k 的两个木条构成三角形，故有(49)(491)(4922)k k k -+--++-+ 对.三角形的最小边长为k （)25>k 时，边长k 为的木条只能与差值为1，2，3，⋯，1-k 的两个木条构成三角形，故有1)149()49(++--+- k k 对. 故总数为(47461)(45441)(43421)(212k k +++++++++++++-+-+++ (321)1++++ 47244523(21)53321k k =⨯+⨯++-⨯++⨯+⨯+()22224231(24231)9500.=+++-+++=二、解答题（共3题，每题10分，写出解答过程）4. 用)(n S 表示自然数n 的数字和，如1)1(=S ，6)123(=S ，10)1234(=S 等等，求自然数n ，使得2011)(=+n S n .答: 1991.解1： 2011)(=+n S n ，20111900<<∴n 则可设y x n ++=101900或y x n ++=102000，其中90,90≤≤≤≤y x ，且y x ,为整数.若y x n ++=101900，则201191101900=++++++y x y x ，即101211=+y x ⎩⎨⎧==∴19y x 1991=n 若y x n ++=102000，则20112102000=+++++y x y x ，即9211=+y x 没有符合条件的整数解.因此，n =1991.解2：因为()(mod9),n S n ≡要使2011)(=+n S n ，只须()2011(mod9),n S n +≡ 即220114(mod9)2(mod9).n n ≡≡⇒≡已知在2011n ≤时()S n 最大为38，所以19832011,n ≤≤其中被9除余2的有1991，2000，2009.其中只有1991满足1991+20=2011，所以1991.n =5. 两个21位自然数m 和n ，每个都由三个1、三个2、三个3、三个4、三个5、三个6和三个7组成，使得nm k =是自然数，问k 能取哪几个自然数？说明你的理由.答：1.解：显然777666555444333222111 1.777666555444333222111k == 假设存在这样的m 和n ，使得数m n 是一个大于1的自然数，则可设m k n=，故m kn =. 两边分别除以9，用数被9除的性质知m 和n 被9除的余数均等于3(1234567)⨯++++++被9除的余数，即84被9除的余数，为3. 因此3与3k 模9同余. 由7776665554443332221117111222333444555666777m k n =≤<，及m 和n 不同（即1k ≠）推得4k =，即4m n =. 考虑数n 最低位的数字7，当把n 乘以4时，这个数字7的下一位（如果有）最多为6，因此乘以4最多进两位，这说明m 中对应位的数字为8（下面不进位,7×4=28）或9（下面进一位）或0（下面进两位），这与m 由三个1、三个2、三个3、三个4、三个5、三个6和三个7组成相矛盾！即不存在满足条件的m 和n .使得数m n是一个大于1的自然数. 所以，只有 1.k =6. 使得关于未知数x 的方程k x x =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡32无解的自然数 k 由小到大排成一行,其前2011个k 的值之和等于多少？解. k0 1 2 3 x 1 2 3 4 23x x ⎡⎤⎡⎤+⎢⎥⎢⎥⎣⎦⎣⎦ 0 1 2 3 设5,0,1,2,3k m r r =+=；令6,x m p p =+待定. 325232323x x p p p p m m m ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+++=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 从上表可知，=,0,1,2,3,23p p r r ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦是有解的. 因此，5,0,1,2,3,(1)k m r r =+=都有解.下面考虑 5 1.k m =-显然，665.23m m m ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦而对于01,q <<66323121115 2.232323m q m q q q q q m m m m m --⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=-+-=-+-+-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦上式对于任意01q <<的q 成立. 所以当51k m =-时，方程无正有理数解.因此，前2011个k 的值之和=20112012(511)(521)(520111)5201110113319.2⨯⨯-+⨯-++⨯-=⨯-=初一组二试试题解答图3 一、填空题（共3题，每题10分）1. 一水池有一进水口，若干同样大小的排水口.如果同时打开进水口和5个排水口，连续30个小时可以将水排尽；如果同时打开进水口和6个排水口，连续20小时可以将水排尽.如果同时打开进水口和15个排水口，几小时可以将水排尽？答：5小时.解：设一水池水为z 立方米，进水口每小时过水y 立方米，一个排水口每小时排水x 立方米.于是 3053020620x y z x y z ⨯=+⎧⎨⨯=+⎩由此此得 2305230232063203x y z xy z ⨯⨯=⨯+⎧⎨⨯⨯=⨯+⎩ 两式两边分别相减得 60x z = ∴ 160x z =；同样可得 120y z =. 设同时打开一进水口和15个排水口，t 小时可以将水排尽. 则1115,6020t z t z z ⨯=⨯+ 即 11 1.420t t =+ 所以 1155t t =⇒=（小时）. 2. 图中，四边形ABCD 是一个长方形，EF //AB ，GH //AD , EF 和GH 相交于点O , 三角形OBD 的面积是m ，求长方形OFCH 的面积和长方形AGOE 的面积差.答：2.m解：从图中可见，1.2BODC BOD ABCD BODA BOD S S S S S ∆∆-==+ 即 22.BODC BODA BOD S S S m ∆-==即 ()()2O F C H B O F D O H A G O E B O G D O ES S S S S S m ∆∆∆∆++-++= 但 ,,BOF BOG DOH DOE S S S S ∆∆∆∆== 因此得2.OFCH AGOE S S m -=3. 自然数a ，b 互质，如果a a b =⎥⎦⎤⎢⎣⎡，n b a b 101⨯=⎭⎬⎫⎩⎨⎧，n 是10进制数b 的位数，则a b = .其中⎥⎦⎤⎢⎣⎡a b 表示不超过a b 的最大整数，⎭⎬⎫⎩⎨⎧a b 表示a b 的小数部分.答：.25 解：设符合题意的最简分数为b a ，a 、b 均为正整数且互质.可知b >a ，根据题意即，则110n b a b a+⨯=，整理成正整数方程为210()n b a -=ab . 从方程中可知2a a b ≤<.因为a 与b 互质，所以b - a 2与ab 也互质.因为若 b -a 2与ab 有公因子p ，那么p 能整除a (或能整除b )，也能整除b -a 2，从而p 也能整除b (或也能整除a )，这样，与题意最简分数(分子与分母互质的分数)矛盾.因此，互质的a 与b 的积只能是10n 与1的乘积或5n 与2n 的乘积两种可能.若10n b =，1a =，这时21b a -≠；若ab =10n =)(52n⨯，b =5n ,2n a =, 这时b -a =1得25(2)1n n -=,即()2521n n -=. 因此，n 只能是1时才成立，即a =2，b =5. 最简分数为.25 二、解答题（共3题，每题10分，写出解答过程）4. 将正整数1，2，3，… ，8分别放置于正方体的8个顶点，每个顶点与相邻3个顶点上的数之和称为该顶点的“众数”.对每一种填法，都可以得到最大“众数”的与最小“众数”的差，那么这个差至少等于多少.答：2解：首先考虑这样的8个众数能否全相等，如果能，因为它们的和等于144，即 1444364)8_321(=⨯=⨯+++，所以每个都等于18，那么最大与最小的众数之差就是0.如果不能全相等，为了求得最小可能值，如果有一个是19，那么相应地得有一个是17，（总和须等于144）所以这个最小的可能值就不能小于21719=-.这样我们只要先证明8个众数不能全相等，然后找出一种布法，其最大与最小众数之差等于2，就可以断定所求的这个最小值是2.设顶点的编号为1，2，3，4，5，6，7，8，如图，记在顶点i 的数为,18,i x i ≤≤.这样，顶点1的众数为1234x x x x +++；顶点5的众数为1568x x x x +++. 若此二顶点的众数相等，则864286515421x x x x x x x x x x x x +=+⇒+++=+++同样地，顶点2的众数为1236x x x x +++，顶点4的众数为1348x x x x +++，若此二顶点的众数相等，则846284316321x x x x x x x x x x x x +=+⇒+++=+++由上面得到的二式相加得 2822,x x =即 28,x x =这是不可能的. 这就证明了8个众数不能全相等.构造一个摆放方式的图例（见右图），最大数和最小数的差等于2，故最小差值等于2.5. 已知三角形边长都是整数，周长不超过28，三个边长两两之差的平方和等于14. 问这样的三角形共有多少个？（三条边长分别对应相等的三角形只算1个）答：12个.解：设三角形三条边长分别为a,b,c ，由已知等式可得：()()()22214a b b c a c -+-+-=. ①令a b m,b c n -=-=，则a c m n -=+，其中m,n 均为自然数.于是，等式①变为 227m n mn ++=. ② 由于m,n 均为自然数，判断易知，2()3737.m n mn mn -+=⇒≤因此，使得等式②成立的m ，n 只有两组：21m n =⎧⎨=⎩ 和 12m n =⎧⎨=⎩. （1）当m ＝2，n ＝1时，b =c +1,a =c +3.又a ，b ，c 为三角形的三边长，所以b c a +>，即13c c c ++>+，解得2c >.又因为三角形的周长不超过28，即3428a b c c ++=+≤，解得8c ≤.因此28c <≤，所以c 可以取值3，4，5，6，7，8，对应可得到6个符合条件的三角形.（2）当12m ,n ==时，23b c ,a c =+=+.a,b,c 又为三角形的三边长，所以b c a +>，即23c c c ++>+.解得1c >.又因为三角形的周长不超过28，即()()3228a b c c c c ++=++++≤，解得233c ≤，因此17c <≤，所以c 可以取值2，3，4，5，6，7，对应可得到6个符合条件的三角形，且和（1）中得到的三角形不同.综合可知：符合条件且周长不超过28的三角形的个数为6612+=个.6. 求最小自然数k , 使得对于任意正整数n , k 个奇数2n +1, 2n +3, ……, 2n +2k -1中至少有一个数, 不能被3, 5, 7, 11中的任何一个整除.解. 试验可知，我们有6个奇数: 115,117,119,121,123,125,它们中每一个都可以被3,5,7,11中的一个或几个数整除.所以,k>6.对于任意的正整数 n , 当 k >6时, 取前7 个数:2n +1, 2n +3, ….., 2n +13 (1)由于2个能被3整除的奇数之差,不小于6; 2个能被5整除的奇数之差,不小于10; 2个能被7整除的奇数之差,不小于14; 2个能被11整除的奇数之差,不小于22. 因此,(1)中能被3整除的数最多有3个,且只能是2n +1, 2n +7, 2n +13.(1)中能被5整除的数最多有2个,且只能是2n +1,2n +11或者2n +3，2n +13;(1)中能被7整除的数最多有1个;(1)中能被11整除的数最多有1个.下面证明(1)中能被3 或5 整除的数的个数不超过4.若能被3整除的数只有2个，显然能能被3 或5 整除的数的个数不超过4. 若能被3整除的数有3个，不管什么情况，能被3整除的数和能被5整除的数，必有一个重合. 能被3整除和能被5整除的数一共不能超过4个.除了能被3 或5 整除的数外，还余下3个.但能被7或11整除的数最多只有2个，因此，必有一个数不能含有质因子3，5，7，11.即这个数不能被3, 5, 7, 11中的任何一个整除.答.k的最小值是7。

第十六届“华杯赛”小学组决赛试题A答案

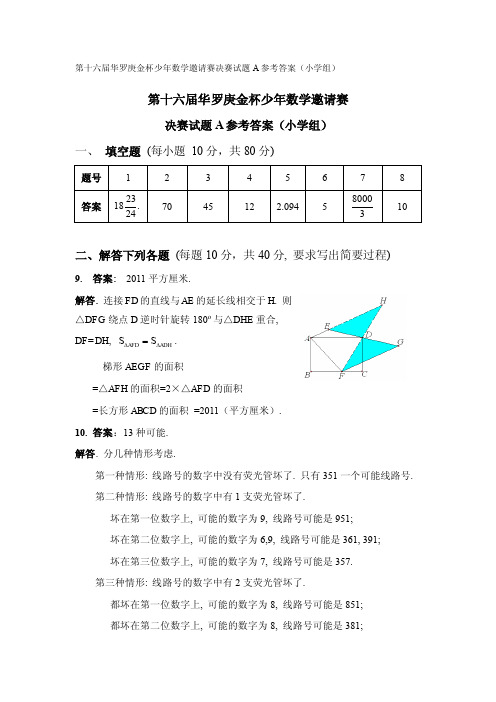
第十六届华罗庚金杯少年数学邀请赛决赛试题A 参考答案（小学组）一、填空题 (每小题 10分，共80分)二、解答下列各题 (每题10分，共40分, 要求写出简要过程)9. 答案: 2011平方厘米.解答. 连接FD 的直线与AE 的延长线相交于H . 则△DFG 绕点D 逆时针旋转180o 与△DHE 重合,DF=DH , ADH AFD S S ∆∆=.梯形AEGF 的面积=△AFH 的面积=2×△AFD 的面积=长方形ABCD 的面积 =2011（平方厘米）.10. 答案：13种可能.解答. 分几种情形考虑.第一种情形: 线路号的数字中没有荧光管坏了. 只有351一个可能线路号. 第二种情形: 线路号的数字中有1支荧光管坏了.坏在第一位数字上, 可能的数字为9, 线路号可能是951;坏在第二位数字上, 可能的数字为6,9, 线路号可能是361, 391;坏在第三位数字上, 可能的数字为7, 线路号可能是357.第三种情形: 线路号的数字中有2支荧光管坏了.都坏在第一位数字上, 可能的数字为8, 线路号可能是851;都坏在第二位数字上, 可能的数字为8, 线路号可能是381;都坏在第三位数字上, 可能的数字为4, 线路号可能是354;坏在第一、二位数字上, 第一位数字可能的数字为9，第二位数字可能的数字为6，9, 线路号可能是961， 991;坏在第一、三位数字上, 第一位数字可能的数字为9，第三位数字可能的数字为7, 线路号可能是957;坏在第二、三位数字上,第二位数字可能的数字为6，9, 第三位数字可能的数字为7，线路号可能是367, 397.所以可能的线路号有13个:351,354,357,361,367,381,391,397,851,951,957,961,991.11. 答案: 3, 5.解答. 设这个月的第一个星期日是a 日（71≤≤a ）, 则这个月内星期日的日期是a k +7, k 是自然数, 317≤+a k . 要求有三个奇数.当a =1时, 要使7k +1是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时,177+=+k a k 分别为1, 15, 29, 这时20号是星期五.当a =2时, 要使7k +2是奇数, k 为奇数, 即k 可取1, 3两个值, 7k +2不可能有三个奇数.当a =3时, 要使7k +3是奇数, k 为偶数, 即k 可取0, 2, 4三个值, 此时377+=+k a k 分别为3, 17, 31, 这时20号是星期三.当74≤≤a 时, a k +7不可能有三个奇数.12. 答案: 253.解：令k m 15=, k 是自然数, 首先考虑满足下式的最大的m ,.201115151153152151≤⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡m m 于是.2011213152)1(1515)1(152151150151511531521512≤-=+-=+⨯-++⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡k k k k k kk m m 因此.402213152≤-k k 又40224114171317152>=⨯-⨯, 40223632161316152<=⨯-⨯,得知k 最大可以取16. 当16=k 时, m =240. 注意到这时312161952363220112131520112+⨯==-=--k k . 注意到20112024131618161513151615121516152151615115161515161511516152151>=⨯+=⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡+⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡-⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ 而201120081216181615121516153152151<=⨯+=⎥⎦⎤⎢⎣⎡+⨯++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ .所以253 是满足题目要求的n的最小值.三、解答下列各题(每小题15分，共30分，要求写出详细过程)13.答案: 312解答. 由于2+0+1+1=4 且0+1+2+3+4+6+7+8+9=40, 4≡40(mod 9), 所以, 九个不同的汉字代表的数字：0, 1, 2, 3, 4, 6, 7, 8, 9.易知：40-4=36, 36÷9=4（次）, 说明此算式共发生四次进位.“4=2+2=1+1+2=1+2+1”显然：①华=1, “4=2+2”无解②华=1, “4=1+1+2”有解A:28+937+1046=2011, 可组成算式36种（6×6×1=36）B：69+738+1204=2011, 可组成算式48种（6×4×2=48）C：79+628+1304=2011, 可组成算式48种（6×4×2=48）③华=1, “4=1+2+1”有解A：46+872+1093=2011, 可组成算式36种（6×6×1=36）B：98+673+1240=2011, 可组成算式72种（6×6×2=72）C：97+684+1230=2011, 可组成算式72种（6×6×2=72）总计：72×3+96=216+96=312（种）.14.解答. 如左下图, 设M, N, P分别为棱GC, GF, GH的中点, 'M, 'N, 'P 分别为棱AE, AD, AB的中点, O为正方体的中心(长方形BDHF的中心).(1)第一只蜘蛛甲可以把爬虫控制在右上图所示的范围内.首先蜘蛛甲做与爬虫关于点O的对称方向的移动, 不妨设爬虫由G沿棱GC 向点M移动, 蜘蛛甲由A沿棱AE向点'M移动, 爬虫被限制在GM上. 当爬虫到达点M时, 蜘蛛甲也同时到达点'M. 然后蜘蛛甲改变策略, 做与爬虫关于平面BDHF对称的方向移动.a) 当爬虫到达点B, D, F, H时, 蜘蛛甲捉住爬虫.b) 当爬虫未到达点B, D, F, H时, 爬虫被控制在左上图所示的范围内.(2) 蜘蛛乙先移动到点G, 由于右上图无环路, 蜘蛛乙可以跟在爬虫后面, 总可以捉住爬虫.。

第十六届华罗庚金杯少年数学邀请赛决赛试卷(七年级组A卷)含答案

二、解答下列各题 (每题 10 分, 共 40 分, 要求写出解题过程)
9、一本书标有 2011 页, 从第一页开始每 11 页就在最后一页的页面加注一个红圈, 直到末页. 然后从末页开始向前, 每 21 页也在最前一页加注一个红圈, 直到第一页. 问一共有多少页加注了两个红圈, 并写出它们的页面号码. 10、如图, M , N 分别为四边形 ABCD对角线 AC、BD 的中点 , 过 M、N 的直线分别交 CD、AB 于 E、F . 如果三角形 ABE 的面积为 45, 求三角形 CDF 的面积. 11、设 S1 | x1 |, S 2 | S1 x2 |, , S n | S n 1 xn | , 将1, 2, 3, , 2011这些数适当地分配给 x1 , x2 , x3 , , x2011 , 使得 S 2011 尽量大, 那么 S 2011 最大是多少？ 12、求所有正整数 x, y, 使得 x2＋3y 与 y2＋3x 都是完全平方数．
m 1 0 0 2k 3， 1
由
100 2k 3 1 2 0 11 k 0 。 8
所以，两圈重合的页面有 9 页。 10. 答案：45 解：因为 M 是 AC 的中点，所以 A与C到EF 的距离相等，因此 S AEF S CEF 。同理： S BEF S DEF 。两式相加可得 S ABE S CDF 。
选手诚信协议：
在参加本次“华杯赛”活动期间，我确定没有就所涉及的问题或结论，与任何人、用任何方式进行交流或讨论．我确定本试卷的答案均为我个人独立完成的成果，否则愿接受本次成绩无效的处罚．我同意遵守以上协议．选手签名： .
一、填空题（每小题 10 分, 共 80 分）
1、公交车的线路号是由数字显示器显示的三位数, 其中每个数字是由横竖放置的七支荧光管显示, 如下图所示.

2011、2012年华罗庚金杯少年数学邀请赛决赛真题及详解

2011、2012年华罗庚金杯少年数学邀请赛决赛真题及详解第十六届华罗庚金杯少年数学邀请赛决赛试题A （小学组）（时间: 2011年4月16日10:00～11:30）一、填空题（每小题 10分, 共80分） 1. 135713572468+++= . 2. 工程队的8个人用30天完成了某项工程的31, 接着增加了4个人完成其余的工程, 那么完成这项工程共用了天. 3. 甲乙两人骑自行车同时从A 地出发去B 地, 甲的车速是乙的车速的1.2倍. 乙骑了5千米后, 自行车出现故障, 耽误的时间可以骑全程的61. 排除故障后, 乙的速度提高了60%, 结果甲乙同时到达B 地. 那么A, B 两地之间的距离为千米. 4. 在火车站的钟楼上装有一个电子报时钟, 在圆形钟面的边界, 每分钟的刻度处都有一个小彩灯. 晚上9时35分20秒时, 在分针与时针所夹的锐角内有个小彩灯. 5. 在边长为1厘米的正方形ABCD 中, 分别以A , B , C , D 为圆心, 1厘米为半径画四分之一圆, 交点E , F , G , H , 如图所示. 则中间阴影部分的周长为厘米.（取圆周率 3.141π=） 6. 用40元钱购买单价分别为2元、5元和11元的三种练习本, 每种至少买一本, 而且钱恰好花完. 则不同的购买方法有种.7. 已知某个几何体的三视图如右图,根据图中标示的尺寸（单位: 厘米）,这个几何体的体积是（立方厘米）.学校____________姓名_________参赛证号密封线内请勿答题8. 将自然数1~22分别填在下面的“□”内(每个“□”只能填一个数), 在形成的11个分数中, 分数值为整数的最多能有个.二、解答下列各题（每题10分, 共40分, 要求写出简要过程）9. 长方形ABCD 的面积是2011平方厘米. 梯形AFGE的顶点F 在BC 上, D 是腰EG 的中点. 试求梯形AFGE 的面积.10. 公交车的线路号是由数字显示器显示的三位数,其中每个数字是由横竖放置的七支荧光管显示,如右图所示. 某公交车的数字显示器有两支坏了的荧光管不亮, 显示的线路号为“351”, 则该公交车的线路号有哪些可能?11. 设某年中有一个月里有三个星期日的日期为奇数, 则这个月的20日可能是星期几?12. 以[]x 表示不超过x 的最大整数, 设自然数n 满足201115151153152151>⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡n n , 则n 的最小值是多少?三、解答下列各题（每小题 15分，共30分，要求写出详细过程）13. 在右面的加法竖式中, 不同的汉字代表不同的数字. 问: 满足要求的不同算式共有多少种?14. 如图, 两只蜘蛛同处在一个正方体的顶点A , 而一只爬虫处在A 的体对顶点G . 假设蜘蛛和爬虫均以同样的速度沿正方体的棱移动, 任何时候它们都知道彼此的位置, 蜘蛛能预判爬虫的爬行方向. 试给出一个两只蜘蛛必定捉住爬虫的方案.2011年“华杯赛”复赛小学组试题及详解第16届华杯赛复赛小学组试题及详解1. 原式=(2+4+6+8)-(1/2+1/4+1/6+1/8)=20-(1+1/24)=18+23/24。

第十六届“华杯赛”小学组决赛试题D答案

第十六届华罗庚金杯少年数学邀请赛决赛试题D 参考答案（小学组）一、填空题 (每小题 10分，共80分)二、解答下列各题 (每题10分，共40分, 要求写出简要过程)9. 答案: 1901解答. 因为华杯决赛是四位数, 十六届是三位数, 兔年是两位数, 所以等式成立时有华杯决赛=19011010020112011=--≤--兔年十六届.当华杯决赛=1901, 十六届=100, 兔年=10时题目要求的等式成立. 10. 答案: 52.5.解答：因为DE AC //，所以COD AOE S S ∆∆=.又CDE COD S S CE OC ∆∆=，EACCODEAC AOE S S S S CE OE ∆∆∆∆==，所以=OE OC CDEEACS S ∆∆. 因为三角形EAC 在边AC 上的高和三角形CDE 在边DE 上的高相等，所以21===∆∆DE AC S S OE OC CDE EAC . 因为21==∆∆OE OC S S DOE COD , 所以202==∆∆COD DOE S S . 因为21==∆∆OE OC S S AOE AOC , 所以52121===∆∆∆COD AOE AOC S S S . 所以15=+=∆∆∆AOE AOC ACE S S S .因为CE AB //，所以21==∆∆CE AB S S ACE ABC ，即5.721==∆∆ACE ABC S S . 所以5.52=+++=∆∆∆∆DOE COD ACE ABC ABCDE S S S S S .11. 答案: 7.解答. 每张卡片, 所写数字有几个约数就被翻过几次. 被翻了奇数次的卡片红色面朝上, 而只有完全平方数才能有奇数个约数, 所以本题也就是求写有完全平方数的卡片有几张, 而50765432112222222<<<<<<<≤,所以红色朝上的卡片共有7张. 12. 答案： 11厘米. 解答. 如图,球的内接正方体ABCD -A 1B 1C 1D 1的顶点在球面上, 它的（体）对角线AC 1就是球的直径, 即201021=⨯=AC (厘米).由图形的对称性, 可知 1111190,90AA C A B C ∠=︒∠=︒. 设正方体的棱长为a 即11111AA A B B C a ===, 连续用勾股定理两次, 得到2222221111112,3AC a AC AA AC a ==+=,则2224001320400,13333a a ====. 显然, 只要一个正方体的棱长a 为整数, 满足2133a ≤, 那么这个正方体一定可以放入球中, 因为 221112113314412=<<=. 故所求的棱长为整数的正方体的最大棱长等于11厘米.三、解答下列各题 (每小题 15分，共30分，要求写出详细过程)13. 答案: 2004, 2032, 2060, 2088.解答. 根据题意, 符合题意的年份必定是闰年(二月有29天), 并且二月一日恰好是星期日, 所以得先找到二十一世纪第一个二月一日是星期日的年份.根据题意, 2011年4月16日是星期六, 可倒推得2004年2月1日是星期日.这样可按每隔4⨯7(28)年为一个周期推算, 二十一世纪符合题意的年份有2004, 2032, 2060和2088年, 共有4个. 14. 答案:51703475，解答. 设这两个最简分数为am bk 和cm dk, 其中:()1b,d =；（1） ()1a,c =；（2） ()1am,bk =；()1cm,dk =. （3）既然cm am m -=, 所以有1a c -=. （4）又因为[]1050123557am,cm ==⨯⨯⨯⨯⨯，并结合（4），可得到: ① 14c =， 15a =，5m =，此时，757056bk dk -=，或 151416bk dk -=；（5） ② 6c =， 7a =，55m =⨯，此时，756516bk dk ⨯⨯-=；（6） ③ 5c =， 6a =，57m =⨯，此时，675716bk dk ⨯⨯-=；（7） ④ 2c =， 3a =，557m =⨯⨯，此时，35725716bk dk ⨯⨯⨯⨯-=；（8） ⑤ 1c =， 2a =，3557m =⨯⨯⨯，此时，235735716bk dk ⨯⨯⨯⨯⨯-=. （9）上面第（6）式中，756576156bk dk bk dk ⨯⨯⎛⎫-=⨯-= ⎪⎝⎭，结合条件（1），必有5k ，即k 有约数5，和（3）矛盾. 即151416b k d k -=无解. 同样，(7) ，(8) 和 (9) 中，必有7k , 均和（3）矛盾，即都无解. 仅考虑（5），151416bk dk -=，151415141161514d bkbd bk dkkbd d b--===-，（10)根据（1），（2）和（3），应当有()()15141 15141b,d b ,d ,d b -=-=，此即意味着：n b d k ⨯-=)1415(，（11）并且（10）变形为11123nbd =⨯⨯，即n,b,d 只能取1，2，3，6. 由（3）和（11），可知：()()151141n,,n,==，因此得1n =. 同样，()151b,=，()141d ,=，因此可得：23b ,d ==. 所以()2151434bk d b =⨯-=，()3151451dk d b =⨯-=. 这两个分数是7534和7051.。

16届华杯赛决赛试题及答案

第十六届华罗庚金杯少年数学邀请赛决赛试题A (初中组)决赛试题A （初中组）（时间: 2011年4月16日14:00～15:30）一、填空题（每小题 10分, 共80分）1. 计算:)161()21()3(12012.13--⨯-÷-+-÷-= .2. 算式: 兔兔兔兔兔兔吉祥如意兔年兔=⨯⨯中的汉字代表0～9的数字, 相同的汉字代表相同的数字, 不同的汉字代表不同的数字, 吉祥如意所代表的四位数是 .3. 将12个小球放入编号为1至4的四个盒子中, 每个盒子中的小球数不小于盒子编号数, 那么共有种不同的放法．4. 有一列数, 第一个数是10, 第二个数是20, 从第三个数开始, 每个数都是前面所有数的平均数, 那么第2011个数是 . 5. 设x 是有理数, 962363-+-+-++=x x x x P , 则P 的最小值为 . 6. 将自然数1~22分别填在下面的“□”内（每个“□”只能填一个数）, 在形成的11个分数中, 分数值为整数的最多能有个.7. 下面两串单项式各有2011个单项式:2457831326028602960316032n n xy ,x y ,x y ,,x y,,xy,xy++10058100571005310052352513128732,,,,,,yxyxy xy xy x y x m m ++其中m n ,为非负整数, 则这两串单项式中共有对同类项.8. 将能被3整除、被5除余2、被11除余4的所有这种正整数依照从小到大的顺序排成一列, 记为1234,,,,a a a a . 如果12011n n a a -<<, 则n 等于二、解答下列各题（每题10分, 共40分, 要求写出简要过程）9. 将9个各不相同的正整数填在3×3表格的格子中, 一个格子填一个数, 使得每个2×2子表格中四个数的和都恰好等于100. 求这9个正整数总和的最小值.10. 右图中, 平行四边形ABCD 的面积等于1, F是BC 上一点, AC 与DF 交于E , 已知3B F F C=,则三角形CEF 的面积是多少？11. 设p n m ,,为非零自然数, p n m ≥≥, 且满足方程:27)38)(38)(38(mnp p n m =---. 问p 的最大值等于多少？12. 如图, 如果将梯形ABCD 分割成一个平行四边形ABCE 和一个三角形AED ,AB =3238米, BC =3226米, CD =72米,AD =20米, 那么四边形ABCE ，三角形AED ，梯形ABCD 的面积分别是多少平方米？三、解答下列各题（每小题 15分, 共30分, 要求写出详细过程）13. 在边长为1厘米的正方形ABCD 中, 分别以A , B , C , D为圆心, 1厘米为半径画圆弧, 交点E , F , G , H , 如图所示. 求中间阴影六边形BEFDGH 的面积.14. 已知m xx =-1, 是否存在整数m 使得441xx +为完全平方数？如果存在, 求出整数m ；若不存在, 请说明理由.图1 图2D第十六届华罗庚金杯少年数学邀请赛决赛试题A 参考答案（初中组）一、填空题 (每小题 10分，共80分)二、解答下列各题 (每题10分，共40分, 要求写出简要过程)9. 答案：121 10. 答案14011. 答案：412. 答案：ABCE 的面积是61832(平方米)三角形ADE 的面积是26632(平方米)梯形的ABCD 面积是88531(平方米)三、解答下列各题 (每小题 15分，共30分，要求写出详细过程)13. 答：12平方厘米.解：如图，连接AF , AE, 则,,ADF AFE AEB ∆∆∆都是顶角为30 ，两腰为1厘米的等腰三角形.其面积相等. 自点F 作FP AD ⊥于P . 则1,2F P =因此三角形ADF 的面积1111.224=⨯⨯= 所以五边形ABEFD 的面积=34（平方厘米）. 同理，五边形BCDGH 的面积=34（平方厘米）.而正方形ABCD 的面积为1平方厘米.D由面积重叠原理可知，重叠部分为阴影六边形BEFDGH ，它的面积为3311442+-=（平方厘米）.14. 答案：不存在解：若存在整数m 使得441xx +为完全平方数，则设存在正整数n 使得，2441n xx =+.因为m x x =-1，所以21222+=+m xx .所以2)2(12244-+=+m xx .所以2222)2(n m =-+. 即2))(2(22=+-+n m n m .因为n m -+22与n m ++22的奇偶性相同，且2是偶数，所以n m -+22与n m ++22都是偶数.因为))(2(22n m n m +-+是4的倍数，但是2不是4的倍数，矛盾！所以不存在整数m 使得441xx +为完全平方数.。

第十六届华罗庚数学奖

第十六届华罗庚数学奖数学是一门深奥的学科，它的研究对象是数量、结构、变化和空间等方面的规律和关系。

数学在现代科技和经济发展中起着至关重要的作用。

而华罗庚数学奖则是中国数学领域的最高荣誉之一，每年评选出杰出的数学家和数学研究成果。

第十六届华罗庚数学奖于2021年9月7日在南京揭晓，共有6名数学家获得了这一殊荣，分别是张益唐、李中华、刘洪涛、刘炳良、郭宇航和杨瑜。

他们的研究领域涉及到了代数几何、微分拓扑、非线性偏微分方程、代数数论等多个方面。

其中，张益唐教授获得了华罗庚数学奖的最高荣誉——华罗庚数学奖特别奖。

张益唐教授是中国科学院数学与系统科学研究院研究员，他在代数几何领域做出了卓越的贡献。

他的主要研究方向是代数几何和算术几何，在代数几何的多个分支领域中都有深入的研究。

他的成果涉及到了代数曲面的分类、有理曲面的有理点、几何不变量、特征类等方面，对代数几何领域的发展做出了重要的贡献。

李中华教授、刘洪涛教授和刘炳良教授获得了华罗庚数学奖一等奖。

李中华教授是北京大学数学科学学院教授，他在微分拓扑领域的研究中取得了卓越的成果。

他主要关注的是微分拓扑中的奇异点理论，他的研究成果包括了拓扑奇异点的分类、拓扑奇异点的同伦不变量、拓扑奇异点的联系等方面。

刘洪涛教授是中国科学院数学与系统科学研究院研究员，他在非线性偏微分方程领域的研究中取得了卓越的成果。

他的研究涉及到了非线性波动方程、非线性双曲方程、非线性抛物方程等多个方面，他的研究成果对非线性偏微分方程理论的发展和应用产生了重要的影响。

刘炳良教授是中国科学院数学与系统科学研究院研究员，他在代数数论领域的研究中取得了卓越的成果。

他的主要研究方向是代数数论中的Galois表示和L函数，他的研究成果包括了Galois表示的结构和分类、L函数的性质和应用等方面，对代数数论领域的发展做出了重要的贡献。

郭宇航教授和杨瑜教授获得了华罗庚数学奖二等奖。

郭宇航教授是中国科学院大学数学科学学院教授，他在代数几何领域的研究中取得了卓越的成果。

第十六届全国“华罗庚金杯”少年数学邀请赛总决赛

第十六届全国“华罗庚金杯”少年数学邀请赛总决赛数学文化节方案一、指导思想第十六届全国“华罗庚金杯”少年数学邀请赛总决赛数学文化节旨在传承华罗庚精神，引导青少年热爱数学，立志成才。

让青少年在活动中感受数学与生活的自然融合，感受数学的奇巧和缜密。

在活动中提升思维、在挑战中享受快乐。

让数学不仅成为智者的游戏，更成就游戏者的智慧。

二、活动主题快乐与数学同行，智慧随思维生长三、活动目的以丰富多彩、趣味纷呈的数学活动为载体，让学生充分感受数学文化，品味数学魅力。

激发学生“爱数学，数学有无尽的乐趣；学数学，数学有无穷的奥妙；用数学，数学有无限的未来”的热情。

四、活动时间2011年7月24日上午9:00---11:30五、活动地点惠州市华罗庚中学六、活动内容及时间安排（一）华罗庚足迹1、参观华罗庚纪念馆负责人：龙静瑶2、华罗庚事迹循环播放负责人：易舒婷（二）数学文化展示1、分“数学之史、数学之美、数学之思、数学之用、数学之语”五个主题布置展板。

地点：华罗庚广场解说：数学社学生负责人：戴辉2、数学文化节优秀宣传语展、数学文化节优秀会标展、数学海报展。

负责人：张启龙实施：由数学社征集数学文化节宣传语和数学文化节会标，集训部、高一和高二开展数学海报比赛3、活动主题展板、活动内容展板、悬挂宣传条幅(每一个游戏场地一条标语)和彩旗。

负责人：刘卫忠4、数学PPT图片和学校简介（电脑播放）（高一阶梯教室）负责人: 熊伟（三）数学智慧活动数学智慧活动九项（专家讲座除外）若晴天则全部放在华罗庚广场举行，各摊位图附后：数学智慧活动九项（专家讲座除外）若雨天则活动地点如下：时间活动内容（雨天）地点学生负责人主要负责人9:00—10:00 专家讲座-罗增高三阶梯课室范恩辉、韩荣兰儒教授9:00—10:30 数学快乐大本营华杯楼报告厅欧阳鑫科甄红、陈宇祥、钟跟、陈皓璇、罗仕平、黄春秀、左静、石丹慧、张丽君9:00—11:30 勇士飞行学生发展中心赖文峰陈冠宁、陈超、邓宏昌、刘勇、黄裕琴、张开河9:00—11:30 挑战24点高三楼下朱舒婷曾中华、黄德华、凡永生9:00—11:30 数学大擂台高二阶梯教室张冬霞向才兵、代军、张小华、张翼帆9:00—11:30 魔方转转转高一楼下刘德彪罗衾、陶艾、温雅萍、张启龙9:00—11:30 数字幻方游戏高二楼下曾育晶何小华、韩建军、刘锦霞、周筱恵、谢龙运9:00—11:30 数学百宝箱高一阶梯教室徐煜淇袁劲竹、曾辉、、艾亚丽、张逸超9:00—11:30 七巧板拼图游戏学生发展中心赵雪儿游兆龙、于中洲、吉世龙、袁丽英、夏玉梅9:00—11:30 数学谜语高二与高三廊黄园芳汪毅刚、刘宝林、徐桂芳、黄琼兰、李伟文七、华杯赛数学文化节活动指南（见附件一）八、组织机构和保障措施（一）成立华杯赛数学文化节领导小组市教育局分管领导：骆平书记组长：戴立波副组长：吴永丹、宋词、黄进添、姜前勇、涂光峰成员：戴辉、杨永强、范恩辉、李京华、陈翰生、谢林海、张毅、丁志勇、刘卫忠、周淼淼、甄红、韩荣兰、张启龙、解凤英、陈冠宁、黄伟周、陈倬飞、黎润秋、刘宝林、陈宇祥、曾中华、向才兵、罗衾、何小华、袁劲竹、游兆龙、汪毅刚、吉世龙、钟跟、石丹慧、左静、谭卉、张丽君宣传接待：杨永强、陈翰生、周淼淼、凌丽聪保卫：杨永强、黄伟周及护校队成员音响：谢林海、张毅、熊伟、曾雨挺奖品：张启龙、吉世龙、熊伟、林惠琦（二）第十六届华杯赛数学文化节所需材料清单（见附件二）、所需奖品清单（见附件三）。

2011-2016年第16-22届华罗庚杯少年数学邀请赛几何试题(小学高年级组)全解析

B
2011年第16届华罗庚杯少年数学邀请赛决赛C几何试题长方形ABCD的面积为70，梯形AFGE的顶点F在BC上，D是EG的中点，则梯形AFGE的的面积是（）。
E A D
G
B
F
C
长方形ABCD的面积为70，梯形AFGE的顶点F在BC上，D是EG的中点，则梯形AFGE的的面积是（）。解1：连接DF， E A D S△ADF= G
��
利用蝴蝶模型，在梯形AFGE中， S□ AFGE
利用蝴蝶模型，在长方形ABCD中， S△ADF=
��
S□ ABCD
B
F
C
故： S□ AFGE= S□ ABCD=70
长方形ABCD的面积为70，梯形AFGE的顶点F在BC上，D是EG的中点，则梯形AFGE的的面积是（）。
一个长40、宽25、高60的无盖长方体容器（厚度忽略不计）盛有水，深度为a，其中0 ˂a ≤60，现将棱长尾10的长方体铁块放在容器底面，问放入铁块后水深是（）。
1
2
3
分析：无盖长方体容器盛有水情况有三种： 1、水很满；放入铁块后，水溢出； 2、水深很浅，放入铁块后，铁块一部分在水中，另一部分露出水面，水面也有升高。
A
由三角形AFC的面积和四边形DBEF的面积相等，得： S△AEC=S△BCD,则：�� × �� = �� × �� 由于BD:AB=DM:AN=1：3，则：EC:BC=1：3
E
A
O C D
B
如图所示，AB∥CE，AC ∥ DE,且AB=AC=5，CE=DE=10。若

少年数学邀请赛总决赛

明确职责，各归其位，确保总决赛顺利开展，特制订本方案。

一、活动名称第十六届“华罗庚金杯”少年数学邀请赛总决赛二、活动宗旨弘扬华罗庚教授的爱国主义精神，学习华罗庚教授勤奋学习，献身科学的优秀品质三、参加单位及人数全国100个城市组队参赛，约1000余人四、时间与地点2011年7月22日至25日在我校举行五、主要工作（一）负责国内代表队接待工作（二）负责笔试考务工作（三）数学文化节活动六、工作领导小组组长：戴立波副组长：吴永丹、宋词、黄进添（协调）、姜前勇、涂光峰、张开河成员：戴辉、杨永强、范恩辉、蓝世剑、陈翰生、章智良、李京华、李茂恒、谢林海、石丽萍、侯粤春、杨元高、唐福东、韩建军、刘刚利、解凤英、张毅、刘卫忠、周淼淼、丁志勇、甄红、周铭耿、范碧珊、王文广、黄伟周、韩荣兰、闵庆田、张启龙、万金花、邓勇威、陈倬飞、邓亚军、张晓红、陈冠宁、邓勇威、黎润秋七、具体相关工作组（一）会务组组长：宋词组员：杨永强、李小艳、黄碧婷、莫永壮、范文静、罗丹主要职责：1、负责贵宾接待工作2、负责活动期间校内相关会议安排3、负责国内代表队派发相关资料（“华杯赛”活动指南、考务手册、文化节活动资料、学校宣传资料等）4、负责组织、安排国内参赛代表每天参加比赛及有关活动5、负责与市会务组联系、沟通协调6、负责车辆安排工作（二）考务组组长：黄进添组员：戴辉、杨永强、范恩辉、谢林海、陈翰生、李京华、丁志勇、甄红、张启龙、韩荣兰、黎润秋、熊伟、林惠琦、曾雨挺、戴慧婷主要职责：1、安排考务办公室、考场、报告厅、休息室、医疗室；2、培训、安排70名监考教师、考务工作人员；3、组织考试等工作。

（三）接待组惠州宾馆接待组：邓振武、高二（11）班4名学生惠州金华悦国际酒店接待组：操瑞英、高一（11）班4名学生学校接待组总负责：戴立波具体负责人：一二组吴永丹，三四五组姜前勇，一组：黑龙江、吉林、辽宁、内蒙古组长：章智良谢凤英组员：陈倬飞、陈婕、龙静瑶、李惠珠、易舒婷、刘智皓二组：河北、山西、山东、陕西、河南、北京、天津组长：张毅张晓虹组员：万金花、朱春悠、林夏、李淑媛、童镜蓉、张莹蓥三组：宁夏、甘肃、青海、新疆、西藏、四川、重庆组长：范碧珊邓勇威组员：宁婧、王慧斌、邱惠茜、陈颖颖、刘蓓蓓、钟妙银四组：江苏、浙江、安徽、湖北、湖南、江西、贵州、上海组长：刘刚利邓亚军组员：杨谷、何贝雅、白晶晶、周锦梅、林丽、邹银芬五组：云南、广西、福建、海南、广东组长：杨元高王文广组员：刘鎏、杨君、黄颖媛、吴珊珊、黄云霞、黄春德主要职责：1、负责国内代表队参赛选手的接待工作（包括吃、住、行等活动）。

2020年第十六届“无悔金杯”少年数学邀请赛决赛试卷c(小学组)

2011年第十六届“华罗庚金杯”少年数学邀请赛决赛试卷C（小学组）一、填空题（每小题10分，共80分）1．（10分）3+5+7＝．2．（10分）工程队的8个人用30天完成了某项工程的，接着增加了4个人完成其余的工程，那么完成这项工程共用了天．3．（10分）甲乙两人骑自行车同时从A地出发去B地，甲的车速是乙的车速的1.2倍．乙骑了4千米后，自行车出现故障，耽误的时间可以骑全程的．排除故障后，乙的速度提高了60%，结果甲乙同时到达B地．那么A，B两地之间的距离为千米．4．（10分）在火车站的钟楼上装有一个电子报时钟，在圆形钟面的边界，每分钟的刻度处都有一个小彩灯．晚上9时37分20秒时，在分针与时针所夹的锐角内有个小彩灯．5．（10分）在边长为2厘米的正方形ABCD中，分别以A，B，C，D为圆心，2厘米为半径画四分之一圆，交点E，F，G，H，如图所示．则中间阴影部分的周长为厘米．（取圆周率π＝3.141）6．（10分）用同一种颜色对4×4方格的7个格子进行涂色，如果某列有涂色的方格则必须从最底下的格子逐格往上涂色，相邻两列中左侧的涂色的方格数大于或等于右侧涂色的方格数（如图）．那么共有种涂色的图案．7．已知某个几何体的三视图如右图，根据图中标示的尺寸（单位：厘米），这个几何体的体积是（立方厘米）8．（10分）公交车的线路号是由数字显示器显示的三位数，其中每个数字是由横竖放置的七支荧光管显示，如图所示．某公交车的数字显示器有一支坏了的荧光管不亮，显示的线路号为“351”，则可能的线路号有个．二、解答下列各题（每题10分，共40分，要求写出简要过程）9．（10分）在如图的加法竖式中，不同的汉字可以代表相同的数字，使得算式成立．在所有满足要求的算式中，四位数的最大值是多少？10．（10分）长方形ABCD的面积是70平方厘米．梯形AFGE的顶点F在BC上，D是腰EG的中点．试求梯形AFGE的面积．11．（10分）不能写成3个不相等的合数之和的最大奇数是．12．（10分）设某年中有一个月里有三个星期日的日期为奇数，则这个月的21日可能是星期几？三、解答下列各题（每小题15分，共30分，要求写出详细过程）13．（15分）以[x]表示不超过x的最大整数，设自然数n满足，则n的最小值是多少？14．（15分）一个长40、宽25、高60的无盖长方体容器（厚度忽略不计）盛有水，深度为a，其中0＜a≤60．现将棱长为10的立方体铁块放在容器的底面，问放入铁块后水深是多少？2011年第十六届“华罗庚金杯”少年数学邀请赛决赛试卷C（小学组）参考答案与试题解析一、填空题（每小题10分，共80分）1．（10分）3+5+7＝17．【分析】直接通分，化为同分母分数相加计算即可．【解答】解：3+5+7＝3+5+7＝17．故答案为：17．2．（10分）工程队的8个人用30天完成了某项工程的，接着增加了4个人完成其余的工程，那么完成这项工程共用了40天．【分析】把这项工程看作单位“1”，用“÷30÷8＝”求出1人1天的工作效率，则8+4＝12个人工作效率和为×12＝，剩下的工作总量是1﹣＝，然后根据：工作总量÷工作效率＝工作时间“求出后来用的时间，进而求出完成这项工程共用的时间．【解答】解：一个人的工作效率是：÷30÷8＝，8+4＝12（人）12个人的工作效率和为：×12＝，共需：（1﹣）÷+30＝10+30＝40（天）答：那么完成这项工程共用了40天．故答案为：40．3．（10分）甲乙两人骑自行车同时从A地出发去B地，甲的车速是乙的车速的1.2倍．乙骑了4千米后，自行车出现故障，耽误的时间可以骑全程的．排除故障后，乙的速度提高了60%，结果甲乙同时到达B地．那么A，B两地之间的距离为36千米．【分析】设A、B相距为X；乙的速度是V，则甲的速度为1.2V；当乙走了4000的时候，甲肯定走了4800；假设乙排除故障的时间为t，那这段时间甲走的距离为1.2V×（×）＝0.2X；我们假设从乙排除故障以后的时间为T，可列出：4800+0.2X+1.2VT＝4000+1.6VT；我们得出800+0.2X＝0.4VT；因为X＝4000+1.6VT，代入得出：VT＝20000，则进而算出X＝36000米＝36千米．【解答】解：设A、B相距为X；乙的速度是V，则甲的速度为1.2V：当乙走了4000的时候，甲走了：4000×1.2＝4800（米）；设乙排除故障的时间为t，那这段时间甲走的距离为：1.2V×（×）＝0.2X；设从乙排除故障以后的时间为T，可列出：4800+0.2X+1.2VT＝4000+1.6VT；得出800+0.2X＝0.4VT；因为X＝4000+1.6VT，代入得出：VT＝20000，把VT＝20000代入4800+0.2X+1.2VT＝4000+1.6VT，得出：X＝36000米＝36千米．答：A，B两地之间的：距离为36千米．故答案为：36．4．（10分）在火车站的钟楼上装有一个电子报时钟，在圆形钟面的边界，每分钟的刻度处都有一个小彩灯．晚上9时37分20秒时，在分针与时针所夹的锐角内有11个小彩灯．【分析】首先分析以整点钟面为例，当9点时再走37分20秒，计算出时针的路程和分针的路程找到中间的格数差即可．【解答】解：依题意可知：从晚上9点开始，分针走了37格20秒时，时针走（37+）×＝3；时针走了3格多．分针果了37，那么就是38到48之间的共有11个．故答案为：11．5．（10分）在边长为2厘米的正方形ABCD中，分别以A，B，C，D为圆心，2厘米为半径画四分之一圆，交点E，F，G，H，如图所示．则中间阴影部分的周长为 4.188厘米．（取圆周率π＝3.141）【分析】如图所示：由题意很容易就可以得出△ABF为等边三角形，则弧为圆的周长，同理弧也为圆的周长，所以弧＝+﹣＝圆的周长，同理其余三段也为圆的周长，故阴影部分图形的周长＝圆的周长，再据圆的周长公式即可得解．【解答】解：依题易知△ABF为等边三角形，故弧为圆的周长，同理弧也为圆的周长，所以弧＝+﹣＝圆的周长，同理其余三段也为圆的周长，故阴影部分的周长＝圆的周长＝＝4.188（厘米）；答：中间阴影部分的周长为4.188厘米．故答案为：4.188．6．（10分）用同一种颜色对4×4方格的7个格子进行涂色，如果某列有涂色的方格则必须从最底下的格子逐格往上涂色，相邻两列中左侧的涂色的方格数大于或等于右侧涂色的方格数（如图）．那么共有9种涂色的图案．【分析】按照要求把4x4方格的7个格子进行涂色，左侧的涂色的方格数大于或等于右侧涂色的方格数，把7分成几个数的和，左边的数最大是4，例如4+3＝7，涂在第一列开始到第三列开始有3种图案；3+2+2＝7，分别从1、2列开始涂色，有2种图案；3+2+1+1，只有从第1列开始涂色，有1种图案；4+1+1+1，只有从第1列开始涂色1种图案；4+2+1＝7，分别从1、2列开始涂色，有2种图案；把它们加起来，即可得解．【解答】解：如图，3+2+1+1+2＝9（种），答：那么共有9种涂色的图案．故答案为：9．7．已知某个几何体的三视图如右图，根据图中标示的尺寸（单位：厘米），这个几何体的体积是9000（立方厘米）【分析】观察三视图可知，原来的几何体是四棱锥，底面积为30×30，高为30，根据锥体的体积公式＝sh计算即可．【解答】解：观察三视图可知，原来的几何体是四棱锥，底面积为30×30，高为30，所以×30×30×30＝9000立方厘米，故答案为9000．8．（10分）公交车的线路号是由数字黑豆网https://黑豆网涵盖电影，电视剧，综艺，动漫等在线观看资源！金马医药招商网:金马医药招商网是专业提供医药代理招商的资讯信息发布平台，科技新闻网:科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料。

第10～16届全国华罗庚金杯少年数学邀请赛决赛试题详细解释答案

答案：10.695；13.计算机中最小的存储单位称为“位”，每个“位”有两种状态：0和1。

一个字节由8个“位”组成，记为B。

常用KB，MB等记存储空间的大小，其中1KB=1024B， 1MB=1024KB。

现将240MB的教育软件从网上下载，已经下载了70%。

如果当前的下载速度为每秒72KB，则下载完毕还需要（）分钟。

（精确到分钟）答案：174．a，b和c都是二位的自然数，a，b的个位分别是7与5，c的十位是1。

如果它们满足等式ab+c=2005，则a+b+c=( )。

答案：13：37．一列自然数0，1，2，3，…，2005，…，2004，第一个数是0，从第二个数开始，每一个都比它前一个大1，最后一个是2024。

现在将这列自然数排成以下数表：规定横排为行，竖排为列，则2005在数表中位于第（）行和第（）列。

答案：20；458．图2中，ABCD是长方形，E，F分别是AB，DA的中点，G是BF和DE的交点，四边形BCDG 的面积是40平方厘米，那么ABCD的面积是（）平方厘米。

图2答案：60二、解答下列各题，要求写出简要过程（每题10分，共40分）9．图3是由风筝形和镖形两种不同的砖铺设而成。