莱斯衰落信道的仿真程序

合集下载

移动通信论文--基于MCM法和Jakes法的Rayleigh信道仿真

基于MCM法和Jakes法的Rayleigh信道仿真组员冯晓东20111060220潘朝云20111060198高忠贤20111060195摘要瑞利衰落信道（Rayleigh fading channel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落”，并且其包络服从瑞利分布。

本次试验我们采用了蒙特克罗法和Jakes法进行Rayleigh信道时域仿真，并根据仿真信号得到仿真的Rayleigh概率密度函数（PDF），累积分布函数（CDF）以及多普勒功率谱，最后把得到的仿真结果与理论计算结果进行对比分析。

目录引言 (4)一、Rayleigh衰落概述 (4)1、瑞利衰落 (4)2、瑞利衰落适用环境 (4)3、模型 (5)4、应用 (6)5、失真和散射效应 (6)二、论题重述 (7)三、Matlab仿真过程 (7)1、蒙特卡罗法Rayleigh信道时域仿真 (7)（1）Rayleigh概率密度函数（PDF） (7)（2）累积分布函数（CDF） (8)（3）多普勒功率谱 (9)2、Jakes法Rayleigh信道时域仿真 (10)（1）Rayleigh概率密度函数（PDF） (10)（2）累积分布函数（CDF） (11)（3）多普勒功率谱 (11)五、仿真结果分析 (12)参考文献 (12)引言由于多径效应和移动台运动等影响因素，使得移动信道对传输信号在时间、频率和角度上造成了色散，即时间色散、频率色散、角度色散等等，因此多径信道的特性对通信质量有着重要的影响，而多径信道的包络统计特性则是我们研究的焦点。

根据不同无线环境，接收信号包络一般服从几种典型分布，如瑞利分布、莱斯分布等。

在此专门针对服从瑞利分布的多径信道进行模拟仿真，进一步加深对多径信道特性的了解。

从网络上参考的文章和资料来看，关于瑞利信道仿真主要使用MATLAB自带的瑞利信道仿真函数和瑞利信道的定义函数，这样做虽然利于仿真和简单的结果分析，但是由于其中部分参数采用定值代替变量，比如多普勒频率和多普勒系数，会使瑞利信道的特性不能够完全展现，本文将使用精确的算法，例如蒙特卡洛算法和Jakes法，会使结果更加准确，更能表现瑞利信道的特性。

莱斯衰落环境下图像信号游程编码和线性分组编码的仿真

莱斯衰落环境下图像信号游程编码和线性分组编码的仿真孟乐（淮阴工学院计算机工程学院，江苏淮安 223003）摘要：给出一副图像，对这幅图像在莱斯衰落环境下进行游程编码和线性分组编码的仿真。

首先我们对图像信号进行游程编码，游程编码是一个无损压缩编码，然后再进行线性分组编码，在进行这些编码后对图像数据中加入莱斯噪声，对图像数据进行译码，比较编码前和解压后图像数据的对比，不同信噪比下仿真的性能，最后得到重建后的图像，比较重建后的图像与原图像的区别。

关键词：图像信号；MATLAB；游程编码；线性分组编码；莱斯噪声中图法分类号：TP391.4 文献标识码：A 文章编号：1674-1374(2011)02-0152-04R i c e f a d i n g i m a g e s i g n a l r u n-l e n g t h e n c o d i n g a n d l i n e a rb l oc k c od i n g s i m u l a t i o ne n v i r o n m e n tMengle（Faculty of Computer Engineering, Huaiyin Institute of Technology, Huai’an Jiangsu, 223003）Abstract:Given a pair of images, the image of the site run-length encoding and linear block coding simulation at Rice fading environment. First, we run the image signal coding, run-length encoding is a lossless compression encoding, and then the linear block code, making these coded image data Royce added noise, the image data is decoded, before comparing the coding and decompression after comparing the image data, different SNR simulation performance, the final reconstructed image is obtained, and the difference between the original image and the comparison of the reconstructed image.Keywords: Image signal;MATLAB; RLE; linear block coding; Royce noise1引言图像是人类最重要、最有效、最常用和最方便的交换信息的方式。

衰落信道中无线通信系统性能的分析与仿真课程设计

******************实践教学*******************兰州理工大学计算机与通信学院2012年秋季学期通信系统综合训练题目：衰落信道中无线通信系统性能的分析与仿真专业班级：姓名：学号：指导教师：成绩：目录 (2)摘要 (3)第1 章前言 (4)第2 章总体设计方案 (5)2.1 64QAM通信系统基本组成 (5)2.2 64QAM通信系统的性能指标 (5)2.3 64QAM的误码率性能 (5)第3 章64QAM调制解调原理 (7)3.1 MQAM调制 (7)3.2 64MQAM调制及相干解调原理框图 (7)第4 章（7，4）循环码编码和译码 (9)4.1 循环码概念 (9)4.2 生成多项式 (9)4.3 循环码的编码及实现 (10)4.4 循环码的译码及实现 (12)第5 章SIMULINK与通信仿真 (15)5.1 SIMULINK简介 (15)5.2 SIMULINK操作 (16)第6 章SIMULINK对64QAM的仿真 (20)6.1 SIMULINK对主要模块及参数设置 (20)6.1.1信号源 (20)6.1.2基带信号处理 (20)6.1.3调制/解调 (21)6.1.4 其他模块参数设置 (22)6.1.5 信噪比--误码曲线实现程序如下。

(23)6.2 64QAM通信系统的仿真图和结果分析 (24)6.3 加入噪声及干扰时系统性能指标的变化分析 (27)6.3.1加入噪声及干扰时系统的仿真 (27)6.3.2结果分析 (31)6.3.3 不足与展望 (31)第7 章总结与致谢 (32)参考文献 (33)以多进制正交幅度调制技术(MQAM)为代表的多载波传输技术已经成为第四代移动通信系统中的关键技术。

MQAM能够有效抵抗多径衰落，并且频谱利用率高，适用于无线环境下的高速数据传输。

SIMULINK是MATLAB软件的扩展，它是实现动态系统建模和仿真的一个软件包，它的模块库包含了许多实现不同功能的模块，使得研究者可以方便地构建功能清晰、结构合理的仿真系统。

衰落信道的无线通信系统的分析与仿真

摘要为了更好的了解和掌握衰落信道中无线通信系统的性能，提出了基于MATLAB的无线衰落信道仿真模型，采用64QAM调制方式，信道编码用了（7,4）线性分组码，利用MATLAB中SIMULINK通信系统仿真模型库进行（7,4）线性分组码建模仿真，并调用通信系统功能函数进行绘制频谱及误码率与信噪比关系曲线图。

在完成衰落信道的性能分析之后，并与高斯信道下的性能进行对比。

关键字：SIMULINK 64QAM 无线衰落高斯信道仿真目录前言 (3)1 64QAM设计原理及衰落信道 (4)1.1 64QAM通信系统基本模型 (4)1.2 无线衰落信道 (4)1.3 64QAM调制技术 (5)1.4 64QAM调制的主要技术指标 (6)2 线性分组码基本原理 (7)2.1 线性分组码 (7)2.2 编码原理 (7)2.3 纠错原理 (9)3 SIMULINK 概述 (11)3.1 Simulink的模块操作 (11)3.1.1 主要模块的简介 (12)3.2 Simulink的功能 (12)4 衰落信道的性能分析与仿真 (14)4.1 SIMULINK中模块仿真 (14)4.1.1 信号源及模块参数 (15)4.1.2 线性分组码（7，4） (15)4.1.3 主要模块参数设置 (16)4.2 64QAM通信系统仿真 (17)4.3 性能分析 (19)总结 (20)参考文献 (21)致谢 (22)前言在卫星移动通信系统、陆地移动通信系统中其电波传播方式主要以视距传播为主。

由于多径和接收端运动等因素的影响，使得无线信道对接收信号在时间、频率和角度上造成了色散，这种色散表现在接收信号幅度上就是所谓的信号衰落，因此，多径效应对通信质量有着至关重要的影响。

正交幅度调制QAM是数字通信系统中一种常用的调制技术。

尤其是多进制QAM，比如64QAM有着非常高的频谱利用率。

它的调制效率高，对传输途径的信噪比要求高，具有带宽利用率高，抗噪声强等特点，适合有线电视电缆传输；我国有线电视网中广泛应用的DVB-C 调制即QAM 调制方式。

Rayleigh无线衰落信道的MATLAB仿真

通信原理课程设计报告书课题名称 Rayleigh 无线衰落信道的MATLAB 仿真姓名学号学院专业通信工程指导教师※※※※※※※※※ ※※ ※※ ※※通信工程专业通信原理课程设计年月日Rayleigh无线衰落信道的MATLAB仿真1 设计目的（1）对瑞利信道的数学分析，得出瑞利信道的数学模型。

（2）利用MATLAB对瑞利无线衰落信道进行编程。

（3）针对服从瑞利分布的多径信道进行模拟仿真，加深对多径信道特性的了解。

（4）对仿真后的结果进行分析，得出瑞利无线衰落信道的特性。

2 设计思路无线衰落信道的MATLAB仿真：（1）分析出无线信道符合瑞利概率密度分布函数，写出数学表达式。

（2）建立多径衰落信道的基本模型。

（3）对符合瑞利信道的路径衰落进行分析，并利用MATLAB进行仿真。

3 设计过程3.1 方案论证3.1.1．瑞利信道环境与数学模型瑞利衰落信道（Rayleigh fading channel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落”，并且其包括服从瑞利分布。

瑞利衰落属于小尺寸的衰落效应，它总是叠加于如阴影、衰减等大尺度衰落效应上。

信道衰落的快慢与发展端和接收端的相对运动速度的大小有关，相对运动对导致接受信号的多普勒频移，一固定信号通过单径的瑞利衰落信道后，在1秒内的能量波动，这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz，在GSM1800MHz的载波频率上，其相应的移动速度分别为约6千米每小时和60千米每小时。

特别需要注意的事信号“深衰落”现象，此时信号能量的衰减达到数千倍，即30到40分贝。

瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。

密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径，而且使得无线信号被衰减、反射、折射、衍射。

在曼哈顿的实验证明，当地的无线信道环境确实接近于瑞利衰落。

通信原理课程设计(Rummler衰落信道的仿真)

一、课程设计目的1．巩固所学的专业技术知识； 2．熟悉SystemView 仿真环境并能在其环境下了解并掌握通信系统的一般设计方法，具备初步的独立设计能力；3．提高综合运用所学理论知识独立分析和解决问题的能力； 4．更好地将理论与实践相结合。

二、设计方案的原理Rummler 衰落信道是一个三路径传输信道模型，由直射和反射能量混合而成，反射信号通过改变直射信道的幅度和相位而形成复合信号，这种三路径的衰落信道广泛应用于视距（LOS ）范围的数字微波中继通信链路的仿真，它是一个基于信道传输函数的统计模型。

三条路径的组成包括：一条直射路径、一个相对于直射路径延迟非常小的多径成分、一个相对于折射路径延时0τ的频率选择性控制路径。

因此接收信号可以描述为()()()()01τβτα-+-+=t x t t x t r这里()t x 表示发射信号，α、β为衰减系数，0τ、1τ表示两个相对延时，则信道的冲激响应可表示为()()()()01ττβτταδδτ-+-+=t h等价的信道低通传输函数为()01221τπτπβαf j f j e e f H --++=假设11<<ωτ，这里ω为调制信号的带宽，则上式进一步化简为021)(τπβαf j e f H -++=令ττ=0，则上式化简为()[]τπ)(201f f j be a f H ---=其中τ、a 、b 、0f 都是模型的统计参数，一般ns 3.6=τ，a 、b 和0f 也取相应的统计参数，a 是整个信号的衰落系数，b 是衰落深度，0f 的取值决定衰落位置。

信道的对应的时域表达式为()()()()()ττπττπ-+--=∧t x f ab t x f ab t ax t y 002sin 2cos )( 其中()τ-∧t x 为()τ-t x 1）的希尔伯特变换。

三、设计、调试及结果分析图（1）是应用Rummler衰落信道模型图符构建的实验仿真电路。

Rayleigh衰落信道的仿真模型_李子

文章编号:1009-3443(2004)02-0001-08Rayleigh 衰落信道的仿真模型李　子,　蔡跃明(解放军理工大学通信工程学院,江苏南京210007)摘　要:Rayleigh 衰落信道的仿真模型是许多信道仿真模型的基础。

用一个统一的表达式归纳和总结了各种Rayleigh 衰落信道仿真模型,根据表达式中参数的假设条件不同,将现有的仿真模型分为4类,分别讨论它们的均值、相关统计特性、平稳特性和各态历经特性。

通过对这些仿真模型的比较分析,可以看出,各态历经特性与相关特性的匹配是一对矛盾,不能同时满足。

在此基础上提出了一个高效的仿真模型应当满足的条件,这将有助于设计新的仿真模型。

关键词:信道模型;瑞利衰落;广义平稳;各态历经中图分类号:TN911.5文献标识码:ASimulation Models for R ayleigh Fading ChannelsL I Zi ,　CAI Yue -m ing(Instit ute o f Communications Engineering ,P L A U niv.of Sci.&T ech.,N anjing 210007,China)Abstract :Rayleigh fading channels are the fo unda tion of all cha nnel m odels.In this paper,sev eral kinds of the sim ula tion m odels of Rayleig h fading cha nnels by a uniform ex pression are sum mariv ed.Acco rding to the differences amo ng the a ssumed co ndition of the pa ram eters in the ex pression ,the simulatio n m odels fall into 4classes.Discussion is also made o f their m ean,cor relatio n,stationa ry and erg odicity.With the help of these discussio ns,it ca n be seen tha t the ergodicity and the fitting o f the sta tionary can 't exist simulta neously .Based on this ,some co nditio ns on an effectiv e channel m odel a re presented .And these conditions a re useful to desig n the new effectiv e channel m odels .Key words :channel m odel;Ray leigh fading;w ide-sense sta tio nary;ergodicity 收稿日期:2003-10-30.基金项目:江苏省自然科学基金资助项目(BK2003015).作者简介:李　子(1980-),男,硕士生. 无线通信系统的性能在很大程度上取决于无线信道。

无线设备测试的衰落仿真

无线设备测试的衰落仿真作者:Noah Schmitz，安捷伦科技公司无线设备产品经理从WLAN到W-CDMA，所有无线设备有一点是共同的，即没有有线连接。

通过空气传送的信号会因大气损伤而失真，会因自然的和人为的障碍而中断，也会因发射机和接收机的相对移动而进一步变化。

这种过程称为衰落。

衰落在现实环境中是不可避免的，因此无线通信系统必须能够在处理这个问题的同时，保持准确的数据传输能力。

对实际信道的衰落损伤进行仿真对无线设备的测试非常关键。

为精确地进行信道仿真，必须理解不同的衰落情形及其影响，并创建这些衰落效应的数学模型。

安捷伦科技提供了一个新型解决方案，用来在无线设备测试过程中仿真衰落，缓和信道仿真中某些最困难的、成本高昂的挑战。

在考虑解决方案之前，理解衰落的不同表现非常重要，衰落的不同表现有不同的成因，它们以各种方式影响着信道。

衰落的成因发射机和接收机之间要能够成功地进行通信，在一定程度上取决于信号在其中传播的信道的衰落特性。

大范围衰落包括信号经过长距离传播的效应（几百个波长或更多波长）。

小范围衰落机制则影响着接收机附近的信号。

大范围衰落包括信号经过一段距离时信号的平均衰减（在理想的视距传播（LOS）条件下，它与距离的平方成正比），以及大型物体（如山脉或摩天大楼）导致的信号衍射。

小范围衰落是多径传播和多普勒频移两者作用的结果。

由于被发送信号在遇到信箱、树木和正在移动的车辆时导致反射、衍射和局部散射，而通过不同的路径到达接收机，所以会发生多径衰落。

因此，接收机在不同的到达时间获得信号的多个拷贝（如图1）。

这些拷贝以不同的相位和功率电平进行接收，导致信号互相干扰而发生功率波动。

图1. 当发送信号在到达接收机的路径上遇到各种物体时，会发生多径衰落，导致其在略微不同的多个时间到达接收机。

多普勒频移衰落是移动的结果。

如果接收机相对于发射机正在移动，那么进入接收机的信号频率会发生变化，具体取决于接收机相对于发射机移动的方向和速度。

莱斯信道中QPSK信Maab仿真

1移动无线信道的定义及分类各类信号从发射端发送出去以后, 在到达接收端之前经历的所有路径统称为信道。

如果其中传输的是无线电信号, 电磁波所经历的路径称之为无线信道。

与其他通信信道相比, 无线信道是最为复杂的一种。

无线传播环境是影响无线通信系统的基本因素。

发射机与接受机之间的无线传播路径,因从经历简单的视距传播, 到遭遇各种复杂的地物（如建筑物、山脉和树林等）所引起的反射、绕射和散射传播等而显得非常复杂。

另外,移动台相对于发射台移动的方向和速度, 甚至收发双方附近的移动物体也对接受信号有很大的影响。

因此, 这使得无线信道具有极度的随机性。

移动通信信号在空间传播中所经历的衰落大体可以分为2类, 即大尺度衰落和小尺度衰落, 如图1所示。

大尺度衰落是因为发射机与接收机之间的距离和两者之间障碍物（如山丘、森林、建筑物等）的遮蔽影响而造成的信号强度的衰减, 它反映了移动信号在较大区域中的平均能量的减少或称为路径损失。

而小尺度衰落是指当移动台在一个较小的范围运动时, 引起接收信号的幅度、相位和到达角等的快速变化。

图1 移动无线信道的分类信号在传播的过程中, 受各种环境的影响会产生反射、衍射和散射, 这样就使得到达接收机的信号是许多路径信号的叠加, 因而这些多径信号的叠加在没有视距传播情况下的包络服从瑞利分布。

当多径信号中包含一条视距传播路径时, 多径信号就服从莱斯分布。

根据信号多径附加时延的大的移动性而导致接收到的信号产生多普勒频移( 频率色散), 根据多普勒扩展的大小, 信道又可以分为快衰落信道和慢衰落信道。

2瑞利分布和莱斯分布的特性在实际情况中对数字通信系统来说, 调制符号的周期比由多径传播引起的时延扩展要大, 因此在一个符号周期内的所有频率分量都会经历相同的衰减和相移。

信道对于所有频率分量来说是平坦的, 因而定义这类信道为平坦衰落信道。

理论分析和实测试验结果表明: 平坦衰落的幅度在大多数情况下, 符合瑞利分布(ray leighdistribution) 或莱斯分布(ricedistribution) 。

莱斯衰落环境下基于信道稀疏特征的MIMO系统信道估计方法

新技术·新业务DOI:10.3969/j.issn.1006-6403.2023.08.013莱斯衰落环境下基于信道稀疏特征的MIMO 系统信道估计方法［王新宇王鹏杜翠凤］提出一种莱斯衰落环境下基于信道稀疏特征的MIMO 系统信道估计方法。

首先，获取信道状态信息矩阵的近似估计值并采用编码器对信道状态信息矩阵进行特征提取；然后采用元素融合规则对不同类终端的信道状态信息矩阵特征进行融合，得到每一类终端的元素特征图；最后，计算各类终端的元素特征图的一致性，求解信道状态信息估计矩阵中每一个元素的权重，根据信道稀疏特征优化MIMO 信道状态信息矩阵，实现信道矩阵的校正。

仿真分析结果显示：在采样数据充足的情况下，方法的信道估计精度较高，其性能接近ReconNet 算法。

由此可知，算法在不需要稀疏度的和LOS 分量未知的情况下仍具有较高的信道估计精度。

王新宇现任职于广州杰赛通信规划设计院有限公司，高级工程师，本科毕业于南京理工大学，研究方向为移动通信无线网络规划关键技术等。

王鹏现任职于中国联合网络通信有限公司陕西省分公司，高级工程师，本科毕业于北京邮电大学，擅长移动通信核心网、物联网规划建设、行业应用，研究方向为移动核心网演进、物联网行业应用。

杜翠凤现任职于中电科普天科技股份有限公司运营商事业部，高级经济师，硕士毕业于广东外语外贸大学，通信创新院研究员。

研究方向为空天地一体化网络、人工智能、边缘计算等。

关键词：莱斯衰落环境信道稀疏特征信道估计 MIMO 系统摘要*1 引言5G 采用毫米波频段时，传播信道中含有丰富直视路径信号分量和多径散射反射信号分量，此时信道服从莱斯分布。

因此，在莱斯分布假设下，本文在LOS （Line of Sight ，视距）分量未知的情况下，在信道状态信息估计值的基础上，对每一个终端获得的信道状态信息估计矩阵进行元素级别特征融合，并采用F2范数求解每一个元素级特征的重要性，以此来优化信道估计矩阵的参数，实现信道估计矩阵的优化。

莱斯信道中QPSK信号Matlab仿真

1 移动无线信道的定义及分类各类信号从发射端发送出去以后,在到达接收端之前经历的所有路径统称为信道。

如果其中传输的是无线电信号,电磁波所经历的路径称之为无线信道。

与其他通信信道相比,无线信道是最为复杂的一种。

无线传播环境是影响无线通信系统的基本因素。

发射机与接受机之间的无线传播路径,因从经历简单的视距传播,到遭遇各种复杂的地物(如建筑物、山脉和树林等)所引起的反射、绕射和散射传播等而显得非常复杂。

另外,移动台相对于发射台移动的方向和速度,甚至收发双方附近的移动物体也对接受信号有很大的影响。

因此,这使得无线信道具有极度的随机性。

移动通信信号在空间传播中所经历的衰落大体可以分为2类, 即大尺度衰落和小尺度衰落,如图1所示。

大尺度衰落是因为发射机与接收机之间的距离和两者之间障碍物(如山丘、森林、建筑物等)的遮蔽影响而造成的信号强度的衰减,它反映了移动信号在较大区域中的平均能量的减少或称为路径损失。

而小尺度衰落是指当移动台在一个较小的范围运动时,引起接收信号的幅度、相位和到达角等的快速变化。

图1 移动无线信道的分类信号在传播的过程中,受各种环境的影响会产生反射、衍射和散射,这样就使得到达接收机的信号是许多路径信号的叠加,因而这些多径信号的叠加在没有视距传播情况下的包络服从瑞利分布。

当多径信号中包含一条视距传播路径时,多径信号就服从莱斯分布。

根据信号多径附加时延的大小,小尺度衰落又可以分为平坦衰落和频率选择性衰落。

另外,由于移动台的移动性而导致接收到的信号产生多普勒频移(频率色散),根据多普勒扩展的大小,信道又可以分为快衰落信道和慢衰落信道。

2 瑞利分布和莱斯分布的特性在实际情况中对数字通信系统来说,调制符号的周期比由多径传播引起的时延扩展要大,因此在一个符号周期内的所有频率分量都会经历相同的衰减和相移。

信道对于所有频率分量来说是平坦的, 因而定义这类信道为平坦衰落信道。

理论分析和实测试验结果表明:平坦衰落的幅度在大多数情况下,符合瑞利分布(ray leighdistribution)或莱斯分布(ricedistribution)。

莱斯分布仿真实现

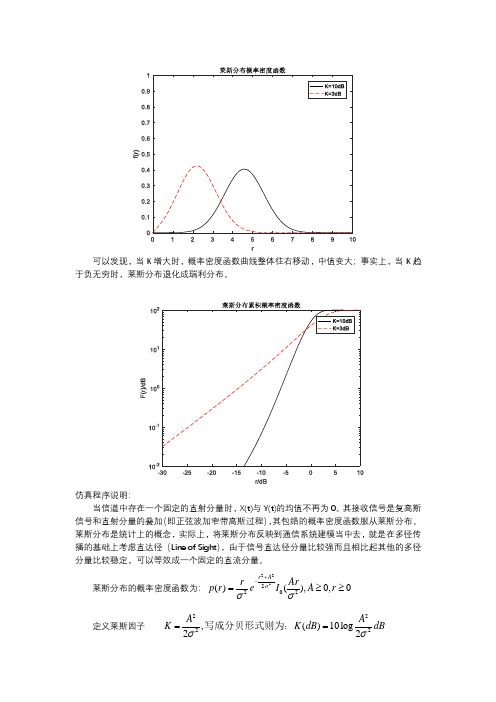
f2=r.*exp(-(r.*r/2+k2)).*besseli(0,sqrt(2*k2).*r);
plot(r,f1,'k',r,f2,'r--');
title('莱斯分布概率密度函数');
legend('K=10dB','K=3dB');
xlabel('r'),ylabel('f(r)');
axis([0 10 0 1]); %标定横纵坐标范围
莱斯分布的概率密度函数为：
p(r)
=
r 2
e−
r
2+ 2
A2
2
I0
( Ar 2
),
A

0, r

0
定义莱斯因子
K = A2 ,写成分贝形式则为：K (dB) = 10 log A2 dB
2 2
2 2
仿真代码如下：
close all;
clear all;
sigma=1;
%初始化方差 sigma 为 1
for i=1:length(f1)
F1(i)=sum(f1(:,1:i))*0.01;
%对概率密度函数求和得到累积概率密度函数
F2(i)=sum(f2(:,1:i))*0.01;
end
ห้องสมุดไป่ตู้
figure(2)
r1=20*log10(r/4.6); %以中值电平为基准，两个中值电平分别为 4.6 和 2 r2=20*log10(r/2.0); semilogy(r1,F1*100,'k',r2,F2*100,'r--'); title('莱斯分布累积概率密度函数'); legend('K=10dB','K=3dB'); xlabel('r/dB'),ylabel('F(r)/dB'); axis([-30 10 0.01 100])%标定横纵坐标范围

瑞利莱斯信道仿真

暑期实习报告一、实习题目用正弦波模拟仿真瑞利信道和莱斯信道二、实习背景在移动通信中，移动台与基站之间的通信往往受到各种障碍物和其他移动物体的影响，作为载体的电磁波会在传输过程中有直射波、反射波、绕射波和散射波之分，以致移动台接收到的信号是由经过不同延时不同路径到达的多路信号合并而成，而这些信号受阴影效应、多普勒效应等的影响，他们的幅度受到不同程度的衰减，同时在存在频移和相移。

三、实习原理瑞利衰落信道是一种无线电信号传播环境的统计模型，这种模型表现为在发射机和接收机之间不存在直射信号，假设信号通过无线信道后，其幅度是随机的。

并且接收机信号的包络服从瑞利分布。

莱斯衰落信道与瑞利信道的区别就是在发射机和接收机之间存在直射波。

瑞利信道模型为：1()c o s (22)N R t C n f t F t T h e a t a ππ=++∑Cn 、F 、Theata 是相互独立的随机变量，Cn 表示信号幅度，F 为频移系数，Theata 表示相移。

莱斯信道模型为：1()cos(2)cos(22)n R t ft Cn ftFt Theata πππ=+++∑Cn 、F 、Theata 是相互独立的随机变量，Cn 表示信号幅度，F 为频移系数，Theata 表示相移四、仿真结果：□1瑞利信道代码：function rayleight=sym('t');n=input('n=');f=8*10^8;%取信号频率为800MhzC=rand(1,n);Theata=-2*pi+4*pi.*rand(1,n);F=-1+2.*rand(1,n);Zx=cos(2*pi*f.*t+2*pi*f.*F*t+Theata);RS=Zx*C'当仿真路数为30路时，得到的接收信号时域图为：0102030405060708090100-8-6-4-2246810当仿真路数为30路时，接收信号的包络：代码：t=0:.2:100;N=501;%采样点总数R=0:0.024:12;%包络幅度范围m=zeros(1,N);q=(8226958330713791*cos((14738544651813039.*t)/2097152 - 6420982962695317/1125899906842624))/9007199254740992 + (8624454854533211*cos((3147546321980441.*t)/2097152 + 1592488907343941/281474976710656))/9007199254740992 + (153933462881711*cos((2922601302899569.*t)/2097152 - 1293881763019091/562949953421312))/281474976710656 + (109820732902227*cos((5056154441375673.*t)/524288 + 572054395085517/140737488355328))/1125899906842624 + (770956303438939*cos((11971310637107755.*t)/2097152 - 976910002155657/281474976710656))/4503599627370496 + (7648276850999985*cos((24678095153207873.*t)/4194304 + 1097200154976001/562949953421312))/9007199254740992 + (55201045594335*cos((15890773575148387.*t)/2097152 - 1129149318181027/562949953421312))/140737488355328 +(3798887910549989*cos((4144792385309751.*t)/2097152 - 384936153162253/562949953421312))/9007199254740992 + (1143795557080799*cos((682689757498656039.*t)/134217728 - 6312399365597953/2251799813685248))/9007199254740992 + (1802071410739743*cos((4897886369182033.*t)/524288 - 8860550568223013/2251799813685248))/2251799813685248 + (8690943295155051*cos((2714506704779073.*t)/1048576 - 823359778227783/140737488355328))/9007199254740992 + (6825116339432507*cos((753288409837281.*t)/262144 - 23146170456561/1125899906842624))/9007199254740992 + (2952009981953243*cos((501305679469463.*t)/131072 + 603204343011701/562949953421312))/4503599627370496 + (525791455320933*cos((46359008585863987.*t)/8388608 - 2386764799977513/562949953421312))/562949953421312 + (3567784634204585*cos((25975981384114555.*t)/4194304 + 740548295201613/281474976710656))/4503599627370496 + (257756635625713*cos((165424021614621.*t)/65536 + 1035053019742027/562949953421312))/281474976710656 + (638999261770491*cos((7378662735005679.*t)/2097152 - 72409097729717/562949953421312))/4503599627370496 + (354913107955861*cos((138474482834837.*t)/16384 - 54167120430423/70368744177664))/2251799813685248 + (7338378580900475*cos((15838866808400863.*t)/2097152 + 1457619014526091/562949953421312))/9007199254740992 + (2953193568373273*cos((926749021084891.*t)/262144 - 49514120493885/17592186044416))/4503599627370496 + (4321169733967891*cos((39913151771089687.*t)/8388608 + 1801714140618479/562949953421312))/4503599627370496 + (8621393422876569*cos((4291865570455739.*t)/524288 + 939164443260505/281474976710656))/9007199254740992 + (1423946432832521*cos((18782798714916921.*t)/2097152 - 712496390568455/140737488355328))/2251799813685248 + (8158648460577917*cos((672267189674085.*t)/262144 - 3311925752416549/562949953421312))/9007199254740992 + (6693542213068579*cos((1995494383059311.*t)/262144 + 1626169033800729/281474976710656))/9007199254740992 + (4371875181445801*cos((5134205601560665.*t)/2097152 + 522078571254719/140737488355328))/9007199254740992 + (6113502781001449*cos((4834269018907937.*t)/524288 - 5390601969460187/1125899906842624))/9007199254740992 + (160831102319495*cos((8758126564219489.*t)/1048576 + 635629730369417/281474976710656))/4503599627370496 + (2185580645132801*cos((2680499240977253.*t)/1048576 - 1675767268482273/1125899906842624))/2251799813685248 +(627122237356493*cos((92294997228769907.*t)/16777216 + 172282999978905/70368744177664))/2251799813685248; y=hilbert(q);%希尔伯特变换z=q+j*y;%解析信号a=z.*exp(-j*16*pi*10^8.*t);%复包络r=abs(a);%包络for l=1:501for n=1:501if r(n)<R(l)m(l)=m(l)+1;endendendmP=m./N;%概率函数figure(1),plot(R,P)figure(2),plot(t,r)包络时域图为：010********60708090100024681012t r概率函数图为：02468101200.10.20.30.40.50.60.70.80.91r P然后对概率函数进行拟合再微分得到概率密度函数：代码为：stan=sqrt(var(r))P_theory=(R./stan^2).*exp(-R.^2./(2*stan^2));coef=polyfit(R,P,10);P_density=polyder(coef);P_density_practice=polyval(P_density,R);plot(R,P_density_practice,'b'),hold onplot(R,P_theory,'r')蓝色表示仿真结果，红色代表理论结果。

基于Matlab的Mpsk信号在莱斯衰落信道下的性能仿真

课程设计（II）通信系统仿真题目MPSK在莱斯衰落信道下的性能专业学号姓名日期1、课程设计目的多进制绝对相移键控MPSK是2PSK的推广，MPSK利用载波的多种不同相位状态来表征数字信息的调制方式。

本次设计以QPSK为主要设计目标，利用MATLAB 对其进行调制解调及在莱斯信道下的传输性能仿真，以此来熟悉掌握相关的知识和MATLAB的使用方法。

2、课程设计内容本次设计主要是对QPSK在莱斯信道下的性能进行仿真。

为此需要先调制出QPSK信号，QPSK信号原理如下：四进制绝对相移键控（4PSK）直接利用载波的四种不同相位来表四进制信息。

如下图由于一个想为代表两个比特信息，因此每个四进制码元可用两个二进制码元的组合来表示。

两个二进制码元中的前一码元用a表示，后一比特用b表示，则双比特ab与载波相位关系如下表4PSK信号等效为两个正交载波进行双边带调制信号之和，这样就把数字调制和线性调制结合起来，为四相波形的产生提供依据。

4PSK的调制方法有正交调制方式，相位选择法，插入脉冲法等。

正交调制法原理如图4PSK可以看作两个正交的2PSK调制器构成。

图中串并转换将输入的二进制序列分为两个速度减慢的两个并行双极性序列a和b，在分别进行极性变换。

再调制到coswt和sinwt载波上。

两路相乘器输出的信号是相互正交的抑制载波的双边带调制信号，相位与各路码元的极性有关，分别由码元a和码元b决定，经相加电路后输出两路的合波即是4PSK信号，图中两个乘法器，一个用于产生0和180两个相位，另一个用于产生90和270两个相位。

相加后可以得到45，135，225，315四种相位状态。

产生4psk信号同样可以采用相位选择法，在一个码元持续时间内，4psk信号为载波4个相位中的某一个，因此，可以用相位选择的方法来产生4psk信号。

其原理图如下：在图中，四相载波发生器产生4psk信号所需要的4种不同相位的载波，输入的二进制数码经串并变换器输出双比特码元，按照输入的双比特码元的不同，逻辑选相电路输出相应相位的在载波。

时间演进非平稳莱斯衰落信道建模及产生方法

第３５卷第１期
２０１７年１月
应
用
科
学
学
报
Ｖｏ１．３５Ｎｏ．１
Ｊａｎ．２０１７
ＪＯＵＲＮＡＬＯＦＡＰＰＬＩＥＤＳＣＩＥＮＣＥＳ— ＥｌｅｃｔｒｏｎｉｃｓａｎｄＩｎｆｏｒｍａｔｉｏｎＥｎｇｉｎｅｅｒｉｎｇ
ａｎｄｂｓｅａｓｔａｔｉｏｎｓ．Ａｇｅｎｅｒａｔｉｏｎｍｅｔｈｏｄｉｓｐｒｏｐｏｓｅｄｆｏｒｎｏｎ－ｓｔａｔｉｏｎａｒｙｆａｄｉｎｇｃｈａｎｎｅｌｓ
ｃｏｍｍｕｎｉｃａｔｉｏｎｓｙｓｔｅｍｉｓｎｏｎ — ｓｔａｔｉｏｎａｒｙ．Ｔｈｉｓｐａｐｅｒｅｓｔａｂｌｉｓｈｅｓａｎｏｎ — ｓｔａｔｉｏｎａｒｙＲｉｃｅｆａｄ — ｉｎｇｃｈａｎｎｅｌｍｏｄｅｌｗｉｔｈｔｉｍｅｅｖｏｌｕｔｉｏｎｏｒｆｔｈｅｄｙｎａｍｉｃｐｒｏｐａｇａｔｉｏｎｌｉｎｋｂｅｔｗｅｅｎｍｏｂｉｌｅ
ＮａｎｊｉｎｇＵｎｉｖｅｒｓｉｔｙｏｆＡｅｒｏｎａｕｔｉｃｓａｎｄＡｓｔｒｏｎａｕｔｉｃｓ，Ｎａｎｊｉｎｇ２１００１６，Ｃｈｉｎａ２．Ｔｈｅ４１ｓｔＩｎｓｔｉｔｕｔｅｆｏＣｈｉｎａＥｌｅｃｔｒｏｎｉｃｓＴｅｃｈｎｏｌｏｇｙＧｒｏｕｐＣｏｒｐｏｒａｔｉｏｎ，

一种可用于莱斯衰落信道的信噪比估计算法

一种可用于莱斯衰落信道的信噪比估计算法陈萍;熊蔚明【摘要】Aimed at the problems in Rician fading channel,i.e.general Non-Data-Aided signal-tonoise ratio(SNR) estimation algorithms were very complex and usually suitable for a certain modulation pattern.This paper proposed an SNR estimation algorithm.On the basis of establishing equivalent system model,the relationship expression of SNR,expectation and variance of received signals were deduced.Under the conditions of the Rician fading channel,the deduced expression had no analytic solutions,thus using the polynomial fitting method to obtain approximate solutions of SNR during a certain range.Simulations and comparison experiments show that,the algorithm does not need any training sequence and is universal for both lower and higher order modulations.If the channel Rician factor K =10 dB and the SNR is between 5 and 25 dB,the normalization bias is lower than 0.2,the computational complexity is comparable with M2M4 algorithm,thus satisfying requirements of general engineering application.%针对莱斯衰落信道条件下,常规非数据辅助信噪比估计算法复杂度高、适用调制类型单一等问题,提出了一种信噪比估计算法.在建立系统等效模型的基础上,推导出信噪比与接收信号期望和方差的关系表达式.由于在莱斯衰落信道下,该表达式无解析解,故提出用多项式拟合法得到一定范围内的信噪比近似解.仿真和对比分析实验表明,提出的信噪比估计算法不需要使用训练序列,不仅对低阶和高阶多种调制方式具有普适性,而且当信道莱斯因子K=10 dB且信噪比为5 ～ 25 dB时,归一化估计偏差均小于0.2,计算时间复杂度与M2M4算法相当,适合一般工程应用需要.【期刊名称】《东南大学学报（自然科学版）》【年(卷),期】2017(047)002【总页数】6页(P209-214)【关键词】信噪比估计;莱斯衰落信道;多项式拟合;非数据辅助【作者】陈萍;熊蔚明【作者单位】中国科学院国家空间科学中心,北京100190;中国科学院大学,北京100049;中国船舶工业系统工程研究院,北京100094;中国科学院国家空间科学中心,北京100190【正文语种】中文【中图分类】TN911.22信噪比是衡量通信质量的重要指标,也是无线通信技术的研究热点之一.由于信号在传输过程中受到复杂传播环境的影响,因此需要针对不同应用场景设计高效的信噪比估计方法[1].目前,对于SNR的估计方法主要分为2类:一类为基于数据辅助(data-aided,DA)的方法,另一类则不需要数据辅助(non-data-aided,NDA).NDA 类算法包括最大似然类算法[2]、矩估计类算法[3-4]、子空间类算法[5]等.NDA类算法无需训练序列,因而被广泛应用.根据样本选取的差异,NDA类信噪比估计算法可以分为:判决域和非判决域的信噪比估计[6].判决域的信噪比估计是指用于估计的信号样本已经经过了同步和均衡操作,其调制方式已知.非判决域的信噪比估计指信号未进行同步和均衡处理(如中频信号),其调制方式未知.针对高斯白噪声(AWGN)信道,许多学者对信噪比估计方法开展了深入研究.经典信噪比估计算法有最大似然(ML)估计、信号噪声方差(SNV)估计、分离符号矩估计(SSME)、二阶-四阶矩估计(M2M4)以及信号-变换比估计(SVR)算法等.Pauluzzi等[7]利用均方误差(MSE)对上述5种估计方法进行了详细的分析和比较,并通过与克拉美罗界(CRB)[8]的比较,得出了M2M4算法、SNV算法和ML算法有较好估计效果的结论.在莱斯衰落信道下,由于存在乘性衰落因子,信噪比估计方法一般比在AWGN信道中更复杂.在准静态平坦衰落信道下,对于恒幅调制信号,矩估计器(如M2M4估计器)可以用于衰落信号信噪比估计[9].针对移动通信中广泛使用的 Nakagami-m信道,Ramesh等[10]给出了一种莱斯衰落信道信噪比估计方法.但这种估计方法只考虑了BPSK调制,无法应用于高阶调制.杨俊等[11]主要针对QPSK提出改进的信噪比估计方法.韩博等[12]提出了一种基于相关向量机的信噪比估计方法,该方法应用相关向量机建立估计模型,通过训练学习得到可靠的模型权值.但是该方法需要进行矩阵求逆运算,复杂度较高,不适用于硬件实现.李晋等[13]提出了一种低复杂度盲信噪比估计方法,但是该方法只针对瑞利(Rayleigh)衰落信道进行了分析,没有针对莱斯衰落信道提出信噪比估计方法.本文从工程应用的角度出发,针对莱斯衰落信道提出一种属于判决域的非数据辅助信噪比估计方法.该方法具有估计精度高、适用范围宽、计算复杂度低的特点,适用于低阶和高阶多种调制信号的信噪比估计.在AWGN信道下,信号输入判决器基本消除了载波偏差和码间干扰,仅混有加性高斯白噪声信号,接收信号rk可表示为式中,xk为真实的星座信号;nk为均值为0、方差为σ2的高斯噪声;L为数据样本长度.假设发送符号有n个不同幅值A1,A2,…,An,取值概率分别为q1,q2,…,qn,定义星座矩为piAi,不失一般性,令发送符号能量归一化.对于莱斯衰落信道,需改进上述信号模型.设tn为信号源,dk为采样后信号,mk为经过成形滤波器后的信号.ri为信道功率因子(对于莱斯衰落信道,信道增益ri服从莱斯分布),ni为噪声信号,si为接收信号,sk为经过匹配滤波器的信号,信噪比估计的系统等效模型如图1所示[14].在本文的分析中,假设系统均衡和同步误差足够小,不会对信噪比估计造成明显影响.过采样和脉冲成形后的信号可表示为式中,hk-n为成形滤波器系数;dk为过采样后的信号.则接收信号表示为匹配滤波器输出信号为则信噪比SNR表示为可见,信噪比SNR估计的关键是对式(5)中接收信号功率以及噪声信号方差进行准确估计.2.1 估计算法原理根据图1所示的系统等效模型,假设用于估计的信号样本经过同步和均衡操作,而且其调制方式已知.设Es为发送符号的能量,接收信号si表示为式中,ni与衰落因子ri为相互独立的随机变量.ri服从莱斯分布,表示为[15]式中,β为直视分量;xi和yi为均值为0、方差为的静态高斯随机变量.定义直视分量β和散射分量的功率比为莱斯因子K,即莱斯因子K可以表示信道的衰落程度,K越大，信道条件越好；反之，则表示多径衰落越严重.K=∞时表示信道条件近似为理想高斯信道,K=0时表示信道条件多径影响严重,可近似认为瑞利信道.可见,瑞利信道是莱斯信道的一种特例.莱斯信道中信号的包络服从莱斯分布,其概率密度函数为式中,I0[·]为修正过的零阶贝塞尔函数,有.莱斯分布的均方值为(K+1).若ri满足)=1,式(7)可进一步表示为接收信号si的计算功率平均值)为考虑到衰落因子ri和信道噪声ni为相互独立的随机变量,故E(rini)=E(ri)E(ni)=0,从而,式(11)改写为又因为,所以接收信号方差表示为对于莱斯衰落信道,有由于式(14)的积分项中有零阶贝塞尔函数经过计算,E(ri)没有显式解.将记为符号信噪比,则有故信噪比表示为对于瑞利衰落信道,E(ri)有显式解[14],则信噪比可以由)/σ2得到.而对于莱斯衰落信道,由于E(ri)无显式解,根据信噪比γ与)/σ2之间的关系式不能直接得到可解析的表达式.本文采用多项式拟合法[16]得到信噪比的近似值.对于给定数据)/σ2,γ)(i=0,1,…,z),设Φ为所有次数不超过c(c≤z)的多项式构成的函数,找到使误差的平方和最小,即使得对于给定数据,采用多项式拟合法需要确定拟合函数的系数.显然,式(18)中2为系数a0,a1,…,ac的多元函数,由多元函数求极值的必要条件解出ar(r=0,1,…,c),从而得到多项式从工程应用角度出发,在保证一定精度的前提下,为降低运算复杂度,本文采用三阶拟合系数.2.2 估计算法基于上述估计算法原理,采用多项式拟合法对接收信号)/σ2进行曲线拟合,得到一定范围内的信噪比γ近似解.由于上述分析严格依赖于莱斯信道参数K,因此需要根据不同莱斯因子K拟合得到不同估计曲线(K因子的估计方法见文献[17-18]).综上,本文提出的信噪比估计算法具体实施步骤如下.① 设接收端收到I路和Q路N个数据分别为Ii和Qi.② 根据下式计算接收数据的幅值Ai和相位φi:③ 按照调制阶数和划分区间的准则将接收到的数据划分为M个区间.④ 根据计算各区间数据的方差).⑤ 对方差和求平均,得到M.⑥ 计算平均比特信号功率M.⑦ 计算).⑧ 对接收数据进行多项式拟合,以p为自变量,理论信噪比γ为应变量,得到拟合多项式f(p),则信噪比估计近似结果γfit=f(p).上述步骤③中,针对不同的调制方式应用如下准则划分区间:1) QPSK调制.区间1为0≤φi<π/2;区间2为π/2≤φi<π;区间3为π≤φi<3π/2;区间4为3π/2≤φi<2π.2) 8PSK调制.区间1为0≤φi<π/8或15π/8≤φi<2π;区间2～区间8为mπ/4-π/8≤φi<mπ/4+π/8,m=1,2, (7)3) 16APSK调制.区间1为Ai<(Rin+Rout)/2,0≤φi<π/4或7π/4≤φi<2π;区间2～区间4为Ai<(Rin+Rout)/2,mπ/2-π/4≤φi<mπ/2+π/4,(m=1,2,3);区间5为Ai≥(Rin+Rout)/2,0≤φi<π/12或23π/12≤φi<2π;区间6～区间16为Ai≥(Rin+Rout)/2,mπ/6-π/12≤φi<mπ/6+π/12,m=1,2,…,11.其中,Rin为内环半径,Rout为外环半径.4) 32APSK调制.区间1为Ai<(Rin+Rmid)/2,0≤φi<π/4或7π/4≤φi<2π;区间2～区间4为Ai<(Rin+Rmid)/2,mπ/2-π/4≤φi<mπ/2+π/4,m=1,2,3;区间5为Ai>(Rout+Rmid)/2,0≤φi<π/16或31π/16≤φi<2π;区间6～区间20为Ai>(Rout+Rmid)/2,mπ/8-π/16≤φi<mπ/8+π/16,m=1,2,3,…,15; 区间21为(Rin+Rmid)/2<Ai<(Rout+Rmid)/2,0≤φi<π/12或23π/12≤φi<2π; 区间22～区间32为(Rin+Rmid)/2<Ai<(Rout+Rmid)/2,mπ/6-π/12≤φi<mπ/6+π/12,m=1,2,3,…,11.其中,Rmid为中间环半径.3.1 归一化估计偏差定义信噪比的归一化估计偏差为[19]式中,b/N0为信噪比估计值;Eb/N0为信噪比理论值或真实值.莱斯衰落信道属于平坦衰落信道,将本文提出的估计算法分别应用于低阶调制QPSK信号和高阶调制16APSK信号信噪比估计,并设定在莱斯因子K=10 dB的情况下与M2M4算法进行性能比较,结果如图2和图3所示.其中,图2(a)和(b)分别是估计数据长度为5 000时QPSK调制信号和16APSK调制信号的信噪比估计仿真结果,图3(a)和(b)是对应信噪比估计结果的归一化偏差.分析图2和图3的结果,得出如下结论:1) 在信道莱斯衰落因子K=10 dB的条件下,本文提出的估计算法归一化偏差不超过0.2,说明该算法在信道衰落较严重时仍然具有较高的估计精度.2) 本文提出的信噪比估计算法对低阶和高阶调制具有普适性:对于低阶QPSK调制和高阶16APSK调制,都具有较精确的估计结果,估计偏差不超过0.2.而M2M4算法在高阶16APSK调制下的估计偏差趋近于1,说明该算法已失效,不适用于高阶调制.3) 本文提出的信噪比估计算法具有较宽的适用范围,在信噪比为5～25 dB范围内都保持较低估计偏差.3.2 计算复杂度本文提出的信噪比估计算法需要计算信号幅值Ai和相位φi,可采用CORDIC(coordinate rotation digital computer, CORDIC)算法完成.CORDIC算法的思想是通过迭代方法,不断旋转特定角度,使得累计旋转角度和无限接近某一设定角度.CORDIC算法的每个迭代需要2次移位、1次查找表和3次加法.设每个用于估计的接收帧长度为N,即利用接收到的N个数据进行信噪比估计,则本文算法的时间复杂度为O(N).本文算法的时间复杂度与M2M4算法的时间复杂度相当,远低于文献[12]算法的时间复杂度O(N3)+O(N2M).针对莱斯衰落信道,提出了一种属于判决域的非数据辅助信噪比估计算法.在推导出信噪比与接收信号期望和方差的关系表达式基础上,对接收数据按照相应准则进行数理统计和分析,采用多项式拟合法得到信噪比估计结果.在同样的信道条件和信号采样长度下,本文算法具有估计结果精度高、适用范围宽、适用于低阶和高阶多种调制类型的特点,且计算时间复杂度与M2M4算法相当,是一种高效的信噪比估计方法.【相关文献】[1]谢显中,刘源源,雷维嘉.高动态环境下基于数据辅助的稳健信噪比估计[J].西南大学学报(自然科学版),2016,38(8):174-181. Xie Xianzhong, Liu Yuanyuan, Lei Weijia. Robust data-aided snr estimation algorithm in high dynamic environment[J]. Journal of Southwest University (Natural Science Edition), 2016, 38(8):174-181. (in Chinese)[2]Li Z X, Yang D W, Wang H, et al. Maximum likelihood SNR estimator for coded MAPSK signals in slow fading channels[C]//Proceedings of 2013 International Conference on Wireless Communications and Signal Processing. Hangzhou, 2013: 1-6.[3]Wang A F, Xu H. Comparison of several SNR estimators for QPSKmodulations[C]//Proceedings of 2012 International Conference on Computer Science and Service System. Nanjing, 2012: 77-80. DOI:10.1109/csss.2012.28.[4]Wang A F, Xu H, Ke J. NDA moment-based SNR estimation for envelope-basedQAM[C]//Proceedings of 2012 IEEE 11th International Conference on Signal Processing. Beijing, 2012: 1341-1344. DOI:10.1109/icosp.2012.6491824.[5]Li W, Zhang Y, Zhang Y, et al. Subspace-based SNR estimator for OFDM system under different channel conditions[C]//Proceedings of 2013 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting. London, UK, 2013: 1-5.DOI:10.1109/bmsb.2013.6621687.[6]许华,王爱粉,杨晓宇.常规数字通信信号信噪比估计综述[J].信号处理,2013,29(6):723-733.DOI:10.3969/j.issn.1003-0530.2013.06.009. Xu Hua, Wang Aifen, Yang Xiaoyu. Survey of the SNR estimation of conventional digital communication signals[J]. Signal Processing, 2013, 29(6): 723-733. DOI:10.3969/j.issn.1003-0530.2013.06.009. (in Chinese)[7]Pauluzzi D R, Beaulieu N C. A comparison of SNR estimation techniques for the AWGN channel[J]. IEEE Transactions on Communications, 2000, 48(10): 1681-1691.DOI:10.1109/26.871393.[8]Alagha N S. Cramer-Rao bounds of SNR estimates for BPSK and QPSK modulated signals[J]. IEEE Commun Letter, 2001, 5(1): 10-12. DOI:10.1109/4234.901810.[9]陈云峰,付永明,张炜.基于矩方法的通信信号信噪比估计算法研究[J].通信技术,2015,48(1):23-26. DOI:10.3969/j.issn.1002-0802.2015.01.005. Chen Yunfeng, Fu Yongming, Zhang Wei. MoM-based SNR estimation algorithms for communication signals [J]. Communication Technology, 2015, 48(1): 23-26. DOI:10.3969/j.issn.1002-0802.2015.01.005. (in Chinese) [10]Ramesh A, Chockalingam A, Milstein L B. SNR estimation in generalized fading channels and its application to Turbo decoding[C]//2001 International Conference on Communication. Helsinki, Finland, 2001, 4: 1094-1098. DOI:10.1109/icc.2001.936822. [11]杨俊,江虹,张秋云.一种改进的非数据辅助SNR估计算法研究[J].计算机科学,2016,43(8):71-73,104. DOI:10.11896/j.issn.1002-137X.2016.8.014. Yang Jun, Jiang Hong, Zhang Qiuyun. Improved non-data-aided SNR estimation algorithm[J]. Computer Science, 2016, 43(8): 71-73, 104. DOI:10.11896/j.issn.1002-137X.2016.8.014. (in Chinese)[12]韩博,吴杰,许华,等.基于相关向量机的信噪比估计算法[J].通信学报,2013,34(4):201-206.DOI:10.3969/j.issn.1000-436x.2013.04.025. Han Bo, Wu Jie, Xu Hua, et al. New SNR estimation algorithm based on relevance vector machine[J]. Journal on Communications, 2013, 34(4): 201-206. DOI:10.3969/j.issn.1000-436x.2013.04.025. (in Chinese)[13]李晋,华惊宇,尤肖虎.一种移动通信中的低复杂度盲信噪比估计算法[J].电子与信息学报,2006,28(6):1054-1058. Li Jin, Hua Jingyu, You Xiaohu. A low complexity blind SNR estimator in mobile communication[J]. Journal of Electronics & Information Technology, 2006, 28(6): 1054-1058. (in Chinese)[14]张金成,彭华,赵国庆.信噪比估计算法研究[J].信息工程大学学报,2011,12(5):535-543.DOI:10.3969/j.issn.1671-0673.2011.05.005. Zhang Jincheng, Peng Hua, Zhao Guoqing. Research on SNR estimation algorithms[J]. Journal of Information Engineering University, 2011, 12(5): 535-543. DOI:10.3969/j.issn.1671-0673.2011.05.005. (in Chinese)[15]Kostov N. Mobile radio channels modeling in Matlab[J]. Radio Engineering, 2003,12(4): 12-16.[16]刘明骞,李兵兵,王婧舒,等.低信噪比下低复杂度的OFDM信号带宽盲估计方法[J].江苏大学学报(自然科学版),2013,34(1):76-80. DOI:10.3969/j.issn.1671-7775.2013.01.015. Liu Mingqian,Li Bingbing,Wang Jingshu,et al. Bandwidth blind estimation scheme of OFDM signals with low complexity at low SNR[J]. Journal of Jiangsu University (Natural Science Edition), 2013, 34(1): 76-80. DOI:10.3969/j.issn.1671-7775.2013.01.015. (in Chinese)[17]郑剑文.特定环境下卫星移动通信信道全阴影模型的研究[D].天津:天津大学电子信息工程学院,2007.[18]周涛,陶成,刘留,等.基于测量的高铁宽带无线信道莱斯K因子研究[J].铁道学报,2013,35(9):72-78. DOI:10.3969/j.issn.1001-8360.2013.09.012. Zhou Tao, Tao Cheng, Liu Liu, et al. Measurement-based research on ricean K-factor of broad-band wireless channel in high-speed railway scenarios[J]. Journal of the China Railway Society, 2013, 35(9): 72-78. DOI:10.3969/j.issn.1001-8360.2013.09.012. (in Chinese)[19]华惊宇,黄清,滑翰,等.一种移动环境下的信噪比估计算法及其在多普勒频移估计中的应用[J].通信学报,2005,26(5):132-137.DOI:10.3321/j.issn:1000-436X.2005.05.022. Hua Jingyu, Huang Qing, Hua Han, et al. SNR estimation scheme and its application in Doppler shift estimation in mobile communication systems[J]. Journal on Communications, 2005, 26(5): 132-137. DOI:10.3321/j.issn:1000-436X.2005.05.022. (in Chinese)。