定性数据分析第二章课后答案教学文案
盖洛普Q12数据分析教学文案

3.5
3.4
3.3
3.2
3.1
3
3.702 中高层经理
3.613 基层经理
3.709 普通员工
总体来看,我公司员工的组织氛围水平中上,优于一般企业,但距离优秀企业 还有距离。参考同行企业的标准来看,联想集团06年的得分为3.58,而我公司 得分为3.7。
Q12调查—1:组织氛围分类调查结果分析
员工组织氛围阶梯数据对比分析
1、10几.有乎要各好类的朋人友员都不认为自己在日常工作经2常9.有09机% 会做32.“50自% 己3擅5.长60%的事34”.7,9%也就25是% 说,3上8%级
9.交致办力于的精工益作求未精必是下级认为最适合自己的工10.作91。% 原因0是.00什% 么?20.是68个% 人1技8.能81%与公2司5%期望4间0%的
Q11:在前六个月中,有同 事跟我谈到我的进步
Q12:近一年来,我有机会 学习和成长
我的发展
我的归属
二号营地
三号营地
Q12调查—1:组织氛围分类调查结果
Q12组织氛围调查对比分析
4
优秀企业:75分位3.91 3.9
3.8
我公司3.701
3.7
一般公司:50分位3.62 2006年联想:3.58
3.6Βιβλιοθήκη 2、8.误公所差司有目?人标还都重是需要沟要通经问常题获、得岗肯位定设,置普问通题员、工任在务3被4.分表55解扬% 问、题关22?.心5需0、%要鼓每2励7.一方03位%面经的2理7满.人1足9%思度考尚3。1可% ,但3职8%位
7.越意高见受,重所视获得的表扬和鼓励就越少。 16.36% 15.00% 12.56% 12.89% 18% 32%
媒体与传播研究中的定性数据分析

媒体与传播研究中的定性数据分析在媒体与传播研究领域,数据分析是一项关键的技术和方法,它可以帮助研究人员深入理解媒体内容和传播现象。
定性数据分析是数据分析中的一种重要方法,它通过对文本、图像、音频和视频等非结构化或半结构化数据的解读和概括,揭示出背后的含义和意义。
本文将介绍媒体与传播研究中的定性数据分析方法,并探讨其在实际研究中的应用和挑战。
一、定性数据分析方法定性数据分析是一种基于主观经验和理解的方法,它强调对数据质量的细致观察和深入解读。
以下是几种常用的定性数据分析方法:1. 文本分析:通过对文本数据的读取和诠释,揭示出其中的主题、情感、意见和观点等信息。
文本分析可以通过手工阅读、编码和分类等方式进行,也可以借助计算机辅助分析工具进行自动化处理。
2. 图像分析:利用计算机视觉和图像处理技术,对图像数据进行特征提取、分类和识别等处理,从而挖掘出其中的视觉信息和智能分析结果。
图像分析可以应用于广告、新闻图片和社交媒体图像等领域。
3. 音频分析:通过对音频数据的转录、分割和标注,从中提取出语音、音调和声音特征等内容,对音频信息进行解读和理解。
音频分析常用于广播、音乐和语音识别等领域。
4. 视频分析:对视频数据进行帧间分析、目标跟踪和动作识别等处理,挖掘出其中的动态信息和视觉模式。
视频分析被广泛应用于电影、电视节目和监控视频等领域。
二、定性数据分析的应用定性数据分析在媒体与传播研究中具有广泛的应用,以下是几个典型的应用案例:1. 新闻分析:通过对新闻报道和社会媒体评论等文本数据的分析,揭示出其中的政治倾向、舆论倾向和话语模式等内容。
新闻分析可以帮助研究人员了解新闻媒体的报道偏向和受众反馈,进而探讨其对社会舆论和政治决策的影响。
2. 品牌分析:通过对广告文案、产品评论和品牌标识等图像数据的分析,评估和比较不同品牌的形象和声誉。
品牌分析可以帮助营销人员了解消费者对品牌的认知和态度,指导品牌策略的制定和推广。
统计学课后答案

统计学课后答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章1.举出你所知道的统计应用的例子。
答:期末考试后统计班里同学的成绩,从而进行排名等;人口普查统计,从而得知男女人口比例,年龄分布等;统计一个生态系统里某种物种的密度;统计股票市场上某一天的各种数据;统计某个城市的人均收入水平,人民幸福指数,对某一电视节目的看法等。
2. 解释定性数据和定量数据的区别,分别给出一个定性数据和一个定量数据的例子。
答:定性数据和定量数据的区别:定性数据是由于我们考虑的是取值为类别的变量,对这些类别用数字来分别代表就得到定性数据;定量数据是我们所考虑的变量的取值为数值,它将在某个区间上连续取值,或在某个区间上取离散的值。
定性数据的例子:例如考察某幼儿园10个人的性别,定义1=男,2=女,则所得到定性数据为:1,1,2,2,2,1,2,1,1,1.定量数据的例子:考察某幼儿园10个人的身高,则此变量取值区间为(0,200)(单位:cm)3. 解释样本和总体的区别。
答:总体是根据一定目的和要求所确定的研究事物的全体。
为了了解总体的分布,我们从总体中随机地抽取一些个体,称这些个体的全体为样本。
样本和总体的区别在于总体是要考虑对象的全体,而样本是从总体中抽取出的一部分具有代表性的个体,从而通过对样本的研究得出关于总体的一些结论。
4. 解释离散型变量和连续型变量的区别,并各举一例。
离散型变量是指其数值只能用自然数或整数单位计算。
例如:某企业里职工的人数连续型变量是如果所考虑变量可以在某个区间内取任一实数,即变量的取值可以是连续的。
例如:生产零件的规格尺寸。
5.阐述四种主要的收集数据方法的区别。
答:观测,访问,问卷,实验区别:观测数据的研究者尽量不干涉研究对象的行为模式;访问在一定程度上对被访问者心理造成干扰,则收集到的数据会有误差;问卷常会产生未响应误差;实验时需要其控制它变量的影响。
定性数据统计分析概要课件

通过降维技术,将行变量与列变量在同一低维空间中表示,以便直观揭示行变量 与列变量间的结构关系。
应用场景
适用于有多个分类变量且变量间存在关联性的情况,如市场调研中的品牌与消费 者特征关系分析、生物学中的物种与环境因子关系分析等。
多维尺度分析原理及应用场景
多维尺度分析原理
通过保持原始数据点间的距离关系,在低维空间中重新排列 数据点,以便揭示数据的潜在结构。
适用于研究公众意见、消费行 为、市场需求等领域。
文本分析法
优点
能够深入挖掘文本中的信息,发现其中的 规律和趋势,同时可以进行大规模的分析。
定义
文本分析法是通过对研究对象产生 的文本进行分析,了解其观点、态 度、情感等,收集相关数据和信息
的方法。
A
B
C
D
应用场景
适用于研究社交媒体言论、新闻报道、广 告文案等领域。
相对频率
计算交叉表中各单元格的相对频率, 以百分比形式表示,便于比较。
卡方检验原理及应用场景
卡方检验原理
基于实际观测频数与期望频数之间的差异,判断两个定性变量是否独立。
应用场景
适用于分析两个定性变量之间的关系,如不同性别对某品牌产品的偏好程度。
04
定性数据探索性统计分析 方法
对应分析原理及应用场景
定义:定性数据也称为分类数据 或品质数据,是说明事物性质、 规定事物类别的非数值型数据, 表现为互不相容的类别或属性。
数据的取值是离散的,且一般无 顺序。
数据之间具有独立性,一个数据 的取值不影响另一个数据的取值。
定性数据统计分析意义
了解数据的分布特征
通过统计定性数据的频数分布,可以了解不同类别或属性数据的 分布情况,从而对数据有一个整体的把握。
数据统计与分析课后习题答案

附录2:《数据统计与分析——SPSS应用教程》习题答案本“习题答案”也适用于《统计分析应用教程—SPSS,LISREL & SAS实例精选》书中的习题。
习题1答案1.(1)答:有错误, 犯了水平互相嵌套的错误; 如“每周去 2次或 2次以上”把第1组的编码嵌套进去了。
又比如:“每周去 3次或 3次以上”又把第2组的编码嵌套进去了。
(2)答:正确的编码方案如下:1=每周去1次2=每周去2次3=每周去3次4=每周去4次或4次以上2.答:该编码问题严重。
(1)80岁不能是缺失值, 缺失值可用00岁。
(2)职业不编码不行, 而必须编码为:1=工人 2=农民等等。
(3)职业变量用全称(Occupation)超出8个字符。
(4)而且栏目位置占1列即可。
(5)颜色的第1个字母作为变量值会引起重复,应该用单词的前3-4个字符。
(6)Color 变量的栏目位置10被嵌套在“4-14”之内,这是严重的错误。
更正后的编码方案见图1-19:图1-19 纠错后的编码方案3.(1) 答:错。
错在变量名超过8个字符。
(2) 答:错。
错在变量名的首字符是数字领头。
(3) 答:错。
错在变量名中间冒出一个空格。
(4) 答:对,#号可以作为变量名。
但不提倡。
习题2答案1.答:合并后的大目标数据文件“BIGab.sav”中仍然有30个Cases、但每个Cases 各有(50+30)=80个变量,即v1、v2、v3、v4……v50、x1、x2、x3、x4……x30。
2.答:合并后的大目标数据文件“BIGab2.sav”中仍然是50个变量,即v1、v2、v3、v4……v50。
但是Cases数目增加为(20+30)=50个Cases。
3.答:请读者照着书中的方法去使用对话框。
排序的命令如下:SORT CASES BY xh (D)sex.LIST xh sex score。
4.答:对话框的解法请按照书中介绍的去举一反三。
命令解法如下:GET File=’9293.sav’.SELECT IF (location=2 AND sex=2).SORT Cases BY xh (D) sex.LIST xh sex score.5.答:对话框的解法请按照书中介绍的去举一反三。
庞皓计量经济学第二章练习题及参考解答(第四版)教学文案
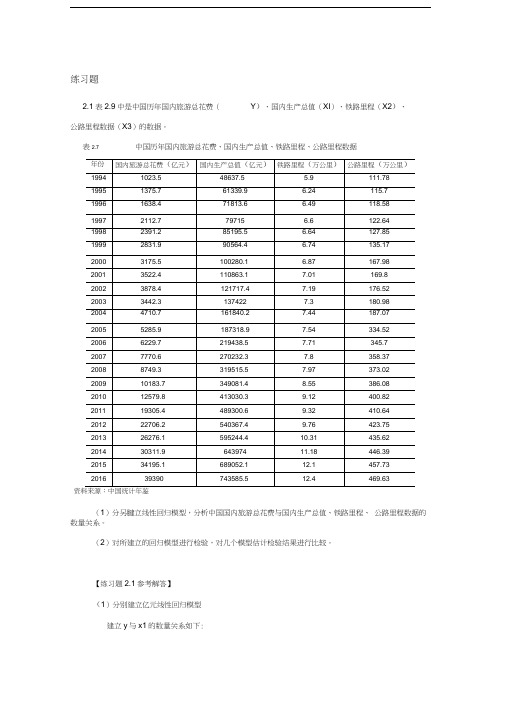
练习题2.1表2.9中是中国历年国内旅游总花费(Y)、国内生产总值(XI)、铁路里程(X2)、公路里程数据(X3)的数据。
表2.7 中国历年国内旅游总花费、国内生产总值、铁路里程、公路里程数据(1)分另腱立线性回归模型,分析中国国内旅游总花费与国内生产总值、铁路里程、公路里程数据的数量关系。
(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
【练习题2.1参考解答】(1)分别建立亿元线性回归模型建立y与x1的数量关系如下:Y t =-3228.€2 + 0.05^1;Depen dent Variable YNetiod: L&astGq^iarBBOdle 03/12f16 Time 2232Sample: 19^42O1&Included o ba avalions: 23Variable Co«fficitnt3cd. Error t'Statistc ProbC-3228.021******* -3 6590^3 3.00JSX10 0501^10 血PVP ?1 879f1 D ODIfl R-squ^red0.9 5^231M早鬲n dependentvar T1Q03.7e-djEted R-squared0,955135s D dependent var11BG6.33S.E. cf re cression2469.548Akaike info criterion18 54440Sum Mqu自「gd「巨Hid1曲Schwair^ criterionLog likelihood-311.2&36Harnan-Qumn enter.16 56923F-Slausuc470.0 U0DurLiln-'.VolsDr seal0.215776Probf-statistic) D.dOUOJU建立y与x2的数量关系如下:歼=-39438.73 + 616525/^Dapan dorrt Variable VMethod. Least 3qusres□ate 03/i2ns lime 2235SamplE 1994 2016Indudcd ote BTVS I on >: 23Varasle Goernci^nr5td. Enor bSlatisic prob.p-*w-304337119&04?2 -23.220200.0003X261SS.25323E.e3iO 25 4?&47&.COODR-scjjared0.97DG57Mean dependent /ar1103176Adjusted R-squar&d机前9574S.D- d-ependentvar11&3 6.S23.E. of regrs55ion3035 056Aka ike in'o enter! on偲15738su-nsquarecresia86&70M4sen wan:rneriicnLoa I kelihood-206.BC9&Hainan-Quinn enter.1fi 16221F^tatisiic70ZD620Du j bm-^atson stat O.5cg7O6Prob FsiarsiQ0.000000建立y与x3的数量关系如下:Pi =-9106.17 + 71.64/^De pendeni Varkab e: YMstiotr LeasiscaresData: 03/12J-g Tirr»:223E sampleIncl idfld Dbwivatlans: 23Variable Coefiicent Stc Eiror 卜Static Prob.c-9105.1053170.97Z -23717270.0091X371 63»3810.20302 7 0213S8O.QOJOR-sau^red0 701250l.'eAr CPnen^ent\Ar110O376Aid justed R-squcr&d0.6670553,0. depenefent ver11&66 63S L cf regression5526.601AKsike irtc Qitenon2048810Sjn squared resid8.95E*-09Schwarz, criterion23.56684Log liKelihoo J-2330132Ha iriaii-Quinr Lii'.er.2951293 tat stir45泗曲Du^hm-Watson stat DR©也PrOj(F-sldlsiic)O.&OOJOI(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
数理统计课后习题答案第二章

30.解:由题意用U统计量
计算得置信区间为
把
代入计算得置信区间
31.解:由题意, 未知,则
则
经计算得
解得 的置信区间为
查表:
带入计算得 的置信区间为: 。
32.
解: 未知,则 即:
有: 则单侧置信下限为:
将 带入计算得
即钢索所能承受平均张力在概率为 的置信度下的置信下限为 。
33.解:总体服从(0,1)分布且样本容量n=100为大子样。
令 为样本均值,由中心极限定理
又因为 所以
则相应的单侧置信区间为 ,
将 =0.06
代入计算得所求置信上限为0.0991
即为这批货物次品率在置信概率为95%情况下置信上限为0.0991。
34.解:由题意:
解得 的单侧置信上限为
其中n=10, =45,查表 3.325
。一元回归的线性模型为 试求 , 的最小二乘估计。
8.对于自变量和因变量都分组的情形,经验回归直线的配置方法如下:对 和 作 次试验得 对试验值,把自变量的试验值分成 组,组中值记为 ,各组以组中值为代表;把因变量的试验值分为 组,组中值记为 ,同样地各组以组中值为代表。如果 取 有 对, , ;而 。用最小二乘法配直线 ,试求 的估计量23
77
7
9.4
44
46
81
8
10.1
31
117
93
9
11.6
29
173
93
10
12.6
58
112
51
11
10.9
37
111
76
12
数据分析文案

数据分析文案一、样本描述1、年龄分布14-25岁占了总样本数量的46.67%,25-55岁占了51.11%,55岁以上占2.22%。
2、收入分布收入1000元以下占了 53.33%,1000-2000元占了22.22%,2000-3000元占了 11.11%,3000-5000元占8.89%,10000元及以上占4.44%。
二、购买渠道分析超市购买占54%排第一;便利店和专实店各占 15.9%,排第二;百货店购买占11.1%,排第三;街边小摊占3.2%,排第四。
三、购买的形式购买袋装的占了样本总数的42.5%,购买散装的占了20%两种都购买的占36%购买袋装的居多四、总结1、消费豆类的人群主要为年轻一代的女性。
2、喜欢级别的人数占总样本46.67%,一般占31.11%,豆类消费市场潜力不错。
3、超市购买占54%排第一;便利店和专卖店各占15.9%,排第二;百货店购买占11.1%,排第三;街边小摊占3.2%,排第四。
4、购买袋装的占了样本总数的 42.5%,购买散装的占了20%两种都购买的占36%购买袋装的居多。
5、在购买散装豆类零食的人群中 59.3%因为散装价格便宜购买,25.9%的人因为味道购买散装。
6、购买袋装的人群中,31.6%因为食品卫生购买,31.6%因为购买便利购买,17.5%因为有固定品牌购买。
原因排名食品卫生,/购买便利、固定品牌、味道、其他(包括营养)、包装精美。
7、竞争对手排名为:馋嘴猴、口水娃/旺旺、没有特定品牌、品忆香、黄飞红、哈牙豆,业五、建议1、品牌定位偏向年轻化路线。
2、豆类零食品种和口味尽可能丰富多样,满足消费者需求。
3、散装食品必须保证卫生度和购买便利性,消除消费者的顾虑。
4、价格设置不宜过高,定位为中档食品。
5、店铺设置做到让消费者购买便利。
2019年咨询工程师实务第二章讲义

第二章数据采集、分析与知识管理本章考情分析:本章属于2019新版改动极大的内容,以文字理解为主,知识较杂,考试题型以记忆为主,不必花费太多的时间,在考前三周进行突击记忆即可。
本章应重点关注“信息鉴别常用方法”、“数据统计分析工作”、“企业建立知识管理系统步骤”几个知识点,考试很有可能不涉及本章题目,也有可能出一个小问的问答题。
一、工程咨询信息及其管理1.工程咨询信息类型及来源(1)信息类型(2)工程咨询对信息的基本要求(3)信息来源2.“互联网+”背景下的工程咨询信息管理(1)任务咨询企业应当利用先进的信息管理手段,建立适合本企业需要的数据库管理系统,加强对本企业内外信息的全面管理,为本企业咨询业务及时提供全面、准确、最新的信息。
(2)方法基本做法:分类与编目检索功能与权限(模糊查询)(3)技术二、信息采集途径和方法1.工程咨询信息采集途径(暗地卷烟)文案调查法、实地调查法、问卷调查法、实验调查法文案调查法:最简单、最一般和常用的方法,也是其他调查方法的基础。
实地调查法:调查周期长,费用高,调查对象容易受调查的心里暗示影响,存在不够客观的可能性。
问卷调查法:适应范围广,简单易行,费用较低,得到大量应用。
实验调查法:用于消费行为调查,最复杂,费用较高,应用范围有限的方法,但调查结果可信度高。
【案例分析】(2011年真题)某企业主要生产A、B两种产品,近期拟投资建设生产C产品的项目。
该企业委托某工程咨询公司提供相关咨询服务。
咨询公司工作过程中,甲咨询工程师提出如下观点:(1)要获得市场相关数据,只能采用实地调查和问卷调查方法。
【问题】3.指出甲咨询工程师的各观点是否正确,并说明理由。
【参考答案】甲的观点(1)不正确。
理由:市场调查的方法除了实地调查和问卷调查外,还有文案调查法和实验调查法。
2.网络信息搜索和提取方法(1)搜索引擎工作原理搜索引擎有信息搜集、信息整理和接受用户查询三部分。
(2)搜索方法与技巧1)关键词索引三、信息鉴别1.信息鉴别常用方法2.信息的综合信息综合有两种方式:一是对已有信息挖掘、延伸,引发创新需求的新信息,达到信息的“增值”;二是通过设计和试验创造新的信息。
第二章 调查方法与技巧(1)--文案调查法

在文案中,对于企业内部资料的收集相对比较容易,调查费用低, 调查的各种障碍少,能够正确把握资料的来源和收集过程,因此,应尽 量利用企业的内部资料。 对于企业外部资料的收集,可以依不同情况,采取不同的方式: (1)具有宣传广告性质的许多资料,如产品目录、使用说明书、图 册、会议资料等,是企事业单位为扩大影响、推销产品、争取客户而免 费面向社会提供的,可以无偿取得;而对于需要采取经济手段获得的资 料,只能通过有偿方式获得,有偿方式取得的资料构成了调查成本,因 此,要对其可能产生的各种效益加以考虑。 (2)对于公开出版、发行的资料,一般可通过订购、邮购、交换、索 取等方式直接获得,而对于对使用对象有一定限制或具有保密性质的资 料,则需要通过间接的方式获取。随着国内外市场竞争的日益加剧,获 取竞争对手的商业秘密已成为市场调查的一个重要内容。
Marketing Research 2007
6
四、文案调查法的优点与局限性
1、优点
(1)时间、费用较少 (2)不受时间和空间的限制 (3)不受调查人员和被调查者主观因素的干扰
Marketing Research 2007
7
2、局限性
第一,这种方法依据的主要是历史资料,过时资料比较多,现实 中正在发展变化的新情况、新问题难以得到即使的反映。 第二,所收集、整理的资料和调查目的往往不能很好地吻合,数 据对解决问题不能完全使用,收集资料时易有遗漏。例如,调查 所需的是分月商品销售额资料,而我们所掌握的是全年商品销售 额资料,尽管可计算平均月销售额,但精确度会受到影响。 第三,文案调查要求调查人员有较广的理论知识、较深的专业知 识及技能,否则将感到无能为力。此外,由于文案调查所收集的 次级资料的准确程度较难把பைடு நூலகம்,有些资料是由专业水平较高的人 员采用科学的方法搜集和加工的,准确度较高,而有的资料只是 估算和推测的,准确度较低,因此,应明确资料的来源并加以说 明。
第二章误差及分析数据的统计处理第六版课后答案

第二章误差及分析数据的统计处理思考题1.正确理解准确度和精密度,误差和偏差的概念。
答:准确度是测定平均值与真值接近的程度,常用误差大小来表示,误差越小,准确度越高。
精密度是指在确定条件下,将测试方法实施多次,所得结果之间的一致程度。
精密度的大小常用偏差来表示。
误差是指测定值与真值之差,其大小可用绝对误差和相对误差来表示。
偏差是指个别测定结果与几次测定结果的平均值之间的差别,其大小可用绝对偏差和相对偏差表示,也可以用标准偏差表示。
2.下列情况分别引起什么误差?如果是系统误差,应如何消除?(1)砝码被腐蚀;(2)天平两臂不等长;(3)容量瓶和吸管不配套;(4)重量分析中杂质被共沉淀;(5)天平称量时最后一位读数估计不准;(6)以含量为99%的邻苯二甲酸氢钾作基准物标定碱溶液。
答:(1)引起系统误差,校正砝码;(2)引起系统误差,校正仪器;(3)引起系统误差,校正仪器;(4)引起系统误差,做对照试验;(5)引起偶然误差;(6)引起系统误差,做对照试验或提纯试剂。
3.用标准偏差和算术平均偏差表示结果,哪一种更合理?答:用标准偏差表示更合理。
因为将单次测定值的偏差平方后,能将较大的偏差显著地表现出来。
4.如何减少偶然误差?如何减少系统误差?答:在一定测定次数范围内,适当增加测定次数,可以减少偶然误差。
针对系统误差产生的原因不同,可采用选择标准方法、进行试剂的提纯和使用校正值等办法加以消除。
如选择一种标准方法与所采用的方法作对照试验或选择与试样组成接近的标准试样做对照试验,找出校正值加以校正。
对试剂或实验用水是否带入被测成分,或所含杂质是否有干扰,可通过空白试验扣除空白值加以校正。
5.某铁矿石中含铁39.16%,若甲分析得结果为39.12%,39.15%和39.18%,乙分析得39.19%,39.24%和39.28%。
试比较甲、乙两人分析结果的准确度和精密度。
解:计算结果如下表所示由绝对误差E 可以看出,甲的准确度高,由平均偏差d 和标准偏差s 可以看出,甲的精密度比乙高。
统计学课后第二章习题答案

第2章练习题1、二手数据的特点是()A。
采集数据的成本低,但搜集比较困难 B. 采集数据的成本低,但搜集比较容易C。
数据缺乏可靠性 D.不适合自己研究的需要2、从含有N个元素的总体中,抽取n个元素作为样本,使得总体中的每一个元素都有相同的机会(概率)被抽中,这样的抽样方式称为()A。
简单随机抽样 B.分层抽样 C.系统抽样 D。
整群抽样3、从总体中抽取一个元素后,把这个元素放回到总体中再抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A。
重复抽样 B.不重复抽样 C.分层抽样 D.整群抽样4、一个元素被抽中后不再放回总体,然后从所剩下的元素中抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.不重复抽样B。
重复抽样C.系统抽样D。
多阶段抽样5、在抽样之前先将总体的元素划分为若干类,然后从各个类中抽取一定数量的元素组成一个样本,这样的抽样方式称为()A。
简单随机抽样B。
系统抽样C.分层抽样D.整群抽样6、先将总体各元素按某种顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个元素,直至抽取n个元素形成一个样本。
这样的抽样方式称为()A. 分层抽样B. 简单随机抽样C。
系统抽样D。
整群抽样7、先将总体划分为若干群,然后以群作为抽样单位从中抽取部分群,再对抽中的各个群中所包含的所有元素进行观察,这样的抽样方式称为()A. 系统抽样B。
多阶段抽样C。
分层抽样D。
整群抽样8、为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生调查,这种调查方是() A。
简单随机抽样B. 整群抽样C.系统抽样D。
分层抽样9、为了调查某校学生的购书费用支出,从全校抽取4个班级的学生进行调查,这种调查方法是()A. 系统抽样B. 简单随机抽样C.分层抽样D。
整群抽样10、为了调查某校学生的购书费用支出,将全校学生的名单按拼音顺序排列后,每隔50名学生抽取一名学生进行调查,这种调查方法是?()A。
报告中的定性数据分析与解释技巧

报告中的定性数据分析与解释技巧
一、引言
描述什么是定性数据,为什么需要对定性数据进行分析和解释。
概述整篇文章的内容和结构。
二、厘定研究目的与问题
在开始进行定性数据分析之前,必须明确研究目的和问题,并将其固化为明确的研究问题。
通过提问和深入讨论的方式,确保研究目的和问题合理合法。
三、准备工作与数据获取
这一部分介绍如何准备工作,选择合适的数据来源和数据收集方法。
同时需要明确研究者的角色和偏好是否可能影响数据的准确性和可信度。
四、编码和分类
在定性数据分析中,编码和分类是基础。
这一部分详细论述如何根据研究目的和问题将数据进行编码和分类,提供一些实用的技巧和方法。
五、模式识别与主题分析
通过模式识别和主题分析,研究者可以发现数据中的潜在模式和主题。
这一部分说明如何进行模式识别和主题分析,引入一些常用的工具和方法。
六、解释和论证
在分析定性数据之后,需要将结果进行解释和论证。
这一部分介绍一些技巧和方法,帮助研究者合理解读和解释结果,并对结果进行有效的论证。
七、结果的可靠性与效度
为了确保结果的可靠性和效度,研究者需要对结果进行验证和确认。
这一部分介绍一些验证的方法和步骤,帮助研究者评估结果的可靠性和效度。
八、结论
对全文进行总结和归纳,重申定性数据分析和解释的重要性,指出可能的不足和改进方向。
通过以上八个小节的展开论述,可以全面且有条理地介绍报告中的定性数据分析与解释技巧。
文章结构紧凑,既有理论分析,又有实践操作,使读者能够全面了解并运用这些技巧,提高研究报告的质量和可信度。
数据分析第二章习题答案

第二章作业
2.4
某公司管理人员为了解某化妆品在一个城市的月销售量Y(单位:箱)与该城市中适合使用该化妆品的人数X1(单位:千人)以及他们人均收入X2(单位:元)之间的关系,在某个月中队15个城市作了调查,得到下述各量的观测值如下:
另外在方差分析表之后,还输出R2值,即R2=SSR
SST =53844.716
53901.600
=0.9989,这些结果均表
明Y与X1,X2,X3之间的线性回归关系式高度显著地参数估计的有关结果
参数估计
(1)得到回归方程为
=Y ^
3.453+0.496X 1+0.009X 1
(3)
β1的置信区间为:(0.483,0.509) β2的置信区间为:(0.007,0.011) (4)
由上表可知对α=0.05时,上表第二行p 均小于α,则X 1,X 2对Y 的影响是显著地;
由SPSS的分析回归线性保存可得当()=(220,2500)是预测值为135.57141,预测区间为(134.08348,137.05934)。
(6)
由上Normal Q-Q Plot of m图知,该正态性近似符合。
XRD数据分析 全面详细教学文案

XRD数据分析 全面详细
一、利用Origin绘图
1)数据的导入
选择曲线
结果
修改X轴
修改Y轴
寻峰
设置找峰范围:
将2theta角变成d值:
选取首列并编辑公式:
三、从findit软件中找到相应的cif 文件
输入第一种物相的含有的元素Sr、S、O
Sr(SO4)的球棒模型为:
同样Na2Zr(Si3O9)(H2O)2 的球棒模型为:
cif文件的输出:
cif文件为
四、运用maud 进行精修
导入cif文件
4.1 修基线
添加参数至5个
右击参数的value值改成refined
结果:
4.2修晶胞参数
结果:
4.3修微结构
4.4修原子位子
两种物相每个原子都要改
4.5修择优取向
• Sr(SO4) , weight %: 60.28361 +- 0.43405727
• Na2Zr(Si3O9)(H2O)2 weight %: 39.71639 +0.43405727
5、用Materials studio绘出球棒形 晶体结构
输入晶胞参数:
Sr(SO4)的球考! 感谢您的支持,我们努力做得更好!谢谢
输入公式:
显示结果:
复制结果:
undo
粘贴至第三列:
隐藏数据列表:
将Y轴表头改为intensity 将X轴表头改为2theta
二、Search Match检索工具进行物相
点击Search Match 进行分析
定性数据分析第二章课后答案
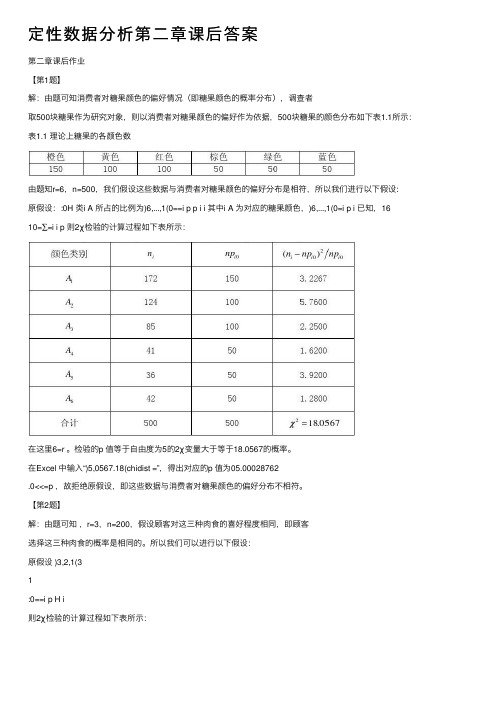
定性数据分析第⼆章课后答案第⼆章课后作业【第1题】解:由题可知消费者对糖果颜⾊的偏好情况(即糖果颜⾊的概率分布),调查者取500块糖果作为研究对象,则以消费者对糖果颜⾊的偏好作为依据,500块糖果的颜⾊分布如下表1.1所⽰:表1.1 理论上糖果的各颜⾊数由题知r=6,n=500,我们假设这些数据与消费者对糖果颜⾊的偏好分布是相符,所以我们进⾏以下假设:原假设::0H 类i A 所占的⽐例为)6,...,1(0==i p p i i 其中i A 为对应的糖果颜⾊,)6,...,1(0=i p i 已知,1610=∑=i i p 则2χ检验的计算过程如下表所⽰:在这⾥6=r 。
检验的p 值等于⾃由度为5的2χ变量⼤于等于18.0567的概率。
在Excel 中输⼊“)5,0567.18(chidist =”,得出对应的p 值为05.00028762.0<<=p ,故拒绝原假设,即这些数据与消费者对糖果颜⾊的偏好分布不相符。
【第2题】解:由题可知,r=3,n=200,假设顾客对这三种⾁⾷的喜好程度相同,即顾客选择这三种⾁⾷的概率是相同的。
所以我们可以进⾏以下假设:原假设 )3,2,1(31:0==i p H i则2χ检验的计算过程如下表所⽰:在这⾥3=r 。
检验的p 值等于⾃由度为2的2χ变量⼤于等于15.72921的概率。
在Excel 中输⼊“)2,72921.15(chidist =”,得出对应的p 值为05.00003841.0<<=p ,故拒绝原假设,即认为顾客对这三种⾁⾷的喜好程度是不相同的。
【第3题】解:由题可知,r=10,n=800,假设学⽣对这些课程的选择没有倾向性,即选各门课的⼈数的⽐例相同,则⼗门课程每门课程被选择的概率都相等。
所以我们可以进⾏以下假设:原假设)10,...,2,1(1.0:0==i p H i 则2χ检验的计算过程如下表所⽰:在这⾥10=r 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定性数据分析第二章课后答案第二章课后作业【第1题】解:由题可知消费者对糖果颜色的偏好情况(即糖果颜色的概率分布),调查者取500块糖果作为研究对象,则以消费者对糖果颜色的偏好作为依据,500块糖果的颜色分布如下表1.1所示:表1.1 理论上糖果的各颜色数由题知r=6,n=500,我们假设这些数据与消费者对糖果颜色的偏好分布是相符,所以我们进行以下假设:原假设::0H 类i A 所占的比例为)6,...,1(0==i p p i i 其中i A 为对应的糖果颜色,)6,...,1(0=i p i 已知,1610=∑=i i p 则2χ检验的计算过程如下表所示:在这里6=r 。
检验的p 值等于自由度为5的2χ变量大于等于18.0567的概率。
在Excel 中输入“)5,0567.18(chidist =”,得出对应的p 值为05.00028762.0<<=p ,故拒绝原假设,即这些数据与消费者对糖果颜色的偏好分布不相符。
【第2题】解:由题可知 ,r=3,n=200,假设顾客对这三种肉食的喜好程度相同,即顾客选择这三种肉食的概率是相同的。
所以我们可以进行以下假设:原假设 )3,2,1(31:0==i p H i则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于15.72921的概率。
在Excel 中输入“)2,72921.15(chidist =”,得出对应的p 值为05.00003841.0<<=p ,故拒绝原假设,即认为顾客对这三种肉食的喜好程度是不相同的。
【第3题】解:由题可知 ,r=10,n=800,假设学生对这些课程的选择没有倾向性,即选各门课的人数的比例相同,则十门课程每门课程被选择的概率都相等。
所以我们可以进行以下假设:原假设)10,...,2,1(1.0:0==i p H i 则2χ检验的计算过程如下表所示:在这里10=r 。
检验的p 值等于自由度为9的2χ变量大于等于5.125的概率。
在Excel 中输入“)9,125.5(chidist =”,得出对应的p 值为05.0823278349.0>>=p ,故接受原假设,即学生对这些课程的选择没有倾向性,各门课选课人数的频率为0.1。
【第4题】解:(1)由题可知,r=3,n=5606,假设1997年8月中国股民投资状况的调查数据和比较流行的说法是相符合。
所以我们可以进行以下假设: 原假设::0H 类i A 所占的比例为)3,2,1(0==i p p i i其中)3,2,1(=i A i 为股票投资中对应的赢、持平和亏,)3,2,1(0=i p i 已知,1310=∑=i i p则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于3511.96137的概率。
在Excel 中输入“)2,72921.15(chidist =”,得出对应的p 值为05.00<<=p ,故拒绝原假设,即认为1997年8月中国股民投资状况的调查数据和比较流行的说法是不相符合的。
(2)解:由题知股票投资中,赢包括盈利10%及以上、盈利10%以下,符合条件的股民共有151+122=273人;持平可以指基本持平,符合条件的股民共有240人;亏包括亏损不足10%和亏损10%及以上,符合条件的股民共有517+240=757人。
由题可知,r=3,n=1270,假设2003年2月上海青年报上的调查数据和比较流行的说法是相符合。
所以我们可以进行以下假设:原假设::0H 类i A 所占的比例为)3,2,1(0==i p p i i其中)3,2,1(=i A i 为股票投资中对应的赢、持平和亏,)3,2,1(0=i p i 已知,1310=∑=i i p则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于188.21372的概率。
在Excel 中输入“)2,21372.188(chidist =”,得出对应的p 值为05.00<<=p ,故拒绝原假设,即认为2003年2月上海青年报上的调查数据和比较流行的说法是不相符合的。
【第5题】解:由题意,我们将“开红花”、“开白花”和“开粉红色花”分别记为321,,A A A ,并记i A 所占的比例为)3,2,1(=i p i ,本题所要检验的原假设为:pq p q p H 2 ,p ,p :322210===其中1=+q p ,这些i p 都依赖一个未知参数p 。
在原假设0H 成立时的似然函数为13210860362242)1()2()()()(p p pq q p p L -∝∝则对L(p)取对数得)1ln(132ln 108)(ln p p p L -+=从而有对数似然方程01132108)(ln =--=∂∂pp p p L 即p p 132)1(108=-。
据此求得p 的极大似然估计45.0ˆ=p,从而得到i p 的极大似然估计 3,2,1),ˆ(ˆ==i p p pi i 。
它们分别为0.2025、0.3025和0.495。
由此得各类的期望频数的估计值3,2,1,ˆ=i pn i 。
它们分别为24.3、36.3、132.20和59.4。
所以2χ统计量的值为0.012244.59)4.5960(3.36)3.3636(3.24)3.2424(2222=-+-+-=χ这里r=3,m=1,r-m-1=1。
检验的p 值等于自由度为1的2χ变量。
利用Excel 可以算出p 值05.0911893.0)1,01224.0(>>==chidist p ,故接受原假设,即我们认为以上数据在0.05的水平下与遗传学理论是相符的。
【第6题】解:由题意,我们可以得到以下信息:① 遗传因子的分布律为:(其中p+q+r=1)②血型的分布律为:将“O ”血型、“A ”血型、“B ”血型和“AB ”血型这四类血型分别记为41A ......, ,A ,并记i A 所占的比例为)4,......,1( =i p i ,本题所要检验的原假设为:pq p qr q p pr p r H 2 ,2 ,2p ,p :42322210=+=+==这些i p 都依赖两个未知参数q p ,。
在原假设0H 成立时的似然函数为5813213243643674858132243623742)2()22()22()1( )2()2()2()(),(pq p q qq p pq p pq qr q pr p r q p L ------∝++∝则对L(p,q)求对数得pqp q q q p p q p q p L 2ln 58)22ln(132ln 132)22ln(436ln 436)1ln(748),(ln +--++--++--=对),(ln q p L 求偏导数得⎪⎪⎩⎪⎪⎨⎧=+---+---+---=∂∂=+---+---+---=∂∂058221321322287201748ln 058222640224364361748ln q p q q q p q p qL p p q q p p q p p L利用Mathematica 软件求解(程序编码及运行结果见附录)解得p 和q 的极大似然估计为100.0ˆ89,2.0ˆ≈≈q p,从而得i p 的极大似然估计4,....,1 ),ˆ,ˆ(ˆ==i q p p pi i 。
它们分别为0.37332、0.43668、0.13220和0.05780。
由此得各类的期望频数的估计值1,....,4i ,ˆ=i pn 。
它们分别为373.32、436.68、132.20和57.80。
所以2χ统计量的值为003292.0 80.57)80.5758(20.132)20.132132(68.436)68.436436(32.373)32.373374(22222=-+-+-+-=χ 这里r=4,m=2,r-m-1=1。
检验的p 值等于自由度为1的2χ变量。
有Excel 可以算出p 值为05.0 954245.0)1 ,003292.0(>>==chidist p ,故接受0H ,我们认为以上数据与遗传学理论是相符的。
附录 ①程序代码:NSolve[{(-748)/(1-p-q)+436/p+(-436)/(2-p-2*q)+0+(-264)/(2-q-2*p)+58/p==0,(-748)/(1-p-q)+0+(-872)/(2-p-2*q)+132/q+(-132)/(2-q-2*p)+58/q==0},{p,q}]//MatrixForm②利用Mathematica 软件运行结果: Out[21] //MatrixForm⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→→→→→→→→0.0999891 q 0.288632 p 0.473295q 0.722065 p 1.50996 q 0.209806 p 0.0900929 q 1.56083p 注:在上述结果中由于p + q = 1-r < 1,所以软件运行的结果中只有第四个解满足条件,即p 和q 的极大似然估计为100.0ˆ89,2.0ˆ≈≈q p。
【第7题】解:由题知,在豌豆实验中,子系从父系(或母系)接受显性因子“黄色”和“青色”的概率分别为p 和1-p ,而子系从父系(或母系)接受显性因子“圆”和“有角”的概率分别为q 和1-q 。
我们将豌豆实验中得到的“黄而圆的”、“青而圆的”、“黄而有角的”和“青而有角的”这四类豌豆分别记为1A ,2A ,3A ,4A ,则这四类豌豆的分布律如下表所示:将豌豆类型i A 所占的比例记为)4,......,1( =i p i ,则本题所要检验的原假设为:224232210)1()1( ,)1)(2( )1)(2(p ),2)(2(p :q p p q p p p p q q q p pq H --=--=--=--=这些i p 都依赖两个未知参数q p ,。
在原假设0H 成立时的似然函数为266280423416423416322210121082315)1()1()2()2( ])1()1[(])1)(2([])1)(2([)]2)(2([),(q p q p q p q p q p p p q q q p pq q p L ----∝--------∝则对L(p,q)求对数得)1ln(266)1ln(280)2ln(423)2ln(416ln 423ln 416),(ln q p q p q p q p L -+-+-+-++=对),(ln q p L 求偏导数得⎪⎪⎩⎪⎪⎨⎧=----=∂∂=----=∂∂012662423423ln 012802416416ln q q q qL p p p p L 即得出下列方程:⎪⎩⎪⎨⎧=+-=+-08322224111208462224111222q q p p 解得p 和q 的极大似然估计为498.0ˆ511,.0ˆ≈≈q p,从而得i p 的极大似然估计4,....,1 ),ˆ,ˆ(ˆ==i q p p pi i 。
