第四章 数据分析(梅长林)习题答案
第三章数据分析(梅长林)习题答案
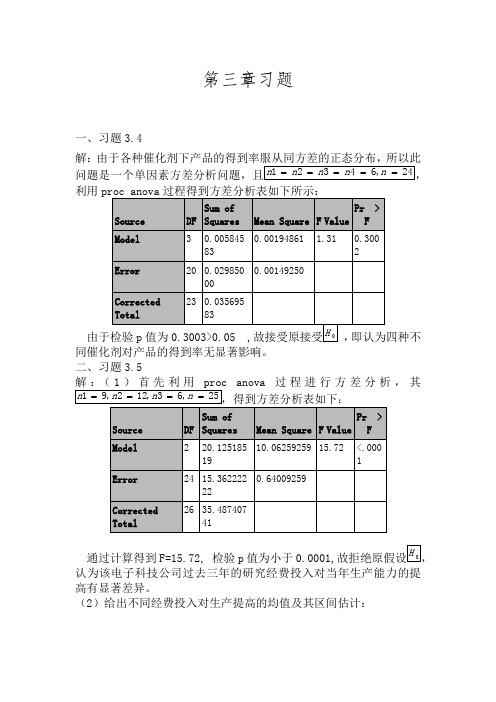
第三章习题一、习题3.4解:由于各种催化剂下产品的得到率服从同方差的正态分布,所以此利用proc anova过程得到方差分析表如下所示:同催化剂对产品的得到率无显著影响。
二、习题3.5anova过程进行方差分析,其通过计算得到F=15.72, 检验p值为小于0.0001,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。
(2)给出不同经费投入对生产提高的均值及其区间估计:为95%的置信区间为:95%的Bonferroni 同时置信区间为:Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高,当年生产能力的改善越显著。
三、习题3.6解:(1)首先利用SAS 的proc anova 过程的means 语句,求出各水平的均值和标准差:如下所示:由上表可知,(a1,b1)组合和(a1,b3)组合的标准差分别为2.030875、2.8067751与其他组合的标准差相差较大,所以我认为假定误差的等方差性不太合理。
故不能直接进行方差分析。
(2)由(1)可知直接进行方差分析是不合理的,所以对观测数据做对数变换,首先来分析个水平组合是否是方差齐性的。
由以上结果可以看出各组合水平上的标准差趋于一致,各组之间的标准差差异比较小。
说明各组合的离散程度比较接近。
故可以利用变换之后的数据在进行方差分析。
(3)由SAS系统的proc anova过程对进行自然对数变换后的数据进行方差分析,得到如下的误差分析表:x1*x2的影响是不显著的,检验P=0.3143>0.05,即两种铁离子残留量的百分比差异在不同剂量水平下可认为是相同的。
而由因素A和因素B对残留量的百分比的影响均显著,检验P值分别为0.0161和<.0001,所以两种铁离子残留量的百分比是有显著差异的,不同剂量水平下残留量的百分比也是有显著差异的。
(4)求出各因素在不同水平下的均值以及估计区间:SAS系统的proc anova过程对数据进行方差分析,得到各因素两两的Bonferroni同时置信区间为:均值之差的置信度为95%(注:可编辑下载,若有不当之处,请指正,谢谢!)。
数据分析方法实验(范金城梅长林)习题报告

习题4.5实验报告一、实验目的问题描述:在习题1.5表1.9中,列出了历年人口出生率、死亡率和自然增长率(单位:%)。
设对应于人口出生率、人口死亡率、自然增长率的数据变量分别为x1,x2,x3。
(1)分别从样本协方差矩阵S及样本相关矩阵R出发,求x1,x2,x3的样本主成分y1,y2,计算各样本主成分的贡献率。
(2)分别从样本协方差矩阵S及样本相关矩阵R出发,将第一样本主成分y1从小到大排序,并给与分析。
二、所用方法及工具(1)主成分分析法与贡献率:主成分分析法即构造原变量的一系列线性组合,使各线性组合在彼此不相关的前提下尽可能多地反映原变量的信息,即使其方差最大。
求的各主成分,等价于求它的协方差矩阵的各特征值及相应的正交单位化特征向量.按特征值由大到小所对应的正交单位化特征向量为组合系数的X,Xz ,…,X,的线性组合分别为X的第一,第二、直至第p个主成分,而各主成分的方差等于相应的特征值。
(2)SAS编程:SAS语言是一种专用的数据管理与分析语言,它提供了一种完善的编程语言。
类似于计算机的高级语言,SAS用户只需要熟悉其命令、语句及简单的语法规则就可以做数据管理和分析处理工作。
因此,掌握SAS编程技术是学习SAS的关键环节。
在SAS中,把大部分常用的复杂数据计算的算法作为标准过程调用,用户仅需要指出过程名及其必要的参数。
这一特点使得SAS编程十分简单。
三、实验内容本次实验采用SAS编程实现,代码如下:data a;set sjfx.rk1;run;proc princomp n=2 cov out=out1;var x1 x2 x3;run;proc sort data=out1 out=a1;by prin1;run;proc print data=a1;run;proc princomp n=2 out=out2;var x1 x2 x3;run;proc sort data=out2 out=a2;by prin1;run;proc print data=a2;run;实验结果:PRINCOMP 过程。
数据分析答案完整版(整理)

x n n x j ( x j x) n 1 n 1 n 1
n2
x j x( j ) x j
服 从 正 态 分 布 。 故 有 E xi x E i
1 n j 0 , n j 1
1 n 1 n n 1 2 D xi x D i j E i j ,故 xi x 服从分 n n n j 1 j 1
N (0, 2 I n ) , (1 , 2 ,
, n ) ,则
,1 .
N (0, 2 ( I n H n )) 。其中:
1
1 1 n 1 , H n n 1, n 1 1
n n 1
n 1 n 2 n n 1 2
——证毕—— 3.条件同第 2 题,证明: (1) x N 0, n
2
(2) N 1 S 2 / 2 x2 n 1 , (4 ) t n
x t n 1
由与此变换为正交变换知, yi 2 xi 2 ,同时 x1 , x2 , , xn 为相互独
i 1 i 1
n
n
立的正态分布。
密度函数 f x1 , x2 ,
xi 1 2 2 i 1 由于正交的雅可比行列 , xn e 2 n
2
1 , n 1 , 1 ,由正交性有 n 1
2 , 3n,
a
第2章 数据分析(梅长林)习题题答案
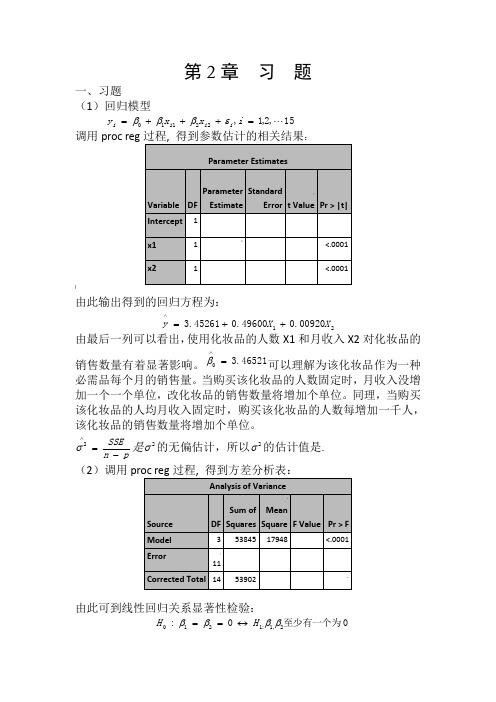
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg:]由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( )2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
数据分析答案梅长林

数据分析答案梅长林【篇一:1.1一维数据数字特征】013学年第一学期主讲教师李晓燕课程名称数据分析课程类别专业限选课学时及学分 68;4授课班级信息101 102使用教材《数据分析方法》系(院.部) 数理系教研室(实验室) 信息和计算科学教研室数据分析总学时:68 理论38.上机28 适用专业:信息和计算科学内容:? sas软件介绍 3学时 ? 数据的描述性分析10学时 ? 线性回归分析 13学时 ? 方差分析 10学时 ? 主成分分析和典型相关分析8学时? 判别分析 8学时 ? 聚类分析 8学时 ? 学生报告 8学时教材:《数据分析方法》,梅长林、范金城编,高等教育出版社.2006. 参考资料:《实用统计方法》,梅长林编,科学出版社;《使用多元统计分析》,高惠璇编,北京大学出版社,2005;《使用统计方法和sas系统》,高惠璇编,北京大学出版社,2001;《多元统计分析》(二版),何晓群编,中国人民大学出版社,2008;《使用回归分析》(二版),何晓群编,中国人民大学出版社,2007;《统计建模和r软件》,薛毅编著,清华大学出版社,2007. 考核:期末成绩(闭卷测试+上机测试):70%。
平时成绩(平时作业+考勤+大报告):30%。
课程作业(1)作业题目在网络教学平台公布,按格式要求,以电子版方式通过平台提交。
(2)大报告:2-3人一组,每组一个选题,成员按相同的成绩计分。
收集数据,撰写小论文,做ppt讲解。
每组讲10-20分钟,提问环节。
同学打分。
课时授课计划课次序号: 01一、课题:1.1 一维数据的数字特征及相关系数二、课型:新授课三、目的要求:1.掌握数据的数字特征(均值、方差等);2.掌握几种描述性分析的sas过程和作图过程计算这些数字特征及进行描述性分析.四、教学重点:均值、方差等数字特征.教学难点:基本概念的理解.五、教学方法及手段:传统教学和上机实验相结合.六、参考资料:1.《实用统计方法》,梅长林,周家良编,科学出版社;2.《sas统计分析使用》,董大钧主编,电子工业出版社.七、作业:1.1八、授课记录:九、授课效果分析:0 绪论0.1 课程内涵数据分析(即多元统计学statistics):是以数据为依据,以统计方法为理论、计算机及软为工具,研究多变量问题、挖掘数据的统计规律的学科. 通过收集数据、整理数据、分析数据和由数据得出结论的一组概念、原则和方法。
数据分析参考答案

数据分析参考答案数据分析参考答案数据分析是一项重要的技能,它帮助我们从大量的数据中提取有用的信息和洞察力。
在当今信息爆炸的时代,数据分析已经成为了各行各业的必备技能。
无论是企业决策、市场营销还是科学研究,数据分析都扮演着重要的角色。
在本文中,我将提供一些数据分析的参考答案,帮助读者更好地理解和应用数据分析。
首先,数据分析的第一步是数据清洗和整理。
在进行数据分析之前,我们需要确保数据的质量和准确性。
这包括删除重复数据、处理缺失值、解决异常值等。
只有经过清洗和整理的数据才能真正反映出问题的本质和规律。
其次,数据分析需要选择合适的方法和工具。
根据问题的性质和数据的类型,我们可以选择不同的数据分析方法。
常见的数据分析方法包括描述性统计、推断统计、机器学习等。
同时,我们还需要选择适合的数据分析工具,如Excel、Python、R等。
选择合适的方法和工具可以提高数据分析的效率和准确性。
第三,数据可视化是数据分析的重要环节。
通过数据可视化,我们可以将抽象的数据转化为直观的图表和图形,更好地理解数据的分布和趋势。
数据可视化不仅可以提高数据分析的效果,还可以帮助我们向他人传达分析结果。
在进行数据可视化时,我们需要选择适当的图表类型,如柱状图、折线图、散点图等,以及合适的颜色和字体。
第四,数据分析需要进行合理的假设和推断。
在进行数据分析时,我们需要建立合理的假设,并通过数据进行验证。
通过统计方法和推断统计学,我们可以对数据进行推断和预测。
然而,我们需要注意的是,数据分析只能提供相关性而非因果性的结论。
因此,在进行数据分析时,我们需要谨慎解读结果,并避免错误的推断。
最后,数据分析需要不断的学习和实践。
数据分析是一个不断发展和演进的领域,新的方法和工具不断涌现。
为了保持竞争力,我们需要不断学习新的数据分析技术,并将其应用到实际问题中。
同时,我们还需要通过实践不断提高自己的数据分析能力,不断优化分析结果和方法。
综上所述,数据分析是一项重要的技能,它帮助我们从大量的数据中提取有用的信息和洞察力。
最新第2章 数据分析(梅长林)习题题答案
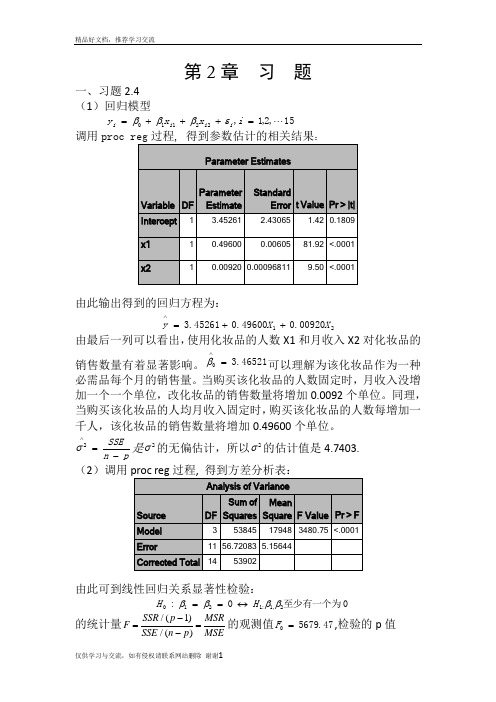
第2章 习 题一、习题2.4 (1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用:由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加0.0092个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加0.49600个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是4.7403. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔== 的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( 2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
第四章数据分析(梅长林)习题答案

第四章 习题一、习题解:(1)通过SAS 的proc princomp 过程对相关系数矩阵R 做主成分分析,得到个主成分的贡献率以及累计贡献率如表1所表 1从表中可以得到特征值向量为:]0.2429 0.4515 0.5396 0.8091 2.8567[=*λ第一主成分贡献率为: % 第二主成分贡献率为: % 第三主成分贡献率为: % 第四主成分贡献率为: % 第五主成分贡献率为: %进一步得到各主成分分析结果如表2所示:(2)由(1)中得到的结果可知前两个主成分的累积贡献率为%,得到第一主成分、第二主成分为:54212.044215.034702.024571.014636.01x x x x x Y ++++=*55820.045257.032604.025093.012404.02x x x x x Y ++---=*由于1*Y 是五个标准化指标的加权和,由此第一主成分更能代表三种化工股票和两种石油股票周反弹率的综合作用效果,1*Y 越大表示各股票的综合周反弹率越大。
*2Y 中关于三种化工股票的周反弹率系数为负,而关于两种石油的系数为正,它放映了两种石油周反弹率和三种化工股票周反弹率的对比,*2Y 的绝对值越大,表明两种石油周反弹率和三种化工股票周反弹率的差距越大。
二、习题解:(1)利用SAS 的proc corr 过程求得相关系数矩阵如表3:(2)从相关系数矩阵出发,通过proc princomp过程对其进行主成分分析,表4给出了各主成分的贡献率以及累积贡献率:表 4第一主成分贡献率为: % 第二主成分贡献率为: %第三主成分贡献率为: % 第四主成分贡献率为: %第五主成分贡献率为: % 第六主成分贡献率为: %其中前两个主成分的累计贡献率为%(3)通过上面的计算得到各主成分,见表5:表 585093.073171.066927.0502169.042541.030185.025192.012496.01x x x x x x x x Y +++++-+=0.0871x8-0.2607x7-0.1347x6+0.5754x5+0.5381x4+0.4754x3+0.0376x2--0.2413x12=Y由于是1Y 八个标准化标值的加权值,因此它反映了平均消费数据的综合指标。
数据分析方法梅长林

数据分析方法梅长林
数据分析是当今社会中非常重要的一项工作,它可以帮助我们更好地理解和利
用数据,从而为决策提供支持。
在数据分析方法中,梅长林是一位非常知名的专家,他的研究成果对于数据分析方法的发展做出了重要贡献。
在本文中,我们将介绍一些梅长林提出的数据分析方法,并探讨它们在实际应用中的价值。
首先,梅长林提出了一种基于统计学原理的数据分析方法。
在这种方法中,他
强调了对数据的有效整理和清洗,以及对数据分布和相关性的深入分析。
通过这种方法,我们可以更好地发现数据中的规律和趋势,从而为后续的决策提供可靠的依据。
其次,梅长林还提出了一种基于机器学习的数据分析方法。
在这种方法中,他
运用了各种算法和模型,对大规模数据进行训练和预测。
通过这种方法,我们可以利用机器学习的能力,发现数据中的复杂关系和模式,从而为业务提供更精准的预测和建议。
此外,梅长林还提出了一种基于数据可视化的分析方法。
在这种方法中,他通
过图表和可视化工具,将数据呈现在我们面前,使得数据的含义一目了然。
通过这种方法,我们可以更直观地理解数据,发现数据中的隐藏信息,为决策提供更直接的参考。
综上所述,梅长林提出的数据分析方法涵盖了统计学、机器学习和数据可视化
等多个领域,为我们提供了丰富的工具和思路。
这些方法在实际应用中,可以帮助我们更好地理解和利用数据,为决策提供更可靠的支持。
因此,我们应该深入学习和应用这些方法,不断提升自己在数据分析领域的能力,为企业和社会创造更大的价值。
多元统计分析应用 第四章课后习题

第四章判别分析习题4.8(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料在该超市试销,其销售价格为3.0,顾客对其口味评分为8,信任度评分平均为5,试预测该饮料的销售情况。
将数据导入SPSS,分析得到以下结果:1.典型判别函数的特征函数的特征值表表1-1 特征值表表1-1所示是典型判别函数的特征值表,只有两个判别函数,所以特征值只有2个。
函数1的特征值为17.791,函数2的特征值为0.720,判别函数的特征值越大,说明函数越具有区别判断力。
函数1方差的累积贡献率高达96.1%,且典型相关系数为0.973,而函数2方差的贡献率仅为3.9%,典型相关系数为0.647。
由此,说明函数1的区别判断力比函数2的强,函数1更具有区别判断力。
2.Wilks检验结果表1-2 Wilks 的Lambda上表中判别函数1和判别函数2的Wilks’Lambda值为0.031,判别函数2的Wilks’Lambda值为0.581。
“1到2”表示两个判别函数的平均数在三个类间的差异情况,P值=0.002<0.05表示差异达到显著水平“2”表示在排除了第一个判别函数后,第二个判别函数在三个组别间的差异情况,P值=0.197>0.05表示判别函数2未达到显著水平。
3.建立贝叶斯判别函数表1-3 贝叶斯判别法函数系数上表为贝叶斯判别函数的系数矩阵,用数学表达式表示各类的贝叶斯判别函数为:第一组:F1=-81.843-11.689X1+12.97X2+16.761X3第二组:F2=-94.536-10.707X1+13.361X2+17.086X3第三组:F3=-17.499-2.194X1+4.960X2+6.447X3将新品牌饮料样品的自变量值分别代入上述三个贝叶斯判别函数,得到三个函数值为:F1=65.271,F2=65.661,F3=47.884比较三个值,可以看出F2=65.661最大,据此得出新品牌饮料样品应该属于第二组,即该饮料的销售情况为平销。
数据分析(梅长林)习题题答案
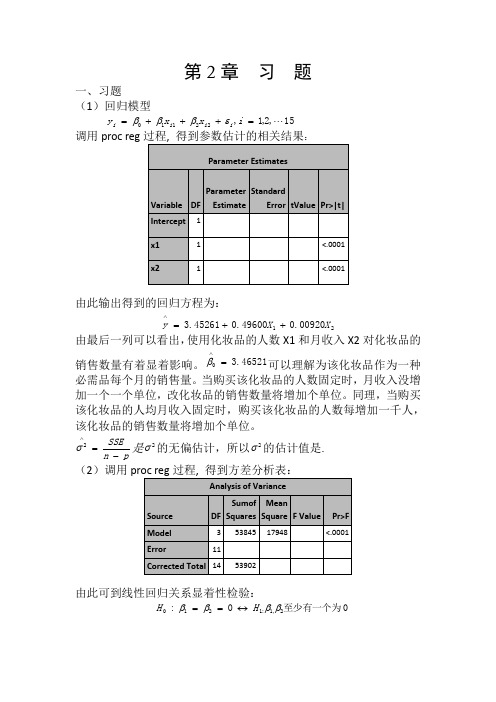
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg :由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显着影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显着性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显着。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( 2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显着性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显着影响。
统计学第四章课后题及答案解析

第四章练习题一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数()A.比例相对数 B.比较相对数 C.结构相对数 D.动态相对数3.某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求()A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
第六章数据分析(梅长林)习题答案
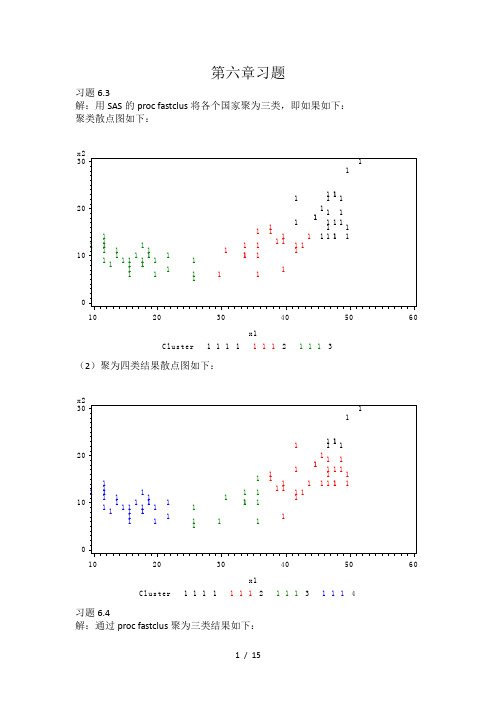
第六章习题习题6.3解:用SAS的proc fastclus将各个国家聚为三类,即如果如下:聚类散点图如下:(2)聚为四类结果散点图如下:习题6.4解:通过proc fastclus聚为三类结果如下:习题6.6解:(1)在proc cluster过程中取选项“method=single”,用最短距离法得到的聚类结果如下所示:上述聚类过程为:首先在最短距离为1的时候,将挪威语和丹麦语聚为一类,得新类CL10={丹麦语,挪威语},其中包含2个样本,这是全部类被分为10类;其次,将法语和意大利语聚为一类,CL9={法语,意大利语};其中包含两个样本,这是全部样本被分为9类,接着在最短距离为2的时候,波兰语被分到CL9当中,也即CL8={CL9,波兰语},然后英语被分到CL10中,的新类CL7={CL10,英语}={丹麦语,挪威语,英语},如此等等,最后在最短距离为8的时候,所有类并入CL2中,这样全部样品归为一类,系统聚类结束。
由谱系聚类法能够细致的看出由小到大的聚类过程,由合并时的距离水平可以看出样本之间的亲疏程度。
然后利用proc tree 过程可以画出最短距离谱系图如下所示:其中以E、N、Da、Du、G、Fr、S、I、P、H、Fi分别代表英语、挪威语、丹麦语、荷兰语、德语、法语、西班牙语、意大利语、波兰语、匈牙利语、芬兰语等11中语言。
(2)最长距离法。
在proc cluster过程中选取”method=conplete”,得到最长距离法聚类过程见下表:不同。
(3)类平均距离法。
在proc cluster过程中选取”method=average”,得到最长距离法聚类过程见下表:与最短距离法聚类过程相比,倒数第二步两种方法合并次序不同,在最长距离聚类中时将匈牙利语和芬兰语先合并为一类在和CL3聚为一类。
最长距离聚类法谱系图如下所示:(4)重心法。
在proc cluster过程中选取”method=centroid”,得到最长距离法聚类过程见下表:其谱系聚类结果如下所示:2.习题6.7解:(1)最长距离法。
数据分析方法 梅长林

数据分析方法梅长林数据分析是指通过收集、整理、加工和解释数据,以提取有用信息、评估假设和支持决策的过程。
数据分析方法是指在数据分析过程中使用的各种技术和工具。
下面将介绍几种常见的数据分析方法。
1. 描述统计分析:描述统计分析是对数据进行总结和描述的方法。
常用的描述统计量包括平均值、中位数、众数、标准差等。
通过描述统计分析,可以对数据的集中趋势、离散程度和分布形态有一个直观的了解。
2. 相关分析:相关分析用于研究变量之间的相关关系。
常见的相关分析方法包括皮尔逊相关系数和斯皮尔曼相关系数。
通过相关分析,可以了解变量之间的线性相关程度和相关方向。
3. 回归分析:回归分析是一种用来研究自变量和因变量之间关系的方法。
回归分析可以分为线性回归分析和非线性回归分析。
通过回归分析,可以估计出自变量对因变量的影响程度,并进行预测和解释。
4. 时间序列分析:时间序列分析主要用于研究随时间变化的数据。
常见的时间序列分析方法包括趋势分析、季节性分析和周期性分析。
时间序列分析可以揭示数据的长期趋势、季节性变化和周期性波动。
5. 聚类分析:聚类分析是一种用于将数据按照某种相似性进行分组的方法。
聚类分析可以帮助我们发现数据中的模式和规律,并进行分类和预测。
6. 因子分析:因子分析是一种用于研究变量之间的潜在结构的方法。
因子分析可以将多个观测指标归纳为几个潜在因子,从而简化数据分析过程,并找出变量之间的内在关系。
7. 假设检验:假设检验是一种用来检验统计推断的方法。
通过对样本数据进行假设检验,可以判断样本数据与总体参数之间是否存在显著差异,以及差异的程度。
以上只是几种常见的数据分析方法,实际数据分析过程中还有其他各种方法和技术。
选择适合的数据分析方法需要根据具体的问题和数据情况进行判断。
同时,数据分析方法的选择也需要结合统计学原理和分析目的,确保结果具有可靠性和实用性。
统计学课后习题答案

第一章统计学及基本概念 1第二章数据的收集与整理 4第三章统计表与统计图7第四章数据的描述性分析 9第五章参数估计 12第六章假设检验 17第七章方差分析 21第八章非参数检验24第九章相关与回归分析27第十章多元统计分析 31第十一章时间序列分析35第十二章指数38第十二章指数38第十三章统计决策42第十四章统计质量管理45第一章统计学及基本概念1.1 统计的涵义(统计工作、统计资料和统计学)1.2 统计学的内容(统计学分类:理论统计学和应用统计学;描述统计学与推断统计学)1.3 统计学的发展史(学派与主要代表人物)1.4 数据类型(定类、定序、定距和定比;时间序列、截面数据和面板数据;绝对数、相对数、平均数)1.5 变量:连续与离散;确定与随机1.6 总体、样本与个体1.7 标志、指标及指标体系1.8 统计计算工具习题一、单项选择题1. 推断统计学研究()。
(知识点:1.2 答案:D)A.统计数据收集的方法B.数据加工处理的方法C.统计数据显示的方法D.如何根据样本数据去推断总体数量特征的方法2. 在统计史上被认为有统计学之名而无统计学之实的学派是()。
(知识点:1.3 答案:D) A.数理统计学派B.政治算术学派C.社会统计学派D.国势学派3. 下列数据中哪个是定比尺度衡量的数据()。
(知识点:1.4 答案:B)A.性别B.年龄C.籍贯D.民族4. 统计对现象总体数量特征的认识是()。
(知识点:1.6 答案:C)A.从定性到定量B.从定量到定性C.从个体到总体D.从总体到个体5. 调查10个企业职工的工资水平情况,则统计总体是()。
(知识点:1.6 答案:C)A.10个企业B.10个企业职工的全部工资C.10个企业的全部职工D.10个企业每个职工的工资6. 从统计总体中抽取出来作为代表这一总体的、由部分个体组成的集合体是().(知识点:1.6 答案:A)A. 样本B. 总体单位C. 个体D. 全及总体7. 三名学生期末统计学考试成绩分别为80分、85分和92分,这三个数字是()。
多元统计分析课后习题解答_第四章

第四章判别分析4.1 简述欧几里得距离与马氏距离的区别和联系。
答:设p维欧几里得空间中的两点X=和Y=。
则欧几里得距离为。
欧几里得距离的局限有①在多元数据分析中,其度量不合理。
②会受到实际问题中量纲的影响。
设X,Y是来自均值向量为,协方差为的总体G中的p维样本。
则马氏距离为D(X,Y)=。
当即单位阵时,D(X,Y)==即欧几里得距离。
因此,在一定程度上,欧几里得距离是马氏距离的特殊情况,马氏距离是欧几里得距离的推广。
4.2 试述判别分析的实质。
答:判别分析就是希望利用已经测得的变量数据,找出一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别的样本点尽可能地区别开来。
设R1,R2,…,Rk 是p 维空间R p 的k 个子集,如果它们互不相交,且它们的和集为,则称为的一个划分。
判别分析问题实质上就是在某种意义上,以最优的性质对p 维空间构造一个“划分”,这个“划分”就构成了一个判别规则。
4.3 简述距离判别法的基本思想和方法。
答:距离判别问题分为①两个总体的距离判别问题和②多个总体的判别问题。
其基本思想都是分别计算样本与各个总体的距离(马氏距离),将距离近的判别为一类。
①两个总体的距离判别问题设有协方差矩阵∑相等的两个总体G 1和G 2,其均值分别是1和2,对于一个新的样品X ,要判断它来自哪个总体。
计算新样品X 到两个总体的马氏距离D 2(X ,G 1)和D 2(X ,G 2),则X ,D 2(X ,G 1)D 2(X ,G 2)X,D 2(X ,G 1)> D 2(X ,G 2,具体分析,2212(,)(,)D G D G -X X 111122111111111222111211122()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ11211212112122()()()2()22()2()---''=-++-'+⎛⎫=--- ⎪⎝⎭''=--=--X ΣμμμμΣμμμμX ΣμμX μααX μ 记()()W '=-X αX μ则判别规则为X ,W(X)X ,W(X)<0②多个总体的判别问题。
数据分析课后答案

1117.00、 习题1.3統計資料(1) .由表可知,全国居民的均值、方差、标准差、偏度、峰度分别为 1031680.286、1015.717、1.025、-0.457。
cv -100* S(%)变异系数有公式 x 计算得90.9325。
(2) 中位数为727.50,上四分位数304.35,下四分位数为1893.50 四分位极差由公式R1 =Q ^Q1得到1579.15A 1 ± 1 ± 1M = —Q 1 +—M +—Q 3三均值由公式 4 2 4得到913.1857。
(3) 直方图(4) 茎叶图全国居民Stem-and-Leaf Plot Freque ncy Stem & Leaf9.00 0 . 1222233445.00 0 . 567882.00 1 . 031.00 1 . 71.00 2 . 33.00 2 . 6891.00 3 . 1Stem width: 1000Each leaf: 1 case(s)4000-3000-1X0-o-(5)由箱图可以看出并不异常点統計資料(1).由图可知农村居民的平均数、方差、标准差、偏度、峰度分别为747.86、399673.838、632.198、1.013、-0.451。
由公式可以算得变异系数为84.5342。
(2)中位数530.50 ,上四分位数239.75 ,下四分位数1197.00。
由公式可得四分位极差为957.25,三均值为624.4375。
(3)茎叶图农村居民Stem-and-Leaf PlotFreque ncy Stem & Leaf10.00 0 . 11112223346.00 0 . 5556782.00 1 . 144.00 1 . 7889Stem width: 1000 Each leaf: 1 case(s)2000-1500- socrQ-农村展民箱图表明了并无异常点統計資料(1) 由表可知城镇居民均值、方差、标准差、偏度、峰度为2336.41、4536136.444、2129.821、0.970、-0.573。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 习题
一、习题4.4
解:(1)通过SAS 的proc princomp 过程对相关系数矩阵R 做主成分分析,得到个主成分的贡献率以及累计贡献率如表1所
表 1
从表中可以得到特征值向量为:
]0.2429 0.4515 0.5396 0.8091 2.8567[=*λ
第一主成分贡献率为:57.13 % 第二主成分贡献率为:16.18 % 第三主成分贡献率为: 10.79% 第四主成分贡献率为:9.03 % 第五主成分贡献率为:6.86 %
进一步得到各主成分分析结果如表2所示:
表 2
(2)由(1)中得到的结果可知前两个主成分的累积贡献率为73.32%,得到第一主成分、第二主成分为:
54212.044215.034702.024571.014636.01x x x x x Y ++++=*
55820.045257.032604.025093.012404.02x x x x x Y ++---=*
由于1*Y 是五个标准化指标的加权和,由此第一主成分更能代表三种化工股票和两种石油股票周反弹率的综合作用效果,1*Y 越大表示各股票的综合周反弹率越大。
*
2Y 中关于三种化工股票的周反弹率系数为
负,而关于两种石油的系数为正,它放映了两种石油周反弹率和三种化工股票周反弹率的对比,*
2Y 的绝对值越大,
表明两种石油周反弹率和三种化工股票周反弹率的差距越大。
二、习题4.5
解:(1)利用SAS 的proc corr 过程求得相关系数矩阵如表3:
表 3
(2)从相关系数矩阵出发,通过proc princomp 过程对其进行主成分分析,表4给出了各主成分的贡献率以及累积贡献率:
表4
第一主成分贡献率为:38.70 % 第二主成分贡献率为:29.59 % 第三主成分贡献率为:11.50% 第四主成分贡献率为:8.82 % 第五主成分贡献率为:6.23 % 第六主成分贡献率为:2.87 % 其中前两个主成分的累计贡献率为68.29%
(3)通过上面的计算得到各主成分,见表5:
表5
8
5093
.
7
3171
.
6
6927
.
5
02169
.
4
2541
.
3
0185
.
2
5192
.
1
2496
.
1
x
x
x
x
x
x
x
x
Y
+
+
+
+
+
-
+ =
0.0871x8
-0.2607x7-0.1347x6
+0.5754x5+0.5381x4+0.4754x3+0.0376x2--0.2413x12 Y
由于是1Y 八个标准化标值的加权值,因此它反映了平均消费数据的综合指标。
对于Y1,它反映了各省人均消费水平,除烟茶酒外,其他支出越高,其人均总体消费水平越高,而烟茶酒对其消费水平评价成反方向。
在Y 2中人均粮食,人均副食品,人均燃料,人均非商品的系数为负;人均烟茶酒、人居其他副食、人均衣着、人均日用品系数为正,说明Y2的绝对值越大,各省人均消费的在生活必需品与高档品差异越大。
根据第一主成分的得分对各个省份进行排序,见表6:
表 6
Obs location Prin1
Obs location Prin1
1 广东 6.89591 16 宁夏 -0.43040
2 上海 3.24842 17 湖南 -0.51802
3 北京 1.7921
4 18 陕西 -0.61274 4 浙江 1.51507 19 云南 -0.66670
5 海南 1.4011
6 20 新疆 -0.81850 6 福建 1.15390 21 青海 -1.11335
7 广西 1.05651 22 安徽 -1.11496
8 天津 0.43543 23 甘肃 -1.18223
9 江苏 0.15329 24 内蒙古 -1.25819 10 辽宁 0.04520 25 贵州 -1.25934 11 西藏 -0.13324 26 吉林 -1.29370 12 四川 -0.13489 27 黑龙江 -1.32567 13 山东 -0.14112 28 河南 -1.48595 14 湖北 -0.17044 29 山西 -1.68448 15 河北
-0.39220
30 江西
-1.96091
三、习题4.6
解:(1)通过SAS的proc princomp过程计算得到样本协方差矩阵见表7:
表7
求得协方差矩阵的特征值以及各样本主成分的贡献率、累计贡献率结果如表8:
表8
从以上结果可看出前三个主成分贡献率已占89.38%,大于剩下三个成分的总和,已包含原始数据的大量信息,所以保留前三个主成分即可。
(2)通过SAS的proc princomp过程对其相关系数矩阵进行主成分分析,首先得到相关系数矩阵见表9:
表9
求得协方差矩阵的特征值以及各样本主成分的贡献率、累计贡献率结果如表10:
表10
从以结果可看出前四个主成分贡献率已占84.59%且第四个主成分的贡献率都占到总信息量的的14.53%,与剩下两个成分的总和差不多,所以保留前四个主成分即可。
我认为基于协方差矩阵S的分析结果更合理。
因为由协方差矩阵S 输出结果可以看出前三个主成分的贡献率就可达到89.38%大于相关系数矩阵R分析得到前四个主成分贡献率总和84.59%,且空腹和摄入食糖的测量数据量纲相等无需进行标准化数据,所以基于协方差矩阵S的分析结果更为合理。
四、习题4.8
(1)通过proc cancorr 过程求得以下结果:
表 11
11
11122221
--R R R R 两个特征值分别为
157698.02
1=∧ρ 0053.02
2=∧
ρ
计算得到各典型变量系数见表下表:
所以有
第一对典型变量为:
2
112114564.01019.10330.12478.1Y Y W X X V -=-=
第一对典型相关系数397.0ˆ1=ρ
; 第二对典型变量为:
2
122120030.10071.07687.03180.0Y Y W X X V +-=+=
第二对典型相关系数07289.0ˆ2=ρ
(2)对典型变量进行显著性检验,结果见表12,其中P1=0.001<0.05,
P2=0.001<0.05,故两对变量都显著相关。
表 12
五、习题4.9
(1)首先计算得到协方差系数矩阵:
进而从协方差系数矩阵计算得到典型变量系数:
所以有
第一对典型变量为:
2
1121180222.05024.007074.005657.0Y Y W X X V -=+=
第一对典型相关系数37716.0ˆ1=ρ
; 第二对典型变量为:
2
1221226208.017615.018695.013997.0Y Y W X X V +-=+-=
第二对典型相关系数99711.0ˆ2=ρ
(2)计算得到样本相关系数矩阵:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢⎢
⎢
⎣⎡= 1.00000.73460.70860.6932
0.73461.00000.70400.71080.70860.69321.00000.73460.70400.71080.73461.0000R
从相关系数矩阵出发,进行典型相关变量分析:
所以有
第一对典型变量为:
*
*
*
*
**-=+=2
112115383.05044.05215.05522.0Y Y W X X V
第一对典型相关系数为:37716.0ˆ1=ρ
第二对典型变量为:
*
**
*
*
*
+-=+-=2
1
22127586.17686.13784.13664.1Y Y
W X X V
第二对典型相关系数为:99711.0ˆ2=ρ
因为样本中测量的数据的量纲都是相同的,所以无论是从协方差系数矩阵还是相关系数矩阵进行典型相关分析,得到的结果是一样的。
对典型变量进行显著性检验,结果见表13:
表13
取显著水平为0.05,其中第一对典型变量的检验p值为0.003,小于0.05,所以第一对典型变量显著相关,而第二对典型变量的检验p值为0.8031,大于0.05,所以第二对典型变量不是显著相关。
