北师大版高一数学必修2试卷及答案
最新高一数学题库 北师大版高一数学必修2试卷及答案

高一数学必修2考试卷十二厂中学 屈丽萍一、选择题(本大题共12小题,每小题5分,共60分)1、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )(A )48 (B )64 (C )96 (D )1922、已知A (x 1,y 1)、B (x 2,y 2)两点的连线平行y 轴,则|AB |=( )A 、|x 1-x 2|B 、|y 1-y 2|C 、 x 2-x 1D 、 y 2-y 13.棱长都是1的三棱锥的表面积为( )B.4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对5、已知正方体外接球的体积是323π,那么正方体的棱长等于 ( D ) (A) (B)3 (C)3 (D)36、若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥C. 若,//l l αβ⊥,则αβ⊥ D .若,l n m n ⊥⊥,则//l m 7、如图,在正方体1111ABCD A B C D -中,E F G H ,,,分别为1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于( )A F D BC G E 1BH 1C 1D1AA.45° B.60° C.90° D.120°8、方程(x-2)2+(y+1)2=1表示的曲线关于点T (-3,2)的对称曲线方程是: ( )A 、 (x+8)2+(y-5)2=1B 、(x-7)2+(y+4)2=2C 、 (x+3)2+(y-2)2=1D 、(x+4)2+(y+3)2=29、已知三点A (-2,-1)、B (x ,2)、C (1,0)共线,则x 为: ( )A 、7B 、-5C 、3D 、-110、方程x 2+y 2-x+y+m=0表示圆则m 的取值范围是 ( )A 、 m ≤2B 、 m<2C 、 m<21D 、 m ≤2111、过直线x+y-2=0和直线x-2y+1=0的交点,且垂直于第二直线的直线方程为 ( )A 、+2y-3=0B 、2x+y-3=0C 、x+y-2=0D 、2x+y+2=012、圆心在直线x=y 上且与x 轴相切于点(1,0)的圆的方程为: ( )A 、(x-1)2+y 2=1B 、(x-1)2+(y-1)2=1C 、(x+1)2+(y-1)2=1D 、(x+1)2+(y+1)2=1二、填空题:(每小题5分,共20分)13、直线x=2y-6到直线x=8-3y 的角是 。
北师大版高中数学必修第二章测试题及答案

高一年级数学学科必修一(第二章)质量检测试卷 (斗鸡中学)一. 一、选择题:共10个小题,每小题6分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 下列判断正确的是( )A 函数22)(2--=x xx x f 是奇函数 B 函数()(1f x x =-是偶函数C 函数()f x x =+D 函数1)(=x f 既是奇函数又是偶函数2 若)(x f 是偶函数,其定义域为()+∞∞-,,且在[)+∞,0上是减函数,则)252()23(2++-a a f f 与的大小关系是( ) A)23(-f >)252(2++a a f B )23(-f <)252(2++a a fC)23(-f ≥)252(2++a a f D )23(-f ≤)252(2++a a f3 已知5)2(22+-+=x a x y 在区间(4,)+∞上是增函数,则a 的范围是( )A 2a ≤-B 2a ≥-C 6-≥aD 6-≤a4 设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,则()0x f x ⋅<的解集是( )A {}|303x x x -<<>或B {}|303x x x <-<<或C {}|33x x x <->或D {}|3003x x x -<<<<或5 已知3()4f x ax bx =+-其中,a b 为常数,若(2)2f -=,则(2)f 的值等于( )A 2-B 4-C 6-D 10-6 已知函数()()0f x x a x a a =+--≠,()()()2200x x x h x x x x ⎧-+>⎪=⎨+≤⎪⎩,则()(),f x h x 的奇偶性依次为( )A 偶函数,奇函数 奇函数,偶函数C 偶函数,偶函数D 奇函数,奇函数7.若函数2()48f x x kx =--在[5,8]上是单调函数,则k 的取值范围是( )A (],40-∞B [40,64]C (][),4064,-∞+∞UD [)64,+∞8 已知函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数,则实数a 的取值范围是( )A 3a ≤-B 3a ≥-C 5a ≤D 3a ≥9. 下列四个命题:(1)函数f x ()在0x >时是增函数,0x <也是增函数,所以)(x f 是增函数;(2)若函数2()2f x ax bx =++与x 轴没有交点,则280b a -<且0a >;(3) 223y x x =--的递增区间为[)1,+∞;(4) 1y x =+和y =表示相等函数其中正确命题的个数是( )A 0B 1C 2D 310 某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( ) 二、填空题:本题共4小题,每小题4分,满分16分,请把答案填在题中横线上 1 设()f x 是R 上的奇函数,且当[)0,x ∈+∞时,()(1f x x =+,则当(,0)x ∈-∞时()f x =_____________________2 若函数()2f x a x b =-+在[)0,x ∈+∞上为增函数,则实数,a b 的取值范围是3 已知221)(x x x f +=,那么)41()4()31()3()21()2()1(f f f f f f f ++++++=_____4 若1()2ax f x x +=+在区间(2,)-+∞上是增函数,则a的取值范围是____________三、解答题1 求下列函数的定义域(本小题共三小题,每小题4分,总分12分)(1)y = (2)11122--+-=x x x y(3)xx y ---=111112(本小题满分12分)判断一次函数,b kx y +=反比例函数x ky =,二次函数c bx ax y ++=2的 单调性3 判断下列函数的奇偶性(本小题满分12分)(1)()22f x x =+- (2)[][]()0,6,22,6f x x =∈--U4 (本小题满分12分)已知函数()f x 的定义域为()1,1-,且同时满足下列条件: (1)()f x 是奇函数; (2)()f x 在定义域上单调递减;(3)2(1)(1)0,f a f a -+-<求a 的取值范围5 (本小题满分12分)已知函数[]2()22,5,5f x x ax x =++∈-① 当1a =-时,求函数的最大值和最小值; ② 求实数a 的取值范围,使()y f x =在区间[]5,5-上是单调函数6 (本小题满分14分)设a 为实数,函数1||)(2+-+=a x x x f ,R x ∈ (1)讨论)(x f 的奇偶性; (2)求)(x f 的最小值参考答案一选择题1C 2 C 3 B 4 D 5 D 6 .D 7 .C 8 . A 9. A 10.B 二填空题 1(1x 2 0a >且0b ≤ 372 4 1(,)2+∞三 解答题1 解:当0k >,y kx b =+解:(1)∵8083,30x x x +≥⎧-≤≤⎨-≥⎩得∴定义域为[]8,3-(2)∵222101011,110x x x x x x ⎧-≥⎪-≥=≠=-⎨⎪-≠⎩得且即∴定义域为{}1-(3)∵0111021101011x x x x x x x x x x ⎧⎪⎧⎪⎪-≠⎪<⎪⎪⎪⎪-≠≠-⎨⎨-⎪⎪⎪⎪≠-≠⎪⎪-⎩⎪-⎪-⎩得∴定义域为11,,022⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭U 2. :当0k >,y kx b =+在R 是增函数,当0k <,y kx b =+在R 是减函数; 当0k >,ky x =在(,0),(0,)-∞+∞是减函数, 当0k <,ky x =在(,0),(0,)-∞+∞是增函数;当0a >,2y ax bx c =++在(,]2b a -∞-是减函数,在[,)2b a -+∞是增函数,当0a <,2y axbx c =++在(,]2b a -∞-是增函数,在[,)2b a -+∞是减函数3 解:(1)定义域为[)(]1,00,1-U ,则22x x +-=,()f x =∵()()f x f x -=-∴()f x =为奇函数(2)∵()()f x f x -=-且()()f x f x -=∴()f x 既是奇函数又是偶函数4 解:22(1)(1)(1)f a f a f a -<--=-,则2211111111a a a a -<-<⎧⎪-<-<⎨⎪->-⎩,5 解:2(1)1,()22,a f x x x =-=-+对称轴min max 1,()(1)1,()(5)37x f x f f x f ===== ∴max m ()37,()1in f x f x ==(2)对称轴,x a =-当5a -≤-或5a -≥时,()f x []5,5-上单调 ∴5a ≥或5a ≤-6 解:(1)当0a =时,2()||1f x x x =++为偶函数, 当0a ≠时,2()||1f x x x a =+-+为非奇非偶函数; (2)当x a <时,2213()1(),24f x x x a x a =-++=-++ 当12a >时,min 13()()24f x f a ==+, 当12a ≤时,min ()f x 不存在;当x a ≥时,2213()1(),24f x x x a x a =+-+=+-+ 当12a >-时,2min ()()1f x f a a ==+, 当12a ≤-时,min 13()()24f x f a =-=-+。
北师大版数学必修试题及答案

高一数学必修二模块考试题命题人:高一年级组 侯雪慧参考公式: 球的表面积公式S球24R π=,其中R 是球半径.锥体的体积公式V锥体13Sh =,其中S 是锥体的底面积,h 是锥体的高. 台体的体积V台体1()3h S S '=,其中,S S '分别是台体上、下底面的面积,h 是台体的高.球的体积公式V 球343R π=,其中R 是球半径.一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、 图(1)是由哪个平面图形旋转得到的 ( )A B C D2.若a ,b 是异面直线,直线c ∥a ,则c 与b 的位置关系是( )A . 相交B . 异面C . 平行D .异面或相交 3.在正方体1111ABCD A B C D -中,下列几种说法正确的是 ( )A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45角 D 、11AC 与1B C 成60角4.正三棱锥的底面边长为6,高为3,则这个三棱锥的全面积为( ) A.39 B.183 C.9(3+6) D.65.如果两个球的体积之比为8:27,那么两个球的表面积之比为 ( ) A.8:27 B. 2:3 C.4:9 D. 2:96、有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为:( )A.24πcm 2,12πcm 3B.15πcm 2,12πcm 3C.24πcm 2,36πcm3D.以上都不正确7) A、8Лcm2B、12Лcm2C、16Лcm2D、20Лcm28、已知在四面体ABCD 中,E 、F 分别是AC 、BD 的中点,若CD=2AB=4,EF ⊥AB ,则EF 与CD 所成的角为( ) A、900B、450C、600D、3009、一个棱柱是正四棱柱的条件是 ( )A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C 、底面是菱形,且有一个顶点处的三条棱两两垂直D 、每个侧面都是全等矩形的四棱柱 10.下列四个命题① 垂直于同一条直线的两条直线相互平行; ② 垂直于同一个平面的两条直线相互平行; ③ 垂直于同一条直线的两个平面相互平行; ④ 垂直于同一个平面的两个平面相互垂直.其中错误..的命题有 ( ) A . 1个 B . 2个 C . 3 个 D . 4个11.已知各面均为等边三角形的四面体的棱长为2,则它的表面积是( )A .B .C .D . 12.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 ( ) A 、23 B 、76 C 、45 D 、56二、填空题(本大题共4小题,每小题6分,共24分)1.长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为_______________.2.如图:四棱锥V-ABCD 中,底面ABCD 是边长为2的正方形,其他四个侧面 都是侧棱长为5的等腰三角形,则二面角V-AB-C 的平面角为 度3. 已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .4. 有下列命题:(m ,n 是两条直线,α是平面)○1若m ║α,n ║α,则m ║n ○2若m ║n ,n ║α,则m ║α ○3若 m ║α则m 平行于α内所有直线 ○4若m 平行于α内无数直线,则m ║α 以上正确的有 个 三、解答题(共66分)1、将圆心角为1200,面积为3π的扇形,作为圆锥的侧面,求圆锥的表面积和体积.2.如图,在四边形ABCD 中,,,,,AD=2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.3.作图(不要求写出作法,请保留作图痕迹)(1) 画出下图几何体的三视图(尺寸自定);(7分)(2) 画出一个底面直径为4cm,高为2cm的圆锥的直观图(6分)4、空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,且AC=BD,判断四边形EFGH的形状,并加以证明。
高中数学 第一章立体几何初步 1.3 三视图练习 北师大版必修2-北师大版高一必修2数学试题
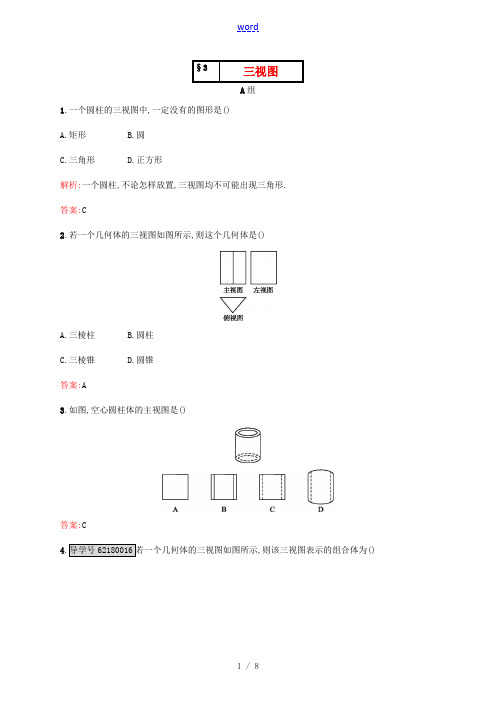
§3三视图A组1.一个圆柱的三视图中,一定没有的图形是()A.矩形B.圆C.三角形D.正方形解析:一个圆柱,不论怎样放置,三视图均不可能出现三角形.答案:C2.若一个几何体的三视图如图所示,则这个几何体是()A.三棱柱B.圆柱C.三棱锥D.圆锥答案:A3.如图,空心圆柱体的主视图是()答案:C4.导学号62180016若一个几何体的三视图如图所示,则该三视图表示的组合体为()A.圆柱与圆锥B.圆柱与三棱锥C.圆柱与四棱锥D.四棱柱与圆锥答案:C5.一个几何体的三视图如图所示,则该几何体的直观图可以是()解析:由俯视图易知,只有选项D符合题意.故选D.答案:D6.如图所示的立体图形,都是由相同的小正方体拼成的.(1)图①的主视图与图②的图相同;(2)图③的主视图与图④的主视图.(填“相同”或“不同”)答案:(1)俯视(2)不同7.如图所示是一个圆锥的三视图,则该圆锥的高为 cm.解析:由三视图知,圆锥的母线长为3 cm,底面圆的直径为3 cm,所以圆锥的轴截面是边长为3 cm 的等边三角形,所以圆锥的高为(cm).答案:8.已知某组合体的主视图与左视图相同(如图1所示,其中AB=AC,四边形BCDE为正方形),则该组合体的俯视图可以是如图2所示的.(把你认为正确的图的序号都填上)图1图2解析:由主视图与左视图可得该几何体可以是由正方体与底面边长相同的四棱锥组合而成的,则其俯视图为图①;可以是由正方体与底面直径与底面正方形边长相同的圆锥组合而成的,则其俯视图为图④;可以是由圆柱与底面相同的圆锥组合而成的,则其俯视图为图③;可以是由圆柱与底面正方形边长等于圆柱底面直径的四棱锥组合而成的,则其俯视图为图②.答案:①②③④9.一个几何体的三视图如图所示,请画出它的实物图.解:由三视图可知,该几何体由正方体和四棱柱组成,如图所示.10.导学号62180017如图所示是一个零件的实物图,画出这个几何体的三视图.解:该零件由一个长方体和一个半圆柱拼接而成,并挖去了一个小圆柱(形成圆孔).主视图反映了长方体的侧面和半圆的底面、小圆柱的底面,左视图反映了长方体的侧面、半圆柱的侧面、小圆柱的侧面,俯视图反映了长方体的底面、半圆柱的侧面和小圆柱的侧面投影后的形状.它的三视图如图所示.B组1.如图①②③分别为三个几何体的三视图,根据三视图可以判断这三个几何体依次分别为()图①图②图③A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:图①②③对应的原几何体分别是三棱柱、正四棱锥、圆锥,故选C.答案:C2.导学号62180018将正方体(如图1-(1)所示)截去两个三棱锥,得到图1-(2)中的几何体,则该几何体的左视图为(如图2所示)()图1图2解析:左侧被截去的三棱锥的底面三条边中,有两条与正方体的棱重合,另一条应为正方形自左上到右下的对角线,是可见的;右侧被截去的三棱锥的底面的三条边中,有两条与正方体的棱重合,另一条应为正方形自右上到左下(从左面看)的对角线,是不可见的.故选B.答案:B3.如图所示,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为()A.6B.3C.3D.6解析:由三视图的画法可知,该几何体的左视图是一个矩形,其宽为2sin 60°=,长为3,故面积S=3.答案:C4.已知一几何体的主视图与左视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:可以结合实物想象,对于①,可认为该几何体的最下部为棱柱,上部为两个圆柱;对于②,可认为该几何体的上部为两个棱柱,下部为圆柱;对于③,可认为该几何体的上部为圆柱,下部为两个棱柱;对于④,可认为该几何体的上部是底面为等腰直角三角形的棱柱,中间为一圆柱,底部为四棱柱;对于⑤,由原几何体最下部的两个视图可知,其俯视图不可能是一个三角形.答案:D5.如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为.解析:根据三视图还原成实物图,即四棱锥P-ABCD,所以最长的一条棱的长为PB=2.答案:26.已知三棱锥的直观图及其俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一直角边长为2的直角三角形,则该三棱锥的主视图面积为.解析:三棱锥的主视图如图所示,故主视图的面积为×2×2=2.答案:27.下图是一个几何体的三视图,试画出其实物图.解:由几何体的三视图容易想到该几何体可以由正方体切割而得到,如图所示.俯视图8.导学号62180019一个棱长均为6的正三棱锥,其俯视图如图所示,求其主视图的面积和左视图的面积.解:作出正三棱锥的直观图如图所示,E为BD的中点,AO为三棱锥的高,由三棱锥的放置方式知,其主视图为三角形,底面边长为BD=6,其高等于AO,其左视图为三角形,底面边长等于CE(中线)的长,其高等于AO.在Rt△BCE中,BC=6,BE=3,得CE=3,CO=×CE=2.在Rt△ACO中,AC=6,CO=2,则AO==2,故主视图面积为×6×2=6,左视图的面积为×3×2=9.。
北师大版高一数学必修2期末试题及答案

斗鸡中学 刘 芳2009-2019学年度高中第一学期期末教学模块测试高一数学(必修2)试题参考公式:1)2S c c h ''+正棱台或圆台侧=(; S ch 正棱柱或圆柱侧=;12S ch '正棱锥或圆锥侧=;24S R π球面=;13V S S h 下台体上=(+;V sh 柱体=; V sh 锥体1=3; 343V R π球=第Ⅰ卷(选择题 共60分)注意事项:1.答第Ⅰ卷前,考生务必将姓名、准考号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.图为某物体的实物图,则其俯视图为( )2.若直线l 只经过第一、二、四象限,则直线l 的斜率k ( )A. 大于零B.小于零 D. 大于零或小于零 D. 以上结论都有可能 3.在空间直角坐标系中Q(1,4,2)到坐标原点的距离为A.21B. 21C.3D.74、 图(1)是由哪个平面图形旋转得到的( )A B C D5.四面体A BCD -中,棱AB AC AD ,,两两互相垂直,则顶点A 在底面BCD 上的投影H 为BCD △的( )A.垂心 B.重心 C.外心 D.内心6.一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ) A.28πcm B.212πcm C.22πcm D.220πcm7.一束光线从点A(-1,1)出发经x 轴反射,到达圆C: (x -2)2+(y -2)2=1上一点的最短路程是A. 4B. 5C. 32-1D.28.如下图,都不是正四面体的表面展开图的是( )A.①⑥ B.④⑤ C.③④ D.④⑥9.已知点(,2)(0)a a >到直线:30l x y -+=的距离为1,则a 等于( )B.21D.1+10.在平面直角坐标系中,直线3x y +=和直线2x y +=的位置关系是( )A.相交但不垂直 B.垂直 C.平行D.重合11.圆:22460x y x y +-+=和圆:2260x y x +-=交于A B ,两点,则AB 的垂直平分线的方程是( ) A.30x y ++=B.250x y --=C.390x y --= D.4370x y -+=12.过点(01)-,)的直线l 与半圆22:430(0)C x y x y +-+=≥有且只有一个交点,则直线l 的斜率k 的取值范围为( ) A.0k =或43k = B.113k <≤ C.43k =或113k <≤D.43k =或113k ≤≤二、填空题:本大题共6小题,每小题5分,共30分。
北师大版高一数学必修2测试题及答案

高一数学必修2测试题斗鸡中学 强彩虹一、 选择题(12×5分=60分)1、下列命题为真命题的是( )A. 平行于同一平面的两条直线平行;B.与某一平面成等角的两条直线平行;C. 垂直于同一平面的两条直线平行;D.垂直于同一直线的两条直线平行。
D.2、下列命题中错误的是:( )A. 如果α⊥β,那么α内一定存在直线平行于平面β;B. 如果α⊥β,那么α内所有直线都垂直于平面β;C. 如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;D. 如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是( )A. 300B.450C. 600D. 9004、右图的正方体ABCD- A ’B ’C ’D ’中,二面角D ’-AB-D 的大小是( )A. 300B.450C. 600D. 9005、直线5x-2y-10=0在x 轴上的截距为a,在y 轴上的截距为b,则( )A.a=2,b=5;B.a=2,b=5-;C.a=2-,b=5;D.a=2-,b=5-.6、直线2x-y=7与直线3x+2y-7=0的交点是( )A (3,-1)B (-1,3)C (-3,-1)D (3,1)7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=08、正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是:( )A BA ’A.3aπ; B.2aπ; C.a π2; D.a π3.9、已知一个铜质的五棱柱的底面积为16cm 2,高为4cm ,现将它熔化后铸成一个正方体的铜块(不计损耗),那么铸成的铜块的棱长是( )A. 2cm;B.cm 34; C.4cm; D.8cm 。
10、圆x 2+y 2-4x-2y-5=0的圆心坐标是:( )A.(-2,-1);B.(2,1);C.(2,-1);D.(1,-2).11、直线3x+4y-13=0与圆1)3()2(22=-+-y x 的位置关系是:( ) A. 相离; B. 相交; C. 相切; D. 无法判定. 12、圆C 1: 1)2()2(22=-++y x 与圆C 2:16)5()2(22=-+-y x 的位置关系是( )A 、外离B 相交C 内切D 外切二、填空题(5×5=25)13、底面直径和高都是4cm 的圆柱的侧面积为 cm 2。
北师大数学必修二测试题附标准答案

x y O x y O x y O xyO高一年级数学学科必修2第二章质量检测试题试卷学校:卧龙寺中学 命题人:吴亮 李丰明第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分)1.下列命题中为真命题地是 ( )A .平行直线地倾斜角相等B .平行直线地斜率相等C .互相垂直地两直线地倾斜角互补D .互相垂直地两直线地斜率互为相反 2. 在同一直角坐标系中,表示直线y ax =与y x a =+正确地是 ( )A .B .C .D .3.已知点(1,2)A 、(3,1)B ,则线段AB 地垂直平分线l 地方程是 ( ) A .524=+y x B .524=-y x C .52=+y x D .52=-y x4.如果直线022=++y ax 与直线023=--y x 平行,那么系数a 为 ( ) A .23-B .6-C .3-D .325.过直线013=-+y x 与072=-+y x 地交点,且与第一条直线垂直地直线l 地方程是( )A .073=+-y xB .0133=+-y xC .072=+-y xD .053=--y x 6.与圆02422=+-+y y x 相切,并在x 轴、y 轴上地截距相等地直线共有 ( ) A.6条 B.5条 C.4条 D.3条7.直线2x =被圆422=+-y a x )(所截得地弦长等于32,则a 地值为 ( )A 、-1或-3B 、22-或C 、1或3D 、3 8.已知1O :06422=+-+y x y x 和2O :0622=-+x y x 交于,A B 两点,则AB 地垂直平分线地方程是 ( )A.30x y ++= B.250x y --= C.390x y --=D.4370x y -+=9.两点)2,2(++b a A 、B ),(b a b --关于直线1134=+y x 对称,则 ( ) A.2,4=-=b a B.2,4-==b a C.2,4==b a D.2,4a b ==10.空间直角坐标系中,点(3,4,0)A -和点(2,1B -地距离是( )A .B .C .9 D二、填空题(本大题共6小题,每小题5分,共30分)把答案填第Ⅱ卷题中横线上11.直线x y 2=关于x 轴对称地直线方程为.12.已知点)1,1(P 和直线l :02043=--y x ,则过P 与直线l 平行地直线方程是,过点P 与l 垂直地直线方程是.13.直线l 经过直线0623=++y x 和0752=-+y x 地交点,且在两坐标轴上地截距相等,则直线l 地方程是______.14.圆心在直线270x y --=上地圆C 与y 轴交于两点(0,4)A -,(0,2)B -,则圆C 地方程为.15.已知点(,)M a b 在直线1543=+y x 上,则22b a +地最小值为16.经过)1,2(-A 和直线1x y +=相切,且圆心在直线x y 2-=上地圆地方程为________________________________.金台区高一年级数学学科必修2第二章质量检测试题参赛试卷第Ⅱ卷二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上)11.________________________12._______________________13._________________________14.______________________15._________________________16._______________________三、解答题(本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(12分)求经过点)2,1(A且到原点地距离等于1地直线方程.18.(14分)已知一曲线是与两个定点(0,0)O 、(3,0)A 距离地比为21地点地轨迹,则求此曲线地方程.19.(14分) 求垂直于直线0743=--y x ,且与两坐标轴构成周长为10地三角形地直线方程20.(15分) 自点A(-3,3)发出地光线L 射到x 轴上,被x 轴反射,其反射光线所在直线与圆x 2+y 2-4x-4y+7=0相切,求光线L 所在直线地方程.21(15分)圆822=+y x 内有一点(1,2)P -,AB 为过点P 且倾斜角为α地弦, (1)当α=1350时,求AB ;(2)当弦AB 被点P 平分时,求出直线AB 地方程;(3)设过P 点地弦地中点为M ,求点M 地坐标所满足地关系式.高一年级数学学科必修2第二章质量检测试题试卷试卷说明学校:卧龙寺中学命题人吴亮李丰明一、命题意图解析几何是新课标中方程与几何部分地重点内容,其中既有一些几何图形基础,也蕴含了丰富地数形结合地思想方法,新课程标准要求重视数学之间地联系应用,培养和发展数学联系意识,所以本章内容一定会成为高考中地热点与重点.本套试题依据“重视基础,考察能力,体现导向,注重发展”地命题原则.注重学生地基础能力,同时考察学生地应用能力,体现了新课程标准数学应用地理念,更考察了学生在数学方面地运用能力以及核心知识地掌握情况,难度中等,对数学学科在新课程地理念下有很好地检测作用.二、试卷结构特点本试题是对高一数学必修2第二章“解析几何”地单元检测,满分150分,时间120分钟,分为Ⅰ卷和Ⅱ卷,共有试题21道,其中10道选择题,共50分;6道填空题,共30分;5道解答题,共70分.难度为中等水平,既有基础能力题,也有拔高扩展题.用基础题考察学生对知识地掌握能力,也同时用拔高题来提高学生地应变能力,为学生对数学意识地培养和在数学方面地应用打好一个基础.三、典型试题例说1.解答第17题:求经过点)2,1(A 且到原点地距离等于1地直线方程.【分析】此题看似简单,但学生极易做错,因为学生只考虑到斜率存在情况,而没有考虑到斜率不存在地情况,因此此题入手容易,得满分难.解:(1)当过点)2,1(A 地直线与x 轴垂直时,则点)2,1(A 到原点地距离为1,所以1=x 为所求直线方程.(2)当过点)2,1(A 且与x 轴不垂直时,可设所求直线方程为)1(2-=-x k y , 即:02=+--k y kx ,由题意有11|2|2=++-k k ,解得43=k , 故所求地直线方程为)1(432-=-x y ,即0543=+-y x . 综上,所求直线方程为1=x 或0543=+-y x .2. 解答第21题:圆822=+y x 内有一点(1,2)P -,AB 为过点P 且倾斜角为α地弦,(1)当α=1350时,求AB ;(2)当弦AB 被点P 平分时,求出直线AB 地方程;(3)设过P 点地弦地中点为M ,求点M 地坐标所满足地关系式.【分析】此题意在使学生理解数形结合地应用思想,要在几何图中勾画函数方程地思想,用函数方程来解决各种问题,正是体现了新课程标准下地“学有价值地数学”地理念.仍要留意不要被斜率不存在所蒙蔽.解:(1)过点O 做OG AB ⊥于G ,连结OA ,当α=1350时,直线AB 地斜率为-1,故直线AB 地方程x+y-1=0,∴OG=d=222100=-+,又∵r=22,∴2OA ===,∴2AB OA == (2)当弦AB 被P 平分时,OP AB ⊥,此时K OP =21-, ∴AB 地点斜式方程为0521212=+-+=-y x x y ),即(.(3)设AB 地中点为(,)M x y ,AB 地斜率为K ,OM AB ⊥,则⎪⎩⎪⎨⎧-=+=-x k y x k y 112)(, 消去K ,得:0222=+-+x y y x ,当AB 地斜率K 不存在时也成立,故过点P 地弦地中点地轨迹方程为:0222=+-+x y y x .参考答案及评分标准一、选择题(本大题共10小题,每小题5分,共50分)二、填空题(本大题共6小题,每小题5分,共30分) 11.x y 2-=. 12.0143=+-y x 或0734=-+y x .13. 340x y +=或10x y ++= 14.22(2)(3)5x y -++= 15.316.22(1)(2)2x y -++=三、解答题(本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(12分)(1)当过点)2,1(A 地直线与x 轴垂直时,则点)2,1(A 到原点地距离为1,所以1=x 为所求直线方程. …………5分(2)当过点)2,1(A 且与x 轴不垂直时,可设所求直线方程为)1(2-=-x k y , 即:02=+--k y kx ,由题意有11|2|2=++-k k ,解得43=k , …………10分故所求地直线方程为)1(432-=-x y ,即0543=+-y x .综上,所求直线方程为1=x 或0543=+-y x . …………12分18.(14分)解:在给定地坐标系里,设点(,)M x y 是曲线上地任意一点,则||1.||2OM AM =…………4分由两点间地距离公式,点M 所适合地条件可以表示为21)3(2222=+-+y x y x ,…………8分 两边平方,得41)3(2222=+-+yx y x ,化简整理有:22230x y x ++-=, 化为标准形式:22(1)4x y ++=, …………12分所以,所求曲线是以C (-1,0)为圆心,2为半径地圆…………14分19.(14分)解:由所求直线能与坐标轴围成三角形,则所求直线在坐标轴上地截距不为0,故可设该直线在x 轴、y 轴上地截距分别为b a ,,又该直线垂直于直线0743=--y x ,且与两坐标轴构成周长为10地三角形,故有⎪⎩⎪⎨⎧=+++=10||||3422b a b a a b , …………9分 解得:52103a b ⎧=⎪⎪⎨⎪=⎪⎩或52103a b ⎧=-⎪⎪⎨⎪=-⎪⎩,…………12分所以所求直线方程为0103y 4x =-+或0103y 4x =++. …………14分20.(15分)解法一:,已知圆地标准方程是:(x-2)2+(y-2)2=1,它关于x 轴地对称圆地方程是(x-2)2+(y+2)2=1. …………5分设光线L 所在地直线地方程是y-3=k(x+3)(其中斜率k 待定), 由题设知对称圆地圆心C ′(2,-2)到这条直线地距离等于1,即…………10分整理得:12k 2+25k+12=0,解得k= -34或k= -43. …………13分故所求直线方程是y-3= -43(x+3),或y-3= -43(x+3),即3x+4y+3=0或4x+3y+3=0. …………15分解法二:已知圆地标准方程是:(x-2)2+(y-2)2=1,设光线L 所在地直线地方程是:y-3=k(x+3)(其中斜率k 待定), 由题意知k ≠0,则L 地反射点地坐标是(-3(1)k k +,0),因为光线地入射角等于反射角, 所以反射光线L '所在直线地方程为y= -k(x+3(1)k k+), 即y+kx+3(1+k)=0.这条直线与已知圆相切,故圆心到直线地距离为1,即以下同解法一21(15分)解:(1)过点O 做OG AB ⊥于G ,连结OA ,当α=1350时,直线AB 地斜率为-1,故直线AB 地方程x+y-1=0,∴OG=d=222100=-+, …………2分又∵r=22,∴OA ===2AB OA = …………5分 (2)当弦AB 被P 平分时,OP AB ⊥,此时K OP =21-, ∴AB 地点斜式方程为0521212=+-+=-y x x y ),即(. …………10分(3)设AB 地中点为(,)M x y ,AB 地斜率为K ,OM AB ⊥,则⎪⎩⎪⎨⎧-=+=-x k y x k y 112)(, 消去K ,得:0222=+-+x y y x ,当AB 地斜率K 不存在时也成立,故过点P 地弦地中点地轨迹方程为:0222=+-+x y y x . …………15分版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.eUts8。
北师大版高中数学必修第二册第一章测试题及答案

北师大版高中数学必修第二册第一章测试题及答案(时间:120分钟满分:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.1弧度的圆心角所对的弧长为6,则这个圆心角所夹的扇形的面积是()A.3B.6C.18D.362.若-π2<α<0,则点P(tan α,cos α)位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知sinα+π6=45,则cosα-π3的值为()A.35B.45C.-45D.-354.若|cos θ|=cos θ,|tan θ|=-tan θ,则θ2的终边在()A.第一、三象限B.第二、四象限C.第一、三象限或在x轴的非负半轴上D.第二、四象限或在x轴的非负半轴上5.函数y=√sinx√|x|-x √log12(x+4)的定义域为()A.(-4,-π]B.[-π,-3]C.[-3,0]D.[0,+∞)6.函数f(x)=sinx+xcosx+x2在[-π,π]的图象大致为()7.把函数f(x)=sin2x+π3图象向左平移π4个单位后所得图象与y轴距离最近的对称轴方程为()A.x=π3B.x=-π6C.x=-π24D.x=11π248.已知函数f(x)=sin(2x+φ)满足f(x)≤f(a)对x∈R恒成立,则函数()A.f(x-a)一定为奇函数B.f(x-a)一定为偶函数C.f(x+a)一定为奇函数D.f(x+a)一定为偶函数二、多项选择题(本题共4小题,每小题5分,共20分)9.给出下列各三角函数值:①sin(-100°);②cos(-220°);③tan(-10);④cos π.其中符号为负的是()A.①B.②C.③D.④10.设函数f(x)=A sin(ωx+φ)A≠0,ω>0,|φ|<π2的图象关于直线x=2π3对称,它的周期是π,则()A.f(x)的图象过点0,12B.f(x)在区间5π12,2π3上是单调递减C.f(x)的一个对称中心是5π12,0 D.f(x)的最大值可能是-A11.将函数f(x)=√3cos2x+π3-1的图象向左平移π3个单位长度,再向上平移1个单位长度,得到函数g(x)的图象,则下列关于函数g(x)的说法正确的是()A.最大值为√3,图象关于直线x=π12对称 B.图象关于y 轴对称 C.最小正周期为π D.图象关于点π4,0对称12.已知函数f (x )=A sin(ωx+φ)(其中A>0,ω>0,0<|φ|<π)的部分图象,则下列结论正确的是( )A.函数f (x )的图象关于直线x=π2对称B.函数f (x )的图象关于点-π12,0对称C.函数f (x )在区间-π3,π6上单调递增 D.函数y=1与y=f (x )-π12≤x ≤23π12的图象的所有交点的横坐标之和为8π3三、填空题(本题共4小题,每小题5分,共20分)13.sin (-23π6)+cos 13π7·tan 4π-cos 13π3= .14.在扇形中,已知半径为8,弧长为12,则圆心角是 弧度,扇形面积是 . 15.函数y=sin (x +π6),x ∈[0,π2]的值域是 .16.已知函数f (x )=12sin 2x,给出下列五个说法:①f (1 921π12)=14;②若f (x 1)=-f (x 2),则x 1=-x 2; ③f (x )在区间[-π6,π3]上单调递增;④将函数f (x )的图象向右平移3π4个单位可得到函数y=12cos 2x 的图象;⑤函数f(x)的图象关于点(-π4,0)成中心对称.其中说法正确的是(填序号).四、解答题(本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(10分)在“①y=f(x)图象的一条对称轴是直线x=π8,②f(0)=-√22,③y=f(x)的图象关于点7π8,0成中心对称”这三个条件中任选一个,补充在下面问题中,并作出详细解答.设函数f(x)=sin(2x+φ)(-π<φ<0),,求函数y=f(x)的单调递增区间.注:如果选择多个条件分别解答,按第一个解答计分.18.(12分)(1)化简:sin(2π-α)tan(α+π)tan(-α)cos(π-α)tan(3π-α);(2)计算:cos25π6+cos25π3+tan-25π4+sin5π6.19.(12分)已知函数f(x)=3tan(2x-π3).(1)求f(x)的定义域;(2)比较f(π2)与f(-π8)的大小.20.(12分)已知函数f(x)=A sin(ωx+φ)x∈R,A>0,ω>0,|φ|<π2的部分图象如图所示.(1)试确定f(x)的解析式;(2)若f(α2π)=12,求cos2π3+α2的值.21.(12分)已知函数f(x)=2sin(2x+π6)+a+1(其中a为常数).(1)求f(x)的单调区间.(2)若x∈[0,π2]时,f(x)的最大值为4,求a的值.(3)求出使f(x)取最大值时x的取值集合.22.(12分)已知点A (x 1,f (x 1)),B (x 2,f (x 2))是函数f (x )=2sin(ωx+φ)ω>0,-π2<φ<0图象上的任意两点,角φ的终边经过点P (1,-√3),且当|f (x 1)-f (x 2)|=4时,|x 1-x 2|的最小值为π3. (1)求函数f (x )的解析式; (2)求函数f (x )的单调递增区间;(3)当x ∈0,π6时,不等式mf (x )+2m ≥f (x )恒成立,求实数m 的取值范围.第一章测评(时间:120分钟 满分:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.1弧度的圆心角所对的弧长为6,则这个圆心角所夹的扇形的面积是( )A.3B.6C.18D.36α,圆心角所对的弧长为l ,半径为r.因为l=|α|r ,所以6=1×r. 所以r=6.所以S=12lr=12×6×6=18.2.若-π2<α<0,则点P (tan α,cos α)位于( ) A.第一象限 B.第二象限 C.第三象限D.第四象限-π2<α<0,所以tan α<0,cos α>0,所以点P (tan α,cos α)位于第二象限.3.已知sin α+π6=45,则cos α-π3的值为( )A.35 B.45 C.-45 D.-35解析cos α-π3=cos α+π6−π2=sin α+π6=45.故选B .4.若|cos θ|=cos θ,|tan θ|=-tan θ,则θ2的终边在( ) A .第一、三象限 B .第二、四象限C .第一、三象限或在x 轴的非负半轴上D .第二、四象限或在x 轴的非负半轴上,cos θ≥0,tan θ≤0,所以θ的终边在x 轴的非负半轴上或在第四象限,故θ2的终边在第二、四象限或在x 轴的非负半轴上.5.函数y=√sinx√|x |-x√log 12(x +4)的定义域为( )A .(-4,-π]B .[-π,-3]C .[-3,0]D .[0,+∞),需满足{sinx ≥0,|x |-x >0,0<x +4≤1,即{2kπ≤x ≤2kπ+π,k ∈Z ,x <0,-4<x ≤-3,解得-4<x ≤-π.6.函数f (x )=sinx+xcosx+x 2在[-π,π]的图象大致为( )f (-x )=-f (x )及区间[-π,π]关于原点对称,得f (x )是奇函数,其图象关于原点对称,排除A .又f (π2)=1+π2(π2)2=4+2ππ2>1,f (π)=π-1+π2>0,排除B,C .故选D .7.把函数f (x )=sin 2x+π3图象向左平移π4个单位后所得图象与y 轴距离最近的对称轴方程为( ) A.x=π3 B.x=-π6 C.x=-π24D.x=11π24解析把函数f (x )=sin 2x+π3图象向左平移π4个单位后所得图象对应的解析式为y=sin 2x+π4+π3=cos 2x+π3,由2x+π3=k π(k ∈Z ),得对称轴方程为x=-π6+kπ2(k ∈Z ).当k=0时,可得对称轴为x=-π6,此时对称轴离y 轴距最近.故选B . 答案B8.已知函数f (x )=sin(2x+φ)满足f (x )≤f (a )对x ∈R 恒成立,则函数( ) A.f (x-a )一定为奇函数 B.f (x-a )一定为偶函数 C.f (x+a )一定为奇函数 D.f (x+a )一定为偶函数解析由题意得f (a )=sin(2a+φ)=1,则2a+φ=2k π+π2,k ∈Z ,所以f (x+a )=sin(2x+2a+φ)=sin 2x+2k π+π2=cos 2x ,此时函数为偶函数. 答案D二、多项选择题(本题共4小题,每小题5分,共20分)9.给出下列各三角函数值:①sin(-100°);②cos(-220°);③tan(-10);④cos π.其中符号为负的是( ) A.①B.②C.③D.④解析因为-100°角是第三象限角,所以sin(-100°)<0;因为-220°角是第二象限角,所以cos(-220°)<0;因为-10∈-72π,-3π,所以-10角是第二象限角,所以tan(-10)<0;cos π=-1<0.故选ABCD . 答案ABCD10.设函数f(x)=A sin(ωx+φ)A≠0,ω>0,|φ|<π2的图象关于直线x=2π3对称,它的周期是π,则()A.f(x)的图象过点0,12B.f(x)在区间5π12,2π3上是单调递减C.f(x)的一个对称中心是5π12,0D.f(x)的最大值可能是-AT=π,所以2πω=π,所以ω=2.又因为f(x)的图象关于直线x=2π3对称,所以2×2π3+φ=π2+kπ,k∈Z,又|φ|<π2,所以φ=π6.所以f(x)=A sin2x+π6.所以f(x)图象过点0,A2.又当x=5π12时,2x+π6=π,即f5π12=0,所以5π12,0是f(x)的一个对称中心.又因为A的值不能确定,所以A,B不一定正确.当A<0时,f(x)的最大值是-A.故D正确.11.将函数f(x)=√3cos2x+π3-1的图象向左平移π3个单位长度,再向上平移1个单位长度,得到函数g(x)的图象,则下列关于函数g(x)的说法正确的是()A.最大值为√3,图象关于直线x=π12对称 B.图象关于y 轴对称 C.最小正周期为πD.图象关于点π4,0对称解析将函数f (x )=√3cos 2x+π3-1的图象向左平移π3个单位长度,得到y=√3cos 2x+π3+π3-1=√3cos(2x+π)-1=-√3cos 2x-1的图象;再向上平移1个单位长度,得到函数g (x )=-√3cos 2x 的图象.对于函数g (x ),它的最大值为√3,由于当x=π12时,g (x )=-32,不是最值,故g (x )的图象不关于直线x=π12对称,故A 错误;由于该函数为偶函数,故它的图象关于y 轴对称,故B 正确;它的最小正周期为2π2=π,故C 正确;当x=π4时,g (x )=0,故函数g (x )的图象关于点π4,0对称,故D 正确.答案BCD12.已知函数f (x )=A sin(ωx+φ)(其中A>0,ω>0,0<|φ|<π)的部分图象,则下列结论正确的是( ) A.函数f (x )的图象关于直线x=π2对称B.函数f (x )的图象关于点-π12,0对称C.函数f (x )在区间-π3,π6上单调递增D.函数y=1与y=f (x )-π12≤x ≤23π12的图象的所有交点的横坐标之和为8π3解析由函数f (x )=A sin(ωx+φ)(其中A>0,ω>0,0<|φ|<π)的图象可得,A=2,T 4=2π3−5π12=π4,因此T=π,所以ω=2ππ=2,所以f (x )=2sin(2x+φ),又因为图象过点2π3,-2,所以f 2π3=2sin 4π3+φ=-2,即sin 4π3+φ=-1,因此4π3+φ=3π2+2k π,k ∈Z ,又0<|φ|<π,所以φ=π6,所以f (x )=2sin 2x+π6.当x=π2时,f π2=-1,故A错;当x=-π12时,f -π12=0,故B 正确;当x ∈-π3,π6,2x+π6∈-π2,π2,所以f (x )=2sin 2x+π6在x ∈-π3,π6上单调递增,故C 正确;当-π12≤x ≤23π12时,2x+π6∈[0,4π],所以y=1与函数y=f (x )有4个交点的横坐标为x 1,x 2,x 3,x 4,x 1+x 2+x 3+x 4=π6×2+7π6×2=8π3,故D 正确. 答案BCD三、填空题(本题共4小题,每小题5分,共20分)13.sin (-23π6)+cos 13π7·tan 4π-cos 13π3= .解析原式=-sin (4π-π6)+cos 13π7·0-cos 4π+π3=-sin (-π6)-cos π3=sin π6-cos π3=12−12=0.答案014.在扇形中,已知半径为8,弧长为12,则圆心角是 弧度,扇形面积是 .θ,则有θ=128=32弧度;扇形面积S=12×12×8=48.4815.函数y=sin (x +π6),x ∈[0,π2]的值域是 .x ∈[0,π2],所以π6≤x+π6≤2π3,所以12≤sin (x +π6)≤1,即原函数的值域为[12,1].[12,1]16.已知函数f (x )=12sin 2x,给出下列五个说法:①f(1921π12)=14;②若f(x1)=-f(x2),则x1=-x2;③f(x)在区间[-π6,π3]上单调递增;④将函数f(x)的图象向右平移3π4个单位可得到函数y=12cos 2x的图象;⑤函数f(x)的图象关于点(-π4,0)成中心对称.其中说法正确的是(填序号).正确,由已知得函数f(x)周期为π,f(1921π12)=f(π12)=12sinπ6=14;②错误,由f(x1)=-f(x2)=f(-x2),知x1=-x2+kπ或x1=π2+x2+kπ(k∈Z);③错误,令-π2+2kπ≤2x≤π2+2kπ(k∈Z),得-π4+kπ≤x≤π4+kπ(k∈Z),函数f(x)在每一个闭区间-π4+kπ,π4+kπ(k∈Z)上都单调递增,但[-π6,π3]不包含于[-π4+kπ,π4+kπ](k∈Z),故函数f(x)在区间[-π6,π3]上不是单调函数;④正确,将函数f(x)的图象向右平移3π4个单位可得到函数y=12sin 2(x-3π4)=12sin(2x-3π2)=12cos2x的图象;⑤错误,函数f(x)的对称中心的横坐标满足2x0=kπ,解得x0=kπ2,即对称中心的坐标为(kπ2,0)(k∈Z),故点(-π4,0)不是其对称中心.四、解答题(本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(10分)在“①y=f (x )图象的一条对称轴是直线x=π8,②f (0)=-√22,③y=f (x )的图象关于点7π8,0成中心对称”这三个条件中任选一个,补充在下面问题中,并作出详细解答.设函数f (x )=sin(2x+φ)(-π<φ<0), ,求函数y=f (x )的单调递增区间. 注:如果选择多个条件分别解答,按第一个解答计分.解选择①:因为x=π8是函数y=f (x )的图象的对称轴,所以sin 2×π8+φ=±1.所以π4+φ=k π+π2,k ∈Z . 因为-π<φ<0,所以φ=-3π4.因此y=sin 2x-3π4.由题意得2k π-π2≤2x-3π4≤2k π+π2,k ∈Z .所以k π+π8≤x ≤k π+5π8,k ∈Z .所以函数y=sin 2x-3π4的单调递增区间为k π+π8,k π+5π8,k ∈Z . 选择②:因为f (0)=-√22,所以sin φ=-√22,又因为-π<φ<0,所以φ=-3π4.因此y=sin 2x-3π4.由题意得2k π-π2≤2x-3π4≤2k π+π2,k ∈Z .所以k π+π8≤x ≤k π+5π8,k ∈Z .所以函数y=sin 2x-3π4的单调递增区间为k π+π8,k π+5π8,k ∈Z .选择③:因为y=f(x)的图象关于点7π8,0成中心对称,所以2×7π8+φ=kπ,k∈Z,φ=kπ-74π,又因为-π<φ<0,所以φ=-3π4.因此y=sin2x-3π4.由题意得2kπ-π2≤2x-3π4≤2kπ+π2,k∈Z.所以kπ+π8≤x≤kπ+5π8,k∈Z.所以函数y=sin2x-3π4的单调递增区间为kπ+π8,kπ+5π8,k∈Z.18.(12分)(1)化简:sin(2π-α)tan(α+π)tan(-α)cos(π-α)tan(3π-α);(2)计算:cos25π6+cos25π3+tan-25π4+sin5π6.原式=sin(-α)tanαtan(-α)-cosα(-tanα)=-sinαtanα(-tanα)cosαtanα=tan αtan α=tan2α.(2)cos25π6+cos25π3+tan-25π4+sin5π6=cos4π+π6+cos8π+π3+tan-6π-π4+sinπ-π6=cosπ6+cosπ3+tan-π4+sinπ6=√3 2+12-1+12=√32.19.(12分)已知函数f(x)=3tan(2x-π3).(2)比较f (π2)与f (-π8)的大小.解(1)由已知得2x-π3≠k π+π2(k ∈Z ),x ≠12k π+5π12(k ∈Z ),所以函数f (x )的定义域为x |x ≠12k π+5π12,k ∈Z . (2)因为f (π2)=3tan (π-π3)=-3tan π3<0,f (-π8)=3tan (-π4-π3)=3tan (-7π12)=3tan (π-7π12)=3tan 5π12>0.所以f (π2)<f (-π8).20.(12分)已知函数f (x )=A sin(ωx+φ)x ∈R ,A>0,ω>0,|φ|<π2的部分图象如图所示. (1)试确定f (x )的解析式;(2)若f (α2π)=12,求cos 2π3+α2的值.由题图可知A=2,T4=56−13=12,则T=2,ω=2πT =π.将点P (13,2)代入y=2sin(πx+φ),得sin (π3+φ)=1, 又|φ|<π2,所以φ=π6.故f (x )的解析式为f (x )=2sin (πx +π6)(x ∈R ).(2)由(1)和f (α2π)=12,得2sin (α2+π6)=12,即sin (α2+π6)=14.所以cos (2π3+α2)=cos (π2+π6+α2)=-sin (π6+α2)=-14.21.(12分)已知函数f (x )=2sin (2x +π6)+a+1(其中a 为常数).(2)若x ∈[0,π2]时,f (x )的最大值为4,求a 的值. (3)求出使f (x )取最大值时x 的取值集合.由-π2+2k π≤2x+π6≤π2+2k π(k ∈Z ),解得-π3+k π≤x ≤π6+k π(k ∈Z ).所以函数f (x )的单调递增区间为-π3+k π,π6+k π(k ∈Z ). 由π2+2k π≤2x+π6≤3π2+2k π,k ∈Z ,解得π6+k π≤x ≤2π3+k π(k ∈Z ).所以函数f (x )的单调递减区间为π6+k π,2π3+k π(k ∈Z ).(2)因为0≤x ≤π2,所以π6≤2x+π6≤7π6, 所以-12≤sin (2x +π6)≤1,所以f (x )的最大值为2+a+1=4,所以a=1. (3)当f (x )取最大值时,2x+π6=π2+2k π,k ∈Z , 所以2x=π3+2k π,k ∈Z , 所以x=π6+k π,k ∈Z .所以当f (x )取最大值时,x 的取值集合是x x=π6+k π,k ∈Z .22.(12分)已知点A (x 1,f (x 1)),B (x 2,f (x 2))是函数f (x )=2sin(ωx+φ)ω>0,-π2<φ<0图象上的任意两点,角φ的终边经过点P (1,-√3),且当|f (x 1)-f (x 2)|=4时,|x 1-x 2|的最小值为π3. (1)求函数f (x )的解析式; (2)求函数f (x )的单调递增区间;(3)当x ∈0,π6时,不等式mf (x )+2m ≥f (x )恒成立,求实数m 的取值范围.因为角φ的终边经过点P (1,-√3),所以tan φ=-√3, 因为-π2<φ<0,所以φ=-π3.由当|f (x 1)-f (x 2)|=4时,|x 1-x 2|的最小值为π3,得T=2π3,即2πω=2π3,所以ω=3.所以f (x )=2sin 3x-π3.(2)由-π2+2k π≤3x-π3≤π2+2k π,k ∈Z , 得-π18+2kπ3≤x ≤5π18+2kπ3,k ∈Z ,故函数f (x )的单调递增区间为-π18+2kπ3,5π18+2kπ3(k ∈Z ).(3)当x ∈0,π6时,-√3≤f (x )≤1,于是2+f (x )>0,则mf (x )+2m ≥f (x )等价于m ≥f (x )2+f (x )=1-22+f (x ).由-√3≤f (x )≤1,得f (x )2+f (x )的最大值为13. 故实数m 的取值范围是13,+∞.。
(常考题)北师大版高中数学必修二第一章《立体几何初步》测试(包含答案解析)
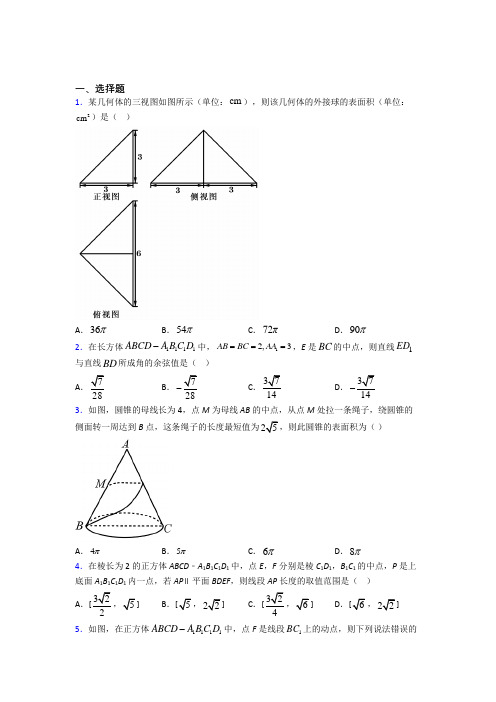
一、选择题1.某几何体的三视图如图所示(单位:cm ),则该几何体的外接球的表面积(单位:2cm )是( )A .36πB .54πC .72πD .90π 2.在长方体1111ABCD A B C D -中,12,3AB BC AA ===,E 是BC 的中点,则直线1ED 与直线BD 所成角的余弦值是( )A .7B .7-C .37D .37- 3.如图,圆锥的母线长为4,点M 为母线AB 的中点,从点M 处拉一条绳子,绕圆锥的侧面转一周达到B 点,这条绳子的长度最短值为25,则此圆锥的表面积为( )A .4πB .5πC .6πD .8π4.在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,P 是上底面A 1B 1C 1D 1内一点,若AP ∥平面BDEF ,则线段AP 长度的取值范围是( ) A .325B .522C .326] D .6,22] 5.如图,在正方体1111ABCD A B C D -中,点F 是线段1BC 上的动点,则下列说法错误的是( )A .无论点F 在上1BC 怎么移动,都有11A FB D ⊥B .当点F 移动至1BC 中点时,才有1A F 与1BD 相交于一点,记为点E ,且12A E EF = C .当点F 移动至1BC 中点时,直线1A F 与平面1BDC 所成角最大且为60°D .无论点F 在1BC 上怎么移动,异面直线1A F 与CD 所成角都不可能是30°6.在正方体1111ABCD A B C D -中,M 是棱1CC 的中点.则下列说法正确的是( ) A .异面直线AM 与BC 所成角的余弦值为5 B .BDM 为等腰直角三角形C .直线BM 与平面11BDD B 所成角的正弦值等于105D .直线1AC 与平面BDM 相交7.一个几何体的三视图如图所示,则该几何体的体积为( )A .4B .8C .12D .148.如图,正方体1111ABCD A B C D -中,P 为线段1A B 上的动点,则下列结论错误的是( )A .1DC PC ⊥B .异面直线AD 与PC 不可能垂直C .1D PC ∠不可能是直角或者钝角D .1APD ∠的取值范围是,62ππ⎛⎫ ⎪⎝⎭ 9.已知长方体1111ABCD A B C D -的顶点A ,B ,C ,D ,在球O 的表面上,顶点1A ,1B ,1C ,1D ,在过球心O 的一个平面上,若6AB =,8AD =,14AA =,则球O 的表面积为( )A .169πB .161πC .164πD .265π 10.设m 、n 是两条不同的直线,α是平面,m 、n 不在α内,下列结论中错误的是( )A .m α⊥,//n α,则m n ⊥B .m α⊥,n α⊥,则//m nC .m α⊥,m n ⊥,则//n αD .m n ⊥,//n α,则m α⊥ 11.如图(1),Rt ABC ,1,3,2AC AB BC ===,D 为BC 的中点,沿AD 将ACD △折起到AC D ',使得C '在平面ABD 上的射影H 落在AB 上,如图(2),则以下结论正确的是( )A .AC BD '⊥B .AD BC '⊥ C .BD C D ⊥' D .AB C D ⊥' 12.已知二面角l αβ--为60,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,45ACD ∠=,则异面直线AB 与CD 所成角的余弦值为( )A .14B .24C .34D .12二、填空题13.3ABCD 中,对角线3AC =ABC 沿AC 折起,使得二面角B AC D --的大小为2π,则三棱锥B ACD -外接球的体积是_________________.14.已知H 是球O 的直径AB 上一点,:1:3AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为__________.15.在正三棱锥P ABC -中,E ,F 分别为棱PA ,AB 上的点,3PE EA =,3BF FA =,且CE EF ⊥.若23PB =,则三棱锥P ABC -的外接球的体积为_________.16.如图,圆柱的体积为16π,正方形ABCD 为该圆柱的轴截面,F 为AB 的中点,E 为母线BC 的中点,则异面直线AC ,EF 所成的角的余弦值为______.17.一个三棱锥的三视图如图所示,该三棱锥中最长棱的长度为_______.18.正四面体ABCD 棱长为2,AO ⊥平面BCD ,垂足为O ,设M 为线段AO 上一点,且90BMC ︒∠=则二面角M BC O --的余弦值为________.19.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.若M 为线段1A C 的中点,则在ADE 翻折过程中,下面四个选项中正确的是______(填写所有的正确选项)(1)BM 是定值 (2)点M 在某个球面上运动(3)存在某个位置,使1DE A C ⊥(4)存在某个位置,使//MB 平面1A DE20.若三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,23AB =,7SA SB SC ===,则该三棱锥的外接球的表面积为__________.三、解答题21.如图,ABC 是边长为2的正三角形,ABD △是以AB 为斜边的等腰直角三角形,且2CD =.(1)求证:平面ABC ⊥平面ABD ;(2)求二面角A-BC-D 的余弦值.22.如图,在正四棱柱1111ABCD A B C D -中,11,2AB AA ==,点E 为1CC 中点,点F 为1BD 中点.(1)求异面直线1BD 与1CC 的距离;(2)求直线1BD 与平面BDE 所成角的正弦值;(3)求点F 到平面BDE 的距离.23.如图,该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成,其中正方形ABCD 的边长为4,H 是线段EF 上(不含端点)的动点,36==FC EB .(1)证明://GH 平面ABCD ;(2)求H 到平面AEC 的距离.24.如图,在直三棱柱111ABC A B C -中,底面ABC 为正三角形,1AB 与1A B 交于点O ,E ,F 是棱1CC 上的两点,且满足112EF CC =.(1)证明://OF 平面ABE ;(2)当1CE C F =,且12AA AB =,求直线OF 与平面ABC 所成角的余弦值. 25.如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面ABC ,AB BC ⊥,D 为AC 的中点,12AA AB ==,3BC =.(1)求证:1//AB 平面1BC D ;(2)求三棱锥1D BCC -的体积.26.如图,四棱锥E ABCD -中,底面ABCD 是边长为2的正方形,平面AEB ⊥平面ABCD ,4EBA π∠=,2EB =,F 为CE 上的点,BF CE ⊥.(1)求证:BF ⊥平面ACE ;(2)求点D 到平面ACE 的距离.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】由三视图知该几何体是底面为等腰直角三角形,且侧面垂直于底面的三棱锥,由题意画出图形,结合图形求出外接球的半径,再计算外接球的表面积.【详解】解:由几何体的三视图知,该几何体是三棱锥P ABC -,底面为等腰ABC ∆, 且侧面PAB ⊥底面ABC ,如图所示;设D 为AB 的中点,又3DA DB DC DP ====,且PD ⊥平面ABC ,∴三棱锥P ABC -的外接球的球心O 在PD 上,设OP R =,则OA R =,3OD R =-, 222(3)3R R ∴=-+,解得3R =,∴该几何体外接球的表面积是32436R cm ππ=.故选:A .【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.2.C解析:C【分析】连接11D B 、1D E 、DE ,先证明四边形11BB D D 为平行四边形,得到11//B D BD ,故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角,由余弦定理可得答案.【详解】连接11D B 、1D E 、DE ,因为棱11//BB DD ,11BB DD =,所以四边形11BB D D 为平行四边形,所以11//B D BD ,故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角11B D E ∠,因为12,3AB AD AA ===,1BE CE ==, 所以2211111122B D D C B C =+=213110B E =+=222415ED CE DC +=+==,所以222115914D E ED D D ==+=+,由余弦定理得, 从而22211111111137cos 24214B D D E B E B D E B D D E +-∠===⨯⨯. 故选:C【点睛】本题考查异面直线所成角的余弦值的求法,关键点是找到异面直线所成的角,考查空间中线线的位置关系等基础知识,考查运算求解能力,是中档题.3.B解析:B【分析】 根据圆锥侧面展开图是一个扇形,且线段25MB =.【详解】设底面圆半径为r ,由母线长4l ,可知侧面展开图扇形的圆心角为22r r l ππα==, 将圆锥侧面展开成一个扇形,从点M 拉一绳子围绕圆锥侧面转到点B ,最短距离为BM ; 如图,在ABM 中,25,2,4MB AM AB ===,所以222AM AB MB +=, 所以2MAB π∠=, 故22rππα==,解得1r =,所以圆锥的表面积为25S rl r πππ=+=,故选:B【点睛】 关键点点睛:首先圆锥的侧面展开图为扇形,其圆心角为2r lπα=,其次从点M 拉一绳子围绕圆锥侧面转到点B ,绳子的最短距离即为展开图中线段MB 的长,解三角即可求解底面圆半径r ,利用圆锥表面积公式求解.4.A解析:A【分析】分别取棱A 1B 1、A 1D 1的中点M 、N ,连接MN ,可证平面AMN ∥平面BDEF ,得P 点在线段MN 上.由此可判断当P 在MN 的中点时,AP 最小;当P 与M 或N 重合时,AP 最大.然后求解直角三角形得答案.【详解】如图所示,分别取棱A 1B 1、A 1D 1的中点M 、N ,连接MN ,连接B 1D 1,∵M 、N 、E 、F 为所在棱的中点,∴MN ∥B 1D 1,EF ∥B 1D 1,∴MN ∥EF ,又MN ⊄平面BDEF ,EF ⊂平面BDEF ,∴MN ∥平面BDEF ;连接NF ,由NF ∥A 1B 1,NF =A 1B 1,A 1B 1∥AB ,A 1B 1=AB ,可得NF ∥AB ,NF =AB ,则四边形ANFB 为平行四边形,则AN ∥FB ,而AN ⊄平面BDEF ,FB ⊂平面BDEF ,则AN ∥平面BDEF .又AN ∩NM =N ,∴平面AMN ∥平面BDEF .又P 是上底面A 1B 1C 1D 1内一点,且AP ∥平面BDEF ,∴P 点在线段MN 上.在Rt △AA 1M 中,AM 222211215AA A M =+=+=同理,在Rt △AA 1N 中,求得AN 5=△AMN 为等腰三角形.当P 在MN 的中点时,AP 最小为222322()22+=, 当P 与M 或N 重合时,AP 最大为5.∴线段AP 长度的取值范围是32,52⎡⎤⎢⎥⎣⎦. 故选:A .【点睛】本题主要考查了空间中点、线、面间的距离问题,其中解答中通过构造平行平面寻找得到点P 的位置是解答的关键,意在考查空间想象能力与运算能力,属于中档试题.5.C解析:C 【分析】A.通过证明线面垂直,证得线线垂直;B.利用相似三角形,求1A EEF的值;C.首先构造直线1A F 与平面1BDC 所成角,再通过数形结合分析最大角,以及最大角的余弦值,判选项;D.将异面直线所成角转化为相交直线所成角,求解判断. 【详解】A.AC BD ⊥,1AC BB ⊥,AC ∴⊥平面1BB D ,1AC B D ∴⊥,11//AC AC ,111B D AC ∴⊥,同理11B D BC ⊥,1111A C BC C ,1B D ∴⊥平面11A BC ,1A F ⊂平面11A BC ,11B D A F ∴⊥,故A 正确;B.连结1A D ,1B C 交1BC 于点F ,11//A B DC ,且11A B DC =,∴四边形11A DCB 是平行四边形,所以11//A D B C ,∴11A DE FB E,得1112A E A DEFB F==,故B 正确;C.1A O ⊥平面1BDC ,1111A B AC A D ==,∴点O1BDC 是等边三角形的中心,11A BC 是等边三角形,111A BC BDC ≅ 当点F 是1BC 的中点时,11A F BC ⊥,此时1A F 是点1A 和1BC 上的点连线的最短距离,设直线1A F 与平面1BDC 所成角为θ,此时11sin A O A F θ=最大,所以此时θ最大,所以111cos 32OF A F θ==<,最大角大于60,故C 不正确;D.11//A B CD ,CD ∴与1A F 所成的角,转化为11B A F ∠的大小,11B A F ∠的最小角是11B A 与平面11A BC 所成的角,即11B A F ∠,此时1111123tan 23FB B A F A B ∠==>,所以11B A F ∠的最小角大于30,故D 正确.故选:C 【点睛】关键点点睛:本题考查利用几何的综合应用,包含线线,线面角,垂直关系,首先会作图,关键选项是C 和D ,C 选项的关键是1A O ⊥平面1BDC ,点O1BDC 是等边三角形的中心,D 选项的关键是知道先与平面中线所成角中,其中线面角是其中的最小角.6.C解析:C 【分析】A 通过平移,找出异面直线所成角,利用直角三角形求余弦即可. B.求出三角形的三边,通过勾股定理说明是不是直角三角形.C.求出点M 到面11BB D D 的距离,再求直线BM 与平面11BDD B 所成角的正弦.D.可通过线线平行证明线面平行. 【详解】 设正方体棱长为2A. 取1BB 的中点为N ,则//BC MN ,则AM 与BC 所成角为AMN ∠ 由BC ⊥面11ABB A ,故MN ⊥面11ABB A ,故MN AN ⊥,在Rt ANM △中,5tan AMN ∠=,故2cos 3AMN ∠=B. BDM 中,5BM =,22BD =,5DM =C. AC BD ⊥,1AC BB ⊥,故AC ⊥面11BB D D ,1//CC 面11BB D D ,故M 到面11BB D D 的距离等于C 到面11BB D D 的距离,即为122d AC ==直线BM 与平面11BDD B 所成角为θ210sin 55d BM θ===直线BM 与平面11BDD B 10D.如图ACBD O =OM 为1ACC △的中位线,有1//OM AC故直线1AC 与平面BDM 平行故选:C 【点睛】本题考查了空间几何体的线面位置关系判定与证明:(1)对于异面直线的判定要熟记异面直线的概念:把既不平行也不相交的两条直线称为异面直线;(2)对于线面位置关系的判定中,熟记线面平行与垂直、面面平行与垂直的定理是关键.7.C解析:C 【分析】根据三视图还原得其几何体为四棱锥,根据题意代入锥体体积公式计算即可. 【详解】解:根据三视图还原得其几何体为四棱锥,图像如下:根据图形可得ABCD 是直角梯形,PA ⊥平面ABCD ,2,4,2,6AB CD PA AD ==== 所以11246212332P ABCD ABCD V S PA -+=⋅=⨯⨯⨯= 故选:C 【点睛】 识别三视图的步骤(1)弄清几何体的结构特征及具体形状、明确几何体的摆放位置;(2)根据三视图的有关定义和规则先确定正视图,再确定俯视图,最后确定侧视图; (3)被遮住的轮廓线应为虚线,若相邻两个物体的表面相交,表面的交线是它们的分界线;对于简单的组合体,要注意它们的组合方式,特别是它们的交线位置.8.D解析:D 【分析】在正方体中根据线面垂直可判断A ,根据异面直线所成角可判断B ,由余弦定理可判断CD. 【详解】 如图,设正方体棱长为2,在正方体中易知1DC ⊥平面11A BCD ,P 为线段1A B 上的动点,则PC ⊂平面11A BCD ,所以1DC PC ⊥,故A 正确;因为异面直线AD 与PC 所成的角即为BC 与PC 所成的角,在Rt PBC 中不可能BC 与PC 垂直,所以异面直线AD 与PC 不可能垂直,故B 正确;由正方体棱长为2,则222222211114480D P PC D C A P BP A P BP +-=+++-=+>,所以由余弦定理知1cos 0D PC ∠>,即1D PC ∠不可能是直角或者钝角,故C 正确;设1(022)A P x x =≤≤,则2214D P x =+,222422cos4224AP x x x x π=+-⨯=+-,由余弦定理,222211111222cos =22AP D P AD x xAP D P A PD P AP D ∠=+--⋅⋅,当2x <1cos 0APD ∠<,所以1APD ∠为钝角,故D 错误.故选:D 【点睛】关键点点睛:判断正方体中的角的范围时,可选择合适三角形,利用正方体中数量关系,位置关系,使用余弦定理,即可判断三角形形状或角的范围,属于中档题.9.C解析:C 【分析】把两个这样的长方体叠放在一起,构成一个长宽高分别为6,8,8的长方体,则球O 就是该长方体的外接球,根据长方体外接球的直径等于体对角线的长,求出直径,即可得出球的表面积. 【详解】如下图所示:把两个这样的长方体叠放在一起,构成一个长宽高分别为6,8,8的长方体,则球O 就是该长方体的外接球,根据长方体的结构特征可得,其外接球直径等于体对角线的长, 所以球O 的半径R 满足2222688164R =++=, 所以球O 的表面积24164S R ππ==. 故选:C.【点睛】关键点点睛:本题主要考查几何体外接球的表面积,熟记长方体结构特征,其外接球的球心和半径与长方体的关系,以及球的表面积公式,是解决此类问题的关键.10.D解析:D 【分析】利用线面平行的性质定理和线面垂直的定义可判断A 选项的正误;由线面垂直的性质定理可判断B 选项的正误;根据已知条件判断直线n 与平面α的位置关系,可判断C 选项的正误;根据已知条件判断直线m 与平面α的位置关系,可判断D 选项的正误. 【详解】 对于A ,//n α,由线面平行的性质定理可知,过直线n 的平面β与平面α的交线l 平行于n ,m α⊥,l α⊂,m l ∴⊥,m n ∴⊥,故A 正确;对于B ,若m α⊥,n α⊥,由直线与平面垂直的性质,可得//m n ,故B 正确; 对于C ,若m α⊥,m n ⊥,则//n α或n ⊂α,又n α⊄,//n α∴,故C 正确; 对于D ,若m n ⊥,//n α,则//m α或m 与α相交或m α⊂, 而m α⊄,则//m α或m 与α相交,故D 错误. 故选:D . 【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳.11.C解析:C 【分析】设AH a =,则BH a =,由线面垂直的性质和勾股定理可求得DH a AH ==,由等腰三角形的性质可证得BD ⊥DH ,再根据线面垂直的判定和性质可得选项. 【详解】设AH a =,则BH a =,因为'C H ⊥面ABD ,AB 面ABD ,DH ⊂面ABD ,所以'C H ⊥AB ,'C H ⊥DH ,'C H ⊥DB ,又Rt ABC ,1,2AC AB BC ===,D 为BC 的中点,所以'1,6C D BD B DAB π==∠=∠=,所以在'Rt AC H 中,'C H ==Rt C HD ’中,()2'222'211DH C D C H a a =-=--=,所以DH a AH ==,所以6ADH DAB π∠=∠=,又23ADB π∠=,所以2HDB π∠=,所以BD ⊥DH ,又'C HDH H =,所以BD ⊥面'C DH ,又'C D ⊂面'C DH ,所以BD ⊥'C D , 故选:C. 【点睛】关键点点睛:在解决折叠问题时,关键在于得出折叠的前后中,线线、线面、面面之间的位置关系的不变和变化,以及其中的边的长度、角度中的不变量和变化的量.12.B解析:B 【分析】作出图形,设2CD =,AD l ⊥,AB =,然后以CA 、CD 为邻边作平行四边形ACDE ,可知BAD ∠为二面角l αβ--的平面角,异面直线AB 与CD 所成角为BAE∠或其补角,计算出ABE △三边边长,利用余弦定理计算出cos BAE ∠,即可得解. 【详解】 如下图所示:设2CD =,AD l ⊥,2AB =CA 、CD 为邻边作平行四边形ACDE ,在平面β内,AD l ⊥,2CD =,45ACD ∠=,则sin 2AD CD ACD =∠=cos 452AC CD ==,AB l ⊥,AD l ⊥,AB α⊂,AD β⊂,所以,BAD ∠为二面角l αβ--的平面角,即60BAD ∠=,2AB AD ==,ABD ∴为等边三角形,则2BD =,四边形ACDE 为平行四边形,//DE AC ∴,即//DE l ,AD l ⊥,AB l ⊥,DE AB ⊥∴,DE AD ⊥, AB AD A =,DE ∴⊥平面ABD ,BD ⊂平面ABD ,DE BD ∴⊥,则222BE BD DE =+=,在平行四边形ACDE 中,//AE CD 且2AE CD ==, 所以,异面直线AB 与CD 所成角为BAE ∠或其补角, 在ABE △中,2AB =2AE BE ==,由余弦定理可得2222cos 24AB AE BE BAE AB AE +-∠==⋅. 因此,异面直线AB 与CD 所成角的余弦值为24. 故选:B. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.二、填空题13.;【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析:556π; 【分析】分析菱形的特点,结合其翻折的程度,判断其外接球球心的位置,放到相应三角形中,利用勾股定理求得半径,利用球的体积公式求得外接球的体积. 【详解】根据题意,画出图形,3的菱形ABCD 中,对角线3AC = 所以ABC 和DBC △都是正三角形, 又因为二面角B AC D --的大小为2π, 所以分别从两个正三角形的中心做面的垂线,交于O , 则O 是棱锥B ACD -外接球的球心,且11,2GD OG GE ===, 所以球的半径2252R GD OG =+=, 所以其体积为3344555(3326V R ππ==⋅=, 故答案为:556π. 【点睛】思路点睛:该题考查的是有关几何体外接球的问题,解题思路如下: (1)根据题中所给的条件,判断菱形的特征,得到两个三角形的形状;(2)根据直二面角,得到两面垂直,近一倍可以确定其外接球的球心所在的位置;(3)利用勾股定理求得半径; (4)利用球的体积公式求得结果;(5)要熟知常见几何体的外接球的半径的求解方法.14.【分析】求出截面圆的半径设可得出从而可知球的半径为根据勾股定理求出的值可得出球的半径进而可求得球的表面积【详解】如下图所示设可得出则球的直径为球的半径为设截面圆的半径为可得由勾股定理可得即即所以球的解析:163π【分析】求出截面圆H 的半径,设AH x =,可得出3HB x =,从而可知,球O 的半径为2x ,根据勾股定理求出x 的值,可得出球O 的半径,进而可求得球O 的表面积. 【详解】如下图所示,设AH x =,可得出3HB x =,则球O 的直径为4AB x =,球O 的半径为2x ,设截面圆H 的半径为r ,可得2r ππ=,1r ∴=,由勾股定理可得()2222OH r x +=,即()22214x AH x -+=,即2214x x +=,33x ∴=, 所以,球O 的半径为232x =,则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 故答案为:163π. 【点睛】方法点睛:在求解有关球的截面圆的问题时,一般利用球的半径、截面圆的半径以及球心到截面圆的距离三者之间满足勾股定理来求解.15.【分析】证明与垂直得线面垂直从而得正三棱锥的三条侧棱两两垂直结合正方体的性质得三条侧棱的平方和为外接球直径的平方求得球半径后可得球体积【详解】∵∴∴又∴取中点连接如图由于是正三棱锥∴而平面∴平面又平解析:36π【分析】证明PB 与,CE AC 垂直得线面垂直,从而得正三棱锥的三条侧棱两两垂直,结合正方体的性质得三条侧棱的平方和为外接球直径的平方,求得球半径后可得球体积. 【详解】∵3PE EA =,3BF FA =,∴AE AFAP AB=,∴//EF PB ,又CE EF ⊥,∴PB CE ⊥,取AC 中点D ,连接,PD BD ,如图,由于P ABC -是正三棱锥,∴,PD AC BD AC ⊥⊥,而PD BD D ⋂=,,PD BD ⊂平面PBD ,∴AC ⊥平面PBD ,又PB ⊂平面PBD , ∴AC PB ⊥,∵ACCE C =,,AC CE ⊂平面PAC ,∴PB ⊥平面PAC ,而,PA PC ⊂平面PAC ,∴,PB PA PB PC ⊥⊥,同理正三棱锥中,PA PC ⊥.设三棱锥P ABC -外接球半径为R ,则22222(2)3(23)R PA PB PC =++=⨯,3R =,球的体积为343363V ππ=⨯=. 故答案为:36π.【点睛】结论点睛:三棱锥的外接球问题,解题关键是找到外接球的球心,三棱锥的外接球球心在过各面外心且与该面垂直的直线上.当从同一顶点出发的三条棱两两垂直时,可以把三棱锥补成一个长方体,而长方体的对角线就是三棱锥外接球的直径.16.【分析】由圆柱体积求得底面半径母线长设底面圆心为可得为异面直线与所成的角(或其补角)在对应三角形中求解可得【详解】设圆柱底面半径为则母线长为由得设底面圆心为连接则所以为异面直线所成的角在中所以故答案 6 【分析】由圆柱体积求得底面半径,母线长,设底面圆心为O ,可得OEF ∠为异面直线AC 与EF所成的角(或其补角).在对应三角形中求解可得. 【详解】设圆柱底面半径为r ,则母线长为2r ,由2216r r ππ⋅=得2r.设底面圆心为O ,连接OE ,OF .则//OE AC ,所以OEF ∠为异面直线AC ,EF 所成的角.在Rt OEF △中,2OF =,22OE =,23EF =. 所以6cos OE OEF EF ∠==. 故答案为:6.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.17.【分析】由三视图还原几何体得到三棱锥P-ABC 分别计算其棱长可得答案【详解】由三视图还原几何体得到三棱锥P-ABC 可将此三棱锥放入棱长为2的正方体内如下图所示所以:BC=所以该三棱锥最长棱的长度为故 解析:3【分析】由三视图还原几何体得到三棱锥P -ABC ,分别计算其棱长,可得答案. 【详解】由三视图还原几何体得到三棱锥P -ABC ,可将此三棱锥放入棱长为2的正方体内,如下图所示,所以:2AB =,BC =2,22,23BP AC PC AP ====.所以该三棱锥最长棱的长度为23. 故答案为:23.【点睛】方法点睛:三视图问题的常见类型及解题策略:(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.18.【分析】连接延长交于则是中点可得是二面角的平面角求出可得结论【详解】由已知是中心连接延长交于则是中点连接则而∴平面平面∴∴是二面角的平面角由对称性又由平面平面得∴故答案为:【点睛】关键点点睛:本题考 3 【分析】连接DO 延长交BC 于E ,则E 是BC 中点,可得MEO ∠是二面角M BC O --的平面角.求出,ME OE 可得结论. 【详解】由已知O 是BCD △中心,连接DO 延长交BC 于E ,则E 是BC 中点,连接AE ,则BC AE ⊥,BC DE ⊥,而AEDE E =,∴BC ⊥平面AED ,ME ⊂平面AED ,∴BC ME ⊥,∴MEO ∠是二面角M BC O --的平面角.2BC =,90BMC ︒∠=,由对称性2BM CM ==112ME BC ==, 又113323323EO DE ==⨯=由AO ⊥平面BCD ,EO ⊂平面BCD ,得AO EO ⊥,∴3cos 3EO MEO ME ∠==. 故答案为:33.【点睛】关键点点睛:本题考查求二面角,解题关键是作出二面角的平面角.这可根据平面角的定义作出(并证明),然后在直角三角形中求角即得.注意一作二证三计算三个步骤.19.(1)(2)(4)【分析】首先取中点连结先判断(4)是否正确再根据平行关系以及等角定理和余弦定理判断(1)再判断(2)假设成立根据直线与平面垂直的性质及判定可得矛盾来判断(3)【详解】取中点连结则平解析:(1)(2)(4) 【分析】首先取CD 中点Q ,连结MQ ,BQ ,先判断(4)是否正确,再根据平行关系,以及等角定理和余弦定理判断(1),再判断(2),假设1DE A C ⊥成立,根据直线与平面垂直的性质及判定,可得11DA A E ⊥矛盾来判断(3). 【详解】取CD 中点Q ,连结MQ ,BQ ,则1//MQ DA ,//BQ DE ,∴平面//MBQ 平面1A DE ,又MB ⊂平面MBQ ,//MB ∴平面1A DE ,故(4)正确;由1A DE MQB ∠=∠,112MQ A D ==定值,QB DE ==定值, 由余弦定理可得2222cos MB MQ QB MQ QB MQB =+-⋅⋅∠ 所以MB 是定值,故(1)正确;B 是定点,M ∴是在以B 为球心,MB 为半径的球面上,故(2)正确;145A DE ADE ∠=∠=,45CDE ∠=,且设1AD =,2AB =,则2DE CE ==,若存在某个位置,使1DE A C ⊥,则因为222DE CE CD +=,即CE DE ⊥,因为1AC CE C =,则DE ⊥平面1A CE ,所以1DE A E ⊥,与11DA A E ⊥矛盾, 故(3)不正确.故答案为:(1)(2)(4) 【点睛】关键点点睛:本题考查线线,线面位置关系时,首先判断(4)是否正确,其他选项就迎刃而解,而判断线面平行时,可根据面面平行证明线面平行.20.【详解】取的中点由题意可得:所以面ABC 所以球心在直线上所以得所以 解析:494π【详解】取AB 的中点,由题意可得:2222,3,SD DC SD DC SC ==+=,所以,SD AB SD DC ⊥⊥,SD ⊥面ABC.所以球心在直线SD 上,所以()2232R R =+-,得74R =, 所以24944S R ππ==.三、解答题21.(1)证明见解析;(2)7. 【分析】(1)取AB 中点O ,连OC 、OD ,即可得到COD ∠是二面角C AB D --的平面角,再由勾股定理逆定理得到222OC OD CD +=,即可得到二面角是直二面角,即可得证; (2)过O 作OM ⊥BC 交BC 于M ,连DM ,即可证明BC ⊥平面DOM ,从而得到ODM ∠为二面角A-BC-D 的平面角,再利用锐角三角函数计算可得; 【详解】(1)证明:取AB 中点O ,连OC 、OD ,因为ABC 是边长为2的正三角形,ABD △是以AB 为斜边的等腰直角三角形, 所以OC AB ⊥,⊥OD AB ,所以COD ∠是二面角C AB D --的平面角. 在OCD 中,因为OC =1OD =,2CD =,所以222OC OD CD +=所以90COD ∠=︒. 所以平面ABC ⊥平面ABD .(2)过O 作OM ⊥BC 交BC 于M ,连DM ,由(1)可知DO ⊥面ABC ,又BC ⊂面ABC ,所以BC DO ⊥,由OMDO O =,,OM DO ⊂面DOM所以BC ⊥平面DOM因为DM ⊂面DOM ,所以BC ⊥DM , 则ODM ∠为二面角A-BC-D 的平面角.在Rt OMD 中,1OD =,2OM =,由勾股定理:DM =,∴二面角A-BC-D 的余弦值为cos OM OMD DM ∠==.【点睛】本题考查了立体几何中的面面垂直的判定和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 22.(1)22;(22;(33 【分析】(1)取BD 中点G ,连接GC ,FG ,根据线面垂直的判定定理及性质,先证明EF 为1BD 与1CC 的公垂线,再由题中数据,计算出EF 的长,即可得出结果;(2)连接1ED ,由(1)得到EF ⊥平面1BDD ,设1D 到平面BDE 的距离为d ,根据等体积法,由11E DBD D DBE V V --=求出d ,记直线1BD 与平面BDE 所成角为θ,由1sin dBD θ=即可得出结果; (3)由(2)得到1D 到平面BDE 的距离d ,根据题中条件,得到F 到平面BDE 的距离为2d,即可得出结果. 【详解】(1)在正四棱柱1111ABCD A B C D -中,取BD 中点G ,连接GC ,FG , ∵F ,G 分别为1,BD BD 的中点,∴1//FG D D 且112FG D D =, 又1//CE D D ,112CE D D =,所以//FG CE 且FG CE =,则四边形EFGC 为平行四边形,又CE ⊥平面ABCD ,CG ⊂平面ABCD ,∴CE CG ⊥,。
最新北师大版高中数学必修二测试题全套含答案解析

最新北师大版高中数学必修二测试题全套含答案解析章末综合测评(一)立体几何初步(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列推理错误的是()A.A∈l,A∈α,B∈l,B∈α⇒lαB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊆/α,A∈l⇒A∉αD.A∈l,lα⇒A∈α【解析】若直线l∩α=A,显然有l⊆/α,A∈l,但A∈α,故C错.【答案】 C2.下列说法中,正确的是()A.经过不同的三点有且只有一个平面B.分别在两个平面内的两条直线一定是异面直线C.垂直于同一个平面的两条直线是平行直线D.垂直于同一个平面的两个平面平行【解析】A中,可能有无数个平面;B中,两条直线还可能平行、相交;D中,两个平面可能相交.【答案】 C3.已知水平放置的△ABC是按“斜二测画法”得到如图1所示的直观图,其中B′O′=C′O′=1,A′O′=32,那么原△ABC的面积是()图1A. 3B.2 2C.32 D.34【解析】由题图可知,原△ABC的高为AO=3,∴S△ABC =12×BC×OA=12×2×3=3,故选A.【答案】 A4.下列四个命题判断正确的是()A.若a∥b,a∥α,则b∥αB.若a∥α,bα,则a∥bC.若a∥α,则a平行于α内所有的直线D.若a∥α,a∥b,b⊆/α,则b∥α【解析】A中b可能在α内;B中a与b可能异面;C中a可能与α内的直线异面;D 正确.【答案】 D5.已知一个圆锥的展开图如图2所示,其中扇形的圆心角为120°,底面圆的半径为1,则该圆锥的体积为()图2A.22π3 B.2π3C.2π3 D.3π【解析】因为扇形弧长为2π,所以圆锥母线长为3,高为22,所求体积V=1 3×π×12×22=22π3.【答案】 A6.如图3所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于()图3A.ACB.BDC.A1DD.A1D1【解析】CE平面ACC1A1,而BD⊥AC,BD⊥AA1,所以BD⊥平面ACC1A1,所以BD⊥CE.【答案】 B7.正方体AC1中,E,F分别是DD1,BD的中点,则直线AD1与EF所成角的余弦值是()A.12 B.32C.63 D.62【解析】连接BD1,则BD1∥EF,∠BD1A是异面直线AD1与EF所成的角.∵AB⊥AD1,∴cos∠BD1A=AD1BD1=63.【答案】 C8.如图4所示,则这个几何体的体积等于()图4 A.4 B.6C.8D.12【解析】由三视图得几何体为四棱锥,如图记作S-ABCD,其中SA⊥平面ABCD,SA=2,AB=2,AD=2,CD=4,且ABCD 为直角梯形, ∠DAB =90°,∴V =13SA ×12(AB +CD )×AD =13×2×12×(2+4)×2=4,故选A. 【答案】 A9.如图5,ABCD -A 1B 1C 1D 1为正方体,下面结论错误的是( )图5A.BD ∥平面CB 1D 1B.AC 1⊥BDC.AC 1⊥平面CB 1D 1D.异面直线AD 与CB 1所成的角为60°【解析】 由于BD ∥B 1D 1,易知BD ∥平面CB 1D 1;连接AC ,易证BD ⊥平面ACC 1,所以AC 1⊥BD ;同理可证AC 1⊥B 1C ,因BD ∥B 1D 1,所以AC 1⊥B 1D 1,所以AC 1⊥平面CB 1D 1;对于选项D ,∵BC ∥AD ,∴∠B 1CB 即为AD 与CB 1所成的角,此角为45°,故D 错.【答案】 D10.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的主视图和俯视图如图6所示.若该几何体的表面积为16+20π,则r =( )图6A.1B.2C.4D.8【解析】如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=12×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选B.【答案】 B11.如图7,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:图7①BD⊥AC;②△BCA是等边三角形;③三棱锥D-ABC是正三棱锥;④平面ADC⊥平面ABC.其中正确的是()A.①②④B.①②③C.②③④D.①③④【解析】由题意知,BD⊥平面ADC,故BD⊥AC,①正确;AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD,所以AB=AC=BC,△BAC是等边三角形,②正确;易知DA=DB=DC,又由②知③正确;由①知④错.故选B.【答案】 B12.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为()A.26 B.36C.23 D.22【解析】由于三棱锥S-ABC与三棱锥O-ABC底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示, S △ABC =34×AB 2=34, 高OD =12-⎝ ⎛⎭⎪⎫332=63,∴V S -ABC =2V O -ABC=2×13×34×63=26. 【答案】 A二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.设平面α∥平面β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且点S 位于平面α,β之间,AS =8,BS =6,CS =12,则SD =________.【解析】 由面面平行的性质得AC ∥BD ,AS BS =CSSD ,解得SD =9. 【答案】 914.如图8所示,将等腰直角△ABC 沿斜边BC 上的高AD 折成一个二面角,此时∠B ′AC =60°,那么这个二面角大小是________.图8【解析】 连接B ′C ,则△AB ′C 为等边三角形,设AD =a , 则B ′D =DC =a ,B ′C =AC =2a , 所以∠B ′DC =90°. 【答案】 90°15.若一个底面边长为62,侧棱长为6的正六棱柱的所有顶点都在一个球面上,则此球的体积为________.【解析】 球的直径等于正六棱柱的体对角线的长.设球的半径为R , 由已知,可得2R =⎝ ⎛⎭⎪⎫62×22+(6)2=23,R = 3.所以球的体积为43πR 3=4π3×(3)3=43π. 【答案】 43π16.将正方形ABCD 沿对角线BD 折成直二面角A -BD -C ,则异面直线AB 与CD 所成的角等于________.【解析】 如图所示,分别取BC ,AC 的中点G 、F , 连接EG ,GF ,EF , 则EG ∥CD ,GF ∥AB ,∴∠EGF 就是AB 与CD 所成的角. 由题意EG =GF =EF =a2,∴△EFG 是等边三角形,∴∠EGF =60°. 【答案】 60°三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)如图9所示,四棱锥V -ABCD 的底面为边长等于2 cm 的正方形,顶点V 与底面正方形中心的连线为棱锥的高,侧棱长VC =4 cm ,求这个正四棱锥的体积.图9【解】 连接AC ,BD 相交于点O ,连接VO , ∵AB =BC =2 cm , 在正方形ABCD 中, 求得CO = 2 cm , 又在直角三角形VOC 中, 求得VO =14 cm , ∴V V -ABCD =13S ABCD ·VO =13×4×14=4314(cm 3). 故这个正四棱锥的体积为4314cm 3.18.(本小题满分12分)如图10所示,P 是▱ABCD 所在平面外一点,E ,F 分别在P A ,BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.图10 【证明】连接AF延长交BC于G,连接PG.在▱ABCD中,易证△BFG∽△DF A,∴GFF A=BFFD=PEEA,∴EF∥PG.而EF⊆/平面PBC,PG平面PBC,∴EF∥平面PBC.19.(本小题满分12分)如图11,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.图11(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.【解】(1)交线围成的正方形EHGF,如图:(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为四边形EHGF为正方形,所以EH=EF=BC=10.于是MH=EH2-EM2=6,AH=10,HB=6.故S四边形A1EHA=12×(4+10)×8=56,S四边形EB1BH=12×(12+6)×8=72.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为97⎝⎛⎭⎪⎫79也正确.20.(本小题满分12分)如图12所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.证明:平面ABM⊥平面A1B1M.图12【证明】由长方体的性质可知A1B1⊥平面BCC1B1,又BM平面BCC1B1,所以A1B1⊥BM.又CC1=2,M为CC1的中点,所以C1M=CM=1.在Rt△B1C1M中,B1M=B1C21+MC21=2,同理BM=BC2+CM2=2,又B1B=2,所以B1M2+BM2=B1B2,从而BM⊥B1M.又A1B1∩B1M=B1,所以BM⊥平面A1B1M,因为BM平面ABM,所以平面ABM⊥平面A1B1M.21.(本小题满分12分)如图13,在四棱锥P-ABCD中,P A⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC的中点.图13(1)求证:AE⊥平面PCD;(2)求二面角A-PD-C的正弦值.【解】(1)证明:在四棱锥P-ABCD中,因P A⊥底面ABCD,CD平面ABCD,故CD⊥P A.由条件CD⊥AC,P A∩AC=A,∴CD⊥平面P AC,又AE平面P AC,∴AE⊥CD.由P A=AB=BC,∠ABC=60°,可得AC=P A.∵E是PC的中点,∴AE⊥PC.又PC∩CD=C,∴AE⊥平面PCD.(2)过点E作EM⊥PD,垂足为M,连接AM,如图所示.由(1)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则AM⊥PD.因此∠AME是二面角A-PD-C的平面角.由已知,可得∠CAD=30°.22.(本小题满分12分)一个空间几何体的三视图及部分数据如图14所示.图14(1)请画出该几何体的直观图,并求它的体积;(2)证明:A1C⊥平面AB1C1;(3)若D是棱CC1的中点,在棱AB上取中点E,判断DE是否平行于平面AB1C1,并证明你的结论.【解】(1)几何体的直观图如图.四边形BB1C1C是矩形,BB1=CC1=3,BC=1,四边形AA1C1C是边长为3的正方形,且垂直于底面BB1C1C,∴其体积V=12×1×3×3=32.(2)证明:∵∠ACB=90°,∴BC⊥AC.∵三棱柱ABC-A1B1C1为直三棱柱,∴BC⊥CC1.∵AC∩CC1=C,∴BC⊥平面ACC1A1,∴BC⊥A1C.∵B1C1∥BC,∴B1C1⊥A1C.∵四边形ACC1A1为正方形,∴A1C⊥AC1.∵B1C1∩AC1=C1,∴A1C⊥平面AB1C1.(3)当E为棱AB的中点时,DE∥平面AB1C1.证明:如图,取BB1的中点F,连接EF,FD,DE,∵D,E,F分别为CC1,AB,BB1的中点,∴EF∥AB1.∵AB1平面AB1C1,EF⊆/平面AB1C1,∴EF∥平面AB1C1.∵FD∥B1C1,∴FD∥平面AB1C1,又EF∩FD=F,∴平面DEF∥平面AB1C1.而DE平面DEF,∴DE∥平面AB1C1.章末综合测评(二)解析几何初步(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.空间两点A(3,-2,5),B(6,0,-1)之间的距离为()A.6B.7C.8D.9【解析】|AB|=(3-6)2+(-2-0)2+(5+1)2=7,故选B.【答案】 B2.过两点A(-2,m),B(m,4)的直线倾斜角是45°,则m的值是()A.-1B.3C.1D.-3【解析】由k AB=m-4-2-m=tan 45°=1,解得m=1.【答案】 C3.过点(-1,3)且平行于直线x -2y +3=0的直线方程为( ) A.x -2y +7=0 B.2x +y -1=0 C.x -2y -5=0D.2x +y -5=0【解析】 ∵直线x -2y +3=0的斜率为12,∴所求直线的方程为y -3=12(x +1),即x -2y +7=0.【答案】 A4.已知直线l 1:ax -y -2=0和直线l 2:(a +2)x -y +1=0互相垂直,则实数a 的值为( ) A.-1 B.0 C.1D.2【解析】 l 1的斜率为a ,l 2的斜率为a +2, ∵l 1⊥l 2,∴a (a +2)=-1, ∴a 2+2a +1=0即a =-1. 【答案】 A5.如图1,在正方体OABC -O 1A 1B 1C 1中,棱长为2,E 是B 1B 上的点,且|EB |=2|EB 1|,则点E 的坐标为( )图1A.(2,2,1)B.⎝ ⎛⎭⎪⎫2,2,23 C.⎝ ⎛⎭⎪⎫2,2,13 D.⎝ ⎛⎭⎪⎫2,2,43 【解析】 ∵|EB |=2|EB 1|,∴|EB |=23|BB 1|=43. 又E 在B 1B 上,∴E 的坐标为⎝ ⎛⎭⎪⎫2,2,43.【答案】 D6.若以点C (-1,2)为圆心的圆与直线x -2y +3=0没有公共点,则圆的半径r 的取值范围为( )A.⎝⎛⎭⎪⎫0,255 B.⎝⎛⎭⎪⎫0,355C.(0,5)D.(0,25)【解析】 设圆心到直线的距离为d ,则d =|-1-4+3|12+(-2)2=255.若直线与圆没有公共点,则0<r <255,故选A.【答案】 A7.已知直线l 1的方程为x +Ay +C =0,直线l 2的方程为2x -3y +4=0,若l 1,l 2的交点在x 轴上,则C 的值为( )A.2B.-2C.±2D.与A 有关【解析】 在2x -3y +4=0中,令y =0,得x =-2,即直线2x -3y +4=0与x 轴的交点为(-2,0).∵点(-2,0)在直线x +Ay +C =0上,∴-2+A ×0+C =0,∴C =2.【答案】 A8.若a ,b 满足a +2b =1,则直线ax +3y +b =0必过定点( ) A.⎝ ⎛⎭⎪⎫-12,-16 B.⎝ ⎛⎭⎪⎫12,-16 C.⎝ ⎛⎭⎪⎫12,16 D.⎝ ⎛⎭⎪⎫-12,16 【解析】 令a =-1,b =1或a =1,b =0,得直线方程分别为-x +3y +1=0,x +3y =0,其交点为⎝ ⎛⎭⎪⎫12,-16,此即为直线所过的定点.故选B. 【答案】 B9.已知平面内两点A (1,2),B (3,1)到直线l 的距离分别是2, 5-2,则满足条件的直线l 的条数为( )A.1B.2C.3D.4【解析】 由题知满足题意的直线l 在线段AB 两侧各有1条,又因为|AB |= 5,所以还有1条为过线段AB 上的一点且与AB 垂直的直线,故共3条.【答案】 C10.若圆心在x 轴上,半径为5的圆O 位于y 轴左侧,且与直线x +2y =0相切,则圆O 的方程是( )A.(x -5)2+y 2=5B.(x +5)2+y 2=5C.(x-5)2+y2=5D.(x+5)2+y2=5【解析】设圆心O(a,0),(a<0),则5=|a|1+22,∴|a|=5,∴a=-5,∴圆O的方程为(x+5)2+y2=5.【答案】 D11.直线y=kx被圆x2+y2=2截得的弦长为()A.2 2B.2C. 2D.与k的取值有关【解析】由于圆x2+y2=2的圆心在直线y=kx上,所以截得弦为圆x2+y2=2的直径,又其半径为2,故截得的弦长为2 2.【答案】 A12.已知点P(x,y)是直线y=22x-4上一动点,PM与PN是圆C:x2+(y-1)2=1的两条切线,M,N为切点,则四边形PMCN的最小面积为()A.43 B.23C.53 D.56【解析】由题意知,圆C的圆心为C(0,1),半径为1,故|PC|2=|PN|2+1.又S四边形PMCN=2×12×|PN|×1=|PN|,故当|PN|最小时,四边形PMCN的面积最小,此时|PC|最小,又|PC|的最小值即为点C到直线的距离d=5(22)2+1=53,此时|PN|=43,故四边形PMCN面积的最小值为43,故选A.【答案】 A二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.两圆x2+y2=1,(x+4)2+(y-a)2=25相切,则实数a=________.【解析】=±25;当两圆内切时,由a2+16=4,得a=0.【答案】 0,±2 514.经过点A (1,1)且在x 轴上的截距等于在y 轴上的截距的直线方程为______.【解析】 当直线过原点时,满足要求,此时直线方程为x -y =0;当直线不过原点时,设直线方程为x a +ya =1,由于点(1,1)在直线上,所以a =2,此时直线方程为x +y -2=0.【答案】 x -y =0或x +y -2=015.已知点M (a ,b )在直线3x +4y =15上,则a 2+b 2的最小值为________. 【解析】 a 2+b 2的最小值为原点到直线3x +4y =15的距离d =|0+0-15|32+42=3. 【答案】 316.设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为________.【解析】 圆C :x 2+y 2-2ay -2=0化为标准方程是C :x 2+(y -a )2=a 2+2, 所以圆心C (0,a ),半径r =a 2+2.|AB |=23,点C 到直线y =x +2a 即x -y +2a =0的距离d =|0-a +2a |2,由勾股定理得⎝⎛⎭⎪⎫2322+⎝ ⎛⎭⎪⎫|0-a +2a |22=a 2+2,解得a 2=2, 所以r =2,所以圆C 的面积为π×22=4π. 【答案】 4π三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知直线l 平行于直线3x +4y -7=0,并且与两坐标轴围成的三角形的面积为24,求直线l 的方程.【解】 设l :3x +4y +m =0,当y =0时,x =-m3; 当x =0时,y =-m4.∵直线l 与两坐标轴围成的三角形面积为24, ∴12·⎪⎪⎪⎪⎪⎪-m 3·⎪⎪⎪⎪⎪⎪-m 4=24, ∴m =±24,∴直线l 的方程为3x +4y +24=0或3x +4y -24=0.18.(本小题满分12分)如图2所示,直三棱柱ABC -A 1B 1C 1中,|C 1C |=|CB |=|CA |=2,AC ⊥CB ,D ,E 分别是棱AB ,B 1C 1的中点,F 是AC 的中点,求DE ,EF 的长度.图2【解】以点C为坐标原点,CA、CB、CC1所在直线为x轴、y轴、z 轴,建立如图所示的空间直角坐标系.∵|C1C|=|CB|=|CA|=2,∴C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),B1(0,2,2),由中点坐标公式可得,D(1,1,0),E(0,1,2),F(1,0,0),∴|DE|=(1-0)2+(1-1)2+(0-2)2=5,|EF|=(0-1)2+(1-0)2+(2-0)2= 6.19.(本小题满分12分)菱形ABCD中,A(-4,7),C(6,-5),BC边所在直线过点P(8,-1).求:(1)AD边所在直线的方程;(2)对角线BD所在直线的方程.【解】(1)k BC=2,∵AD∥BC,∴k AD=2,∴直线AD方程为y-7=2(x+4),即2x-y+15=0.(2)k AC=-65,∵菱形对角线互相垂直,∴BD⊥AC,∴k BD=56,而AC中点(1,1),也是BD的中点,∴直线BD的方程为y-1=56(x-1),即5x-6y+1=0.20.(本小题满分12分)已知圆C:(x-1)2+y2=9内有一点P(2,2),过点P作直线l交圆C 于A、B两点.(1)当l经过圆心C时,求直线l的方程;(2)当弦AB被点P平分时,写出直线l的方程.【解】(1)已知圆C:(x-1)2+y2=9的圆心为C(1,0),因直线l过点P、C,所以直线l 的斜率为2,直线l的方程为y=2(x-1),即2x-y-2=0.(2)当弦AB被点P平分时,l⊥PC,直线l的方程为y-2=-12(x-2),即x +2y -6=0.21.(本小题满分12分)自点A (-3,3)发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆x 2+y 2-4x -4y +7=0相切,求光线l 所在直线的方程.【解】 如图所示,已知圆C :x 2+y 2-4x -4y +7=0关于x 轴对称的圆为C 1:(x -2)2+(y +2)2=1,其圆心C 1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C 1相切.设l 的方程为y-3=k (x +3),即kx -y +3+3k =0. 则|5k +5|1+k 2=1,即12k 2+25k +12=0,∴k 1=-43,k 2=-34. 则l 的方程为4x +3y +3=0或3x +4y -3=0.22.(本小题满分12分)已知圆x 2+y 2+x -6y +m =0与直线x +2y -3=0相交于P ,Q 两点,O 为原点,若OP ⊥OQ ,求实数m 的值.【解】 设P ,Q 两点坐标为(x 1,y 1)和(x 2,y 2),由OP ⊥OQ 可得x 1x 2+y 1y 2=0, 由⎩⎨⎧x 2+y 2+x -6y +m =0,x +2y -3=0, 可得5y 2-20y +12+m =0, ①所以y 1y 2=12+m5,y 1+y 2=4.又x 1x 2=(3-2y 1)(3-2y 2)=9-6(y 1+y 2)+4y 1y 2 =9-24+45(12+m ),所以x 1x 2+y 1y 2=9-24+45(12+m )+12+m 5=0, 解得m =3.将m =3代入方程①,可得Δ=202-4×5×15=100>0, 可知m =3满足题意,即实数m 的值为3.模块综合测评(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线x 3-y3=1的倾斜角的大小为( )A.30°B.60°C.120°D.150°【解析】 由x 3-y 3=1,得该直线的斜率k =33,故倾斜角为30°.【答案】 A2.在空间直角坐标系中,点B 是A (1,2,3)在yOz 坐标平面内的射影,O 为坐标原点,则|OB |等于( )A.14B.13C.2 3D.11【解析】 点A (1,2,3)在yOz 坐标平面内的投影为B (0,2,3), ∴|OB |=02+22+32=13. 【答案】 B3.点(a ,b )关于直线x +y +1=0的对称点是( ) A.(-a -1,-b -1) B.(-b -1,-a -1) C.(-a ,-b )D.(-b ,-a )【解析】 设对称点为(x ′,y ′), 则⎩⎪⎨⎪⎧y ′-b x ′-a ×(-1)=-1,x ′+a 2+y ′+b 2+1=0,解得:x ′=-b -1,y ′=-a -1. 【答案】 B4.已知M ,N 分别是正方体AC 1的棱A 1B 1,A 1D 1的中点,如图1是过M ,N ,A 和D ,N ,C 1的两个截面截去两个角后所得的几何体,则该几何体的主视图为( )图1【解析】由主视图的性质知,几何体的正投影为一正方形,正面有可见的一棱和背面有不可见的一棱,故选B.【答案】 B5.若{(x,y)|ax+2y-1=0}∩{(x,y)|x+(a-1)y+1=0}=∅,则a等于()A.32 B.2C.-1D.2或-1【解析】依题意,两直线平行.由a(a-1)-2×1=0,得a2-a-2=0,a=2或-1.又当a=-1时,两直线重合,故选B.【答案】 B6.已知m是平面α的一条斜线,点A∉α,l为过点A的一条动直线,那么下列情形中可能出现的是()A.l∥m,l⊥αB.l⊥m,l⊥αC.l⊥m,l∥αD.l∥m,l∥α【解析】如图l可以垂直m,且l平行α.【答案】 C7.已知A,B,C,D是空间不共面的四个点,且AB⊥CD,AD⊥BC,则直线BD与AC()A.垂直B.平行C.相交D.位置关系不确定【解析】过点A作AO⊥平面BCD,垂足为O,连接BO,CO并延长分别交CD,BD于F,E两点,连接DO.因为AB⊥CD,AO⊥CD,所以CD⊥平面AOB,所以BO⊥CD,同理DO ⊥BC ,所以O 为△BCD 的垂心,所以CO ⊥BD , 所以BD ⊥AC .故选A. 【答案】 A8.已知一个正六棱锥的体积为12,底面边长为2,则它的侧棱长为( ) A.4 B.433 C. 6D.2【解析】 由正六棱锥可知,底面是由六个正三角形组成的,∴底面积S =6×12×2×3=63,∴体积V =13Sh =12, ∴h =36S =3663=23,在直角三角形SOB 中,侧棱长为SB =OB 2+h 2=4+12=4. 故选A. 【答案】 A9.过点P (-3,-1)的直线l 与圆x 2+y 2=1有公共点,则直线l 的倾斜角的取值范围是( )A.(0°,30°]B.(0°,60°]C.[0°,30°]D.[0°,60°]【解析】 如图,过点P 作圆的切线P A ,PB ,切点为A ,B . 由题意知|OP |=2,|OA |=1, 则sin α=12,所以α=30°,∠BP A =60°.故直线l 的倾斜角的取值范围是[0°,60°].选D. 【答案】 D10.若M (2,-1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程是( ) A.x -y -3=0 B.2x +y -3=0 C.x +y -1=0D.2x -y -5=0【解析】 设圆心为C ,其坐标为(1,0).则AB ⊥CM ,k CM =-1, ∴k AB =1,∴直线AB 的方程为y -(-1)=1×(x -2),即x -y -3=0,故选A. 【答案】 A11.过点P (-3,4)作圆x 2+y 2=4的两条切线,切点分别为A ,B ,则直线AB 的方程为( ) A.3x +4y -7=0 B.3x -4y +25=0 C.3x -4y +4=0D.3x -4y =0【解析】 先求出以PO (O 为原点)为直径的圆C 的方程为⎝ ⎛⎭⎪⎫x +322+(y -2)2=⎝ ⎛⎭⎪⎫522,即x 2+y 2+3x -4y =0,再将两圆方程相减得3x -4y +4=0,因为这条直线经过两圆的交点即切点A ,B ,所以3x -4y +4=0就是直线AB 的方程,故选C.【答案】 C12.若直线y =kx -1与曲线y =-1-(x -2)2有公共点,则k 的取值范围是( ) A.⎝ ⎛⎦⎥⎤0,43 B.⎣⎢⎡⎦⎥⎤13,43 C.⎣⎢⎡⎦⎥⎤0,12 D.[0,1]【解析】 曲线y =-1-(x -2)2可化为(x -2)2+y 2=1它表示以(2,0)为圆心,1为半径的x 轴下方的半圆,直线y =kx -1过定点(0,-1),要使直线与曲线有公共点(如图),易知0≤k ≤1.【答案】 D二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.已知一个正方体的所有顶点在一个球面上,若球的体积为9π2,则正方体的棱长为________.【解析】 设正方体的棱长为x ,其外接球的半径为R ,则由球的体积为9π2,得43πR 3=9π2,解得R =32.由2R =3x ,得x =2R3= 3.【答案】314.在空间四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,对角线AC =BD =2,且AC ⊥BD ,则四边形EFGH 的面积为______.【解析】 如图,由条件,易判断EH ═∥FG ═∥12BD ,所以EH =FG =1,同样有EF ═∥GH ═∥12AC ,EF =GH =1,又BD ⊥AC ,所以EF ⊥EH ,所以四边形EFGH 是边长为1的正方形,其面积S =12=1.【答案】 115.已知圆O :x 2+y 2=5和点A (1,2),则过点A 且与圆O 相切的直线与两坐标轴围成的三角形的面积为______.【解析】 由题意知,点A 在圆上,切线斜率为-1k OA=-121=-12,用点斜式可直接求出切线方程为y -2=-12(x -1),即x +2y -5=0,从而求出在两坐标轴上的截距分别是5和52, 所以所求面积为12×52×5=254. 【答案】 25416.如图2,三棱柱ABC -A 1B 1C 1中,侧棱AA 1垂直于底面A 1B 1C 1,底面三角形A 1B 1C 1是正三角形,E 是BC 的中点,则下列叙述正确的是________.图2①CC 1与B 1E 是异面直线; ②AC ⊥平面ABB 1A 1;③AE 与B 1C 1是异面直线,且AE ⊥B 1C 1; ④A 1C 1∥平面AB 1E .【解析】 ①中,直线CC 1与B 1E 都在平面BCC 1B 1中,不是异面直线;②中,平面ABC ⊥平面ABB 1A 1,而AC 与AB 不垂直,则AC 与平面ABB 1A 1不垂直; ③中,AE 与B 1C 1不平行也不相交,是异面直线,又由已知得平面ABC ⊥平面BCC 1B 1,由△ABC 为正三角形,且E 为BC 的中点知AE ⊥BC ,所以AE ⊥平面BCC 1B 1,则AE ⊥B 1C 1;④中,A 1C 1与平面AB 1E 相交,故错误. 【答案】 ③三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)将圆心角为120°,面积为3π的扇形作为圆锥的侧面,求圆锥的表面积和体积.【解】 设扇形的半径和圆锥的母线都为l ,圆锥的半径为r ,则 120360πl 2=3π,l =3;2π3×3=2πr ,r =1; S 表面积=S 侧面+S 底面=πrl +πr 2=4π, V =13Sh =13×π×12×22=223π.18.(本小题满分12分)已知直线l 过两直线3x -y -10=0和x +y -2=0的交点,且直线l 与点A (1,3)和点B (5,2)的距离相等,求直线l 的方程.【解】 由⎩⎨⎧3x -y -10=0,x +y -2=0,得交点为(3,-1),当直线l 斜率存在时,设直线l 的方程为y +1=k (x -3), 则|-2k -4|k 2+1=|2k -3|k 2+1,解得k =-14,所以直线l 的方程为y +1=-14(x -3), 即x +4y +1=0;又当直线l 的斜率不存在时,其方程为x =3,也满足题意. 故x +4y +1=0或x =3为所求方程.19.(本小题满分12分)如图3,在直三棱柱ABC -A 1B 1C 1中,A 1B 1=A 1C 1,D ,E 分别是棱BC ,CC 1上的点(点D 不同于点C ),且AD ⊥DE ,F 为B 1C 1的中点.图3求证:(1)平面ADE ⊥平面BCC 1B 1; (2)直线A 1F ∥平面ADE .【证明】 (1)因为ABC -A 1B 1C 1是直三棱柱,所以CC 1⊥平面ABC . 又AD 平面ABC ,所以CC 1⊥AD .又因为AD ⊥DE ,CC 1,DE 平面BCC 1B 1,CC 1∩DE =E ,所以AD ⊥平面BCC 1B 1.又AD平面ADE,所以平面ADE⊥平面BCC1B1.(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F平面A1B1C1,所以CC1⊥A1F.又因为CC1、B1C1平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD平面ADE,A1F⊆/平面ADE,所以A1F∥平面ADE.20.(本小题满分12分)已知点A(-3,0),B(3,0),动点P满足|P A|=2|PB|.(1)若点P的轨迹为曲线C,求此曲线的方程;(2)若点Q在直线l1:x+y+3=0上,直线l经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.【解】(1)设点P的坐标为(x,y),则(x+3)2+y2=2(x-3)2+y2,化简可得(x-5)2+y2=16,此即为所求.(2)曲线C是以点(5,0)为圆心,4为半径的圆,如图,则直线l是此圆的切线,连接CQ,则|QM|=|CQ|2-|CM|2=|CQ|2-16.当CQ⊥l1时,|CQ|取最小值,|CQ|=|5+3|2=42,∴|QM|最小=4.21.(本小题满分12分)如图4,多面体EF -ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.图4(1)若M,N分别是AB,CD的中点,求证:平面MNE∥平面BCF;(2)若△BCF中,BC边上的高FH=3,求多面体EF -ABCD的体积V.【解】 (1)若M ,N 分别是AB ,CD 的中点, 则MN ∥BC ,MN ⊆/平面BCF ,BC 平面BCF , ∴MN ∥平面BCF .又EF ∥AB ,EF =2=12AB , ∴EF =MB ,∴四边形BMEF 是平行四边形,∴ME ∥BF , 又∵ME ⊆/平面BCF ,BF 平面BCF , ∴ME ∥平面BCF ,又ME ∩MN =M ,由面面平行的判定定理知,平面MNE ∥平面BCF . (2)∵平面FBC ⊥平面ABCD ,FH ⊥BC ,AB ⊥BC , ∴FH ⊥平面ABCD ,AB ⊥平面BCF ,∴FH 是四棱锥E -AMND 的高,MB 是三棱柱BCF -MNE 的高, ∴多面体EF -ABCD 的体积 V =V E -AMND +V BCF -MNE =13S AMND ·FH +S △BCF ·MB =13×4×2×3+12×4×3×2=20.22.(本小题满分12分)在一个居民小区内设计一个边长为5 m 的菱形喷水池,规划者要求,菱形的一条对角线长不大于6 m ,另一条长不小于6 m ,试问该菱形喷水池的两条对角线的长度之和的最大值为多少?【解】 设菱形喷水池的两条对角线的长度分别为x ,y ,则⎝ ⎛⎭⎪⎫x 22+⎝ ⎛⎭⎪⎫y 22=52,即x 2+y 2=100且x ≥6,y ≤6.如图作圆x 2+y 2=100,又作直线x =6,y =6,且y =6交圆周上一点P (8,6),则满足条件的点(x ,y )应在阴影部分及AP ︵上变动.令b =x +y ,则b 是直线y =-x +b 在y 轴上的截距,当直线y =-x +b 过点P (8,6)时,b =x +y 取得最大值8+6=14,即两条对角线的长度之和的最大值为14 m.。
高中数学 第二章 解析几何初步章末综合测评(含解析)北师大版必修2-北师大版高一必修2数学试题

章末综合测评(二) 解析几何初步(满分:150分 时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.空间两点A (3,-2,5),B (6,0,-1)之间的距离为( )A .6B .7C .8D .9 B [|AB |=(3-6)2+(-2-0)2+(5+1)2=7,故选B.]2.过两点A (-2,m ),B (m,4)的直线倾斜角是45°,则m 的值是( )A .-1B .3C .1D .-3 C [由k AB =m -4-2-m=tan 45°=1,解得m =1.] 3.过点(-1,3)且平行于直线x -2y +3=0的直线方程为( )A .x -2y +7=0B .2x +y -1=0C .x -2y -5=0D .2x +y -5=0A [∵直线x -2y +3=0的斜率为12,∴所求直线的方程为y -3=12(x +1),即x -2y +7=0.]4.已知直线l 1:ax -y -2=0和直线l 2:(a +2)x -y +1=0互相垂直,则实数a 的值为( )A .-1B .0C .1D .2A [l 1的斜率为a ,l 2的斜率为a +2,∵l 1⊥l 2,∴a (a +2)=-1,∴a 2+2a +1=0即a =-1.]5.如图,在正方体OABC -O 1A 1B 1C 1中,棱长为2,E 是B 1B 上的点,且|EB |=2|EB 1|,则点E 的坐标为( )A .(2,2,1) B.⎝⎛⎭⎫2,2,23 C.⎝⎛⎭⎫2,2,13D.⎝⎛⎭⎫2,2,43 D [∵|EB |=2|EB 1|,∴|EB |=23|BB 1|=43. 又E 在B 1B 上,∴E 的坐标为⎝⎛⎭⎫2,2,43.] 6.若以点C (-1,2)为圆心的圆与直线x -2y +3=0没有公共点,则圆的半径r 的取值X 围为( )A.⎝⎛⎭⎫0,255 B.⎝⎛⎭⎫0, 355 C .(0,5) D .(0,25)A [设圆心到直线的距离为d ,则d =|-1-4+3|12+(-2)2=255.若直线与圆没有公共点,则0<r <255,故选A.] 7.已知直线l 1的方程为x +Ay +C =0,直线l 2的方程为2x -3y +4=0,若l 1,l 2的交点在x 轴上,则C 的值为( )A .2B .-2C .±2D .与A 有关A [在2x -3y +4=0中,令y =0,得x =-2,即直线2x -3y +4=0与x 轴的交点为(-2,0).∵点(-2,0)在直线x +Ay +C =0上,∴-2+A ×0+C =0,∴C =2.]8.若a ,b 满足a +2b =1,则直线ax +3y +b =0必过定点( )A.⎝⎛⎭⎫-12,-16B.⎝⎛⎭⎫12,-16 C.⎝⎛⎭⎫12,16D.⎝⎛⎭⎫-12,16B [令a =-1,b =1或a =1,b =0,得直线方程分别为-x +3y +1=0,x +3y =0,其交点为⎝⎛⎭⎫12,-16,此即为直线所过的定点.故选B.] 9.已知平面内两点A (1,2),B (3,1)到直线l 的距离分别是2, 5-2,则满足条件的直线l 的条数为( )A.1B.2 C.3D.4C[由题知满足题意的直线l在线段AB两侧各有1条,又因为|AB|=5,所以还有1条为过线段AB上的一点且与AB垂直的直线,故共3条.]10.若圆心在x轴上,半径为5的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O 的方程是()A.(x-5)2+y2=5B.(x+5)2+y2=5C.(x-5)2+y2=5D.(x+5)2+y2=5D[设圆心O(a,0)(a<0),则5=|a|1+22,∴|a|=5,∴a=-5,∴圆O的方程为(x+5)2+y2=5.]11.直线y=kx被圆x2+y2=2截得的弦长为()A.2 2 B.2C. 2 D.与k的取值有关A[由于圆x2+y2=2的圆心在直线y=kx上,所以截得弦为圆x2+y2=2的直径,又其半径为2,故截得的弦长为2 2.]12.已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.52-4 B.17-1C.6-22D.17A[由题意知,圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9的圆心分别为C1(2,3),C2(3,4),且|PM|+|PN|=|PC1|+|PC2|-4,点C1(2,3)关于x轴的对称点为C(2,-3),所以|PC1|+|PC2|=|PC|+|PC2|≥|CC2|=52,即|PM |+|PN |=|PC 1|+|PC 2|-4≥52-4.]二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.在如图所示的长方体ABCD -A 1B 1C 1D 1中,已知A 1(a,0,c ),C (0,b,0),则点B 1的坐标为________.(a ,b ,c )[由题中图可知,点B 1的横坐标和竖坐标与点A 1的横坐标和竖坐标相同,点B 1的纵坐标与点C 的纵坐标相同,所以B 1(a ,b ,c ).]14.两圆x 2+y 2=1,(x +4)2+(y -a )2=25相切,则实数a =________.0或±25[当两圆外切时,由a 2+16=6,得a =±25;当两圆内切时,由a 2+16=4,得a =0.]15.经过点A (1,1)且在x 轴上的截距等于在y 轴上的截距的直线方程为______. x -y =0或x +y -2=0[当直线过原点时,满足要求,此时直线方程为x -y =0;当直线不过原点时,设直线方程为x a +y a =1,由于点(1,1)在直线上,所以a =2,此时直线方程为x +y -2=0.]16.已知点M (a ,b )在直线3x +4y =15上,则a 2+b 2的最小值为________.3[a 2+b 2的最小值为原点到直线3x +4y =15的距离d =|0+0-15|32+42=3.] 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知直线l 平行于直线3x +4y -7=0,并且与两坐标轴围成的三角形的面积为24,求直线l 的方程.[解] 设l :3x +4y +m =0,当y =0时,x =-m 3; 当x =0时,y =-m 4. ∵直线l 与两坐标轴围成的三角形面积为24,∴12·⎪⎪⎪⎪-m3·⎪⎪⎪⎪-m4=24,∴m=±24,∴直线l的方程为3x+4y+24=0或3x+4y-24=0.18.(本小题满分12分)如图所示,直三棱柱ABC-A1B1C1中,|C1C|=|CB|=|CA|=2,AC⊥CB,D,E分别是棱AB,B1C1的中点,F是AC的中点,求DE,EF的长度.[解]以点C为坐标原点,CA、CB、CC1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.∵|C1C|=|CB|=|CA|=2,∴C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),B1(0,2,2),由中点坐标公式可得,D(1,1,0),E(0,1,2),F(1,0,0),∴|DE|=(1-0)2+(1-1)2+(0-2)2=5,|EF|=(0-1)2+(1-0)2+(2-0)2= 6.19.(本小题满分12分)菱形ABCD中,A(-4,7),C(6,-5),BC边所在直线过点P(8,-1).求:(1)AD边所在直线的方程;(2)对角线BD所在直线的方程.[解](1)k BC=2,∵AD∥BC,∴k AD=2,∴直线AD 方程为y -7=2(x +4),即2x -y +15=0.(2)k AC =-65,∵菱形对角线互相垂直,∴BD ⊥AC ,∴k BD =56,而AC 中点(1,1),也是BD 的中点,∴直线BD 的方程为y -1=56(x -1),即5x -6y +1=0. 20.(本小题满分12分)已知圆C :(x -1)2+y 2=9内有一点P (2,2),过点P 作直线l 交圆C 于A 、B 两点.(1)当l 经过圆心C 时,求直线l 的方程;(2)当弦AB 被点P 平分时,写出直线l 的方程.[解] (1)已知圆C :(x -1)2+y 2=9的圆心为C (1,0),因直线l 过点P ,C ,所以直线l 的斜率为2,直线l 的方程为y =2(x -1),即2x -y -2=0.(2)当弦AB 被点P 平分时,l ⊥PC ,直线l 的方程为y -2=-12(x -2), 即x +2y -6=0.21.(本小题满分12分)自点A (-3,3)发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆x 2+y 2-4x -4y +7=0相切,求光线l 所在直线的方程.[解] 如图所示,已知圆C :x 2+y 2-4x -4y +7=0关于x 轴对称的圆为C 1:(x -2)2+(y +2)2=1,其圆心C 1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C 1相切.设l 的方程为y -3=k (x +3),即kx -y +3+3k =0.则|5k +5|1+k 2=1,即12k 2+25k +12=0,∴k 1=-43,k 2=-34. 则l 的方程为4x +3y +3=0或3x +4y -3=0.22.(本小题满分12分)已知圆x 2+y 2+x -6y +m =0与直线x +2y -3=0相交于P ,Q 两点,O 为原点,若OP ⊥OQ ,某某数m 的值.[解] 设P ,Q 两点坐标为(x 1,y 1)和(x 2,y 2),由OP ⊥OQ 可得x 1x 2+y 1y 2=0,由⎩⎪⎨⎪⎧x 2+y 2+x -6y +m =0,x +2y -3=0, 消去x 可得5y 2-20y +12+m =0,①所以y 1y 2=12+m 5,y 1+y 2=4. 又x 1x 2=(3-2y 1)(3-2y 2)=9-6(y 1+y 2)+4y 1y 2=9-24+45(12+m ), 所以x 1x 2+y 1y 2=9-24+45(12+m )+12+m 5=0, 解得m =3.将m =3代入方程①,可得Δ=202-4×5×15=100>0,可知m =3满足题意,即实数m 的值为3.。
北师大版高一数学必修2测试题及答案

高一年级必修二试题考试时间:100分钟 满分:100分 命题人:杨丁一、选择题(每小题4分共40分)1、圆锥过轴的截面是( )A 圆B 等腰三角形C 抛物线D 椭圆2、若一条直线与两个平行平面中的一个平行,则这条直线与另一个平面的位置关系是( )。
A 平行B 相交C 在平面内D 平行或在平面内3、一个西瓜切3刀,最多能切出( )块。
A 4B 6C 7D 84.下图中不可能成正方体的是( )5.三个球的半径之比是1:2:3,那么最大的球的表面积是其余两个球的表面积之和的( )A .1倍B .2倍C .541倍D .431倍 6.以下四个命题中正确命题的个数是( )①过空间一点作已知平面的垂线有且只有一条②过空间一点作已知平面的平行线有且只有一条③过空间一点作已知直线的垂线有且只有一条④过空间一点作已知直线的平行线有且只有一条A .1B .2C .3D .47.若)0,(),4,9(),2,3(x C B A --三点共线,则x 的值是( )A .1B .-1C .0D .78.已知直线06:1=++my x l 和直线023)2(:2=++-m y x m l 互相平行,则实数m 的值是( )A .-1或3B .-1C .-3D .1或-39.已知直线l 的方程为02543=-+y x ,则圆122=+y x 上的点到直线l A BC D的最大距离是( )A .1B .4C .5D .610.点)1,3,2(-M 关于坐标原点的对称点是( )A .(-2,3,-1)B .(-2,-3,-1)C .(2,-3,-1)D .(-2,3,1)二、填空题(每题4分共16分)11、从长方体一个顶点出发的三个面的面积分别为6、8、12,则其对角线长为12.将等腰三角形绕底边上的高旋转180o ,所得几何体是______________;13.圆C :1)6()2(22=-++y x 关于直线0543=+-y x 对称的圆的方程是___________________;14.经过点)4,3(--P ,且在x 轴、y 轴上的截距相等的直线l 的方程是______________________。
高一北师大版数学必修2第二章 解析几何初步单元测试题试卷含答案解析

第一章测试时间120分钟满分150分一、选择题(本大题共10小题,每小题5分,共50分.在下列四个选项中,只有一项是符合题意的)1.下列说法正确的是()A.三点确定一个平面B.四边形一定是平面图形C.梯形一定是平面图形D.平面α与平面β有不同在一条直线上的三个交点解析梯形有两条边平行,过两条平行直线有且只有一个平面.答案C2.室内有直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在的直线()A.异面B.相交C.平行D.垂直答案D3.若直线a⊥b,且直线a∥平面α,则直线b与平面α的位置关系是()A.bαB.b∥αC.bα或b∥αD.b与α相交或bα或b∥α答案D4.若三球的半径之比是1:2:3,则半径最大的球的体积是其余两球的体积和的()A.4倍B.3倍C.2倍D.1倍解析设三个球的半径依次为a,2a,3a,V最大=43π(3a)3=36πa3,V1+V2=43πa3+43π(2a)3=363πa3=12πa3,V最大V1+V2=3.答案B5.一个长方体去掉一个小长方体,所得几何体的主视图与左视图分别如图所示,则该几何体的俯视图为()答案C①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c;③若a ∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.A.①②B.②③C.①④D.③④解析根据公理4,知①正确;根据垂直于同一平面的两直线平行可知④正确.答案C7.在空间四边形ABCD中,若AD⊥BC,BD⊥AD,则有() A.面ABC⊥面DBC B.面ABC⊥面ADCC.面ABC⊥面ADB D.面ADC⊥面DBC解析如图,在四面体ABCD中,∵AD⊥BC,AD⊥BD,BD∩BC=B,∴AD⊥面BCD.又AD面ADC,∴面ADC⊥面BCD.答案D8.在直三棱柱ABC-A1B1C1中,AC=BC,D为AB的中点,下列说法中正确的个数有()①CD⊥面ABB1A1;②BC1∥面A1DC;③面ADC⊥面ABB1A1.A.0个B.1个C.2个D.3个解析 ∵ABC -A 1B 1C 1为直三棱柱,AC =BC ,D 为AB 的中点,∴CD ⊥AB ,由两平面垂直的性质定理,可知CD ⊥面ABB 1A 1,又CD 面ADC ,故面ADC ⊥面ABB 1A ,故①、③正确,对于②连接AC 1,BC 1,设A 1C ∩AC 1=O ,则O 为AC 1的中点,又D 为AB 的中点,∴OD ∥BC 1.又OD 面A 1DC ,BC 1面A 1DC ,∴BC 1∥面A 1DC ,故②正确. 答案 D9.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )A.73 m 3B.92 m 3C.72 m 3D.94 m 3解析 由三视图可知,原几何体如图所示,故V =3×13+12×13=3+12=72 m 3.答案 C10.如图,平行四边形ABCD 中,AB ⊥BD ,沿BD 将△ABD 折起到A ′BD ,使面A ′BD ⊥面BCD ,连接A ′C ,则在四面体A ′BCD 的四个面中,互相垂直的平面有( )①面ABD ⊥面BCD ;②面A ′CD ⊥面ABD ;③面A ′BC ⊥面BCD ;④面ACD ⊥面ABC .A .1个B .2个C .3个D .4个解析 由于面ABD ⊥面BCD ,故①正确.又AB ⊥BD 则A ′B ⊥BD ,则A ′B ⊥BD ,∴A ′B ⊥面BCD ,故面A ′BC ⊥面BCD ,又CD ⊥BD ,∴面A ′CD ⊥面ABD ,故②③正确,④显然不正确.答案 C二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)11.某几何体的三视图如图所示,则该几何体的体积是________. 解析 由三视图知,该几何体是由圆柱中间除去正四棱柱得到的,所以体积是4π×4-2×2×4=16π-16.答案 16π-1612.若正三棱台的上、下底面的边长分别为2和8,侧棱长为5,则这个棱台的高为________.解析 由题可知,上底面三角形的高为2sin60°=3,下底面三角形的高为8sin60°=43,故棱台的高h =52-⎣⎢⎡⎦⎥⎤(43-3)×232=13. 答案1313.已知圆锥的表面积为a m 2,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为________.解析 设圆锥的底面半径为r ,母线长为l ,则πl =2πr ,即l =2r,S圆锥表=πr2+πrl=3πr2=a,则r=3πa 3π.答案3πa3πm14.如图四棱锥S-ABCD中,底面ABCD为平行四边形,E为SA上的点,当E满足条件:________时,SC∥面EBD.解析当E为SA的中点时,设AC∩BD=O,连接EO,EB,ED,∵ABCD为平行四边形,∴O为AC的中点.∴EO∥SC,又SC面EBD,OE面EBD,∴SC∥面EBD.答案E为SA的中点15.如图所示,平面α⊥平面β,在α与β的交线l上,取线段AB=4,AC、BD分别在平面α和平面β内,AC⊥l,BD⊥l,AC=3,BD=12,则线段CD的长为________.解析连接BC,∵AC⊥l,∴∠CAB=90°,CB=AC2+AB2=32+42=5.又BD⊥l,α⊥β,∴BD⊥平面α.又BCα,∴BD⊥BC.∴CD=BD2+BC2=122+52=13.答案13三、解答题(本大题共6小题,共75分.解答时应写出必要的文字说明,证明过程或演算步骤)16.(12分)已知圆台的上、下底面半径分别是2,5,且侧面积等于两底面面积之和,求该圆台的母线长.解 设圆台的母线长为l ,则圆台的上、下底面面积为S 上=π·22=4π,S 下=π·52=25π,∴圆台的两底面面积之和S =S 上+S 下=29π, 又圆台的侧面积S 侧=π(2+5)·l =7πl , 由7πl =29π,得l =297, 即母线长为297.17.(12分)如图所示,已知E ,F ,G ,H 分别为空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且EH ∥FG .求证:EH ∥BD .证明 ∵EH ∥FG ,EH ⃘面BDC ,FG 面BDC ,∴EH ∥面BDC , 又EH面ABD ,面ABD ∩面BDC =BD ,∴EH ∥BD .18.(12分)如图,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°.(1)证明:AB⊥A1C;(2)若AB=CB=2,A1C=6,求三棱柱ABC-A1B1C1的体积.解(1)取AB的中点O,连接OC,OA1,A1B.因为CA=CB,所以OC⊥AB.由于AB=AA1,∠BAA1=60°,故△AA1B为等边三角形,所以OA1⊥AB.因为OC∩OA1=O,所以AB⊥平面OA1C.又A1C平面OA1C,故AB⊥A1C.(2)由题设知△ABC与△AA1B都是边长为2的等边三角形,所以OC=OA1= 3.又A1C=6,则A1C2=OC2+OA21,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC-A1B1C1的高.又△ABC的面积S△ABC=3,故三棱柱ABC-A1B1C1的体积V=S△ABC×OA1=3.19.(13分)如图,已知P A垂直于正方形ABCD所在平面,E,F 分别是AB,PC的中点,∠PDA=45°.(1)求证:EF∥面P AD;(2)求证:面PCE⊥面PCD.证明(1)设PD中点为G,连接FG,AG,∵F,G分别为PC,PD的中点,∴FG綊12CD.又E为AB的中点,∴AE綊FG.即四边形EFGA为平行四边形.∴EF∥AG.又EF面P AD,AG面P AD,∴EF∥面P AD.(2)P A⊥面ABCD,∴P A⊥AD,P A⊥CD.又∵在Rt△P AD中,∠PDA=45°,∴P A=AD,∴AG⊥PD.又CD⊥AD,CD⊥P A,且P A∩AD=A,∴CD⊥面P AD,CD⊥AG,又PD∩CD=D,∴AG⊥面PCD.由(1)知EF∥AG,∴EF⊥面PCD,又EF面PCE,∴面PCE⊥面PCD.20.(13分)如图①,△ABC是等腰直角三角形,AC=BC=4,E,F分别为AC,AB的中点,将△AEF沿EF折起,使A′在平面BCEF 上的射影O恰为EC的中点,得到图②.(1)求证:EF⊥A′C;(2)求三棱锥F—A′BC的体积.解(1)证法1:在△ABC中,EF是等腰直角△ABC的中位线,在四棱锥A′—BCEF中,EF⊥A′E,EF⊥EC,∴EF⊥平面A′EC,又A′C平面A′EC,∴EF⊥A′C.证法2:同证法1 EF⊥EC,∴A′O⊥EF,∴EF⊥平面A′EC.又A ′C 平面A ′EC ,∴EF ⊥A ′C .(2)在直角梯形EFBC 中,EC =2,BC =4,∴S △FBC =12BC ·EC =4.又∵A ′O 垂直平分EC ,∴A ′O =A ′E 2-EO 2=3,∴三棱锥F —A ′BC 的体积V F —A ′BC =V A ′—FBC =13S △FBC ·A ′O =13×4×3=433.21.(13分)如图所示,已知正方体ABCD —A 1B 1C 1D 1,O 是底面ABCD 对角线的交点.(1)求证:C 1O ∥平面AB 1D 1;(2)求证:A 1C ⊥平面AB 1D 1;(3)若AA 1=2,求三棱锥A 1—AB 1D 1的体积. 解 (1)证明:设B 1D 1的中点为O 1,∵ABCD —A 1B 1C 1D 1为正方体,∴C 1O 1綊AO .故AOC 1O 1为平行四边形.∴AO 1∥C 1O ,又AO 1面AB 1D 1,C 1O 面AB 1D 1,∴C 1O ∥面AB 1D 1.(2)证明:∵B 1D 1⊥A 1C 1,B 1D 1⊥CC 1,A 1C 1∩C 1C =C 1. ∴B 1D 1⊥面ACC 1A 1,A 1C 面ACC 1A 1.∴B 1D 1⊥A 1C . 同理可证A 1C ⊥AB 1.又AB 1∩B 1D 1=B 1,∴A 1C ⊥面AB 1D 1.(3)VA 1—AB 1D 1=VA —A 1B 1D 1=13×12×2×2×2=43.。
2024-2025年北师大版数学必修第二册全书综合测评卷(带答案)

全书综合测评卷时间:120分钟 满分:150分一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.关于向量a ,b ,下列命题中,正确的是( ) A .若|a |=|b |,则a =b B .若a =-b ,则a ∥bC .若a ∥b ,b ∥c ,则a ∥cD .若|a |>|b |,则a >b2.已知i 为虚数单位,复数z 1=1+2i ,z 2=2-i ,则( ) A .z 1的共轭复数为-1+2i B .z 1的虚部是2i C .z 1+z 2为实数 D .z 1z 2=4+3i3.三个数sin 1.5·sin 2·sin 3.1,cos 4.1·cos 5·cos 6,tan 7·tan 8·tan 9中,值为负数的个数有( )A .0个B .1个C .2个D .3个4.已知函数f (x )=cos (ωx +2π3 )(ω>0)的最小正周期为4π,则下面结论正确的是( )A .函数f (x )在区间(0,π)上单调递增B .函数f (x )在区间(0,π)上单调递减C .函数f (x )的图象关于直线x =2π3 对称D .函数f (x )的图象关于点(2π3 ,0)对称5.宜昌奥林匹克体育中心为了迎接湖北省第十六届运动会开幕式,将中心内一块平面四边形ABCD 区域设计灯带.已知灯带AB =CD =10米,BC =20米,AD =102 米,且∠A +∠C =3π4,则cos ∠BCD =( ) A .35 B .0 C .45 D .2106.已知△ABC 中,3AB → +AC → -6AD →=0,延长BD 交AC 于E ,则AE AC=( )A .23B .12C .13D .14 7.如图,已知三棱柱ABC A 1B 1C 1的各条棱长都相等,且CC 1⊥底面ABC ,M 是侧棱CC 1的中点,则异面直线AB 1和BM 所成的角为( )A .90° B.45° C .30° D.60°8.当函数y =sin ⎝ ⎛⎭⎪⎫π3+x cos ⎝ ⎛⎭⎪⎫π3-x 取得最大值时,tan x 的值为( ) A .1 B .±1 C.3 D .-1二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,选对但不全的得2分,有选错的得0分)9.设z 1,z 2为复数,则下列命题中一定成立的是( ) A .如果z 1-z 2>0,那么z 1>z 2B .如果|z 1|=|z 2|,那么z 1z - 1=z 2z -2 C .如果⎪⎪⎪⎪⎪⎪z 1z 2 >1,那么|z 1|>|z 2|D .如果z 21 +z 22 =0,那么z 1=z 2=010.已知函数f (x )=cos (sin x ),g (x )=sin (cos x ),则下列说法不正确的是( ) A .f (x )与g (x )的定义域都是[-1,1] B .f (x )为奇函数,g (x )为偶函数C .f (x )的值域为[cos 1,1],g (x )的值域为[-sin 1,sin 1]D .f (x )与g (x )都不是周期函数11.已知f (x )=sin ⎝ ⎛⎭⎪⎫x -π4 cos ⎝⎛⎭⎪⎫x -π4 +3.给出下列结论,其中不正确的是( )A .最小正周期为πB .对称轴为直线x =k π(k ∈Z )C .对称中心为⎝ ⎛⎭⎪⎫k2π+π4,0D .最大值为312.如图,已知四棱台ABCD A 1B 1C 1D 1的上、下底面均为正方形,其中AB =22 ,A 1B 1=2 ,AA 1=BB 1=CC 1=DD 1=2,则下列叙述正确的是( )A.该四棱台的高为3 B .AA 1⊥CC 1C .该四棱台的表面积为26D .该四棱台外接球的表面积为16π三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.复数z =(m 2+4m +3)+(m +3)i ,m ∈R 为纯虚数,则m =________.14.已知tan α,tan β是方程2x 2+3x -5=0的两个实数根,则tan (α+β)=________.15.已知函数f (x )=2sin (ωx +φ)(ω>0)满足f ⎝ ⎛⎭⎪⎫π4 =2,f (π)=0,且f (x )在区间⎝⎛⎭⎪⎫π4,π3 上单调,则ω的最大值为________.16.记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a -3 c )sin A =b sin B -c sin C ,若△ABC 外接圆面积为π,则△ABC 面积的最大值为________.四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明,证明过程或演算步骤)17.(本小题满分10分)(1)已知复数z =m 2-5m +6+(2m 2-3m -2)i ,m ∈R .若z 为纯虚数,求m 的值;(2)已知复数z =a +b i(a ,b ∈R ),若z 满足z ·z -+i z =15+3i ,求a ,b 的值. 18.(本小题满分12分)函数f (x )=A cos (ωx +φ)(A >0,ω>0,|φ|<π2 )的部分图象如图所示.(1)求函数f (x )的解析式;(2)若函数f (x )在区间[0,m ]有5个零点,求m 的取值范围.19.(本小题满分12分)如图,在长方体ABCD A1B1C1D1中,AD=AA1=1,AB=2,点E 是AB的中点.(1)证明:D1E⊥A1D;(2)在棱DD1上是否存在一点P,使得AP∥平面D1EC,若存在,求DPDD1,若不存在,说明理由;(3)求D到平面D1EC的距离.20.(本小题满分12分)在①2cos2B+cos2B=0,②b cos A+a cos B=3+1这两个条件中任选一个,补充在下面问题的横线中,并解决相应问题.已知在锐角△ABC中,角A,B,C的对边分别为a,b,c,△ABC的面积为S,若4S=b2+c2-a2,b=6,________,求△ABC的面积S的大小.注:如果选择多个条件分别解答,按第一个解答计分.21.(本小题满分12分)矩形ABCD 中,AB =2AD =2,P 为线段DC 的中点,将△ADP 沿AP 折起,使得平面ADP ⊥平面ABCP .(1)在DC 上是否存在点E 使得AD ∥平面PBE ?若存在,求出点E 的位置;若不存在,请说明理由;(2)求二面角P AD B 的余弦值. 22.(本小题满分12分)已知向量m =(1,cos ωx ),n =(sin ωx ,3 )(ω>0),函数f (x )=m ·n ,且f (x )图象上的一个最高点为P ⎝ ⎛⎭⎪⎫π12,2 ,与P 最近的一个最低点的坐标为⎝⎛⎭⎪⎫7π12,-2 .(1)求函数f (x )的解析式;(2)设a 为常数,判断方程f (x )=a 在区间⎣⎢⎡⎦⎥⎤0,π2 上的解的个数;(3)在锐角△ABC 中,若cos ⎝ ⎛⎭⎪⎫π3-B =1,求f (A )的取值范围.全书综合测评卷1.答案:B解析:向量是既有大小又有方向的量,大小相等,但方向不一定相同,故A 错误;若a =-b ,得a ,b 方向相反,则a ∥b ,故B 正确;当b =0,a 与c 不一定平行,故C 错误;尽管两个向量的模有大小之分,但两个向量是不能比较大小的,故D 错误.故选B.2.答案:D解析:z 1=1+2i ,z -1=1-2i ,故A 错误;z 1的虚部是2,故B 错误;z 1+z 2=3+i为虚数,故C 错误;z 1·z 2=(1+2i)(2-i)=2-i +4i -2i 2=4+3i ,故D 正确.故选D.3.答案:B解析:0<1.5<π,0<2<π,0<3.1<π,∴sin 1.5·sin 2·sin 3.1>0;π<4.1<3π2,cos 4.1<0,3π2 <5<2π,3π2 <6<2π,cos 5>0,cos 6>0,∴cos 4.1·cos 5·cos 6<0;2π<7<5π2 ,5π2 <8<3π,5π2<9<3π,∴tan 7>0,tan 8<0,tan 9<0,tan 7·tan 8·tan9>0;只有一个负数.故选B.4.答案:C解析:由题意知:2πω =4π⇒ω=12 ,∴f (x )=cos (12 x +2π3)A ,B 选项,当x ∈(0,π)时,12 x +2π3 ∈(2π3 ,7π6 ),当12 x +2π3 ∈(2π3,π)时,f (x )单调递减,12 x +2π3 ∈(π,7π6 )时,f (x )单调递增.因此,A 和B 都错误;C 选项,x =2π3 时,12 x +2π3 =π;x =π是cos x 的对称轴,则x =2π3是f (x )的对称轴.因此,C 正确;D 选项,由C 可知,x =2π3是对称轴的位置,则必不是对称中心,D 错误.故选C.5.答案:A 解析:如图,连接BD .在△ABD 中,由余弦定理有:BD 2=BA 2+AD 2-2BA ×AD ×cos A =300-2002 cos A ①, 在△CBD 中,由余弦定理有:BD 2=BC 2+CD 2-2BC ×CD ×cos C =500-400cos C ②, 由①②得:-2 cos A =1-2cos C ,又∠A +∠C =3π4 ,∴-2 cos (3π4-C )=1-2cos C ,∴-sin C =1-3cos C ,又∵sin 2C +cos 2C =1.∴(3cos C -1)2+cos 2C =1,∴cos C =0或cos C =35,∵C ∈(0,3π4),∴sin C >0,若cos C =0,则sin C =-1(舍),∴cos C =35.故选A.6.答案:C解析:依题意,设AE → =λAC → ,BE → =μBD → ,则AE → =λAC → =λ(-3AB → +6AD →)=-3λAB → +6λAD → .又AE → =AB → +BE → =AB → +μBD → =AB → +μ·(AD → -AB → )=(1-μ)AB → +μAD → ,所以⎩⎪⎨⎪⎧-3λ=1-μ,6λ=μ, 两式相加得λ=13 ,即AE →=13 AC → ,所以AE AC =|AE →||AC →|=13 .故选C.7.答案:A 解析:设棱长为a ,将三棱柱ABC A 1B 1C 1补成正三棱柱A 1B 1C 1 A 2B 2C 2(如图),使AA 1=AA 2.平移AB 1至A 2B ,连接A 2M ,∠MBA 2(或其补角)即为AB 1与BM 所成的角,在△A 2BM 中,A 2B =2a ,BM =a 2+⎝ ⎛⎭⎪⎫a 22 =52 a ,A 2M =a 2+⎝ ⎛⎭⎪⎫3a 22 =132 a ,∴A 2B 2+BM 2=A 2M 2,∴∠MBA 2=90°.故选A.8.答案:A解析:y =⎝ ⎛⎭⎪⎫32cos x +12sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x =34 (sin 2x +cos 2x )+14 sin x cosx +34sin x cos x =34 +12 sin 2x .当sin 2x =1时,y max =3+24 ,此时2x =2k π+π2 (k ∈Z ),即x =k π+π4(k ∈Z ),∴tan x =1.故选A.9.答案:BC解析:取z 1=3+i ,z 2=1+i 时,z 1-z 2=2>0,但虚数不能比较大小,故A 项错误;由|z 1|=|z 2|,得|z 1|2=|z 2|2.又z 1z - 1=|z 1|2,z 2z - 2=|z 2|2,所以z 1z - 1=z 2z - 2,故B 项正确;因为⎪⎪⎪⎪⎪⎪z 1z 2 =|z 1||z 2|>1,所以|z 1|>|z 2|,故C 项正确;取z 1=1,z 2=i ,满足z 21 +z 22=0,但是z 1≠z 2≠0,故D 项错误.故选BC.10.答案:ABD解析:f (x )与g (x )的定义域是R ,故A 错误;f (-x )=cos (sin (-x ))=cos (sin x )=f (x ),则f (x )是偶函数,故B 错误;∵-1≤sin x ≤1,-1≤cos x ≤1,∴f (x )的值域为[cos 1,1],g (x )的值域为[-sin 1,sin 1],故C 正确;f (x +2π)=cos (sin (x +2π))=cos (sin x )=f (x ),则f (x )是周期函数,故D 错误.故选ABD.11.答案:BCD解析:因为f (x )=sin ⎝ ⎛⎭⎪⎫x -π4 cos ⎝ ⎛⎭⎪⎫x -π4 +3=12 sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π4 +3=12 sin⎝⎛⎭⎪⎫2x -π2 +3=-12 cos2x +3,所以f (x )的最小正周期T =π,图象的对称轴为直线x =k 2 π,k ∈Z ,对称中心为⎝ ⎛⎭⎪⎫π4+k 2π,3 ,k ∈Z ,最大值为3+12 =72 ,故只有A 正确.故选BCD.12.答案:AD 解析:给四棱台ABCD A 1B 1C 1D 1补上一个小四棱锥S A 1B 1C 1D 1即可得到四棱锥S ABCD ,如图.连接A 1C 1,B 1D 1交于点O 1,连接AC ,BD 交于点O ,连接SO .由AB =22 ,A 1B 1=2 ,可知△SA 1B 1与△SAB 的相似比为1∶2,则SA =2AA 1=4.由题意可得AO =2,则SO =23 ,则OO 1=3 ,故该四棱台的高为3 ,A 正确;因为SA =SC =AC =4,所以AA 1与CC 1的夹角为60°,B 错误;由题意可得该四棱台侧面的高为22-⎝ ⎛⎭⎪⎫22-222=142 ,则四棱台的表面积S =S上底+S下底+S 侧=2+8+4×2+222 ×142=10+67 ,C 错误;因为四棱台ABCD A 1B 1C 1D 1的上、下底面都是正方形,所以其外接球的球心在OO 1上.连接OB 1,在平面B 1BOO 1中,由OO 1=3 ,B 1O 1=1,得OB 1=2=OB ,即点O 到点B 与到点B 1的距离相等,则外接球半径r =OB =2,所以该四棱台外接球的表面积为4πr 2=16π,D 正确.故选AD.13.答案:-1解析:因为复数z =(m 2+4m +3)+(m +3)i ,m ∈R 为纯虚数,所以⎩⎪⎨⎪⎧m 2+4m +3=0,m +3≠0, 所以m =-1.14.答案:-37解析:∵tan α,tan β是方程2x 2+3x -5=0的两个实数根,∴tan α+tan β=-32 ,tan αtan β=-52 ,由tan (α+β)=tan α+tan β1-tan αtan β =-321-⎝ ⎛⎭⎪⎫-52 =-37 . 15.答案:343解析:因为f (x )在区间⎝ ⎛⎭⎪⎫π4,π3 上单调,所以T 2 ≥π3 -π4 =π12 ,解得T ≥π6 ,所以2πω ≥π6 ,解得0<ω≤12.因为f ⎝ ⎛⎭⎪⎫π4 =2,f (π)=0,所以2k +14 T =π-π4 =3π4 ,k ∈N *,所以T =3π2k +1 ,所以2πω =3π2k +1 ,所以ω=4k +23 ,k ∈N *,当ω=4k +23 ≤12时,解得k ≤172 ,k ∈N ,所以ωmax =4×8+23 =343.16.答案:2+34解析:由已知及正弦定理得a 2-3 ac =b 2-c 2,所以a 2+c 2-b 2=3 ac ,所以cos B =a 2+c 2-b 22ac =32 ,又B ∈(0,π),所以B =π6.由△ABC 的外接圆面积为π,得外接圆的半径R =1. 由正弦定理得b =2R sin B =1,所以a 2+c 2-1=3 ac ,所以a 2+c 2=3 ac +1≥2ac ,解得ac ≤2+3 ,所以△ABC 的面积S =12 ac sin B =14 ac ≤2+34,当且仅当a =c 时等号成立.17.解析:(1)因为z 是纯虚数,所以⎩⎪⎨⎪⎧m 2-5m +6=0,2m 2-3m -2≠0, 解得m =3.(2)设z =a +b i ,所以z -=a -b i , z ·z -+i z =(a +b i)(a -b i)+i(a +b i)=a 2+b 2-b +a i =15+3i.所以⎩⎪⎨⎪⎧a =3,a 2+b 2-b =15, 解得⎩⎪⎨⎪⎧a =3b =3 或⎩⎪⎨⎪⎧a =3,b =-2. 18.解析:(1)因为A >0,由图象可知A =2,且有T 2 =πω =2π3 -π6 =π2,所以ω=2,因为图象过点(π6 ,2),所以2cos (2·π6+φ)=2,即φ+π3 =2k π,解得φ=2k π-π3 ,k ∈Z ,因为|φ|<π2 ,所以φ=-π3 ,故f (x )=2cos (2x -π3).(2)由(1)知f (x )=2cos (2x -π3 ),因为x ∈[0,m ],所以2x -π3 ∈[-π3 ,2m -π3],由函数f (x )在区间[0,m ]上有5个零点,令2x -π3=t ,即y =2cos t 在区间[-π3 ,2m -π3]有5个零点,由y =cos t 的图象知,只需9π2 ≤2m -π3 <11π2即可,解得29π12 ≤m <35π12 ,故m ∈[29π12 ,35π12).19.解析:(1)如图所示,连接AD 1交A 1D 于点O ,则O 为AD 1的中点,由题意可知,四边形ADD 1A 1是正方形,∴A 1D ⊥AD 1. ∵AB ⊥平面ADD 1A 1,A 1D ⊂平面ADD 1A 1,∴AB ⊥AD 1. 又∵AB ⊂平面AD 1E ,AD 1⊂平面AD 1E ,AB ∩AD 1=A , ∴A 1D ⊥平面AD 1E ,又D 1E ⊂平面AD 1E ,∴A 1D ⊥D 1E ,即D 1E ⊥A 1D .(2)存在一点P 满足DP DD 1 =12时,使得AP ∥平面ED 1C ,当点P 满足DP DD 1 =12,即P 为DD 1的中点,取CD 1的中点Q ,连接PQ ,EQ , 在△DD 1C 中,P ,Q 为中点,∴PQ ∥DC ,PQ =12DC ,∵在长方体AC 1中,E 是AB 的中点,∴AE ∥DC 且AE =12DC ,∴AE ∥PQ 且AE =PQ ,∴四边形AEQP 为▱AEQP ,∴AP ∥EQ , 又EQ ⊂平面D 1EC ,AP ⊄平面D 1EC ,∴AP ∥平面D 1EC . (3)连接DE ,设D 到平面D 1EC 的距离为h , ∵在长方体AC 1中,DD 1⊥平面ABCD , ∵矩形ABCD ,点E 是AB 的中点,∴S △DCE =12 S 矩形ABCD =12×1×2=1,∴VD 1-DCE =13 S △DCE ·DD 1=13 ×1×1=13,在Rt△D 1DC 中,D 1C =DD 21+DC 2=5 , 在Rt△ADE 中,DE =AD 2+AE 2=2 ,∵DD 1⊥平面ABCD ,DE ⊂平面ABCD ,∴DD 1⊥DE , 在Rt△D 1DE 中,D 1E =DD 21 +DE 2=3 , 在Rt△BCE 中,EC =BC 2+BE 2=2 ,∴D 1E 2+EC 2=CD 21 ,∴ED 1⊥CE ,∴S △D 1CE =12 D 1E ×EC =12 ×3 ×2 =62 ,又VD D 1CE =VD 1DCE ,∴13 S △D 1EC ×h =13 ,h =63 ,∴D 到平面D 1EC 的距离为63. 20.解析:因为4S =b 2+c 2-a 2,cos A =b 2+c 2-a 22bc,S =12bc sin A ,所以2bc sin A =2bc cos A , 显然cos A ≠0,所以tan A =1,又A ∈⎝⎛⎭⎪⎫0,π2 ,所以A =π4 . 若选择①,由2cos 2B +cos2B =0得, cos 2B =14. 又B ∈⎝⎛⎭⎪⎫0,π2 ,∴B =π3 , 由a sin A =b sin B 得,a =b sin A sin B =6×2232=2. 又sin C =sin [π-(A +B )]=sin (A +B )=sin A cos B +cos A sin B =22 ×12 +22 ×32 =6+24 , 所以S =12 ab sin C =3+32. 若选择②,b cos A +a cos B =3 +1,则b cos A +a cos B =b ·b 2+c 2-a 22bc +a ·a 2+c 2-b 22ac =b 2+c 2-a 22c +a 2+c 2-b 22c =c =3 +1,所以S =12 bc sin A =12 ×6 ×(3 +1)×22 =3+32. 21.解析:(1)存在.如图所示:连接AC ,BP ,设AC 交BP 于点F ,∵CP ∥AB ,且CP =12AB , ∴CF CA =PF PB =13. 取DC 的三等分点E ,使CE CD =13,连接EF ,PE ,BE ,则EF ∥AD , 又EF ⊂平面PBE ,AD ⊄平面PBE ,∴AD ∥平面PBE .故存在满足条件的点E ,且E 是线段CD 上靠近点C 的三等分点.(2)在矩形ABCD 中,AP =BP =2 ,AB =2,∴AP 2+BP 2=AB 2,∴AP ⊥BP ,又平面ADP ⊥平面ABCP ,BP ⊂平面ABCP ,平面ADP ∩平面ABCP =AP ,∴BP ⊥平面ADP ,∴BP ⊥DP ,∴BD 2=DP 2+BP 2=1+2=3.在△ADB 中,AB 2=AD 2+BD 2,∴AD ⊥DB ,又PD ⊥AD ,PD ⊂平面ADP ,BD ⊂平面ADB ,平面ADP ∩平面ADB =AD ,∴∠PDB 为二面角P AD B 的平面角,在Rt△PDB 中,cos ∠PDB =DP BD =13=33 ,∴二面角P AD B 的余弦值为33. 22.解析:(1)f (x )=m ·n =sin ωx +3 cos ωx =2(12 sin ωx +32cos ωx )=2sin ⎝⎛⎭⎪⎫ωx +π3 . ∵f (x )图象上的一个最高点为P ⎝ ⎛⎭⎪⎫π12,2 ,与P 最近的一个最低点的坐标为⎝ ⎛⎭⎪⎫7π12,-2 , ∴T 2 =7π12 -π12 =π2,∴T =π, 又ω>0,∴ω=2πT=2. ∴f (x )=2sin ⎝⎛⎭⎪⎫2x +π3 . (2)当x ∈⎣⎢⎡⎦⎥⎤0,π2 时,π3 ≤2x +π3 ≤4π3 , 由f (x )=2sin ⎝⎛⎭⎪⎫2x +π3 的图象(图略)可知, 当a ∈[3 ,2)时,f (x )=a 在区间⎣⎢⎡⎦⎥⎤0,π2 上有两解; 当a ∈[-3 ,3 )或a =2时,f (x )=a 在区间⎣⎢⎡⎦⎥⎤0,π2 上有一解; 当a <-3 或a >2时,f (x )=a 在区间⎣⎢⎡⎦⎥⎤0,π2 上无解. (3)在锐角△ABC 中,0<B <π2 ,-π6 <π3 -B <π3, 又cos ⎝ ⎛⎭⎪⎫π3-B =1,∴π3 -B =0,∴B =π3 . 在锐角△ABC 中,0<A <π2 ,A +B >π2, ∴π6 <A <π2 ,∴2π3 <2A +π3 <4π3, ∴sin ⎝ ⎛⎭⎪⎫2A +π3 ∈⎝ ⎛⎭⎪⎫-32,32 , ∴f (A )=2sin ⎝ ⎛⎭⎪⎫2A +π3 ∈(-3 ,3 ). ∴f (A )的取值范围是(-3 ,3 ).GS -2。
2024-2025年北师大版数学必修第二册2.5.2向量数量积的坐标表示(带答案)

5.2 向量数量积的坐标表示必备知识基础练知识点一 数量积的坐标运算1.若a =(1,2),b =(x ,3)且a ·b =4,则x =( )A .-2B .-12C .12D .102.如图所示,在矩形ABCD 中,AB =2 ,BC =2,点E 在边CD 上,且DE → =2EC → ,则AE → ·BE →=________.3.已知向量a =(1,3),b =(2,5),c =(2,1). 求:(1)2a ·(b -a );(2)(a +2b )·c .知识点二 向量的模与夹角4.设x ∈R ,向量a =(x ,1),b =(1,-2),且a ⊥b ,则|a +b |=( ) A .5 B .10 C .25 D .105.已知向量a =(1,1),2a +b =(4,2),则向量a ,b 的夹角为( ) A .π6 B .π4 C .π3 D .π26.平面直角坐标系xOy 中,A (1,0),B (0,1),C (2,5),D 是AC 上的动点,满足AD → =λAC →(λ∈R ).(1)求|2AB → +AC →|的值; (2)求cos ∠BAC ;(3)若BD → ⊥BA →,求实数λ的值.知识点三 求点到直线的距离7.已知点A (-1,2),向量m =(3 ,1),过点A 以向量m 为方向向量的直线为l ,求点P (3,-1)到直线l 的距离.关键能力综合练一、选择题1.已知向量a =(1,-1),b =(2,x ).若a ·b =1,则x =( )A .-1B .-12C .12D .12.已知向量a =(1,-2),b =(-3,5),若(2a +b )⊥c ,则c 的坐标可以是( ) A .(-2,3) B .(-2,-3) C .(4,-4) D .(4,4)3.已知向量a =(1,3 ),b =(3,m ),若向量a ,b 的夹角为π6,则实数m =( )A .23B .3C .0D .-34.已知向量a =(1,2),b =(-2,-4),|c |=5 .若(a +b )·c =52,则a 与c 的夹角为( )A .30°B .60° C.120° D .150°5.(探究题)已知点A (4,3)和点B (1,2),O 为坐标原点,则|OA → +tOB →|(t ∈R )的最小值为( )A .52B .5C .3D .5 二、填空题6.若a =(2,3),b =(-4,7),则a 在b 方向上的投影为________.7.(易错题)已知向量a =(1,0),b =(0,1).若向量k a +b 与a +2b 的夹角为锐角,则实数k 的取值范围为________.8.在矩形ABCD 中,已知AB =2,BC =1,点P 是对角线AC 上一动点,则AP → ·BP →的最小值为________.三、解答题9.设平面向量a =(cos α,sin α)(0≤α<2π),b =(-12 ,32).(1)求证:向量a +b 与a -b 垂直;(2)若向量3 a +b 与a -3 b 的模相等,求角α.学科素养升级练1.(多选题)已知a =(1,3 ),b =(cos θ,sin θ),则下列命题正确的有( )A .若a ⊥b ,则θ=π3B .a ·b 的最大值为2C .存在θ,使|a +b |=|a |+|b |D .|a -b |的最大值为32.(学科素养——逻辑推理)如图,在四边形ABCD 中,∠B =60°,AB =3,BC =6,且AD →=λBC → ,AD → ·AB →=-32.(1)求实数λ的值;(2)若M 是线段BC 上的动点,求DM → ·BC →的取值范围.5.2 向量数量积的坐标表示必备知识基础练1.答案:A解析:因为a =(1,2),b =(x ,3)且a ·b =4,所以a ·b =1×x +2×3=x +6=4,所以x =-2.故选A.2.答案:329解析:以A 为原点,AB ,AD 所在直线分别为x ,y 轴,建立平面直角坐标系,如图所示. 则A (0,0),B (2 ,0),C (2 ,2),D (0,2).由DE → =2EC →得,E ⎝ ⎛⎭⎪⎫223,2 .∴AE → =⎝ ⎛⎭⎪⎫223,2 ,BE → =⎝ ⎛⎭⎪⎫-23,2 .∴AE → ·BE →=223 ×⎝ ⎛⎭⎪⎫-23 +2×2=329 .3.解析:方法一 (1)∵2a =2(1,3)=(2,6), b -a =(2,5)-(1,3)=(1,2),∴2a ·(b -a )=(2,6)·(1,2)=2×1+6×2=14.(2)∵a +2b =(1,3)+2(2,5)=(1,3)+(4,10)=(5,13), ∴(a +2b )·c =(5,13)·(2,1)=5×2+13×1=23.方法二 (1)2a ·(b -a )=2a ·b -2a 2=2(1×2+3×5)-2(1+9)=14. (2)(a +2b )·c =a ·c +2b ·c=(1×2+3×1)+2(2×2+5×1)=23. 4.答案:B解析:由a ⊥b ,可得a ·b =0,即x -2=0,解得x =2,所以a +b =(3,-1),故|a+b |=32+(-1)2=10 .故选B.5.答案:B解析:由2a +b =(4,2),a =(1,1)得,b =2a +b -2a =(2,0), 故a ·b =2,|a |=2 ,|b |=2.设向量a ,b 的夹角为θ,则cos θ=a·b |a ||b | =22 .又因为θ∈[0,π],所以θ=π4.故选B.6.解析:(1)由题意得AB → =(-1,1),AC → =(1,5),所以2AB → +AC → =(-1,7),|2AB →+AC → |=(-1)2+72=52 .(2)因为cos ∠BAC =AB →·AC→|AB →||AC →|,所以cos ∠BAC =(-1)×1+1×5(-1)2+12×12+52=21313. (3)由题意得BD → =AD → -AB →=λ(1,5)-(-1,1)=(λ+1,5λ-1),因为BD → ⊥BA → ,所以BD → ·BA →=0,又BA →=(1,-1),所以(λ+1)×1+(5λ-1)×(-1)=0,解得λ=12.7.解析:设n ⊥l ,即n ⊥m .设n =(x ,y ), 由n ⊥m ,得n ·m =(x ,y )·(3 ,1)=0,即3 x +y =0,令x =1,得y =-3 ,n =(1,-3 ).由A (-1,2),P (3,-1),得AP →=(4,-3). ∴点P 到直线l 的距离d =⎪⎪⎪⎪⎪⎪AP →·n |n | =⎪⎪⎪⎪⎪⎪(4,-3)·(1,-3)12+(-3)2 =4+332 . 关键能力综合练1.答案:D解析:a·b =(1,-1)·(2,x )=2-x =1,解得x =1.故选D. 2.答案:D解析:因为2a +b =(-1,1),所以当c =(4,4)时,(2a +b )⊥c .故选D. 3.答案:B 解析:∵a ·b =|a ||b |cos θ,根据题意可得(1,3 )·(3,m )=1+3 ×9+m 2 ×cos π6 ,即3+3 m =1+3 ×9+m 2 ×32,两边平方化简得m =3 .故选B. 4.答案:C解析:依题意,得a +b =(-1,-2),|a |=5 .设c =(x ,y ),a 与c 的夹角为θ,∵(a +b )·c =52 ,∴x +2y =-52 .又∵a ·c =x +2y ,∴cos θ=a ·c |a ||c | =x +2y5×5 =-525=-12.∴a 与c 的夹角为120°.故选C.5.答案:D解析:由题意可得OA → =(4,3),OB → =(1,2),则|OA → +tOB →|=|(4,3)+t (1,2)|=|(4+t ,3+2t )|=(4+t )2+(3+2t )2 =5t 2+20t +25 =5(t +2)2+5 ,结合二次函数的性质可得,当t =-2时,|OA → +tOB →|min =5 .故选D.6.答案:655解析:设a 与b 的夹角为θ,由题意得a ·b =|a ||b |cos θ=13,∴|a |·cos θ=a ·b|b |=655. 7.答案:⎝ ⎛⎭⎪⎫-2,12 ∪⎝ ⎛⎭⎪⎫12,+∞ 解析:∵a =(1,0),b =(0,1),∴k a +b =(k ,1),a +2b =(1,2).∵向量k a +b 与a +2b 的夹角为锐角,∴(k a +b )·(a +2b )=(k ,1)·(1,2)=k +2>0,解得k >-2.又当k =12 时,两个向量方向相同,∴k ∈(-2,12 )∪⎝ ⎛⎭⎪⎫12,+∞ . 8.答案:-45解析:以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴建立直角坐标系,又因为AB =2,BC =1,所以A (0,0),B (2,0),C (2,1),D (0,1),则直线AC 的方程为y =12x ,所以设P (2m ,m ),且0≤m ≤1,而AP → =(2m ,m ),BP → =(2m -2,m ),所以AP → ·BP →=2m (2m -2)+m 2=5m 2-4m ,结合二次函数的性质可知,当m =25 时,AP → ·BP → 有最小值,且最小值为5×⎝ ⎛⎭⎪⎫25 2-4×25 =-45.9.解析:(1)由题意,知a +b =⎝ ⎛⎭⎪⎫cos α-12,sin α+32 ,a -b =⎝⎛⎭⎪⎫cos α+12,sin α-32 .∵(a +b )·(a -b )=cos 2α-14 +sin 2α-34=0,∴(a +b )⊥(a -b ).(2)易得|a |=1,|b |=1.由题意,知(3 a +b )2=(a -3 b )2,化简得a ·b =0,∴-12 cos α+32 sin α=0,∴tan α=33.又0≤α<2π,∴α=π6 或α=7π6.学科素养升级练1.答案:BCD解析:依题意,对于A :a ⊥b ⇒a ·b =0,即a ·b =(1,3 )·(cos θ,sin θ)=3sin θ+cos θ=2sin (θ+π6 )=0,所以θ+π6 =k π(k ∈Z )⇒θ=k π-π6(k ∈Z ),故A 错误;对于B :由A 知a ·b =2sin (θ+π6 ),所以当θ+π6 =π2+2k π(k ∈Z )⇒θ=2k π+π3(k ∈Z )时,有最大值2,故B 正确; 对于C :当θ=π3 时,a =(1,3 ),b =(12 ,32 ),a +b =(1,3 )+(12 ,32 )=(32 ,332),所以|a +b |=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫3322=3,|a |=1+(3)2 =2,|b |= ⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫322=1,所以|a +b |=|a |+|b |,故C 正确; 对于D :a -b =(1,3 )-(cos θ,sin θ)=(1-cos θ,3 -sin θ),所以|a-b |2=(1-cos θ)2+(3 -sin θ)2=5-(23 sin θ+2cos θ)=5-4sin (θ+π6),当sin (θ+π6 )=-1,即θ+π6 =-π2 +2k π(k ∈Z )⇒θ=-2π3+2k π(k ∈Z )时,|a -b |2取得最大值9,所以|a -b |的最大值为3,故D 正确.故选BCD.2.解析:(1)由于AD → =λBC →,所以AD ∥BC ,所以∠BAD =120°,AD → ·AB → =|AD → |·|AB → |·cos 120°=-32 |AD → |=-32,所以|AD →|=1,所以AD → =16 BC →,λ=16.(2)以B 为原点建立如图所示平面直角坐标系,A (32 ,332 ),D (52 ,332),C (6,0), 设M (t ,0),0≤t ≤6,DM → =(t -52 ,332 ),BC →=(6,0),DM →·BC →=(t -52 ,332 )·(6,0)=6(t -52)=6t -15,由于0≤t ≤6,0≤6t ≤36,-15≤6t -15≤21,所以DM → ·BC →的取值范围是[-15,21].。
北师大版高一数学必修2试卷及答案

A 、(x+8)2+(y-5)2=1B 、(x-7)2+(y+4)2=2C 、(x+3)2+(y-2)2=lD 、(x+4)2+(y+3)2=2 高一数学必修2考试卷 十二厂中学屈丽萍 一、选择题(本大题共12小题,每小题5分,共60分) 1、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰 三角形,侧视图(或称左视图)是一个底边长为6、高为4的几何体的体积为() (A)48(B)64(C)96(D)192 2、已知A (x i ,y i )、B (x 2,y 2)两点的连线平行y 轴, A 、|x-x|B 、|y-y|C 、x-x D 、 121221 3•棱长都是1的三棱锥的表面积为() A.<3B.2朽C.3朽D.4©3 4、长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是() A .25兀B .55C .125兀D .都不对 325、已知正方体外接球的体积是3“,那么正方体的棱长等于(D ) 3 (A )2迈(B )叵(C )包(D )痘333 6、若1、m 、n 是互不相同的空间直线,a 、B 是不重合的平面,则下列命题中为真命题的是()A.若a //P ,/u a ,n u R ,则l //nB.若a 丄B ,/u a ,则1丄B 等腰三角形•则该 则|AB |=() y 2-y 1C.若l 丄a ,l 〃B ,则a 丄BD.若l 丄n,m 丄n ,则 7、如图,在正方体ABCD -ABCD 中,EF ,G ,H 分别为1111 BC 的中点,则异面直线EF 与GH 所成的角等于() 11 A.45°B.60°C.90°D.120° 8、方程(x-2)2+(y+l )2=l 表示的曲线关于点T (-3,2)的对l //m AA ,AB ,BB , 11 称曲线方程是:。
北师大版高一数学必修2测试题及答案

高一数学必修2测试题一、 选择题(12×5分=60分)1、下列命题为真命题的是( )A. 平行于同一平面的两条直线平行;B.与某一平面成等角的两条直线平行;C. 垂直于同一平面的两条直线平行;D.垂直于同一直线的两条直线平行。
D.2、下列命题中错误的是:( )A. 如果α⊥β,那么α内一定存在直线平行于平面β;B. 如果α⊥β,那么α内所有直线都垂直于平面β;C. 如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;D. 如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是( )A. 300B.450C. 600D. 9004、右图的正方体ABCD- A ’B ’C ’D ’中,二面角D ’-AB-D 的大小是( )A. 300B.450C. 600D. 9005、直线5x-2y-10=0在x 轴上的截距为a,在y 轴上的截距为b,则( )A.a=2,b=5;B.a=2,b=5-;C.a=2-,b=5;D.a=2-,b=5-.6、直线2x-y=7与直线3x+2y-7=0的交点是( )A (3,-1)B (-1,3)C (-3,-1)D (3,1)7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=08、正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是:( )A BD A ’ B ’D ’ C C ’A.3aπ; B.2aπ; C.a π2; D.a π3.9、已知一个铜质的五棱柱的底面积为16cm 2,高为4cm ,现将它熔化后铸成一个正方体的铜块(不计损耗),那么铸成的铜块的棱长是( )A. 2cm;B.cm 34; C.4cm; D.8cm 。
10、圆x 2+y 2-4x-2y-5=0的圆心坐标是:( )A.(-2,-1);B.(2,1);C.(2,-1);D.(1,-2).11、直线3x+4y-13=0与圆1)3()2(22=-+-y x 的位置关系是:( ) A. 相离; B. 相交; C. 相切; D. 无法判定. 12、圆C 1: 1)2()2(22=-++y x 与圆C 2:16)5()2(22=-+-y x 的位置关系是( )A 、外离B 相交C 内切D 外切二、填空题(5×5=25)13、底面直径和高都是4cm 的圆柱的侧面积为 cm 2。
2024-2025年北师大版数学必修第二册1.7.1-2正切函数(带答案)

§7 正切函数7.1 正切函数的定义7.2 正切函数的诱导公式必备知识基础练知识点一 正切函数的定义1.点A (x ,y )是60°角的终边与单位圆的交点,则y x =( )A .3B .-3C .33D .-332.已知sin α=45 ,且P (-1,m )是角α的终边上一点,则tan α=( )A .-43 B .-34C .34D .43知识点二 求值3.cos ⎝ ⎛⎭⎪⎫-17π4 ·tan 17π6 =________.4.已知角α终边上的一点A (3 ,-1),则sin (2π-α)tan (π+α)tan ⎝ ⎛⎭⎪⎫π2+αsin (-α)cos (π-α)tan (3π-α) =________.5.已知α为第四象限角,且tan α是方程x 2-x -12=0的一个根,求tan (2π-α)-tan (π+α)tan (π-α)tan (-α) 的值.知识点三 化简6.化简:tan (π+α)cos (2π+α)sin ⎝ ⎛⎭⎪⎫α-3π2cos (-α-3π)sin (-3π-α) .7.求证:tan (2π-α)sin (-2π-α)cos (6π-α)cos (α-π)sin (5π-α)=-tan α.关键能力综合练一、选择题1.若tan θsin θ<0,则θ的终边在( )A .第一或第二象限B .第一或第三象限C .第二或第三象限D .第二或第四象限2.已知角α的终边落在直线y =2x 上,则tan α=( )A .2B .±2 C.255 D .±2553.已知角α终边上有一点P (5n ,4n )(n ≠0),则tan (180°-α)=( )A .-45B .-35C .±35D .±454.已知cos ⎝ ⎛⎭⎪⎫3π2-φ =32 ,且|φ|<π2 ,则tan φ=( ) A .-33 B .33C .3D .-3 5.(易错题)记cos (-80°)=k ,那么tan 100°=( )A .1-k 2kB .-1-k 2kC .k 1-k 2D .k 1-k 2 二、填空题6.已知P (x ,5)是角θ终边上一点,且tan θ=53434,则x =________. 7.已知tan ⎝ ⎛⎭⎪⎫π6-α =33 ,则tan ⎝ ⎛⎭⎪⎫5π6+α =________. 8.tan 315°+tan 570°tan (-60°)·tan 675°=________. 三、解答题9.(探究题)如图,设A 是单位圆和x 轴正半轴的交点,P ,Q 是单位圆上的两点,O 是坐标原点,∠AOP =π6,∠AOQ =α,α∈[0,π).(1)若已知角θ的终边与OP 所在的射线关于x 轴对称,求tan θ.(2)若已知Q (35 ,45),试求tan α.学科素养升级练1.(多选题)化简y =sin x |sin x | +|cos x |cos x +tan x |tan x |的值可以是( ) A .1 B .-1C .3D .-32.(学科素养——逻辑推理)已知A ,B ,C 为△ABC 的内角.(1)求证:cos 2A +B 2 +cos 2C 2=1; (2)若cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan (C -π)<0,求证:△ABC 为钝角三角形.7.1 正切函数的定义7.2 正切函数的诱导公式必备知识基础练1.答案:A解析:因为tan 60°=3 ,所以y x=3 .故选A.2.答案:A解析:∵sin α=45 ,且P (-1,m )是角α的终边上一点,∴m 1+m2 =45 ,解得m =43 ,∴tan α=m -1 =-m =-43.故选A. 3.答案:-66 解析:因为cos ⎝ ⎛⎭⎪⎫-17π4 =cos 17π4 =cos ⎝ ⎛⎭⎪⎫4π+π4 =cos π4 =22 ,tan 17π6 =tan ⎝ ⎛⎭⎪⎫3π-π6 =-tan π6 =-33 ,所以cos ⎝ ⎛⎭⎪⎫-17π4 ·tan 17π6 =-66 . 4.答案:12解析:原式=(-sin α)·tan α·⎝ ⎛⎭⎪⎫-1tan α·(-sin α)(-cos α)·(-tan α)=-sin α,而sin α=-12 ,所以原式=12. 5.解析:tan (2π-α)-tan (π+α)tan (π-α)tan (-α) =-tan α-tan α(-tan α)(-tan α)=-2tan αtan αtan α =-2tan α. 方程x 2-x -12=0的两根分别为4,-3,由α为第四象限角知,tan α<0,∴tan α=-3,∴tan (2π-α)-tan (π+α)tan (π-α)tan (-α) =-2-3 =23. 6.解析:原式=tan αcos αsin ⎣⎢⎡⎦⎥⎤-2π+⎝ ⎛⎭⎪⎫α+π2cos (3π+α)sin (π-α)=tan αcos αsin ⎝ ⎛⎭⎪⎫π2+α(-cos α)sin α =tan αcos αcos α(-cos α)sin α=-tan αcos αsin α =-sin αcos α ·cos αsin α=-1. 7. 证明:左边=-tan αsin (-α)cos (-α)cos (π-α)sin (π-α)=-tan α(-sin α)cos α-cos αsin α=-tan α=右边.所以原式得证. 关键能力综合练1.答案:C解析:由tan θsin θ<0得,tan θ>0,sin θ<0或tan θ<0,sin θ>0,故θ的终边在第二或第三象限.故选C.2.答案:A解析:在角α的终边上任取一点P (a ,2a )(a ∈R 且a ≠0),则tan α=2a a=2.故选A.3.答案:A解析:∵角α终边上有一点P (5n ,4n )(n ≠0),∴tan α=45. ∴tan (180°-α)=-tan α=-45.故选A. 4.答案:D解析:∵cos ⎝ ⎛⎭⎪⎫3π2-φ =-sin φ=32 ,∴sin φ=-32 ,又|φ|<π2 ,∴φ为第四象限角,∴cos φ=1-sin 2φ =12 ,则tan φ=sin φcos φ =-3 .故选D. 5.答案:B解析:∵cos (-80°)=k ,∴cos 80°=k ,∴sin 80°=1-k 2 , ∴tan 80°=1-k 2k ,∴tan 100°=-tan 80°=-1-k 2k.故选B. 6.答案:34解析:∵tan θ=5x =53434,∴x =34 . 7.答案:-33解析:∵tan ⎝ ⎛⎭⎪⎫π6-α =33 , ∴tan ⎝ ⎛⎭⎪⎫5π6+α =tan ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-α =-tan ⎝ ⎛⎭⎪⎫π6-α =-33 . 8.答案:1-33解析:原式=tan (360°-45°)+tan (3×180°+30°)tan (-60°)·tan (2×360°-45°)=-tan 45°+tan 30°-tan 60°·(-tan 45°) =-1+33-3×(-1) =1-33 .9.解析:(1)∵角θ的终边与OP 所在的射线关于x 轴对称,且P (32 ,12), ∴θ的终边与单位圆交于P ′(32 ,-12 ), 则tan θ=-1232=-33 . (2)已知Q (35 ,45 ),∴tan α=y x =4535 =43. 学科素养升级练1.答案:BC解析:由函数解析式,可知sin x ≠0,cos x ≠0,且tan x ≠0,所以角x 的终边不能落在坐标轴上,①当角x 是第一象限角时,sin x >0,cos x >0,tan x >0,此时y =3.②当角x 是第二、三、四象限角时,sin x ,cos x ,tan x 的值都是一个正值两个负值,此时y =-1.故选BC.2.证明:(1)∵在△ABC 中,A +B =π-C , ∴A +B 2 =π2 -C 2, ∴cos A +B 2 =cos ⎝ ⎛⎭⎪⎫π2-C 2 =sin C 2 , ∴cos 2A +B 2 +cos 2C 2 =sin 2C 2 +cos 2C 2=1. (2)∵cos ⎝ ⎛⎭⎪⎫π2+A sin ⎝ ⎛⎭⎪⎫3π2+B tan (C -π)<0, ∴-sin A ·(-cos B )·tan C <0,即sin A cos B tan C <0.又A ,B ,C ∈(0,π),∴sin A >0,∴cos B tan C <0,即cos B <0,tan C >0或tan C <0,cos B >0,∴B 为钝角或C 为钝角,∴△ABC 为钝角三角形.。
最新高一数学题库 北师大版高中数学必修2测试题及答案

必修2测试卷石油中学 齐宗锁一、选择题(每小题4分共40分)1、圆锥过轴的截面是( )A 圆B 等腰三角形C 抛物线D 椭圆2、若一条直线与两个平行平面中的一个平行,则这条直线与另一个平面的位置关系是( )。
A 平行B 相交C 在平面内D 平行或在平面内3、一个西瓜切3刀,最多能切出( )块。
A 4B 6C 7D 84.下图中不可能成正方体的是( )5.三个球的半径之比是1:2:3,那么最大的球的表面积是其余两个球的表面积之和的( )A .1倍B .2倍C .541倍D .431倍 6.以下四个命题中正确命题的个数是( )①过空间一点作已知平面的垂线有且只有一条②过空间一点作已知平面的平行线有且只有一条③过空间一点作已知直线的垂线有且只有一条④过空间一点作已知直线的平行线有且只有一条A .1B .2C .3D .47.若)0,(),4,9(),2,3(x C B A --三点共线,则x 的值是( )A .1B .-1C .0D .78.已知直线06:1=++my x l 和直线023)2(:2=++-m y x m l 互相平行,则实数m 的值是( )A .-1或3B .-1C .-3D .1或-39.已知直线l 的方程为02543=-+y x ,则圆122=+y x 上的点到直线l 的最大距离是( ) A BC DA .1B .4C .5D .610.点)1,3,2(-M 关于坐标原点的对称点是( )A .(-2,3,-1)B .(-2,-3,-1)C .(2,-3,-1)D .(-2,3,1)二、填空题(每题4分共16分)11、从长方体一个顶点出发的三个面的面积分别为6、8、12,则其对角线长为12.将等腰三角形绕底边上的高旋转180o ,所得几何体是______________;13.圆C :1)6()2(22=-++y x 关于直线0543=+-y x 对称的圆的方程是___________________;14.经过点)4,3(--P ,且在x 轴、y 轴上的截距相等的直线l 的方程是______________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修2考试卷
一、选择题(本大题共12小题,每小题5分,共60分)
1、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边
长为8、高为4的等腰三角形,侧视图(或称左视图)是一个
底边长为6、高为4的等腰三角形.则该几何体的体积为
( )
(A )48 (B )64 (C )96 (D )192
2、已知A (x 1,y 1)、B (x 2,y 2)两点的连线平行y 轴,则|AB |=( )
A 、|x 1-x 2|
B 、|y 1-y 2|
C 、 x 2-x 1
D 、 y 2-y 1
3.棱长都是1的三棱锥的表面积为( )
B.
4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,
则这个球的表面积是( )
A .25π
B .50π
C .125π
D .都不对
5、已知正方体外接球的体积是
323π,那么正方体的棱长等于 ( D ) (A
) (B
) (C
(D
6、若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为
真命题的是( )
A .若//,,l n αβαβ⊂⊂,则//l n
B .若,l αβα⊥⊂,则l β⊥
C. 若,//l l αβ⊥,则αβ⊥ D .若,l n m n ⊥⊥,则
//l m 7、如图,在正方体1111ABCD A B C D -中,E F G H ,,,分别为
1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于( )
A F D B
C G E 1B
H 1C 1D 1A
A.45° B.60° C.90° D.120°
8、方程(x-2)2+(y+1)2=1表示的曲线关于点T (-3,2)的对称曲线方程是: ( )
A 、 (x+8)2+(y-5)2=1
B 、(x-7)2+(y+4)2=2
C 、 (x+3)2+(y-2)2=1
D 、(x+4)2+(y+3)2=2
9、已知三点A (-2,-1)、B (x ,2)、C (1,0)共线,则x 为: ( )
A 、7
B 、-5
C 、3
D 、-1
10、方程x 2+y 2-x+y+m=0表示圆则m 的取值范围是 ( )
A 、 m ≤2
B 、 m<2
C 、 m<21
D 、 m ≤2
1
11、过直线x+y-2=0和直线x-2y+1=0的交点,且垂直于第二直线的直线方程
为 ( )
A 、+2y-3=0
B 、2x+y-3=0
C 、x+y-2=0
D 、2x+y+2=0
12、圆心在直线x=y 上且与x 轴相切于点(1,0)的圆的方程为: ( )
A 、(x-1)2+y 2=1
B 、(x-1)2+(y-1)2=1
C 、(x+1)2+(y-1)2=1
D 、(x+1)2+(y+1)2=1
二、填空题:(每小题5分,共20分)
13、直线x=2y-6到直线x=8-3y 的角是 。
14、圆:x 2+y 2-2x-2y=0的圆心到直线xcos θ +ysin θ=2的最大距离
是 。
15.正方体的内切球和外接球的半径之比为_____
16如图,△ABC 是直角三角形,∠ACB=︒90,PA ⊥平面ABC ,此图形中有 个直
角三角形。
三 解答题:(共70分)
17.(10分)如图,PA ⊥平面ABC ,平面PAB ⊥平面
PBC 求证:AB ⊥BC
P A C
18.在长方体1111D C B A ABCD -中,已知
3,41===DD DC DA ,求异面直线B A 1与C B 1所
成角的余弦值 。
(10分)
19、求过原点且与直线x=1及圆(x-1)2+(y-2)2=1
相切的圆的方程。
(12分)
20、在△ABC 中,BC 边上的高所在直线方程为x-2y+1=0,∠A 的平分线所在直线方程为y=0若点B 坐标为(1,2),求点A 和C 的坐标。
(12分)
21.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD AC CD ⊥⊥,, 60ABC ∠=°,PA AB BC ==,E 是PC 的中点.(14分) (Ⅰ)求PB 和平面PAD 所成的角的大小;
(Ⅱ)证明AE ⊥平面PCD ;
(Ⅲ)求二面角A PD C --的正弦值.
22、设圆:(1)截y 轴所得弦长为2;(2)被x 轴分成两段圆弧,其弧长的比为3∶1。
则在满足条件(1)、(2)的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程。
(12分)
A B C
D P
E
答案:一选择题:1B 2.B 3.B 长方体对角线是球直径,
2
2,450
2
l R R S R
ππ
======
4.D 5、C6、B
7.A
因为四个面是全等的正三角形,则44
4
S S
==⨯=
表面积底面积
8.A;9A;10.C;11.B;12.B
二填空题13.
4
3π
;14 2+2;15、正方体的棱长是内切球的直径,正方体的对角线是外接球的直径,设棱长是a
22,3
22
a
a r r r r r r
=====
内切球内切球外接球外接球内切球外接球
,,:
16、4
三解答题:
17、证明:过A作AD⊥PB于D,由平面PAB⊥平面PBC ,得AD⊥平面PBC,故AD⊥BC,
又BC⊥PA,故BC⊥平面PAB,所以BC⊥AB
18、连接D
A
1
,D
BA
C
B
D
A
1
1
1
,
//∠
∴
为异面直线B
A
1
与C
B
1
所成的角.
连接BD,在△DB
A
1
中,2
4
,5
1
1
=
=
=BD
D
A
B
A,
则
D
A
B
A
BD
D
A
B
A
D
BA
1
1
2
2
1
2
1
12
cos
⋅
⋅
-
+
=
∠
25
9
5
5
2
32
25
25
=
⋅
⋅
-
+
=
19. (x-
8
3
)2+(y-
2
1
)=
24
25
.
20.(1)k≠-9且k≠1;(2)k=
2
13
1±
;(3)k=-9;(4)k=1.
20. A (-1,0) , C (5, -6) .
21、(Ⅰ)解:在四棱锥P ABCD
-中,因PA⊥底面ABCD,AB⊂平面ABCD,故PA AB
⊥.
又AB AD
⊥,PA AD A
=
,从而AB⊥平面PAD.故PB在平面PAD内的射影为PA,从而APB
∠为PB和平面PAD所成的角.
在Rt PAB
△中,AB PA
=,故45
APB=
∠.
所以PB和平面PAD所成的角的大小为45 .
(Ⅱ)证明:在四棱锥P ABCD
-中,
因PA⊥底面ABCD,CD⊂平面ABCD,故CD PA
⊥.
由条件CD AC
⊥,PA AC A
=
,CD
∴⊥面PAC.又AE⊂面PAC,AE CD
∴⊥.由PA AB BC
==,60
ABC=
∠,可得AC PA
=.E
是PC的中点,AE PC
∴⊥,
A
B
C
D
P
E
M
PC CD C ∴= .综上得AE ⊥平面PCD .
(Ⅲ)解:过点E 作EM PD ⊥,垂足为M ,连结AM .由(Ⅱ)知,AE ⊥平面PCD ,AM 在平面PCD 内的射影是EM ,则AM PD ⊥.
因此AME ∠是二面角A PD C --的平面角.由已知,得30CAD =
∠.设AC a =,得 PA a =
,3AD a =
,3PD a =
,2
AE a =. 在Rt ADP △中,AM PD ⊥ ,AM PD PA AD ∴= ,则
a PA AD AM PD == .在Rt AEM △
中,sin 4AE AME AM == 22. 设所求圆的圆心为P (a,b ),半径为r ,则P 到x 轴、y 轴的距离分别为|b|、|a|.
由题设得:⎪⎩⎪⎨⎧+==1
22222a r b r ∴ 2b 2-a 2=1 又点P (a,b )到直线 x -2y =0距离为 d =5|
2|b a - .
∴5d 2=|a -2b|2= a 2+4b 2-4ab ≥a 2+4b 2-2(a 2+b 2)=2b 2-a 2=1 .
当且仅当a=b 时,上式等号成立,d 取得最小值. ∴ ⎪⎩⎪⎨
⎧=-=1222a b b a ∴⎩⎨⎧==11b a 或⎩⎨⎧-=-=1
1b a 故所求圆的方程为(x ±1)2+(y ±1)2=2 .。
