工程光学-浙大2005年答案
工程光学-浙大光学课堂练习2

1.在夫琅和费单缝衍射实验中,以钠黄光(波长为589nm)垂直入射,若缝宽为0.1mm,则第1极小岀现在()弧度的方向上。
2•—束准直的单色光正入射到一个直径为lcm的汇聚透镜,透镜焦距为50cm, 测得透镜焦平面上衍射图样中央亮斑的直径是6.66xl0-3cm?则光波波长为()nmo3・已知闪耀光栅的闪耀角为15。
,光栅常数d=l屮m平行光垂直于光栅平面入射时在一级光谱处得到最大光强,则入射光的波长为()nm。
4.晶体的旋光现象是(5.渥拉斯棱镜的作用(()O10・在两块平板玻璃A和B之间夹一薄纸片G,形成空气劈尖。
用单色光垂直照射劈尖,如图1所示。
半稍稍用力下汗玻璃板A时,干涉条纹间距(儿条纹向()移动。
若使平行单色光倾斜照射玻璃板(入射角‘1 >°),形成的干涉条纹与垂直照射时相比,条纹间距()。
1.简要分析如图2所示夫琅和费衍射装置如有以下变动时,衍射图样会发生怎样的变化?1)增大透镜L2的焦距;2)减小透镜L2的口径;3)衍射屏作垂直于光轴的移动(不超出入射光束照明范圉)o一.填空(每题2分,共20分)),其规律是()。
),要使它获得较好的作用效果应利用此关系可() 7 •波片快轴的定义:(8.光源的相干长度与相干时间的关系为(明光源的时间相干性(9.获得相干光的方法有()和()O相干长度愈长,说)O二问答(请选作5题并写明题号,每6分,共30分)2.以迈克尔逊(M)干涉仪的等倾圆环和牛顿(N)环为例,对“条纹形状”作一简要讨论,(从中央级次、条纹移动分析它们的相同点与不同点)。
答案一、填空题(每题2分,共20分)1.在夫琅和费单缝衍射实验中,以钠黄光(波长为589nm)垂直入射,若缝宽为0.1 mm, 则第1极小岀现在(5.89x10-3 )弧度的方向上。
2.一朿准直的单色光正入射到一个直径为lcm的汇聚透镜,透镜焦距为50cm,测得透镜焦平而上衍射图样中央亮斑的直径是6.66x10-3 cm,则光波波长为(546) nm。
工程光学-浙大2005年答案

05年答案一.1.C 2.B 3.B 4.D 5.D 6.C 7.C 8.C 9.B 10.A 二.1.会聚球面波:E=(A/r)exp(-ikr)发散球面波:E=(A/r)exp(ikr)2.ε(x)=asin(2えx/d)+t03.扩展光源上的两点SS’发出的同倾角的光线经过平板后到达观察屏上时有相同的光程差,故可见度不受影响。
p4.让偏振光通过¼波片,旋转偏振器,能找到消光位置者为椭圆偏振光5.望远镜分辨率用θ=1.22λ/D三.1.同02年试题2.条纹移动112个,表示光程差为112λ,而这时两束光程差为(n-1)l,其中l=500mm;所以(n-1)×500=112×589.3×10-63.同01年试题4.d=1/2000mm,设闪耀角为γ对一级闪耀波长,2dsinγ=λ则,γ=17.46º由光栅方程d(sini-sin θ)=m λ i=γd(sin γ-sin θ)=m λ 取sin θ=1,得m=-1.17取sin θ=-1, 得m=2.17因此,最多可看见500nm 的-1,0,+1,+2级光谱6.建立如图坐标,则,投射系数为:t(x)=rect(x/a)+rect[(x-3/2a-d)/2a]频谱为E(u)=F[t(x)] a d 2a=asinc[(ax)/(λz 1)]+2aexp[-i2えu(3/2a+d)]sinc[(2ax)/ (λz 1)]I=<E.E*>=a 2sinc 2[(2ax)/ (λz 1)]+4 a 2sinc 2[(ax)/ (λz 1)]+ 4 a 2sinc [(ax)/ (λz 1)] sinc [(2ax)/ (λz 1)]cos[えx(3a+2d)/( λz 1)]7.同02年试题8.从起偏器透出偏振光的琼斯矢量为【 】 待测波片的琼斯矩阵为:m=21 法线0-10 1cos δ/21/4波片的矩阵为:通过1/4波片以后的矩阵为cos δ/2=即出射光为与x 轴成δ/2的线偏振光,利用检偏器确定夹角即可得到待测波片的相位延迟角9.(1)振幅为2的平面波经过的振幅分布为:ε(x )=1+cos(2えu 0x) 傅立叶频谱为E(u)=δ(u)+1/2[δ(u+u 0)+ δ(u-u 0)]条纹是平行y 轴的平行直条纹三个频谱分量对应三个夫琅和费衍射0级和±级极大值,位置为x o ’=0, x ±1’=±u 0λf一级极大为零级极大强度的1/41 -itg δ/2-itg δ/2 1 1 0 0 i2 -itg δ/2 -itg δ/2 1 2 0 0 i 1 0cos δ/2 sin δ/2(2)I=【1+cos(2えu0x)】2(3)挡住0级,I= cos2(2えu0x) u=2u0(4)挡住-1级,I=(1+e-i2えu0x)2=5/4+ cos(2えu0x)u=u0。
工程光学第一章练习参考答案

l 2 ' 15 mm
第一章 16
(2)凸面镀反射膜 r1
l , r 30 , n 1 , n ' 1 n' l' l' n l n' n ' n n ' n r r 1 11 30 15 mm
第一章 16
(3)凹面镀反射膜 (a)在左球面折射
l 2 ' 10 mm
第一章 16
(4)凹面镀反射膜 (a)在左球面折射 (b)在右球面第二次反射
r1
r2
l 2 ' 10 mm
(c)再左球面第三次折射
l 50 mm , r 30 , n 1 . 5 , n ' 1 n' l' 1 l' n l 1 .5 50 n ' n r 1 1 .5 30
n1
I2’
n 1 sin I 1 n 1 sin I 2 ' I1 I 2'
第一章 8
I1’ I1 n 0 sin I 1 n 1 sin I 1 ' n 1 sin I 2 n 2 sin 90 n 2 I 1 ' 90 I 2 I2
n0 n2 n1
3 10 1 . 526
8
1 . 966 10 m / s
8 8
3 10 2 . 417
1 . 241 10 m / s
第一章 4
D=?
h=200mm
全反射问题. (1)
n sin I 1 sin 90 sin I 1 I 41 . 81 n
I
1
工程光学第二章练习参考答案

(5)
n sinU NA sinU 0.1
U 5.73917 D 2( ltgU ) 2(45 tg 5.73917 ) 9.045mm
(5)
lz 160 D D' 1.667 9.00mm lz ' 29.63
(6)
-l (6)
l’ 180 -lz
h3 h2 d 2 tgu2 ' 12 10 0.04 11.6 tgu3 ' tgu3 h3 11.6 0.04 0.156 f3' 100
第二章 17
F’ 求物方参数。反向算。 h1=10
H’
u3’
f’
h1 10 f ' 64.102564 tgu3 ' 0.156 h3 11.6 lF ' 74.35897 tgu3 ' 0.156
第二章 17
求物方参数。反向算。
h1=10
H’
u3’
F’
f1 ' 50, f 2 ' 50, f 3 ' 100 d1 d 2 10
f’
lF’
tgu1 ' tgu2
h1
f1 '
10
50
0.2
h2 h1 d1tgu1 ' 10 10 ( 0.2) 12 tgu2 ' tgu3 tgu2 h2 f2' 0.2 12 50 0.04
第二章 3
y H -f d 1140mm 7200mm H’ f’ y’
l ' l 10
l d l ' 7200 2 f ' d 1140 1 1 1 l' l f'
工程光学习题参考答案第七章典型光学系统

⼯程光学习题参考答案第七章典型光学系统第七章典型光学系统1.⼀个⼈近视程度是D 2-(屈光度),调节范围是D 8,求:(1)远点距离;(2)其近点距离;(3)配戴100度近视镜,求该镜的焦距;(4)戴上该近视镜后,求看清的远点距离;(5)戴上该近视镜后,求看清的近点距离。
解:① 21-==rl R )/1(m ∴ m l r 5.0-=②P R A -= D A 8= D R 2-= ∴D A R P 1082-=--=-=m P l p 1.01011-=-== ③fD '=1∴m f 1-=' ④D D R R 1-=-='m l R1-=' ⑤P R A '-'= D A 8= D R 1-='D A R P 9-=-'='m l P11.091-=-=' 2.⼀放⼤镜焦距mm f 25=',通光孔径mm D 18=,眼睛距放⼤镜为mm 50,像距离眼睛在明视距离mm 250,渐晕系数为%50=k ,试求(1)视觉放⼤率;(2)线视场;(3)物体的位置。
eye已知:放⼤镜 mm f 25=' mm D 18=放 mm P 50=' mm l P 250='-'%50=K求:①Γ② 2y ③l 解:①fDP '-'-=Γ1 25501252501250-+=''-+'=f P f 92110=-+=②由%50=K 可得: 18.050*2182=='='P D tg 放ωωωtg tg '=Γ∴02.0918.0==ωtg Dytg =ω∴mm Dtg y 502.0*250===ω∴mm y 102= ⽅法⼆:18.0='ωtg mm tg y 45*250='='ω mm l 200-=' mm fe 250='mm l 2.22-= yy l l X '==='=92.22200β mm y 102=③ l P D '-'= mm D P l 20025050-=-=-'='f l l '=-'11125112001=--l mm l 22.22-=3.⼀显微镜物镜的垂轴放⼤率为x3-=β,数值孔径1.0=NA ,共扼距mm L 180=,物镜框是孔径光阑,⽬镜焦距mm f e 25='。
工程光学第四章参考答案

第四章光学系统中的光束限制1.设照相物镜的焦距等于75mm,底片尺寸为55×55㎜2,求该照相物镜的最大视场角等于多少?解:2.略。
3. 在本章第二节中的双目望远镜系统中,假定物镜的口径为30mm,目镜的通光口径为20mm,如果系统中没有视场光阑,问该望远镜最大的极限视场角等于多少?渐晕系数k =0.5的视场角等于多少?解:(1)151018108=++x xmm x 252=1081825218252108181815+++=+++=x x y714286.10=y︒=33.112目ω(2) 0793651.0181081021=+=+=’目‘物目f f D tg ω ︒︒==∴08.932492‘’‘ω答:极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。
总黄酮生物总黄酮是指黄酮类化合物,是一大类天然产物,广泛存在于植物界,是许多中草药的有效成分。
在自然界中最常见的是黄酮和黄酮醇,其它包括双氢黄(醇)、异黄酮、双黄酮、黄烷醇、查尔酮、橙酮、花色苷及新黄酮类等。
简介近年来,由于自由基生命科学的进展,使具有很强的抗氧化和消除自由基作用的类黄酮受到空前的重视。
类黄酮参与了磷酸与花生四烯酸的代谢、蛋白质的磷酸化、钙离子的转移、自由基的清除、抗氧化活力的增强、氧化还原作用、螯合作用和基因的表达。
它们对健康的好处有:( 1 )抗炎症( 2 )抗过敏( 3 )抑制细菌( 4 )抑制寄生虫( 5 )抑制病毒( 6 )防治肝病(7 )防治血管疾病(8 )防治血管栓塞(9 )防治心与脑血管疾病(10 )抗肿瘤(11 )抗化学毒物等。
天然来源的生物黄酮分子量小,能被人体迅速吸收,能通过血脑屏障,能时入脂肪组织,进而体现出如下功能:消除疲劳、保护血管、防动脉硬化、扩张毛细血管、疏通微循环、活化大脑及其他脏器细胞的功能、抗脂肪氧化、抗衰老。
近年来国内外对茶多酚、银杏类黄酮等的药理和营养性的广泛深入的研究和临床试验,证实类黄酮既是药理因子,又是重要的营养因子为一种新发现的营养素,对人体具有重要的生理保健功效。
1995-2016年浙江大学841工程光学基础考研真题及答案解析-汇编

1995-2016年浙江大学841工程光学基础考研真题及答案解析-汇编2017版浙江大学《841工程光学基础》全套考研资料我们是布丁考研网浙大考研团队,是在读学长。
我们亲身经历过浙大考研,录取后把自己当年考研时用过的资料重新整理,从本校的研招办拿到了最新的真题,同时新添加很多高参考价值的内部复习资料,保证资料的真实性,希望能帮助大家成功考入浙大。
此外,我们还提供学长一对一个性化辅导服务,适合二战、在职、基础或本科不好的同学,可在短时间内快速把握重点和考点。
有任何考浙大相关的疑问,也可以咨询我们,学长会提供免费的解答。
更多信息,请关注布丁考研网。
以下为本科目的资料清单(有实物图及预览,货真价实):2017年浙江大学《工程光学基础》全套资料包括:一、浙江大学《工程光学基础》历年考研真题及答案解析2016年浙江大学《工程光学基础》考研真题2015年浙江大学《工程光学基础》考研真题2014年浙江大学《工程光学基础》考研真题(含答案解析)2013年浙江大学《工程光学基础》考研真题(含答案解析)2012年浙江大学《工程光学基础》考研真题(含答案解析)2011年浙江大学《工程光学基础》考研真题(含答案解析)2010年浙江大学《工程光学基础》考研真题(含答案解析)2009年浙江大学《工程光学基础》考研真题(含答案解析)2008年浙江大学《工程光学基础》考研真题(含答案解析)2007年浙江大学《工程光学基础》考研真题(含答案解析)2006年浙江大学《工程光学基础》考研真题(含答案解析)2005年浙江大学《工程光学基础》考研真题(含答案解析)2004年浙江大学《工程光学基础》考研真题(含答案解析)2003年浙江大学《工程光学基础》考研真题(含答案解析)2002年浙江大学《工程光学基础》考研真题(含答案解析)2001年浙江大学《工程光学基础》考研真题(含答案解析)2000年浙江大学《工程光学基础》考研真题(含答案解析)1999年浙江大学《工程光学基础》考研真题(含答案解析)1998年浙江大学《工程光学基础》考研真题(含答案解析)1997年浙江大学《工程光学基础》考研真题(含答案解析)1996年浙江大学《工程光学基础》考研真题(含答案解析)1995年浙江大学《工程光学基础》考研真题(含答案解析)二、浙江大学《工程光学基础》期中期末试题汇编三、浙江大学《工程光学基础》考研复习笔记1、浙江大学物理光学笔记2、浙江大学最新光学笔记四、浙江大学《工程光学基础》考研复习题1、习题与答案五、浙江大学《工程光学基础》赠送资料(电子版,发邮箱)1、浙江大学《光学工程基础》复试题目以下为截图及预览:2016年考研真题:2012年考研真题:2012年真题答案解析:期中期末试题:考研复习笔记:。
工程光学习题解答(第1章)

第一章1.举例说明符合光传播基本定律的生活现象及各定律的应用。
答:(1)光的直线传播定律影子的形成;日蚀;月蚀;均可证明此定律.应用:许多精密的测量,如大地测量(地形地貌测量),光学测量,天文测量.(2)光的独立传播定律定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独立传播。
说明:各光束在一点交会,光的强度是各光束强度的简单叠加,离开交会点后,各光束仍按各自原来的方向传播。
2.已知真空中的光速c≈3×108m/s,求光在水(n=1。
333)、冕牌玻璃(n=1。
51)、火石玻璃(n=1。
65)、加拿大树胶(n=1。
526)、金刚石(n=2.417)等介质中的光速。
解:v=c/n(1)光在水中的速度:v=3×108/1。
333=2.25×108 m/s(2)光在冕牌玻璃中的速度:v=3×108/1。
51=1。
99×108 m/s(3)光在火石玻璃中的速度:v=3×108/1。
65=1。
82×108 m/s(4)光在加拿大树胶中的速度:v=3×108/1。
526=1。
97×108 m/s(5)光在金刚石中的速度:v=3×108/2.417=1。
24×108m/s*背景资料:最初用于制造镜头的玻璃,就是普通窗户玻璃或酒瓶上的疙瘩,形状类似“冠”,皇冠玻璃或冕牌玻璃的名称由此而来。
那时候的玻璃极不均匀,多泡沫。
除了冕牌玻璃外还有另一种含铅量较多的燧石玻璃(也称火石玻璃).3.一物体经针孔相机在屏上成像的大小为60mm,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:⇒l=300mm4.一厚度为200mm的平行平板玻璃(设n=1。
5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:本题是关于全反射条件的问题。
工程光学习题参考答案第一章几何光学基本定律

⼯程光学习题参考答案第⼀章⼏何光学基本定律第⼀章⼏何光学基本定律1. 已知真空中的光速c =3810?m/s ,求光在⽔(n=1.333)、冕牌玻璃(n=1.51)、⽕⽯玻璃(n=1.65)、加拿⼤树胶(n=1.526)、⾦刚⽯(n=2.417)等介质中的光速。
解:则当光在⽔中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在⽕⽯玻璃中,n =1.65时,v=1.82 m/s ,当光在加拿⼤树胶中,n=1.526时,v=1.97 m/s ,当光在⾦刚⽯中,n=2.417时,v=1.24 m/s 。
2. ⼀物体经针孔相机在屏上成⼀60mm ⼤⼩的像,若将屏拉远50mm ,则像的⼤⼩变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则⽅向不变,令屏到针孔的初始距离为x ,则可以根据三⾓形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. ⼀厚度为200mm 的平⾏平板玻璃(设n =1.5),下⾯放⼀直径为1mm 的⾦属⽚。
若在玻璃板上盖⼀圆形的纸⽚,要求在玻璃板上⽅任何⽅向上都看不到该⾦属⽚,问纸⽚的最⼩直径应为多少?2211sin sin I n I n =66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射⽅式传播时在⼊射端⾯的最⼤⼊射⾓)。
解:位于光纤⼊射端⾯,满⾜由空⽓⼊射到光纤芯中,应⽤折射定律则有: n 0sinI 1=n 2sinI 2 (1)⽽当光束由光纤芯⼊射到包层的时候满⾜全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联⽴得到n 0 .5. ⼀束平⾏细光束⼊射到⼀半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题解答第十章光的干涉

第十一章 光的干涉1. 双缝间距为1mm,离观察屏1m,用钠光灯做光源,它发出两种波长的单色光nm 0.5891=λ和nm 6.5892=λ,问两种单色光的第十级亮条纹之间的间距是多少?解:由题知两种波长光的条纹间距分别为961131589105891010D e m d λ---⨯⨯===⨯ 962231589.610589.61010D e m d λ---⨯⨯===⨯ ∴第十级亮纹间距()()65211010589.6589100.610e e m -∆=-=⨯-⨯=⨯2. 在杨氏实验中,两小孔距离为1mm,观察屏离小孔的距离为50cm,当用一片折射率为1.58的透明薄片贴住其中一个小孔时(见图11-17),发现屏上的条纹系统移动了0.5场面,试决定试件厚度。
解:设厚度为h ,则前后光程差为()1n h ∆=- ()1x dn h D∆⋅∴-=230.510100.580.5h --⨯⨯=21.7210h mm -=⨯3. 一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长nm 28.656=λ,空气折射率000276.10=n 。
试求注入气室内气体的折射率。
图11-47 习题2 图解:设气体折射率为n ,则光程差改变()0n n h ∆=- ()02525x d dn n h e D Dλ∆⋅∴-==⋅= 9025656.2810 1.000276 1.0008230.03m n n h λ-⨯⨯=+=+= 4. ** 垂直入射的平面波通过折射率为n 的玻璃板,投射光经投射会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面(见图11-18)的直线发生光波波长量级的突变d ,问d 为多少时,焦点光强是玻璃板无突变时光强的一半。
解:无突变时焦点光强为04I ,有突变时为02I ,设',.d D 200'4cos 2xd I I I Dπλ== ()'104xd m m D λ⎛⎫∴∆==+≥ ⎪⎝⎭又()1n d ∆=- 114d m n λ⎛⎫∴=+ ⎪-⎝⎭5. 若光波的波长为λ,波长宽度为λ∆,相应的频率和频率宽度记为ν和ν∆,证明λλνν∆=∆,对于nm 8.632=λ的氦氖激光,波长宽度nm 8102-⨯=∆λ,求频率宽度和相干长度。
工程光学习题库

模拟试题与答案工程光学2005——2006年底第一学期期末考试试题A一、填空(20分)1、照明系统与成像系统之间的衔接关系为:__照明系统的拉赫不变量要大于成像系统的拉赫不变量_、______保证两个系统的光瞳衔接和成像关系__________________________________________2、转像系统分__棱镜式___________和___透镜式__________两大类,其作用是:_使物镜所成的倒像转变为正像。
3、角放大率、轴向放大率和垂轴放大率三者之间的关系为、拉赫不变J=nuy 、牛顿公式以焦点为坐标原点。
4产生偏振光的方法有反射和折射、二向色性、双折射、散射。
5、麦克斯韦方程组的微分形式为6.获得相干光的方法有分波前法、分振幅法。
7、水槽中盛水,深20mm,槽底中央置一点光源,水的折射率n=1.33,水面上浮一个既不透光又不反射光的纸片,使人从水面上无论哪个角度都看不到光,纸片面积最小为1634.33mm2。
8、光源的相干长度与相干时间的关系为。
三、名词解释(15分)1、光的直线传播定律:在各向同性的均匀介质中,光是沿直线传播的。
2、节点:光学系统中放大率为+1的一对共轭点称为节点。
3、空间相干性:光源的大小与相干空间成反比关系,给定一个光源尺寸,就限制着一个相干空间,这就是空间相干性的问题,即通过光波场横方向上两点的光在空间相遇时能够发生干涉,则称通过空间这两点的光具有空间相干性。
4、费马原理:光从一点传播到另一点,其间无论经过多少次折射或反射,其光程为极值,即光是沿光程的极值的路径传播的。
5、出瞳:孔径光阑经它前面的透镜或透镜组在光学系统像空间所成的像称为出射光瞳。
四、作图(20分)1、设输入为右手坐标系,画出经图中棱镜后的输出坐标系(图1)。
2、求AB的像(图2)。
3、判断棱镜的成像方向(图3)。
4、求轴上物点A所成的像(图4)。
图4五、计算题(45分)1、用等厚条纹测量玻璃楔板的楔角时,在长达5cm的范围内共有15个亮条纹,玻璃楔板的折射率n=1.52,所用光波波长,求楔角?(10分)解:……………………………………..………………….5分e=50mm/15……………………………5分2、已知,的双凸透镜,置于空气中。
浙江大学2005高代答案

" # $ %
qso
p n n p ) o
n n r rq )
: : ¬ 5 / )« tu 8 + 7 £S ¤¥¦ §7 ¨EF © 7 + ª0« + 0 © 0 ® 55 5 ¯ °
lF f I lF f I
" # $ %
f`mF@
! !
lF ] p F@ C A C C^ q2 cWstu4stvw2 x4y f n( )o +, r z{H| I p l F l I l I 4{ r 4 cWst2 f} r ~r pFI p }F pF
12345 6 789
o 0 ¢* ¢ ¡பைடு நூலகம் +
+ 0
5 ¬ / )7 ª ® ¯ 5 °
! !
12345 6 789
&) # ( # $ 8< ! %./ 0123 45 687 9:%;123 45 7 "! * %' $ '+ , &) &) ? ( ( ( ) 7 > 9:%=1 @$ $ $"&A "! " > * + * + * + ' ' ,> > , , CDE3 F <8 71GH25%IJKLJMNOPG5QRST F <8 7RUVW F ) Q1X%Y 7 QZ[\]59:%^_`La9: b%cd ! %. F$( <#7 * ,>+ F ) i$ # %./ & j kl # ( /F %gh & & > ' 3 4eLaf:%IJ F$! * + ,>Lam F F& ) ) > # # $! ( Ld @$F &i $!#( & > ' '#%n= b%k%F %& L * + * + > > >
(完整版)工程光学习题参考答案第十四章光的偏振和晶体光学.doc

工程光学习题解答第十四章 光的偏振和晶体光学1. 一束自然光以 30 度角入射到玻璃 -空气界面, 玻璃的折射率 n 1.54 ,试计算 ( 1)反射光的偏振度;( 2)玻璃 -空气界面的布儒斯特角; ( 3)以布儒斯特角入射时透射光的偏振度。
解:光由玻璃到空气,n 1 1.54,n 2 1,130o , 2 sin 1n 1sin 1 50.354n 2① r ssin 12tan120.06305sin0.3528, r p12tan12I maxI min22Pr sr p93.80 0I maxI min22r sr p② B1n 2tan 1133 otann 11.54③ 1B时, 290B57 0 , r p 0, r ssin 12 0.4067sin 12T s 1 r s 2 0.8364, T p 1P 1 0.8364 9 0 010.8364注:若n 2 cos 2 , T st s 2 ,T pt p2n 1 cos 1ImaxT p I 0, IminT s I 0故Pt p 2t s 2或 T scos 2(12)t p 2 t s 2T p2. 自然光以布儒斯特角入射到由10 片玻璃片叠成的玻片堆上,试计算透射光的偏振度。
10 片玻璃透射率 T s 1 r s20 0.028解:每片玻璃两次反射,故20.836420而 T p 1,令I min ,则p1 IIm ax1Im axm axII m in m in1 0.02689 0.94761 0.026893. 选用折射率为 2.38 的硫化锌和折射率为 1.38 的氟化镁作镀膜材料,制作用于氟氖激光(632.8nm )的偏振分光镜。
试问(1)分光镜的折射率应为多少?(2)膜层的厚度应为多少?解:( 1)n3sin 45 n2 sin 2n1 n3tg 2 (起偏要求)n2n3 452n2 sin 1 n3n3 2 2n2tg 22 n22 1 tg 2n1 n1 1 n1 n2 n22 n2n2 1 n1 2 2 n2 2 n1 2 1.6883n2(2)满足干涉加强 2 2n2 h2 cos 22 ,2 sin 1 n3 30.1065n2 sin 45则 h2 2 76.84 nmcos2n2 2而1 90 2 59.8934 , h12 228.54 nm 2n1 cos 14. 线偏振光垂直入射到一块光轴平行于界面的方解石晶体上,若光矢量的方向与警惕主截面成( 1)30 度( 2)45 度( 3)60 度的夹角,求o光和e光从晶体透射出来后的强度比?解:垂直入射 1 2 3, S 波与 p 波分阶r s 2 r p 2n1 cos 1 n2 cos 2 n1 n2r sn2 cos n1 n2n1 cos 1 2n2 cos 1 n1 cos 2 n2 n1r pn1 cos n2 n1n2 cos 1 2o 光此时对应 s 波r0 1 n0 ,T0 1 r02 4n0 22 21 n0 1 n02e 光此时对应 p 波r en e 1 , T e1 224n en e1 r e21 n e2T 0 sin 224I 0E s T 0 tg 2n 0 1 n e I eE p 2T e cos 2 T en e1 n 0取 n 0 1.6584 , n e 1.4864则Itg 20.9526I e( 1)30 ,I 01 0.9526 0.3175I e3( 2)45 ,I 00.9526I e( 3)60 ,I 03 0.95262.8578I e5. 方解石晶片的厚度 d 0.013mm ,晶片的光轴与表面成60 度角, 当波长632.8nm的氦氖激光垂直入射晶片时(见图14-64),求( 1)晶片内 o 、 e 光线的夹角;( 2) o 光和 e 光的振动方向; ( 3) o 、 e 光通过晶片后的相位差。
工程光学习题解答

36.2( mm), l F
第二章 理想光学系统
17、有三个薄透镜,其焦距分别为 f1 100mm, f 2 50mm, f 3 50mm, 其间隔 d1 10mm, d 2 10mm 求组合系统的 基点。 h h1 100mm, tan U 2 tan U1 2 解:物方参数 f
lH f
l F l H f 1560mm, l F l H f 1360mm
第二章 理想光学系统
10、解:
f f1f 2
100mm,
f1f 2 f
50mm
d f1 f 2 100mm lH f lH f d f2 d f1 100mm, l F l H f 0
A
OB 50 OB OB 30mm
A
A
n 6、解:0 sin I1 n1 sin I 2 I 2 90 I m
0
n1 sin I m n2 sin 90 sin I m n2 n1 n2 n1
2 2
0
cos I m 1
n0 sin I1 n1 1
H
lH
F2
F1
F
d
l F (lk )
L
f
第二章 理想光学系统
9、已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 , 求其焦距、光焦度、基点位置。 nr1r2 解: f 1440mm 1.44m
( n 1)[ n( r2 r1 ) ( n 1)] 1 f 0.69 D n 1 n d1 120mm, l H f n 1 n d 2 80mm
工程光学习题参考答案第二章 理想光学系统.doc
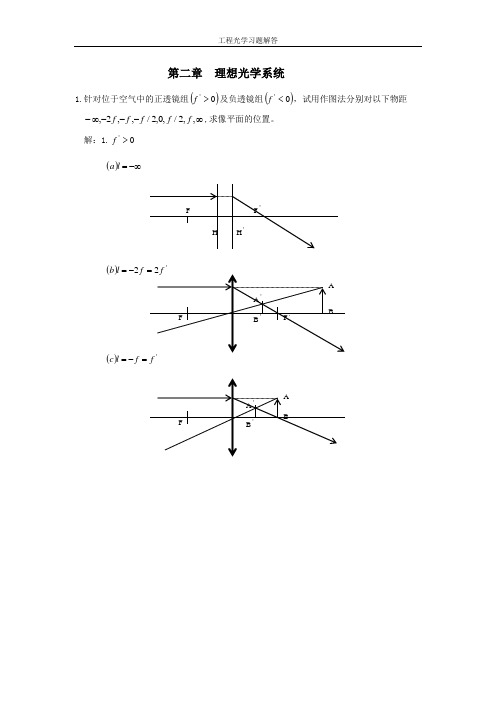
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c=-=()/f l d -=()0=l e()/f lf =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′=0.5625 (3)x ′=0.703 (4)x ′=0.937 (5)x ′=1.4(6)x ′=2.813.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=βΘ143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少? 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm,则所得像与物同大小,求该正透镜组的焦距。
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
