自动控制原理课程设计报告
自动控制原理专业课程设计方案报告

自控课程设计 课程设计(论文)设计(论文)题目 单位反馈系统中传输函数研究学院名称 Z Z Z Z 学院 专业名称 Z Z Z Z Z学生姓名 Z Z Z 学生学号 Z Z Z Z Z Z Z Z Z Z 任课老师 Z Z Z Z Z设计(论文)成绩单位反馈系统中传输函数研究一、设计题目设单位反馈系统被控对象传输函数为 )2)(1()(00++=s s s K s G (ksm7)1、画出未校正系统根轨迹图,分析系统是否稳定。
2、对系统进行串联校正,要求校正后系统满足指标: (1)在单位斜坡信号输入下,系统速度误差系数=10。
(2)相角稳定裕度γ>45º , 幅值稳定裕度H>12。
(3)系统对阶跃响应超调量Mp <25%,系统调整时间Ts<15s3、分别画出校正前,校正后和校正装置幅频特征图。
4、给出校正装置传输函数。
计算校正后系统截止频率Wc和穿频率Wx。
5、分别画出系统校正前、后开环系统奈奎斯特图,并进行分析。
6、在SIMULINK中建立系统仿真模型,在前向通道中分别接入饱和非线性步骤和回环非线性步骤,观察分析非线性步骤对系统性能影响。
7、应用所学知识分析校正器对系统性能影响(自由发挥)。
二、设计方法1、未校正系统根轨迹图分析根轨迹简称根迹,它是开环系统某一参数从0变为无穷时,闭环系统特征方程式根在s平面上改变轨迹。
1)、确定根轨迹起点和终点。
根轨迹起于开环极点,最终开环零点;本题中无零点,极点为:0、-1、-2 。
故起于0、-1、-2,最终无穷处。
2)、确定分支数。
根轨迹分支数和开环有限零点数m和有限极点数n中大者相等,连续而且对称于实轴;本题中分支数为3条。
3)、确定根轨迹渐近线。
渐近线和实轴夹角为φa,交点为:σa。
且:φa=(2k+1)πn−m k=0,1,2······n-m-1; σa=∈pi−∈zin−m;则:φa=π3、3π3、5π3;σa=0−1−23=−1。
自动控制原理课程设计

审定成绩:自动控制原理课程设计报告题目:单位负反馈系统设计校正学生姓名罗衡班级0903班院别物理与电子学院专业电子科学与技术学号14092500060 指导老师杜健嵘设计时间2011.12目录一、设计题目 (1)二、设计要求 (1)三、设计思路 (1)四、设计方法与步骤 (1)(1)确定系统开环增益 (2)(2)分析校正前系统性能指标 (2)(3)选择校正方案 (4)(4)设置校正装置的参数 (5)(5)分析校正后系统性能指标 (6)五、验证与对比 (8)六、参考文献 (9)自动控制原理课程设计一、设计题目设单位负反馈系统的开环传递函数为)12.0)(11.0()(0++=s s s K s G ,用相应的频率域校正方法对系统进行校正设计,使系统满足如下动态和静态性能:(1)相角裕度045≥γ(2)在单位斜坡输入下的稳态误差05.0<ss e (3)系统的剪切频率s /rad 3<c ω二、设计要求(1)分析设计要求,说明校正的设计思路(超前校正,滞后校正或滞后-超前校正)(2)详细设计(包括的图形有:校正结构图,校正前系统的Bode 图,校正装置的Bode 图,校正后系统的Bode 图)(3)用MATLAB 编程代码及运行结果(包括图形、运算结果) (4)校正前后系统的单位阶跃响应图。
三、设计思路根据题目要求的稳态误差 e ss 的值,确定开环增益 K ,再得到校正前系统的传递函数及频率特性,利用matlab 画出其 bode 图,从图形及结果可以得到校正前系统的相角裕度γ和剪切频率ωc ,判断这两项指标是否符合要求,若不符合,则选择合适的校正装置,确定并计算出校正装置的参数 a 和 T 。
即得校正装置的传递函数,然后得到校正后系统的开环传递函数及频率特性,最后验证已校正系统的γ和ωc 是否都达到要求。
如果有指标仍未达标。
则须另取合适的w c 的四、设计方法与步骤(1)确定系统开环增益单位负反馈系统的误差传递函数为:)12.0)(11.0()12.0)(11.0()()(11)()s (K s s s s s s s H s G s R E +++++=+= 根据稳态误差的定义,在单位斜坡输入信号t t r =)((2s 1)(=s R )作用下的稳态误差为:K1)()(1)(lim)]([lim )(lim =+=⋅==∞→∞→∞→s H s G s sR s E s t e e s s s ss现要使稳态误差05.0<ss e ,则K>20,取开环增益K=21即可满足系统对稳态误差的要求。
自动控制原理 课程设计报告 范文

目录一、课设的任务与要求 (1)I、课设的题目与问题 (1)II课设的范化要求 (1)二、设计正文 (2)I、第一问 (3)1-1 题目的处理 (3)1-2 题目的代码 (3)1-3 运行的的结果 (3)1-4 比较 (4)II 、第二问 (4)2-1 题目的处理 (5)2-2 题目的代码 (5)2-3 运行的结果 (5)K>0 (6)K<0 (6)III、第三问 (6)3-1 题目的处理 (6)3-3 运行的结果 (7)3-4 结论 (8)IV、第四问 (8)第四问中的第一小题 (8)4-1-1题目的分析 (8)4-1-2题目的代码 (8)4-1-3运行结果 (9)4-1-4 系统的校正 (9)4-1-4-1 超前校正 (9)4-1-4-2 滞后校正 (10)第四问中的第二小题 (11)4-2-1题目的分析 (11)4-2-2题目的代码 (11)4-2-3 运行的结果 (12)4-2-4 系统校正 (12)4-2-4-1 超前校正 (12)4-2-4-2 滞后校正 (13)三、附录 (16)第一问 (16)第二问 (17)K>0 (17)K<0 (17)第三问 (18)第四问 (19)第一题 (19)未校正的单位阶跃响应图 (19)未校正前的BODE 图 (19)超前校正 (19)滞后校正 (21)第二题 (21)未校正的单位阶跃响应图 (22)可得未校正前的BODE 图 (22)超前校正 (22)滞后校正 (23)滞后—超前校正 (24)四、总结 (26)五、参考文献 (26)一、课设的任务与要求I 、课设的题目与问题题目:已知单位负反馈系统被控制对象的开环传递函数)11.0()(+=s s K s G k问题: 1. 分析系统单位阶跃响应的时域性能指标2. 当(),k ∈-∞+∞时,绘制系统的根轨迹,分析系统的稳定性3. 对系统进行频域分析,绘制其Nyquist 图及Bode 图,确定闭环系统的稳定性4. 用串联校正的频率域方法对系统进行串联校正设计,使系统满足如下动态及静态性能指标:4.1设计串联校正满足下列性能指标(1)在单位斜坡信号t t r =)(作用下,系统的稳态误差01.0≤ss e ;(2)系统校正后,相位裕量0''45)(>c ωγ。
《自动控制原理》课程设计

名称:《自动控制原理》课程设计题目:基于自动控制原理的性能分析设计与校正院系:建筑环境与能源工程系班级:学生姓名:指导教师:目录一、课程设计的目的与要求------------------------------3二、设计内容2.1控制系统的数学建模----------------------------42.2控制系统的时域分析----------------------------62.3控制系统的根轨迹分析--------------------------82.4控制系统的频域分析---------------------------102.5控制系统的校正-------------------------------12三、课程设计总结------------------------------------17四、参考文献----------------------------------------18一、课程设计的目的与要求本课程为《自动控制原理》的课程设计,是课堂的深化。
设置《自动控制原理》课程设计的目的是使MATLAB成为学生的基本技能,熟悉MATLAB这一解决具体工程问题的标准软件,能熟练地应用MATLAB软件解决控制理论中的复杂和工程实际问题,并给以后的模糊控制理论、最优控制理论和多变量控制理论等奠定基础。
使相关专业的本科学生学会应用这一强大的工具,并掌握利用MATLAB对控制理论内容进行分析和研究的技能,以达到加深对课堂上所讲内容理解的目的。
通过使用这一软件工具把学生从繁琐枯燥的计算负担中解脱出来,而把更多的精力用到思考本质问题和研究解决实际生产问题上去。
通过此次计算机辅助设计,学生应达到以下的基本要求:1.能用MATLAB软件分析复杂和实际的控制系统。
2.能用MATLAB软件设计控制系统以满足具体的性能指标要求。
3.能灵活应用MATLAB的CONTROL SYSTEM 工具箱和SIMULINK仿真软件,分析系统的性能。
自控原理课程实验报告

一、实验目的1. 理解并掌握自动控制原理的基本概念和基本分析方法。
2. 熟悉自动控制系统的典型环节,包括比例环节、积分环节、比例积分环节、惯性环节、比例微分环节和比例积分微分环节。
3. 通过实验,验证自动控制理论在实践中的应用,提高分析问题和解决问题的能力。
二、实验原理自动控制原理是研究自动控制系统动态和稳态性能的学科。
本实验主要围绕以下几个方面展开:1. 典型环节:通过搭建模拟电路,研究典型环节的阶跃响应、频率响应等特性。
2. 系统校正:通过在系统中加入校正环节,改善系统的性能,使其满足设计要求。
3. 系统仿真:利用MATLAB等仿真软件,对自动控制系统进行建模和仿真,分析系统的动态和稳态性能。
三、实验内容1. 典型环节实验(1)比例环节:搭建比例环节模拟电路,观察其阶跃响应,分析比例系数对系统性能的影响。
(2)积分环节:搭建积分环节模拟电路,观察其阶跃响应,分析积分时间常数对系统性能的影响。
(3)比例积分环节:搭建比例积分环节模拟电路,观察其阶跃响应,分析比例系数和积分时间常数对系统性能的影响。
(4)惯性环节:搭建惯性环节模拟电路,观察其阶跃响应,分析时间常数对系统性能的影响。
(5)比例微分环节:搭建比例微分环节模拟电路,观察其阶跃响应,分析比例系数和微分时间常数对系统性能的影响。
(6)比例积分微分环节:搭建比例积分微分环节模拟电路,观察其阶跃响应,分析比例系数、积分时间常数和微分时间常数对系统性能的影响。
2. 系统校正实验(1)串联校正:在系统中加入串联校正环节,改善系统的性能,使其满足设计要求。
(2)反馈校正:在系统中加入反馈校正环节,改善系统的性能,使其满足设计要求。
3. 系统仿真实验(1)利用MATLAB等仿真软件,对自动控制系统进行建模和仿真,分析系统的动态和稳态性能。
(2)根据仿真结果,优化系统参数,提高系统性能。
四、实验步骤1. 搭建模拟电路:根据实验内容,搭建相应的模拟电路,并连接好测试设备。
自动控制原理课程设计报告材料

自动控制原理课程设计报告材料一、引言自动控制原理是现代工程领域中一门重要的学科,它涉及到控制系统的设计、分析和优化。
本课程设计报告旨在介绍我所完成的自动控制原理课程设计,并详细阐述设计过程、实验结果及分析。
二、设计目标本次课程设计的目标是设计一个能够实现温度控制的自动控制系统。
通过该系统,能够实时监测温度变化并根据设定的温度范围自动调节加热器的工作状态,以保持温度在设定范围内稳定。
三、设计原理1. 系统框架设计的自动控制系统由传感器、控制器和执行器组成。
传感器负责实时监测温度变化,控制器根据传感器的反馈信号进行判断和控制决策,执行器则根据控制器的指令调节加热器的工作状态。
2. 控制算法本次设计采用了经典的比例-积分-微分(PID)控制算法。
PID控制器通过计算误差的比例、积分和微分部分的权重,来调节执行器的输出信号,以实现对温度的精确控制。
3. 系统建模为了进行系统控制算法的设计和分析,我们需要对系统进行建模。
本次设计中,我们采用了一阶惯性环节模型来描述加热器和温度传感器之间的关系。
四、实验步骤1. 硬件搭建首先,我们搭建了一个实验平台,包括加热器、温度传感器、控制器和执行器等硬件设备。
确保各个设备之间的连接正确并稳定。
2. 参数调节接下来,我们通过对PID控制器的参数进行调节,使得系统能够快速响应、稳定控制。
通过试验和调整,我们得到了最优的PID参数。
3. 实验数据采集在实验过程中,我们采集了一系列的温度数据,包括初始温度、设定温度和实际温度等。
同时,记录了控制器的输出信号和执行器的工作状态。
4. 数据分析与结果验证通过对实验数据的分析,我们验证了设计的自动控制系统的性能。
分析结果表明,该系统能够准确地控制温度在设定范围内波动,并具有良好的稳定性和鲁棒性。
五、实验结果与讨论1. 温度控制精度经过多次实验,我们得到了控制系统的温度控制精度。
结果表明,系统能够将温度控制在设定范围内,误差较小。
2. 响应时间实验结果显示,系统对温度变化的响应时间较短,能够快速调节加热器的工作状态以保持温度稳定。
自动控制原理课程设计报告-北京科技大学

北京科技大学自动控制原理课程设计学院:班级:学号:指导教师:姓名:目录一.引言 (3)二.系统模型的建立 (3)三.系统控制的优化 (3)3.1 PID调节参数的优化 (3)3.2 积分分离PID的应用 (3)四,结语 (3)双轮自平衡智能车行走伺服控制算法摘要:全国第八届“飞思卡尔”智能汽车大赛已经结束。
光电组使用大赛提供的D车模,双轮站立前进,相对于以前的四轮车,双轮车的控制复杂度大大增加。
行走过程中会遇到各种干扰,经过多次的实验,已经找到了一套能够控制双轮车的方法。
双轮机器人已经广泛用于城市作战,排爆,反恐,消防以及空间消防等领域。
实验使用单片机控制双电机的转速,达到了预期的效果。
关键词:自平衡;智能;控制算法Motion Servo Control Algorithm forDual Wheel Intelligent CarAbstract: The 8th freescale cup national Intelligent Car competition of has been end.The led team must used D car which has only 2tires.It is more difficult to control prefer to control A car which has 4tires.There is much interference on the track. A two-wheeled robots have been widely used in urban warfare, eod, counter-terrorism, fire control and space fire control and other fields。
We has searched a good ways to control it.We used MCU to control the speed of motors and get our gates.Key Words: balance by self; intelligent; control algorithm一.引言双轮自平衡车是智能汽车中一个重要的组成部分。
自动控制原理课程设计

总结词
自动控制系统是一种无需人为干 预,能够根据输入信号和系统内 部参数自动调节输出信号,以实 现特定目标的系统。
详细描述
自动控制系统通过传感器检测输 入信号,经过控制器处理后,输 出控制信号驱动执行机构,以调 节被控对象的输出参数。
自动控制系统分类
总结词
根据不同的分类标准,可以将自动控制系统分为多种类型。
生对自动控制原理的理解和应用能力。
03
教学效果
通过本次课程设计,学生能够掌握自动控制系统的基本原理和设计方法,
具备一定的系统分析和设计能力,为后续的专业学习和实践打下坚实的
基础。
课程设计展望
加强实践环节
在未来的课程设计中,可以进一步增加实践环节的比重,通过更多的实验和项目实践,提 高学生的动手能力和解决实际问题的能力。
软件测试与调试
对软件进行测试和调试,确保软件功能正确、 稳定。
控制系统应用实例
温度控制系统
以温度为被控量,实现温 度的自动控制,应用于工 业、农业等领域。
液位控制系统
以液位为被控量,实现液 位的自动控制,应用于化 工、水处理等领域。
电机控制系统
以电机转速或位置为被控 量,实现电机的自动控制, 应用于工业自动化、电动 车等领域。
详细描述
根据控制方式,自动控制系统可以分为开环控制系统和闭环 控制系统;根据任务类型,可以分为调节系统、随动系统和 程序控制系统;根据控制对象的特性,可以分为线性控制系 统和非线性控制系统。
自动控制系统基本组成
总结词
自动控制系统通常由输入环节、控制环节、执行环节和被控对象组成。
详细描述
输入环节负责接收外部信号并将其传输给控制环节;控制环节通常由控制器组 成,用于处理输入信号并产生控制信号;执行环节接收控制信号并驱动执行机 构;被控对象是受控对象,其输出参数由执行机构调节。
自动控制原理课程设计报告

1、 设计内容开环传递函数:()(0.011)(1)KG s s s s =++,对传递函数进行分析,包括时域、频域、根轨迹分析。
要求校正后系统的性能指标为: 45γ>°,05.0<ss e2、 设计要求分析函数,说明校正的设计思路(超前校正,滞后校正或滞后-超前校正;),详细设计(包括的图形有:校正前系统的Bode 图,校正后系统的Bode 图;),用MATLAB 编程代码及运行结果(包括图形、运算结果;),校正前后系统的单位阶跃响应图。
3、 校正前系统分析3.1时域指标的计算与MATLAB 分析3.1.1由05.0<ss e 得出,系统型别v=1,K=20。
3.1.2将开环传递函数求出闭环传递函数:系统为为单位负反馈系统,得出:自然振荡频率 ωn =4.47 rad/s ,阻尼角β=4.17º,阻尼比 ξ=0.11,衰减系数 б=0.49,振荡频率 ωd =4.423.1.3时域性能指标:由公式得 超调量 σ%=49%,峰值时间 t p=π/ωd =0.70S调节时间t s=9.81S(Δ=0.02)上升时间t r=π-β/ ωd=0.25S3.1.4MATLAB分析:输入为单位阶跃响应, MATLAB程序参看附录;MATLAB图如下:图3-1 单位阶跃响应及其动态性能指标3.1.5动态性能指标:超调量:σ%=75% ,调节时间:t s=9.34S (Δ=0.02)上升时间:t r=0.251S (取由稳态值的10%到90%),峰值时间:t p=0.703s3.1.6MATLAB分析得出:通常由上升时间或峰值时间来评价系统的响应速度;用超调量来评价系统的阻尼程度;而调节时间是同时反映响应速度和阻尼程度的综合性能指标。
系统的单位阶跃响应曲线为衰减振荡曲线,最后趋于稳定。
2图3-1 单位阶跃响应及其动态性能指标图3-2 稳态值的10%到90%3.2根轨迹稳定分析3.2.1根轨迹分析:由开环传递函数得出有三个极点,分别为:s=-100,-1,0 极点数N=3,零点数M=0S=-100为非主导极点(舍去),s=-1和s=0为主导极点,无零点。
自动控制原理课程设计报告

自动控制原理课程设计报告自动控制是工程学的重要组成部分,它是一种数学模型,可以控制复杂的过程和系统,从而使其稳定运行,并获得最佳的性能。
自动控制的原理在许多工程领域中都有广泛的应用,如化工、航空航天、机械、电力等。
本文将介绍如何利用自动控制原理来设计一个系统,以优化系统性能。
首先要设计一个控制系统,可以实现对系统的自动控制。
控制系统的第一步是定义系统模型。
一般来说,系统模型有两种:非线性模型和线性模型,其中线性模型更为简单,也是设计自动控制系统的常用模型。
接下来,需要确定控制系统的类型。
一般来说,自动控制系统可以分为闭环控制系统和开环控制系统,其中闭环控制系统具有更高的精度和更好的稳定性,它通过检测控制量的反馈信号与设定值进行比较,以实现对系统的控制。
此外,还需要为控制系统设计一个优化的控制器,用于控制系统的运行状态。
一般来说,有两种主要的控制器:PID控制器和经验模型控制器。
PID控制器是最常用的控制器,它可以控制系统的振荡和滞后,并且可以根据不同情况自动调整参数。
另一种控制器是经验模型控制器,它主要用于复杂的非线性系统,可以有效的抑制噪声,并对系统的响应时间进行调节。
完成了以上步骤后,就可以搭建出一个自动控制系统,以达到优化系统性能的目的。
实际的设计过程要根据实际的应用场景进行相应的调整,实现最佳的系统性能。
例如,在机器人控制系统中,需要使用传感器和控制器来实现对机器人运动的控制,以达到最佳性能。
综上所述,自动控制原理在设计控制系统时十分重要,可以有效的解决复杂的控制问题,并有助于优化系统性能。
本文只是简要介绍了自动控制系统的基本原理,实际的设计和实现过程要根据具体的应用环境而定,还需要从不同的方面进行充分的研究。
自动控制原理课程设计报告_3

自动控制原理课程设计专业:自动化班级:姓名:学号:指导教师:自动化与电气工程学院2013 年 01月 11日目录1、设计目的 (2)2、设计内容 (2)3、设计过程和步骤 (2)4、软件仿真 (6)5、电路模拟以及结果分析 (7)6、思考题 (9)7、设计小结 (10)8、参考文献 (10)连续定常系统的频率法超前校正1.设计目的(1)了解串联超前校正环节对系统稳定性及过渡过程的影响;(2)掌握用频率特性法分析自动控制系统动态特性的方法;(3)掌握串联超前校正装置的设计方法和参数调试技术;(4)掌握设计给定系统超前校正环节的方法,并用仿真技术验证校正环节理论设计的正确性;(5)掌握设计给定系统超前校正环节的方法,并模拟实验验证校正环节理论设计的正确性。
2.设计内容已知单位反馈控制系统的开环传递函数为:G0(s)=Ks(0.2s+1)(0.01s+1)设计超前校正装置,使校正后系统满足:K v=100s−1, ωc≥30s−1,σ%≤36% 3.设计过程和步骤3.1 确定开环增益K根据给定静态误差系数的要求,确定开环增益KK v=lims→0sG0(s)=lims→0sKs(0.2s+1)(0.01s+1)=100s−1得K=100。
3.2画出未校正系统的伯德图未校正系统的开环函数:G0(s)=100s(0.2s+1)(0.01s+1)=50000s(s+5)(s+100)MATLAB中输入以下语句:>> Go=zpk([],[0 -5 -100],50000);>> bode(Go)>> margin(Go)得到未校正系统的Bode图,如图1所示,并由图可知未校正系统的相角余P m=γ1= 0.596deg ,剪切频率ωc=21.8s−1。
图1未校正系统的Bode图3.3 确定最大超前相角由题目要求可知,校正后的系统的超调量σ%≤36%,高阶系统有以下公式,超调量:σ%=0.16+0.4(Mγ−1)谐振峰值:Mγ=1 sinγ由以上公式可得,当σ%=36%时,γ=41.8°,由于系统的开环对数幅频特性在剪切频率处的斜率为−40db/dec,一般取ε=5~10。
自动控制原理课程设计报告

成绩摘要本设计通过对开环传递函数的串联滞后校正,改善了系统的各项性能指标,使校正后的剪切频率和相角裕度满足题目所给要求,并通过MATLAB编程给出了校正前和校正后的Bode图,Nyquist曲线,以及各个频域响应曲线。
运用Nyquist 稳定判据和对数频率稳定判据成功判出校正前和校正后系统的稳定性。
关键字:滞后,Bode图,稳定性,校正目录设计题目 (4)一.概述 (4)1.1设计题目 (4)1.2 设计目的 (4)1.3 设计要求 (4)二.串联滞后校正的设计 (4)2.1校正前的性能指标 (4)2.2设计滞后校正 (5)2.3校验 (6)三.判断系统稳定性 (7)3.1利用MATLAB求校正前与校正后的特征根 (7)3.2校正前与校正后的动态性能 (7)3.绘制根轨迹 (13)3.4绘制Nyquist曲线并判断稳定性 (15)3.5根据Bode图判断系统稳定性 (16)3.6绘制校正前后幅相特性曲线 (16)课程设计体会 (18)参考文献 (18)一、概述:1.1设计条件:已知单位负反馈系统的开环传递函数0()(0.11)(0.21)K G S S S S =++试用频率法设计串联滞后校正装置,使(1)校正后系统的静态误差系数25V K = (2)相位裕度045γ≥, (3)截止频率为2.5rad s 。
2.2设计目的a. 了解控制系统设计的一般方法、步骤。
b. 掌握对系统进行稳定性分析、稳态误差分析以及动态特性分析的方法。
c. 掌握利用MATLAB 对控制理论内容进行分析和研究的技能。
d. 提高分析问题解决问题的能力。
3.3设计要求(1)、能用MATLAB 解复杂的自动控制理论题目。
(2)、能用MATLAB 设计控制系统以满足具体的性能指标。
(3)、能灵活应用MATLAB 的CONTROL SYSTEM 工具箱和SIMULINK 仿真软件,分析系统的性能二、串联滞后校正的设计本设计使用串联滞后校正来改善系统的各项性能指标。
自动化控制原理课程设计报告(一)

自动化控制原理课程设计报告(一)自动化控制原理课程设计报告引言•简要介绍自动化控制原理的重要性和应用场景。
•阐述课程设计报告的目的和意义。
课程设计目标•描述本次课程设计的具体目标和要求。
•解释该目标的意义和对学习者的影响。
设计思路•分析课程设计要求,确定设计思路的基本框架。
•阐述设计思路的合理性和可行性。
•介绍所采用的主要方法和技术。
实施步骤1.项目准备阶段–研究相关资料和文献,了解当前的研究进展和应用场景。
–调研市场上已有的自动化控制系统,分析其特点和优缺点。
2.系统设计阶段–定义系统的功能和性能指标。
–利用系统理论和数学模型设计控制策略。
–根据系统需求和参数设计硬件电路和软件程序。
3.系统实施与调试阶段–制作自动化控制系统的原型。
–进行系统实施和集成测试。
–进行系统调试和优化。
4.系统性能评估阶段–测试和评估系统在不同情况下的性能和稳定性。
–分析评估结果,并对系统进行改进和优化。
5.报告撰写和展示阶段–撰写课程设计报告,并整理相关实验数据和图表。
–准备课程设计的展示材料和演示文稿。
–展示和演示课程设计成果,并回答相关问题。
实施结果与分析•分析所设计的自动化控制系统在实际应用中的性能和稳定性。
•对系统的优点和局限性进行分析和总结。
•提出改进和优化的方向和建议。
结论•简要总结整个课程设计的过程和成果。
•强调该课程设计对学习者的价值和意义。
参考文献•列出参考文献的主要信息。
以上是一篇关于自动化控制原理课程设计报告的相关文章,通过标题和副标题的形式来呈现内容。
文章采用markdown格式,按照列点的方式生成,遵守了不出现html字符、网址、图片和电话号码等内容的规则。
希望对您有所帮助!。
自动控制原理课程设计报告书
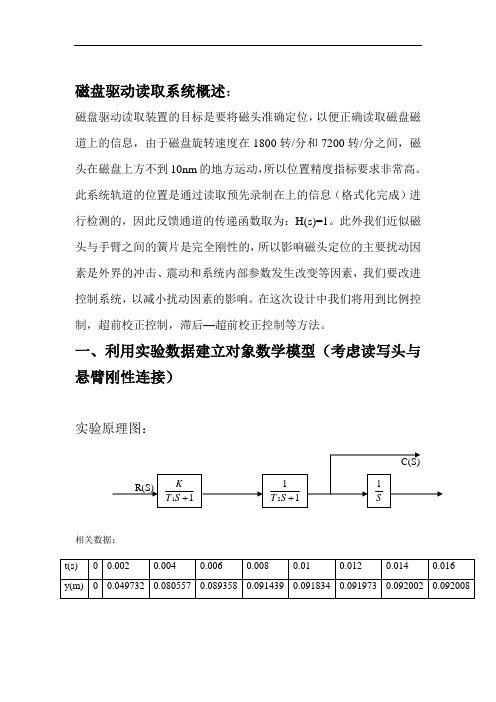
磁盘驱动读取系统概述:磁盘驱动读取装置的目标是要将磁头准确定位,以便正确读取磁盘磁道上的信息,由于磁盘旋转速度在1800转/分和7200转/分之间,磁头在磁盘上方不到10nm的地方运动,所以位置精度指标要求非常高。
此系统轨道的位置是通过读取预先录制在上的信息(格式化完成)进行检测的,因此反馈通道的传递函数取为:H(s)=1。
此外我们近似磁头与手臂之间的簧片是完全刚性的,所以影响磁头定位的主要扰动因素是外界的冲击、震动和系统内部参数发生改变等因素,我们要改进控制系统,以减小扰动因素的影响。
在这次设计中我们将用到比例控制,超前校正控制,滞后—超前校正控制等方法。
一、利用实验数据建立对象数学模型(考虑读写头与悬臂刚性连接)实验原理图:相关数据:飞升曲线标幺曲线根据程序:t=t(15:30);y1=y(15:30);y2=y1/0.092008;y3=1-y2;y4=log(y3);plot(t,y4)gridp=polyfit(t,y4,1)并得到:p =-829.6900 1.5860所以:K=-829.69,b=1.586 得到斜率坐标曲线如下图:斜率坐标图计算如下:所以对象传递函数:G(s)=0.92008/(1.156×10-6S3+2.16×10-3S2+S)二、采用比例控制,系统的性能指标要求:超调量%<5%,调整时间t s <200ms ,单位扰动的最大响应小于5‰1、控制系统方块图:R(S) C(S2、根据根轨迹程序:a=[0.92008];b=[1.156e-006 0.00216 1 0]; sys=tf(a,b); rlocus(sys); gridrlocfind(sys)>> Select a point in the graphics window selected_point =-7.4426e+002 -8.3668e+000ians =26.5803得到如图根轨迹:Ka 0.92008/(0.00121S+1)1/(0.000958S+1)1/s 1根轨迹图在保证系统稳定的前提下,折中选出比例增益,系统稳定要求闭环系统的极点位于S平面的右半面,通过根轨迹图可知当%=4.88%时,系统Ka=2473、系统的稳定裕度编程:ka=247;sys1=tf([0.92008*ka],[ 0.00121 1])sys2=tf([1],[0.000958 1 0])sys3=series(sys1,sys2);bode(sys3)gridmargin(sys3)[h r wg wc]=margin(sys3)运行结果:Transfer function:227.3-------------0.00121 s + 1Transfer function:1----------------0.000958 s^2 + sh =8.2297 (幅值欲量h)r =63.7349 (相角欲量r)wg =928.8050 (交接频率w g)wc =215.3773 (截止频率w c)BODE图4、单位阶跃给定作用下的响应曲线编程:ka=247;t=0:0.0001:10;sys1=tf([0.92008*ka],[ 0.00121 1])sys2=tf([1],[0.000958 1 0])sys3=series(sys1,sys2);sys4=feedback(sys3,[1])[y,t]=step(sys4,t);plot(t,y)grid得到曲线如图:5、单位扰动作用下的响应曲线编程:ka=247;t=0:0.001:2;sys1=tf( 1,[0.000958 1 0])sys2=tf(0.92008*ka,[0.00121 1])sys3=feedback(sys1,sys2)[y,t]=step(sys3,t);plot(t,y)grid得到曲线如图:5、小结通过多次改变Ka的可得到以下表中的多组数据:Ka 225 235 247 255 265超调量 3.14% 3.95% 4.88% 5.57% 6.4%调节时间(s)0.014 0.013 0.012 0.012 0.0130.0049 0.0048 0.0046 0.0045 0.0044对单位阶跃扰动的响应的最大值由此折中选择Ka=247为合适的。
自控实验报告终极版

自动控制原理课程设计实验报告一、 实验目的1、了解自动控制原理的数学和系统稳定验证的方法。
2、了解自动控制系统的放大系数对系统的稳态误差和稳定性的影响。
3、 熟悉MABLAB 系统仿真的应用,加强对MABLAB 软件应用的认识。
二、 实验内容1、设单位反馈控制系统的开环传递函数如下,试用MATLAB 绘制闭环根轨迹图。
33*)2()1()(++=s s K s G2、两个系统的传递函数分别为:)65)(1)(254()144)(3(50)()()1(2232++-++++-=s s s s s s s s s s H s G )1)(2)(6())(133(3)()()2(2222323+++-+++++=s s s s s s s s s s s s H s G 计算上述所给系统在2=ω和20=ω时的幅频特性)(ωA ,对数幅频特性)(ωL 以及相频特性)(ωϕ。
(用MATLAB 验证) 3、设单位反馈的开环传递函数为)15.0)(1()(0++=s s s Ks G要求设计一串联校正网络,使校正后系统的开环增益K=5,相角裕度不低于40°,幅值裕度不小于10dB.(用MATLAB 验证)三、实验步骤及MATLAB 验证仿真1、设单位反馈控制系统的开环传递函数如下,试用MATLAB 绘制闭环根轨迹图。
33*)2()1()(++=s s K s G 解:33*)2()1()(++=s s K s G用MATLAB 绘制闭环根轨迹图如下:程序:num=conv([1 1],conv([1 1],[1 1])); den=conv([1 2],conv([1 2],[1 2])); sys=tf(num,den); rlocus(sys); grid on其闭环根轨迹图如下:2、两个系统的传递函数分别为:)65)(1)(254()144)(3(50)()()1(2232++-++++-=s s s s s s s s s s H s G )1)(2)(6())(133(3)()()2(2222323+++-+++++=s s s s s s s s s s s s H s G(1) 解:)(lg 20)(3462541)14(5094116)25()14(950)()()()3)(2)(1)(425()12)(3(50))H(j ()3)(2)(1)(254()12)(3(50)()(42222222222222222ωωωωωωωωωωωωωωωωωωωωωωωωωωωωωA L j H j G A j j j j j j j j G s s s s s s s s s H s G =+-+++=++++-++==++-+-+-=+--+++-=当ω<5时,o2o2o o 90)2arctan()arctan()254arctan()2arctan(2)32arctan(-)3arctan()2arctan())arctan(180(254arctan90)2arctan(2)3arctan(-180)(--+--+-=---+----++=ωωωωωωωωωωωωωωϕ当ω>5时,o2o2o o 270)2arctan()arctan()254arctan()2arctan(2)32arctan(-)3arctan()2arctan())arctan(180(254arctan90)2arctan(2)3arctan(-180)(--+--+-=---+----++=ωωωωωωωωωωωωωωϕ当ω=2时,87.7904543.6385.2093.15138.6790)22arctan()2arctan()22524arctan()42arctan()322arctan()2(513.999.2lg 20)2lgA(20)2L(99.224346254414214450)2(o o24-=--+-+-=--+-⨯-+-=≈==≈+⨯-+++⨯⨯=ϕ)(A当ω=20时,9. 24027029.8414.8704.1214.17793. 162270)220arctan()20arctan()2025204arctan()402arctan()3202arctan( )20(7.31026.0lg20)20lgA(20)20L(026.0204003462544001400 201400450) 20 (o o2 4-=--+++-=--+-⨯-+-=-≈==≈+⨯-+++⨯⨯=ϕ)(A用MATLAB验证如下:程序:num=conv(50,conv([1 -3],[4 4 1]));den=conv([1 4 25 0],conv([1 -1],[1 5 6]));sys=tf(num,den);margin(sys);grid on其MABLAB验证图如下:由计算值和MATLAB 验证可知,当ω=2时,()()%032.0%100)2()2()2(:16.8251.92L ,87.7)2(513.9)2(99.2)2()2(≈⨯'-=-='='-===L L L L A L δϕϕ故其误差值分别为,,仿真值:,,理论值:%68.3%100)22()2()2(-≈⨯'-=()ϕϕϕδϕ当时20=ω理论值:()(),)(,, 9.240207.3120L 026.020A -=-≈≈ϕ仿真值:()(),, 241207.3120L -='-='ϕ故其误差值分别为:()()()()()()%04.0%1002020200%10020L 20L 20L 2020L -≈⨯'-==⨯'-=ϕϕϕδδϕ)()((2)解:)1)(2)(2)(3()1(3)1)(2)(6())(133(3)()(242222323+++-++=+++-+++++=s s s s s s s s s s s s s s s s s s s H s G )1)(2)(2)(3()1(3)()(24ωωωωωωωωωj j j j j j j H j G +-+-++=422222222222221)4(9)1(3)1(449)1(3|)()(|)(ωωωωωωωωωωωωωωωω+-+++=+-++++==j H j G A )(lg 20)(ωβωA L =()()()()()05.027087.247.8155.34827020120arctan 320arctan 20arctan 42077.908.3lg 2020lg 202008.320201420920120203)20(,2026.162702arctan 4270212arctan 32arctan 2arctan 4)2(18.35275lg 20)2(lg 20)2(44.1221)42(92)12(23)2(,22701arctan3arctan arctan 4)1arctan 180(2arctan )]7arctan(180[3arctan arctan 490)(,1242222242222222-=-+-≈----=≈==≈+-+++⨯⨯==-≈-=----====≈+-+++⨯⨯==----=-+---+--+=>ϕωϕωωωωωωωωωωωωϕωA L A A L A 时当时当时当用MATLAB 验证如下:程序:num=conv(3,conv([1 3 3 1],[1 1 0 0])); den=conv([1 1 -6],conv([1 2 0],[1 1 1])); sys=tf(num,den); margin(sys); grid on其MATLAB 验证图如下:(下一页)由计算值和MATLAB 验证可知; 当时,2=ω理论值:()()() 26.162,18.32,44.12-≈=≈ϕL A 验证值:()() 2.162,17.32-='='ϕL 故其误差值分别为:()%14.3%100)2()2(2)2(≈⨯'-=L L L L δ%37.0%100)2()2()2()2(≈⨯'-=ϕϕϕδϕ当时,20=ω理论值:()()() 05.02077.920L 08.320A -=≈≈ϕ,, 验证值:()() 0512.02041.920L -='='ϕ, 故其误差值分别为:()()()()%68.3%10020L 20L 2020L ≈⨯'-=L δ()()()%4.2%10020202020-=⨯'-=ϕϕϕδϕ)(3、设单位反馈的开环传递函数为)15.0)(1()(0++=s s s Ks G要求设计一串联校正网络,使校正后系统的开环增益K=5,相角裕度不低于40°,幅值裕度不小于10dB.(用MATLAB 验证)解:设校正后c ω截止频率为r c ''",ω为指标求值,通过串联滞后校正,设滞后校正传递函数为()sss G c 71671++=()()())12)(1(1015.01++=++=s s s s s s s s G()()()12110++=ωωωωj j j j G()2110lg2022++=ωωωωL() 902arctanarctan ---=ωωωψ由()()c c c r r ωψω''+''''='' ,且()c c ωψ''取为 14- ,得()() 541440=+=''-''=''''c r c r ωψω由()()c c r ''+=''''ωψω 180得 () 126180540-=-=''x ωψ通过Bode 图得 442.0="c ω程序: num=[10]; den=[1,3,2,0]; G=tf(num,den); margin(G); grid on其MATLAB 伯德图如下:则()1.202442.01442.0442.010log20442.02≈++='=⎪⎭⎫ ⎝⎛"'L L c ω所以有:()()()()()ss s s s s s s s s s G s G s G c 266.30449.45383.1501083.15083.1501083.15115.0152340++++=++⋅++=⋅=程序:num1=[10];den1=[1,3,2,0]; num2=[150.83,10];den2=[150.83,453.49,304.66,2,0]; G1=tf(num1,den1); margin(G1); hold onG2=tf(num2,den2); margin(G2); bode(G1,':'); grid on其MATLAB 验证图如下()sss G T b bTl b c cc 83.1501083.15183.1501.015.010lg 20++=⎩⎨⎧==⎪⎩⎪⎨⎧''==⎪⎭⎫ ⎝⎛"'+得ωω校正前系统阶跃响应如下:程序:num=[10];den=[1,3,2,0];G=tf(num,den);figure(1);step(feedback(G,1,-1));grid on其MATLAB验证图如下校正后系统阶跃响应如下:程序:num=[150.83,10];den=[150.83,453.49,304.66,2,0]; G=tf(num,den);figure(1);step(feedback(G,1,-1));grid on其MATLAB验证图如下校正方法分析:ω附近很窄的频率范围内在此题中,采用相位超前校正是不怎么有效的,此例在c对数幅频和相频特性衰减很快,若采用相位超前校正,虽然校正环节可提供超前相角,ω右移,又将使系统的相位产生较大的滞后量,而使系统的相位裕量不会有但又会使c明显的改善。
自动控制原理课程设计报告_2

《自动控制原理》课程设计报告班级姓名学号2013 年12 月26 日初始条件: 设单位反馈控制系统的开环传递函数为,试设计一串联校正装置, 使系统满足如下性能指标:静态速度误差系数, 相角裕度。
1.1设计原理所谓校正, 就是在系统中加入一些其参数可以根据需要而改变的机构或装置, 使系统整个特性发生变化, 从而满足给定的各项性能指标。
系统校正的常用方法是附加校正装置。
按校正装置在系统中的位置不同, 系统校正分为串联校正、反馈校正和复合校正。
按校正装置的特性不同, 又可分为超前校正、滞后校正和滞后-超前校正、PID校正。
这里我们主要讨论串联校正。
一般来说, 串联校正设计比反馈校正设计简单, 也比较容易对信号进行各种必要的形式变化。
在直流控制系统中, 由于传递直流电压信号, 适于采用串联校正;在交流载波控制系统中, 如果采用串联校正, 一般应接在解调器和滤波器之后, 否则由于参数变化和载频漂移, 校正装置的工作稳定性很差。
串联超前校正是利用超前网络或PD控制器进行串联校正的基本原理, 是利用超前网络或PD控制器的相角超前特性实现的, 使开环系统截止频率增大, 从而闭环系统带宽也增大, 使响应速度加快。
在有些情况下采用串联超前校正是无效的, 它受以下两个因素的限制:1)闭环带宽要求。
若待校正系统不稳定, 为了得到规定的相角裕度, 需要超前网络提高很大的相角超前量。
这样, 超前网络的a值必须选得很大, 从而造成已校正系统带宽过大, 使得通过系统的高频噪声电平很高, 很可能使系统失控。
2) 在截止频率附近相角迅速减小的待校正系统, 一般不宜采用串联超前校正。
因为随着截止频率的睁大, 待校正系统相角迅速减小, 使已校正系统的相角裕度改善不大, 很难得到足够的相角超调量。
串联滞后校正是利用滞后网络PID控制器进行串联校正的基本原理, 利用其具有负相移和负幅值的特斜率的特点, 幅值的压缩使得有可能调大开环增益, 从而提高稳定精度, 也能提高系统的稳定裕度。
自动控制原理课程设计报告

自动控制原理课程设计专业:自动化设计题目:控制系统的综合设计班级:自动化0943学生姓名:XXX学号:XX指导教师:XX分院院长:XXX教研室主任:XX电气工程学院目录第一章 课程设计内容与要求分析1.1设计内容针对二阶系统)1()(+=s s Ks W ,利用有源串联超前校正网络(如图所示)进行系统校正。
当开关S 接通时为超前校正装置,其传递函数11)(++-=Ts Ts K s W cc α,其中132R R R K c +=,1)(132432>++=αR R R R R ,C R T 4=,“-”号表示反向输入端。
若Kc=1,且开关S 断开,该装置相当于一个放大系数为1的放大器(对原系统没有校正作用)。
1.2 设计要求11.0)(≤∞e ,开环截止频率 2 3) 4)设校正装置网络元件参数R4、5R=100K ,C=1F 、10F 若干个);6)利用Matlab 仿真软件辅助分析,绘制校正前、后及校正装置对数频率特性曲线,并验算设计结果;7)在Matlab-Simulink 下建立系统仿真模型,求校正前、后系 统单位阶跃响应特性,并进行系统性能比较;8)利用自动控制原理实验箱完成硬件设计过程,包括:搭建校正前后c系统电路、输入阶跃信号并通过示波器观察校正前后系统输出响应曲线。
1.3 Matlab软件1.3.1基本功能MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
MATLAB和Mathematica、Maple并称为三大数学软件。
自动控制原理_课程设计_报告

青岛理工大学琴岛学院设计报告课题名称:自动控制原理课程设计学院:青岛理工大学琴岛学院专业班级:学号:学生:指导教师:青岛理工大学琴岛学院教务处2013年 7 月 12 日学 生 指导教师课题名称自动控制原理 课程设计设计时间2013.7.1-2013.7.12设计地点 实验楼315设计目的通过本次课程设计,掌握控制设计的原理、方法、目标实现等等,以及能用相关信息去分析、改善系统稳定性。
设计内容(包括设计过程、主要收获、存在问题、解决措施、建议,不少于2000字)一、设计过程: 1、软件介绍:MATLAB 是Mathworks 公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算应用软件。
MATLAB 不仅可以处理代数问题和数值分析问题,而且还具有强大的图形处理及仿真模拟等功能。
从而能够很好的帮助工程师及科学家解决实际的技术问题。
MATLAB 的含义是矩阵实验室(Matrix Laboratory ),最初主要用于方便矩阵的存取,其基本元素是无需定义维数的矩阵。
经过十几年的扩充和完善,现已发展成为包含大量实用工具箱(Toolbox )的综合应用软件,不仅成为线性代数课程的标准工具,而且适合具有不同专业研究方向及工程应用需求的用户使用。
MATLAB 最重要的特点是易于扩展。
它允许用户自行建立完成指定功能的扩展MATLAB 函数(称为M 文件),从而构成适合于其它领域的工具箱,大大扩展了MATLAB 的应用范围。
目前,MATLAB 已成为国际控制界最流行的软件,控制界很多学者将自己擅长的CAD 方法用MATLAB 加以实现,出现了大量的MATLAB 配套工具箱,如控制系统工具箱(control systems toolbox ),系统识别工具箱(system identification toolbox ),鲁棒控制工具箱(robust control toolbox ),信号处理工具箱(signal processing toolbox )以及仿真环境SIMULINK 等2、实际应用:Simulink 建模方法在一些实际应用中,如果系统的结构过于复杂,不适合用前面介绍的方法建模。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理课程设计专业:自动化设计题目:控制系统的综合设计班级:自动化0943学生姓名:XXX学号:XX指导教师:XX分院院长:XXX教研室主任:XX电气工程学院目录目录第一章课程设计内容与要求分析 (1)1.1设计内容 (1)1.2 设计要求 (1)1.3 Matlab软件 (2)1.3.1基本功能 (2)1.3.2应用 (3)第二章控制系统程序设计 (4)2.1 校正装置计算方法 (4)2.2 课程设计要求计算 (4)第三章利用Matlab仿真软件进行辅助分析 (6)3.1校正系统的传递函数 (6)3.2用Matlab仿真 (6)3.3利用Matlab/Simulink求系统单位阶跃响应 (10)3.2.1原系统单位阶跃响应 (10)3.2.2校正后系统单位阶跃响应 (11)3.2.3校正前、后系统单位阶跃响应比较 (12)3.4硬件设计 (13)3.4.1在计算机上运行出硬件仿真波形图 (14)课程设计心得体会 (16)参考文献 (18)第一章 课程设计内容与要求分析1.1设计内容针对二阶系统)1()(+=s s Ks W ,利用有源串联超前校正网络(如图所示)进行系统校正。
当开关S 接通时为超前校正装置,其传递函数11)(++-=Ts Ts K s W cc α,其中132R R R K c +=,1)(132432>++=αR R R R R ,C R T 4=,“-”号表示反向输入端。
若Kc=1,且开关S 断开,该装置相当于一个放大系数为1的放大器(对原系统没有校正作用)。
1.2 设计要求1)引入该校正装置后,单位斜坡输入信号作用时稳态误差1.0)(≤∞e ,开环截止频率ωc’≥4.4弧度/秒,相位裕量γ’≥45°;2)根据性能指标要求,确定串联超前校正装置传递函数;3)利用对数坐标纸手工绘制校正前、后及校正装置对数频率特性曲线;cR 234)设校正装置R1=100K,R2=R3=50K,根据计算结果确定有源超前校正网络元件参数R4、C值;5)绘制引入校正装置后系统电路图(设给定的电阻和电容:R=100K,C=1μF、10μF若干个);6)利用Matlab仿真软件辅助分析,绘制校正前、后及校正装置对数频率特性曲线,并验算设计结果;7)在Matlab-Simulink下建立系统仿真模型,求校正前、后系统单位阶跃响应特性,并进行系统性能比较;8)利用自动控制原理实验箱完成硬件设计过程,包括:搭建校正前后系统电路、输入阶跃信号并通过示波器观察校正前后系统输出响应曲线。
1.3 Matlab软件1.3.1基本功能MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
MATLAB和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连 matlab开发工作界面接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多,并且MATLAB也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。
在新的版本中也加入了对C,FORTRAN,C++,JAVA的支持。
可以直接调用,用户也可以将自己编写的实用程序导入到MATLAB函数库中方便自己以后调用,此外许多的MATLAB爱好者都编写了一些经典的程序,用户可以直接进行下载就可以用。
1.3.2应用1、MA TLAB 产品族可以用来进行以下各种工作:●数值分析●数值和符号计算●工程与科学绘图●控制系统的设计与仿真●数字图像处理技术●数字信号处理技术●通讯系统设计与仿真●财务与金融工程2、MA TLAB在通讯系统设计与仿真的应用MATLAB 的应用范围非常广,包括信号和图像处理、通讯、控制系统设计、测试和测量、财务建模和分析以及计算生物学等众多应用领域。
附加的工具箱(单独提供的专用MA TLAB 函数集)扩展了MATLAB 环境,以解决这些应用领域内特定类型的问题。
第二章 控制系统程序设计2.1 校正装置计算方法设超前校正装置传递函数为:11)(++=s TTs s W dc γ,rd>1若校正后系统的截止频率ωc '=ωm ,原系统在ωc '处的对数幅值为L(ωc '),则:d c L γ=ω-lg 10)('由此得:10)('10c Ld ω-=γ由T d d c 11'γ=ωγ=ω,得时间常数T 为:'c dT ωγ= 2.2 课程设计要求计算解答过程:对于Ⅰ型系统,10=k ,1.01)(≤==∞ke kss e得 10k k ≥ 故取 K=10。
因此)1(10)(+=s s s ω要求4.4≥c ω取:4.4=c ω则有L cϖ()+10lg rd=0。
即 20lg10-20lg ωc -20lg ωc +10lg rd=0 41074.510≈=⇒r d其相位欲度:45.04.42'1'1≈==⇒⨯==ωωcddc rrT Tr w d。
1445.0145.041)(++⨯=∴s s s c ω校正后传递函数:)145.0)(1()145.0(10+++s s s sD=KΩ=⇒=⨯⨯⇒=++3.8310050504)(14423432R R R R R RR因此C=F F Tk μ1410014.0103.8445.0334=⨯=⨯⨯=-第三章 利用Matlab 仿真软件进行辅助分析3.1校正系统的传递函数设:原系统传递函数为)()(a s s Ks W +=,校正装置传递函数为11)(++=cs bs s W c ,则校正后传递函数为11)()()()('+++==cs bs a s s K s W s W s W c3.2用Matlab 仿真num=[10]; den=[1,1,0];W=tf(num,den); %求原系统传递函数W(s) bode(W); %绘制原系统对数频率特性margin(W); %求原系统幅值裕度、相位裕度、相位穿越频率和幅值穿越频率[Gm,Pm,wj,wc]=margin(W);grid; %绘制网格线令a=1:进行仿真,得到下图:校正前系统伯德图M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , Pm = 18 deg (at 3.08 rad/sec)Frequency (rad/sec)图3-1 校正前系统伯德图numc=[b,1]; denc=[c,1];Wc=tf(numc,denc); %求校正装置传递函数Wc(s) bode(Wc); %绘制校正装置对数频率特性grid; %绘制网格线(该条指令可有可无)已知求得:b=1/2.412(0.46),c=1/7.236。
进行仿真得下图:系统校正装置伯德图。
M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)图3-2 系统校正装置伯德图numh=conv(num,numc); denh=conv(den,denc);Wh=tf(numh,denh); %求校正后系统传递函数W (s) bode(Wh); %绘制校正后系统对数频率特性margin(Wh); %求校正后系统幅值裕度、相位裕度、相位穿越频率和幅值穿越频率[Gm,Pm,wj,wc]=margin(Wh);grid; %绘制网格线(该条指令可有可无M a g n i t u d e (d B )1010101010103P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , Pm = 50.1 deg (at 4.42 rad/sec)Frequency (rad/sec)图3-3 校正后系统伯德图bode(W,':'); %绘制原系统对数频率特性hold on; %保留曲线,以便在同一坐标系内绘制其他特性bode(Wc,'-.'); %绘制校正装置对数频率特性 hold on; %保留曲线,以便在同一坐标系内绘制其他特性bode(Wh); %绘制校正后系统对数频率特性 grid; %绘制网格线(该条指令可有可无)-100-50050100M a g n i t u d e (d B )1010101010103-180-135-90-45045P h a s e (d e g )Bode DiagramFrequency (rad/sec)图3-4 校正前、后校正装置伯德图 3.3利用Matlab/Simulink 求系统单位阶跃响应3.2.1原系统单位阶跃响应原系统仿真模型如图3-5所示。
图3-5 校正前系统图系统运行后,其输出阶跃响应如图3-6所示:图3-6 校正前输出阶跃响应曲线3.2.2校正后系统单位阶跃响应校正后系统仿真模型如图3-7所示:图3-7 矫正后系统图系统运行后,其输出阶跃响应如图3-8所示:图3-8 校正后系统阶跃响应波形图3.2.3校正前、后系统单位阶跃响应比较仿真模型如图3-9所示:图3-9 校正前、后系统仿真模型系统运行后,其输出阶跃响应如图3-10所示:图3-10 校正前、后系统输出阶跃响应波形图3.4硬件设计绘制硬件校正装置原理图:图3-11 硬件校正装置原理图3.4.1在计算机上运行出硬件仿真波形图未校正系统硬件波形:图3-12 未校正系统硬件仿真波形图校正后系统硬件波形:图3-13 校正后系统硬件波形图课程设计心得体会通过自动控制原理课程设计,加强了我们动手、思考和解决问题的能力。
这个方案使用了Matlab软件,使我们有掌握了一个软件的应用。
我觉得做课程设计同时也是对课本知识的巩固和加强,由于课本上的知识太多,平时课间的学习并不能很好的理解和运用各个原理的功能,而且考试内容有限,所以在这次课程设计过程中,我们了解了很多原理的功能。
