重庆中考25题二次函数题专练
2022年重庆中考数学25题专题复习二次函数综合题平移基础类

2022级重庆中考数学25题专题复习二次函数综合题平移基础类1.如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.(1)线段OA所在直线的函数解析式是______;(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.2.如图1,已知直线l:y=-x+2与y轴交于点A,抛物线y=(x-1)2+m也经过点A,其顶点为B,将该抛物线沿直线l平移使顶点B落在直线l的点D处,点D的横坐标n(n >1).(1)求点B的坐标;(2)平移后的抛物线可以表示为______(用含n的式子表示);(3)若平移后的抛物线与原抛物线相交于点C,且点C的横坐标为a.①请写出a与n的函数关系式.②如图2,连接AC,CD,若∠ACD=90°,求a的值.3. 如图,在平面直角坐标系中,抛物线y =√33x 2-2√33x -√3与x 轴交于A 、B 两点(点A 在点B的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,点E (4,n )在抛物线上.(1)求直线AE 的解析式;(2)点P 为直线CE 下方抛物线上的一点,连接PC ,PE .当△PCE 的面积最大时,求P 点坐标?(3)点G 是线段CE 的中点,将抛物线y =√33x 2-2√33x -√3沿x 轴正方向平移得到新抛物线y ′,y ′经过点D ,y ′的顶点为点F .在新抛物线y ′的对称轴上,是否存在点Q ,使得△FGQ 为等腰三角形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.4. 如图,已知二次函数y =ax 2+bx +3(a ≠0)的图象经过点A (3,0),B (4,1),且与y轴交于点C ,连接AB 、AC 、BC . (1)求此二次函数的关系式;(2)判断△ABC 的形状;若△ABC 的外接圆记为⊙M ,请直接写出圆心M 的坐标; (3)若将抛物线沿射线BA 方向平移,平移后点A 、B 、C 的对应点分别记为点A 1、B 1、C 1,△A 1B 1C 1的外接圆记为⊙M 1,是否存在某个位置,使⊙M 1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.5.如图,已知抛物线C1:y=ax2+4ax+4a-5的顶点为D,与x轴相交于A、B两点(点A在点B的左边),且AB=6.(1)求抛物线C1的解析式及顶点D的坐标;x沿y轴向下平移m个单位(m>0),若平移后的直线与抛物线C1(2)将直线y=-13相交于点M、N(点M在点N的左边),且MN=√10,求m的值;(3)点P是x轴正半轴上一点,将抛物线C1绕点P旋转180°后得到抛物线C2,抛物线C2的顶点为C,与x轴相交于E、F两点(点E在F的左边),当以点D、C、F为顶点的三角形是直角三角形时,求点C的坐标.6.如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3)(1)求此抛物线解析式;(2)在抛物线上存在点D,使点D到直线AC的距离是√10,求点D的坐标;(3)如图2,将原抛物线向左平移1个单位,得到新抛物线C1,若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m 翻折交新抛物线C1于N,过Q作QS∥y轴,求证:QS必定平分MN.7.如图,抛物线C:y=ax2+bx+3与x轴的两个交点坐标为A(-3,0),B(-1,0).(Ⅰ)求抛物线C的解析式;(Ⅱ)设抛物线C的顶点为M,直线y=-2x+9与y轴交于点E,交直线OM于点F.现保持抛物线C的形状和开口方向,使顶点沿直线OM移动(O为坐标原点).在平移过程中,当抛物线与线段EF(含端点E、F)只有一个公共点时,求它的顶点横坐标的值或取值范围;(Ⅲ)将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于M,N两点.问在y轴的负半轴上是否存在点P,使△PMN的内心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2).(1)探究与猜想:若A(1,y a)、B(0,y b)、C(-1,y c)三点均在C1上,连接BC,作AE∥BC交抛物线C1于E.①探究,取a=1,则点E的坐标为______.②猜想:当a值变化时,E点总在直线______上,验证你的猜想.(2)如图2,若a=1,将抛物线C1先向右平移3个单位,再向下平移4个单位得到抛物线C2,C2交x轴于M,交y轴于N,直线y=kx-9交抛物线C2于P,Q,当PM∥QN时,求k的值.9.在平面直角坐标系中,已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a>0),且经过点(0,1).(1)求a的值;(2)如图1,将抛物线C1向下平移h(h>0)个单位长度得到抛物线C2,过点M(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A、B、C、D四点,且A、C两点关于y轴对称.①点G在抛物线C1上,当m为何值时,四边形APCG是平行四边形?②如图2,若抛物线C1的对称轴与抛物线C2交于点Q,试证明:在M点的运动过程中,MC PQ =34恒成立.10.如图,已知抛物线y=12x2+bx+c与x轴交于A(-3,0),B两点,四边形ABCD是边长为4的正方形,且抛物线的顶点E落在过B的直线l上.(1)求顶点E的坐标;(2)将抛物线沿着射线EB方向平移,使顶点仍落在直线l上,且平移后的抛物线过点C,求平移后抛物线的解析式.11.如图1,抛物线C1:y=ax2-2x+3与x轴交于A、B两点(点A在点B左边),与y轴交于C点,B(1,0),第二象限内有一点P在抛物线C1上运动,OP交线段AC于点E.(1)求抛物线C1的解析式及点A坐标;(2)若PE:OE=2:3,求P点坐标;(3)如图2,将抛物线C1向右平移,使平移后的摊物线C2的顶点D在y轴上,P是抛物线C2在第二象限图象上的动点,作P关于y轴的对称点P′,连接PO并延长交抛物线C2于点Q,连接QP′并延长交y轴于点N,求证:ND=OD.12.在平面直角坐标系中,已知抛物线y=-1x2+bx+c(b,c为常数)的顶点为P,等腰直角2三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,取BC的中点N,连接NP,BQ,试探究PQ是否存在最大值?若存在,求出该最大值;NP+BQ若不存在,请说明理由.13.如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-1)2为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N(1)求出抛物线的表达式及直线BC的表达式(2)在点D运动的过程中,点FN的值最大时,在线段BC上是否存在一点H,使得△FNH 与△ABC相似,如果存在,求出此时H点的坐标(3)当DF=4时,连接DC,四边形ABCD先向上平移一定单位长度后,使点D落在x 轴上,然后沿x轴向左平移n(1<n<4)个单位长度,用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S(直接写出结果)14.如图所示,已知二次函数y=x2-3x+2的图象l1的顶点为点D,与x轴的交点为点A、E(点A位于点E的左侧),与y轴的交点为B.连接AB,将△ABO绕点A顺时针旋转90°后,点B落到点C的位置,得到△ACF.(1)如图①,求点C的坐标;(2)如图②,将二次函数y=x2-3x+2的图象l1沿y轴向下平移后,得到的二次函数y=ax2+bx+c的图象l2经过点C、顶点为D1、与y轴的交点为B1,连接DD1.①求二次函数y=ax2+bx+c的解析式;②点N为平移后得到的二次函数图象l2上的动点,点N的坐标为(n,m),且n>0.是否存在这样的点N,使△NBB1的面积是△NDD1面积的2倍,若存在,求点N的坐标;若不存在,请说明理由.15. 如图,在平面直角坐标系中,抛物线y =-√33x 2+bx +c 与x 轴交于B 、C 两点(点B 在点C的左侧),与y 轴交于点A ,抛物线的顶点为D ,B (-3,0),A (0,√3) ((1)求抛物线解析式及D 点坐标;(2)如图1,P 为线段OB 上(不与O 、B 重舍)一动点,过点P 作y 轴的平行线交线段AB 于点M ,交抛物线于点N ,点N 作NK ⊥BA 交BA 于点K ,当△MNK 与△MPB 的面积相等时,在X 轴上找一动点Q ,使得12CQ +QN 最小时,求点Q 的坐标及12CQ +QN 最小值;(3)如图2,在(2)的条件下,将△ODN 沿射线DN 平移,平移后的对应三角形为△O ′D ′N ′,将△AOC 绕点O 逆时针旋转到A 1OC 1的位置,且点C 1恰好落在AC 上,△A 1D ′N ′是否能为等腰三角形,若能求出N ′的坐标,若不能,请说明理由.16.在平面直角坐标系xOy中,抛物线M:y=ax2-4ax-5a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l与抛物线M交于另一点D,且D点的横坐标为6.(1)求A、B两点的坐标及抛物线的对称轴.(2)若点E是直线L上方抛物线上的动点,且△ADE的面积的最大值为49,求a的值.(3)将抛物线平移到顶点与原点重合,过点F(0,-2)的直线与平移后的抛物线交于点G、H.若∠GOH=90°,△GOH的面积为4√2,求直线GH的解析式.第11页,共11页。
2022年重庆中考数学25题专题复习练习 二次函数综合题7周长最值类

2021-2022学年重庆中考数学25题专题复习二次函数综合题7周长最值类1.如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.(1)求抛物线的解析式;(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.2.综合与探究已知如图,ΔOAB为直角三角形,∠OBA=90°,∠AOB=30°,OA=4,点O与坐标原点重合,点A在x轴的正半轴上,点B在第一象限内,(1)求经过点O,A,B三点的抛物线的表达式并求出顶点C的坐标;(2)若点M为(1)中所求抛物线的对称轴上一动点,当ΔABM的周长最小时,判断ΔMBC的形状并说明理由。
(3)在(2)题的条件下,在抛物线的对称轴上是否存在点P,使ΔPOM为直角三角形,若存在,请直接写出所有符合条件的点P的坐标;若不存在,说明理由。
3.如图,边长为2的正方形ABCO的顶点O在原点,AO和CO在坐标轴上,点D的坐标为(2,1),连接AD,将△ABD绕点A顺时针方向旋转90°,与点D对应的点为F.(1)求点F的坐标;(2)求四边形ADCF的面积;(3)求过A,D,F三点的抛物线的解析式;(4)在抛物线的对称轴上是否存在点P,使得△APF的周长最短?若存在,请求出点P的坐标;若不存在,请说明理由.4.如图,抛物线y=x2-ax-3经过点A(4,5),与x轴正半轴交于B点,与y轴交于C点.(1)求直线AC的解析式;(2)设点P为直线AC下方抛物线上一点,连接PC、PA,当△PAC面积最大时,求点P的坐标;(3)在(2)的条件下,直线y=x+b过直线AC与x轴的交点D.设BC的中点为F,H是直线y=x+b 上一点,E是直线PC上一点,求△EHF周长的最小值.5.如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.(1)求抛物线的解析式;(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.6.如图,抛物线y=-x2+bx+c与x轴交于A(2,0),B(-4,0)两点.(1)求抛物线的解析式;(2)若一元二次方程-x2+bx+c-m=0有实数根,则m的取值范围为__________________;(3)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.7.如图1,抛物线y=ax2+bx+4交x轴于A、B两点(点A在点B的左侧),交y于点C,连接AC、BC,其中CO=BO=2AO。
2024重庆中考复习第25题-二次函数综合题

2024重庆中考复习第25题-二次函数综合题2024年重庆中考复习第25题为一道关于二次函数的综合题。
由于题目没有具体给出,我将为您提供一道关于二次函数的综合题,并给出一个详细的解答,希望能对您的复习有所帮助。
题目:已知函数f(x) = ax^2 + bx + c,其中a、b、c均为实数,且a ≠ 0。
已知f(1) = 0,f(3) = 0,f(4) = 6、求函数f(x)的表达式。
解答:根据题目已知条件,我们可以列出以下方程组:1)f(1)=0:a(1)^2+b(1)+c=0a+b+c=0--(1)2)f(3)=0:a(3)^2+b(3)+c=09a+3b+c=0--(2)3)f(4)=6:a(4)^2+b(4)+c=616a+4b+c=6--(3)现在我们有一个包含三个未知数(a,b,c)的方程组。
我们可以通过解这个方程组来求出函数f(x)的表达式。
首先,我们可以通过方程(1)和方程(2)的消元法得到一个新的方程。
(2)-(1)得:9a+3b+c-(a+b+c)=08a+2b=04a+b=0--(4)然后,我们可以通过方程(4)和方程(3)的消元法得到另一个新的方程。
(4)×4得:16a+4b=0将这个方程代入到方程(3)中,得到:16a+4b+c=6将16a+4b=0代入到上式,得到:c=6现在我们已经得到了a、b和c的值。
将这些值代入到函数f(x) =ax^2 + bx + c中,即可得到函数f(x)的表达式。
将a=-1、b=4和c=6代入到函数f(x)中,得到:f(x)=-x^2+4x+6所以,函数f(x)的表达式为f(x)=-x^2+4x+6以上就是针对2024年重庆中考复习第25题的一道关于二次函数的综合题的解答。
希望能对您的复习有所帮助。
如果您有任何其他问题,请随时提问。
重庆中考数学25题二次函数专项训练:平行四边形的存在性
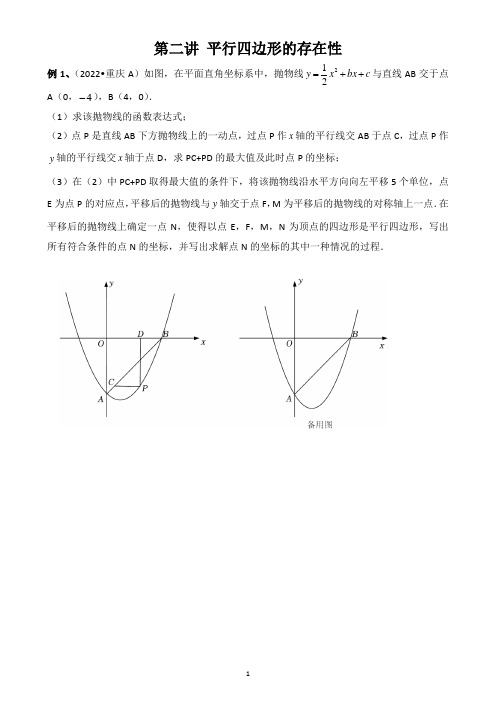
第二讲 平行四边形的存在性例1、(2022•重庆A )如图,在平面直角坐标系中,抛物线c bx x y ++=221与直线AB 交于点A (0,4-),B (4,0).(1)求该抛物线的函数表达式;(2)点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点C ,过点P 作y 轴的平行线交x 轴于点D ,求PC+PD 的最大值及此时点P 的坐标;(3)在(2)中PC+PD 取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,M 为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N ,使得以点E ,F ,M ,N 为顶点的四边形是平行四边形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.练习1、(2022•重庆B )如图,在平面直角坐标系中,抛物线c bx x y ++-=243与x 轴交于点A (4,0),与y 轴交于点B (0,3).(1)求抛物线的函数表达式;(2)点P 为直线AB 上方抛物线上一动点,过点P 作PQ⊥x 轴于点Q ,交AB 于点M ,求PM+56AM 的最大值及此时点P 的坐标; (3)在(2)的条件下,点P′与点P 关于抛物线c bx x y ++-=243的对称轴对称.将抛物线c bx x y ++-=243向右平移,使新抛物线的对称轴l 经过点A .点C 在新抛物线上,点D 在l 上,直接写出所有使得以点A 、P′、C 、D 为顶点的四边形是平行四边形的点D 的坐标,并把求其中一个点D 的坐标的过程写出来.练习2、如图1,抛物线)0(2≠++=a c bx ax y 与x 轴交于A (4-,0),B (1,0)两点,交y 轴于点C (0,3).(1)求抛物线的解析式;(2)如图2,点P 为直线AC 上方且抛物线对称轴左侧的抛物线上一点,过点P 作x 轴的平行线交抛物线于点D ,过点P 作y 轴的平行线交AC 于点H ,求PD+PH 的最大值及此时点P 的坐标;(3)把抛物线)0(2≠++=a c bx ax y 向右平移23个单位,再向上平移165个单位得新抛物线,在新抛物线对称轴上找一点M ,在新抛物线上找一点N ,直接写出所有使得以点A ,C ,M ,N 为顶点的四边形是平行四边形的点M 的坐标,并把求其中一个点M 的坐标的过程写出来.练习3、(选讲)在平面直角坐标系中,抛物线)0(32≠++=a bx ax y 与x 轴的交点为A(1-,0),B(3,0),与y 轴交于点C .(1)求抛物线的函数解析式;(2)如图1,连接AC ,BC ,P 是第一象限内抛物线上一动点,过点P 作PT ⊥x 轴交BC 于点T ,过点P 作PR//AC 与BC 交于点R .求△PRT 的周长的最大值以及此时点P 的坐标;(3)如图2,将抛物线沿CA 方向平移,使得新抛物线'y 刚好经过点A ,设M 为新抛物线上一点,N 为原抛物线对称轴上一点,当点B ,C ,M ,N 组成的四边形为平行四边形时,直接写出点N 的纵坐标.自我巩固1、(2021•重庆B )如图,在平面直角坐标系中,抛物线)0(42≠-+=a bx ax y 与x 轴交于点A (1-,0),B (4,0),与y 轴交于点C .(1)求该抛物线的解析式;(2)直线l 为该抛物线的对称轴,点D 与点C 关于直线l 对称,点P 为直线AD 下方抛物线上一动点,连接PA ,PD ,求⊥PAD 面积的最大值.(3)在(2)的条件下,将抛物线)0(42≠-+=a bx ax y 沿射线AD 平移24个单位,得到新的抛物线1y ,点E 为点P 的对应点,点F 为1y 的对称轴上任意一点,在1y 上确定一点G ,使得以点D ,E ,F ,G 为顶点的四边形是平行四边形,写出所有符合条件的点G 的坐标,并任选其中一个点的坐标,写出求解过程.。
重庆中考数学三轮冲刺第25题二次函数综合专题专训一

2021年重庆中考数学三轮冲刺第25题二次函数综合专题专训一1.综合与探究如图,抛物线y=ax2+bx−4与x轴交于A(−3,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线解析式:(2)抛物线对称轴上存在一点H,连接AH、CH,当|AH−CH|值最大时,求点H坐标:(3)若抛物线上存在一点P(m,n),mn>0,当S ABC=S ABP时,求点P坐标:(4)若点M是∠BAC平分线上的一点,点N是平面内一点,若以A、B、M、N为顶点的四边形是矩形,请直接写出点N坐标.2.如图,已知抛物线经过点A(-1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是线段AB上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.(1)求该抛物线所表示的二次函数的表达式;(2)在点P运动过程中,是否存在点Q,使得△BQM是直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)连接AC,将△AOC绕平面内某点H顺时针旋转90°,得到△A1O1C1,点A、O、C的对应点分别是点A、O1、C1、若△A1O1C1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A1的横坐标.3.如图,二次函数y=−x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点(1)求m的值及C点坐标;(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由(3)P为抛物线上一点,它关于直线BC的对称点为Q,当四边形PBQC为菱形时,求点P的坐标(直接写出答案);4.如图,抛物线y=ax2−2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).(1)求该抛物线的解析式;(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;(3)点Q是线段AB上的动点,过点Q作QE//AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P 不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.6.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC.点D 在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1)求b、c的值;(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F 的坐标;(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.7.如图1,抛物线y=ax2+bx+4过A(2,0)、B(4,0)两点,交y轴于点C,过点C作x 轴的平行线与抛物线上的另一个交点为D,连接AC、BC.点P是该抛物线上一动点,设点P 的横坐标为m(m>4).(1)求该抛物线的表达式和∠ACB的正切值;(2)如图2,若∠ACP=45°,求m的值;(3)如图3,过点A、P的直线与y轴于点N,过点P作PM⊥CD,垂足为M,直线MN与x 轴交于点Q,试判断四边形ADMQ的形状,并说明理由.8.已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.9.如图,抛物线y=−x2+bx+c交X轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3 .图①图②(1)求抛物线的函数表达式及其顶点C的坐标;(2)如图①,点P(m,0)是线段AO上的一个动点,其中−3<m<0,作直线DP⊥x轴,交直线AB于D,交抛物线于E,作EF∥X轴,交直线AB于点F,四边形DEFG为矩形.设矩形DEFG的周长为L,写出L与m的函数关系式,并求m为何值时周长L最大;(3)如图②,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形是以AB为腰的等腰三角形.若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.10.如图,抛物线y=ax2+bx+c经过点A(2,﹣3),且与x轴交点坐标为(﹣1,0),(3,0)(1)求抛物线的解析式;(2)在直线AB下方抛物线上找一点D,求出使得△ABD面积最大时点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.11.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线上的一个动点,求使△BPC为直角三角形的点P的坐标.(直接写出)12.综合与探究如图,已知抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C.其顶点为D,对称轴是直线l,且与x轴交于点H.(1)求点A,B,C,D的坐标;(2)若点P是该抛物线对称轴l上的﹣个动点,求△PBC周长的最小值;(3)若点E是线段AC上的一个动点(E与A.C不重合),过点E作x轴的垂线,与抛物线交于点F,与x轴交于点G.则在点E运动的过程中,是否存在EF=2EG?若存在,求出此时点E的坐标;若不存在,请说明理由.13.如图1,在平面直角坐标系xOy 中,直线l :y =34x +π与x 轴、y 轴分别交于点A 和点B (0,﹣1),抛物线y =12x 2+bx +c 经过点B ,且与直线l 的另一个交点为C (4,n ).(1)求n 的值和抛物线的解析式;(2)点D 在抛物线上,且点D 的横坐标为t (0<t <4).DE ∥y 轴交直线l 于点E ,点F 在直线l 上,且四边形DFEG 为矩形(如图2).若矩形DFEG 的周长为p ,求p 与t 的函数关系式以及p 的最大值;(3)M 是平面内一点,将△AOB 绕点M 沿逆时针方向旋转90°后,得到△A 1O 1B 1,点A 、O 、B 的对应点分别是点A 1、O 1、B 1.若△A 1O 1B 1的两个顶点恰好落在抛物线上,请直接写出点A 1的横坐标.14.如图,抛物线y=14x 2+ 14x+c 与x 轴的负半轴交于点A ,与y 轴交于点B ,连结AB ,点C(6,152)在抛物线上,直线AC 与y 轴交于点D.(1)求c 的值及直线AC 的函数表达式;(2)点P 在x 轴正半轴上,点Q 在y 轴正半轴上,连结PQ 与直线AC 交于点M ,连结MO 并延长交AB 于点N ,若M 为PQ 的中点. ①求证:△APM ∽△AON ;②设点M 的横坐标为m ,求AN 的长(用含m 的代数式表示).15.如图,抛物线y=x2﹣4x﹣5与x轴交于A,B两点(电B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.(1)求A,B,C三点的坐标及抛物线的对称轴.(2)如图1,点E(m,n)为抛物线上一点,且2<m<5,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,求四边形EHDF周长的最大值.(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,B,C为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.16.如图,抛物线y=13x2−13x−4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P 作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.。
重庆中考二次函数(25题)专练

1、(12分)如图,在平面直角坐标系中,四边形OABC 是平行四边形,A 、B 两点的坐标分别是()3,0A ,()0,2B 。
若抛物线2y ax bx c =++经过点A 、B 、C ,且与x 轴的另一个交点为点D 。
(1)求抛物线的解析式; (2)若点P 是第二象限内抛物线上一点,直线OP 将四边形OBCD 的面积分成1:2两部分。
求出此时点P 的坐标;(3)设点Q 是抛物线对称轴上的一个动点,当点Q 的坐标为何值时QD QC +最小?并求出最小值。
19.如图1,抛物线y=x 2-4x+c 交x 轴于点A 和B (-1,0)交y 轴于点C ,且抛物线的对称轴交x 轴于点D(1)求这个抛物线的解析式;(2)若点E 在抛物线上,且位于第四象限,当四边形ADCE 面积最大时,求点E 的坐标; (3)如图2,在抛物线上是否存在这样的点P ,使△PAB 中的内角中有一边与x 轴所夹锐角的正切值为21?若存在,求出点P 的坐标;若不存在,请说明理由.20.如图,抛物线y=-21x 2+bx+c 与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于点C ,对称轴为直线x=21,OA=2,OD 平分∠BOC 交抛物线于点D (点D 在第一象限).(1)求抛物线的解析式和点D 的坐标;(2)在抛物线的对称轴上,是否存在一点P ,使得△BPD 的周长最小?若存在,请求出点P 的坐标;若不存在,请说明理由.(3)点M 是抛物线上的动点,在x 轴上是否存在点N ,使A 、D 、M 、N 四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M 点坐标;如果不存在,请说明理由.28. 如图①,抛物线2y ax bx c =++与x 轴相交于O A 、两点直线3y x =-+与y 轴交于B 点,与该抛物线交于,A D 两点,已知点D 横坐标为-1. (1)求这条抛物线的解析式;(2)如图①,在线段OA 上有一动点H (不与O A 、重合),过H 作x 轴的垂线分别交AB 于P 点,交抛物线于Q 点,若x 轴把POQ ∆分成两部分的面积之比为1:2,请求出H 点的坐标;(3)如图②,在抛物线上是否存在点C ,使ABC ∆为直角三角形?若存在,求出点C 的坐标;若不存在,请说明理由.26.已知:二次函数y=ax 2﹣2x+c 的图象与x 于A 、B ,A 在点B 的左侧),与y 轴交于点C ,对称轴是直线x=1,平移一个单位后经过坐标原点O (1)求这个二次函数的解析式; (2)直线交y 轴于D 点,E 为抛物线顶点.若∠DBC=α,∠CBE=β,求α﹣β的值;(3)在(2)问的前提下,P 为抛物线对称轴上一点,且满足PA=PC ,在y 轴右侧的抛物线上是否存在点M ,使得△BDM 的面积等于PA 2?若存在,求出点M 的坐标;若不存在,请说明理由.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式.(2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?26. 如图,直线434+-=x y 与x 轴交于点A ,与y 轴交于点C ,已知二次函数的图象经过点A 、C 和点()0,1-B .(1)求该二次函数的关系式;(2)设该二次函数的图象的顶点为M ,求四边形AOCM 的面积; (3)有两动点D 、E 同时从点O 出发,其中点D 以每秒23个单位长度的速度沿折线OAC 按O →A →C 的路线运动,点E 以每秒4个单位长度的速度沿折线OCA 按O →C →A 的路线运动,当D 、E 两点相遇时,它们都停止运动.设D 、E 同时从点O 出发t 秒时,ODE ∆的面积为S .①请问D 、E 两点在运动过程中,是否存在DE ∥OC ,若存在,请求出此时t 的值;若不存在,请说明理由;②请求出S 关于t 的函数关系式,并写出自变量t 的取值范围; ③设0S 是②中函数S 的最大值,那么0S = .26.如图,在平面直角坐标系中,一抛物线的对称轴为直线1=x ,与y 轴负半轴交于C 点,与x 轴交于A 、B 两点,其中B 点的坐标为(3,0),C 点坐标为(0,-3). ⑴求此抛物线的解析式;⑵若点G (2,-3)是该抛物线上一点,点E 是直线AG 下方的抛物线上一动点,当点E 运动到什么位置时,△AEG 的面积最大?求出此时E 点的坐标和△AEG 的最大面积.⑶若平行于x 轴的直线与该抛物线交于M 、N 两点(其中点M 在点N 的右侧),在x 轴上是否存在点Q ,使△MNQ25.如图,在平面直角坐标系中,直线122y x =+与坐标轴分别交于A 、B 两点,过A 、B 两点的抛物线为2y x bx c =-++,点E 为第二象限内抛物线上一动点,连接AE,BE.(1)求抛物线的解析式;(2)当ABE ∆面积最大时,求点E 的坐标,并求出此时ABE ∆的面积; (3)当EAB OAB ∠=∠时,求点E 的坐标.26.已知:矩形ABCD 中,M 为BC 边上一点, AB=BM=10,MC=14,如图1,正方形EFGH 的顶点E 和点B 重合,点F 、G 、H 分别在边AB 、AM 、BC 上.如图2,P 为对角线AC 上一动点,正方形EFGH 从图1的位置出发,以每秒1个单位的速度沿BC 向点C 匀速移动;同时,点P 从C 点出发,以每秒1个单位的速度沿CA向点A 匀速移动.当点F 到达线段AC 上时,正方形EFGH 和点P 同时停止运动.设运动时间为t 秒,解答下列问题:(1)在整个运动过程中,当点F 落在线段AM 上和点G 落在线段AC 上时,分别求出对应t 的值; (2)在整个运动过程中,设正方形EFGH 与AMC ∆重叠部分面积为S,请直接写出S 与t 之间的函数关系式以及自变量t 的取值范围;26.已知:如图,抛物线)0(22≠+-=a c ax ax y 与y 轴交于点C (0,4),与x 轴交于点A 、B ,点A 的坐标为(4,0)。
重庆中考数学第25题二次函数综合专题训练3

2021级重庆中考数学 第25题二次函数综合专题训练31.如图1,直线l :y =34x +m 与x 轴、y 轴分别交于点A 和点B (0,﹣1),抛物线y =12x 2+bx +c 经过点B ,与直线l 的另一个交点为C (4,n ). (1)求n 的值和抛物线的解析式;(2)点D 在抛物线上,DE ∥y 轴交直线l 于点E ,点F 在直线l 上,且四边形DFEG 为矩形(如图2),设点D 的横坐标为t (0<t <4),矩形DFEG 的周长为p ,求p 与t 的函数关系式以及p 的最大值;(3)将△AOB 绕平面内某点M 旋转90°或180°,得到△A 1O 1B 1,点A 、O 、B 的对应点分别是点A 1、O 1、B 1.若△A 1O 1B 1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A 1的横坐标.2.如图,顶点为C 的抛物线y=ax 2+bx (a >0)经过点A 和x 轴正半轴上的点B ,连接OC 、OA 、AB ,已知OA=OB=2,∠AOB=120°.(1)求这条抛物线的表达式;(2)过点C 作CE ⊥OB ,垂足为E ,点P 为y 轴上的动点,若以O 、C 、P 为顶点的三角形与△AOE 相似,求点P 的坐标;(3)若将2.的线段OE 绕点O 逆时针旋转得到OE′,旋转角为α(0°<α<120°),连接E′A 、E′B ,求E′A+12E′B 的最小值.3.如图,抛物线y=﹣x2+4x+5与x轴,y轴分别交于A,B,C三点.(1)请直接写出A,B,C三点坐标:A(_____,_____)、B(_____,______)、C(______,______)(2)若⊙M过A、B、C三点,求圆心M的坐标,并求⊙M的面积;(3)在2.的条件下,在抛物线上是否存在点N,使得由A,C,M,N四点构成的四边形为平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.4.如图①,直线L:y=mx+n(m < 0,n > 0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做L的关联抛物线,而L叫做P的关联直线.x2−x+4,则L表示的(1)若L:y=-x+2,则P表示的函数解析式为______;若P:y=−12函数解析式为_______.(2)如图②,若L:y=-3x+3,P的对称轴与CD相交于点E,点F在L上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;(3)如图③,若L:y=mx+1,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=√5,求出L,P表示的函数解析式.65.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=-1 上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标.6.如图,已知抛物线y=ax2+3ax−4a与x轴负半轴相交于点A,与y轴正半轴相交于点B,OB=OA,直线l过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.(1)求抛物线的解析式;(2)若抛物线与x轴正半轴交于点F,设点D的横坐标为x,四边形F AEB的面积为S,请写出S与x的函数关系式,并判断S是否存在最大值,如果存在,求出这个最大值;并写出此时点E的坐标;如果不存在,请说明理由.(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D的坐标;若不存在,说明理由.7.如图,已知抛物线的顶点坐标是(2,﹣1),且经过点A(5,8)(1)求该抛物线的解析式;(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;(3)设点P是x轴任一点,连接AP、BP.试求当AP+BP取得最小值时点P的坐标.8.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y =x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标;(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.9.如图,抛物线y=ax2+bx+c为x轴的一交点为A(﹣6,0),与y轴的交点为C(0,3),且经过点G(﹣2,3).(1)求抛物线的表达式.(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值.(3)若点B是抛物线与x轴的另一定点,点D、M在线段AB上,点N在线段AC上,∠DCB=∠CDB,CD是MN的垂直平分线,求点M的坐标.x+π与x轴、y轴分别交于点A和点10.如图1,在平面直角坐标系xOy中,直线l:y=34x2+bx+c经过点B,且与直线l的另一个交点为C(4,n). B(0,﹣1),抛物线y=12(1)求n的值和抛物线的解析式;(2)点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.11.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.(1)求抛物线及直线AC的函数关系式;(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM 周长的最小值;若不存在,请说明理由.12.如图,抛物线y=﹣x2﹣2x+3 的图象与x 轴交于A、B 两点(点A 在点B 的左边),与y轴交于点C,点D 为抛物线的顶点.(1)求点A、B、C 的坐标;(2)点M(m,0)为线段AB 上一点(点M 不与点A、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E,与抛物线交于点P,过点P 作PQ∥AB 交抛物线于点Q,过点Q 作QN⊥x 轴于点N,可得矩形PQNM.如图,点P 在点Q 左边,试用含m 的式子表示矩形PQNM 的周长;(3)当矩形PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积;(4)在(3)的条件下,当矩形PMNQ 的周长最大时,连接DQ,过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G(点G 在点F 的上方).若FG=2√2DQ,求点F 的坐标.x2+bx+c经过点A(﹣2,0),点B(0,4).13.如图,抛物线y=−12(1)求这条抛物线的表达式;(2)P是抛物线对称轴上的点,联结AB、PB,如果∠PBO=∠BAO,求点P的坐标;(3)将抛物线沿y轴向下平移m个单位,所得新抛物线与y轴交于点D,过点D作DE∥x轴交新抛物线于点E,射线EO交新抛物线于点F,如果EO=2OF,求m的值.14.如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.(1)求该抛物线所表示的二次函数的表达式;(2)已知点F(0,1),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边2形?15.如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).(1)求抛物线的解析式;(2)若点M是抛物线上在x轴下方的动点,过M作MN//y轴交直线BC于点N,求线段MN的最大值;(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.16.已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A、B.(1)A点坐标,B点坐标,抛物线解析式;(2)点C(m,0)在线段OA上(点C不与A、O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=√2AD,求m的值;(3)点M在抛物线上,点N在抛物线的对称轴上,在2.的条件下,是否存在以点D、B、M、N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.。
最新重庆中考数学25题专题及答案
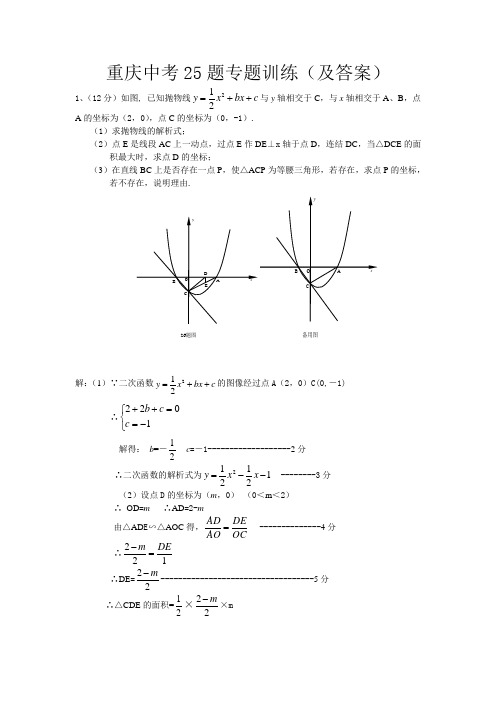
重庆中考25题专题训练(及答案)1、(12分)如图, 已知抛物线c bx x y ++=221与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1).(1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.解:(1)∵二次函数c bx x y ++=221的图像经过点A (2,0)C(0,-1) ∴⎩⎨⎧-==++1022c c b解得: b =-21c =-1-------------------2分 ∴二次函数的解析式为121212--=x x y --------3分(2)设点D 的坐标为(m ,0) (0<m <2)∴ OD =m ∴AD =2-m 由△AD E ∽△AOC 得,OCDEAO AD = --------------4分 ∴122DEm =- ∴DE =22m ------------------------------------5分∴△CDE 的面积=21×22m-×mABCxyo备用图ABCED xyo题图26=242m m +-=41)1(412+--m 当m =1时,△CDE 的面积最大∴点D 的坐标为(1,0)--------------------------8分 (3)存在 由(1)知:二次函数的解析式为121212--=x x y 设y=0则1212102--=x x 解得:x 1=2 x 2=-1 ∴点B 的坐标为(-1,0) C (0,-1)设直线BC 的解析式为:y =kx +b∴ ⎩⎨⎧-==+-10b b k 解得:k =-1 b =-1∴直线BC 的解析式为: y =-x -1在Rt △AOC 中,∠AOC=900OA=2 OC=1 由勾股定理得:AC=5 ∵点B(-1,0) 点C (0,-1) ∴OB=OC ∠BCO=450①当以点C 为顶点且PC=AC=5时,设P(k , -k -1)过点P 作PH ⊥y 轴于H ∴∠HCP=∠BCO=450CH=PH=∣k ∣ 在Rt △PCH 中k 2+k 2=()25 解得k 1=210, k 2=-210 ∴P 1(210,-1210-) P 2(-210,1210-)---10分 ②以A 为顶点,即AC=AP=5 设P(k , -k -1)过点P 作PG ⊥x 轴于GAG=∣2-k ∣ GP=∣-k -1∣ 在Rt △APG 中 AG 2+PG 2=AP 2 (2-k )2+(-k -1)2=5 解得:k 1=1,k 2=0(舍)∴P 3(1, -2) ----------------------------------11分③以P 为顶点,PC=AP 设P(k , -k -1) 过点P 作PQ ⊥y 轴于点Q PL ⊥x 轴于点L∴L(k ,0)∴△QPC 为等腰直角三角形 PQ=CQ=k 由勾股定理知 CP=PA=2k∴AL=∣k -2∣, PL=|-k -1| 在Rt △PLA 中(2k)2=(k -2)2+(k +1)2 解得:k =25∴P 4(25,-27) ------------------------12分2、(本题满分12分)已知抛物线2y x bx c =++交x 轴于A (1,0)、B (3,0)两点,交y 轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴;(2)连接BC ,过点O 作直线OE ⊥BC 交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形;(3)抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求点Q 的坐标;若不存在,请说明理由.2、(1)求出:4-=b ,3=c ,抛物线的对称轴为:x=2(2) 抛物线的解析式为342+-=x x y ,易得C 点坐标为(0,3),D 点坐标为(2,-1) 设抛物线的对称轴DE 交x 轴于点F ,易得F 点坐标为(2,0),连接OD ,DB ,BE∵∆OBC 是等腰直角三角形,∆DFB 也是等腰直角三角形,E 点坐标为(2,2), ∴∠BOE= ∠OBD=45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分 在ODF Rt ∆和EBF Rt ∆中,OD=5122222=+=+DF OF ,BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ………………7分(3) 存在, ………………8分由题意得:29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分 设点Q 坐标为(x ,y ), 由题意得:y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时,即1342=+-x x ,∴ 221+=x , 222-=x ,∴Q 点坐标为(2+2,1)或(2-2,1) ………………11分 当y=-1时,即1342-=+-x x , ∴x=2, ∴Q 点坐标为(2,-1)综上所述,抛物线上存在三点Q 1(2+2,1),Q 2 (2-2,1) ,Q 3(2,-1) 使得OBQ S 三角形=ODBE S 四边形31. ………………12分3、(11分)如图,已知抛物线(1)233(0)y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .EFQ 1 Q 3Q 2(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 解:(1)抛物线2(1)33(0)y a x a =-+≠经过点(20)A -,,309333a a ∴=+∴=-························· 1分 ∴二次函数的解析式为:232383333y x x =-++ ············· 3分 (2)D 为抛物线的顶点(133)D ∴,过D 作DN OB ⊥于N ,则33DN =, 2233(33)660AN AD DAO =∴=+=∴∠=,° ·············· 4分OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形 66(s)OP t ∴=∴= ············· 5分 ②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH =(如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =)55(s)OP DH t ∴=== ·························· 6分 ③当PD OA =时,四边形DAOP 是等腰梯形 26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. 7分yMCDPxyM CDPQO AB N E H(3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形 则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则32PE t =···················· 8分 113633(62)222BCPQ S t t ∴=⨯⨯-⨯-⨯=233633228t ⎛⎫-+ ⎪⎝⎭ ··························· 9分 当32t =时,BCPQ S 的面积最小值为6338··················· 10分 ∴此时3339333324444OQ OP OE QE PE ==∴=-==,=, 222233933442PQ PE QE ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭ ··············· 11分4.(本小题满分13分)如图,抛物线经过(40)(10)(02)A B C -,,,,,三点. (1)求出抛物线的解析式;(2)P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标. 解:(1)该抛物线过点(02)C -,,∴可设该抛物线的解析式为22y ax bx =+-. 将(40)A ,,(10)B ,代入, O xyAB C4 1 2-(第26题图)得1642020a b a b .+-=⎧⎨+-=⎩,解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩,∴此抛物线的解析式为215222y x x =-+-. ··············· (3分)(2)存在. ······························ (4分) 如图,设P 点的横坐标为m ,则P 点的纵坐标为215222m m -+-,当14m <<时,4AM m =-,215222PM m m =-+-.又90COA PMA ∠=∠=°, ∴①当21AM AO PM OC ==时, APM ACO △∽△,即21542222m m m ⎛⎫-=-+- ⎪⎝⎭.解得1224m m ==,(舍去),(21)P ∴,. ················ (6分) ②当12AM OC PM OA ==时,APM CAO △∽△,即2152(4)222m m m -=-+-. 解得14m =,25m =(均不合题意,舍去)∴当14m <<时,(21)P ,. ······················ (7分)类似地可求出当4m >时,(52)P -,. ·················· (8分) 当1m <时,(314)P --,. 综上所述,符合条件的点P 为(21),或(52)-,或(314)--,. ········ (9分)(3)如图,设D 点的横坐标为(04)t t <<,则D 点的纵坐标为215222t t -+-. 过D 作y 轴的平行线交AC 于E . 由题意可求得直线AC 的解析式为122y x =-. ·············· (10分) O xy A BC41 2-(第26题图)D PM EE ∴点的坐标为122t t ⎛⎫- ⎪⎝⎭,.2215112222222DE t t t t t ⎛⎫∴=-+---=-+ ⎪⎝⎭. ············· (11分)22211244(2)422DAC S t t t t t ⎛⎫∴=⨯-+⨯=-+=--+ ⎪⎝⎭△.∴当2t =时,DAC △面积最大.(21)D ∴,.5.如图,二次函数的图象经过点D(0,397),且顶点C 的横坐标为4,该图象在x 轴上截得的线段AB 的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P ,使PA+PD 最小,求出点P 的坐标;⑶在抛物线上是否存在点Q ,使△QAB 与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由.⑴设二次函数的解析式为:y=a(x-h)2+k∵顶点C 的横坐标为4,且过点(0,397)∴y=a(x-4)2+k k a +=16397 ………………①又∵对称轴为直线x=4,图象在x 轴上截得的线段长为6 ∴A(1,0),B(7,0) ∴0=9a+k ………………② 由①②解得a=93,k=3-∴二次函数的解析式为:y=93(x-4)2-3⑵∵点A 、B 关于直线x=4对称 ∴PA=PB∴PA+PD=PB+PD ≥DB∴当点P 在线段DB 上时PA+PD 取得最小值 ∴DB 与对称轴的交点即为所求点P 设直线x=4与x 轴交于点M∵PM ∥OD ,∴∠BPM=∠BDO ,又∠PBM=∠DBO ∴△BPM ∽△BDO∴BO BM DO PM = ∴3373397=⨯=PM ∴点P 的坐标为(4,33)⑶由⑴知点C(4,3-),又∵AM=3,∴在Rt △AMC 中,cot ∠ACM=33,∴∠ACM=60o,∵AC=BC ,∴∠ACB=120o①当点Q在x轴上方时,过Q作QN⊥x轴于N如果AB=BQ,由△ABC∽△ABQ有BQ=6,∠ABQ=120o,则∠QBN=60o∴QN=33,BN=3,ON=10,此时点Q(10,33),如果AB=AQ,由对称性知Q(-2,33)②当点Q在x轴下方时,△QAB就是△ACB,此时点Q的坐标是(4,3-),经检验,点(10,33)都在抛物线上3)与(-2,3综上所述,存在这样的点Q,使△QAB∽△ABC点Q的坐标为(10,3-).3)或(-2,33)或(4,36、(12分) 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标;(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.解:(1)设该抛物线的解析式为c bx ax y ++=2,由抛物线与y 轴交于点C (0,-3),可知3-=c .即抛物线的解析式为32-+=bx ax y . ………………………1分把A (-1,0)、B (3,0)代入, 得30,9330.a b a b --=⎧⎨+-=⎩解得2,1-==b a .∴ 抛物线的解析式为y = x 2-2x -3. ……………………………………………3分 ∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分 说明:只要学生求对2,1-==b a ,不写“抛物线的解析式为y = x 2-2x -3”不扣分. (2)以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分 理由如下:过点D 分别作x 轴、y 轴的垂线,垂足分别为E 、F.在Rt △BOC 中,OB=3,OC=3,∴ 182=BC . …………………………6分 在Rt △CDF 中,DF=1,CF=OF-OC=4-3=1,∴ 22=CD . …………………………7分 在Rt △BDE 中,DE=4,BE=OB-OE=3-1=2,∴ 202=BD . …………………………8分∴ 222BD CD BC =+, 故△BCD 为直角三角形. …………………………9分 (3)连接AC ,可知Rt △COA ∽ Rt △BCD ,得符合条件的点为O (0,0). ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1,可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD ,求得符合条件的点为)31,0(1P . …………………………………………11分 过C 作CP 2⊥AC 交x 轴正半轴于P 2,可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD , 求得符合条件的点为P 2(9,0). …………………………………………12分 ∴符合条件的点有三个:O (0,0),)31,0(1P ,P 2(9,0).7、如图,抛物线21y ax bx =++与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C .(1)求抛物线的解析式;(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;(3)在x 轴下方的抛物线上是否存在一点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为顶点的三角形与△BCD 相似?若存在,则求出点M 的坐标;若不存在,请说明理由.解:(1)解:(1)把A (1,0)- B (1,0)代入21y ax bx =++得:1010a b a b -+=⎧⎨++=⎩解得:10a b =-⎧⎨=⎩ 21y x ∴=-+………………………………………………………………………3分(2)令0x =,得1y = ∴()0,1C ……………………………………………4分∵OA=OB=OC=1 ∴∠BAC=∠ACO=∠BCO=∠ABC =45 ∵BD ∥CA , ∴∠AB D=∠BA C 45=︒过点D 作DE ⊥x 轴于E ,则∆BDE 为等腰直角三角形 令OE k = ()0k >,则1DE k =+ ∴(),1D k k --- ∵点D 在抛物线21y x ∴=-+上 ∴ ()211k k --=--+解得12k =,21k =-(不合题意,舍去) ()2,3D -- ∴DE=3(说明:先求出直线BD 的解析式,再用两个解析式联立求解得到点D 的坐标也可) ∴四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯=………………………………7分 (说明:也可直接求直角梯形ACBD 的面积为4)(3)存在这样的点M ……………………………………………………………………8分∵∠ABC=∠ABD=45 ∴∠DBC=90 ∵MN ⊥x 轴于点N , ∴∠ANM=∠DBC =90 在Rt △BOC 中,OB=OC=1 有BC=2 在Rt △DBE 中,BE=DE=3 有BD=32设M 点的横坐标为m ,则M ()2,1m m -+ ①点M 在y 轴左侧时,则1m <- (ⅰ) 当∆A MN ∽∆CDB 时,有AN MNBC BD=∵21,1AN m MN m =--=-即 211232m m ---=解得:1m =-(舍去) 22m =- 则()2,3M --(ⅱ) 当∆AMN ∽∆DCB 时,有AN MNBD BC=即211322m m ---=解得11m =-(舍去) 223m =(舍去)…………10分② 点M 在y 轴右侧时,则1m > (ⅰ) 当∆AMN ∽∆DCB 时,有AN MNBD BC=∵21,1AN m MN m =+=-∴ 211322m m +-=解得11m =-(舍去) 243m =∴47,39M ⎛⎫-⎪⎝⎭ (ⅱ) 当∆A MN ∽∆CDB 时,有AN MNBC BD=即 211232m m +-=解得:11m =-(舍去) 24m = ∴()4,15M -∴M 点的坐标为()()472,3,,,4,1539⎛⎫---- ⎪⎝⎭…………………………12分8、在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b )。
二次函数专题练习(重庆中考25题)

重庆中考复习25题专题训练一.解答题(共30小题)1.(2013•雅安)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.2.(2013•新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.3.(2013•湘潭)如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx﹣2的图象过C点.(1)求抛物线的解析式;(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.4.(2013•梧州)如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x轴交于点C.(1)求此抛物线的解析式.(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.5.(2013•威海)如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.(1)求抛物线的函数表达式;(2)设P为对称轴上一动点,求△APC周长的最小值;(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为.6.(2013•铜仁地区)如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C 是抛物线与x轴的另一个交点(与A点不重合).(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.7.(2013•泰安)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0)(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.。
重庆中考25题:二次函数
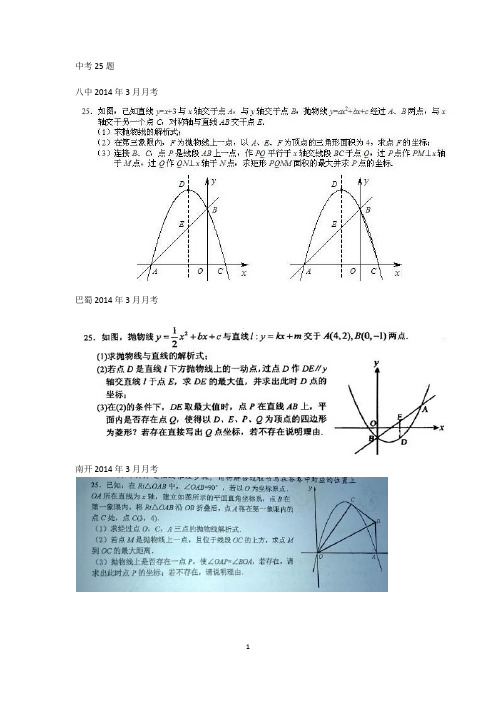
中考25题八中2014年3月月考巴蜀2014年3月月考南开2014年3月月考一中2013年3月月考2013-2014一中期末考试25.如图,在平面直角坐标系中,直线交轴于点,交轴于点,过、两点的抛物线交轴于另一点,点是抛物线的顶点.(1)求此抛物线的解析式.(2)点是直线上方的抛物线上一点,(不与点、重合),过点作轴的垂线交轴于点,交直线于点,作⊥于点.求出△的周长最大值; (3)在抛物线上是否存在除点D 以外的点M ,使得△ABM 与△ABD 的面积相等? 若存在,请求出此时点M 的坐标,若不存在,请说明理由.xoy 3+=x y x A y B A B 2y x bx c =-++x C D P AB A B P x x H AB F PG AB G PFG c bx ax y ++=22013-2014南开期末考试25.如图,已知抛物线的对称轴是直线x=4,顶点A 的纵坐标为2,点B(8,0)在此抛物线上。
(1)求此抛物线的解析式:(2)若此抛物线的对称轴与x 轴交于点C ,点D(m,n)为抛物线上一动点,过点D 作直线y=4的垂线,垂足为E 。
①用含n 的代数式表示CD 2,并猜想CD 2与DE 2之间的数量关系,请给出证明;②在此抛物线上是否存在点D ,使∠EDC =120°?如果存在,请求出D 点坐标:如果不存在,请说明理由。
巴蜀2013-2014期末考试25、如图,抛物线22y ax bx =++与x 轴交于A 、B 两点,点A 的坐标为()1,0-,抛物线的对称轴为直线 1.5x =,点M 为线段AB 上一点,过M 作x 轴的垂线交抛物线于P ,交过点A 的直线y x n =-+于点C 。
(1)求直线AC 及抛物线的解析式;(2)M 位于线段AB 的什么位置时,PC 最长,并求出此时P 点的坐标; (3)若在(2)的条件下,在x 轴上方的抛物线上是否存在点Q ,使23ABQ APB S S ∆∆=,求点Q 的坐标。
重庆中考25题典型例题(二次函数题)---重点中学考题

25. 重庆市巴蜀中学2012-2013学年度第二学期第一次定时作业如图,一次函数122y x =-+分别交y 轴、x 轴于A 、B 两点,抛物线2y x bx c =-++过A 、B 两点。
(1)求这个抛物线的解析式;(2)作垂直x 轴的直线x =t ,在第一象限交直线AB 于M ,交这个抛物线于N 。
求当t 取何值时,MN 有最大值?最大值是多少?(3)在(2)的情况下,以A 、M 、N 、D 为顶点作平行四边形,求第四个顶点D 的坐标。
22、重庆巴蜀中学2012级初三下第五次6月考试押题题卷 如图,在平面直角坐标系中,二次函数bx x y +-=223经过点O 、A 、B 三点,且A 点坐标为(4,0),B 的坐标为(m ,32),点C 是抛物线在第三象限的一点,且横坐标为-2 (1)求抛物线的解析式和直线BC 的解析式。
(2)直线BC 与 x 轴相交于点D ,求△OBC 的面积 AOCD 22题图xyB25.重庆市巴蜀中学2012-2013学年度第二学期第一次模拟考试 如图,抛物线y=ax 2+bx+c (a <0)与双曲线ky=x相交于点A ,B ,且抛物线经过坐标原点,点A 的坐标为(﹣2,2),点B 在第四象限内,过点B 作直线BC ∥x 轴,点C 为直线BC 与抛物线的另一交点,已知直线BC与x 轴之间的距离是点B 到y 轴的距离的4倍,记抛物线顶点为E . (1)求双曲线和抛物线的解析式; (2)计算△ABC 与△ABE 的面积;(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABE 的面积的8倍?若存在,请求出点D 的坐标;若不存在,请说明理由.22、重庆南开中学初2013级初三(下)3月月考如图,在平面直角坐标系中,直线()0y kx b k =+≠分别交双曲线()0my m x =≠于A 、B 两点,交x 轴于点D ,在x 轴上有一点()3,0C ,且5,4AD CD ==,4sin 5ADC ∠=,()3,B n -。
{word试卷}年重庆中考25题:二次函数专题练习(12月月考考试试题集)(仅供参考)

20XX年高中测试高中试题试卷科目:年级:考点:监考老师:日期:2021年重庆年中考25题二次函数专题练习(12月月考考试试题集)1(八中2021级初三上定时训练12)如图,二次函数21(0)2y x bx c a=++≠的图象与x轴相交于点A、B(A在B左侧),点A的坐标为(-2,0),与y轴正半轴交于点C,点D 在抛物线上,CD//x轴,且CD=6,(1)求抛物线的解析式;(2)如图①,点P为线段CD上方抛物线上一点,连接OP交CD于点E,点Q是线段AB上一点,求四边形PEQD面积的最大值,并求出此时点P的坐标;(3)如图②,抛物线上一点F的横坐标为2,直线CF交x轴于点G,点M为y轴右侧上一点,过点M作直线CF的垂线,垂足为Q,若∠MCN=∠BGC,直接写出点N的坐标.2(八中2021级初三定时训练11)如图1,抛物线2y ax bx c=++与x轴交于点A、B两点,与y轴交于点C,点D为抛物线的顶点,对称轴为直线x=2,已知经过点B、C两点的直线解析式为5 y x=-+(1)求此抛物线的解析式;(2)如图1,点E为直线BC上方抛物线上一点,过点E作EF⊥x轴于F,交BC于点M,作EG⊥BC于G,求△EGM周长的最大值,以及此时点E的坐标;(3)如图2,连接BD,将抛物线向右平移,使得新抛物线过原点,点P为直线BD上一点,在新抛物线上是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,请直接写出点Q坐标,若不存在,请说明理由.3(八中2020级初三第三次月考)如图在平面直角坐标系中,已知抛物线2(0)y ax bx c a =++≠交x 轴于A (-4,0),B (1,0),交y 轴于C (0,3)(1)求此抛物线解析式;(2)如图1,点P 为直线AC 上方抛物线上一点,过点P 作PQ ⊥x 轴于点Q ,再过点Q 作QR//AC 交y 轴于点R ,求PQ+QR 的最大值及此时点P 的坐标;(3)如图2,点E 在抛物线上,横坐标为-3,连接AE ,将线段AE 沿直线AC 平移,得到线段''A E ,连接'CE ,当△''A E C 为等腰三角形时,只写写出点'A 的坐标。
重庆中考数学25题二次函数专项训练之三角形的存在性

第一讲 三角形的存在性问题例1、如图,抛物线822++-=x x y 与x 轴交于A 、B 两点,过点A 的直线2+=x y 与抛物线交于点C ,与y 轴交于点D .(1)求△ABC 的面积;(2)若点P 为直线AC 上方抛物线上的动点,求点P 到直线AC 距离的最大值;(3)将抛物线沿射线AC 的方向平移23个单位长度,平移后的顶点记作M ,原抛物线的顶点关于新抛物线的对称轴的对称点记作N ,E 为直线AC 上的动点,是否存在点E ,使得以M 、N 、E 为顶点的三角形是等腰三角形?若存在,请直接写出点E 的坐标;若不存在,请说明理由.与y 轴交于点C ,对称轴交抛物线于点Q ,交x 轴于点M .其中点A (﹣2,0),点B (4,0).(1)求抛物线的解析式;(2)如图2,连接BC ,在第一象限的抛物线上有一点P ,且点P 位于对称轴右侧,过P 作PD△BC 于点D ,PE△MQ 于点E ,求5PD+PE 的最大值及此时点P 的坐标.(3)将抛物线向右平移2个单位长度后得到新抛物线1y ,新抛物线1y 与原抛物线相交于点N ,在新抛物线1y 的对称轴上有一点H ,点F 为1y 与x 轴正半轴的交点,若△NFH 是以NH 为腰的等腰三角形,请直接写出点H 的坐标,并写出求解其中一个H 点的过程.与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD 的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.练习2、已知抛物线c bx ax y ++=2与x 轴交于A (2-,0)、B (6,0)两点,与y 轴交于点C (0,3-).(1)求抛物线的表达式;(2)点P 在直线BC 下方的抛物线上,连接AP 交BC 于点M ,当AMPM 最大时,求点P 的坐标及AM PM 的最大值; (3)在(2)的条件下,过点P 作x 轴的垂线l ,在l 上是否存在点D ,使△BCD 是直角三角形,若存在,请直接写出点D 的坐标;若不存在,请说明理由.自我巩固1、如图,抛物线343832++-=x x y 与x 轴相交于点A ,点B (A 在B 的左侧),与y 轴相交于点C ,连接AC ,BC .(1)求△ABC 的面积;(2)如图,点P 是第一象限内抛物线上的动点,过点P 作PE△y 轴,交直线BC 于点E ,当PE+54CE 有最大值时,求PE+54CE 的最大值与点P 的坐标; (3)将抛物线343832++-=x x y 向右平移2个单位得到新抛物线y ′,点F 为原抛物线y 与新抛物线y ′的交点,点M 是原抛物线y 对称轴上一点,当△AFM 是以FM 为腰的等腰三角形时,直接写出点M 的坐标.。
重庆中考数学第25题二次函数综合专题训练2

2021级重庆中考数学第25题二次函数综合专题训练21.如图,直线y=−x+3与x轴、y轴分别交于点B、C,对称轴为x=1的抛物线经过B、C 两点,与x轴的另一个交点为A,顶点为D、点P是该抛物线上的一个动点,过点P作PE⊥x 轴于点E,分别交线段BD、BC于点F、G,设点P的横坐标为t(1<t<3).(1)求该抛物线所对应的函数关系式及顶点D的坐标;(2)求证:①FG=GE;②∠BDC=∠CAO;(3)当△FCG为等腰三角形时,求t的值.2.如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.(1)求该抛物线的解析式;(2)阅读理解:在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1•k2=﹣1.解决问题:①若直线y=2x﹣1与直线y=mx+2互相垂直,则m的值是____;②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.3.如图,在平面直角坐标系中,二次函数的图像交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点C使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.4.如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(2,1),将此矩形绕点O逆时针旋转90°得矩形DEFO,抛物线y=-x2+bx+c过B、E两点.(1)求此抛物线的函数解析式.(2)将矩形DEFO向右平移,当点E的对应点E’在抛物线上时,求线段DF扫过的面积.(3)若将矩形ABCO向上平移d个单位长度后,能使此抛物线的顶点在此矩形的边上,求d 的值.5.抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(32,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.6.如图,直线y=−34x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+34x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?(3)3.在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.7.如图,抛物线y=﹣x2+bx+c经过点A,B,C,已知点A(﹣1,0),点C(0,3).(1)求抛物线的表达式;(2)P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)设E是抛物线上的一点,在x轴上是否存在点F,使得A,C,E,F为顶点的四边形是平行四边形?若存在,求点F的坐标;若不存在,请说明理由.8.如图,已知二次函数y=ax2+bx+c 的图象经过点A(﹣4,0),B(﹣1,3),C(﹣3,3).(1)求此二次函数的解析式(2)设此二次函数的对称轴为直线l,该图象上的点P(m,n)在第三象限,其关于直线1 的对称点为M,点M 关于y 轴的对称点为N,若四边形OAPN 的面积为20,求m,n 的值;(3)在对称轴直线l 上是否存在一点D,使△ADC 的周长最短,如果存在,求出点D 的坐标;如果不存在,请说明理由.9.已知抛物线y=a(x﹣1)2过点(3,4),D为抛物线的顶点.(1)求抛物线的解析式;(2)若点B、C均在抛物线上,其中点B(0,1),且∠BDC=90°,求点C的坐标:(3)如图,直线y=kx+1﹣k与抛物线交于P、Q两点,∠PDQ=90°,求△PDQ面积的最小值.10.如图,在平面直角坐标系xoy中,把抛物线y=x2先向右平移1个单位,再向下平移4个单位,得到抛物线y=(x−ℎ)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M;(1)写出h、k的值以及点A、B的坐标;(2)判断三角形BCM的形状,并计算其面积;(3)点P是抛物线上一动点,在y轴上找点Q.使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标.(不用写过程)(4)点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标.(不写过程)11.如图,抛物线y =ax 2+bx +c 与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,且当x =0和x =2时,y 的值相等,直线y =3x -7与这条抛物线交于两点,其中一点横坐标为4,另一点是这条抛物线的顶点M.(1)求顶点M 的坐标.(2)求这条抛物线对应的函数解析式.(3)P 为线段BM 上一点(P 不与点B ,M 重合),作PQ ⊥x 轴于点Q ,连接PC ,设OQ =t ,四边形PQAC 的面积为S ,求S 与t 的函数解析式,并直接写出t 的取值范围.(4)在线段BM 上是否存在点N ,使△NMC 为等腰三角形?若存在,求出点N 的坐标,若不存在,说明理由.12.已知顶点为A 的抛物线y =a(x −12)2−2 经经经B(−32经2)经经C(52经2).(1)经经经经经经经经经(2)经经1经经经AB经x经经经经经M经经y经经经经经E经经经经经y经经经经经F经经经经AB经经经经P经经经OPM经经MAF经经经POE经经经经(3)经经2经经Q经经经A经B经C经经经经经经Q经QN经y经经经经E经EN经x经经经经QN经经经EN经经经经N 经经经QE经经经QEN经QE经经经经经QEN′经经经N′经经x经经经经经经经经Q经经经经.13.经经经经经y =−x −2经经经经经经经经经A经经B经经经A经y经经经经经经经经经C经经经经(3,1).(1)经经经经经经经经经(2)经P经经经AB经经经经经经经PM//x经经经经经BC经经经经经经经经经M经N经经经P经PE⊥x经经经E经经PE经PM经经经经经经经经y经经经经经Q经经|PQ−CQ|经经经经经经|PQ−CQ|经经经经经经经Q经经经经(3)经经经经经经经经D经经△ABD经经经经经经经经D经经经经.x+3经y经经经经C经14. .经经经经经经y经经x2+bx+c经x经经经A经经1经0经经B经5经0经经经经经经y经经34经x经经经经D.经P经经经CD经经经经经经经经经经经经经P经PF经x经经经F经经经经CD经经E经经经P经经经经经m.(1)经经经经经经经经经(2)经PE经经经经经m经经.(3)Q经经经经经经经经经经经经经2.经经经经经经PQCD经经经经经经经经经经经经经经经经经经经经经经经经经经经Q经经经经经经经经经经经经经经.15.如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.(1)求该抛物线所表示的二次函数的表达式;(2)已知点F(0,1),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边2形?16. 如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.。
2021-2022学年重庆中考数学25题专题复习:二次函数综合题八 面积最值类

2021-2022学年重庆中考数学25题专题复习二次函数综合题8面积最值类1.如图,直线y=1x+4分别交x、y轴于B、C两点,经过B、C两点的抛物线交x轴于点2A,且A点坐标为(4,0).2.(1)求抛物线的解析式及顶点D的坐标;(2)如图1,若点P是BC上方抛物线上一点,求四边形ABPC面积S的最大值,并求此时点P的坐标;(3)如图2,抛物线对称轴交直线BC于点E,点Q是抛物线上任意一点,过点Q作QH//y轴交直线BC于点H,当以D、E、H、Q为顶点的四边形是平行四边形时,求点Q的坐标.3.如图①,已知抛物线y=ax2+bx−3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.4.(1)求抛物线的表达式;(2)设抛物线的对称轴与x轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)如图②,若点E为第三象限抛物线上一动点,连结BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.5.已知抛物线y=a x2+3x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点2A右侧),与y轴交于点C.6.(1)求抛物线的解折式和A,B两点的坐标;(2)如上图,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由.x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于7.已知:如图,抛物线y=34点C(0,-3).8.9.(1)求抛物线的解析式;10.(2)若点D是线段BC下方抛物线上的动点,求四边形ABDC面积的最大值;(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点的平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.12.(1)填空:点A坐标为________;抛物线的解析式为_____.(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ与△OCE相似?(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?13.如图,已知抛物线y=ax2+bx+3√3与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.14.(1)求抛物线的解析式;15.(2)如图1,过点C的直线交抛物线于另一点E,若∠ACE=60°,求点E的坐标.16.(3)如图2,直线y=kx-2k+√3交抛物线于P,Q两点,求△DPQ面积的最小值.17.如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,连接BC.(1)求抛物线的解析式;(2)若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;(3)在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由。
2021年重庆中考数学二次函数25题专题训练解析版

2021重庆中考数学二次函数25题专题训练1.如图,抛物线y=﹣x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.2.如图1,二次函数y=﹣x2+x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.(1)求点D的坐标;(2)如图2,已知点E是该二次函数图象的顶点,在线段AO上取一点F,过点F作FH ⊥CD,交该二次函数的图象于点H(点H在点E的右侧),当五边形FCEHB的面积最大时,求点H的横坐标;(3)如图3,在直线BC上取一点M(不与点B重合),在直线CD的右上方是否存在这样的点N,使得以C、M、N为顶点的三角形与△BCD全等?若存在,请求出点N的坐标;若不存在,请说明理由.3. 二次函数2y -与x 轴分别交于A 、B 两点,与y 轴交于点C ,点D 为抛物线的顶点,连接BD .(1)如图1,点P 为抛物线上的一点,且在线段BD 的下方(包括线段的端点),连接PA ,PC ,AC .求PAC ∆的最大面积;(2)如图2,直线1l 过点B 、D .过点A 作直线21//l l 交y 轴于点E ,连接点A 、E ,得到OAE ∆,将OAE ∆绕着原点O 顺时针旋转(0180)αα︒<<得到△11OA E ,旋转过程中直线1OE 与直线1l 交于点M ,直线11A E 与直线1l 交于点N .当△1E MN 为等腰三角形时,直接写出点1E 的坐标并写出相应的α值.4.已知二次函数3332332--=x x y 与x 轴交于B A 、两点(点A 在点B 左侧),与y 轴交于点C ,抛物线的对称轴与抛物线交于点D ,连接BD AD 、.(1)如图1,求ABD ∆的周长;(2)如图2,点P 是线段CB 下方抛物线上一点,过点P 作y 轴的平行线交BC 于点M ,交BD 于点N ,BC PH ⊥,点Q 是以P 为圆心PN 为半径的圆周上的动点,点R 是直线AD 上的动点,当PHM ∆周长最大时,求RQ BR +的最小值;(3)将抛物关于y 轴对称,对称后的抛物线与x 轴分别交于11B A 、点(点1A 在点1B 的左侧),连接D A 1,将D B A 11∆绕点1A 顺时针旋转α(0180α<≤),记旋转后的图形为121D B A ∆,旋转过程中直线12D B 分别与直线D A 1和x 轴交于点E 、点F ,当EF A 1∆是等腰三角形时,请直接写出F B 2的长度.5.已知抛物线y=﹣x2+x+9与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)如图1,点P为线段BC上方抛物线上的任意一点,当四边形PCAB面积最大时,连接OP并延长至点Q,使PQ=OP,在对称轴上有一动点E,将△ACE沿边CE翻折得到△A′CE,取BA′的中点N,求BQ+QN的最大值;(2)如图2,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为A1,C1,且点A1落在线段AC上,再将△A1OC1沿y轴平移得△A2O1C2,其中直线O1C2与x轴交于点K,点T是抛物线对称轴上的动点,连接KT,O1T,△O1KT能否成为以O1K为直角边的等腰直角三角形?若能,请直接写出所有符合条件的点T的坐标;若不能,请说明理由.(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物1.解:(1)在直线解析式y=x+2中,令x=0,得y=2,∴C(0,2).∵点C(0,2)、D(3,)在抛物线y=﹣x2+bx+c上,∴,解得b=,c=2,∴抛物线的解析式为:y=﹣x2+x+2.(2)∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,∴PF=OC=2,∴将直线y=x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.将直线y=x+2沿y轴向上平移2个单位,得到直线y=x+4,联立,解得x1=1,x2=2,∴m1=1,m2=2;将直线y=x+2沿y轴向下平移2个单位,得到直线y=x,联立,解得x3=,x4=(不合题意,舍去),∴m3=.∴当m为值为1,2或时,以O、C、P、F为顶点的四边形是平行四边形.(3)存在.理由:设点P的横坐标为m,则P(m,﹣m2+m+2),F(m,m+2).如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=2,∴FM=y F﹣EM=m,∴tan∠CFM=2.在Rt△CFM中,由勾股定理得:CF=m.过点P作PN⊥CD于点N,则PN=FN•tan∠PFN=FN•tan∠CFM=2FN.∵∠PCF=45°,∴PN=CN,而PN=2FN,∴FN=CF=m,PN=2FN=m,在Rt△PFN中,由勾股定理得:PF==m.∵PF=y P﹣y F=(﹣m2+m+2)﹣(m+2)=﹣m2+3m,∴﹣m2+3m=m,整理得:m2﹣m=0,解得m=0(舍去)或m=,∴P(,);同理求得,另一点为P(,).∴符合条件的点P的坐标为(,)或(,).2.解:(1)令x=0,则y=3,∴C(0,3),∴OC=3.令y=0,则﹣x2+x+3=0,解得:x1=﹣4,x2=6,∴A(﹣4,0),B(6,0),∴OA=4,OB=6.∵CD⊥AC,∴∠ACD=90°,∵CO⊥AD,∴OC2=OA•OD,∴OD=,∴D(,0).(2)∵y=﹣x2+x+3=﹣(x﹣1)2+,∴E(1,).如图2,连接OE、BE,作HG⊥x轴于点G,交BE于点P.由B、E两点坐标可求得直线BE的解析式为:y=﹣x+.设H(m,﹣m2+m+3),则P(m,﹣m+).∴HG=﹣m2+m+3,HP=y H﹣y P=﹣m2+m﹣.∴S△BHE=(x B﹣x E)•HP=(﹣m2+m﹣)=﹣m2+m﹣.∵FH⊥CD,AC⊥CD,∴AC∥FH,∴∠HFG=∠CAO,∵∠AOC=∠FGH=90°,∴△ACO∼△FHG,∴==,∴FG=HG=﹣m2+m+4,∴AF=AG﹣FG=m+4+m2﹣m﹣4=m2+m,∴S△AFC=AF•OC=(m2+m)=m2+m,∵S四边形ACEB=S△ACO+S△OCE+S△OEB=×4×3+×3×1+6×=,∴S五边形FCEHB=S四边形ACEB+S△BHE﹣S△AFC=+(﹣m2+m﹣)﹣(m2+m)=﹣m2+m+15=﹣(m﹣)2+,∴当m=时,S五边形FCEHB取得最大值.此时,H的横坐标为.(3)∵B(6,0),C(0,3),D(,0),∴CD=BD=,BC=3,∴∠DCB=∠DBC.①如图3﹣1,△CMN≌△DCB,MN交y轴于K,则CM=CN=DC=DB=,MN=BC=3,∠CMN=∠CNM=∠DBC=∠DCB,∴MN∥AB,∴MN⊥y轴,∴∠CKN=∠COB=90°,MK=NK=MN=,∴△CKN∼△COB,∴==,∴CK=,∴OK=OC+CK=,∴N(,).②如图3﹣2,△MCN≌△DBC,则CN=CB=3,∠MCN=∠DBC,∴CN∥AB,∴N(3,3).③如图3﹣3,△CMN≌△DBC,则∠CMN=∠DCB,CM=CN=DC=DB=,MN=BC=3,∴MN∥CD,作MR⊥y轴于R,则===,∴CR=,RM=,∴OR=3﹣,作MQ∥y轴,NQ⊥MQ于点Q,则∠NMQ=∠DCO,∠NQM=∠DOC=90°,∴△COD ∼△MQN , ∴==,∴MQ =MN =,NQ =MN =, ∴NQ ﹣RM =,OR +MQ =,∴N (﹣,).综上所述,满足要标的N 点坐标有:(,)、(3,3)、(﹣,).3. (1)222333333(23)(1)232222y x x x x x =--=--=--, ∴顶点D 的坐标为(1,23)-,令0y =,则23(23)02x x --=, 1x ∴=-或3x =,(1,0)A ∴-,(3,0)B ,令0x =,则332y =-, 33(0,)2C ∴-, AC ∴是定值,要ACP ∆的面积最大,则点P 到AC 的距离最大,即当点P 在点B 位置时,点P 到AC 的距离最大, ()33113133222ABC ACP S S AB OC ∆∆∴==⋅=+⋅=最大; (2)由(1)知,(3,0)B ,(1,23)D -,∴直线1l 的解析式为333y x =-,12//l l ,且1l 过点A ,∴直线2l 的解析式为33y x =+,(0,3)E ∴, 3OE ∴=,在Rt AOE ∆中,1OA =, 3tan 3OA AEO OE ∴∠==,30AEO ∴∠=︒, 12//l l ,60DBO ∴∠=︒,由旋转知,1OE OE ==,1130A E O AEO ∠=∠=︒, 130ME N ∴∠=︒如图,△1E MN 为等腰三角形,∴①当1111E N M N =时,1111130E M N A E O ∴∠=∠=︒,603060BOM α∴=∠=︒-︒=︒,过点1E 作1E F x ⊥轴于F ,1112E F OE ∴==,132OF F ∴=,13(2E ∴,②当2222E M E N =时,2222221(18030)752E N M E M N ∠=∠=︒-︒=︒,2756015BOM ∴∠=︒-︒=︒,105α∴=︒,过点2E 作2E H x ⊥轴,在OH 上取一点Q ,使2OQ E Q =, 230E QH ∴∠=︒,设2E H a =,则22E Q a =,HQ =,22OQ E Q a ∴==,(2OH a =+,在2Rt OHE ∆中,根据勾股定理得,22[(2]3a a ++=,a ∴(舍去负值),2E ∴.③当3333E M M N =时,33333330E N M M E N ∠=∠=, 333120E M N ∴∠=︒,360BOM ∴∠=︒,150α∴=︒, 360OBM ∠=︒,33330E N M ∠=︒, 390N GB ∴∠=︒,32OG ∴=,332E G =, 33(2E ∴,3)2-. 4. 解:(1)⎪⎪⎭⎫⎝⎛-∴334,1D当0=y 时,03332332=--x x 1,321-==∴x x ())0,1(,0,3-∴A B 4=∴AB2213AD BD ∴==42143ABD C AB AD BD ∆=++=+(2)PMN ∆ ∽BOC ∆PM HM PH PM C PMH 233+=++=∴∆ ∴当PM 最大时,PHM C ∆最大设⎪⎪⎭⎫ ⎝⎛---333233,),333,(2m m m P m m M ∴m m PM 3332+-= 23=∴m 时,⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-3,23,435,23N P43=∴PN B 点关于直线AD 的对称点)7316,711(1--BRQ BR +∴最小=432899191-=-PN P B(3)283843433B F =±或或5. 解:(1)针对于抛物线y =﹣x 2+x +9,令x =0,则y =9, ∴C (0,9), 令y =0, ∴0=﹣x 2+x +9,∴x =﹣3,或x =9,∴A (﹣3,0),B (9,0), ∵S 四边形ABPC =S △ABC +S △BPC =×(9+3)×9+S △BPC =45+S △BPC ,要四边形ABPC 的面积最大,只要△BPC 的面积最大, ∵B (9,0),C (0,9)∴直线BC 的解析式为y =﹣x +9,如图1,过点P 作PD '∥y 轴交BC 于D ', 设点P (m ,﹣ m 2+m +9)(0<m <9),∴D (m ,﹣ m +9), ∴PD '=﹣m 2+m +9﹣(﹣m +9)=﹣m 2+m =﹣(m ﹣)2+,∴S △BPC = [﹣(m ﹣)2+]×9=﹣(m ﹣)2+∴当m=时,△BPC的面积最大,即:四边形ABPC的面积最大,∴P(,),∵点Q在OP的延长线上,且PQ=OP,∴Q(9,),∵B(9,0)∴BQ⊥x轴,BQ=,如图2,延长BQ至F,使QF=BQ,连接A'F,∴BF=45,∴F(9,45),∵点N是A'B的中点,∴QN是△A'BF的中位线,∴A'F=2QN,∵BQ+QN=9+QN,最大,∴QN最大,即:A'F最大,由折叠知,点A'在以点C为圆心,AC=6为半径的圆上,∴FA'过点C时,A'F最大,∵C(0,9),F(9,45),∴直线CF的解析式为y=x+9,令y=0,∴x=﹣>3,∴点A'在x轴下方,如图3,过点C作CD⊥BF于D,在Rt△CDF中,CF==9,=CF+A'C=9+6,∴A'F最大=,∴QN最大∴(QN+QB)=+=;最大(2)在Rt△AOC中,OA=3,OC=9,∴tan∠OAC==,∴∠OAC=60°,由旋转知,OA=OA1,∴△AOA1是等边三角形,∠A1OA=60°=∠OA1C1,∴A1C1∥x轴,∴∠OC1A1=30°,C1(9,3)∴直线OC1的解析式为y=x,∵OC1∥O1C2,∴设直线O1C2的解析式为y=x+b,∴O1(0,b),K(﹣b,0),∴OO1=|b|,OK=|b|,∵抛物线的解析式为y=﹣x2+x+9,∴此抛物线的对称轴为x=3,①当∠O1KT=90°时,b<0,OO1=﹣b,OK=﹣b,如图4,易证,△O1OK≌△KHT(AAS),∴OO1=KT,OK=HT,∴|b|+|b|=3,∴b=.∴HT=OK=,∴T(3,);②当∠KO1T=90°时,当b>0时,如图5,OO1=b,OK=b,易证,△O1OK≌△O1HT(AAS),∴OO 1=HT ,OK =O 1H , ∴b =3,∴OH =O 1H ﹣OO 1=OK ﹣OO 1=9﹣3,∴T (3,9﹣3);当∠KO 1T =90°时,当b <0时,如图6, OO 1=﹣b ,OK =﹣b ,易证,△O 1OK ≌△O 1HT (AAS ), ∴OO 1=HT ,OK =O 1H , ∴b =﹣3,∴OH =O 1H +OO 1=OK +OO 1=9+3,∴T (3,﹣9﹣3); 即:(3,)或(3,9﹣3)或(3,﹣9﹣3).6.(1)∵3332332--=x x y , ∴()()3133-+=x x y . ∴A (-1,0),B (3,0). 当x =4时,335=y . ∴E (4,335), 设直线AE 的解析式为y=kx+b ,将点A 和点E 的坐标代入得:⎪⎩⎪⎨⎧=+=+-33540b k b k , 计算得出:33,33==b k , ∴直线AE 的解析式为3333+=x y (2)设直线CE 的解析式为3-=mx y ,将点E 的坐标代入得33534==m ,计算出332=m . ∴直线CE 的解析式为3332-=x y . 过点P 作PF ∥y 轴,交CE 与点F.设点P 的坐标为⎪⎪⎭⎫ ⎝⎛--333233,2x x x ,则点F ⎪⎪⎭⎫ ⎝⎛-3332,x x , 则FP=x x x x x 33433333233333222+-=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-, ∴△EPC 的面积=x x x x 3383324334332122+-=⨯⎪⎪⎭⎫ ⎝⎛+-⨯ ∴当x =2时,△EPC 的面积最大.∴P (2,3-).如图2所示:作点K 关于CD 和CP 的对称点G 、H,连接G 、H 交CD 和CP 与N 、M.∵K 是CB 的中点. ∴k (23,23-).∵点H 与点K 关于CP 对称,∴点H 的坐标为(23,23-).∵点G 与点K 关于CD 对称, ∴点G (0,0),∴KM+MH+NK=MH+MN+GN.当点O 、N 、M 、H 在条直线上时,KM+MH+NK 有最小值,最小值=GH.∴GH=32322322=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛. ∴KM+MH+NK 的最小值为3. (3)如图3所示:∵y′经过点D ,y′的顶点为点F , ∴点F (3,334-). ∵点G 为CE 的中点, ∴G (2,33). ∴FG=3212335122=⎪⎪⎭⎫ ⎝⎛+ ∴当PG=PQ 时,点Q (3,321234+-),Q′(3,321234--).当GF=GQ 时,点F 与点Q″关于33=y 对称, ∴点Q″(3,32). 当QG=QF 时,设点Q 1的的坐标为(3,a ).由两点间的距离公式可以知道:22331334⎪⎪⎭⎫ ⎝⎛-+=+a a ,计算得出:532-=a . ∴点Q 1的坐标为(3,532-). 综上所述,点Q 的坐标为(3,321234+-)或(3,321234--)或(3,32)或(3,532-).。
重庆中考二次函数25题专题
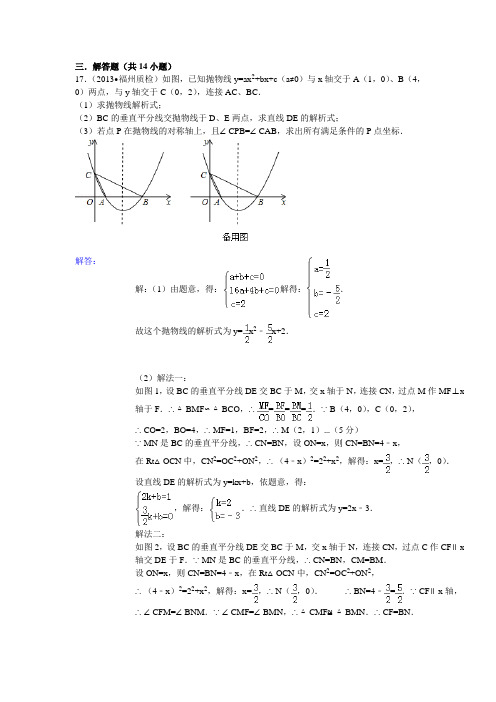
三.解答题(共14小题)17.(2013•福州质检)如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(1,0)、B(4,0)两点,与y轴交于C(0,2),连接AC、BC.(1)求抛物线解析式;(2)BC的垂直平分线交抛物线于D、E两点,求直线DE的解析式;(3)若点P在抛物线的对称轴上,且∠CPB=∠CAB,求出所有满足条件的P点坐标.)由题意,得:解得:y=﹣,∴===x=,∴(,解得:,∴,﹣.∵,,解得:x x+2x=(GA=的坐标为(,﹣,∴NH==1=,点的坐标为(,﹣)或(,18.如图,抛物线y=ax+bx+3与x轴交于A(﹣1,0)、B (3,0)两点,与y轴交于点C,此抛物线的对称轴与抛物线相交于点P,与直线BC相交于点M,连接PB.(1)求点C坐标以及该抛物线的关系式;(2)连接AC,在x轴下方的抛物线上有点D,使S△ABD=S△ABC,求点D的坐标;(3)抛物线上是否存在点Q,使△QMB与△PMB的面积相等?若存在,直接写出点Q的坐标;若不存在,说明理由;(4)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,直接写出点R的坐标;若不存在,说明理由.解得:×,∴±,﹣联立,解得:或)或或﹣=1+C(5,8)两点,点D是抛物线顶点,E是对称轴与直线AC的交点,F与E关于点D对称.(1)求抛物线的解析式;(2)求证:∠AFE=∠CFE;(3)在抛物线的对称轴上是否存在点P,使△AFP与△FDC相似?若有,请求出所有符合条件的点P的坐标;若没有,请说明理由.,解得,===只需=之间)或(点20.如图,抛物线y=ax+bx过点A(4,0)正方形OABC的边BC与抛物线的一个交点为D,点D的横坐标为3,点M在y轴的负半轴上,直线L过点D、M两点且与抛物线的对称轴将于点H,tan∠OMD=.(1)写出D点坐标(3,4),a=﹣,b=,抛物线的对称轴为x=2.(2)求M点坐标,H点坐标;(3)如果点Q是抛物线对称轴上一个动点,那么是否存在点Q使得以点O、M、Q、H为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.得,解得=,得解得21.(2011•莆田)已知抛物线y=ax+bx+c的对称轴为直线x=2,且与x轴交于A、B两点,与y轴交于点C,其中A(1,0),C(0,﹣3).(1)求抛物线的解析式;(2)若点P在抛物线上运动(点P异于点A).①如图1.当△PBC面积与△ABC面积相等时.求点P的坐标;②如图2.当∠PCB=∠BCA时,求直线CP的解析式.)由题意,得,解得解方程组,得解方程组得),((∴,∴∴的解析式为22.(2005•山西)矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A (6,0)、C(0,3),直线y=x与BC边相交于点D.(1)求点D的坐标;(2)若抛物线y=ax2+bx经过D、A两点,试确定此抛物线的表达式;(3)P为x轴上方(2)中抛物线上一点,求△POA面积的最大值;(4)设(2)中抛物线的对称轴与直线OD交于点M,点Q为对称轴上一动点,以Q、O、M为顶点的三角形与△OCD相似,求符合条件的Q点的坐标.xx得解之得﹣+<×==3。
2021年重庆中考数学第25题二次函数综合专题训练1

2021级重庆中考数学第25题二次函数综合专题训练11.如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.2.如图,抛物线y =−x 2−2x +3的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.(1)求A 、B 、C 的坐标;(2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N.若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ.过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG=DQ ,求点F 的坐标.3.已知:如图,二次函数y =﹣12x 2+32x +2的图象交x 轴于A 点和B 点(A 点在B 点左则),交y 轴于E 点,作直线EB ,D 是直线EB 上方抛物线上的一个动点,过D 点作直线l 平行于直线EB.M 是直线EB 上的任意点,N 是直线l 上的任意点,连接MO ,NO 始终保持∠MON 为90°,以MO 和ON 为边,做矩形MONC.(1)在D 点移动过程中,求出当△DEB 的面积最大时点D 的坐标:在△DEB 的面积最大时,求矩形MONC 的面积的最小值;(2)在△DEB 的面积最大时,线段ON 交直线EB 于点G ,当点D ,N ,G ,B 四个点组成平行四边形时,求此时线段ON 与抛物线的交点坐标.4.如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.(1)求出抛物线C1的解析式,并写出点G的坐标;(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:(3)在2.的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.5.如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.6.如图1,在平面直角坐标系中,抛物线y=﹣√33x 2+2√33x+√3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D.(1)求直线BC 的解析式;(2)如图2,点P 为直线BC 上方抛物线上一点,连接PB 、PC.当△PBC 的面积最大时,在线段BC 上找一点E (不与B 、C 重合),使PE+12BE 的值最小,求点P 的坐标和PE+12BE 的最小值;(3)如图3,点G 是线段CB 的中点,将抛物线y=﹣√33x 2+2√33x+√3沿x 轴正方向平移得到新抛物线y′,y′经过点D ,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q ,使得△FGQ 为直角三角形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.7.如图,抛物线y=ax 2+bx 过点B (1,﹣3),对称轴是直线x=2,且抛物线与x 轴的正半轴交于点A.(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x 的取值范围; (2)在第二象限内的抛物线上有一点P ,当PA ⊥BA 时,求△PAB 的面积.8.如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y 轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.①求线段PM的最大值;②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.9.如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.(1)求直线OA及抛物线的解析式;(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为1,8如果存在,求出P的坐标;如果不存在,请说明理由.x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10.如图,已知抛物线y=1310),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.m的顶点为A,与y轴交于点11.如图①,在平面直角坐标系中,抛物线y=x2﹣2mx+m2+43B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.(1)分别用含有m的代数式表示点A、B的坐标.(2)判断点B能否落在y轴负半轴上,并说明理由.(3)连结AC,设l=AC+BD,求l与m之间的函数关系式.(4)过点A作y轴的垂线,交y轴于点P,以AP为边作正方形APMN,MN在AP上方,如图②,当正方形APMN与四边形ABCD重叠部分图形为四边形时,直接写出m的取值范围.12.如图,已知抛物线y=ax2+bx+c(a<0)分别交x轴、y轴于点A(2,0)、B(0,4),点P 是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若a+b=0.①求抛物线的解析式;②当线段PD的长度最大时,求点P的坐标;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B,P,D为顶点的三角形与ΔAOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.x2 bxc经过△ABC 的三个顶点,其中点A(0,1),点B(9,10),13.如图,已知抛物线y13AC∥x 轴,点P 是直线AC 下方抛物线上的动点,过点P 且与y 轴平行的直线l 与直线AB、AC 分别交于点E、F.(1)求抛物线的函数表达式;(2)如图1,当四边形AECP 的面积最大时,求点P 的坐标和四边形AECP 的最大面积;(3)如图2,当点P 为抛物线的顶点时,在直线AC 上是否存在点Q,使得以C,P,Q 为顶点的三角形与△ABC 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.14.如图1,已知二次函数y=mx 2+3mx ﹣274m 的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),顶点D 和点B 关于过点A 的直线l :y=﹣√33x ﹣3√32对称.(1)求A 、B 两点的坐标及二次函数解析式;(2)如图2,作直线AD ,过点B 作AD 的平行线交直线1于点E ,若点P 是直线AD 上的一动点,点Q 是直线AE 上的一动点.连接DQ 、QP 、PE ,试求DQ+QP+PE 的最小值;若不存在,请说明理由:(3)将二次函数图象向右平移32个单位,再向上平移3√3个单位,平移后的二次函数图象上存在一点M ,其横坐标为3,在y 轴上是否存在点F ,使得∠MAF=45°?若存在,请求出点F 坐标;若不存在,请说明理由.15.如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.(1)求经过B、E、C三点的抛物线的解析式;(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.16.抛物线y=ax2+bx的顶点M(√3,3)关于x轴的对称点为B,点A为抛物线与x轴的一个交点,点A关于原点O的对称点为A′;已知C为A′B的中点,P为抛物线上一动点,作CD⊥x轴,PE⊥x轴,垂足分别为D,E.(1)求点A的坐标及抛物线的解析式;(2)当0<x<2√3时,是否存在点P使以点C,D,P,E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.。
重庆中考数学三轮冲刺第25题二次函数综合专题专训三

2021年重庆中考数学三轮冲刺第25题二次函数综合专题专训三1.如如如如如如如y如如x如2如如如如如如如如y如ax2+bx如4如如如如如x如如如如A如如y如如如如B如如x如如如如如如C.如如如如如如y如ax2+bx如4如如如如y如如如如D如如如如如如如x如n如n如0如如n如如如2x2如3x 如2如0如如如如如如如AD.(1)如如如如如如如如如.(2)如S如ACB如3S如ADB如如如如C如如如.(3)如如如如如如如如如如如如如如如C如如如如如A如B如C如如如如如如如如ADB如如如如如如如如如如如C如如如如如如如如如如如如如如.2.如如如如如如如x如如如A如B如如如如y如如C如如如A如如如如如2如0如如如B如如如如如如3如0如如如C如如如如如0如3如如(1)如如如如如如如如如(2)如如如如如如如如如如如如H如如CH+AH如如如如如如如如H如如如如(3)如如如如如如如如P如如如S如AOP=5如如如如如P如如如如x如1如x如如y如如如如如如如A如B如如x=如1如如如如如如如如y=x2+bx 3.如如如如如如如如如如如如如y=如13+c如x如如如如如如A如C如如如x=如1如x如如如如D.(1)如如如如如如如如如(2)如如如AB如如如如如如如P如如如A如D如P如如如如如如如如如AOB如如如如如如如如如如P如如如如如如如如如如如如如如如如(3)如如Q如如如如如如如如tan如AQD=2如如如CQ如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如.4.如如如如如如如如如如如如如如如如y=ax2+bx+3如如A(如3如0)如B(1如0)如如如如如如如D如如如AD如如P如如如AD如如如如如如如如A如D如如如.(1)如如如如如如如如如如如如如如如如D如如如如(2)如如1如如如P如PE如y如如如E如如如AE.如如PAE如如S如如如如如(3)如如2如如如如如如如如如如如Q如如如如如如OAPQ如如如如如如如如如如如如Q如如如如如如如如如如如如如.5.如图1,在平面直角坐标系xOy中,直线l:y=34x+π与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=12x2+bx+c如如如B如如如如如l如如如如如如如C如4如n如.(1)如n如如如如如如如如如如如(2)如D如如如如如如如如D如如如如如t如0如t如4如.DE如y如如如如l如如E如如F如如如l如如如如如如DFEG如如如如如如2如.如如如DFEG如如如如p如如p如t如如如如如如如如p如如如如如(3)M如如如如如如如如如AOB如如M如如如如如如如如90°如如如如如A1O1B1如如A如O如B如如如如如如如如A1如O1如B1.如如A1O1B1如如如如如如如如如如如如如如如如如如如如A1如如如如.6.如图,抛物线y=−14x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,52),直线y=kx−32过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD 于点N.(1)填空:b=__________,c=__________,k=__________如(2)探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在,请求出点P如如如如如如如如如如如如如如如(3)设ΔPMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l如如如如.7.如如如如如如如如如如如如如如如如如如ABOC如如如如如如如如如如如如如如O如如如如如90°如如如如如如如A′B′OC′.如如如y如如x2+2x+3如如如A如C如A′如如.(1)如A如A′如C如如如如如如(2)如如如如如如ABOC如如如如如如A′B′OC′如如如如如C′OD如如如如(3)如M如如如如如如如如如如如如如如如如如M如如如如如如AMA′如如如如如如如如如如如如如如如如如如如M 如如如.8.如如如Rt如ABC如如如如如5如如如如如如如2如如如如如如如如如如如如如如如如如如如如如如如如如AB如x 如如如如如如OA如OB如如如如如如C如如y如如如如如如如如1如.(1)如如如OA如OB如如如如如如A如B如C如如如如如如如如.(2)如如2如如D如如如如如2如0如如如P如m如n如如如如如如如如如如如如如如如m如0如n如0如如如如DP如B C如如E.如如如BDE如如如如如如如如如如如如如如如E如如如.如如如如CD如CP如如如3如如如CDP如如如如如如如如如如如如如如CDP如如如如如如如如如P如如如如如如如如如如如如如.x2+bx+4如x如如如如A如B如如如如y如如如如如C如如如如B如如如如如B如8如0如9.如如如如如如如如y=如14.(1)如如如如如如如如如如如如如如如.(2)如如AC如BC如如如如如AOC如如COB如如如如如如如如如如.(3)如如如如如BC如如如如如如如如D如如如如DBC如如如如如如如如如如如如如D如如如如如DBC如如如如如如如如如如如如如如.10.如如如如如如如如如如如如O如如如如A如1如1如如如如如如y=x如2如如B如C如如.(1)如如如如如如如如如如C如如如如(2)如如如如ABC如如如如如如如(3)如如N如x如如如如如如如如如如N如MN如x如如如如如如如如M如如如如如如如O如M如N如如如如如如如如如ABC如如如如如如如如如如如N如如如如如如如如如如如如如如.11.如如如如如如如如如如如y=如x2+2mx如m如0如如x如如如如如如如如A如如如P如1如m如如如如PA如x如如如M如如如如如如如B.如如B如如如如如如如如如如如如如C如如B如C如如如如如如如CB如CP.(1)如m=3如如如如A如如如如BC如如如(2)如m如1如如如如CA如如CA如CP如如m如如如(3)如如P如PE如PC如如PE=PC如如如E如如如如如如如如如m如如如如如如如如如如如E如如如.x+c如x如如如A如B如如如如y如如如C如如12.已知:如图,抛物线y=ax2−32如B(4如0)如C(0如-2)如如D如如如如如如如如如如如如如如如如如如D如如如DF如x如如如如如如F如如如如B C如如E.(1)如如如如如如如如如如A如如如;(2)如DE=2EF如如如如D如如如;(3)如y如_如如如如如P如如如如如P AC如如AC如如如如如如如如?如如如如如如如如如P如如如;如如如如如如如如如如.13.如如如如如如 y=-x2 + bx + c如x如如如A如B如如如如y如如如如如C如如D如如如如如如如如A如-3如0如如B如1如0如.(1)如如如如如如如如如如.(2)如如P如x如如如如如PCA=如CAD如如如P如如如.(3)如x如如如如如如如如如如如如如如Q如如如如Q如C如A如O如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如Q如如如如如如如如如如如如如如如.14.在平面直角坐标系中,抛物线y=−x2−2x+3如x如如如A如B如如如A如B如如如如如如y如如如如C如如如如D.(1)如如如如如如A如C如D如如如如(2)如如如1如如如x如如如如如E如如如如CDE如如如如如如如如E如如如如(3)如如如2如如F如如如AC如如如如如如如如如如如如如如如P如如如如AFP如如如如如如如如如如如如如如如如P如如如如如如如如如如如如如如.15.如图,在平面直角坐标系中,抛物线y=ax2+bx+1如y如如如A如)如如x如如如如如如B如4如0如如如如A如如如如如如如如如如D(3,52如如D如DC如x如如如如如C.(1)如如如如如如如如如(2)如P如如如OC如如如如如O如C如如如如如如P如PN如x如如如如如AD如M如如如如如如如N如如如CM如如如PCM如如如如如如如(3)如如P如x如如如如如如如如如如如OP如如如t如如如如如t如如如M如C如D如N如如如如如如如如如如如如如如如如如如如如t如如如如如如如如如如如如如.16.如如如如如如y=ax2+bx+c如x如如如如A如如B如1如0如如如y如如如如C如0如3如如如如如如l如x=如1.(1)如如如如如如如如如如如如如如如如如(2)如如如P如如如如如如如如如如如如如如N如如如如l如.如如PA如NA如如PA=NA如如如如如如P如如如如如如如如如PABC如如如如如如如如如如如PABC如如如如如如如如如如P如如如.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 如图,抛物线42
12
-+=
x x y 交x 轴于A 、B 两点,交y 轴于点C ,顶点为H ,其对称轴交x 轴于点N 。
直线l 经过B 、D 两点,交抛物线的对称轴于点M ,其中点D 的横坐标为5-. (1)连接AM ,求∆ABM 的周长;
(2)若P 是抛物线位于直线BD 的下方且在其对称轴左侧上的一点,当四边形DPHM 的面积最大时,求点P
(3)连接AC ,若F 为y
轴上一点,当∠MBN =点的坐标.
2. 如图,在平面直角坐标系中,抛物线2
7922x x --
+与直线1
2
y x b =+交于A 、B 两点,其中点A 在x 轴上,点P 是直线AB 上方的抛物线上一动点(不与点A 、B 重合),连接PA 、
PB 。
(1)求直线的解析式及A 、B 两点的坐标;
(2)过点P 作x 轴的垂线,交直线AB 于点C ,当线段PC 最大时,求此时点C 的坐标及PC 的最大值:
(3)当∠PAB=90°时,求此时点P 的坐标。
3.如图,抛物线22y ax bx =++与x 轴交于A 、B 两点,点A 的坐标为()1,0-,抛物线的对称轴为直线 1.5x =,点M 为线段AB 上一点,过M 作x 轴的垂线交抛物线于P ,交过点A 的直线y x n =-+于点C 。
(1)求直线AC 及抛物线的解析式;
(2)M 位于线段AB 的什么位置时,PC 最长,并求出此时P 点的坐标;
(3)若在(2)的条件下,在x 轴上方的抛物线上是否存在点Q ,使2
3
ABQ APB S S ∆∆=,求点Q 的坐标。
4.如图,二次函数32-+=bx ax y 的图象与x 轴交于B 、C 两点(点B 在点C 的左侧),一
次函数n mx y +=的图象经过点B 和二次函数图象上另一点A . 点A 的坐标(4 ,3),
2
1
t a n =
∠ABC . (1)求二次函数函数和一次函数解析式;
(2)若抛物线上的点P 在第四象限内,求ABP ∆面积S 的最大值并求出此时点P 的坐标;
(3)若点M 在直线AB 上,且与点A 的距离是到x 轴距离的
2
5
倍,求点M 的坐标.
5.如图,在平面直角坐标系中,抛物线y=a x2+bx-3(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段B C上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△P BQ存在时,求运动多少秒使△PB Q的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S
△C B K :S
△P B Q
=5:
2,求K点坐标.
6.如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y 轴交于点C,连接B C.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BC M的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△C NQ为直角三角形,求点Q的坐标.
7.如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD、BD、DP,延长DP交x轴正半轴于点E,且S
△O C E =S
四边形OC D B
,求此时
P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.
8.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A 和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC 的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
9.如图,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3.
(1)求抛物线的函数表达式及其顶点C的坐标;
(2)如图①,点P(m,0)是线段AO上的一个动点,其中-3<m<0,作直线DP ⊥x轴,交直线AB于D,交抛物线于E,作EF∥x轴,交直线AB于点F,四边形D EFG 为矩形.设矩形DE FG的周长为L,写出L与m的函数关系式,并求m为何值时周长L最大;
(3)如图②,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形是以AB为腰的等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.。
