第一章第二章算法题(精品文档)
高中数学 第一章 算法初步 1.1.1 算法的概念练习(含解析)新人教A版必修3-新人教A版高一必修

1.1.1 算法的概念A级基础巩固一、选择题1.下列四种自然语言叙述中,能称作算法的是()A.在家里一般是妈妈做饭B.做米饭需要刷锅、淘米、添水、加热这些步骤C.在野外做饭叫野炊D.做饭必须要有米解析:算法是做一件事情或解决一类问题的程序或步骤,故B正确.答案:B2.下面的结论正确的是()A.一个程序的算法步骤是可逆的B.一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D.设计算法要本着简单方便的原则解析:算法需每一步都按顺序进行,并且结果唯一,不能保证可逆,故A不正确;一个算法必须在有限步内完成,不然就不是问题的解了,故B不正确;一般情况下,完成一件事情的算法不止一个,但是存在一个比较好的,故C不正确;设计算法要尽量运算简单,节约时间,故D正确.答案:D3.一个算法的步骤如下,若输入x的值为-3,则输出z的值为()第一步,输入x的值.第二步,计算x的绝对值y.第三步,计算z=2y-y.第四步,输出z的值.A.4B.5C.6 D.8解析:因为x=-3,所以y=|x|=3.所以z=23-3=5.答案:B4.阅读下面的算法:第一步,输入两个实数a,b.第二步,若a<b,则交换a,b的值;否则,不交换a,b的值.第三步,输出a.这个算法输出的是()A.a,b中较大的数B.a,b中较小的数C.原来的a的值D.原来的b的值解析:第二步中,若a<b,则交换a,b的值,那么a是a,b中较大的数,即a≥b.答案:A5.给出算法:第一步,输入n=6.第二步,令i=1,S=0.第三步,判断i≤n是否成立.若不成立,则输出S,结束算法;若成立,则执行下一步.第四步,令S的值加i,仍用S表示,令i的值加1,仍用i表示,返回第三步.则该算法的功能为()A.计算1+2+3+4+5+6的值B.计算1+2+3+4+5的值C.计算1+2+3+4+5+6+7的值D.以上答案皆不正确解析:该算法的运行过程是:n=6,i=1,S=0,i=1≤6成立;S=0+1=1,i=1+1=2,i=2≤6成立;S=1+2,i=2+1=3,i=3≤6成立;S=1+2+3,i=3+1=4,i=4≤6成立;S=1+2+3+4,i=4+1=5,i=5≤6成立;S=1+2+3+4+5,i=5+1=6,i=6≤6成立;S=1+2+3+4+5+6,i=6+1=7,i=7≤6不成立,输出S=1+2+3+4+5+6=21.答案:A二、填空题6.给出下列算法:第一步,输入x 的值.第二步,当x >4时,计算y =x +2;否则执行下一步.第三步,计算y =4-x .第四步,输出y .当输入x =0时,输出y =________.解析:因为0<4,执行第三步,所以y =4-0=2.答案:27.已知直角三角形两直角边长为a ,b ,求斜边长c 的一个算法分下列三步:①计算c =a 2+b 2.②输入直角三角形两直角边长a ,b 的值.③输出斜边长c 的值.其中正确的顺序是________________.解析:算法的步骤是有先后顺序的,第一步是输入,最后一步是输出,中间的步骤是赋值、计算.答案:②①③8.如下算法:第一步,输入x 的值.第二步,若x ≥0,则y =x .第三步,否则,y =x 2.第四步,输出y 的值.若输出的y 值为9,则x =________.解析:根据题意可知,此为求分段函数y =⎩⎪⎨⎪⎧x ,x ≥0,x 2,x <0的函数值的算法.当x ≥0时,x =9;当x <0时,x 2=9,所以x =-3.答案:9或-3三、解答题9.试设计一个判断圆(x -a )2+(y -b )2=r 2与直线Ax +By +C =0(A 、B 不同时为零)位置关系的算法.解:算法步骤如下:第一步,输入圆心的坐标(a ,b )、半径r 和直线方程的系数A ,B ,C .第二步,计算z 1=Aa +Bb +C .第三步,计算z 2=A 2+B 2.第四步,计算d =|z 1|z 2. 第五步,如果d >r ,则输出“相离”;如果d =r ,则输出“相切”;如果d <r ,则输出“相交”.10.某商场举办优惠促销活动.若购物金额在800 元以上(不含800 元),打7折;若购物金额在400 元以上(不含400 元),800 元以下(含800 元),打8折;否则,不打折.请为商场收银员设计一个算法,要求输入购物金额x ,输出实际交款额y .解:算法步骤如下:第一步,输入购物金额x (x >0).第二步,判断“x >800”是否成立,若是,则y =0.7x ,转第四步;否则,执行第三步. 第三步,判断“x >400”是否成立,若是,则y =0.8x ;否则,y =x .第四步,输出y ,结束算法.B 级 能力提升1.给出算法:第一步,输入x .第二步,判断x 是否小于0,若是,则输出x +2;否则,执行第三步.第三步,输出x -1.当输入的x 的值为-1,0,1时,输出的结果分别为()A .-1,0,1B .-1,1,0C .1,-1,0D .0,-1,1解析:根据x 值与0的关系选择执行不同的步骤.答案:C2.以下为输出1至1 000的正整数中3的倍数的一个算法,请将算法补充完整: 第一步,令i =1.第二步,i 被3除,得余数r .第三步,若________,则输出i ,否则不输出.第四步,令i =i +1.第五步,若i ≤1 000,则返回第二步继续执行,否则结束算法.解析:由定义可知,可被3整除的数即3的倍数,所以此处余数是否为0可以作为判断是否输出该数的条件.答案:r=03.“韩信点兵”问题:韩信是汉高祖手下的大将,他英勇善战,谋略超群,为汉朝的建立立下了不朽功勋.据说他在一次点兵的时候,为保住军事秘密,不让敌人知道自己部队的军事实力,采用下述点兵方法:①先令士兵从1~3报数,结果最后一个士兵报2;②又令士兵从1~5报数,结果最后一个士兵报3;③又令士兵从1~7报数,结果最后一个士兵报4.这样韩信很快算出自己部队里士兵的总数.请设计一个算法,求出士兵至少有多少人.解:第一步,首先确定最小的满足除以3余2的正整数:2.第二步,依次加3就得到所有除以3余2的正整数:2,5,8,11,14,17,20,….第三步,在上列数中确定最小的满足除以5余3的正整数:8.第四步,在自然数内的8的基础上依次加上15,得到8,23,38,53,….第五步,在上列数中确定最小的满足除以7余4的正整数:53.即士兵至少有53人.。
算法和程序设计及试题附答案-08-算法和程序设计资料

算法和程序设计及试题附答案-08-算法和程序设计资料选修1:算法与程序设计第一单元算法一、知识内容(一)使用计算机解决问题的一般过程考试要求:对所列知识要知道其内容及含义,并能用自己的语言或动作进行表达、判断和直接运用。
1.一般过程(1)分析问题确定要使用计算机来“做什么”,即确定解题的任务。
(2)寻求解决问题的途径和方法。
(3)用计算机进行处理。
2.确定解决问题的方法及步骤化确定了解决问题的方法后,必须把解决问题的方法步骤化,即用某种方式告诉计算机每个需做什么。
计算机开始计算之前,需把解决问题的程序存储在内存中。
通常一个程序包括指令和数据两部分。
(1)指令部分:指令是对计算机操作类型和操作数地址做出规定的一组符号。
(2)数据部分:计算所需的原始数据、计算的中间结果或最终结果。
3.设计程序时需要考虑的问题(1)数据的存储:计算所需要的原始数据、计算产生的中间结果需要存储在不同的变量中。
(2)计算的过程:把解决问题的方法步骤化,并用计算机能执行的指令来有序地实现对应的步骤。
(3)典型的指令类型有输入指令、输出指令、算术运算指令、逻辑运算指令和控制转移指令。
(二)算法及算法的表示方法考试要求:对所列知识要理解其确切含义及与其它知识的联系,能够用所学的信息技术知识和操作方法解决实际问题,熟练应用信息技术进行信息的处理。
1.算法的特征(1)有穷性。
一个算法必须保证它的执行步骤是有限的,即它是能终止的。
(2)确定性。
算法中的每个步骤必须有确切的含义,不应当有模棱两可的。
(3)能行性。
算法中的每一个步骤都要足够简单,能实际能作的,而且在能在有限的时间内完成。
(4)有0个或多个输入。
(5)有一个或多个输出。
(三)用自然语言、流程图、伪代码表示算法考试要求:对所列知识要理解其确切含义及与其它知识的联系,能够用所学的信息技术知识和操作方法解决实际问题,熟练应用信息技术进行信息的处理。
1.自然语言就像写文章时所列的提纲一样,可以有序地用简洁的自然语言加数学符号来描述算法。
算法_精品文档

一、算法的定义
有三个牧师和三个野人过河,只有一条能装下 两个人的船,在河的任何一方或者船上,如果野人 的人数大于牧师的人数,那么牧师就会有危险(被 野人吃掉)。你能找出一种安全的渡河方案吗?请 记录详细的方法和步骤!
第一步:两个野人划船到B岸 一个野人划船回到A岸
第二步:两个野人划船到B岸 一个野人划船回到A岸
请大家把书本打开翻到68页,快速浏览 本页的内容。
流程图的常用符号
起止框;输入输出框;处理框;判断框;流程线。
图形符号
名称
说明
起止框 算法的开始或结束
输入输出框 输入和输出数据
处理框 指出要处理的内容
判断框 条件判断及产生分支的情况
流程线 从一个步骤到下一个步骤
五、程序的三种基本结构
顺序结构 早晨起床
第二步:在含有假币的那组金币中任意取2枚分别放在天平两边,若平衡,则剩下 的那枚是假币;若不平衡,较轻的那枚是假币。
自然语言表示
开始 将9枚金币平均分成3组
任取其中2组分别放在天平两边
Y
N
是否平衡?
输出Y 结束
假币在剩下的那组中
任取其中2枚分别放在天平两边
Y
N
是否平衡?
假币在较轻的那组中
三、算法的表示形式
请设计一个算法,求键盘输入两数之和并输出结果。
自然语言
用键盘先输入一个数, 再输入另一个数, 计算两数和, 输出“和”的结果。
流程图
开始 输入一个加数 输入另一个加数 计算两数之和
输出和 结束
计算机语言
Private Sub Command1_Click()
a = Val(Text1.Text) b = Val(Text2.Text) sum = a + b Print sum End Sub
浙教版(2019)必修1《第二章_算法与问题解决》2022年单元测试卷(1)+答案解析(附后)

浙教版(2019)必修1《第二章算法与问题解决》2022年单元测试卷(1)1. 以下对算法的叙述,错误的是( )A. 算法结果不唯一B. 实现算法的语言可以是多样的C. 算法具有确定性D. 解决同一问题的算法可以有多种2. 以下程序的运行结果是( )i=0sum=0while i<10:ifi%3==0:sum+=iii+1print('sum=',sum)A. sum=18B. sum=9C. sum=sumD. sum=03. 以下程序的运行结果是( )t=1for i in range(1,4):t=t*iprint(i,“!=“,t)A. i!=tB. i!=1C. i!=6D. 3!=64. 在下面程序中,分别输入两个数2和3,运行的结果是( )a=input( )b=input( )print(a+b)A. 2B. 3C. 5D. “23“5. 已知a=5,b=6,则执行下列语句后,a和b的值分别是( )a=a+bb-atbA. 11;17B. 11;11C. 17:11D. 5;66. 有关顺序结构的说法不正确的是( )A. 顺序结构是算法的基本结构之一B. 任何的程序设计中都有顺序结构C. 顺序结构在程序设计中可有可无D. 顺序结构、选择结构、循环结构是程序设计的三种基本结构7. 近年来,很多APP通过“AI算法”分析推测用户偏好,并据此推荐用户喜爱的信息内容。
关于“AI算法”,下列说法错误的是( )A. AI算法使用了大数据分析技术B. AI算法是一种先进的技术,没有缺点C. AI算法容易使用广沉迷于自己的喜好,陷入“信息茧房”D. AI算法使用了人工智能技术8. 以下流程图中,执行后会出错的是( )A. B.C. D.9. 计算机完成了一个加法操作,执行的是一个( )A. 程序B. 判断C. 软件D. 指令10. 使用欧式距离度量法对未知鸢尾花进行分类预测,其实施步骤的正确顺序是( )①计算待测鸢尾花各属性值与三类鸢尾花属性平均值之间的欧式距离②读入鸢尾花训练集相关数据③计算三类鸢尾花各自特征属性的平均值④读入待测鸢尾花的数据⑤找出欧氏距离的最小值,并确定其对应的鸢尾花类别A. ④③②①⑤B. ②③④①⑤C. ②④③①⑤D. ③①④②⑤11. 计算机执行程序语句“s=3>0”时,相关说法不正确的是( )A. 该程序语句需要被转换成二进制的指令后才能被执行B. 该程序语句编译后的指令被存放在存储器中C. 控制器能根据程序语句的指令识别、读取待运算的数据D. 运算器执行完算术运算后,将执行结果送回到存储器中12. K-近邻算法是机器学习中用于解决分类任务的基础算法。
(2021年整理)线性代数1-2章精选练习题

线性代数1-2章精选练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(线性代数1-2章精选练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为线性代数1-2章精选练习题的全部内容。
第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( )。
(A) 24315 (B ) 14325 (C ) 41523 (D )24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( )。
(A )k (B )k n - (C)k n -2! (D)k n n --2)1(3。
n 阶行列式的展开式中含1122a a 的项共有( )项。
(A ) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( )。
(A) 0 (B)1- (C ) 1 (D ) 25. =0001100000100100( )。
(A) 0 (B )1- (C ) 1 (D) 26.在函数10323211112)(x x x xx f ----=中3x 项的系数是( )。
(A) 0 (B)1- (C) 1 (D ) 27。
若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ).(A) 4 (B ) 4- (C ) 2 (D ) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( )。
浙教版(2019)必修1《第二章 算法与问题解决》2023年单元测试卷+答案解析(附后)

浙教版(2019)必修1《第二章算法与问题解决》2023年单元测试卷1. 下面关于算法的描述,正确的是( )A. 一个算法只能有一个输入B. 算法只能用框图来表示C. 一个算法的执行步骤可以是无限的D. 一个完整的算法,不管用什么方法来表示,都至少有一个输出结果2. 求矩形面积s的部分流程图如图所示,矩形的长、宽分别用变量a、b表示,对于框①和框②的作用,下列说法正确的是( )A. 框①用于输入a和b的值,框②用于输出s的值B. 框①用于输出a和b的值,框②用于输出s的值C. 框①用于输入a和b的值,框②用于输入s的值D. 框①用于输出a和b的值,框②用于输入s的值3. 有流程图如图所示,其功能是将键盘输入的数进行相加,当输入的数为0时输出它们的和,则图中虚线部分的内容是( )A. B.C. D.4. 下面流程图中依次输入x的值为3、2、1、-1该算法的输出结果n和s分别为( )A. 5,2B. 6,3C. 6,4D. 5,35. 某算法流程图如图所示,算法执行时若输入n的值为3,则输出s的值是( )A. 4B. 8C. 9D. 166. ( )是编程加工的核心.A. 算法设计B. 界面设计C. 代码编写D. 调试运行7. 在地铁站自动售票机买票的算法描述如下:步骤1:选择地铁线路步骤2:选择目的地站点步骤3:选择需要购买的地铁票数量步骤4:放入一张纸币或一枚硬币步骤5:如果多次投入纸币执行步骤4步骤6:若投入的纸币已达到或超出票价则执行步骤7步骤7:出票及找零上述算法的描述采用了( )A. 自然语言B. 伪代码C. 流程图D. 程序设计8. 下列关于算法的错误说法是( )A. 算法必须有输出B. 表示算法的语言可以是自然语言C. 同一个算法只能用一种程序设计语言来实现D. 算法必须在执行有限步后结束9. Python语言属于( )A. 自然语言B. 汇编语言C. 机器语言D. 高级语言10. 图形符号““在算法流程图描述中表示( )A. 算法的开始或结束B. 输入输出操作C. 处理或运算的功能D. 用来判断条件是否满足需求11. 下列问题不能用算法描述的是( )A. 求所有自然数之和B. 将四位十进制数转换为对应的二进制数C. 将100个实数按升序排列D. 求100个整数中的最大值和最小值12. 已知三角形三条边的长度分别为A、B、C,用海伦公式计算此三角形的面积S的步骤如下,其正确的顺序是( )。
高中数学必修三课后习题答案

高中数学必修三课后习题答案第一章 算法初步 1.1算法与程序框图练习(P5) 1、算法步骤:第一步,给定一个正实数r .第二步,计算以r 为半径的圆的面积2S r π=.第三步,得到圆的面积S .2、算法步骤:第一步,给定一个大于1的正整数n .第二步,令1i =.第三步,用i 除n ,等到余数r .第四步,判断“0r =”是否成立. 若是,则i 是n 的因数;否则,i 不是n 的因数. 第五步,使i 的值增加1,仍用i 表示.第六步,判断“i n >”是否成立. 若是,则结束算法;否则,返回第三步.练习(P19)算法步骤:第一步,给定精确度d ,令1i =.的到小数点后第i 位的不足近似值,赋给a 的到小数点后第i 位的过剩近似值,赋给b . 第三步,计算55b am =-.第四步,若m d <,则得到5a;否则,将i 的值增加1,仍用i 表示.返回第二步. 第五步,输出5a.程序框图:习题1.1 A 组(P20)1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7 m 3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m 3的部分,每立方收费1.5元,并加收0.4元的城市污水处理费.设某户每月用水量为x m 3,应交纳水费y 元,那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤:第一步:输入用户每月用水量x .第二步:判断输入的x 是否不超过7. 若是,则计算 1.2y x =;若不是,则计算 1.9 4.9y x =-.第三步:输出用户应交纳的水费y .程序框图:2、算法步骤:第一步,令i =1,S=0.第二步:若i ≤100成立,则执行第三步;否则输出S. 第三步:计算S=S+i 2.第四步:i = i +1,返回第二步.程序框图:3、算法步骤:第一步,输入人数x ,设收取的卫生费为m 元.第二步:判断x 与3的大小. 若x >3,则费用为5(3) 1.2m x =+-⨯;若x ≤3,则费用为5m =.第三步:输出m .程序框图:B 组 1、算法步骤:第一步,输入111222,,,,,a b c a b c ..第二步:计算21121221b c b c x a b a b -=-.第三步:计算12211221a c a c y ab a b -=-.第四步:输出,x y .程序框图:INPUT “a ,b=”;a ,bsum=a+b diff=a -b pro=a*b quo=a/bPRINT sum ,diff ,pro ,quoEND2、算法步骤:第一步,令n =1第二步:输入一个成绩r ,判断r 与6.8的大小. 若r ≥6.8,则执行下一步;若r<6.8,则输出r ,并执行下一步.第三步:使n 的值增加1,仍用n 表示.第四步:判断n 与成绩个数9的大小. 若n ≤9,则返回第二步;若n >9,则结束算法.程序框图:说明:本题在循环结构的循环体中包含了一个条件结构.1.2基本算法语句 练习(P24) 1、程序:2、程序:3、程序:练习(P29) 1、程序:INPUT “a ,b ,c=”;a ,b ,cIF a+b>c AND a+c>b AND b+c>a THEN PRINT “Yes.” ELSEPRINT “No.” END IF INPUT “a ,b ,c=”;a ,b ,cp=(a+b+c)/2 s=SQR(p*(p -a) *(p -b) *(p -c)) PRINT “s=”;s END INPUT “F=”;F C=(F -32)*5/9 PRINT “C=”;C END4、程序: INPUT “a ,b ,c=”;a ,b ,csum=10.4*a+15.6*b+25.2*c PRINT “sum =”;sum END2、本程序的运行过程为:输入整数x . 若x 是满足9<x <100的两位整数,则先取出x 的十位,记作a ,再取出x 的个位,记作b ,把a ,b 调换位置,分别作两位数的个位数与十位数,然后输出新的两位数. 如输入25,则输出52. 34练习(P32) 1 2习题1.2 A 组(P33)1、1(0)0(0)1(0)x x y x x x -+<⎧⎪==⎨⎪+>⎩23、程序: 习题1.2 B 组(P33) 1、程序:23 41.3算法案例 练习(P45) 1、(1)45; (2)98; (3)24; (4)17. 2、2881.75.3、2200811111011000=() ,820083730=() 习题1.3 A 组(P48) 1、(1)57; (2)55. 2、21324.3、(1)104; (2)7212() (3)1278; (4)6315().4、习题1.3 B 组(P48)1、算法步骤:第一步,令45n =,1i =,0a =,0b =,0c =.第二步,输入()a i .第三步,判断是否0()60a i ≤<. 若是,则1a a =+,并执行第六步. 第四步,判断是否60()80a i ≤<. 若是,则1b b =+,并执行第六步. 第五步,判断是否80()100a i ≤≤. 若是,则1c c =+,并执行第六步. 第六步,1i i =+. 判断是否45i ≤. 若是,则返回第二步.2、如“出入相补”——计算面积的方法,“垛积术”——高阶等差数列的求和方法,等等. 第二章复习参考题A组(P50)1、(1)程序框图:程序:1、(2)程序框图:程序:2、见习题1.2 B组第1题解答.INPUT “x=”;x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”;y ENDINPUT “x=”;x IF x<0 THENy=(x+2)^2 ELSEIF x=0 THENy=4ELSEy=(x-2)^2 END IFEND IFPRINT “y=”;y END34、程序框图:程序:INPUT “t=0”;t IF t<0 THEN PRINT “Please input again.”ELSE IF t>0 AND t<=180 THENy=0.2ELSEIF (t -180) MOD 60=0 THENy=0.2+0.1*(t-180)/60ELSEy=0.2+0.1*((t-180)\60+1)END IFEND IFPRINT “y=”;yEND IF END INPUT “n=”;n i=1 S=0WHILE i<=n S=S+1/i i=i+1 WENDPRINT “S=”;S END5、 (1)向下的运动共经过约199.805 m (2)第10次着地后反弹约0.098 m (3)全程共经过约299.609 m 第二章 复习参考题B 组(P35)1、 2、3、算法步骤:第一步,输入一个正整数x 和它的位数n . 第二步,判断n 是不是偶数,如果n 是偶数,令2n m =;如果n 是奇数,令12n m -=. 第三步,令1i =i=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i /2 k=k+1 WEND PRINT “(1)”;sum PRINT “(2)”;i PRINT “(3)”;2*sum -100 ENDINPUT “n=”;n IF n MOD 7=0 THEN PRINT “Sunday ” END IF IF n MOD 7=1 THEN PRINT “Monday ” END IF IF n MOD 7=2 THEN PRINT “Tuesday ” END IF IF n MOD 7=3 THEN PRINT “Wednesday ” END IF IF n MOD 7=4 THEN PRINT “Thursday ” END IF IF n MOD 7=5 THEN PRINT “Friday ” END IF IF n MOD 7=6 THEN PRINT “Saturday ” END IF END第四步,判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是,则使i 的值增加1,仍用i 表示;否则,x 不是回文数,结束算法.第五步,判断“i m >”是否成立. 若是,则n 是回文数,结束算法;否则,返回第四步.第二章 统计 2.1随机抽样 练习(P57)1、.况之间有误差. 如抽取的部分个体不能很好地代表总体,那么我们分析出的结果就会有偏差. 2、(1)抽签法:对高一年级全体学生450人进行编号,将学生的名字和对应的编号分别写在卡片上,并把450张卡片放入一个容器中,搅拌均匀后,每次不放回地从中抽取一张卡片,连续抽取50次,就得到参加这项活动的50名学生的编号. (2)随机数表法:第一步,先将450名学生编号,可以编为000,001, (449)第二步,在随机数表中任选一个数. 例如选出第7行第5列的数1(为了便于说明,下面摘取了附表的第6~10行).16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28第三步,从选定的数1开始向右读,得到一个三位数175,由于175<450,说明号码175在总体内,将它取出;继续向右读,得到331,由于331<450,说明号码331在总体内,将它取出;继续向右读,得到572,由于572>450,将它去掉. 按照这种方法继续向右读,依次下去,直到样本的50个号码全部取出,这样我们就得到了参加这项活动的50名学生. 3、用抽签法抽取样本的例子:为检查某班同学的学习情况,可用抽签法取出容量为5的样本. 用随机数表法抽取样本的例子:部分学生的心理调查等.抽签法能够保证总体中任何个体都以相同的机会被选到样本之中,因此保证了样本的代表性.4、与抽签法相比,随机数表法抽取样本的主要优点是节省人力、物力、财力和时间,缺点是所产生的样本不是真正的简单样本. 练习(P59)1、系统抽样的优点是:(1)简便易行;(2)当对总体结构有一定了解时,充分利用已有信息对总体中的个体进行排队后再抽样,可提高抽样调查;(3)当总体中的个体存在一种自然编号(如生产线上产品的质量控制)时,便于施行系统抽样法.系统抽样的缺点是:在不了解样本总体的情况下,所抽出的样本可能有一定的偏差. 2、(1)对这118名教师进行编号;(2)计算间隔1187.37516k==,由于k不是一个整数,我们从总体中随机剔除6个样本,再来进行系统抽样. 例如我们随机剔除了3,46,59,57,112,93这6名教师,然后再对剩余的112位教师进行编号,计算间隔7k=;(3)在1~7之间随机选取一个数字,例如选5,将5加上间隔7得到第2个个体编号12,再加7得到第3个个体编号19,依次进行下去,直到获取整个样本.3、由于身份证(18位)的倒数第二位表示性别,后三位是632的观众全部都是男性,所以这样获得的调查结果不能代表女性观众的意见,因此缺乏代表性.练习(P62)1、略2、这种说法有道理,因为一个好的抽样方法应该能够保证随着样本容量的增加,抽样调查结果会接近于普查的结果. 因此只要根据误差的要求取相应容量的样本进行调查,就可以节省人力、物力和财力.3、可以用分层抽样的方法进行抽样. 将麦田按照气候、土质、田间管理水平的不同而分成不同的层,然后按照各层麦田的面积比例及样本容量确定各层抽取的面积,再在各层中抽取个体(这里的个体是单位面积的一块地).习题2.1 A组(P63)1、产生随机样本的困难:(1)很难确定总体中所有个体的数目,例如调查对象是生产线上生产的产品.(2)成本高,要产生真正的简单随机样本,需要利用类似于抽签法中的抽签试验来产生非负整值随机数.(3)耗时多,产生非负整数值随机数和从总体中挑选出随机数所对的个体都需要时间.2、调查的总体是所有可能看电视的人群.学生A的设计方案考虑的人数是:上网而且登录某网址的人群,那些不能上网的人群,或者不登录某网址的人群就被排除在外了. 因此A方案抽取的样本的代表性差.学生B的设计方案考虑的人群是小区内的居民,有一定的片面性. 因此B方案抽取的样本的代表性差.学生C的设计方案考虑的人群是那些有电话的人群,也有一定的片面性. 因此C方案抽取的样本的代表性.所以,这三种调查方案都有一定的片面性,不能得到比较准确的收视率.3、(1)因为各个年级学习任务和学生年龄等因素的不同,影响各年级学生对学生活动的看法,所以按年级分层进行抽样调查,可以得到更有代表性的样本.(2)在抽样的过程中可能遇到的问题如敏感性问题:有些学生担心提出意见对自己不利;又如不响应问题:由于种种原因,有些学生不能发表意见;等等.(3)前面列举的两个问题都可能导致样本的统计推断结果的误差.(4)为解决敏感性问题,可以采用阅读与思考栏目“如何得到敏感性问题的诚实反应”中的方法设计调查问卷;为解决不响应问题,可以事先向全体学生宣传调查的意义,并安排专人负责发放和催收调查问卷,最大程度地回收有效调查问卷.4、将每一天看作一个个体,则总体由365天组成. 假设要抽取50个样本,将一年中的各天按先后次序编号为0~364天用简单随机抽样设计方案:制作365个号签,依次标上0~364. 将号签放到容器内充分搅拌均匀,从容器中任意不放回取出50个号签. 以签上的号码所对应的那些天构成样本,检测样本中所有个体的空气质量.用系统抽样设计抽样方案:先通过简单随机抽样方法从365天中随机抽出15天,再把剩下的350天重新按先后次序编号为0~349. 制作7个分别标有0~7的号签,放在容器中充分搅拌均匀. 从容器中任意取出一个号签,设取出的号签的编号为a,则编号为7(050)a k k +≤<所对应的那些天构成样本,检测样本中所有个体的空气质量.显然,系统抽样方案抽出的样本中个体在一年中排列的次序更规律,因此更好实施,更受方案的实施者欢迎.5、田径队运动员的总人数是564298+=(人),要得到28人的样本,占总体的比例为27.于是,应该在男运动员中随机抽取256167⨯=(人),在女运动员中随机抽取281612-=(人).这样我们就可以得到一个容量为28的样本.6、以10为分段间隔,首先在1~10的编号中,随机地选取一个编号,如6,那么这个获奖者奖品的编号是:6,16,26,36,46.7、说明:可以按年级分层抽样的方法设计方案. 习题2.1 B 组(P64)1、说明:可以按年级分层抽样的方法设计方案,调查问卷由学生所关心的问题组成. 例如:(1)你最喜欢哪一门课程? (2)你每月的零花钱平均是多少? (3)你最喜欢看《新闻联播》吗? (4)你每天早上几点起床? (5)你每天晚上几点睡觉?要根据统计的结果和具体的情况解释结论,主要从引起结论的可能原因及结论本身含义来解释.2、说明:这是一个开放性的题目,没有一个标准的答案. 2.2用样本估计总体 练习(P71) 1、说明:由于样本的极差为364.41362.51 1.90-=,取组距为0.19,将样本分为10组. 可以按照书上的方法制作频率分布表、频率分布直观图和频率折线图. 2、说明:此题目属于应用题,没有标准的答案.3、茎叶图为:由该图可以看出30名工人的日加工零件个数稳定在120件左右. 练习(P74)这里应该采用平均数来表示每一个国家项目的平均金额,因为它能反应所有项目的信息. 但平均数会受到极端数据2000万元的影响,所以大多数项目投资金额都和平均数相差比较大.练习(P79)1、甲乙两种水稻6年平均产量的平均数都是900,但甲的标准差约等于23.8,乙的标准差约等于41.6,所以甲的产量比较稳定.2、(1)平均重量496.86x ≈,标准差 6.55s ≈.(2)重量位于(,)x s x s -+之间有14袋白糖,所占的百分比约为66.67%.3、(1)略. (2)平均分19.25x ≈,中位数为15.2,标准差12.50s ≈.这些数据表明这些国家男性患该病的平均死亡率约为19.25,有一半国家的死亡率不超过15.2,15.2x >说明存在大的异常数据,值得关注. 这些异常数据使标准差增大. 习题2.2 A 组(P81) 1、(1)茎叶图为:(2)汞含量分布偏向于大于1.00 ppm 的方向,即多数鱼的汞含量分布在大于1.00 ppm 的区域. (3)不一定. 因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同. 即使各批鱼的汞含量分布相同,上面的数据只能为这个分布作出估计,不能保证平均汞含量大于1.00 ppm. (4)样本平均数 1.08x ≈,样本标准差0.45s ≈.(5)有28条鱼的汞含量在平均数与2倍标准差的和(差)的范围内.2比较短,所以在这批棉花中混进了一些次品.3、说明:应该查阅一下这所大学的其他招生信息,例如平均数信息、最低录取分数线信息等. 尽管该校友的分数位于中位数之下,而中位数本身并不能提供更多录取分数分布的信息.在已知最低录取分数线的情况下,很容易做出判断;在已知平均数小于中位数很多,则说明最低录取分数线较低,可以推荐该校友报考这所大学,否则还要获取其他的信息(如标准差的信息)来做出判断. 4、说明:(1)对,从平均数的角度考虑; (2)对,从标准差的角度考虑;(3)对,从标准差的角度考虑; (4)对,从平均数和标准差的角度考虑; 5、(1)不能. 因为平均收入和最高收入相差太多,说明高收入的职工只占极少数. 现在已知知道至少有一个人的收入为50100x =万元,那么其他员工的收入之和为4913.55010075ii x==⨯-=∑(万元)每人平均只有1.53. 如果再有几个收入特别高者,那么初进公司的员工的收入将会很低. (2)不能,要看中位数是多少.(3)能,可以确定有75%的员工工资在1万元以上,其中25%的员工工资在3万元以上.(4)收入的中位数大约是2万. 因为有年收入100万这个极端值的影响,使得年平均收入比中位数高许多.6、甲机床的平均数=1.5x 甲,标准差=1.2845s 甲;乙机床的平均数 1.2z y =,标准差0.8718z s =. 比较发现乙机床的平均数小而且标准差也比较小,说明乙机床生产出的次品比甲机床少,而且更为稳定,所以乙机床的性能较好. 7、(1)总体平均数为199.75,总体标准差为95.26. (2)可以使用抓阄法进行抽样. 样本平均数和标准差的计算结果和抽取到的样本有关. (3) (4)略 习题2.2 B 组(P82)1、(1)由于测试1T 的标准差小,所以测试1T 结果更稳定,所以该测试做得更好一些. (2)由于2T 测出的值偏高,有利于增强队员的信心,所以应该选择测试2T .2、说明:此题需要在本节开始的时候就布置,先让学生分头收集数据,汇总所收集的数据才能完成题目.2.3变量间的相关关系 练习(P85)1、从已经掌握的知识来看,吸烟会损害身体的健康. 但除了吸烟之外,还有许多其他的随机因素影响身体健康,人体健康是很多因素共同作用的结果. 我们可以找到长寿的吸烟者,也更容易发现由于吸烟而引发的患病者,所以吸烟不一定引起健康问题. 但吸烟引起健康问题的可能性大,因此“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法是不对的.2、从现在我们掌握的知识来看,没有发现根据说明“天鹅能够带来孩子”,完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素(例如独特的环境因素),即天鹅与婴儿出生率之间没有直接的关系,因此“天鹅能够带来孩子”的结论不可靠.而要证实此结论是否可靠,可以通过试验来进行. 相同的环境下将居民随机地分为两组,一组居民和天鹅一起生活(比如家中都饲养天鹅),而另一组居民的附近不让天鹅活动,对比两组居民的出生率是否相同. 练习(P92)1、当0x =时,147.767y =,这个值与实际卖出的热饮杯数150不符,原因是:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差;即使截距和斜率的估计没有误差,也不可能百分之百地保证对应于x ,预报值y 能够等于实际值y . 事实上:y bx a e =++. (这里e 是随机变量,是引起预报值y 与真实值(1)散点图如下: y 之间的误差的原因之一,其大小取决于e 的方差.)2、数据的散点图为:从这个散点图中可以看出,鸟的种类数与海拔高度应该为正相关(事实上相关系数为0.793). 但是从散点图的分布特点来看,它们之间的线性相关性不强. 习题2.3 A 组(P94)1、教师的水平与学生的学习成绩呈正相关关系. 又如,“水涨船高”“登高望远”等.2、(3)基本成正相关关系,即食品所含热量越高,口味越好.(4)因为当回归直线上方的食品与下方的食品所含热量相同时,其口味更好. 3、(1)散点图如下:(2)回归方程为:0.66954.933y x =+.(2)回归直线如下图所示:(3)加工零件的个数与所花费的时间呈正线性相关关系. 4、(1)散点图为:(2)回归方程为:0.546876.425y x =+.(3)由回归方程知,城镇居民的消费水平和工资收入之间呈正线性相关关系,即工资收入水平越高,城镇居民的消费水平越高. 习题2.3 B 组(P95) 1、(1)散点图如下:(2)回归方程为: 1.44715.843y x =-.(3)如果这座城市居民的年收入达到40亿元,估计这种商品的销售额为42.037y ≈(万元). 2、说明:本题是一个讨论题,按照教科书中的方法逐步展开即可.第二章 复习参考题A 组(P100)1、A .2、(1)该组的数据个数,该组的频数除以全体数据总数; (2)nmN. 3、(1)这个结果只能说明A 城市中光顾这家服务连锁店的人比其他人较少倾向于选择咖啡色,因为光顾连锁店的人使一种方便样本,不能代表A 城市其他人群的想法. (2)这两种调查的差异是由样本的代表性所引起的. 因为A 城市的调查结果来自于该市光顾这家服装连锁店的人群,这个样本不能很好地代表全国民众的观点.4、说明:这是一个敏感性问题,可以模仿阅读与思考栏目“如何得到敏感性问题的诚实反应”来设计提问方法.5、表略. 可以估计出句子中所含单词的分布,以及与该分布有关的数字特征,如平均数、标准差等.6、(1)可以用样本标准差来度量每一组成员的相似性,样本标准差越小,相似程度越高. (2)A 组的样本标准差为 3.730A S ≈,B 组的样本标准差为11.789B S ≈. 由于专业裁判给分更符合专业规则,相似程度应该高,因此A 组更像是由专业人士组成的.7、(1)中位数为182.5,平均数为217.1875.(2)这两种数字特征不同的主要原因是,430比其他的数据大得多,应该查找430是否由某种错误而产生的. 如果这个大数据的采集正确,用平均数更合适,因为它利用了所有数据的信息;如果这个大数据的采集不正确,用中位数更合适,因为它不受极端值的影响,稳定性好. 8、(1)略.(2)系数0.42是回归直线的斜率,意味着:对于农村考生,每年的入学率平均增长0.42%.(3)城市的大学入学率年增长最快. 说明:(4)可以模仿(1)(2)(3)的方法分析数据.第二章 复习参考题B 组(P101)1、频率分布如下表:从表中看出当把指标定为17.46千元 时,月65%的推销员 经过努力才能完成销 售指标.2、(1)数据的散点图如下:(2)用y 表示身高,x 表示年龄,则数据的回归方程为 6.31771.984y x =+. (3)在该例中,斜率6.317表示孩子在一年中增加的高度.(4)每年身高的增长数略. 3~16岁的身高年均增长约为6.323 cm. (5)斜率与每年平均增长的身高之间之间近似相等.第三章 概率3.1随机事件的概率 练习(P113) 1、(1)试验可能出现的结果有3个,两个均为正面、一个正面一个反面、两个均为反面. (2)通过与其他同学的结果汇总,可以发现出现一个正面一个反面的次数最多,大约在50次左右,两个均为正面的次数和两个均为反面的次数在25次左右. 由此可以估计出现一个正面一个反面的概率为0.50,出现两个均为正面的概率和两个均为反面的概率均为0.25. 2、略 3、(1)例如:北京四月飞雪;某人花两元钱买福利彩票,中了特等奖;同时抛10枚硬币,10枚都正面朝上.(2)例如:在王府井大街问路时,碰到会说中文的人;去烤鸭店吃饭的顾客点烤鸭;在1~1000的自然数任选一个数,选到的数大于1. 练习(P118)1、说明:例如,计算机键盘上各键盘的安排,公交线路及其各站点的安排,抽奖活动中各奖项的安排等,其中都用到了概率. 学生可能举出各种各样的例子,关键是引导他们正确分析例子中蕴涵的概率思想.2、通过掷硬币或抽签的方法,决定谁先发球,这两种方法都是公平的. 而猜拳的方法不太公平,因为出拳有时间差,个人反应也不一样.3、这种说法是错误的. 因为掷骰子一次得到2是一个随机事件,在一次试验中它可能发生也可能不发生. 掷6次骰子就是做6次试验,每次试验的结果都是随机的,可能出现2也可能不出现2,所以6次试验中有可能一次2都不出现,也可能出现1次,2次,…,6次. 练习(P121)1、0.72、0.6153、0.44、D5、B 习题3.1 A 组(P123) 1、D . 2、(1)0; (2)0.2; (3)1.3、(1)430.067645≈; (2)900.140645≈; (3)7010.891645-≈.4、略5、0.136、说明:本题是想通过试验的方法,得到这种摸球游戏对先摸者和后摸者是公平的结论. 最好把全班同学的结果汇总,根据两个事件出现的频率比较近,猜测在第一种情况下摸到红球的概率为110,在第二种下也为110. 第4次摸到红球的频率与第1次摸到红球的频率应该相差不远,因为不论哪种情况,第4次和第1次摸到红球的概率都是1 10.习题3.1 B组(P124)1、D.2、略. 说明:本题是为了学生根据实际数据作出一些推断. 一般我们假定每个人的生日在12个月中哪一个月是等可能的,这个假定是否成立,引导学生通过收集的数据作出初步的推断.3.2古典概率练习(P130)1、110. 2、17. 3、16.练习(P133)1、38,38.2、(1)113;(2)1213;(3)14;(4)313;(5)0;(6)213;(7)12;(8)1.说明:模拟的方法有两种.(1)把1~52个自然数分别与每张牌对应,再用计算机做模拟试验.(2)让计算机分两次产生两个随机数,第一次产生1~4的随机数,代表4个花色;第二次产生1~13的随机数,代表牌号.3、(1)不可能事件,概率为0;(2)随机事件,概率为49;(3)必然事件,概率为1;(4)让计算机产生1~9的随机数,1~4代表白球,5~9代表黑球.4、(1)16;(2)略;(3)应该相差不大,但会有差异. 存在差异的主要原因是随机事件在每次试验中是否发生是随机的,但在200次试验中,该事件发生的次数又是有规律的,所以一般情况下所得的频率与概率相差不大.习题3.2 A组(P133)1、游戏1:取红球与取白球的概率都为12,因此规则是公平的.游戏2:取两球同色的概率为13,异色的概率为23,因此规则是不公平的.游戏3:取两球同色的概率为12,异色的概率为12,因此规则是公平的.2、第一位可以是1~9这9个数字中的一个,第二位可以是0~9这10个数字中的一个,所以(1)190;(2)18919090-=;(3)9919010-=3、(1)0.52;(2)0.18.4、(1)12;(2)16;(3)56;(4)16.5、(1)25;(2)825.6、(1)920;(2)920;(3)12.习题3.2 B组(P134)1、(1)13;(2)14.2、(1)35;(2)310;(3)910.说明:(3)先计算该事件的对立事件发生的概率会比较简单.3、具体步骤如下:①建立概率模型. 首先要模拟每个人的出生月份,可用1,2,…,11,12表示月份,用产生取整数值的随机数的办法,随机产生1~12之间的随机数. 由于模拟的对象是一个有10个人的集体,故把连续产生的10个随机数作为一组模拟结果,可模拟产生100组这样的结果.②进行模拟试验. 可用计算器或计算机进行模拟试验.如使用Excel软件,可参看教科书125页的步骤,下图是模拟的结果:其中,A,B,C,D,E,F,G,H,I,J的每一行表示对一个10人集体的模拟结果. 这样的试验一共做了100次,所以共有100行,表示随机抽取了100个集体.③统计试验的结果. K,L,M,N列表示统计结果. 例如,第一行前十列中至少有两个数相同,表示这个集体中至少有两个人的生日在同一月. 本题的难点是统计每一行前十列中至少有两个数相同的个数. 由于需要判断的条件态度,所以用K,L,M三列分三次完成统计.其中K列的公式为“=IF(OR(A1=B1,A1=C1,A1=D1,A1=E1,A1=F1,A1=G1,A1=H1,A1=I1,A1=J1,B1=C1,B1=D1,B1=E1,B1=F1,B1=G1,B1=H1,B1=I1,B1=J1,C1=D1,C1=E1,C1=F1,C1=G1,C1=H1,C1=I1,C1=J1,D1=E1,D1=F1,D1=G1,D1=H1,D1=I1,D1=J1),1,0)”,L列的公式为“=IF(OR(E1=F1,E1=G1,E1=H1,E1=I1,E1=J1,F1=G1,F1=H1,F1=I1,F1=J1,G1=H1,G1=I1,G1=J1,H1=I1,H1=J1,I1=J1),1,0)”,M列的公式为“=IF(OR(K1=1,L1=1),1,0)”,M列的值为1表示该行所代表的10人集体中至少有两个人的生日在同一个月. N1表示100个10人集体中至少有两个人的生日在同一个月的个数,其公式为“=SUM(M$1:M$100)”. N1除以100所得的结果0.98,就是用模拟方法计算10人集体中至少有两个人的生日在同一个月的概率的估计值. 可以看出,这个估计值很接近1.3.3几何概率。
工程力学(静力学答案)
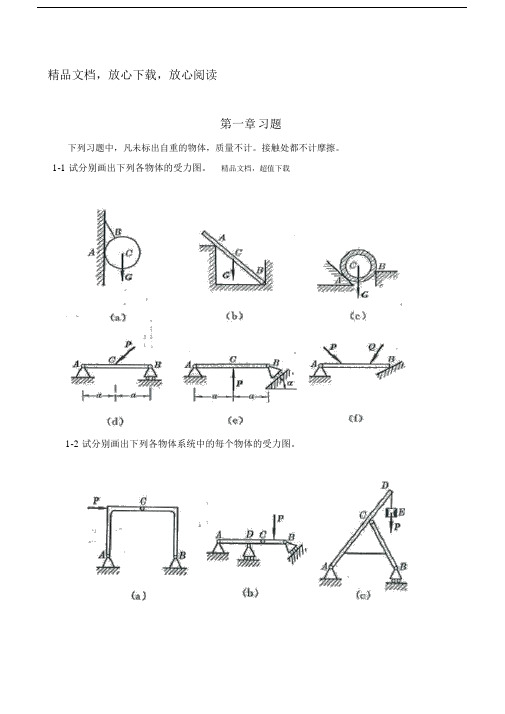
精品文档,放心下载,放心阅读第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1 试分别画出下列各物体的受力图。
精品文档,超值下载1-2 试分别画出下列各物体系统中的每个物体的受力图。
1-3 试分别画出整个系统以及杆BD ,AD ,AB(带滑轮 C,重物 E 和一段绳索)的受力图。
1-4 构架如图所示,试分别画出杆HED ,杆 BDC 及杆 AEC 的受力图。
1-5 构架如图所示,试分别画出杆BDH ,杆 AB ,销钉 A 及整个系统的受力图。
1-6 构架如图所示,试分别画出杆AEB ,销钉 A 及整个系统的受力图。
1-7 构架如图所示,试分别画出杆AEB ,销钉 C,销钉 A 及整个系统的受力图。
1-8 结构如图所示,力 P 作用在销钉 C 上,试分别画出 AC ,BCE 及 DEH 部分的受力图。
参考答案1-1 解:1-2 解:1-3 解:1-4 解:1-5 解:1-6 解:1-7 解:1-8 解:第二章 习题参考答案2-1 解:由解析法, F RX X P 2 cos P 3 80NF RYY P 1 P 2 sin 140NF R F 2 F 2 161.2N故: RX RY(F R , P 1) arccos F RY 29 44F R2-2 解:即求此力系的合力,沿OB建立 x 坐标,由解析法,有F RX X P1 cos45 P2P3 cos453KNF RY Y P1 sin45 P3 sin 450故:F R F RX2F RY23KN 方向沿OB。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a)由平衡方程有:X 0 F AC sin 30F AB0Y 0 F AC cos30W0联立上二式,解得:F AB0.577W (拉力)FAC 1.155W(压力)(b)由平衡方程有:X 0 F AC F AB cos700Y 0 F AB sin 70W0联立上二式,解得:FAB 1.064W(拉力)F AC0.364W (压力)(c)由平衡方程有:X 0 F AC cos60F AB cos300Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:FAB 0.5W(拉力)FAC 0.866W(压力)(d)由平衡方程有:X 0 F AB sin 30F AC sin 300Y 0 F AB cos30F AC cos30 W0联立上二式,解得:FAB 0.577W(拉力)FAC 0.577W(拉力)2-4 解:( a)受力分析如图所示:x 0 F RA4P cos 45 0 42由22F RA15.8 KNF RA2F RB P sin 45 042由Y 022F RB7.1KN(b)解:受力分析如图所示:由x 0 F RA 3F RB cos45 P cos45 0 10FRA 1F RB sin 45 P sin 45 0Y 010联立上二式,得:F RA22.4KNF RB10KN2-5 解:几何法:系统受力如图所示三力汇交于点 D,其封闭的力三角形如图示所以:FRA5KN(压力)F RB 5KN(与X轴正向夹150度)2-6 解:受力如图所示:已知, F R G1,F AC G2x 0F r 0由F AC coscos G1 G2由Y 0 F AC sinF N W 0F N W G2 sin W G22G122-7 解:受力分析如图所示,取左半部分为研究对象x 0由P F RA cos 45 F CB cos45 0 Y 0 F CB sin 45F RA sin 450联立后,解得:FRA0.707 PF RB0.707 P由二力平衡定理FRBFCBFCB0.707 P2-8 解:杆 AB,AC均为二力杆,取 A 点平衡x 0由F AC cos 60 F AB cos30 W 0Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:F AB7.32KN (受压)FAC 27.3KN(受压)2-9 解:各处全为柔索约束,故反力全为拉力,以D, B 点分别列平衡方程(1)取 D 点,列平衡方程x 0T DB sinW cos0由T DB Wctg0(2)取 B 点列平衡方程由Y 0 T sinT BD cos0T T BD ctg Wctg 230KN 2-10 解:取 B 为研究对象:FBC由Y 0 F BC sinP 0Psin取 C 为研究对象:x 0F DC sin F CE sin0由F BC cos由Y 0F BC sin F DC cos F CE cos0联立上二式,且有FBCFBC解得:P cos1 FCEsin2cos2取 E 为研究对象:由 Y 0 F NH F CE cos0F CE F CE 故有:F NH P cos 1 P2 sin 2 cos cos22sin 2-11 解:取 A 点平衡:x 0F AB sin 75 F AD sin 75 0Y 0 F AB cos75 F AD cos75 P 0PF AD F AB联立后可得: 2cos 75取 D 点平衡,取如图坐标系:x 0F AD cos5 F ND cos80 0cos5F ND F ADcos80由对称性及F AD F ADF N2F ND2 cos5FAD2 cos5P166.2KNcos80cos802cos 75 2-12 解:整体受力交于O点,列 O点平衡x 0由F RA cosF DC P cos30 0Y 0 F RA sin P sin 300联立上二式得:F RA 2.92 KNFDC 1.33KN(压力)列 C点平衡4x0FDC FAC53Y0FBCFAC5联立上二式得:FAC1.67KN(拉力)F BC 1.0KN (压力)2-13 解:(1)取 DEH部分,对 H点列平衡x 0 F RD 2F RE 0 5Y0FRD1Q 05联立方程后解得:FRD5QF RE2Q(2)取 ABCE部分,对 C 点列平衡x0F RE F RA cos 450Y 0 F RB F RA sin 45 P0且F RE F RE联立上面各式得:FRA2 2QF RB 2Q P(3)取 BCE 部分。
全国通用高中数学第一章算法初步1.1.1算法的概念练习新人教B版必修3(2021年整理)

(全国通用版)2018-2019高中数学第一章算法初步1.1.1 算法的概念练习新人教B版必修3编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国通用版)2018-2019高中数学第一章算法初步 1.1.1 算法的概念练习新人教B版必修3)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国通用版)2018-2019高中数学第一章算法初步 1.1.1 算法的概念练习新人教B版必修3的全部内容。
1.1。
1 算法的概念课时过关·能力提升1下列关于算法的说法正确的有()①算法必须在有限步操作后终止;②算法的每一步操作必须是明确的,不能有歧义;③算法执行后一定产生确定的结果。
A。
1个B。
2个 C.3个D。
0个解析算法具有有穷性和确定性,则①②③均正确。
答案C2指出下列哪个不是算法()A。
解方程3x-6=0的过程是移项和系数化为1B.从济南到温哥华要先乘火车到北京,再转乘飞机到温哥华C.解方程2x2+x—1=0D。
利用公式S=πr2计算半径为3的圆的面积就是计算π×32解析C选项没给出解这个方程的程序或步骤.答案C3已知直角三角形的两条直角边长分别为a,b,求斜边长c的一个算法分为以下三步:①计算cA。
①②③B。
②③①C.①③②D。
②①③答案D4对于一般的二元一次方程A.a1≠0B。
a2≠0C.a1b2-a2b1≠0D。
a1b1-a2b2≠0答案C5用Scilab指令解二元一次方程A.A=[2,3,7,-2];B=[1;5];B。
A=[2,3;7,—2];B=[1;5];C。
A=[2,7,3,-2];B=[1;5];D。
第一章 算法初步 1.2.2有详细答案
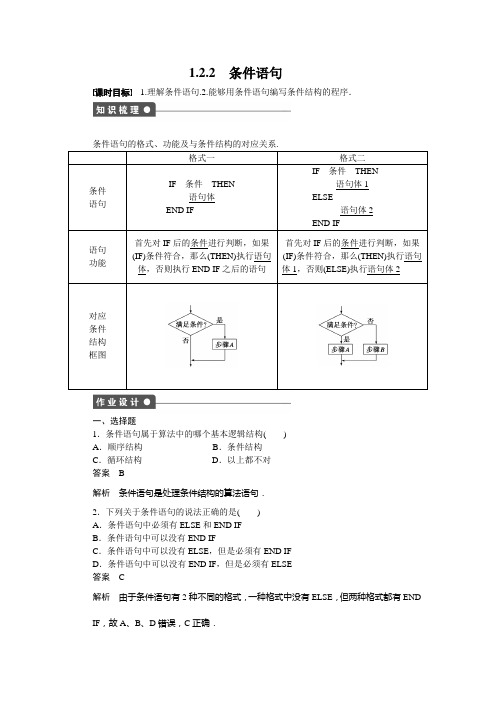
6.下面给出的是条件语句编写的程序,该程序的功能是求函数________的函数值.
INPUTx
IFx<=3THEN
y=2*x
ELSE IF
PRINT y
END
答案f(x)=
解析该程序的主要功能是对分段函数f(x)求值.
当x≤3时,y=2x;当x>3时,y=x2-1.
所以函数为f(x)=.
7.如下图所给出的是一个算法的程序.如果输出的y的值是20,则输入的x的值是________.
(4)为了程序的可读性,一般IF、ELSE与ENDIF顶格书写,其他的语句体前面则空两格.
2.计算机能识别的数学符号:
加号“+”
减号“-”
乘号“*”如a乘以b写作:a*b
除号“/”如a除以b写作:a/b
乘方“^”如a的平方写作:a^2
大于或等于“≥”写作:>=
不等式“≠”写作:< >
首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句
体1,否则(ELSE)执行语句体2
对应
条件
结构
框图
一、选择题
1.条件语句属于算法中的哪个基本逻辑结构()
A.顺序结构B.条件结构
C.循环结构D.以上都不对
答案B
解析条件语句是处理条件结构的算法语句.
2.下列关于条件语句的说法正确的是()
A.条件语句中必须有ELSE和END IF
B.条件语句中可以没有END IF
C.条件语句中可以没有ELSE,但是必须有END IF
D.条件语句中可以没有END IF,但是必须有ELSE
答案C
解析由于条件语句有2种不同的格式,一种格式中没有ELSE,但两种格式都有END IF,故A、B、D错误,C正确.
管理会计计算题及答案
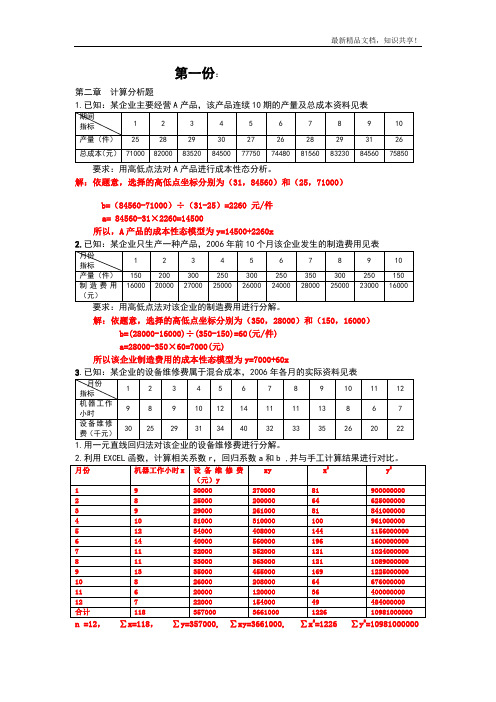
第一份:第二章计算分析题1.已知:某企业主要经营A产品,该产品连续10期的产量及总成本资料见表要求:用高低点法对A产品进行成本性态分析。
解:依题意,选择的高低点坐标分别为(31,84560)和(25,71000)b=(84560-71000)÷(31-25)=2260 元/件a= 84560-31×2260=14500所以,A产品的成本性态模型为y=14500+2260x2.已知:某企业只生产一种产品,2006年前10个月该企业发生的制造费用见表要求:用高低点法对该企业的制造费用进行分解。
解:依题意,选择的高低点坐标分别为(350,28000)和(150,16000)b=(28000-16000)÷(350-150)=60(元/件)a=28000-350×60=7000(元)所以该企业制造费用的成本性态模型为y=7000+60x3.已知:某企业的设备维修费属于混合成本,2006年各月的实际资料见表1.用一元直线回归法对该企业的设备维修费进行分解。
2.利用EXCEL函数,计算相关系数r,回归系数a和b ,并与手工计算结果进行对比。
r=(12×3661000-118×357000)÷(12×1226-1182)×(12×10981000000-3570002)≈0.9785→+1 (x与y基本正相关)b=(12×3661000-118×357000)÷(12×1226-1182)=2292 元/小时a=(357000-2292×118)÷12=7212 元因此,该企业的成本性态模型为:y=7212+2292x第三章变动成本法计算成本题(注:计算变动非生产成本的业务量用销售量)1.已知:某公司从事单一产品生产,连续三年销售量均为1000件,而三年的产量分别为1000件、1200件和800件。
(完整版)1-1算法的概念练习题及答案(可编辑修改word版)

[当堂达标]1.我们已学过的算法有一元二次方程的求根公式、加减消元法求二元一次方程组的解、二分法求函数零点等,对算法的描述有:①对一类问题都有效;②对个别问题有效;③计算可以一步一步进行,每一步都有唯一结果;④是一种通法,只要按部就班地做,总能得到结果.以上描述正确的有( )A.1 个B.2 个C.3 个D.4 个答案:C 解析:设计的算法应该是对一类问题都有效,而不是只对个别问题有效.所以①对,②不对.由算法的确定性、有限性、顺序性易知③④都是正确的,故描述正确的有3 个.2.下列所给问题中,不能设计一个算法求解的是( )A.用二分法求方程x2-3=0 的近似解(精确到0.01)B.解方程组Error!C.求半径为2 的球的体积D.判断y=x2 在R 上是否具有单调性答案:D 解析:选项A,B,C 中的问题都可以设计算法求解,而D 项中的问题则不能设计算法求解.3.“已知直角三角形两直角边长为a,b,求斜边长c”的一个算法分下列三步:①计算c=a2+b2;②输入直角三角形两直角边长a,b 的值;③输出斜边长c 的值.= 其中正确的顺序是 .答案:②①③ 解析:根据运算顺序,易知算法顺序应是②①③. 4.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99, 求它的总分和平均分的一个算法如下,请将其补充完整:第一步:取 A =89,B =96,C =99. 第二步, . 第三步,.第四步,输出计算结果. 答案:计算总分 D =A +B +C计算平均分 E D35.已知函数 y =Error!试设计一个算法,输入 x 的值,求对应的函数值.解:算法如下: 第一步,输入 x 的值;第二步,当 x ≤-1 时,计算 y =-x 2-1,否则执行第三步; 第三步,计算 y =x 3; 第四步,输出 y .[课堂小结]1. 算法的特点:有限性、确定性、逻辑性、不唯一性、普遍性.2. 算法设计的要求:(1) 写出的算法必须能够解决一类问题(如判断一个整数是否为质数,求任意一个方程的近似解等),并且能够重复使用.(2) 要使算法尽量简单,步骤尽量少.(3) 要保证算法正确,且算法步骤能够一步一步执行,每一步执行的操作必须确切,不能含混不清,而且在有限步后能得到结果.教材习题答案第一章算法初步1.1算法与程序框图1.1.1算法的概念[教材习题答案与解析][练习]1.解:第一步,输入任意正实数r.第二步,计算S=πr2.第三步,输出圆的面积S.2.解:根据因数的定义,可设计出下面的一个算法:第一步,判断n 是否等于2.若n=2,则n 的因数为1,n;若n>2,则执行第二步.第二步,依次从1 到n 检验是不是能整除n.若能整除n,则是n 的因数;若不能整除n,则不是n 的因数.第三步,输出n 的所有因数.= + + +…+ ; = + + +…+ +…; = + + +…+ (n ≥1 且 n ∈N ).[易错误区] 对算法含义及特征理解不清致误[典例] 计算下列各式中 S 的值,能设计算法求解的是( )①S1 1 1 12 4 8 ②S1 1 12 4 8 ③S 1 1 1 2100 121001 *2 4 8 2nA .①②B .①③C .②③D .①②③[答案] B[解析] 算法是用来求解一类问题的,在实际算法中 n 的值是具体确定的,算法会根据具体确定的 n 来求值计算,所以①③是正确的, 而算法的步骤是有限的,即执行有限步骤后一定能解决问题,而②显然不符合有限性,所以②不正确.[常见误区]明确算法的含义(1) 算法是为解决某一类问题而设计的一系列可操作或可计算的步骤,通过这些步骤能够有效地解决问题.(2) 算法具有有限性、确定性、有序性和不唯一性的特征,在解题中要灵活应用,如本例中主要考查算法的有限性.[类题试解] 给出下列说法:①从北京到上海先乘出租车到火车站,再坐高铁到上海;②解方程2x+1=0 的过程是先移项再把x 的系数化为1;③利用公式C=2πr 计算半径为2 的圆的周长为2π×2;④解不等式x2+x-1>0.其中是算法的是.答案:①②③ 解析:①②给出了解决问题的方法和步骤,是算法;③利用公式计算属于算法;④没有给出解决问题的方法,不是算法.。
2020高中数学 第一章 算法初步 1.1.1 算法的概念练习(含解析)(1)

1.1。
1 算法的概念[A 基础达标]1.下列关于算法的描述正确的是( )A.算法与求解一个问题的方法相同B.算法只能解决一个问题,不能重复使用C.算法过程要一步一步执行,每步执行的操作必须确切D.有的算法执行完后,可能无结果解析:选C.算法与求解一个问题的方法既有区别又有联系,故A 不对;算法能重复使用,故B不对;每个算法执行后必须有结果,故D不对;由算法的有序性和确定性可知C正确.2.关于一元二次方程x2-5x+6=0的求根问题,下列说法正确的是( )A.只能设计一种算法B.可以设计两种算法C.不能设计算法D.不能根据解题过程设计算法解析:选B。
算法具有不唯一性,对于一个问题,我们可以设计不同的算法.3.下列所给问题中,不能设计一个算法求解的是()A.用二分法求方程x2-3=0的近似解(精确度0.01)B.解方程组错误!C.求半径为2的球的体积D.求S=1+2+3+…的值解析:选D.对于D,S=1+2+3+…,不知道需要多少步完成,所以不能设计一个算法求解.4.对于算法:第一步,输入n.第二步,判断n是否等于2,若n=2,则n满足条件;若n〉2,则执行第三步.第三步,依次从2到(n-1)检验能不能整除n,若不能整除n,则执行第四步;若能整除n,则执行第一步.第四步,输出n.满足条件的n是()A.质数B.奇数C.偶数D.约数解析:选A.此题首先要理解质数,只能被1和自身整除的大于1的整数叫质数。
2是最小的质数,这个算法通过对2到(n-1)一一验证,看是否有其他约数,来判断其是否为质数.5.求过P(a1,b1),Q(a2,b2)(a1,b1,a2,b2∈R)两点的直线的斜率有如下算法,请在横线上填上适当的步骤:第一步,取x1=a1,y1=b1,x2=a2,y2=b2.第二步,若x1=x2,则输出“斜率不存在”,结束算法;否则,执行第三步.第三步,________________.第四步,输出k。
高一数学算法初步练习题及答案

第一章算法初步算法与程序框图算法的概念1.下面的结论正确的是【】A.一个程序的算法步骤是可逆的B.一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D.设计算法要本着简单方便的原则2.下面对算法描述正确的一项是【】A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同;结果必然不同3.下面哪个不是算法的特征【】A.抽象性B.精确性C.有穷性D.唯一性4.算法的有穷性是指【】A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤;从下列选项中选最好的一种算法【】洗脸刷牙、S2刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播吃饭同时听广播、S2泡面;S3烧水同时洗脸刷牙;S4刷水壶6.看下面的四段话;其中不是解决问题的算法是【】A.从济南到北京旅游;先坐火车;再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程210x-=有两个实根D.求1+2+3+4+5的值;先计算1+2=3;再计算3+3=6;6+4=10;10+5=15;最终结果为157.写出求1+2+3+4+5+6+…+100的一个算法.可运用公式1+2+3+…+n=(1)2n n+直接计算.第一步______①_______;第二步_______②________;第三步输出计算的结果.8.写出1×2×3×4×5×6的一个算法.1.1.2 程序框图1.算法的三种基本结构是【】A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2.给出以下四个问题;①输入x;输出它的相反数;②求面积为6的正方形的周长;③在三个不等实数,,a b c中;求一个数的最大数;④求函数1,0()2,0x xf xx x-≥⎧=⎨+<⎩的函数值。
算法与程序框图练习题及答案

第一章算法初步1.1算法与程序框图1.1.1算法的概念1•已知直角三角形两直角边长为d ",求斜边长C 的一个算法分下列三步:①计算C = Ja2:②输入直角三角形两直角边长α,b 的值;③输出斜边长C 的值,其中正确的顺序是【 ]A.①®®B.②③①C.®@②D.②①③ 2•若/ (x)在区间0b]内单调,且< O ,则f (Λ)在区间",对内【 A.至多有一个根B.至少有一个根C.恰好有一个根D.不确定 3. 已知一个学生的语文成绩为89,数学成绩为96.外语成绩为99•求他的总分和平均成绩的一个算法为:第一步:取 A=89 .B=96 .C=99;第二步: ______ ①_______ :第三步: ______ ② ________:第四步:输出计算的结果.4•写出按从小到大的顺序重新排列x,y,z 三个数值的算法.1. 1. 2程序框图1. 在程序框图中,算法中间要处理数据或计算,可分别写在不同的A.处理框内B.判断框内C.终端框内D.输入输出框内2. 将两个数a=10, b=18交换,使a=18, b=10,下而语句正确一组是3指出下列语句的错误,并改正:(1)(2)(3)(4)(5)(6) 4. 2000年我国人口为13亿,如果人口每年的自然增长率为7%o,那么多少年 后我国人口将达到15亿?设计一个算法的程序・5 •儿童乘坐火车时,若身髙不超过l.lm,则不需买票;若身髙超过Llm 但不超过1.4m,则需买 匕票:若身髙超过l ・4m,则需买全票•试设计一个买票的算法,并画出相应的程序框图及程序。
1・2基本算法语句1.2.1输入语句、输出语句和赋值语句1 •在输入语句中,若同时输入多个变量,则变量之间的分隔符号是A.逗号B.空格C.分号D.顿号Λ=β=50 .x=l, y t =2t ∑=3 INPUT INPUT PRINT PRINT HOW Old are you ' X ,X A+B=; C GOOd-bve!b = 4a=b b = a输出a,h以上程序输出的结果是A34 B. 4,4 3请从下而具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内・ 一般画成 ----------------- f 麺1 ---- ( )圆箱爼形[结束I4. 设计一个算法,要求输入一个圆的半径,便能输出该圆的周长和而积 5 取3.14)o1.2.2-1.2.3条件语句和循环语句Io 给出程序:INPUT ΛIF Λ>9 AND XVloo THENα=Λβ∖10b=x MOD 10 (注:“\"是X 除以10的商,“MOD"是X 除以10的余数)x=10*b+ΛPRINT XEND IFEND上述程序输岀A-的含义是— _____________________2某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算:0.53d? (Q ≤50),* j50 X 0.53 + (ω 一 50) X 0.85(6? > 50).C.3,3 DA3—般画成卩行四边形 彳输入仇卜∕¾⅛n∕通第画成菱形通常画成矩形岀相应的程序框图.3如果学生的成绩大于或等于60分,则输岀“及格“,否则输出“不及格“用程序框图表示这一算法过程.4•火车站对乘客退票收取一泄的费用,具体办法是:按票价每10元(不足10元按10元计算)核收2 元:2元以下的票不退.试写出票价为X元的车票退掉后,返还的金额y元的算法的程序框图.5.写出计算12÷32 +52+∙..+9992的程序,并画出程序框图.13算法案例1•用秦九韶算法求多项式/(x)= 7√+3√ -5x + ll在X = 23时的值,在运算过程中下列数值不会出现的是【】A. 164B. 3767C. 86652D. 851692.三位七进制的数表示的最大的十进制的数是【】A.322 B .402 C.342 D.3653•将十进制下的数72转化为八进制下的数为【】A. Oll⑻B. IOI mC. IIO mD. IlI m4.将十进制数3344化为七进制等于 _____________ ■5.我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五:鸡母一, 值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?6.写出用二分法求方程A j-A-I= 0在区间[1, 1.5]上的一个解的算法(误差不超过0.001),并画岀相应的程序框图及程序.第一章算法初步参考答案1.1算法与程序框图1.1.1算法的概念1.D2.C3.① S = A + B + C i ®X=A^B^C34・算法:(1)输入X,y,z三个数值;(2)从三个数值中挑出最小者并换到兀中:(3)从y,z中挑出最小者并换到y中;(4)输出排序的结果.1. 1. 2程序框图1. A2. B3(1)变量不能够连续赋值.可以改为A==50B=A(2)一个赋值语句只能给一个变量赋值.可以改为Λ= 1>-24=3(3)INPUT语句“提示内容”后面有个分号(:)改为INPUT “ HOW Old are you? xINPUT X(5)PRINT语句"提示内容”部分要加引号("”)改为PRINT “A+B=”;C(6)PRINT语句可以没有表达式部分,但提示内容必须加引号(“”)改为PRINT U GOOd-bye!"4.A=13R=0.007/=1DOA=A* (1+R)i=i+lLOOP UNTIL A>=15i=i-1PRINT “达到或超过15亿人口需要的年数为:";/END5.是否买票,买何种票,都是以身高作为条件进行判断的,此处形成条件结构嵌套.程序框图是:(开始〕/输入身>⅜h∕/输出买半票信思/ /输出买全票信息/(≡iΓ)程序是:INPUT “请输入身高h (米):”;hIF h<=l.l THENPRINT “ 免票”ELSEIF h<=1.4 THENPRINT “买半票”ELSEPRINT “买全票”END IFEND IFEND1.2基本算法语句1.2.1输入、输出语句和赋值语句L A 2. B 3.终端框(起止框):表示•个平勰癡成/输出n/---------------- ; ------------- 流程线(指向线):农示操作的先后次序⅛4.输入RC=2*3.14*/?S=3.14*/输出该圆的周长为C输出该圆的而积为S1.2.2-1.2.3条件语句和循环语句1・交换十位数与个位数的位麗2.算法:第一步:输入物品重疑3:第二步:如果ω≤50,那么/=0.53 6>,否则,∕=5OXO∙53+(3 —50) X0.85;第三步:输出物品重疑G和托运费.人相应的程序框图./输入co // ⅜U ITIG) , f/3∙[W½J/输入成绩A/是/输出“及格”/ /输出“木及格”/l⅞⅞J4.5.程序:/==1DOS=S+∕Λ2/=∕+2LOOP UNTlL ∕>999PRINT SEND 1・3算法案例LD 2.C 3.C 4. 12515⑺5•设鸡翁.母、雏各八八Z只,则5A +3>-+∣=1OO,χ + y + Z = 100,由②•得Z=IOO—x—y,③代入①,得5A÷3y÷1(K) ~-~ v-=100,7.v+4y∙=100 ・④求方程④的解,可由程序解之.程序:x=ly=lWHILE x<=14WHILE y<=25IF 7*x+4*y=100 THEN2=100—A—yPRINT “鸡翁、母、雏的个数别为:S X, y t ZEND IF y=y+ιWENDX=X+\y=lWENDEND6.用二分法求方程的近似值一般取区间[“,h^]具有以下特征: f (U) <0, / (b) >0.由于/ (1) =P-I-I=-KO, f (1.5) =L53-1.5-1=O.875>O,所以取[1, 1.5]中点上导=1.25研究,以下同求X2-2=0的根的方法.相应的程序框图是:c=0. OOla=x b=x/输冷κ/程序:a=∖b=\.5c=0.001DOΛ =(a+h ) /2f (a) =a 3~a~ 1f (X y) =X 3—A— 1IF f (x) =0 THENPRINT W: XELSEIF f(t∕)(X) <0 THENb=xELSE a=xEND IFEND IFLOOP UNTIL ABS (u~∕?) <=cPRINT "方程的一个近似解.= ”:XEND谢谢大家。
第一章 算法初步1.1.2.2 Word版

(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题5分,共20分)1.下列四种说法中正确的有( )①任何一个算法都离不开顺序结构;②程序框图中,根据条件是否成立有不同的流向;③循环体是指按照一定条件,反复执行某一处理步骤;④循环结构中有条件结构,条件结构中有循环结构.A .1个B .2个C .3个D .4个解析: 因为顺序结构是任何一个算法都离不开的基本结构,所以①正确;在一个算法中,经常会遇到一些条件的判断,算法流程根据条件是否成立有不同的流向,因此②正确;根据循环体的定义知,③正确;④不正确.因为在条件结构中可以不含循环结构.综上分析知①②③正确,④不正确.故选C.答案: C2.(2015·四川卷)执行如图所示的程序框图,输出S 的值为( )A .-32 B.32C .-12 D.12解析: 根据题中程序框图,可知k =1,k =1+1=2<4,k =2+1=3<4,k =3+1=4,k =4+1=5>4,S =sin 5π6=12.故输出S 的值为12.故选D. 答案: D3.(2015·天津卷)阅读如图的程序框图,运行相应的程序,则输出i 的值为( )A.2 B.3C.4 D.5解析:第一次执行,i=1,S=10-1=9;第二次执行,i=2,S=9-2=7;第三次执行,i=3,S=7-3=4;第四次执行,i=4,S=4-4=0,满足条件,则退出循环,所以输出i的值为4.故选C.答案: C4.(2015·菏泽模拟)如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为()A.S=S(n+1) B.S=Sx n+1C.S=Sn D.S=Sx n解析:赋值框内应为累乘积,累乘积=前面项累乘积×第n项,即S=Sx n,故选D.答案: D二、填空题(每小题5分,共15分)5.阅读如图所示的程序框图,运行相应的程序.如果输入某个正整数n后,输出的S∈(10,20),那么n的值为________.解析: 先读出框图的计算功能,再结合等比数列求和公式求解.框图功能为求和,即S =1+21+22+…+2n -1.由于S =1×(1-2n )1-2=2n -1∈(10,20), ∴10<2n -1<20,∴11<2n <21,∴n =4,即求前4项和.∴判断框内的条件为k >4?,即n =4.答案: 46.按下列程序框图运算:规定:程序运行到“判断结果是否大于244”为1次运算,若x =5,则运算进行________次才停止.解析: 第一次运算得13,第二次运算得37,第三次运算得109,第四次运算得325,大于244,程序终止,故运算进行4次.答案: 47.(2015·黄石模拟)如果执行如图所示的程序框图,输入x =4.5,则输出的数i =________.解析:开始x=4.5,i=1,进入循环体,x=3.5;不符合x<1,则i=2,x=2.5;不符合x<1,则i=3,x=1.5;不符合x<1,则i=4,x=0.5,符合x<1,输出i=4.答案: 4三、解答题(每小题10分,共20分)8.设计程序框图,计算1×2×3×4×…×n的值.解析:程序框图(1),含有当型循环结构,如图(1)所示.程序框图(2),含有直到型循环结构,如图(2)所示.9.某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分以上)的成绩,试设计一个算法,并画出程序框图.解析:算法步骤如下:第一步,把计数变量n的初始值设为1.第二步,输入一个成绩r,比较r与60的大小.若r≥60,则输出r,然后执行下一步;若r<60,则执行下一步.第三步,使计数变量n的值增加1.第四步,判断计数变量n与学生个数50的大小,若n≤50,返回第二步,若n大于50,则结束.程序框图如图.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4、试编写算法,求一元多项式P n(x)=a0+a1x+a2x2+a3x3+…a n x n的值P n(x0),并确定算法中的每一语句的执行次数和整个算法的时间复杂度,要求时间复杂度尽可能小,规定算法中不能使用求幂函数。
注意:本题中的输入a i(i=0,1,…,n),x和n,输出为P n(x0)。
通常算法的输入和输出可采用下列两种方式之一:(1)通过参数表中的参数显式传递。
(2)通过全局变量隐式传递。
试讨论这两种方法的优缺点,并在本题算法中以你认为较好的一种方式实现输入和输出【解答】(1)通过参数表中的参数显式传递优点:当没有调用函数时,不占用内存,调用结束后形参被释放,实参维持,函数通用性强,移置性强。
缺点:形参须与实参对应,且返回值数量有限。
(2)通过全局变量隐式传递优点:减少实参与形参的个数,从而减少内存空间以及传递数据时的时间消耗缺点:函数通用性降低,移植性差算法如下:通过全局变量隐式传递参数PolyValue(){ int i,n;float x,a[],p;printf(“\nn=”);scanf(“%f”,&n);printf(“\nx=”);scanf(“%f”,&x);for(i=0;i<n;i++)scanf(“%f ”,&a[i]); /*执行次数:n次*/p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x; /*执行次数:n次*/x=x*x;}printf(“%f”,p);}算法的时间复杂度:T(n)=O(n)通过参数表中的参数显式传递float PolyValue(float a[ ], float x, int n){float p,s;int i;p=x;s=a[0];for(i=1;i<=n;i++){s=s+a[i]*p; /*执行次数:n次*/p=p*x;}return(p);}算法的时间复杂度:T(n)=O(n)[techer's]#include <stdio.h>#define MAXSIZE 10float pnx(float a[],float x,int n){ int j;float sum=0.0;for(j=n;j>0;j--) /*a[0]=a0,[a1]=a1,...*/sum=(sum+a[j])*x;sum=sum+a[0];return(sum);}void main(){int n,i;float a[MAXSIZE],x,result;printf("Input the value of x:\n");scanf("%f",&x);printf("\n");printf("Input The n:\n");scanf("%d",&n);printf("\n");printf("Input a0,a1,...an:");for(i=0;i<=n;i++) scanf("%f",&a[i]);printf("\n");result=pnx(a,x,n);printf("The result is:%f\n",result);}2.4 已知线性表L递增有序。
试写一算法,将X插入到L的适当位置上,以保持线性表L的有序性。
Status Insert_SqList(SqList &va,int x)//把x插入递增有序表va中{if(va.length+1>va.listsize) return ERROR;va.length++;for(i=va.length-1;va.elem[i]>x&&i>=0;i--)va.elem[i+1]=va.elem[i];va.elem[i+1]=x;return OK;}//Insert_SqList[teacher's]int InsList_Sort(SeqList *L,elemtype e){int i;if(L->last>=MAXSIZE-1) {printf("表已满无法插入!");return(0);}i=L->last;while((i>=0)&&(e<L->elem[i]))/*寻找插入位置并移动元素*/{ L->elem[i+1]=L->elem[i];i--;}L->elem[i+1]=e;/*即使L为空,处理也相同*/L->last++;return (1);}2.5 写一算法,从顺序表中删除自第i个元素开始的k个元素。
[提示]:注意检查i和k的合法性。
(集体搬迁,“新房”、“旧房”)< 方法1 > 以待移动元素下标m(“旧房号”)为中心,计算应移入位置(“新房号”):for ( m= i-1+k; m<= L->last; m++)L->elem[ m-k ] = L->elem[ m ];< 方法2 > 同时以待移动元素下标m和应移入位置j为中心:< 方法2 > 以应移入位置j为中心,计算待移动元素下标:[teacher's]int DelList_k(SeqList *L,int i,int k){ /*假定从i往后的元素个数不足k个时,仅删除其后的所有元素*/int count,j;if ((i>L->last+1)||(k<1)) return(0);count=L->last-i+1;/*计算i后的元素个数*/j=i+k-1;while(j<=L->last)/*将i+k位置以后的元素向前移动*/{ L->elem[j-k]=L->elem[j];j++;/*原算法中的count--;去掉*/}if(count>=k) L->last=L->last-k;/*改变指向尾元的位置值*/else L->last=L->last-count;/*被删元素数少于k个时*/return (1);}2.6已知线性表中的元素(整数)以值递增有序排列,并以单链表作存储结构。
试写一高效算法,删除表中所有大于mink且小于maxk的元素(若表中存在这样的元素),分析你的算法的时间复杂度(注意:mink 和maxk是给定的两个参变量,它们的值为任意的整数)。
Status Delete_Between(Linklist &L,int mink,int maxk)//删除元素递增排列的链表L中值大于mink且小于maxk的所有元素{p=L;while(p->next->data<=mink) p=p->next; //p是最后一个不大于mink的元素if(p->next) //如果还有比mink更大的元素{q=p->next;while(q->data<maxk) q=q->next; //q是第一个不小于maxk的元素p->next=q;}}//Delete_Between2.7试分别以不同的存储结构实现线性表的就地逆置算法,即在原表的存储空间将线性表(a1, a2..., a n)逆置为(a n, a n-1,..., a1)。
(1)以一维数组作存储结构,设线性表存于a(1:arrsize)的前elenum个分量中。
(2)以单链表作存储结构。
[方法1]:在原头结点后重新头插一遍[方法2]:可设三个同步移动的指针p, q, r,将q的后继r改为p[teacher's]#include <stdio.h> //2.7.1#define MAXSIZE 10void createdata(int x[],int n){int i;if(n>=MAXSIZE) {printf("ERROR!");exit();}for(i=0;i<n;i++) x[i]=i+i;}void reverse1(int x[],int n){ int tmp,i,k;if(n>=MAXSIZE) {printf("OverFlow!");exit();}k=0;for(i=n-1;i>=n/2;i--){tmp=x[i];x[i]=x[k];x[k]=tmp;k++;}}void disparray(int x[],int n){int i;if(n>=MAXSIZE) {printf("ERROR!");exit();}for(i=0;i<n;i++) printf("%d ",x[i]);}void main(){int a[MAXSIZE];createdata(a,8);reverse1(a,8);disparray(a,8);}#include <stdio.h> //2.7.2typedef struct node{ int x;struct node *next;}snode,*Linklist;Linklist create(){ snode *head,*rear,*s;int y;head=(Linklist)malloc(sizeof(snode));rear=head;scanf("%d",&y);while(y!=-1){ s=(Linklist)malloc(sizeof(snode));s->x=y;rear->next=s;rear=s;scanf("%d",&y);}rear->next=NULL;return(head);}Linklist reverse2(snode *head){ Linklist p,q;p=head->next;head->next=NULL;while(p){ q=p;/*采用头插法,q指向待插节点,p指向下一个*/p=p->next;q->next=head->next;head->next=q;}return(head);}main(){ Linklist h,p;h=create();p=h->next;while(p){ printf("%5d",p->x);p=p->next;}h=reverse(h);printf("\n");p=h->next;while(p){ printf("%5d",p->x);p=p->next;}}2.8假设两个按元素值递增有序排列的线性表A和B,均以单链表作为存储结构,请编写算法,将A表和B表归并成一个按元素值递减有序的排列的线性表C,并要求利用原表(即A表和B表的)结点空间存放表C.[teacher's]/*ch2_8合并并逆置链表*/#include <stdio.h>typedef struct node{ int x;struct node *next;}snode,*Linklist;Linklist create(){ snode *head,*rear,*s;int y;head=(Linklist)malloc(sizeof(snode));rear=head;scanf("%d",&y);while(y!=-1){ s=(Linklist)malloc(sizeof(snode));s->x=y;rear->next=s;rear=s;scanf("%d",&y);}rear->next=NULL;return(head);}Linklist merge(snode *head1,snode *head2){ Linklist head,p,q,s;p=head1->next;/*指向A的首元节点*/q=head2->next;/*指向B的首元节点*/head=head1; /*以链表A的头节点做C的头节点*/head->next=NULL;free(head2); /*释放B的头节点*/while(p!=NULL&&q!=NULL)/*用头插法挑选元素插入*/ { if(p->x<q->x){ s=p;p=p->next;}else{s=q;q=q->next;}s->next=head->next;head->next=s;}if(p==NULL) p=q;while(p){ s=p;p=p->next;s->next=head->next;head->next=s;} return(head);}main(){ Linklist h,h1,h2,p,q;h1=create();h2=create();printf("\n******************************\n");p=h1->next;while(p) /*显示链表A的数据*/{ printf("%5d",p->x);p=p->next;}printf("\n******************************\n");q=h2->next;while(q) /*显示链表B的数据*/{ printf("%5d",q->x);q=q->next;}h=merge(h1,h2);p=h->next;printf("\n******************************\n");while(p) /*显示链表C的数据*/{printf("%5d",p->x);p=p->next;}}2.9假设有一个循环链表的长度大于1,且表中既无头结点也无头指针。
